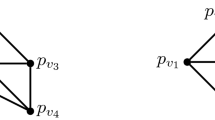Minimum Size Highly Redundantly Rigid Graphs in the Plane

Abstract

A graph G is said to be k-vertex rigid in $\mathbb {R}^d$ if $G-X$ is rigid in $\mathbb {R}^d$ for all subsets X of the vertex set of G with cardinality less than k. We determine the smallest number of edges in a k-vertex rigid graph on n vertices in $\mathbb {R}^2$, for all $k\ge 4$. We also consider k-edge-rigid graphs, defined by removing edges, as well as k-vertex globally rigid and k-edge globally rigid graphs in $\mathbb {R}^d$. For $d=2$ we determine the corresponding tight bounds for each of these versions, for all $k\ge 3$. Our results complete the solutions of these extremal problems in the plane. The result on k-vertex rigidity verifies a conjecture of Kaszanitzky and Király (Graphs Combin, 32:225–240, 2016). We also determine the degree of vertex redundancy of powers of cycles, with respect to rigidity in the plane, answering a question of Yu and Anderson (Int J Robust Nonlinear Control, 19(13):1427–1446, 2009).

1 Introduction

A d-dimensional framework (or geometric graph) is a pair (G, p), where G is a simple graph and $p:V(G)\rightarrow \mathbb {R}^d$ is a map. We also call (G, p) a realization of G in $\mathbb {R}^d$. The length of an edge uv in the framework is defined to be the distance between the points p(u) and p(v). The framework is said to be rigid in $\mathbb {R}^d$ if every continuous motion of its vertices in $\mathbb {R}^d$ that preserves all edge lengths preserves all pairwise distances. It is globally rigid in $\mathbb {R}^d$ if the edge lengths uniquely determine all pairwise distances. A relization (G, p) is generic if the set of the d|V(G)| coordinates of the vertices is algebraically independent over the rationals. It is known that for generic frameworks rigidity and global rigidity in $\mathbb {R}^d$ depends only on the graph of the framework, for every $d\ge 1$. So we may call a graph G rigid (resp. globally rigid) in $\mathbb {R}^d$ if every (or equivalently, if some) d-dimensional realization of G is rigid (resp. globally rigid). We refer the reader to [6, 8, 12] for more details on the theory of rigid and globally rigid frameworks and graphs.

Rigid and globally rigid graphs occur in several applications, including sensor network localization [5], molecular conformation [3], formation control [16], and statics [10]. In some applications it is desirable to have a graph which remains rigid or globally rigid even if some vertices or edges are removed. This motivates the next definitions.

We say that a graph $G=(V,E)$ is k-vertex rigid (resp. k-vertex globally rigid) in $\mathbb {R}^d$ if $G-X$ is rigid (resp. globally rigid) for all $X\subseteq V$ with $|X|\le k-1$. A graph $G=(V,E)$ on n vertices is said to be strongly minimally k-vertex rigid (resp. strongly minimally k-vertex globally rigid) in $\mathbb {R}^d$ if it is k-vertex rigid (resp. k-vertex globally rigid) and no graph on n vertices with less than |E| edges satisfies this property. We can define (strongly minimal) k-edge-rigidity and k-edge-global rigidity in a similar way, by the deletion of edge sets, rather than vertex sets. It will be convenient to use the following graph parameters. For a graph G we use $R^d_v(G)$ to denote the largest integer $\ell$ for which G is $\ell$-vertex rigid in $\mathbb {R}^d$. The other parameters, corresponding to the other three versions, are denoted by $R^d_{gv}(G)$, $R^d_e(G)$, and $R^d_{ge}(G)$, respectively.

In this paper our goal is to obtain tight bounds for the number of edges of a strongly minimally k-vertex rigid (k-vertex globally rigid, k-edge rigid, k-edge globally rigid, resp.) graph on n vertices in $\mathbb {R}^2$. To be more precise, we look for a lower bound on the size of such a graph in terms of n and k, and an infinite family of graphs, with the required property, for which this bound is attained. In some special cases the tight bounds have already been determined for these extremal problems in the plane. The smallest size of a 1-vertex rigid (2-vertex rigid, 3-vertex rigid, resp.) graph on n vertices is equal to $2n-3$ ($2n-1$, $2n+2$, resp.). Here the first bound is well-known, the other two are from [13, 16]. The smallest size of a 1-vertex globally rigid (2-vertex globally rigid, 3-vertex globally rigid, resp.) graph on n vertices is equal to $2n-2$ (2n, $\frac{5n}{2}$, resp.). Again, the first bound is easy, the other two can be found in [11, 16]. These results are valid for n large enough (compared to k). The edge versions and the problems for higher values of k remained open. For the status of the higher dimensional ($d\ge 3$) problems see Section 6.

Table 1 The extremal values in $\mathbb {R}^2$ for the four versions and for all $k\ge 1$

It is worth noting that the case $d=1$ is, in a sense, exceptional, and has an easy solution. It is well-known that a graph G is rigid (resp. globally rigid) in $\mathbb {R}^1$ if and only if G is connected (resp. 2-vertex connected). This implies that a k-vertex connected graph is k-vertex (edge) rigid as well as $(k-1)$-vertex (edge) globally rigid in $\mathbb {R}^1$, for every $k\ge 1$. Observe that the minimum degree of a graph satisfying one of these properties is at least k. Hence a k-regular k-vertex connected graph is strongly minimal with respect to each of these four properties. Since infinite families of k-regular k-vertex connected graphs exist for all $k\ge 2$, the tight bound $\frac{kn}{2}$ follows. The strongly minimally 1-vertex (edge) rigid graphs are the trees. Verifying k-vertex connectivity is also an easy task: it can be done locally, by showing k internally disjoint paths (rigid subgraphs) containing u and v, for all pairs of vertices u, v.

This approach fails for $d\ge 2$. A typical proof method for determining the extremal value for, say, k-vertex rigidity in $\mathbb {R}^d$ consists of the following steps: (i) give a lower bound for the number of edges in a graph satisfying the property, (ii) construct an infinite family of graphs attaining this bound, (iii) show that each member in this family is indeed k-vertex rigid in $\mathbb {R}^d$. The last step is usually a rather lengthy case analysis: for each graph in the family and for every vertex set X of size (at most) $k-1$ one has to show that $G-X$ is rigid. The standard way to verify that $G-X$ is rigid is by showing that it can be obtained from a small complete graph by a sequence of operations (called Henneberg operations or extensions) that add one vertex at a time and preserve rigidity. Even though the extremal graphs tend to be symmetric, the number of cases to deal with and the number of operations used grow quickly as one increases k and the size of the graph, which makes this method inconvenient or even infeasible. We shall use a different approach, based on a key lemma on chains and merging rigid subgraphs.

The structure of the paper is as follows. In the next section we prove several preliminary results, including ones that establish connections between the four different parameters we are dealing with. In Sect. 3 we consider powers of cycles, which play a fundamental role in our constructions. The results of these sections are valid in $\mathbb {R}^d$ for all d. Then we focus on the two-dimensional case and analyse the extremal graphs in Sect. 4 for all $k\ge 4$. The tight bounds for k-vertex rigidity as well as for the other three versions are deduced in Sect. 5. The extremal values are summarized in Table 1. Section 6 contains a few concluding remarks on higher dimensional extensions.

2 Preliminary Results

The next lemma shows that in the definition of k-vertex (global) rigidity it suffices to consider the removal of vertex sets of cardinality exactly $k-1$. This useful observation was made and used earlier for k-vertex rigidity [9, 16]. For completeness we give a proof for both versions, and for all dimensions $d\ge 1$. Note that the corresponding observation for k-edge (global) rigidity is straightforward, since edge addition preserves rigidity as well as global rigidity.

Lemma 1

Let $G=(V,E)$ be a graph on $n\ge k+1$ vertices. Then

• (i) G is k-vertex rigid in $\mathbb {R}^d$ if and only if $G-X$ is rigid in $\mathbb {R}^d$ for all $X\subseteq V$ with $|X|=k-1$, and

• (ii) G is k-vertex globally rigid in $\mathbb {R}^d$ if and only if $G-X$ is globally rigid in $\mathbb {R}^d$ for all $X\subseteq V$ with $|X|=k-1$.

Proof

Necessity is clear from the definition in both cases. In order to prove sufficiency in (i) suppose, for a contradiction, that $G-X'$ is not rigid for some $X'\subset V$ with $|X'|\le k-2$. This implies that for any fixed generic d-dimensional realization $(G-X',p)$ there is a flex (a continuous deformation that preserves edge lengths) which changes the distance between two vertices $u,v\in V$. Since $n\ge k+1$, there is a set X with $|X|=k-1$ and $X'\subset X\subseteq V-\{u,v\}$. Then the restriction of the same flex to $V-X$ shows that $G-X$ is not rigid, a contradiction.□

The proof in case (ii) is similar. Suppose that $G-X'$ is not globally rigid for some $X'\subset V$ with $|X'|\le k-2$. Then for any fixed generic d-dimensional realization $(G-X',p)$ there exists an equivalent but non-congruent realization $(G-X',q)$. This means that there is a pair $u,v\in V$ for which the distance between u and v in $(G-X',p)$ is different from that in $(G-X',q)$. Since $n\ge k+1$, there is a set X with $|X|=k-1$ and $X'\subset X\subseteq V-\{u,v\}$. Then the restrictions of these realizations to $V-X$ show that $G-X$ is not globally rigid, a contradiction. □

It is easy to see that a graph G on at most $d+1$ (resp. $d+2$) vertices is rigid (resp. globally rigid) in $\mathbb {R}^d$ if and only if it is complete. A similar observation yields that a rigid (resp. globally rigid) graph G in $\mathbb {R}^d$ on at least $d+1$ (resp. $d+2$) vertices has minimum degree at least d (resp. $d+1$). Hence we have the following lower bounds on the minimum degree.

Lemma 2

If G is a k-vertex rigid (k-vertex globally rigid, resp.) graph on at least $d+k$ ($d+k+1$, resp.) vertices, then the minimum degree of G is at least $d+k-1$ ($d+k$, resp.). If G is a k-edge rigid (k-edge globally rigid, resp.) graph on at least $d+k$ ($d+k+1$, resp.) vertices, then the minimum degree of G is at least $d+k-1$ ($d+k$, resp.).

Lemma 2 implies, among others, that a $(d+k-1)$-regular k-vertex rigid graph in $\mathbb {R}^d$ is strongly minimally k-vertex rigid. We shall use this observation later.

In the rest of this section we focus on the connections between the four redundancy parameters. The one-dimensional case of the next lemma is easy to deduce from the characterization of rigid and globally rigid graphs in $\mathbb {R}^1$ mentioned earlier. The two-dimensional case was proved in [16], using the characterization of globally rigid graphs in $\mathbb {R}^2$ from [4]. Here we point out that the inequality holds for all $d\ge 1$.

Lemma 3

Let $G=(V,E)$ be a k-vertex rigid graph in $\mathbb {R}^d$ for some $k\ge 2$. Then G is $(k-1)$-vertex globally rigid. Hence for all $d\ge 1$ we have

$$\begin{aligned} R^d_{gv}(G)\ge R^d_v(G)-1. \end{aligned}$$

(1)

Proof

By Lemma 1 it suffices to show that $G-X$ is globally rigid for all $X\subset V$ with $|X|=k-2$. Since G is k-vertex rigid, $G-X$ is 2-vertex rigid. Tanigawa [15] proved that every 2-vertex rigid graph in $\mathbb {R}^d$ is globally rigid in $\mathbb {R}^d$. Thus $G-X$ is globally rigid in $\mathbb {R}^d$, as required. □

Yu and Anderson [16] showed—in the special case $d=2$— that every non-complete k-vertex rigid graph is k-edge rigid. It is easy to extend their proof to higher dimensions. Here we give a (similar) proof for the globally rigid version. It will be convenient to assume that the number of vertices is not too small (rather than assuming the graph is non-complete).

Theorem 1

Let G be a k-vertex rigid (resp. k-vertex globally rigid) graph in $\mathbb {R}^d$ on at least $d+k$ (resp. $d+k+1$) vertices. Then G is k-edge rigid (resp. k-edge globally rigid) in $\mathbb {R}^d$.

Proof

Since the proofs are similar, we only prove the globally rigid version. The proof is by induction on k. For $k=1$ the statement is obvious. Suppose that $k=2$. Let $e=uv$ be an edge of G. The graph $G-u$ is globally rigid. Since G has at least $d+k+1$ vertices, Lemma 2 implies that the degree of u in G is at least $d+k$. It follows that $G-e$ can be obtained from $G-u$ by adding a new vertex u and at least $d+k-1=d+1$ edges incident with u. This operation preserves global rigidity. Therefore $G-e$ is globally rigid. Since the choice of e was arbitrary, it follows that $R^d_{ge}(G)\ge 2$, as required.

Now consider the general case. Suppose that $k\ge 3$ and that the statement of the theorem holds up to $k-1$. It suffices to show that $R^d_{gv}(G-e)\ge k-1$ for every edge e of G. To see this fix an edge e and let S be a vertex-set of size $k-2$ in $G-e$.

If e is incident with a vertex of S, then $G-e-S=G-S$, and hence $G-e-S$ is globally rigid by our assumption on G. If e is disjoint from S, then consider $G-S$. Since G is k-vertex globally rigid, $G-S$ is 2-vertex globally rigid. Thus $G-S$ is 2-edge globally rigid (by the case $k=2$), and hence $G-e-S$ is globally rigid. Hence for every edge e the graph $G-e$ is indeed $(k-1)$-vertex globally rigid, which implies, by induction, that $G-e$ is also $(k-1)$-edge globally rigid. Now $R^d_{ge}(G)\ge k$ follows, and the proof is complete. □

Yet another useful inequality involving the parameters is as follows.

Lemma 4

Let $G=(V,E)$ be a globally rigid graph in $\mathbb {R}^d$ on $n\ge d+2$ vertices. Then

$$\begin{aligned} R^d_{e}(G)\ge R^d_{ge}(G)+1. \end{aligned}$$

(2)

Proof

Let $R^d_{ge}(G)=k\ge 1$ and let $\emptyset \not = F\subset E$ with $|F|\le k$. Choose an edge $f\in F$ and let $F'=F-\{f\}$. Since $|F'|=k-1$, $G-F'$ is globally rigid. By a theorem due to Hendrickson [2] every globally rigid graph on at least $d+2$ vertices in $\mathbb {R}^d$ is 2-edge rigid in $\mathbb {R}^d$. This implies that $G-F=G-F'-\{f\}$ is rigid. Hence $R^d_{e}(G)\ge k+1$, as claimed. □

2.1 Operations

In our proofs we shall frequently use the following graph operations. The (d-dimensional) 0-extension operation adds a new vertex v to the graph as well as d new edges incident with v. The 1-extension operation removes an edge $v_iv_j$ and adds a new vertex v as well as a set of $d+1$ new edges which includes $vv_i$ and $vv_j$. It is well-known that both of these operations preserve rigidity in $\mathbb {R}^d$, and the d-dimensional 1-extension operation preserves global rigidity in $\mathbb {R}^d$, see e.g. [8, 12].

3 Powers of Cycles

Let $C_n$ be a cycle on n vertices, with vertex set $V=\{v_1,v_2,\ldots , v_n\}$, where the indices follow the cyclic ordering. The k-th power of $C_n$, denoted by $C_n^k$, is obtained from $C_n$ by adding all edges $v_iv_j$ for which the distance from $v_i$ to $v_j$ in $C_n$ is at most k.

Consider a cycle $C_n=(V,E)$ with $|V|=n$ and fix a set $S\subseteq V$ of its vertices. To simplify notation let $C=C_n$ and $H=C_n^k$. We call a set $I\subseteq V$ of consecutive vertices on C an interval. A chain $J\subseteq V$ is the union of consecutive intervals in $C-S$. That is, $J=I-S$ for some interval I.

Fig. 1

A chain J in $C-S$, its neighbours $v_1,v_2$, and its ends $K_1,K_2$. The vertices of the cycle C are cyclically ordered. The edges are not visible. The vertices of S are black. In this example $|S|=5$ and $k=3$

Let $G=(V,E)$ be a graph. For a set $X\subseteq V$ the subgraph of G induced by X is denoted by G[X].

Lemma 5

Suppose that $k\ge d$. Then for every interval I the graph H[I] is rigid in $\mathbb {R}^d$.

Proof

Intervals on at most d vertices induce complete (and hence rigid) subgraphs in H. Since $k\ge d$, it is easy to see that for an interval I with $|I|\ge d+1$ the subgraph H[I] contains a spanning subgraph which can be obtained from a complete subgraph on d vertices by a sequence of d-dimensional 0-extensions. Hence H[I] is rigid. □

Suppose that $n\ge k+1$. Let J be a chain in $C-S$. If V and S are clear from the context, we shall use the notation $\bar{J}=V-S-J$. Suppose that ${\bar{J}}\not = \emptyset$. A neighbour of J is a vertex $v\in {\bar{J}}$ which comes right after (or before) J in $C-S$ with respect to the cyclic ordering of C. Equivalently, a vertex v is a neighbour of J if $J\cup \{v\}$ is a chain in $C-S$. Thus a chain has at most two distinct neighbours. Let $v_1,v_2$ be the (not necessarily distinct) neighbours of J. The set of k vertices that preced $v_i$ on C (in the direction of J) is called an end of J and is denoted by $K_i$, $i=1,2$. Thus J has two ends. We define two ends in a natural way, even if $v_1=v_2$. See Fig. 1.

We are ready to prove a key lemma which will be used several times. In order to be able to use it in a more general setting, we formulate it for supergraphs of H.

Lemma 6

Suppose that $k\ge d$. Let H be a graph obtained from $C_n^k$ by adding a (possibly empty) set of edges. Let J be a chain in $C-S$ which contains an interval I of size at least d, for which H[J] is rigid, and which is maximal with respect to these properties. Suppose that ${\bar{J}}\not = \emptyset$ and let $K_1,K_2$ be the ends of J. Then

• (i) $|S\cap K_i|\ge k-d+1$, for $i=1,2$, and

• (ii) $K_1\cap K_2\cap S=\emptyset$.

Proof

First observe that $K_i\subseteq J\cup S$ for $i=1,2$, that is, the ends are disjoint from the neighbours of J. This follows from the maximality of J and the fact that $H[K_i-S]$ is a complete, and hence rigid subgraph of $H-S$.□

Suppose that $|S\cap K_i|\le k-d$ for some $i\in \{1,2\}$. Then the end $K_i$ contains at least d vertices from J, which are all connected to the neighbour $v_i$ of J in $H-S$. Thus $v_i$ could be added to J by a 0-extension, preserving rigidity. It contradicts the maximality of J. This proves (i). To see the second claim suppose that $K_1$ and $K_2$ intersect. Then J is a subset of $K_1\cup K_2$. If there is a vertex of S in $K_1\cap K_2$ then $I\subseteq K_i$ for some $i\in \{1,2\}$. Since $|I|\ge d$, it would contradict (i). □

Next we show a lower bound on $R^d_v(C_n^k)$ for all d, k (for $k\ge d$ and sufficiently large n), which is tight for $d=2$. It is easy to observe, by counting the number of edges, that if $k\le d-1$ and $n\ge {d+1\atopwithdelims ()2}+1$ then $C_n^k$ is not rigid. Hence we may indeed assume that $k\ge d$. The proof of the next lemma illustrates the proof method we shall use later in our main result.

Theorem 2

Let $k\ge d$ and $n\ge d(2k-2d+1)+1$. Then

$$\begin{aligned} R^d_v(C_n^k)\ge 2k-2d+2. \end{aligned}$$

Proof

Let $H=C_n^k$. By Lemma 1 it suffices to show that $H-S$ is rigid for all $S\subset V$ with $|S|=2k-2d+1$. Since $n\ge d(2k-2d+1)+1= d|S|+1$, there is an interval I in $C-S$ of size at least d, by the pigeon-hole principle. Let J be a maximal chain in $C-S$ for which $I\subseteq J$ and H[J] is rigid. Since $k\ge d$, H[I] is rigid by Lemma 5. Thus J indeed exists. If ${\bar{J}}=\emptyset$ then $V-S=J$ and $H-S=H[J]$. Thus $H-S$ is rigid, as required. Otherwise, when ${\bar{J}}\not =\emptyset$, consider the ends $K_1,K_2$ of J. We can use Lemma 6 to deduce that

$$\begin{aligned} |S|\ge |S\cap K_1|+|S\cap K_2|\ge 2k-2d+2, \end{aligned}$$

a contradiction. This completes the proof. □

Yu and Anderson [16, Theorem 4] considered the two-dimensional special case and proved that $k\le R^2_v(C_n^k) \le 2k-2$, provided $k\ge 2$ and $n\ge 2k+2$. They left the problem of determining the exact degree of vertex-redundancy of $C_n^k$ open. The answer follows by putting $d=2$ in Theorem 2.

Corollary 1

Let $k\ge 2$ and $n\ge \max \{2k+2, 4k-5\}$. Then $R^2_v(C_n^k)=2k-2$.

Note that a set $S\subset V$ of size $2k-2$ for which $C_n^k-S$ is not rigid in $\mathbb {R}^2$ can be obtained by choosing $S=\{v_1,v_2\ldots v_{k-1},v_{k+2},v_{k+3},\ldots v_{2k}\}$.

4 Strongly Minimal k-Vertex Rigid Graphs in $\mathbb {R}^2$

In this section we assume that $d=2$. We define two families of graphs which are obtained from the k’th power of a cycle by adding one (resp. two) longest diagonals incident with each vertex and show that they are strongly minimally 2k-vertex rigid ($(2k+1)$-vertex rigid, resp.) in $\mathbb {R}^2$.

Fig. 2

The graphs $L_{10}^3$ and $\bar{L}_{11}^2$

4.1 The Case of Even Vertex-Redundancy

Consider a cycle $C_n$. For simplicity suppose that n is even. Then for each vertex $v_i$ there is a unique vertex $v_j$ for which the distance from $v_i$ to $v_j$ in $C_n$ is equal to $\frac{n}{2}$. The edge $v_iv_j$ is called a longest diagonal of $C_n$.

Let $D_n$ be the set of longest diagonals of $C_n$ and let $L_n^k=C_n^k + D_n$. Note that if $n\le 2k+2$ then $L_n^k$ is complete. If $n\ge 2k+4$ then $L_n^k$ is a non-complete $(2k+1)$-regular graph in which the edges of $D_n$ are disjoint from the edges of $C_n^k$. See Fig. 2 for an example.

We shall use the following lemma, which is easy to verify.

Lemma 7

Let $G_1,G_2$ be two disjoint rigid graphs and let $F=\{e,f,g\}$ be a set of three edges from $G_1$ to $G_2$ such that e and f are disjoint. Then $G_1\cup G_2\cup F$ is rigid.

The next theorem shows that the addition of the $\frac{n}{2}$ longest diagonals to $C_n^k$ increases its vertex redundancy by two.

Theorem 3

Suppose that $k\ge 2$ and $n\ge 4k+5$ is even. Then

$$\begin{aligned} R^2_v\left(L_n^k\right)=2k. \end{aligned}$$

Proof

Let $L=L_n^k$ and let $C=C_n$, $H=C_n^k$, and $D=D_n$ denote the corresponding graphs on vertex set V with $|V|=n$. Since L is $(2k+1)$-regular, it can be made non-rigid by removing 2k vertices. This gives $R^2_v(L)\le 2k$.

To prove that equality holds it suffices to show, by Lemma 1, that $L-S$ is rigid for every $S\subset V$ with $|S|=2k-1$. Fix such an S for the rest of the proof. Since $n\ge 4k+5\ge 2(2k-1)+1$, there is an interval in $C-S$ of size at least 2, by the pigeon-hole principle. Let J be a maximum length (and hence also maximal) chain in $C-S$ which contains an interval of size at least 2, and for which L[J] is rigid. Recall that $\bar{J}=V-S-J$. If ${\bar{J}}=\emptyset$, then $V-S=J$ and $L-S=L[J]$. Thus $L-S$ is rigid, as required.

Thus we may suppose that ${\bar{J}}\not = \emptyset$. Let $v_1,v_2$ be the neighbours of J in $C-S$ and let $K_1,K_2$ be the ends of J. First we show that $v_1\not =v_2$. Indeed, if $v_1=v_2$ then there is only one vertex in ${\bar{J}}$. Since it has degree $2k+1$ in L and $|S|=2k-1$, it has at least two neighbours in J. Thus $L[J\cup \{v_1\}]=L-S$ is rigid, as required.

Let $J^*$ be the maximal interval of C which contains J and which is disjoint from the neighbours of J. Lemma 6, applied to L, implies that $K_1\cap K_2\cap S=\emptyset$ and

$$\begin{aligned} 2k-1=|S|\ge |S\cap K_1|+|S\cap K_2|\ge 2k-2. \end{aligned}$$

(3)

Thus S has at most one vertex in $V-(K_1\cup K_2)$. In particular, there is at most one vertex of S in $V-J^*$. First we deal with the case when there is no vertex of S in $V-J^*$.

Case 1. $S\cap (V-J^*)=\emptyset$.

In this case ${\bar{J}}$ is an interval of size at least two (since $v_1\not = v_2$). By Lemma 5$H[{\bar{J}}]$, and hence also $L[{\bar{J}}]$ is rigid. Thus the choice of J implies that $|J|\ge |{\bar{J}}|$.

We claim that each of the longest diagonals incident with ${\bar{J}}$ connects ${\bar{J}}$ to a vertex in $J^*-(K_1\cup K_2)$. To see this suppose, for a contradiction, that there is a longest diagonal from a vertex of ${\bar{J}}$ to, say, ${\bar{J}}\cup K_2$. Then $|{\bar{J}}|\ge \frac{n}{2} - (k-1)$. This in turn gives $|J|= n - |{\bar{J}}| - (2k-1)\le \frac{n}{2} - k$, which contradicts the maximality of J.

Now focus on the two neighbours $v_1,v_2$. If the longest diagonal incident with $v_1$ has the other end-vertex in J and $v_1$ has a neighbour in $J\cap K_1$, too, then $v_1$ can be added to J, preserving rigidity. It would contradict the maximality of J. Otherwise either the longest diagonal ends in a vertex of S or $|S\cap K_1|=k$ (and hence $S\subset K_1\cup K_2$). In both cases $v_2$ satisfies that the longest diagonal incident with $v_2$ has the other end-vertex in J and $v_2$ has a neighbour in $J\cap K_2$. Thus $v_2$ can be added to J, preserving rigidity, a contradiction.

Case 2. There exists a vertex $w\in (S\cap (V-J^*))$.

In this case ${\bar{J}}$ is a chain, which is the union of two disjoint intervals $I_1,I_2$, with $v_i\in I_i$, $i=1,2$. We can use Lemma 6 and the fact that $|S|=2k-1$ to deduce that $|S\cap K_i|=k-1$, that is, $v_i$ is connected to exactly one vertex of $J\cap K_i$, for $i=1,2$.

Suppose that $k\ge 3$. Then we can use an argument similar to that of the proof of Lemma 5 to show that $H[I_1\cup I_2]$ is rigid. We claim that each of the longest diagonals incident with $(I_1\cup I_2)-\{v_1,v_2\}$ has the other end-vertex in $J^*-(K_1\cup K_2)$. To see this suppose, for a contradiction, that there is a longest diagonal from, say, $v_1'$ to a vertex of $\bar{J}\cup \{w\}\cup K_2$, where $v_1'$ is the vertex of $I_1$ next to $v_1$ on C. Then $|{\bar{J}}|\ge \frac{n}{2} - (k-1)$. This in turn gives $|J|= n - |{\bar{J}}| - (2k-1)\le \frac{n}{2} - k$, which contradicts the maximality of J.

Therefore if $|{\bar{J}}|\ge 3$ then there is at least one longest diagonal connecting ${\bar{J}}$ to J. Together with the edges from $v_i$ to $K_i$, $i=1,2$ they form a set of three disjoint edges from J to ${\bar{J}}$. Thus $L-S=L[J\cup {\bar{J}}]$ is rigid by Lemma 7, as required. If $|I_1|=|I_2|=1$ then, since $n\ge 4k+5\ge 2k+6$, each of the longest diagonals incident with $v_1$ or $v_2$ has the other end in J. In this case $v_1$ and $v_2$ can be added to L[J] by two 0-extensions. This shows that $L-S$ is rigid.

So we may assume that $k=2$. In this case we have $|S|=3$. First suppose $|I_1|=|I_2|=1$. Then, since $n\ge 10$, the longest diagonals from $v_1$ and $v_2$ both go to J. We can use these diagonals and the edges from $v_i$ to $J\cap K_i$, $i=1,2$ to add $v_1$ and $v_2$ to J by 0-extensions and to show that $L-S$ is rigid.

Next suppose that, say, $|I_1|\ge 2$. Let x and y be the vertices in $I_1$ closest to w, that is, x is next to w and y is next to x in the cyclic ordering of C. Focus on the longest diagonals incident with x and y. The maximality of J implies that the other end-vertices of these diagonals cannot be in $I_1\cup K_1$ (since otherwise $|I_1|\ge \frac{n}{2}-1$ and $|J|\le \frac{n}{2}-3$ would follow). Thus either they both end in J or at least one of them ends in $I_2\cup K_2$. In the former case $L[J\cup I_1]$ is rigid, contradicting the maximality of J (rigidity follows from Lemma 7, applied to J, $I_1$, the longest diagonals incident with x, y, and the edge from $v_1$ to $J\cap K_1$). In the latter case we must have $|I_2|\ge \frac{n}{2}-3$. In this case we apply the same argument to $I_2$. Since we cannot simultaneously have $|I_2|\ge \frac{n}{2}-3$ and $|I_1|\ge \frac{n}{2}-3$ (for otherwise $|J|\le 3$ follows, contradicting the maximality of J, since $C-S$ has an interval of size at least 4, when $n\ge 13$ and $|S|=3$), we obtain that $L[J\cup I_2]$ is rigid, contradicting the maximality of J. This completes the proof. □

We can extend the definition of $L_n^k$ to the case when n is odd by adding $\frac{n-1}{2}$ disjoint longest diagonals plus one more, to make it almost regular. (Note that the definition of longest diagonals is slightly different when n is odd, see the next paragraph.) A similar proof shows that these odd examples are also 2k-vertex rigid, for n sufficiently large.

4.2 The Case of Odd Vertex-Redundancy

Consider a cycle $C_n$. For simplicity suppose that n is odd. Then for each vertex $v_i$ there are two vertices $v_j,v_j'$ for which the distance from $v_i$ to $v_j$ and $v_j'$ in $C_n$ is equal to $\frac{n-1}{2}$. The edges $v_iv_j, v_iv_j'$ are called longest diagonals of $C_n$.

Let ${\bar{D}}_n$ be the set of longest diagonals of $C_n$ and let ${\bar{L}}_n^k=C_n^k + {\bar{D}}_n$. Note that if $n\le 2k+3$ then $\bar{L}_n^k$ is complete. If $n\ge 2k+5$ then ${\bar{L}}_n^k$ is a non-complete $(2k+2)$-regular graph in which the edges of ${\bar{D}}_n$ are disjoint from the edges of $C_n^k$. See Fig. 2 for an example.

The next theorem shows that the addition of the n longest diagonals to $C_n^k$ increases its vertex redundancy by three. The proof is similar to that of the even case, except for one new subcase (Case 3. below).

Theorem 4

Suppose that $k\ge 2$ and $n\ge 6k+23$ is odd. Then

$$\begin{aligned} R^d_v\left({\bar{L}}_n^k\right)=2k+1. \end{aligned}$$

Proof

Let ${\bar{L}}={\bar{L}}_n^k$ and let $C=C_n$, $H=C_n^k$, and ${\bar{D}}=\bar{D}_n$ denote the corresponding graphs on vertex set V with $|V|=n$. Since ${\bar{L}}$ is $(2k+2)$-regular, it can be made non-rigid by removing $2k+1$ vertices. This gives $R^2_v({\bar{L}})\le 2k+1$. □

To prove that equality holds it suffices to show, by Lemma 1, that $L-S$ is rigid for every $S\subset V$ with $|S|=2k$. Fix such an S for the rest of the proof. Since $n\ge 6k+23\ge 2(2k)+1$, there is an interval in $C-S$ of size at least 2, by the pigeon-hole principle. Let J be a maximum length (and hence also maximal) chain in $C-S$ which contains an interval of size at least 2, and for which ${\bar{L}}[J]$ is rigid. Recall that ${\bar{J}}=V-S-J$. If ${\bar{J}}=\emptyset$, then $V-S=J$ and $\bar{L}-S={\bar{L}}[J]$. Thus ${\bar{L}}-S$ is rigid, as required.

Thus we may suppose that ${\bar{J}}\not = \emptyset$. Let $v_1,v_2$ be the neighbours of J in $C-S$ and let $K_1,K_2$ be the ends of J. First we show that $v_1\not =v_2$. Indeed, if $v_1=v_2$ then there is only one vertex in ${\bar{J}}$. Since it has degree $2k+2$ in ${\bar{L}}$ and $|S|=2k$, it has at least two neighbours in J. Thus $\bar{L}[J\cup \{v_1\}]={\bar{L}}-S$ is rigid, as required.

Let $J^*$ be the maximal interval of C which contains J and which is disjoint from the neighbours of J. Lemma 6, applied to ${\bar{L}}$, implies that $K_1\cap K_2\cap S=\emptyset$ and

$$\begin{aligned} 2k=|S|\ge |S\cap K_1|+|S\cap K_2|\ge 2k-2. \end{aligned}$$

(4)

Thus S has at most two vertices in $V-(K_1\cup K_2)$. In particular, there are at most two vertices of S in $V-J^*$. First we deal with the case when there is no vertex of S in $V-J^*$.

Case 1. $S\cap (V-J^*)=\emptyset$.

In this case ${\bar{J}}$ is an interval of size at least two (since $v_1\not = v_2$). By Lemma 5$H[{\bar{J}}]$, and hence also $L[{\bar{J}}]$ is rigid. Thus the choice of J implies that $|J|\ge |{\bar{J}}|$.

We claim that each of the longest diagonals incident with ${\bar{J}}$ connects ${\bar{J}}$ to a vertex in $J^*-(K_1\cup K_2)$. To see this suppose, for a contradiction, that there is a longest diagonal from a vertex of ${\bar{J}}$ to, say, ${\bar{J}}\cup K_2$. Then $|{\bar{J}}|\ge \frac{n-1}{2} - (k-1)$. This in turn gives $|J|= n - |{\bar{J}}| - 2k\le \frac{n+1}{2} - k-1$, which contradicts the maximality of J.

Now focus on the two neighbours $v_1,v_2$. The other end-vertices of the two longest diagonals incident with $v_1$ may belong to J and $v_1$ may also have a neighbour in $J\cap K_1$. If two out of these three potential neighbours in J exist then $v_1$ can be added to J by a 0-extension, preserving rigidity. This would contradict the maximality of J. On the other hand, if two out of these three vertices belong to S, then $v_2$ must have at least two edges to J, a contradiction.

Case 2. There exists a unique vertex $w\in (S\cap (V-J^*))$.

In this case ${\bar{J}}$ is a chain, which is the union of two disjoint intervals $I_1,I_2$, with $v_i\in I_i$, $i=1,2$. We can use Lemma 6 and the fact that $|S|=2k$ to deduce that for at least one of the two neighbours $v_i$ of J, $i\in \{1,2\}$, $v_i$ is connected to a vertex of $J\cap K_i$.

Suppose that $k\ge 3$. Then we can use an argument similar to that of the proof of Lemma 5 to show that $H[I_1\cup I_2]$ is rigid. We claim that at least one of the two longest diagonals incident with $v_1$ has the other end-vertex in $J^*-(K_1\cup K_2)$. To see this suppose, for a contradiction, that both longest diagonals connect $v_1$ to a vertex of ${\bar{J}}\cup \{w\}\cup K_2$. Then $|{\bar{J}}|\ge \frac{n+1}{2} - k$. This in turn gives $|J|= n - |{\bar{J}}| - 2k\le \frac{n-1}{2} - k$, contradicting the maximality of J. A similar argument works for $v_2$.

Therefore there exist three edges from ${\bar{J}}$ to J such that two of them are disjoint: two longest diagonals incident with $v_1$ and $v_2$, respectively, and an edge from $v_i$ to $J\cap K_i$, for some $i\in \{1,2\}$. Thus ${\bar{L}}-S={\bar{L}}[J\cup {\bar{J}}]$ is rigid by Lemma 7, as required.

Thus we may assume that $k=2$. Then $|S|=4$. First suppose $|I_1|=|I_2|=1$. Then, since $n\ge 10$, all the longest diagonals incident with $v_1$ and $v_2$ have the other end-vertices in $J^*-(K_1\cup K_2)$. We can use these diagonals and an edge from a neighbour $v_i$ to $J\cap K_i$, $i\in \{1,2\}$ to add $v_1$ and $v_2$ to J by two 0-extension operations. Therefore ${\bar{L}}-S$ is rigid, as required.

Next suppose that, say, $|I_1|\ge 2$. Let x, y be the vertices in $I_1$ closest to w on C. The maximality of J implies that either each of the longest diagonals from x, y go to $J^*-(K_1\cup K_2)$, or $|I_2|\ge \frac{n-1}{2}-3$. Note that there is at most one vertex of S in $J^*-(K_1\cup K_2)$. Thus in the former case ${\bar{L}}[J\cup I_1]$ is rigid, contradicting the maximality of J (rigidity follows from Lemma 7, using the longest diagonals incident with x, y and, if one of them leads to vertex of S, the edge from $v_1$ to $J\cap K_1$). In the latter case we apply the same argument to $I_2$: then either we obtain a similar contradiction, or it follows that $|I_1|\ge \frac{n-1}{2}-3$. But then we can use these bounds and $n\ge 15$ to deduce that $|J|\le 3$ and $|I_1|\ge 4$, a contradiction.

Case 3. There exist two vertices $w,z\in (S\cap (V-J^*))$.

In this case ${\bar{J}}$ consist of three intervals $I_1,I_2,I^*$, where $v_i\in I_i$, $i=1,2$, and $I^*$ may be empty (when w and z are consecutive vertices on C). By Lemma 6 we have $|S\cap K_i|=k-1$ for $i=1,2$. Hence there is an edge from $v_i$ to $J\cap K_i$ for $i=1,2$.

If $|J|\ge \frac{n-1}{2}-k+1$ then at least one of the longest diagonals incident with $v_1$ ends in J. With this diagonal and the edge from $v_1$ to $J\cap K_1$ we could add $v_1$ to J by a 0-extension, contradicting the maximality of J. Thus we may assume that

$$\begin{aligned} |J|\le \frac{n-1}{2}-k. \end{aligned}$$

(5)

First suppose $k\ge 3$. If $|I^*|\ge 2$ then we can show, as in the previous proofs, that $H[I_1\cup I^* \cup I_2]$ is rigid. Thus, by the maximality of J, we have $|J|\ge |{\bar{J}}|$. Hence $|J|\ge \frac{n-2k}{2} \ge 2k\ge 6$. The upper bound in (5) implies that every longest diagonal incident with J has the other end-vertex in $V-J^*$. Since $|S\cap (V-J^*)|=2$, all but four diagonals incident with $V-J^*$ are incident with ${\bar{J}}=I_1\cup I^* \cup I_2$. By using $|J|\ge 6$ we can now deduce that there is at least one longest diagonal that connects J and ${\bar{J}}$. This longest diagonal, together with the edges from $v_i$ to $J\cap K_i$, $i=1,2$, verifies that ${\bar{L}}-S$ is rigid, by Lemma 7. If $|I^*|\le 1$ then we proceed as follows. We consider the vertex $x\in I_1$ next to w. If both longest diagonals incident with x go to J then we have that ${\bar{L}}[J\cup I_1]$ is rigid, by using Lemma 7 (when $|I_1|\ge 2$) or simply a 0-extension (when $|I_1|=1$), which contradicts the maximality of J. So we may suppose that there is a longest diagonal xa with $a\notin J$. If $a\in I_1\cup K_1$ then $|I_1|\ge \frac{n-1}{2}-(k-1)$ follows, which contradicts the maximality of J by (5). Thus we must have $a\in I_2\cup K_2$, and hence $|I_2|\ge \frac{n-1}{2}-k-3$ follows. By applying the same argument to $I_2$ and the vertex of $I_2$ next to w we can also deduce that $|I_1|\ge \frac{n-1}{2}-k-3$. This gives $|J|\le n-|I_1|-|I_2|-2k\le 7$. Moreover, since $n\ge 6n+12$, we have $|I_1|+|I_2|\ge 4k+4$. Hence $|I_i|\ge 8$ for some $i\in \{1,2\}$, contradicting the maximality of J.

Finally consider the case when $k=2$. If a longest diagonal incident with J ends in $J^*$ then $|J|\ge \frac{n-1}{2}-1$ follows, contradicting (5). So all longest diagonals leaving J end in $V-J^*$. If at least two of these diagonals go to $I_i$ for some $i\in \{1,2\}$, then ${\bar{L}}[J\cup I_i]$ is rigid by Lemma 7, a contradiction. Thus we may assume that we have at most one longest diagonal from J to $I_i$, for $i=1,2$. Since the pair $\{w,z\}$ is incident with four longest diagonals, it follows that all but six longest diagonals incident with J end in $I^*$. Since $n\ge 24$, we have $|J|\ge 5$, and hence at least 10 longest diagonals leave J. We can now deduce that at least four of them end in $I^*$, implying that ${\bar{L}}[J\cup I^*]$ is rigid by Lemma 7. Note that two edges of H connect $I_i$ to $J\cup I^*$, for $i=1,2$. Thus if one of $I_1$ or $I_2$ is a singleton then it can be added to $J\cup I^*$ by a 0-extension, contradicting the maximality of J. Therefore we may assume that $|I_1|,|I_2|\ge 2$ hold. We may also assume that no longest diagonal connects $J\cup I^*$ to $I_1\cup I_2$ (for otherwise Lemma 7 can be used to deduce that ${\bar{L}}[J\cup I^*\cup I_i]$ is rigid for some $i\in \{1,2\}$). Hence the longest diagonals incident with $I_1$ end in $I_2$ (or at some vertex of S next to $I_2$) and the longest diagonals incident with $I_2$ end in $I_1$ (or at some vertex of S next to $I_1$). Moreover, the end-vertices of the longest diagonals incident with $I_i$ form an interval on C, for $i=1,2$. These facts, and the assumption $|I_1|,|I_2|\ge 2$ imply that at least three longest diagonals connect $I_1$ and $I_2$. Hence $\bar{L}[I_1\cup I_2]$ is rigid by Lemma 7. Now three edges out of the four edges of H that connect $J\cup I^*$ to $I_1\cup I_2$ and Lemma 7 show that ${\bar{L}}-S$ is also rigid. This completes the proof. □

5 Strongly Minimally Rigid and Globally Rigid Graphs in $\mathbb {R}^2$

In this section we deduce the solutions of our extremal problems in $\mathbb {R}^2$ for each of the four versions and for all missing cases.

5.1 Rigidity

As we noted in the Introduction, the problems for k-vertex rigidity have been solved earlier for $k\le 3$. For $k\ge 4$ we have the following bound, which shows that the minimum degree based lower bound is tight in this range. It was conjectured by Kaszanitzky and Király [9].

Theorem 5

Let $k\ge 4$ and $n\ge 6k+23$. Then the number of edges in a strongly minimally k-vertex rigid graph on n vertices in $\mathbb {R}^2$ is $\lceil \frac{(k+1)n}{2} \rceil$.

Proof

The lower bound follows from Lemma 2. The constructions given in Theorems 3 and 4 for k even and odd, respectively, show that it is tight. □

For k-edge rigidity the tight bound is $2n-3$ for $k=1$ and $2n-2$ for $k=2$. The extremal graphs are the minimally rigid graphs and the generic circuits. These facts follow from basic results in rigidity theory. For $k\ge 4$ Theorem 5, Lemma 2, and Theorem 1 give the next result.

Theorem 6

Let $k\ge 4$ and $n\ge 6k+23$. Then the number of edges in a strongly minimally k-edge rigid graph on n vertices in $\mathbb {R}^2$ is $\lceil \frac{(k+1)n}{2} \rceil$.

It remains to consider the case $k=3$. Here we have the following bound.

Theorem 7

The number of edges in a strongly minimally 3-edge rigid graph on $n\ge 5$ vertices in $\mathbb {R}^2$ is 2n.

Proof

The lower bound follows from Lemma 2. To see that equality holds we claim that $C_n^2$ is (strongly minimally) 3-edge-rigid for all $n\ge 5$. It was shown by Summers, Yu, and Anderson [14], that $C_n^2$ is 2-vertex globally rigid. By Theorem 1 it is also 2-edge globally rigid if $n\ge 5$ holds. Hence, by Lemma 4, $C_n^2$ is 3-edge rigid. □

5.2 Global Rigidity

For k-vertex global rigidity it is not hard to show that the tight bound is $2n-2$ for $k=1$ (see e.g. Theorem 11 below), and the bounds have also been determined for $k=2,3$ in previous work. For $k\ge 3$ we obtain the following.

Theorem 8

Let $k\ge 3$ and $n\ge 6k+23$. Then the number of edges in a strongly minimally k-vertex globally rigid graph on n vertices in $\mathbb {R}^2$ is $\lceil \frac{(k+2)n}{2} \rceil$.

Proof

The lower bound follows from Lemma 2. To see that it is tight consider a strongly minimally $(k+1)$-vertex rigid graph. By Theorem 5 and Lemma 3 it is strongly minimally k-vertex globally rigid. □

The special case $k=3$ of Theorem 8 was proved earlier by Motevallian, Yu and Anderson [11], who showed that $L_n^2$ is 3-vertex globally rigid. Our proof method gives a more general statement by showing that it is in fact 4-vertex rigid.

In the case of k-edge global rigidity Theorem 8 and Theorem 1 yield the following corollary.

Theorem 9

Let $k\ge 3$ and $n\ge 6k+23$. Then the number of edges in a strongly minimally k-edge globally rigid graph on n vertices in $\mathbb {R}^2$ is $\lceil \frac{(k+2)n}{2} \rceil$.

As we noted above, for 1-edge global rigidity (which is the same as 1-vertex global rigidity) the tight bound is $2n-2$. So it remains to consider the case when $k=2$. By rereading the proof of Theorem 7 and using Lemma 2 we obtain:

Theorem 10

The number of edges in a strongly minimally 2-edge globally rigid graph on $n\ge 5$ vertices in $\mathbb {R}^2$ is 2n.

6 Concluding Remarks

In this section we summarize the known results about our extremal problems for $d\ge 3$. Kaszanitzky and Király [9] considered the k-vertex rigidity version and solved the corresponding problems for $k=2$ (for all $d\ge 2$) and when $d=k=3$. In a recent manuscript [7] we determined the tight bounds in the 3-dimensional case for all k and for each of the four versions, with the exception of four special cases. The rigidity versions for $d\ge 4$ and $k\ge 3$ remain open.

For global rigidity there are no results available for $d\ge 4$, except for the case $k=1$, for which we give a short proof below.

Theorem 11

The number of edges in a strongly minimally 1-vertex (or 1-edge) globally rigid graph on $n\ge d+2$ vertices in $\mathbb {R}^d$ is equal to $dn-{d+1\atopwithdelims ()2}+1$.

Proof

A graph is 1-vertex or 1-edge globally rigid if it is globally rigid. Since globally rigid graphs on at least $d+2$ vertices are 2-edge-rigid by Hendrickson’s theorem [2], and a rigid graph in $\mathbb {R}^d$ on $n\ge d+2$ vertices has at least $dn-{d+1\atopwithdelims ()2}$ edges, the lower bound follows. The complete graph $K_{d+2}$ is globally rigid in $\mathbb {R}^d$ and satisfies the lower bound with equality. By a result of Connelly [1], every graph obtained from $K_{d+2}$ by a sequence of d-dimensional 1-extensions is globally rigid in $\mathbb {R}^d$. Since the 1-extension operation preserves the edge count, the theorem follows. □