Skip to main content
SpringerLink
Log in

Optimization of weight and cost of cantilever retaining wall by a hybrid metaheuristic algorithm

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

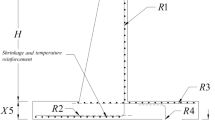
A retaining wall is a structure used to resist the lateral pressure of soil or any backfill material. Cantilever retaining walls provide resistance to overturning and sliding by using backfill weight. In this paper, the weight and cost of the cantilever retaining wall have been minimized using a hybrid metaheuristic optimization technique, namely, h-BOASOS. The algorithm has been developed by the ensemble of two popular metaheuristics, butterfly optimization algorithm (BOA) and symbiosis organism search (SOS) algorithm. BOA’s exploratory intensity is coupled with SOS’s greater exploitative capacity to find the superior algorithm h-BOASOS. The newly developed algorithm has been tested with a suite of 35 classical benchmark functions, and the results are compared with several state-of-the-art metaheuristic algorithms. The results are evaluated statistically by the Friedman rank test, and convergence curves measure the convergence speed of the algorithm. It is observed in both cases that h-BOASOS is superior to other algorithms. The suggested approach is then used to solve four real-world engineering design problems to examine the problem-solving capacity of the proposed algorithm, and the results are contrasted with a wide range of algorithms. The proposed h-BOASOS is considered to be the winner on each occasion. Finally, the newly suggested algorithm is applied to find the cost and weight of the cantilever retaining wall problems of two different heights, 3.2 m and 6.3 m. The obtained results are compared with the component algorithms and found that the new algorithm works better than the compared algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Dede T (2018) Jaya algorithm to solve single objective size optimization problem for steel grillage structures. Steel Compos Struct 26(2):163–170. https://doi.org/10.12989/scs.2018.26.2.163

    Article  MathSciNet  Google Scholar 

  2. Mohammad RB, Morteza M (2019) Application of an improved genetic algorithm for optimal design of planar steel frames. Period Polytech Civ Eng 63(1):141–151. https://doi.org/10.3311/PPci.13039

    Article  Google Scholar 

  3. Kaveh A, Mohammad F (2019) Optimal seismic design of steel plate shear walls using metaheuristic algorithms. Period Polytech Civ Eng 63(1):1–17. https://doi.org/10.3311/PPci.12119

    Article  Google Scholar 

  4. Kaveh A, Seyed RHV, Pedram H (2019) Performance of the modified dolphin monitoring operator for weight optimization of skeletal structures. Period Polytech Civ Eng 63(1):30–45. https://doi.org/10.3311/PPci.12544

    Article  Google Scholar 

  5. Ali K, Mohammad ZK, Mahdi B (2019) Optimal design of multi-span pitched roof frames with tapered members. Period Polytech Civ Eng 63(1):77–86. https://doi.org/10.3311/PPci.13107

    Article  Google Scholar 

  6. Ahmadi NB, Varaee H Optimal design of reinforced concrete retaining walls using a swarm intelligence technique. Proc 1st Int Conf Soft Comput Technol Civil, Structural Environ Eng Civ Comp Press, Stirlingshire, UK

  7. Khajehzadeh M, Taha MR, El-Shafie A, Eslami M (2010) Economic design of retaining wall using particle swarm optimization with passive congregation. Aust J Basic Appl Sci 4(11):5500–5507

    Google Scholar 

  8. Khajehzadeh M, Taha M R, El-Shafie A, Eslami M Modified particle swarm optimization for optimum design of spread footing and retaining wall. J Zhejiang Univ-Sci A (Appl Physics Eng) 011; 12(6):415–4272. https://doi.org/10.1631/jzus.A1000252

  9. Khajehzadeh M, Eslami M (2011) Gravitational search algorithm for optimization of retaining structures. Indian J Sci Technol 5(1):1821–1827. https://doi.org/10.1007/s12205-017-1627-1

    Article  Google Scholar 

  10. Yepes V, Alcala A, Perea C, Gonzalez-Vidosa F (2008) A parametric study of optimum earth-retaining walls by simulated annealing. Eng Struct 30(3):821–830. https://doi.org/10.1016/j.engstruct.2007.05.023

    Article  Google Scholar 

  11. Ghazavi M, Bonab SB (2011) Learning from ant society in optimizing concrete retaining walls. J Technol Educ 5(3):205–212

    Google Scholar 

  12. Kaveh A, Abadi ASM (2010) Harmony search based algorithm for the optimum cost design of reinforced concrete cantilever retaining walls. Int J Civ Eng 9(1):1–8

    Google Scholar 

  13. Kaveh A, Behnam AF (2013) Charged system search algorithm for the optimum cost design of reinforced concrete cantilever retaining walls. Arab J Sci Eng 38(3):563–570

    Article  Google Scholar 

  14. Camp CV, Akin C (2012) Design of retaining walls using big bang-big crunch optimization optimum design of cantilever retaining walls. J Struct Eng 138:438–448

    Article  Google Scholar 

  15. Gandomi AH, Kashani AR, Mousavi M (2015) Boundary constraint handling affection on slope stability analysis. Engineering and Applied Sciences Optimization 2015. Springer International Publishing, Switzerland 341–358

  16. Nama S, Saha AK, Ghosh S (2015) Parameters optimization of geotechnical problem using different optimization algorithm. Geotech Geol Eng 33(5):1235–1253. https://doi.org/10.1007/s10706-015-9898-0

    Article  Google Scholar 

  17. Nabeel AJ, Ahmed MAY (2016) Optimum Design of Tied Back Retaining Wall. Open Journal of Civil Engineering 6:139–155. https://doi.org/10.4236/ojce.2016.62013

    Article  Google Scholar 

  18. Kumar VN, Suribabu CR (2017) Optimal design of cantilever retaining wall using differential evolution algorithm. Int J Optim Civil Eng 7(3):433–449

    Google Scholar 

  19. Bath GS, Dhillon JS, Walia BS (2018) Optimization of geometric design of retaining wall by differential evolution technique. Int J Comput Eng Res 8(6):67–77

    Google Scholar 

  20. Neda M, Sadjad G, Vagelis P (2019) Cost-based optimum design of reinforced concrete retaining walls considering different methods of bearing capacity computation. Journal 7:1232. https://doi.org/10.3390/math7121232

    Article  Google Scholar 

  21. Nama S, Saha AK, Ghosh S (2017) Improved backtracking search algorithm for pseudo dynamic active earth pressure on retaining wall supporting c-\(\phi\) backfill. Appl Soft Comput 52:885–897

    Article  Google Scholar 

  22. Prayogo D, Cheng MY, Wu YW, Tran D-H (2020) Combining machine learning models via adaptive ensemble weighting for prediction of shear capacity of reinforced-concrete deep beams. Eng Comput 36:1135–1153. https://doi.org/10.1007/s00366-019-00753-w

    Article  Google Scholar 

  23. Saha A, Saha AK , Ghosh S (2018) Pseudodynamic bearing capacity analysis of shallow strip footing using the advanced optimization technique “hybrid symbiosis organisms search algorithm” with numerical validation. Adv Civ Eng. https://doi.org/10.1155/2018/3729360

  24. Stefanos S, George K, Nikos DL (2020) Conceptual design of structural systems based on topology optimization and prefabricated components. Comput Struct 226:106–136. https://doi.org/10.1016/j.compstruc.2019.106136

    Article  Google Scholar 

  25. Lohar G, Sharma S, Saha AK, Ghosh G (2020) Optimization of geotechnical parameters used in slope stability analysis by metaheuristic algorithms. Appl IoT 223–231

  26. Francisco JM, Fernando GV, Antonio H, Victor Y (2010) Heuristic optimization of RC bridge piers with rectangular hollow sections. Comput Struct 88(5–6):375–386. https://doi.org/10.1016/j.compstruc.2009.11.009

    Article  Google Scholar 

  27. Degertekin SO, Hayalioglu MS (2013) Sizing truss structures using teaching–learning-based optimization. Comput Struct 119:177–188. https://doi.org/10.1016/j.compstruc.2012.12.011

    Article  Google Scholar 

  28. Nama S, Saha AK, Saha A (2020) The hDEBSA global optimization method: a comparative study on CEC2014 test function and application to geotechnical problem. Bio-inspir Neurocomput 225–258

  29. Gordan B, Koopialipoor M, Clementking A, Tootoonchi H, Mohamda ET (2019) Estimating and optimizing safety factors of retaining wall through neural network and bee colony techniques. Eng Comput 35:945–954. https://doi.org/10.1007/s00366-018-0642-2

    Article  Google Scholar 

  30. Kaveh A, Biabani Hamedani K, Zaerreza A (2020) A set theoretical shuffled shepherd optimization algorithm for optimal design of cantilever retaining wall structures. Eng Comput. https://doi.org/10.1007/s00366-020-00999-9

    Article  Google Scholar 

  31. Koopialipoor M, Murlidhar BR, Hedayat A, Armaghani DJ, Gordan B, Mohamad ET (2020) The use of new intelligent techniques in designing retaining walls. Eng Comput 36:283–294. https://doi.org/10.1007/s00366-018-00700-1

    Article  Google Scholar 

  32. Kumar S, Tejani GG, Mirjalili S (2019) Modified symbiotic organisms search for structural optimization. Eng Comput 35:1269–1296. https://doi.org/10.1007/s00366-018-0662-y

    Article  Google Scholar 

  33. Arora S, Singh S (2019) Butterfly optimization algorithm: a novel approach for global optimization. Soft Comput 23:715–734

    Article  Google Scholar 

  34. Sharma S, Saha AK (2019) m-MBOA: a novel butterfly optimization algorithm enhanced with mutualism scheme. Soft Comput. https://doi.org/10.1007/s00500-019-04234-6

  35. Guo Y, Liu X, Chen L (2020) Improved butterfly optimisation algorithm based on guiding weight and population restart. J Exp Theor Artif Intell 1–19

  36. Sharma S, Saha AK, Nama S (2020) An Enhanced Butterfly Optimization Algorithm for Function Optimization. In: Pant M, Kumar Sharma T, Arya R, Sahana B, Zolfagharinia H (eds) Soft Computing: Theories and Applications (2020). Advances in Intelligent Systems and Computing, vol 1154. Springer, Singapore. https://doi.org/10.1007/978-981-15-4032-5_54

  37. Sharma S, Saha AK, Ramasamy V, Sarkar JL, Panigrahi CR (2020) hBOSOS: an ensemble of butterfly optimization algorithm and symbiosis organisms search for global optimization. In: Pati B, Panigrahi C, Buyya R, Li KC (eds) Advanced Computing and Intelligent Engineering. Advances in Intelligent Systems and Computing (2020), vol 1089. Springer, Singapore. https://doi.org/10.1007/978-981-15-1483-8_48

  38. Sharma S, Saha AK, Majumder A, Nama S MPBOA - A novel hybrid butterfly optimization algorithm with symbiosis organisms search for global optimization and image segmentation. Multimed Tools Appl

  39. Cheng MY, Prayogo D (2014) Symbiotic Organisms Search: A new metaheuristic optimization algorithm. Computers & Structures 139:98–112

    Article  Google Scholar 

  40. Nama S, Saha AK, Ghosh S (2016) Improved symbiotic organisms search algorithm for solving unconstrained function optimization. Decis Sci Lett 5(3):361–380

    Article  Google Scholar 

  41. Nama S, Saha AK, Ghosh S (2017) A hybrid symbiosis organisms search algorithm and its application to real world problems. Mem Comput 9(3):261–280

    Article  Google Scholar 

  42. Nama S, Saha AK (2018) An ensemble symbiosis organisms search algorithm and its application to real world problems. Decis Sci Lett 7(2):103–118

    Article  Google Scholar 

  43. Nama S, Saha AK, Sharma S (2020) A novel improved symbiotic organisms search algorithm. Comput Intell. https://doi.org/10.1111/coin.12290

  44. Ezugwu AE, Prayogo D (2019) Symbiotic organisms search algorithm: theory, recent advances and applications. Expert Syst Appl 119:184–209

    Article  Google Scholar 

  45. Storn R, Price K (1997) Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J Glob Optim 4:341–359

    Article  MathSciNet  Google Scholar 

  46. Kennedy J , Eberhart R (1995) Particle swarm optimization. In: Proceedings of the 1995 IEEE international conference on neural networks 1942–8

  47. Basturk B, Karaboga D (2006) An artificial bee colony (ABC) algorithm for numeric function optimization. In: Proceedings of the IEEE swarm intelligence symposium 12–14

  48. Rao R (2016) Jaya: a simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int J Ind Eng Comput 7(1):19–34

    Google Scholar 

  49. Mirjalili S (2016) SCA: a sine cosine algorithm for solving optimization problems. Knowl Based Syst 96:120–133

    Article  Google Scholar 

  50. Mirjalili S (2015) Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm. Knowl Based Syst 89:228–249

    Article  Google Scholar 

  51. Yang XS, Deb S (2009) Cuckoo search via lévy flights. World congress on nature and biologically inspired computing, NaBIC 2009; IEEE, 210–214

  52. Yang XS (2009) Firefly algorithm, levy flights and global optimization. Bramer M, Ellis R, Petridis M (eds) Research and development in intelligent systems XXVI 2009; Springer, Berlin, 209–218

  53. Goldberg DE, Holland JH (1988) Genetic algorithms and machine learning. Mach Learn 3(2):95–99

    Article  Google Scholar 

  54. Wang GG, Deb S, Cui Z (2009) Monarch butterfly optimization. Neural Comput Appl 24(3–4):853–871. https://doi.org/10.1007/s00521-015-1923-y

    Article  Google Scholar 

  55. Chakraborty S, Saha AK, Sharma S, Mirjalili S, Chakraborty R (2020) A novel enhanced whale optimization algorithm for global optimization. Comput Ind Eng. 107086, ISSN 0360-8352. https://doi.org/10.1016/j.cie.2020.107086

  56. Wang Z, Luo Q, Zhou Y-Q (2020) Hybrid metaheuristic algorithm using butterfly and flower pollination base on mutualism mechanism for global optimization problems. Eng Comput. https://doi.org/10.1007/s00366-020-01025-8

  57. Mirjalili S (2015) The Ant Lion optimizer. Adv Eng Softw 83:80–98

    Article  Google Scholar 

  58. Sable KS, Patil AA (2012) Optimization of retaining wall by using optimtool matlab. Int J Eng Res Technol 01(06):1–11

    Google Scholar 

Download references

Acknowledgements

The authors would like to express their sincere thanks to the editor and the anonymous reviewers for their useful remarks and important inputs for improving the manuscript.

Author information

Authors and Affiliations

  1. National Institute of Technology, Agartala, India

    Sushmita Sharma, Apu Kumar Saha & Geetanjali Lohar

Authors
  1. Sushmita Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Apu Kumar Saha
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Geetanjali Lohar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Apu Kumar Saha.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sharma, S., Saha, A.K. & Lohar, G. Optimization of weight and cost of cantilever retaining wall by a hybrid metaheuristic algorithm. Engineering with Computers 38, 2897–2923 (2022). https://doi.org/10.1007/s00366-021-01294-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-021-01294-x

Keywords

Search

Navigation