1 Introduction

The study of the population mean of a random variable is a central problem in Statistics (Rohatgi and Saleh 2015). Several methods for its estimation have been developed, some of them focused on the use of the order statistics (Lloyd 1952). In particular, the use of linear combinations of them, known as L-statistics, has been deeply studied in the specialized literature (Gao et al. 2021; Kumar et al. 2020).

In some approaches, the weights (coefficients) of such a linear combination are computed by integrating a weight-generating function \(h:[0,1]\rightarrow \mathbb {R}\) (Hosking 1998). In particular, for a sample size n, the k-th weight is computed as:

$$\begin{aligned} w_k=\int _{\frac{k-1}{n}}^{\frac{k}{n}} h(t)dt \text { }\forall \text { }k =1,2,...,n. \end{aligned}$$

Afterwards, given a random sample \(\textbf{X}\) of a random variable X, the L-statistic is computed as \(L(\textbf{X},\textbf{w})=\sum _{k=1}^n w_kX_{(k)}\), where \(X_{(k)}\) is the \(k-th\) lower value in the random sample \(\textbf{X}\). A similar approach, usually called Yager’s method to derive ordered weighted averaging (OWA) weights (Yager 1993; García-Zamora et al. 2022), consists of considering an increasing bijection \(g:[0,1]\rightarrow [0,1]\) and computing these weights as

$$\begin{aligned} w_k=g\left( \frac{k}{n}\right) -g\left( \frac{k-1}{n}\right) , \text { }\forall \text { }k =1,2,...,n. \end{aligned}$$

From the mean estimation point of view, the weights which minimize the mean squared error (MSE) are especially interesting. Even though, these MSE-minimizing weights may be computed if the distribution belongs to a scale-location family or there are some available data, the resulting weights are only defined for a particular sample size. Nevertheless, in real-world problems, the sample size may change and therefore the so-computed optimal weights are no longer applicable. The most prominent example is the case of censored samples (Almongy et al. 2021; Alzeley et al. 2021; Narisetty and Koenker 2022), which appear naturally in survival analysis (Klein and Moeschberger 2003), missing observations (Little and Rubin 2019) or the changing sampling frequency that may appear in signal analysis (Baraniuk 2015). Consequently, in order to face real-world scenarios, it is essential to provide a method that allows the sample size to be modified.

In this sense, given a distribution, it would be convenient to be able to find a certain generating function g, as the one used in Yager’s method (1993), to derive a weighting vector of the required size. However, given a distribution, it is not easy, in general, to find such a function g to generate the optimal weights, in the sense of minimizing the MSE in mean estimation. Only some distributions, such as the Gaussian and the Uniform distributions, have a simple pattern for the optimal weights that allows their computation from a generating function. Consequently, we raise the following research questions:

  • How to define optimal-weights generating functions for symmetric distributions?

  • How to compute flexible-dimensional L-statistics for the mean estimation of classical symmetric distributions?

Therefore, in this paper, we aim to define a methodology that permits estimating the mean of a symmetric distribution through L-statistics by allowing flexible sample sizes. To do so, we first prove several theoretical results related to the theory of order statistics (David and Nagaraja 2004), then we propose a family of functions for fitting the optimal cumulative weights and finally, we study the behavior of the resulting estimator by numerical procedures.

As main theoretical results, we study, under certain assumptions, the convergence of the optimal weights when the sample size of a random sample of a symmetric distribution tends to infinity. In addition, we show the convergence to the real value of the resulting estimator. Afterward, to define a method to fit the optimal weights, we introduce a parametric family of functions which is defined as a linear combination of extreme valued reductions (EVRs) and extreme value amplifications (EVAs) (García-Zamora 2021, 2022). The simulation results show that such a family presents a good performance when computing the weights for many classical symmetric distributions. Finally, for these classical distributions, such a parametric family is used to derive a flexible-dimensional L-statistic for the mean estimation of the respective distribution. The resulting estimator has a similar behavior as the optimal one for close sample sizes and outperforms significantly the sample mean. Consequently, the presented method provides good estimations for closer sample sizes even if no information about the optimal weights is known.

This method can be used in two different scenarios. In the first one, the expression of the underlying distribution is known, but it is complicated to derive the optimal weights analytically. This is a common situation since the distributions of L-statistics are usually hard to handle (see Chapter 6 in David and Nagaraja (2004)). By simulation, it is possible to compute a good approximation of the optimal weights. However, it is necessary to perform such a simulation for each sample size and, for big sample sizes, the computational time can be unfeasible. In this regard, the results and the method provided in this paper allow obtaining an approximation to derive the optimal weights in a simple way for different sample sizes, especially for big ones.

In the second one, a quantity of interest is supposed to be independently measured when it is perturbed by an additive symmetric noise with a mean of 0. For each of the values of this quantity, several measures are made. If we have a dataset in which we have different true values of the quantity and their associated measurements, it is possible to fit an L-statistic that minimizes the MSE in the dataset. Then, the constructed L-statistic can be applied to new data to obtain estimations of the quantity of interest. However, if the sample size changes, the fitted weights are no longer valid, since they were computed for a fixed length. In this sense, for small variations of sample sizes, the proposed method allows obtaining new weights that will lead to an estimator with a small MSE and defined with the correct dimension.

Although the conditions of the theoretical result may be difficult to check for an arbitrary distribution, the presented method is illustrated for several classical symmetric distributions, showing good behavior.

The remainder of the paper is organized as follows. In Sect. 2 we present the basic definitions and results regarding mean estimation, L-statistics, and EVRs/EVAs functions. The expression for the optimal weights and their convergence are studied in Sect. 3. The flexible-dimensional L-statistic for mean estimation of symmetric distributions is defined in Sects. 5 and 4, giving several examples of its good performance for classical distributions. The conclusions are discussed in Sect. 6.

2 Preliminaries

In this section, the basic concepts needed to understand the contribution are recalled. We start with some elementary notions about mean estimation, then L-statistics are defined, and, finally, we introduce extreme value reductions and amplifications as a tool for generating the weights of L-statistics.

2.1 Mean estimation and L-statistics

Let us start by stating some definitions of estimation from a probabilistic approach, following (Rohatgi and Saleh 2015) as the main reference. Let us assume a quantity of interest associated with a continuous random variable X, with cumulative distribution function F(t), density function f(t) and quantile function \(F^{-1}(t)\). Additionally, the support of the random variable is defined as \(S=\{t\in \mathbb {R}: f(t)>0\}\).

It is common to have an expression for the density and cumulative distribution function of X depending on some unknown parameters. Denoting the set of possible values for the unknown parameters \(\theta \) as \(\Theta \), an estimator of \(\theta \) is a function from the random sample to \(\Theta \) that does not depend on the value of \(\theta \).

In this paper we will consider the population’s mean estimation, focusing on efficiency, which is related to the MSE, defined as \(MSE(T,\theta )=E\left[ \left( T-\theta \right) ^2\right] \), where \(E[\cdot ]\) denotes the expectation operator.

Definition 1

Let \(X_1,\dots ,X_n\) be a sequence of iid random variables with density function \(f_{\theta }\) depending on the unknown parameter \(\theta \in \Theta \) and \(T_1,T_2\) two estimators of \(\theta \). It is said that \(T_1\) is more efficient than \(T_2\) if \(MSE(T_1)\le MSE(T_2)\) for any \(\theta \in \Theta \) and exists \(\theta _0\in \Theta \) such that \(MSE(T_1)< MSE(T_2)\).

Below, we introduce the concept of an L-statistic. They are based on the order statistics, which are the ordered values (from the smallest to the greatest) of a sequence \(X_1,\dots ,X_n\) of iid random variables. They are denoted as \(X_{(1)},\dots ,X_{(n)}\).

Linear combinations of the latter statistics are defined using a weight vector \(\textbf{w}\) of, in general, real numbers. Conceptually, we are sorting the random sample, multiplying the elements by the weights and then adding the results.

Definition 2

Let \(\textbf{X}=X_1,\dots ,X_n\) be a sequence of random variables and \(\textbf{w}\) a weighting real vector. Then, the L-statistics is defined as \(L(\textbf{X},\textbf{w})=\sum _{k=1}^n w_kX_{(k)}\).

L-statistics and order statistics are widely use in estimation. We address some of the foundational papers (Lloyd 1952; Sarhan 1954, 1955a, b) and also some examples of the relevancy of the topic nowadays (Ahsanullah and Alzaatreh 2018; Dytso et al. 2019; Gao et al. 2021; Hassan and Abd-Allah 2018; Kumar et al. 2020).

2.2 The EVR-OWA operator

This section provides a brief introduction to EVR-OWA operators, i.e., OWA operators (Yager 1993, 1996) based on EVRs (García-Zamora et al. 2022), which are essential to provide ordered aggregations whose weights are positive, symmetric, and prioritize the intermediate information.

OWA operators are a family of aggregation functions (Beliakov et al. 2016) which were proposed to ensure that the importance of the aggregated values depends on their position with respect to the median value (Yager 1993). Formally:

Definition 3

(Yager 1993) Let \(w\in [0,1]^n\) be a weighting vector such that \(\sum _{i=1}^m{w_i}=1\). The OWA Operator \(\Psi _w:[0,1]^n\rightarrow [0,1]\) associated to w is defined by:

$$\begin{aligned} \Psi _w(\textbf{x})=\sum _{k=1}^n{w_kx_{\sigma (k)}}\text { }\forall \text { }\textbf{x}\in [0,1]^n, \end{aligned}$$

where \(\sigma \) is a permutation of the n-tuple (1, 2, ..., n) such that \(x_{\sigma (1)}\ge x_{\sigma (2)}\ge \cdots \ge x_{\sigma (n)}\).

OWA operators generalize other aggregation functions (Beliakov et al. 2016). For example, the weighting vector \(w=(\frac{1}{n},\frac{1}{n},...,\frac{1}{n})\in [0,1]^n\), produces the arithmetic mean, whereas the vectors \(w=(1,0,...,0)\in [0,1]^n\) and \(w=(0,...,0,1)\in [0,1]^n\) produce the maximum and the minimum operators, respectively.

It should be highlighted that OWA operators decreasingly order the elements to be aggregated, while L-statistics are defined through an increasing order. However, when symmetric distributions are considered (which will lead to symmetric weights), these two approaches are equivalent.

To derive weights for OWA operators, Yager (1996) proposed the use of regular increasing monotonous quantifiers (RIMQs) (Zadeh 1983), i.e., functions \(Q:[0,1]\rightarrow [0,1]\) such that \(Q(0)=0\), \(Q(1)=1\), and \(Q(x)\le Q(y)\text { }\forall \text { }x,y\in [0,1]\) such that \(x\le y\). For such a RIMQ, the weights for an OWA operator to fuse \(n\in \mathbb {N}\) values are computed as follows:

$$\begin{aligned} w_k=Q\left( \frac{k}{n}\right) -Q\left( \frac{k-1}{n}\right) \text { }\text { for }k=1,2,...,n. \end{aligned}$$

A widely-extended choice for such RIMQ (Palomares et al. 2014; Herrera-Viedma et al. 2002) is the linear RIMQ defined as \(Q_{\alpha ,\beta }:[0,1]\rightarrow [0,1]\), \(0\le \alpha <\beta \le 1\) defined by:

$$\begin{aligned} Q_{\alpha ,\beta }(x) = \left\{ \begin{array}{cc} 0&{} \hspace{5mm} 0\le x<\alpha \\ \frac{x-\alpha }{\beta -\alpha } &{} \hspace{5mm} \alpha \le x\le \beta \\ 1 &{} \hspace{5mm} x\ge \beta \end{array} \right. . \end{aligned}$$
Fig. 1
figure 1

Sketch of an EVR and an EVA

Full size image

Even though, it could seem that changing the values of \(\alpha \) and \(\beta \) provides a flexible method to derive weights, the use of the linear RIMQ presents several drawbacks such as unrealistic aggregations that ignore too much information or biased results (García-Zamora et al. 2022).

The EVR-OWA operator was proposed as a mechanism to guarantee non-biased aggregations that take into account all the available information (García-Zamora et al. 2022). The EVR-OWA operator assumes that the RIMQ is given as an EVR:

Definition 4

(García-Zamora et al. 2021) Let \(\hat{D}:[0,1]\rightarrow [0,1]\) be a function satisfying:

  1. 1.

    \(\hat{D}\) is an automorphism in the interval \([0,1]\),

  2. 2.

    \(\hat{D}\) is a function of class \(\mathcal {C}^1\),

  3. 3.

    \(\hat{D}\) satisfies \(\hat{D}(x)=1-\hat{D}(1-x)\text { }\forall \text { }x\in [0,1]\),

  4. 4.

    \(\hat{D}'(0)<1\) and \(\hat{D}'(1)<1\),

  5. 5.

    \(\hat{D}\) is convex in a neighborhood of 0 and concave in a neighborhood of 1,

then \(\hat{D}\) will be called extreme values reduction (EVR) in the interval \([0,1]\).

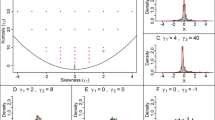
These EVRs remap the values of the interval \([0,1]\) such that the distance between the most extreme points is reduced (García-Zamora et al. 2021) (see Fig. 1). In the same way, the notion of EVA was also introduced as a function that amplifies the distance between the extreme values of the interval \([0,1]\):

Definition 5

(García-Zamora et al. 2021) Let \(D:[0,1]\rightarrow [0,1]\) be a function satisfying:

  1. 1.

    D is an automorphism on the interval \([0,1]\),

  2. 2.

    D is a function of class \(\mathcal {C}^1\),

  3. 3.

    D satisfies \(D(x)=1-D(1-x)\text { }\forall \text { }x\in [0,1]\),

  4. 4.

    \(D'(0)>1\) and \(D'(1)>1\),

  5. 5.

    D is concave in a neighborhood of 0 and convex in a neighborhood of 1,

then D will be called extreme values amplification (EVA) in the interval \([0,1]\).

Consequently, the EVR-OWA operator was defined as an OWA operator whose weights were computed by using an EVR as RIMQ (García-Zamora et al. 2022):

Definition 6

(García-Zamora et al. 2022) Let \(\hat{D}\) be an extreme values reduction and consider \(n\in \mathbb {N}\). Then, the family \(W=\{w_1,w_2,...,w_n\}\), where

$$\begin{aligned} w_k=\hat{D}\left( \frac{k}{n}\right) -\hat{D}\left( \frac{k-1}{n}\right) \text { }\forall \text { }k\in \{1,2,...,n\}, \end{aligned}$$

receives the name of order n weights associated with the EVR \(\hat{D}\), and the OWA operator \(\Psi _{\hat{D}}\) defined using these weights is called EVR-OWA operator.

The use of EVRs to derive OWA weights ensure symmetric aggregations that do not neglect the extreme information and prioritize the intermediate values (García-Zamora et al. 2022).

3 Optimal L-statistics for mean estimation

This section is devoted to analyzing the optimal L-statistic which minimizes the mean squared error (MSE) when estimating the mean of a distribution.

Consider a quantity of interest \(\mu \in \mathbb {R}\) and assume that several measures of this quantity, perturbed by a symmetric noise, are given. The result is a sequence of random variables \(X_1,\dots ,X_n\) in which all the variables are independent, symmetric, and with mean \(\mu \in \mathbb {R}\).

Let us denote the random vector consisting of the order statistics of the random sample as \(\textbf{Z}=\left( X_{(1)},\dots ,X_{(n)}\right) \) and consider its covariance matrix \(\Sigma =\text {Var}\left[ \textbf{Z}\right] \) and the vector \(\mathbf {\Delta }=E\left[ \textbf{Z}\right] -\mu \textbf{1}\), the mean drift from \(\mu \) of the components of \(\textbf{Z}\).

Since the L-statistics \(L\left( \textbf{X},\textbf{w}\right) \) is a linear combination of the order statistics, the MSE to estimate \(\mu \) has the following expression:

$$\begin{aligned} E\left[ \left( \mu -L\left( \textbf{X},\textbf{w}\right) \right) ^2\right] =\textbf{w}'\left( \Sigma +\mathbf {\Delta }\mathbf {\Delta }'\right) \textbf{w}. \end{aligned}$$

Thus, using the latter expression, the optimal weights can be computed by solving an optimization problem. Its resolution it is immediate using Lagrange’s multipliers procedure, therefore we omit the proof.

Proposition 1

Let \(X_1,\dots ,X_n\) be a random sample in which all the variables have mean \(\mu \). Then, the weighting vector \(\textbf{w}\) (verifying that \(\sum _{i=1}^n w_i=1\), \(i=1,2,...,n\)) which minimize \(E\left[ \left( \mu -L\left( \textbf{X},\textbf{w}\right) \right) ^2\right] \) is

$$\begin{aligned} \textbf{w}=\frac{\left( \Sigma +\mathbf {\Delta }\mathbf {\Delta }'\right) ^{-1}\textbf{1}}{\textbf{1}'\left( \Sigma +\mathbf {\Delta }\mathbf {\Delta }'\right) ^{-1}\textbf{1}}. \end{aligned}$$

Remark 1

We want to remark that the resulting weights may be negative. Notice also that if the noise is multiplied by a scalar quantity, \(\Sigma \) and \(\mathbf {\Delta }\mathbf {\Delta }'\) are multiplied by the square of the quantity, thus the optimal weights remain the same.

The optimal weights basically depend on the noise distribution and the sample size, since they characterize the order statistics of the sample. Since our aim is to construct a flexible-dimensional method, we have to explore the relation of the weights for the same distribution with different sample sizes. However, comparing two vectors of different lengths is not straightforward. Therefore, inspired by the EVR-OWA theory to derive weights (García-Zamora et al. 2022), given a weighting vector \(\textbf{w}\in \mathbb {R}^n\) of dimension n, its cumulative weight function \(W:\left\{ 0,\frac{1}{n},\dots ,\frac{n-1}{n},1\right\} \rightarrow \mathbb {R}\) is defined as \(W\left( \frac{k}{n}\right) =\sum _{i=1}^k w_i \text { }\forall \text { }k=1,2,...,n\) and \(W(0)=0\).

In the following, we will denote the optimal cumulative weight function for a fixed distribution and a sample size n as \(W^{(n)}\). The graphical representation of the cumulative weights for some classical distributions suggests a sort of convergence. For instance, when working with the Hyperbolic secant or the Logistic distribution and sample sizes close to 20, the behavior of the cumulative weights seems to be distributed in a common line (see Fig. 2).

Fig. 2
figure 2

Cumulative optimal weights for the Logistic (left) and Hyperbolic secant (right) distributions for \(n\in \{18,19,20,21,22\}\)

Full size image

4 Convergence of optimal cumulative weights

As illustrated in Fig. 2, the cumulative weights for different sample sizes seem to fit to a common function defined on the unit interval. This section is devoted to showing that, under certain conditions on a symmetric distribution, the optimal cumulative weights converge to a function defined on the interval \([0,1]\). This convergence is based on the convergence of order statistics. The following lemma combines the results of (Stephens 1990), which gives a more convenient definition of the sequence, and (Stigler 1969), in which the uniform convergence part is proved.

Lemma 1

(Stephens 1990; Stigler 1969) Let \(X_1,\dots ,X_n\) be a sequence of iid random variables with density function f and cumulative distribution function F such that f is continuous and strictly positive in \(F^{-1}(0,1)\) and there exists \(\epsilon >0\) for which \(\lim _{x\rightarrow \infty }|x|^\epsilon \left[ 1-F(x)+F(-x)\right] =0\). Then, for any \(\delta >0\):

$$\begin{aligned} \lim _{n\rightarrow \infty } (n+2)Cov\left( X_{(nq)},X_{(np)}\right) =\frac{(1-p)q}{f\left( F^{-1}(p)\right) f\left( F^{-1}(q)\right) }, \end{aligned}$$

uniformly for \(p,q\in [\delta ,1-\delta ]\) such that \(p\le q\).

As a consequence, the inverse of this covariance matrix, when n goes to infinity, can be approximated as \(\Sigma ^{-1}\sim (n+1)(n+2)DQD\) (Stephens 1990), where D is a diagonal matrix satisfying that \(D_{i,i}=f\left( F^{-1}(\frac{i}{n+1})\right) \) for any \(i\in \{1,\dots ,n\}\) and Q is a tridiagonal matrix:

$$\begin{aligned} Q=\begin{pmatrix} 2 &{} - 1 &{} 0 &{} 0 &{} 0 &{}\dots \\ - 1 &{} 2 &{} - 1 &{} 0 &{} 0&{}\dots \\ 0 &{} - 1 &{} 2 &{} - 1 &{} 0&{}\dots \\ 0 &{} 0 &{} - 1 &{} 2 &{} - 1&{}\dots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots \\ \end{pmatrix} \end{aligned}$$

The formula \(\Sigma ^{-1}\sim (n+1)(n+2)DQD\) is interesting, but we need a formal result regarding this convergence. In particular, if we suppose a fast convergence of \(nCov\left( X_{(nq)},X_{(np)}\right) f\left( F^{-1}(p)\right) f\left( F^{-1}(q)\right) \) uniformly on (0, 1), we have that the convergence of the elements of \(\Sigma ^{-1}\) is uniform, and moreover, eliminating some of the first elements we obtain a dominated sequence. Let us introduce first an useful lemma:

Lemma 2

(Hager 1989) (Woodbury matrix identity) Let A, B two matrices such that A and \(A{-}B\) are invertible. Then:

$$\begin{aligned} (A-B)^{-1}=A^{-1}+A^{-1}B(A-B)^{-1},\\ (A-B)^{-1}=\sum _{k=0}^\infty \left( A^{-1}B\right) ^kA^{-1}. \end{aligned}$$

The next proposition establishes the convergence of the inverse of the covariance matrix of the order statistics.

Proposition 2

Let \(X_1,\dots ,X_n\) be a sequence of iid random variables with density function f(x) and cumulative distribution F(x) such that f(x) is bounded and strictly positive on \(F^{-1}(0,1)\). Suppose that:

$$\begin{aligned} \lim _{n\rightarrow \infty } k(n)(n+1)^2\left( (n+2)f\left( F^{-1}\left( p\right) \right) f\left( F^{-1}\left( q\right) \right) \Sigma _{np,nq}-p(1-q)\right) =0, \end{aligned}$$

uniformly for \(p,q\in (0,1)\) such that \(p\le q\) for a sequence k(n) such that \(k(n)\rightarrow \infty \). Then, for any \(\epsilon >0\) exists \(m\in \mathbb {N}\) such that for any \(m\le n\in \mathbb {N}\) we have that:

$$\begin{aligned} \left| \frac{1}{(n+1)(n+2)}\left( \Sigma ^{-1}\right) _{i,j}-(DQD)_{i,j}\right| <\frac{\epsilon }{k(n)}, \end{aligned}$$

for any \(i,j\in \{1,\dots ,n\}\), being Q and D the matrices defined after Lemma 1.

Proof

Let us set \(\epsilon >0\). Using the uniform limit of the hyphotesis, for any \(\epsilon _0>0\), there exists \(m\in \mathbb {N}\) such that for any \(m\le n\in \mathbb {N}\) we have:

$$\begin{aligned}{} & {} k(n)(n+1)^2\left| (n+2)f\left( F^{-1}\left( \frac{i}{n+1}\right) \right) f\left( F^{-1}\left( \frac{j}{n+1}\right) \right) \Sigma _{i,j}\right. \\{} & {} \left. \quad -\frac{1}{n+1}\left( Q^{-1}\right) _{i,j}\right| < \epsilon _0, \end{aligned}$$

where \(1 \le i\le j\le n\). Then, since f(x) is strictly positive in \(F^{-1}(0,1)\) the latter expression is equivalent to:

$$\begin{aligned}{} & {} \left| (n+2)(n+1)\Sigma _{i,j}-\left( (DQD)^{-1}\right) _{i,j}\right| \\{} & {} <\frac{\epsilon _0}{f\left( F^{-1}\left( \frac{i}{n+1}\right) \right) f\left( F^{-1}\left( \frac{j}{n+1}\right) \right) (n+1)k(n)}. \end{aligned}$$

Therefore, we can write \((n+2)(n+1)\Sigma =(DQD)^{-1}-\epsilon _1 X\), with \(\epsilon _1=\frac{\epsilon _0}{f\left( F^{-1}\left( \frac{i}{n+1}\right) \right) f\left( F^{-1}\left( \frac{j}{n+1}\right) \right) k(n)}\) and \(\left| X_{i,j}\right| <1\) for any \(i,j\in \{1,\dots ,n\}\). Using the Woodbury matrix identity:

$$\begin{aligned} \frac{1}{(n+2)(n+1)}\Sigma ^{-1}{} & {} =\left( (DQD)^{-1}-\epsilon _1 X\right) ^{-1}\\{} & {} =\sum _{k=0}^\infty \left( DQD\epsilon _1 X\right) ^kDQD=DQD+\sum _{k=1}^\infty \left( DQD\epsilon _1 X\right) ^kDQD. \end{aligned}$$

If we apply the infinite norm (the maximum over the sum of all the row sums) and denote \(M=\max f(x)\) (f is bounded), we obtain the following inequality for the second term in the previous sum:

$$\begin{aligned} \left| \left| \sum _{k=1}^\infty \left( FQF\epsilon _1 X\right) ^kDQD\right| \right| _\infty{} & {} \le \sum _{k=1}^\infty ||D||^{2(k+1)}||Q||^{k+1}||X||^k\epsilon _1^k \\{} & {} \le 4M^2\sum _{k=1}^\infty \left( 4nM^2\epsilon _1\right) ^k. \end{aligned}$$

Now, set \(\epsilon _0=\frac{\min \{\epsilon ,1\}}{32\left( \max \{M,1\}\right) ^2}\). Therefore, we have:

$$\begin{aligned} \epsilon _1{} & {} \le \frac{\min \{\epsilon ,1\}}{32(n+1)k(n)\left( \max \{M,1\}\right) ^4} \left| \left| \sum _{k=1}^\infty \left( FQF\epsilon _1 X\right) ^k(FQF)\right| \right| _\infty \\{} & {} \le 4M^2\frac{\frac{\min \{\epsilon ,1\}}{16k(n)\left( \max \{M,1\}\right) ^2}}{1-\frac{\min \{\epsilon ,1\}}{16k(n)\left( \max \{M,1\}\right) ^2}}\\{} & {} \le \frac{\frac{\epsilon }{4k(n)}}{1-\frac{1}{16}}=\frac{4}{15k(n)}\epsilon < \frac{\epsilon }{k(n)}. \end{aligned}$$

Since the absolute value of any element of a matrix is less than or equal to the infinite norm of the matrix, we have that, for any \(\epsilon >0\) there exists \(m\in \mathbb {N}\) such that for any \(m\le n\in \mathbb {N}\):

$$\begin{aligned} \left| \frac{1}{(n+1)(n+2)}\left( \Sigma ^{-1}\right) _{i,j}-(DQD)_{i,j}\right| <\frac{\epsilon }{k(n)}, \end{aligned}$$

for any \(i,j\in \{1,\dots ,n\}\). \(\square \)

In Proposition 2, we have done two important assumptions that must be discussed. The first one is the convergence of the presented sequence. We know that, according to Lemma 1, the difference must converge to 0, but including the factor \(k(n)(n+1)^2\) implies a requirement for faster convergence. The second one is the uniform convergence rate. Using Lemma 1, the uniform convergence on any closed interval contained in (0, 1) is guaranteed, but not on (0, 1) itself.

The following theorem states the convergence of the cumulative weights (denoted as \(\left( W^{(n)},n\in \mathbb {N}\right) \)) when the distribution is fixed and some requirements are fulfilled. More precisely, fast convergence and uniform convergence of the order statistics are needed, as well as some properties of the density function.

Theorem 1

Let \(X_1,\dots ,X_n\) be a sequence of symmetric iid random variables with support S, density function f and cumulative distribution F, such that f is bounded, continuous, with second derivative on S and strictly positive on \(F^{-1}(0,1)\). Suppose that:

  • Exists a sequence k(n) such that \(\frac{k(n)}{n^3}\rightarrow \infty \) satisfying that for any \(p,q\in (0,1), p\le q\):

    $$\begin{aligned} \lim _{n\rightarrow \infty }k(n) (n+1)^2\left( (n+2)f\left( F^{-1}\left( p\right) \right) f\left( F^{-1}\left( q\right) \right) \Sigma _{np,nq}-p(1-q)\right) =0, \end{aligned}$$

    uniformly.

  • The integral

    $$\begin{aligned} \int _0^1 f\left( F^{-1}(x)\right) \left( \frac{d^2}{dx^2} f\left( F^{-1}(x)\right) \right) dx, \end{aligned}$$

    is finite.

  • The limit

    $$\begin{aligned} \lim _{x\rightarrow \inf S} \frac{f(x)}{F(x)}\left( 2f(x)-f\left( \left( F^{-1}(2F(x)\right) \right) \right) , \end{aligned}$$

    is not oscillatory.

Then, the sequence of optimal cumulative weights \(\left( W^{(n)},n\in \mathbb {N}\right) \) satisfy \(W^{(n)}(0)=0\), \(W^{(n)}(1)=1\) for any \(n\in \mathbb {N}\) and for any \(q\in (0,1)\cap \mathbb {Q}\) with irreducible fraction \(\frac{a}{b}\):

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } W^{(nb)}\left( q\right) =\frac{L+\int _0^q f\left( F^{-1}(x)\right) \left( \frac{d^2}{dx^2} f\left( F^{-1}(x)\right) \right) dx}{2L+\int _0^1 f\left( F^{-1}(x)\right) \left( \frac{d^2}{dx^2} f\left( F^{-1}(x)\right) \right) dx}, \end{aligned}$$

if \(\lim _{x\rightarrow \inf S} \frac{f(x)}{F(x)}\left( 2f(x)-f\left( \left( F^{-1}(2F(x)\right) \right) \right) =L\) is finite and \(\lim \limits _{n\rightarrow \infty } W^{(nb)}\left( q\right) =0.5\) otherwise.

Proof

If X is symmetric, then the matrix \(\Sigma \) is persymmetric (see Golub and Van Loan 1996), since \(E[X_{(i)},X_{(j)}]=E[X_{(n+1-i)},X_{(n+1-j)}]\) for any \(i,j\in \{1,\dots ,n\}\). Thus, since the inverse of a persymmetric matrix is persymmetric (Golub and Van Loan 1996), \(\Sigma ^{-1}\) is also persymmetric. Then, the weights that minimize the variance, which are, similarly as in Proposition 1, \(\textbf{w}=\frac{\Sigma ^{-1}\textbf{1}}{\textbf{1}\Sigma ^{-1}\textbf{1}}\) satisfy \(w_i=w_{n+1-i}\) for any \(i\in \{1,\dots ,n\}\). Also, since X is symmetric, we have \(\Delta _i=-\Delta _{n+1-i}\) for any \(i\in \{1,\dots ,n\}\), which implies \(\textbf{w}'\Delta =0\). Thus, in the symmetric case minimizing the variance and minimizing the MSE is equivalent. Therefore, we just need to compute \(\textbf{w}=\frac{\Sigma ^{-1}\textbf{1}}{\textbf{1}\Sigma ^{-1}\textbf{1}}\) for minimizing the MSE.

Notice that we can express

$$\begin{aligned} W^{(n)}\left( \frac{k}{n+1}\right) =\frac{\sum _{i=1}^k \sum _{j=1}^n \left( \Sigma ^{-1}\right) _{i,j}}{\sum _{i=1}^n\sum _{j=1}^n \left( \Sigma ^{-1}\right) _{i,j}}. \end{aligned}$$

For clarity, let us denote \(\Sigma (n)^{-1}\) the inverse of the covariance matrix of the order statistics of dimension n. Let us consider the sequence:

$$\begin{aligned} W^{(nb)}\left( q\right) =\frac{\sum _{i=1}^{na} \sum _{j=1}^{nb} \left( \Sigma (nb)^{-1}\right) _{i,j}}{\sum _{i=1}^{nb}\sum _{j=1}^{nb}\left( \Sigma (nb)^{-1}\right) _{i,j}}. \end{aligned}$$

We can divide the numerator and denominator by \((nb+1)(nb+2)\) and then apply Proposition 2. Firstly, we can express the limit of the numerator as:

$$\begin{aligned} \lim _{n\rightarrow \infty } \left( \sum _{i=1}^{na} \sum _{j=1}^{nb} \left( DQD\right) _{i,j} + \left( \sum _{i=1}^{na} \sum _{j=1}^{nb} \frac{\left( \Sigma (nb)^{-1}\right) _{i,j}}{(nb+1)(nb+2)}-\left( DQD\right) _{i,j}\right) \right) . \end{aligned}$$

Secondly, applying Proposition 2, exists \(m\in \mathbb {N}\) such that for any \(m\le n\in \mathbb {N}\) and the absolute value of the second term can be bounded as follows:

$$\begin{aligned} \left| \sum _{i=1}^{na} \sum _{j=1}^{nb} \frac{\left( \Sigma (nb)^{-1}\right) _{i,j}}{(nb+1)(nb+2)}-\left( DQD\right) _{i,j}\right| \le \sum _{i=1}^{na} \sum _{j=1}^{nb}\frac{\epsilon }{k(n)}=\frac{ab\epsilon n^2}{k(n)}. \end{aligned}$$

Let us suppose that this term is negligible in the limit compared to the other terms. With this assumption:

$$\begin{aligned}{} & {} \lim _{n\rightarrow \infty } \sum _{i=1}^{na} \sum _{j=1}^{nb} \left( DQD\right) _{i,j}\\{} & {} \quad =\lim _{n\rightarrow \infty } f\left( F^{-1}\left( \frac{1}{n+1}\right) \right) \left( 2f\left( F^{-1}\left( \frac{1}{n+1}\right) \right) -f\left( F^{-1}\left( \frac{2}{n+1}\right) \right) \right) \\{} & {} \qquad +\sum _{i=2}^{na} f\left( F^{-1}\left( \frac{i}{n+1}\right) \right) \left( 2f\left( F^{-1}\left( \frac{i}{n+1}\right) \right) -f\left( F^{-1}\left( \frac{2}{n+1}\right) \right) \right. \\{} & {} \left. \qquad -f\left( F^{-1}\left( \frac{i-1}{n+1}\right) \right) \right) . \end{aligned}$$

The limit of the latter line can be expressed in terms of an integral, that is convergent by hypothesis, and the second derivative of f, which is finite:

$$\begin{aligned}{} & {} \lim _{n\rightarrow \infty } \sum _{i=2}^{na} f\left( F^{-1}\left( \frac{i}{n+1}\right) \right) \left( 2f\left( F^{-1}\left( \frac{i}{n+1}\right) \right) -f\left( F^{-1}\left( \frac{i+1}{n+1}\right) \right) \right. \\{} & {} \left. -f\left( F^{-1}\left( \frac{i-1}{n+1}\right) \right) \right) \\{} & {} =\lim _{n\rightarrow \infty } \frac{1}{n}\sum _{i=2}^{na} f\left( F^{-1}\left( \frac{i}{n+1}\right) \right) \left( \frac{2f\left( F^{-1}\left( \frac{i}{n+1}\right) \right) -f\left( F^{-1}\left( \frac{i+1}{n+1}\right) \right) -f\left( F^{-1}\left( \frac{i-1}{n+1}\right) \right) }{1/n^2}\right) \frac{1}{n}\\{} & {} =\lim _{n\rightarrow \infty } \frac{1}{n} \int _0^q f\left( F^{-1}\left( x\right) \right) \left( \frac{d^2}{dx^2}f\left( F^{-1}\left( x\right) \right) \right) dx. \end{aligned}$$

Applying the same process to the denominator, we reach the following expression:

$$\begin{aligned} \lim _{n\rightarrow \infty } W^{(nb)}\left( q\right) =\lim _{n\rightarrow \infty }\frac{f\left( F^{-1}\left( \frac{1}{n+1}\right) \right) \left( 2f\left( F^{-1}\left( \frac{1}{n+1}\right) \right) -f\left( F^{-1}\left( \frac{2}{n+1}\right) \right) \right) +}{2f\left( F^{-1}\left( \frac{1}{n+1}\right) \right) \left( 2f\left( F^{-1}\left( \frac{1}{n+1}\right) \right) -f\left( F^{-1}\left( \frac{2}{n+1}\right) \right) \right) }\\\frac{+\frac{1}{n}\int _0^q f\left( F^{-1}(x)\right) \left( \frac{d^2}{dx^2} f\left( F^{-1}(x)\right) \right) dx}{\frac{1}{n}\int _0^1 f\left( F^{-1}(x)\right) \left( \frac{d^2}{dx^2} f\left( F^{-1}(x)\right) \right) dx}, \end{aligned}$$

where we have used \(f\left( F^{-1}\left( \frac{1}{n+1}\right) \right) =f\left( F^{-1}\left( \frac{n}{n+1}\right) \right) \) and \(f\left( F^{-1}\left( \frac{2}{n+1}\right) \right) =f\left( F^{-1}\left( \frac{n-1}{n+1}\right) \right) \), as a consequence of the symmetry of the distribution. Thus, if:

$$\begin{aligned}{} & {} \lim _{n\rightarrow \infty } nf\left( F^{-1}\left( \frac{1}{n}\right) \right) \left( 2f\left( F^{-1}\left( \frac{1}{n}\right) \right) -f\left( F^{-1}\left( \frac{2}{n}\right) \right) \right) \\ {}{} & {} \quad =\lim _{x\rightarrow \inf S} \frac{f(x)}{F(x)}\left( 2f(x)-f\left( \left( F^{-1}(2F(x)\right) \right) \right) =L, \end{aligned}$$

we have the first case of the statement we want to proof. If the limit diverges, the integral terms are negligible and we have 0.5 as the limit. Notice that we have assumed that the latter limit cannot be oscillatory.

In order to end the proof only remains to prove that the term bounded by \(\frac{ab\epsilon n^2}{k(n)}\) is negligible with respect to the other terms in the denominator. Notice that we can express the integral, integrating by parts:

$$\begin{aligned}{} & {} \int _0^1 f\left( F^{-1}(x)\right) \left( \frac{d^2}{dx^2} f\left( F^{-1}(x)\right) \right) dx\\ \nonumber{} & {} \quad =\lim _{q\rightarrow 0} f\left( F^{-1}(q)\right) \left( \frac{d}{dx} f\left( F^{-1}(q)\right) \right) \\{} & {} \qquad -\lim _{q\rightarrow 1} f\left( F^{-1}(q)\right) \left( \frac{d}{dx} f\left( F^{-1}(q)\right) \right) -\int _0^1 \left( \frac{d}{dx} f\left( F^{-1}(x)\right) \right) ^2 dx. \end{aligned}$$

Applying the symmetry of the distribution, the first and the second terms (with sign) equal the same value. If the latter expression is different from 0, then we have that the term by \(\frac{ab\epsilon n^2}{k(n)}\) is negligible with respect to the integral divided by n. Otherwise, one case is being \(f'(x)=0\). Then, f(x) is constant and strictly positive. But then \(L\ne 0\) (moreover, the associated limit diverges), thus the term \(\frac{ab\epsilon n^2}{k(n)}\) is also negligible. The other case is \(f'(x)\ne 0\), and then the latter expression is 0 if and only if \(\lim _{x\rightarrow \inf S} f(x)\ne 0\) and in this case we also have that the associated limit with L diverges. \(\square \)

The previous result only makes sense for the rational numbers on [0, 1]. However, we can extend the limit function to the unit interval numbers straightforwardly considering its continuous extension when it is available.

Theorem 1 also allows us to expect a smaller difference between the fitting function and the exact solution when the sample size increases. This is very important since, in general, it is not easy to derive the explicit expression of the latter limit, since the integrals can be hard to compute. We can see this in the case of the hyperbolic secant distribution, see 1. This example will be used later to analyze the difference between the fitting function and the limit function.

Example 1

Consider the distribution of a random variable defined as \(Y=\mu +\lambda X\), \(\mu ,\lambda \in \mathbb {R}\) with X having hyperbolic secant distribution. Then, \(f(x)=\frac{1}{2}\text {sech}\left( \frac{\pi }{2}x\right) \), \(F(x)=\frac{2}{\pi }\arctan \left( e^{\frac{\pi }{2}x}\right) \) and \(F^{-1}(x)=\frac{2}{\pi }\ln \left( \text {tan}\left( \frac{\pi }{2}x\right) \right) \). The limit L equals 0:

$$\begin{aligned} \lim _{x\rightarrow -\infty } \frac{\pi \text {sech}\left( \frac{\pi }{2}x\right) }{4\arctan \left( e^{\frac{\pi }{2}x}\right) }\left( \text {sech}\left( \frac{\pi }{2}x\right) -\frac{\text {tan}\left( 2 \text {arctan}\left( e^{\frac{\pi }{2}x}\right) \right) }{\text {tan}^2\left( 2 \text {arctan}\left( e^{\frac{\pi }{2}x}\right) \right) + 1}\right) =0, \end{aligned}$$

since the first fraction converges and the second term tends to 0. Then,

$$\begin{aligned} \frac{d^2}{dx^2}\frac{1}{2}\text {sech}\left( \ln \left( \text {tan}\left( \frac{\pi }{2}x\right) \right) \right) =\frac{d}{dx}\frac{\pi }{2}\cos (\pi x)=-\frac{\pi ^2}{2}\sin (\pi x), \end{aligned}$$

and therefore the integral term in Theorem 1 is the following:

$$\begin{aligned} \int _0^x -\frac{\pi ^4}{4}\text {sech}\left( \ln \left( \text {tan}\left( \frac{\pi }{2}t\right) \right) \right) \sin (\pi t)=\frac{\pi }{4}(1-\cos (\pi x)). \end{aligned}$$

It is concluded that the limit function is \(g(x)=\frac{1}{2}(1-\cos (\pi x))\).

We end this section by stating the asymptotic convergence of the estimators build with the limits of the optimal cumulative weights to the real value of the mean.

Proposition 3

In the conditions of Theorem 1, one has:

$$\begin{aligned} \sum _{i=1}^n \left( W\left( \frac{i}{n}\right) -W\left( \frac{i-1}{n}\right) \right) X_{(i)}\xrightarrow {L^2} \mu , \end{aligned}$$

with \(W:[0,1]\rightarrow \mathbb {R}\) defined as

$$\begin{aligned} W\left( t\right) =\frac{L+\int _0^t f\left( F^{-1}(x)\right) \left( \frac{d^2}{dx^2} f\left( F^{-1}(x)\right) \right) dx}{2L+\int _0^1 f\left( F^{-1}(x)\right) \left( \frac{d^2}{dx^2} f\left( F^{-1}(x)\right) \right) dx}, \end{aligned}$$

if \(\lim _{x\rightarrow \inf S} \frac{f(x)}{F(x)}\left( 2f(x)-f\left( \left( F^{-1}(2F(x)\right) \right) \right) =L\) is finite and \(W(0)=0, W(1)=1\) and \(W(t)=0.5\) for any \(t\in (0,1)\) otherwise.

Proof

Since both the function W(t) and the distribution are symmetric, it is clear that the expectation of the estimator is \(\mu \) for any sample size. It remains to prove that its variance converges to 0.

Suppose that \(\lim _{x\rightarrow \inf S} \frac{f(x)}{F(x)}\left( 2f(x)-f\left( \left( F^{-1}(2F(x)\right) \right) \right) =L\) is finite. Denote as \(\lambda \) the finite quantity in the denominator of W(t). Then, using the same notation as the previous proof, the variance can be decomposed as follows.

$$\begin{aligned}{} & {} Var\left( \sum _{i=1}^n \left( W\left( \frac{i}{n}\right) -W\left( \frac{i-1}{n}\right) \right) X_{(i)}\right) \\{} & {} \quad =\frac{L^2}{\lambda }\Sigma (n)_{1,1}+\Sigma (n)_{n,n}\\{} & {} \qquad +\frac{L}{\lambda }\sum _{i=2}^{n-1}\left( \Sigma (n)_{1,i}+\Sigma (n)_{n,i}+\Sigma (n)_{i,1}+\Sigma (n)_{i,n}\right) \left( \int _{\frac{j-1}{n}}^{\frac{j}{n}} f\left( F^{-1}(x)\right) \left( \frac{d^2}{dx^2} f\left( F^{-1}(x)\right) \right) dx\right) \\{} & {} \qquad +\frac{1}{\lambda }\sum _{i,j=1}^n \left( \int _{\frac{i-1}{n}}^{\frac{i}{n}} f\left( F^{-1}(x)\right) \left( \frac{d^2}{dx^2} f\left( F^{-1}(x)\right) \right) dx\right) \\{} & {} \qquad \times \left( \int _{\frac{j-1}{n}}^{\frac{j}{n}} f\left( F^{-1}(x)\right) \left( \frac{d^2}{dx^2} f\left( F^{-1}(x)\right) \right) dx\right) \Sigma (n)_{i,j}. \end{aligned}$$

We will prove that the limit of each of the three summands is 0.

First summand If \(L=0\), the first summand is 0. Suppose that \(L\ne 0\). In that case, using the uniform convergence of the covariance matrix of the order statistics one has,

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{L^2}{\lambda } \Sigma (n)_{1,1}{} & {} =\frac{L^2}{\lambda } \lim _{n\rightarrow \infty } \frac{1}{n+2} \frac{\frac{1}{n}\left( 1-\frac{1}{n}\right) }{f\left( F^{-1}\left( \frac{1}{n}\right) \right) ^2} \\{} & {} \le \frac{L^2}{\lambda } \lim _{n\rightarrow \infty } \frac{1}{n} \frac{\frac{1}{n}\left( 1-\frac{1}{n}\right) }{f\left( F^{-1}\left( \frac{1}{n}\right) \right) ^2} =\frac{L^2}{\lambda }\lim _{x\rightarrow \inf S} F(x)\frac{F(x)(1-F(x))}{f(x)^2}\\{} & {} \le \frac{L^2}{\lambda } \lim _{x\rightarrow \inf S}\frac{F(x)^2}{f(x)^2}= \frac{L^2}{\lambda } \lim _{x\rightarrow \inf S}\frac{F(x)^2}{f(x)^2}\frac{\left( 2f(x)-f\left( \left( F^{-1}(2F(x)\right) \right) \right) ^2}{\left( 2f(x)-f\left( \left( F^{-1}(2F(x)\right) \right) \right) ^2}\\{} & {} = \frac{1}{\lambda }\lim _{x\rightarrow \inf S} \left( 2f(x)-f\left( \left( F^{-1}(2F(x)\right) \right) \right) ^2. \end{aligned}$$

The latter limit is 0 if \(\lim _{x\rightarrow \inf S} f(x)=0\), which should holds since, if not, \(\lim _{x\rightarrow \inf S} \frac{f(x)}{F(x)}\left( 2f(x)-f\left( \left( F^{-1}(2F(x)\right) \right) \right) \) is not finite. A similar reasoning can be applied to \(\lim _{n\rightarrow \infty }\frac{L^2}{\lambda } \Sigma (n)_{n,n}\), thus the limit of the first summand is 0.

Second summand If \(L=0\), the first summand is 0. Suppose that \(L\ne 0\). Using the inequality \(\Sigma (n)_{1,i}\le \sqrt{\Sigma (n)_{1,1}\Sigma (n)_{i,i}}\) and the hyphotesis of uniform convergence of the covariances of the order statistics, we can express

$$\begin{aligned}{} & {} \lim _{n\rightarrow \infty }\frac{L}{\lambda }\sum _{i=2}^{n-1} \Sigma (n)_{1,i}\left( \int _{\frac{j-1}{n}}^{\frac{j}{n}} f\left( F^{-1}(x)\right) \left( \frac{d^2}{dx^2} f\left( F^{-1}(x)\right) \right) dx\right) \le \\{} & {} \le \lim _{n\rightarrow \infty }\frac{L \sqrt{\Sigma (n)_{1,1}}}{\lambda }\sum _{i=2}^{n-1} \sqrt{\Sigma (n)_{i,i}}\left( \int _{\frac{j-1}{n}}^{\frac{j}{n}} f\left( F^{-1}(x)\right) \left( \frac{d^2}{dx^2} f\left( F^{-1}(x)\right) \right) dx\right) \\{} & {} < \lim _{n\rightarrow \infty }\frac{L \sqrt{\Sigma (n)_{1,1}}}{\lambda }\int _0^1 \sqrt{\frac{p(1-p)}{f\left( F^{-1}(p)\right) ^2}} f\left( F^{-1}(p)\right) \left( \frac{d^2}{dp^2} f\left( F^{-1}(p)\right) \right) dp\\{} & {} = \lim _{n\rightarrow \infty }\frac{L \sqrt{\Sigma (n)_{1,1}}}{\lambda }\int _0^1 \sqrt{p(1-p)}\left( \frac{d^2}{dp^2} f\left( F^{-1}(p)\right) \right) dp \\{} & {} \le \lim _{n\rightarrow \infty }\frac{L \sqrt{\Sigma (n)_{1,1}}}{\lambda } M\int _0^1 f\left( F^{-1}(p)\right) \left( \frac{d^2}{dp^2} f\left( F^{-1}(p)\right) \right) dp, \end{aligned}$$

where M a constant that bounds the density function, which is bounded by hyphotesis. Also by hyphotesis, the latter integral is finite. Then, since the first part of the product goes to 0, as proved when working with the first summand, the limit is 0.

Third summand Changing again the covariances of the order statistics by its limits and the sums for integrals, we obtain the following expression.

$$\begin{aligned}{} & {} \lim _{n\rightarrow \infty } \frac{1}{\lambda }\sum _{i,j{=}1}^n \left( \int _{\frac{i{-}1}{n}}^{\frac{i}{n}} f\left( F^{{-}1}(x)\right) \left( \frac{d^2}{dx^2} f\left( F^{-1}(x)\right) \right) dx\right) \left( \int _{\frac{j{-}1}{n}}^{\frac{j}{n}} f\left( F^{-1}(x)\right) \left( \frac{d^2}{dx^2} f\left( F^{-1}(x)\right) \right) dx\right) \Sigma (n)_{i,j}\\{} & {} = \lim _{n\rightarrow \infty } \frac{1}{\lambda (n+2)} \int _0^1\int _0^1 \frac{p(1-q) f\left( F^{-1}(p)\right) \left( \frac{d^2}{dp^2} f\left( F^{-1}(p)\right) \right) f\left( F^{-1}(q)\right) \left( \frac{d^2}{dq^2} f\left( F^{-1}(q)\right) \right) }{f\left( F^{-1}(p)\right) f\left( F^{-1}(q)\right) }dpdq\\{} & {} = \lim _{n\rightarrow \infty } \frac{1}{\lambda (n+2)} \int _0^1\int _0^1 p(1-q)\left( \frac{d^2}{dp^2} f\left( F^{-1}(p)\right) \right) \left( \frac{d^2}{dq^2} f\left( F^{-1}(q)\right) \right) dpdq\le \\{} & {} \le \lim _{n\rightarrow \infty } \frac{M^2}{\lambda n} \left( \int _0^1 f\left( F^{-1}(p)\right) \left( \frac{d^2}{dp^2} f\left( F^{-1}(p)\right) \right) dp\right) ^2. \end{aligned}$$

The integral is convergent by the same previous arguments. Then the limit goes to 0.

It remains the case when the limit \(\lim _{x\rightarrow \inf S} \frac{f(x)}{F(x)}\left( 2f(x)-f\left( \left( F^{-1}(2F(x)\right) \right) \right) \) diverges. In this case, we have that the estimator is just \(\frac{1}{2}\left( X_{(n)}+X_{(1)}\right) \) and its variance is \(\frac{1}{4}\left( \Sigma (n)_{1,1}+\Sigma (n)_{1,n}+\Sigma (n)_{n,1}+\Sigma (n)_{n,n}\right) \). Proceeding similarly as in the first summand of the other case,

$$\begin{aligned}{} & {} \lim _{n\rightarrow \infty }\frac{1}{4} \Sigma (n)_{1,1}\le \frac{1}{4} \lim _{x\rightarrow \inf S}\frac{F(x)^2}{f(x)^2}\\{} & {} \quad =\frac{1}{4} \lim _{x\rightarrow \inf S}\left[ \frac{F(x)^2}{f(x)^2}\frac{1}{\left( 2f(x)-f\left( \left( F^{-1}(2F(x)\right) \right) \right) ^2}\right] \left( 2f(x)-f\left( \left( F^{-1}(2F(x)\right) \right) \right) ^2. \end{aligned}$$

The part between the brackets goes to 0, by the divergence of its inverse, and the limit of the other part is finite, thus it is concluded that the limit is 0.

We have proved that the mean of the estimator converges to \(\mu \) and the variance converges to 0, therefore the result holds. \(\square \)

5 Flexible-dimensional L-statistic for mean estimation of symmetric distributions

The main result of the previous section, the numerical results shown in Fig. 2 and the performance of the EVR-OWA operator (García-Zamora et al. 2021, 2022) to provide symmetrically ordered aggregations, serve as inspiration for a method to construct a flexible-dimensional L-statistic for mean estimation.

In particular, given some optimal weights, the associated cumulative weights are fitted using a function \(g:[0,1]\rightarrow \mathbb {R}\). Then, if aggregating a vector with a different dimension, the fitted function is used to generate new weights that suit the new dimension. Keeping in mind Theorem 1 and Fig. 2, it is reasonable to think that the generated weights will be similar to the optimal weights if both dimensions are sufficiently great and close.

Table 1 Parameters of the fitted function to the optimal cumulative weights of the considered distributions with a sample size \(n=20\)
Full size table
Table 2 Mean squared error (multiplied by \(10^{-7}\)) between the fitted function using the cumulative weights for \(n=20\) and the cumulative weights for \(n\in \{10,18,19,20,21,22,30\}\) for the considered distributions
Full size table
Table 3 Mean squared error of L-estimators when considering the optimal weights, the fitted weights and the balanced weights for sample sizes \(n\in \{10,18,19,20,21,22,30\}\) for the considered distributions
Full size table

5.1 Fitting functions

Even if the limit function is known, the optimal cumulative weights can be far from it for small sample sizes. Therefore, one of the main challenges faced by this procedure is the correct choice of a family of functions for fitting the cumulative weights. Although more elections might be done, here we consider a family of functions based on extreme value amplifications (EVAs) (García-Zamora et al. 2021) and extreme value reductions (EVRs) (García-Zamora et al. 2022) due to their convenient behavior when applied in OWA aggregations (Baz et al. 2022).

In particular, the following families of functions are considered:

  • Sin-based EVAs/EVRs The function \(s_\alpha :[0,1]\rightarrow [0,1]\) defined as

    $$\begin{aligned} s_\alpha (x)=x+\sum _{k=0}^n \alpha _k\sin (2\pi kx)\text { }\forall \text { }x\in [0,1], \end{aligned}$$

    is an EVA if \(\alpha =(\alpha _1,...,\alpha _n)\) satisfy \(\sum _{k=1}^{n}\alpha _kk<\frac{1}{2\pi }\), \(\alpha _k>0\). In addition, if \(\alpha =(\alpha _1,...,\alpha _n)\) satisfy \(\sum _{k=1}^{n}\alpha _kk>-\frac{1}{2\pi }\), \(\alpha _k<0\), the function \(s_{\alpha }\) is an EVR.

  • Grade 3 polynomials The function \(p^3_\beta :[0,1]\rightarrow [0,1]\), defined as

    $$\begin{aligned} p^3_\beta (x)=(1-\beta )x+3\beta x^2-2\beta x^3\text { }\forall \text { }x\in [0,1], \end{aligned}$$

    is an EVR for \(\beta \in ]0,1]\) and an EVA for \(\beta \in [-1,0[\).

  • Spline-based EVAs and EVRs The functions \(sp_\gamma :[0,1]\rightarrow [0,1]\) defined as

    $$\begin{aligned} sp_\gamma (x) = \left\{ \begin{array}{cc} \frac{1}{2}-\frac{1}{2}(1-2x)^\gamma &{} \hspace{5mm} 0\le x<\frac{1}{2} \\ \frac{1}{2}+\frac{1}{2}(2x-1)^\gamma &{} \hspace{5mm} \frac{1}{2}\le x\le 1\\ \end{array} \right. , \end{aligned}$$

    are EVAs for \(\gamma >1\) and behave like EVRs for \(0<\gamma <1\).

  • Pseudo-constant function Finally, we include the function \(c:[0,1]\rightarrow [0,1]\) defined as:

    $$\begin{aligned} c(x) = \left\{ \begin{array}{cc} 0 &{} x=0 \\ \frac{1}{2} &{} 0<x<1\\ 1&{}x=1 \end{array} \right. . \end{aligned}$$

Remark 2

The proof of the above statements is straightforward and follows arguments similar to those developed in García-Zamora et al. (2021, 2022).

For the family \(s_{\mathbf {\alpha }}\), in which the parameter \(\mathbf {\alpha }\) can be a vector with possibly infinite elements, we just consider a vector with dimension 4, \(\mathbf {\alpha }=\left( \alpha _1,\alpha _2,\alpha _3,\alpha _4\right) \).

We consider a linear combination of the aforementioned families with coefficients \(\mathbf {\lambda }=\left( \lambda _1,\lambda _2,\lambda _3,\lambda _4\right) \) in order to obtain a unique function with a better behavior. We define the family of functions \(g_{\mathbf {\alpha },\beta ,n,\mathbf {\lambda }}:[0,1]\rightarrow \mathbb {R}\) given by

$$\begin{aligned} g_{\mathbf {\alpha },\beta ,\gamma ,\mathbf {\lambda }}(x)=\lambda _1s_{\mathbf {\alpha }}(x)+\lambda _2 p^3_\beta (x)+\lambda _3 sp_{\gamma }(x)+\lambda _4 c(x). \end{aligned}$$

5.2 Numerical results

For eight different symmetric distributions, the optimal weights for \(n=20\) are computed through simulation. Then, the cumulative weights are fitted using the latter family of functions, with the aim to minimize the mean squared error between the points and the fitted function. The resulting function is compared to the optimal weights for \(n\in \{18,19,21,22\}\), the dimensional sizes closest to 20 and \(n\in \{10,30\}\), further ones. The election of \(n=20\) is adequate for illustrating the method working on small sample sizes, in which small differences between sample sizes are relevant. Additional experiments with larger samples sizes have been also done, with better results as a consequence of the convergence of Theorem 1. For too small samples, the differences between sample sizes are relatively very large, and the behavior gets worse.

In particular, the considered distributions are the Laplace distribution, the Hyperbolic secant distribution, the Student’s T distribution (with 30 degrees of freedom), two Generalized Normal (or G-normal) distributions (with parameters \(s=3\) and \(s=1.5\)), two Beta distribution (with \(\alpha =\beta =0.5\) and \(\alpha =\beta =2\)) and the Logistic distribution. They are a good sample of classical and relevant distribution in theoretical and applied problems in statistics. For a detailed review of the aforementioned distributions, we refer to Ding (2014), Dytso et al. (2018) and Johnson et al. (1995). The uniform or the normal distribution have not been addressed because the optimal weights are straightforward to compute for any sample size, \(\left( \frac{1}{2},0,\dots ,0,\frac{1}{2}\right) \) and \(\left( \frac{1}{n},\dots ,\frac{1}{n}\right) \) (Rohatgi and Saleh 2015).

We want to remark that the here-proposed method is not restricted to the distributions considered in this section. As guaranteed by Theorem 1, for a sufficient regular distribution, this procedure can also be used but perhaps using a broader family of fitting functions.

The resulting parameters of the fitted functions can be found in Table 1. If a coefficient of the linear combination is 0, the parameters of the associated function are not provided.

The limit function for the Logistic distribution, derived in Example 1 equals \(3x^2-2x^3\), and the fitted function, using the optimal weights for \(n=20\), is \(0.584(x- 0.099\sin (2\pi x-\pi )+0.012\sin (4\pi x-\pi ) -0.004\sin (6\pi x-\pi )) - 0.001\sin (8\pi x-\pi )+0.416(3.066x^2-2.044x^3)\). Although the second summand of the fitted function is similar to the limit function, there is a notable difference between them. For bigger sample sizes, the fitted function will converge to the limit function, as already proved in Theorem 1.

In Fig. 3, the fitted functions and the cumulative weights can be seen for different values of n, for all the considered distributions. It can be seen that the fitted function also serves as a good approximation for the cumulative weights when \(n\in \{18,19,21,22\}\), although we have not used them to fit the function. As expected, the behavior is worse for the cases \(n\in \{10,30\}\).

Fig. 3
figure 3

Fitted cumulative weights when \(n=20\) and its comparison with cumulative weights when \(n\in \{10,18,19,21,22,30\}\) for several symmetric distributions

Full size image

In addition, we have computed the mean squared error between the points and the fitted function for all the cases. In Table 2, it can be seen that the MSE does not increase considerably when moving from \(n=20\) to closer sample sizes (even in a particular case it decreases) and it is of the order of \(10^{-6}{-}10^{-8}\) (notice that the values in the table are multiplied by \(10^{-7}\)) for all the cases. The MSE for the further sample sizes increases in some cases to the order of \(10^{-4}{-}10^{-6}\).

The small difference between the optimal and the fitted weights should lead to a small difference in the behavior between the obtained L-estimators. In this regard, we have computed it for each of the cases, as well as the value for the sample mean (balanced weights), and its Mean Squared Error by simulation. The results can be found in Table 3.

As it can be seen, the L-estimators with fitted weights behave similarly to the optimal one. Their MSE is always between the optimal, which cannot be improved, and the sample mean, which can be seen as a naive flexible-dimensional method. Indeed, it is almost the same for most of the considered cases. The difference is greater for the sample sizes that are further to \(n=20\), since, as already seen in Table 2, the fitted function is a better approximation for closer sample sizes.

6 Conclusion

A method for the definition of flexible-dimensional L-statistics for the mean estimation of symmetric distributions is provided. In particular, given some optimal weights for a specific sample size, the cumulative optimal weights are fitted using a family of weighting functions inspired by Extreme Value Reductions and Amplifications.

The feasibility of the method is justified using Theorem 1, which states a convergence of the cumulative weights to a limiting weighting function. Given a distribution, although checking whether the conditions of the Theorem are fulfilled is not straightforward, numerical results support the good performance of the method. In particular, the method has been illustrated for different classical symmetric distributions. In conclusion, it can be seen that the weights constructed using the fitted function are similar to the optimal weights when considering sample sizes near to initial sample size. In particular, the MSE between the fitted functions and the optimal weights is of the order \(10^{-6}{-}10^{-7}\), illustrating the good behavior of the family of fitting functions.

Our main next objective is to apply this procedure to real data. In this scenario, we may have data for specific sample sizes to compute the optimal weights, which can be extended to other sample sizes with the presented method if necessary. In this regard, we should generalize Theorem 1 for non-symmetric random variables and also give a greater family of fitting functions to fulfill the theoretical and practical necessities when working in a more general case. In addition, we wonder if this method could be applied to censored samples, which in general are not equivalent to simple random samples of variable dimension.