Confidence distributions and hypothesis testing

Abstract

The traditional frequentist approach to hypothesis testing has recently come under extensive debate, raising several critical concerns. Additionally, practical applications often blend the decision-theoretical framework pioneered by Neyman and Pearson with the inductive inferential process relied on the p-value, as advocated by Fisher. The combination of the two methods has led to interpreting the p-value as both an observed error rate and a measure of empirical evidence for the hypothesis. Unfortunately, both interpretations pose difficulties. In this context, we propose that resorting to confidence distributions can offer a valuable solution to address many of these critical issues. Rather than suggesting an automatic procedure, we present a natural approach to tackle the problem within a broader inferential context. Through the use of confidence distributions, we show the possibility of defining two statistical measures of evidence that align with different types of hypotheses under examination. These measures, unlike the p-value, exhibit coherence, simplicity of interpretation, and ease of computation, as exemplified by various illustrative examples spanning diverse fields. Furthermore, we provide theoretical results that establish connections between our proposal, other measures of evidence given in the literature, and standard testing concepts such as size, optimality, and the p-value.

1 Introduction

In applied research, the standard frequentist approach to hypothesis testing is commonly regarded as a straightforward, coherent, and automatic method for assessing the validity of a conjecture represented by one of two hypotheses, denoted as ${{{\mathcal {H}}}_{0}}$ and ${{{\mathcal {H}}}_{1}}$. The probabilities $\alpha$ and $\beta$ of committing type I and type II errors (reject ${{{\mathcal {H}}}_{0}}$, when it is true and accept ${{{\mathcal {H}}}_{0}}$ when it is false, respectively) are controlled through a carefully designed experiment. After having fixed $\alpha$ (usually at 0.05), the p-value is used to quantify the measure of evidence against the null hypothesis. If the p-value is less than $\alpha$, the conclusion is deemed significant, suggesting that it is unlikely that the null hypothesis holds. Regrettably, this methodology is not as secure as it may seem, as evidenced by a large literature, see the ASA’s Statement on p-values (Wasserstein and Lazar 2016) and The American Statistician (2019, vol. 73, sup1) for a discussion of various principles, misconceptions, and recommendations regarding the utilization of p-values. The standard frequentist approach is, in fact, a blend of two different views on hypothesis testing presented by Neyman-Pearson and Fisher. The first authors approach hypothesis testing within a decision-theoretic framework, viewing it as a behavioral theory. In contrast, Fisher’s perspective considers testing as a component of an inductive inferential process that does not necessarily require an alternative hypothesis or concepts from decision theory such as loss, risk or admissibility, see Hubbard and Bayarri (2003). As emphasized by Goodman (1993) “the combination of the two methods has led to a reinterpretation of the p-value simultaneously as an ‘observed error rate’ and as a ‘measure of evidence’. Both of these interpretations are problematic...”.

It is out of our scope to review the extensive debate on hypothesis testing. Here, we briefly touch upon a few general points, without delving into the Bayesian approach.

i) The long-standing caution expressed by Berger and Sellke (1987) and Berger and Delampady (1987) that a p-value of 0.05 provides only weak evidence against the null hypothesis has been further substantiated by recent investigations into experiment reproducibility, see e.g., Open Science Collaboration OSC (2015) and Johnson et al. (2017). In light of this, 72 statisticians have stated “For fields where the threshold for defining statistical significance for new discoveries is $p<0.05$, we propose a change to $p<0.005$”, see Benjamin et al. (2018).

ii) The ongoing debate regarding the selection of a one-sided or two-sided test leaves the standard practice of doubling the p-value, when moving from the first to the second type of test, without consistent support, see e.g., Freedman (2008).

iii) There has been a longstanding argument in favor of integrating hypothesis testing with estimation, see e.g. Yates (1951, pp. 32–33) or more recently, Greenland et al. (2016) who emphasize that “... statistical tests should never constitute the sole input to inferences or decisions about associations or effects ... in most scientific settings, the arbitrary classification of results into significant and non-significant is unnecessary for and often damaging to valid interpretation of data”.

iv) Finally, the p-value is incoherent when it is regarded as a statistical measure of the evidence provided by the data in support of a hypothesis ${{{\mathcal {H}}}_{0}}$. As shown by Schervish (1996), it is possible that the p-value for testing the hypothesis ${{{\mathcal {H}}}_{0}}$ is greater than that for testing ${{{\mathcal {H}}}_{0}}^{\prime } \supset {{{\mathcal {H}}}_{0}}$ for the same observed data.

While theoretical insights into hypothesis testing are valuable for elucidating various aspects, we believe they cannot be compelled to serve as a unique, definitive practical guide for real-world applications. For example, uniformly most powerful (UMP) tests for discrete models not only rarely exist, but nobody uses them because they are randomized. On the other hand, how can a test of size 0.05 be considered really different from one of size 0.047 or 0.053? Moreover, for one-sided hypotheses, why should the first type error always be much more severe than the second type one? Alternatively, why should the test for ${{{\mathcal {H}}}_{0}}: \theta \le \theta _0$ versus ${{{\mathcal {H}}}_{1}}: \theta >\theta _0$ always be considered equivalent to the test for ${{{\mathcal {H}}}_{0}}: \theta = \theta _0$ versus ${{{\mathcal {H}}}_{1}}: \theta >\theta _0$? Furthermore, the decision to test ${{{\mathcal {H}}}_{0}}: \theta =\theta _0$ rather than ${{{\mathcal {H}}}_{0}}: \theta \in [\theta _0-\epsilon , \theta _0+\epsilon ]$, for a suitable positive $\epsilon$, should be driven by the specific requirements of the application and not solely by the existence of a good or simple test. In summary, we concur with Fisher (1973) that “no scientific worker has a fixed level of significance at which from year to year, and in all circumstances, he rejects hypotheses; he rather gives his mind to each particular case in the light of his evidence and his ideas”.

Considering all these crucial aspects, we believe it is essential to seek an applied hypothesis testing approach that encourages researchers to engage more deeply with the specific problem, avoids relying on standardized procedures, and is consistently integrated into a broader framework of inference. One potential solution can be found resorting to the “confidence distribution” (CD) approach. The modern CD theory was introduced by Schweder and Hjort (2002) and Singh et al. (2005) and relies on the idea of constructing a data-depending distribution for the parameter of interest to be used for inferential purposes. A CD should not be confused with a Bayesian posterior distribution. It is not derived through the Bayes theorem, and it does not require any prior distributions. Similar to the conventional practice in point or interval estimation, where one seeks a point or interval estimator, the objective of this theory is to discover a distribution estimator. Thanks to a clarification of this concept and a formalized definition of the CD within a purely frequentist setting, a wide literature on the topic has been developed encompassing both theoretical developments and practical applications, see e.g. for a general overview Schweder and Hjort (2016), Singh et al. (2007), and Xie and Singh (2013). We also remark that when inference is required for a real parameter, it is possible to establish a relationship between CDs and fiducial distributions, originally introduced by Fisher (1930). For a modern and general presentation of the fiducial inference see Hannig (2009) and Hannig et al. (2016), while for a connection with the CDs see Schweder and Hjort (2016) and Veronese and Melilli (2015, 2018a). Some results about the connection between CDs and hypothesis testing are presented in Singh et al. (2007, Sec. 3.3) and Xie & Singh (2013, Sec. 4.3), but the focus is only on the formal relationships between the support that a CD can provide for a hypothesis and the p-value.

In this paper we discuss in details the application of CDs in hypothesis testing. We show how CDs can offer valuable solutions to address the aforementioned difficulties and how a test can naturally be viewed as a part of a more extensive inferential process. Once a CD has been specified, everything can be developed straightforwardly, without any particular technical difficulties. The core of our approach centers on the notion of support provided by the data to a hypothesis through a CD. We introduce two distinct but related types of support, the choice of which depends on the hypothesis under consideration. They are always coherent, easy to interpret and to compute, even in case of interval hypotheses, contrary to what happens for the p-value. The flexibility, simplicity, and effectiveness of our proposal are illustrated by several examples from various fields and a simulation study. We have postponed the presentation of theoretical results, comparisons with other proposals found in the literature, as well as the connections with standard hypothesis testing concepts such as size, significance level, optimality, and p-values to the end of the paper to enhance its readability.

The paper is structured as follows: In Sect. 2, we provide a review of the CD’s definition and the primary methods for its construction, with a particular focus on distinctive aspects that arise when dealing with discrete models (Sect. 2.1). Section 3 explores the application of the CD in hypothesis testing and introduces the two notions of support. In Sect. 4, we discuss several examples to illustrate the benefits of utilizing the CD in various scenarios, offering comparisons with traditional p-values. Theoretical results about tests based on the CD and comparisons with other measures of support or plausibility for hypotheses are presented in Sect. 5. Finally, in Sect. 6, we summarize the paper’s findings and provide concluding remarks. For convenience, a table of CDs for some common statistical models can be found in Appendix A, while all the proofs of the propositions are presented in Appendix B.

2 Confidence distributions

The modern definition of confidence distribution for a real parameter $\theta$ of interest, see Schweder & Hjort (2002; 2016, sec. 3.2) and Singh et al. (2005; 2007) can be formulated as follows:

Definition 1

Let $\{P_{\theta ,\varvec{\lambda }},\theta \in \Theta \subseteq \mathbb {R}, \varvec{\lambda }\in \varvec{\Lambda }\}$ be a parametric model for data $\textbf{X}\in {\mathcal {X}}$; here $\theta$ is the parameter of interest and $\varvec{\lambda }$ is a nuisance parameter. A function H of $\textbf{X}$ and $\theta$ is called a confidence distribution for $\theta$ if: i) for each value $\textbf{x}$ of $\textbf{X}$, $H(\textbf{x},\cdot )=H_{\textbf{x}}(\cdot )$ is a continuous distribution function on $\Theta$; ii) $H(\textbf{X},\theta )$, seen as a function of the random element $\textbf{X}$, has the uniform distribution on (0, 1), whatever the true parameter value $(\theta , \varvec{\lambda })$. The function H is an asymptotic confidence distribution if the continuity requirement in i) is removed and ii) is replaced by: ii)$^{\prime }$ $H(\textbf{X},\theta )$ converges in law to the uniform distribution on (0, 1) for the sample size going to infinity, whatever the true parameter value $(\theta , \varvec{\lambda })$.

The CD theory is placed in a purely frequentist context and the uniformity of the distribution ensures the correct coverage of the confidence intervals. The CD should be regarded as a distribution estimator of a parameter $\theta$ and its mean, median or mode can serve as point estimates of $\theta$, see Xie and Singh (2013) for a detailed discussion. In essence, the CD can be employed in a manner similar to a Bayesian posterior distribution, but its interpretation differs and does not necessitate any prior distribution. Closely related to the CD is the confidence curve (CC) which, given an observation $\textbf{x}$, is defined as $CC_{\textbf{x}}(\theta )=|1-2H_{\textbf{x}}(\theta )|$; see Schweder and Hjort (2002). This function provides the boundary points of equal-tailed confidence intervals for any level $1-\alpha$, with $0<\alpha <1$, and offers an immediate visualization of their length.

Various procedures can be adopted to obtain exact or asymptotic CDs starting, for example, from pivotal functions, likelihood functions and bootstrap distributions, as detailed in Singh et al. (2007), Xie and Singh (2013), Schweder and Hjort (2016). A CD (or an asymptotic CD) can also be derived directly from a real statistic T, provided that its exact or asymptotic distribution function $F_{\theta }(t)$ is a continuously monotonic function in $\theta$ and its limits are 0 and 1 as $\theta$ approaches its boundaries. For example, if $F_{\theta }(t)$ is nonincreasing, we can define

$$\begin{aligned} H_t(\theta )=1-F_\theta (t). \end{aligned}$$

(1)

Furthermore, if $H_t(\theta )$ is differentiable in $\theta$, we can obtain the CD-density $h_t(\theta )=-({\partial }/{\partial \theta }) F_{\theta }(t)$, which coincides with the fiducial density suggested by Fisher. In particular, when the statistical model belongs to the real regular natural exponential family (NEF) with natural parameter $\theta$ and sufficient statistic T, there always exists an “optimal” CD for $\theta$ which is given by (1), see Veronese and Melilli (2015).

The CDs based on a real statistic play an important role in hypothesis testing. In this setting remarkable results are obtained when the model has monotone likelihood ratio (MLR). We recall that if $\textbf{X}$ is a random vector distributed according to the family $\{p_\theta , \theta \in \Theta \subseteq \mathbb {R}\}$, this family is said to have MLR in the real statistic $T(\textbf{X})$ if, for any $\theta _1 <\theta _2$, the ratio $p_{\theta _2}(\textbf{x})/p_{\theta _1}(\textbf{x})$ is a nondecreasing function of $T(\textbf{x})$ for values of $\textbf{x}$ that induce at least one of $p_{\theta _1}$ and $p_{\theta _2}$ to be positive. Furthermore, for such families, it holds that $F_{\theta _2}(t) \le F_{\theta _1}(t)$ for each t, see Shao (2003, Sec. 6.1.2). Families with MLR not only allow the construction of Uniformly Most Powerful (UMP) tests in various scenarios but also identify the statistic T, which can be employed in constructing the CD for $\theta$. Indeed, because $F_\theta (t)$ is nonincreasing in $\theta$ for each t, $H_t(\theta )$ can be defined as in (1) provided the conditions of continuity and limits of $F_{\theta }(t)$ are met. Of course, if the MLR is nonincreasing in T a similar result holds and the CD for $\theta$ is $H_t(\theta )=F_\theta (t)$.

An interesting characteristic of the CD that validates its suitability for use in a testing problem is its consistency, meaning that it increasingly concentrates around the “true” value of $\theta$ as the sample size grows, leading to the correct decision.

Definition 2

The sequence of CDs $H(\textbf{X}_n, \cdot )$ is consistent at some $\theta _0 \in \Theta$ if, for every neighborhood U of $\theta _0$, $\int _U dH(\textbf{X}_n, \theta ) \rightarrow 1$, as $n\rightarrow \infty$, in probability under $\theta _0$.

The following proposition provides some useful asymptotic properties of a CD for independent identically distributed (i.i.d.) random variables.

Proposition 1

Let $X_1,X_2,\ldots$ be a sequence of i.i.d. random variables from a distribution function $F_{\theta }$, parameterized by a real parameter $\theta$, and let $H_{\textbf{x}_n}$ be the CD for $\theta$ based on $\textbf{x}_n=(x_1, \ldots , x_n)$. If $\theta _0$ denotes the true value of $\theta$, then $H(\textbf{X}_n, \cdot )$ is consistent at $\theta _0$ if one of the following conditions holds:

• i) $F_{\theta }$ belongs to a NEF;

• ii) $F_{\theta }$ is a continuous distribution function and standard regularity assumptions hold;

• iii) its expected value and variance converge for $n\rightarrow \infty$ to $\theta _0$, and 0, respectively, in probability under $\theta _0$.

Finally, if i) or ii) holds the CD is asymptotically normal.

Table 8 in Appendix A provides a list of CDs for various standard models. Here, we present two basic examples, while numerous others will be covered in Sect. 4 within an inferential and testing framework.

Example 1

(Normal model) Let $\textbf{X}=(X_1,\ldots ,X_n)$ be an i.i.d. sample from a normal distribution N$(\mu ,\sigma ^2)$, with $\sigma ^2$ known. A standard pivotal function is $Q({\bar{X}}, \mu )=\sqrt{n}({\bar{X}}-\mu )/ \sigma$, where $\bar{X}=\sum X_i/n$. Since $Q({\bar{X}}, \mu )$ is decreasing in $\mu$ and has the standard normal distribution $\Phi$, the CD for $\mu$ is $H_{\bar{x}}(\mu )=1-\Phi (\sqrt{n}({\bar{x}}-\mu )/ \sigma )=\Phi (\sqrt{n}(\mu -{\bar{x}})/ \sigma )$, that is a N$({\bar{x}},\sigma /\sqrt{n})$. When the variance is unknown we can use the pivotal function $Q({\bar{X}}, \mu )=\sqrt{n}({\bar{X}}-\mu )/S$, where $S^2=\sum (X_i-\bar{X})^2/(n-1)$, and the CD for $\mu$ is $H_{{\bar{x}},s}(\mu )=1-F^{T_{n-1}}(\sqrt{n}({\bar{x}}-\mu )/ \sigma )=F^{T_{n-1}}(\sqrt{n}(\mu -{\bar{x}})/ \sigma )$, where $F^{T_{n-1}}$ is the t-distribution function with $n-1$ degrees of freedom.

Example 2

(Uniform model) Let $\textbf{X}=(X_1,\ldots ,X_n)$ be an i.i.d. sample from the uniform distribution on $(0,\theta )$, $\theta >0$. Consider the (sufficient) statistic $T=\max (X_1, \ldots ,X_n)$ whose distribution function is $F_\theta (t)=(t/\theta )^n$, for $0<t<\theta$. Because $F_\theta (t)$ is decreasing in $\theta$ and the limit conditions are satisfied for $\theta >t$, the CD for $\theta$ is $H_t(\theta )=1-(t/\theta )^n$, i.e. a Pareto distribution $\text {Pa}(n, t)$ with parameters n (shape) and t (scale). Since the uniform distribution is not regular, the consistency of the CD follows from condition iii) of Proposition 1. This is because $E^{H_{t}}(\theta )=nt/(n-1)$ and $Var^{H_{t}}(\theta )=nt^2/((n-2)(n-1)^2)$, so that, for $n\rightarrow \infty$, $E^{H_{t}}(\theta ) \rightarrow \theta _0$ (from the strong consistency of the estimator T of $\theta$, see e.g. Shao 2003, p.134) and $Var^{H_{t}}(\theta )\rightarrow 0$ trivially.

2.1 Peculiarities of confidence distributions for discrete models

When the model is discrete, clearly we can only derive asymptotic CDs. However, a crucial question arises regarding uniqueness. Since $F_{\theta }(t)=\text{ Pr}_\theta \{T \le t\}$ does not coincide with Pr$_\theta \{T<t\}$ for any value t within the support ${\mathcal {T}}$ of T, it is possible to define two distinct “extreme” CDs. If $F_\theta (t)$ is non increasing in $\theta$, we refer to the right CD as $H_{t}^r(\theta )=1-\text{ Pr}_\theta \{T\le t\}$ and to the left CD as $H_{t}^\ell (\theta )=1-\text{ Pr}_\theta \{T<t\}$. Note that $H_{t}^r(\theta ) < H_{t}^\ell (\theta )$, for every $t \in {{\mathcal {T}}}$ and $\theta \in \Theta$, so that the center (i.e. the mean or the median) of $H_{t}^r(\theta )$ is greater than that of $H_{t}^\ell (\theta )$. If $F_\theta (t)$ is increasing in $\theta$, we define $H_{t}^\ell (\theta )=F_\theta (t)$ and $H^r_t(\theta )=\text{ Pr}_\theta \{T<t\}$ and one again $H_{t}^r(\theta ) < H_{t}^\ell (\theta )$. Veronese & Melilli (2018b, sec. 3.2) suggest overcoming this nonuniqueness by averaging the CD-densities $h_t^r$ and $h_t^\ell$ using the geometric mean $h_t^g(\theta )\propto \sqrt{h_t^r(\theta )h_t^\ell (\theta )}$. This typically results in a simpler CD compared to the one obtained through the arithmetic mean, with smaller confidence intervals. Note that the (asymptotic) CD defined in (1) for discrete models corresponds to the right CD, and it is more appropriately referred to as $H_t^r(\theta )$ hereafter. Clearly, $H_{t}^\ell (\theta )$ can be obtained from $H_{t}^r(\theta )$ by replacing t with its preceding value in the support ${\mathcal {T}}$. For discrete models, the table in Appendix A reports $H_{t}^r(\theta )$, $H_{t}^\ell (\theta )$ and $H_t^g(\theta )$. Compared to $H^{\ell }_t$ and $H^r_t$, $H^g_t$ offers the advantage of closely approximating a uniform distribution when viewed as a function of the random variable T.

Proposition 2

Given a discrete statistic T with distribution indexed by a real parameter $\theta \in \Theta$ and support ${{\mathcal {T}}}$ independent of $\theta$, assume that, for each $\theta \in \Theta$ and $t\in {\mathcal {T}}$, $H^r_t(\theta )< H^g_t(\theta ) < H^{\ell }_t(\theta )$. Then, denoting by $G^j$ the distribution function of $H^j_T$, with $j=\ell ,g,r$, we have $G^\ell (u) \le u \le G^r(u)$. Furthermore,

$$\begin{aligned} \int ^1_0 |G^g(u)-u |\, du < \int ^1_0 |G^{\ell }(u)-u | \, du =\int ^1_0 |G^r(u)-u|\, du. \end{aligned}$$

(2)

Notice that the assumption in Proposition 2 is always satisfied when the model belongs to a NEF, see Veronese and Melilli (2018a).

The possibility of constructing different CDs using the same discrete statistic T plays an important role in connection with standard p-values, as we will see in Sect. 5.

Example 3

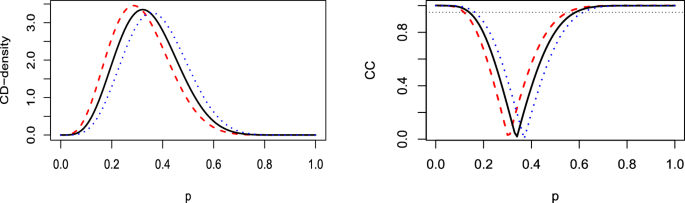
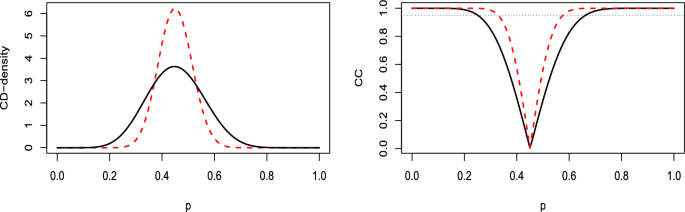
(Binomial model) Let $\textbf{X}=(X_1,\ldots , X_n)$ be an i.i.d. sample from a binomial distributions Bi(1, p) with success probability p. Then $T=\sum _{i=1}^n X_i$ is distributed as a Bi(n, p) and by (1), recalling the well-known relationship between the binomial and beta distributions, it follows that the right CD for p is a Be($t+1,n-t$) for $t=0,1,\ldots , n-1$. Furthermore, the left CD is a Be($t,n-t+1$) and it easily follows that $H_t^g(p)$ is a Be($t+1/2,n-t+1/2$). Figure 1 shows the corresponding three CD-densities along with their respective CCs, emphasizing the central position of $h_t^g(p)$ and its confidence intervals in comparison to $h_t^\ell (p)$ and $h^r_t(p)$.

Fig. 1

(Binomial model) CD-densities (left plot) and CCs (right plot) corresponding to $H_t^g(p)$ (solid lines), $H_t^{\ell }(p)$ (dashed lines) and $H_t^r(p)$ (dotted lines) for the parameter p with n = 15 and $t=5$. In the CC plot, the horizontal dotted line is at level 0.95

3 Confidence distributions in testing problems

As mentioned in Sect. 1, we believe that introducing a CD can serve as a valuable and unifying approach, compelling individuals to think more deeply about the specific problem they aim to address rather than resorting to automatic rules. In fact, the availability of a whole distribution for the parameter of interest equips statisticians and practitioners with a versatile tool for handling a wide range of inference tasks, such as point and interval estimation, hypothesis testing, and more, without the need for ad hoc procedures. Here, we will address the issue in the simplest manner, referring to Sect. 5 for connections with related ideas in the literature and additional technical details.

Given a set $A \subseteq \Theta \subseteq \mathbb {R}$, it seems natural to measure the “support” that the data $\textbf{x}$ provide to A through the CD $H_{\textbf{x}}$, as $CD(A)=H_{\textbf{x}}(A)= \int _{A} dH_{\textbf{x}}(\theta )$. Notice that, with a slight abuse of notation widely used in literature (see e.g., Singh et al. 2007, who call $H_{\textbf{x}}(A)$ strong-support), we use $H_{\textbf{x}}(\theta )$ to indicate the distribution function on $\Theta \subseteq \mathbb {R}$ evaluated at $\theta$ and $H_{\textbf{x}}(A)$ to denote the mass that $H_{\textbf{x}}$ induces on a (measurable) subset $A\subseteq \Theta$. It immediately follows that to compare the plausibility of k different hypotheses ${{\mathcal {H}}}_{i}: \theta \in \Theta _i$, $i=1,\ldots ,k$, with $\Theta _i \subseteq \Theta$ not being a singleton, it is enough to compute each $H_{\textbf{x}}(\Theta _i)$. We will call $H_{\textbf{x}}(\Theta _i)$ the CD-support provided by $H_{\textbf{x}}$ to the set $\Theta _i$. In particular, consider the usual case in which we have two hypotheses ${{{\mathcal {H}}}_{0}}: \theta \in \Theta _0$ and ${{{\mathcal {H}}}_{1}}: \theta \in \Theta _1$, with $\Theta _0 \cap \Theta _1= \emptyset$, $\Theta _0 \cup \Theta _1 = \Theta$ and assume that ${{{\mathcal {H}}}_{0}}$ is not a precise hypothesis (i.e. is not of type $\theta =\theta _0$). As in the Bayesian approach one can compute the posterior odds, here we can evaluate the confidence odds $CO_{0,1}$ of ${{{\mathcal {H}}}_{0}}$ against ${{{\mathcal {H}}}_{1}}$

$$\begin{aligned} CO_{0,1}=\frac{H_{\textbf{x}}(\Theta _0)}{H_{\textbf{x}}(\Theta _1)}=\frac{H_{\textbf{x}}(\Theta _0)}{1-H_{\textbf{x}}(\Theta _0)}. \end{aligned}$$

If $CO_{0,1}$ is greater than one, the data support ${{{\mathcal {H}}}_{0}}$ more than ${{{\mathcal {H}}}_{1}}$ and this support clearly increases with $CO_{0,1}$. Sometimes this type of information can be sufficient to have an idea of the reasonableness of the hypotheses, but if we need to take a decision, we can include the confidence odds in a full decision setting. Thus, writing the decision space as ${{\mathcal {D}}}=\{0,1\}$, where i indicates accepting ${{{\mathcal {H}}}}_i$, for $i=0,1$, a penalization for the two possible errors must be specified. A simple loss function is

$$\begin{aligned} \ell (\theta ,\delta ) = \left\{ \begin{array}{cl} a_0 &{} \text {if } \theta \in \Theta _0 \text { and } \delta =1 \\ a_1 &{} \text {if } \theta \in \Theta _1 \text { and } \delta =0\\ 0 &{} \text {otherwise, } \end{array}\right. \end{aligned}$$

(3)

where $\delta$ denotes the decision taken and $a_i >0$, $i=0,1$. The optimal decision is the one that minimizes the (expected) confidence loss

$$\begin{aligned} L(\delta ,H_x)=\int _{\Theta }\ell (\theta ^{\prime },\delta )d H_x(\theta ^{\prime })=a_0 H_x(\Theta _0)I_{\{1\}}(\delta ) + a_1 H_x(\Theta _1)I_{\{0\}}(\delta ). \end{aligned}$$

Therefore, we will choose ${{{\mathcal {H}}}_{0}}$ if $a_0 H_{\textbf{x}}(\Theta _0) > a_1 H_{\textbf{x}}(\Theta _1)$, that is if $CO_{0,1}>a_1/a_0$ or equivalently if $H_{\textbf{x}}(\Theta _0)>a_1/(a_0+a_1)=\gamma$. Clearly, if there is no reason to penalize differently the two errors by setting an appropriate value for the ratio $a_1/a_0$, we assume $a_0=a_1$ so that $\gamma =0.5$. This implies that the chosen hypothesis will be the one receiving the highest level of the CD-support. Therefore, we state the following

Definition 3

Given the two (non precise) hypotheses ${{\mathcal {H}}}_i: \theta \in \Theta _i$, $i=0,1$, the CD-support of ${{\mathcal {H}}}_i$ is defined as $H_{\textbf{x}}(\Theta _i)$. The hypothesis ${{{\mathcal {H}}}_{0}}$ is rejected according to the CD-test if the CD-support is less than a fixed threshold $\gamma$ depending on the loss function (3) or, equivalently, if the confidence odds $CO_{0,1}$ are less than $a_1/a_0=\gamma /(1-\gamma )$.

Unfortunately, the previous notion of CD-support fails for a precise hypothesis ${{{\mathcal {H}}}_{0}}:\theta =\theta _0$, since in this case $H_{\textbf{x}}(\{\theta _0\})$ trivially equals zero. Notice that the problem cannot be solved by transforming ${{{\mathcal {H}}}_{0}}:\theta =\theta _0$ into the seemingly more reasonable ${{{\mathcal {H}}}_{0}}^{\prime }:\theta \in [\theta _0-\epsilon , \theta _0+\epsilon ]$ because, apart from the arbitrariness of $\epsilon$, the CD-support for very narrow range intervals would typically remain negligible. We thus introduce an alternative way to assess the plausibility of a precise hypothesis or, more generally, of a “small” interval hypothesis.

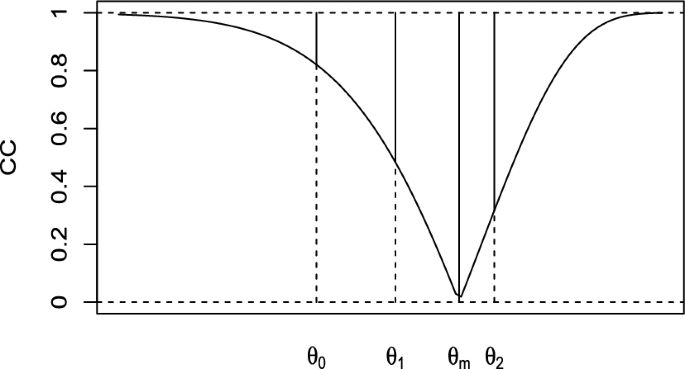
Consider first ${{{\mathcal {H}}}_{0}}:\theta =\theta _0$ and assume, as usual, that $H_{\textbf{x}}(\theta )$ is a CD for $\theta$, based on the data $\textbf{x}$. Looking at the confidence curve $CC_{\textbf{x}}(\theta )=|1-2H_{\textbf{x}}(\theta )|$ in Fig. 2, it is reasonable to assume that the closer $\theta _0$ is to the median $\theta _m$ of the CD, the greater the consistency of the value of $\theta _0$ with respect to $\textbf{x}$. Conversely, the complement to 1 of the CC represents the unconsidered confidence relating to both tails of the distribution. We can thus define a measure of plausibility for ${{{\mathcal {H}}}_{0}}:\theta =\theta _0$ as $(1-CC_{\textbf{x}}(\theta ))/2$ and this measure will be referred to as the CD*-support given by $\textbf{x}$ to the hypothesis. It is immediate to see that

$$\begin{aligned} \text{ CD* }(\{\theta _0\})= & {} \frac{1}{2}(1- CC_{\textbf{x}}(\theta _0))\nonumber \\= & {} \left\{ \begin{array}{ll} \frac{1}{2}(1-(1-2H_{\textbf{x}}(\theta _0)))=H_{\textbf{x}}(\theta _0) &{} \hspace{5mm} \text{ if } H_{\textbf{x}}(\theta _0)\le \frac{1}{2} \\ \frac{1}{2}(1-(2H_{\textbf{x}}(\theta _0)-1))=1-H_{\textbf{x}}(\theta _0) &{} \hspace{5mm} \text{ if } H_{\textbf{x}}(\theta _0) > \frac{1}{2} \end{array} \right. \nonumber \\= & {} \min \{H_{\textbf{x}}(\theta _0), 1-H_{\textbf{x}}(\theta _0)\}. \end{aligned}$$

(4)

In other words, if $\theta _0 < \theta _m$ $[\theta _0 > \theta _m]$ the CD*-support is $H_{\textbf{x}}(\theta _0)$ $[1-H_{\textbf{x}}(\theta _0)]$ and corresponds to the CD-support of all $\theta$’s that are less plausible than $\theta _0$ among those located on the left [right] side of the CC. Clearly, if $\theta _0 = \theta _m$ the CD*-support equals 1/2, its maximum value. Notice that in this case no alternative hypothesis is considered and that the CD*-support provides a measure of plausibility for $\theta _0$ by examining “the direction of the observed departure from the null hypothesis”. This quotation is derived from Gibbons and Pratt (1975) and was originally stated to support their preference for reporting a one-tailed p-value over a two-tailed one. Here we are in a similar context and we refer to their paper for a detailed discussion of this recommendation.

Fig. 2

The CD*-supports of the points $\theta _0$, $\theta _1$, $\theta _m$ and $\theta _2$ correspond to half of the solid vertical lines and are given by $H_{\textbf{x}}(\theta _0)$, $H_{\textbf{x}}(\theta _1)$, $H_{\textbf{x}}(\theta _m)=1/2$ e $1-H_{\textbf{x}}(\theta _2)$, respectively

An alternative way to intuitively justify formula (4) is as follows. Since $H_{\textbf{x}}(\{\theta _0\})=0$, we can look at the set K of values of $\theta$ which are in some sense “more consistent” with the observed data $\textbf{x}$ than $\theta _0$, and define the plausibility of ${{{\mathcal {H}}}_{0}}$ as $1-H_{\textbf{x}}(K)$. This procedure was followed in a Bayesian framework by Pereira et al. (1999) and Pereira et al. (2008) who, in order to identify K, relay on the posterior distribution of $\theta$ and focus on its mode. We refer to these papers for a more detailed discussion of this idea. Here we emphasize only that the evidence $1-H_{\textbf{x}}(K)$ supporting ${{{\mathcal {H}}}_{0}}$ cannot be considered as evidence against a possible alternative hypothesis. In our context, the set K can be identified as the set $\{\theta \in \Theta : \theta < \theta _0\}$ if $H_{\textbf{x}}(\theta _0)>1-H_{\textbf{x}}(\theta _0)$ or as $\{\theta \in \Theta : \theta >\theta _0\}$ if $H_{\textbf{x}}(\theta _0)\le 1-H_{\textbf{x}}(\theta _0)$. It follows immediately that $1-H_{\textbf{x}}(K)=\min \{H_{\textbf{x}}(\theta _0), 1-H_{\textbf{x}}(\theta _0)\}$, which coincides with the CD*-support given in (4).

We can readily extend the previous definition of CD*-support to interval hypotheses ${{{\mathcal {H}}}_{0}}:\theta \in [\theta _1, \theta _2]$. This extension becomes particularly pertinent when dealing with small intervals, where the CD-support may prove ineffective. In such cases, the set K of $\theta$ values that are “more consistent” with the data $\textbf{x}$ than those falling within the interval $[\theta _1, \theta _2]$ should clearly exclude this interval. Instead, it should include one of the two tails, namely, either ${\theta \in \Theta : \theta < \theta _1}$ or ${\theta \in \Theta : \theta > \theta _2}$, depending on which one receives a greater mass from the CD. Then

$$\begin{aligned} K = \left\{ \begin{array}{cl} \{\theta \in \Theta : \theta < \theta _1\} &{} \text {if } H_{\textbf{x}}(\theta _1)>1-H_{\textbf{x}}(\theta _2)\\ \{\theta \in \Theta : \theta >\theta _2\} &{} \text {if } H_{\textbf{x}}(\theta _1)\le 1-H_{\textbf{x}}(\theta _2) \end{array}\right. \end{aligned}$$

so that the CD*-support of the interval $[\theta _1,\theta _2]$ is $\text{ CD* }([\theta _1,\theta _2])=1-H_{\textbf{x}}(K)=\min \{H_{\textbf{x}}(\theta _2), 1-H_{\textbf{x}}(\theta _1)\}$, which reduces to (4) in the case of a degenerate interval (i.e., when $\theta _1=\theta _2=\theta _0$). Therefore, we can establish the following

Definition 4

Given the hypothesis ${{{\mathcal {H}}}_{0}}: \theta \in [\theta _1,\theta _2]$, with $\theta _1 \le \theta _2$, the CD*-support of ${{{\mathcal {H}}}_{0}}$ is defined as $\min \{H_{\textbf{x}}(\theta _2), 1-H_{\textbf{x}}(\theta _1)\}$. If $H_{\textbf{x}}(\theta _2) <1-H_{\textbf{x}}(\theta _1)$ it is more reasonable to consider values of $\theta$ greater than those specified by ${{{\mathcal {H}}}_{0}}$, and conversely, the opposite holds true in the reverse situation. Furthermore, the hypothesis ${{{\mathcal {H}}}_{0}}$ is rejected according to the CD*-test if its CD*-support is less than a fixed threshold $\gamma ^*$.

The definition of CD*-support has been established for bounded interval (or precise) hypothesis. However, it can be readily extended to one-sided intervals such as $(-\infty , \theta _0]$ or $[\theta _0, +\infty )$, but in these cases, it is evident that the CD*- and the CD-support are equivalent. For a general interval hypothesis we observe that $H_{\textbf{x}}([\theta _1, \theta _2])\le \min \{H_{\textbf{x}}(\theta _2), 1-H_{\textbf{x}}(\theta _1)\}$. Consequently, the CD-support can never exceed the CD*-support, even though they exhibit significant similarity when $\theta _1$ or $\theta _2$ resides in the extreme region of one tail of the CD or when the CD is highly concentrated (see examples 4, 6 and 7).

Remark 1

It is crucial to emphasize that both CD-support and CD*-support are coherent measures of the evidence provided by the data for a hypothesis. This coherence arises from the fact that if ${{{\mathcal {H}}}_{0}}\subset {{{\mathcal {H}}}_{0}}^{\prime }$, both the supports for ${{{\mathcal {H}}}_{0}}^{\prime }$ cannot be less than those for ${{{\mathcal {H}}}_{0}}$. This is in stark contrast to the behavior of p-values, as demonstrated in Schervish (1996), Peskun (2020), and illustrated in Examples 4 and 7.

Finally, as seen in Sect. 2.1, various options for CDs are available for discrete models. Unless a specific problem suggests otherwise (see Sect. 5.1), we recommend using the geometric mean $H_t^g$ as it offers a more impartial treatment of ${{{\mathcal {H}}}_{0}}$ and e ${{{\mathcal {H}}}_{1}}$, as shown in Proposition 2.

4 Examples

In this section, we illustrate the behavior, effectiveness, and simplicity of CD- and CD*-supports in an inferential context through several examples. We examine various contexts to assess the flexibility and consistency of our approach and compare it with the standard one. It is worth noting that the computation of the p-value for interval hypotheses is challenging and does not have a closed form.

Example 4

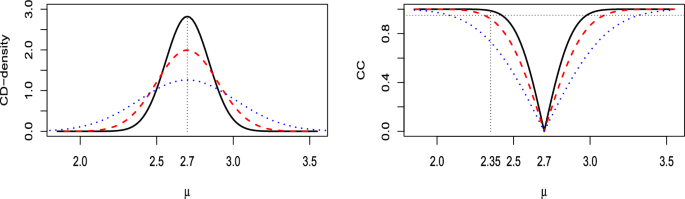
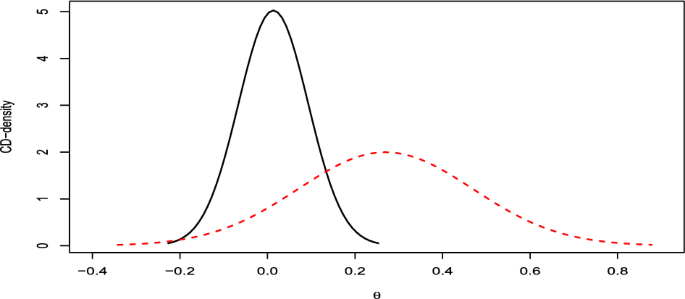
(Normal model) As seen in Example 1, the CD for the mean $\mu$ of a normal model is N$({\bar{x}},\sigma /\sqrt{n})$, for $\sigma$ known. For simplicity, we assume this case; otherwise, the CD would be a t-distribution. Figure 3 shows the CD-density and the corresponding CC for ${\bar{x}}=2.7$ with three different values of $\sigma /\sqrt{n}$: $1/\sqrt{50}=0.141$, $1/\sqrt{25}=0.2$ and $1/\sqrt{10}=0.316$.

The observed ${\bar{x}}$ specifies the center of both the CD and the CC, and values of $\mu$ that are far from it receive less support the smaller the dispersion $\sigma /\sqrt{n}$ of the CD. Alternatively, values of $\mu$ within the CC, i.e., within the confidence interval of a specific level, are more reasonable than values outside it. These values become more plausible as the level of the interval decreases. Table 1 clarifies these points by providing the CD-support, confidence odds, CD*-support, and the p-value of the UMPU test for different interval hypotheses and different values of $\sigma /\sqrt{n}$.

Fig. 3

(Normal model) CD-densities (left plot) and CCs (right plot) for $\mu$ with ${\bar{x}}=2.7$ and three values of $\sigma /\sqrt{n}$: $1/\sqrt{50}$ (solid line), $1/\sqrt{25}$ (dashed line) and $1/\sqrt{10}$ (dotted line). In the CC plot the dotted horizontal line is at level 0.95

It can be observed that when the interval is sufficiently large, e.g., [2.0, 2.5], the CD- and the CD*-supports are similar. However, for smaller intervals, as in the other three cases, the difference between the CD- and the CD*-support increases with the variance of the CD, $\sigma /\sqrt{n}$, regardless of whether the interval contains the observation ${\bar{x}}$ or not. These aspects are general depending on the form of the CD. Therefore, a comparison between these two measures can be useful to clarify whether an interval is smaller or not, according to the problem under analysis. Regarding the p-value of the UMPU test (see Schervish 1996, equation 2), it is similar to the CD*-support when the interval is large (first case). However, the difference increases with the growth of the variance in the other cases. Furthermore, enlarging the interval from [2.4, 2.6] to [2.3, 2.6], not reported in Table 1, while the CD*-supports remain unchanged, results in p-values reducing to 0.241, 0.331, and 0.479 for the three considered variances. This once again highlights the incoherence of the p-value as a measure of the plausibility of a hypothesis.

Now, consider a precise hypothesis, for instance, ${{{\mathcal {H}}}_{0}}:\mu =2.35$. For the three values used for $\sigma /\sqrt{n}$, the CD*-supports are 0.007, 0.040, and 0.134, respectively. From Fig. 3, it is evident that the point $\mu =2.35$ lies to the left of the median of the CD. Consequently, the data suggest values of $\mu$ larger than 2.35. Furthermore, looking at the CC, it becomes apparent that 2.35 is not encompassed within the confidence interval of level 0.95 when $\sigma /\sqrt{n}=1/\sqrt{50}$, contrary to what occurs in the other two cases. Due to the symmetry of the normal model, the UMPU test coincides with the equal tailed test, so that the p-value is equal to 2 times the CD*-support (see Remark 4 in Sect. 5.2). Furthermore, the size of the CD*-test is $2\gamma ^*$, where $\gamma ^*$ is the threshold fixed to decide whether to reject the hypothesis or not (see Proposition 5. Thus, if a test of level 0.05 is desired, it is sufficient to fix $\gamma ^*=0.025$, and both the CD*-support and the p-value lead to the same decision, namely, rejecting ${{{\mathcal {H}}}_{0}}$ only for the case $\sigma /\sqrt{n}=0.141$.

Table 1 (Normal model) CD-support, confidence odds $CO_{0,1}$, CD*-support and p-value of the UMPU test for different hypotheses, when ${\bar{x}}=2.7$ under different values of $\sigma /\sqrt{n}$

Table 2 (Normal model) Simulation for various values of $\mu$ and $\sigma /\sqrt{n}$, for the hypothesis ${{{\mathcal {H}}}_{0}}:\mu \in [2.0,2.5]$. Proportion of values of the CD*-support in the intervals [0, 0.4), [0.4, 0.6) and [0.6, 1] and proportion of errors of the p-values for a threshold of 0.05. Error proportion are in boldface

To assess the effectiveness of the CD*-support, we conduct a brief simulation study. For different values of $\mu$, we generate 100000 values of ${\bar{x}}$ from a normal distribution with mean $\mu$ and various standard deviation $\sigma /\sqrt{n}$. We obtain the corresponding CDs with the CD*-supports and compute also the p-values. In Table 2, we consider ${{{\mathcal {H}}}_{0}}: \mu \in [2.0, 2.5]$ and the performance of the CD*-support can be evaluated looking for example at the proportions of values in the intervals [0, 0.4), [0.4, 0.6) and [0.6, 1]. Values of the CD*-support in the first interval suggest a low plausibility of ${{{\mathcal {H}}}_{0}}$ in the light of the data, while values in the third one suggest a high plausibility. We highlight the proportions of incorrect evaluations in boldface. The last column of the table reports the proportion of errors resulting from the use of the standard procedure based on the p-value for a threshold of 0.05. Note how the proportion of errors related to the CD*-support is generally quite low with a maximum value of 0.301, contrary to what happens for the automatic procedure based on the p-value, which reaches a proportion of error of 0.845. Notice that the maximum error due to the CD*-support is obtained when ${{{\mathcal {H}}}_{0}}$ is true, while that due to the p-value is obtained in the opposite, as expected.

We consider now the two hypotheses ${{{\mathcal {H}}}_{0}}:\mu =2.35$ and ${{{\mathcal {H}}}_{0}}: \mu \in [2.75,2.85]$. Notice that the interval in the second hypothesis should be regarded as small, because it can be checked that the CD- and CD*-supports consistently differ, as can be seen for example in Table 1 for the case ${\bar{x}}=2.7$. Thus, this hypothesis can be considered not too different from a precise one. Because for a precise hypothesis the CD*-support cannot be larger than 0.5, to evaluate the performance of the CD*-support we can consider the three intervals [0, 0.2), [0.2, 0.3) and [0.3, 0.5].

Table 3 reports the results of the simulation including again the proportion of errors resulting from the use of the p-value with threshold 0.05. For the precise hypothesis ${{{\mathcal {H}}}_{0}}: \mu =2.35$, the proportion of values of the CD*-support less than 0.2 when $\mu =2.35$ is, whatever the standard deviation, approximately equal to 0.4. This depends on the fact that for a precise hypothesis, the CD*-support has a uniform distribution on the interval [0, 0.5], see Proposition 5. This aspect must be taken into careful consideration when setting a threshold for a CD*-test. On the other hand, the proportion of values of the CD*-support in the interval [0.3, 0.5], which wrongly support ${{{\mathcal {H}}}_{0}}$ when it is false, goes from 0.159 to 0.333 for $\mu =2.55$ and from 0.010 to 0.193 for $\mu =2.75$, which are surely better than those obtained from the standard procedure based on the p-value. Take now the hypothesis ${{{\mathcal {H}}}_{0}}: \mu \in [2.75,2.85]$. Since it can be considered not too different from a precise hypothesis, we consider the proportion of values of the CD*-support in the intervals [0, 0.2), [0.2, 0.3) and [0.3, 1]. Notice that, for simplicity, we assume 1 as the upper bound of the third interval, even though for small intervals, the values of the CD*-support can not be much larger than 0.5. In our simulation it does not exceed 0.635. For the different values of $\mu$ considered the behavior of the CD*-support and p-value is not too different from the previous case of a precise hypothesis even if the proportion of errors when ${{{\mathcal {H}}}_{0}}$ is true decreases for both while it increases when ${{{\mathcal {H}}}_{0}}$ is false.

Table 3 (Normal model) Simulation for various values of $\mu$ and $\sigma /\sqrt{n}$, for the hypotheses ${{{\mathcal {H}}}_{0}}:\mu =2.35$ and ${{{\mathcal {H}}}_{0}}:\mu \in [2.75,2.85]$. Proportion of values of the CD*-support in the three specified intervals and proportion of errors of the p-values for a threshold of 0.05. Error proportions are in boldface

Example 5

Binomial model Suppose we are interested in assessing the chances of candidate A winning the next ballot for a certain administrative position. The latest election poll based on a sample of size $n=20$, yielded $t=9$ votes in favor of A. What can we infer? Clearly, we have a binomial model where the parameter p denotes the probability of having a vote in favor of A. The standard estimate of p is $\hat{p}=9/20=0.45$, which might suggest that A will lose the ballot. However, the usual (Wald) confidence interval of level 0.95 based on the normal approximation, i.e. $\hat{p} \pm 1.96 \sqrt{\hat{p}(1-\hat{p})/n}$, is (0.232, 0.668). Given its considerable width, this interval suggests that the previous estimate is unreliable. We could perform a statistical test with a significance level $\alpha$, but what is ${{{\mathcal {H}}}_{0}}$, and what value of $\alpha$ should we consider? If ${{{\mathcal {H}}}_{0}}: p \ge 0.5$, implying ${{{\mathcal {H}}}_{1}}: p <0.5$, the p-value is 0.327. This suggests not rejecting ${{{\mathcal {H}}}_{0}}$ for any usual value $\alpha$. However, if we choose ${{{\mathcal {H}}}_{0}}^\prime : p \le 0.5$ the p-value is 0.673, and in this case, we would not reject ${{{\mathcal {H}}}_{0}}^\prime$. These results provide conflicting indications. As seen in Example 3, the CD for p, $H_t^g(p)$, is Be(9.5,11.5) and Fig. 4 shows its CD-density along with the corresponding CC, represented by solid lines. The dotted horizontal line at 0.95 in the CC plot highlights the (non asymptotic) equal-tailed confidence interval (0.251, 0.662), which is shorter than the Wald interval. Note that our interval can be easily obtained by computing the quantiles of order 0.025 and 0.975 of the beta distribution.

Fig. 4

(Binomial model) CD-densities (left plot) and CCs (right plot) corresponding to $H_t^g(p)$, for the parameter p, with $\hat{p}=t/n=0.45$: $n=20$, $t=9$ (solid lines) and $n=60$, $t=27$ (dashed lines). In the CC plot the horizontal dotted line is at level 0.95

The CD-support provided by the data for the two hypotheses ${{{\mathcal {H}}}_{0}}:p \ge 0.5$ and ${{{\mathcal {H}}}_{1}}:p < 0.5$ (the choice of what is called $H_0$ being irrelevant), is $1-H_t^g(0.5)=0.328$ and $H_t^g(0.5)=0.672$ respectively. Therefore, the confidence odds are $CO_{0,1}=0.328/0.672=0.488$, suggesting that the empirical evidence in favor of the victory of A is half of that of its defeat. Now, consider a sample of size $n=60$ with $t=27$, so that again $\hat{p}=0.45$. While a standard analysis leads to the same conclusions (the p-values for ${{{\mathcal {H}}}_{0}}$ and ${{{\mathcal {H}}}_{0}}^{\prime }$ are 0.219 and 0.781, respectively), the use of the CD clarifies the differences between the two cases. The corresponding CD-density and CC are also reported in Fig. 4 (dashed lines) and, as expected, they are more concentrated around $\hat{p}$. Thus, the accuracy of the estimates of p is greater for the larger n and the length of the confidence intervals is smaller. Furthermore, for $n=60$, $CO_{0,1}=0.281$ reducing the chance that A wins to about 1 to 4.

As a second application on the binomial model, we follow Johnson and Rossell (2010) and consider a stylized phase II trial of a new drug designed to improve the overall response rate from 20% to 40% for a specific population of patients with a common disease. The hypotheses are ${{{\mathcal {H}}}_{0}}:p \le 0.2$ versus ${{{\mathcal {H}}}_{1}}: p>0.2$. It is assumed that patients are accrued and the trial continues until one of the two events occurs: (a) data clearly support one of the two hypotheses (indicated by a CD-support greater than 0.9) or (b) 50 patients have entered the trial. Trials that are not stopped before the 51st patient accrues are assumed to be inconclusive.

Based on a simulation of 1000 trials, Table 4 reports the proportions of trials that conclude in favor of each hypothesis, along with the average number of patients observed before each trial is stopped, for $\theta =0.1$ (the central value of ${{{\mathcal {H}}}_{0}}$) and for $\theta =0.4$. A comparison with the results reported by Johnson and Rossell (2010) reveals that our approach is clearly superior with respect to Bayesian inferences performed with standard priors and comparable to that obtained under their non-local prior carefully specified. Although there is a slight reduction in the proportion of trials stopped for ${{\mathcal {H}}}_0$ (0.814 compared to 0.91), the average number of involved patients is lower (12.7 compared to 17.7), and the power is higher (0.941 against 0.812).

Table 4 (Binomial model) Proportions of trials ended in favor of ${{{\mathcal {H}}}_{0}}$ and in favor of ${{{\mathcal {H}}}_{1}}$, with the average number of patients enrolled for ${{{\mathcal {H}}}_{0}}$ true $(p=0.1)$ and for ${{{\mathcal {H}}}_{1}}$ true $(p=0.4)$

Example 6

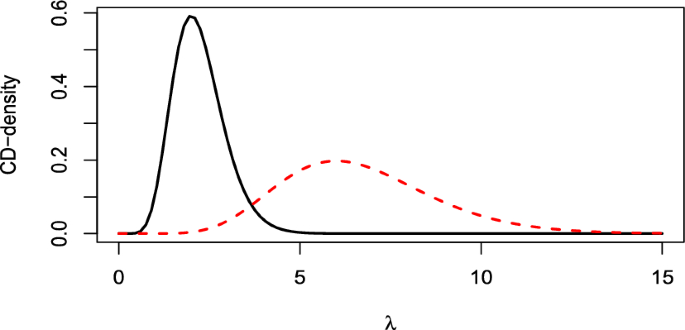
(Exponential distribution) Suppose an investigator aims to compare the performance of a new item, measured in terms of average lifetime, with that of the one currently in use, which is 0.375. To model the item lifetime, it is common to use the exponential distribution with rate parameter $\lambda$, so that the mean is $1/\lambda$. The typical testing problem is defined by ${{\mathcal {H}}}_0: \lambda =1/0.375=2.667$ versus ${{\mathcal {H}}}_1: \lambda \ne 2.667$. In many cases, it would be more realistic and interesting to consider hypotheses of the form ${{\mathcal {H}}}_0: \lambda \in [\lambda _1,\lambda _2]$ versus ${{\mathcal {H}}}_1: \lambda \notin [\lambda _1,\lambda _2]$, and if ${{{\mathcal {H}}}_{0}}$ is rejected, it becomes valuable to know whether the new item is better or worse than the old one. Note that, although an UMPU test exists for this problem, calculating its p-value is not simple and cannot be expressed in a closed form. Here we consider two different null hypotheses: ${{\mathcal {H}}}_0: \lambda \in [2, 4]$ and ${{\mathcal {H}}}_0: \lambda \in [2.63, 2.70]$, corresponding to a tolerance in the difference between the mean lifetimes of the new and old items equal to 0.125 and 0.005, respectively. Given a sample of n new items with mean ${\bar{x}}$, it follows from Table 8 in Appendix A that the CD for $\lambda$ is Ga(n, t), where $t=n\bar{x}$. Assuming $n=10$, we consider two values of t, namely, 1.5 and 4.5. The corresponding CD-densities are illustrated in Fig. 5 showing how the observed value t significantly influences the shape of the distribution, altering both its center and its dispersion, in contrast to the normal model. Specifically, for $t=1.5$, the potential estimates of $\lambda$, represented by the mean and median of the CD, are 6.67 and 6.45, respectively. For $t=4.5$, these values change to 2.22 and 2.15.

Table 5 provides the CD- and the CD*-supports corresponding to the two null hypotheses considered, along with the p-values of the UMPU test. Figure 5 and Table 5 together make it evident that, for $t=1.5$, the supports of both interval null hypotheses are very low and leading to their rejection, unless the problem requires a loss function that strongly penalizes a wrong rejection. Furthermore, it is immediately apparent that the data suggest higher values of $\lambda$, indicating a lower average lifetime of the new item. Note that the standard criterion “p-value $< 0.05$” would imply not rejecting ${{{\mathcal {H}}}_{0}}: \lambda \in [2,4]$. For $t=4.5$, when ${{{\mathcal {H}}}_{0}}: \lambda \in [2,4]$, the median 2.15 of the CD falls within the interval [2, 4]. Consequently, both the CD- and the CD*-supports are greater than 0.5, leading to the acceptance of ${{{\mathcal {H}}}_{0}}$, as also suggested by the p-value. When ${{{\mathcal {H}}}_{0}}: \lambda \in [2.63, 2.70]$, the CD-support becomes meaningless, whereas the CD*-support is not negligible (0.256) and should be carefully evaluated in accordance with the problem under analysis. This contrasts with the indication provided by the p-value (0.555).

For the point null hypothesis $\lambda =2.67$, the analysis is similar to that for the interval [2.63, 2.70]. Note that, in this case, in addition to the UMPU test, it is also possible to consider the simpler and most frequently used equal-tailed test. The corresponding p-value is 0.016 for $t=1.5$ and 0.484 for $t=4.5$; these values are exactly two times the CD*-support, see Remark 4.

Fig. 5

(Exponential model) CD-densities for the rate parameter $\lambda$, with $n=10$ and $t=1.5$ (dashed line) and $t=4.5$ (solid line)

Table 5 (Exponential model) CD-support, CD*-support and p-value of the UMPU test for different hypotheses with a sample of size $n=10$ and $t=1.5$ and $t=4.5$

Example 7

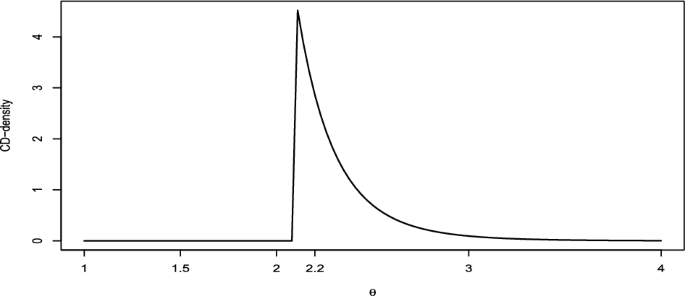
(Uniform model) As seen in Example 2, the CD for the parameter $\theta$ of the uniform distribution $\text {U}(0, \theta )$ is a Pareto distribution $\text {Pa}(n, t)$, where t is the sample maximum. Figure 6 shows the CD-density for $n=10$ and $t=2.1$.

Consider now ${{{\mathcal {H}}}_{0}}: \theta \in [\theta _1, \theta _2]$ versus ${{{\mathcal {H}}}_{1}}: \theta \notin [\theta _1, \theta _2]$. As usual, we can identify the interval $[\theta _1, \theta _2]$ on the plot of the CD-density and immediately recognize when the CD-test trivially rejects ${{{\mathcal {H}}}_{0}}$ (the interval lies on the left of t, i.e. $\theta _2<t$), when the value of $\theta _1$ is irrelevant and only the CD-support of $[t,\theta _2]$ determines the decision ($\theta _1<t<\theta _2$), or when the whole CD-support of $[\theta _1,\theta _2]$ must be considered ($t<\theta _1<\theta _2$). These facts are not as intuitive when the p-value is used. Indeed, for this problem, there exists the UMP test of level $\alpha$ (see Eftekharian and Taheri 2015) and it is possible to write the p-value as

$$\begin{aligned} p-\text{ value }=\left\{ \begin{array}{lll} \frac{t^n}{\theta _1^n} &{} \hspace{5mm} t<\theta _1 \\ \frac{\theta _2^n-t^n}{\theta _2^n-\theta _1^n} &{} \hspace{5mm} \theta _1\le t \le \theta _2 \\ 0 &{} \hspace{5mm} t > \theta _2,\\ \end{array} \right. \end{aligned}$$

(we are not aware of previous mention of it). Table 6 reports the p-value of the UMP test, as well as the CD and CD*-supports, for the two hypotheses ${{{\mathcal {H}}}_{0}}: \theta \in [1.5, 2.2]$ and ${{{\mathcal {H}}}_{0}}^\prime : \theta \in [2.0, 2.2]$ for a sample of size $n=10$ and various values of t.

It can be observed that, when t belongs to the interval $[\theta _1, \theta _2]$, the CD- and CD*-supports do not depend on $\theta _1$, as previously remarked, while the p-value does. This reinforces the incoherence of the p-value shown by Schervish (1996). For instance, when $t=2.19$, the p-value for ${{{\mathcal {H}}}_{0}}$ is 0.046, while that for ${{{\mathcal {H}}}_{0}}^{\prime }$ (included in ${{{\mathcal {H}}}_{0}}$) is larger, namely 0.072. Thus, assuming $\alpha =0.05$, the UMP test leads to the rejection of ${{{\mathcal {H}}}_{0}}$ but it results in the acceptance of the smaller hypothesis ${{{\mathcal {H}}}_{0}}^{\prime }$.

Fig. 6

(Uniform model) CD-density for $\theta$ with $n=10$ and $t=2.1$

Table 6 (Uniform model) CD-support, CD*-support and the p-value of the UMP test, for two different hypotheses and three different values of t, with fixed sample size $n=10$

Example 8

(Sharpe ratio) The Sharpe ratio is one of the most widely used measures of performance of stocks and funds. It is defined as the average excess return relative to the volatility, i.e. $SR=\theta =(\mu _R-R_f)/\sigma _R$, where $\mu _R$ and $\sigma _R$ are the mean and standard deviation of a return R and $R_f$ is a risk-free rate. Under the typical assumption of constant risk-free rate, the excess returns $X_1, X_2, \ldots , X_n$ of the fund over a period of length n are considered, leading to $\theta =\mu /\sigma$, where $\mu$ and $\sigma$ are the mean and standard deviation of each $X_i$. If the sample is not too small, the distribution and the dependence of the $X_i$’s are not so crucial, and the inference on $\theta$ is similar to that obtained under the basic assumption of i.i.d. normal random variables, as discussed in Opdyke (2007). Following this article, we consider the weekly returns of the mutual fund Fidelity Blue Chip Growth from 12/24/03 to 12/20/06 (these data are available for example on Yahoo! Finance, https://finance.yahoo.com/quote/FBGRX) and assume that the excess returns are i.i.d. normal with a risk-free rate equal to 0.00052. Two different samples are analyzed: the first one includes all $n_1=159$ observations from the entire period, while the second one is limited to the $n_2=26$ weeks corresponding to the fourth quarter of 2005 and the first quarter of 2006. The sample mean, the standard deviation, and the corresponding sample Sharpe ratio for the first sample are $\bar{x}_1=0.00011$, $s_1=0.01354$, $t_1=\bar{x}_1/s_1=0.00842$. For the second sample, the values are $\bar{x}_2=0.00280$, $s_2=0.01048$, $t_2=\bar{x}_2/s_2=0.26744$.

We can derive the CD for $\theta$ starting from the sampling distribution of the statistic $W=\sqrt{n}T=\sqrt{n}\bar{X}/S$, which has a noncentral t-distribution with $n-1$ degrees of freedom and noncentrality parameter $\tau =\sqrt{n}\mu /\sigma =\sqrt{n}\theta$. This family has MLR (see Lehmann and Romano 2005, p. 224) and the distribution function $F^W_\tau$ of W is continuous in $\tau$ with $\lim _{\tau \rightarrow +\infty } F^W_\tau (w)=0$ and $\lim _{\tau \rightarrow -\infty } F^W_\tau (w)=1$, for each w in $\mathbb {R}$. Thus, from (1), the CD for $\tau$ is $H^\tau _w(\tau )=1-F^W_\tau (w)$. Recalling that $\theta =\tau /\sqrt{n}$, the CD for $\theta$ can be obtained using a trivial transformation which leads to $H^\theta _w(\theta )=H^\tau _{w}(\sqrt{n}\theta )=1-F_{\sqrt{n}\theta }^W(w)$, where $w=\sqrt{n}t$. In Figure 7, the CD-densities for $\theta$ relative to the two samples are plotted: they are symmetric and centered on the estimate t of $\theta$, and the dispersion is smaller for the one with the larger n.

Now, let us consider the typical hypotheses for the Sharpe ratio ${{\mathcal {H}}}_0: \theta \le 0$ versus ${{\mathcal {H}}}_1: \theta >0$. From Table 7, which reports the CD-supports and the corresponding odds for the two samples, and from Fig. 7, it appears that the first sample clearly favors neither hypothesis, while ${{{\mathcal {H}}}_{1}}$ is strongly supported by the second one. Here, the p-value coincides with the CD-support (see Proposition 3), but choosing the the usual values 0.05 or 0.01 to decide whether to reject ${{{\mathcal {H}}}_{0}}$ or not may lead to markedly different conclusions.

When the assumption of i.i.d. normal returns does not hold, it is possible to show (Opdyke 2007) that the asymptotic distribution of T is normal with mean and variance $\theta$ and $\sigma ^2_T=(1+\theta ^2(\gamma _4-1)/4-\theta \gamma _3)/n$, where $\gamma _3$ and $\gamma _4$ are the skewness and kurtosis of the $X_i$’s. Thus, the CD for $\theta$ can be derived from the asymptotic distribution of T and is N($t,\hat{\sigma }^2_T)$, where $\hat{\sigma }^2_T$ is obtained by estimating the population moments using the sample counterparts. The last column of Table 7 shows that the asymptotic CD-supports for ${{{\mathcal {H}}}_{0}}$ are not too different from the previous ones.

Fig. 7

(Sharpe ratio) CD-densities for $\theta =\mu /\sigma$ with $n_1=159, t_1=0.008$ (solid line) and $n_2$=26, $t_2=0.267$ (dashed line)

Table 7 (Sharpe ratio) Exact CD-support, confidence odds $CO_{0.1}$ and asymptotic CD-support for the hypothesis ${{{\mathcal {H}}}_{0}}: \theta \le 0$ versus ${{{\mathcal {H}}}_{1}}: \theta > 0$ for $n_1$=159, $t_1=0.008$ and $n_2$=26, $t_2=0.267$

Example 9

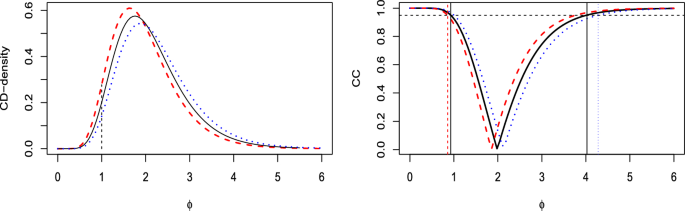
(Ratio of Poisson rates) The comparison of Poisson rates $\mu _1$ and $\mu _2$ is important in various contexts, as illustrated for example by Lehmann & Romano (2005, sec. 4.5), who also derive the UMPU test for the ratio $\phi =\mu _1/\mu _2$. Given two i.i.d. samples of sizes $n_1$ and $n_2$ from independent Poisson distributions, we can summarize the data with the two sufficient sample sums $S_1$ and $S_2$, where $S_i \sim$ Po($n_i\mu _i$), $i=1,2$. Reparameterizing the joint density of $(S_1, S_2)$ with $\phi =\mu _1/\mu _2$ and $\lambda =n_1\mu _1+n_2\mu _2$, it is simple to verify that the conditional distribution of $S_1$ given $S_1+S_2=s_1+s_2$ is Bi($s_1+s_2, w\phi /(1+w\phi )$), with $w=n_1/n_2$, while the marginal distribution of $S_1+S_2$ depends only on $\lambda$. Thus, for making inference on $\phi$, it is reasonable to use the CD for $\phi$ obtained from the previous conditional distribution. Referring to the table in Appendix A, the CD $H^g_{s_1,s_2}$ for $w\phi /(1+w\phi )$ is Be$(s_1+1/2, s_2+1/2)$, enabling us to determine the CD-density for $\phi$ through the change of variable rule:

$$\begin{aligned} h^G_{s_1,s_2}(\phi ){} & {} = \frac{1}{\texttt {B}(s_1+1/2,s_2+1/2)}w^{s_1+1/2}\phi ^{s_1-1/2}(1+w\phi )^{-s_1-s_2-1},\,\,\, \phi >0.\qquad \end{aligned}$$

(5)

We compare our results with those derived by the standard conditional test implemented through the function poisson.test in R. We use the “eba1977” data set available in the package ISwR, (https://CRAN.R-project.org/package=ISwR), which contains counts of incident lung cancer cases and population size in four neighboring Danish cities by age group. Specifically, we compare the $s_1=11$ lung cancer cases in a population of $n_1=800$ people aged 55–59 living in Fredericia with the $s_2=21$ cases observed in the other cities, which have a total of $n_2=3011$ residents. For the hypothesis ${{{\mathcal {H}}}_{0}}: \phi =1$ versus ${{{\mathcal {H}}}_{1}}: \phi \ne 1$, the R-output provides a p-value of 0.080 and a 0.95 confidence interval of (0.858, 4.277). If a significance level $\alpha =0.05$ is chosen, ${{{\mathcal {H}}}_{0}}$ is not rejected, leading to the conclusion that there should be no reason for the inhabitants of Fredericia to worry.

Looking at the three CD-densities for $\phi$ in Fig. 8, it is evident that values of $\phi$ greater than 1 are more supported than values less than 1. Thus, one should test the hypothesis ${{{\mathcal {H}}}_{0}}: \phi \le 1$ versus ${{{\mathcal {H}}}_{1}}: \phi >1$. Using (5), it follows that the CD-support of ${{{\mathcal {H}}}_{0}}$ is $H^g_{s_1,s_2}(1)=0.037$, and the confidence odds are $CO_{0,1}=0.037/(1-0.037)=0.038$. To avoid rejecting ${{{\mathcal {H}}}_{0}}$, a very asymmetric loss function should be deemed suitable. Finally, we observe that the confidence interval computed in R, is the Clopper-Pearson one, which has exact coverage but, as generally recognized, is too wide. In our context, this corresponds to taking the lower bound of the interval using the CC generated by $H^\ell _{s_1, s_2}$ and the upper bound using that generated by $H^r_{s_1, s_2}$ (see Veronese and Melilli 2015). It includes the interval generated by $H_{s_1, s_2}^g$, namely (0.931, 4.026), as shown in the right plot of Fig. 8.

Fig. 8

(Poisson-rates) CD-densities (left plot) and CCs (right plot) corresponding to $H^g_{s_1,s_2}(\phi )$ (solid lines), $H^\ell _{s_1,s_2}(\phi )$ (dashed lines) and $H^r_{s_1,s_2}(\phi )$ (dotted lines) for the parameter $\phi$. In the CC plot the vertical lines identify the Clopper-Pearson confidence interval (dashed and dotted lines) and that based on $H^g_{s_1,s_2}(\phi )$ (solid lines). The dotted horizontal line is at level 0.95

5 Properties of CD-support and CD*-support

5.1 One-sided hypotheses

The CD-support of a set is the mass assigned to it by the CD, making it a fundamental component in all inferential problems based on CDs. Nevertheless, its direct utilization in hypothesis testing is rare, with the exception of Xie and Singh (2013). It can also be viewed as a specific instance of evidential support, a notion introduced by Bickel (2022) within a broader category of models known as evidential models, which encompass both posterior distributions and confidence distributions as specific cases.

Let us now consider a classical testing problem. Let $\textbf{X}$ be an i.i.d. sample with a distribution depending on a real parameter $\theta$ and let ${{{\mathcal {H}}}_{0}}: \theta \le \theta _0$ versus ${{{\mathcal {H}}}_{1}}: \theta >\theta _0$, where $\theta _0$ is a fixed value (the case ${{{\mathcal {H}}}_{0}}^\prime : \theta \ge \theta _0$ versus ${{{\mathcal {H}}}_{1}}^\prime : \theta <\theta _0$ is perfectly specular and will not be analyzed). In order to compare our test with the standard one, we assume that the model has MLR in $T=T(\textbf{X})$. Suppose first that the distribution function $F_\theta (t)$ of T is continuous and that the CD for $\theta$ is $H_t(\theta )=1- F_{\theta }(t)$. From Sect. 3, the CD-support for ${{{\mathcal {H}}}_{0}}$ (which coincides with the CD*-support) is $H_t(\theta _0)$. In this case, the UMP test exists, as established by the Karlin-Rubin theorem, and rejects ${{{\mathcal {H}}}_{0}}$ if $t > t_\alpha$, where $t_\alpha$ depends on the chosen significance level $\alpha$, or alternatively, if the p-value $\text{ Pr}_{\theta _0}(T\ge t)$ is less than $\alpha$. Since $\text{ Pr}_{\theta _0}(T\ge t)=1-F_{\theta _0}(t)=H_t(\theta _0)$, the p-value coincides with the CD-support. Thus, to define a CD-test with size $\alpha$, it is enough to fix its rejection region as $\{t: H_t(\theta _0)<\alpha \}$, and both tests lead to the same conclusion.

When the statistic T is discrete, we have seen that various choices of CDs are possible. Assuming that $H^r_t(\theta )< H^g_t(\theta ) < H^{\ell }_t(\theta )$, as occurs for models belonging to a real NEF, it follows immediately that $H^{r}_t$ provides stronger support for ${{\mathcal {H}}}_0: \theta \le \theta _0$ than $H^g_t$ does, while $H^{\ell }_t$ provides stronger support for ${{\mathcal {H}}}_0^\prime : \theta \ge \theta _0$ than $H^g_t$ does. In other words, $H_t^{\ell }$ is more conservative than $H^g_t$ for testing ${{{\mathcal {H}}}_{0}}$ and the same happens to $H^r_t$ for ${{{\mathcal {H}}}_{0}}^{\prime }$. Therefore, selecting the appropriate CD can lead to the standard testing result. For example, in the case of ${{{\mathcal {H}}}_{0}}:\theta \le \theta _0$ versus ${{{\mathcal {H}}}_{1}}: \theta > \theta _0$, the p-value is $\text{ Pr}_{\theta _0}(T\ge t)=1-\text{ Pr}_{\theta _0}(T<t)=H^{\ell }_t(\theta _0)$, and the rejection region of the standard test and that of the CD-test based on $H_t^{\ell }$ coincide if the threshold is the same. However, as both tests are non-randomized, their size is typically strictly less than the fixed threshold.

The following proposition summarizes the previous considerations.

Proposition 3

Consider a model indexed by a real parameter $\theta$ with MLR in the statistic T and the one-sided hypotheses ${{{\mathcal {H}}}_{0}}: \theta \le \theta _0$ versus ${{{\mathcal {H}}}_{1}}: \theta >\theta _0$, or ${{{\mathcal {H}}}_{0}}^\prime : \theta \ge \theta _0$ versus ${{{\mathcal {H}}}_{1}}^\prime : \theta <\theta _0$. If T is continuous, then the CD-support and the p-value associated with the UMP test are equal. Thus, if a common threshold $\alpha$ is set for both rejection regions, the two tests have size $\alpha$. If T is discrete, the CD-support coincides with the usual p-value if $H^\ell _t [H^r_t]$ is chosen when ${{{\mathcal {H}}}_{0}}: \theta \le \theta _0$ $[{{{\mathcal {H}}}_{0}}^\prime : \theta \ge \theta _0]$. For a fixed threshold $\alpha$, the two tests have a size not greater than $\alpha$.

Remark 2

The CD-tests with threshold $\alpha$ mentioned in the previous proposition have significance level $\alpha$ and are, therefore, valid, that is $\sup _{\theta \in \Theta _0} Pr_\theta (H(T)\le \alpha ) \le \alpha$ (see Martin and Liu 2013). This is no longer true if, for a discrete T, we choose $H^g_t$. However, Proposition 2 implies that its average size is closer to $\alpha$ compared to those of the tests obtained using $H^\ell _t$ $[H^r_t]$, making $H^g_t$ more appropriate when the problem does not strongly suggest that the null hypothesis should be considered true “until proven otherwise”.

5.2 Precise and interval hypotheses

The notion of CD*-support surely demands more attention than that of CD-support. Recalling that the CD*-support only accounts for one direction of deviation from the precise or interval hypothesis, we will first briefly explore its connections with similar notions.

While the CD-support is an additive measure, meaning that for any set $A \subseteq \Theta$ and its complement $A^c$, we always have $\text{ CD }(A) +\text{ CD }(A^c)=1$, the CD*-support is only a sub-additive measure, that is $\text{ CD* }(A) +\text{ CD* }(A^c)\le 1$, as can be easily checked. This suggests that the CD*-support can be related to a belief function. In essence, a belief function $\text{ bel}_\textbf{x}(A)$ measures the evidence in $\textbf{x}$ that supports A. However, due to its sub-additivity, it alone cannot provide sufficient information; it must be coupled with the plausibility function, defined as $\text {pl}_\textbf{x}(A) = 1 - \text {bel}_\textbf{x}(A^c)$. We refer to Martin and Liu (2013) for a detailed treatment of these notions within the general framework of Inferential Models, which admits a CD as a very specific case. We only mention here that they show that when $A=\{\theta _0\}$ (i.e. a singleton), $\text{ bel}_\textbf{x}(\{\theta _0\})=0$, but $\text{ bel}_\textbf{x}(\{\theta _0\}^c)$ can be different from 1. In particular, for the normal model N$(\theta ,1)$, they found that, under some assumptions, $\text{ bel}_\textbf{x}(\{\theta _0\}^c) =|2\Phi (x-\theta _0)-1|$. Recalling the definition of the CC and the CD provided in Example 1, it follows that the plausibility of $\theta _0$ is $\text {pl}_\textbf{x}(\{\theta _0\})=1-\text{ bel}_\textbf{x}(\{\theta _0\}^c)=1-|2\Phi (x-\theta _0)-1|= 1-CC_\textbf{x}(\theta _0)$, and using (4), we can conclude that the CD*-support of $\theta _0$ corresponds to half their plausibility.

The CD*-support for a precise hypothesis ${{{\mathcal {H}}}_{0}}: \theta =\theta _0$ is related to the notion of evidence, as defined in a Bayesian context by Pereira et al. (2008). Evidence is the posterior probability of the set $\{\theta \in \Theta : p(\theta |\textbf{x})<p(\theta _0|\textbf{x})\}$, where $p(\theta |\textbf{x})$ is the posterior density of $\theta$. In particular, when a unimodal and symmetric CD is used as a posterior distribution, it is easy to check that the CD*-support coincides with half of the evidence.

The CD*-support is also related to the notion of weak-support defined by Singh et al. (2007) as $\sup _{\theta \in [\theta _1,\theta _2]} 2 \min \{H_{\textbf{x}}(\theta ), 1-H_{\textbf{x}}(\theta )\}$, but important differences exist. If data give little support to ${{{\mathcal {H}}}_{0}}$, our definition highlights better whether values of $\theta$ on the right or on the left of ${{{\mathcal {H}}}_{0}}$ are more reasonable. Moreover, if ${{{\mathcal {H}}}_{0}}$ is highly supported, that is $\theta _m \in [\theta _1,\theta _2]$, the weak-support is always equal to one, while the CD*-support assumes values in the interval [0.5, 1], allowing to better discriminate between different cases. Only if ${{{\mathcal {H}}}_{0}}$ is a precise hypothesis the two definitions agree, leaving out the multiplicative constant of two.

There exists a strong connection between the CD*-support and the e-value introduced by Peskun (2020). Under certain regularity assumptions, the e-value can be expressed in terms of a CD and coincides with the CD*-support, so that the properties and results originally established by Peskun for the e-value also apply to the CD*-support. More precisely, let us first consider the case of an observation x generated by the normal model $\text {N}(\mu ,1)$. Peskun shows that for the hypothesis ${{{\mathcal {H}}}_{0}}: \mu \in [\mu _1,\mu _2]$, the e-value is equal to $\min \{\Phi (x-\mu _1), \Phi (\mu _2-x)\}$. Since, as shown in Example 1, $H_x(\mu )=1-\Phi (x-\mu )=\Phi (\mu -x)$, it immediately follows that $\min \{H_x(\mu _2),1-H_x(\mu _1)\}= \min \{\Phi (\mu _2-x), \Phi (x-\mu _1)\}$, so that the e-value and the CD*-support coincide. For a more general case, we present the following result.

Proposition 4

Let $\textbf{X}$ be a random vector distributed according to the family of densities $\{p_\theta , \theta \in \Theta \subseteq \mathbb {R}\}$ with a MLR in the real continuous statistic $T=T(\textbf{X})$, with distribution function $F_\theta (t)$. If $F_\theta (t)$ is continuous in $\theta$ with limits 0 and 1 for $\theta$ tending to $\sup (\Theta )$ and $\inf (\Theta )$, respectively, then the CD*-support and the e-value for the hypothesis ${{{\mathcal {H}}}_{0}}: \theta \in [\theta _1,\theta _2]$, $\theta _1 \le \theta _2$, are equivalent.

We emphasize, however, that the advantage of the CD*-support over the e-value relies on the fact that knowledge of the entire CD allows us to naturally encompass the testing problem into a more comprehensive and coherent inferential framework, in which the e-value is only one of the aspects to be taken into consideration.

Suppose now that a test of significance for ${{\mathcal {H}}}_0: \theta \in [\theta _1,\theta _2]$, with $\theta _1 \le \theta _2$, is desired and that the CD for $\theta$ is $H_t(\theta )$. Recall that the CD-support for ${{{\mathcal {H}}}_{0}}$ is $H_t([\theta _1,\theta _2]) = \int _{\theta _1}^{\theta _2} dH_{t}(\theta ) = H_t(\theta _2)-H_t(\theta _1)$, and that when $\theta _1=\theta _2=\theta _0$, or the interval $[\theta _1,\theta _2]$ is “small”, it becomes ineffective, and the CD*-support must be employed. The following proposition establishes some results about the CD- and the CD*-tests.

Proposition 5

Given a statistical model parameterized by the real parameter $\theta$ with MLR in the continuous statistic T, consider the hypothesis ${{{\mathcal {H}}}_{0}}: \theta \in [\theta _1,\theta _2]$ with $\theta _1 \le \theta _2$. Then,

• (i) both the CD- and the CD*-tests reject ${{{\mathcal {H}}}_{0}}$ for all values of T that are smaller or larger than suitable values;

• (ii) if a threshold $\gamma$ is fixed for the CD-test, its size is not less than $\gamma$;

• (iii) for a precise hypothesis, i.e., $\theta _1=\theta _2$, the CD*-support, seen as function of the random variable T, has the uniform distribution on (0, 0.5);

• (iv) if a threshold $\gamma ^*$ is fixed for the CD*-test, its size falls within the interval $[\gamma ^*, \min (2\gamma ^*,1)]$ and equals $\min (2\gamma ^*,1)$ when $\theta _1=\theta _2$, (i.e. when ${{{\mathcal {H}}}_{0}}$ is a precise hypothesis);

• (v) the CD-support is never greater than the CD*-support, and if a common threshold is fixed for both tests, the size of the CD-test is not smaller than that of the CD*-test.

Remark 3

Point i) highlights that the rejection regions generated by the CD- and CD*-tests are two-sided, resembling standard tests for hypotheses of this kind. However, even when $\gamma = \gamma ^*$, the rejection regions differ, with the CD-test being more conservative for ${{{\mathcal {H}}}_{0}}$. This becomes crucial for small intervals, where the CD-test tends to reject the null hypothesis almost invariably.

Remark 4

Under the assumption of Proposition 5, the p-value corresponding to the commonly used equal tailed test for a precise hypothesis ${{{\mathcal {H}}}_{0}}:\theta =\theta _0$ is $2\min \{F_{\theta _0}(t), 1-F_{\theta _0}(t)\}$, so that it coincides with 2 times the CD*-support.

For interval hypotheses, a UMPU test essentially exists only for models within a NEF, and an interesting relationship can be established with the CD-test.

Proposition 6

Given the CD based on the sufficient statistic of a continuous real NEF with natural parameter $\theta$, consider the hypothesis ${{\mathcal {H}}}_0: \theta \in [\theta _1,\theta _2]$ versus ${{\mathcal {H}}}_1: \theta \notin [\theta _1,\theta _2]$, with $\theta _1 < \theta _2$. If the CD-test has size $\alpha _{CD}$, it is the UMPU test among all $\alpha _{CD}$-level tests.

For interval hypotheses, unlike one-sided hypotheses, when the statistic T is discrete, there is no clear reason to prefer either $H_t^{\ell }$ or $H_t^r$. Neither test is more conservative, as their respective rejection regions are shifted by just one point in the support of T. Thus, $H^g_t$ can be considered again a reasonable compromise, due to its greater proximity to the uniform distribution. Moreover, while the results stated for continuous statistics may not hold exactly for discrete statistics, they remain approximately valid for not too small sample sizes, thanks to the asymptotic normality of CDs, as stated in Proposition 1.

6 Conclusions

In this article, we propose the use of confidence distributions to address a hypothesis testing problem concerning a real parameter of interest. Specifically, we introduce the CD- and CD*-supports, which are suitable for evaluating one-sided or large interval null hypotheses and precise or small interval null hypotheses, respectively. This approach does not necessarily require identifying the first and second type errors or fixing a significance level a priori. We do not propose an automatic procedure; instead, we suggest a careful and more general inferential analysis of the problem based on CDs. CD- and CD*-supports are two simple coherent measures of evidence for a hypothesis with a clear meaning and interpretation. None of these features are owned by the p-value, which is more complex and generally does not exist in closed form for interval hypothesis.

It is well known that the significance level $\alpha$ of a test, which is crucial to take a decision, should be adjusted according to the sample size, but this is almost never done in practice. In our approach, the support provided by the CD to a hypothesis trivially depends on the sample size through the dispersion of the CD. For example, if ${{{\mathcal {H}}}_{0}}: \theta \in [\theta _1,\theta _2]$, you can easily observe the effect of sample size on the CD-support of ${{{\mathcal {H}}}_{0}}$ by examining the interval $[\theta _1, \theta _2]$ on the CD-density plot. The CD-support can be non-negligible also when the length $\Delta =\theta _2-\theta _1$ is small for a CD that is sufficiently concentrated on the interval. The relationship between $\Delta$ and the dispersion of the CD highlights again the importance of a thoughtful choice of the threshold used for decision-making and the unreasonableness of using standard values. Note that the CD- and CD*-tests are similar in many standard situations, as shown in the examples presented.

Finally, we have investigated some theoretical aspects of the CD- and CD*-tests which are crucial in standard approach. While for one-sided hypotheses, an agreement with standard tests can be established, there are some distinctions to be made for two-sided hypotheses. If a threshold $\gamma$ is fixed for a CD- or CD*-test, then its size exceeds $\gamma$ reaching $2\gamma$ for a CD*-test relative to a precise hypothesis. This is because the CD*-support only considers the appropriate tail suggested by the data and it does not adhere to the typical procedure of doubling the one-sided p-value, a procedure that can be criticized, as seen in Sect. 1. Of course, if one is convinced of the need to double the p-value, in our context, it is sufficient to double the CD*-support. In the case of a precise hypothesis ${{{\mathcal {H}}}_{0}}: \theta = \theta _0$, this leads to a valid test because $Pr_{\theta _0}\left( 2\min \{H_{\textbf{x}}(\theta _0),1-H_{\textbf{x}}(\theta _0)\}\le \alpha \right) \le \alpha$, as can be deduced by considering the relationship of the CD*-support with the e-value and the results in Peskun (2020, Sec. 2).

Appendices

Appendix A. Table of confidence distributions

Table 8 CDs related to some important statistical models under an i.i.d. sample of size n

Appendix B. Proof of propositions

Proof of Proposition 1

The asymptotic normality and the consistency of the CD in i) and ii) follow from Veronese & Melilli (2015, Thm. 3) for models belonging to a NEF and from Veronese & Melilli (2018b, Thm. 1) for continuous arbitrary models. Part iii) of the proposition follows directly using the Chebyshev’s inequality. $\diamond$

Proof of Proposition 2

Denote by $F_{\theta }(t)$ the distribution function of T, assume that its support ${{\mathcal {T}}}=\{t_1,t_2,\ldots ,t_k\}$ is finite for simplicity and let $p_j=p_j(\theta )=\text{ Pr}_\theta (T=t_j)$, $j=1,2,\ldots ,k$ for a fixed $\theta$. Consider the case $H_t^r(\theta )=1-F_{\theta }(t)$ (if $H_t^r(\theta )=F_{\theta }(t)$ the proof is similar) so that, for each $j=2,\ldots ,k$, $H_{t_j}^\ell (\theta )=H_{t_{j-1}}^r(\theta )$ and $H_{t_1}^\ell (\theta )=1$. The supports of the random variables $H^r_T(\theta )$, $H^\ell _T(\theta )$ and $H^g_T(\theta )$ are, respectively,

$$\begin{aligned} {{\mathcal {S}}}_{H^r_T}= & {} \{H^r_{t_{k-j+1}}(\theta ),j=1,2,\ldots ,k\}=\{0,p_k,p_k+p_{k-1},\ldots , p_k+p_{k-1}+\ldots +p_2\}, \nonumber \\ {{\mathcal {S}}}_{H^\ell _T}= & {} \{H^\ell _{t_{k-j+1}}(\theta ),j=1,2,\ldots ,k\}=\{p_k,p_k+p_{k-1},\ldots , p_k+p_{k-1}+\ldots +p_2,1\}, \nonumber \\ {{\mathcal {S}}}_{H^g_T}= & {} \{H^g_{t_{k-j+1}}(\theta ) =c_{j}, j=1,2,\ldots ,k\},\quad \text{ with } \nonumber \\{} & {} c_1 \in (0,p_k), c_{2} \in (p_k,p_k+p_{k-1}),\ldots ,c_k \in (p_k+p_{k-1}+\ldots +p_2,1), \end{aligned}$$

(6)

where (6) holds because $H^r_{t_j}(\theta )< H^g_{t_j}(\theta ) < H^{\ell }_{t_j}(\theta )$. The probabilities corresponding to the points included in the three supports are of course the same, that is $p_k,p_{k-1},\ldots ,p_1$, in this order, so that $G^\ell (u) \le u \le G^r(u)$.

Let $d(Q,R)=\int |Q(x)-R(x)|dx$ be the distance between the two arbitrary distribution functions Q and R. Denoting $G^u$ as the uniform distribution function on (0, 1), we have

$$\begin{aligned} d(G^r,G^u)= & {} d(G^\ell ,G^u)=\frac{1}{2} \sum _{j=1}^{k} p_j^2\\ d(G^g,G^u)= & {} \frac{1}{2} \sum _{j=1}^{k} p_j^2+ \sum _{j=1}^{k-1} [c_{j+1}-(p_k+\ldots +p_{k-j+1})] \\{} & {} \quad [c_{j+1}-(p_k+\ldots +p_{k-j})]+c_1\cdot (c_1-p_k)\\< & {} \frac{1}{2} \sum _{j=1}^{k} p_j^2, \end{aligned}$$

where the last inequality follows from (6). Thus, the distance from uniformity of $H_T^g(\theta )$ is less than that of $H_T^\ell (\theta )$ and of $H_T^r(\theta )$ and (2) is proven.$\diamond$

Proof of Proposition 4

Given the statistic T and the hypothesis ${{{\mathcal {H}}}_{0}}: \theta \in [\theta _1,\theta _2]$, the e-value, see Peskun 2020, equation 12), is $\min \bigg \{\max _{\theta \in [\theta _1,\theta _2]} F_\theta (t), \max _{\theta \in [\theta _1,\theta _2]} (1-F_\theta (t))\bigg \}$. Under the assumptions of the proposition, it follows that $F_t(\theta )$ is monotonically nonincreasing in $\theta$ for each t (see Section 2). As a result, the e-value simplifies to:

$$\begin{aligned} e\text{-value } =\min \left\{ F_{\theta _1}(t), 1-F_{\theta _2}(t)\right\} =\min \left\{ 1-H_t(\theta _1), H_t(\theta _2)\right\} , \end{aligned}$$

where the last expression coincides with the CD*-support of ${{{\mathcal {H}}}_{0}}$. Note that the same result holds if the MLR is nondecreasing in T ensuring that $F_t(\theta )$ is monotonically nondecreasing. $\diamond$

Proof of Proposition 5

Point i). Consider first the CD-test and let $g(t)=H_t([\theta _1,\theta _2])=H_t(\theta _2)-H_t(\theta _1)=F_{\theta _1}(t)-F_{\theta _2}(t)$ , which is a nonnegative, continuous function with $\lim _{t\rightarrow \pm \infty }g(t)=0$ and with derivative $g^\prime (t)=f_{\theta _1}(t)- f_{\theta _2}(t)$. Let $t_0 \in \mathbb {R}$ be a point such that g is nondecreasing for $t<t_0$ and strictly decreasing for $t \in (t_0,t_1)$, for a suitable $t_1>t_0$; the existence of $t_0$ is guaranteed by the properties of g. It follows that $g^\prime (t) \ge 0$ for $t<t_0$ and $g^\prime (t)<0$ in $(t_0,t_1)$. We show that $t_0$ is the unique point at which the function $g^\prime$ changes sign. Indeed, if $t_2$ were a point greater than $t_1$ such that $g^\prime (t)>0$ for t in a suitable interval $(t_2,t_3)$, with $t_3> t_2$, we would have, in this interval, $f_{\theta _1}(t)>f_{\theta _2}(t)$. Since $f_{\theta _1}(t)<f_{\theta _2}(t)$ for $t \in (t_0,t_1)$, this implies $f_{\theta _2}(t)/f_{\theta _1}(t)>1$ for $t \in (t_0,t_1)$ and $f_{\theta _2}(t)/f_{\theta _1}(t)<1$ for $t \in (t_2,t_3)$, which contradicts the assumption of the (nondecreasing) MLR in T. Thus, g(t) is nondecreasing for $t<t_0$ and nonincreasing for $t>t_0$, and the set $\{t: H_t([\theta _1,\theta _2])< \gamma \}$ coincides with $\{t: t<t^\prime$ or $t>t^{\prime \prime }\}$ for suitable $t^\prime$ and $t^{\prime \prime }$.

Consider now the CD*-test. The corresponding support is $\min \{H_t(\theta _2), 1-H_t(\theta _1)\}= \min \{1-F_{\theta _2}(t), F_{\theta _1}(t)\}$, which is a continuous function of t and approaches zero as $t \rightarrow \pm \infty$. Moreover, it equals $F_{\theta _1}(t)$ for $t\le t^*=\inf \{t: F_{\theta _1}(t)=1-F_{\theta _2}(t)\}$ and $1-F_{\theta _2}(t)$ for $t\ge t^*$. Thus, the function is nondecreasing for $t \le t^*$ and nonincreasing for $t \ge t^*$, and the result is proven.

Point ii). Suppose having observed $t^\prime = F_{\theta _1}^{-1}(\gamma )$, then the CD-support for ${{{\mathcal {H}}}_{0}}$ is

$$\begin{aligned} H_{t^\prime }([\theta _1,\theta _2])= & {} H_{t^\prime }(\theta _2)-H_{t^\prime }(\theta _1)=F_{\theta _1}({t^\prime })-F_{\theta _2}({t^\prime }) = F_{\theta _1}(F_{\theta _1}^{-1}(\gamma )) -F_{\theta _2}(F_{\theta _1}^{-1}(\gamma )) \\= & {} \gamma -F_{\theta _2}(F_{\theta _1}^{-1}(\gamma )) \le \gamma , \end{aligned}$$

so that $t^\prime$ belongs to the rejection region defined by the threshold $\gamma$. Due to the structure of this region specified in point i), all $t\le t^{\prime }$ belong to it. Now,

$$\begin{aligned} \sup _{\theta \in [\theta _1,\theta _2]}\text{ Pr}_\theta \{T\le t^{\prime }\}=\sup _{\theta \in [\theta _1,\theta _2]}F_{\theta }(F_{\theta _1}^{-1}(\gamma ))=F_{\theta _1}(F_{\theta _1}^{-1}(\gamma ))=\gamma \end{aligned}$$

because $F_{\theta }(t) \le F_{\theta _1}(t)$ for each t and $\theta \in [\theta _1,\theta _2]$. It follows that the size of the CD-test with threshold $\gamma$ is not smaller than $\gamma$.

Point iii). The result follows from the equality of the CD*-support with the e-value, as stated in Proposition 4, and the uniformity of the e-value as proven in Peskun (2020, Sec. 2).

Point iv). The size of the CD*-test with threshold $\gamma ^*$ is the supremum on $[\theta _1,\theta _2]$ of the following probability

$$\begin{aligned}{} & {} \text{ Pr}_\theta \{\min [H_T(\theta _2), 1-H_T(\theta _1)]< \gamma ^*\}= \text{ Pr}_\theta \{\min [1-F_{\theta _2}(T), F_{\theta _1}(T)]<\gamma ^*\}\nonumber \\{} & {} \quad = 1-\text{ Pr}_\theta \{1-F_{\theta _2}(T)>\gamma ^*, F_{\theta _1}(T)>\gamma ^*\}\nonumber \\{} & {} \quad = 1-\text{ Pr}_\theta \{T<F_{\theta _2}^{-1}(1-\gamma ^*), T>F_{\theta _1}^{-1}(\gamma ^*)\}\nonumber \\{} & {} \quad = 1-\text{ Pr}_\theta \{F_{\theta _1}^{-1}(\gamma ^*)<T<F_{\theta _2}^{-1}(1-\gamma ^*)\}\nonumber \\{} & {} \quad = 1-[F_\theta (F_{\theta _2}^{-1}(1-\gamma ^*)) - F_\theta (F_{\theta _1}^{-1}(\gamma ^*))], \end{aligned}$$

(7)

under the assumption that $F_{\theta _1}^{-1}(\gamma ^*) <F_{\theta _2}^{-1}(1-\gamma ^*)$, otherwise the probability is one. Because $F_{\theta _2}(t) \le F_{\theta }(t) \le F_{\theta _1}(t)$ for each t and $\theta \in [\theta _1,\theta _2]$, it follows that $F_{\theta }(F_{\theta _1}^{-1}(\gamma ^*)) \le F_{\theta _1}(F_{\theta _1}^{-1}(\gamma ^*))=\gamma ^*$, and $F_{\theta }(F_{\theta _2}^{-1}(1-\gamma ^*)) \ge F_{\theta _2}(F_{\theta _2}^{-1}(1-\gamma ^*)) = 1-\gamma ^*$ so that the size is

$$\begin{aligned}{} & {} \sup _{\theta \in [\theta _1,\theta _2]} \{1-[F_\theta (F_{\theta _2}^{-1}(1-\gamma ^*)) - F_{\theta }(F_{\theta _1}^{-1}(\gamma ^*))]\} \nonumber \\{} & {} \quad \le 1-[F_{\theta _2}(F_{\theta _2}^{-1}(1-\gamma ^*)) - F_{\theta _1}(F_{\theta _1}^{-1}(\gamma ^*))] = 2\gamma ^*. \end{aligned}$$

Finally, if $\theta =\theta _2$, from (7) we have

$$\begin{aligned} 1-[F_{\theta _2}(F_{\theta _2}^{-1}(1-\gamma ^*)) - F_{\theta _2}(F_{\theta _1}^{-1}(\gamma ^*))]= 1-1+\gamma ^*+F_{\theta _2}(F_{\theta _1}^{-1}(\gamma ^*)) \ge \gamma ^* \end{aligned}$$

and thus the size of the CD*-test must be included in the interval $[\gamma ^*,2\gamma ^*]$, provided that $2\gamma ^*$ is less than 1. For the case $\theta _1=\theta _2$, it follows from (7) that the size of the CD*-test is $2\gamma ^*$.

Point v). Because $H_t([\theta _1,\theta _2]=H_t(\theta _2)-H_t(\theta _1)\le H_t(\theta _2)$ and also $H_t(\theta _2)-H_t(\theta _1) \le 1-H_t(\theta _1)$, recalling Definition 4, it immediately follows that the CD-support is not greater than the CD*-support. Thus if the same threshold is fixed for the two tests, the rejection region of the CD-test includes that of the CD*-test, and the size of the first test is not smaller than that of the second one. $\diamond$

Proof of Proposition 6

Recall from point i) of Proposition 5, that the CD-test with threshold $\gamma$ rejects ${{{\mathcal {H}}}_{0}}: \theta \in [\theta _1,\theta _2]$ for values of T less than $t^\prime$ or greater than $t^{\prime \prime }$, with $t^\prime$ and $t^{\prime \prime }$ solutions of the equation $F_{\theta _1}(t)-F_{\theta _2}(t)=\gamma$. Denoting with $\pi _{CD}$ its power function, we have

$$\begin{aligned} \pi _{CD}(\theta _1)-\pi _{CD}(\theta _2)= & {} [\text{ Pr}_{\theta _1}(T<t^\prime )+\text{ Pr}_{\theta _1}(T>t^{\prime \prime })] -[\text{ Pr}_{\theta _2}(T <t^\prime )+\text{ Pr}_{\theta _2}(T >t^{\prime \prime })] \nonumber \\= & {} [F_{\theta _1}(t^\prime )+1-F_{\theta _1}(t^{\prime \prime })]-[F_{\theta _2}(t^\prime )+1-F_{\theta _2}(t^{\prime \prime })] \nonumber \\= & {} [F_{\theta _1}(t^\prime )-F_{\theta _2}(t^{\prime })]-[F_{\theta _1}(t^{\prime \prime })-F_{\theta _2}(t^{\prime \prime })]=0. \end{aligned}$$

Thus the power function of the CD-test is equal in $\theta _1$ and $\theta _2$ and this condition characterizes the UMPU test for the exponential families, see Lehmann & Romano (2005, p. 135). $\diamond$