Inference of improved adaptive progressively censored competing risks data for Weibull lifetime models

Abstract

Recently, an improved adaptive Type-II progressive censoring scheme is proposed to ensure that the experimental time will not pass a pre-fixed time and ends the test after recording a pre-fixed number of failures. This paper studies the inference of the competing risks model from Weibull distribution under the improved adaptive progressive Type-II censoring. For this goal, we used the latent failure time model with Weibull lifetime distributions with common shape parameters. The point and interval estimation problems of parameters, reliability and hazard rate functions using the maximum likelihood and Bayesian estimation methods are considered. Moreover, making use of the asymptotic normality of classical estimators and delta method, approximate intervals are constructed via the observed Fisher information matrix. Following the assumption of independent gamma priors, the Bayes estimates of the scale parameters have closed expressions, but when the common shape parameter is unknown, the Bayes estimates cannot be formed explicitly. To solve this difficulty, we recommend using Markov chain Monte Carlo routine to compute the Bayes estimates and to construct credible intervals. A comprehensive Monte Carlo simulation is conducted to judge the behavior of the offered methods. Ultimately, analysis of electrodes data from the life-test of high-stress voltage endurance is provided to illustrate all proposed inferential procedures.

1 Introduction

Censored data occurs when an experimenter or reliability practitioner desires to stop a life test before getting the entire sample. Type-I (time) and Type-II (failure) censoring schemes are the most practised schemes in reliability studies. Recently, a more general censoring scheme termed progressive Type-II censoring scheme (PCS-T2) has been commonly employed in reliability analysis because it saves both time and cost associated with an experiment and is also beneficial when the units being tested are costly. For an exhaustive bibliography list and more details on PCS-T2, we mention readers to an extraordinary book by Balakrishnan and Cramer (2014). Unfortunately, if one considers the PCS-T2 life test, the total experimental time may be too long due to the high lifespan of numerous modern products. Therefore, Kundu and Joarder (2006) suggested a progressive Type-II hybrid censoring scheme (PHCS-T2) as a mixture of PCS-T2 and hybrid censoring schemes. It has been investigated and considered by several authors, see for example Tian et al. (2015) and Shi et al. (2017).

Using the PHCS-T2, the test time is insured and will not pass a planned time. But the experiment ended at a prefixed time, which causes the number of failed members to be random and perhaps small or even zero. This is a direct effect due to industrial-technological progress; thus, today’s products are more reliable. In this case, the outcomes of statistical procedures may be inadequate or inefficient. To defeat this limitation, an adaptive progressively Type-II censoring scheme (APCS-T2), introduced by Ng et al. (2009), enables the test time to exceed a pre-specified time. Many authors considered this scheme in the literature using some lifetime distributions, see for example (Sobhi and Soliman 2016; Nassar and Abo-Kasem 2017; Nassar et al. 2018; Okasha et al. 2021; Elshahhat and Nassar 2021). Nevertheless, as shown by Ng et al. (2009) that the APCS-T2 is efficient in parameter estimation when the total duration of the test is not of significant interest. At the same time, if the test units are highly reliable products, then the experiment time will be very long, and the APCS-T2 does not ensure a satisfactory total test duration. Newly, to overcome this obstacle, Yan et al. (2021) suggested a new life-test plan called an improved adaptive progressive Type-II censoring scheme (IAPCS-T2). It has two desirable properties. The first one is that it can effectively ensure that the experiment stops within a designated period, and the second one is that it can be considered as a generalization of some existing censoring schemes such as PCS-T2, PHCS-T2 and APCS-T2. Accordingly, if the researcher wants to terminate the test within a certain time, then the suggested IAPCS-T2 can be applied. A detailed description of the IAPCS-T2 is presented in the next section.

In medical studies and life-testing analysis, the failure of units may be associated with more than one risk factor. These risk factors or causes of failures in some sense competing with each other for the breakdown of the test unit. Due to the aforementioned reason, in the statistical literature, it is well identified as the competing risks model. Many examples can be seen, see for instance (Crowder 2001), where failure may happen due to more numerous than one cause. In investigating the competing risks data, the researcher is typically interested in the evaluation of a specific risk in presence of other risk factors. When analyzing such a data set, ideally, the data consist of the lifetime of the failed unit and an indicator variable that expresses the cause of failure. The causes of failure may be considered to be independent or dependent. In this article, we assume the latent failure time model suggested by Cox (1959), where the competing causes of failures are independently distributed. Many studies have been performed under this assumption using different lifetime distributions and different censoring schemes. See for example, Kundu et al. (2003), Pareek et al. (2009), Cramer and Schmiedt (2011), Ashour and Nassar (2017), and Ren and Gui (2021a, b).

To the best of our knowledge, we have not come across any study that investigates the estimation of the parameters and some reliability characteristics under improved progressive Type-II censored competing risks data. So, to close this gap, our objectives in this study are: First, developing some inferential approaches of an improved adaptive progressively Type-II censored competing risks data for Weibull lifetime models. To achieve this goal, we consider the same latent failure time model formulations, and it is assumed that the latent failure times are distributed as independent Weibull random variables with the same shape parameter and different scale parameters. In the context of the point inference scenario, the maximum likelihood and Bayesian estimates of the unknown parameters, reliability function (RF) and hazard rate function (HRF) are obtained. Utilizing the asymptotic properties of the maximum likelihood estimates (MLEs), the approximate confidence intervals (ACIs) of the different quantities are obtained. The Bayesian estimates are reached by assuming independent gamma priors and using the squared error loss (SEL) function. As expected, the Bayesian estimates under the SEL function cannot be obtained in closed forms. Thus, we suggest using Markov chain Monte Carlo (MCMC) procedure to approximate the Bayes estimates of the unknown parameters and the associated credible intervals. Finally, the different proposed methods are compared through a simulation study and the analysis of competing risks data sets. The main contributions of this article essentially involve (i) Introducing the IAPCS-T2 in the presence of the competing risks model; (ii) Assuming the latent failure times are independent Weibull distributions, the classical and Bayesian estimations of the unknown parameters, RF and HRF are investigated; (iii) An extensive numerical study is done to compare the efficiency of the different proposed estimates.

The rest of this paper is organized as follows: The model assumptions and the corresponding likelihood function of IAPCS-T2 are described in Sect. 2. Point and interval estimates of parameters, reliability, hazard rate functions and relative risks via maximum likelihood and Bayesian approaches when the common shape parameter is known and/or unknown are discussed in Sects. 3 and 4, respectively. In Sect. 5, a Monte Carlo simulation study is performed. Analysis of one real-life data set is discussed in Sect. 6. Finally, we conclude our study in Sect. 7.

2 Model description

Consider n identical units are placed on a life test and their lifetimes are characterized by independent and identically distributed (i.i.d.) random variables indicated by ${{X}_{1}},\dots ,{{X}_{n}}$. Also, without loss of generality, we assume that there are just two competing risks, then one has

$$\begin{aligned} {{X}_{i}}=\min \left\{ {{X}_{1i}},{{X}_{2i}} \right\} ;\,\,i=1,2,\dots ,n, \end{aligned}$$

where ${{X}_{ji}},\ j=1,2$ refers to the latent failure time of the $i^{th}$ experimental unit under $j^{th}$ cause of failure. Furthermore, we assume independence of the causes of failure, i.e., the latent failure times $X_{1i}$ and $X_{2i}$ (for $i=1,2,\dots ,n$) are stochastically independent. Also, the pairs $(X_{1i},X_{2i})$, $i = 1,\dots , n$ are assumed to be i.i.d. such as when the $i^{th}$ failure is noted it is assumed that the cause of failure is identified and signed by the indicator $\xi _i, i=1,\dots ,n$, $\xi _i\in \{1,2\}$, where $\xi _i=1$ if the $i^{th}$ failure is due to the first cause and $\xi _i=2$ otherwise. It is also assumed that for each i, ${{X}_{i}}$ follows the two-parameter Weibull distribution with common shape parameter $\alpha >0$ and different scale parameters ${{\theta }_{j}}>0,\ j=1,2$, with the following probability density function (PDF) and cumulative distribution function (CDF)

$$\begin{aligned} {{f}_{j}}\left( x;\alpha ,{{\theta }_{j}} \right) =\alpha {{\theta }_{j}}{{x}^{\alpha -1}}e^{-\theta _{j} x^{\alpha }},\ \text {and}\ F_{j}\left( x;\alpha ,\theta _{j} \right) =1-e^{-\theta _{j} x^{\alpha }}, \end{aligned}$$

(1)

respectively. The Weibull distribution with the PDF furnished by (1) will be indicated as $WD\left( \alpha ,{{\theta }_{j}} \right)$, $j=1,2$.

Remark 1

If the failure times ${{X}_{1}}$ and ${{X}_{2}}$ are i.i.d random variables following $WD\left( \alpha ,{{\theta }_{1}} \right)$ and $WD\left( \alpha ,{{\theta }_{2}} \right)$, respectively, then the random variable $X=\min \left\{ {{X}_{1}},{{X}_{2}} \right\}$ follows $WD(\alpha ,\theta _{1}+\theta _{2})$, where $\alpha$ is the shape parameter and $({{\theta }_{1}}+{{\theta }_{2}})$ is the scale parameter.

Using Remark 1, the RF of the random variable X, say ${\mathcal {R}}_{X}(x)$, is given by

$$\begin{aligned} {{\mathcal {R}}_{X}}(x)&=\Pr \left( X>x \right) \nonumber \\&\quad =\Pr \left( {{X}_{1}}>x\right) \, \Pr \left( {{X}_{2}}>x \right) \nonumber \\&\quad =e^{-(\theta _{1}+\theta _{2})x^{\alpha }}, \end{aligned}$$

(2)

consequently, the HRF of the random variable X is

$$\begin{aligned} {{h}_{X}}(x)=\alpha \left( {{\theta }_{1}}+{{\theta }_{2}} \right) {{x}^{\alpha -1}}. \end{aligned}$$

(3)

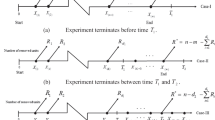
Suppose we have n identical units in the experiment, and the lifetime of these are expressed by ${{X}_{1}},{{X}_{2}},\dots ,{{X}_{n}}$. It is assumed that ${{X}_{i}}=\min \{{{X}_{1i}},{X}_{2i}\}$, $i=1,2,\dots ,n$, where ${{X}_{1i}}\sim WD\left( \alpha ,{{\theta }_{1}} \right)$ and ${{X}_{2i}}\sim WD\left( \alpha ,{{\theta }_{2}} \right)$, are independently distributed. Before beginning the test, the failure number $m<n$ and a progressive censoring scheme (PCS) $\Re =\left( {{R}_{1}},{{R}_{2}},\dots ,{{R}_{m}} \right)$, $R_i>0$, are determined in advance with the understanding that some values of $R_i$ may be changed during the experiment. Also, let ${{T}_{1}},{{T}_{2}}\in (0,\infty )$, where ${{T}_{1}}<{{T}_{2}}$, be two thresholds that are both determined in advance. Suppose $T_1$ is the initial threshold, and it is a notice about the test time. If the test proceeds to $T_1$, which implies that the test needs to be hurried up. Suppose $T_2$ is the secondary threshold, showing the highest time permitted by the experiment. The experiment must be stopped at $T_2$ if the number of failures does not reach the wanted number of failures m. At the time of the first failure ${{X}_{1:m:n}}$, the associated cause of failure ${{\xi }_{1}}$ is indicated and ${{R}_{1}}$ of the left items are randomly picked and discarded from the experiment. Similarly, at the time of the second failure ${{X}_{2:m:n}}$, the corresponding cause of failure ${{\xi }_{2}}$ is determined and ${{R}_{2}}$ items are randomly withdrawn from the remaining items, and so on. If ${{X}_{m:m:n}}<{{T}_{1}}$ (Case-I), the experiment stops at the time of $m^{th}$ failure and the remaining survival items $R_{m}=n-m-\sum \nolimits _{i=1}^{{m-1}}{{{R}_{i}}}$ are removed, which is just the conventional PCS-T2. If ${{X}_{{{d}_{1}}:m:n}}<{{T}_{1}}<{{X}_{{{d}_{1}}+1:m:n}}$ (Case-II), where $d_{1}$ is the number of failures before time $T_{1}$ and $({{d}_{1}}+1)<m$, then we put $R_{d_{1}+1}=\dots =R_{m-1}=0$ and terminate the experiment at the time of $m^{th}$ failure and then all the remaining $R_{m}=n-m-\sum \nolimits _{i=1}^{{{d}_{1}}}{{{R}_{i}}}$ units are removed. The reader can observe that Case II is the well-known APCS-T2. On the other hand, if ${{X}_{m:m:n}}>{{T}_{2}}$ (Case-III), the experiment stops at $T_{2}$, with the understanding that no items will be removed when the test time exceeds the first threshold $T_1$. In this case we have $d_{2}<m$ number of observed failures, where $d_{2}$ is the number of failures before time $T_{2}$. At the time $T_{2}$, all remaining units are removed, i.e., $R^{*}=n-{{d}_{2}}-\sum \nolimits _{i=1}^{{{d}_{1}}}{{{R}_{i}}}$. Therefore, based on an improved adaptive progressively Type-II censored competing risk data, we can perceive one of the different observations given by Table 1.

Table 1 Types of observations for an improved adaptive progressively Type-II censored competing risk data

Furthermore, we define the indicator function

$$\begin{aligned} \textbf{1}(\xi _{i}=j)= {\left\{ \begin{array}{ll} 1, &{}\xi _{i}=j, \,j=1,2\\ 0, &{}\text{ else }. \end{array}\right. } \end{aligned}$$

Thus, ${{D}_{1}}=\sum \nolimits _{i=1}^{D}{\textbf{1}\left( {{\xi }_{i}}=1 \right) }$ and ${{D}_{2}}=\sum \nolimits _{i=1}^{D}{\textbf{1}\left( {{\xi }_{i}}=2 \right) }$ denote the total number of observed failures due to causes 1 and 2, respectively, and $D=D_{1}+D_{2}$, $D>0$. It is observed here that for cases I and II, we have $m=D_{1}+D_{2}$, while $d_{2}=D_{1}+D_{2}$ for Case III, and in all the cases we use $D=D_{1}+D_{2}$ to denote to the number of observed failures.

Remark 2

Using the independence of the latent failure times, the relative risk due to cause 1 is given by

$$\begin{aligned} \pi _{1}&= \int _{0}^{\infty }{\alpha {{\theta }_{1}}{{y}^{\alpha -1}}{{e}^{-\left( {{\theta }_{1}}+{{\theta }_{2}} \right) {{y}^{\alpha }}}}dy} \nonumber \\&\quad =\frac{{{\theta }_{1}}}{{{\theta }_{1}}+{{\theta }_{2}}}\cdot \end{aligned}$$

(4)

Furthermore, the relative risk due to cause 2 can be obtained using the same approach in Remark 2, or simply as $\pi _{2}=1-\pi _{1}$. Then, we have $D_{j}\sim Binomial(D,\pi _{j}),\ j=1,2$.

Now, based on the observed data given by Table 1, we can write the likelihood function as follows

$$\begin{aligned} L(\underline{\theta })&={{A}^{*}}\prod \limits _{i=1}^{D}{\left\{ {{\left[ {{f}_{1}}({{x}_{i:m:n}}){\bar{F}_{2}}({{x}_{i:m:n}}) \right] }^{\textbf{1}\left( {{\xi }_{i}}=1 \right) }}{{\left[ {{f}_{2}}({{x}_{i:m:n}}){\bar{F}_{1}}({{x}_{i:m:n}}) \right] }^{\textbf{1}\left( {{\xi }_{i}}=2 \right) }} \right\} }\nonumber \\&\quad \times \prod \limits _{i=1}^{J}{\left\{ {{\left[ {\bar{F}_{1}}({{x}_{i:m:n}}){\bar{F}_{2}}({{x}_{i:m:n}}) \right] }^{{{R}_{i}}}} \right\} }{\left[ {\bar{F}_{1}}({{T}^{*}}){\bar{F}_{2}}({{T}^{*}}) \right] }^{R^{*}}, \end{aligned}$$

(5)

where $\bar{F}_{j}(\cdot )=1-F_{j}(\cdot )$, $\underline{\theta }$ is the vector of unknown parameters, ${A}^{*}$ is a constant which does not depend on the parameters, and the notation J, D, $T^{*}$ and $R^{*}$ are displayed in Table 2 for the cases I, II and III.

Table 2 Notation of the IAPCS-T2

In the next sections, the point and interval estimations for the unknown parameter of $WD(\theta _{j},\alpha )$, reliability characteristics and relative risks will be investigated using the frequentist and Bayesian approaches.

3 Maximum likelihood estimation

In this section, the MLEs and the corresponding ACIs of the unknown parameters $\theta _{j},\ j=1,2$ and $\alpha$, the reliability characteristics ${\mathcal {R}}(x)$ and h(x), and the relative risks $\pi _{j},\ j=1,2$ are derived under the improved adaptive progressively Type-II censored competing risk data.

3.1 Point estimates

Based on the observations as explained in the preceding section, the likelihood function (ignoring the constant term) can be formulated from (1) and (5) as follows

$$\begin{aligned} L\left( \theta _{1},\theta _{2},\alpha |\underline{\textbf{x}} \right) ={{\alpha }^{{{D}}}}\theta _{1}^{{{D}_{1}}}\theta _{2}^{{{D}_{2}}}\exp \left[ -\left( {{\theta }_{1}}+{{\theta }_{2}} \right) \psi \left( \underline{\textbf{x}};\alpha \right) \right] \prod \limits _{i=1}^{D}{x_{i}^{\alpha }}, \end{aligned}$$

(6)

where $x_{i}=x_{i:m:n}$ for simplicity, $\underline{\textbf{x}}$ is the observed data vector, $\psi \left( \underline{\textbf{x}};\alpha \right) =R^{*}T^{*^\alpha } +\sum \nolimits _{i=1}^{D}{x_{i}^{\alpha }}+\sum \nolimits _{i=1}^{J}R_{i}x_{i}^{\alpha }$. Correspondingly, the log-likelihood function, denoted by $l(\cdot )$, of (6) becomes

$$\begin{aligned} {{l}_{ }}\left( {{\theta }_{1}},{{\theta }_{2}},\alpha |\underline{\textbf{x}} \right)= & {} {{D}}\log (\alpha )+{{D}_{1}}\log ({{\theta }_{1}})+{{D}_{2}}\log ({{\theta }_{2}})-\left( {{\theta }_{1}}+{{\theta }_{2}} \right) \psi \left( \underline{\textbf{x}};\alpha \right) \nonumber \\{} & {} +\alpha \sum \nolimits _{i=1}^{D}{\log ({{x}_{i}})}. \end{aligned}$$

(7)

Firstly, we consider the case when the scale parameters are unknown and the common shape parameter $\alpha$ is known. In this case, the MLEs of $\theta _j, j=1,2$ are obtained by taking the first derivatives of (7) with respect to ${{\theta }_{j}}$ then equating them to zeros. The outcomes are as follow

$$\begin{aligned} {{\hat{\theta }}_{1}}=\frac{{{D}_{1}}}{\psi \left( \underline{\textbf{x}};\alpha \right) }\quad \text{ and }\quad {{\hat{\theta }}_{2}}=\frac{{{D}_{2}}}{\psi \left( \underline{\textbf{x}};\alpha \right) }\cdot \end{aligned}$$

(8)

On the other hand, we consider the most practical case when the common shape parameter is unknown. In this case, the MLEs of $\theta _j, j=1,2$ are obtained as displayed in (8) as a function in the unknown parameter $\alpha$, i.e. $\hat{\theta }_{1}(\alpha )$ and $\hat{\theta }_{2}(\alpha )$, respectively. Substituting $\hat{\theta }_{1}(\alpha )$ and $\hat{\theta }_{2}(\alpha )$ in (7), the profile log-likelihood of $\alpha$ can be expressed as follows

$$\begin{aligned} p\left( \alpha \right) ={{D}}\log \left[ \frac{\alpha }{\psi (\underline{\textbf{x}};\alpha )} \right] +\alpha \sum \nolimits _{i=1}^{D}{\log ({{x}_{i}})}. \end{aligned}$$

(9)

Directly, the MLE of $\alpha$ denoted by $\hat{\alpha }$, can be obtained by maximizing (9) with respect to $\alpha$. Since $p\left( \alpha \right)$ is unimodal, as pointed out by Pareek et al. (2009), then by differentiating (9) with respect to $\alpha$ and then equating the result to zero, the MLE of $\alpha$ such as $\alpha =q\left( \alpha \right)$ takes the form

$$\begin{aligned} q\left( \alpha \right) ={{\left[ \frac{{\psi }'\left( \underline{\textbf{x}};\alpha \right) }{\psi \left( \underline{\textbf{x}};\alpha \right) }-\frac{1}{{{D}}}\sum \nolimits _{i=1}^{D}{\log ({{x}_{i}})} \right] }^{-1}}, \end{aligned}$$

(10)

where ${\psi }'\left( \underline{\textbf{x}};\alpha \right) =R^{*}{{T}^{*}}^{\alpha }\log ({{T}^{*}})+\sum \nolimits _{i=1}^{D}{x_{i}^{\alpha }}\log ({{x}_{i}})+\sum \nolimits _{i=1}^{J}R_{i}x_{i}^{\alpha }\log (x_{i})$. From (10), it is clear that the MLE $\hat{\alpha }$ is difficult to reach mathematically. Therefore, to reach $\hat{\alpha }$ from (10), a simple iterative procedure proposed by Pareek et al. (2009) can be easily used for this purpose. Once we get $\hat{\alpha }$, then the MLEs ${{\hat{\theta }}_{1}}$ and ${{\hat{\theta }}_{2}}$ can be obtained directly from (8).

Remark 3

From (6), several works can be obtained as special cases, such as: (i) progressively Type-II censored competing risks by Pareek et al. (2009) when ${{T}_{1}}\rightarrow \infty$; (ii) adaptive progressively Type-II censored competing risks Weibull models with common shape parameter by Ren and Gui (2021a) when ${{T}_{2}}\rightarrow \infty$; (iii) improved adaptive Type-II progressively censored competing risks exponential data by Dutta and Kayal (2021) when $\alpha =1$.

According to the invariance property of the MLEs, the reliability characteristics ${\mathcal {R}}(t)$ and h(t) , at the distinct time t, can be obtained from (2) and (3) by replacing the original values $\theta _{1}, \theta _{2}$ and $\alpha$ by their MLEs ${{\hat{\theta }}_{1}}$, ${{\hat{\theta }}_{2}}$ and $\hat{\alpha }$, respectively, as follow

$$\begin{aligned} \widehat{{\mathcal {R}}}(t)=e^{-(\hat{\theta }_{1}+\hat{\theta }_{2})t^{\hat{\alpha }}}\quad \text{ and }\quad \hat{h}(t)=\hat{\alpha }( {{{\hat{\theta }}}_{1}}+{{{\hat{\theta }}}_{2}} ){{t}^{\hat{\alpha }-1}}. \end{aligned}$$

Similarly, the MLE of the relative risk due to cause j can be obtained from (4) as follows

$$\begin{aligned} \widehat{\pi }_{j}&=\frac{\hat{\theta }_{j}}{\hat{\theta }_{1}+\hat{\theta }_{2}} \\&\quad =\frac{D_{j}}{D}, j=1,2 \cdot \end{aligned}$$

3.2 Asymptotic interval estimates

The $100(1-\gamma )\%$ two-sided ACIs of the parameters, reliability characteristics and relative risks are formed employing the normality of MLEs in this subsection. Let $\varvec{\varphi } ={({{\theta }_{1}},{{\theta }_{2}},\alpha )}^{\top }$ be the vector of unknown parameters, where ${{\varphi }_{1}}={{\theta }_{1}}$, ${{\varphi }_{2}}={{\theta }_{2}}$ and ${{\varphi }_{3}}=\alpha$, then the asymptotic distribution of $\widehat{\varvec{\varphi } }$ is approximately multivariate normal with mean vector $\varvec{\varphi }$ and variance-covariance matrix $\textbf{I}^{-1}(\varvec{\varphi })$, i.e. $\hat{\varvec{\varphi }}\sim {N}_{3}\left[ \varvec{\varphi },{{\textbf{I}}^{-1}}\left( \varvec{\varphi } \right) \right]$, where $\textbf{I}(\varvec{\varphi })$ is the $3\times 3$ Fisher information matrix with elements ${{\textbf{I}}_{ij}}(\varvec{\varphi } )=E\left( -{{{\partial }^{2}}l}/{\partial {{\varphi }_{i}}\partial {{\varphi }_{j}}}\; \right) , i,j=1,2,3$. In this case, the second-order partial derivatives are obtained from (7) as follow

$$\begin{aligned} {{l}_{11}}= & {} \frac{{{D}_{1}}}{\theta _{1}^{2}},\ {{l}_{22}}=\frac{{{D}_{2}}}{\theta _{2}^{2}},\ {{l}_{33}}=\frac{{{D}}}{{{\alpha }^{2}}}+\left( {{\theta }_{1}}+{{\theta }_{2}} \right) {\psi }''\left( \underline{\textbf{x}};\alpha \right) ,\ {{l}_{13}}={{l}_{23}}\\{} & {} ={\psi }'\left( \underline{\textbf{x}};\alpha \right) ,\ \text{ and }\ {{l}_{12}}={{l}_{21}}=0, \end{aligned}$$

where ${\psi }''\left( \underline{\textbf{x}};\alpha \right) =R^{*}{{T}^{*}}^{\alpha } \log ^{2}({{T}^{*}}) +\sum \nolimits _{i=1}^{D}{x_{i}^{\alpha }}\log ^{2}({{x}_{i}}) +\sum \nolimits _{i=1}^{J}{x_{i}^{\alpha }{{R}_{i}}}\log ^{2}({{x}_{i}})$.

Because the expected information matrix is in a highly complex form and needs numerical integration, consequently, the approximate asymptotic variance-covariance matrix $\textbf{I}^{-1}(\widehat{\varvec{\varphi }})$ is utilized to build the ACIs, see for more details Lawless (2003). Hence, the approximate asymptotic variance-covariance matrix is given by

$$\begin{aligned} {{\textbf{I}}^{-1}}\left( {\hat{\varvec{\varphi } }} \right) =\left[ \begin{matrix} {{l}_{11}} &{} {} &{} {} \\ {{l}_{12}} &{} {{l}_{22}} &{} {} \\ {{l}_{31}} &{} {{l}_{32}} &{} {{l}_{33}} \\ \end{matrix} \right] _{\varphi =\hat{\varphi }}^{-1}=\left[ \begin{matrix} {{{\hat{\sigma }}}_{11}} &{} {} &{} {} \\ {{{\hat{\sigma }}}_{21}} &{} {{{\hat{\sigma }}}_{22}} &{} {} \\ {{{\hat{\sigma }}}_{31}} &{} {{{\hat{\sigma }}}_{32}} &{} {{{\hat{\sigma }}}_{33}} \\ \end{matrix} \right] . \end{aligned}$$

(11)

Then, for arbitrary $0<\gamma <1$, the two-sided $100(1-\gamma )\%$ ACI of ${{\varphi }_{i}},\ i=1,2,3$ can be expressed as

$$\begin{aligned} {{\hat{\varphi }}_{i}}\mp {{z}_{{\gamma }/{2}\;}}\sqrt{{{{\hat{\sigma }}}_{ii}}},\ i=1,2,3, \end{aligned}$$

(12)

where ${{\hat{\sigma }}_{ii}}, i=1,2,3$ are the main diagonal components of (11) and ${{z}_{{\gamma }/{2}}}$ is the upper $({\gamma }/{2})^{th}$ percentile of the standard normal distribution.

Moreover, based on the asymptotic normality of the MLEs it is known that $\widehat{{\mathcal {R}}}(t)\sim N[{\mathcal {R}}(t),\hat{\sigma }^{2}_{{\mathcal {R}}}]$, $\hat{h}(t)\sim N[h(t),\hat{\sigma }^{2}_{h}]$ and $\hat{\pi }_{j}(t)\sim N[\pi _{j}(t),\hat{\sigma }^{2}_{\pi _{j}}],\ j=1,2$. Therefore, the ACIs for ${\mathcal {R}}(t), h(t)$ and $\pi _{j}$ can be constructed using the corresponding normality. To get these ACIs, we need to compute the variances of the estimators of ${\mathcal {R}}(t), h(t)$ and $\pi _{j}$. For this purpose, we use the delta method as proposed by Greene (2000) to approximate these variances. Let $\Delta _{{\mathcal {R}}}, \Delta _{h}$ and $\Delta _{\pi _{j}}, j=1,2,$ are three partial derivative vectors for ${\mathcal {R}}(t), h(t)$ and $\pi _{j}$, respectively, as follow

$$\begin{aligned} \Delta _{{\mathcal {R}}}=\left( \frac{\partial {\mathcal {R}}(t) }{\partial \theta _{1}}, \frac{\partial {\mathcal {R}}(t) }{\partial \theta _{2}}, \frac{\partial {\mathcal {R}}(t) }{\partial \alpha } \right) , \,\,\Delta _{h}=\left( \frac{\partial h(t) }{\partial \theta _{1}}, \frac{\partial h(t) }{\partial \theta _{2}}, \frac{\partial h(t) }{\partial \alpha } \right) \end{aligned}$$

and

$$\begin{aligned} \Delta _{\pi _{j}}=\left( \frac{\partial \pi _{j} }{\partial \theta _{1}}, \frac{\partial \pi _{j} }{\partial \theta _{2}}, \frac{\partial \pi _{j} }{\partial \alpha } \right) , j=1,2, \end{aligned}$$

with the following components

$$\begin{aligned} \frac{\partial {\mathcal {R}}(t) }{\partial \theta _{j}}= & {} -t^{\alpha }e^{-(\theta _{1}+\theta _{2})t^{\alpha }}, \,\, \frac{\partial {\mathcal {R}}(t) }{\partial \alpha }=- (\theta _{1}+\theta _{2})t^{\alpha } \log (t) e^{-(\theta _{1}+\theta _{2})t^{\alpha }},\\ \frac{\partial h(t) }{\partial \theta _{j}}= & {} \alpha t^{\alpha -1}, \,\, \frac{\partial h }{\partial \alpha }=(\theta _{1}+\theta _{2})t^{\alpha -1} \left[ 1+\alpha \log (t)\right] \end{aligned}$$

and

$$\begin{aligned} \frac{\partial \pi _{j} }{\partial \theta _{j}}=\frac{\theta _{3-j}}{(\theta _{1}+\theta _{2})^{2}}, \,\,\frac{\partial \pi _{j} }{\partial \theta _{3-j}}=-\frac{\theta _{j}}{(\theta _{1}+\theta _{2})^{2}}, \,\,\frac{\partial \pi _{j} }{\partial \alpha }=0, \, j=1,2. \end{aligned}$$

Thus, the approximate variances of $\hat{{\mathcal {R}}}(t), \hat{h}(t)$ and $\hat{\pi }_{j}, j=1,2$ can be obtained, respectively, as

$$\begin{aligned}&\displaystyle \hat{\sigma }_{{\mathcal {R}}}^{2}=\left[ \Delta _{{\mathcal {R}}}\, \textbf{I}^{-1}(\varvec{\varphi }) \, \Delta _{{\mathcal {R}}}^{\top }\right] \big |_{\varphi =\hat{\varphi }}, \,\,\, \hat{\sigma }_{h}^{2}=\left[ \Delta _{h}\, \textbf{I}^{-1}(\varvec{\varphi }) \, \Delta _{h}^{\top }\right] \big |_{\varphi =\hat{\varphi }}\, \text {and}&\\&\displaystyle \hat{\sigma }_{\pi _{j}}^{2}=\left[ \Delta _{\pi _{j}}\, \textbf{I}^{-1}(\varvec{\varphi }) \, \Delta _{\pi _{j}}^{\top }\right] \big |_{\varphi =\hat{\varphi }}, j=1,2.&\end{aligned}$$

Now, the $100(1-\gamma )\%$ ACIs for ${\mathcal {R}}(t), h(t)$ and $\pi _{j}$ are given, respectively, by

$$\begin{aligned} \hat{{\mathcal {R}}}(t)\mp {{z}_{{\gamma }/{2}\;}}\sqrt{\hat{\sigma }_{{\mathcal {R}}}^{2}}, \,\, \,\, \hat{h}(t)\mp {{z}_{{\gamma }/{2}\;}}\sqrt{\hat{\sigma }_{h}^{2}}\,\,\, \text {and}\,\,\, \hat{\pi }_{j}\mp {{z}_{{\gamma }/{2}\;}}\sqrt{\hat{\sigma }_{\pi _{j}}^{2}}, j=1,2. \end{aligned}$$

4 Bayesian estimators

Over the past years, Bayes’ paradigm has grown to become the most popular approach in many fields; including but not limited to engineering, clinical, biology, etc. The capability of combining prior information in the analysis makes it so worthy in reliability studies where one of the significant challenges is the short availability of data. This section deals with deriving the Bayes estimates as well as the corresponding and highest posterior density (HPD) and Bayes credible intervals (BCIs) of the unknown parameters under an improved adaptive progressively Type-II censoring competing risks data by considering two cases. The first one is when the common shape parameter is known, and the second case is when the common shape parameter is unknown. Before progressing forward, we mainly consider the most important symmetric loss function called SEL function which is defined as

$$\begin{aligned} \ell \left( \eta ,\tilde{\eta } \right) ={{\left( \eta -\tilde{\eta } \right) }^{2}}. \end{aligned}$$

(13)

Using (13), the Bayes estimate $\tilde{\eta }$ of $\eta$ is given by the posterior mean. It is important to mention here that other symmetric and/or asymmetric loss functions can be easily used without much of an intractable. For more detail about the effectiveness of the Bayesian estimation procedure in estimating model parameters in the presence of the competing risks data, one can refer to the work of Kundu and Gupta (2007), Kundu and Pradhan (2011) and Nassar et al. (2022).

4.1 Shape parameter known

Electing prior for the unknown model parameter is an essential matter in Bayesian analysis. The class of gamma prior densities is quite flexible because it permits us to model a variety of prior information, see for more details (Kundu and Howlader 2010; Dey et al. 2018, 2021). Therefore, we assume that the random variables ${{\theta }_{1}}$ and ${{\theta }_{2}}$ have an independent gamma prior distributions. Suppose that ${{\theta }_{j}}\sim Gamma(a_{j},b_{j}), j=1,2,$ then the joint prior distribution of ${{\theta }_{1}}$ and ${{\theta }_{2}}$ can be written as

$$\begin{aligned} g_{1}({{\theta }_{1}},{{\theta }_{2}})\propto \theta _{1}^{{{a}_{1}}-1}\theta _{2}^{{{a}_{2}}-1}\exp [-({{\theta }_{1}}{{b}_{1}}+{{\theta }_{2}}{{b}_{2}})]. \end{aligned}$$

(14)

The hyper-parameters $({{a}_{j}},{{b}_{j}}),\ j=1,2,$ are chosen to show the prior awareness about the unknown parameters and they necessity be known and non-negative. Setting ${{a}_{j}}={{b}_{j}}=0,\ j=1,2,$ in (14), one can obtain the improper priors of ${{\theta }_{1}}$ and ${{\theta }_{2}}$ given by ${{({{\theta }_{1}}{{\theta }_{2}})}^{-1}}$. Combining (6) with (14) and substituting in the continuous Bayes’ theorem, the joint posterior PDF, denoted by ${{\Psi }_{1}}(\cdot )$, of ${{\theta }_{1}}$ and ${{\theta }_{2}}$, can be written up to proportional as

$$\begin{aligned} {{\Psi }_{1}}\left( {{\theta }_{1}},{{\theta }_{2}}|\underline{\textbf{x}} \right) \propto \theta _{1}^{a_{1}^{*}-1}\theta _{2}^{a_{2}^{*}-1}\exp \left[ -({{\theta }_{1}}b_{1}^{*}+{{\theta }_{2}}b_{2}^{*}) \right] , \end{aligned}$$

(15)

where $a_{1}^{*}={{a}_{1}}+{{D}_{1}}$, $a_{2}^{*}={{a}_{2}}+{{D}_{2}}$, $b_{1}^{*}={{b}_{1}}+\psi \left( \underline{\textbf{x}};\alpha \right)$ and $b_{2}^{*}={{b}_{2}}+\psi \left( \underline{\textbf{x}};\alpha \right)$.

Remark 4

It follows from (15) that the posterior distributions of ${{\theta }_{1}}$ and ${{\theta }_{2}}$ are gamma distributions, respectively, such that

$$\begin{aligned} {{\theta }_{1}}|\underline{\textbf{x}} \ {\sim }\ Gamma\left( a_{1}^{*},b_{1}^{*} \right) \,\, \text{ and }\,\, {{\theta }_{2}} |\underline{\textbf{x}} \ {\sim }\ Gamma\left( a_{2}^{*},b_{2}^{*} \right) . \end{aligned}$$

Then, the Bayes estimators ${{\tilde{\theta }}_{1}}$ and ${{\tilde{\theta }}_{2}}$ of ${{\theta }_{1}}$ and ${{\theta }_{2}}$ under the SEL function can be obtained using Remark 4 as the posterior expectation, respectively, as

$$\begin{aligned} {{\tilde{\theta }}_{1}}=\frac{a_{1}^{*}}{b_{1}^{*}}\quad \text{ and }\quad {{\tilde{\theta }}_{2}}=\frac{a_{2}^{*}}{b_{2}^{*}}\cdot \end{aligned}$$

(16)

From (16), under the assumptions of improper priors ${{a}_{i}}={{b}_{i}}=0,\ i=1,2$, it is clear that the Bayes estimators ${{\tilde{\theta }}_{1}}$ and ${{\tilde{\theta }}_{2}}$ of ${{\theta }_{1}}$ and ${{\theta }_{2}}$ are obtained in explicit expressions and they will be coincide with corresponding MLEs given by (8).

As it is pointed out in Remark 4 that posterior distributions of ${{\theta }_{1}}$ and ${{\theta }_{2}}$ are gamma distributions, then one can show that the random variable ${{\zeta }_{j}}=2{{\theta }_{j}}b_{j}^{*}, j=1,2,$ follows ${{\chi }^{2}}$ distributions with ${{\upsilon }_{j}}=2a_{j}^{*}$ degree of freedom. Thus, the two-sided $100(1-\gamma )\%$ BCIs for ${{\theta }_{j}},\ j=1,2$ are given, respectively, by

$$\begin{aligned} \left( \frac{1}{{{\zeta }_{1}}}\chi _{\left( {{\upsilon }_{1}},1-\left( {\alpha }/{2}\; \right) \right) }^{2},\frac{1}{{{\zeta }_{1}}}\chi _{\left( {{\upsilon }_{1}},\left( {\alpha }/{2}\; \right) \right) }^{2} \right) \ \text{ and }\ \left( \frac{1}{{{\zeta }_{2}}}\chi _{\left( {{\upsilon }_{2}},1-\left( {\alpha }/{2}\; \right) \right) }^{2},\frac{1}{{{\zeta }_{2}}}\chi _{\left( {{\upsilon }_{2}},\left( {\alpha }/{2}\; \right) \right) }^{2} \right) . \end{aligned}$$

(17)

Clearly; one can use the gamma distribution instead of chi-squared distribution to construct these BCIs when ${{\upsilon }_{j}},\ j=1,2$ are not integer values. Moreover, the $100(1-\gamma )\%$ HPD credible intervals of ${{\theta }_{j}}$ (for $j=1,2,$) are the intervals $\left( H_{L}^{{{\theta }_{j}}},H_{U}^{{{\theta }_{j}}} \right) , j=1,2,$ which satisfying

$$\begin{aligned} 1-\gamma =\int _{H_{L}^{{{\theta }_{j}}}}^{H_{U}^{{{\theta }_{j}}}}{\Psi _{j}^{{{\theta }_{j}}}\left( {{\theta }_{j}} |\underline{\textbf{x}} \right) d{{\theta }_{j}}}\, \text {and}\, \ \Psi _{j}^{{{\theta }_{j}}}\left( H_{L}^{{{\theta }_{j}}}\big |\underline{\textbf{x}} \right) =\Psi _{j}^{{{\theta }_{j}}}\left( H_{U}^{{{\theta }_{j}}} \big |\underline{\textbf{x}} \right) , \end{aligned}$$

(18)

where $\Psi _{j}^{{{\theta }_{j}}}\left( \cdot \right)$ is the posterior distribution of ${{\theta }_{j}},\ j=1,2.$ From (18) and after some algebraic manipulations, the two-sided $100(1-\gamma )\%$ HPD credible intervals, $\left( H_{L}^{{{\theta }_{j}}},H_{U}^{{{\theta }_{j}}} \right)$, of ${{\theta }_{j}}$ (for $j=1,2$) can be obtained by solving

$$\begin{aligned}&\displaystyle 1-\gamma =\frac{\Gamma \left( a_{j}^{*},H_{U}^{{{\theta }_{j}}}b_{j}^{*} \right) -\Gamma \left( a_{j}^{*},H_{L}^{{{\theta }_{j}}}b_{j}^{*} \right) }{\Gamma \left( a_{j}^{*} \right) }\quad \text{ and }&\nonumber \\&\displaystyle {{\left( \frac{H_{U}^{{{\theta }_{j}}}}{H_{L}^{{{\theta }_{j}}}} \right) }^{a_{j}^{*}-1}}=\exp \left[ -b_{j}^{*}\left( H_{U}^{{{\theta }_{j}}}-H_{L}^{{{\theta }_{j}}} \right) \right] , j=1,2,&\end{aligned}$$

(19)

where $\Gamma (a,b)=\int _{0}^{b}{x^{a-1}}e^{-x}dx$ is the incomplete gamma function. Clearly; the two nonlinear equations (19) must be solved simultaneously to provide the HPD credible intervals of ${{\theta }_{j}},\ j=1,2$.

Subsequently, from (15), the Bayesian estimators of the reliability characteristics ${\mathcal {R}}(\cdot )$ and $h(\cdot )$ at mission time t are given respectively as follows

$$\begin{aligned} \widetilde{{\mathcal {R}}}(t)=\int _{{{\theta }_{1}}}{\int _{{{\theta }_{2}}}{{\mathcal {R}}(t;{{\theta }_{1}},{{\theta }_{2}},\alpha ){{\Psi }_{1}}\left( {{\theta }_{1}},{{\theta }_{2}}|\underline{\textbf{x}} \right) d{{\theta }_{1}}d{{\theta }_{2}}}}, \end{aligned}$$

and

$$\begin{aligned} \tilde{h}(t)=\int _{{{\theta }_{1}}}{\int _{{{\theta }_{2}}}{h(t;{{\theta }_{1}},{{\theta }_{2}},\alpha ){{\Psi }_{1}}\left( {{\theta }_{1}},{{\theta }_{2}} | \underline{\textbf{x}} \right) d{{\theta }_{1}}d{{\theta }_{2}}}}. \end{aligned}$$

After some simplifications, we get

$$\begin{aligned} \widetilde{{\mathcal {R}}}(t)=\frac{b_{1}^{*a_{1}^*}b_{2}^{*a_{2}^*}}{\left( b_{1}^{*}+{{t}^{\alpha }} \right) ^{a_{1}^*}\left( b_{2}^{*}+{{t}^{\alpha }} \right) ^{a_{2}^*}},\ t>0,\quad \text {and}\quad \tilde{h}(t)=\alpha t^{\alpha -1}\left[ \frac{a_{1}^{*}}{b_{1}^{*}}+ \frac{a_{2}^{*}}{b_{2}^{*}} \right] ,\ t>0. \end{aligned}$$

Using the same approach, we can obtain the Bayes estimates of the relative risks ${\pi }_{j},\ j=1,2$ as

$$\begin{aligned} \tilde{\pi }_{j}=\int _{\theta _{1}}\int _{\theta _{2}}\pi _{j}(\theta _{1},\theta _{2}) {{\Psi }_{1}}\left( {{\theta }_{1}},{{\theta }_{2}} | \underline{\textbf{x}} \right) \ d{{\theta }_{1}}d{{\theta }_{2}},\ j=1,2, \end{aligned}$$

which cannot be obtained in closed forms and one can use numerical integration for this purpose. Although the BCI/HPD credible intervals of the unknown scale parameters are expressed in explicit forms, it is not easy to construct the same intervals for the reliability characteristics and relative risks. To solve this problem, the MCMC approach can be used to generate samples by direct sampling from the joint posterior distribution and then approximate the desired HPD credible intervals.

4.2 Shape parameter unknown

Analyzing the competing risks data under the assumption that the common shape parameter to be known may be an unrealistic assumption. Therefore, this subsection is devoted to studying the estimation problems when the common shape parameter is unknown, which is most likely to occur in practice. In this case, we assume that the random variable $\alpha$ follows a gamma distribution, i.e. $\alpha \sim Gamma(a_{3},b_{3})$. Then, joint prior distribution of ${{\theta }_{1}}$, ${{\theta }_{2}}$ and $\alpha$ can be written as

$$\begin{aligned} {g_{2}}({{\theta }_{1}},{{\theta }_{2}},\alpha )\propto \theta _{1}^{{{a}_{1}}-1}\theta _{2}^{{{a}_{2}}-1}{{\alpha }^{{{a}_{3}}-1}}\exp (-({{\theta }_{1}}{{b}_{1}}+{{\theta }_{2}}{{b}_{2}}+\alpha {{b}_{3}})). \end{aligned}$$

(20)

It is observed that when ${{a}_{i}},{{b}_{i}}=0,\ i=1,2,3$ in (20), the improper prior of ${{\theta }_{1}}$, ${{\theta }_{2}}$ and $\alpha$ is given by ${{({{\theta }_{1}}{{\theta }_{2}}\alpha )}^{-1}}$. Using (6) and (20), the joint posterior distribution of ${{\theta }_{1}}$, ${{\theta }_{2}}$ and $\alpha$ can be written as

$$\begin{aligned} {{\Psi }_{2}}\left( {{\theta }_{1}},{{\theta }_{2}},\alpha |\underline{\textbf{x}} \right) =C\,\theta _{1}^{a_{1}^{*}-1}\theta _{2}^{a_{2}^{*}-1}{{\alpha }^{a_{3}^{*}-1}}\exp \left[ -\left( {{\theta }_{1}}b_{1}^{*}+{{\theta }_{2}}b_{2}^{*}+\alpha b_{3}^{*} \right) \right] , \end{aligned}$$

(21)

where $a_{3}^{*}={{a}_{3}}+{{D}}$ and $b_{3}^{*}={{b}_{3}}-\sum \nolimits _{i=1}^{D}{\log \left( {{x}_{i}} \right) }$ and C is the normalized constant. The Bayes estimators, based on (21), cannot be obtained analytically because they are expressed in the ratio of multiple integrals. In literature, several approaches can be used to approximate the posterior density function to obtain the Bayesian point estimates namely; Lindley and Tierney–Kadane methods. But these approaches do not provide the HPD credible intervals, hence, we propose to use MCMC samples generated from the target distribution to approximate the Bayesian (point and interval) estimates. In the present context, the Gibbs sampler along with the Metropolis–Hastings (M–H) algorithm can be used to draw samples, for more details on the various applications of MCMC algorithms, one may refer to Gelman et al. (2004) and Lynch (2007).

The Gibbs sampling and M–H algorithm are the two most usually applied MCMC techniques. We apply a hybrid procedure that mixes the M–H algorithm within Gibbs sampler to produce samples from the posterior distribution. To establish the MCMC algorithm from (21), we first need to find the conditional posterior distributions of ${{\theta }_{j}},\ j=1,2$ and $\alpha$, respectively, as

$$\begin{aligned} \phi _{j}(\theta _{j}|\theta _{3-j},\alpha ,\underline{\textbf{x}})\propto \theta _{j}^{a^{*}_{j}-1}\, e^{-b_{j}^{*}\theta _{j}}, j=1,2 \end{aligned}$$

(22)

and

$$\begin{aligned} \phi _{3}\left( \alpha |{{\theta }_{1}},{{\theta }_{2}},\underline{\textbf{x}} \right) \propto {{\alpha }^{a_{3}^{*}-1}}\exp \left\{ -\left[ \alpha b_{3}^{*}+\left( {{\theta }_{1}}+{{\theta }_{2}} \right) \psi \left( \underline{\textbf{x}};\alpha \right) \right] \right\} . \end{aligned}$$

(23)

It is clear that the conditional posterior distributions of ${{\theta }_{1}}$ and ${{\theta }_{2}}$ given by (22) follow the gamma distributions, respectively. Thus, the samples of the unknown scale parameters can be easily simulated. It is also noted that the conditional posterior distribution of $\alpha$ given by (23) cannot be reduced to any standard distribution. But it follows from Theorem 2 by Kundu (2008) that $\phi _{3}\left( \alpha |\underline{\textbf{x}} \right)$ is log-concave in the form

$$\begin{aligned} \phi _{3}\left( \alpha |\underline{\textbf{x}} \right) \propto \frac{{{\alpha }^{{{a}_{3}}+{{D}}-1}}\exp \left( -\alpha b_{3}^{*} \right) }{{{\left[ {{b}_{1}}+\psi \left( \underline{\textbf{x}};\alpha \right) \right] }^{{{a}_{1}}+{{D}_{1}}}}{{\left[ {{b}_{2}}+\psi \left( \underline{\textbf{x}};\alpha \right) \right] }^{{{a}_{2}}+{{D}_{2}}}}}. \end{aligned}$$

Hence, we use the hybrid algorithm (M–H within Gibbs) for updating the unknown parameters ${{\theta }_{1}}$, ${{\theta }_{2}}$ and $\alpha$ in order to obtain the Bayes (point and interval) estimates for any related function of them. Now, to carry out the proposed hybrid algorithm, do the following steps for the sample generation process:

Step 1:

Set initial guesses of ${{\theta }_{1}}$, ${{\theta }_{2}}$ and $\alpha$ as ${{\theta }^{(0)}_{1}}$, ${{\theta }^{(0)}_{2}}$ and $\alpha ^{(0)}$, respectively.

Step 2:

Set $g=1$.

Step 3:

Use M–H steps to generate $\alpha ^{(g)}$ from $\phi _{3}(\alpha ^{(g-1)}|\underline{\textbf{x}})$ with the normal proposal distribution as

• (a) Generate ${{\alpha }^{*}}$ from $N(\alpha ^{(g-1)},\sigma _{33})$.

• (b) Obtain ${{\delta }}\left( {{\alpha }^{(g-1)}},{{\alpha }^{*}} \right) =\min \left\{ 1,\frac{{{\phi _{3}}}( {{\alpha }^{*}} |\underline{\textbf{x}})}{{{\phi _{3} }}( {{\alpha }^{(g-1)}} |\underline{\textbf{x}}) } \right\} .$

• (c) Generate a sample variate u from U(0, 1) .

• (d) If ${{u}}\leqslant {{\delta }}$ set ${{\alpha }^{(g)}}={{\alpha }^{*}}$, else set ${{\alpha }^{(g)}}={{\alpha }^{(g-1)}}$.

Step 4 :

Generate ${{\theta }^{(g)}_{j}}, j=1,2$ from (22).

Step 5 :

Obtain ${{\mathcal {R}}^{(g)}}(t)$ and ${{h}^{(g)}}(t)$, for a specified time $t>0$ and $\pi _{j}^{(g)}, j=1,2,$ by replacing ${{\theta }_{1}}$, ${{\theta }_{2}}$ and $\alpha$ with their ${{\theta }^{(g)}_{1}}$, ${{\theta }^{(g)}_{2}}$ and $\alpha ^{(g)}$, respectively.

Step 6 :

Set $g=g+1$.

Step 7 :

Redo steps 3–6 M times to get $\vartheta ^{(g)}=\left( {{\theta }^{(g)}_{1}},{{\theta }^{(g)}_{2}},\alpha ^{(g)},{\mathcal {R}}^{(g)}(t),h^{(g)}(t), \pi _{1}^{(g)},\pi _{2}^{(g)} \right) ,\ g=1,2,\dots ,M$.

To remove the affection of the selection of start value and to guarantee the chain convergence, the first samples, say ${{M}_{0}}$, are discarded. So, for large M, the remaining MCMC samples with size $M-M_{0}$ can be used to develop the Bayesian inference. Thus, the approximate Bayes estimate, $\tilde{\vartheta }$, and the corresponding posterior variance, $\tilde{V}(\tilde{\vartheta })$, of $\vartheta$ with respect to SEL function are given respectively by

$$\begin{aligned} {\tilde{\vartheta }}=\frac{1}{M-M_{0}}\sum \limits _{g={{M}_{0}}+1}^{M}{{{\vartheta }^{(g)}}}\quad \text{ and }\quad \tilde{V}(\tilde{\vartheta })=\frac{1}{M-M_{0}}\sum \limits _{g={{M}_{0}}+1}^{M}{({\vartheta }^{(g)}-\tilde{\vartheta })^2}. \end{aligned}$$

To construct the two-sided BCI of the parameter $\vartheta$, order the simulated MCMC samples of $\vartheta ^{(g)}$ as $\vartheta _{(M_0+1)},\vartheta _{(M_0+2)},\dots ,\vartheta _{(M)}$. Hence, the $100(1-\gamma )\%$ two-sided BCIs of $\vartheta$ is given by

$$\begin{aligned} \left( {\vartheta _{(M-M_0)\left( {{\gamma /2}} \right) },\vartheta _{(M-M_0)\left( {1 - \left( {{\gamma /2}} \right) } \right) } } \right) . \end{aligned}$$

On the other hand, one can choose the shortest interval, that involves values of the highest probability density, which is referred to HPD credible interval. According to the procedure proposed by Chen and Shao (1999), the HPD credible interval of the unknown parameter $\vartheta$ can be constructed. First, order the simulated MCMC variates of ${{\vartheta }^{(g)}}$ for $g=M_0+1,\dots ,M$. Hence, the $100(1 - \gamma )\%$ two-sided HPD credible interval of the unknown parameter $\vartheta$ is given by

$$\begin{aligned} \left( {{\vartheta }_{({{g}^{*}})}},{{\vartheta }_{({{g}^{*}}+(1-\gamma )(M-{{M}_{0}}))}} \right) , \end{aligned}$$

where ${{g}^{*}}={{M}_{0}}+1,\dots ,M$ is chosen such that

$$\begin{aligned} {{\vartheta }_{\left( {{g}^{*}}+[(1-\gamma )(M-{{M}_{0}})] \right) }}-{{\vartheta }_{({{g}^{*}})}}=\underset{1\leqslant g\leqslant \gamma \left( M-{{M}_{0}} \right) }{\mathop {\min }}\,\left( {{\vartheta }_{\left( g+[(1-\gamma )(M-{{M}_{0}})] \right) }}-{{\vartheta }_{\left( g \right) }} \right) . \end{aligned}$$

Here [y] denotes the largest integer less than or equal to y.

5 Monte Carlo simulation

To evaluate the performance of the theoretical results including point and interval estimators using the maximum likelihood and Bayesian methods, an extensive Monte Carlo simulation study is performed when true values of $\left( {{\theta }_{1}},{{\theta }_{2}},\alpha \right)$ are taken as $\left( 0.2,0.4,0.6 \right)$. Thus, the corresponding actual value of the reliability parameters ${\mathcal {R}}(t)$ and h(t) are 0.6036 and 0.4039, for mission time $t=0.75$, respectively. By considering different combinations of n(total test units), m(effective sample size), R(removal pattern) and ${{T}_{i}},\ i=1,2$(threshold points), we generate a large 1000 improved adaptive Type-II progressive censored samples from Weibull distribution. Two various choices of n and ${{T}_{i}},\ i=1,2$ are used such as $n(=40,80)$, ${{T}_{1}}(=0.5,0.8)$ and ${{T}_{2}}(=0.8,1.5)$. It is to be mentioned here that, when the number of failures m achieves, the experiment is terminated. In this study, the percentages of failure information $({m}/{n})100\%$ are considered to be such as 50 and $75\%$. To evaluate the performance of removal patterns, for each combination of (n, m) , different four censoring schemes are considered namely; uniform ($\textsf{U}$), left ($\textsf{L}$), middle ($\textsf{M}$) and right ($\textsf{R}$) censoring schemes.

To generate an improved adaptive Type-II progressive censored competing risks data from Weibull distribution, do the following algorithm:

Step 1:

Set the parameter values of $\theta _{j},\ j=1,2$ and $\alpha$.

Step 2:

Carried out Type-II progressively censored competing risks sample using the algorithm described by Balakrishnan and Sandhu (1995) as

(a):

Generate independent observations of size m as ${{\omega }_{1}},{{\omega }_{2}},\dots ,{{\omega }_{m}}$ from uniform distribution.

(b):

For a specific values of n, m and ${{R}_{i}},\ i=1,2,\dots ,m$, set ${{\upsilon }_{i}}=\omega _{i}^{{{\left( i+\sum \nolimits _{j=m-i+1}^{m}{{{R}_{j}}} \right) }^{-1}}},\ i=1,2,\dots ,m.$.

(c):

Set ${{U}_{i}}=1-{{\upsilon }_{m}}{{\upsilon }_{m-1}}\cdots {{\upsilon }_{m-i+1}}$ for $i=1,2,\dots ,m$.

(d):

Generate PCS-T2 competing risks sample from $WD(\alpha ,\theta _{j})$ by ${{X}_{i}}={F^{-1}}({{u}_{i}};\alpha ,\theta _{j}),\ j=1,2,\ i=1,2,\dots ,m$.

Step 3:

Determine ${{d}_{1}}$ at the threshold time ${{T}_{1}}$ and discard $X_{i},\ i={{d}_{1}}+2,\dots ,m$ for Case-II and -III.

Step 4:

Generate the first $m-{{d}_{1}}-1$ order statistics from a truncated distribution ${f\left( x \right) }/{\bar{F}\left( {{x}_{{{d}_{1}}+1}} \right) }$ with sample size $n-{{d}_{1}}-1-\sum \nolimits _{i=1}^{{{d}_{1}}}{{{R}_{i}}}$ as ${{X}_{{{d}_{1}}+2}},\dots ,{{X}_{m}}$, where $f(\cdot )$ and $F(\cdot )$ are given by (1) and $\bar{F}(\cdot )=1-F(\cdot )$.

Step 5:

Assign the cause of failure for each sample point as 1 or 2 with probability $\pi _{1}$ and $\pi _{2}$, respectively.

Step 6:

Collect one of the data observations of improved adaptive progressively Type-II censored competing risks as depicted in Table 1.

Using each simulated data, the MLEs and associated ACIs (when the significance level is set to be $\gamma =0.05$) of $\theta _{1}$, $\theta _{2}$, $\alpha$, ${\mathcal {R}}(t)$ and h(t) are computed. Here, we suggest to apply the Newton–Raphson method via ’maxLik’ package in $\textsf {R}$ programming software in order to evaluate any MLE of the unknown parameters $\alpha$ and $\theta _{j},\ j=1,2$. For Bayesian estimation, we took two informative priors for $\alpha$ and $\theta _{j},\ j=1,2$ called; Prior I $(a_{1},a_{2},a_{3})=(0.4,0.8,1.2)$ and $b_{i}=2,\ i=1,2,3$ also Prior II $(a_{1},a_{2},a_{3})=(2,4,6)$ and $b_{i}=10,\ i=1,2,3$. It is clear that the values of both priors I and II are selected in such a way that prior means are the same as the original expected value of the corresponding parameter. In practice, if one does not have prior information about the unknown parameters of interest, it is better to use the frequentist method rather than the Bayesian method because the latter is computationally more expensive. As described in Sect.  4, we use the M–H algorithm within the Gibbs sampler to generate 12,000 MCMC samples and discard the first 2000 values as ’burn-in’. Hence, using 10,000 MCMC samples, the average Bayes MCMC estimates and the associated 95% HPD credible intervals are computed. To get the objective posterior samples, we recommend utilizing the ‘coda’ package proposed by Plummer et al. (2006). Comparison of the point estimates are examined in terms of their root mean squared errors (RMSEs) and mean relative absolute biases (MRABs) using the following formulas

$$\begin{aligned} \text {RMSE}=\sqrt{\frac{1}{G}\sum \nolimits _{j=1}^{G}{{{\left( \hat{\vartheta }_{s }^{(j)}-{{\vartheta }_{s }} \right) }^{2}}}},\ s =1,2,3,4,5, \end{aligned}$$

and

$$\begin{aligned} \text {MRAB}=\frac{1}{G}\sum \nolimits _{j=1}^{G}{\frac{| \hat{\vartheta }_{s }^{(j)}-{{\vartheta }_{s }} |}{{{\vartheta }_{s }}},}\ s =1,2,3,4,5, \end{aligned}$$

respectively, where $\hat{\vartheta }_{s }^{(j)}$ denotes the obtained estimate using any estimation method at the $j-th$ sample of the unknown parameter ${{\vartheta }_{s }}$, G is the number of generated sequence data, ${{\vartheta }_{1}}=\theta _{1}$, ${{\vartheta }_{2}}=\theta _{2}$, ${{\vartheta }_{3}}=\alpha$, ${{\vartheta }_{4}}={{\mathcal {R}}}(t)$ and ${{\vartheta }_{5}}=h(t)$.

Also, the performances of the interval estimates are compared by their average confidence lengths (ACLs) and the coverage probabilities (CPs) based on samples generated by direct sampling as

$$\begin{aligned} \text {AC}{{\text {L}}_{{{\vartheta }_{s }}}}\left( 1-\gamma \right) \%=\frac{1}{G}\sum \nolimits _{j=1}^{G}{\left( {{U}_{\hat{\vartheta }_{s }^{(j)}}}\left( 1-\gamma \right) \%-{{L}_{\hat{\vartheta }_{s }^{(j)}}}\left( 1-\gamma \right) \% \right) },\ s =1,2,3,4,5, \end{aligned}$$

and

$$\begin{aligned} \text {CP}_{{{\vartheta }_{s }}}\left( 1-\gamma \right) \%=\frac{1}{G}\sum \nolimits _{j=1}^{G}{{{\textbf{1}^{*}}_{\left( {{L}_{\hat{\vartheta }_{s }^{(j)}}}\left( 1-\gamma \right) \%;{{U}_{\hat{\vartheta }_{s }^{(j)}}}\left( 1-\gamma \right) \% \right) }}}\left( {{\vartheta }_{s }} \right) ,\ s =1,2,3,4,5, \end{aligned}$$

where $\textbf{1}^{*}(\cdot )$ is the indicator function, $L(\cdot )$ and $U(\cdot )$ denote the lower and upper bounds, respectively, of the interval estimate of $\vartheta _{s }$. The average point estimates with their respective RMSEs and MRABs are reported in Tables 3, 4, 5, 6 and 7, while the ACLs with their CPs are listed in Tables 8 and 9. It is important to mention here that the outcomes of the relative risks and BCIs are not reported here due to space limitations. All necessary computational algorithms are coded in $\textsf {R}$ statistical programming language version 4.0.4.

Table 3 The average estimates with their (RMSEs, MRABs) of $\theta _{1}$

Table 4 The average estimates with their (RMSEs, MRABs) of $\theta _{2}$

Table 5 The average estimates with their (RMSEs, MRABs) of $\alpha$

Table 6 The average estimates with their (RMSEs, MRABs) of ${{\mathcal {R}}}(t)$

Table 7 The average estimates with their (RMSEs, MRABs) of h(t)

Table 8 The ACLs with their (CPs) of $\theta _{1}$, $\theta _{2}$ and $\alpha$

Table 9 The ACLs with their (CPs) of ${{\mathcal {R}}}(t)$ and h(t)

From the simulation results declared in Tables 3, 4, 5, 6, 7, 8 and 9, we have the following findings. In general, it can be noticed that the classical and Bayes estimates of the unknown parameters $\theta _{1}$, $\theta _{2}$, $\alpha$, ${\mathcal {R}}(t)$ and h(t) are satisfactory in terms of minimum RMSEs and MRABs. As n(or m) grows, for all estimates, the RMSEs, MRABs and ACLs decrease while their associated CPs increase. The same aforementioned outcome can be found when the values of the progressive censoring, $R_{i}$’s, decreases. The alike pattern is observed in asymptotic/Bayes interval estimates, when (n or m increases), such that their ACLs tend to decrease but their CPs tend to increase. Thus, to get better estimation results, one may dispose to raise n.

Further, it can be seen that the Bayes (point/interval) estimate for each unknown parameter has a significant behaviour compared to the other estimate with respect to the least RMSE, MRAB and ACL values as well as the highest CP values. This consequence is anticipated due to the fact that Bayesian estimates include additional prior information about the unknown parameter of interest. When the thresholds $T_1$ and $T_2$ increase, in most cases, it is observed that the RMSEs and MRABs associated with all unknown parameters decrease. Besides, the ACLs of ACI/HPD credible intervals tend to decrease while associated CPs tend to increase. This may not be too surprising, because when the values of the thresholds $T_1$ and $T_2$ increase, the investigator gathers more extra information.

Comparing the impact of different scenarios of the censoring schemes, for each set based on the lowest RMSEs, MRABs and ACLs as well as the highest CPs, the simulation results indicate that both classical and Bayes estimates have better performance based on scheme $\textsf{U}$ (next, scheme $\textsf{L}$) than other schemes. This effect is due to the fact that the expected duration test under scheme $\textsf{U}$ (or scheme $\textsf{L}$), where the remaining $n-m$ live units are removed via the uniform (or left) pattern, is greater than any other competing censoring scheme.

One of the major problems in Bayesian analysis is evaluating the convergence of the MCMC chain. Therefore, the trace and autocorrelation plots of the simulated MCMC draws of each unknown parameter are displayed (when $(n,m)=(40,20)$, $(T_1,T_2)=(0.4,0.8)$, and censoring scheme $\textsf{U}$ as an example) in Fig. 1. The trace plots of the MCMC results look like random noise and the autocorrelation values close to zero as the lag value increases. However, Fig. 1 showed that the MCMC draws are mixed adequately and thus the estimation results are reasonable. To sum up, the Bayesian estimation utilising the hybrid MCMC algorithm is recommended to estimate the unknown parameters and the reliability indices of WD under an improved adaptive progressive Type-II censored competing risks data.

Fig. 1

Trace and autocorrelation plots for MCMC draws of $\theta _{1}$, $\theta _{2}$, $\alpha$, ${\mathcal {R}}(t)$ and h(t) under MCMC method

6 Electrodes data analysis

To illustrate the relevance of the offered inference procedures to a real phenomenon, we shall apply the real-life test data set reported by Doganaksoy et al. (2002). Recently, this dataset has also been investigated by Ahmed et al. (2020) and Ren and Gui (2021a). The dataset includes 58 electrodes that were placed on a high-stress voltage endurance life test. The failures were attributed to one of two (modes) causes, the first cause named Mode E (insulation defect due to a processing problem which tends to occur early in life), and the second cause called Mode D (degradation of the organic material which typically occurs at a later stage). Nevertheless, the total number of observed failures due to causes of Mode E and D are 18 and 27, respectively. Also, the other 13 unfilled electrodes due to the missing cause (denoted by ‘$+$’) were still running. For computational convenience, each observed value in the original dataset has been divided by one thousand. The transformed failure times of the insulation voltage endurance test are shown in Table 10. In this application, from the full competing risks samples, we particularly concentrate only on those observations which were completely observed and left those observations which were still running.

Table 10 Voltage endurance life-test results (in 1000’s hours) of 58 electrodes

Firstly, to indicate whether the Weibull distribution can furnish an acceptable fit for the given data, the Kolmogorov–Smirnov (K–S) test is employed. Considering that the latent cause of failures has independent Weibull distributions, using the null and alternative hypotheses, $H_{0}:$ Data follows Weibull distribution v.s $H_{1}:$ Data do not follow Weibull distribution, respectively. The MLEs via the Newton–Raphson procedure are employed to inspect the validity of the Weibull distribution to fit the data. For the sample with failures due to Mode E (cause 1) and the sample with failures due to Mode D (cause 2), the K–S distance between empirical and fitted distribution functions, at a significance level $\gamma =0.05$, and the corresponding P-value for each sample are computed and reported in Table 11. It is seen from Table 11 that the P-values are greater than the specified significance level which indicates that the null hypothesis of the underlying Weibull distribution cannot be rejected. For further explanation, the probability–probability (P–P) plots and the fitted reliability plots, where the K–S distances are marked with blue lines, are plotted in Fig. 2. It shows that the fitted reliability functions are quite close to the corresponding empirical reliability functions.

Table 11 Fitting of Weibull models for the electrodes dataset

Fig. 2

Fitted RFs and P–P plots for electrodes dataset

Table 12 Improved adaptive progressively Type-II censored samples generated from electrodes data

Fig. 3

Profile log-likelihood functions of $\alpha$

Fig. 4

Density (left) and Trace (right) plots from electrodes dataset

Now, for specified $m=25$ and progressive censoring $R=(0^{*}2,1^{*}20,0^{*}3)$, where $0^{*}n$ stands 0 is repeated for n times, three different improved adaptive progressively Type-II censored samples under different choices of $T_{i},\ i=1,2$ are generated and provided in Table 12. Before proceeding to calculate the desired (point and interval) estimates, using the three generated data samples reported in Table 12, the corresponding profile log-likelihood functions (9) are calculated and plotted in Fig. 3, where the best starting points are the maximum points with a vertical dashed line. It shows that the profile log-likelihood functions of $\alpha$, based on samples 1, 2 and 3, are unimodal and their MLEs are close to 1.2, 0.45 and 1.0, respectively. So, we suggest assuming these starting points as initial values to run any further computational iteration.

Currently, based on the three generated samples in Table 12, the proposed point estimates as well as the interval estimates of the unknown parameters $\alpha$ and $\theta _{i},\ i=1,2$; the relative risk rates $\pi _{i},\ i=1,2$; and the reliability characteristics ${\mathcal {R}}(t)$ and h(t) at distinct time $t=0.1$, are calculated. In the Bayesian estimation procedure, because we do not have any prior information about the unknown parameters, the hyperparameters are taken into account as $a_{i}=b_{i}=0.001$. Using the M–H algorithm within the Gibbs sampler proposed in Sect. 4, we generate 50,000 MCMC samples and discard the first 10,000 iterations. To visually explore the convergence and blending of Markovian chains, using each generated sample, both density and trace plots of the unknown parameters based on 40,000 MCMC simulated variates are displayed in Fig. 4. The horizontal solid line in each histogram (or density) plot represents the sample mean while the horizontal dashed lines in each histogram plot represent the two bounds of HPD credible interval estimates. Figure 4 shows, for each unknown parameter, that the posterior density is almost symmetrical and its MCMC variates are mixed well. The MLEs and Bayes estimates (with their standard errors (SEs)), as well as the asymptotic/HPD credible intervals (with their lengths), are calculated and shown in Table 13. It is found that the point estimates of $\alpha$, $\theta _{i}$, $\pi _{i}$ (for $i=1,2$), ${\mathcal {R}}(t)$ and h(t) obtained via the maximum likelihood and Bayesian estimation methods are quite close to each other. Also, the outcomes of Table 13 indicated that the HPD credible intervals are slightly shorter than the other confidence intervals in terms of their interval lengths. It can also be seen that the pre-specified of $T_1$ and $T_2$ play an important role in estimation problems of any parametric function of the unknown parameters. Thus, the results of the proposed methods under an electrodes dataset give a good explanation to our model.

Table 13 The point and interval estimation from electrodes data

7 Conclusion remarks

In this paper, we have investigated the estimation problems of Weibull distribution based on improved adaptive Type-II progressively censored competing risks data. To achieve our objective, the maximum likelihood and Bayesian estimation methods are considered. The point and approximate confidence interval estimates for the unknown parameters as well as the reliability and hazard rate functions are studied. In the Bayesian paradigm, the Metropolis-Hastings algorithm within Gibbs sampler is offered to acquire the Bayesian estimates under the squared error loss function and the associated credible intervals are also obtained. Through Monte Carlo simulation investigations, it is evident that the Bayesian estimation is more satisfactory than the maximum likelihood estimation method and both are applicable and feasible. It is also shown that the predetermined thresholds provide a significant effect on the proposed point and interval estimates of the unknown parameters. Furthermore, the real-life data analysis using electrodes data set confirms that our methods are practicable. This study is primarily related to the analysis of an improved adaptive Type-II progressively censored competing risks data, where the lifetime items of the individual failure causes are independent and follow Weibull distribution. It is worth saying that although the problem of only two competing risks factors is considered, the same inferential methodologies suggested here can be easily generalized to multiple failure factors and other censoring schemes.