1 Introduction

Numerous designs of fluidic oscillators have been present since the 1950s. Still, there is a renewed interest in their design, optimization, and application in recent years, due to their significant potential for flow control. They are also simple to fabricate, since they do not involve any moving parts, and can be fairly easily implemented. These oscillators have been designed as feedback-free (Raghu 2013), with one feedback channel (Wassermann et al. 2013), or with two feedback channels (Bobusch et al. 2013a). A version with two separate outlets is used as a pulsing jet (Wang et al. 2019). A family of suction and oscillatory-blowing (SaOB) actuators introduced by Arwatz et al. (2008) reflects the versatility of fluidic oscillator designs. The Sweeping Jet (SWJ) actuator with two feedback channels is one of the most common fluidic oscillator designs, with oscillation frequencies ranging from a few Hertz to several kilo-Hertz. It has been widely studied for many applications, such as: heat transfer enhancement  (Wen et al. 2019), combustion control  (Crittenden and Raghu 2009), cavity tones suppression (Raman and Raghu 2004), noise control  (Horne and Burnside 2016), atomizing high-viscosity liquids (Fu et al. 2017), flow measurement (Meng et al. 2013), dynamic calibration (Gregory et al. 2002), boundary-layer control (Seifert et al. 1993), and separation control (Wilson et al. 2013; Shtendel and Seifert 2014; Schatzman et al. 2014; Kara et al. 2018), to name just a few. Its most common application in aerodynamics, as an active vortex generator, is based on its production of streamwise vorticity (Woszidlo and Wygnanski 2011) due to the sweeping motion of the external jet.

The basic working principle of such actuator is to provoke and harness a bi-stable internal flow, which causes the sweeping of the external flow in a given plane. Bi-stable flows are ubiquitous in many fields of fluid engineering; they can occur in strongly separated three-dimensional flows (Fabre et al. 2008; Herry et al. 2011; Grandemange et al. 2012), where the origins of the bi-stability are still unclear. Other common cases of flow bi-stability, which are far better understood, are situations where the flow alternates between separation and re-attachment, as in fluid-structure interaction (Alben and Shelley 2008), different arrangements of two-dimensional cylinders (Alam et al. 2003; Afgan et al. 2011), in heat transfer (Abed and Afgan 2017), and passive flow control (Parezanović et al. 2015). In the case of the fluidic oscillators, the usual chaotic behavior of the bi-stable flow is forced by the internal geometry of the oscillator, such that the switching between the two flow states becomes almost perfectly periodic.

Very recently, several important contributions to understanding of the governing mechanisms of the internal oscillator flows have been made. For example, Bobusch et al. (2013a) found that the oscillation mechanism is dependent on the flow feeding a separation bubble between the jet and the mixing chamber wall, which causes the jet to switch to the other side and restart the process. They further conclude that the switching mechanism period is driven by the mass flow through the feedback channel, not the pressure wave. Woszidlo et al. (2015) gave a definitive characterization of the SWJ oscillation frequency as primarily dependent on how fast the specific total mass is transported into the separation bubble through the feedback channels. They concluded that regardless of the mass flow rate through the actuator, a constant volume of the working fluid is used to grow the recirculation bubble to its maximum size and perform a full switch cycle of the jet. Since a constant volume is provided at an increased rate when the mass flow rate is increased, the jet oscillates at a higher frequency. While the mass flow governs the process, recent work (Wu et al. 2019; Baghaei and Bergada 2019) confirms that the pressure gradient between the feedback channel inlet and outlet is initiating the switching.

The internal geometry of the SWJ is the determining factor of the oscillation frequency and other jet parameters. Therefore, recent research is focused on exploring the different internal geometry features and their importance in enhancing the performance of SWJs. Bobusch et al. (2013b) and Seo et al. (2018) demonstrated that the feedback channel length and height have little effect on the oscillation frequency, but do affect the oscillation amplitude and periodicity. On the other hand, the variation in the length of the mixing chamber significantly affects the jet oscillation frequency, where frequency scales as \(\frac{1}{L^2}\) (Metka et al. 2015). More recently, Park et al. (2020) have similarly characterized the actuator flow in a supersonic regime, using Taguchi’s Design of Experiment to perform a systematic exploration of the impact of several key geometric parameters.

Besides the jet oscillation frequency, the pressure loss or the flow resistance in an actuator is also a determining factor for the applicability of a certain design (Woszidlo et al. 2019). It is noteworthy that both higher and lower supply pressure can be desirable, depending on the intended application. By applying minor geometrical modifications Yang et al. (2007) obtained a significant improvement in the actuator signal to noise ratio, which is crucial for certain applications. It has also been recommended (Gaertlein et al. 2014; Ostermann et al. 2015a) that the mixing chamber and feedback channel geometry can be further streamlined to avert flow separation and increase actuator efficiency.

Hence, the current work presented in this paper investigates the effects of localized geometry modifications on one of the common fluidic oscillator designs; the curved SWJ actuator. Designs with different feedback channel width, feedback channel outlet diameter, and alternative shapes of the mixing chamber wall, i.e., the Coanda surface are tested. We characterize the effects of the geometry variations on the performance parameters of the SWJ such as the oscillation frequency, the pressure fluctuation intensity, the required supply pressure, and the maximum jet deflection angle. The main objective is to isolate the impact of specific geometry elements on the global properties of the jet.

This article is structured as follows. The experimental setup, measurements, and geometry modifications are described in Sect. 2. In Sect. 3, we present the reference geometry flow characteristics and the comparative results with respect to the modified geometries. Discussion of the results is presented in Sect. 4 and the concluding remarks are given in Sect. 5.

2 Experimental setup and actuator geometry

2.1 Experimental model and measurements

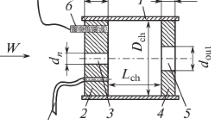
The reference geometry corresponds to a curved (also called Type-II) SWJ actuator with two feedback channels (Fig. 1). The working fluid is air, and the actuator is expelling the jet into a quiescent environment. The SWJ actuator’s main body with the oscillator cavity and the cover has been machined from acrylic glass. The actuator cavity depth is \(h = 6.35\) mm, equal to the outlet throat width \(h = d_{\mathrm{out}}\), while inlet width is \(d_{\mathrm{in}} = 6.07\) mm. The outlet nozzle half-angle is \(\theta = 50^\circ \), and the streamwise length of the diffuser is \(L_d \approx 3.3h\) for all geometries in the experiment. Spatial coordinates \(x^*\) and \(y^*\) are presented as non-dimensional quantities with respect to the cavity depth h.

Fig. 1
figure 1

A schematic of the curved SWJ actuator used in the experiment, with major geometry elements indicated. Static pressure port locations are denoted with \((\bullet ),\) and hot-wire measurement locations with \((\times )\) symbols

Full size image

A 7-bar compressed air source provides the pressurized air at a temperature of 25 \(^{\circ }{\mathrm{C}}\). The inlet control parameter is the actuator mass flow rate \({\dot{m}}\), managed by an Alicat MCR-1500SLPM mass flow meter/controller. Mass flow rates used in the experiment range from 2 to 7 g/s, and the controller can maintain the desired value with a precision better than 0.1 g/s.

The internal flow of the actuator is characterized by time-resolved local static pressure, measured using Kulite XTL-140 high-frequency, absolute pressure transducers. The transducers are mounted flush with the floor of the actuator, at locations shown in Fig. 1. The pressure measurement locations correspond to: the throat of the actuator inlet \(p_{\mathrm{in}}\), the middle of the feedback channel \(p_f\), and \(p_d\) at location \(x^*,y^*=(1.57,0)\) in the diffuser. A National Instruments cDAQ\(^{\mathrm{TM}}\)-917 data acquisition system is used to acquire data simultaneously from all three channels, with a sampling rate of \(f_s= 10\) kHz and the acquisition period of \(T= 10\) s.

External properties of the jet are evaluated using a TSI IFA-300 anemometer with a single hot-wire TSI Model 1211. A TSI model 1129 automatic calibrator was used to calibrate the hot-wires over the range of 0–150 m/s, and a fourth-order polynomial was used to fit the velocity versus voltage curve. The typical uncertainty of the hot-wire velocity measurements across the entire range is less than \(3\%\). The probe was mounted on a two-axis computer-controlled translation stage, enabling the wire to traverse in the xy-plane located at the middle of the cavity depth h at \(z^*=0\). The hot-wire is placed perpendicular to the xy-plane, measuring a modulus of velocity \(U(t)=\sqrt{u^2(t)+v^2(t)}\) in that plane. In further text we represent the mean value of the velocity modulus as \({\overline{U}}\), and Root-Mean-Square (RMS) of its fluctuating part \(U'(t)=U(t)-{\overline{U}}\) as \(U'_{\mathrm{rms}}\). The velocity measurements are obtained at 21 locations in the spanwise direction with the distance between two adjacent measurements \(\Delta y = 5\) mm, as shown in Fig. 1. The data is acquired with a sampling rate of \(f_s=10\) kHz and the acquisition period of \(T= 10\) s.

2.2 Actuator geometries

The schematic representation of the three groups of modified designs of the SWJ actuator are shown in Fig. 2. The modified designs are superimposed on the reference geometry to highlight the changes. The geometric modifications focus on the variations of the feedback channel width \(D_1\), feedback channel outlet diameter \(D_2\), and the mixing chamber Coanda surface shape \(S_i\).

For the variations of \(D_1\), the diameter of the feedback channel is changed, while length of the straight part of the feedback channel is kept constant and identical to the reference geometry. We can also note that the connections between the straight part of the feedback channel (where we define \(D_1\)) and the main mixing chamber have been adapted to maintain the general shape of the original actuator as much as possible. The test cases include one geometry where the feedback channel width is smaller (\(D_1\times 0.5\)), and two where the width is larger (\(D_1\times 2.0\) and \(D_1\times 3.0\)) than the reference.

Fig. 2
figure 2

Geometric variations of the reference curved Sweeping Jet actuator. Structure of the unmodified Coanda surface is shown in the detail (dashed box)

Full size image

The modification of \(D_2\) has been implemented by moving the location of the inlet throat and the adjoining feedback outlet wall, with respect to the leading edges of the two Coanda surfaces. Again, we test three cases, where one outlet is smaller (\(D_2\times 0.5\)), and two other are larger than the reference (\(D_2\times 1.5\) and \(D_2\times 1.75\)). It must be noted that the modifications of \(D_2\) maintain a constant length of the mixing chamber \(L_{\mathrm{mc}}\), but the total actuator length \(L_{\mathrm{osc}}\) is modified. As shown in Fig. 1, the length of the mixing chamber \((L_{\mathrm{mc}})\) is defined as the horizontal distance between the Coanda surface leading edge and the feedback channel inlet corner. It is well-documented (Metka 2015; Seo et al. 2018) that \(L_{\mathrm{mc}}\) plays a crucial role in the determination of the oscillation frequency of the SWJ. Since, in our case \(L_{\mathrm{mc}}\) is constant, any modifications of the oscillation frequencies of \(D_2\) geometries must originate elsewhere.

Lastly, the modifications of the mixing chamber Coanda surface \(S_i\) are shown in Fig. 2. The portion of the reference geometry Coanda surface which will be modified in our experiment consists of three parts: part-I is a straight line of approximately 16\(^\circ \)  slope, part-II is a spline profile, and part-III is straight, horizontal line (see detail in Fig. 2). Firstly, we aim to simplify the Coanda surface profile; for \(S_1\), part-I, -II, and -III are substituted with an angled straight line of approximately 12\(^\circ \)  slope. The \(S_2\) actuator replaces the three segments with a 2nd-order polynomial curve. The \(S_3\) actuator features a Backward-Facing Step (BFS) profile, which consists of a straight line with a 2\(^\circ \)  slope (part-I), a spline profile (part-II), and a horizontal line similar to the reference geometry (part-III). The intention behind this design is to force a flow separation at a fixed streamwise location in the mixing chamber.

3 Results

3.1 The reference actuator

Fig. 3
figure 3

Flow properties of the reference geometry: a comparison of PSDs of pressure and velocity for \({\dot{m}} = 5\) g/s, b PSDs of \(p_d'(t)\) for \({\dot{m}} = 2{-}7\) g/s (in log-log scale, amplitudes shifted by a decade for clarity), profiles of c mean velocity \({\overline{U}}(y^*)\) and d RMS of velocity fluctuations \(U'_{\mathrm{rms}}(y^*)\) at \(x^*=4.88\), and e reference performance parameters \(f_0^{\mathrm{ref}}\), \(f_1^{\mathrm{ref}}\), \(p_{\sigma }^{\mathrm{ref}}\), \(p_s^{\mathrm{ref}}\), and \(\theta _{\mathrm{max}}^{\mathrm{ref}}\)

Full size image

The sweeping frequency of fluidic oscillators such as the curved SWJ is usually estimated using data from the mixing chamber (Ostermann et al. 2015a) or the feedback channels (Gaertlein et al. 2014; Yang et al. 2007). In the present experiment, both the feedback channels and the mixing chamber are independently modified, which means that the pressure signals obtained there may not be comparable between the designs. The detection of the SWJ frequency and its dispersion is then performed using sensor signals \(p_d'(t)\) in the diffuser (see Fig. 1), since data at this location comprise all of the effects of the modifications in the internal geometric features. The data from the pressure sensor in the center of the feedback channel \(p_f'(t)\) is only used to verify that our reference geometry (the non-modified curved SWJ) results correspond to literature. The comparative Power Spectral Density (PSD) of \(p_f'(t)\) and \(p_d'(t)\), together with PSDs of velocity fluctuations \(U'(t,y^*)\) from the hot wire measurements, are shown in Fig. 3a for reference. We can see that the fluctuations of both pressure and velocity are globally dominated by the well-defined periodic oscillations at the fundamental frequency, or by the first harmonic when the sensor is placed at the streamwise axis of the actuator, as in the case of \(p_d'(t)\) and \(U'(t,0)\).

The SWJ oscillation frequency is automatically detected from the PSDs using the FindPeaks function in MATLAB 2021a Signal Processing Toolbox. \(f_0\) is the sweeping jet fundamental frequency and \(f_1\), \(f_2\) and \(f_3\) are the harmonics. However, the fundamental frequency \(f_0\) is not clearly distinguishable for every SWJ geometry from the \(p_d'(t)\) sensor data; therefore, we use the first harmonic frequency \(f_1\) as the basis for the SWJ oscillation frequency detection. The PSD(\(p_d'\)) of the reference geometry for different mass flow rates are shown in Fig. 3b. The \(f_1\) frequency peak is clearly the more prominent in the \(p_d'(t)\) signal since the sweeping jet passes the horizontal symmetry axis twice per every oscillation cycle.

The properties of the jet downstream of the exit nozzle are investigated using a stationary hot-wire probe as described in Sect. 2. The resulting \({\overline{U}}\) and \(U'_{\mathrm{rms}}\) profiles for different mass flow rates are shown in Fig. 3c, d, respectively. Both the mean and RMS profiles feature two clear peaks, indicating a bifurcated jet typical for this type of the SWJ actuator. In fact, the RMS profiles for all actuator geometries in the current study follow the same patterns observable in their respective mean velocity profiles. Since they do not provide any additional insight, the RMS profiles are only shown here for the baseline geometry, but will be omitted from results on the modified actuator geometries in the subsequent sections.

The inlet velocities \({\overline{U}}_{\mathrm{in}}\) of the actuator are estimated to be in the range of 44–154 m/s for the range of mass flow rates used in the experiment. This estimation is based on the principle of mass conservation and the assumption of incompressibility (constant density of \(\rho = 1.18~{\mathrm{kg/m}^{3}}\)). The associated maximum Mach number \(M={\overline{U}}_{\mathrm{in}} / c\) is M = 0.48 for the mass flow rate of \({\dot{m}} = 7\) g/s. In a similar setup in Slupski et al. (2019), it is shown that the true Mach number is around M(7 g/s) = 0.38. Thus, the flow in the current experiment can be considered to be incompressible for \({\dot{m}}< 6\) g/s and the maximum Mach number is overestimated. However, since the current experimental model is not exactly the same as in the latter paper, we prefer using the estimated \({\overline{U}}_{\mathrm{in}}\) and \(\rho =const\) for obtaining dimensionless values, which does not qualitatively change any of the results presented in this paper.

The Reynolds number at the inlet of the actuator is defined as \(Re = {\overline{U}}_{\mathrm{in}} h/\nu \), where the kinematic viscosity has a value of \(\nu = 1.552 \times 10^{-5}\) \({\mathrm{m}^2/\mathrm{s}}\). The Reynolds number is in a range of \(1.8\times 10^4<Re<6.3\times 10^4\), well within the turbulent regime of a pipe flow. We can also estimate the Strouhal number of the actuator as \(St = f_0 h / {\overline{U}}_{\mathrm{in}}\). The Strouhal number of the reference geometry is in the range of \(0.013< St < 0.016\), which corresponds well to the values in literature (Woszidlo et al. 2019; Slupski et al. 2019; Oz and Kara 2020).

From the pressure and velocity measurements, described above, we can extract several important performance parameters, which will then be used as a benchmark for modified actuator geometries. These parameters are presented in Fig. 3d. From the pressure measurements we obtain the true sweeping frequency \(f_0\) and its harmonic \(f_1\), the intensity of the pressure fluctuations in the diffuser \(p_{\sigma }\), and the required supply pressure \(p_s\). Pressure fluctuations are estimated as the standard deviation of the static pressure in the diffuser \(p_d (t)\):

$$\begin{aligned} p_{\sigma }=\sqrt{\frac{1}{N}\sum _{t=1}^{N}{\left[ p_d(t) - \overline{p_d} \right] ^2}}, \end{aligned}$$
(1)

where N is the number of samples.

The time-averaged required supply pressure is expressed as \(p_s={\overline{p}}_{\mathrm{in}}-{\overline{p}}_{\infty }\), and is a useful indicator of the actuator’s overall efficiency (Woszidlo et al. 2019). Here, \({\overline{p}}_{\mathrm{in}}\) is the time-averaged static pressure at the inlet of the actuator (see Fig. 1), and \({\overline{p}}_{\infty }\) is the time-averaged ambient static pressure. The standard deviation of \(p_s\) for all actuator geometries is noted to be less than \(\pm 3\%\), regardless of the mass flow rate.

From the velocity data in Fig. 3c, the jet half-width is quantified as \(\delta \), which is the distance between \(y^*=0\) and \(y^*\) where \({\overline{U}}(y^*)\ge 0.5{\overline{U}}_{\mathrm{max}}(y^*)\) (Woszidlo et al. 2015; Koklu 2016). The jet half-width relates to the maximum jet deflection angle \(\theta _{\mathrm{max}}\) (Woszidlo et al. 2015) as:

$$\begin{aligned} \theta _{\mathrm{max}} =\tan ^{-1}{\left( \frac{\delta }{x^*}\right) }. \end{aligned}$$
(2)

For the reference actuator at \(x^*=4.88\) the average jet half-width is almost constant \(\delta ^{\mathrm{ref}} =7.46\), which corresponds to \(\theta _{\mathrm{max}}^{\mathrm{ref}} \approx 56.8^{\circ }\) throughout the studied mass flow rates (Fig. 3d).

In the following sections we will benchmark the performance of different actuator geometries with respect to the reference geometry described here. All the performance parameters (\(f_0\), \(p_{\sigma }\), \(p_s\), and \(\theta _{\mathrm{max}}\)) will be presented as a relative change of a given variable \(\psi \), with respect to the value \(\psi ^{\mathrm{ref}}\) of the reference geometry as: \(\Delta \psi = (\psi -\psi ^{\mathrm{ref}})/ \psi ^{\mathrm{ref}}\).

3.2 Modifications of the feedback channel width \(D_1\)

Fig. 4
figure 4

Flow properties of actuators with a modified feedback channel width \(D_1\), for \({\dot{m}} = 2{-}7\) g/s: a PSDs of \(p_d'(t)\) (in log-log scale, amplitudes shifted by a decade for clarity), b mean velocity profiles \({\overline{U}}(y^*)\) at \(x^*=4.88\), c relative performance parameters with respect to the reference geometry \(\Delta f_0\), \(\Delta p_{\sigma }\), \(\Delta p_s\), and \(\Delta \theta _{\mathrm{max}}\)

Full size image

The results of the modifications of the feedback channel width \(D_1\) (see Fig. 2) are showcased using the PSD(\(p_d'\)) in Fig. 4a. In the PSDs of the \(D_1\times 0.5\) actuator, with the contracted feedback channel, we can note that the fundamental and first harmonic frequency peaks are not as well defined as in the reference case (see Sect. 3.1), while the higher harmonics become indistinguishable for some mass flow rates. On the contrary, the enlarged feedback channel actuators \(D_1\times 2.0\) and \(D_1\times 3.0\) show the fundamental and harmonic peaks to be comparable to the reference at all mass flow rates, with common features throughout the spectrum. It can be concluded that the flow regime is similar for the reference, \(D_1\times 2.0\) and \(D_1\times 3.0\) actuators, while the smaller \(D_1\times 0.5\) actuator is subject to different phenomena.

The external jet properties of these actuators are represented through \({\overline{U}}(y^*)\) profiles in Fig. 4b. For the \(D_1\times 2.0\) and \(D_1\times 3.0\) geometries, the \({\overline{U}}(y^*)\) distributions are featuring a bifurcated jet profile for all mass flow rates. The \(D_1\times 3.0\) distributions are slightly asymmetric and have a flatter profile around the axis of symmetry. On the other hand, \(D_1\times 0.5\) provokes velocity distributions centered around the axis of symmetry for low mass flow rates of \({\dot{m}}\) = 2–3 g/s. For higher mass flow rates of \({\dot{m}}\) = 4–6 g/s there is a clear change in the flow regime to a much flatter jet profile, with some features of the asymmetric bifurcated jet. However, at \({\dot{m}}\) = 7 g/s the velocity distribution again becomes shifted toward the axis of symmetry, although the remnants of the two peaks around \(y^*\approx \pm 6\) are still visible, indicating that the jet mostly oscillates near the middle but is also capable of exploring larger deflection angles. These flow regime changes are quite clearly observable in the PSDs (see Fig. 4a) for this geometry, where we can note a wider \(f_0\) peak and a damping of the fundamental frequency for mass flow rates of \({\dot{m}}\) = 2, 3, and 7 g/s.

The performance parameters of the modified \(D_1\) geometries are shown in Fig. 4c, where the dashed line denotes reference values from the unmodified actuator geometry. The sweeping frequency for \(D_1\times 0.5\) is globally reduced with a minimum of \(\Delta f_0\approx -8\%\), while the slope of the evolution changes above \({\dot{m}}\) = 3 g/s, corresponding to the flow regime change observed from the \({\overline{U}}(y^*)\) distributions. For \(D_1\times 2.0\) and \(D_1\times 3.0\), the frequency is generally increased in a range of \(+2\%<\Delta f_0 < +10\%\). The slope of \(\Delta f_0\), in the former case, relaxes above \({\dot{m}}\) = 4 g/s, while the slope for the latter case is largely constant. Going back to Fig. 4b, we can see that the higher slope for \(D_1\times 2.0\) corresponds to the two profiles (\({\dot{m}}\) = 2 and 3 g/s) with a higher velocity around \(y^*=0\) compared to their maximum values.

The relative pressure oscillation amplitude is on the average \(\Delta p_{\sigma }\approx -45\%\) for the \(D_1\times 0.5\), as corroborated by the lower peak amplitudes in the appropriate PSDs in Fig. 4a for all mass flow rates. For \(D_1\times 2.0\), \(p_{\sigma }\) is equivalent to the reference, while for For \(D_1\times 3.0\), it can be as low as \(\Delta p_{\sigma }= -12\%\) for some mass flow rates.

The relative supply pressure \(\Delta p_s\), shown in Fig. 4c, is generally negative for all \(D_1\) geometries. The smaller feedback channel geometry \(D_1\times 0.5\) has a minimum of \(\Delta p_s\) around \(-15\) to \(-20\%,\) for the mass flow rates associated with a non-bifurcating jet (\({\dot{m}}\) = 2 and 3 g/s). For \(D_1\times \) 3.0, \(\Delta p_s\) exhibits a minimum value of around \(-10\%.\) We can note a nice correlation between the general trends in behavior between \(\Delta p_{\sigma }\) and \(\Delta p_s\) for all three geometries.

The velocity information from the hot-wire data are presented as the maximum deflection angle \(\Delta \theta _{\mathrm{max}}\) in Fig. 4c. The enlarged \(D_1\)s feature a near constant jet spreading regardless of the mass flow rate. The \(\Delta \theta _{\mathrm{max}}\) values are, however, slightly below the reference actuator. This smaller \(\Delta \theta _{\mathrm{max}}\) and the flatter distribution (albeit irregular) of the velocity profiles between the two maxima could be an indicator that the instantaneous jet is wider and more diffused for these geometries. The exception to this behavior is again the \(D_1\times 0.5\) actuator which features a much reduced \(\Delta \theta _{\mathrm{max}}\) at low mass flow rates. When the flatter jet profile is present for intermediate mass flow rates, \(\Delta \theta _{\mathrm{max}}\) becomes similar to the reference actuator, but it drops off again at the highest tested mass flow rate of 7 g/s.

We can conclude that the enlarged feedback channel provokes an increase in the sweeping frequency, which is obtained at a slightly lower required supply pressure and a marginal reduction in maximum jet deflection. On the other hand, the smaller diameter of the feedback channel causes a reduction of oscillation frequency. For small mass flow rates, the feedback flow appears to be too weak to cause a clear bifurcated behavior of the external flow, with significantly reduced deflection angles. At higher mass flow rates, the deflection angle is recovered, but the frequency is still lower than the reference actuator. It is interesting to note here that the frequency is not strongly coupled with the deflection angle.

3.3 Modifications of the feedback channel outlet diameter \(D_2\)

Fig. 5
figure 5

Flow properties of actuators with modified feedback channel outlet diameter \(D_2\). See caption of Fig. 4 for details

Full size image

The effects of a modified feedback channel outlet diameter \(D_2\) (see Fig. 2) on the PSDs of the pressure fluctuations \(p_d'(t)\) are shown in Fig. 5a. Similar as in the case of a smaller \(D_1\) geometry, the \(D_2\times 0.5\) exhibits a poorly defined peak at \(f_0\), throughout the range of different mass flow rates. However, whereas the larger \(D_1\)s featured a similar spectrum to the reference actuator, the larger \(D_2\)s show a significant departure from it. For certain mass flow rates, both the \(D_2\times 1.5\) and \(D_2\times 1.75\) geometries feature fluctuations at very high frequencies (\(f\sim 3\times 10^3\) Hz). For mass flow rates of \({\dot{m}}\) = 3 g/s, for the \(D_2\times 1.5\), and \({\dot{m}}\) = 3–4 g/s for the \(D_2\times 1.75\), these fluctuations are very well defined and produce multiple harmonics in the spectrum. Even more striking is the complete damping of the jet oscillation for the \(D_2\times 1.75\), at a mass flow rate of \({\dot{m}}\) = 5 g/s, where the expected sweeping frequency peak is completely absent. We suspect that the same phenomenon is responsible for the sudden decrease in the peak amplitude and definition of the jet sweeping frequency for the \(D_2\times 1.5\) geometry at \({\dot{m}}\) = 7 g/s. That there is still a peak in the spectrum of \(D_2\times 1.5\) could be a consequence of the flow regime becoming compressible or the set mass flow rate not being the exact needed for the oscillation extinction. It would be interesting to explore if a similar resonance occurs for even larger \(D_2\)s.

Velocity profiles of the external jet for \(D_2\) geometries are shown in Fig. 5b. For mass flow rates \({\dot{m}}\) = 2 and 3 g/s, the \(D_2\times 0.5\) actuator produces a jet profile similar to a free jet, with a very sharp bell curve distribution around the axis of symmetry. From the PSDs, however, it turns out that even this jet is capable of oscillating at a specific (if poorly defined) sweeping frequency. The jet velocity profile changes significantly for \({\dot{m}} \ge \) 4 g/s, where the mean velocity is still high around the axis of symmetry, but the distribution is quite different around the extremes of the profile (\(y^*\sim \pm 5\)). For the \(D_2\times 1.5\) and \(D_2\times 1.75\) geometries, velocity distributions are that of a bifurcated jet, which are not as self-similar as those in the case of the actuators with enlarged feedback channel width \(D_1\times 2.0\) and \(D_1\times 3.0\) (see dimensionless velocity profiles in Fig. 7). In addition, we see a bell-curve distribution for \(D_2\times 1.75\) at \({\dot{m}}\) = 5 g/s which is related to the interruption of the sweeping process, as observed earlier from spectral data. We can immediately note that this profile is very similar to the one occurring at low mass flow rates for \(D_2\times 0.5\), but this time the effects on the sweeping process are much more significant.

The general trends of variations of \(\Delta f_0\), can be observed in Fig. 5c. The decrease of \(D_2\) diameter provokes a globally higher oscillation frequency. However, the behavior of \(\Delta f_0\) is erratic for the increased outlet diameters; for \(D_2\times 1.5\) the detected frequencies vary in a non-monotonic manner around the reference. In the case of \(D_2\times 1.75\), the frequency evolution clearly changes at \({\dot{m}}\) = 5 g/s, where the sweeping oscillations are extinguished, and there is no detected frequency. From the PSD in Fig. 5a the frequency of this jet might be related to the broadband bump visible around \(f\sim 1.5\times 10^3\) Hz. The \(\Delta p_{\sigma }\) in Fig. 5c is very low for \(D_2\times 0.5\), reminiscent of the effects observed in the case of \(D_1\times 0.5\). For \(D_2\times 1.5\), the trend of \(\Delta p_{\sigma }\) follows the reference until \({\dot{m}}\) = 5 g/s, after which the fluctuations are quickly reduced. For the case of \(D_2\times 1.75\) where the sweeping process is arrested, the \(\Delta p_{\sigma }\) value features a very low minimum \((-70\%).\) The relative required supply pressure \(\Delta p_s\), in Fig. 5c, is lower for \(D_2\times 0.5\), but generally higher for designs with larger feedback channel outlet diameter.

The effects of \(D_2\) modifications on the relative jet deflection angle \(\Delta \theta _{\mathrm{max}}\) are also summarized in Fig. 5c. We can note the significant reduction of the jet deflection for \(D_2\times 0.5\), especially in the lower mass flow regime. Also, the change of the jet regime for \(D_2\times 1.5\) at \({\dot{m}}\) = 7 g/s produces a noticeably lower \(\Delta \theta _{\mathrm{max}}\), although this reduction is small compared to the \(\Delta \theta _{\mathrm{max}}\) of \(D_2\times 1.75\) at \({\dot{m}}\) = 5 g/s, where the sweeping process is extinguished.

The geometries with the enlarged feedback channel outlet diameter \(D_2\times 1.5\) and \(D_2\times 1.75\) cause the sweeping frequency to fluctuate around the mean value of the reference. The associated required supply pressure \(p_s\) is higher, whereas the jet deflection \(\theta _{\mathrm{max}}\) is similar to the reference in most cases. The contracted feedback channel outlet causes a significant increase in oscillation frequency of \(D_2\times 0.5\), accompanied by a very different external flow and its associated global reductions of \(p_{\sigma }\), \(p_s\), and \(\theta _{\mathrm{max}}\). We will revisit these observations in the discussion in Sect. 4.3.

3.4 Modifications of the Coanda surface \(S_i\)

Fig. 6
figure 6

Flow properties of actuators with modified Coanda surface \(S_i\). See caption of Fig. 4 for details

Full size image

The effects of different Coanda surfaces on the spectral properties of the flow are shown in Fig. 6a. The PSD(\(p_d'\)) clearly show a strong influence of different \(S_i\) shapes on both the frequency and the peak definition. The straight Coanda surface profile \(S_1\) actuator features a very well-defined system of harmonics throughout the examined mass flow rates, resembling closely the reference actuator spectral distributions. The 2nd-order polynomial profile \(S_2\), and the BFS profile \(S_3\) have relatively poorly defined first harmonic peaks and almost indistinguishable fundamental frequency peak. It can also be observed, that for \(S_2\) at \({\dot{m}} \ge 4\) g/s, the occupied bandwidth of the first harmonic increases drastically.

External jet velocity distributions in Fig. 6b reveal a rich pattern of external flow behaviors, corresponding to what is observed in the PSDs. Well-defined frequency peaks correspond to a bifurcated jet profile for \(S_1\), while badly-defined frequency peaks correspond to velocity distributions around the axis of symmetry \(y^*=0\), which is the case for both \(S_2\) and \(S_3\). A major feature of the velocity profile of \(S_1\) is a generally lower magnitude of mean velocity across the entire \({\overline{U}}(y^*)\) profile, in comparison to the reference (see Fig. 3c).

The \(S_2\) actuator velocity profiles feature two small peaks close to the axis of symmetry (\(y^*\approx \pm 1.5\)), for \({\dot{m}}\) = 2,3 and 5 g/s. For \({\dot{m}} = 4\) g/s, however, we can observe an abrupt change to a sharp bell-curve distribution, which then returns for \({\dot{m}}\ge 6\) g/s. A similar two-peak distribution, even closer around \(y^*=0\), is observed for \(S_3\) for all mass flow rates except \({\dot{m}} = 6\) g/s, where a sharper bell-curve distribution exists. These two-peak velocity profiles are a strong confirmation that the flow is still a bifurcated sweeping jet, and relate well to the appropriate PSDs in Fig. 6a, which have a higher amplitude and better definition of the oscillation frequency peaks.

Figure 6c summarizes the changes in \(\Delta f_0\), \(\Delta p_{\sigma }\), \(\Delta p_s\), and \(\Delta \theta _{\mathrm{max}}\) values with respect to the increasing \({\dot{m}}\). The relative oscillation frequency is noticeably higher for \(S_2\) and \(S_3\), where we note an average increase of 6 and \(11\%\) in \(\Delta f_0\). The same is marginally positive for \(S_1\) as \(\Delta f_0\) is in a range of 0–4%. For \(S_2\), we observe a change of the slope of \(\Delta f_0\) for \({\dot{m}} > 4\) g/s, corresponding to the noted changes in the \({\overline{U}}(y^*)\) profile.

For both \(S_2\) and \(S_3\), \(\Delta p_{\sigma }\) values are drastically negative, with a slope change for \({\dot{m}} > 4\) g/s. \(S_1\) provokes again a marginally lower \(p_{\sigma }\) compared to the reference actuator. The relative required supply pressure \(\Delta p_s\) for \(S_2\) and \(S_3\) has an average value of around \(-25\%\) and \(-18\%,\) respectively. In the case of \(S_1\) the required pressure is only slightly lower than the reference (\(-5\%\) on average). The relative jet deflection angles \(\Delta \theta _{\mathrm{max}}\), shown in Fig. 6c, capture well the transitory changes in the flow regimes of \(S_2\) and \(S_3\).

In summary, the \(S_1\) actuator performs very similarly to the reference curved geometry, although its Coanda surface shape is much simpler. The \(S_2\) and \(S_3\) actuators adopt a completely different flow regime, which is somewhat similar to what was observed earlier for \(D_2\times 0.5\). There, the oscillation frequencies are higher, but the deflection angles are significantly reduced compared to the reference geometry. Again this smaller deflection angle is strongly correlated with a decrease in the pressure losses and pressure fluctuations. It should be also noted that \(S_1\) maintains a very consistent performance throughout the examined range of mass flow rates, while the flow patterns and performance parameters for both \(S_2\) and \(S_3\) are much more sensitive to the mass flow rate set point.

4 Discussion

4.1 Flow regimes of the modified geometries

Fig. 7
figure 7

Categorization of flow regimes of all modified actuator geometries, based on non-dimensional velocity profiles \(U^*(y^*)\) at \(x^*=4.88\)

Full size image

Our experiment focused on limited local modifications in order to isolate the impact of specific geometric elements to the performance of the actuator. Nevertheless, local geometry modifications were capable of provoking very different external jet flows. The general behavior of the external flow for all geometries is categorized in Fig. 7 using the non-dimensional velocity profiles \(U^* = {\overline{U}}(y^*) / {\overline{U}}_{\mathrm{in}}\), where \({\overline{U}}(y^*)\) is the mean velocity at a given span-wise location, and \({\overline{U}}_{\mathrm{in}}\) is the estimated mean velocity at the inlet of the actuator.

Two major flow behaviors can be clearly distinguished in Fig. 7: a bifurcated velocity profile, and a homogeneous velocity profile. The former velocity profile is similar to what is obtained from a canonical curved SWJ actuator, whose data is shown from our reference geometry. The homogeneous velocity profile is similar to the velocity profile obtained from the angled SWJ actuator, sketched in Fig. 7. Some actuator geometries fall in-between these two categories as their behavior changes from a bifurcated to a homogeneous velocity profile depending on the mass flow rate. All actuator designs feature mean velocity profiles which vary depending on the mass flow rate, as it can be seen in Fig. 7 in cases where the non-dimensional velocity does not collapse perfectly. However, these variations are much more pronounced for the actuators which produce a homogeneous jet profile. Some jet velocity profiles in this group are broadly similar to a plain jet profile (for example, \(D_2\times 0.5\) and \(S_2\) at certain mass flow rates), but the associated PSDs of pressure signals confirm that they still oscillate at a specific frequency related to the Strouhal number of the sweeping. The single exception is the case of \(D_2\times 1.75\) at \({\dot{m}} = 5\) g/s where there is no discernible frequency around the expected Strouhal number, rather the broadband, high-frequency fluctuations (see Fig. 5a) bear a strong resemblance to the natural instabilities of plain jet shear layers. Thus, the term “homogeneous” in the above discussion refers to the mean velocity profile that does not represent a typical twin-peak distribution expected from a bi-stable jet, but is still dominated by a well-defined oscillation period accompanied by a lower jet deflection angle.

Vatsa et al. (2012) performed the first direct comparison of the external flows between a curved and an angled SWJ. Some experimental details and results are shown next to the angled actuator sketch in Fig. 7 as reference. It should be noted that the magnitudes of \(U^*\) in this experiment are not directly comparable to ours, since Vatsa et al. (2012) uses a shorter diffuser length \(L_d=1h\) and the velocity is measured at \(x^*=2\). Nevertheless, their results demonstrate a clear difference between the two external flow regimes.

An even more detailed comparison of the spatially resolved flow fields between the angled and curved actuators can be found in Ostermann et al. (2015a). From time-resolved velocity fields of the internal flow, the angled actuator is found to have a higher deflection angle of the internal jet (compared with the curved SWJ), as it interacts with the converging internal part of the exit nozzle (just upstream of the throat). Opposite of what would be then expected, the resulting external flow is a homogeneous jet with a lower deflection angle. Ostermann et al. (2015a) attribute this discrepancy to the larger diffuser opening angle of \(125^\circ \) of the angled actuator, which is deemed too large for the external jet to re-attach to, thus oscillating closer to the axis of symmetry and producing a completely different external flow pattern.

In our experiment, the mixing chamber of the \(S_3\) (BFS Coanda surface) actuator is broadly similar to the mixing chamber of the angled actuator (see Fig. 7); they both feature a sharp backward facing step, followed by a horizontal flat surface. Comparing \(S_3\) to the reference (curved) geometry, the Coanda surface shape is the only feature of difference between the two actuators (the exit nozzle and the diffuser geometries are identical). We can conclude that the BFS profile is the main reason for \(S_3\) producing an external jet which is quite reminiscent of the angled SWJ external jet. A similar effect on the external flow is also observed for \(S_2\) (2nd-order polynomial Coanda surface) actuator. For this design, the distance between two opposing Coanda surfaces is curtailed substantially. Wen et al. (2020) reported that by reducing the distance between the mixing chamber walls, the size of the recirculation bubble reduces, resulting in a lower jet spreading, similar to our case. We can reasonably conclude that the different Coanda surfaces modify the dynamics of the flow separation and recirculation, and thus the properties of the periodic symmetry breaking of the flow inside the mixing chamber. These changes are the dominant factor determining the external flow regime, everything else being identical between different actuator geometries.

A homogeneous velocity profile of the jet persisting throughout the entire range of tested mass flow rates is also observed for the \(D_2\times 0.5\) actuator. In this case, the feedback channel outlet is smaller but the geometry of the Coanda surface is not altered. We can hypothesize that the initial properties of the jet are modified before it enters the mixing chamber, consequently impacting the dynamics of the flow in the mixing chamber. Actuators \(D_1\times 0.5\) and \(D_2\times 1.5\) also feature a homogeneous jet velocity profile, albeit only for certain mass flow rates (see Fig. 7). We shall discuss this further in Sect. 4.3.

4.2 The impact of the flow regime on actuator performance parameters

Fig. 8
figure 8

Relationships between the non-dimensional required supply pressure \(p_s / q_{\mathrm{in}}\) and: a Strouhal number St, b jet deflection angle \(\theta _{\mathrm{max}}/\theta \), and c static pressure fluctuations in the diffuser \(p_{\sigma }/q_{\mathrm{in}}\), where \(q_{\mathrm{in}}=\frac{1}{2}\rho {\overline{U}}_{\mathrm{in}}^2\), and \(\rho =\hbox {const}\). Data points are represented based on their association to a bifurcated (\(+\)), or a homogeneous (\(\triangleright \)) jet velocity profile. See Fig. 7 for details

Full size image

In this section, we examine how St, \(\theta _{\mathrm{max}}\), and \(p_{\sigma }\) are modified by the two different flow regimes as a function of \(p_s\), since the required supply pressure determines how efficient is the actuator in flow control applications.

The first comparison presented in Fig. 8a relates the required supply pressure \(p_s / q_{\mathrm{in}}\) to the resulting Strouhal number St. Here, we can see that most data points for both external flow regimes are located around a typical Strouhal number for sweeping jets of \(St \approx 0.015\). Bifurcated jets tend to require a higher supply pressure and yield oscillations in a mid-to-low Strouhal number range, while homogeneous jets yield a mid-to-high Strouhal number associated with lower required pressure for their operation. Still, there is a large overlap in Strouhal numbers of both groups and we can conclude that the non-dimensional sweeping frequency is only weakly dependent on the flow regime, or its associated pressure requirement.

Second, we examine the relationship between supply pressure \(p_s / q_{\mathrm{in}}\) and the maximum jet deflection angles \(\theta _{\mathrm{max}}/\theta \) in Fig. 8b. Immediately, it can be observed that all of the actuator geometries which feature a bifurcated jet experience a saturation of the maximum jet deflection angle. It is well known that the jet deflection is significantly affected by the diffuser length (Koklu 2016) and the nozzle exit angle (Woszidlo et al. 2015). For actuators with a long diffuser, the Coanda effect between the jet and the diffuser side-walls enhances the jet deflection, provided that the right conditions are met in terms of jet’s capacity to re-attach. The relatively long diffuser in our case plausibly causes any bifurcating jet to re-attach to the diffuser wall, yielding \(\theta _{\mathrm{max}} / \theta > 1\). The values greater than one are a consequence of the measurement location downstream of the end of the diffuser at \(x^*=4.88\), where the separated jet can be expected to spread much more rapidly (Ostermann et al. 2015a), as beautifully visualized in Sieber et al. (2015). On the other hand, geometries with the homogeneous jet distribution demonstrate a progressive reduction of \(\theta _{\mathrm{max}} / \theta \) generally correlated with a lower \(p_s / q_{\mathrm{in}}\). The two data points associated with the homogeneous jet but having a high values of \(p_s / q_{\mathrm{in}}> 1.6\) are special cases of enlarged \(D_2\) actuators. Regardless of flow regime, most data points above the value of \(p_s / q_{\mathrm{in}}= 1.4\) belong to \(D_2\times 1.5\) and \(D_2\times 1.75\) actuators which require an increased supply pressure throughout the range of the tested mass flow rates (see Fig. 5c). In these cases, it is reasonable to conclude that the additional pressure losses are a result of the enlarged feedback channel outlet geometry and its effects on the internal flow.

Finally, the relationship between \(p_s / q_{\mathrm{in}}\) and non-dimensional pressure fluctuations in the diffuser \(p_\sigma / q_{\mathrm{in}}\) is shown in Fig. 8c. Here we see a very nice correlation between the two; high pressure fluctuations correlate well with the bifurcated jet, and vice versa. The correlation between the flow regime and values of \(p_\sigma / q_{\mathrm{in}}\) indicate that the pressure is dominated by the large scale unsteadiness due to the global sweeping motion, and is less sensitive to the turbulence properties of the jet. In a flow control scenario where the sweeping characteristics of the actuator are important, the \(p_\sigma \) can be taken as a simple measure of the effectiveness of the actuator, broadly similar to the switching quality \(\kappa \) defined by Schatzman et al. (2014).

4.3 External jet characterization

In this section we present a more detailed characterization of the external flow, through phase-average and auto-correlation of the local velocity data from the hot-wire sensor.

Fig. 9
figure 9

Spanwise location \(y^*\) (\(+\)) of the phase-averaged velocity \(U^*_{\mathrm{max}}(\phi )\) at \(x^*=4.88\) for \({\dot{m}} = 2{-}7\) g/s. Instantaneous jet width \(w^*(\phi )\) is represented with the two continuous lines. The dashed line represents the barycenter of the \(U^*(\phi ,y^*)\) profile

Full size image

The dimensionless velocity \(U^*(t,y^*)\) from hot-wire measurements is phase-averaged to obtain \(U^*(\phi , y^*)\). From the phase-locked velocity profiles we extract the instantaneous spanwise location of the maximum of the jet velocity \(U^*_{\mathrm{max}}(\phi )\) and the corresponding jet width \(w^*(\phi )\). The jet width is defined as the distance between two spanwise locations on either side of \(U^*_{\mathrm{max}}(\phi )\) where local velocity first becomes \(U^*(\phi , y^*)\le 0.6 U^*_{\mathrm{max}}(\phi )\). The threshold of 60% of the local maximum velocity is arbitrary. Figure 9 shows the resulting trajectory of the phase-averaged velocity maximum and the associated jet width for all actuator designs and mass flow rates.

The major difference between the previously discussed two flow regimes is clearly observed here, as the ability of the jet to deflect and linger beyond \(y^*=\pm 5\), indicating that the flow has re-attached to the wall of the diffuser (see for example Ref. in Fig. 9). For \(D_1\times 2.0\) and \(D_1\times 3.0\) actuators, the velocity maximum remains beyond \(y^*=\pm 5\) for a shorter time compared to the baseline actuator. This implies a shorter dwelling time of the jet and correlates well with the increased sweeping frequency of these two actuators. However, the jet becomes more diffused, especially in the range of \(90^{\circ }<\phi <180^{\circ }\) where it starts to move away from the spanwise extreme toward the center (the same occurs for \(270^{\circ }<\phi <360^{\circ }\) as the jet starts back from the opposite state). This modified velocity distribution is reflected in the flatter mean velocity profiles observed earlier for \(D_1\times 2.0\) and \(D_1\times 3.0\). We can conclude that the enlarged feedback channel diameter causes the jet dwelling time to be reduced, and the switch between the two states to be less well defined.

Actuators with enlarged feedback channel outlet \(D_2\times 1.5\) and \(D_2\times 1.75\) also show a clear bi-stable behavior, with exceptions for specific mass flow rates as pointed out earlier. Their phase-averaged velocity profiles are mostly unremarkable compared to the baseline actuator. Only a small reduction of \(w^*(\phi )\) and dwelling time can be observed around \(\phi =90^{\circ }\) and \(270^{\circ }\), when the jet is in one of the two stable states. Hence, enlarging the feedback channel outlet does not significantly change the external flow, except for mass flow rates where the sweeping is damped or extinguished.

The straight Coanda surface actuator \(S_1\) has a very similar phase-averaged velocity profile as the baseline actuator; it exhibits an abrupt switch between the two stable states, with comparable dwelling times. We can also note that these properties are stable across the entire range of the mass flow rates, which makes \(S_1\) and the baseline actuator the most consistent performers of all the configurations tested.

On the other hand, for \(D_1\times 0.5\) we can observe an overall thinner jet, with state changes which appear more gradual. Even for mass flow rates (\({\dot{m}}\) = 4–6 g/s) when the jet is deflected beyond the re-attachment threshold of \(y^*=\pm 5\), the maximum velocity remains there for a much shorter time, followed by a gradual trajectory across the axis of symmetry. It is noteworthy that the reduction of the sweeping frequency of \(D_1\times 0.5\) is accompanied by the maximum deflection angle which is very similar to the baseline actuator. We can then conclude that the contraction of the feedback channel can directly modify the angular velocity of the sweeping jet.

In the case of \(D_2\times 0.5\), \(S_2\), and \(S_3\) actuators, the sweeping motion is clearly curtailed. For \(D_2\times 0.5\) at \({\dot{m}}\) = 2, 3 g/s, and \(S_2\) at \({\dot{m}}\) = 4, 6, 7 g/s, we observe a thin jet which meanders periodically around the axis of symmetry, with minimal changes in its \(w^*(\phi )\). At other mass flow rates, these three actuator designs show an increase in jet deflection and an increase in \(w^*(\phi )\) for the two stable states around \(\phi =90^{\circ }\) and \(270^{\circ }\). This, however, is not enough to cause the jet to reach the re-attachment threshold, and so the dwelling time is small and the switching between the states is gradual.

Fig. 10
figure 10

External flow coherence maps of the auto-correlation function r of \(U(t, x^*=4.88, y^*)\) vs. the dimensionless oscillation period \(\tau ^*\), for \({\dot{m}} = 2{-}7\) g/s

Full size image

We can further quantify the evolution of the velocity signal spectral properties using the Auto-Correlation Function (ACF). Ostermann et al. (2015b) reported that ACF yields the most promising results in identifying the oscillation period since it is less prone to local fluctuations, attributable to the fact that the calculation of the correlation coefficient takes the local mean and RMS values into account. The ACF measures the similarity between time series \(Y_t\) and the lagged versions of the same time series \(Y_{t+k}\) as a function of the lag, where \(k=\) 0 to K. According to Box (1994), the auto-correlation for lag k can be expressed as:

$$\begin{aligned} r = \frac{\ 1/T\sum _{t=1}^{T-k} (Y_t - {{\overline{Y}}}) (Y_{t+k} - {{\overline{Y}}})}{\ \sigma ^2} \end{aligned}$$
(3)

where \(\sigma ^2\) is the sample variance of the time series. The values of auto-correlation r for each hot wire signal \(U(t, y^*)\) are shown as the color map in Fig. 10, versus a number of time lags k which correspond to 10 non-dimensional oscillation periods \(\tau ^*\) of the baseline actuator at a given mass flow rate: \(\tau ^*=kf_s/f_{0}^{\mathrm{ref}}({\dot{m}})\).

Figure 10 clearly shows the differences in the spatio-temporal coherence of the sweeping jet for the two external flow regimes. Actuator geometries Ref., \(D_1\times 2.0\), \(D_1\times 3.0\), and \(S_1\) which feature a bifurcated jet profile (see Fig. 7), have a long flow memory and the periodic motion is clearly visible across the entire hot-wire profile. In these cases, the fundamental frequency \(f_0\) is detected near the extremes of \(y^*\), while a double frequency (\(f_1\)) dominates the middle of the spanwise profile. The waviness observed for ACF profiles at higher time lags is due to minute differences in the detected frequency of the hot-wire signals for different \(y^*\), since the measurements of \(U(t,y^*)\) are not synchronous. The maximum standard deviation of detected \(f_0\) is less than 0.5% of the mean value for most mass flow rates, but sharply increase to a maximum of 1.3% for \({\dot{m}}\) = 7 g/s. These deviations are not correlated with the \(y^*\) of the measurement and are most likely caused by small fluctuations in the mass flow rate and the compressed air supply, between velocity data acquisitions.

The second group of actuators, which are producing a homogeneous velocity profile (see Fig. 7), can cause two distinct coherency patterns. In the cases where the periodic motion is well-defined (for example, \(S_3\) for all mass flow rates), the high values of r are restricted to a spanwise band delimited by the jet’s lower sweeping angle. Comparing the phase-averaged data for \(S_3\) in Fig. 9 and its auto-correlation map in Fig. 10, we see that there is a strong correlation between the sweeping angle \(\theta _{\mathrm{max}}\) and the vanishing of \(r(\tau ^*)\). The flow history is more preserved for lower \({\dot{m}}\) where the \(\theta _{\mathrm{max}}\) is larger, although re-attachment to the diffuser is not achieved by the \(S_3\) actuator for any mass flow rate. When the \(\theta _{\mathrm{max}}\) is low (for example \(S_2\) for \({\dot{m}}\) = 4 g/s), we can see a high positive r value beyond \(y^*=\pm 5\) and for small \(\tau ^*\). In such cases, the sweeping jet is not reaching far along the spanwise direction (on either side), and the undisturbed hot-wire sensor signal has a high auto-correlation value. To a various degree, this coherency pattern is common for all the cases where we observe a sharp, bell-curve mean velocity profile: \(D_2\times 0.50\) at \({\dot{m}}\) = 2, 3 g/s, \(D_2\times 1.75\) at \({\dot{m}}\) = 5 g/s, and \(S_2\) at \({\dot{m}}\) = 4, 6, 7 g/s (see Figs. 5b and 6b, respectively).

5 Conclusions

We experimentally investigated the impact of the internal geometry modifications on the performance of a curved sweeping jet actuator. Specifically, the effects of the feedback channel width (\(D_1\)), its outlet diameter (\(D_2\)), and the Coanda surface structure (\(S_i\)) are examined.

The major effect of geometry modifications is that the resulting flow regimes resemble either a classical curved actuator featuring a bifurcated jet profile, or the flow becomes similar to the homogeneous jet profile commonly found for the angled actuator. An important observation is that by changing only the Coanda surface shape of a curved SWJ actuator, the external flow can be made to resemble the flow out of the angled SWJ actuator. It is also found that the jet deflection angles and static pressure fluctuations in the diffuser are well correlated to the required supply pressure. Thus, the differences in the pressure losses and the associated efficiency of the actuator can be attributed mainly to the external flow regime. It is also observed that the coherence of the external flow is always improved as the sweeping angle is increased, even in cases when the jet does not re-attach to the diffuser wall.

The sweeping frequency is found to be only weakly related to the flow regime, although a bifurcated jet profile is typically accompanied by a lower sweeping frequency than the homogeneous jet profile. An exception is the \(D_1\times 0.5\) which produces a lower frequency despite having low jet deflection angles, which is a probable consequence of a lower possible volume flux through the contracted feedback channel. However, an even more intriguing result is the increase in frequency of the enlarged \(D_1\) actuators, which was unexpected given the results in literature for similar modifications of the angled actuator geometry. In this case, the phase-averaged, phase-locked velocity profiles reveal a lower jet dwelling time at the two stable states, and a more diffused jet during transitions.

The actuator \(S_1\) with a straight Coanda surface performed equally well as the reference case in all aspects, which implies that the canonical curved geometry could be simplified without any significant loss in performance. Furthermore, we observe a striking difference between the external flows of \(S_1\) and \(S_2\) actuators, whereas their respective simple geometries are only slightly different. We propose that an actuator could be made with a shape memory alloy for the Coanda surface wall, which could change from straight to curved geometry based on external input. Such a hybrid actuator could work in both bifurcated and homogeneous jet regimes, as desired.

We can conclude that the performance of the canonical curved SWJ can be improved, or at least, that the geometry can be simplified. However, several modified geometries experience transitional phenomena and inconsistent performance throughout the examined range of the mass flow rates. It is, therefore, evident that further full field information on the internal flow is needed to characterize and optimize these designs, either from Particle Image Velocimetry (PIV) or numerical simulations. In addition, using a shorter diffuser, or none at all, might reveal more on the sensitivity of the jet deflection angles and the jet coherence to internal geometry modifications. Finally, we recommend further investigation of the properties of the recirculation bubble for different mixing chamber designs, which we suspect to be the determining cause for different external flow regimes.