Abstract
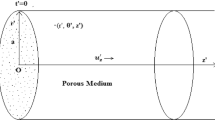
An experimental investigation of the flow inside a rectangular cylinder with air injected continuously along the wall is performed. This kind of flow is a two-dimensional approximation of what happens inside a solid rocket motor, where the lateral grain burns expelling exhaust gas or in processes with air filtration or devices to attain uniform flows. We propose a brief derivation of some analytical solutions and a comparison between these solutions and experimental data, which are obtained using the particle image velocimetry technique, to provide a global reconstruction of the flowfield. The flow, which enters orthogonal to the injecting wall, turns suddenly its direction being pushed towards the exit of the chamber. Under the incompressible and inviscid flow hypothesis, two analytical solutions are reported and compared. The first one, known as Hart–McClure solution, is irrotational and the injection velocity is non-perpendicular to the injecting wall. The other one, due to Taylor and Culick, has non-zero vorticity and constant, vertical injection velocity. The comparison with laminar solutions is useful to assess whether transition to turbulence is reached and how the disturbance thrown in by the porous injection influences and modifies those solutions.
















Similar content being viewed by others
Notes
We proved that this form of \(\psi\) is a consequence of the conservation of mass under the zero vorticity hypothesis. Without this hypothesis, we are not able to prove that \(\beta\) is zero.
In addition, the error should be scaled by \(U_\mathrm {inj}\). Then, we obtain a maximum error, the one relative to the third section, of the order of 0.06.
Abbreviations
- A :
-
Area of the porous plate; \(A = {120}\hbox { cm}^2\)
- \(A_0\) :
-
Amplitude of acoustic waves
- \(B_j\) :
-
jth bin of the histogram representation
- H :
-
Height of the channel; \(H = {2}\hbox { cm}\)
- I :
-
Turbulence intensity; \(I = \sqrt{\langle u'u'\rangle + \langle v'v'\rangle }\)
- \(I_{\mathrm {p}}\) :
-
Turbulence intensity peak; \(\max _y I\)
- L :
-
Length of the channel; \(L = {24}\hbox { cm}\)
- \(N_\mathrm {bin}\) :
-
Total number of bins
- P :
-
Divergence of a two-dimensional flow, first invariant of \(\nabla \mathbf {u}\); \(P = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}\)
- Q :
-
Third invariant of \(\nabla \mathbf {u}\); \(Q = \frac{\partial u}{\partial x}\frac{\partial v}{\partial y} - \frac{\partial u}{\partial y}\frac{\partial v}{\partial x}\)
- \(U_\mathrm {inj}\) :
-
Injection velocity
- \({\varDelta }\) :
-
Discriminant of the eigenvalues characteristic equation for the two-dimensional \(\nabla \mathbf {u}\); \({\varDelta }= P^2 - 4Q\)
- \(\varOmega _z\) :
-
Transversal component of vorticity
- \(\bar{\cdot }\) :
-
Spatial average; i.e., a discrete approximation of the integral \(\frac{1}{L}\int _0^L s(x) \,\mathrm{{d}}x\)
- \(\cdot '\) :
-
Fluctuation of a variable with respect the mean
- \(\cdot ^*\) :
-
Dimensional variable
- \(\dot{m}\) :
-
Volume flow rate
- \(\lambda\) :
-
Wavelength
- \(\langle \cdot \rangle\) :
-
Ensemble average; e.g., \(\langle s \rangle = \frac{1}{N} \sum \nolimits _{i=1}^N s_i\) where N is the number of data
- \(Re_{\mathrm {inj}}\) :
-
Injection Reynolds number; \(Re_{\mathrm {inj}} = HU_{\mathrm {inj}}/\nu\)
- \(\nu\) :
-
Kinematic viscosity of fluid
- \(\psi\) :
-
Stream function
- \({\varvec{\Omega }}\) :
-
Vorticity
- \(\mathbf {u}\) :
-
Velocity vector
- \(h_i\) :
-
ith horizontal acoustic eigenmode; \(h_i =A_0 \sin \left( i\frac{2\pi }{4L}x\right)\)
- k :
-
Wavenumber
- p :
-
Pressure
- u :
-
Horizontal component of velocity
- v :
-
Vertical component of velocity
- \(v_i\) :
-
ith vertical acoustic eigenmode; \(v_i = A_0\sin \left( i\frac{2\pi }{2H}x\right)\)
- w :
-
Transversal component of velocity
- x :
-
Horizontal direction. Distance with the head end of the channel
- y :
-
Vertical direction
- z :
-
Transversal direction
- HC:
-
Hart–McClure solution
- PDF:
-
Probability density function
- TC:
-
Taylor–Culick solution
References
Avalon G, Casalis G, Griffond J (1998) Flow instabilities and acoustic resonance of channels with wall injection. Am Inst Aeronaut Astron. https://doi.org/10.2514/6.1998-3218
Avalon G, Ugurtas B, Grisch F, Bresson A (2001) Numerical computations and visualization tests of the flow inside a cold gas simulation with characterization of a parietal vortex shedding. Tiré à part—pOffice national d’études et de recherches aerospatiales
Beddini RA (1986) Injection-induced flows in porous-walled ducts. AIAA J 24(11):1766–1773. https://doi.org/10.2514/3.9522
Casalis G, Avalon G, Pineau JP (1998) Spatial instability of planar channel flow with fluid injection through porous walls. Phys Fluids (1994-present) 10(10):2558–2568
Casalis G, Chedevergne F, Feraille T, Avalon G (2006) A new stability approach for the flow induced by wall injection. Springer, Netherlands
Chedevergne F, Casalis G, Feraille T (2006) Biglobal linear stability analysis of the flow induced by wall injection. Phys Fluids (1994-present) 18(1):14–103
Culick F (1966) Rotational axisymmetric mean flow and damping of acoustic waves in asolid propellant rocket. AIAA J 4(8):1462–1464
Féraille T, Casalis G (2005) Global stability of the flow induced by wall injection. Tiré à part—Office national d’études et de recherches aerospatiales
Flandro GA (1986) Vortex driving mechanism in oscillatory rocket flows. J Propuls Power 2(3):206–214. https://doi.org/10.2514/3.22871
Griffond J, Casalis G, Pineau JP (2000) Spatial instability of flow in a semiinfinite cylinder with fluid injection through its porous walls. Eur J Mech B Fluids 19(1):69–87. https://doi.org/10.1016/S0997-7546(00)00105-9. URL http://www.sciencedirect.com/science/article/pii/S0997754600001059
Hart RW, McClure FT (1959) Combustion instability: Acoustic interaction with a burning propellant surface. J Chem Phys 30(6):1501–1514. https://doi.org/10.1063/1.1730226. URL http://scitation.aip.org/content/aip/journal/jcp/30/6/10.1063/1.1730226
Huesmann K, Eckert ERG (1968) Studies of the laminar flow and the transition to turbulence in porous tubes with uniform injection through the tube wall. Warme-und Stoffubertragung
Jeong J, Hussain F (1995) On the identification of a vortex. J Fluid Mech 285:69–94. https://doi.org/10.1017/S0022112095000462. https://www.cambridge.org/core/article/div-class-title-on-the-identification-of-a-vortex-div/D26006DDB95FB28DA80E28A581182DF1
Laboureur D, Tóth B, Anthoine J (2010) Investigation of the Taylor–Culick flow through particle image velocimetry and numerical simulation. AIAA J 48(6):1077–1084. https://doi.org/10.2514/1.44616
Majdalani J, Fist A (2014) Improved mean flow solution for solid rocket motors with a naturally developing swirling motion. In: Propulsion and Energy Forum, AIAA
McClure FT, Lure FT, Cantrell RH, Hart RW (1963) Interaction between sound and flow: stability of T-burners. AIAA J 1(3):586–590. https://doi.org/10.2514/3.54846
Olson RM, Eckert ERG (1966) Experimental studies of turbulent flow in a porous circular tube with uniform fluid injection through the tube wall. J Appl Mech 33(1):7–17. https://doi.org/10.1115/1.3625030
Perrotta A, Gnisci S, Romano GP (2017) Resolving the flow fine structure generated downstream a permeable plate using single-pixel correlation in comparison to window correlation. In: The 12th international symposium on particle image velocimetry
Pimenta M, Moffat RJ (1974) Stability of flow through porous plates: coalescent jets effect. AIAA J 12(10):1438–1440. https://doi.org/10.2514/3.49512
Taylor G (1956) Fluid flow in regions bounded by porous surfaces. Proc R Soc Lond Ser A Math Phys Sci 234(1199):456–475
Thielicke W, Stamhuis E (2014) Pivlab-towards user-friendly, affordable and accurate digital particle image velocimetry in matlab. J Open Res Softw 2(1):p.e30. https://doi.org/10.5334/jors.bl
Varapaev V, Yagodkin V (1969) Flow stability in a channel with porous walls. Fluid Dyn 4(5):60–62
Yagodkin V (1980) Use of channels with porous walls for studying flows which occur during combustion of solid propellants. Technical Report, No. FTD-ID (RS) T-0323-80, pp 1–10
Yamada K, Ishikawa N (1976) Simulative study on the erosive burning of solid rocket motors. AIAA J 14(9):1170–1176. https://doi.org/10.2514/3.61451
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Perrotta, A., Romano, G.P. & Favini, B. An experimental study of wall-injected flows in a rectangular cylinder. Exp Fluids 59, 11 (2018). https://doi.org/10.1007/s00348-017-2472-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-017-2472-1