1 Introduction

Ammonia has become a strong candidate as an alternative energy carrier in a carbon-neutral society with an energy density half of that of liquefied natural gas [1]. It is ranked as a hazardous gas and therefore environmental emissions from the industrial new-energy infrastructure need to be strictly monitored. NH\(_3\) has absorption near a central wavelength of 1030 nm [2], due to the second overtone of the \(\nu _1\) mode. The narrow gas absorption lines have a bandwidth well below 0.3 cm\(^{-1}\) [3], which could not be resolved using a conventional spectrometer with a typical resolution of \(\sim \)1 cm\(^{-1}\). This can make Yb-doped laser oscillators a useful tool in a laboratory dedicated to laser spectroscopy of gases for environmental monitoring using high-resolution detection techniques. Besides, Yb-doped laser gain media could be also investigated to evaluate the crystal quality and the effects of doped impurities.

To increase the signal to noise ratio, a laser oscillator with a high repetition rate is required so as the intensity of each frequency comb line would be high enough to resolve the narrowband gas absorption lines after conversion of the optical signal to a radio signal in the frequency domain. A fast and high-resolution technique of dual-frequency-comb spectroscopy has been successfully applied to environmental monitoring by taking advantage of two frequency combs with a slightly different repetition rate so that a heterodyne detection becomes possible without the need of any delay scanning equipment [4]. Phase locking of two laser sources is required in dual-frequency-comb spectroscopy, which is technically difficult. Therefore, a free-running single laser source that could generate two frequency combs simultaneously [5, 6] becomes a key technique to facilitate laser spectroscopy for environmental monitoring.

Among Yb-doped laser gain media, Yb:KGd(WO\(_4\))\(_2\) (Yb:KGW) has shown superior properties such as a broad bandwidth at a very high output power not easily achievable by other Yb-doped laser gain media in a bulk geometry [7]. It can be pumped at the zero-phonon line at 981 nm using commercially available laser diodes (LDs) resulting in a low quantum defect of only \(\sim \)5.6%, which is even slightly lower than that of Yb:YAG pumped at 969 nm. Wavelength-stabilized high-power LDs at 981 nm are commercially available at a more reasonable cost compared to 969 nm LDs, which suggests an advantage of Yb:KGW bulk lasers. On the other hand, unlike Yb:YAG having a cubic structure, Yb:KGW is birefringent and the polarization direction of the pump laser with respect to the crystal axis needs to be finely tuned to achieve the best performance. These characteristic features have made Yb:KGW a challenging laser medium for thin-disk laser fabrication [8] although it was initially thought to be the most promising candidate among Yb-doped gain media [9]. However, it has still remained as a strong candidate for the development of high-power bulk lasers due to the high laser efficiency not easily achievable by the other gain media [10].

Since multimode LDs are used for pumping a Yb:KGW laser crystal, they yield a large beam spot diameter above 100 \(\upmu \)m in the crystal even though LDs with a high-brightness are coupled into a multimode fiber with a core diameter of \(\sim \)100 \(\upmu \)m with a low numerical aperture (N.A.). This requires a large fundamental laser mode diameter in the cavity matched to the pump spot size to obtain single-transverse-mode oscillation, which is absolutely necessary for mode-locking. As a result, a strong Kerr effect is difficult to be obtained in such laser cavities, and consequently, using a semiconductor saturable absorber mirror (SESAM) [11] has been commonly used for mode-locking in Yb:KGW laser oscillators [12]. Although it is possible to separate the loosely focused laser crystal from a tightly focused Kerr medium in a hybrid design, in which an ultrafast Kerr lens mode-locked (KLM) laser oscillator is pumped by a high-power multimode LD [13], the repetition rate becomes low because an extra pair of concave mirrors and a Kerr medium need to be inserted in the cavity to get a strong Kerr effect. Currently, the highest average power obtained by a purely KLM linear Yb:KGW laser oscillator is limited to only 2.3 W at a repetition rate of 86.8 MHz with a pulse duration of 240 fs, corresponding to the peak power of 97 kW and the pulse energy of 26 nJ [14].

In this paper, we report the development of a ring Yb:KGW laser oscillator with an average power of 4.22 ± 0.01 W, corresponding to a pulse energy of 19.5 nJ at a repetition rate of 216 MHz. Considering a Sech\(^2\) temporal profile, the pulse duration is measured by a home-built intensity auto-correlator to be 312 fs, which is very close to the Fourier-limit pulse duration of 303 fs. Due to the ring geometry of the laser oscillator, a large fundamental mode diameter is possible in the laser crystal even in a compact cavity to achieve single-transverse-mode oscillation [15, 16], when the crystal is pumped by a multimode LD with a spot size less than 140 \(\upmu \)m. Besides, a ring geometry yields a lower magnitude of intra-cavity dispersion and a broad spectrum thanks to the easier dispersion compensation [17]. Thanks to the high nonlinear refractive index of the Yb:KGW crystal, the Kerr effect inside the gain medium is sufficiently large to start mode-locking and achieve CW-free spectra due to a high magnitude of intra-cavity negative dispersion assured by using a pair of customized high-dispersion mirrors. Since no extra Kerr element is inserted in the cavity, a high repetition rate beyond 200 MHz is achieved limited to multimode LD pumping. Measuring the repetition rate fluctuations after initial warm-up of the cavity, a peak to valley (PV) of only 354.28 Hz during 30 min of free-running operation has been achieved. This could make a free-running ring cavity a suitable light source for application to laser spectroscopy. As a proof of principle, we have applied the ring laser oscillator to the measurements of the second-overtone transition of the \(\nu _1\) mode of NH\(_3\) to resolve the absorption line profiles. We have also measured absorption spectra of the Yb:KGW crystal to evaluate the quality of the crystal affected by the doped impurities.

2 Laser development

2.1 Structure of the ring laser

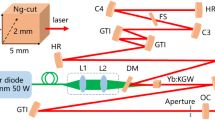
At the core of the ring laser cavity, two concave mirrors with the radius of curvature (R) of 250 mm are used to focus the laser inside a Ng-cut Yb:KGW (4Lasers, 7054M9008) crystal with the thickness of 5 mm and a doping concentration of 2 at.%. The laser crystal antireflection (AR) coated on two sides in a spectral range of 970–1070 nm has a square shape with a length of 5 mm. It has a high damage threshold of 10 J/cm\(^2\) for 10 ns pulses. The laser crystal is wrapped in an indium foil with the thickness of 100 \(\mu \)m and clamped in a copper holder, which is water cooled to 20 \(^\circ \)C. A dichroic mirror (Optogama, 6202HT) is used to send the pump multimode LD into the laser crystal. It has a transmission of 98% in a spectral range of 965–982 nm at the incidence angle of 22.5\(^\circ \) placed after the first concave mirror.

To minimize astigmatism, we have placed the concave mirrors at the incidence angle less than 9\(^\circ \). The pump LD (Photontec Berlin, M981 ± 0.5-27-F105/22-T4R) with the highest output power of 27 W is coupled into a multimode fiber with a core diameter of 105 \(\mu \)m and N.A. of 0.22, the image of which is relayed into the laser crystal using a combination of f = 50 mm and f = 60 mm achromatic doublets to obtain a pump spot size less than 140 \(\upmu \)m inside the crystal. To control the laser polarization of the pump LD and achieve the highest possible pump absorption, a polarizing beamsplitter is used to transmit only the \(\Pi \) horizontal polarization light used for pumping the crystal through the dichroic mirror. We dump the remaining \(\Sigma \) vertically polarized laser to a water-cooled beam dump (OptoSigma, BD-80). By doing so, only 12 W of the \(\Pi \)-polarized laser power has remained for pumping the crystal. In this way, the spectral power near 981 nm becomes higher than using 12 W of unpolarized pump power at a lower LD-driving current.

Fig. 1
figure 1

Schematic of the ring laser oscillator. OC output coupler, LD laser diode, PD photodiodes to monitor the pulse trains in both left and right rotating directions, Brw Brewster plate to control laser polarization, CMOS beam profiler equipped with a CMOS (complementary metal oxide semiconductor) camera. A picture of the Yb:KGW ring laser oscillator is also shown

Full size image

To balance the intra-cavity self-phase modulation (SPM) with negative dispersion, two highly dispersive mirrors (Tokai Optics, TypeT2k) are inserted in the cavity, which result in a group delay dispersion (GDD) of −8000 fs\(^2\) at the central wavelength of 1030 nm by making two reflections on each mirror. Dispersion of the crystal is estimated from the values reported for the host material KGW [18, 19]. A fused silica plate at the Brewster’s angle with the thickness of 1.25 mm is used to control the laser polarization of the ring cavity. The cavity is folded using a turning mirror and an output coupler (Layertec, 157174) used in the position of another turning mirror with a reflectance of 92% in the spectral range of 1020–1040 nm, for \(\Pi \) horizontally polarized laser. Since the output coupler is used at an incidence angle of 45\(^\circ \), its reflectance is highly dependent on the laser polarization. Therefore, removing the fused silica plate will force the laser to operate in \(\Sigma \) vertical polarization due to the higher reflectance. This will drastically decrease the laser efficiency due to a poor output coupling ratio. Folding by these turning mirrors results in a compact cavity with the length of \(\sim \)1.4 m. A schematic of the ring laser cavity is shown in Fig. 1. The whole setup including the pump LD are placed on an aluminum breadboard (300 \(\times \) 900 mm\(^2\)) enclosed inside an acrylic box to reduce environmental perturbations and protect the optics from dust particles in a rough environment outside a clean room.

The pump LD has two peaks. One broad peak is located at \(\sim \) 972 nm, which is not wavelength stabilized, and its central wavelength shifts towards 976 nm by increasing the current of the LD. The other peak having a narrow width of \(\sim \) 0.6 nm is located at 981 nm, which is stabilized. The first peak is not efficiently absorbed in the laser crystal crystal, so that only up to \(\sim \) 60% of the pump is absorbed in non-lasing conditions. We use an iris behind the second concave mirror to cut the unabsorbed pump power that would easily heat up the edge of mirror holders. The pump LD has a beam quality of \(M^2(x)\)=30.2 in the horizontal direction and \(M^2(y)\)=31.9 in the vertical direction with a Rayleigh range of only \(\sim \) 1 mm. Therefore, the pump spot size increases very quickly as soon as it passes the focal point in the laser crystal. Using such a multimode LD, due to matching of the fundamental laser mode to the pump spot, achieving a strong Kerr effect inside the laser crystal is rather difficult given the large fundamental mode size of 83 \(\upmu \)m obtained based on the ABCD matrix formalism. However, thanks to the very high nonlinear refractive index (24 \(\times \) 10\(^{-14}\) mm\(^2\)/W) of Yb:KGW [20], which is \(\sim \) 3.8 times larger than that of Yb:YAG, we are able to achieve KLM directly inside the laser crystal without using a hard aperture. This has yielded a compact cavity without the need of tight focusing inside another Kerr medium.

Fig. 2
figure 2

Properties of the mode-locked laser oscillator. a Broadband spectrum at a central wavelength of 1038 nm. The beam profile is shown in the inset. b Intensity autocorrelation trace indicating a pulse duration of 312 fs. c Pulse trains indicating a repetition rate of 216 MHz without any Q-switching instabilities

Full size image

2.2 Experimental results

First, we align the laser cavity to obtain the highest possible CW laser output in the unidirectional mode. We carefully align the cavity to obtain a single-transverse-mode oscillation, which is not easy due to the large pump spot size inside the crystal. A mirror is placed behind the OC to achieve unidirectional CW oscillation by sending one of the laser outputs back into the ring cavity to destabilize the laser oscillation in this arm of the cavity [21, 22]. In this cavity configuration, we obtained the highest output power of 6.1 W with a slope efficiency of 68.5% and a maximum optical to optical efficiency of 50.6%. As we increase the power of the LD beyond 10 W, the sub-peak located initially at \(\sim \) 972 nm shifts towards 976 nm and gets much weaker in intensity and the laser efficiency increases as a result of a higher pump power available at 981 nm. All we need to achieve a stable mode-locking is a gentle tapping of the second concave mirror placed behind the laser crystal. Although KLM could be initiated when the laser oscillator is uncapped, KLM start-up is much easier when the box is fully enclosed. We have to slightly tilt the laser crystal so that reflections from the AR coating does not interfere with the mode-locking [23]. Using a laser crystal with a more suitable AR coating or a Brewster-cut crystal should be helpful to avoid such a crystal tilt.

When KLM is stabilized, the maximum pump power is 9.9 W, above which obtaining a stable KLM without Q-switching instabilities is difficult. We monitor the beam profile using a CMOS camera, and as soon as KLM is initiated, the beam profile turns into a smooth and nearly Gaussian shape shown in the inset of Fig. 2a. It has a beam radius of 0.42 mm in the horizontal direction and 0.44 mm in the vertical direction. The broadband spectrum obtained after KLM with a bandwidth of 3.64 nm is shown in Fig. 2a, which has a Fourier-limit pulse duration of 303 fs. Using a home-built intensity auto-correlator with a scanning range larger than 60 ps, we measure a pulse duration of 312 fs considering a Sech\(^2\) temporal profile shown in Fig. 2b. We use a t=1 mm BBO crystal with a GaP photodiode (Thorlabs, SM05PD7A) to record the auto-correlation trace. The auto-correlation trace is magnified in the range of ± 3 ps for clarity while we did not see any indication of double pulsing in the range of ±30 ps.

The pulse trains are measured using an oscilloscope (Tektronix, DPO7254C) with a bandwidth of 2.5 GHz and a fast InGaAs photodiode (EOT, ET-3000). They do not show any Q-switching instabilities or double pulsing as shown in Fig. 2c. The pulse trains have a separation of 4.63 ns, corresponding to a repetition rate of 216.07 MHz, consistent with the cavity length. Although a higher repetition rate could be obtained by further making the laser cavity compact, the limit should be \(\sim \)250 MHz and further scaling towards a repetition rate beyond 500 MHz requires a single-transverse-mode pump laser source such as a fiber laser at a central wavelength of 981 nm so that tight focusing inside the laser cavity becomes possible. In this way, it would be easier to match the mode size of the fundamental laser to the pump spot using a much more compact cavity setup using a R = 100 mm concave mirror pair. As a result, a stronger Kerr effect can be obtained yielding a shorter pulse duration.

Depending on the position of the second concave mirror, it is possible to operate the ring cavity unidirectionally in the left rotating arm (OC\(\rightarrow \)Crystal\(\rightarrow \)Brw), or in the right rotating arm (OC\(\rightarrow \)Brw\(\rightarrow \)Crystal). We choose to operate the ring cavity in the left rotating arm on a daily basis for laser spectroscopy experiments. Once the laser is adjusted to be operated unidirectionally in the left rotating arm, it operates in that mode upon turning the laser off and on reinitiating KLM as many times as required without any sophisticated adjustments provided that a single transverse mode is obtained during CW oscillation, which is sensitive to the direction of the pump LD. We have used a lens mount (Thorlabs, LM1XY/M) which can not be locked to hold the second achromatic doublet lens focusing the pump LD into the crystal. Using another type of lens mount should result in a much more robust performance provided that we had more space for the pump optics. Note that bidirectional laser operation requires placing the crystal much closer to the focal point of the concave mirrors to increase the SPM and as a result, double pulsing in the unidirectional mode or bidirectional single pulse operation is very difficult to be observed in the current setup unless we first decrease the magnitude of the intra-cavity dispersion to − 4000 fs\(^2\).

Once KLM is initiated after a suitable alignment of the second achromatic lens, it stays mode-locked for 1–3 h until dust particles are accumulated on the mirrors due to operation of the laser cavity outside a clean room. We need to clean the optics and reinitiate KLM. Therefore, we have not been able to operate KLM non-stop for a period longer than \(\sim \) 3 h thus far due the dust accumulation problem. Besides, the achromatic lens holder could be another reason of a minor alignment change. Placing the ring oscillator in a clean room or hermetically sealing it from the ambient environment should be necessary to achieve a longer stability. A spectrogram indicating the stability of mode-locking is shown in Fig. 3a. Since the spectrogram used to suffer from speckle pattern formation, we had to shake the multimode fiber connected to the spectrometer (Broadcom, AFBR-S20M2NI) using a vibrator to obtain a smooth spectrogram. We did not observe any spectral narrowing or spectral shift during operation of the ring laser cavity on a daily basis up to \(\sim \) 2 months of daily operations.

Using a frequency counter (Keysight Technologies, 53210A), we measured fluctuations of the repetition rate with an average value of 215.964 MHz shown in Fig. 3b by a dashed curve during start-up phase of the laser oscillator and a solid curve after \(\sim \)40 min warm-up. The fluctuations have a PV of only 354.28 Hz during 30 min of free-running operation. This is equal to expansion or contraction of the laser cavity length of up to \(\sim \)2.3 \(\mu \)m at this level of repetition rate. Note that such a cavity length change should happen in a much shorter time period in a linear laser cavity. A ring cavity is automatically sustaining a stable performance due to the traveling nature of the laser beam [15, 16], while a linear cavity can easily change its alignment due to the standing waves confined between an end mirror and the OC. This indicates that a ring laser geometry could be useful in obtaining a lower drift of the the repetition rate, making it a suitable source for application to laser spectroscopy at a fast data acquisition rate. Moreover, locking the repetition rate using a cavity mirror placed on a Piezo stage should require less frequent feedbacks with such a slow cavity length change. The output power was measured by a convection-cooled thermal head (Thorlabs, S350C) having a resolution of 1 mW. The power stability achieved during mode-locking is shown in Fig. 3c. The output power was 4.22 ± 0.01 W (RMS 0.22%) corresponding to a pulse energy of \(\sim \) 19.5 nJ. The estimated peak power is 55 kW considering a Sech\(^2\) temporal profile, making these laser pulses suitable for certain applications such as laser spectroscopy, two-photon microscopy, pumping optical parametric oscillators, or laser micro-machining at a high repetition rate.

Fig. 3
figure 3

Stability of the mode-locked laser oscillator. a Spectrogram showing no indication of spectral shift or narrowing. b Fluctuation of the repetition rate upon starting mode-locking shown by a dashed curve compared to that recorded after \(\sim \) 40 min of laser warm-up shown by a solid curve. c The power stability during mode-locking

Full size image

After operating the laser for \(\sim \)2 months on a daily basis, we noticed that the beam profile of the leaked pump LD had turned into three vertical lines after passing through the crystal instead of a usual round profile, and consequently, obtaining single transverse mode oscillation became impossible. As a result, it was too difficult to reinitiate KLM by any cavity realignment, even though there was no visible damage on the surface of the crystal. We guess this should be due to a refractive index change of the Yb:KGW laser crystal due to a high SPM, diffracting the pump laser. Such behavior must be highly linked to the crystal quality. In order to achieve single-transverse-mode CW oscillation and initiate KLM by a gentle tap, we had to slightly shift the position of the crystal and use a fresh surface, which resulted a round beam profile leaked from the crystal as usual. We noticed this issue repeated itself every \(\sim \) 2 months of laser operation. Further ongoing investigation is necessary to find the reason of the laser crystal degradation and any link to the humidity level.

Fig. 4
figure 4

Laser spectroscopy using a FTIR setp. a Schematic of the FTIR setup. BS beamsplitter, PBS polarizing beamsplitter, SMF single-mode fiber, ND neutral density filter. b Correlation trace when the gas cell is evacuated to below 0.1 torr. c Correlation trace when the gas cell is filled with NH\(_3\) gas up to a pressure of 600 torr. d The background spectrum retrieved from b is shown by a dashed curve compared to that in the sample arm retrieved from c shown by a solid curve

Full size image

3 Application to laser spectroscopy

Towards measuring the absorption spectra at a high resolution, we have prepared a Fourier-transform infrared spectroscopy (FTIR) setup to apply the developed ring laser oscillator to the spectroscopy of NH\(_3\), which is considered to be an alternative energy carrier in a carbon-neutral society. The FTIR setup can be also applied to the spectroscopy of solids such as Yb-doped laser crystals to detect any abnormal properties due to doped impurities. The schematic of the FTIR setup is shown in Fig. 4a. The laser pulses are sent to a Michelson interferometer composed of two gold-coated mirrors and a cubic beamsplitter (SigmaKoki, NPCH-10-10640). While one arm is fixed, the other arm of the interferometer is scanned by a stepper motor translation stage (Thorlabs, LNR25ZFS/M) with a maximum scanning range of 25 mm at a velocity of \(\sim \) 0.35 mm/s.

Beyond the interferometer, we have placed another cubic beamsplitter to send the fringes to two InGaAs photodiodes (EOT, ET3010) simultaneously. We have placed a lens in front of the photodiodes to make sure that the fringes are fully detected by the small aperture of the photodiodes and have balanced the intensity using neutral density (ND) filters. One photodiode records a reference signal and the other the main signal after transmission through the sample. The sample being a gas cell or a Yb-doped crystal is set between the cubic beamsplitter and a photodiode in the sample arm. The polarization of the laser is set to \(\Pi \), which is horizontal to the optical table. Since measurement of Yb-doped crystals requires a wide bandwidth to cover a spectral range of 970–1100 nm, we have coupled the laser pulses into a single-mode fiber with a core diameter of 6 \(\upmu \)m to achieve spectral broadening while keeping a smooth and not spiky spectrum. The polarization of the broadened light is controlled to send only the \(\Pi \) output into the interferometer. Note that in the case of absorption measurement of NH\(_3\), no spectral broadening is necessary due to the very narrow gas absorption lines near the central wavelength of \(\sim \) 1038.1 nm.

The gas cell has a length of 0.9 m and the effective length becomes 1.8 m after using a roof mirror to reflect the fringes back into the gas cell and pick them up using a side-coated prism (Thorlabs, MRA20L-E03). Once the gas cell is evacuated to below 0.1 torr, the interferogram magnified in a range of ±20 ps shown in Fig. 4b is recorded. The fringes are recorded at a frequency of 677 Hz with \(\sim \) 118 points in each fringe. The resolution of the spectra was 0.031 nm (0.288 cm\(^{-1}\)). Given this resolution, each measurement takes up to 50 s. We obtain the spectrum shown in Fig. 4d by a dashed curve. The tiny peaks near 1022, 1025, and 1048 nm may be due to artifacts of Fourier transformation, the movement of the stage, or effects of air turbulence. We may be able to get an improved result by placing the FTIR setup in an acrylic box.

Once the gas cell is filled with 600 torr of NH\(_3\), we clearly observe satellite fringes in the interferogram as shown in Fig. 4c separated from the main fringes at the center. The more these satellite fringes are separated from the center, the narrower the resultant absorption spectra will be. After Fourier transform, we can retrieve the spectrum shown in Fig. 4d by a solid curve. Currently, we have used the central wavelength of 1038.1 nm to retrieve the spectra from the interferogram. Using a narrowband light source such as a He-Ne laser to measure a reference interferogram simultaneously could decrease the uncertainty in calibration of the wavelength axis of the spectra.

Comparison of the spectrum retrieved in the sample arm with that retrieved in the reference arm, we can measure the absorption of hazardous gases or Yb-doped crystals placed in the sample arm. Since we use a pulsed laser, satellite fringes do not show up when the pulses have no temporal overlap if there is no spectral absorption. As a result, they are an indicator of narrowband absorption in the spectrum. Broadband absorption spectra are detectable from the main fringes near the center of the interferogram. Compared to the absorption spectrum when the gas cell is evacuated shown in Fig. 5a by a dashed curve, NH\(_3\) has an absorption of up to \(\sim \) 40% with tiny and narrowband absorption lines shown by a solid curve in Fig. 5a. The absorption spectrum is suffering from pressure broadening in the gas cell. We need to operate the stage of the interferometer in closed loop and average the interferogram to improve the signal to noise ratio.

Fig. 5
figure 5

Absorption spectra measured using the FTIR setup. a Absorption of NH\(_3\) gas shown by a solid curve compared to that shown by a dashed curve when the cell is evacuated. BG background. b The spectrum retrieved from the correlation after inserting a Yb:KGW crystal shown by a solid curve compared to the background spectrum after spectral broadening. c Absorption of a Yb:KGW crystal when laser polarization is parallel to the N\(_\text {m}\) axis (\(E\) \(\parallel \) \(N_\text {m}\)) shown by a solid curve compared to that when the crystal is rotated by 90\(^\circ \) (\(E\) \(\parallel \) \(N_\text {p}\)) shown by a dashed curve

Full size image

After spectral broadening, we have retrieved a spectrum shown by a dashed curve in Fig. 5b in the reference arm compared to placing a 3 at% doped Yb:KGW crystal with a thickness of 5 mm in the sample arm shown by a solid curve in Fig. 5b. Since the satellite fringes indicating narrow absorption lines were not present, we limited the resolution to 0.14 nm (1.3 cm\(^{-1}\)) while recording the fringes at a frequency of 766 Hz with 130 points in each fringe. Each measurement took only 10 s. In this case, the laser polarization is parallel to the \(N_\text {m}\) axis of the crystal (\(E\) \(\parallel \) \(N_\text {m}\)). From these spectra, we can measure absorption of the Yb:KGW crystal shown by a solid curve in Fig. 5c. We see a sharp absorption near 981 nm, followed by another peak near 994 nm and slowly decreasing broadband absorption up to 1050 nm in the fundamental region of Yb:KGW laser oscillation. While the peak near 981 nm originates from the absorption of Yb ions, the peak near 994 nm is far from where it should be (near 1000 nm) and could indicates a crystal deformation or absorption by impurities.

By rotating the crystal so that the polarization of the laser is parallel to the \(N_\text {p}\) axis (\(E\) \(\parallel \) \(N_\text {p}\)), we likewise measured the crystal absorption shown by a dashed curve in Fig. 5c. In the latter case, although absorption near 981 nm is lower than the initial case, we see a much lower absorption in the fundamental spectral range of 1020–1040 nm. This indicates that, in the latter case of \(E\) \(\parallel \) \(N_\text {p}\), the center of the lasing spectrum should become closer to 1030 nm with a broader bandwidth due to the lower and flatter absorption. Likewise, in case of \(E\) \(\parallel \) \(N_\text {m}\) the center of the lasing spectrum should become closer to 1040 nm due to the decreasing absorption in the fundamental spectral range towards a longer wavelength. Since the beamsplitter used to separate the sample and reference arms does not have a flat spectral response, we observe an absorption below 0% when the absorption is low. Using a beamsplitter with a flatter spectral response, a D-shaped gold-coated mirror to split the beam in space, or an uncoated sapphire window should result in a flatter spectral response and decrease the uncertainty when the absorption of the sample is low.

To find an ideal Yb:KGW laser crystal, we will need to measure the crystal absorption at the configuration of \(E\) \(\parallel \) \(N_\text {p}\) to confirm a high absorption near 981 nm and a low absorption in the fundamental spectral range. Therefore, we can use the FTIR setup to evaluate the quality and performance of Yb-doped crystals prior to any lasing experiments. This can save a huge time during the initial development phase of a laser oscillator making this simple spectroscopy setup an indispensable tool in a laser laboratory. To reduce the measurement time while keeping the current resolution and sufficient data points in each fringe, using a rotating mirror pair in front of an end mirror [24] instead of a stepper motor translation stage, could be more effective.

Fig. 6
figure 6

Properties of the ring laser oscillator in bidirectional mode. a Repetition frequency subtracted from the average repetition frequency of the left rotating arm is shown by a solid curve compared to that in the right rotating arm shown by a dashed curve. b Difference of the repetition frequency in the two arms indicating random frequency differences near a zero offset

Full size image

Towards non-scanning high-resolution spectroscopy, we can also operate the ring laser oscillator in the bidirectional mode to obtain two laser outputs from a single laser cavity. We just need to place the laser crystal close to the focal point and reduce the magnitude of intra-cavity GDD to − 4000 fs\(^2\). Such a configuration could be useful in dual-frequency-comb spectroscopy to use a free-running laser without locking the repetition rate and carrier envelope phase (CEP) of the pulses due to the short time required for retrieving the absorption spectra provided that there is a frequency difference between the two laser outputs (\(\Delta f_\text {rep}\)). This could reduce the time of measurement from 10–50 s in the FTIR setup to a value in the ms range making the measurement at least 10\(^3\) times faster since no delay scanning would be necessary. To examine if there was any \(\Delta f_\text {rep}\), we used two frequency counters and measured the repetition rate of the laser pulses obtained in both arms simultaneously. The result is shown in Fig. 6a after subtracting from the average repetition rate of 215.542 MHz. After subtracting the two data, we could observe only a random frequency difference with an amplitude of \(\sim \) 10 Hz as shown in Fig. 6b. The amplitude can become larger when the laser is Q-switch mode-locked. However, the laser is not very stable in this condition and we could not find any cavity configuration by which a \(\Delta f_\text {rep}\) useful for application to dual-frequency-comb spectroscopy was present when KLM was stable and we had CW mode-locking. Further ongoing experiments are required to find out a mechanism to obtain \(\Delta f_\text {rep}\) between the two laser outputs using a Brewster-cut crystal taking advantage of the birefringence.

4 Conclusion

We have developed a ring laser oscillator with a unidirectional output power of 4.22 W, pulse duration of 312 fs at a repetition rate of 216 MHz using a Yb:KGW crystal. A pulse energy of 19.5 nJ is obtained at a peak power of 55 kW, making the laser pulses suitable for a variety of applications such as laser spectroscopy, two-photon microscopy, pumping optical parametric oscillators, or laser micro-machining at a high repetition rate. Thanks to the ring geometry, the repetition rate has a PV fluctuation of only 354.28 Hz during 30 min of free-running operation making the ring laser geometry a superior candidate for locking the repetition rate or application to laser spectroscopy experiments. To the best of our knowledge, this is the highest output power obtained from a Kerr lens mode-locked Yb:KGW ring laser oscillator.

As an application of this laser oscillator, we have measured the absorption spectra of NH\(_3\) and a Yb:KGW crystal at two crystal axes orientations. We have been able to use the spectroscopy setup to evaluate the crystal quality before any lasing experiments. Operating the ring laser oscillator in the bidirectional mode, no noticeable frequency difference between the two arms of the cavity has been observed thus far. By using a single-transverse-mode pump laser and building a much more compact ring laser cavity to yield a repetition rate beyond 500 MHz while taking advantage of the birefringence of a Brewster-cut laser crystal, we expect to obtain a frequency difference in the two cavity arms to facilitate experiments in dual-frequency-comb spectroscopy.