1 Introduction

High-power lasers operating in the \(2 {\upmu{\text{m}}}\) spectral region can be used for a variety of applications, ranging from medical treatments and countermeasures to the pumping of mid-infrared optical parametric oscillators (OPOs). For the latter application, solid-state lasers have shown great potential given the high pulse energies that these laser sources allow to reach. Thulium-based lasers are often used in this spectral region, because they can be pumped with highly efficient laser diodes at 800nm and have the advantage of high conversion efficiencies. However, \(\hbox {Ho}^{3+}\)doped media like \(\hbox {Ho}^{3+}\):YAG are efficient for emitting at wavelengths greater than \(2 {\upmu{\text{m}}}\) and, therefore, may be preferred for some applications, such as ZGP OPO pumping, by taking advantage of lower background absorption for wavelengths around 2.1\(\upmu{\text{m}}\) and beyond [1]. The increasing availability of high-power thulium-based fiber lasers has made \(\hbox {Ho}^{3+}\):YAG more attractive for these applications. Since the absorption cross section of holmium is at a maximum at around 1.9\(\upmu{\text{m}}\) depending on the host material, thulium fiber lasers are ideal high power pump sources at this spectral region. One of the main limitations for power-scaling solid-state laser resonators is the loss of resonator stability due to thermal lensing in the laser crystal. This can get even more problematic in holmium crystals, due to high energy transfer upconversion (ETU) depending on the doping concentration of the crystal. Consequently, the optimization of such a system can be much more difficult. A simulation model can greatly assist in the design and optimization of \(\hbox {Ho}^{3+}\):YAG resonators for high power, efficiency, and good beam quality by allowing more insight into the internal processes of the system.

In this work, we present a powerful model developed for accurately describing end-pumped \(\hbox {Ho}^{3+}\):YAG lasers. The general approach is based on a sequential field propagation method. A modular simulation environment allows for the inclusion of a variety of different element operators, like mirrors and laser crystals. By combining these operators, a linear or ring resonator can be modeled. To calculate the laser gain of the system, rate equations are used to describe the radiative and non-radiative processes in a spatially resolved crystal. The model for holmium includes all the relevant manifolds and their respective energy transfer processes. By applying the rate equation model, not only the laser gain but also the heat load of the crystal is accurately modeled. Subsequently, the temperature distribution as well as the displacement distribution and resulting mechanical stresses are calculated. The respective differential equations are solved with finite difference methods (FDMs), which are chosen for their simplicity. Resulting thermal effects like thermal lensing and birefringence can then be calculated for the crystal. In the last section, a continuous-wave \(\hbox {Ho}^{3+}\):YAG resonator setup is used to validate the model by comparing the laser output for the model and experiment. All the procedures described in this manuscript where implemented using the MATLAB language, in some cases incorporating the underlying theory and algorithms described in the references.

2 Fundamental simulation model

2.1 CW simulation approach

The fundamental cw approach is based on the sequential field propagation of a two-dimensional complex field. Using a modular environment, different element operators are placed in between the propagation steps to accurately model a laser resonator. Each element operator uses unique algorithms to transform the field for their appropriate application. They include mirrors, lenses, glasses, polarizers, and laser crystals. Using these operators, a linear or ring resonator can be modeled by following the approach of Fox and Li [2].

The resonator gain is recalculated iteratively over a certain amount of roundtrip steps until an end condition is met. The flowchart depicted in Fig. 1 shows the modular structure and basic operation of the model. When the laser gain in the resonator has stabilized, the thermal steady state of the laser crystal is calculated in between the roundtrip steps. This process is repeated until the thermal recalculation reaches a convergence criteria. Resulting thermal lensing and birefringence effects can have a large influence on the generated power output and beam quality of the laser.

Fig. 1
figure 1

Flowchart for the simulation of an example resonator, showing the modular structure

Full size image

2.2 Propagation method


Two-dimensional field propagation is usually achieved by solving Maxwell’s equations for transverse electromagnetic waves. Here, a variety of different solvers can be used. Direct Maxwell solvers [3, 4] like finite element methods (FEM) or finite difference time domain methods (FDTD) provide the highest accuracy at the cost of high simulation effort. More simplified approaches like Gaussian beam propagation [5] use specific field distributions and typically have less accuracy, but may provide lower simulation efforts. However, the beam propagation method (BPM) provides a good compromise between accuracy and numerical effort. For this model, a split step BPM approach developed by Fleck et al. [6] is used. The method is based on the slowly varying envelope approximation, which simplifies Maxwell’s equations by assuming the complex amplitude only varies slowly in time and space. This may cause problems for some applications where a broad-band spectrum is to be propagated, but has proven to be very compatible with this model. Maxwell’s wave equation is solved in the parabolic form

$$\begin{aligned} 2ik \left( \frac{n}{c} \frac{\partial {\mathcal {E}}}{\partial t} + \frac{\partial {\mathcal {E}}}{\partial z} \right) = \nabla ^2 {\mathcal {E}} + k^2 \left( n^2 - 1 \right) {\mathcal {E}}, \end{aligned}$$
(1)

where n is the refractive index, \({\mathcal {E}}\) is the slowly varying field amplitude with the Intensity I given by \(I \propto \vert {\mathcal {E}} \vert ^2\) and k is the wave number \(k=2 \pi / \lambda\). For the numerical solution, equation (1) is solved in a discretized form as a finite two-dimensional Fourier series

$$\begin{aligned} {\mathcal {E}} \left( x,y,z+\varDelta z \right) = \sum _{m=\frac{-N}{2}}^{N/2} \sum _{n=\frac{-N}{2}}^{N/2} {\mathcal {E}}_{mn}(z) e^{\frac{2\pi i(mx+ny)}{N}} \end{aligned}$$
(2)

wherein a square of the size \(L=N\varDelta x=N\varDelta y\) is discretized in m and n pixels in x-y space. With this, the initial field \({\mathcal {E}}_{mn}(z)\) is propagated along the distance \(\varDelta z\). In between the propagation step, at half the step length the phase delay through a refractive medium is added to the complex field as shown in Fig. 2. To include polarization effects in the later simulation, this propagation model can be extended vectorially by propagating one field for each polarization component and coupling the fields at specific element operators. In this model, the split step BPM is used to propagate the laser field as well as the pump field, so that all relevant refraction and diffraction effects are considered.

Fig. 2
figure 2

Schematic example of a propagation step in the vectorial split step BPM

Full size image

2.3 \(\hbox {Ho}^{3+}\) rate equations


To calculate the laser gain and internal heat load of the active laser crystal, a rate equation model is used to determine the energy state population of the relevant manifolds. For quasi-three-level laser ions like \(\hbox {Ho}^{3+}\), the simplified laser process by stimulated emission can be described by just the upper laser level and the ground level, since the lower laser level gets depopulated quickly due to fast thermal transitions. The temporal population dynamic of the upper laser level can be expressed by the following rate equation in differential form [7]

$$\begin{aligned} \frac{\partial N_{I7}}{\partial t} = W_P N_{I8} - \left( W_L+M_{7 \rightarrow 8}+\frac{1}{\tau _{7,sp}} \right) N_{I7}, \end{aligned}$$
(3)

where \(M_{ij}\) stands for the rate constant of phonon relaxation from the i to the j manifold, \(\frac{1}{\tau _{i,sp}}\) describes the rate constant of spontaneous emission and \(W_L\) and \(W_P\) are the rates of stimulated laser emission and pump absorption, respectively. In this simplified model the upper laser level population \(N_{I7}\) and the ground state population \(N_{I8}\) can be calculated analytically in the steady state. The heat load in this model only depends on the quantum defect between the pump wavelength and the laser wavelength, as well as heat generation due to phonon transitions of the upper laser level.

A more accurate rate equation model also has to take into account energy transfer upconversion (ETU) and cross-relaxation processes, since especially ETU is an important contributing factor to heat loss in holmium, as mentioned earlier. By including these transfer processes, more manifolds have to be considered. For the laser transition at 2.09\(\upmu{\text{m}}\) from the \(I7 \rightarrow I8\) manifold, the I8, I7, I6, and I5 manifolds now have to be taken into account. The expanded set of rate equations is based on a 2D model for \(\hbox {Er}^{3+}\):YAG described by Eichhorn [8] and is changed to fit the specific requirements for holmium at this laser transition. In this case, the rate equations have to be solved for all four relevant energy levels resulting in the following set of nonlinear equations:

$$\begin{aligned} \frac{\partial N_{I5}}{\partial t}&= N_{I7}^2 k_{7 \rightarrow 5} \nonumber \\&\quad - N_{I5} \left( C_{5 \rightarrow 7} N_{I8} + M_{5 \rightarrow 6} + \frac{1}{\tau _{5,sp}} \right) \end{aligned}$$
(4)
$$\begin{aligned} \frac{\partial N_{I6}}{\partial t}&= N_{I7}^2 k_{7 \rightarrow 6} \nonumber \\&\quad - N_{I6} \left( C_{6 \rightarrow 7} N_{I8} + M_{6 \rightarrow 7} + \frac{1}{\tau _{6,sp}} \right) \nonumber \\&\quad + N_{I5} \left( M_{5 \rightarrow 6} + \frac{1}{\tau _{5,sp}} \beta _{5 \rightarrow 6} \right) \end{aligned}$$
(5)
$$\begin{aligned} \frac{\partial N_{I7}}{\partial t}&= -2 N_{I7}^2 (k_{7 \rightarrow 6}+k_{7 \rightarrow 5}) \nonumber \\&\quad - N_{I7} \left( M_{7 \rightarrow 8} + \frac{1}{\tau _{7,sp}} \right) \nonumber \\&\quad + N_{I6} \left( 2 C_{6 \rightarrow 7} N_{I8} + M_{6 \rightarrow 7} + \frac{1}{\tau _{6,sp}} \beta _{6 \rightarrow 7} \right) \nonumber \\&\quad + N_{I5} \left( 2 C_{5 \rightarrow 7} N_{I8} + \frac{1}{\tau _{5,sp}} \beta _{5 \rightarrow 7} \right) \nonumber \\&\quad + N_{I8} \left( W_{P,abs} + W_{L,abs} \right) \nonumber \\&\quad - N_{I7} \left( W_{P,emi} + W_{L,emi} \right) \end{aligned}$$
(6)
$$\begin{aligned} \frac{\partial N_{I8}}{\partial t}&= N_{I7}^2 (k_{7 \rightarrow 6}+k_{7 \rightarrow 5}) \nonumber \\&\quad - N_{I8} \left( C_{5 \rightarrow 7} N_{I5} + C_{6 \rightarrow 7} N_{I6} \right) \nonumber \\&\quad + N_{I7} \left( M_{7 \rightarrow 8} + \frac{1}{\tau _{7,sp}} \right) \nonumber \\&\quad + N_{I6} \frac{1}{\tau _{6,sp}} \beta _{6 \rightarrow 8} + N_{I5} \frac{1}{\tau _{5,sp}} \beta _{5 \rightarrow 8} \nonumber \\&\quad - N_{I8} \left( W_{P,abs} + W_{L,abs} \right) \nonumber \\&\quad + N_{I7} \left( W_{P,emi} + W_{L,emi} \right) \end{aligned}$$
(7)

Figure 3 shows the schematic laser level diagram of the relevant manifolds for holmium, including all energy transfer processes of interest. The constants describing ETU \(k_{ij}\) and cross-relaxation \(C_{ij}\) quantify the ion-pair transitions taking place at different energy levels and are typically dependent on the doping concentration of the material [9]. Another level of complexity stems from the branching ratios for spontaneous emission \(\beta _{ij}\), which determine the probability of the spontaneous decay from i to a certain manifold j [10]. Many of the constants describing the population dynamics and spectral properties of holmium can be found in literature [11,12,13]. However, as the relevant literature shows variation in values, it may be useful to validate some of the properties in experiments to achieve more precise simulation results. The spectroscopic material parameters used for an example simulation with this model are presented in Appendix A (Table 1).

Fig. 3
figure 3

Energy level diagram of \(\hbox {Ho}^{3+}\), showing the relevant manifolds and energy transfer processes for the \(I7 \rightarrow I8\) laser transition

Full size image

Using the population dynamics of the spatially resolved crystal, the laser gain and absorption of the electromagnetic field \({\mathcal {E}}\) can be calculated by applying the Lambert-Beer law to consider the attenuation in the gain medium. Subsequently, the heat load in the crystal can be determined by the following equation: [8]

$$\begin{aligned} { H }&= \frac{1}{C \rho } \left( \frac{\partial I^{+}_{P}}{\partial z} - \frac{\partial I^{-}_{P}}{\partial z} + \frac{\partial I^{+}_{L}}{\partial z} - \frac{\partial I^{-}_{L}}{\partial z} \right) \nonumber \\&\quad - \frac{1}{C \rho } \left( \frac{N_{I7}}{\tau _{7,sp}} E_{7 \rightarrow 8} \beta _{7 \rightarrow 8} + \frac{N_{I6}}{\tau _{7,sp}} E_{6 \rightarrow 7} \beta _{6 \rightarrow 7} \right. \nonumber \\&\quad + \frac{N_{I6}}{\tau _{7,sp}} E_{6 \rightarrow 8} \beta _{6 \rightarrow 8} + \frac{N_{I5}}{\tau _{7,sp}} E_{5 \rightarrow 6} \beta _{5 \rightarrow 6} \nonumber \\&\quad + \left. \frac{N_{I5}}{\tau _{7,sp}} E_{5 \rightarrow 7} \beta _{5 \rightarrow 7} + \frac{N_{I5}}{\tau _{7,sp}} E_{5 \rightarrow 8} \beta _{5 \rightarrow 8} \right) . \end{aligned}$$
(8)

The first term in equation (8) accounts for the heat load by the absorption or emission of photons. The change of the intensity distributions in z direction \(I^{\pm }_{P,L}\) is accounted for the pump and laser fields respectively in negative and positive propagation direction. To include the radiative power loss, the spontaneous emission from the different manifolds is subtracted in the second term. Here, \(E_{i \rightarrow j}=\frac{h c}{\bar{\lambda _{i}}}\) is the average photon energy for a specific \(i \rightarrow j\) manifold transition. The rate equations (4–7) are unique to each active laser material at a specific laser transition and may be modified accordingly, if a different material has to be simulated.

3 Thermal effects in the \(\hbox {Ho}^{3+}\):YAG crystal

3.1 Temperature distribution


The heating of the crystal can lead to a variety of detrimental effects, for example, stability loss due to thermal lensing, power losses by depolarization due to birefringence, and the temperature dependence of different material parameters like the emission and absorption cross sections. Solid-state laser crystals for high power applications typically have a heat sink in place, leading to a specific thermal distribution. Therefore, the crystal temperature has an important influence on the overall resonator performance and should not be neglected in a precise simulation model. With the heat load in the crystal accurately calculated by the rate equation model in a three-dimensional grid, the temperature distribution can be solved numerically with high accuracy. The following second-order partial differential equation (PDE) describes the thermal diffusion

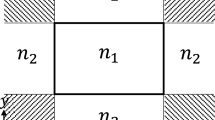
$$\begin{aligned} \frac{\partial T(x,y,z)}{\partial t} = \frac{k}{C \rho } \left( \nabla ^2 T(x,y,z) \right) + H(x,y,z), \end{aligned}$$
(9)

where k is the heat transfer coefficient, C is the heat capacity, and \(\rho\) is the density of the material. The heat load calculated by the rate equation model is included through the internal energy deposition H. There are several numerical solving methods suitable to this problem. For this model, the finite difference method (FDM) was chosen for its relative simplicity. More specifically, the three-dimensional alternating-direction implicit method (ADI) is used, as it has high stability and accuracy [14]. The method is based on an iterative approach, splitting the individual time steps in the three spatial directions as depicted in Fig. 4. To achieve an accurate representation of the real temperature in a crystal, the boundary conditions play an important role and have to be chosen correctly. In the case of the temperature diffusion, the boundary can either be defined by a Dirichlet or a Neumann condition. For the Dirichlet condition, the temperate values at the boundary are set to constant values \(T_{lat}\) and \(T_{end}\) for the lateral surface and the endfaces respectively. In cases where the temperature at the surface is not kept constant, a Neumann boundary condition can be chosen for higher accuracy. Here, the boundary is defined by the effective heat transfer coefficients \(k_{e,lat}\) and \(k_{e,end}\), calculated for the thermal resistances at the surface.

Fig. 4
figure 4

Schematic approach of the FDM ADI method [14]. The distribution is solved iteratively by splitting the time step in the three spatial directions

Full size image

3.2 Displacement distribution

Besides the temperature, the displacement due to thermal expansion also plays an important role in laser performance, since some contributions to thermal lensing and birefringence depend on the stress distribution in the crystal. With the temperature distribution calculated in a three-dimensional mesh, the displacement distribution can be calculated numerically by solving the respective differential equations. However, while the temperature can be calculated by a single parabolic PDE, the displacement distribution in this model is described by a set of coupled second-order hyperbolic PDEs, which adds more complexity to the respective model. The solution is based on Hooke’s generalized law in the three spatial dimensions given by the following set of equations [15]

$$\begin{aligned} \sigma _{xx}&= \frac{E}{1+\nu }\left \{ \frac{\partial u}{\partial x} + \frac{\nu }{1-2\nu } \left( \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} \right) \right\} \nonumber \\&\quad - \frac{E \alpha \varDelta T}{1-2\nu } \end{aligned}$$
(10)
$$\begin{aligned} \sigma _{yy}&= \frac{E}{1+\nu } \left\{ \frac{\partial v}{\partial y} + \frac{\nu }{1-2\nu } \left( \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} \right) \right\} \nonumber \\&\quad - \frac{E \alpha \varDelta T}{1-2\nu } \end{aligned}$$
(11)
$$\begin{aligned} \sigma _{zz}&= \frac{E}{1+\nu }\left \{ \frac{\partial w}{\partial z} + \frac{\nu }{1-2\nu } \left( \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} \right) \right\} \nonumber \\&\quad - \frac{E \alpha \varDelta T}{1-2\nu } \end{aligned}$$
(12)
$$\begin{aligned} \tau _{xy}&= \frac{E}{2(1+\nu )} \left( \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \right) \end{aligned}$$
(13)
$$\begin{aligned} \tau _{xz}&= \frac{E}{2(1+\nu )} \left( \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} \right) \end{aligned}$$
(14)
$$\begin{aligned} \tau _{yz}&= \frac{E}{2(1+\nu )} \left( \frac{\partial v}{\partial z} + \frac{\partial w}{\partial y} \right) \end{aligned}$$
(15)

wherein \(\sigma _{xx}\), \(\sigma _{yy}\), \(\sigma _{zz}\) are the normal stresses and \(\tau _{xy}\), \(\tau _{xz}\), \(\tau _{yz}\) are the shear stresses between the discretized mesh grid points as shown in Fig. 5. The displacements in the three spatial directions are given by u, v, w. E describes the elastic modulus, \(\nu\) the Poisson’s ratio of the material. The initial thermal expansion is included by the thermal expansion factor \(\alpha\) and the temperature \(\varDelta T\). By equating all the volume forces in the system and solving the resulting set of differential equations, the displacement is calculated. In this model, the set of equations is yet again solved by the ADI FDM, which is also suitable for this problem. However, to model more complex crystal shapes, a FEM algorithm should be considered. A control volume-based FDM approach using a staggered grid is detailed in [16]. As a simple solution for the boundary conditions, the degrees of freedom at a given surface can be set for the displacements in x,y, and z. For a cylindrical crystal rod, the boundary at the lateral surface \(DoF_{lat}\) and the endfaces \(DoF_{end}\) are defined to fit the realistic mounting condition of the crystal. With the resulting displacement distribution, the relevant stresses in the crystal can be calculated analytically with equations (10–15).

Fig. 5
figure 5

Components of stress in three dimensions in the Cauchy stress tensor

Full size image

3.3 Thermal lensing

Due to the heating of the laser crystal and resulting thermal effects, the crystal in a solid-state resonator typically displays lens-like behavior as depicted in Fig. 6. This is usually unwanted, limiting the power scalability of the system. Minimizing thermal lensing is, therefore, an important part of resonator design. In this model, thermal lensing is implemented by including the thermooptic effect, the photoelastic effect, and endface bulging [7].


Typically, the greatest impact to the thermal lens can be expected from the thermooptic effect, which describes the temperature-dependent change of the refractive index quantified with the material constant \(\frac{\partial n}{\partial T}\). By taking the highly resolved temperature distribution calculated prior, the change in refractive index is implemented with [17]

$$\begin{aligned} n(x,y,z)=n_0(\lambda ) \frac{\partial n}{\partial T} (T(x,y,z) - T_0), \end{aligned}$$
(16)

where \(n_0\) is the initial wavelength-dependent refractive index, \(T_o\) is the initial crystal temperature, and T(x, y, z) describes the temperature distribution due to the heat load in the crystal. Depending on the sign of the constant \(\frac{\partial n}{\partial T}\), this effect can contribute to a focusing or defocusing in the crystal, for \(\hbox {Ho}^{3+}\):YAG a focusing effect can be expected. Another contribution stems from the photoelastic effect, which describes the change in refractive index with the mechanical stresses due to thermal expansion. This effect is tied to the stress induced birefringence discussed in the next section. The last contributing factor in this model comes from the endface bulging of the crystal, which causes a lensing effect due to the deformation caused by thermal expansion at the endfaces. This can be implemented by adjusting the crystal length with the highly resolved displacement distribution calculated prior and using the intrinsic refraction functionality of the BPM.

Fig. 6
figure 6

Schematic depiction of thermal lensing in a laser crystal

Full size image

3.4 Stress-induced birefringence

Birefringence describes the optical property of a material, where the refractive index depends on the polarization direction incident on the material. Depending on the crystal structure, anisotropic materials can be inherently birefringent. \(\hbox {Ho}^{3+}\):YAG is an isotropic material, which typically does not exhibit this behavior. However, mechanical stresses in the crystal due to thermal expansion can deform the local optical indicatrix as shown in Fig. 7. This changes the refractive properties of the crystal to act birefringent, depending on the specific temperature profile. For end-pumped laser crystals, this will usually result in a radial stress profile, which acts birefringent towards an optical field incident along the optical crystal axis.

Fig. 7
figure 7

Stress-induced changes of the local optical indicatrix due to thermal expansion in isotropic media

Full size image

The implementation of stress-induced birefringence in this model is based on an approximate approach by Koechner and Rice [18]. The polarization dependent refractive index \(n_{\pm }=\frac{1}{\sqrt{B'_{\pm }}}\) that describes the resulting optical indicatrix in this approach, is expressed by the dielectric impermeability B.

$$\begin{aligned} B'_{\pm }&= \frac{1}{2} [ (B_{xx} + B_{yy}) \pm \left( (B_{xx} - B_{yy})^2 + 4B_{xy}^2 \right) ] \end{aligned}$$
(17)

The specific impermeability values used in equation (17) are calculated with the stress data derived from the displacement distribution and the photoelastic tensor \(p_{ij}\), which is a material tensor dependent on the specific crystal structure.

$$\begin{aligned} \begin{bmatrix} B_{xx} \\ B_{yy} \\ B_{zz} \\ B_{xy} \\ B_{xz} \\ B_{yz} \end{bmatrix}&= \begin{bmatrix} B_{0,xx} \\ B_{0,yy} \\ B_{0,zz} \\ 0 \\ 0 \\ 0 \end{bmatrix} \nonumber \\&+ \begin{bmatrix} p_{11} &{} p_{12} &{} p_{13} &{} p_{14} &{} p_{15} &{} 0 \\ p_{12} &{} p_{11} &{} p_{13} &{} -p_{14} &{} -p_{15} &{} 0 \\ p_{13} &{} p_{13} &{} p_{33} &{} 0 &{} 0 &{} 0 \\ p_{14} &{} -p_{14} &{} 0 &{} p_{44} &{} 0 &{} -p_{15} \\ p_{15} &{} -p_{15} &{} 0 &{} 0 &{} p_{44} &{} p_{14} \\ 0 &{} 0 &{} 0 &{} -p_{15} &{} p_{14} &{} p_{66} \end{bmatrix} \begin{bmatrix} \sigma _{xx} \\ \sigma _{yy} \\ \sigma _{zz} \\ \sigma _{xy} \\ \sigma _{xz} \\ \sigma _{yz} \end{bmatrix} \end{aligned}$$
(18)

The birefringent behavior in YAG is investigated in greater detail by Ostermeyer et al. in [19]. Unlike the slab geometry described in their work, cylindrical \(\hbox {Ho}^{3+}\):YAG rods are typically cut in the \(<111>\) crystal axis at a cut angle of \(\phi _{cut}=\pi\) relative to the [101] direction. This has to be considered when choosing the photoelastic tensor values for equation (18).

4 Model validation

4.1 Experimental setup

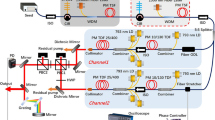
The combination of the aforementioned algorithms results in a powerful model for simulating cw \(\hbox {Ho}^{3+}\):YAG resonators. To validate the model, a resonator is set up in the laboratory and the experimental results are compared to the model results. Figure 8 shows a schematic depiction of the resonator used. The active medium is pumped with a \(\hbox {Tm}^{3+}\)-fiber laser operating at around 1908nm, with a maximum cw output power of 100W and a \(M^2<1.1\). A two-lens telescope is used to focus the pump beam in the crystal at a \(D4\sigma\) waist diameter of around 1000\(\upmu{\text{m}}\). The diameter of was measured at the crystal position without thermal effects and is expected to change in operation due to thermal lensing. The resonator itself is Z-shaped, where the pump beam passes through two dichroic mirrors at a \(45^{\circ }\) angle with high reflection at 2090nm and high transmission at 1908nm. This Z-shaped cavity was chosen to keep the resonator simple by utilizing a single pass pump design. The high reflector (HR, Mirror 1) has a concave surface with a curvature of 100cm. The plane outcoupling mirror (OC, Mirror 2) has a reflectivity of \(50\%\) at 2090nm. A 1.1 at.\(\%\)-doped \(\hbox {Ho}^{3+}\):YAG crystal rod with a diameter of 4mm and a length of 18mm acts as the active medium of the system. Both end faces are anti-reflection coated for the pump and laser wavelength. For cooling, the crystal was mounted into a copper heat sink to dissipate the heat load. The crystal is placed at half the resonator length, while the whole resonator from HR to OC has a length of 29cm. To produce a linear polarized output, a Brewster’s angle thin film polarizer is placed in the resonator in front of the OC. This basic setup allows for a good fundamental comparison between model and experiment.

Fig. 8
figure 8

Experimental \(\hbox {Ho}^{3+}\):YAG resonator setup used to validate the model

Full size image

4.2 Comparison between model and experiment

For many thermal and spectroscopic material properties, different values can be found in literature. The parameters used for the validation were therefore chosen in such a manner as to assure agreement with the literature and different experiments, like the measured absorption through the crystal at varying pump powers. The specific spectroscopic and thermal material parameters of the \(\hbox {Ho}^{3+}\):YAG crystal used for this simulation are summarized in Appendix A. The experimental setup is computed with the simulation model at different pump powers. The resulting output power plotted over the pump power is compared to the experiment in Fig. 9a. The comparison shows a similar slope of \(44.2\%\) for the experiment and \(42.9\%\) for the model. It is also notable, that at around 60W of pump power, the output power drops significantly. This is most likely due to the thermal lens in the resonator getting too strong and higher order modes getting more dominant, and it is also very well replicated in the model. The residual pump power over the incident pump power is plotted in Fig. 9b.

Fig. 9
figure 9

Comparison of an experimental \(\hbox {Ho}^{3+}\):YAG resonator setup with the model. In (a), the laser output power is compared, in (b) the residual pump power

Full size image

The measured data as well as the simulation show an irregular pump absorption, a rise in the residual pump power is notable at around 60W of pump power. We believe that this is due to the same reason as the drop in output power. Since the mode overlap between pump and laser mode likely changes due to thermal effects and the stronger higher order mode content, this will have a direct impact on the pump absorption efficiency.

Another important validation can be made by comparing the output field distributions at certain pump powers, as shown in Fig. 10. Here, the upper row shows the simulated output fields, while the lower row shows the output fields generated in the laboratory. The field distributions and \(D4\sigma\) diameters at the centroid were measured at a distance of 35cm behind the OC mirror. The evolution of the fields over the output power shows a clear degradation of the fundamental mode into higher order modes, with an especially strong degradation between 50W and 65W, where the drop in output power takes place. The simulated fields show a very similar evolution, further validating the accuracy of the model. One thing to note is that the Z-shaped \(\hbox {Ho}^{3+}\):YAG resonator used in this experiment was not optimized for a gaussian beam output. This approach was deliberately chosen to test the model at suboptimal beam qualities, where a resonator reaches its stability limit.

Fig. 10
figure 10

Comparison of the output field distributions and \(D4\sigma\) diameters at different pump powers. The upper row shows the simulated fields and the lower row shows the fields measured in experiment

Full size image

A further comparison between model and experiment can be made by taking a look at the depolarization field ejected at the polarizer in the resonator, where the power losses due to depolarization take place. Figure 11 shows the depolarization field measured in the experiment (a) and in the model (b). They both show a four-lobe intensity distribution, as expected from an end-pumped cylindrical laser crystal with isotropic properties. While the general fields look similar, there are some differences in the specific intensity distribution on the lobes. Some accuracy issues are to be expected here, since the birefringence implementation is an approximation and some material parameters may not be chosen correctly. Nonetheless, this comparison shows that in general, the birefringence algorithm does work as intended.

Fig. 11
figure 11

Comparison of the depolarization field ejected at the polarizer at a pump power of 50W. (a) shows the experiment and (b) the simulated field distribution

Full size image

5 Conclusion

We developed a powerful model for simulating end-pumped \(\hbox {Ho}^{3+}\):YAG resonators in continuous-wave operation. The fundamental model is based on a modular approach, where the propagation between different element operators is achieved with the split-step BPM field propagation algorithm. Thermal effects in the active laser crystal are included by a combination of different algorithms. The heat load in the crystal is calculated with the rate equations considering the population dynamics of holmium. The resulting temperature and displacement distributions are included by solving the respective differential equations with an FDM approach. These distributions allow for the inclusion of the most important thermal effects like thermal lensing and birefringence. The model is then compared to an experimental \(\hbox {Ho}^{3+}\):YAG linear cavity, where the model shows a good agreement in the evolution of output power and the resulting field distribution.

To achieve a high simulation accuracy, finding the right set of material parameters for the active laser medium can be a challenge, since literature values can vary between publications and may be incomplete. However, if the parameters are chosen in a suitable range, the model can be an powerful tool for simulating resonators with high precision.