Dynamics of a Stochastic SVEIR Epidemic Model Incorporating General Incidence Rate and Ornstein–Uhlenbeck Process

Abstract

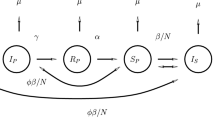
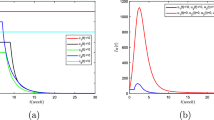
In this paper, considering the inevitable effects of environmental perturbations on disease transmission, we mainly study a stochastic SVEIR epidemic model in which the transmission rate satisfies the log-normal Ornstein–Uhlenbeck process and the incidence rate is general. To analyze the dynamic properties of the stochastic model, we firstly verify that there is a unique positive global solution. By constructing several suitable Lyapunov functions and using the ergodicity of the Ornstein–Uhlenbeck process, we establish sufficient conditions for the existence of stationary distribution, which means the disease will prevail. The sufficient condition for disease extinction is also given. Next, as a special case, we investigate the asymptotic stability of equilibria for the deterministic model and establish the exact expression of the probability density function of stationary distribution for the stochastic model. Finally, we calculate the mean first passage time from the initial value to the stationary state or extinction state to study the influence of environmental perturbations; meanwhile, some numerical simulations are carried out to demonstrate theoretical conclusions.

Appendices

Appendix A

We give the specific calculation process of

$$\begin{aligned} \lim _{t\rightarrow \infty }\left( \frac{1}{t}\int _{0}^{t}(\beta (\tau )-{\bar{\beta }})^2\textrm{d}\tau \right) ^{\frac{1}{2}}. \end{aligned}$$

A necessary integral should be first illustrated.

Lemma A

$\int _{-\infty }^{+\infty }e^{-At^{2}}\textrm{d}t=\frac{\sqrt{\pi }}{\sqrt{A}}.$

Proof

Let $y=\sqrt{A}t$, then we obtain

$$\begin{aligned} \int _{-\infty }^{+\infty }e^{-At^{2}}\textrm{d}t=\frac{1}{\sqrt{A}}\int _{-\infty }^{+\infty }e^{-y^{2}}\textrm{d}y. \end{aligned}$$

Denote $\Gamma (x)$ as the Gamma function, then we know $\Gamma (\frac{1}{2})=\sqrt{\pi }$. Let $x=y^2$, then we have

$$\begin{aligned} \int _{-\infty }^{+\infty }e^{-y^{2}}\textrm{d}y&=2 \int _{0}^{+\infty }e^{-y^{2}}\textrm{d}y =\int _{0}^{+\infty }\frac{1}{\sqrt{x}}e^{-x}\textrm{d}x =\Gamma (\frac{1}{2}) =\sqrt{\pi }. \end{aligned}$$

Therefore, we get

$$\begin{aligned} \int _{-\infty }^{+\infty }e^{-At^{2}}\textrm{d}t=\frac{\sqrt{\pi }}{\sqrt{A}}. \end{aligned}$$

$\square$

Next, we calculate $\lim _{t\rightarrow \infty }\left( \frac{1}{t}\int _{0}^{t}(\beta (\tau )-{\bar{\beta }})^2\textrm{d}\tau \right) ^{\frac{1}{2}}$. To make the calculation clear, let $y(t)=\log \beta (t)$ and ${\bar{y}}=\log {\bar{\beta }}$. According to the analysis in Sect. 2, y(t) obeys the Gaussian distribution ${\mathcal {N}}({\bar{y}},\frac{\lambda ^{2}}{2\gamma })$ as $t\rightarrow +\infty$ with the probability density function

$$\begin{aligned} \zeta (y)=\frac{\sqrt{\gamma }}{\sqrt{\pi }\lambda }e^{-\gamma \left( \frac{y -{\bar{y}}}{\lambda }\right) ^{2}}. \end{aligned}$$

From the ergodicity of $\beta (t)$, we have

$$\begin{aligned} \begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t}\int _{0}^{t}(\beta (\tau )-{\bar{\beta }})^2\textrm{d}\tau&=\int _{-\infty }^{+\infty }\left( e^y-e^{{\bar{y}}}\right) ^2\zeta (y)\textrm{d}y\\&=\int _{-\infty }^{+\infty }\left( e^y-e^{{\bar{y}}}\right) ^2\frac{\sqrt{\gamma }}{\sqrt{\pi }\lambda }e^{-\gamma \left( \frac{y -{\bar{y}}}{\lambda }\right) ^{2}}\textrm{d}y\\&={\bar{\beta }}^2\frac{\sqrt{\gamma }}{\sqrt{\pi }\lambda }\int _{-\infty }^{+\infty }\left( e^{y-{\bar{y}}}-1\right) ^2e^{-\gamma \left( \frac{y -{\bar{y}}}{\lambda }\right) ^{2}}\textrm{d}y \end{aligned} \end{aligned}$$

(48)

Let $x=y-{\bar{y}}$, then (48) turns into

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t}\int _{0}^{t}(\beta (\tau )-{\bar{\beta }})^2\textrm{d}\tau ={\bar{\beta }}^2\frac{\sqrt{\gamma }}{\sqrt{\pi }\lambda }\int _{-\infty }^{+\infty }\left( e^{x}-1\right) ^2e^{-\gamma \frac{x^2}{\lambda ^2}}\textrm{d}x. \end{aligned}$$

(49)

Let $t=\frac{x}{\lambda }$, then (49) transforms into

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t}\int _{0}^{t}(\beta (\tau )-{\bar{\beta }})^2\textrm{d}\tau&={\bar{\beta }}^2\frac{\sqrt{\gamma }}{\sqrt{\pi }}\int _{-\infty }^{+\infty }\left( e^{\lambda t}-1\right) ^2e^{-\gamma t^2}\textrm{d}t\\&={\bar{\beta }}^2\frac{\sqrt{\gamma }}{\sqrt{\pi }}\int _{-\infty }^{+\infty }\left( e^{2\lambda t-\gamma t^2}-2e^{\lambda t-\gamma t^2}+e^{-\gamma t^2}\right) \textrm{d}t\\&:={\bar{\beta }}^2\frac{\sqrt{\gamma }}{\sqrt{\pi }}\left( I_{1}-2I_{2}+I_{3}\right) . \end{aligned}$$

By Lemma A, we calculate $I_{1}$, $I_{2}$ and $I_{3}$, respectively.

$$\begin{aligned} I_{1}&=\int _{-\infty }^{+\infty }e^{2\lambda t-\gamma t^2}\textrm{d}t=\int _{-\infty }^{+\infty }e^{-\gamma (t-\frac{\lambda }{\gamma })^2+\frac{\lambda ^2}{\gamma }}\textrm{d}t\\&=e^{\frac{\lambda ^2}{\gamma }}\int _{-\infty }^{+\infty }e^{-\gamma (t-\frac{\lambda }{\gamma })^2}\textrm{d}t=e^{\frac{\lambda ^2}{\gamma }}\frac{\sqrt{\pi }}{\sqrt{\gamma }}.\\ I_{2}&=\int _{-\infty }^{+\infty }e^{\lambda t-\gamma t^2}\textrm{d}t =\int _{-\infty }^{+\infty }e^{-\gamma (t-\frac{\lambda }{2\gamma })^2+\frac{\lambda ^2}{4\gamma }}\textrm{d}t \\&=e^{\frac{\lambda ^2}{4\gamma }}\int _{-\infty }^{+\infty }e^{-\gamma (t-\frac{\lambda }{2\gamma })^2}\textrm{d}t=e^{\frac{\lambda ^2}{4\gamma }}\frac{\sqrt{\pi }}{\sqrt{\gamma }}.\\ I_{3}&=\int _{-\infty }^{+\infty }e^{-\gamma t^2}\textrm{d}t=\frac{\sqrt{\pi }}{\sqrt{\gamma }}. \end{aligned}$$

Finally, we have

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t}\int _{0}^{t}(\beta (\tau )-{\bar{\beta }})^2\textrm{d}\tau ={\bar{\beta }}^2\left( e^{\frac{\lambda ^2}{\gamma }}+2e^{\frac{\lambda ^2}{4\gamma }}+1\right) . \end{aligned}$$

Hence,

$$\begin{aligned} \lim _{t\rightarrow \infty }\left( \frac{1}{t}\int _{0}^{t}(\beta (\tau )-{\bar{\beta }})^2\textrm{d}\tau \right) ^{\frac{1}{2}}={\bar{\beta }}\left( e^{\frac{\lambda ^2}{\gamma }}+2e^{\frac{\lambda ^2}{4\gamma }}+1\right) ^{\frac{1}{2}}. \end{aligned}$$

Appendix B

We verify the local asymptotic stability of equilibria in the deterministic system (41).

Theorem B

Assuming that ${\hat{R}}_{0}<1$, then disease-free equilibrium $P_0$ is locally asymptotically stable (LAS). Furthermore, if ${\hat{R}}_{0}>1$, then the endemic equilibrium ${\hat{P}}^{*}$ is LAS, but $P_0$ is unstable.

Proof

The Jacobian matrix of system (41) is

$$\begin{aligned} J=\left( \begin{array}{cccc} -({\bar{\beta }}I+\mu +\rho )&{}\omega &{}0&{}-{\bar{\beta }}S\\ \rho &{}-({\bar{\beta }}I+\mu +\omega )&{}0&{}-{\bar{\beta }}V\\ {\bar{\beta }}I&{}{\bar{\beta }}I&{}-(\mu +\theta )&{}{\bar{\beta }}(S+V)\\ 0&{}0&{}\theta &{}-(\mu +\alpha ) \end{array}\right) . \end{aligned}$$

Evaluating the matrix J at $P_0$ leads us to

$$\begin{aligned} J_{0}=\left( \begin{array}{cccc} -(\mu +\rho )&{}\omega &{}0&{}-{\bar{\beta }}S_{0}\\ \rho &{}-(\mu +\omega )&{}0&{}-{\bar{\beta }}V_{0}\\ 0&{}0&{}-(\mu +\theta )&{}{\bar{\beta }}(S_{0}+V_{0})\\ 0&{}0&{}\theta &{}-(\mu +\alpha ) \end{array}\right) . \end{aligned}$$

The eigenvalues of $|\lambda {\mathbb {I}}_{4}-J_{0}|$ are determined by the following equation

$$\begin{aligned}&\left[ \lambda ^{2}+\left( 2\mu +\omega +\rho \right) \lambda +\mu (\mu +\omega +\rho )\right] \\&\quad \left[ \lambda ^{2}+(2\mu +\alpha +\theta )\lambda +(\mu +\theta )(\mu +\alpha )-\theta {\bar{\beta }}(S_{0}+V_{0})\right] =0. \end{aligned}$$

Apparently,

$$\begin{aligned} 2\mu +\omega +\rho>0,\ \mu (\mu +\omega +\rho )>0,\ 2\mu +\alpha +\theta >0. \end{aligned}$$

It is easy to check that $(\mu +\theta )(\mu +\alpha )-\theta {\bar{\beta }}(S_{0}+V_{0})>0$ when ${\hat{R}}_0<1$. By definition 2.1 in Yang et al. (2022), all eigenvalues of $J_{0}$ have the negative real part. Hence, $P_0$ is locally asymptotically stable if ${\hat{R}}_{0}<1$.

Next, we concentrate on the LAS of endemic equilibrium ${\hat{P}}^{*}=({\hat{S}}^{*},{\hat{V}}^{*},{\hat{E}}^{*},{\hat{I}}^{*})$. Taking ${\hat{P}}^*$ into the matrix J reads

$$\begin{aligned} J_*=\left( \begin{array}{cccc} -({\bar{\beta }}{\hat{I}}^*+\mu +\rho )&{}\omega &{}0&{}-{\bar{\beta }}{\hat{S}}^*\\ \rho &{}-({\bar{\beta }}{\hat{I}}^*+\mu +\omega )&{}0&{}-{\bar{\beta }}{\hat{V}}^*\\ {\bar{\beta }}{\hat{I}}^*&{}{\bar{\beta }}{\hat{I}}^*&{}-(\mu +\theta )&{}{\bar{\beta }}({\hat{S}}^*+{\hat{V}}^*)\\ 0&{}0&{}\theta &{}-(\mu +\alpha ) \end{array}\right) . \end{aligned}$$

From the third and fourth equations of (41), we have

$$\begin{aligned} {\bar{\beta }}({\hat{S}}^{*}+{\hat{V}}^{*}) =\frac{(\mu +\theta ){\hat{E}}^{*}}{{\hat{I}}^{*}}=\frac{(\mu +\theta )(\mu +\alpha )}{\theta }, \end{aligned}$$

which means

$$\begin{aligned} \theta {\bar{\beta }}({\hat{S}}^{*}+{\hat{V}}^{*})=(\mu +\theta )(\mu +\alpha ). \end{aligned}$$

(50)

Combining (50), the characteristic equation of $J_*$ is calculated as

$$\begin{aligned} \lambda ^{4}+a_{1}\lambda ^{3}+a_{2}\lambda ^{2}+a_{3}\lambda +a_{4}=0, \end{aligned}$$

(51)

in which

$$\begin{aligned} a_{1}=&2{\bar{\beta }}{\hat{I}}^{*}+4\mu +\omega +\rho +\theta +\alpha ,\\ a_{2}=&({\bar{\beta }}{\hat{I}}^{*}+\mu )({\bar{\beta }}{\hat{I}}^{*} +\mu +\omega +\rho )+(2\mu +\theta +\alpha )(2{\bar{\beta }}{\hat{I}}^{*}+2\mu +\omega +\rho ),\\ a_{3}=&\theta {\bar{\beta }}^{2}{\hat{I}}^{*}({\hat{S}}^{*}+{\hat{V}}^{*}) +(2\mu +\theta +\alpha )({\bar{\beta }}{\hat{I}}^{*}+\mu )({\bar{\beta }}{\hat{I}}^{*}+\mu +\omega +\rho ),\\ a_{4}=&\theta {\bar{\beta }}^{2}{\hat{I}}^{*}({\hat{S}}^{*}+{\hat{V}}^{*}) ({\bar{\beta }}{\hat{I}}^{*}+\mu +\omega +\rho ). \end{aligned}$$

It is obvious that $a_{1}>0,\ a_{2}>0,\ a_{3}>0,\ a_{4}>0$. To make the calculation briefer, define $b_{1}={\bar{\beta }}{\hat{I}}^{*}+\mu>0,\ b_{2}={\bar{\beta }}{\hat{I}}^{*}+\mu +\omega +\rho>0,\ b_{3}=2\mu +\theta +\alpha>0,\ b_{4}=\theta {\bar{\beta }}^{2}{\hat{I}}^{*}({\hat{S}}^{*}+{\hat{V}}^{*})={\bar{\beta }}{\hat{I}}^{*}(\mu +\theta )(\mu +\alpha )>0,$ then $a_1,\ a_2,\ a_3,\ a_4$ can be equivalently expressed as

$$\begin{aligned} a_{1}=b_{1}+b_{2}+b_{3},\ a_{2}=b_{1}b_{2}+b_{1}b_{3}+b_{2}b_{3},\ a_{3}=b_{4}+b_{1}b_{2}b_{3},\ a_{4}=b_{2}b_{4}. \end{aligned}$$

From

$$\begin{aligned} b_{1}b_{3}^{2}-b_{4}&=({\bar{\beta }}I^{*}+\mu )(2\mu +\theta +\alpha )^2-{\bar{\beta }}I^{*}(\mu +\theta )(\mu +\alpha )\\&={\bar{\beta }}I^{*}\left[ (\mu +\theta )^2+(\mu +\alpha )^2+(\mu +\theta )(\mu +\alpha )\right] \\&\quad +\mu (2\mu +\theta +\alpha )^2>0,\\ b_{2}b_{3}^{2}-b_{4}&=({\bar{\beta }}I^{*}+\mu +\omega +\rho )(2\mu +\theta +\alpha )^2-{\bar{\beta }}I^{*}(\mu +\theta )(\mu +\alpha )\\&={\bar{\beta }}I^{*}\left[ (\mu +\theta )^2+(\mu +\alpha )^2+(\mu +\theta )(\mu +\alpha )\right] \\&\quad +(\mu +\omega +\rho )(2\mu +\theta +\alpha )^2 >0, \end{aligned}$$

we obtain

$$\begin{aligned} a_{1}a_{2}-a_{3}&=(b_{1}+b_{2}+b_{3})(b_{1}b_{2}+b_{1}b_{3}+b_{2}b_{3})-(b_{4} +b_{1}b_{2}b_{3})\\&=b_{1}^{2}(b_{2}+b_{3})+b_{2}(b_{1}b_{2}+b_{1}b_{3} +b_{2}b_{3})\\&\quad +b_{1}b_{3}(b_{2}+b_{3})+b_{2}b_{3}^{2}-b_{4}>0, a_{1}(a_{2}a_{3}-a_{1}a_{4})-a_{3}^{2}\\&=(b_{1}b_{2})^{2}(b_{1}b_{3}+b_{2}b_{3}+b_{3}^{2}) +b_{1}^{2}b_{3}(b_{4}+b_{1}b_{2}b_{3})\\&\quad +(b_{1}b_{2}^{2}+b_{2}^{2}b_{3}+b_{2}^{3}+b_{1}b_{2}b_{3}+b_{4})(b_{1}b_{3}^{2}-b_{4}) >0. \end{aligned}$$

Therefore, all roots of (51) have the negative real part. We get the result that ${\hat{P}}^*$ is LAS when ${\hat{R}}_{0}>1$. The proof ends. $\square$