Impact of State-Dependent Dispersal on Disease Prevalence

Abstract

Based on a susceptible-infected-susceptible patch model, we study the influence of dispersal on the disease prevalence of an individual patch and all patches at the endemic equilibrium. Specifically, we estimate the disease prevalence of each patch and obtain a weak order-preserving result that correlated the patch reproduction number with the patch disease prevalence. Then we assume that dispersal rates of the susceptible and infected populations are proportional and derive the overall disease prevalence, or equivalently, the total infection size at no dispersal or infinite dispersal as well as the right derivative of the total infection size at no dispersal. Furthermore, for the two-patch submodel, two complete classifications of the model parameter space are given: one addressing when dispersal leads to higher or lower overall disease prevalence than no dispersal, and the other concerning how the overall disease prevalence varies with dispersal rate. Numerical simulations are performed to further investigate the effect of movement on disease prevalence.

1 Introduction

Infectious diseases pose a serious threat to public health and economic stability around the globe. The globalization, urbanization, and economic growth have strengthened both regional and global connectivity to an unprecedented level. However, large human movement facilitates pathogen spread and hinders disease control and elimination. For example, the COVID-19 outbreak was first detected in the city of Wuhan in China in December 2019 and was declared by the World Health Organization as a pandemic on March 11, 2020. As of October 5, 2020, the disease has caused more than 34.8 million confirmed cases and over 1 million deaths in more than 188 countries and territories (World Health Organization 2020). To mitigate the disease burden, many countries have imposed travel restrictions including entry-exit screening, flight cancellations, and city lockdown.

Mathematical modeling of the spatial-temporal spread of infectious diseases has attracted considerable attention in the past two decades (Rass and Radcliffe 2003; Sattenspiel and Lloyd 2009). A large number of spatial epidemic models have been proposed to describe disease spread through discrete diffusion (Wang 2007), continuous diffusion (Ruan and Wu 2009), and nonlocal diffusion (Yang et al. 2019). Among these, we refer to Wang and Mulone (2003), Wang and Zhao (2004), Salmani and van den Driessche (2006), Allen et al. (2007), Cosner et al. (2009), Gao and Ruan (2011, 2012), Tien et al. (2015) and Gao (2019) for epidemic patch models, Allen et al. (2008), Peng (2009), Huang et al. (2010), Lou and Zhao (2010), Ge et al. (2015), Wu and Zou (2016), Cui et al. (2017), Li et al. (2017), Song et al. (2019) for reaction-diffusion epidemic models, and Kuniya and Wang (2018), Yang et al. (2019), Zhang and Liu (2019) for nonlocal diffusion epidemic models. Most of these works focus on studying the effect of diffusion on the dynamic behavior of the model systems and particularly establishing threshold-type results in terms of the basic reproduction number.

It is important to know whether a disease can spread or not and how it goes in the long term, but that should not be the whole story. Disease eradication is rather difficult or even impossible for many infectious diseases. Smallpox is the only human disease that has been eradicated globally. Thus, reducing disease prevalence to a low level is usually a more feasible and cost-effective goal. This requires us to explore the impact of population dispersal on the infection size (i.e., the number of infections) or disease prevalence (i.e., the proportion of individuals in a given population having a specific disease or a particular condition). To our knowledge, there are only sporadic numerical investigations on this topic (Gao 2019; Gao et al. 2019; Hsieh et al. 2007) except one recent work (Gao 2020). It should be pointed out that the topic is highly related to a fundamental question in spatial ecology, that is, how does animal dispersal affect the population abundance and distribution in a heterogenous environment (DeAngelis et al. 2016b). Since the pioneering work of Freedman and Waltman (1977), extensive theoretical and experimental works have been done (Arditi et al. 2018; DeAngelis et al. 2016a; He et al. 2019; Lou 2006; Wang et al. 2020; Zhang et al. 2017, 2015).

In this paper, we consider a susceptible-infected-susceptible (SIS) patch model

$$\begin{aligned} \begin{aligned} \dfrac{dS_i}{dt}&=-\beta _i\frac{S_iI_i}{N_i}+\gamma _i I_i+\delta \sum \limits _{j\in \Omega } L_{ij}S_j,\&i\in \Omega ,\\ \dfrac{dI_i}{dt}&=\beta _i\frac{S_iI_i}{N_i}-\gamma _i I_i+\varepsilon \sum \limits _{j\in \Omega } L_{ij}I_j,\&i\in \Omega , \end{aligned} \end{aligned}$$

(1.1)

where $\Omega =\{1,2,...,n\}$, $n\ge 2$. Here $S_i(t)$ and $I_i(t)$ denote the number of susceptible and infected individuals in patch i at time t, respectively, and $N_i(t)=S_i(t)+I_i(t)$ is the total number of individuals in patch i at time t. The parameters $\beta _i$ and $\gamma _i$ are transmission and recovery rates in patch i, respectively; $L_{ij}$ represents the degree of incoming movement from patch j to patch i for $i\ne j$ and $-L_{ii}=\sum _{j\ne i}L_{ji}$ is the degree of outgoing movement from patch i to all other patches; $\delta$ and $\varepsilon$ are the dispersal rates of the susceptible and infected populations (i.e., the dispersal rate is dependent upon the disease state), respectively. We assume that $\beta _i$, $\gamma _i$, $\delta$, and $\varepsilon$ are all positive constants, independent of time t.

The model (1.1) was originally proposed and analyzed by Allen et al. (2007) and later studied from the aspects of asymptotic profiles and global stability of endemic equilibrium, and the monotonicity of the basic reproduction number with respect to dispersal rate of the infected populations by Li and Peng (2019), Gao (2019), Gao and Dong (2020), and Chen et al. (2020). To facilitate the analysis and presentation, the following assumptions will be required throughout the paper:

• (B1) $S_i(0)\ge 0$ and $I_i(0)>0$ for $i\in \Omega$;

• (B2) $L=(L_{ij})_{n\times n}$ is essentially nonnegative, irreducible, and $\sum _{j\in \Omega } L_{ji}=0$ holds for $i\in \Omega$.

Then by assumption (B2) and the Perron–Frobenius theorem, model (1.1) has a unique disease-free equilibrium $E_0=(S^0_1,\dots ,S^0_n,0,\dots ,0)$, where ${\varvec{S}}^0=(S^0_1,\dots ,S^0_n)$ is the unique positive solution of

$$\begin{aligned} \begin{aligned} \sum \limits _{j\in \Omega } L_{ij}S_j=0,\ i\in \Omega \quad \text{ and } \quad \sum \limits _{i\in \Omega }S_i=N, \end{aligned} \end{aligned}$$

where N is the total population size over all patches at time $t=0$, given by

$$\begin{aligned} N:=\sum \limits _{i\in \Omega }(S_i(0)+I_i(0)). \end{aligned}$$

By assumption (B1), N is positive.

Furthermore, it follows from, e.g., Lemma 3.1 in Gao and Dong (2020), that

$$\begin{aligned} \begin{aligned} (S^0_1,\dots ,S^0_n)=N(\alpha _1,\dots ,\alpha _n):=\frac{N}{\sum _{i\in \Omega }L_{ii}^*}(L_{11}^*,\dots ,L_{nn}^*) , \end{aligned} \end{aligned}$$

where $L_{ii}^*$ represents the (i, i) cofactor of L and $\mathop {{\mathrm {sgn}}}(L_{ii}^*)=(-1)^{n-1}$. That is,

$$\begin{aligned} \alpha _i=\frac{L_{ii}^*}{\sum _{i\in \Omega } L_{ii}^*}, \quad i\in \Omega ,\end{aligned}$$

satisfying $0<\alpha _i<1$ for all $i\in \Omega$ and $\sum _{i\in \Omega }\alpha _i=1$. In particular, if L is symmetric or line-sum-symmetric (i.e., the sum of elements in each of its rows equals the sum of elements in the corresponding column), then $L_{11}^*=\dots =L_{nn}^*$ and hence $\alpha _1=\dots =\alpha _n=1/n$.

Using the next-generation matrix method (Diekmann et al. 1990; van den Driessche and Watmough 2002), the basic reproduction number of model (1.1) is defined as ${\mathcal {R}}_0=\rho (FV^{-1})$, where

$$\begin{aligned}F=\mathop {{\mathrm {diag}}}\{\beta _1,\dots ,\beta _n\}\quad \text{ and } \quad V=\mathop {{\mathrm {diag}}}\{\gamma _1,\dots ,\gamma _n\}-\varepsilon L.\end{aligned}$$

Obviously, the basic reproduction number of patch i in isolation is ${\mathcal {R}}_0^{(i)}=\beta _i/\gamma _i$. When ${\mathcal {R}}_0>1$, by constructing an equivalent equilibrium problem, Allen et al. (2007) and Chen et al. (2020) showed the existence and uniqueness of the endemic equilibrium with symmetric and asymmetric connectivity matrix L, respectively.

Lemma 1.1

(Lemma 3.12 in Allen et al. (2007) and Theorem 3.3 in Chen et al. (2020)) For model (1.1), if ${\mathcal {R}}_0\le 1$ then $E_0$ is globally asymptotically stable in ${\mathbb {R}}^{2n}_+$, whereas if ${\mathcal {R}}_0>1$ then the disease is uniformly persistent and there exists a unique endemic equilibrium

$$\begin{aligned} \begin{aligned} E^*=({\varvec{S}}^*,{\varvec{I}}^*)=(S_1^*,\dots ,S_n^*,I_1^*,\dots ,I_n^*) =\left( \kappa {\check{S}}_1^*,\dots ,\kappa {\check{S}}_n^*, \frac{\kappa }{\varepsilon }{\check{I}}_1^*,\dots , \frac{\kappa }{\varepsilon }{\check{I}}_n^*\right) , \end{aligned} \end{aligned}$$

(1.2)

where

$$\begin{aligned} \begin{aligned} {\check{S}}_i^*=\frac{\alpha _i-{\check{I}}_i^*}{\delta },\ i\in \Omega ,\quad \text{ and } \quad \kappa =\frac{\varepsilon N}{\sum \limits _{j\in \Omega }(\varepsilon {\check{S}}_j^*+{\check{I}}_j^*)} =\frac{\varepsilon N}{\theta +(1-\theta )\sum \limits _{j\in \Omega }{\check{I}}_j^*}, \end{aligned} \end{aligned}$$

$\theta :=\varepsilon /\delta \in (0,\infty )$, and $\check{{\varvec{I}}}^*=({\check{I}}_1^*,\dots ,{\check{I}}_n^*)$ is the unique positive solution to

$$\begin{aligned} \begin{aligned} h_i(\check{{\varvec{I}}}):={\check{I}}_i\left( \beta _i-\gamma _i- \frac{\beta _i{\check{I}}_i}{\theta (\alpha _i-{\check{I}}_i)+{\check{I}}_i}\right) +\varepsilon \sum \limits _{j\in \Omega } L_{ij}{\check{I}}_j=0,\quad i\in \Omega , \end{aligned} \end{aligned}$$

(1.3)

in the region $\Gamma =\{({\check{I}}_1,\dots ,{\check{I}}_n)\in {\mathbb {R}}_+^n\ |\ 0\le {\check{I}}_i\le \alpha _i,\ i\in \Omega \}$. Moreover, ${\check{I}}_i^*$ is monotone increasing in parameter $\theta$ for all $i\in \Omega$.

In reality, the relative mobility of infected individuals to susceptible individuals, $\theta$, is probably below one for human diseases but may be above one for animal diseases such as rabies (Ruan and Wu 2009). The following assumption will also be required throughout the paper to reflect the environmental heterogeneity across the habitat:

• (B3) ${\mathcal {R}}_0^{(i)}$ is nonconstant in $i\in \Omega$.

Otherwise, the reproduction number ${\mathcal {R}}_0={\mathcal {R}}_0^{(i)}$ for all $i\in \Omega$ and the endemic equilibrium $E^*=({\varvec{S}}^0/{\mathcal {R}}_0,(1-1/{\mathcal {R}}_0){\varvec{S}}^0)$ are independent of dispersal rates.

Using the theory of monotone dynamical systems (Smith 1995; Zhao 2017), Gao and Ruan showed that $E^*$ is globally asymptotically stable if susceptible and infected individuals disperse at the same rates (Gao and Ruan 2011). Recently Li and Peng (2019) established the global asymptotic stability of $E^*$ in the case of constant patch reproduction number ${\mathcal {R}}_0^{(i)}$. Extensive numerical simulations suggest that the global attractivity of $E^*$ holds for general model (1.1).

In the next two sections, we will investigate some quantitative properties of $E^*$, i.e., how human movement affects the disease prevalence of an individual patch and all patches at the endemic equilibrium (when it exists), denoted by,

$$\begin{aligned}\frac{I_i^*}{S_i^*+I_i^*}\ \text{ and } \ \frac{T_n}{N},\end{aligned}$$

respectively, where $T_n=\sum \nolimits _{i\in \Omega }I_i^*$ denotes the total infection size over all patches. Since the total population size N is constant, we use total infection size and overall disease prevalence interchangeably.

In Sect. 4, we completely answer two epidemiologically meaningful questions for two-patch case: (1) when does dispersal cause higher or lower overall disease prevalence than no dispersal? (2) when is it detrimental or beneficial to disease control in terms of overall disease prevalence by implementing or relaxing travel restrictions? One of the key ingredients in the proofs is to show that the total abundance of infected population at equilibrium, as a function of the dispersal rate, has at most one local maximum.

In Sect. 5, numerical simulations are conducted to demonstrate the impact of human migration on the overall disease prevalence. A brief discussion of the main results and their implications is given at the end. We extend the main results in Gao (2020) from a special case ($\delta =\varepsilon$) to a general setting with substantial improvements and new findings.

2 General Results

This section is mainly devoted to the study of the effect of population dispersal on the disease prevalence of an individual patch. We first present a lemma on the basic reproduction number ${\mathcal {R}}_0$ which guarantees that if the disease eventually dies out in every patch for some dispersal rate $\varepsilon _0\in [0,\infty )$ then it remains extinct for $\varepsilon >\varepsilon _0$.

Lemma 2.1

(Lemma 3.1 in Gao (2020) and Gao and Dong (2020)) For model (1.1), the basic reproduction number ${\mathcal {R}}_0(\varepsilon )=\rho (FV^{-1})$ and the spectral bound $s(\varepsilon ):=s(F-V)=s(F-D+\varepsilon L)$ are strictly decreasing and strictly convex in $\varepsilon \in [0,\infty )$ if ${\mathcal {R}}_0^{(i)}=\beta _i/\gamma _i$ and $\beta _i-\gamma _i$ are, respectively, nonconstant in $i\in \Omega$, and constant otherwise, where $D=\mathop {{\mathrm {diag}}}\{\gamma _1,\dots ,\gamma _n\}$. Moreover, we have

$$\begin{aligned}\min \limits _{i\in \Omega }{\mathcal {R}}_0^{(i)}<{\mathcal {R}}_0(\infty )=\sum _{i\in \Omega } \beta _iL_{ii}^*\Big /\sum _{i\in \Omega } \gamma _iL_{ii}^*<{\mathcal {R}}_{0}(\varepsilon )<{\mathcal {R}}_0(0)=\max \limits _{i\in \Omega }{\mathcal {R}}_0^{(i)},\quad \forall \varepsilon >0,\end{aligned}$$

where ${\mathcal {R}}_0^{(i)}$ is nonconstant in $i\in \Omega$ and $L_{ii}^*$ is the (i, i) cofactor of L. In addition, if ${\mathcal {R}}_0(0)>1$, then the followings hold:

• (a) If ${\mathcal {R}}_0(\infty )<1$, then there exists a unique critical value $\varepsilon ^*\in (0,\infty )$ such that ${\mathcal {R}}_0(\varepsilon )>1$ for $\varepsilon <\varepsilon ^*$, ${\mathcal {R}}_0(\varepsilon )=1$ for $\varepsilon =\varepsilon ^*$, and ${\mathcal {R}}_0(\varepsilon )<1$ for $\varepsilon >\varepsilon ^*$.

• (b) If ${\mathcal {R}}_0(\infty )\ge 1$, then we have ${\mathcal {R}}_0(\varepsilon )>1$ for all $\varepsilon \ge 0$.

For convenience, we introduce the following notations:

$$\begin{aligned} \begin{aligned}&{\check{f}}_i({\check{I}}_i)={\check{g}}_i({\check{I}}_i){\check{I}}_i\quad \text{ and } \quad {\check{g}}_i({\check{I}}_i)=\beta _i-\gamma _i- \frac{\beta _i{\check{I}}_i}{\theta (\alpha _i-{\check{I}}_i)+{\check{I}}_i},\quad i\in \Omega . \end{aligned} \end{aligned}$$

Like the relation between patch reproduction numbers and multipatch reproduction number (Gao and Ruan 2011), the disease prevalence over all connected patches is bounded below and above by the minimum and maximum values of the single patch disease prevalences.

Proposition 2.2

For model (1.1), if ${\mathcal {R}}_0>1$ for some $\delta >0$ and $\varepsilon >0$, then the disease prevalence at the endemic equilibrium $E^*=({\varvec{S}}^*,{\varvec{I}}^*)=({\varvec{N}}^*-{\varvec{I}}^*,{\varvec{I}}^*)$ satisfies

$$\begin{aligned}\left( 1-\frac{1}{\min \limits _{j\in \Omega }{\mathcal {R}}_0^{(j)}}\right) ^+< \frac{I_i^*}{N_{i}^*}< 1-\frac{1}{\max \limits _{j\in \Omega }{\mathcal {R}}_0^{(j)}},\quad i\in \Omega ,\end{aligned}$$

where $\zeta ^+=\max \{\zeta ,0\}$. Furthermore, the same estimate holds for the overall disease prevalence $\frac{T_n}{N}= \sum \limits _{i\in \Omega }I_i^*\big / \sum \limits _{i\in \Omega }N_i^*$.

Proof

It follows from Lemma 1.1 that

$$\begin{aligned} \begin{aligned}&S_i^*=\kappa {\check{S}}_i^*=\frac{\varepsilon N}{\theta +(1-\theta )\sum \limits _{j\in \Omega }{\check{I}}_j^*}\cdot \frac{\alpha _i-{\check{I}}_i^*}{\delta }=\frac{\theta (\alpha _i-{\check{I}}_i^*)}{\theta +(1-\theta )\sum _{j\in \Omega }{\check{I}}_j^*}N,\\&I_i^*=\frac{\kappa }{\varepsilon }{\check{I}}_i^* =\frac{\varepsilon N}{\theta +(1-\theta )\sum \limits _{j\in \Omega }{\check{I}}_j^*}\cdot \frac{1}{\varepsilon } {\check{I}}_i^*=\frac{{\check{I}}_i^*}{\theta +(1-\theta )\sum _{j\in \Omega }{\check{I}}_j^*}N. \end{aligned} \end{aligned}$$

(2.1)

Thus, the disease prevalence of patch i at the endemic equilibrium $E^*$ is

$$\begin{aligned} \begin{aligned} \frac{I_i^*}{S_i^*+I_i^*}=\frac{{\check{I}}_i^*}{\theta (\alpha _i-{\check{I}}_i^*)+{\check{I}}_i^*}, \end{aligned} \end{aligned}$$

(2.2)

which is strictly increasing in ${\check{I}}_i^*\in [0,\alpha _i]$. Denote

$$\begin{aligned} \begin{aligned}&\bar{{\varvec{I}}}=({\bar{I}}_1,\dots ,{\bar{I}}_n) =\left( 1-\frac{1}{1+\theta \max \limits _{i\in \Omega }({\mathcal {R}}_0^{(i)}-1)^+}\right) (\alpha _1,\dots ,\alpha _n),\\&\underline{{\varvec{I}}}=({\underline{I}}_1,\dots ,{\underline{I}}_n) =\left( 1-\frac{1}{1+\theta \min \limits _{i\in \Omega }({\mathcal {R}}_0^{(i)}-1)^+}\right) (\alpha _1,\dots ,\alpha _n). \end{aligned} \end{aligned}$$

Assume that ${\mathcal {R}}_0^{(i)}>1$ for all $i\in \Omega$. Otherwise, the lower bound of $I_i^*/N_{i}^*$ immediately holds. It follows from

$$\begin{aligned} \begin{aligned} h_i(\bar{{\varvec{I}}})={\check{f}}_i({\bar{I}}_i)\le 0\ \text{ and } \ h_i(\underline{{\varvec{I}}})={\check{f}}_i({\underline{I}}_i)\ge 0,\ i\in \Omega \end{aligned} \end{aligned}$$

that $\bar{{\varvec{I}}}$ and $\underline{{\varvec{I}}}$ are the upper and lower solutions of (1.3), respectively. By the strong monotonicity of the system generated by (1.3) and assumption (B3), we know

$$\begin{aligned} \begin{aligned} \underline{{\varvec{I}}}\ll \check{{\varvec{I}}}^*\ll \bar{{\varvec{I}}}. \end{aligned} \end{aligned}$$

(2.3)

The proof is completed by substituting the estimate (2.3) into (2.2). $\square$

We next generalize the weak order-preserving result in Gao (2020) from $\theta =1$ (i.e., $\delta =\varepsilon$) to arbitrary $\theta >0$ (i.e., $\forall \varepsilon >0$ and $\delta >0$) and the proof is postponed to Appendix A.

Theorem 2.3

For model (1.1), suppose ${\mathcal {R}}_0^{(1)}\ge \dots \ge {\mathcal {R}}_0^{(n)}$ and ${\mathcal {R}}_0>1$ for some $\delta >0$ and $\varepsilon >0$, then the disease prevalence at the unique endemic equilibrium $E^*=({\varvec{N}}^*-{\varvec{I}}^*,{\varvec{I}}^*)$ satisfies

$$\begin{aligned}\min \limits _{i\in \Omega }\frac{I^*_i}{N^*_i}<\frac{I^*_1}{N^*_1}<1-\frac{1}{{\mathcal {R}}_0^{(1)}}\quad \text{ and } \quad \left( 1-\frac{1}{{\mathcal {R}}_0^{(n)}}\right) ^+<\frac{I^*_n}{N^*_n}<\max \limits _{i\in \Omega } \frac{I^*_i}{N^*_i}.\end{aligned}$$

In particular, for the two-patch case, we have $I^*_1/N^*_1>I^*_2/N^*_2$, i.e., the disease prevalence of the high-risk patch is always larger than that of the low-risk patch; for the three-patch case, we have $I^*_1/N^*_1>I^*_3/N^*_3$, i.e., the disease prevalence of the highest-risk patch is always larger than that of the lowest-risk patch.

Remark 2.4

Under the condition of Theorem 2.3, it follows from Proposition 2.2 that

$$\begin{aligned}\frac{I^*_1}{N^*_1}<1-\frac{1}{{\mathcal {R}}_0^{(1)}}\quad \text{ and } \quad \left( 1-\frac{1}{{\mathcal {R}}_0^{(n)}}\right) ^+<\frac{I^*_n}{N^*_n}\end{aligned}$$

and hence

$$\begin{aligned} \begin{aligned}&f_1(I_1^*)=\beta _1I_1^*\left( 1-\frac{1}{{\mathcal {R}}_0^{(1)}}-\frac{I_1^*}{N_1^*}\right)>0>\sum \limits _{j\in \Omega } L_{1j}I_j^*,\\&f_n(I_n^*)=\beta _nI_n^*\left( 1-\frac{1}{{\mathcal {R}}_0^{(n)}}-\frac{I_n^*}{N_n^*}\right)<0 <\sum \limits _{j\in \Omega } L_{nj}I_j^*. \end{aligned} \end{aligned}$$

Thus, combining with the last part of the proof of Theorem 2.3, an alternative proof of the above theorem can be given. We will numerically show that the conclusions of Proposition 2.2 and Theorem 2.3 may fail if the susceptible and infected populations have different connectivity matrices.

Following Remark 2.4, we can see that

$$\begin{aligned} \begin{aligned} \sum \limits _{j\in \Omega } L_{ij}N_j^*=\sum \limits _{j\in \Omega } L_{ij}S_j^*+\sum \limits _{j\in \Omega } L_{ij}I_j^*=(1-\varepsilon /\delta )\sum \limits _{j\in \Omega } L_{ij}I_j^* \end{aligned} \end{aligned}$$

can be positive or negative if $\theta =\varepsilon /\delta \ne 1$, which suggests that the state-dependent dispersal also affects the distribution of hosts. In particular, for two-patch case, dispersal increases/decreases the population size of the high-risk patch but decreases/increases that of the low-risk patch if and only if infections reduce/increase host mobility.

Corollary 2.5

For (1.1), suppose ${\mathcal {R}}_0^{(1)}\ge \dots \ge {\mathcal {R}}_0^{(n)}$ and ${\mathcal {R}}_0>1$ for some $\delta >0$ and $\varepsilon >0$, then the population distribution at the unique endemic equilibrium $E^*=({\varvec{N}}^*-{\varvec{I}}^*,{\varvec{I}}^*)$ satisfies

$$\begin{aligned}\sum \limits _{j\in \Omega }L_{1j}N_j^*>(=,<)\;0>(=,<)\;\sum \limits _{j\in \Omega }L_{nj}N_j^*,\end{aligned}$$

if and only if $\theta =\varepsilon /\delta >(=,<)\;1$. In particular, for the two-patch case, we have

$$\begin{aligned}\frac{N^*_1}{\alpha _1 N}>(=,<)\;1>(=,<)\;\frac{N^*_2}{\alpha _2 N},\end{aligned}$$

if and only if $\theta =\varepsilon /\delta <(=,>)\;1$, where $\alpha _1=L_{12}/(L_{12}+L_{21})$ and $\alpha _2=1-\alpha _1$.

It is worth pointing out that results similar to Proposition 2.2, Theorem 2.3, and Remark 2.4 can be established for the unique positive solution of (1.3). In particular, we can rewrite (2.3) to give an estimate of ${\check{I}}_i^*/\alpha _i$ or ${\check{I}}_i^*$ which will be used later.

Corollary 2.6

For system of equations (1.3), if ${\mathcal {R}}_0>1$ for some $\varepsilon >0$ and $\theta >0$, then the unique positive solution $\check{{\varvec{I}}}^*=({\check{I}}_1^*,\dots ,{\check{I}}_n^*)$ satisfies

$$\begin{aligned} \min \limits _{j\in \Omega } \frac{{\check{I}}_j^*(0)}{\alpha _j}<\frac{{\check{I}}_i^*}{\alpha _i}< \max \limits _{j\in \Omega } \frac{{\check{I}}_j^*(0)}{\alpha _j},\quad i\in \Omega ,\end{aligned}$$

where ${\check{I}}^*_j(0)=\Big (1-\frac{1}{1+\theta ({\mathcal {R}}_0^{(j)}-1)^+}\Big )\alpha _j,\ j\in \Omega .$ If, in addition, L is line-sum-symmetric, then

$$\begin{aligned} \min \limits _{j\in \Omega } {\check{I}}_j^*(0)<{\check{I}}_i^*< \max \limits _{j\in \Omega } {\check{I}}_j^*(0),\quad i\in \Omega .\end{aligned}$$

At the end of this section, we consider the total infection size over all patches at the positive steady state (when it exists) or the disease-free steady state and its limit as the dispersal rate $\delta$ or $\varepsilon$ approaches zero or infinity. In case where the patchy environment consists of both high-risk and low-risk patches satisfying ${\mathcal {R}}_0^{(i)}>1>{\mathcal {R}}_0^{(j)}$ for some $i,j\in \Omega$, the asymptotic profile of the endemic equilibrium $E^*$ as $\delta \rightarrow 0$ or $\varepsilon \rightarrow 0$ was discussed by Allen et al. (2007), Li and Peng (2019), and Chen et al. (2020).

Proposition 2.7

For model (1.1), the total infection size, denoted by $T_n(\delta ,\varepsilon )$, satisfies

$$\begin{aligned} \begin{aligned} T_n(\delta ,\varepsilon ):=\sum \limits _{i\in \Omega } I^*_i(\delta ,\varepsilon ) =\frac{{\check{T}}_n(\delta ,\varepsilon )}{\theta +(1-\theta ){\check{T}}_n(\delta ,\varepsilon )}N,\quad \forall \varepsilon >0, \end{aligned} \end{aligned}$$

where

$$\begin{aligned}I^*_i(\delta ,\varepsilon )=\frac{{\check{I}}_i^*(\delta ,\varepsilon )}{\theta +(1-\theta ){\check{T}}_n(\delta ,\varepsilon )}N\quad \text{ and } \quad {\check{T}}_n(\delta ,\varepsilon ):= \sum \limits _{i\in \Omega }{\check{I}}_i^*(\delta ,\varepsilon )\in [0,1). \end{aligned}$$

In addition, we have

$$\begin{aligned} \begin{aligned}&T_n(0+,\varepsilon ):=\lim \limits _{\delta \rightarrow 0+} T_n(\delta ,\varepsilon )=\frac{1}{1+\sum \limits _{i\in \Omega }\frac{\alpha _i}{({\mathcal {R}}_0^{(i)}-1)^+}}N,\quad \forall \varepsilon \in (0,\infty ],\\&T_n(\delta ,0+):=\lim \limits _{\varepsilon \rightarrow 0+} T_n(\delta ,\varepsilon )=\Big (1-\frac{1}{1+\sum \limits _{i\in \Omega }\alpha _i({\mathcal {R}}_0^{(i)}-1)^+}\Big )N,\quad \forall \delta \in (0,\infty ],\\&T_n(\infty ,\varepsilon ):=\lim \limits _{\delta \rightarrow \infty } T_n(\delta ,\varepsilon )=\Big (1- \frac{1}{1+\sum \limits _{i\in \Omega }{\hat{I}}_i}\Big )N,\quad \forall \varepsilon \in (0,\infty ],\\&T_n(\delta ,\infty ):=\lim \limits _{\varepsilon \rightarrow \infty } T_n(\delta ,\varepsilon )=\frac{1}{1+\sum \limits _{i\in \Omega }{\hat{S}}_i}N,\quad \forall \delta \in (0,\infty ], \end{aligned} \end{aligned}$$

where $T_n(0+,\varepsilon )=0$ if ${\mathcal {R}}_0^{(i)}\le 1$ for some $i\in \Omega$, and $({\hat{I}}_1,\dots ,{\hat{I}}_n)$ and $({\hat{S}}_1,\dots ,{\hat{S}}_n)$ are, respectively, the unique positive solutions to

$$\begin{aligned}\varepsilon \sum \limits _{j\in \Omega }L_{ij}{\hat{I}}_j +\beta _i\frac{\alpha _i}{\alpha _i+{\hat{I}}_i}{\hat{I}}_i-\gamma _i{\hat{I}}_i=0,\quad i\in \Omega ,\end{aligned}$$

and

$$\begin{aligned}\delta \sum \limits _{j\in \Omega }L_{ij}{\hat{S}}_j -\beta _i\frac{\alpha _i}{\alpha _i+{\hat{S}}_i}{\hat{S}}_i+\gamma _i\alpha _i=0,\quad i\in \Omega ,\end{aligned}$$

provided that ${\mathcal {R}}_0(\varepsilon )>1$ and ${\mathcal {R}}_0(\infty )>1$.

Proof

It follows from (2.1) that

$$\begin{aligned} \begin{aligned} T_n(\delta ,\varepsilon )&=\sum \limits _{i\in \Omega } I^*_i(\delta ,\varepsilon ) =\sum \limits _{i\in \Omega }\frac{{\check{I}}_i^*(\delta ,\varepsilon )}{\theta +(1-\theta )\sum \limits _{j\in \Omega }{\check{I}}_j^*(\delta ,\varepsilon )}N=\frac{{\check{T}}_n(\delta ,\varepsilon )}{\theta +(1-\theta ){\check{T}}_n(\delta ,\varepsilon )}N. \end{aligned} \end{aligned}$$

We omit the proof of the remaining parts which are similar to these of Lemma 4.1 in Allen et al. (2007), Lemma 3.4 in Chen et al. (2020) and Theorem 3.6 in Gao and Dong (2020). It suffices to note that no low-risk patch with ${\mathcal {R}}_0^{(i)}<1$ is required. $\square$

3 Model with Restrictions

In this section, we further work on the total infection size, or equivalently, the overall disease prevalence of model (1.1) under two additional assumptions as follows:

• (B4) The diffusion coefficients of the susceptible and infected subpopulations are proportional, i.e., $\delta =\varepsilon /\theta$ with constant $\theta$ and variable $\varepsilon$;

• (B5) The population distribution by patch at no dispersal obeys the limiting case of $\varepsilon \rightarrow 0+$.

The assumption (B4) here is a generalization of (B5) in Gao (2020), and (B5) here was labeled (B4) in Gao (2020). Under assumption (B4), model (1.1) takes the form

$$\begin{aligned} \begin{aligned} \dfrac{dS_i}{dt}&=-\beta _i\frac{S_iI_i}{N_i}+\gamma _i I_i+\frac{\varepsilon }{\theta }\sum \limits _{j\in \Omega } L_{ij}S_j,\quad&i\in \Omega ,\\ \dfrac{dI_i}{dt}&=\beta _i\frac{S_iI_i}{N_i}-\gamma _i I_i+\varepsilon \sum \limits _{j\in \Omega } L_{ij}I_j,\quad&i\in \Omega . \end{aligned} \end{aligned}$$

(3.1)

In correspondence to Proposition 2.7, we get the following result on the total number of infections for model (3.1) as the diffusion coefficient $\varepsilon \rightarrow 0+$ or $\infty$.

Theorem 3.1

For model (3.1), the total infection size, denoted by $T_n(\varepsilon )$, satisfies

$$\begin{aligned} \begin{aligned} T_n(\varepsilon ):=\sum \limits _{i\in \Omega } I^*_i(\varepsilon ) =\frac{{\check{T}}_n(\varepsilon )}{\theta +(1-\theta ){\check{T}}_n(\varepsilon )}N,\quad \forall \varepsilon >0, \end{aligned} \end{aligned}$$

where

$$\begin{aligned}I^*_i(\varepsilon )=\frac{{\check{I}}_i^*(\varepsilon )}{\theta +(1-\theta ){\check{T}}_n(\varepsilon )}N\quad \text{ and } \quad {\check{T}}_n(\varepsilon ):= \sum \limits _{i\in \Omega }{\check{I}}_i^*(\varepsilon )\in [0,1). \end{aligned}$$

In addition, we have

$$\begin{aligned} \begin{aligned} T_n(0)&=\sum _{i\in \Omega }I^*_i(0)=\frac{1-\sum \limits _{i\in \Omega }\frac{\alpha _i}{1+\theta ({\mathcal {R}}_0^{(i)}-1)^+}}{\theta +(1-\theta ) \left( 1-\sum \limits _{i\in \Omega }\frac{\alpha _i}{1+\theta ({\mathcal {R}}_0^{(i)}-1)^+}\right) }N, \\ T_n(\infty )&=\sum _{i\in \Omega }I^*_i(\infty )= \Big (1-\frac{1}{{\mathcal {R}}_0(\infty )}\Big )^+ N, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} {\check{I}}^*_i(0)&:=\lim \limits _{\varepsilon \rightarrow 0+}{\check{I}}^*_i(\varepsilon )=\Big (1-\frac{1}{1+\theta ({\mathcal {R}}_0^{(i)}-1)^+}\Big )\alpha _i,\quad&i\in \Omega , \\ {\check{I}}^*_i(\infty )&:= \lim \limits _{\varepsilon \rightarrow \infty }{\check{I}}^*_i(\varepsilon )= \Big (1-\frac{1}{1+\theta ({\mathcal {R}}_0(\infty )-1)^+}\Big )\alpha _i,\quad&i\in \Omega . \end{aligned} \end{aligned}$$

Proof

The first part directly follows from Proposition 2.7. As $\varepsilon \rightarrow 0+$, equations (1.3) become ${\check{f}}_i({\check{I}}_i^*(0))=0$ for $i\in \Omega$, which implies that

$$\begin{aligned}{\check{I}}^*_i(0)=\frac{\theta \alpha _i(\beta _i-\gamma _i)}{\theta (\beta _i-\gamma _i)+\gamma _i} =\Big (1-\frac{\gamma _i}{\theta (\beta _i-\gamma _i)+\gamma _i}\Big )\alpha _i =\Big (1-\frac{1}{1+\theta ({\mathcal {R}}_0^{(i)}-1)}\Big )\alpha _i \end{aligned}$$

if ${\mathcal {R}}_0^{(i)}>1$ and ${\check{I}}^*_i(0)=0$ otherwise (Chen et al. 2020; Li and Peng 2019).

Suppose ${\mathcal {R}}_0(\infty )>1$. Then there exists some $m={\check{T}}_n(\infty )\in (0,1]$ such that

$$\begin{aligned}\lim \limits _{\varepsilon \rightarrow \infty }({\check{I}}^*_1(\varepsilon ),\dots ,{\check{I}}^*_n(\varepsilon )) =m(\alpha _1,\dots ,\alpha _n).\end{aligned}$$

Summing up (1.3) over $i\in \Omega$ gives

$$\begin{aligned} \begin{aligned}&\sum \limits _{i\in \Omega }\left( \beta _i-\gamma _i- \frac{\beta _i{\check{I}}_i^*}{\theta (\alpha _i-{\check{I}}_i^*)+{\check{I}}_i^*}\right) {\check{I}}_i^* =\sum \limits _{i\in \Omega }\left( \beta _i-\gamma _i-\frac{\beta _i m\alpha _i}{\theta (\alpha _i-m\alpha _i)+m\alpha _i} \right) m\alpha _i=0, \end{aligned} \end{aligned}$$

(3.2)

which implies

$$\begin{aligned}&\sum \limits _{i\in \Omega }(\beta _i-\gamma _i)\alpha _i =\frac{ m}{\theta (1-m)+m}\sum \limits _{i\in \Omega }\beta _i\alpha _i\\ \Rightarrow&\frac{ m}{\theta (1-m)+m}=\frac{\sum \limits _{i\in \Omega }(\beta _i-\gamma _i)\alpha _i}{\sum \limits _{i\in \Omega }\beta _i\alpha _i} =1-\frac{1}{{\mathcal {R}}_0(\infty )}\\ \Rightarrow&T_n(\infty )=\frac{{\check{T}}_n(\infty )}{\theta +(1-\theta ){\check{T}}_n(\infty )}N=\frac{m}{\theta +(1-\theta )m}N=\Big (1-\frac{1}{{\mathcal {R}}_0(\infty )}\Big )N. \end{aligned}$$

The proof is completed by solving m from the above equation. $\square$

Remark 3.2

As $\varepsilon \rightarrow 0+$ and $\infty$, by (2.1) and (2.2), the disease prevalence and total population size of patch i at the equilibrium satisfy, respectively,

$$\begin{aligned} \begin{aligned}&\lim _{\varepsilon \rightarrow 0+}\frac{I_i^*}{S_i^*+I_i^*}=\lim _{\varepsilon \rightarrow 0+}\frac{{\check{I}}_i^*}{\theta (\alpha _i-{\check{I}}_i^*)+{\check{I}}_i^*}=\left( 1-\frac{1}{{\mathcal {R}}_0^{(i)}}\right) ^+ \text{ and } \\&\lim _{\varepsilon \rightarrow \infty }\frac{I_i^*}{S_i^*+I_i^*}=\left( 1-\frac{1}{{\mathcal {R}}_0(\infty )}\right) ^+, \end{aligned} \end{aligned}$$

and

$$\begin{aligned}&\lim _{\varepsilon \rightarrow 0+}N_i^*=\lim _{\varepsilon \rightarrow 0+}\frac{\theta \alpha _i+(1-\theta ){\check{I}}^*_i}{\theta +(1-\theta ){\check{T}}_n}N =\frac{\left( 1-\frac{1-\theta }{1+\theta \left( {\mathcal {R}}_0^{(i)}-1\right) ^+}\right) \alpha _i}{\sum \limits _{i\in \Omega }\left( 1-\frac{1-\theta }{1+\theta \left( {\mathcal {R}}_0^{(i)}-1\right) ^+}\right) \alpha _i} N \text{ and } \\&\lim _{\varepsilon \rightarrow \infty }N_i^*=\alpha _i N.\end{aligned}$$

3.1 $T_n(0)$ vs $T_n(\infty )$

We shall make a comparison of $T_n(0)$ and $T_n(\infty )$ to see the difference of small and large dispersal. Note that $T_n(\infty )$ is independent of $\theta$ but $T_n(0)$ does. Only in this subsection, to highlight the dependence of $T_n(0)$ and ${\check{T}}_n(0)$ on $\theta$, we write $T_n(0)$ and ${\check{T}}_n(0)$ as ${\mathcal {T}}_n(\theta )$ and $\check{{\mathcal {T}}}_n(\theta )$ or simply ${\mathcal {T}}_n$ and $\check{{\mathcal {T}}}_n$ for $\theta \in (0,\infty )$, respectively.

Lemma 3.3

${\mathcal {T}}_n(\theta )$ is strictly decreasing in $\theta$ as long as ${\mathcal {R}}_0(0)=\max \limits _{i\in \Omega }{\mathcal {R}}_0^{(i)}>1$.

Proof

In fact, the derivative of ${\mathcal {T}}_n(\theta )$ with respect to $\theta$ is

$$\begin{aligned} \frac{d{\mathcal {T}}_n}{d\theta }= \frac{\theta \frac{d\check{{\mathcal {T}}}_n}{d\theta }-\check{{\mathcal {T}}}_n(\theta )(1-\check{{\mathcal {T}}}_n(\theta ))}{(\theta +(1-\theta )\check{{\mathcal {T}}}_n(\theta ))^2}N.\end{aligned}$$

Denote $p_i=\theta ({\mathcal {R}}_0^{(i)}-1)^+$. Direct calculation yields

$$\begin{aligned} \begin{aligned}&\theta \frac{d\check{{\mathcal {T}}}_n}{d\theta }-\check{{\mathcal {T}}}_n(\theta )(1-\check{{\mathcal {T}}}_n(\theta ))\\ =&\,\,\theta \sum \limits _{i\in \Omega }\frac{\left( {\mathcal {R}}_0^{(i)}-1\right) ^+}{\left( 1+\theta \left( {\mathcal {R}}_0^{(i)}-1\right) ^+\right) ^2}\alpha _i -\sum \limits _{i\in \Omega }\left( 1-\frac{1}{1+\theta \left( {\mathcal {R}}_0^{(i)}-1\right) ^+}\right) \\&\quad \times \alpha _i\cdot \sum \limits _{i\in \Omega }\frac{\alpha _i}{1+\theta \left( {\mathcal {R}}_0^{(i)}-1\right) ^+} \\ =&\sum \limits _{i\in \Omega }\frac{p_i}{(1+p_i)^2}\alpha _i -\left( 1-\sum \limits _{i\in \Omega }\frac{\alpha _i}{1+p_i}\right) \cdot \sum \limits _{i\in \Omega }\frac{\alpha _i}{1+p_i} \\ =&\sum \limits _{i\in \Omega }\frac{\alpha _i}{1+p_i} -\sum \limits _{i\in \Omega }\frac{\alpha _i}{(1+p_i)^2} -\left( 1-\sum \limits _{i\in \Omega }\frac{\alpha _i}{1+p_i}\right) \cdot \sum \limits _{i\in \Omega }\frac{\alpha _i}{1+p_i}\\ =&\left( \sum \limits _{i\in \Omega }\frac{\alpha _i}{1+p_i}\right) ^2- \sum \limits _{i\in \Omega }\frac{\alpha _i}{(1+p_i)^2}\cdot \sum \limits _{i\in \Omega }\alpha _i<0, \end{aligned} \end{aligned}$$

which is implied by the Cauchy–Schwarz inequality. $\square$

So, we have

$$\begin{aligned}\lim \limits _{\theta \rightarrow \infty } {\mathcal {T}}_n(\theta )<{\mathcal {T}}_n(\theta )<\lim \limits _{\theta \rightarrow 0+} {\mathcal {T}}_n(\theta ),\ \forall \theta \in (0,\infty ),\end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \lim \limits _{\theta \rightarrow 0+} {\mathcal {T}}_n(\theta )&=\left( 1-\frac{1}{1+\sum \limits _{i\in \Omega }\alpha _i\left( {\mathcal {R}}_0^{(i)}-1\right) ^+}\right) N=T_n(\delta ,0+),\\ \lim \limits _{\theta \rightarrow \infty } {\mathcal {T}}_n(\theta )&= \dfrac{1}{1+\sum \limits _{i\in \Omega }\frac{\alpha _i}{\left( {\mathcal {R}}_0^{(i)}-1\right) ^+}}N=T_n(0+,\varepsilon ) \end{aligned} \end{aligned}$$

with the understanding that $\lim \limits _{\theta \rightarrow \infty } {\mathcal {T}}_n(\theta )=0$ if ${\mathcal {R}}_0^{(i)}\le 1$ for some $i\in \Omega$. Based on these discussions and Lemma 3.3, we obtain the following result on comparing ${\mathcal {T}}_n(\theta )$ and $T_n(\infty )$.

Theorem 3.4

For model (3.1), suppose ${\mathcal {R}}_0(0)=\max \limits _{i\in \Omega }{\mathcal {R}}_0^{(i)}>1$. Then the following statements hold:

• (a) if $\lim \limits _{\theta \rightarrow \infty }{\mathcal {T}}_n(\theta )< T_n(\infty )<\lim \limits _{\theta \rightarrow 0+} {\mathcal {T}}_n(\theta )$, then there exists a unique $\theta ^*>0$ such that ${\mathcal {T}}_n(\theta )>T_n(\infty )$ for $\theta \in (0,\theta ^*)$, ${\mathcal {T}}_n(\theta )=T_n(\infty )$ for $\theta =\theta ^*$, and ${\mathcal {T}}_n(\theta )<T_n(\infty )$ for $\theta \in (\theta ^*,\infty )$;

• (b) if $\lim \limits _{\theta \rightarrow 0+} {\mathcal {T}}_n(\theta )\le T_n(\infty )$, then ${\mathcal {T}}_n(\theta )<T_n(\infty )$ for $\theta \in (0,\infty )$;

• (c) if $\lim \limits _{\theta \rightarrow \infty } {\mathcal {T}}_n(\theta )\ge T_n(\infty )$, then ${\mathcal {T}}_n(\theta )>T_n(\infty )$ for $\theta \in (0,\infty )$.

In what follows, we compare ${\mathcal {T}}_n(\theta )$ and $T_n(\infty )$ in some special cases.

Corollary 3.5

For model (3.1), suppose ${\mathcal {R}}_0^{(i)}>1$ for all $i\in \Omega$. Then the following statements hold:

• (a) if $\beta _i=\beta$ for all $i\in \Omega$, then ${\mathcal {T}}_n(\theta )<(=,>)\;T_n(\infty )$ if and only if $\theta >(=,<)\;1$;

• (b) if $\gamma _i=\gamma$ for all $i\in \Omega$, then ${\mathcal {T}}_n(\theta )<T_n(\infty )$ for $\theta \in (0,\infty )$;

• (c) if $\beta _i-\gamma _i=c>0$ for all $i\in \Omega$, then ${\mathcal {T}}_n(\theta )>T_n(\infty )$ for $\theta \in (0,\infty )$.

Proof

We give a simple proof by using Theorem 3.4, whereas a direct proof by comparing $\check{{\mathcal {T}}}_n(\theta )$ and ${\check{T}}_n(\infty )$ and applying the Cauchy–Schwarz inequality is feasible.

Case (a). It suffices to show that $\lim \limits _{\theta \rightarrow 1} {\mathcal {T}}_n(\theta )= T_n(\infty )$, i.e.,

$$\begin{aligned}\left( 1-\sum \limits _{i\in \Omega }\frac{\alpha _i}{{\mathcal {R}}_0^{(i)}}\right) N =\left( 1-\frac{1}{{\mathcal {R}}_0(\infty )}\right) N\Leftrightarrow \sum \limits _{i\in \Omega }\frac{\alpha _i}{{\mathcal {R}}_0^{(i)}} =\sum \limits _{i\in \Omega }\frac{\gamma _i\alpha _i}{\beta } =\frac{\sum \limits _{i\in \Omega }\gamma _i\alpha _i}{\sum \limits _{i\in \Omega }\beta \alpha _i} =\frac{1}{{\mathcal {R}}_0(\infty )}.\end{aligned}$$

Case (b). It suffices to show that $\lim \limits _{\theta \rightarrow 0+} {\mathcal {T}}_n(\theta )= T_n(\infty )$, or equivalently,

$$\begin{aligned} \begin{aligned}&1+\sum \limits _{i\in \Omega }\alpha _i({\mathcal {R}}_0^{(i)}-1)= \sum \limits _{i\in \Omega }\alpha _i{\mathcal {R}}_0^{(i)}= \sum \limits _{i\in \Omega }\frac{\beta _i\alpha _i}{\gamma } =\frac{\sum \limits _{i\in \Omega }\beta _i\alpha _i}{\sum \limits _{i\in \Omega }\gamma \alpha _i}={\mathcal {R}}_0(\infty ). \end{aligned} \end{aligned}$$

Case (c). It suffices to show that $\lim \limits _{\theta \rightarrow \infty } {\mathcal {T}}_n(\theta )=T_n(\infty )$, or equivalently,

$$\begin{aligned} \begin{aligned}&\left( 1+\sum \limits _{i\in \Omega }\frac{\alpha _i}{({\mathcal {R}}_0^{(i)}-1)}\right) \left( 1-\frac{1}{{\mathcal {R}}_0(\infty )}\right) =\left( 1+\sum \limits _{i\in \Omega }\frac{\gamma _i\alpha _i}{c}\right) \left( 1-\frac{\sum \limits _{i\in \Omega }\gamma _i\alpha _i}{\sum \limits _{i\in \Omega }\beta _i\alpha _i}\right) \\ =&\left( 1+\sum \limits _{i\in \Omega }\frac{\gamma _i\alpha _i}{c}\right) \frac{c}{\sum \limits _{i\in \Omega }\beta _i\alpha _i} =\frac{\sum \limits _{i\in \Omega }\beta _i\alpha _i}{c} \cdot \frac{c}{\sum \limits _{i\in \Omega }\beta _i\alpha _i}=1, \end{aligned} \end{aligned}$$

by noting that $\beta _i-\gamma _i=c$ and $c+\gamma _i=\beta _i$ for all $i\in \Omega$. $\square$

Additionally, similar to Remark 3.4 in Gao (2020), if the connectivity matrix L is line-sum-symmetric, then ${\mathcal {T}}_n(\theta )\ge T_n(\infty )$ as one of the sequences $\{{\mathcal {R}}_0^{(i)}\}_{i\in \Omega }$ and $\{\beta _i+\frac{1-\theta }{\theta }\gamma _i\}_{i\in \Omega }$ is nondecreasing and the other is nonincreasing, and ${\mathcal {T}}_n(\theta )\le T_n(\infty )$ as both sequences are nondecreasing or nonincreasing. We can see from the above analysis that the state-dependent dispersal does make a difference to infection size or disease prevalence.

Remark 3.6

For model (1.1), if $\delta$ is a fixed constant, then $T_n(\delta ,\infty )$ may vary with $\delta$, i.e.,

$$\begin{aligned}T_n(\delta ,\infty )=\lim \limits _{\varepsilon \rightarrow \infty } T_n(\delta ,\varepsilon )=\sum \limits _{i\in \Omega } I_i^*(\delta ,\infty )\not \equiv \left( 1-\frac{1}{{\mathcal {R}}_0(\infty )}\right) ^+ N.\end{aligned}$$

It is sufficient to consider the case of ${\mathcal {R}}_0(\infty )>1$. Since $0<{\check{I}}^*_i<\alpha _i$ for all $i\in \Omega$, it follows from (1.3) that

$$\begin{aligned}({\check{I}}^*_1(\delta ,\varepsilon ),\dots {\check{I}}^*_n(\delta ,\varepsilon ))\rightarrow k(\alpha _1,\dots ,\alpha _n),\ \text{ as } \varepsilon \rightarrow \infty ,\end{aligned}$$

for some $k\in [0,1]$. By using (3.2), we find $k=1$ by contradiction and thus $T_n(\delta ,\infty )$ cannot be solved from (1.2) and (1.3). However, according to Proposition 2.7, we have

$$\begin{aligned}T_n(0+,\infty )=\lim \limits _{\theta \rightarrow \infty } {\mathcal {T}}_n(\theta )= \dfrac{1}{1+\sum \limits _{i\in \Omega }\frac{\alpha _i}{({\mathcal {R}}_0^{(i)}-1)^+}}N .\end{aligned}$$

Meanwhile, $T_n(\infty ,\infty )=(1-1/{\mathcal {R}}_0(\infty ))N$ and all patches have the same disease prevalence. They are generally not the same, e.g., $T_n(0+,\infty )<T_n(\infty ,\infty )$ if $\beta _i=\beta$ or $\gamma _i=\gamma$ for all $i\in \Omega$, but $T_n(0+,\infty )=T_n(\infty ,\infty )$ if $\beta _i-\gamma _i=c$ for all $i\in \Omega$. Hence, $T_n(\delta ,\infty )$ is generally nonconstant in $\delta \in [0,\infty ]$.

3.2 Monotonicity of $T_n(\varepsilon )$ for small $\varepsilon$

We next compute the right derivative of $T_n(\varepsilon )$ with respect to $\varepsilon$ at zero to determine the monotonicity of $T_n(\varepsilon )$ under sufficiently small dispersal. It can also enable us to establish a sufficient condition for the nonmonotonicity of $T_n(\varepsilon )$ (Gao 2020).

Theorem 3.7

For model (3.1), if ${\mathcal {R}}_0^{(i)}\ne 1$ for all $i\in \Omega$, then

$$\begin{aligned}T_n'(0+)=\frac{\theta N}{(\theta +(1-\theta ){\check{T}}_n(0))^2}{\check{T}}_n'(0+),\end{aligned}$$

where

$$\begin{aligned}{\check{T}}_n'(0+)=-\sum \limits _{i\in \Omega } \left( \frac{1}{\chi _i}\sum \limits _{j\in \Omega }L_{ij}{\check{I}}^*_j(0)\right) \end{aligned}$$

and

$$\begin{aligned} \chi _i= {\left\{ \begin{array}{ll} \beta _i-\gamma _i,&{} \text{ if } \ {\mathcal {R}}_0^{(i)}<1,\\ -(\beta _i-\gamma _i)\frac{\gamma _i+\theta (\beta _i-\gamma _i)}{\beta _i},&{} \text{ if } \ {\mathcal {R}}_0^{(i)}>1. \end{array}\right. } \end{aligned}$$

Proof

Since $T_n(\varepsilon )$ can be viewed as a strictly increasing function of ${\check{T}}_n(\varepsilon )$, we only need to calculate ${\check{T}}_n'(0+)$ to decide the sign of $T_n'(0+)$.

Suppose ${\mathcal {R}}_0(0)=\max \limits _{i\in \Omega }{\mathcal {R}}_0^{(i)}>1$. Otherwise, $T_n(\varepsilon )\equiv 0$ for $\varepsilon \ge 0$ and the conclusion immediately holds. Thus, for sufficiently small $\varepsilon$, we have ${\mathcal {R}}_0(\varepsilon )>1$ and there exists a unique positive solution $({\check{I}}^*_1,\dots ,{\check{I}}^*_n)$ to the equilibrium equations

$$\begin{aligned} \begin{aligned} M_n({\check{I}}^*_1,\dots ,{\check{I}}^*_n)^T={\varvec{0}}, \end{aligned} \end{aligned}$$

(3.3)

where

$$\begin{aligned}M_n=F-V-\mathop {{\mathrm {diag}}}\left\{ \frac{\beta _1{\check{I}}_1^*}{\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*},\dots ,\frac{\beta _n{\check{I}}_n^*}{\theta (\alpha _n-{\check{I}}_n^*)+{\check{I}}_n^*}\right\} .\end{aligned}$$

Differentiating both sides of (3.3) with respect to $\varepsilon$ gives

$$\begin{aligned} \begin{aligned} {\tilde{M}}_n\left( \frac{d{\check{I}}_1^{*}}{d\varepsilon },\dots , \frac{d{\check{I}}_n^{*}}{d\varepsilon }\right) ^T =-\left( \sum _{j\in \Omega }L_{1j}{\check{I}}_j^*,..., \sum _{j\in \Omega } L_{nj} {\check{I}}_j^*\right) ^T, \end{aligned} \end{aligned}$$

(3.4)

where

$$\begin{aligned}{\tilde{M}}_n=M_n-\mathop {{\mathrm {diag}}}\left\{ \frac{\theta \beta _1\alpha _1{\check{I}}_1^*}{(\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*)^2},\dots , \frac{\theta \beta _n\alpha _n{\check{I}}_n^*}{(\theta (\alpha _n-{\check{I}}_n^*)+{\check{I}}_n^*)^2}\right\} .\end{aligned}$$

The essential nonnegativity and irreducibility of $M_n$ imply that $s(M_n)=0$ and hence $s({\tilde{M}}_n)<s(M_n)=0$ and $\mathop {{\mathrm {sgn}}}(|{\tilde{M}}_n|)=(-1)^n\ne 0$. So, ${\tilde{M}}^{-1}_n$ exists and it is negative (see e.g., Corollary 4.3.2 in Smith (1995)). Solving $d{\check{I}}_i^*/d\varepsilon$ from (3.4) gives

$$\begin{aligned} \begin{aligned} \left( \frac{d{\check{I}}_1^{*}}{d\varepsilon },\dots , \frac{d{\check{I}}_n^{*}}{d\varepsilon }\right) ^T=-{\tilde{M}}^{-1}_n\left( \sum \limits _{j\in \Omega }L_{1j}{\check{I}}_j^*,\dots , \sum \limits _{j\in \Omega }L_{nj}{\check{I}}_j^*\right) ^T . \end{aligned} \end{aligned}$$

(3.5)

As $\varepsilon \rightarrow 0+$, we have

$$\begin{aligned} \begin{aligned} {\tilde{M}}_n&\rightarrow \mathop {{\mathrm {diag}}}(\chi _i):=\mathop {{\mathrm {diag}}}\left( \beta _i-\gamma _i-\frac{\beta _i{\check{I}}_i^*(0)}{\theta (\alpha _i-{\check{I}}_i^*(0))+{\check{I}}_i^*(0)}-\frac{\theta \beta _i\alpha _i{\check{I}}_i^*(0)}{(\theta (\alpha _i-{\check{I}}_i^*(0))+{\check{I}}_i^*(0))^2}\right) , \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \chi _i&=\beta _i-\gamma _i-\frac{\beta _i{\check{I}}_i^*(0)}{\theta (\alpha _i-{\check{I}}_i^*(0))+{\check{I}}_i^*(0)}-\frac{\theta \beta _i\alpha _i{\check{I}}_i^*(0)}{(\theta (\alpha _i-{\check{I}}_i^*(0))+{\check{I}}_i^*(0))^2}\\&=-\frac{\theta \beta _i\alpha _i{\check{I}}_i^*(0)}{(\theta (\alpha _i-{\check{I}}_i^*(0))+{\check{I}}_i^*(0))^2} =-\frac{\theta \beta _i\alpha _i}{{\check{I}}_i^*(0)}\left( \frac{{\check{I}}_i^*(0)}{\theta (\alpha _i-{\check{I}}_i^*(0))+{\check{I}}_i^*(0)}\right) ^2\\&=-\frac{\theta \beta _i\alpha _i}{\Big (1-\frac{1}{1+\theta ({\mathcal {R}}_0^{(i)}-1)}\Big )\alpha _i}\left( 1-\frac{1}{{\mathcal {R}}_0^{(i)}}\right) ^2 =-\beta _i(1+\theta ({\mathcal {R}}_0^{(i)}-1))\frac{{\mathcal {R}}_0^{(i)}-1}{({\mathcal {R}}_0^{(i)})^2}\\&=-(\beta _i-\gamma _i)\frac{\gamma _i+\theta (\beta _i-\gamma _i)}{\beta _i}<0,\ \end{aligned} \end{aligned}$$

if ${\mathcal {R}}_0^{(i)}>1$, and $\chi _i=\beta _i-\gamma _i<0$ if ${\mathcal {R}}_0^{(i)}<1$. $\square$

Remark 3.8

For $n=2$, if ${\mathcal {R}}_0^{(1)}>{\mathcal {R}}_0^{(2)}$ and ${\mathcal {R}}_0(\varepsilon )>1$, then we have $L_{21}{\check{I}}_1^*(\varepsilon )-L_{12}{\check{I}}_2^*(\varepsilon )>0$, or equivalently, $L_{21}I_1^*(\varepsilon )-L_{12}I_2^*(\varepsilon )>0$ due to Remark 2.4. It suffices to consider the case of $\varepsilon =0$ with ${\mathcal {R}}_0^{(1)}>{\mathcal {R}}_0^{(2)}>1$. In fact,

$$\begin{aligned} \begin{aligned} L_{21}{\check{I}}_1^*(0)-L_{12}{\check{I}}_2^*(0)&=L_{21}\left( 1-\frac{1}{1+\theta ({\mathcal {R}}_0^{(1)}-1)}\right) \alpha _1 -L_{12}\left( 1-\frac{1}{1+\theta ({\mathcal {R}}_0^{(2)}-1)}\right) \alpha _2 \\&=-\frac{L_{21}\alpha _1}{1+\theta ({\mathcal {R}}_0^{(1)}-1)} +\frac{L_{12}\alpha _2}{1+\theta ({\mathcal {R}}_0^{(2)}-1)} \\&=\frac{\theta L_{21}\alpha _1({\mathcal {R}}_0^{(1)}-{\mathcal {R}}_0^{(2)})}{(1+\theta ({\mathcal {R}}_0^{(1)}-1))(1+\theta ({\mathcal {R}}_0^{(2)}-1))}>0. \end{aligned} \end{aligned}$$

4 Two-patch Case

In this section, we present two complete classifications of the model parameter space in two-patch case: the first classification concerns when dispersal leads to more or less infections across patches (or equivalently, higher or lower overall disease prevalence) and the second addresses how the total number of infections (or equivalently, the overall disease prevalence) varies with dispersal rate. To this end, we consider the two-patch submodel

$$\begin{aligned} \begin{aligned} \dfrac{dS_i}{dt}&=-\beta _i\frac{S_iI_i}{N_i}+\gamma _i I_i+\frac{\varepsilon }{\theta }\sum \limits _{j=1}^2 L_{ij}S_j,\quad&1\le i\le 2,\\ \dfrac{dI_i}{dt}&=\beta _i\frac{S_iI_i}{N_i}-\gamma _i I_i+\varepsilon \sum \limits _{j=1}^2 L_{ij}I_j,\quad&1\le i\le 2. \end{aligned} \end{aligned}$$

(4.1)

The auxiliary system associated to the equivalent equilibrium problem is

$$\begin{aligned} \begin{aligned} \dfrac{d{\check{I}}_1}{dt}&={\check{I}}_1\left( \beta _1-\gamma _1- \frac{\beta _1{\check{I}}_1}{\theta (\alpha _1-{\check{I}}_1)+{\check{I}}_1}\right) +\varepsilon (-L_{21}{\check{I}}_1+L_{12}{\check{I}}_2),\\ \dfrac{d{\check{I}}_2}{dt}&={\check{I}}_2\left( \beta _2-\gamma _2- \frac{\beta _2{\check{I}}_2}{\theta (\alpha _2-{\check{I}}_2)+{\check{I}}_2}\right) +\varepsilon (L_{21}{\check{I}}_1-L_{12}{\check{I}}_2), \end{aligned} \end{aligned}$$

(4.2)

where $\theta =\varepsilon /\delta >0$ is constant and $({\check{I}}_1,{\check{I}}_2)\in [0,\alpha _1]\times [0,\alpha _2]$. Without loss of generality, we assume that the first patch has higher risk of infection, i.e., ${\mathcal {R}}_0^{(1)}>{\mathcal {R}}_0^{(2)}$.

4.1 $T_2(\varepsilon )$ vs $T_2(0)$

Lemma 4.1

For system (4.2), if $0<{\check{T}}_2(\varepsilon _0)\le {\check{T}}_2(0)$ for some $\varepsilon _0>0$, then ${\check{T}}_2'(\varepsilon _0)<0$. In particular, if ${\check{T}}_2'(0+)<0$, then ${\check{T}}_2'(\varepsilon )<0$ for all $\varepsilon \in (0,\infty )$ as ${\mathcal {R}}_0(\infty )\ge 1$ or $\varepsilon \in (0,\varepsilon ^*)$ as ${\mathcal {R}}_0(\infty )<1$. Here

$$\begin{aligned} {\mathcal {R}}_0(\infty )=\frac{\beta _1L_{12}+\beta _2L_{21}}{\gamma _1L_{12}+\gamma _2L_{21}}\ \text{ and } \ \varepsilon ^*=\frac{(\beta _1-\gamma _1)(\beta _2-\gamma _2)}{(\beta _1-\gamma _1)L_{12}+(\beta _2-\gamma _2)L_{21}} \end{aligned}$$

is the unique positive solution to ${\mathcal {R}}_0(\varepsilon )=1$ as ${\mathcal {R}}_0(\infty )<1$.

Proof

According to (3.5), we have

$$\begin{aligned} \begin{aligned} \left( \dfrac{d{\check{I}}_1^*}{d\varepsilon },\dfrac{d{\check{I}}_2^*}{d\varepsilon }\right) ^T&= \frac{L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*}{|{\tilde{M}}_2|}\\&\quad \times \begin{pmatrix} \varepsilon L_{21}\frac{{\check{I}}_1^*}{{\check{I}}_2^*} +\frac{\theta \beta _2\alpha _2{\check{I}}_2^*}{(\theta (\alpha _2-{\check{I}}^*_2)+{\check{I}}^*_2)^2} &{} \varepsilon L_{12}\\ \varepsilon L_{21} &{} \varepsilon L_{12}\frac{{\check{I}}_2^*}{{\check{I}}_1^*}+\frac{\theta \beta _1\alpha _1{\check{I}}_1^*}{(\theta (\alpha _1-{\check{I}}^*_1)+{\check{I}}^*_1)^2} \end{pmatrix} \begin{pmatrix} -1 \\ 1 \end{pmatrix}, \end{aligned} \end{aligned}$$

where ${\tilde{M}}_2$ is defined as in the proof of Theorem 3.7 with $|{\tilde{M}}_2|>0$. It indicates that

$$\begin{aligned}&\frac{|{\tilde{M}}_2|}{L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*}{\check{T}}_2'(\varepsilon ) =\frac{|{\tilde{M}}_2|}{L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*} \sum \limits _{i=1}^2\frac{d}{d\varepsilon }\left( {\check{I}}_i^*(\varepsilon )\right) \nonumber \\ =&\sum \limits _{i=1}^2(-1)^{j}\left( \varepsilon L_{ij} -\varepsilon L_{ji}\frac{{\check{I}}_i^*}{{\check{I}}_j^*} -\frac{\theta \beta _j\alpha _j{\check{I}}^*_j}{(\theta (\alpha _j-{\check{I}}^*_j)+{\check{I}}^*_j)^2} \right) \nonumber \\ =&\frac{\theta \beta _1\alpha _1{\check{I}}^*_1}{(\theta (\alpha _1-{\check{I}}^*_1)+{\check{I}}^*_1)^2} -\frac{\theta \beta _2\alpha _2{\check{I}}^*_2}{(\theta (\alpha _2-{\check{I}}^*_2)+{\check{I}}^*_2)^2} -\frac{\varepsilon ({\check{I}}_1^*+{\check{I}}_2^*)}{{\check{I}}_1^*{\check{I}}_2^*} (L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*) \end{aligned}$$

(4.3)

$$\begin{aligned} =&\sum \limits _{i=1}^2(-1)^{j}\left( \beta _j-\gamma _j-\frac{\beta _j{\check{I}}^*_j}{\theta (\alpha _j-{\check{I}}^*_j)+{\check{I}}^*_j} -\frac{\theta \beta _j\alpha _j{\check{I}}^*_j}{(\theta (\alpha _j-{\check{I}}^*_j)+{\check{I}}^*_j)^2}\right) \end{aligned}$$

(4.4)

$$\begin{aligned} =&\sum \limits _{i=1}^2(-1)^{j} \left( \frac{-(\theta (\beta _j-\gamma _j)+\gamma _j){\check{I}}^*_j+ (\beta _j-\gamma _j)\theta \alpha _j}{\theta (\alpha _j-{\check{I}}^*_j)+{\check{I}}^*_j} -\frac{\theta \beta _j\alpha _j{\check{I}}^*_j}{(\theta (\alpha _j-{\check{I}}^*_j)+{\check{I}}^*_j)^2}\right) \nonumber \\ =&\sum \limits _{i=1}^2(-1)^{j}\left( -\frac{(\theta (\beta _j-\gamma _j)+\gamma _j){\check{I}}_j^*}{\theta (\alpha _j-{\check{I}}_j^*)+{\check{I}}_j^*} +\frac{\theta \alpha _j}{\theta (\alpha _j-{\check{I}}_j^*)+{\check{I}}_j^*} \left( \beta _j-\gamma _j-\frac{\beta _j{\check{I}}_j^*}{\theta (\alpha _j-{\check{I}}_j^*)+{\check{I}}_j^*}\right) \right) \end{aligned}$$

(4.5)

$$\begin{aligned} =&\left( \frac{(\theta (\beta _1-\gamma _1)+\gamma _1){\check{I}}_1^*}{\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*} - \frac{(\theta (\beta _2-\gamma _2)+\gamma _2){\check{I}}_2^*}{\theta (\alpha _2-{\check{I}}_2^*)+{\check{I}}_2^*}\right) +\nonumber \\&\frac{\theta \alpha _1}{\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*} \left( \frac{\beta _1{\check{I}}_1^*}{\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*} -(\beta _1-\gamma _1)\right) + \nonumber \\&\frac{\theta \alpha _2}{\theta (\alpha _2-{\check{I}}_2^*)+{\check{I}}_2^*} \left( (\beta _2-\gamma _2)-\frac{\beta _2{\check{I}}_2^*}{\theta (\alpha _2-{\check{I}}_2^*)+{\check{I}}_2^*}\right) , \end{aligned}$$

(4.6)

where $1\le j\le 2$ and $j\ne i$.

Case 1: ${\mathcal {R}}_0^{(1)}>{\mathcal {R}}_0^{(2)}>1$. If follows from the difference of equilibrium equations

$$\begin{aligned} \begin{aligned}&{\check{I}}_1^*\left( \beta _1-\gamma _1- \frac{\beta _1{\check{I}}_1^*}{\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*}\right) +\varepsilon (-L_{21}{\check{I}}_1^*+L_{12}{\check{I}}_2^*)=0,\\&{\check{I}}_1^*(0)\left( \beta _1-\gamma _1- \frac{\beta _1{\check{I}}_1^*(0)}{\theta (\alpha _1-{\check{I}}_1^*(0))+{\check{I}}_1^*(0)}\right) =0 \end{aligned} \end{aligned}$$

that

$$\begin{aligned} \begin{aligned}&\frac{\varepsilon (L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*)}{{\check{I}}^*_1} =-\frac{\beta _1{\check{I}}_1^*}{\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*} +\frac{\beta _1{\check{I}}_1^*(0)}{\theta (\alpha _1-{\check{I}}_1^*(0))+{\check{I}}_1^*(0)} \\ =&\frac{\theta \beta _1\alpha _1({\check{I}}_1^*(0)-{\check{I}}_1^*)}{(\theta (\alpha _1-{\check{I}}_1^*(0))+{\check{I}}_1^*(0))(\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*)} =\frac{\theta (\beta _1-\gamma _1)+\gamma _1}{\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*}({\check{I}}_1^*(0)-{\check{I}}_1^*)\\ \Leftrightarrow&\frac{{\check{I}}^*_1-{\check{I}}^*_1(0)}{\varepsilon (L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*)} =-\frac{1}{\theta (\beta _1-\gamma _1)+\gamma _1}\cdot \frac{\theta (\alpha _1-{\check{I}}^*_1)+{\check{I}}^*_1}{{\check{I}}^*_1}. \end{aligned} \end{aligned}$$

Similarly, we have

$$\begin{aligned}\frac{{\check{I}}^*_2-{\check{I}}^*_2(0)}{\varepsilon (L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*)} =\frac{1}{\theta (\beta _2-\gamma _2)+\gamma _2}\cdot \frac{\theta (\alpha _2-{\check{I}}^*_2)+{\check{I}}^*_2}{{\check{I}}^*_2}.\end{aligned}$$

The above two equalities give

$$\begin{aligned} \begin{aligned} \frac{{\check{T}}_2(\varepsilon )-{\check{T}}_2(0)}{\varepsilon (L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*)} =&\frac{\theta (\alpha _2-{\check{I}}_2^*)+{\check{I}}_2^*}{(\theta (\beta _2-\gamma _2)+\gamma _2){\check{I}}_2^*}- \frac{\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*}{(\theta (\beta _1-\gamma _1)+\gamma _1){\check{I}}_1^*}, \end{aligned} \end{aligned}$$

and hence it follows from $L_{21}{\check{I}}_1^*(\varepsilon )-L_{12}{\check{I}}_2^*(\varepsilon )>0$ for any $\varepsilon \ge 0$ that

$$\begin{aligned} \begin{aligned} {\check{T}}_2(\varepsilon )\le {\check{T}}_2(0)\Leftrightarrow \frac{(\theta (\beta _1-\gamma _1)+\gamma _1){\check{I}}_1^*}{\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*} \le \frac{(\theta (\beta _2-\gamma _2)+\gamma _2){\check{I}}_2^*}{\theta (\alpha _2-{\check{I}}_2^*)+{\check{I}}_2^*}, \end{aligned} \end{aligned}$$

(4.7)

which implies that ${\check{T}}_2'(\varepsilon )<0$ by applying (4.6) and Remark 2.4 or Corollary 2.6.

Case 2: ${\mathcal {R}}_0^{(1)}>{\mathcal {R}}_0^{(2)}=1$. Direct calculation yields

$$\begin{aligned}{\check{I}}^*_2-{\check{I}}^*_2(0)={\check{I}}^*_2= \frac{1}{\beta _2}\cdot \frac{\theta (\alpha _2-{\check{I}}^*_2)+{\check{I}}^*_2}{{\check{I}}^*_2}\varepsilon (L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*)\end{aligned}$$

and hence

$$\begin{aligned} \begin{aligned} \frac{{\check{T}}_2(\varepsilon )-{\check{T}}_2(0)}{\varepsilon (L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*)} = \frac{\theta (\alpha _2-{\check{I}}_2^*)+{\check{I}}_2^*}{\beta _2{\check{I}}_2^*}- \frac{\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*}{(\theta (\beta _1-\gamma _1)+\gamma _1){\check{I}}_1^*}, \end{aligned} \end{aligned}$$

which implies that

$$\begin{aligned} \begin{aligned} {\check{T}}_2(\varepsilon )\le {\check{T}}_2(0)\Leftrightarrow \frac{(\theta (\beta _1-\gamma _1)+\gamma _1){\check{I}}_1^*}{\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*} \le \frac{\beta _2{\check{I}}_2^*}{\theta (\alpha _2-{\check{I}}_2^*)+{\check{I}}_2^*}. \end{aligned} \end{aligned}$$

(4.8)

Similarly, we obtain ${\check{T}}_2'(\varepsilon )<0$ provided that ${\check{T}}_2(\varepsilon )\le {\check{T}}_2(0)$.

Case 3: ${\mathcal {R}}_0^{(1)}>1>{\mathcal {R}}_0^{(2)}$. Direct calculation yields

$$\begin{aligned}\frac{{\check{I}}^*_2}{\varepsilon (L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*)} =-\left( \beta _2-\gamma _2-\frac{\beta _2{\check{I}}_2^*}{\theta (\alpha _2-{\check{I}}_2^*)+{\check{I}}_2^*}\right) ^{-1}=-\left( {\check{g}}_2({\check{I}}^*_2)\right) ^{-1}\end{aligned}$$

and hence

$$\begin{aligned} \begin{aligned} \frac{{\check{T}}_2(\varepsilon )-{\check{T}}_2(0)}{\varepsilon (L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*)} = -\left( {\check{g}}_2({\check{I}}^*_2)\right) ^{-1}- \frac{\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*}{(\theta (\beta _1-\gamma _1)+\gamma _1){\check{I}}_1^*}, \end{aligned} \end{aligned}$$

which implies that

$$\begin{aligned} \begin{aligned} {\check{T}}_2(\varepsilon )\le {\check{T}}_2(0)\Leftrightarrow \frac{(\theta (\beta _1-\gamma _1)+\gamma _1){\check{I}}_1^*}{\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*} \le -{\check{g}}_2({\check{I}}^*_2)=\gamma _2-\beta _2+ \frac{\beta _2{\check{I}}_2^*}{\theta (\alpha _2-{\check{I}}_2^*)+{\check{I}}_2^*}. \end{aligned} \end{aligned}$$

(4.9)

On the other hand, it follows from (4.6) and (4.9) that

$$\begin{aligned} \begin{aligned} \frac{|{\tilde{M}}_2|}{L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*}{\check{T}}_2'(\varepsilon )<&\left( -{\check{g}}_2({\check{I}}^*_2) -\frac{(\theta (\beta _2-\gamma _2)+\gamma _2){\check{I}}_2^*}{\theta (\alpha _2-{\check{I}}_2^*)+{\check{I}}_2^*}\right) +\frac{\theta \alpha _2}{\theta (\alpha _2-{\check{I}}_2^*)+{\check{I}}_2^*}{\check{g}}_2({\check{I}}^*_2)\\ <&\left( \gamma _2-\beta _2+\frac{(\beta _2-\gamma _2){\check{I}}_2^*}{\theta (\alpha _2-{\check{I}}_2^*)+{\check{I}}_2^*}-\frac{\theta (\beta _2-\gamma _2){\check{I}}_2^*}{\theta (\alpha _2-{\check{I}}_2^*)+{\check{I}}_2^*}\right) \\&\quad +\frac{\theta \alpha _2(\beta _2-\gamma _2)}{\theta (\alpha _2-{\check{I}}_2^*)+{\check{I}}_2^*}\\ =&\gamma _2-\beta _2+(\beta _2-\gamma _2)\frac{{\check{I}}_2^*-\theta {\check{I}}_2^* +\theta \alpha _2}{\theta (\alpha _2-{\check{I}}_2^*)+{\check{I}}_2^*}=0. \end{aligned} \end{aligned}$$

The proof is complete. $\square$

Remark 4.2

One can give a simpler proof of the above lemma in the case of ${\mathcal {R}}_0^{(1)}>{\mathcal {R}}_0^{(2)}>1$ and $\theta >1$. In fact, it follows from ${\check{I}}_1^*<{\check{I}}_1^*(0)$ and ${\check{I}}_2^*>{\check{I}}_2^*(0)$ that

$$\begin{aligned} \begin{aligned} \theta (\beta _1-\gamma _1)+\gamma _1>\frac{\theta \beta _1\alpha _1}{\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*} \ \text{ and } \ \theta (\beta _2-\gamma _2)+\gamma _2<\frac{\theta \beta _2\alpha _2}{\theta (\alpha _2-{\check{I}}_2^*)+{\check{I}}_2^*}, \end{aligned} \end{aligned}$$

respectively. Thus, if ${\check{T}}_2(\varepsilon )\le {\check{T}}_2(0)$, i.e., (4.7), for some $\varepsilon >0$ then we have

$$\begin{aligned} \begin{aligned}&\frac{\theta \beta _1\alpha _1}{\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*}\cdot \frac{{\check{I}}_1^*}{\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*}< (\theta (\beta _1-\gamma _1)+\gamma _1)\cdot \frac{{\check{I}}_1^*}{\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*}\\ \le&(\theta (\beta _2-\gamma _2)+\gamma _2)\cdot \frac{{\check{I}}_2^*}{\theta (\alpha _2-{\check{I}}_2^*)+{\check{I}}_2^*} <\frac{\theta \beta _2\alpha _2}{\theta (\alpha _2-{\check{I}}^*_2)+{\check{I}}^*_2} \cdot \frac{{\check{I}}^*_2}{\theta (\alpha _2-{\check{I}}^*_2)+{\check{I}}^*_2} \end{aligned} \end{aligned}$$

and hence ${\check{T}}_2'(\varepsilon )<0$ because of (4.3).

Remark 4.3

It follows from Remark 2.4 and (4.4) that $\frac{d{\check{I}}_1^*}{d\varepsilon }<0$ for $\varepsilon \in [0,\infty )$ as ${\mathcal {R}}_0(\infty )\ge 1$ or $\varepsilon \in [0,\varepsilon ^*)$ as ${\mathcal {R}}_0(\infty )<1<{\mathcal {R}}_0(0)$. Meanwhile, the second part of (4.4) has the same sign as $\frac{d{\check{I}}_2^*}{d\varepsilon }$ and it is strictly increasing in ${\check{I}}^*_1$. Thus, if

$$\begin{aligned}\phi _I:=\beta _1-\gamma _1-\frac{\beta _1{\check{I}}_1^*(\infty )}{\theta (\alpha _1-{\check{I}}_1^*(\infty ))+{\check{I}}_1^*(\infty )}- \frac{\theta \beta _1\alpha _1{\check{I}}_1^*(\infty )}{(\theta (\alpha _1-{\check{I}}_1^*(\infty ))+{\check{I}}_1^*(\infty ))^2}\le 0,\end{aligned}$$

then $\frac{d{\check{I}}_2^*}{d\varepsilon }>0$ for $\varepsilon \in [0,\infty )$; otherwise there exists a unique ${\bar{\varepsilon }}>0$ such that $\frac{d{\check{I}}_2^*}{d\varepsilon }>0$ for $\varepsilon \in [0,{\bar{\varepsilon }})$, $\frac{d{\check{I}}_2^*}{d\varepsilon }=0$ for $\varepsilon ={\bar{\varepsilon }}$, and $\frac{d{\check{I}}_2^*}{d\varepsilon }<0$ for $\varepsilon \in ({\bar{\varepsilon }},\infty )$ as ${\mathcal {R}}_0(\infty )\ge 1$ or $\varepsilon \in ({\bar{\varepsilon }},\varepsilon ^*)$ as ${\mathcal {R}}_0(\infty )<1<{\mathcal {R}}_0(0)$.

The proof of Lemma 4.1 is irrelevant to the relation between $(\alpha _1,\alpha _2)$ and L, so the result can be generalized to a more general model. The strict monotonicity of $T_2(\varepsilon )$ in terms of ${\check{T}}_2(\varepsilon )$ implies that Lemma 4.1 can be directly transformed to model (4.1).

Lemma 4.4

For model (4.1), if $0<T_2(\varepsilon _0)\le T_2(0)$ for some $\varepsilon _0>0$, then $T_2'(\varepsilon _0)<0$. In particular, if $T_2'(0+)<0$, then $T_2'(\varepsilon )<0$ for all $\varepsilon \in (0,\infty )$ as ${\mathcal {R}}_0(\infty )\ge 1$ or $\varepsilon \in (0,\varepsilon ^*)$ as ${\mathcal {R}}_0(\infty )<1$.

Next we give a complete classification of the parameter space for model (4.1) on whether dispersal is beneficial or detrimental to disease control in terms of total infection size.

Theorem 4.5

Suppose ${\mathcal {R}}_0^{(1)}>\max \{{\mathcal {R}}_0^{(2)},1\}$ for model (4.1). Then we have

• (a) if $T_2'(0+)\le 0$, then $T_2(\varepsilon )<T_2(0)$ for $\varepsilon \in (0,\infty )$;

• (b) if $0<T_2'(0+)\le \infty$ and $T_2(0)>T_2(\infty )$, then there exists a unique ${\hat{\varepsilon }}>0$ such that $T_2(\varepsilon )>T_2(0)$ for $\varepsilon \in (0,{\hat{\varepsilon }})$, $T_2(\varepsilon )=T_2(0)$ for $\varepsilon ={\hat{\varepsilon }}$, and $T_2(\varepsilon )<T_2(0)$ for $\varepsilon \in ({\hat{\varepsilon }},\infty )$;

• (c) if $T_2(0)\le T_2(\infty )$, then $T_2(\varepsilon )>T_2(0)$ for $\varepsilon \in (0,\infty )$ (and $T_2'(0+)>0$).

Proof

By applying Lemma 4.4, we need only consider the cases of $T_2'(0+)=0$ and $\infty$, or equivalently, ${\check{T}}_2'(0+)=0$ and $\infty$. If ${\check{T}}_2'(0+)=0$, i.e., $\chi _1=\chi _2$, then

• (1) ${\mathcal {R}}_0^{(1)}>{\mathcal {R}}_0^{(2)}>1$. It follows from Theorem 2.3 and $\chi _1=\chi _2$ that

  $$\begin{aligned} \begin{aligned}&(\theta (\beta _1-\gamma _1)+\gamma _1)\frac{{\check{I}}_1^*}{\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*}<(\theta (\beta _1-\gamma _1)+\gamma _1)\frac{{\check{I}}_1^*(0)}{\theta (\alpha _1-{\check{I}}_1^*(0))+{\check{I}}_1^*(0)}\\ =&(\theta (\beta _2-\gamma _2)+\gamma _2)\frac{{\check{I}}_2^*(0)}{\theta (\alpha _2-{\check{I}}_2^*(0))+{\check{I}}_2^*(0)} <(\theta (\beta _2-\gamma _2)+\gamma _2)\frac{{\check{I}}_2^*}{\theta (\alpha _2-{\check{I}}_2^*)+{\check{I}}_2^*}, \end{aligned} \end{aligned}$$

  which means that ${\check{T}}_2(\varepsilon )<{\check{T}}_2(0)$ for $\varepsilon >0$ by using (4.7).

• (2) ${\mathcal {R}}_0^{(1)}>1>{\mathcal {R}}_0^{(2)}$. It follows from Theorem 2.3 and $\chi _1=\chi _2$ that

  $$\begin{aligned} \begin{aligned}&(\theta (\beta _1-\gamma _1)+\gamma _1)\frac{{\check{I}}_1^*}{\theta (\alpha _1-{\check{I}}_1^*)+{\check{I}}_1^*}<(\theta (\beta _1-\gamma _1)+\gamma _1)\frac{{\check{I}}_1^*(0)}{\theta (\alpha _1-{\check{I}}_1^*(0))+{\check{I}}_1^*(0)}\\ =&\gamma _2-\beta _2 <\gamma _2-\beta _2+ \frac{\beta _2{\check{I}}_2^*}{\theta (\alpha _2-{\check{I}}_2^*)+{\check{I}}_2^*}, \end{aligned} \end{aligned}$$

  which again means that ${\check{T}}_2(\varepsilon )<{\check{T}}_2(0)$ for $\varepsilon >0$ by applying (4.9).

If $T_2'(0+)=\infty$, i.e., ${\mathcal {R}}_0^{(2)}=1$, then ${\check{T}}_2(\varepsilon )>{\check{T}}_2(0)$ holds for $0<\varepsilon \ll 1$ by using (4.8). $\square$

The following comparison result of $T_2(0)$ and $T_2(\infty )$ somewhat generalizes Corollary 3.5 when only two patches are concerned. We also decide the sign of $T_2'(0+)$ afterwards. These are crucial for applying Theorem 4.5.

Proposition 4.6

Suppose ${\mathcal {R}}_0^{(1)}>\max \{{\mathcal {R}}_0^{(2)},1\}$ for model (4.1). Then the following statements concerning the relation between $T_2(0)$ and $T_2(\infty )$ hold as $\theta \in (0,\infty )$:

• (a) if ${\mathcal {R}}_0^{(1)}>{\mathcal {R}}_0^{(2)}\ge 1$, then

  • (i) if $\gamma _1<\gamma _2$ and $\beta _1-\gamma _1>\beta _2-\gamma _2$, then $\mathop {{\mathrm {sgn}}}(T_2(\infty )-T_2(0))=\mathop {{\mathrm {sgn}}}(\theta -\theta ^*_a)$ where $\theta ^*_a=\frac{\gamma _2-\gamma _1}{(\beta _1-\gamma _1)-(\beta _2-\gamma _2)}>0$;

  • (ii) if $\gamma _1\ge \gamma _2$, then $T_2(0)<T_2(\infty )$;

  • (iii) if $\beta _1-\gamma _1\le \beta _2-\gamma _2$, then $T_2(0)>T_2(\infty )$;

• (b) if ${\mathcal {R}}_0^{(1)}>{\mathcal {R}}_0(\infty )>1>{\mathcal {R}}_0^{(2)}$, then

  • (i) if $\Delta :=(\beta _1-\gamma _1)(\gamma _1-\gamma _2)\alpha _1-(\gamma _2-\beta _2)\gamma _1\ge 0$, then $T_2(\infty )>T_2(0)$;

  • (ii) if $\Delta <0$, then $\mathop {{\mathrm {sgn}}}(T_2(\infty )-T_2(0))=\mathop {{\mathrm {sgn}}}(\theta -\theta ^*_b)$ where $\theta ^*_b=\frac{(\gamma _2-\beta _2)\gamma _1-(\beta _1-\gamma _1)(\gamma _1-\gamma _2)\alpha _1}{(\beta _1-\gamma _1)(\beta _1\alpha _1+\beta _2\alpha _2-\gamma _1\alpha _1-\gamma _2\alpha _2)}$;

• (c) if ${\mathcal {R}}_0^{(1)}>1\ge {\mathcal {R}}_0(\infty )>{\mathcal {R}}_0^{(2)}$, then $T_2(0)>T_2(\infty )=0$.

Proof

Using $T_2(0)$ and $T_2(\infty )$ from Theorem 3.1, direct calculation yields

• (a) if ${\mathcal {R}}_0^{(1)}>{\mathcal {R}}_0^{(2)}\ge 1$, then

  $$\begin{aligned}T_2(\infty )-T_2(0)=\frac{\alpha _1\alpha _2(\beta _1\gamma _2-\beta _2\gamma _1) (\theta (\beta _1-\gamma _1-\beta _2+\gamma _2)+(\gamma _1-\gamma _2))}{(\beta _1\alpha _1+\beta _2\alpha _2) (\beta _1\alpha _1(\theta (\beta _2-\gamma _2)+\gamma _2)+\beta _2\alpha _2(\theta (\beta _1-\gamma _1)+\gamma _1))}N;\end{aligned}$$

• (b) if ${\mathcal {R}}_0^{(1)}>{\mathcal {R}}_0(\infty )>1>{\mathcal {R}}_0^{(2)}$, then

  $$\begin{aligned}T_2(\infty )-T_2(0)=\frac{\alpha _2(\theta (\beta _1-\gamma _1)(\beta _1\alpha _1+\beta _2\alpha _2-\gamma _1\alpha _1-\gamma _2\alpha _2)+\Delta )}{(\beta _1\alpha _1+\beta _2\alpha _2)(\beta _1\alpha _1+(\theta (\beta _1-\gamma _1)+\gamma _1)\alpha _2)}N\end{aligned}$$

  with $\Delta =(\beta _1-\gamma _1)(\gamma _1-\gamma _2)\alpha _1-(\gamma _2-\beta _2)\gamma _1$;

• (c) if ${\mathcal {R}}_0^{(1)}>1\ge {\mathcal {R}}_0(\infty )>{\mathcal {R}}_0^{(2)}$, then

  $$\begin{aligned}T_2(\infty )-T_2(0)=-T_2(0)=-\frac{(\beta _1-\gamma _1)\alpha _1}{\beta _1\alpha _1+(\theta (\beta _1-\gamma _1)+\gamma _1)\alpha _2}N<0.\end{aligned}$$

The proof is completed by noting that the numerator of $T_2(\infty )-T_2(0)$ is either a constant or a linear function of $\theta$ and the denominator of $T_2(\infty )-T_2(0)$ is always positive. $\square$

Proposition 4.7

Suppose ${\mathcal {R}}_0^{(1)}>\max \{{\mathcal {R}}_0^{(2)},1\}$ for model (4.1). Then the following statements concerning the sign of $T_2'(0+)$ hold as $\theta \in (0,\infty )$:

• (a) if ${\mathcal {R}}_0^{(1)}>{\mathcal {R}}_0^{(2)}>1$, then

  • (i) if $\Phi _0:=\gamma _1\left( 1-\frac{\gamma _1}{\beta _1}\right) -\gamma _2\left( 1-\frac{\gamma _2}{\beta _2}\right) \ge 0$, then $T_2'(0+)>0$ (and $\Phi _1:=\frac{(\beta _1-\gamma _1)^2}{\beta _1} -\frac{(\beta _2-\gamma _2)^2}{\beta _2}>0$). Particularly, $T_2'(0+)>0$ if $\gamma _1\ge \gamma _2$;

  • (ii) if $\Phi _0<0$ and $\Phi _1>0$, then $\mathop {{\mathrm {sgn}}}(T_2'(0+))=\mathop {{\mathrm {sgn}}}(\theta -\theta ^*_{0a})$ where $\theta ^*_{0a}=-\frac{\Phi _0}{\Phi _1}>0$;

  • (iii) if $\Phi _1\le 0$, then $T_2'(0+)<0$ (and $\Phi _0<0$);

• (b) if ${\mathcal {R}}_0^{(1)}>1>{\mathcal {R}}_0^{(2)}$, then

  • (i) if $\Psi _0:=\gamma _1\left( 1-\frac{\gamma _1}{\beta _1}\right) -(\gamma _2-\beta _2)\ge 0$, then $T_2'(0+)>0$;

  • (ii) if $\Psi _0<0$, then $\mathop {{\mathrm {sgn}}}(T_2'(0+))=\mathop {{\mathrm {sgn}}}(\theta -\theta ^*_{0b})$ where $\theta ^*_{0b}=\frac{\beta _1(\gamma _2-\beta _2)-\gamma _1(\beta _1-\gamma _1)}{(\beta _1-\gamma _1)^2}>0$;

• (c) if ${\mathcal {R}}_0^{(1)}>1={\mathcal {R}}_0^{(2)}$, then $T_2'(0+)=+\infty >0$.

Proof

Using Theorem 3.7, if ${\mathcal {R}}_0^{(1)}>\max \{{\mathcal {R}}_0^{(2)},1\}$ and ${\mathcal {R}}_0^{(2)}\ne 1$ then

$$\begin{aligned} \begin{aligned} \mathop {{\mathrm {sgn}}}(T_2'(0+))&=\mathop {{\mathrm {sgn}}}({\check{T}}_2'(0+))= \mathop {{\mathrm {sgn}}}\left( \frac{\chi _2-\chi _1}{\chi _1\chi _2} (L_{21}{\check{I}}_1^*(0)-L_{12}{\check{I}}_2^*(0))\right) \\&=\mathop {{\mathrm {sgn}}}\left( \frac{\chi _2-\chi _1}{\chi _1\chi _2}\right) =\mathop {{\mathrm {sgn}}}(\chi _2-\chi _1), \end{aligned} \end{aligned}$$

where $\chi _i=\beta _i-\gamma _i<0$ if ${\mathcal {R}}_0^{(i)}<1$ and $-(\beta _i-\gamma _i)\frac{\gamma _i+\theta (\beta _i-\gamma _i)}{\beta _i}<0$ if ${\mathcal {R}}_0^{(i)}>1$. Therefore,

• (a) for ${\mathcal {R}}_0^{(1)}>{\mathcal {R}}_0^{(2)}>1$,

  $$\begin{aligned}\chi _2-\chi _1&=\left( \frac{(\beta _1-\gamma _1)^2}{\beta _1} -\frac{(\beta _2-\gamma _2)^2}{\beta _2}\right) \theta +\gamma _1\left( 1-\frac{\gamma _1}{\beta _1}\right) -\gamma _2\left( 1-\frac{\gamma _2}{\beta _2}\right) \\&=\Phi _1 \theta +\Phi _0. \end{aligned}$$

• (b-c) for ${\mathcal {R}}_0^{(1)}>1\ge {\mathcal {R}}_0^{(2)}$,

  $$\begin{aligned} \chi _2-\chi _1=\frac{(\beta _1-\gamma _1)^2}{\beta _1}\theta +\gamma _1\left( 1-\frac{\gamma _1}{\beta _1}\right) -(\gamma _2-\beta _2) =\frac{(\beta _1-\gamma _1)^2}{\beta _1}\theta +\Psi _0. \end{aligned}$$

The proof is completed by noting that $\chi _2-\chi _1$ is a linear function of $\theta$. $\square$

In terms of the signs of $T_2'(0+)$ and $T_2(\infty )-T_2(0)$, and the values of single and multi-patch reproduction numbers, ${\mathcal {R}}_0^{(i)}$ and ${\mathcal {R}}_0(\infty )$, a more detailed classification of the relation between $T_2(\varepsilon )$ and $T_2(0)$ similar to Theorem 4.3 in Gao (2020) can be given. In particular, we now have a clearer understanding of the relation between $T_2(\varepsilon )$ and $T_2(0)$ under the special conditions listed in Corollary 3.5.

4.2 Monotonicity of $T_2(\varepsilon )$

To identify the shape of $T_2(\varepsilon )$, it is necessary to know its change trend or monotonicity for small and large dispersal rates. The former is discussed in Proposition 4.7 while the latter is considered below.

Remark 4.8

For model (4.1) with ${\mathcal {R}}_0^{(1)}>{\mathcal {R}}_0^{(2)}$ and ${\mathcal {R}}_0(\infty )=\frac{\beta _1\alpha _1+\beta _2\alpha _2}{\gamma _1\alpha _1+\gamma _2\alpha _2}\ge 1$, the monotonicity of $T_2(\varepsilon )$ for sufficiently large $\varepsilon$ can be determined by (4.4) and Theorem 3.1. Indeed, substituting ${\check{I}}^*_i$ by ${\check{I}}_i^*(\infty )$ for $i=1,2$ into (4.4) gives

$$\begin{aligned} {\mathbb {T}}_2'(\infty ):=&\sum _{i=1}^2(-1)^j\left( \alpha _i\frac{\beta _j\gamma _i-\beta _i\gamma _j}{\beta _i\alpha _i+\beta _j\alpha _j} -\frac{(\beta _i-\gamma _i)\alpha _i+(\beta _j-\gamma _j)\alpha _j}{\beta _i\alpha _i+\beta _j\alpha _j}\right. \\&\quad \cdot \left. \beta _j\frac{(\theta (\beta _i-\gamma _i)+\gamma _i)\alpha _i+(\theta (\beta _j-\gamma _j)+\gamma _j)\alpha _j}{\beta _i\alpha _i+\beta _j\alpha _j}\right) \\ =&\frac{\beta _2\gamma _1-\beta _1\gamma _2}{\beta _1\alpha _1+\beta _2\alpha _2} +\Big (1-\frac{1}{{\mathcal {R}}_0(\infty )}\Big )\Big (\theta +(1-\theta )\frac{1}{{\mathcal {R}}_0(\infty )}\Big )(\beta _1-\beta _2), \end{aligned}$$

which has the same sign as $T_2'(\varepsilon )$ for large enough $\varepsilon$ as long as ${\mathbb {T}}_2'(\infty )\ne 0$. Clearly,

• (a) if $\beta _1>\beta _2$ and $\theta >\theta ^*_{\infty }:= \frac{1}{\beta _1-\beta _2}\cdot \frac{\beta _1\gamma _2-\beta _2\gamma _1}{\gamma _1\alpha _1+\gamma _2\alpha _2} \cdot \frac{{\mathcal {R}}_0(\infty )}{({\mathcal {R}}_0(\infty )-1)^2}-\frac{1}{{\mathcal {R}}_0(\infty )-1}$, then ${\mathbb {T}}_2'(\infty )>0$;

• (b) if $\beta _1>\beta _2$ and $\theta =\theta ^*_{\infty }>0$, then ${\mathbb {T}}_2'(\infty )=0$;

• (c) if $\beta _1\le \beta _2$ or $0<\theta <\theta ^*_{\infty }$, then ${\mathbb {T}}_2'(\infty )<0$.

In particular, $T_2'(\varepsilon )<0$ for $\varepsilon \gg 1$ as $\beta _1\le \beta _2$ or ${\mathcal {R}}_0(\infty )=1$.

Lemma 4.9

For system (4.2), if ${\check{T}}_2'(\varepsilon _0)=0$ and ${\mathcal {R}}_0(\varepsilon _0)>1$ for some $\varepsilon _0>0$, then ${\check{T}}_2''(\varepsilon _0)<0$, i.e., any nontrivial critical point (the corresponding critical value is nonzero) of ${\check{T}}_2(\varepsilon )$ on ${\mathbb {R}}_+$ corresponds to a local maximum. Furthermore, ${\check{T}}_2(\varepsilon )$ has at most one nontrivial critical point $\varepsilon _0\in {\mathbb {R}}_+$ and $T_2'(\varepsilon )<0$ for all $\varepsilon \in (\varepsilon _0,\infty )$ as ${\mathcal {R}}_0(\infty )\ge 1$ or $\varepsilon \in (\varepsilon _0,\varepsilon ^*)$ as ${\mathcal {R}}_0(\infty )<1$.

Proof

If ${\mathcal {R}}_0(\varepsilon )>1$, then differentiating the equilibrium equations

$$\begin{aligned} \begin{aligned}&{\check{I}}^*_i\left( \beta _i-\gamma _i- \frac{\beta _i{\check{I}}^*_i}{\theta (\alpha _i-{\check{I}}^*_i)+{\check{I}}^*_i}\right) +\varepsilon \sum \limits _{j=1}^2 L_{ij}{\check{I}}^*_j=0,\ 1\le i\le 2, \end{aligned} \end{aligned}$$

with respect to $\varepsilon$ yields

$$\begin{aligned} \begin{aligned}&({\check{I}}^*_i)'\left( \beta _i-\gamma _i- \frac{\beta _i{\check{I}}^*_i}{\theta (\alpha _i-{\check{I}}^*_i)+{\check{I}}^*_i} -\frac{\theta \beta _i\alpha _i{\check{I}}_i^*}{(\theta (\alpha _i-{\check{I}}_i^*)+{\check{I}}_i^*)^2}\right) +\varepsilon \sum \limits _{j=1}^2 L_{ij}({\check{I}}^*_j)'\\&\quad +\sum \limits _{j=1}^2 L_{ij}{\check{I}}^*_j=0. \end{aligned} \end{aligned}$$

(4.10)

Summing (4.10) over i gives

$$\begin{aligned} \begin{aligned}&\sum \limits _{i=1}^2({\check{I}}^*_i)'\left( \beta _i-\gamma _i- \frac{\beta _i{\check{I}}^*_i}{\theta (\alpha _i-{\check{I}}^*_i)+{\check{I}}^*_i} -\frac{\theta \beta _i\alpha _i{\check{I}}_i^*}{(\theta (\alpha _i-{\check{I}}_i^*)+{\check{I}}_i^*)^2}\right) =0. \end{aligned} \end{aligned}$$

(4.11)

It follows from ${\check{T}}_2'(\varepsilon _0)=0$, i.e., $({\check{I}}^*_1)'(\varepsilon _0)=-({\check{I}}^*_2)'(\varepsilon _0)$, that $({\check{I}}^*_1)'(\varepsilon _0)=({\check{I}}^*_2)'(\varepsilon _0)=0$ or

$$\begin{aligned} \begin{aligned}&\beta _i-\gamma _i- \frac{\beta _i{\check{I}}^*_i(\varepsilon _0)}{\theta (\alpha _i-{\check{I}}^*_i(\varepsilon _0))+{\check{I}}^*_i(\varepsilon _0)} -\frac{\theta \beta _i\alpha _i{\check{I}}_i^*(\varepsilon _0)}{(\theta (\alpha _i-{\check{I}}_i^*(\varepsilon _0))+{\check{I}}_i^*(\varepsilon _0))^2}:=\eta <0 ,\ i=1,2. \end{aligned} \end{aligned}$$

(4.12)

In the former case, equations (4.10) imply that $L_{21}{\check{I}}_1^*(\varepsilon _0)-L_{12}{\check{I}}_2^*(\varepsilon _0)=0$, which contradicts Remark 3.8. Thus, (4.12) holds and the negativity of $\eta$ follows from Remark 4.3. Differentiating (4.11) in $\varepsilon$ yields

$$\begin{aligned} \begin{aligned}&\sum \limits _{i=1}^2({\check{I}}^*_i)''\Big (\beta _i-\gamma _i- \frac{\beta _i{\check{I}}^*_i}{\theta (\alpha _i-{\check{I}}^*_i)+{\check{I}}^*_i} -\frac{\theta \beta _i\alpha _i{\check{I}}_i^*}{(\theta (\alpha _i-{\check{I}}_i^*)+{\check{I}}_i^*)^2}\Big )\\ =&\sum \limits _{i=1}^2(({\check{I}}^*_i)')^2 \Big (\frac{\theta \beta _i\alpha _i}{(\theta (\alpha _i-{\check{I}}_i^*)+{\check{I}}_i^*)^2} +\theta \beta _i\alpha _i\frac{(\theta (\alpha _i-{\check{I}}_i^*)+{\check{I}}_i^*)-2(1-\theta ){\check{I}}_i^*}{(\theta (\alpha _i-{\check{I}}_i^*)+{\check{I}}_i^*)^3}\Big )\\ =&\sum \limits _{i=1}^2(({\check{I}}^*_i)')^2\theta \beta _i\alpha _i \frac{2\theta \alpha _i}{(\theta (\alpha _i-{\check{I}}_i^*)+{\check{I}}_i^*)^3}>0, \end{aligned} \end{aligned}$$

which indicates that at $\varepsilon =\varepsilon _0$ we have

$$\begin{aligned}\sum \limits _{i=1}^2({\check{I}}^*_i)''(\varepsilon _0)\eta =\eta {\check{T}}_2''(\varepsilon _0)>0\Rightarrow {\check{T}}_2''(\varepsilon _0)<0.\end{aligned}$$

The remaining part can be shown by contradiction and the differentiable continuity of $T_2(\varepsilon )$ on $(0,\infty )$ as ${\mathcal {R}}_0(\infty )\ge 1$ or $(0,\varepsilon ^*)$ as ${\mathcal {R}}_0(\infty )<1$. $\square$

Lemma 4.10

For model (4.1), if $T_2'(\varepsilon _0)=0$ and ${\mathcal {R}}_0(\varepsilon _0)>1$ for some $\varepsilon _0>0$, then $T_2''(\varepsilon _0)<0$, i.e., any nontrivial critical point of $T_2(\varepsilon )$ on ${\mathbb {R}}_+$ corresponds to a local maximum. Furthermore, $T_2(\varepsilon )$ has at most one nontrivial critical point $\varepsilon _0\in {\mathbb {R}}_+$ and $T_2'(\varepsilon )<0$ for all $\varepsilon \in (\varepsilon _0,\infty )$ as ${\mathcal {R}}_0(\infty )\ge 1$ or $\varepsilon \in (\varepsilon _0,\varepsilon ^*)$ as ${\mathcal {R}}_0(\infty )<1$.

Proof

The first and second derivatives of

$$\begin{aligned} \begin{aligned} T_n(\varepsilon ) =\frac{{\check{T}}_n(\varepsilon )}{\theta +(1-\theta ){\check{T}}_n(\varepsilon )}N \end{aligned} \end{aligned}$$

with respect to $\varepsilon$ are

$$\begin{aligned} \begin{aligned} T_n'(\varepsilon ) =\frac{\theta N}{(\theta +(1-\theta ){\check{T}}_n(\varepsilon ))^2}{\check{T}}_n'(\varepsilon ) \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} T_n''(\varepsilon ) =\frac{\theta N}{(\theta +(1-\theta ){\check{T}}_n(\varepsilon ))^3} \left( (\theta +(1-\theta ){\check{T}}_n(\varepsilon )){\check{T}}_n''(\varepsilon ) -2(1-\theta )({\check{T}}_n'(\varepsilon ))^2\right) , \end{aligned} \end{aligned}$$

respectively. So, if $T_2'(\varepsilon _0)=0$ for some $\varepsilon _0>0$, then ${\check{T}}_2'(\varepsilon _0)=0$. It follows from Lemma 4.9 that ${\check{T}}_2''(\varepsilon _0)<0$ and hence $T_2''(\varepsilon _0)<0$. This completes the proof. $\square$

Lemma 4.11

For model (4.1), if ${\mathcal {R}}_0(\infty )>1$ and ${\mathbb {T}}_2'(\infty )=0$, then $T_2'(\varepsilon )>0$ for all $\varepsilon \in [0,\infty )$.

Proof

Denote $p=\alpha _1+\alpha _2/2$ and $\sigma \in {\mathbb {R}}_+$. We introduce an axillary system

$$\begin{aligned} \begin{aligned} \dfrac{d{\check{I}}_1}{dt}&={\check{I}}_1\Big ({\tilde{\beta }}_1-{\tilde{\gamma }}_1- \frac{{\tilde{\beta }}_1{\check{I}}_1}{\theta (\alpha _1-{\check{I}}_1)+{\check{I}}_1}\Big )+\varepsilon (-L_{21}{\check{I}}_1+L_{12}{\check{I}}_2),\\ \dfrac{d{\check{I}}_2}{dt}&={\check{I}}_2\Big ({\tilde{\beta }}_2-{\tilde{\gamma }}_2- \frac{{\tilde{\beta }}_2{\check{I}}_2}{\theta (\alpha _2-{\check{I}}_2)+{\check{I}}_2}\Big )+\varepsilon (L_{21}{\check{I}}_1-L_{12}{\check{I}}_2), \end{aligned} \end{aligned}$$

(4.13)

where

$$\begin{aligned}{\tilde{\beta }}_i=\beta _i+\sigma ,\ i=1,2,\ \ {\tilde{\gamma }}_1=\gamma _1+\frac{p}{\alpha _1{\mathcal {R}}_0(\infty )}\sigma ,\ \text{ and } \ {\tilde{\gamma }}_2=\gamma _2+\frac{1-p}{\alpha _2{\mathcal {R}}_0(\infty )}\sigma .\end{aligned}$$

Let ${\check{T}}_{2\sigma }(\varepsilon )$ be the sum of ${\check{I}}_1$ and ${\check{I}}_2$ at the unique positive equilibrium of system (4.13) and ${\mathbb {T}}_{2\sigma }'(\infty )$ the limit of (4.6) as $\varepsilon \rightarrow \infty$ associated to system (4.13). Note that ${\check{T}}_{20}(\varepsilon )={\check{T}}_2(\varepsilon )$ and ${\mathbb {T}}_{20}'(\infty )={\mathbb {T}}_{2}'(\infty )$. The limiting reproduction number as $\varepsilon \rightarrow \infty$ associated to system (4.13) is the same as that of system (4.2), i.e.,

$$\begin{aligned} \begin{aligned} {\mathcal {R}}_{\sigma }(\infty ):=&\frac{{\tilde{\beta }}_1\alpha _1+{\tilde{\beta }}_2\alpha _2}{{\tilde{\gamma }}_1\alpha _1+{\tilde{\gamma }}_2\alpha _2}= \frac{\beta _1\alpha _1+\beta _2\alpha _2+\sigma }{\gamma _1\alpha _1+\gamma _2\alpha _2+\sigma /{\mathcal {R}}_0(\infty )}\\ =&\frac{\beta _1\alpha _1+\beta _2\alpha _2+\sigma }{(\gamma _1\alpha _1+\gamma _2\alpha _2)(1+\sigma /(\beta _1\alpha _1+\beta _2\alpha _2))} =\frac{\beta _1\alpha _1+\beta _2\alpha _2}{\gamma _1\alpha _1+\gamma _2\alpha _2}={\mathcal {R}}_0(\infty )>1. \end{aligned} \end{aligned}$$

A straightforward but tedious computation gives

$$\begin{aligned} \begin{aligned} {\mathbb {T}}_{2\sigma }'(\infty ):=&\frac{{\tilde{\beta }}_2{\tilde{\gamma }}_1-{\tilde{\beta }}_1{\tilde{\gamma }}_2}{{\tilde{\beta }}_1\alpha _1+{\tilde{\beta }}_2\alpha _2} +\Big (1-\frac{1}{{\mathcal {R}}_{\sigma }(\infty )}\Big )\Big (\theta +(1-\theta )\frac{1}{{\mathcal {R}}_{\sigma }(\infty )}\Big )({\tilde{\beta }}_1-{\tilde{\beta }}_2)\\ =&\frac{{\tilde{\beta }}_2{\tilde{\gamma }}_1-{\tilde{\beta }}_1{\tilde{\gamma }}_2}{{\tilde{\beta }}_1\alpha _1+{\tilde{\beta }}_2\alpha _2} +\Big (1-\frac{1}{{\mathcal {R}}_0(\infty )}\Big )\Big (\theta +(1-\theta )\frac{1}{{\mathcal {R}}_0(\infty )}\Big )(\beta _1-\beta _2)\\ =&\frac{\beta _2\gamma _1-\beta _1\gamma _2}{\beta _1\alpha _1+\beta _2\alpha _2}+\frac{1}{\alpha _1\alpha _2{\mathcal {R}}_0(\infty )}(p-\alpha _1)\sigma -\frac{\beta _2\gamma _1-\beta _1\gamma _2}{\beta _1\alpha _1+\beta _2\alpha _2}\\ =&\frac{1}{\alpha _1\alpha _2{\mathcal {R}}_0(\infty )}(p-\alpha _1)\sigma =\frac{1}{2\alpha _1{\mathcal {R}}_0(\infty )}\sigma >0 \end{aligned} \end{aligned}$$

for any $\sigma >0$, where the second and third equalities are due to ${\mathcal {R}}_{\sigma }(\infty )={\mathcal {R}}_0(\infty )$ and ${\mathbb {T}}_2'(\infty )=0$. So it follows from Lemmas 4.1 and 4.9 that ${\check{T}}_{2\sigma }'(\varepsilon )>0$ for any $\varepsilon \ge 0$ and $\sigma >0$. By the smoothness of ${\check{T}}_{2\sigma }(\varepsilon )$ in $\sigma \in {\mathbb {R}}_+$, we known ${\check{T}}_{2\sigma }(\varepsilon )$ is uniformly convergent to ${\check{T}}_{20}(\varepsilon )={\check{T}}_{2}(\varepsilon )$ as $\sigma \rightarrow 0+$ for $\varepsilon$ in every bounded set on ${\mathbb {R}}_+$. The monotonicity of ${\check{T}}_{2\sigma }(\varepsilon )$ in $\varepsilon$ implies that ${\check{T}}_{2}(\varepsilon )$ is nondecreasing in $\varepsilon$, i.e., ${\check{T}}_{2}'(\varepsilon )\ge 0$ for any $\varepsilon \ge 0$. Again by applying Lemma 4.9, we have ${\check{T}}_{2}'(\varepsilon )>0$ and hence $T_{2}'(\varepsilon )>0$ on ${\mathbb {R}}_+$. $\square$

A combination of Lemmas 2.1, 4.4, 4.10 and 4.11, and Remark 4.8 produce the following theorem which means that $T_2(\varepsilon )$ is either constant (if and only if ${\mathcal {R}}_0^{(1)}={\mathcal {R}}_0^{(2)}$ or ${\mathcal {R}}_0(0)\le 1$), or strictly decreasing, or strictly increasing, or initially strictly increasing then strictly decreasing with respect to diffusion coefficient $\varepsilon$.

Theorem 4.12

Suppose ${\mathcal {R}}_0^{(1)}>\max \{{\mathcal {R}}_0^{(2)},1\}$ for model (4.1). Then we have

• (a) if $T_2'(0+)\le 0$, then $T_2'(\varepsilon )<0$ for all $\varepsilon \in (0,\infty )$ as ${\mathcal {R}}_0(\infty )\ge 1$ (or $(0,\varepsilon ^*)$ and $T_2'(\varepsilon )=0$ for $\varepsilon \in (\varepsilon ^*,\infty )$ as ${\mathcal {R}}_0(\infty )<1$);

• (b) if $0<T_2'(0+)\le \infty$ and ${\mathcal {R}}_0(\infty )<1$, then there exists $\varepsilon _1\in (0,\varepsilon ^*)$ such that $T_2'(\varepsilon )>0$ for $\varepsilon \in (0,\varepsilon _1)$, $T_2'(\varepsilon )=0$ for $\varepsilon =\varepsilon _1$, $T_2'(\varepsilon )<0$ for $\varepsilon \in (\varepsilon _1,\varepsilon ^*)$, and $T_2'(\varepsilon )=0$ for $\varepsilon \in (\varepsilon ^*,\infty )$;

• (c) if $0<T_2'(0+)\le \infty$, ${\mathcal {R}}_0(\infty )\ge 1$ and ${\mathbb {T}}_2'(\infty )\ge 0$, then $T_2'(\varepsilon )>0$ for all $\varepsilon \in (0,\infty )$;

• (d) if $0<T_2'(0+)\le \infty$, ${\mathcal {R}}_0(\infty )\ge 1$ and ${\mathbb {T}}_2'(\infty )<0$, then there exist $\varepsilon _2>0$ such that $T_2'(\varepsilon )>0$ for $\varepsilon \in (0,\varepsilon _2)$, $T_2'(\varepsilon )=0$ for $\varepsilon =\varepsilon _2$, and $T_2'(\varepsilon )<0$ for $\varepsilon \in (\varepsilon _2,\infty )$.

We can see that the shape of $T_2(\varepsilon )$ is completely determined by the signs of ${\mathcal {R}}_0(\infty )-1$, $T_2'(0+)$ and ${\mathbb {T}}_2'(\infty )$. It is noteworthy that ${\mathbb {T}}_2'(\infty )\ge 0$ implies ${\mathcal {R}}_0(\infty )>1$, $T_2'(0+)>0$ and $T_2(\infty )>T_2(0)$ provided that ${\mathcal {R}}_0(\infty )\ge 1$. An alternative way for clarification of the shape of $T_2(\varepsilon )$ can be given in terms of $\mathop {{\mathrm {sgn}}}(T_2(\infty )-T_2(0))$.

In what follows, we present some results on how population dispersal affects the disease prevalence, the population size and the infection size of the high-risk patch. The proof can be found in Appendix B.

Proposition 4.13

Suppose ${\mathcal {R}}_0^{(1)}>{\mathcal {R}}_0^{(2)}$ and ${\mathcal {R}}_0(\varepsilon )>1$ for model (4.1). Then

• (a) the difference of the disease prevalences of patches 1 and 2 satisfies $\frac{d}{d\varepsilon }\left( \frac{I_1^*}{N_1^*}-\frac{I_2^*}{N_2^*}\right) <0$;

• (b) the disease prevalence in patch 1 satisfies $\frac{d}{d\varepsilon }\left( \frac{I_1^*}{N_1^*}\right) <0$;

• (c)

  • (i) if $0<\theta <1$, then the total population size of patch 1 satisfies $\frac{dN_1^*}{d\varepsilon }<0$;

  • (ii) if $\theta =1$, then $\frac{dN_1^*}{d\varepsilon }\equiv 0$ and $N_1^*(\varepsilon )\equiv \alpha _1 N$ for $\varepsilon \in [0,\infty )$;

  • (iii) if $\theta >1$, then $\frac{dN_1^*}{d\varepsilon }>0$;

• (d) if $0<\theta \le 1$, or $\theta >1$ and $T_2'(0+)\le 0$, then the infection size in patch 1 satisfies $\frac{dI_1^*}{d\varepsilon }<0$;

• (e) the population sizes of the susceptible and the infectious in patches 1 and 2 satisfy $\frac{d}{d\varepsilon }\left( \frac{I_1^*}{\alpha _1}-\frac{I_2^*}{\alpha _2}\right) <0$ and $\frac{d}{d\varepsilon }\left( \frac{S_1^*}{\alpha _1}-\frac{S_2^*}{\alpha _2}\right) >0$, respectively.

Remark 4.14

When only two patches are considered and $0<\theta \le 1$, increasing dispersal is good for the high-risk patch in reducing its infection size and disease prevalence, but can be harmful to the whole patchy environment. The condition in part (d) can probably be weakened through a delicate analysis. However, under some parameter setting, we find that $I^*_1(\varepsilon )$ may not be decreasing for sufficiently small or large $\varepsilon$ once $\frac{dI_1^*}{d\varepsilon }(0+)>0$ or $I^*_1(0)<I^*_1(\infty )$ holds (e.g., $\beta _1=4, \beta _2=2, \gamma _1=\gamma _2=1$, $L_{12}=L_{21}=1$ and $\theta =4$), respectively. By Corollary 2.5 and Remark 3.2, it is not surprising that $N_1^*(\varepsilon )$ changes its monotonicity with respect to $\varepsilon$ as $\theta$ varies from less than one to greater than one. It is easy to see that $I_2^*/N_2^*$ may constantly increase or initially increase then decrease with respect to $\varepsilon$, whereas $I_2^*$ can be decreasing, increasing or nonmonotone in $\varepsilon$ (e.g., ${\mathcal {R}}_0(\infty )<1$).

Remark 4.15

The disease persistence/extinction and the total infection size as $\varepsilon \rightarrow \infty$, characterized by $(1-1/{\mathcal {R}}_0(\infty ))^+N$, are independent of $\theta =\varepsilon /\delta$, the relative mobility of infected population to susceptible population, but the total infection size is affected by $\theta$ when $\varepsilon$ is finite. More specifically, the infection-caused change in mobility affects $T_2'(0+), T_2(\infty )-T_2(0)$ and ${\mathbb {T}}_2'(\infty )$, and hence the sign pattern of $T_2(\varepsilon )-T_2(0)$ and the change pattern of $T_2(\varepsilon )$. In addition, the population size of a given patch and its change pattern also depend on $\theta$ if the disease can persist.

Remark 4.16

The methods here can be applied to two-patch models with logistic growth for a single species, introduced by Freedman and Waltman (1977) in 1977 to study the effect of dispersal on total population abundance. Since then, many related theoretical and experimental works have been done; see (Arditi et al. 2018; DeAngelis et al. 2016a; He et al. 2019; Lou 2006; Wang et al. 2020; Zhang et al. 2017, 2015) and the references therein for more details. We will further address this ecological question and its applications to two competing species models in a forthcoming work (Gao and Lou 2021).

5 Numerical Simulations

We will use a numerical approach to further explore the impact of the movement of susceptible and infected populations on the local and global disease prevalence, $I_i^*/N_i^*$ and $T_n/N$, respectively. For simplicity, the total population size across patches is fixed at one, i.e., $N=1$, such that the overall disease prevalence and the total infection size have the same quantity. The ranges of parameters used below are chosen for illustrative purpose only and may not necessarily be epidemiologically realistic.

Fig. 1

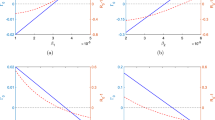
The contour plots of $T_2$ versus $\delta$ and $\varepsilon$ under four parameter settings: a $\beta _1=0.3, \gamma _1=0.11, \beta _2=0.1, \gamma _2=0.05, L_{12}=0.2, L_{21}=0.3$; b $\beta _1=0.15, \gamma _1=0.05, \beta _2=0.4, \gamma _2=0.2, L_{12}=0.2, L_{21}=0.2$; c $\beta _1=0.11, \gamma _1=0.071, \beta _2=0.15, \gamma _2=0.109, L_{12}=0.2, L_{21}=0.1$; d $\beta _1=0.14, \gamma _1=0.1, \beta _2=0.06, \gamma _2=0.057, L_{12}=0.03, L_{21}=0.18$

Example 5.1

($T_2$ versus $\delta$ and $\varepsilon$) For model (1.1) with two patches, we make four contour plots of the total infection size $T_2(\delta ,\varepsilon )$ under different parameter settings in Fig. 1. In all four scenarios, both patches are sources with patch 1 having higher infection risk, i.e., ${\mathcal {R}}_0^{(1)}>{\mathcal {R}}_0^{(2)}>1$. Figure 1a and b shows that $T_2$ can simultaneously increase and decrease with respect to $\delta$ and $\varepsilon$, the dispersal rates of susceptible and infected populations, respectively. Moreover, near y-axis in Fig. 1a and x-axis in Fig. 1b, $T_2$ is increasing in $\delta$ but decreasing in $\varepsilon$. Figure 1c and d illustrates the nonmonotonic dependence of $T_2$ in terms of $\delta$ and $\varepsilon$, respectively. So even though ${\check{T}}_2$ is increasing in $\theta =\varepsilon /\delta$ for fixed $\varepsilon$ (i.e., decreasing in $\delta$), $T_2(\delta ,\varepsilon )$ can increasingly, or decreasingly, or nonmonotonically depend on $\delta$ and $\varepsilon$. However, for a source-sink patchy environment, i.e., ${\mathcal {R}}_0^{(1)}>1>{\mathcal {R}}_0^{(2)}$, the endemic equilibrium $E^*$ approaches a limiting disease-free equilibrium as $\delta \rightarrow 0+$, so we have $T_2(0+,\varepsilon )=0$ and $T_2(\delta ,\varepsilon )$ must strictly decrease in $\delta$ near zero (Allen et al. 2007; Chen et al. 2020). We can see from Fig. 1 that $T_2(\delta ,\varepsilon )$ still changes significantly in $\varepsilon$ or $\delta$ for large $\delta$ or $\varepsilon$. This suggests that $T_2(\infty ,\varepsilon )$ and $T_2(\delta ,\infty )$ are nonconstant which agrees with Remark 3.6.

Fig. 2

The curves of $(T_2(\infty )-T_2(\varepsilon ))\varepsilon$ against $\varepsilon$ (in logarithmic scale) with $\theta =0.2$ (blue solid), 1 (red dashed), and 5 (black dotted) for a source–source and b source–sink patchy environment. See main text for parameter settings (Color figure online)

In Fig. 1, all points on a ray passing through the origin in the interior of the first quadrant have the same slope $\theta =\varepsilon /\delta$. Thus, $T_2(\varepsilon )$ is strictly increasing in $\varepsilon$ in Fig. 1a, strictly decreasing in $\varepsilon$ in Fig. 1b and c, and initially increasing then decreasing in $\varepsilon$ for small and medium $\theta$ but strictly increasing in $\varepsilon$ for large $\theta$ in Fig. 1d. The dependence of $T_n$ on $\delta$ and $\varepsilon$ becomes more complicated and some properties of the two-patch submodel like Lemmas 4.4 and 4.10 may fail for model (1.1) with three or more patches (Gao 2020). It should be noted that the threshold quantity ${\mathcal {R}}_0$ is independent of $\delta$ but strictly decreasing in $\varepsilon$ for the model with an arbitrary number of patches.

Example 5.2

(rate of convergence for $T_n(\varepsilon )\rightarrow T_n(\infty )$ as $\varepsilon \rightarrow \infty$) For model (3.1) with ${\mathcal {R}}_0(\infty )>1$, it follows from Theorem 3.1 that $T_n(\varepsilon )\rightarrow T_n(\infty )=(1-1/{\mathcal {R}}_0(\infty ))N$ as $\varepsilon \rightarrow \infty$. It is biologically meaningful and mathematically interesting to examine how fast the convergence speed is. Consider the two-patch submodel (4.2) with the parameter setting: $\beta _1=0.3, \gamma _1=0.15, \beta _2=0.25, \gamma _2=0.2, L_{12}=0.05, L_{21}=0.1$, which gives ${\mathcal {R}}_0^{(1)}=2>{\mathcal {R}}_0(\infty )=1.45>{\mathcal {R}}_0^{(2)}=1.25$ and $T_2(\infty )=0.31$. The dependence of $W_2(\varepsilon ):=(T_2(\infty )-T_2(\varepsilon ))\varepsilon$ in $\varepsilon$ for $\theta =0.2, 1, 5$ are illustrated in Fig. 2a. Clearly, $W_2(\varepsilon )$ converges to a constant as $\varepsilon \rightarrow \infty$, which suggests that $T_2(\varepsilon )=T_2(\infty )+O(1/\varepsilon )$. The limit of $W_2(\varepsilon )$ varies with $\theta$ and for fixed $\varepsilon$ larger $W_2(\varepsilon )$ in $\theta$ corresponds to smaller $T_2(\varepsilon )$. Using the same parameter set except that $\beta _2=0.15$ so that ${\mathcal {R}}_0^{(1)}=2>{\mathcal {R}}_0(\infty )=1.09>{\mathcal {R}}_0^{(2)}=0.75$ and $T_2(\infty )=0.083$. Now patch 2 changes from a source patch to a sink patch, but the function $W_2(\varepsilon )$ remains convergent as $\varepsilon \rightarrow \infty$ (see Fig. 2b).

Moreover, for 2-, 3- and 4-patch cases, we use the Latin hypercube sampling (LHS) method to randomly generate $10^4$ parameter sets with $\beta _i, \gamma _i, L_{ij}\in (0,1]$ and $\theta \in (0,5]$ and obtain 5007, 5082, and 5037 qualified scenarios whose corresponding ${\mathcal {R}}_0(\infty )>1$, respectively. We calculate the relative change of $W_n(\varepsilon )$ from $\varepsilon =10^5$ to $10^6$ for each qualified scenario,

$$\begin{aligned}\frac{W_n(10^6)-W_n(10^5)}{W_n(10^5)}=\frac{W_n(10^6)}{W_n(10^5)}-1,\end{aligned}$$

and find that the average and maximum values are $2.94\times 10^{-5}$ and $6.22\times 10^{-3}$, $4.31\times 10^{-3}$ and 1.83, $2.46\times 10^{-3}$ and 0.54 for $n=2,3,4$, respectively. These simulation results strongly suggest that

$$\begin{aligned}T_n(\varepsilon )=T_n(\infty )+O(1/\varepsilon ),\ \text{ or } \text{ equivalently },\ {\check{T}}_n(\varepsilon )={\check{T}}_n(\infty )+O(1/\varepsilon ),\end{aligned}$$

as $\varepsilon \rightarrow \infty$ provided that $n\ge 2$ and ${\mathcal {R}}_0(\infty )>1$. Furthermore, we numerically find that even $I_i^*(\varepsilon )=I_i^*(\infty )+O(1/\varepsilon )$ holds as $\varepsilon \rightarrow \infty$ for each $i\in \Omega$ provided that $n\ge 2$ and ${\mathcal {R}}_0(\infty )>1$. We leave the rigorous proof of this observation for a future work. It is worth mentioning that ${\mathcal {R}}_0(\varepsilon )={\mathcal {R}}_0(\infty )+O(1/\varepsilon )$ also holds as $\varepsilon \rightarrow \infty$ (Tien et al. 2015).

Example 5.3

(failure of order preservation) The conclusion that the disease prevalence of each patch in connection is between the maximum and minimum of the set of the disease prevalences of each isolated patch may fail if the connectivity matrices for susceptible and infectious populations, respectively, denoted by L and K, are different. Namely, consider a generalized model as follows

$$\begin{aligned} \begin{aligned} \dfrac{dS_i}{dt}&=-\beta _i\frac{S_iI_i}{N_i}+\gamma _i I_i+\varepsilon \sum \limits _{j\in \Omega } L_{ij}S_j,&\quad i\in \Omega ,\\ \dfrac{dI_i}{dt}&=\beta _i\frac{S_iI_i}{N_i}-\gamma _i I_i+\varepsilon \sum \limits _{j\in \Omega } K_{ij}I_j,&\quad i\in \Omega \end{aligned} \end{aligned}$$

(5.1)

with nonnegative initial condition satisfying

$$\begin{aligned}\sum \nolimits _{i\in \Omega } (S_i(0)+I_i(0)):=N>0\ \text{ and } \ \sum \nolimits _{i\in \Omega } I_i(0)>0.\end{aligned}$$

For the two-patch case, we choose the following parameter set

$$\begin{aligned}\beta _1=0.4, \gamma _1=0.28, \beta _2=0.4, \gamma _2=0.3, L_{12}=0.5, L_{21}=0.1, K_{12}=0.1, K_{21}=0.5.\end{aligned}$$

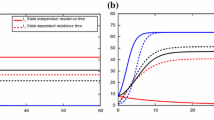
The disease prevalences of patch 1, patch 2, and both patches at the endemic equilibrium versus the diffusion coefficient $\varepsilon$ are plotted in Fig. 3a. When the two patches are isolated, the disease prevalences of patches 1 and 2 are 0.3 and 0.25, respectively. As the dispersal rate increases, the disease prevalence of patch 1 is constantly decreasing while that of patch 2 is initially increasing then decreasing. For larger dispersal rate, the disease prevalence of patch 1 is less than that of patch 2 (low-risk patch) in isolation, the disease prevalence of patch 2 exceeds that of patch 1 (high-risk patch) in isolation, and the overall disease prevalence is below the minimum of the disease prevalences of the two isolated patches. Figure 3b is illustrated by using the same parameter set except that the connectivity matrices L and K are changed to their respective transposes. The disease prevalence of the high-risk patch becomes even larger while that of the low-risk patch becomes even smaller when population dispersal presents. The choices of L and K make less susceptible individuals but more infected individuals move from low-risk patch to high-risk patch, which results in an even higher disease prevalence for the high-risk patch.

Fig. 3

The disease prevalences of patch 1 (blue solid), patch 2 (red dashed) and both patches (black dotted) versus diffusion coefficient for (5.1) in two scenarios. See main text for parameter settings (Color figure online)

6 Discussion

In most theoretical studies on spatial epidemic models, the central objective is to explore the influence of human movement on the disease dynamics. Usually a sharp threshold result between disease persistence and extinction can be gained in terms of the basic reproduction number. When a disease is endemic in a discrete or continuous space, it is important to know how population dispersal affects the local and global disease prevalence at the endemic equilibrium or other attractors. Although the reproduction number can determine whether an emerging infectious disease can spread in a population or not, it can hardly measure the endemic level in most cases. This motivates us to study the quantitative property of the positive steady state. It appears there are rather few analytical studies in this topic (Gao 2020).

In the current paper, based on an SIS patch model, we first gave an estimate of the disease prevalence of each connected patch with respect to those of all isolated patches and established a weak order-preserving result associated with patch disease prevalence and patch reproduction number. Dispersal reduces the disease prevalence of the highest-risk patch but promotes that of the lowest-risk patch. In case of two patches, high-risk patch still has high disease prevalence in the presence of human migration. Then we studied the total infection size, or equivalently, the overall disease prevalence in case the dispersal rate of the susceptible population is proportional to that of the infected population. The total infection sizes at no dispersal and infinite dispersal were calculated and compared. In particular, if the recovery rate is unanimous then fast dispersal leads to more infections than slow dispersal. Furthermore, for the two-patch submodel, we completely answered the questions of when dispersal causes more or less infections and how the total number of infections changes with dispersal rate. Finally, three numerical examples were given to investigate the relationship between the total infection size and dispersal rates, the convergence speed of the total infection size $T_n(\varepsilon )$ as $\varepsilon \rightarrow \infty$, and the occurrence of non-order-preserving phenomenon, respectively. The strict monotonicity of ${\mathcal {R}}_0(\varepsilon )$ in $\varepsilon$ implies that ${\mathcal {R}}_0(0)$ and ${\mathcal {R}}_0(\infty )$ are the supremum and infimum of ${\mathcal {R}}_0(\varepsilon )$, respectively. However, the two-patch case indicates that $T_n(\varepsilon )$ can at least increase, or decrease, or initially increase then decrease in $\varepsilon$. Thus, $T_n(0)$ and $T_n(\infty )$ could be the supremum, infimum or neither of $T_n(\varepsilon )$. The inconsistence between the basic reproduction number and the overall disease prevalence with respect to dispersal rates indicates that public agencies should not focus solely on reducing the basic reproduction number in the fight against infectious diseases.

We extensively generalized and improved the results of our recent work (Gao 2020) from the very special case of $\theta =1$ to the general case of $\theta >0$. The infection-caused change in mobility for the infected people impacts population distribution, total infection size, and its distribution and change pattern. For the two-patch submodel with any positive constant $\theta$, it is no longer easy, if not impossible, to use the graphical method to classify the model parameter space on when dispersal results in more or less infections than no dispersal (Arditi et al. 2018; Gao 2020). The approach used in proving Lemma 4.1 is quite skillful in factoring ${\check{T}}_2'(\varepsilon )$ and deriving ${\check{T}}_2(\varepsilon )-{\check{T}}_2(0)$. Importantly, in Lemma 4.10 we showed that any nontrivial critical point of $T_2(\varepsilon )$ must be a local maximum point. The relation between $T_2(\varepsilon )$ and $T_2(0)$ is wholly governed by the signs of $T'_2(0+)$ and $T_2(\infty )-T_2(0)$, while the shape of $T_2(\varepsilon )$ is completely determined by the signs of ${\mathcal {R}}_0(\infty )-1$, $T_2'(0+)$ and ${\mathbb {T}}_2'(\infty )$. Here the terms $T_2(0)$, $T'_2(0+)$ and ${\mathbb {T}}_2'(\infty )$ are dependent of $\theta$ (Proposition 4.6, Proposition 4.7 and Remark 4.8). One application of this finding is that it enables us to have a much better understanding of dispersal on total population abundance for the two-patch logistic model (Arditi et al. 2018; Freedman and Waltman 1977; Gao and Lou 2021).

When vital dynamics are incorporated into model (1.1) (Wang and Mulone 2003), we get

$$\begin{aligned} \begin{aligned} \dfrac{dS_i}{dt}&=\mu _iN_i-\mu _iS_i-\beta _i\frac{S_iI_i}{N_i}+\gamma _i I_i+\delta \sum \limits _{j\in \Omega } L_{ij}S_j,\quad&i\in \Omega ,\\ \dfrac{dI_i}{dt}&=\beta _i\frac{S_iI_i}{N_i}-(\mu _i+\gamma _i) I_i+\varepsilon \sum \limits _{j\in \Omega } L_{ij}I_j,\quad&i\in \Omega , \end{aligned} \end{aligned}$$

where $\mu _i$ is the birth rate and death rate of the population in patch i. The main results in this paper remain valid since a result similar to Lemma 1.1 on the existence and uniqueness of the endemic equilibrium as ${\mathcal {R}}_0>1$ can be similarly proved. This study is also applicable to an SIS patch model with different contact rates $c_i$ and $k c_i$ but equal dispersal rates for the susceptible and infectious populations.

There is still room for improvement. It will be nice to compute the derivative of $T_n(\varepsilon )$ with respect to large $\varepsilon$ for $n\ge 3$ and determine its sign to see the change trend of $T_n(\varepsilon )$ for large dispersal. The observation on the rate of convergence for $T_n(\varepsilon )$ as $\varepsilon \rightarrow \infty$ desires a rigorous proof (DeAngelis et al. 2016a; Lou 2006). What happens to $T_n(\varepsilon )$ if there are three or more patches? A detailed study of the dependence of $T_n$ on $\delta$, $\varepsilon$ and $L_{ij}$ is helpful to evaluate the effectiveness of border screening and travel restrictions, especially during the ongoing COVID-19 pandemic. The global asymptotic stability of the unique endemic equilibrium is generally unknown (Gao and Ruan 2011; Li and Peng 2019). We are interested in generalizing the current work in various ways, e.g., by considering complicated vital dynamics (Wang and Zhao 2004), state-dependent connectivity matrices (Gao and Ruan 2011), temporal variations (Gao et al. 2014), different model structures (Cosner et al. 2009; Gao and Ruan 2012; Salmani and van den Driessche 2006), and continuous or nonlocal diffusion (Allen et al. 2008; Lou and Zhao 2010; Yang et al. 2019).

Appendices

Appendix A: Proof of Theorem 2.3

Proof

We only prove the first part while the second part can be shown similarly. Suppose not, then there exists some $\delta _0>0$ and $\varepsilon _0>0$ such that $I^*_1/N^*_1=\min \limits _{i\in \Omega } I^*_i/N^*_i$.

Claim 1: $I^*_1/N^*_1=\dots =I^*_n/N^*_n$ if and only if ${\mathcal {R}}_0^{(1)}=\dots ={\mathcal {R}}_0^{(n)}$. Suppose $I^*_i/N^*_i=\tau \in (0,1)$ for all $i\in \Omega$, then

$$\begin{aligned}\sum \limits _{j\in \Omega } L_{ij}I_j^*=\sum \limits _{j\in \Omega } L_{ij}\tau N_j^*=\tau \left( \sum \limits _{j\in \Omega } L_{ij}S_j^*+\sum \limits _{j\in \Omega } L_{ij}I_j^*\right) \end{aligned}$$

implies that

$$\begin{aligned}\sum \limits _{j\in \Omega } L_{ij}S_j^*=\frac{1-\tau }{\tau }\sum \limits _{j\in \Omega } L_{ij}I_j^*\end{aligned}$$

and hence

$$\begin{aligned}0=\delta \sum \limits _{j\in \Omega } L_{ij}S_j^*+\varepsilon \sum \limits _{j\in \Omega } L_{ij}I_j^* =\left( \delta \frac{1-\tau }{\tau }+\varepsilon \right) \sum \limits _{j\in \Omega } L_{ij}I_j^*.\end{aligned}$$

Thus, we have

$$\begin{aligned}\sum \limits _{j\in \Omega } L_{ij}I_j^*=0 \Rightarrow f_i(I_i^*):=\beta _i\left( 1-\dfrac{I_i^*}{N^*_i}\right) I_i^*-\gamma _i I_i^*=0\Rightarrow \dfrac{I_i^*}{N^*_i}=1-\dfrac{1}{{\mathcal {R}}_0^{(i)}}=\tau \end{aligned}$$

and hence ${\mathcal {R}}_0^{(i)}=1/(1-\tau )$ for all $i\in \Omega$. On the other hand, if ${\mathcal {R}}_0^{(1)}=\dots ={\mathcal {R}}_0^{(n)}$, then ${\mathcal {R}}_0={\mathcal {R}}_0^{(1)}>1$ and the unique endemic equilibrium $E^*=({\varvec{S}}^*,{\varvec{I}}^*)$ of system (1.1) satisfies

$$\begin{aligned}S_i^*=\frac{1}{{\mathcal {R}}_0}\alpha _i N\quad \text{ and } \quad I_i^*=\left( 1-\frac{1}{{\mathcal {R}}_0}\right) \alpha _i N,\quad i\in \Omega .\end{aligned}$$

So, $I^*_i/N^*_i=1-1/{\mathcal {R}}_0$ for $i\in \Omega$.

Claim 2: $f_i(I_i^*)\not \equiv 0$ for $i\in \Omega$. Suppose not, then

$$\begin{aligned}f_i(I_i^*)=0\Leftrightarrow \sum \limits _{j\in \Omega }L_{ij}I_j^*=0 \Leftrightarrow \sum \limits _{j\in \Omega }L_{ij}S_j^*=0,\ i\in \Omega \end{aligned}$$

implies that $I_i^*/N_i^*$ is constant in $i\in \Omega$, which is impossible by Claim 1.

Claim 3: If $f_k(I_k^*)>0$ for some $k\in \Omega$ then $f_1(I_1^*)>0$. Indeed, it follows that

$$\begin{aligned} \begin{aligned} \frac{f_1(I_1^*)}{\gamma _1I_1^*}=\frac{\beta _1}{\gamma _1}\cdot \frac{S_1^*}{N_1^*}-1 \ge \frac{\beta _k}{\gamma _k}\cdot \frac{S_k^*}{N_k^*}-1= \frac{f_k(I_k^*)}{\gamma _kI_k^*}>0 \end{aligned} \end{aligned}$$

due to ${\mathcal {R}}_0^{(1)}=\frac{\beta _1}{\gamma _1}\ge {\mathcal {R}}_0^{(k)}=\frac{\beta _k}{\gamma _k}$ and $\frac{I_1^*}{N_1^*}\le \frac{I_k^*}{N_k^*}$.

It follows from the above claims and the fact

$$\begin{aligned}\sum \limits _{i\in \Omega }\left( f_i(I_i^*)+\varepsilon \sum \limits _{j\in \Omega } L_{ij}I_j^*\right) =\sum \limits _{i\in \Omega }f_i(I_i^*)=0\end{aligned}$$

that there exist $k,l\in \Omega$ such that $f_k(I_k^*)>0$ and $f_l(I_l^*)<0$. In particular, $f_1(I^*_1)>0$.

On the other hand, we have

$$\begin{aligned} \begin{aligned}&\sum \limits _{j\in \Omega } L_{1j}I_j^* \ge \sum \limits _{j\in \Omega }L_{1j}\frac{I_1^*}{N_1^*}N_j^* =\frac{I_1^*}{N_1^*}\sum \limits _{j\in \Omega }L_{1j}N_j^*\\ \Rightarrow&\left( 1-\frac{I_1^*}{N_1^*}\right) \sum \limits _{j\in \Omega } L_{1j}I_j^*\ge \frac{I_1^*}{N_1^*}\sum \limits _{j\in \Omega }L_{1j}S_j^* =\frac{I_1^*}{N_1^*}\left( -\frac{\varepsilon }{\delta }\right) \sum \limits _{j\in \Omega }L_{1j}I_j^*\\ \Rightarrow&\sum \limits _{j\in \Omega } L_{1j}I_j^*\ge 0. \end{aligned} \end{aligned}$$

So the left-hand side of the equilibrium equation for $I^*_1$ is positive, a contradiction. $\square$

Appendix B: Proof of Proposition 4.13

Proof

(a) Suppose ${\mathcal {R}}_0(\varepsilon )>1$ for some $\varepsilon >0$. It follows from (4.4) that

$$\begin{aligned}&\dfrac{d}{d\varepsilon }\left( \sum \limits _{i=1}^2 (-1)^{j}\frac{I_i^*}{N_i^*}\right) \\ =&\dfrac{d}{d\varepsilon }\left( \sum _{i=1}^2(-1)^{j}\frac{{\check{I}}_i^*}{\theta (\alpha _i-{\check{I}}_i^*)+{\check{I}}_i^*}\right) =\sum _{i=1}^2(-1)^{j}\frac{\theta \alpha _i ({\check{I}}_i^*)'}{(\theta (\alpha _i-{\check{I}}_i^*)+{\check{I}}_i^*)^2}\\ =&\sum _{i=1}^2(-1)^{j}\frac{\theta \alpha _i}{(\theta (\alpha _i-{\check{I}}_i^*)+{\check{I}}_i^*)^2}\cdot \frac{L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*}{|{\tilde{M}}_2|}\cdot (-1)^{j}\\&\quad \times \left( \varepsilon L_{ij} -\varepsilon L_{ji}\frac{{\check{I}}_i^*}{{\check{I}}_j^*} -\frac{\theta \beta _j\alpha _j{\check{I}}^*_j}{(\theta (\alpha _j-{\check{I}}^*_j)+{\check{I}}^*_j)^2} \right) \\ =&\frac{L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*}{|{\tilde{M}}_2|} \sum _{i=1}^2 \frac{\theta \alpha _i}{(\theta (\alpha _i-{\check{I}}_i^*)+{\check{I}}_i^*)^2}\\&\quad \times \left( \beta _j-\gamma _j-\frac{\beta _j{\check{I}}^*_j}{\theta (\alpha _j-{\check{I}}^*_j)+{\check{I}}^*_j} -\frac{\theta \beta _j\alpha _j{\check{I}}^*_j}{(\theta (\alpha _j-{\check{I}}^*_j)+{\check{I}}^*_j)^2}\right) , \end{aligned}$$

where $1\le j\le 2$ and $j\ne i$. Thus, using (4.5), if ${\mathcal {R}}_0^{(2)}\ge 1-1/\theta$ then

$$\begin{aligned} \begin{aligned}&\sum _{i=1}^2 \frac{\alpha _i}{(\theta (\alpha _i-{\check{I}}_i^*)+{\check{I}}_i^*)^2} \left( \beta _j-\gamma _j-\frac{\beta _j{\check{I}}^*_j}{\theta (\alpha _j-{\check{I}}^*_j)+{\check{I}}^*_j} -\frac{\theta \beta _j\alpha _j{\check{I}}^*_j}{(\theta (\alpha _j-{\check{I}}^*_j)+{\check{I}}^*_j)^2}\right) \\ =&\sum _{i=1}^2 \frac{\alpha _i}{(\theta (\alpha _i-{\check{I}}_i^*)+{\check{I}}_i^*)^2} \left( -\frac{(\theta (\beta _j-\gamma _j)+\gamma _j){\check{I}}_j^*}{\theta (\alpha _j-{\check{I}}_j^*)+{\check{I}}_j^*} +\frac{\theta \alpha _j}{\theta (\alpha _j-{\check{I}}_j^*)+{\check{I}}_j^*}{\check{g}}_j({\check{I}}_j^*)\right) \\<&\sum _{i=1}^2 \frac{\alpha _i}{(\theta (\alpha _i-{\check{I}}_i^*)+{\check{I}}_i^*)^2} \cdot \frac{\theta \alpha _j}{\theta (\alpha _j-{\check{I}}_j^*)+{\check{I}}_j^*} {\check{g}}_j({\check{I}}_j^*)<0, \end{aligned} \end{aligned}$$

by noting that

$$\begin{aligned} \begin{aligned}&\sum _{j=1}^2(\theta (\alpha _j-{\check{I}}_j^*)+{\check{I}}_j^*)\left( \beta _j-\gamma _j-\frac{\beta _j{\check{I}}_j^*}{\theta (\alpha _j-{\check{I}}_j^*)+{\check{I}}_j^*}\right) \\ =&\sum _{j=1}^2(\theta (\alpha _j-{\check{I}}_j^*)+{\check{I}}_j^*) \frac{\varepsilon (L_{ij}{\check{I}}_j^*-L_{ji}{\check{I}}_i^*)}{{\check{I}}_j^*}\\ =&\varepsilon (L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*) \left( \frac{\theta \alpha _1}{{\check{I}}_1^*}-\frac{\theta \alpha _2}{{\check{I}}_2^*}\right) =\theta \varepsilon (L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*) \frac{\alpha _1{\check{I}}_2^*-\alpha _2{\check{I}}_1^*}{{\check{I}}_1^*{\check{I}}_2^*}\\ =&-\frac{\theta \varepsilon }{(L_{12}+L_{21}){\check{I}}_1^*{\check{I}}_2^*} (L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*)^2<0. \end{aligned} \end{aligned}$$

(B.1)

On the other hand, if $\theta >1/2$ then the conclusion follows from

$$\begin{aligned}&\sum _{i=1}^2 \alpha _i (\theta (\alpha _j-{\check{I}}_j^*)+{\check{I}}_j^*)^2 \left( \beta _j-\gamma _j-\frac{\beta _j{\check{I}}^*_j}{\theta (\alpha _j-{\check{I}}^*_j)+{\check{I}}^*_j} -\frac{\theta \beta _j\alpha _j{\check{I}}^*_j}{(\theta (\alpha _j-{\check{I}}^*_j)+{\check{I}}^*_j)^2}\right) \\<&\sum _{i=1}^2 \alpha _i(\theta \alpha _j+(1-\theta ){\check{I}}_j^*)^2 \left( \beta _j-\gamma _j-\frac{\beta _j{\check{I}}^*_j}{\theta (\alpha _j-{\check{I}}^*_j)+{\check{I}}^*_j}\right) \\ =&\sum _{i=1}^2 (\theta ^2\alpha _1\alpha _2\alpha _j+(1-\theta )^2\alpha _i({\check{I}}^*_j)^2) \left( \beta _j-\gamma _j-\frac{\beta _j{\check{I}}^*_j}{\theta (\alpha _j-{\check{I}}^*_j)+{\check{I}}^*_j}\right) \\ =&\sum _{i=1}^2 (\theta ^2\alpha _1\alpha _2\alpha _j+(1-\theta )^2\alpha _i({\check{I}}^*_j)^2) \frac{\varepsilon (L_{ij}{\check{I}}^*_j-L_{ji}{\check{I}}^*_i)}{{\check{I}}^*_j}\\ =&\varepsilon (L_{21}{\check{I}}^*_1-L_{12}{\check{I}}^*_2) \left( \theta ^2\alpha _1\alpha _2\left( \frac{\alpha _1}{{\check{I}}^*_1} -\frac{\alpha _2}{{\check{I}}^*_2}\right) +(1-\theta )^2(\alpha _2{\check{I}}^*_1-\alpha _1{\check{I}}^*_2)\right) \\ =&\varepsilon (L_{21}{\check{I}}^*_1-L_{12}{\check{I}}^*_2)\left( \frac{\alpha _1}{{\check{I}}^*_1} -\frac{\alpha _2}{{\check{I}}^*_2}\right) {\check{I}}^*_1{\check{I}}^*_2\left( \theta ^2\frac{\alpha _1\alpha _2}{{\check{I}}^*_1{\check{I}}^*_2} -(1-\theta )^2\right) <0, \end{aligned}$$

where the first equality is due to ${\check{f}}_1({\check{I}}_1^*)+{\check{f}}_2({\check{I}}_2^*)=0$.

(b) It immediately follows from the calculation of $\frac{d}{d\varepsilon }\left( \frac{I_1^*}{N_1^*}\right)$ in part (a).

(c) By (2.1), a straightforward calculation gives

$$\begin{aligned} \begin{aligned} \frac{d N_1^*}{d\varepsilon }&=\frac{d}{d\varepsilon }(S_1^*+I_1^*) =\frac{d}{d\varepsilon }\left( \frac{\theta \alpha _1+(1-\theta ){\check{I}}^*_1}{\theta +(1-\theta ){\check{T}}_2}N\right) \\&=\frac{(\theta (\alpha _2-{\check{I}}^*_2)+{\check{I}}^*_2)({\check{I}}^*_1)' -(\theta (\alpha _1-{\check{I}}^*_1)+{\check{I}}^*_1)({\check{I}}^*_2)'}{(\theta +(1-\theta ){\check{T}}_2)^2}(1-\theta )N. \end{aligned} \end{aligned}$$

So, it remains to prove the negativity of

$$\begin{aligned} \begin{aligned}&(\theta (\alpha _2-{\check{I}}^*_2)+{\check{I}}^*_2)({\check{I}}^*_1)' -(\theta (\alpha _1-{\check{I}}^*_1)+{\check{I}}^*_1)({\check{I}}^*_2)') =\sum \limits _{i=1}^2(-1)^i(\theta (\alpha _i-{\check{I}}^*_i)+{\check{I}}^*_i)({\check{I}}^*_j)'\\ =&\sum _{i=1}^2(-1)^i(\theta (\alpha _i-{\check{I}}^*_i)+{\check{I}}^*_i) \cdot \frac{L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*}{|{\tilde{M}}_2|} (-1)^i\left( {\check{g}}_i({\check{I}}_i^*)-\frac{\theta \beta _i\alpha _i{\check{I}}^*_i}{(\theta (\alpha _i-{\check{I}}^*_i)+{\check{I}}^*_i)^2}\right) , \end{aligned} \end{aligned}$$

which is guaranteed by

$$\begin{aligned} \begin{aligned}&\sum _{i=1}^2(\theta (\alpha _i-{\check{I}}^*_i)+{\check{I}}^*_i) \left( \beta _i-\gamma _i-\frac{\beta _i{\check{I}}^*_i}{\theta (\alpha _i-{\check{I}}^*_i)+{\check{I}}^*_i} -\frac{\theta \beta _i\alpha _i{\check{I}}^*_i}{(\theta (\alpha _i-{\check{I}}^*_i)+{\check{I}}^*_i)^2}\right) \\<&\sum _{i=1}^2(\theta (\alpha _i-{\check{I}}^*_i)+{\check{I}}^*_i)\left( \beta _i-\gamma _i-\frac{\beta _i{\check{I}}^*_i}{\theta (\alpha _i-{\check{I}}^*_i)+{\check{I}}^*_i}\right) <0. \end{aligned} \end{aligned}$$

The second inequality is due to (B.1).

(d) Direct calculation yields

$$\begin{aligned} \begin{aligned} \frac{d I_1^*}{d\varepsilon }&=\frac{d}{d\varepsilon }\left( \frac{{\check{I}}^*_1}{\theta +(1-\theta ){\check{T}}_2}N\right) =\frac{\theta ({\check{I}}^*_1)'+(1-\theta )(({\check{I}}^*_1)'{\check{I}}^*_2 -{\check{I}}^*_1({\check{I}}^*_2)')}{(\theta +(1-\theta ){\check{T}}_2)^2}N\\&<\frac{({\check{I}}^*_1)'{\check{I}}^*_2 -{\check{I}}^*_1({\check{I}}^*_2)'}{(\theta +(1-\theta ){\check{T}}_2)^2}(1-\theta )N. \end{aligned} \end{aligned}$$

So, if $0<\theta \le 1$ then it suffices to determine the sign of

$$\begin{aligned} \begin{aligned}&\frac{|{\tilde{M}}_2|}{L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*} (({\check{I}}^*_1)'{\check{I}}^*_2 -{\check{I}}^*_1({\check{I}}^*_2)')=\frac{|{\tilde{M}}_2|}{L_{21}{\check{I}}_1^*-L_{12}{\check{I}}_2^*} \sum \limits _{i=1}^2(-1)^i {\check{I}}^*_i({\check{I}}^*_j)'\\ =&\sum \limits _{i=1}^2(-1)^i {\check{I}}^*_i (-1)^{i}\left( \beta _i-\gamma _i-\frac{\beta _i{\check{I}}^*_i}{\theta (\alpha _i-{\check{I}}^*_i)+{\check{I}}^*_i} -\frac{\theta \beta _i\alpha _i{\check{I}}^*_i}{(\theta (\alpha _i-{\check{I}}^*_i)+{\check{I}}^*_i)^2}\right) \\ <&\sum \limits _{i=1}^2{\check{I}}^*_i\left( \beta _i-\gamma _i-\frac{\beta _i{\check{I}}^*_i}{\theta (\alpha _i-{\check{I}}^*_i)+{\check{I}}^*_i} \right) =\sum \limits _{i=1}^2 \varepsilon (L_{ij}{\check{I}}_j^*-L_{ji}{\check{I}}_i^*)=0, \end{aligned} \end{aligned}$$

where $1\le j\le 2$ and $j\ne i$. This can also be directly proved by applying parts (b) and (c) due to $\frac{I_1^*}{N_1^*}N_1^*=I_1^*$. Meanwhile, it follows from the proof of part (c) and Lemma 4.1 that the inequality

$$\begin{aligned} \begin{aligned}&\theta ({\check{I}}^*_1)'+(1-\theta )(({\check{I}}^*_1)'{\check{I}}^*_2 -{\check{I}}^*_1({\check{I}}^*_2)')\\&\quad =({\check{I}}^*_1)'(\theta (\alpha _2-{\check{I}}^*_2)+{\check{I}}^*_2)- ({\check{I}}^*_2)'(\theta (\alpha _1-{\check{I}}^*_1)+{\check{I}}^*_1)\\&\qquad +\theta \alpha _1({\check{I}}^*_1+{\check{I}}^*_2)'<\theta \alpha _1{\check{T}}_2'(\varepsilon )\le 0 \end{aligned} \end{aligned}$$

holds whenever $T_2'(0+)\le 0$.

(e) It follows from $\varepsilon (L_{21}I_1^*-L_{12}I_2^*)+\delta (L_{21}S_1^*-L_{12}S_2^*)=0$ that

$$\begin{aligned} \begin{aligned} L_{21}N_1^*-L_{12}N_2^*&=(L_{21}+L_{12})N_1^*-L_{12}N =(L_{21}S_1^*-L_{12}S_2^*)+(L_{21}I_1^*-L_{12}I_2^*)\\&=(1-\theta )(L_{21}I_1^*-L_{12}I_2^*)=(1-1/\theta )(L_{21}S_1^*-L_{12}S_2^*). \end{aligned} \end{aligned}$$

Thus, we can draw the conclusion by applying parts (a) and (c) for $\theta \!=\! 1$ and $\theta \! \ne \! 1$. $\square$