Perihelion Librations in the Secular Three-Body Problem

Abstract

A normal form theory for non-quasiperiodic systems is combined with the special properties of the partially averaged Newtonian potential pointed out in Pinzari (Celest Mech Dyn Astron 131(5):22, 2019) to prove, in the averaged, planar three-body problem, the existence of a plenty of motions where, periodically, the perihelion of the inner body affords librations about one equilibrium position and its ellipse squeezes to a segment before reversing its direction and again decreasing its eccentricity (perihelion librations).

1 Introduction

This paper deals with certain motions of three point masses undergoing Newtonian attraction. More precisely, we study the case of two light bodies orbiting their common center of mass (a “binary asteroid system”) while interacting with a heavier mass (a “planet”), whose position is external to their trajectories. As no Newtonian interaction can be neglected, there is no reason to claim that the system undergoes the “Keplerian” approximation, successfully used in the so-called planetary model¹ (Arnold 1963b; Féjoz 2004; Laskar and Robutel 1995; Pinzari 2009; Chierchia and Pinzari 2011). We think to the case that the time of mutual revolution of the lighter bodies is much shorter than the timescale of the motions of the massive body. We also assume that the ratio $\epsilon$ between the semi-axis of the ellipse of the asteroids and the position ray of the heavier one keeps to be less than $\frac{1}{2}$, so that collisions between the asteroids and the planet are not possible. Recall in fact that a body moving on a Keplerian ellipse does not go beyond twice the semimajor axis from its focus. We look at the system from a reference frame centered with one of the asteroids or with their center of mass, so as to deal with an effective two-particle system, given by the other asteroid and the planet. We shall refer as “asteroidal ellipse” the instantaneous ellipse of this asteroid, focused on the center of the reference frame. We are interested to its motions. To simplify the analysis a little bit, we introduce three assumptions. The main one is based on the belief that, as long as the difference between the timescales persists, the system is “well represented” by a certain “averaged” problem, which we call secular problem. We remark that such average is meant with respect to the proper time of the asteroid, so it should not be confused with the homonymous procedure often studied in the literature (e.g., Féjoz and Guardia 2016), where the Keplerian approximation is used for two particles about their common sun, and the average is done with respect to both their mean anomalies.

The secular system is simpler than the original problem, as we lose information concerning the position of the asteroid. In particular, collisions between the lighter particles are not observable. The degrees of freedom of the system are the motions of the eccentricity (or of the angular momentum) and of the pericenter direction of the asteroidal ellipse and the motions of the massive body. We associate with such system a certain “limiting system” which is similarly defined, but with the massive body being firm. From now on, we refer to such limiting problem as “unperturbed” and to the full secular problem as “perturbed.” The terminology is here used with abuse, as we do not assume that the massive body has slow velocity in the full problem. For the unperturbed system, only movements of the asteroidal ellipse occur. By Pinzari (2019), the unperturbed problem turns out to be integrable, in the sense that it possesses a complete family of independent and commuting first integrals. More importantly, it reveals a surprising property, which we named renormalizable integrability. Such property (recalled for completeness in Sect. 2.2) offers a remarkable shortcut to the knowledge of movements of the asteroidal ellipse. By Pinzari (2020), in the case that the interacting particles are constrained on a plane (this is actually our second assumption), and $\varepsilon <\frac{1}{2}$, there are two stable equilibria such that the pericenter direction of the asteroidal ellipse in the unperturbed problem affords small oscillations about them, while its angular momentum oscillates about zero, affording a periodic change of sign. Physically, this means that the asteroidal ellipse is highly eccentric at any time and, moreover, there are two times (“squeezing times”) in a period of oscillation of the pericenter when the eccentricity is equal to one. Namely, at those times, the ellipse becomes a segment. After the squeezing times, the eccentricity of the ellipse decreases while the sense of the motion is reversed. We call “perihelion librations” such kind of motions. The question which here we address is whether perihelion librations do persist in the full perturbed problem, when the massive body moves. We are able to give a positive answer to this question under our third assumption, which consists in taking the total angular momentum of the system (which is preserved during the motion) equal to zero. Under this assumption, the symmetries of the Hamiltonian ensure that the equilibria persist also in the perturbed problem, even though the integrability is lost. On the other side, such assumption is a source of difficulty, as the angular momenta of the two particles will simultaneously vanish, and hence collisions of the heavy body with the center of the system are to be controlled. We shall formulate our result below, after we have introduced some mathematical tool.

In terms of Jacobi coordinates,² the three-body problem Hamiltonian with masses $m_0$, $\mu m_0$, $\kappa m_0$ is the translation-free function

$$\begin{aligned} {{\mathrm{H}}_1}= & {} {\frac{\Vert {\mathbf {y}}\Vert ^2}{2m_0}\left( 1+\frac{1}{\mu }\right) +\frac{\Vert {\mathbf {y}}^{\prime }\Vert ^2}{2m_0}\left( \frac{1}{1+\mu }+\frac{1}{\kappa }\right) -\frac{ \mu m^2_0}{\Vert {\mathbf {x}}\Vert }-\frac{\mu \kappa m_0^2}{\Vert {\mathbf {x}}^{\prime }-\frac{1}{1+\mu }{\mathbf {x}}\Vert }-\frac{ \kappa m_0^2}{\Vert {\mathbf {x}}^{\prime }+\frac{\mu }{1+\mu }{\mathbf {x}}\Vert }}. \end{aligned}$$

Here, $({{\mathbf {y}}}^{\prime }, {{\mathbf {y}}}, {{\mathbf {x}}}^{\prime }, {{\mathbf {x}}})\in ({{\mathbb {R}}}^3)^4$ (or $({{\mathbb {R}}}^2)^4$), $\Vert \cdot \Vert$ denotes Euclidean distance and the gravity constant has been taken equal to one, by a proper choice of the units system. We rescale impulses and positions

$$\begin{aligned} {{\mathbf {y}}\rightarrow \frac{\mu }{1+\mu }{\mathbf {y}} ,\quad {\mathbf {x}}\rightarrow {(1+\mu )}{{\mathbf {x}}},\quad {\mathbf {y}}^{\prime }\rightarrow \mu \beta {{\mathbf {y}}^{\prime }} ,\quad {\mathbf {x}}^{\prime }\rightarrow \beta ^{-1}{\mathbf {x}}^{\prime }} \end{aligned}$$

(1)

multiply the Hamiltonian by $\frac{1+\mu }{\mu }$ (by a rescaling of time) and obtain

$$\begin{aligned} {\mathrm{H}_1=\frac{\Vert {\mathbf {y}}\Vert ^2}{2m_0}-\frac{m_0^2}{\Vert {\mathbf {x}}\Vert }+\gamma \left( \frac{\Vert {\mathbf {y}}^{\prime }\Vert ^2}{2m_0} -\frac{{\overline{\beta }}}{\beta +{\overline{\beta }}}\frac{ m_0^2 }{\Vert {\mathbf {x}}^{\prime }-\beta {\mathbf {x}}\Vert } -\frac{\beta }{\beta +{\overline{\beta }}}\frac{ m_0^2 }{\Vert {\mathbf {x}}^{\prime }+{\overline{\beta }}{\mathbf {x}}\Vert } \right) } \end{aligned}$$

(2)

with

$$\begin{aligned} {\gamma =\frac{\kappa ^3(1+\mu )^4}{\mu ^3(1+\mu +\kappa )} ,\quad \beta =\frac{\kappa ^2(1+\mu )^2}{\mu ^2(1+\mu +\kappa )} ,\quad {\overline{\beta }}=\mu \beta }. \end{aligned}$$

(3)

Likewise, one might consider the problem written in the so-called $m_0$-centric³ coordinates, and in this case the Hamiltonian is

$$\begin{aligned} {\mathrm{H}_2=\frac{1}{2m_0}\left( 1+\frac{1}{\mu }\right) \Vert {{\mathbf {y}}}\Vert ^2+\frac{1}{2m_0}\left( 1+\frac{1}{\kappa }\right) \Vert {{\mathbf {y}}}^{\prime }\Vert ^2-\frac{\mu m_0^2}{\Vert {{\mathbf {x}}}\Vert }-\frac{\kappa m_0^2}{\Vert {{\mathbf {x}}}^{\prime }\Vert }-\frac{\mu \kappa m_0^2}{\Vert {{\mathbf {x}}}-{{\mathbf {x}}}^{\prime }\Vert }+\frac{{{\mathbf {y}}}\cdot {{\mathbf {y}}}^{\prime }}{m_0}.} \end{aligned}$$

We apply an analogue rescaling, but with

$$\begin{aligned} {\gamma =\frac{\kappa ^3(1+\mu )^3}{\mu ^3(1+\kappa )},\quad \beta =\frac{\kappa ^2(1+\mu )}{\mu ^2(1+\kappa )},\quad {\overline{\beta }}=\mu \beta .} \end{aligned}$$

(4)

We arrive at

$$\begin{aligned} {\mathrm{H}_2=\frac{\Vert {{\mathbf {y}}}\Vert ^2}{2m_0}-\frac{m_0^2}{\Vert {{\mathbf {x}}}\Vert }+\gamma \left( \frac{\Vert {{\mathbf {y}}}^{\prime }\Vert ^2}{2m_0}-\frac{\beta }{\beta +{\overline{\beta }}}\frac{ m_0^2}{\Vert {{\mathbf {x}}}^{\prime }\Vert }-\frac{{\overline{\beta }}}{\beta +{\overline{\beta }}}\frac{m_0^2}{\Vert {{\mathbf {x}}}^{\prime }-(\beta +{\overline{\beta }}){{\mathbf {x}}}\Vert } \right) +{\overline{\beta }} \frac{{{\mathbf {y}}}^{\prime }\cdot {{\mathbf {y}}}}{m_0}.} \end{aligned}$$

(5)

We remark that in the case, of our interest, that $\kappa \gg \mu \sim 1$, the above definition of Jacobi coordinates differs substantially from the usual one, because the barycentric reduction begins with one of the two lighter masses, rather than with the heavier one. A similar observation holds for the $m_0$-centric reduction, which here is not centered on the most massive body, contrarily to the usual convention. We look at the Hamiltonians ${\mathrm{H}}_i$ in (2) and (5). The assumptions mentioned above are:

$(A_1)$:

If $\ell$ is the mean anomaly associated with the Keplerian motions of the term

$$\begin{aligned} \frac{\Vert {\mathbf {y}}\Vert ^2}{2m_0}-\frac{m_0^2}{\Vert {\mathbf {x}}\Vert }=-\frac{m_0^5}{2{\Lambda }^2}, \end{aligned}$$

(6)

we replace the Hamiltonians (2) and (5) with their respective $\ell$-averages

$$\begin{aligned} \overline{\mathrm{H}}_i=-\frac{m_0^5}{2{\Lambda }^2}+\gamma {\widehat{{\mathrm{H}}}}_i; \end{aligned}$$

(7)

where $\widehat{\mathrm{H}}_i$ are the $\ell$-averages of the terms inside parentheses in (2), (5).

$(A_2)$:

The coordinates ${{\mathbf {x}}}$, ${{\mathbf {x}}}^{\prime }$ and the impulses ${{\mathbf {y}}}$, ${{\mathbf {y}}}^{\prime }$ are constrained on the plane ${{\mathbb {R}}}^2$;

$(A_3)$:

The total angular momentum ${\mathbf {C}}={{\mathbf {x}}}^{\prime }\times {{\mathbf {y}}}^{\prime }+{{\mathbf {x}}}\times {{\mathbf {y}}}$ of the system vanishes.

As mentioned above, the main assumption is $(A_1)$. It allows us to exploit facts highlighted in Pinzari (2019, 2020), as now we describe.

Since the $\overline{\mathrm{H}}_i$’s in (7) are $\ell$-independent, $\Lambda$ is a first integral; hence, the term $-\frac{m_0^5}{2{\Lambda }^2}$ may be neglected. After a further rescaling of time $t\rightarrow \gamma t$, we are led to look at the Hamiltonians ${\widehat{{\mathrm{H}}}}_i$ in (7), which are given by

$$\begin{aligned} {\widehat{{\mathrm{H}}}}_1&:=\frac{\Vert {{\mathbf {y}}}^{\prime }\Vert ^2}{2 m_0}-\frac{m_0^2{\overline{\beta }}}{\beta +{\overline{\beta }}}{\mathrm{U}} _{\beta }-\frac{m_0^2\beta }{\beta +{\overline{\beta }}}{\mathrm{U}} _{-{\overline{\beta }}}\nonumber \\ {\widehat{{\mathrm{H}}}}_2&:=\frac{\Vert {{\mathbf {y}}}^{\prime }\Vert ^2}{2 m_0}-\frac{m_0^2{\overline{\beta }}}{\beta +{\overline{\beta }}}{\mathrm{U}} _{\beta +{\overline{\beta }}}-\frac{m_0^2\beta }{\beta +{\overline{\beta }}}\frac{1}{\Vert {{\mathbf {x}}}^{\prime }\Vert } \end{aligned}$$

(8)

where

$$\begin{aligned} {\mathrm{U}} _{\beta }:=\frac{1}{2\pi }\int _0^{2\pi }\frac{\hbox {d}\ell }{\Vert {{\mathbf {x}}}^{\prime }-\beta {{\mathbf {x}}}(\ell )\Vert } \end{aligned}$$

(9)

is the $\ell$-average of the Newtonian potential. Remark that ${{\mathbf {y}}}(\ell )$ has vanishing $\ell$-average,⁴ so that the last term in (5) does not survive. In the case of the planar problem, after the reduction in rotation invariance, the Hamiltonians ${\widehat{{\mathrm{H}}}}_i$ have two degrees of freedom. We use the following canonical coordinates:

$$\begin{aligned}&{\mathrm{R}}=\frac{{{\mathbf {y}}}^{\prime }\cdot {{\mathbf {x}}}^{\prime }}{\Vert {{\mathbf {y}}}^{\prime }\Vert },\quad \mathrm{r}=\Vert {{\mathbf {x}}}^{\prime }\Vert \\&{\mathrm{G}}=\Vert {{\mathbf {x}}}\times {{\mathbf {y}}}\Vert ,\quad {\mathrm{g}}=\text { anomaly of } {{\mathbf {P}}}\, \text { with respect to a fixed direction } {{\mathbf {a}}} \end{aligned}$$

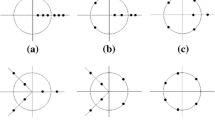
where ${{\mathbf {P}}}$ is the perihelion of (6), and the direction ${{\mathbf {a}}}$, orthogonal to ${{\mathbf {x}}}\times {{\mathbf {y}}}$, will be specified later. Note the coordinates above are fit to describe motions of Keplerian elements for $({{\mathbf {y}}}, {{\mathbf {x}}})$, but not of $({{\mathbf {y}}}^{\prime }, {{\mathbf {x}}}^{\prime })$. If ${{\mathbf {y}}}^{\prime }$ is set to zero, the ${\widehat{{\mathrm{H}}}}_i$’s reduce to sums of averaged Newtonian potentials, which are integrable, as do not depend on ${\mathrm{R}}$. The function ${\mathrm{U}}_\beta |_{\beta =1}$ has been thoroughly studied in Pinzari (2019). Its phase portrait in the plane $({\mathrm{g}}, {\mathrm{G}})$, while the ratio $\varepsilon =a/{\mathrm{r}}$ (where $a={\Lambda }^2/m_0^3$ is the semimajor axis associated with (6)) varies, is as follows.

• (i) Case $0<\varepsilon <\frac{1}{2}$. There exist two centers, (0, 0) and $(0, \pi )$, surrounded by librational motions (Fig. 1).

• (ii) Case $\frac{1}{2}<\varepsilon <1$. The equilibrium (0, 0) becomes a saddle, with its own separatrix (the light blue curve), while $(0, \pi )$ is still stable. Two more equilibria appear on the ${\mathrm{G}}$-axis (Fig. 2).

• (iii) Case $\varepsilon >1$. The equilibria on the $\mathrm{G}$-axis and the saddle persist. There is the birth of rotational motions (Fig. 3).

The purpose of this paper is to prove that motions of the kind (i) do persist in ${\widehat{{\mathrm{H}}}}_i$, when ${{\mathbf {y}}}^{\prime }\ne 0$. Note that we shall not require $\Vert {{\mathbf {y}}}^{\prime }\Vert$ small.

To state the result, we introduce the following quantities, which will be used as mass parameters, at the place of $\mu$ and $\kappa$:

$$\begin{aligned} \beta _*:=\left\{ \begin{array}{ll} \displaystyle \frac{\beta {\overline{\beta }}}{\beta +{\overline{\beta }}}&{}\quad {\mathrm{if}}\quad i=1\\ \\ \displaystyle {\overline{\beta }}&{}\quad {\mathrm{if}}\quad i=2 \end{array}\right. \quad \beta ^*:=\left\{ \begin{array}{ll}\displaystyle \max \{\beta , {\overline{\beta }}\}&{}\quad {\mathrm{if}}\quad i=1\\ \displaystyle \beta +{\overline{\beta }}&{}\quad {\mathrm{if}}\quad i=2 \end{array}\right. \end{aligned}$$

(10)

where $\beta$ and ${\overline{\beta }}$ are as in (3), (4), respectively. Observe that $\beta _*< \beta ^*$ and the case, of our interest, $\kappa \gg \mu \sim 1$ corresponds to $\beta _*\sim \beta ^*/2\gg 1$.

We shall prove the following result.

Theorem 1.1

(Perihelion librations about (0, 0)) Fix an arbitrary neighborhood ${\mathrm{U}}_0$ of (0, 0) and an arbitrary neighborhood ${\mathrm{V}}_0$ of an unperturbed curve $\gamma _0(t)=({\mathrm{G}}_0(t), {\mathrm{g}}_0(t))\in {\mathrm{U}}_0$ in Fig. 1. Then, it is possible to find six numbers $0<c<1$, $0<\beta _-<\beta _+$, $0<\alpha _-<\alpha _+$$T>0$, such that, for any $\beta _-<\beta _*\le \beta ^*<\beta _+$ the projections $\Gamma _0(t)=({\mathrm{G}}(t), {\mathrm{g}}(t))$ of all the orbits $\Gamma (t)=({\mathrm{R}}(t), {\mathrm{G}}(t), {\mathrm{r}}(t), {\mathrm{g}}(t))$ of $\overline{\mathrm{H}}_1$, $\overline{\mathrm{H}}_2$ with initial datum $(\mathrm{R}_0, {\mathrm{r}}_0, {\mathrm{G}}_0, {\mathrm{g}}_0)\in [\frac{1}{\sqrt{c\alpha _+}}, \frac{1}{\sqrt{c\alpha _-}}]\times [c\alpha _-, \alpha _+]\times {\mathrm{U}}_0$ belong to ${\mathrm{V}}_0$ for all $0\le t\le T$. Moreover, the angle $\gamma (t)$ between the position ray of $\Gamma _0(t)$ and the ${\mathrm{g}}$-axis affords a variation larger than $2\pi$ during the time T.

Fig. 1

Case $0<\varepsilon <\frac{1}{2}$

A similar statement concerning perihelion librations about $(0,\pi )$ holds true. The statement of Theorem 1.1 deserves two remarks. The former regards the motions involved, which are quasi-rectilinear, hence, close to be collisional. Generally speaking, for a three-body system composed of two asteroids and one planet, three kinds of collisions are possible: (1) collisions between the two asteroids; (2) collision between one of the asteroids and the planet; and (3) triple collision. The system under investigation is, as stressed above, an averaged problem derived from the full above problem. For this, averaged problem collisions of kind (1) or (3) do not exist, as the position of the asteroids is treated only in averaged meaning. Collisions of the kind (2) may exist, but they are to be intended as collisions between the planet and the average ellipse, rather than with a single particle on this ellipse. They are prevented by the assumption that the orbit of the planet is sufficiently far from the orbit of the asteroids, namely, with a careful choice of the domain of the coordinates. Under this assumption, the averaged Hamiltonians ${\widehat{{\mathrm{H}}}}_i$ keep finite. Incidentally, their regularity is studied in Proposition 3.3. During the proof of Theorem 1.1, in Sect. A, the trajectory of the massive planet is controlled to keep outside the trajectory of the asteroid for all the time of a perihelion libration.

Fig. 2

Case $\frac{1}{2}<\varepsilon <1$

Fig. 3

Case $\varepsilon >1$

The second remark concerns the thesis of Theorem 1.1. It holds in an open subset of phase space. In a sense, it recalls the statement of Nekhoroshev’s theorem (Nehorošev 1977). However, differently from it, Theorem 1.1 is not an application of perturbation theory, nor it uses trapping arguments. The reason is the following. In Sect. 4, we shall see that the manifolds

$$\begin{aligned} {{\mathcal {M}}}_0:=\{({\mathrm{R}}, {\mathrm{G}}, {\mathrm{r}}, {\mathrm{g}}):\ (\mathrm{G}, {\mathrm{g}})=(0, 0)\},\quad {{\mathcal {M}}}_\pi :=\{({\mathrm{R}}, \mathrm{G}, {\mathrm{r}}, {\mathrm{g}}):\ ({\mathrm{G}}, {\mathrm{g}})=(0, \pi )\}\nonumber \\ \end{aligned}$$

(11)

are in fact invariant for ${\widehat{{\mathrm{H}}}}_i$. On such invariant manifold, by $A_3$, we have

$$\begin{aligned} \Vert {{\mathbf {x}}}^{\prime }\times {{\mathbf {y}}}^{\prime }\Vert =\Vert -{{\mathbf {x}}}\times {{\mathbf {y}}}\Vert ={\mathrm{G}}, \end{aligned}$$

(12)

so

$$\begin{aligned} \left. \Vert {{\mathbf {y}}}^{\prime }\Vert ^2\right| _{{{\mathcal {M}}}_0, {{\mathcal {M}}}_\pi }=\left. {\mathrm{R}}^2+\frac{{\mathrm{G}}^2}{\mathrm{r}^2}\right| _{{{\mathcal {M}}}_0, {{\mathcal {M}}}_\pi }= {\mathrm{R}}^2. \end{aligned}$$

Moreover, the functions ${\mathrm{U}}_\beta$, $\mathrm{U}_{-{\overline{\beta }}}$, ${\mathrm{U}}_{\beta +{\overline{\beta }}}$ in (8) are asymptotic (as $\varepsilon \rightarrow 0$) to $\frac{1}{{\mathrm{r}}}$. Hence, the motion of the coordinates $({\mathrm{R}}, {\mathrm{r}})$ on ${{\mathcal {M}}}_0$ and ${{\mathcal {M}}}_\pi$ is ruled by an Hamiltonian asymptotic to

$$\begin{aligned} \frac{{\mathrm{R}}^2}{2m_0}-\frac{m_0^2}{{\mathrm{r}}}. \end{aligned}$$

This Hamiltonian generates unbounded (hence, non-quasiperiodic) motions, for both positive and negative energies: For positive energies, both ${\mathrm{R}}$ and ${\mathrm{r}}$ are unbounded; for negative energies, only ${\mathrm{R}}$ is so. In any case, these motions are not quasiperiodic and hence we cannot apply the machinery of perturbation theory. In Sect. , we develop a theory suited to the case (see Fortunati and Wiggins 2016 for a result of the same kind). In this theory, no small denominators will arise, which is the reason why no trapping argument is needed.

Before switching to full statements and proofs, we quote three open questions arising from the present setting.

$({\mathrm{Q}}_1)$:

Let us consider the cases $\frac{1}{2}<\varepsilon <1$ or $\varepsilon >1$ (Figs. 2, 3, respectively). Does the separatrix split so as to produce chaotic dynamics in the partially averaged planar problem?

$({\mathrm{Q}}_2)$:

Again in the cases above, let us consider the full three-body problem. It has three degrees of freedom. Does the separatrix split so as to produce Arnold instability (Arnol’d 1964; Delshams et al. 2019)?

$({\mathrm{Q}}_3)$:

What is the scenario in the case of the spatial problem?

This paper is organized as follows. In Sect. 2, we provide a review of the main results of Pinzari (2019, 2020). In particular, we recall the mathematical formulation of the mentioned renormalizable integrability and we carry from Pinzari (2020) a set of action-angle like coordinates suited to our needs. In Sect. , we refine the analysis of Pinzari (2019) to the case of the planar secular problem, in the region of phase space where $0<\varepsilon <\frac{1}{2}$. In this case, we are able to obtain simpler formulae compared to Pinzari (2019) and hence to study the regularity region of ${\widehat{{\mathrm{H}}}}_i$ completely. In Sect. 4, we state a normal form theory without small divisors (Theorem 4.1), suited for aperiodic systems. The proof of Theorem 4.1 is deferred to Appendix A. In Sect. 5, we provide the proof of Theorem 1.1, as well as of a more precise version of it (Theorem 5.1), as an application of Theorem 4.1.

2 Review of the Results of Pinzari (2019, 2020)

2.1 ${{\mathcal {K}}}$ Coordinates

We describe canonical coordinates suited to our problem.

We fix an arbitrary orthonormal frame

$$\begin{aligned} {\mathrm{F}}_0:\quad {{\mathbf {i}}}=\left( \begin{array}{lll} 1\\ 0\\ 0 \end{array} \right) ,\quad {{\mathbf {j}}}=\left( \begin{array}{lll} 0\\ 1\\ 0 \end{array} \right) ,\quad {{\mathbf {k}}}=\left( \begin{array}{lll} 0\\ 0\\ 1 \end{array} \right) \end{aligned}$$

in ${{\mathbb {R}}}^3$, that we call inertial frame.

For given $m_0>0$, fix a region of phase space (i.e., a set of values of $({{\mathbf {y}}}^{\prime }, {{\mathbf {y}}},{{\mathbf {x}}}^{\prime }, {{\mathbf {x}}})$) where the Kepler Hamiltonian (6) takes negative values. Consider the motion generated by (6) with initial datum $({{\mathbf {y}}}, {{\mathbf {x}}})$, and denote:

• a the semimajor axis;

• ${{\mathbf {P}}}$, with $\Vert {{\mathbf {P}}}\Vert =1$, the direction of perihelion, assuming the ellipse is not a circle;

• $\ell$: the mean anomaly, defined, mod $2\pi$, as the area of the elliptic sector spanned by ${{\mathbf {x}}}$ from ${{\mathbf {P}}}$, normalized to $2\pi$.

Denote also:

$$\begin{aligned} {{\mathbf {M}}}={{\mathbf {x}}}\times {{\mathbf {y}}},\quad {{\mathbf {M}}}^{\prime }={{\mathbf {x}}}^{\prime }\times {{\mathbf {y}}}^{\prime },\quad {{\mathbf {C}}}={{\mathbf {M}}}^{\prime }+{{\mathbf {M}}}, \end{aligned}$$

where “$\times$” denotes skew-product in ${{{\mathbb {R}}}}^3$. Observe the following relations:

$$\begin{aligned} {{{\mathbf {x}}}^{\prime }}\cdot {{{\mathbf {C}}}}={{{\mathbf {x}}}^{\prime }}\cdot {\big ({{\mathbf {M}}}+{{\mathbf {M}}}^{\prime }\big )}={{{\mathbf {x}}}^{\prime }}\cdot {{{\mathbf {M}}}}\ ,\quad {{\mathbf {P}}}\cdot {{\mathbf {M}}}=0. \end{aligned}$$

(13)

Let

$$\begin{aligned} {{\mathbf {i}}}_1:={{\mathbf {k}}}\times {{\mathbf {C}}},\quad {{\mathbf {i}}}_2:={{\mathbf {C}}}\times {{\mathbf {x}}}^{\prime },\quad {{\mathbf {i}}}_3:={{\mathbf {x}}}^{\prime }\times {{\mathbf {M}}},\quad {{\mathbf {i}}}_4:={{\mathbf {M}}}\times {{\mathbf {P}}} \end{aligned}$$

(14)

and assume

$$\begin{aligned} {{\mathbf {i}}}_{j}\ne 0\quad j=1, 2, 3, 4. \end{aligned}$$

Given three vectors ${{\mathbf {i}}}$, ${{\mathbf {i}}}^{\prime }$ and ${{\mathbf {k}}}$, with ${{\mathbf {i}}}$, ${{\mathbf {i}}}^{\prime }\perp {{\mathbf {k}}}$, we denote as $\alpha _{{\mathbf {k}}}({{\mathbf {i}}}, {{\mathbf {i}}}^{\prime })$ the oriented angle from ${{\mathbf {i}}}$ to ${{\mathbf {i}}}^{\prime }$ relatively to the positive orientation established by ${{\mathbf {k}}}$.

We define the coordinates

$$\begin{aligned} {{{\mathcal {K}}}}=(Z, C, R, \Lambda , G, \Theta , z, \gamma , r, \ell , g, \vartheta ) \end{aligned}$$

as

$$\begin{aligned} \left\{ \begin{array}{llll} \displaystyle {\mathrm{Z}}={{\mathbf {C}}}\cdot {\mathrm{k}}\\ \displaystyle {\mathrm{C}}=\Vert {{\mathbf {C}}}\Vert \\ \displaystyle {\mathrm{R}}=\frac{{{\mathbf {y}}}^{\prime }\cdot {{\mathbf {x}}}^{\prime }}{\Vert {{\mathbf {x}}}^{\prime }\Vert }\\ \displaystyle \Lambda =\sqrt{m_0^3 a}\\ \displaystyle {\mathrm{G}}=\Vert {{\mathbf {M}}}\Vert \\ \displaystyle \Theta =\frac{{{\mathbf {M}}}\cdot {{\mathbf {x}}}^{\prime }}{\Vert {{\mathbf {x}}}^{\prime }\Vert }\\ \end{array}\right. \quad \left\{ \begin{array}{llll} \displaystyle {\mathrm{z}}=\alpha _{{\mathrm{k}}}({{\mathbf {i}}}, {{\mathbf {i}}}_1)\\ \displaystyle \gamma =\alpha _{{{\mathbf {C}}}}({{\mathbf {i}}}_1, {{\mathbf {i}}}_2)\\ \displaystyle {\mathrm{r}}=\Vert {{\mathbf {x}}}^{\prime }\Vert \\ \displaystyle \ell ={\mathrm{mean\ anomaly\ of}}\, {{\mathbf {x}}}\, {\mathrm{on}}\, {\mathbb {E}} \\ \displaystyle {\mathrm{g}}=\alpha _{{{\mathbf {M}}}}({{\mathbf {i}}}_3, {{\mathbf {i}}}_4) \\ \displaystyle \vartheta =\alpha _{{{\mathbf {x}}}^{\prime }}({{\mathbf {i}}}_2, {{\mathbf {i}}}_3) \end{array}\right. \end{aligned}$$

(15)

The canonical character of ${{{\mathcal {K}}}}$ has been discussed in Pinzari (2019), based on Pinzari (2013).

Using the formulae in the previous section, we provide the expressions of the following functions:

$$\begin{aligned} \mathrm{U}=\frac{1}{2\pi }\int _{0}^{2\pi }\frac{\hbox {d}\ell }{\Vert {{\mathbf {x}}}_{{\mathcal {K}}}^{\prime }-{{\mathbf {x}}}_{{\mathcal {K}}}\Vert }\ ,\quad {\mathrm{E}}=\Vert {{\mathbf {x}}}_{{\mathcal {K}}}\times {{\mathbf {y}}}_{{\mathcal {K}}}\Vert ^2-m_0^3 {\mathrm{e}}_{{\mathcal {K}}} {{\mathbf {P}}}_{{\mathcal {K}}}\cdot {{\mathbf {x}}}_{{\mathcal {K}}}^{\prime } \end{aligned}$$

(where ${{\mathbf {x}}}_{{\mathcal {K}}}:={{\mathbf {x}}}\circ {{\mathcal {K}}}$, etc.) which will be mentioned in the next section. They are:

$$\begin{aligned} {\mathrm{U}}( \Lambda , {\mathrm{G}}, \Theta , {\mathrm{r}} , \ell , \mathrm{g})= & {} \frac{1}{2\pi }\int _0^{2\pi }\frac{\hbox {d}\ell }{\sqrt{{{\mathrm{r}} }^2+2{\mathrm{r}} a(\Lambda )\sqrt{1-\frac{\Theta ^2}{{\mathrm{G}}^2}} \mathrm{p}(\Lambda , {\mathrm{G}}, \ell , {\mathrm{g}})+{a(\Lambda )}^2\varrho (\Lambda , {\mathrm{G}}, {\mathrm{g}})^2}}\nonumber \\ {\mathrm{E}}(\Lambda , {\mathrm{G}}, \Theta , {\mathrm{r}} , \ell , {\mathrm{g}})= & {} \mathrm{G}^2+m_0^3{\mathrm{r}} \sqrt{1-\frac{\Theta ^2}{\mathrm{G}^2}}\sqrt{1-\frac{{\mathrm{G}}^2}{{\Lambda }^2}}\cos {\mathrm{g}} \end{aligned}$$

(16)

where $a=a(\Lambda )$, the semimajor axis; ${\mathrm{e}}=\mathrm{e}(\Lambda , {\mathrm{G}})$, the eccentricity of the ellipse; $\varrho =\varrho (\Lambda , {\mathrm{G}}, \ell )$; ${\mathrm{p}}={\mathrm{p}}( \Lambda , {\mathrm{G}}, \ell , {\mathrm{g}})$ are defined as

$$\begin{aligned} a(\Lambda )= & {} \frac{{\Lambda }^2}{m_0^3}\nonumber \\ {\mathrm{e}}(\Lambda , {\mathrm{G}}):= & {} \sqrt{1-\frac{\mathrm{G}^2}{{\Lambda }^2}}\nonumber \\ \varrho (\Lambda , {\mathrm{G}}, \ell ):= & {} 1-{\mathrm{e}}(\Lambda , \mathrm{G})\cos \xi ( \Lambda , {\mathrm{G}}, \ell )\nonumber \\ {\mathrm{p}}(\Lambda , {\mathrm{G}}, \ell , {\mathrm{g}}):= & {} (\cos \xi ( \Lambda , \mathrm{G}, \ell )-{\mathrm{e}}(\Lambda , {\mathrm{G}}))\cos {\mathrm{g}}-\frac{\mathrm{G}}{\Lambda }\sin \xi ( \Lambda , {\mathrm{G}}, \ell ), \end{aligned}$$

(17)

with $\xi =\xi (\Lambda , {\mathrm{G}}, \ell )$ the eccentric anomaly, defined as the solution of Kepler equation

$$\begin{aligned} \xi -{\mathrm{e}}(\Lambda , {\mathrm{G}})\sin \xi =\ell . \end{aligned}$$

(18)

These formulae have been discussed in Pinzari (2020).

2.2 Renormalizable Integrability

We recall some results concerning the functions ${\mathrm{U}}$ and $\mathrm{E}$ in (16). We refer to Pinzari (2019) for full details.

Definition 2.1

(Pinzari 2019, Definition 1) Let f, g be two functions of the form

$$\begin{aligned} f(p, q, y, x)={\widehat{f}}({\mathrm{I}}(p,q), y, x),\quad g(p, q, y, x)={\widehat{g}}({\mathrm{I}}(p,q), y, x) \end{aligned}$$

(19)

where

$$\begin{aligned} (p, q, y, x)\in {{\mathcal {D}}}:={{\mathcal {B}}}\times U \end{aligned}$$

(20)

with $U\subset {{\mathbb {R}}}^2$, ${{\mathcal {B}}}\subset {{\mathbb {R}}}^{2n}$ open and connected, $(p,q)=$$(p_1$, $\dots$, $p_n$, $q_1$, $\ldots$, $q_n)$ conjugate coordinates with respect to the two-form ${\omega }=dy\wedge \hbox {d}x+\sum _{i=1}^{n}\hbox {d}p_i\wedge \hbox {d}q_i$ and ${\mathrm{I}}(p,q)=({\mathrm{I}}_1(p,q), \dots , {\mathrm{I}}_n(p,q))$, with

$$\begin{aligned} {\mathrm{I}}_i:\ {{\mathcal {B}}}\rightarrow {{\mathbb {R}}},\quad i=1,\ldots , n \end{aligned}$$

pairwise Poisson commuting:

$$\begin{aligned} \big \{{\mathrm{I}}_i,{\mathrm{I}}_j\big \}=0\quad \forall \ 1\le i<j\le n\quad i=1,\ldots , n. \end{aligned}$$

(21)

We say that f is renormalizably integrable bygvia${\widetilde{f}}$ (or renormalizably integrable byg, or simply renormalizably integrable), if there exists a function

$$\begin{aligned} {\widetilde{f}}:\quad \mathrm{I}({{\mathcal {B}}})\times g(U)\rightarrow {{\mathbb {R}}}, \end{aligned}$$

such that

$$\begin{aligned} f(p,q,y,x)={\widetilde{f}}({\mathrm{I}}(p,q), {\widehat{g}}(\mathrm{I}(p,q),y,x)) \end{aligned}$$

(22)

for all $(p, q, y, x)\in {{\mathcal {D}}}$.

Proposition 2.1

(Pinzari 2019, Proposition 4) If f is renormalizably integrable by g, then:

• (i) ${\mathrm{I}}_1$, $\ldots$, ${\mathrm{I}}_n$ are first integrals to f and g;

• (ii) f and g Poisson commute.

Observe that, if f is renormalizably integrable via g, then, generically, their respective time laws for the coordinates (y, x) are the same, up to rescaling the time. Formally:

Proposition 2.2

(Pinzari 2019, Proposition 5) Let f be renormalizably integrable via g. Fix a value $\mathrm{I}_0$ for the integrals ${\mathrm{I}}$ and look at the motion of (y, x) under f and g, on the manifold ${\mathrm{I}}={\mathrm{I}}_0$. For any fixed initial datum $(y_0, x_0)$, let $g_0:=g({\mathrm{I}}_0, y_0, x_0)$. If ${\omega }({\mathrm{I}}_0, g_0):=\partial _{g}{\tilde{f}}({\mathrm{I}}, g)|_{(\mathrm{I}_0, g_0)}\ne 0$, the motion $(y^f(t), x^f(t))$ with initial datum$(y_0, x_0)$ under f is related to the corresponding motion $(y^g(t), x^g(t))$ under g via

$$\begin{aligned} y^f(t)=y^g({\omega }({\mathrm{I}}_0, g_0) t),\quad x^f(t)=x^g({\omega }({\mathrm{I}}_0, g_0) t). \end{aligned}$$

In particular, under this condition, all the fixed points of g in the plane (y, x) are fixed points to f. Values of $({\mathrm{I}}_0, g_0)$ for which ${\omega }({\mathrm{I}}_0, g_0)= 0$ provide, in the plane (y, x), curves of fixed points for f (which are not necessarily curves of fixed points to g).

We observe that ${\mathrm{U}}$ and ${\mathrm{E}}$ have the form in (19), with ${\mathrm{I}}=({\mathrm{I}}_1, {\mathrm{I}}_2, {\mathrm{I}}_3)=({\mathrm{r}}, \Lambda , \Theta )$ verifying (21) and $(y, x)=({\mathrm{G}}, {\mathrm{g}})$.

Proposition 2.3

(Pinzari 2019, Proposition 6) ${\mathrm{U}}$ is renormalizably integrable via ${\mathrm{E}}$. Namely, there exists a function ${\mathrm{F}}$ such that

$$\begin{aligned} {\mathrm{U}}(\Lambda , {\mathrm{G}}, \Theta , {\mathrm{G}}, {\mathrm{g}}, {\mathrm{r}})=\mathrm{F}\big (\Lambda , \Theta , {\mathrm{r}}, {\mathrm{E}}(\Lambda , {\mathrm{G}}, \Theta , {\mathrm{G}}, {\mathrm{g}}, {\mathrm{r}})\big ). \end{aligned}$$

(23)

The phase portrait of ${\mathrm{E}}$ in the planar case is shown in Figs. 1, 2 and 3, accordingly to the values of $\varepsilon$.

2.3 Asymptotic Action-Angle Coordinates

In this section, we focus on the planar case, i.e., when ${\mathbf {y}}^{\prime }$, ${\mathbf {y}}$, ${\mathbf {x}}^{\prime }$, ${\mathbf {x}}\in {{\mathbb {R}}}^2$. In that case, the following 8-dimensional diffeomorphism replaces ${{\mathcal {K}}}$ in (15):

$$\begin{aligned} {{\mathcal {K}}}_0:\quad \left\{ \begin{array}{llll}\displaystyle {\mathrm{C}}=\Vert {\mathbf {C}}\Vert \\ \displaystyle {\mathrm{G}}=\Vert {\mathbf {M}}\Vert \\ \displaystyle {\mathrm{R}}=\frac{{\mathbf {y}}^{\prime }\cdot {\mathbf {x}}^{\prime }}{\Vert {\mathbf {x}}^{\prime }\Vert }\\ \displaystyle \Lambda ={\mathrm{m}} \sqrt{{{\mathcal {M}}} a} \end{array}\right. \quad \qquad \left\{ \begin{array}{llll}\displaystyle \gamma =\alpha _{{\mathbf {k}}}({\mathbf {i}}, {\mathbf {x}}^{\prime })+\frac{\pi }{2}\\ \displaystyle {\mathrm{g}}=\alpha _{{\mathbf {k}}}({{\mathbf {x}}^{\prime }},{\mathbf {P}})+\pi \\ \displaystyle {\mathrm{r}}=\Vert {\mathbf {x}}^{\prime }\Vert \\ \displaystyle \ell =\mathrm{mean\ anomaly\ of\ {{\mathbf {x}}}\ in\ {\mathbb {E}}} \end{array}\right. \end{aligned}$$

(24)

${{\mathcal {K}}}_0$ may be regarded as the natural limit of ${{\mathcal {K}}}$, once $\Theta$ and $\vartheta$ are fixed to (0, 0), (0, $\pi$) (which are the values they take in the planar case), respectively, and $({\mathrm{Z}}, {\mathrm{z}})$ are neglected. The functions ${\mathrm{U}}$ and ${\mathrm{E}}$ in (16) become

$$\begin{aligned} {\mathrm{U}}(\Lambda , {\mathrm{G}}, {\mathrm{g}}, \mathrm{r}):= & {} \frac{1}{2\pi }\int _0^{2\pi }\frac{\hbox {d}\ell }{\sqrt{{\mathrm{r}}^2+2 a(\Lambda ) {\mathrm{r}}{\mathrm{p}}(\Lambda , {\mathrm{G}},\ell , {\mathrm{g}})+ a(\Lambda )^2\varrho ( \Lambda , {\mathrm{G}}, \ell )^2 }},\nonumber \\ {\mathrm{E}}(\Lambda , {\mathrm{G}}, {\mathrm{g}}, {\mathrm{r}})= & {} {\mathrm{G}}^2+m_0^3\mathrm{r}\,\sqrt{1-\frac{{\mathrm{G}}^2}{{\Lambda }^2}}\cos {\mathrm{g}} \end{aligned}$$

(25)

where $a(\Lambda )$, $\varrho ( \Lambda , {\mathrm{G}}, \ell )$, $\mathrm{p}( \Lambda , {\mathrm{G}}, \ell , {\mathrm{g}})$ are given in (17).

Unfortunately, the action-angle coordinates associated with ${\mathrm{E}}$ are not explicit, since they are defined via inversion of elliptic integrals. However, it is possible to define, explicitly, action-angle coordinates associated with the leading part of $\mathrm{E}$ in the case of large ${\mathrm{r}}$:

$$\begin{aligned} {\mathrm{E}}_1:= m_0^3{\mathrm{r}}\, \sqrt{1-\frac{{\mathrm{G}}^2}{{\Lambda }^2}} \cos {\mathrm{g}}. \end{aligned}$$

As discussed in Pinzari (2020), these coordinates, denoted as⁵$({{\mathcal {G}}}, \gamma )$, are defined via the canonical⁶ change

$$\begin{aligned} \left\{ \begin{array}{llll} \displaystyle {\mathrm{G}}=\sqrt{{\Lambda }^2-{{\mathcal {G}}}^2}\cos \gamma \\ \displaystyle {\mathrm{g}}=-\tan ^{-1}\left( \frac{\Lambda }{{{\mathcal {G}}}} \sqrt{1-\frac{{{\mathcal {G}}}^2}{{\Lambda }^2}}\sin \gamma \right) +k\pi \\ {\mathrm{with}} \quad k=\left\{ \begin{array}{llll}0\ \ {\mathrm{if}} \ 0<{{\mathcal {G}}}<\Lambda \\ 1\ \ {\mathrm{if}}\ -\Lambda<{{\mathcal {G}}}<0 \end{array}\right. \end{array}\right. \end{aligned}$$

(26)

for any fixed value of $\Lambda$. Observe that positive values of ${{\mathcal {G}}}$ (hence, $k=0$) provide coordinates with the image $({\mathrm{G}}, {\mathrm{g}})$ in a neighborhood of (0, 0); negative values ($k=1$) are for $({\mathrm{G}}, {\mathrm{g}})$ in a neighborhood of $(0,\pi )$. Using these “approximate” coordinates, one obtains the expression of ${\mathrm{E}}$ as a close-to-be-integrable system for large $\mathrm{r}$:

$$\begin{aligned} {\mathrm{E}}=m_0^3\mathrm{r}\,\frac{{{\mathcal {G}}}}{\Lambda }+({\Lambda }^2-{{\mathcal {G}}}^2)\cos ^2\gamma \end{aligned}$$

(27)

The coordinates $({{\mathcal {G}}}, \gamma )$ will be used in Sect. 5.

3 A Deeper Look at the Planar Case

In the planar case, the relation (23) becomes very special.

Instead of ${\mathrm{U}}$ and ${\mathrm{E}}$, it is convenient to switch to the functions

$$\begin{aligned}&{\widehat{{\mathrm{U}}}}_{\varepsilon }(\Lambda , {\mathrm{G}}, \mathrm{g}):=\frac{1}{2\pi }\int _0^{2\pi }\frac{\hbox {d}\ell }{\sqrt{1+2 \varepsilon {\mathrm{p}}(\Lambda , {\mathrm{G}},\ell , \mathrm{g})+\varepsilon ^2\varrho ( \Lambda , {\mathrm{G}}, \ell )^2 }}\nonumber \\&{\widehat{{\mathrm{E}}}}_{\varepsilon }(\Lambda , {\mathrm{G}}, {\mathrm{g}}):= \sqrt{1-\frac{{\mathrm{G}}^2}{{\Lambda }^2}}\cos \mathrm{g}+\varepsilon \frac{{\mathrm{G}}^2}{{\Lambda }^2}, \end{aligned}$$

(28)

which are related to the previous ones via

(29)

with

$$\begin{aligned} \varepsilon (\Lambda , {\mathrm{r}}):= \frac{{\Lambda }^2}{m_0^3{\mathrm{r}}}=\frac{a(\Lambda )}{{\mathrm{r}}} \end{aligned}$$

if $a=a(\Lambda )$ is as in (15). We rewrite relation (23) as

$$\begin{aligned} {\widehat{{\mathrm{U}}}}_{\varepsilon (\Lambda , {\mathrm{r}})}(\Lambda , {\mathrm{G}}, {\mathrm{g}})={\widehat{{\mathrm{F}}}}_{\varepsilon (\Lambda , \mathrm{r})}\big ({\widehat{{\mathrm{E}}}}_{\varepsilon (\Lambda , {\mathrm{r}})}(\Lambda , {\mathrm{G}}, {\mathrm{g}})\big ). \end{aligned}$$

(30)

Here, we have used that ${\widehat{{\mathrm{F}}}}_\varepsilon$ does not depend explicitly on $\Lambda$, since both ${\mathrm{U}}$ and ${\mathrm{E}}$ depend on $\Lambda$ only via $\frac{{\mathrm{G}}}{\Lambda }$. We claim that

Proposition 3.1

In the planar problem, if $|\varepsilon | < \frac{1}{2}$ and $|\widehat{E}_\varepsilon |\le 1$, (30) holds with

$$\begin{aligned} {\widehat{{\mathrm{F}}}}_{\varepsilon }(t)=\frac{1}{2\pi }\int _0^{2\pi }\frac{(1-\cos \xi ) d\xi }{\sqrt{1-2 \varepsilon (1-\cos \xi ) t+\varepsilon ^2(1-\cos \xi )^2 }}. \end{aligned}$$

(31)

To prove Proposition 3.1, we need to recall the following result from Pinzari (2019).

Proposition 3.2

(Pinzari 2019, Theorem 4 and Remark 3) Let $f({\mathrm{P}}, y, x)$ and $g({\mathrm{P}}, y, x)$ Poisson commute. Assume that, for any fixed ${\mathrm{P}}$, the level sets $\{(y, x):\ g({\mathrm{P}}, y, x)={{\mathcal {G}}}\}$ are union of graphs

$$\begin{aligned} y=g_{1, i}({\mathrm{P}}, x, {{\mathcal {G}}})\quad {\mathrm{or}} \quad x=g_{2, j}({\mathrm{P}}, y, {{\mathcal {G}}}). \end{aligned}$$

Then, f renormalizably integrable by g through ${\widetilde{f}}$, and ${\widetilde{f}}$ can be chosen to be

$$\begin{aligned} {\widetilde{f}}({\mathrm{P}},{{\mathcal {G}}})=f({\mathrm{P}}, y_j, g_{2, j}(y_j, {{\mathcal {G}}}))= f({\mathrm{P}}, g_{1, i}(x_i, {{\mathcal {G}}}), x_i). \end{aligned}$$

(32)

for some fixed $x_i$, $y_j$.

Proof of Proposition 3.1

We apply Proposition 3.2 to the functions ${\widehat{{\mathrm{U}}}}_{\varepsilon (\Lambda , {\mathrm{r}})}(\Lambda , {\mathrm{G}}, {\mathrm{g}})$, ${\widehat{{\mathrm{E}}}}_{\varepsilon (\Lambda , {\mathrm{r}})}(\Lambda , {\mathrm{G}}, {\mathrm{g}})$ in (29). Such two functions do commute since $\mathrm{U}(\Lambda , {\mathrm{G}}, {\mathrm{g}}, {\mathrm{r}})$ and ${\mathrm{E}}(\Lambda , \mathrm{G}, {\mathrm{g}}, {\mathrm{r}})$ do, and they both commute with ${\mathrm{r}}$. Moreover, the level sets $\{(\Lambda , {\mathrm{G}}, {\mathrm{g}}):\ {\widehat{{\mathrm{E}}}}_{\varepsilon (\Lambda , {\mathrm{r}})}(\Lambda , {\mathrm{G}}, {\mathrm{g}})=t\}$ are graphs

$$\begin{aligned} {\mathrm{g}}=\pm \cos ^{-1}\left( \frac{t-\varepsilon (\Lambda , \mathrm{r})\frac{{\mathrm{G}}^2}{{\Lambda }^2}}{\sqrt{1-\frac{\mathrm{G}^2}{{\Lambda }^2}}}\right) +2j\pi =:g^\pm _j({\mathrm{r}}, \Lambda , \mathrm{G}, t),\quad j\in {{\mathbb {Z}}}. \end{aligned}$$

We use the formula in (32) with ${\mathrm{P}}=(\Lambda , {\mathrm{r}})$, $g_{2, j}=g^\pm _j({\mathrm{r}}, \Lambda , {\mathrm{G}}, t)$, $f={\mathrm{U}}$ and $y_j={\mathrm{G}}_j=0$ for all j. When ${\mathrm{G}}=0$, the functions $\mathrm{g}^\pm _j$ take the value

$$\begin{aligned} {\mathrm{g}}^\pm _j|_{{\mathrm{G}}=0}=\pm \cos ^{-1}t+2j\pi \quad \forall \ {r},\ \Lambda \end{aligned}$$

which is well defined as $|t|=|\widehat{E}_ \varepsilon |\le 1$. Then, by (32),

$$\begin{aligned} {\widehat{{\mathrm{F}}}}_{\varepsilon }(t)= & {} {\widehat{{\mathrm{U}}}}_{\varepsilon }( 0, \pm \cos ^{-1}t+2j\pi )\\= & {} \frac{1}{2\pi }\int _0^{2\pi }\frac{(1-\cos \xi ) d\xi }{\sqrt{1-2 \varepsilon (1-\cos \xi ) t+\varepsilon ^2(1-\cos \xi )^2 }}. \end{aligned}$$

$\square$

A first consequence of the formula in (31) is underlined in the following.

Remark 3.1

Equation (31) can also be used to provide an expansion of ${\widehat{{\mathrm{U}}}}_\varepsilon$ about the equilibria (0, 0) and $(0, \pi )$. Indeed, ${\widehat{{\mathrm{E}}}}_{\varepsilon }(\Lambda , {\mathrm{G}}, \mathrm{g})$ takes the value $+1$ at $(\Lambda , {\mathrm{G}}, {\mathrm{g}})=(0, 0)$, and the value $-1$ at $(\Lambda , {\mathrm{G}}, {\mathrm{g}})=(0, \pi )$. Therefore, an expansion of ${\widehat{{\mathrm{F}}}}_{\varepsilon }(t)$ about $\pm 1$ provides, via (30), an expansion ${\widehat{{\mathrm{U}}}}_{\varepsilon }$ about the corresponding equilibrium. On the other hand, the value of ${\widehat{{\mathrm{F}}}}_{\varepsilon }(t)$ and of its derivatives at $t=+ 1$ or $t=- 1$ can be explicitly computed, using the residue theorem. For example, for $0<\varepsilon <\frac{1}{2}$,

$$\begin{aligned} {\widehat{\mathrm{F}}}_{\varepsilon }(1)=\frac{1}{2\pi }\int _0^{2\pi }\frac{(1-\cos \xi )d\xi }{1-\varepsilon (1-\cos \xi )}=\frac{2}{\sqrt{1-2\varepsilon }(1+\sqrt{1-2\varepsilon })}. \end{aligned}$$

(33)

Another consequence of (31) is:

Proposition 3.3

Let $|\varepsilon |<\frac{1}{2}$. The complex function $(\varepsilon , t)\rightarrow {\widehat{{\mathrm{F}}}}_{\varepsilon }(t)$ loses its holomorphy if and only if

$$\begin{aligned} {4\varepsilon ^2-4\varepsilon t+1=0}. \end{aligned}$$

(34)

Proof

We equivalently write

$$\begin{aligned} {\widehat{{\mathrm{F}}}}_{\varepsilon }(t)=\frac{1}{\pi }\int _0^{\pi }\frac{(1-\cos \xi ) d\xi }{\sqrt{1-2 \varepsilon (1-\cos \xi ) t+\varepsilon ^2(1-\cos \xi )^2 }}. \end{aligned}$$

Then, we change variable, letting $x=1-\cos \xi$. The integral becomes

$$\begin{aligned} {\widehat{{\mathrm{F}}}}_{\varepsilon }(t)=\frac{1}{\pi }\int _0^{2}\frac{x\hbox {d}x}{\sqrt{x(2-x)}\sqrt{1-2 \varepsilon x t+\varepsilon ^2x^2 }}. \end{aligned}$$

The only possibility it diverges is that there are two coinciding roots of the denominator on the real interval [0, 2]. The polynomial under the second square root has not coinciding roots on [0, 2] for $|\varepsilon |<\frac{1}{2}$ and never has the root $x=0$. The only possibility is that it has the root $x=2$. This happens when $t=\varepsilon +\frac{1}{4\varepsilon }$. $\square$

Remark 3.2

The formula in (31) (and its consequences below) is pretty specific for the planar case. In Pinzari (2019, Equation 49), we proposed a general formula (holding for the planar and the spatial case), which, unfortunately, does not seem equally exploitable.

4 Set Out and Analytic Tools

For definiteness, we refer to perihelion librations about (0, 0), the case $(0, \pi )$ being specular.

Using the identity in (30), the assumption $A_3$ in the introduction, which gives

$$\begin{aligned} \Vert {{\mathbf {x}}}^{\prime }_{{{\mathcal {K}}}_0}\times {{\mathbf {y}}}^{\prime }_{{{\mathcal {K}}}_0}\Vert =\Vert {{\mathbf {x}}}_{{{\mathcal {K}}}_0}\times {{\mathbf {y}}}_{{{\mathcal {K}}}_0}\Vert ={\mathrm{G}}, \end{aligned}$$

(35)

and the relation

$$\begin{aligned} \Vert {{\mathbf {y}}}^{\prime }_{{{\mathcal {K}}}_0}\Vert ^2= & {} \frac{|{{\mathbf {y}}}^{\prime }_{{{\mathcal {K}}}_0}\cdot {\mathbf {x}}^{\prime }_{{{\mathcal {K}}}_0}|^2}{\Vert {\mathbf {x}}^{\prime }_{{{\mathcal {K}}}_0}\Vert ^2}+\frac{\Vert {{\mathbf {y}}}^{\prime }_{{{\mathcal {K}}}_0}\times {\mathbf {x}}^{\prime }_{{{\mathcal {K}}}_0}\Vert ^2}{\Vert {\mathbf {x}}^{\prime }_{{{\mathcal {K}}}_0}\Vert ^2}=\mathrm{R}^2+\frac{{\mathrm{G}}^2}{{\mathrm{r}}^2}, \end{aligned}$$

(36)

we rewrite the Hamiltonians (8) as

$$\begin{aligned} {\widehat{{\mathrm{H}}}}_1({\mathrm{R}}, {\mathrm{G}}, {\mathrm{r}}, {\mathrm{g}})= & {} \frac{\mathrm{R}^2}{2m_0}+\frac{{\mathrm{G}}^2}{2m_0\mathrm{r}^2}-\frac{{\overline{\beta }}}{\beta +{\overline{\beta }}}\frac{m_0^2}{\mathrm{r}}{\widehat{{\mathrm{F}}}}_{\beta \varepsilon ({\mathrm{r}})}\Big ({\widehat{{\mathrm{E}}}}_{\beta \varepsilon ({\mathrm{r}})}({\mathrm{G}}, {\mathrm{g}})\Big )\nonumber \\&-\frac{\beta }{\beta +{\overline{\beta }}}\frac{m_0^2}{\mathrm{r}}{\widehat{{\mathrm{F}}}}_{-{\overline{\beta }}\varepsilon (\mathrm{r})}\Big ({\widehat{{\mathrm{E}}}}_{-{\overline{\beta }}\varepsilon (\mathrm{r})}({\mathrm{G}}, {\mathrm{g}})\Big )\nonumber \\ {\widehat{{\mathrm{H}}}}_2({\mathrm{R}}, {\mathrm{G}}, {\mathrm{r}}, {\mathrm{g}})= & {} \frac{\mathrm{R}^2}{2m_0}+\frac{{\mathrm{G}}^2}{2m_0\mathrm{r}^2}-\frac{{\overline{\beta }}}{\beta +{\overline{\beta }}}\frac{m_0^2}{\mathrm{r}}{\widehat{{\mathrm{F}}}}_{(\beta +{\overline{\beta }})\varepsilon (\mathrm{r})}\Big ({\widehat{{\mathrm{E}}}}_{(\beta +{\overline{\beta }})\varepsilon (\mathrm{r})}({\mathrm{G}}, {\mathrm{g}})\Big )\nonumber \\&-\frac{\beta }{\beta +{\overline{\beta }}}\frac{m_0^2}{{\mathrm{r}}} \end{aligned}$$

(37)

having neglected to write (as well as we shall do below) the dependence on $\Lambda$.

We suddenly remark that ${\widehat{{\mathrm{H}}}}_1$ and ${\widehat{{\mathrm{H}}}}_2$ are both even with respect to ${\mathrm{G}}$ and ${\mathrm{g}}$ separately, because so are the functions ${\widehat{{\mathrm{E}}}}_\varepsilon ({\mathrm{G}}, {\mathrm{g}})$ and the⁷ term $\frac{{\mathrm{G}}^2}{2m_0\mathrm{r}^2}$. Then, the manifolds

$$\begin{aligned} {{\mathcal {M}}}_0:=\{({\mathrm{R}}, {\mathrm{G}}, {\mathrm{r}}, \mathrm{g}):\ ({\mathrm{G}}, {\mathrm{g}})=(0, 0)\},\quad {{\mathcal {M}}}_\pi :=\{({\mathrm{R}}, {\mathrm{G}}, {\mathrm{r}}, {\mathrm{g}}):\ (\mathrm{G}, {\mathrm{g}})=(0, \pi )\}\nonumber \\ \end{aligned}$$

(38)

which, by the discussions of Sect. 2, are invariant for ${\widehat{{\mathrm{E}}}}_\varepsilon ({\mathrm{G}}, {\mathrm{g}})$, keep to be so also for ${\widehat{{\mathrm{H}}}}_i$. We focus on ${{\mathcal {M}}}_0$. On ${{\mathcal {M}}}_0$, the motions of the coordinates $({\mathrm{R}}, \mathrm{r})$ are governed by the Hamiltonians

$$\begin{aligned} {\mathrm{h}}_i({\mathrm{R}}, {\mathrm{r}})=\frac{{\mathrm{R}}^2}{2m_0}+{\mathrm{V}}_i(\mathrm{r}) \end{aligned}$$

(39)

where (using (33) and dehomogenizating)

$$\begin{aligned} {\mathrm{V}}_1({\mathrm{r}})= & {} -\frac{{\overline{\beta }}}{\beta +{\overline{\beta }}}\frac{2m_0^2}{\sqrt{\mathrm{r}-2\beta a}\left( \sqrt{\mathrm{r}}+\sqrt{{\mathrm{r}}-2\beta a}\right) }-\frac{\beta }{\beta +{\overline{\beta }}}\frac{2 m_0^2}{\sqrt{{\mathrm{r}}+2{\overline{\beta }} a}\left( \sqrt{\mathrm{r}}+\sqrt{{\mathrm{r}}+2{\overline{\beta }} a}\right) } \nonumber \\ {\mathrm{V}}_2({\mathrm{r}})= & {} -\frac{{\overline{\beta }}}{\beta +{\overline{\beta }}}\frac{2m_0^2}{\sqrt{\mathrm{r}-2(\beta +{\overline{\beta }})a}\left( \sqrt{\mathrm{r}}+\sqrt{\mathrm{r}-2(\beta +{\overline{\beta }})a}\right) }-\frac{\beta }{\beta +{\overline{\beta }}}\frac{ m_0^2}{{\mathrm{r}}}. \end{aligned}$$

(40)

The “potentials” ${\mathrm{V}}_1$ and ${\mathrm{V}}_2$ are well defined and increasing from $-\infty$ to 0 for ${\mathrm{r}}>2\beta a$, $r>2(\beta +\overline{\beta })a$, respectively, so action-angle coordinates do not exist. In other words, closely to ${{\mathcal {M}}}_0$, ${\widehat{{\mathrm{H}}}}_i$ has not close to an integrable system in the sense of Liouville–Arnold (Arnold (1963a)) and hence standard perturbation theory does not apply. In the next section, we develop an analytic theory suited to this case. It will be used to “decouple” the Hamiltonians.

4.1 A Normal Form Theory Without Quasiperiodic Unperturbed Motions

In this section, we describe a procedure for eliminating the angles⁸${\varvec{\varphi }}$ at high orders, given Hamiltonian of the form

$$\begin{aligned} {\mathrm{H}}({{\mathbf {I}}}, {\varvec{\varphi }}, {{\mathbf {p}}}, {{\mathbf {q}}}, y, x)={\mathrm{h}}({{\mathbf {I}}},{{\mathbf {J}}}({{\mathbf {p}}}, {{\mathbf {q}}}), y)+f({{\mathbf {I}}}, {\varvec{\varphi }}, {{\mathbf {p}}}, {{\mathbf {q}}}, y, x) \end{aligned}$$

(41)

which we assume to be holomorphic on the neighborhood

$$\begin{aligned} {{\mathbb {P}}}_{\rho , s, \delta , r, \xi }={{\mathbb {I}}}_\rho \times {{{\mathbb {T}}}}^n_s\times {{\mathbb {B}}}_{\delta }\times {{\mathbb {Y}}}_r\times {{\mathbb {X}}}_\xi \supset {{\mathbb {P}}}={{\mathbb {I}}} \times {{{\mathbb {T}}}}^n\times {{\mathbb {B}}}\times {{\mathbb {Y}}}\times {{\mathbb {X}}}, \end{aligned}$$

and

$$\begin{aligned} {{\mathbf {J}}}({{\mathbf {p}}}, {{\mathbf {q}}})=(p_1q_1,\dots , p_mq_m). \end{aligned}$$

Here, ${{\mathbb {I}}}\subset {{\mathbb {R}}}^n$, ${{\mathbb {B}}}\subset {{\mathbb {R}}}^{2m}$, ${{\mathbb {Y}}}\subset {{\mathbb {R}}}$, ${{\mathbb {X}}}\subset {{\mathbb {R}}}$ are open and connected; ${\mathbb {T}}={\mathbb {R}}/(2\pi {\mathbb {Z}})$ is the standard torus.

We denote as ${{\mathcal {O}}}_{\rho , s, \delta , r, \xi }$ the set of complex holomorphic functions

$$\begin{aligned} \phi :\quad {{\mathbb {P}}}_{{\hat{\rho }}, {\hat{s}}, {\hat{\delta }}, {\hat{r}}, {\hat{\xi }}}\rightarrow {{{\mathbb {C}}}} \end{aligned}$$

for some ${\hat{\rho }}>\rho$, ${\hat{s}}>s$, ${\hat{\delta }}>\delta$, ${\hat{r}}>r$, ${\hat{\xi }}>\xi$, equipped with the norm

$$\begin{aligned} \Vert \phi \Vert _{\rho , s, \delta , r, \xi }:=\sum _{k,h,j}\Vert \phi _{khj}\Vert _{\rho , r,\xi }e^{s|k|}\delta ^{h+j} \end{aligned}$$

where $\phi _{khj}({{\mathbf {I}}}, y, x)$ are the coefficients of the Taylor–Fourier expansion⁹

$$\begin{aligned} \phi =\sum _{k,h,j}\phi _{khj}({{\mathbf {I}}},y, x)e^{{\mathrm{i}} k s}{{\mathbf {p}}}^h {{\mathbf {q}}}^j,\quad \Vert \phi \Vert _{\rho , r,\xi }:=\sup _{{{\mathbb {I}}}_\rho \times {{\mathbb {Y}}}_r\times {{\mathbb {X}}}_\xi }|\phi ({{\mathbf {I}}}, y, x)|. \end{aligned}$$

If $\phi$ is independent of x, we simply write $\Vert \phi \Vert _{\rho , r}$ for $\Vert \phi \Vert _{\rho , r,\xi }$.

If $\phi \in {{\mathcal {O}}}_{\rho , s, \delta , r, \xi }$, we define its “off-average” ${\widetilde{\phi }}$ and “average” ${\overline{\phi }}$ as

$$\begin{aligned}&{\widetilde{\phi }}:=\sum _{\begin{array}{c} k,h,j:\\ (k,h-j)\ne (0,0) \end{array}}\phi _{khj}({{\mathbf {I}}}, y, x)e^{{\mathrm{i}} k s}{{\mathbf {p}}}^h {{\mathbf {q}}}^j\\&{\overline{\phi }}:=\phi -{\widetilde{\phi }}=\frac{1}{2\pi ^2}\int _{[0,2\pi ]^n}\Pi _{{{\mathbf {p}}}{\mathbf {q}}}\phi ({{\mathbf {I}}}, {\varvec{\varphi }}, {{\mathbf {J}}}({{\mathbf {p}}}, {{\mathbf {q}}}), y, x)d{\varvec{\varphi }} , \end{aligned}$$

with

$$\begin{aligned} \Pi _{{{\mathbf {p}}}{\mathbf {q}}}\phi ({{\mathbf {I}}}, {\varvec{\varphi }}, {{\mathbf {J}}}({{\mathbf {p}}}, {{\mathbf {q}}}), y, x):=\sum _{k,h}\phi _{khh}({{\mathbf {I}}}, y, x)e^{{\mathrm{i}} k s}{{\mathbf {p}}}^h {{\mathbf {q}}}^h. \end{aligned}$$

We decompose

$$\begin{aligned} {{\mathcal {O}}}_{\rho , s, \delta , r, \xi }={{\mathcal {Z}}}_{\rho , s, \delta , r, \xi }\oplus {{\mathcal {N}}}_{\rho , s, \delta , r, \xi }\ , \end{aligned}$$

where ${{\mathcal {Z}}}_{\rho , s, \delta , r, \xi }$, ${{\mathcal {N}}}_{\rho , s, \delta , r, \xi }$ are the “zero-average” and the “normal” classes

$$\begin{aligned}&{{\mathcal {Z}}}_{\rho , s, \delta , r, \xi }:=\{\phi \in {{\mathcal {O}}}_{\rho , s, \delta , r, \xi }:\quad \phi ={\widetilde{\phi }}\}=\{\phi \in {{\mathcal {O}}}_{\rho , s, \delta , r, \xi }:\quad {\overline{\phi }}=0\} \end{aligned}$$

(42)

$$\begin{aligned}&{{\mathcal {N}}}_{\rho , s, \delta , r, \xi }:=\{\phi \in {{\mathcal {O}}}_{\rho , s, \delta , r, \xi }:\quad \phi ={\overline{\phi }}\}=\{\phi \in {{\mathcal {O}}}_{\rho , s, \delta , r, \xi }:\quad {\widetilde{\phi }}=0\}, \end{aligned}$$

(43)

respectively. We finally let $\omega _{y,{{\mathbf {I}}},{{\mathbf {J}}}}:=\partial _{y,{{\mathbf {I}}},{{\mathbf {J}}}} {\mathrm{h}}$.

We shall prove the following result. Its peculiarity is that it does not need any non-resonance condition on the frequencies $\omega _{{\mathbf {I}}}$, which, as a matter of fact, might also be zero.

Theorem 4.1

For any n, m, there exists a number ${\mathrm{c}}_{n,m}\ge 1$ such that, for any $N\in {{\mathbb {N}}}$ such that, the following inequalities are satisfied:

$$\begin{aligned} 4N{{\mathcal {X}}}\left\| \mathfrak {I}\frac{\omega _{{\mathbf {I}}}}{\omega _y}\right\| _{\rho , r}< s ,\quad 4N{{\mathcal {X}}}\left\| \frac{\omega _{{\mathbf {J}}}}{\omega _y}\right\| _{\rho , r}< 1,\quad {{\widetilde{{\mathrm{c}}}}_{n,m}N\frac{{{\mathcal {X}}}}{\mathrm{d}} \left\| {f}\right\| _{\rho , s, \delta , r, \xi }\left\| \frac{1}{\omega _y}\right\| _{\rho , s, \delta , r, \xi } <1}\nonumber \\ \end{aligned}$$

(44)

with ${\mathrm{d}}:=\min \big \{\rho s, r\xi , {\delta }^2\big \}$, ${{\mathcal {X}}}:=\sup \big \{|x|:\ x\in {{\mathbb {X}}}_\xi \big \}$, one can find an operator

$$\begin{aligned} \Psi _*:\quad {{\mathcal {O}}}_{\rho , s, \delta , r, \xi }\rightarrow {{\mathcal {O}}}_{1/3 (\rho , s, \delta , r, \xi )} \end{aligned}$$

(45)

which carries ${\mathrm{H}}$ to

$$\begin{aligned} {\mathrm{H}}_*={\mathrm{h}}+g_*+f_* \end{aligned}$$

where $g_*\in {{\mathcal {N}}}_{1/3 (\rho , s, \delta , r, \xi )}$, $f_*\in {{\mathcal {O}}}_{1/3 (\rho , s, \delta , r, \xi )}$ and, moreover, the following inequalities hold:

$$\begin{aligned}&\Vert g_*-{\overline{f}}\Vert _{1/3 (\rho , s, \delta , r, \xi )}\le 162{\widetilde{{\mathrm{c}}}}_{n, m} \frac{{{\mathcal {X}}}}{\mathrm{d}}\left\| {\frac{{\widetilde{f}}}{\omega _y}}\right\| _{\rho , s, \delta , r, \xi }\Vert f\Vert _{\rho , s, \delta , r, \xi }\nonumber \\&\quad \Vert f_*\Vert _{1/3 (\rho , s, \delta , r, \xi )}\le \frac{1}{2^{N+1}} \Vert f\Vert _{\rho , s, \delta , r, \xi }. \end{aligned}$$

(46)

The transformation $\Psi _*$ can be obtained as a composition of time-one Hamiltonian flows and satisfies the following. If

$$\begin{aligned} ({{\mathbf {I}}}, {\varvec{\varphi }}, {{\mathbf {p}}}, {{\mathbf {q}}}, y, x):=\Psi _*({{\mathbf {I}}}_*, {\varvec{\varphi }}_*, {{\mathbf {p}}}_*, {{\mathbf {q}}}_*, {\mathrm{R}}_*, {\mathrm{r}}_*), \end{aligned}$$

the following uniform bounds hold:

$$\begin{aligned}&{\mathrm{d}}\max \Big \{\frac{|{{\mathbf {I}}}-{{\mathbf {I}}}_*|}{\rho },\ \frac{|{\varvec{\varphi }} -{\varvec{\varphi }} _*|}{s},\ \frac{|{{\mathbf {p}}}-{{\mathbf {p}}}_*|}{\delta },\ \frac{ |{{\mathbf {q}}}-{{\mathbf {q}}}_*|}{\delta },\ \frac{|y-y_*|}{r},\frac{ |x-x_*|}{\xi } \Big \}\nonumber \\&\quad \le \max \Big \{s|{{\mathbf {I}}}-{{\mathbf {I}}}_*|,\ \rho |{\varvec{\varphi }} -{\varvec{\varphi }} _*|,\ \delta |{{\mathbf {p}}}-{{\mathbf {p}}}_*|,\ \delta |{{\mathbf {q}}}-{{\mathbf {q}}}_*|,\ \xi |y-y_*|,\ r |x-x_*| \Big \}\nonumber \\&\quad \le {{19\, {{\mathcal {X}}} \left\| \frac{ f}{\omega _y}\right\| _{\rho , s, \delta , r, \xi } }} . \end{aligned}$$

(47)

Remark 4.1

(Extensions)

• (i) There is an obvious extension to the case that ${{\mathbb {I}}}_\rho$, ${{\mathbb {T}}}^n_s$ are replaced with $({{\mathbb {I}}}_1)_{\rho _1}\times \cdots \times ({{\mathbb {I}}}_n)_{\rho _n}$, ${{\mathbb {T}}}_{s_1}\times \cdots \times {{\mathbb {T}}}_{s_n}$. In this case, the number s in the former equation in (44) is to be replaced with $\min _i\{s_i\}$. Moreover, the product $\rho \, s$ in the definition of ${\mathrm{d}}$ is to be replaced with $\min _i\{\rho _i\,s_i\}$. Finally, the bound in (47) is to be changed taking into account the different sizes.

• (ii) If f does not depend on some angle $\varphi _1$, $\dots$, $\varphi _p$, the vector $\omega _{{\mathbf {I}}}$ in (44) is to be replaced with ${\widehat{\omega }}_{{\mathbf {I}}}:=(\omega _{{{\mathbf {I}}}_{p+1}},\dots , \omega _{{{\mathbf {I}}}_{n}})$.

4.2 Outline of the Proof

The complete proof of Theorem 4.1 is provided in Appendix A, but here we aim to spend some word, so as to highlight the main ideas.

We proceed by recursion. We assume that, at a certain step, we have a system of the form

$$\begin{aligned} {\mathrm{H}}({{\mathbf {I}}}, {\varvec{\varphi }}, {{\mathbf {J}}}({{\mathbf {p}}}, {{\mathbf {q}}}), y)={\mathrm{h}}({{\mathbf {I}}}, {{\mathbf {J}}}({{\mathbf {p}}}, {{\mathbf {q}}}), y)+g({{\mathbf {I}}}, {{\mathbf {J}}}({{\mathbf {p}}}, {{\mathbf {q}}}), y, x)+f({{\mathbf {I}}}, {\varvec{\varphi }}, {{\mathbf {J}}}({{\mathbf {p}}}, {{\mathbf {q}}}), y, x)\nonumber \\ \end{aligned}$$

(48)

where $f\in {{\mathcal {O}}}_{\rho , s, \delta , r, \xi }$, $g\in {{\mathcal {N}}}_{\rho , s, \delta , r, \xi }$. At the first step, just take $g\equiv 0$.

After splitting f on its Taylor–Fourier basis

$$\begin{aligned} f=\sum _{k,h,j} f_{khj}({{\mathbf {I}}},y, x)e^{{\mathrm{i}} k \cdot {\varvec{\varphi }}}{{\mathbf {p}}}^h {{\mathbf {q}}}^j, \end{aligned}$$

one looks for a time-one map

$$\begin{aligned} \Phi =e^{{{\mathcal {L}}}_\phi }=\sum _{k=0}^{\infty }\frac{{{\mathcal {L}}}_\phi ^k}{k!}\quad {{\mathcal {L}}}_\phi (f):=\big \{\phi ,\ f\big \} \end{aligned}$$

generated by a small Hamiltonian $\phi$ which will be taken in the class ${{\mathcal {Z}}}_{\rho , s, \delta , r, \xi }$ in (42). Here,

$$\begin{aligned} \big \{\phi ,\ f\big \}:= & {} \sum _{i=1}^n(\partial _{{{\mathbf {I}}}_i}\phi \partial _{{\varvec{\varphi }}_i}f-\partial _{{{\mathbf {I}}}_i}f\partial _{{\varvec{\varphi }}_i}\phi )\\&+\sum _{i=1}^m(\partial _{{{\mathbf {p}}}_i}\phi \partial _{{\mathbf {q}}_i}f-\partial _{{{\mathbf {p}}}_i}f\partial _{{\mathbf {q}}_i}\phi )+(\partial _{y}\phi \partial _{x}f-\partial _{y}f\partial _{x}\phi ) \end{aligned}$$

denotes the Poisson parentheses of $\phi$ and f. One lets

$$\begin{aligned} \phi =\sum _{\begin{array}{c} (k,h,j):\\ {(k,h-j)\ne (0,0)} \end{array}} \phi _{khj}({{\mathbf {I}}},y, x)e^{{\mathrm{i}} k\cdot {\varvec{\varphi }}}{{\mathbf {p}}}^h {{\mathbf {q}}}^j. \end{aligned}$$

(49)

The operation

$$\begin{aligned} \phi \rightarrow \{\phi ,{\mathrm{h}}\} \end{aligned}$$

acts diagonally on the monomials in the expansion (49), carrying

$$\begin{aligned} \phi _{khj}\rightarrow -\big (\omega _y\partial _x \phi _{khj}+\lambda _{khj} \phi _{khj}\big ),\quad {\mathrm{with}}\quad \lambda _{khj}:=(h-j)\cdot \omega _{{\mathbf {J}}}+{\mathrm{i}} k\cdot \omega _{{\mathbf {I}}}. \end{aligned}$$

(50)

Therefore, one defines

$$\begin{aligned} \{\phi ,{\mathrm{h}}\}=:-D_\omega \phi . \end{aligned}$$

The formal application of $\Phi =e^{{{\mathcal {L}}}_\phi }$ yields:

$$\begin{aligned} e^{{{\mathcal {L}}}_\phi } {\mathrm{H}}=e^{{{\mathcal {L}}}_\phi } (\mathrm{h}+g+f)={\mathrm{h}}+g-D_\omega \phi +f+\Phi _2(\mathrm{h})+\Phi _1(g)+\Phi _1(f)\qquad \end{aligned}$$

(51)

where the $\Phi _h$’s are the tails of $e^{{{\mathcal {L}}}_\phi }$, defined in Appendix A.

Next, one requires that the residual term $-D_\omega \phi +f$ lies in the class ${{\mathcal {N}}}_{\rho , s, \delta , r, \xi }$ in (43)

$$\begin{aligned} {(-D_\omega \phi +f )}\in {{\mathcal {N}}}_{\rho , s, \delta , r, \xi } \end{aligned}$$

(52)

for $\phi$.

Since we have chosen $\phi \in {{\mathcal {Z}}}_{\rho , s, \delta , r, \xi }$, by (50), we have that also $D_\omega \phi \in {{\mathcal {Z}}}_{\rho , s, \delta , r, \xi }$. So, Eq. (52) becomes

$$\begin{aligned} -D_\omega \phi +{\widetilde{f}}=0. \end{aligned}$$

In terms of the Taylor–Fourier modes, the equation becomes

$$\begin{aligned} \omega _y\partial _x \phi _{khj}+\lambda _{khj} \phi _{khj}=f_{khj}\quad \forall \ (k,h,j):\ (k,h-j)\ne (0,0). \end{aligned}$$

(53)

In the standard situation, one typically proceeds to solve such equation via Fourier series:

$$\begin{aligned} f_{khj}({{\mathbf {I}}},y, x)=\sum _{\ell }f_{khj\ell }({{\mathbf {I}}}, y)e^{{\mathrm{i}} \ell x},\quad \phi _{khj}({{\mathbf {I}}},y, x)=\sum _{\ell }\phi _{khj\ell }({{\mathbf {I}}}, y)e^{{\mathrm{i}} \ell x} \end{aligned}$$

so as to find $\displaystyle \phi _{khj\ell }=\frac{f_{khj\ell }}{\mu _{khj\ell }}$ with the usual denominators $\mu _{khj\ell }:=\lambda _{khj}+{\mathrm{i}}\ell \omega _y$ which one requires not to vanish via, e.g., a “diophantine inequality” to be held for all $(k,h,j,\ell )$ with $(k,h-j)\ne (0,0)$. In this standard case, there is not much freedom in the choice of $\phi$. In fact, such solution is determined up to solutions of the homogenous equation

$$\begin{aligned} D_\omega \phi _0=0 \end{aligned}$$

(54)

which, in view of the Diophantine condition, has the only trivial solution $\phi _0\equiv 0$. The situation is different iffis not periodic inx, or$\phi$is not needed so. In such a case, it is possible to find a solution of (53), corresponding to a non-trivial solution of (54), where small divisors do not appear. This is

$$\begin{aligned} \phi _{khj}({{\mathbf {I}}}, y, x)=\left\{ \begin{array}{ll}\displaystyle \frac{1}{\omega _y}\int _0^xf_{khj}({{\mathbf {I}}}, y, \tau )e^{\frac{\lambda _{khj}}{\omega _y}(\tau -x)}\hbox {d}\tau &{}\quad {\mathrm{if}}\ \ (k,h-j)\ne (0,0)\\ \\ \displaystyle 0&{}\quad \mathrm{otherwise .} \end{array}\right. \end{aligned}$$

(55)

Multiplying by $e^{ik\varphi }$ and summing over k, h and j, we obtain

$$\begin{aligned} \phi ({{\mathbf {I}}}, {{\varvec{\varphi }}}, p, q, y, x)=\frac{1}{\omega _y}\int _0^x {\widetilde{f}}\left( {{\mathbf {I}}}, {{\varvec{\varphi }}}+\frac{\omega _{{\mathbf {I}}}}{\omega _y}(\tau -x), p e^{\frac{\omega _{{\mathbf {J}}}}{\omega _y}(\tau -x)}, q e^{-\frac{\omega _{{\mathbf {J}}}}{\omega _y}(\tau -x)}, y, \tau \right) \hbox {d}\tau . \end{aligned}$$

(56)

In Appendix A, we shall prove that, under the assumptions (44), this function can be used to obtain a convergent time-one map and that the construction can be iterated so as to provide the proof of Theorem 4.1. The construction of the iterations and the proof of its convergence are obtained adapting the techniques of Pöschel (1993) to the present case.

5 Proof of Theorem 1.1

The purpose of this section is state and prove a more precise version of Theorem 1.1 (Theorem 5.1). We shall obtain it as an application of Theorem 4.1 to the Hamiltonians ${\widehat{{\mathrm{H}}}}_i$. Therefore, we need to introduce a change in new coordinates ${{\mathcal {C}}}$ which put the ${\widehat{{\mathrm{H}}}}_i$’s in the suited form (41). Since the potentials ${\mathrm{V}}_i$ in (40) are, for large ${\mathrm{r}}$, asymptotic to $-\frac{m_0^2}{{\mathrm{r}}}$, it is convenient to rewrite the functions ${\widehat{{\mathrm{H}}}}_i$ in (37) as

$$\begin{aligned} {\widehat{{\mathrm{H}}}}_1({\mathrm{R}}, {\mathrm{G}}, {\mathrm{r}}, \mathrm{g})= & {} \left( \frac{{\mathrm{R}}^2}{2m_0}-\frac{m_0^2}{\mathrm{r}}\right) +\frac{{\mathrm{G}}^2}{2m_0\mathrm{r}^2}-\frac{{\overline{\beta }}}{\beta +{\overline{\beta }}}\frac{m_0^2}{\mathrm{r}}\left( {\widehat{{\mathrm{F}}}}_{-{\overline{\beta }}\varepsilon (\mathrm{r})}\Big ({\widehat{{\mathrm{E}}}}_{\beta \varepsilon ({\mathrm{r}})}({\mathrm{G}}, \mathrm{g})\Big )-1\right) \\&-\frac{\beta }{\beta +{\overline{\beta }}}\frac{m_0^2}{\mathrm{r}}\left( {\widehat{{\mathrm{F}}}}_{-{\overline{\beta }}\varepsilon (\mathrm{r})}\Big ({\widehat{{\mathrm{E}}}}_{-{\overline{\beta }}\varepsilon (\mathrm{r})}({\mathrm{G}}, {\mathrm{g}})\Big )-1\right) \\ {\widehat{{\mathrm{H}}}}_2({\mathrm{R}}, {\mathrm{G}}, {\mathrm{r}}, \mathrm{g})= & {} \left( \frac{{\mathrm{R}}^2}{2m_0}-\frac{m_0^2}{\mathrm{r}}\right) +\frac{{\mathrm{G}}^2}{2m_0\mathrm{r}^2}-\frac{{\overline{\beta }}}{\beta +{\overline{\beta }}}\frac{m_0^2}{\mathrm{r}}\left( {\widehat{{\mathrm{F}}}}_{(\beta +{\overline{\beta }})\varepsilon (\mathrm{r})}\Big ({\widehat{{\mathrm{E}}}}_{-{\overline{\beta }}\varepsilon (\mathrm{r})}({\mathrm{G}}, {\mathrm{g}})\Big )-1\right) \end{aligned}$$

and take ${{\mathcal {C}}}$ as the composition of two independent and canonical changes

$$\begin{aligned} {{\mathcal {C}}}_1:\ ({{\mathcal {G}}}, \gamma )\rightarrow ({\mathrm{G}}, {\mathrm{g}})\ ,\quad {{\mathcal {C}}}_2:\ (y, x)\rightarrow ({\mathrm{R}}, \mathrm{r}) \end{aligned}$$

where ${{\mathcal {C}}}_1$ is defined as in (26), with $k=0$, while ${{\mathcal {C}}}_2$ is defined via the formulae

$$\begin{aligned} \left\{ \begin{array}{llll}\displaystyle {\mathrm{R}}(y, x)=\frac{m_0^3}{y}\sqrt{ \frac{\cos \xi ^{\prime }(x)+1}{1-\cos \xi ^{\prime }(x)}} \\ \\ \displaystyle {\mathrm{r}}(y, x)=\frac{y^2}{m_0^3}(1-\cos \xi ^{\prime }(x))\end{array}\right. \end{aligned}$$

(57)

where $\xi ^{\prime }(x)$ solves

$$\begin{aligned} \xi ^{\prime }-\sin \xi ^{\prime }= x. \end{aligned}$$

(58)

${{\mathcal {C}}}_2$ has been chosen so that

$$\begin{aligned} {\mathrm{H}}_\omega \circ {{\mathcal {C}}}_1=\left( \frac{\mathrm{R}^2}{2m_0}-\frac{m_0^2}{\mathrm{r}}\right) \circ {{\mathcal {C}}}_1=-\frac{m_0^5}{2y^2}. \end{aligned}$$

Using the new coordinates, we have

$$\begin{aligned} {\widehat{{\mathrm{H}}}}_1= & {} -\frac{m_0^5}{2y^2}+\frac{m_0^2}{{\mathrm{r}}(y, x)}\left( \varepsilon (y, x)\frac{({\Lambda }^2-{{\mathcal {G}}}^2)}{2{\Lambda }^2}\cos ^2\gamma -\frac{{\overline{\beta }}}{\beta +{\overline{\beta }}}\left( {\widehat{{\mathrm{F}}}} _{\beta \varepsilon (y, x)}\Big ({\widehat{{\mathrm{E}}}}_{\beta \varepsilon (y, x)}({{\mathcal {G}}}, \gamma )\Big )-1\right) \right. \\&\left. -\frac{\beta }{\beta +{\overline{\beta }}}\left( {\widehat{{\mathrm{F}}}}_{-{\overline{\beta }}\varepsilon (y, x)}\Big ({\widehat{{\mathrm{E}}}}_{-{\overline{\beta }}\varepsilon (y, x)}({{\mathcal {G}}}, \gamma )\Big )-1\right) \right) \\ {\widehat{{\mathrm{H}}}}_2= & {} -\frac{m_0^5}{2y^2}+\frac{m_0^2}{{\mathrm{r}}(y, x)}\left( \varepsilon (y, x)\frac{({\Lambda }^2-{{\mathcal {G}}}^2)}{2{\Lambda }^2}\cos ^2\gamma \right. \\&\left. - \frac{{\overline{\beta }}}{\beta +{\overline{\beta }}}\frac{m_0^2}{{\mathrm{r}}(y, x)}\left( {\widehat{{\mathrm{F}}}} _{(\beta +{\overline{\beta }})\varepsilon (y, x)}\Big ({\widehat{{\mathrm{E}}}}_{(\beta +{\overline{\beta }})\varepsilon (y, x)}({{\mathcal {G}}}, \gamma )\Big )-1\right) \right) \end{aligned}$$

having abusively denoted as $\varepsilon (y, x)$ the function $\varepsilon ({\mathrm{r}}(y, x))$, and using the formulae in (27)–(29)

$$\begin{aligned} {\widehat{{\mathrm{E}}}}_\varepsilon ({{\mathcal {G}}}, \gamma ):=\frac{{{\mathcal {G}}}}{\Lambda }+\varepsilon \left( 1-\frac{{{\mathcal {G}}}^2}{{\Lambda }^2}\right) \cos ^2\gamma . \end{aligned}$$

(59)

We now determine a domain of holomorphy of ${\widehat{{\mathrm{H}}}}_i$. Recall that we use, as mass parameters, the numbers $\beta _*$, $\beta ^*$ in (10). For the coordinates (y, x), we choose the complex domains ${{\mathbb {Y}}}_{\sqrt{m_0^3\alpha _-}}$, ${{\mathbb {X}}}_{\sqrt{\varepsilon _0}}$, where

$$\begin{aligned} {{\mathbb {Y}}}{:=}\Big \{y\in {{\mathbb {R}}}:\ 2\sqrt{m_0^3\alpha _-}<y<\sqrt{m_0^3\alpha _+}\Big \},\quad {{\mathbb {X}}}{:=}\Big \{x\in {{\mathbb {R}}}:\ |x-\pi |\le \pi -2\sqrt{\varepsilon _0}\Big \}\nonumber \\ \end{aligned}$$

(60)

with $0<\varepsilon _0<1$, $0<\alpha _-<\alpha _+{/4}$ verifying

$$\begin{aligned} \alpha _-\varepsilon _0>\frac{4\beta ^* a}{c_0}\quad \mathrm{with} \end{aligned}$$

(61)

with $\beta ^*$ as in (10) and $c_0$ being such that for any $0<\varepsilon _0<1$ and for any $x\in {{\mathcal {X}}}_{\sqrt{\varepsilon _0}}$, Eq. (58) has a unique solution $\xi ^{\prime }(x)$ which depends analytically on x and verifies

$$\begin{aligned} |1-\cos \xi ^{\prime }(x)|\ge c_0\varepsilon _0. \end{aligned}$$

(62)

(The existence of such a number $c_0$ is well known.) For the coordinates ${{\mathcal {G}}}$, $\gamma$, we choose the domains ${{\mathbb {G}}}_\delta$, ${{\mathbb {T}}}_{s_0}$, with $0<\delta <\Lambda$, $s_0$ fixed, and ${{\mathbb {G}}}:=\Big \{{{\mathcal {G}}}\in {{\mathbb {R}}}:\ \Lambda -\delta<{{\mathcal {G}}}<\Lambda \Big \}$. Remark that, since, in ${\widehat{{\mathrm{H}}}}_i$, there is no dependence of ${\mathrm{G}}$, but only on ${\mathrm{G}}^2$, ${{\mathcal {G}}}=\Lambda$ is a regular point for ${\widehat{{\mathrm{H}}}}_i$. Then, we let

$$\begin{aligned} {{\mathbb {D}}}:= {{\mathbb {G}}}\times {{\mathbb {T}}}\times {{\mathbb {Y}}}\times {{\mathbb {X}}}\subset {{\mathbb {R}}}^4 \end{aligned}$$

and

$$\begin{aligned} {{\mathbb {D}}}_{\delta , s_0, \sqrt{m_0^3\alpha _-},\sqrt{\varepsilon _0}}:= {{\mathbb {G}}}_\delta \times {{\mathbb {T}}}_{s_0}\times {{\mathbb {Y}}}_{\sqrt{m_0^3\alpha _-}}\times {{\mathbb {X}}}_{\sqrt{\varepsilon _0}}\subset {{\mathbb {C}}}^4. \end{aligned}$$

We now check that, under the further assumptions

$$\begin{aligned} 0<\delta \le \frac{\Lambda }{4},\quad C^*(s_0)\frac{\delta }{\Lambda }<1\quad C^*(s_0):=16\left( \sup _{ {{\mathbb {T}}}_{s_0}}|\sin \gamma |\right) ^2 \end{aligned}$$

(63)

${\widehat{{\mathrm{H}}}}_i$ are holomorphic functions on the domain

$$\begin{aligned} {{\mathbb {D}}}_{\delta , s_0, \sqrt{m_0^3\alpha _-},\sqrt{\varepsilon _0}}:={{\mathbb {Y}}}_{\sqrt{m_0^3\alpha _-}}\times {{\mathbb {X}}}_{\sqrt{\varepsilon _0}}\times {{\mathbb {G}}}_\delta \times {{\mathbb {T}}}_{s_0}. \end{aligned}$$

(64)

By (62), the first equation in (60) and the expression of ${\mathrm{r}}(y, x)$ in (57), we have

$$\begin{aligned} |{\mathrm{r}}(y, x)|\ge c_0\alpha _-\varepsilon _0 \end{aligned}$$

(65)

and hence, because of (61),

$$\begin{aligned} |\beta ^*\varepsilon (y, x)|=\left| \frac{\beta ^*a}{{\mathrm{r}}(y, x)}\right| \le \frac{\beta ^* a}{c_0\alpha _-\varepsilon _0}<\frac{1}{4}\ . \end{aligned}$$

(66)

By inequalities (65)–(66) and Proposition 3.3, we only need to check that, if $\varepsilon _*\in \{\beta \varepsilon , -{\overline{\beta }}\varepsilon \}$ for $i=1$ and $\varepsilon _*=(\beta +{\overline{\beta }})\varepsilon$ for $i=2$, then Eq. (34) with $\varepsilon =\varepsilon _*$ and $t={\widehat{{\mathrm{E}}}}_{\varepsilon _*}({{\mathcal {G}}}, \gamma )$ has not solutions in ${{\mathbb {D}}}_{\delta , s_0, \sqrt{m_0^3\alpha _-},\sqrt{\varepsilon _0}}$. We prove that any such solution would verify $|\varepsilon _*|\ge \frac{1}{4}$, which would contradict (66), as $|\beta ^*\varepsilon |\ge |\varepsilon _*|$. Using (59), Eq. (34) with $\varepsilon =\varepsilon _*$ and $t={\widehat{{\mathrm{E}}}}_{\varepsilon _*}({{\mathcal {G}}}, \gamma )$ is

$$\begin{aligned} 4\varepsilon _*^2\left( 1-\left( 1-\frac{{{\mathcal {G}}}^2}{{\Lambda }^2}\right) \cos ^2\gamma \right) -4\frac{{{\mathcal {G}}}}{\Lambda }\varepsilon _*+1=0\ . \end{aligned}$$

We solve for $\varepsilon _*$:

$$\begin{aligned} \varepsilon _*=\frac{1}{2}\left( \frac{{{\mathcal {G}}}}{\Lambda }+\sin \gamma \sqrt{\frac{{{\mathcal {G}}}^2}{{\Lambda }^2}-1}\right) \end{aligned}$$

with the double determination of the square root. Since $\left| \frac{{{\mathcal {G}}}}{\Lambda }\right| \ge 1-\frac{\delta }{\Lambda }\ge \frac{3}{4}$ and, if $c_*(s_0):=\sup _{{{\mathbb {T}}}_{s_0}}|\sin \gamma |$, $\left| \sin \gamma \sqrt{\frac{{{\mathcal {G}}}^2}{{\Lambda }^2}-1}\right| \le c^*(s_0)\sqrt{\frac{\delta }{\Lambda }}\le \frac{1}{4}$, we have $|\varepsilon _*|\ge \frac{1}{2}\left( \frac{3}{4}-\frac{1}{4}\right) =\frac{1}{4}$, as claimed.

We are now ready to state the result. Observe that the motions

$$\begin{aligned} {{\mathcal {G}}}={{\mathcal {G}}}_0={\mathrm{constant}},\quad |\gamma (T)-\gamma (0)|=2\pi \end{aligned}$$

correspond, using the coordinates $({\mathrm{G}}, {\mathrm{g}})$, to librations about (0, 0) if $0<{{\mathcal {G}}}_0<\Lambda$; about $(0, \pi )$ if $-\Lambda<{{\mathcal {G}}}_0<0$. We shall prove the existence, in ${\widehat{{\mathrm{H}}}}_i$’s, of motions close to these ones.

Theorem 5.1

Let $\alpha _-$, $\alpha _+$, $\beta$, ${\overline{\beta }}$, $\delta$, $\varepsilon _0$ and $s_0$ be fixed; $\beta _*$, $\beta ^*$ as in  (10). There exist two numbers $C^*>C_*>1$, both independent of $\alpha _-$, $\alpha _+$, $\beta$, ${\overline{\beta }}$, $\delta$, $\varepsilon _0$, with $C^*$ possibly depending on $s_0$, while $C_*$ independent of $s_0$, such that, if the following inequalities are satisfied

$$\begin{aligned}&0<\varepsilon _0<1,\quad 0<\delta \le \frac{\Lambda }{4},\quad \frac{4\beta ^* a}{c_0\alpha _-\varepsilon _0}<1,\quad \frac{C^*\delta }{\beta _*\Lambda }\le 1\nonumber \\&\quad \frac{1}{N_0}:=C_*\max \left\{ \frac{\beta _*\Lambda }{c_0^2\varepsilon _0^2\delta s_0}\sqrt{\frac{a}{\alpha _-}}\ , \quad {\frac{\beta _*}{c_0^2\varepsilon _0^{5/2}}{\frac{a}{\alpha _-}}} \right\} \frac{\alpha _+^{3/2}}{\alpha _-^{3/2}}<\frac{c_0^2\varepsilon _0^2\alpha _-^2}{2\alpha _+^2} \end{aligned}$$

(67)

it is possible to find new coordinates $({{\mathcal {G}}}_*, \gamma _*, y_*, x_*)$ and a time T such that any solution $\Gamma _*(t)=({{\mathcal {G}}}_*(t), \gamma _*(t), y_*(t), x_*(t))$ of ${\widehat{{\mathrm{H}}}}_i$ with initial datum $\Gamma _*(0)$$=$$({{\mathcal {G}}}_*(0)$, $\gamma _*(0)$, $y_*(0)$, $x_*(0))$$\in {{\mathbb {D}}}$ such that

$$\begin{aligned} |{{\mathcal {G}}}(0)-\Lambda |\le \frac{\delta }{2},\quad 2\sqrt{m_0^3\alpha _-}\le |y_*(0)|{\le \frac{\sqrt{m_0^3\alpha _-}+\sqrt{m_0^3\alpha _+}}{2} } ,\quad x_*(0)=\pi \end{aligned}$$

(68)

stays in ${{\mathbb {D}}}$ for all $0\le t\le T$ and ${{\mathcal {G}}}_*$ varies a little in the course of such time:

$$\begin{aligned} |{{\mathcal {G}}}_*(t)-{{\mathcal {G}}}_*(0)|\le C_*\frac{2^{-N_0}}{s_0}\frac{m_0^2a\beta _*}{c^2_0\varepsilon ^2_0\alpha ^2_-}t \ \quad \mathrm{for\ all}\ 0\le t\le T. \end{aligned}$$

If, in addition,

$$\begin{aligned} {\eta }:=C_*\max \left\{ \frac{\alpha _+^2}{\beta _*\sqrt{\alpha _-^3 a}}\ ,\ \frac{\alpha _+^2}{c^2_0\varepsilon ^{5/2}_0\alpha ^2_-}\sqrt{\frac{a}{\alpha _-}}\ ,\ \frac{\alpha _+^2}{c^2_0\varepsilon ^{2}_0\alpha ^2_-} \frac{\Lambda }{s_0\delta }2^{-N_0} \right\} <1, \end{aligned}$$

(69)

then motions close to librations occur, in the sense that, also

$$\begin{aligned} |\gamma _*(T)-\gamma _*(0)|\ge 3\pi . \end{aligned}$$

The time T can be taken to be

$$\begin{aligned} {T=\frac{\Lambda \alpha _+^3}{\beta _*m_0^2a}\frac{3\pi }{\eta }}. \end{aligned}$$

(70)

Finally, the change

$$\begin{aligned} ({{\mathcal {G}}}_*, \gamma _*, y_*, x_*)\rightarrow ({{\mathcal {G}}}, \gamma , y, x) \end{aligned}$$

is real-analytic and close to the identity, in the sense that

$$\begin{aligned} |{{\mathcal {G}}}-{{\mathcal {G}}}_*|\le \frac{\Lambda }{N_0},\quad |\gamma -\gamma _*|\le \frac{s_0}{N_0},\quad |y-y_*|\le \frac{\sqrt{m_0^3\alpha _-}}{N_0},\quad |x-x_*|\le \frac{\sqrt{\varepsilon _0}}{N_0}. \end{aligned}$$

Remark 5.1

(Proof of Theorem 1.1) Inequalities (67), (68) and (69) are simultaneously satisfied provided that the following holds. Fix $0<\varepsilon _0<1$ and $0<\delta \le \frac{\Lambda }{4}$ once forever. Then, identify $\delta$ as the size of ${\mathrm{U}}_0$ and $2^{-N_0}$ as the size of ${\mathrm{V}}_0$. Take

$$\begin{aligned}&s_0\rhd \frac{\Lambda }{\delta \varepsilon _0^4},\quad \frac{\alpha _+}{a}=2^8\frac{\alpha _-}{a}\rhd \frac{{C^*(s_0)}^2}{\varepsilon _0^8}\\&\min \left\{ \varepsilon _0^4\frac{\delta }{\Lambda }s_0\sqrt{\frac{\alpha _-}{a}},\ \varepsilon _0^{9/2}\frac{\alpha _-}{a} \right\} \rhd \beta ^*\ge \beta _*\rhd \max \left\{ C^*\frac{\delta }{\Lambda },\ \sqrt{\frac{\alpha _-}{a}}\right\} . \end{aligned}$$

For short, we have written “$a\rhd b$” if there exist $c>1$, independent of $\delta$, $\Lambda$, $\alpha _-$, $\alpha _+$, a and $s_0$ such that $a>cb$. Note that here it is essential that $\alpha _-$, $s_0$, $\beta _*$ and $\beta ^*$ can be chosen arbitrarily large.

Proof

During the proof, we shall make extensive use of Cauchy¹⁰ inequalities.

We aim to apply Theorem 4.1, with ${{\mathbf {I}}}={{\mathcal {G}}}$, ${\varvec{\varphi }}=\gamma$, (y, x) as in (57), ${\mathrm{h}}(y)=-\frac{m_0^5}{2y^2}$ and, finally

$$\begin{aligned} f({{\mathcal {G}}}, \gamma , y, x)=\left\{ \begin{array}{llll}\frac{m_0^2}{{\mathrm{r}}(y, x)}\left( \varepsilon (y, x)\frac{({\Lambda }^2-{{\mathcal {G}}}^2)}{2{\Lambda }^2}\cos ^2\gamma -\frac{{\overline{\beta }}}{\beta +{\overline{\beta }}}\left( {\widehat{{\mathrm{F}}}} _{\beta \varepsilon (y, x)}\Big ({\widehat{{\mathrm{E}}}}_{\beta \varepsilon (y, x)}({{\mathcal {G}}}, \gamma )\Big )-1\right) \right. \\ \left. -\frac{\beta }{\beta +{\overline{\beta }}}\left( {\widehat{{\mathrm{F}}}}_{-{\overline{\beta }}\varepsilon (y, x)}\Big ({\widehat{{\mathrm{E}}}}_{-{\overline{\beta }}\varepsilon (y, x)}({{\mathcal {G}}}, \gamma )\Big )-1\right) \right) \quad i=1\\ \\ \frac{m_0^2}{{\mathrm{r}}(y, x)}\left( \varepsilon (y, x)\frac{({\Lambda }^2-{{\mathcal {G}}}^2)}{2{\Lambda }^2}\cos ^2\gamma \right. \\ \left. -\frac{{\overline{\beta }}}{\beta +{\overline{\beta }}}\frac{m_0^2}{\mathrm{r}(y, x)}\left( {\widehat{{\mathrm{F}}}} _{(\beta +{\overline{\beta }})\varepsilon (y, x)}\Big ({\widehat{{\mathrm{E}}}}_{(\beta +{\overline{\beta }})\varepsilon (y, x)}({{\mathcal {G}}}, \gamma )\Big )-1\right) \right) \\ \quad i=2 \end{array}\right. \end{aligned}$$

(71)

In our case, ${{\mathbf {p}}}$, ${{\mathbf {q}}}$ do not exist and the unperturbed term ${\mathrm{h}}$ does not depend on ${{\mathbf {I}}}={{\mathcal {G}}}$. Therefore, we have only to verify the last condition in (44). We have

$$\begin{aligned} \omega _y=\frac{m_0^5}{y^3},\quad {\mathrm{d}}=\min \{\delta s_0,\ \sqrt{m_0^3\alpha _-\varepsilon _0}\},\quad {{\mathcal {X}}}=\sqrt{4\pi ^2+\varepsilon _0}\le 3\pi \end{aligned}$$

(having used $\varepsilon _0<1$) and

$$\begin{aligned}&{\left\| \frac{1}{\omega _y}\right\| _{\sqrt{m_0^3\alpha _-}, \sqrt{\varepsilon _0}, \delta , s_0}\le 2\sqrt{\frac{\alpha _+^3}{m_0}}}\nonumber \\&{\left. \Vert f\Vert \right| _{\sqrt{m_0^3\alpha _-}, \sqrt{\varepsilon _0}, \delta , s_0}\le \frac{m_0^2a}{c^2_0\varepsilon ^2_0\alpha ^2_-}\left( C_1\frac{\delta }{\Lambda }+C_2\beta _* \right) \le C_*\frac{m_0^2a\beta _*}{c^2_0\varepsilon ^2_0\alpha ^2_-}=:\Delta } \end{aligned}$$

(72)

with¹¹$C_1$, $C_2$, $C_*$ independent of $\alpha _-$, $\alpha _+$, $\delta$, $\beta _*$, $\beta ^*$ but $C_1$ possibly depending on $s_0$, while $C_2$, $C_*$ independent of $s_0$. We have chosen the number $C^*$ in (67) larger than or equal to $2C_1/C_2$ and the number $C_*$ larger than or equal to $3C_2/2$, so that $\left( C_1\frac{\delta }{\Lambda } +C_2\beta _*\right) \le \frac{3}{2}C_2\beta _*{\le C_*\beta _*}$. We have

$$\begin{aligned}&{\widetilde{{\mathrm{c}}}}_{1, 0}\frac{\chi }{\mathrm{d}}\big \Vert f\big \Vert _{\sqrt{m_0^3\alpha _-}, \sqrt{\varepsilon _0}, \delta , s_0}\left\| \frac{1}{\omega _y}\right\| _{\sqrt{m_0^3\alpha _-}, \sqrt{\varepsilon _0}, \delta , s_0}\\&\quad \le C_*\max \left\{ \frac{\beta _*\Lambda }{c_0^2\varepsilon _0^2\delta s_0}\sqrt{\frac{a}{\alpha _-}}\ , \frac{\beta _*\Lambda }{c_0^2\varepsilon _0^2\sqrt{m_0^3\alpha _-\varepsilon _0}}\sqrt{\frac{a}{\alpha _-}} \right\} \frac{\alpha _+^{3/2}}{\alpha _-^{3/2}}\\&\quad ={ C_*\max \left\{ \frac{\beta _*\Lambda }{c_0^2\varepsilon _0^2\delta s_0}\sqrt{\frac{a}{\alpha _-}}\ , \frac{\beta _*}{c_0^2\varepsilon _0^{\frac{5}{2}}}{\frac{a}{\alpha _-}} \right\} \frac{\alpha _+^{3/2}}{\alpha _-^{3/2}} }\\&\quad \le \frac{1}{N_0}. \end{aligned}$$

Therefore, the last condition in (44) is immediately implied by $N<N_0$, with $N_0$ as in (67). We then find a real-analytic transformation

$$\begin{aligned} \phi _*:\quad ({{\mathcal {G}}}_*, \gamma _*, y_*, x_*)\in {{\mathbb {D}}}_{\sqrt{m_0^3\alpha _-}/3,\sqrt{\varepsilon _0}/3, \delta /3, s_0/3}\rightarrow ({{\mathcal {G}}}, \gamma , y, x)\in {{\mathbb {D}}}_{\delta , s_0, \sqrt{m_0^3\alpha _-},\sqrt{\varepsilon _0}} \end{aligned}$$

which leads ${\widehat{{\mathrm{H}}}}_i$ to

$$\begin{aligned} {\widehat{{\mathrm{H}}}}_{*}={\mathrm{h}}(y_*)+g_{*}(y_*, x_*, {{\mathcal {G}}}_*)+f_{*}({{\mathcal {G}}}_*, \gamma _*, y_*, x_*)\end{aligned}$$

(73)

where $g_*$ and $f_*$ satisfy the following bounds:

$$\begin{aligned} \Vert g_*{-{\overline{f}}}\Vert \le 2 \Delta ,\quad \Vert g_*\Vert \le 2^{-N}\Delta \end{aligned}$$

with ${\overline{f}}(y_*, x_*, {{\mathcal {G}}}_*)$ the $\gamma _*$-average of $f(y_*, x_*, {{\mathcal {G}}}_*, \gamma _*)$ and $\Delta$ as in (72). Let now $\Gamma _*(t)=({{\mathcal {G}}}_*(t), \gamma _*(t), y_*(t), x_*(t))$ be a solution of ${\widehat{{\mathrm{H}}}}_i$ with initial datum $\Gamma _*(0)$$=$$({{\mathcal {G}}}_*(0)$, $\gamma _*(0)$, $y_*(0)$, $x_*(0))$$\in {{\mathbb {D}}}$ and verifying (68). We look for a time $T>0$ such that $\Gamma _*(t)\in {{\mathbb {D}}}$ for all $0\le t\le T$. We show that we can take T as in (70), which, for convenience, we rewrite as

$$\begin{aligned} T=\min \left\{ \sqrt{\frac{\alpha _-^3}{m_0}},\ {\frac{\sqrt{m_0^3\alpha _-\varepsilon _0}}{\Delta }},\ 2^{N_0}\frac{s_0\delta }{\Delta }\right\} \end{aligned}$$

(74)

where $\Delta$ is as in (72). Equation (73) implies

$$\begin{aligned} \left| y_*(t)-y_*(0)\right| \le \frac{\Delta t}{\sqrt{\varepsilon _0}}. \end{aligned}$$

So, for $t\le \frac{\sqrt{m_0^3\alpha _-\varepsilon _0}}{\Delta }$, we have

$$\begin{aligned} t \le \frac{|y_*(0)|-\sqrt{m_0^3\alpha _-}}{\Delta }\sqrt{\varepsilon _0}\quad \Longrightarrow \quad |y_*(t)-y_*(0)|\le |y_*(0)|-\sqrt{m_0^3\alpha _-} \end{aligned}$$

namely, $y_*(t)\in {{\mathbb {Y}}}$ for $0\le t\le T$. Since $|y|\ge \sqrt{m_0^3 \alpha _-}$ for all this time, we also have

$$\begin{aligned} \left| x_*(t)-x_*(0)\right| \le \left( \sqrt{\frac{m_0}{\alpha _-^3}}+\frac{\Delta }{\sqrt{m_0^3\alpha _-}}\right) t. \end{aligned}$$

Inequalities $0<\varepsilon _0<1$ and $t\le \min \left\{ \sqrt{\frac{\alpha _-^3}{m_0}},\ \frac{\sqrt{m_0^3\alpha _-}}{\Delta } \right\}$ imply

$$\begin{aligned} t\le \frac{2}{2\max \left\{ \sqrt{\frac{m_0}{\alpha _-^3}},\ \frac{\Delta }{\sqrt{m_0^3\alpha _-}}\right\} } \le \frac{\pi -\sqrt{\varepsilon _0}}{\sqrt{\frac{m_0}{\alpha _-^3}}+\frac{\Delta }{\sqrt{m_0^3\alpha _-}}}\quad \Longrightarrow \quad |x_*(t)-x_*(0)|\le \pi -\sqrt{\varepsilon _0} \end{aligned}$$

and hence $x_*(t)\in {{\mathbb {X}}}$ for $0\le t\le T$. Since $0\le t\le 2^N\frac{s_0\delta }{\Delta }$, we have

$$\begin{aligned} |{{\mathcal {G}}}_*(t)-{{\mathcal {G}}}_*(0)|\le \frac{2^{-(N+1)}\Delta t}{s_0}\le \frac{\delta }{2} \end{aligned}$$

and hence ${{\mathcal {G}}}_*(t)\in {{\mathbb {G}}}$. Let us now evaluate the variation of $\gamma _*$ during the time T. We have

$$\begin{aligned} |\gamma _*(T)-\gamma _*(0)|\ge & {} \inf |\partial _{{{\mathcal {G}}}_*}(g_*+f_*)|t\ge \left( \inf |\partial _{{{\mathcal {G}}}_*}{\overline{f}}|-\sup |\partial _{{{\mathcal {G}}}_*}(|g_*-{\overline{f}}|+|f_*|)| \right) T\\\ge & {} \left( \inf |\partial _{{{\mathcal {G}}}_*}{\overline{f}}|-\frac{\Delta }{\Lambda } N_0^{-1} \right) T. \end{aligned}$$

Proceeding as in (72) and using Cauchy inequalities, one sees that $\inf |\partial _{{{\mathcal {G}}}_*}{\overline{f}}|\ge c^*\beta _*{m_0^2}\frac{a}{\Lambda \alpha _+^2}$. So, using (72) and $N_0^{-1}<\frac{c_0^2\varepsilon _0^2\alpha _-^2}{2\alpha _+^2}$,

$$\begin{aligned} |\gamma _*(T)-\gamma _*(0)|\ge & {} c^*\beta _*{m_0^2}\frac{a}{\Lambda \alpha _+^2}\left( 1-\frac{\alpha _+^2}{c_0^2\varepsilon _0^2\alpha _-^2N_0}\right) T\ge \frac{c^*}{2}\beta _*{m_0^2}\frac{a}{\Lambda \alpha _+^2}T\\= & {} \frac{c^*}{2}m_0^2\beta _*\frac{a}{\Lambda \alpha _+^2}\min \left\{ \sqrt{\frac{\alpha _-^3}{m_0}}\ ,\ \frac{\sqrt{m_0^3\alpha _-\varepsilon _0}}{\Delta } ,\ 2^N\frac{s_0\delta }{\Delta }\right\} \\= & {} c^\circ \min \left\{ \beta _*\sqrt{\frac{\alpha _-^3 a}{\alpha _+^4}},\ \frac{c^2_0\varepsilon ^{5/2}_0\alpha ^2_-}{\alpha _+^2}\sqrt{\frac{\alpha _-}{a}},\ \frac{c^2_0\varepsilon ^{2}_0\alpha ^2_-}{\alpha _+^2}2^{N_0} s_0\frac{\delta }{\Lambda } \right\} {=:\frac{3\pi }{\eta }} \end{aligned}$$

with $c^*$, $c^\circ$ independent of $\alpha _-$, $\alpha _+$, $\beta$, ${\overline{\beta }}$, $\delta$, $\varepsilon _0$ and $s_0$. We then see that $|\gamma _*(T)-\gamma _*(0)|$ is lower-bounded by $3\pi$ as soon as the condition in (69) is satisfied. $\square$

Proof of Theorem 4.1

In this section, we use the definitions and the notations introduced in Sect. 4.1, plus the following further ones.

Definition A.1

Given ${\mathrm{h}}$ and f as in (41), we call¹² the function (56) nqp-primitive offrelatively to${\mathrm{h}}$ or, simply, nqp-primitive off.

Example A.1

Let $n=1$ and $f(I, \varphi )=a(I)\cos \varphi$. The nqp-primitive of f is

$$\begin{aligned} \phi (I, \varphi , y, x)= & {} \frac{ 1}{\omega _y}\int _0^x a(I)\cos \left( \varphi +\frac{\omega _{ I}}{\omega _y}(\tau -x)\right) \hbox {d}\tau =\frac{ a(I)}{\omega _I}\int _{-\frac{\omega _{ I}}{\omega _y}x}^0 \cos (\varphi +\psi )\hbox {d}\psi \\= & {} \frac{a(I)}{\omega _I}\left( \sin \varphi -\sin \left( \varphi -\frac{\omega _{ I}}{\omega _y}x\right) \right) \end{aligned}$$

having changed variable $\tau \rightarrow \psi =\frac{\omega _{ I}}{\omega _y}(\tau -x)$.

Definition A.2

(Time-one flow) Let ${{\mathcal {L}}}_\phi (\cdot ):=\big \{\phi , \cdot \big \}$. For a given $\phi \in {{\mathcal {O}}}_{\rho , s, \delta , r, \xi }$ and $h\in {{\mathbb {N}}}$, we denote as $\Phi _h$ the formal series

$$\begin{aligned} \Phi _h:=\sum _{j\ge h}\frac{{{\mathcal {L}}}_\phi ^j}{j!}\ .\end{aligned}$$

(75)

We call $\Psi :=\Phi _0:=e^{{{\mathcal {L}}}_\phi }$time-one flow generated by $\phi$.

Definition A.3

We call nqp-homological transformation the time-one flow $\Psi :=\Phi _0=e^{{{\mathcal {L}}}_\phi }$ generated by $\phi$ in (49), with $\phi _{khj}$ as in (55).

Below, we prove that the nqp-homological transformation is well defined. Later, we shall prove that the composition of $N+1$nqp-homological transformations $\Psi _1=e^{{{\mathcal {L}}}_{\phi _1}}$, $\dots$, $\Psi _{N+1}=e^{{{\mathcal {L}}}_{\phi _{N+1}}}$, where

$$\begin{aligned} \Psi _j:\quad {\mathrm{H}}_{j-1}\rightarrow {\mathrm{H}}_{j} \end{aligned}$$

with ${\mathrm{H}}_0={\mathrm{H}}$ provides the transformation $\Psi _*$ in (45).

Lemma A.1

(Pöschel 1993) There exists an integer number $\overline{\mathrm{c}}_{n,m}$ such that, for any $\phi \in {{\mathcal {O}}}_{\rho , s, \delta , r, \xi }$ and any $r^{\prime }<r$, $s^{\prime }<s$, $\rho ^{\prime }<\rho$, $\xi ^{\prime }<\xi$, $\delta ^{\prime }<\delta$ such that

$$\begin{aligned} \frac{\overline{\mathrm{c}}_{n,m}\Vert \phi \Vert _{\rho , s, \delta , r, \xi }}{d}<1\quad d:=\min \big \{\rho ^{\prime }\sigma ^{\prime }, r^{\prime }\xi ^{\prime }, {\delta ^{\prime }}^2\big \} \end{aligned}$$

then the series in (75) converge uniformly so as to define the family $\{\Phi _h\}_{h=0,1,\dots }$ of operators

$$\begin{aligned} \Phi _h:\quad {{\mathcal {O}}}_{\rho , s, \delta , r, \xi }\rightarrow {{\mathcal {O}}}_{\rho -\rho ^{\prime }, s-s^{\prime }, \delta -\delta ^{\prime }, r-r^{\prime }, \xi -\xi ^{\prime }}\ . \end{aligned}$$

Moreover, the following bound holds (showing, in particular, uniform convergence):

$$\begin{aligned} \Vert {{\mathcal {L}}}^j_\phi [g]\Vert _{\rho -\rho ^{\prime }, s-s^{\prime }, \delta -\delta ^{\prime }, r-r^{\prime }, \xi -\xi ^{\prime }}\le j!\big (\frac{\overline{\mathrm{c}}_{n,m}\Vert \phi \Vert _{\rho , s, \delta , r, \xi }}{d}\big )^j\Vert g\Vert _{\rho , s, \delta , r, \xi } \end{aligned}$$

(76)

for all $g\in {{\mathcal {O}}}_{\rho , s, \delta , r, \xi }$.

Remark A.1

(Pöschel 1993) The bound (76) immediately implies

$$\begin{aligned} \Vert \Phi _hg\Vert _{\rho -\rho ^{\prime }, s-s^{\prime }, \delta -\delta ^{\prime }, r-r^{\prime }, \xi -\xi ^{\prime }}\le \frac{\big (\frac{\overline{\mathrm{c}}_{n,m}\Vert \phi \Vert _{\rho , s, \delta , r, \xi }}{d}\big )^h}{1-\frac{\overline{\mathrm{c}}_{n,m}\Vert \phi \Vert _{\rho , s, \delta , r, \xi }}{d}}\Vert g\Vert _{\rho , s, \delta , r, \xi }\quad \forall g\in {{\mathcal {O}}}_{\rho , s, \delta , r, \xi }.\nonumber \\ \end{aligned}$$

(77)

Lemma A.2

(Iterative lemma) There exists a number ${\widetilde{{\mathrm{c}}}}_{n,m}>1$ such that the following holds. For any choice of positive numbers $r^{\prime }$, $\rho ^{\prime }$, $s^{\prime }$, $\xi ^{\prime }$, $\delta ^{\prime }$ satisfying

$$\begin{aligned}&{2\rho ^{\prime }<\rho ,\quad 2r^{\prime }<r,\quad 2\xi ^{\prime }<\xi } \end{aligned}$$

(78)

$$\begin{aligned}&2s^{\prime }<s,\quad 2\delta ^{\prime }<\delta ,\quad { {{\mathcal {X}}}\left\| \mathfrak {I}\frac{\omega _{{\mathbf {I}}}}{\omega _y}\right\| _{\rho , r}<s-2s^{\prime },\quad {{\mathcal {X}}}\left\| \frac{\omega _{{\mathbf {J}}}}{\omega _y}\right\| _{\rho , r}< \log \frac{\delta }{2\delta ^{\prime }} } \end{aligned}$$

(79)

and provided that the following inequality holds true

$$\begin{aligned} {\widetilde{{\mathrm{c}}}}_{n,m}\frac{{{\mathcal {X}}}}{d} \left\| \frac{{\widetilde{f}}}{\omega _y}\right\| _{\rho , s, \delta , r, \xi } <1\quad d:=\min \big \{\rho ^{\prime }\sigma ^{\prime }, r^{\prime }\xi ^{\prime }, {\delta ^{\prime }}^2\big \}, \end{aligned}$$

(80)

one can find an operator

$$\begin{aligned} \Phi :\quad {{\mathcal {O}}}_{\rho , s, \delta , r, \xi }\rightarrow {{\mathcal {O}}}_{\rho _+, s_+, \delta _+, r_+, \xi _+} \end{aligned}$$

with

$$\begin{aligned}&r_+:=r-2r^{\prime },\quad \rho _+:=\rho -2\rho ^{\prime },\quad \xi _+:=\xi -2\xi ^{\prime }\ ,\quad s_+:=s-2s^{\prime }-{{\mathcal {X}}}\left\| \mathfrak {I}\frac{\omega _{{\mathbf {I}}}}{\omega _y}\right\| _{\rho , r}\\&\delta _+:=\delta e^{-{{\mathcal {X}}}\left\| \frac{\omega _{{\mathbf {J}}}}{\omega _y}\right\| _{\rho , r}}-2\delta ^{\prime } \end{aligned}$$

which carries the Hamiltonian ${\mathrm{H}}$ in (48) to

$$\begin{aligned} {\mathrm{H}}_+:=\Phi [{\mathrm{H}}]={\mathrm{h}}+g+{\overline{f}}+f_+ \end{aligned}$$

where

$$\begin{aligned}&\Vert f_+\Vert _{r_+,\rho _+, \xi _+, s_+,\delta _+}\nonumber \\&\le {\widetilde{{\mathrm{c}}}}_{n,m}\left( \frac{{{\mathcal {X}}}}{d}\left\| \frac{{\widetilde{f}}}{\omega _y}\right\| _{\rho , s, \delta , r, \xi }\Vert f\Vert _{\rho , s, \delta , r, \xi }+ \Vert \{\phi , g\}\Vert _{\rho _1-\rho ^{\prime }, s_1-s^{\prime }, \delta _1-\delta ^{\prime }, r_1-r^{\prime }, \xi _1-\xi ^{\prime }}\right) \qquad \qquad \end{aligned}$$

(81)

with

$$\begin{aligned} \rho _1:=\rho ,\quad s_1:=s-{{\mathcal {X}}}\left\| \mathfrak {I}\frac{\omega _{{\mathbf {I}}}}{\omega _y}\right\| _{\rho , r},\quad \delta _1:=\delta e^{-{{\mathcal {X}}}\left\| \frac{\omega _{{\mathbf {J}}}}{\omega _y}\right\| _{\rho , r}},\quad r_1:=r,\quad \xi _1:=\xi \end{aligned}$$

for a suitable $\phi \in {{\mathcal {O}}}_{\rho _1, s_1, \delta _1, r_1, \xi _1}$ verifying

$$\begin{aligned} \Vert \phi \Vert _{\rho _1, s_1, \delta _1, r_1, \xi _1 }\le {{\mathcal {X}}} \left\| \frac{{\widetilde{f}}}{\omega _y}\right\| _{\rho , s, \delta , r, \xi } .\end{aligned}$$

(82)

Furthermore, if

$$\begin{aligned} ({{\mathbf {I}}}_+, {\varvec{\varphi }}_+, {{\mathbf {p}}}_+, {{\mathbf {q}}}_+, y_+, x_+):=\Phi ({{\mathbf {I}}}, {\varvec{\varphi }}, {{\mathbf {p}}}, {{\mathbf {q}}}, y, x) \end{aligned}$$

the following uniform bounds hold:

$$\begin{aligned}&\max \Big \{s^{\prime }|{{\mathbf {I}}}-{{\mathbf {I}}}_+|,\ \rho ^{\prime }|{\varvec{\varphi }} -{\varvec{\varphi }} _+|,\ \delta ^{\prime } |{{\mathbf {p}}}-{{\mathbf {p}}}_+|,\ \delta |{{\mathbf {q}}}-{{\mathbf {q}}}_+|,\ \xi ^{\prime } |y-y_+|,\ r^{\prime } |x-x_+| \Big \}\nonumber \\&\quad \le 2\, {{\mathcal {X}}} \left\| \frac{{\widetilde{f}}}{\omega _y}\right\| _{\rho , s, \delta , r, \xi } . \end{aligned}$$

(83)

Remark A.2

The right-hand side of (81) benefits of the absence of small divisors, as no “ultraviolet” (i.e., with size $\sim e^{-Ns}\Vert f\Vert$) term appears.

Proof

Let $\overline{\mathrm{c}}_{n,m}$ be as in Lemma A.1. We shall choose ${\widetilde{{\mathrm{c}}}}_{n,m}$ suitably large with respect to $\overline{\mathrm{c}}_{n,m}$.

Let $\phi _{khj}$ as in (55). Let us fix

$$\begin{aligned} 0<{\overline{r}}\le r,\quad 0<{\overline{\rho }}\le \rho ,\quad 0<{\overline{\xi }}\le \xi ,\quad 0<{\overline{s}}< s,\quad 0<{\overline{\delta }}< \delta \end{aligned}$$

(84)

and assume that

$$\begin{aligned} {{\mathcal {X}}}\left\| \mathfrak {I}\frac{\omega _{{\mathbf {I}}}}{\omega _y}\right\| _{\rho , r} \le s-{\overline{s}},\quad {{\mathcal {X}}}\left\| \frac{\omega _{{\mathbf {J}}}}{\omega _y}\right\| _{\rho , r} \le \log \frac{\delta }{{\overline{\delta }}}. \end{aligned}$$

(85)

Then, we have

$$\begin{aligned} \Vert \phi _{khj}\Vert _{{\overline{\rho }},{\overline{r}},{\overline{\xi }}}\le \left\| \frac{f_{khj}}{\omega _y}\right\| _{{\overline{\rho }}, {\overline{r}},{\overline{\xi }}}\left\| \int _0^x |e^{-\frac{\lambda _{khj}}{\omega _y}\tau }|\right\| _{{\overline{\rho }}, {\overline{r}},{\overline{\xi }}}\hbox {d}\tau \le {{\mathcal {X}}} \left\| \frac{f_{khj}}{\omega _y}\right\| _{{\overline{\rho }}, {\overline{r}},{\overline{\xi }}} e^{{{\mathcal {X}}}\left\| \frac{\lambda _{khj}}{\omega _y}\right\| _{{\overline{\rho }}, {\overline{r}}}}. \end{aligned}$$

Since

$$\begin{aligned} \Vert \frac{\lambda _{khj}}{\omega _y}\Vert _{{\overline{\rho }}, {\overline{r}}} \le (h+j)\left\| \frac{\omega _{{\mathbf {J}}}}{\omega _y}\right\| _{{\overline{\rho }}, {\overline{r}}} +|k|\left\| \mathfrak {I}\frac{\omega _{{\mathbf {I}}}}{\omega _y}\right\| _{{\overline{\rho }}, {\overline{r}}}, \end{aligned}$$

we have

$$\begin{aligned} \Vert \phi _{khj}\Vert _{{\overline{\rho }},{\overline{r}},{\overline{\xi }}}\le {{\mathcal {X}}} \left\| \frac{{\widetilde{f}}_{khj}}{\omega _y}\right\| _{{\overline{\rho }},{\overline{r}},{\overline{\xi }}} e^{(h+j){{\mathcal {X}}}\left\| \frac{\omega _{{\mathbf {J}}}}{\omega _y}\right\| _{{\overline{\rho }}, {\overline{r}}} +|k|{{\mathcal {X}}}\left\| \mathfrak {I}\frac{\omega _{{\mathbf {I}}}}{\omega _y}\right\| _{{\overline{\rho }}, {\overline{r}}} } \end{aligned}$$

which yields (after multiplying by $e^{|k|{\overline{s}}}({\overline{\delta }})^{j+h}$ and summing over k, j, h with $(k,h-k)\ne (0,0)$) to

$$\begin{aligned} \Vert \phi \Vert _{{\overline{\rho }},{\overline{r}},{\overline{\xi }}, {\overline{s}},{\overline{\delta }}}\le {{\mathcal {X}}} \left\| \frac{{\widetilde{f}}}{\omega _y}\right\| _{{\overline{r}},{\overline{\rho }},{\overline{\xi }},{\overline{s}}+{{\mathcal {X}}}\left\| \mathfrak {I}\frac{\omega _{{\mathbf {I}}}}{\omega _y}\right\| _{{\overline{\rho }}, {\overline{r}}} ,{\overline{\delta }} e^{{{\mathcal {X}}}\left\| \frac{\omega _{{\mathbf {J}}}}{\omega _y}\right\| _{{\overline{\rho }}, {\overline{r}}} }}. \end{aligned}$$

Note that the right-hand side is well defined because of (85). In the case of the choice

$$\begin{aligned}&{\overline{r}}=r=:r_1,\quad {\overline{\rho }}=\rho =: \rho _1\ ,\quad {\overline{\xi }}=\xi =:\xi _1,\quad {\overline{s}}=s-{{\mathcal {X}}}\left\| \mathfrak {I}\frac{\omega _{{\mathbf {I}}}}{\omega _y}\right\| _{\rho , r}=:s_1\\&{\overline{\delta }}=\delta e^{-{{\mathcal {X}}}\left\| \frac{\omega _{{\mathbf {J}}}}{\omega _y}\right\| _{\rho , r}}=:\delta _1 \end{aligned}$$

(which, in view of the two latter inequalities in (79), satisfies (84)–(85)) the inequality becomes (82). An application of Lemma ,with r, $\rho$, $\xi$, s, $\delta$ replaced by $r_1-r^{\prime }$, $\rho _1-\rho ^{\prime }$, $\xi _1-\xi ^{\prime }$, $s_1-s^{\prime }$, $\delta _1-\delta ^{\prime }$, concludes with a suitable choice of ${\widetilde{{\mathrm{c}}}}_{n,m}>\overline{\mathrm{c}}_{n,m}$ and (by (51))

$$\begin{aligned} f_+:=\Phi _2({\mathrm{h}})+\Phi _1(g)+\Phi _1(f). \end{aligned}$$

Observe that the bound (81) follows from Eqs. (77) and (76) and the identities

$$\begin{aligned} \Phi _2[{\mathrm{h}}]= & {} \sum _{j=2}^\infty \frac{{{\mathcal {L}}}^j_\phi ({\mathrm{h}})}{j!}=\sum _{j=1}^\infty \frac{{{\mathcal {L}}}^{j+1}_\phi ({\mathrm{h}})}{(j+1)!}=-\sum _{j=1}^\infty \frac{{{\mathcal {L}}}^{j}_\phi ({\widetilde{f}})}{(j+1)!} \\ \Phi _1[g]= & {} \sum _{j=1}^\infty \frac{{{\mathcal {L}}}^j_\phi (g)}{j!}=\sum _{j=0}^\infty \frac{{{\mathcal {L}}}^{j+1}_\phi (g)}{(j+1)!}=\sum _{j=0}^\infty \frac{{{\mathcal {L}}}^{j}_\phi (g_1)}{(j+1)!} \end{aligned}$$

with $g_1:={{\mathcal {L}}}_\phi (g)=\{\phi , g\}$. The bounds in (83) are a consequence of equalities of the kind

$$\begin{aligned} {{\mathbf {I}}}_+-{{\mathbf {I}}}=\sum _{j=0}^\infty \frac{{{\mathcal {L}}}^{j+1}_\phi ({{\mathbf {I}}})}{(j+1)!}=\sum _{j=0}^\infty \frac{{{\mathcal {L}}}^{j}_\phi (-\partial _\varphi \phi )}{(j+1)!} \end{aligned}$$

(and similar). $\square$

The proof of the Theorem 4.1 goes through iterate applications of Lemma A.2.

We premise the following

Remark A.3

Replacing conditions in (79) with the stronger ones¹³

$$\begin{aligned} {3s^{\prime }<s,\quad 3\delta ^{\prime }<\delta ,\quad {{\mathcal {X}}}\left\| \mathfrak {I}\frac{\omega _{{\mathbf {I}}}}{\omega _y}\right\| _{\rho , r}<s^{\prime },\quad {{\mathcal {X}}}\left\| \frac{\omega _{{\mathbf {J}}}}{\omega _y}\right\| _{\rho , r}< \frac{\delta ^{\prime }}{\delta }} \end{aligned}$$

(86)

[and keeping (78), (80) unvaried] one can take, for $s_+$, $\delta _+$, $s_1$, $\delta _1$ the simpler expressions

$$\begin{aligned} {s_{+\mathrm new}=s-3s^{\prime },\quad \delta _{+\mathrm new}=\delta -3\delta ^{\prime }\ ,\quad s_{1\mathrm new}:=s-s^{\prime },\quad \delta _{1\mathrm new}=\delta -\delta ^{\prime }\ } \end{aligned}$$

(while keeping $r_+$, $\rho _+$, $\xi _+$, $r_1$, $\rho _1$, $\xi _1$ unvaried). Indeed, since $1-e^{-x}\le x$ for all x,

$$\begin{aligned} \delta _1=\delta e^{-{{\mathcal {X}}}\left\| \frac{\omega _{{\mathbf {J}}}}{\omega _y}\right\| _{\rho , r}} = \delta -\delta (1- e^{-{{\mathcal {X}}}\left\| \frac{\omega _{{\mathbf {J}}}}{\omega _y}\right\| _{\rho , r}})\ge \delta -\delta {{\mathcal {X}}}\left\| \frac{\omega _{{\mathbf {J}}}}{\omega _y}\right\| _{\rho , r}\ge \delta -\delta ^{\prime } =\delta _{1\mathrm new}. \end{aligned}$$

This also implies $\xi _+=\delta _1-\delta ^{\prime }\ge \delta -2\delta ^{\prime }=\xi _{+\mathrm new}$. That $s_+\ge s_{+\mathrm new}$, $s_1\ge s_{1\mathrm new}$ is even more immediate.

Now, we can proceed with the

Proof of Theorem 4.1

Let ${\widetilde{{\mathrm{c}}}}_{n,m}$ be as in Lemma A.2. We shall choose $\overline{\mathrm{c}}_{n,m}$ suitably large with respect to ${\widetilde{{\mathrm{c}}}}_{n,m}$.

We apply Lemma A.2 with

$$\begin{aligned} {2}\rho ^{\prime }=\frac{\rho }{3},\quad {3}s^{\prime }=\frac{s}{3},\quad {3}\delta ^{\prime }=\frac{\delta }{3},\quad {2}r^{\prime }=\frac{r}{3},\quad {2}\xi ^{\prime }=\frac{\xi }{3},\quad g\equiv 0. \end{aligned}$$

We make use of the stronger formulation described in Remark A.3. Conditions in (78) and the two former conditions in (86) are trivially true. The two latter inequalities in (86) reduce to

$$\begin{aligned} {{\mathcal {X}}}\left\| \mathfrak {I}\frac{\omega _{{\mathbf {I}}}}{\omega _y}\right\| _{\rho , r}<\frac{s}{9},\quad {{\mathcal {X}}}\left\| \frac{\omega _{{\mathbf {J}}}}{\omega _y}\right\| _{\rho , r}< \frac{1}{9}, \end{aligned}$$

and they are certainly satisfied by assumption (44), for $N>2$. Since

$$\begin{aligned} d=\min \{ \rho ^{\prime } s^{\prime }, r^{\prime }\xi ^{\prime }, {\delta ^{\prime }}^2 \}=\min \{ \rho s/{36}, r\xi /{54}, {\delta }^2/{81} \}\ge \frac{1}{{81}} \min \{ \rho s, r\xi , {\delta }^2 \}=\frac{{d}}{{81}}, \end{aligned}$$

we have that condition (80) is certainly implied by the last inequality in (44), once one chooses ${\mathrm{c}}_{n,m}>{81} {\widetilde{{\mathrm{c}}}}_{n,m}$. By Lemma A.2, it is then possible to conjugate $\mathrm{H}$ to

$$\begin{aligned} {\mathrm{H}}_1={\mathrm{h}}_0+{\overline{f}}+f_1 \end{aligned}$$

with $f_1\in {{\mathcal {O}}}_{\rho ^{(1)},s^{(1)},\delta ^{(1)}, r^{(1)},\xi ^{(1)},}$, where $(\rho ^{(1)},s^{(1)},\delta ^{(1)}, r^{(1)},\xi ^{(1)},):=2/3 (\rho , s, \delta , r, \xi )$ and

$$\begin{aligned} \Vert f_1\Vert _{\rho ^{(1)},s^{(1)},\delta ^{(1)}, r^{(1)},\xi ^{(1)},}\le {81}{\widetilde{{\mathrm{c}}}}_{n,m} \frac{{{\mathcal {X}}}}{\mathrm{d}} \left\| \frac{{\widetilde{f}}}{\omega _y}\right\| _{\rho , s, \delta , r, \xi }\Vert f\Vert _{\rho , s, \delta , r, \xi }\le \frac{\Vert f\Vert _{\rho , s, \delta , r, \xi }}{2}\nonumber \\ \end{aligned}$$

(87)

since ${\mathrm{c}}_{n,m}\ge {162} {\widetilde{{\mathrm{c}}}}_{n,m}$ and $N\ge 1$. Now, we aim to apply Lemma A.2N times, again as described in Remark A.3, each time with parameters

$$\begin{aligned} \rho _j^{\prime }=\frac{\rho }{6N},\quad s_j^{\prime }=\frac{s}{{9}N},\quad \delta _j^{\prime }=\frac{\delta }{{9}N},\quad r_j^{\prime }=\frac{r}{6N},\quad \xi _j^{\prime }=\frac{\xi }{6N}. \end{aligned}$$

(88)

Therefore, we find, at each step

$$\begin{aligned}&\rho ^{(j+1)}:=\rho ^{(1)}-j\frac{\rho }{3N},\quad s^{(j+1)}:=s^{(1)}-j\frac{s}{3N},\quad \delta ^{(j+1)}:=\delta ^{(1)}-j\frac{\delta }{3N}\nonumber \\&r^{(j+1)}:=r^{(1)}-j\frac{r}{3N},\quad \xi ^{(j+1)}:=\xi ^{(1)}-j\frac{\xi }{3N}\nonumber \\&\rho _1^{(j)}:=\rho ^{(j)},\quad s_1^{(j)}:=s^{(j)}-\frac{s}{9N},\quad \delta _1^{(j)}:=\delta ^{(j)}-\frac{\delta }{9N}\nonumber \\&r_1^{(j)}:=r^{(j)},\quad \xi _1^{(j)}:=\xi ^{(j)},\quad {{\mathcal {X}}}_j:=\sup \{|x|:\ x\in {{\mathbb {X}}}_{\xi _j}\} \end{aligned}$$

(89)

with $1\le j\le N$.

We assume that for a certain $1\le i\le N$ and all $1\le j\le i$, we have ${\mathrm{H}}_j\in {{\mathcal {O}}}_{\rho ^{(j)},s^{(j)},\delta ^{(j)}, r^{(j)},\xi ^{(j)},}$ of the form

$$\begin{aligned}&{\mathrm{H}}_j={\mathrm{h}}_0+g_{j-1}+f_j, \quad g_{j-1}\in {{\mathcal {N}}}_{\rho ^{(j)},s^{(j)},\delta ^{(j)}, r^{(j)},\xi ^{(j)},},\quad g_{j-1}-g_{j-2}={\overline{f}}_{j-1} \nonumber \\\end{aligned}$$

(90)

$$\begin{aligned}&\Vert f_j\Vert _{\rho ^{(j)},s^{(j)},\delta ^{(j)}, r^{(j)},\xi ^{(j)},}\le \frac{\Vert f_1\Vert _{\rho ^{(1)},s^{(1)},\delta ^{(1)}, r^{(1)},\xi ^{(1)},}}{2^{j-1}} \end{aligned}$$

(91)

with $g_{-1}\equiv 0$, $g_0={\overline{f}}$. We want to prove that, if $i<N$, Lemma A.2 can be applied once again, so as to conjugate ${\mathrm{H}}_i$ to a suitable ${\mathrm{H}}_{i+1}$ such that (90)–(91) are true with $j=i+1$. To this end, according to the discussion in Remark A.3, we check the stronger inequalities

$$\begin{aligned}&{2{\rho ^{\prime }_i}<\rho ^{(i)},\quad 2r^{\prime }_i<r^{(i)},\quad 2\xi ^{\prime }_i<\xi ^{(i)}}\end{aligned}$$

(92)

$$\begin{aligned}&{{\mathcal {X}}}_i\left\| \mathfrak {I}\frac{\omega _{{\mathbf {I}}}}{\omega _y}\right\| _{\rho _i, r_i}<s^{\prime }_i ,\quad {{\mathcal {X}}}_i\left\| \frac{\omega _{{\mathbf {J}}}}{\omega _y}\right\| _{\rho _i, r_i}< \frac{\delta ^{\prime }_i}{\delta _i} \end{aligned}$$

(93)

$$\begin{aligned}&{\widetilde{{\mathrm{c}}}}_{n,m}\frac{{{\mathcal {X}}}_i}{d_i} \left\| \frac{f_i}{\omega _y}\right\| _{\rho _i,s_i,\delta _i, r_i,\xi _i}<1. \end{aligned}$$

(94)

where $d_i:=\min \{ \rho _i^{\prime } s_i^{\prime }, r_i^{\prime }\xi _i^{\prime }, {\delta ^{\prime }}_i^2 \}$. Conditions (92) and (93) are certainly verified, since in fact they are implied by the definitions above (using also $\delta _i\le \frac{2}{3}\delta$, ${{\mathcal {X}}}_i\le {{\mathcal {X}}}$) and the two former inequalities in (44). To check the validity of (94), we firstly observe that

$$\begin{aligned} d_i=\min \{\rho ^{\prime (i)} s^{\prime (i)},\ (\delta ^{\prime (i)})^2,\ r^{\prime (i)}\xi ^{\prime }_j,\}\ge \frac{\mathrm{d}}{{81}N^2}. \end{aligned}$$

(95)

Using then ${\mathrm{c}}_{n,m}>{162} {\widetilde{{\mathrm{c}}}}_{n,m}$,${{\mathcal {X}}}_i<{{\mathcal {X}}}$, Eq. (87), the inequality in (91) with $j=i$ and the last inequality in (44), we easily conclude

$$\begin{aligned}&\Vert f_i\Vert _{\rho ^{(i)},s^{(i)},\delta ^{(i)}, r^{(i)},\xi ^{(i)}}\le \Vert f_1\Vert _{\rho ^{(1)},s^{(1)},\delta ^{(1)}, r^{(1)},\xi ^{(1)},}\le {81}{\widetilde{{\mathrm{c}}}}_{n,m} \frac{{{\mathcal {X}}}}{\mathrm{d}} \left\| \frac{{\widetilde{f}}}{\omega _y}\right\| _{\rho , s, \delta , r, \xi }\Vert { f}\Vert _{\rho , s, \delta , r, \xi }\\&\quad \le \frac{1}{{\widetilde{{\mathrm{c}}}}_{n,m}}\frac{\mathrm{d}}{{81} N^2}\frac{1}{{{\mathcal {X}}}} \left\| \frac{1}{\omega _y}\right\| _{\rho , r}^{-1}\le \frac{1}{{\widetilde{{\mathrm{c}}}}_{n,m}}\frac{d_i}{{{\mathcal {X}}}_i} \left\| \frac{1}{\omega _y}\right\| _{\rho ^{(i)}, r^{(i)}}^{-1} \end{aligned}$$

which implies (94).

Then, the iterative lemma is applicable to ${\mathrm{H}}_i$, which is conjugated to

$$\begin{aligned} {\mathrm{H}}_{i+1}={\mathrm{h}}_0+g_{i}+f_{i+1}, \quad g_{i}\in {{\mathcal {N}}}_{\rho ^{(i+1)},s^{(i+1)},\delta ^{(i+1)}, r^{(i+1)},\xi ^{(i+1)}},\quad g_{i}-g_{i-1}={\overline{f}}_{i}\nonumber \\ \end{aligned}$$

(96)

with $g_{i}$, $f_{i+1}$ satisfying (90) with $j=i+1$. We prove that (91) holds with $j=i+1$, so as to complete the inductive step. By the thesis of the iterative lemma,

$$\begin{aligned} \left\| f_{i+1}\right\| _{\rho ^{(i+1)}, s^{(i+1)}, \delta ^{(i+1)}, r^{(i+1)}, \xi ^{(i+1)}}\le & {} {\widetilde{{\mathrm{c}}}}_{n,m}\Big (\frac{{{\mathcal {X}}}_i}{{d}_i}\left\| \frac{{\widetilde{f}}_i}{\omega _y}\right\| _{\rho ^{(i)}, s^{(i)}, \delta ^{(i)}, r^{(i)}, \xi ^{(i)}}\Vert f_i\Vert _{\rho ^{(i)}, s^{(i)}, \delta ^{(i)}, r^{(i)}, \xi ^{(i)}}\\&+\, \Vert \{\phi _i, g_{i-1}\}\Vert _{\rho ^{(i)}_1-{\rho ^{\prime }}^{(i)}, s^{(i)}_1-{s^{\prime }}^{(i)}, \delta ^{(i)}_1-{\delta ^{\prime }}^{(i)}, r^{(i)}_1-{r^{\prime }}^{(i)}, \xi ^{(i)}_1-{\xi ^{\prime }}^{(i)}}\Big ) \end{aligned}$$

On the other hand, using (87), (95) and the last assumption in (44) and (91) with $j=i$, we obtain

$$\begin{aligned} \frac{{{\mathcal {X}}}_i}{{d}_i}\left\| \frac{{\widetilde{f}}_i}{\omega _y}\right\| _{\rho ^{(i)}, s^{(i)}, \delta ^{(i)}, r^{(i)}, \xi ^{(i)}}\le & {} \frac{81N^2\chi _0}{\mathrm{d}}\left\| \frac{1}{\omega _y}\right\| \left\| {\widetilde{f}}_i\right\| \le \frac{81N^2\chi _0}{{\mathrm{d}}}\left\| \frac{1}{\omega _y}\right\| \left\| f_i\right\| \\\le & {} \frac{81N^2\chi _0}{\mathrm{d}}\left\| \frac{1}{\omega _y}\right\| \left\| f_1\right\| \\\le & {} \frac{(81)^2 {\widetilde{{\mathrm{c}}}}_{n, m} N^2\chi ^2_0}{\mathrm{d}^2}\left\| \frac{1}{\omega _y}\right\| \left\| \frac{{\widetilde{f}}}{\omega _y}\right\| _{\rho , s, \delta , r, \xi }\Vert f\Vert _{\rho , s, \delta , r, \xi } \\\le & {} \frac{1}{6{\widetilde{{\mathrm{c}}}}_{n, m}}. \end{aligned}$$

Furthermore, using (76) with $j=1$, (82) and

$$\begin{aligned} \Vert g_0\Vert _{\rho ^{(i)}_1-{\rho ^{\prime }}^{(i)}, s^{(i)}_1-{s^{\prime }}^{(i)}, \delta ^{(i)}_1-{\delta ^{\prime }}^{(i)}, r^{(i)}_1-{r^{\prime }}^{(i)}, \xi ^{(i)}_1-{\xi ^{\prime }}^{(i)}}\le & {} \Vert f\Vert _{\rho ^{(i)}_1-{\rho ^{\prime }}^{(i)}, s^{(i)}_1-{s^{\prime }}^{(i)}, \delta ^{(i)}_1-{\delta ^{\prime }}^{(i)}, r^{(i)}_1-{r^{\prime }}^{(i)}, \xi ^{(i)}_1-{\xi ^{\prime }}^{(i)}}\\\le & {} \Vert f\Vert _{\rho ^{(0)}, s^{(0)}, \delta ^{(0)}, r^{(0)}, \xi ^{(0)}} \end{aligned}$$

and, with $j=1$, $\dots$, $i-1$

$$\begin{aligned} \Vert g_j-g_{j-1}\Vert _{\rho ^{(i)}_1-{\rho ^{\prime }}^{(i)}, s^{(i)}_1-{s^{\prime }}^{(i)}, \delta ^{(i)}_1-{\delta ^{\prime }}^{(i)}, r^{(i)}_1-{r^{\prime }}^{(i)}, \xi ^{(i)}_1-{\xi ^{\prime }}^{(i)}}\le & {} \Vert f_j\Vert _{\rho ^{(i)}_1-{\rho ^{\prime }}^{(i)}, s^{(i)}_1-{s^{\prime }}^{(i)}, \delta ^{(i)}_1-{\delta ^{\prime }}^{(i)}, r^{(i)}_1-{r^{\prime }}^{(i)}, \xi ^{(i)}_1-{\xi ^{\prime }}^{(i)}} \nonumber \\\le & {} \Vert f_j\Vert _{\rho ^{(j)},s^{(j)},\delta ^{(j)}, r^{(j)},\xi ^{(j)},}\nonumber \\\le & {} \frac{\Vert f_1\Vert _{\rho ^{(1)},s^{(1)},\delta ^{(1)}, r^{(1)},\xi ^{(1)},}}{2^{j-1}} \end{aligned}$$

(97)

we obtain

$$\begin{aligned}&\Vert \{\phi _i, g_{i-1}\}\Vert _{\rho ^{(i)}_1-{\rho ^{\prime }}^{(i)}, s^{(i)}_1-{s^{\prime }}^{(i)}, \delta ^{(i)}_1-{\delta ^{\prime }}^{(i)}, r^{(i)}_1-{r^{\prime }}^{(i)}, \xi ^{(i)}_1-{\xi ^{\prime }}^{(i)}}\\&\quad \le \Vert \{\phi _i, g_{0}\}\Vert _{\rho ^{(i)}_1-{\rho ^{\prime }}^{(i)}, s^{(i)}_1-{s^{\prime }}^{(i)}, \delta ^{(i)}_1-{\delta ^{\prime }}^{(i)}, r^{(i)}_1-{r^{\prime }}^{(i)}, \xi ^{(i)}_1-{\xi ^{\prime }}^{(i)}}\\&\qquad +\sum _{j=1}^{i-1}\Vert \{\phi _i, g_{j}-g_{j-1}\}\Vert _{\rho ^{(i)}_1-{\rho ^{\prime }}^{(i)}, s^{(i)}_1-{s^{\prime }}^{(i)}, \delta ^{(i)}_1-{\delta ^{\prime }}^{(i)}, r^{(i)}_1-{r^{\prime }}^{(i)}, \xi ^{(i)}_1-{\xi ^{\prime }}^{(i)}}\\&\quad \le 2\frac{\overline{\mathrm{c}}_{n, m}\chi _i}{d_i}\left\| \frac{{\widetilde{f}}_i}{\omega _y}\right\| _{\rho ^{(i)}, s^{(i)}, \delta ^{(i)}, r^{(i)}, \xi ^{(i)}}\Big (\frac{1}{N} \Vert g_0\Vert _{\rho ^{(i)}_1-{\rho ^{\prime }}^{(i)}, s^{(i)}_1-{s^{\prime }}^{(i)}, \delta ^{(i)}_1-{\delta ^{\prime }}^{(i)}, r^{(i)}_1-{r^{\prime }}^{(i)}, \xi ^{(i)}_1-{\xi ^{\prime }}^{(i)}}\\&\qquad +\sum _{j=1}^{i-1}\Vert g_{j}-g_{j-1}\Vert _{\rho ^{(i)}_1-{\rho ^{\prime }}^{(i)}, s^{(i)}_1-{s^{\prime }}^{(i)}, \delta ^{(i)}_1-{\delta ^{\prime }}^{(i)}, r^{(i)}_1-{r^{\prime }}^{(i)}, \xi ^{(i)}_1-{\xi ^{\prime }}^{(i)}} \Big )\\&\quad \le 162 N^2\frac{\overline{\mathrm{c}}_{n, m}\chi _i}{\mathrm{d}}\left\| \frac{1}{\omega _y}\right\| \left( \frac{\Vert f\Vert _{\rho , s, \delta , r, \xi }}{N}+2\times {81}{\widetilde{{\mathrm{c}}}}_{n,m} \frac{{{\mathcal {X}}}}{\mathrm{d}} \left\| \frac{{\widetilde{f}}}{\omega _y}\right\| _{\rho , s, \delta , r, \xi }\Vert { f}\Vert _{\rho , s, \delta , r, \xi } \right) \\&\qquad \times \left\| f_i\right\| _{\rho ^{(i)}, s^{(i)}, \delta ^{(i)}, r^{(i)}, \xi ^{(i)}}\le \frac{1}{3}\left\| f_i\right\| _{\rho ^{(i)}, s^{(i)}, \delta ^{(i)}, r^{(i)}, \xi ^{(i)}} \end{aligned}$$

where the last summand is to be taken into account only when $i\ge 2$ and we have used that, when $j=0$, $d_i$ can be replaced with $N d_i$. Collecting the bounds above, we find (91) holds with $j=i+1$. Then, the iterative lemma can be applied N times, and we get (46) as a direct consequence of (87) and (97) and of the validity of (91) for all $1\le i\le N$. The inequalities in (47) follow from (83) and (88). For example,

$$\begin{aligned} |{{\mathbf {I}}}_*-{{\mathbf {I}}}_0|\le \sum _{j=1}^N|{{\mathbf {I}}}^{(j)}-{{\mathbf {I}}}^{(j-1)}|\le 2\frac{\chi _{0}}{{s^{\prime }}^{(0)}}\left\| \frac{f_0}{\omega _y}\right\| + 4\frac{\chi _{1}}{{s^{\prime }}^{(1)}}\left\| \frac{1}{\omega _y}\right\| \Vert f_1\Vert \le 19\frac{\chi _{0}}{{s}^{(0)}}\left\| \frac{f_0}{\omega _y}\right\| , \end{aligned}$$

etc. $\square$