Heteroclinic Dynamics of Localized Frequency Synchrony: Stability of Heteroclinic Cycles and Networks

Abstract

Coupled populations of identical phase oscillators with higher-order interactions can give rise to heteroclinic cycles between invariant sets where populations show distinct frequencies. For these heteroclinic cycles to be observable, they have to have some stability properties. In this paper, we complement the existence results for heteroclinic cycles given in a companion paper by proving stability results for heteroclinic cycles for coupled oscillator populations consisting of two oscillators each. Moreover, we show that for systems with four coupled phase oscillator populations, there are distinct heteroclinic cycles that form a heteroclinic network. While such networks cannot be asymptotically stable, the local attraction properties of each cycle in the network can be quantified by stability indices. We calculate these stability indices in terms of the coupling parameters between oscillator populations. Hence, our results elucidate how oscillator coupling influences sequential transitions along a heteroclinic network where individual oscillator populations switch sequentially between a high and a low frequency regime; such dynamics appear relevant for the functionality of neural oscillators.

1 Introduction

Interacting populations of identical oscillators can generate a range of collective dynamics (Strogatz 2004), ranging from complete (global) synchronization to synchrony patterns where synchrony is localized in some populations. These synchrony patterns include patterns of localized frequency synchrony where some populations oscillate faster (or slower) than others (Ashwin and Burylko 2015; Bick and Ashwin 2016; Omel’chenko 2018). For coupled oscillator populations with higher-order interactions—including higher harmonics or nonlinear interactions between three or more oscillators (nonpairwise terms)—which arise naturally in phase reductions (Ashwin and Rodrigues 2016; León and Pazó 2019), heteroclinic structures between patterns of localized frequency synchrony are possible (Bick 2018, 2019). Heteroclinic dynamics are not only of interest in their own right (see Weinberger and Ashwin 2018 for a recent review), but have also been related, for example, to computation in neural systems (Rabinovich et al. 2006; Neves and Timme 2012; Ashwin et al. 2016). In the companion paper (Bick 2019), we showed the existence of heteroclinic cycles between invariant sets with localized frequency synchrony in three coupled populations. In particular, we obtained explicit existence conditions for heteroclinic cycles in terms of the interaction between the phase oscillator populations.

For heteroclinic dynamics between invariant set with localized frequency synchrony to be observable over extended timescales, the heteroclinic cycles and networks have to attract some initial conditions. Apart from asymptotic stability and instability, heteroclinic cycles can display various intermediate forms of nonasymptotic stability: These range from fragmentary asymptotic stability (“attracting more than nothing”) to essential asymptotic stability (“attracting almost everything”). Podvigina and Ashwin (2011) introduced a stability index to quantify attraction along trajectories. This stability index is defined for any dynamically invariant set and thus provides a convenient tool to describe the stability of heteroclinic trajectories within a cycle or network.¹ Recently, Garrido-da-Silva and Castro (2019) derived explicit expressions for the stability indices for the fairly general class of quasi-simple heteroclinic cycles. Such expressions are particularly useful to describe the stability of heteroclinic cycles that are part of a network consisting of more than one cycle.

The main contributions of this paper are stability results for heteroclinic cycles and networks between invariant sets with localized frequency synchrony in coupled populations of phase oscillators. In particular, we prove stability results which allow to obtain explicit relations between the coupling parameters of the oscillator populations and the stability properties of heteroclinic structures in phase space. Importantly, this progress contributes to the question how the coupling properties (its topology and functional form) of interacting oscillatory units shape the overall collective dynamics. The implications of the coupling properties on the dynamics local to synchrony have been studied extensively; see, for example, Pecora and Carroll (1998), Pereira et al. (2014). By contrast, our results relate to how the coupling properties shape global dynamical features (such as heteroclinic cycles and networks) for a class of vector fields relevant to describe real-world coupled nonlinear oscillator populations.

We focus on three and four coupled phase oscillator populations with two oscillators per population. Due to the existence of invariant subspaces, the heteroclinic cycles are quasi-simple. Consequently, we apply the stability results of Garrido-da-Silva and Castro (2019) to calculate the stability indices. We first consider three coupled oscillator populations to calculate stability indices for the heteroclinic cycles in Bick (2019). We then show that four coupled oscillator populations support a heteroclinic network which contains two distinct heteroclinic cycles of the type considered before. Their stability properties are then calculated using the tools developed for three populations and we comment on the stability of the whole network. Since our stability conditions explicitly depend on the coupling parameters of the oscillator populations, our results elucidate how the coupling structure of the system shapes the asymptotic dynamical behavior. Moreover, they highlight the utility of the general stability results for quasi-simple heteroclinic cycles (Garrido-da-Silva and Castro 2019) for heteroclinic cycles on arbitrary manifolds.

The remainder of this paper is structured as follows. The following section summarizes facts on (robust) heteroclinic cycles, nonasymptotic stability, and coupled populations of phase oscillators. In Sect. 3, we calculate the stability indices along the heteroclinic cycle in the companion paper (Bick 2019) for a system of three populations. Such cycles are contained in a heteroclinic network for four coupled populations as shown in Sect. 4, and we calculate their stability properties. We also give some numerical results and comment on the stability of the network as a whole. Finally, we give some concluding remarks in Sect. 5.

2 Preliminaries

To set the stage, we review some results about heteroclinic cycles, their stability properties, and coupled populations of phase oscillators; the notation here follows the companion paper (Bick 2019).

2.1 Heteroclinic Cycles and Their Stability

Let ${\mathcal {M}}$ be a smooth d-dimensional manifold and let X be a smooth vector field on ${\mathcal {M}}$. For a hyperbolic equilibrium $\xi \in {\mathcal {M}}$, define the stable manifold $W^\text {s}(\xi )$ and unstable manifold $W^\text {u}(\xi )$ as usual.

Definition 2.1

A heteroclinic cycle ${{\mathbf {\mathsf{{C}}}} }$ consists of a finite number of hyperbolic equilibria $\xi _q\in {\mathcal {M}}$, $q=1,\ldots ,Q$, together with heteroclinic trajectories

$$\begin{aligned}{}[\xi _q\rightarrow \xi _{q+1}] \subset W^\text {u}(\xi _q)\cap W^\text {s}(\xi _{q+1})\ne \emptyset \end{aligned}$$

where indices are taken modulo Q.

A heteroclinic network ${{\mathbf {\mathsf{{N}}}} }$ is a connected union of two or more distinct heteroclinic cycles.

For simplicity, we write ${{\mathbf {\mathsf{{C}}}} }=(\xi _1, \ldots , \xi _Q)$. If ${\mathcal {M}}$ is a quotient of a higher-dimensional manifold and ${{\mathbf {\mathsf{{C}}}} }$ is a heteroclinic cycle in ${\mathcal {M}}$, we also call the lift of ${{\mathbf {\mathsf{{C}}}} }$ a heteroclinic cycle. The same goes for a heteroclinic network ${{\mathbf {\mathsf{{N}}}} }$.

While heteroclinic cycles are in general a nongeneric phenomenon, they can be robust if all connections are of saddle–sink type in (lower-dimensional) subspaces. Let ${{\mathbf {\mathsf{{C}}}} }=(\xi _1, \ldots , \xi _Q)$ be a heteroclinic cycle. If there are flow-invariant submanifolds $P_q\subset {\mathcal {M}}$ such that $[\xi _q\rightarrow \xi _{q+1}]\subset P_q$ is a saddle–sink connection, then ${{\mathbf {\mathsf{{C}}}} }$ is robust with respect to perturbations of X which preserve the invariant sets $P_q$.

Robust heteroclinic cycles may arise for example in dynamical systems with symmetry. Let $\Gamma$ be a finite group which acts on ${\mathcal {M}}$. For a subgroup $H\subset \Gamma$, define the set ${{\,\mathrm{Fix}\,}}(H) = \left\{ \, x\in {\mathcal {M}}\,\left| \;\gamma x=x\ \forall \gamma \in H\right. \right\}$ of points fixed under H; this is invariant under the flow generated by X. For $x\in {\mathcal {M}}$, let $\Gamma x=\left\{ \, \gamma x\,\left| \;\gamma \in \Gamma \right. \right\}$ denote its group orbit and $\Sigma (x) = \left\{ \, \gamma \in \Gamma \,\left| \;\gamma x = x\right. \right\}$ its isotropy subgroup. Now assume that the smooth vector field X is a $\Gamma$-equivariant vector field on ${\mathcal {M}}$, that is, the action of the group commutes with X. Any heteroclinic cycle with $P_q = {{\,\mathrm{Fix}\,}}(\Sigma _q)$ where $\Sigma _q$ are isotropy subgroups is robust to $\Gamma$-equivariant perturbations of X, that is, $\Gamma$-equivariant vector fields close to X will have a heteroclinic cycle close to ${{\mathbf {\mathsf{{C}}}} }$; see Krupa (1997) for more details.

2.1.1 Nonasymptotic Stability

Heteroclinic cycles may have intricate nonasymptotic stability properties. We briefly recall some definitions that formalize these; we state them for $\mathbb {R}^d$ but they generalize to more general manifolds ${\mathcal {M}}$.

For $\varepsilon >0$, write $B_{\varepsilon }(A)$ for an $\varepsilon$-neighborhood of a set $A \subset {\mathbb {R}}^d$ and ${\mathcal {B}}(A)$ for its basin of attraction, i.e., the set of points $x \in {\mathbb {R}}^d$ with $\omega$-limit set in A. For $\delta >0$, the $\delta$-local basin of attraction is

$$\begin{aligned} {\mathcal {B}}_\delta (A):=\left\{ \, x \in {\mathcal {B}}(A)\,\left| \;\forall t>0:\Phi _t(x) \in B_\delta (A)\right. \right\} , \end{aligned}$$

where $\Phi _t$ is the flow generated by X. Let $\ell$ denote the Lebesgue measure.

Definition 2.2

(Podvigina 2012) An invariant set A is fragmentarily asymptotically stable (f.a.s.) if $\ell ({{\mathcal {B}}}_\delta (A))>0$ for any $\delta >0$.

Being f.a.s. is not necessarily a very strong form of attraction. A set that is not even f.a.s. is usually called completely unstable, see also Podvigina (2012). Melbourne (1991) introduces the stronger notion of essential asymptotic stability, which we quote here in the formulation of Brannath (1994).

Definition 2.3

(Brannath 1994, Definition 1.2) A compact invariant set A is called essentially asymptotically stable (e.a.s.) if it is asymptotically stable relative² to a set $\Upsilon \subset {\mathbb {R}}^d$ with the property that

$$\begin{aligned} \lim \limits _{\varepsilon \rightarrow 0} \frac{\ell (B_{\varepsilon }(A) \cap \Upsilon )}{\ell (B_\varepsilon (A))} = 1. \end{aligned}$$

(1)

Podvigina and Ashwin (2011) introduced the concept of a local stability index³${\mathfrak {s}}(x)\in [-\infty ,+\infty ]$ to quantify stability and attraction. It is constant along trajectories, so to characterize stability/attraction of a heteroclinic cycle with one-dimensional connections, it suffices to consider finitely many stability indices. Let ${\mathfrak {s}}_q$ denote the stability index along $[\xi _{q-1}\rightarrow \xi _{q}]$. For our purposes, it is enough to note that (under some mild assumptions) a heteroclinic cycle ${{\mathbf {\mathsf{{C}}}} }=(\xi _1, \ldots ,\xi _Q)$ is completely unstable if ${\mathfrak {s}}_q=-\infty$ for all q, it is f.a.s. as soon as ${\mathfrak {s}}_q>-\infty$ for some q, and it is e.a.s. if and only if ${\mathfrak {s}}_q>0$ for all $q=1,\ldots ,Q$. See Lohse (2015, Theorem 3.1) for details.

2.1.2 Stability of Quasi-Simple Heteroclinic Cycles

The stability indices can be calculated for specific classes of heteroclinic cycles. Let ${{\mathbf {\mathsf{{C}}}} }=(\xi _1, \ldots , \xi _Q)$ be a robust heteroclinic cycle on ${\mathcal {M}}$. As above, let $P_q$ denote the flow-invariant sets which contain the heteroclinic connections. Let $T_q := \mathrm {T}_{\xi _q}{\mathcal {M}}$ denote the tangent space of ${\mathcal {M}}$ at $\xi _q$. For subspaces $V\subset W\subset T_q$, write $W\ominus V$ for the orthogonal complement of V in W. In slight abuse of notation, define $P_q^- := \mathrm {T}_{\xi _q} P_{q-1}$ and $P_q^{+} := \mathrm {T}_{\xi _q} P_{q}$ to be the tangent spaces of $P_{q-1}$ and $P_q$ in $T_q$, respectively. These are linear subspaces of $T_q$ of the same dimension as $P_{q-1}$ (which contains the incoming saddle connection) and $P_q$ (containing the outgoing connection), respectively. Set $L_q := P_{q}^- \cap P_q^+$.

Definition 2.4

The robust heteroclinic cycle ${{\mathbf {\mathsf{{C}}}} }$ is quasi-simple if $\dim (P_q^- \ominus L_q)=\dim (P_q^+ \ominus L_q)=1$ for all $q\in \left\{ 1, \ldots , Q\right\}$.

Remark 2.5

Note that this is a slight generalization of the definition given by Garrido-da-Silva and Castro in (2019) to arbitrary manifolds. In particular, the condition in Definition 2.4 implies that $\dim (P_{q-1})=\dim (P_q)$.

As usual, an eigenvalue of the Jacobian $\mathrm {d}X(\xi _q)$ is radial if its associated eigenvector is in $L_q$, contracting if the associated eigenvector is in $P_{q}^-\ominus L_q$, expanding if the associated eigenvector is in $P_{q}^+\ominus L_q$, and transverse otherwise. In other words, a cycle is quasi-simple if it has unique expanding and contracting directions at each equilibrium, and thus one-dimensional saddle connections.

The standard way to analyze the stability of heteroclinic cycles is to write down a Poincaré return map with linearized dynamics local to the equilibria as well as globally along the connecting orbits; cf. Krupa and Melbourne (1995). For quasi-simple cycles whose global maps are rescaled permutations of the local coordinate axes Garrido-da-Silva and Castro (2019) showed how their (asymptotic or nonasymptotic) stability can be calculated solely from the properties of the linearization at the equilibria of the cycle. More precisely, the stability of each equilibrium $\xi _q$ along the cycle is encoded in a transition matrix ${{{\textsf {\textit{M}}}}}_q$ whose entries are rational functions of the eigenvalues at $\xi _q$. The stability of the cycle is determined by properties of these matrices. We explain this technique in more detail when we apply it in Sect. 3. Note that this immediately implies that the results in Garrido-da-Silva and Castro (2019) carry over to our definition of a quasi-simple heteroclinic cycle since the stability does not depend on other global properties.

For ease of reference, we recall the stability results from Garrido-da-Silva and Castro (2019, Theorems 3.4, 3.10) in a condensed form. For a heteroclinic cycle ${{\mathbf {\mathsf{{C}}}} }=(\xi _1,\ldots ,\xi _Q)$ with transition matrices ${{{\textsf {\textit{M}}}}}_q$, set ${{{\textsf {\textit{M}}}}}^{(q)}:={{{\textsf {\textit{M}}}}}_{q-1}\cdots {{{\textsf {\textit{M}}}}}_1{{{\textsf {\textit{M}}}}}_Q\cdots {{{\textsf {\textit{M}}}}}_{q+1}{{{\textsf {\textit{M}}}}}_q$. All ${{{\textsf {\textit{M}}}}}^{(q)}$ have the same eigenvalues. If none of the ${{{\textsf {\textit{M}}}}}_q$ has a negative entry—there are no repelling transverse directions—we have the following result, which is a dichotomy between asymptotic stability and complete instability.

Proposition 2.6

(Garrido-da-Silva and Castro 2019, Theorem 3.4) Let ${{\mathbf {\mathsf{{C}}}} }$ be a quasi-simple heteroclinic cycle with rescaled permutations of the local coordinate axes as global maps and transition matrices ${{{\textsf {\textit{M}}}}}_q$, $q=1,\ldots ,Q$. Suppose that all entries of all ${{{\textsf {\textit{M}}}}}_q$ are nonnegative.

• (i) If ${{{\textsf {\textit{M}}}}}^{(1)}$ satisfies $\left| \lambda ^{\max }\right| >1$, then ${\mathfrak {s}}_q=+\infty$ for all $q=1,\ldots ,Q$ and the cycle ${{\mathbf {\mathsf{{C}}}} }$ is asymptotically stable.

• (ii) Otherwise, ${\mathfrak {s}}_q=-\infty$ for all $q=1,\ldots ,Q$ and ${{\mathbf {\mathsf{{C}}}} }$ is completely unstable.

If the transition matrices ${{{\textsf {\textit{M}}}}}_q$ contain negative entries—there are transversely repelling directions, for example, if the cycle is part of a network—then additional criteria have to be satisfied in order for the cycle to possess some form of nonasymptotic stability. For a matrix ${{{\textsf {\textit{M}}}}}$, let $\lambda ^{\max }$ denote the maximal eigenvalue and $u^\text {max}=(u^\text {max}_1,\ldots ,u^\text {max}_d)$ the corresponding eigenvector. Define the conditions (cf. Garrido-da-Silva and Castro 2019, Lemma 3.2)

• (C1) $\lambda ^{\max }$ is real,

• (C2) $\lambda ^{\max }>1$,

• (C3) $u^\text {max}_m u^\text {max}_n>0$ for all $m,n=1, \ldots , d$.

Generally, stability indices are evaluated as a function of the local stability properties at the equilibrium points (Podvigina and Ashwin 2011); for quasi-simple cycles in arbitrary dimension (Garrido-da-Silva and Castro 2019), denote this function by $F^{\text {ind}}$. Later on, we will consider three-dimensional transition matrices and for $\beta =(\beta _1, \beta _2, \beta _3) \in {\mathbb {R}}^3\smallsetminus \left\{ 0\right\}$, this function reads

$$\begin{aligned} F^{\text {ind}}(\beta ):= {\left\{ \begin{array}{ll} +\infty \quad&\begin{array}{l} \text {if }\min (\beta _1,\beta _2,\beta _3)\ge 0, \end{array}\\ -\frac{\beta _1+\beta _2+\beta _3}{\min (\beta _1,\beta _2,\beta _3)} \quad &{} \begin{array}{l} \text {if }\beta _1+\beta _2+\beta _3>0\\ \quad \text { and }\min (\beta _1,\beta _2,\beta _3)<0, \end{array}\\ 0 \quad &{} \begin{array}{l} \text {if}\ \beta _1+\beta _2+\beta _3=0, \end{array}\\ \frac{\beta _1+\beta _2+\beta _3}{\max (\beta _1,\beta _2,\beta _3)} \quad &{} \begin{array}{l} \text {if}\ \beta _1+\beta _2+\beta _3<0\\ \quad \text { and }\max (\beta _1,\beta _2,\beta _3)>0, \end{array}\\ -\infty \quad &{} \begin{array}{l} \text {if }\max (\beta _1,\beta _2,\beta _3)\le 0. \end{array}\\ \end{array}\right. } \end{aligned}$$

The following proposition summarizes the second stability result adapted to our setting.

Proposition 2.7

(Garrido-da-Silva and Castro 2019, Theorem 3.10) Let ${{\mathbf {\mathsf{{C}}}} }$ be a quasi-simple heteroclinic cycle with rescaled permutations of the local coordinate axes as global maps and transition matrices ${{{\textsf {\textit{M}}}}}_q$, $q=1,\ldots ,Q$. Suppose that at least one ${{{\textsf {\textit{M}}}}}_q$ has at least one negative entry.

• (a) If there is at least one q such that the matrix ${{{\textsf {\textit{M}}}}}^{(q)}$ does not satisfy conditions (C1)–(C3), then ${\mathfrak {s}}_q=-\infty$ for all $q=1,\ldots ,Q$ and ${{\mathbf {\mathsf{{C}}}} }$ is completely unstable.

• (b) If all ${{{\textsf {\textit{M}}}}}^{(q)}$ satisfy conditions (C1)–(C3), then ${{\mathbf {\mathsf{{C}}}} }$ is f.a.s. and there exist $\beta ^{(1)},\ldots ,\beta ^{(s)} \in {\mathbb {R}}^3$ such that the stability indices for ${{\mathbf {\mathsf{{C}}}} }$ are given by

  $$\begin{aligned}{\mathfrak {s}}_q=\min \limits _{l=1,\ldots ,s}F^\mathrm{ind}\big (\beta ^{(l)}\big ).\end{aligned}$$

The vectors $\beta ^{(l)}$ that determine the stability indices depend on the local stability at the equilibria: They are rows of the transition matrices (and their products) with at least one negative entry. The number s relates to the number of such rows in the transition matrices (and their products), see Garrido-da-Silva and Castro (2019) for details.

2.2 Coupled Populations of Phase Oscillators

Consider $M$ populations of $N$ phase oscillators where $\theta _{\sigma ,k}\in {\mathbf {T}}:={\mathbb {R}}/2\pi {\mathbb {Z}}$ denotes the phase of oscillator k in population $\sigma$. Hence, the state of the coupled oscillator populations is determined by $\theta =(\theta _{1}, \ldots , \theta _{M})\in {\mathbf {T}}^{MN}$ where $\theta _\sigma = (\theta _{\sigma , 1}, \ldots , \theta _{\sigma , N})\in {\mathbf {T}}^N$ is the state of population $\sigma$. Let ${\mathbf {S}}_N$ denote the permutation group of $N$ elements. Suppose that the phase evolution is given by

$$\begin{aligned} {\dot{\theta }}_{\sigma ,k} := \frac{\mathrm {d}}{\mathrm {d}t}\theta _{\sigma ,k} = \omega + Y_{\sigma ,k}(\theta ) \end{aligned}$$

(2)

where $\omega$ is the intrinsic frequency of each oscillator and the vector field $Y=(Y_{\sigma ,k})$ is $({\mathbf {S}}_N\times {\mathbf {T}})^M$-equivariant. Here, each copy of ${\mathbf {T}}$ acts by shifting all oscillator phases of a given population $\sigma$ by a common constant, while ${\mathbf {S}}_N$ permutes the oscillator indices k.

The symmetry implies that certain phase configurations are dynamically invariant. For a single population of $N$ oscillators, the subset

$$\begin{aligned} \mathrm{S}&:= \left\{ (\phi _1, \ldots , \phi _N)\in {\mathbf {T}}^N\; \Big |\;\phi _k=\phi _{k+1}\right\} \end{aligned}$$

(3)

corresponds to phases being in full phase synchrony and

$$\begin{aligned} \mathrm{D}&:= \left\{ \, (\phi _1, \ldots , \phi _N)\in {\mathbf {T}}^N\,\left| \;\phi _{k+1}=\phi _{k}+\frac{2\pi }{N}\right. \right\} \end{aligned}$$

(4)

denotes a splay phase configuration—typically we call any element of the group orbit ${\mathbf {S}}_N\mathrm{D}$ a splay phase. For interacting oscillator populations, we use the shorthand notation

$$\begin{aligned} \theta _1\cdots \theta _{\sigma -1}\mathrm{S}\theta _{\sigma +1}\cdots \theta _{M}&= \left\{ \left. \theta \in {\mathbf {T}}^{MN}\;\right| \,\theta _\sigma \in \mathrm{S}\,\right\} \end{aligned}$$

(5a)

$$\begin{aligned} \theta _1\cdots \theta _{\sigma -1}\mathrm{D}\theta _{\sigma +1}\cdots \theta _{M}&= \left\{ \left. \theta \in {\mathbf {T}}^{MN}\;\right| \,\theta _\sigma \in \mathrm{D}\,\right\} \end{aligned}$$

(5b)

to indicate that population $\sigma$ is fully phase synchronized or in splay phase. Because of the ${\mathbf {S}}_N^M$ symmetry, the sets (5) are invariant (Ashwin and Swift 1992). We extend this notation to intersections of sets (5): In particular, for $\mathrm {X}_\tau \in \left\{ \mathrm{S},\mathrm{D}\right\}$ we write

$$\begin{aligned} \mathrm {X}_1\cdots \mathrm {X}_M= \bigcap _{\tau =1}^M\theta _1\cdots \theta _{\tau -1}\mathrm {X}_\tau \theta _{\tau +1}\cdots \theta _{M}. \end{aligned}$$

(6)

For example, $\mathrm{S}\cdots \mathrm{S}$ ($M$ times) is the set of cluster states where all populations are fully phase synchronized and $\mathrm{D}\cdots \mathrm{D}$ the set where all populations are in splay phase.

To reduce the continuous phase-shift symmetry ${\mathbf {T}}^{M}$, we may rewrite (2) in terms of phase differences $\psi _{\sigma ,k} := \theta _{\sigma , k+1} - \theta _{\sigma , 1}$, $k=1, \ldots , N-1$. Hence, with $\psi _\sigma \in {\mathbf {T}}^{N-1}$ we also write for example $\psi _1\mathrm{S}\cdots \mathrm{S}$ (or simply $\psi \mathrm{S}\cdots \mathrm{S}$ if the index is obvious) to indicate that all but the first population is phase synchronized. Note that the sets (6) are equilibria relative to ${\mathbf {T}}^{M}$, that is, they are equilibria for the reduced system in terms of phase differences on ${\mathbf {T}}^{M(N-1)}$. While the linearization of (2) on ${\mathbf {T}}^{MN}$ at the relative equilibria (6) has $M$ zero eigenvalues (corresponding to perturbations along the group orbits of each of the $M$ phase-shift symmetries), linear stability of (6) on the reduced phase space ${\mathbf {T}}^{M(N-1)}$ is given by the remaining $M(N-1)$ eigenvalues.

2.2.1 Frequencies and Localized Frequency Synchrony

Suppose that $M> 1$ and let $\theta :[0,\infty )\rightarrow {\mathbf {T}}^{MN}$ be a solution of (2) with initial condition $\theta (0)=\theta ^0$. While ${\dot{\theta }}_{\sigma ,k}(t)$ is the instantaneous angular frequency of oscillator $(\sigma , k)$, define the asymptotic average angular frequency of oscillator $(\sigma , k)$ by

$$\begin{aligned} \Omega _{\sigma ,k}(\theta ^0):=\lim _{T\rightarrow \infty }\frac{1}{T}\int _0^T{\dot{\theta }}_{\sigma ,k}(t)\,\mathrm {d}t. \end{aligned}$$

(7)

Here, we assume that these limits exist for all oscillators, but this notion can be generalized to frequency intervals; see also Bick and Ashwin (2016), Bick (2017).

Definition 2.8

A connected flow-invariant set $A\subset {\mathbf {T}}^{MN}$ has localized frequency synchrony if for any $\theta ^0\in A$ and fixed $\sigma$ we have $\Omega _{\sigma ,k} = \Omega _{\sigma }$ for all k and there exist indices $\sigma \ne \tau$ such that

$$\begin{aligned} \Omega _{\sigma } \ne \Omega _{\tau }. \end{aligned}$$

(8)

Remark 2.9

Note that a chain-recurrent set A with localized frequency synchrony is a weak chimera as defined by Ashwin and Burylko (2015).

3 Three Coupled Oscillator Populations

Here, we derive explicit stability results for the heteroclinic cycles in $M=3$ coupled populations of $N=2$ phase oscillators (2) with interaction functions that include higher harmonics and nonpairwise interactions; such terms arise naturally in phase reductions of nonlinear oscillators (Ashwin and Rodrigues 2016; León and Pazó 2019). Specifically, interactions between pairs of oscillators are mediated by the coupling function

$$\begin{aligned} g(\vartheta ) = \sin (\vartheta +\alpha )-r\sin (a(\vartheta +\alpha )) \end{aligned}$$

(9)

and the interaction between populations is determined by the nonpairwise interaction function

$$\begin{aligned} {\tilde{G}}^{(4)}(\theta _\tau ; \vartheta )&= -\frac{1}{4}\big (\cos (\theta _{\tau , 1}-\theta _{\tau ,2}+\vartheta +\alpha )+\cos (\theta _{\tau , 2}-\theta _{\tau ,1}+\vartheta +\alpha )\big ). \end{aligned}$$

(10)

For coupling strength $K>0$ between populations, the phase of oscillator $k\in \left\{ 1,2\right\}$ in population $\sigma \in \left\{ 1,2,3\right\}$ evolves according to

$$\begin{aligned} \begin{aligned} {\dot{\theta }}_{\sigma ,k}&= \omega +g(\theta _{\sigma ,3-k}-\theta _{\sigma ,k}) +K{\tilde{G}}^{(4)}(\theta _{\sigma -1}; \theta _{\sigma ,3-k}-\theta _{\sigma ,k}) \\&\quad \quad -\,K{\tilde{G}}^{(4)}(\theta _{\sigma +1}; \theta _{\sigma ,3-k}-\theta _{\sigma ,k}). \end{aligned} \end{aligned}$$

(11)

These are the equations of motion considered in the companion paper (Bick 2019) with phase shifts parametrized by $\alpha := \alpha _2= \alpha _4-\frac{\pi }{2}$ and use the notation introduced there.⁴

The interactions between populations in (11)—which include nonpairwise coupling—are a special case of (2). More precisely, with ${\mathbb {Z}}_M:={\mathbb {Z}}/M{\mathbb {Z}}$ the system (11) is $({\mathbf {S}}_N\times {\mathbf {T}})^M\rtimes {\mathbb {Z}}_M$-equivariant. Each copy of ${\mathbf {T}}$ acts by shifting all oscillator phases of one population by a common constant, while ${\mathbf {S}}_N$ permutes its oscillators. The action of ${\mathbb {Z}}_M$ permutes the populations cyclically. These actions do not necessarily commute. The phase space of (11) is organized by invariant subspaces and there are relative equilibria ${\mathrm{D}\mathrm{S}\mathrm{S}}$, ${\mathrm{D}\mathrm{D}\mathrm{S}}$ and their images under the ${\mathbb {Z}}_3$ action. In this section, we consider the dynamics of (11) on the reduced phase space ${\mathbf {T}}^{M(N-1)}={\mathbf {T}}^3$ where the coordinates represent the phase differences in each population. In particular, on ${\mathbf {T}}^3$ the sets ${\mathrm{D}\mathrm{S}\mathrm{S}}, {\mathrm{D}\mathrm{D}\mathrm{S}}$ are equilibria ${\mathrm{D}\mathrm{S}\mathrm{S}}= (\pi , 0, 0)$, ${\mathrm{D}\mathrm{D}\mathrm{S}}= (\pi , \pi , 0)$.

3.1 Heteroclinic Cycles and Local Stability

The coupled oscillator populations (11) with interaction functions (9), (10) support a robust heteroclinic cycle (Bick 2018, 2019). More specifically, on ${\mathbf {T}}^3$ the linear stability of the equilibria ${\mathrm{D}\mathrm{S}\mathrm{S}}$, ${\mathrm{D}\mathrm{D}\mathrm{S}}$ is given by the eigenvalues

$$\begin{aligned} \lambda ^{\mathrm{D}\mathrm{S}\mathrm{S}}_1&= 2\cos (\alpha )+4r\cos (2\alpha ), \end{aligned}$$

(12a)

$$\begin{aligned} \lambda ^{\mathrm{D}\mathrm{S}\mathrm{S}}_2&= 2K\sin (\alpha )-2\cos (\alpha )+4r\cos (2\alpha ),\end{aligned}$$

(12b)

$$\begin{aligned} \lambda ^{\mathrm{D}\mathrm{S}\mathrm{S}}_3&= -2K\sin (\alpha )-2\cos (\alpha )+4r\cos (2\alpha ), \end{aligned}$$

(12c)

and

$$\begin{aligned} \lambda ^{\mathrm{D}\mathrm{D}\mathrm{S}}_1&= 2K\sin (\alpha )+2\cos (\alpha )+4r\cos (2\alpha ),\end{aligned}$$

(13a)

$$\begin{aligned} \lambda ^{\mathrm{D}\mathrm{D}\mathrm{S}}_2&= -2K\sin (\alpha )+2\cos (\alpha )+4r\cos (2\alpha ),\end{aligned}$$

(13b)

$$\begin{aligned} \lambda ^{\mathrm{D}\mathrm{D}\mathrm{S}}_3&= -2\cos (\alpha )+4r\cos (2\alpha ). \end{aligned}$$

(13c)

Conditions for the existence of a robust heteroclinic cycle can now be given in terms of the local stability properties of ${\mathrm{D}\mathrm{S}\mathrm{S}}$, ${\mathrm{D}\mathrm{D}\mathrm{S}}$ (which, in turn, depend on the interaction parameters):

Lemma 3.1

(See Bick 2018 and Lemma 3.2 in Bick 2019) Suppose that $\lambda ^{\mathrm{D}\mathrm{S}\mathrm{S}}_3<0<\lambda ^{\mathrm{D}\mathrm{S}\mathrm{S}}_2$ and $\lambda ^{\mathrm{D}\mathrm{D}\mathrm{S}}_2<0<\lambda ^{\mathrm{D}\mathrm{D}\mathrm{S}}_1$. Then the $M=3$ coupled populations of $N=2$ phase oscillators (11) with interaction functions (9), (10) have a robust heteroclinic cycle

$$\begin{aligned} {{\mathbf {\mathsf{{C}}}} }_2 = ({\mathrm{D}\mathrm{S}\mathrm{S}}, {\mathrm{D}\mathrm{D}\mathrm{S}}, {\mathrm{S}\mathrm{D}\mathrm{S}}, {\mathrm{S}\mathrm{D}\mathrm{D}}, {\mathrm{S}\mathrm{S}\mathrm{D}}, {\mathrm{D}\mathrm{S}\mathrm{D}}) \end{aligned}$$

between relative equilibria.

For $\alpha$ fixed with $|\alpha -\frac{\pi }{2}|$ sufficiently small, the assumptions of Lemma 3.1 define a cone-shaped region in $(K,r)$ parameter space: there is an affine linear function L such that $K>K_0$ where $L(K_0)=0$ and r between $-L(K)$ and L(K). For the remainder of this section, we assume that the assumptions of Lemma 3.1 hold.

Lemma 3.2

The cycle ${{\mathbf {\mathsf{{C}}}} }_2$ is quasi-simple.

Proof

It suffices to consider the equilibria ${\mathrm{D}\mathrm{S}\mathrm{S}}$ and ${\mathrm{D}\mathrm{D}\mathrm{S}}$ due to the symmetry which permutes populations. We have $W^\text {u}({\mathrm{D}\mathrm{S}\mathrm{S}})\subset {\mathrm{D}\psi \mathrm{S}}$, $W^\text {u}({\mathrm{D}\mathrm{D}\mathrm{S}})\subset {\psi \mathrm{D}\mathrm{S}}$ which implies that each saddle has one contracting, expanding, and transverse eigenvalue; there are no radial eigenvalues since ${\mathrm{D}\mathrm{S}\psi }\cap {\mathrm{D}\psi \mathrm{S}}= {\mathrm{D}\mathrm{S}\mathrm{S}}$ and ${\mathrm{D}\psi \mathrm{S}}\cap {\psi \mathrm{D}\mathrm{S}}= {\mathrm{D}\mathrm{D}\mathrm{S}}$. $\square$

Subject to nonresonance conditions, we may linearize the flow around the equilibria; see also Aguiar and Castro (2010, Proposition 4.1).

Lemma 3.3

Suppose that $\lambda ^{\mathrm{D}\mathrm{S}\mathrm{S}}_1, \lambda ^{\mathrm{D}\mathrm{D}\mathrm{S}}_3\ne 0$, and

$$\begin{aligned} 0&\ne 2r\cos (2\alpha )\pm 3\cos (\alpha ), \end{aligned}$$

(14a)

$$\begin{aligned} 0&\ne 4K\sin (\alpha )\pm 4r\cos (2\alpha )\pm 2\cos (\alpha ) \end{aligned}$$

(14b)

(in the second line we allow any combination of $+$ and −). Then we can linearize the flow at the equilibria in ${{\mathbf {\mathsf{{C}}}} }_2$. For $\alpha =\frac{\pi }{2}$, these conditions reduce to $r\ne 0$ and $r\ne \pm K$.

Proof

According to the $C^1$ linearization theorem (Ruelle 1989), we can linearize the flow if the eigenvalues $\lambda _l$ of the linearization satisfy ${{\,\mathrm{Re}\,}}{\lambda _l} \ne {{\,\mathrm{Re}\,}}{\lambda _j} + {{\,\mathrm{Re}\,}}\lambda _k$ when ${{\,\mathrm{Re}\,}}{\lambda _j}<0<{{\,\mathrm{Re}\,}}{\lambda _k}$. Given (12), conditions (14) are just these nonresonance conditions. Substituting $\alpha =\frac{\pi }{2}$ yields the second assertion. $\square$

3.2 Cross Sections, Transition Matrices, and Stability

Using standard notation, we write

$$\begin{aligned} -c_{\mathrm{D}\mathrm{S}\mathrm{S}}&:= \lambda ^{\mathrm{D}\mathrm{S}\mathrm{S}}_3, \quad e_{\mathrm{D}\mathrm{S}\mathrm{S}}:= \lambda ^{\mathrm{D}\mathrm{S}\mathrm{S}}_2, \quad t_{\mathrm{D}\mathrm{S}\mathrm{S}}:= \lambda ^{\mathrm{D}\mathrm{S}\mathrm{S}}_1, \end{aligned}$$

(15)

$$\begin{aligned} -c_{\mathrm{D}\mathrm{D}\mathrm{S}}&:= \lambda ^{\mathrm{D}\mathrm{D}\mathrm{S}}_2, \quad e_{\mathrm{D}\mathrm{D}\mathrm{S}}:= \lambda ^{\mathrm{D}\mathrm{D}\mathrm{S}}_1, \quad t_{\mathrm{D}\mathrm{D}\mathrm{S}}:= \lambda ^{\mathrm{D}\mathrm{D}\mathrm{S}}_3, \end{aligned}$$

(16)

for the contracting, expanding, and transverse eigenvalues. Thus $e_q, c_q>0$, $q\in \left\{ {\mathrm{D}\mathrm{S}\mathrm{S}}, {\mathrm{D}\mathrm{D}\mathrm{S}}\right\}$. The ratios between contraction/transverse stability and expansion are given by

$$\begin{aligned} a_q&:= \frac{c_q}{e_q},\quad b_q := -\frac{t_q}{e_q} \end{aligned}$$

(17)

for $q\in \left\{ {\mathrm{D}\mathrm{S}\mathrm{S}}, {\mathrm{D}\mathrm{D}\mathrm{S}}\right\}$; we have $a_q>0$ by definition and $b_q>0$ if $t_q<0$.

3.2.1 Poincaré Map and Transition Matrices

We first consider the linearized flow at the equilibria to calculate the local transition maps. Introduce local coordinates (v, w, z) which correspond to the contracting, expanding, and transverse directions, respectively. After appropriate rescaling, consider the cross sections

$$\begin{aligned} H^{\text {in}}_q&= \left\{ \, (v,w,z)\,\left| \;\left| v\right| = 1, \left| w\right| \le 1, \left| z\right| \le 1\right. \right\} , \end{aligned}$$

(18)

$$\begin{aligned} H^{\text {out}}_q&= \left\{ \, (v,w,z)\,\left| \;\left| v\right| \le 1, \left| w\right| = 1, \left| z\right| \le 1\right. \right\} \end{aligned}$$

(19)

at $q\in \left\{ {\mathrm{D}\mathrm{S}\mathrm{S}}, {\mathrm{D}\mathrm{D}\mathrm{S}}\right\}$. The linearized flow at $\xi _q$ is

$$\begin{aligned} \Phi ^\tau _q(v, w, z) = \left( \exp (-c_q\tau )v, \exp (e_q\tau )w, \exp (t_q\tau )z\right) . \end{aligned}$$

Hence the time of flight is $\tau =-\log (w)/e_q$ which implies that the local map at $\xi _q$ is

$$\begin{aligned} h^{\text {loc}}_q:H^{\text {in}}_q\rightarrow H^{\text {out}}_q, (\pm 1,w,z)\mapsto (w^{a_q}, \pm 1, w^{b_q}z). \end{aligned}$$

Considering the invariant subspaces, we see that the global maps are rescaled permutations. More specifically, we have

$$\begin{aligned}h^{\text {gl}}_q:H^{\text {out}}_q\rightarrow H^{\text {in}}_{q+1}, (v,w,z)\mapsto (A_q w,B_q z,D_q v).\end{aligned}$$

Write $h_q := h^{\text {gl}}_q\circ h^{\text {loc}}_q: H^{\text {in}}_q\rightarrow H^{\text {in}}_{q+1}$. Ignoring v, this yields a map between the incoming 2-dimensional sections of subsequent equilibria

$$\begin{aligned} h_q(w,z) = (B_q w^{b_q}z,D_q w^{a_q}). \end{aligned}$$

Taken together, the Poincaré return map for the linearized dynamics around the heteroclinic cycle (modulo the ${\mathbb {Z}}_3$ group action) is

$$\begin{aligned} h= h_{\mathrm{D}\mathrm{D}\mathrm{S}}\circ h_{\mathrm{D}\mathrm{S}\mathrm{S}}. \end{aligned}$$

If we introduce logarithmic coordinates, we can write the return map in terms of transition matrices (Field and Swift 1991; Garrido-da-Silva and Castro 2019). Restrict to the (w, z) coordinates and introduce logarithmic variables $\eta = \log (w)$, $\zeta = \log (z)$. In the new variables, the maps $h_q$ become linear,

$$\begin{aligned} {\hat{h}}_q(\eta , \zeta ) = {{{\textsf {\textit{M}}}}}_q\left( \begin{array}{c}\eta \\ \zeta \end{array}\right) + \left( \begin{array}{c}\log B_q\\ \log D_q\end{array}\right) \end{aligned}$$

(20)

with

$$\begin{aligned} {{{\textsf {\textit{M}}}}}_q&= \left( \begin{array}{cc}b_q &{} 1 \\ a_q &{} 0\end{array}\right) \end{aligned}$$

(21)

Note that these transition matrices are the same as the ones for simple cycles in ${\mathbb {R}}^4$ of type C (Podvigina and Ashwin 2011).

The transition matrix for the Poincaré map $h$ is ${{{\textsf {\textit{M}}}}}_{\mathrm{D}\mathrm{D}\mathrm{S}}{{{\textsf {\textit{M}}}}}_{\mathrm{D}\mathrm{S}\mathrm{S}}$. These transition matrices govern the stability of the cycle (Garrido-da-Silva and Castro 2019, Theorem 3.4).

3.2.2 Stability of ${{\mathbf {\mathsf{{C}}}} }_2$ for $\alpha =\frac{\pi }{2}$

The stability properties at the saddles are symmetric, and stability is governed by the properties of the transition matrix

$$\begin{aligned} {{{\textsf {\textit{M}}}}}&= \left( \begin{array}{c@{\quad }c}b &{} 1 \\ a &{} 0\end{array}\right) . \end{aligned}$$

(22)

Here, we omitted the index q of the saddle since ${{{\textsf {\textit{M}}}}}_{\mathrm{D}\mathrm{S}\mathrm{S}}={{{\textsf {\textit{M}}}}}_{\mathrm{D}\mathrm{D}\mathrm{S}}={{{\textsf {\textit{M}}}}}$. This is the same transition matrix as for a simple heteroclinic cycle in ${\mathbb {R}}^4$ of type $C_1^-$ (Podvigina and Ashwin 2011).

Lemma 3.4

(Podvigina and Ashwin 2011, Section 4.2.2) A heteroclinic cycle whose stability is given by the transition matrix ${{{\textsf {\textit{M}}}}}$ is asymptotically stable if $b \ge 0$ (that is, $t \le 0$) and $a+b>1$; otherwise, it is completely unstable.

In terms of the oscillator coupling parameters, we can now show that the heteroclinic cycle loses stability completely in a (degenerate) transverse bifurcation at $r=0$ as both transverse eigenvalues pass through zero.

Theorem 3.5

For $\alpha =\frac{\pi }{2}$, the heteroclinic cycle ${{\mathbf {\mathsf{{C}}}} }_2$ is asymptotically stable if $r>0$ and completely unstable if $r<0$.

Proof

Substituting the stability properties (12), (13), we obtain

$$\begin{aligned} a&= \frac{c}{e} = \frac{2K+4r}{2K-4r}&b&= -\frac{t}{e} = \frac{4r}{2K-4r}. \end{aligned}$$

(23)

Simplifying the expressions $b \ge 0$ and $a + b > 1$ now proves the assertion. $\square$

3.2.3 Stability for $\alpha \ne \frac{\pi }{2}$

If $\alpha \ne \frac{\pi }{2}$, then the two transverse eigenvalues $t_1 = 2\cos (\alpha )+4r\cos (2\alpha )$, $t_2 = -2\cos (\alpha )+4r\cos (2\alpha )$ are distinct. Consequently, there are two transverse bifurcations as the oscillator coupling parameters are varied: We have

• $t_1, t_2 < 0$ if $r>\frac{\left| \cos (\alpha )\right| }{4\cos ^2(\alpha )-2}$,

• $t_1, t_2 > 0$ if $r<\frac{-\left| \cos (\alpha )\right| }{4\cos ^2(\alpha )-2}$, and

• one positive and one negative transverse eigenvalue otherwise.

The stability of the heteroclinic cycle is now determined by the properties of the transition matrix

$$\begin{aligned} {{{\textsf {\textit{M}}}}}&= {{{\textsf {\textit{M}}}}}_{\mathrm{D}\mathrm{D}\mathrm{S}}{{{\textsf {\textit{M}}}}}_{\mathrm{D}\mathrm{S}\mathrm{S}}=\left( \begin{array}{c@{\quad }c}b_1b_2+a_2 &{} b_1\\ a_1b_2 &{} a_1\end{array}\right) . \end{aligned}$$

(24)

The stability calculations are analogous to those for simple heteroclinic cycles in ${\mathbb {R}}^4$ of type $C_2^-$ (Podvigina and Ashwin 2011; Lohse 2015); for such cycles, we have the following result.

Lemma 3.6

(Stability conditions for $C_2^-$ cycles given in Podvigina and Ashwin 2011; Lohse 2015) For asymptotic stability, we need $t_1, t_2 < 0$ and

$$\begin{aligned} \max \left\{ b_1b_2 + a_2 + a_1, 2(b_1b_2 + a_2 + a_1-a_1a_2)\right\} > 2. \end{aligned}$$

If $t_2<0<t_1$ and $b_1b_2-a_1+a_2<0$, then the cycle is completely unstable.

These results can now be used to show that the heteroclinic cycle loses stability completely as one of the transverse eigenvalues becomes positive.

Theorem 3.7

The heteroclinic cycle ${{\mathbf {\mathsf{{C}}}} }_2$ is asymptotically stable if

$$\begin{aligned} r>\frac{\left| \cos (\alpha )\right| }{4\cos ^2(\alpha )-2} \end{aligned}$$

and completely unstable otherwise.

Proof

First, observe that there are relations between the eigenvalues (12), (13) of the linearization at the saddle points. Set $S=2K\sin (\alpha )$. We have $e_1 = S+t_2$, $c_1 = S-t_2$, $e_2 = S+t_1$, $c_2 = S-t_1$ which are all positive. Consequently, $S>0$ and $c_1 = e_1 - 2t_2$, $c_2 = e_2 - 2t_1$.

If $t_1, t_2 < 0$ (the hypothesis of the theorem is satisfied), we have

$$\begin{aligned} b_1b_2 + a_2 + a_1&= 2+\frac{t_1t_2 -2t_1e_1 -2t_2e_2}{e_1e_2}>2 \end{aligned}$$

(25)

since all terms are positive. Hence by Lemma 3.6, the heteroclinic cycle is asymptotically stable.

Now suppose that $t_2<0<t_1$ (the case $t_1<0<t_2$ is analogous). We have

$$\begin{aligned} b_1b_2-a_1+a_2&= \frac{t_1t_2 -2St_1+2St_2}{e_1e_2}<0 \end{aligned}$$

(26)

since all terms are negative. By Lemma 3.6, the heteroclinic cycle is completely unstable. $\square$

The dichotomy between asymptotic stability and complete instability appears to be nongeneric for $C_2^-$-cycles compared to Lohse (2015, Corollary 4.8). This is due to the fact that $e_2$ and $c_2$ are not independent of $t_1$. In fact, the case $t_1=0$ coincides with the degenerate situation $c_2=e_2$. Therefore, the assumption in Lohse (2015, Corollary 4.8) that $b_1b_2-a_1+a_2>0$ even for small $t_1>0$ cannot be satisfied here.

3.3 Eigenvalues and Eigenvectors of the Transition Matrix Products

In the previous section, we used results from Podvigina and Ashwin (2011), Lohse (2015) (stated as Lemmas 3.4 and 3.6) to determine the stability of the cycle. We now relate these to the hypotheses in Propositions 2.6 and 2.7 by calculating eigenvalues and eigenvectors of the transition matrix products. This is useful for our stability analysis in the higher-dimensional system in Sect. 4.

For $\alpha \ne \frac{\pi }{2}$, the transition matrix product ${{{\textsf {\textit{M}}}}}$ as defined in (24) has eigenvalues $\lambda _1>\lambda _2$ given by

$$\begin{aligned} \lambda _1&=\frac{1}{2}\left( a_1+a_2+b_1b_2+\sqrt{(a_1-a_2-b_1b_2)^2+4a_1b_1b_2}\right) ,\\ \lambda _2&=\frac{1}{2}\left( a_1+a_2+b_1b_2-\sqrt{(a_1-a_2-b_1b_2)^2+4a_1b_1b_2} \right) \end{aligned}$$

and corresponding eigenvectors

$$\begin{aligned} u_1&=(u_{11},u_{12})=\left( 1,\frac{a_1-a_2-b_1b_2+\sqrt{(a_1-a_2-b_1b_2)^2+4a_1b_1b_2}}{2b_1}\right) ,\\ u_2&=(u_{21},u_{22})=\left( 1,\frac{a_1-a_2-b_1b_2-\sqrt{(a_1-a_2-b_1b_2)^2+4a_1b_1b_2}}{2b_1}\right) . \end{aligned}$$

Recall from (17) that $a_q=\frac{c_q}{e_q}$ and $b_q=-\frac{t_q}{e_q}$. So if $t_1,t_2<0$, then both eigenvalues are real and hence condition (C1) is satisfied. Moreover, by the calculations in the proof of Theorem 3.7, we have

$$\begin{aligned} \lambda _1&>\frac{1}{2}(a_1+a_2+b_1b_2)>1, \end{aligned}$$

so (C2) is satisfied as well. Since in this case all transition matrices have only nonnegative entries, Proposition 2.6 applies and the cycle is asymptotically stable. We note that (C3) is also satisfied, because $4a_1b_1b_2>0$ implies that

$$\begin{aligned} u_{11}u_{12}=u_{12}>\frac{a_1-a_2-b_1b_2+|a_1-a_2-b_1b_2|}{2b_1}>0. \end{aligned}$$

Similarly, for the components of the other eigenvector we get

$$\begin{aligned} u_{21}u_{22}=u_{22}<\frac{a_1-a_2-b_1b_2-|a_1-a_2-b_1b_2|}{2b_1}<0. \end{aligned}$$

This is not directly related to condition (C3), but will also be used in the following section.

On the other hand, if $t_2<0<t_1$, the transition matrix ${{{\textsf {\textit{M}}}}}_1$ has a negative entry. Again by the calculations in the proof of Theorem 3.7, we have $a_1-a_2-b_1b_2>0$, and therefore

$$\begin{aligned} u_{11}u_{12}=u_{12}<\frac{a_1-a_2-b_1b_2}{2b_1}<0. \end{aligned}$$

Thus, (C3) is violated and by Proposition 2.7(a) the cycle is completely unstable. The case $t_1<0<t_2$ is analogous for the other transition matrix product.

4 Four Coupled Oscillator Populations

4.1 Four Interacting Populations Support a Heteroclinic Network

In this section, we consider $M=4$ coupled populations with $N=2$ phase oscillators each. For the coupling function g as in (9) and parameter $\delta \in [-1, 1]$, define the interaction functions

$$\begin{aligned} {\tilde{G}}^{(4)}(\theta _\tau ; \vartheta )&= -\frac{1}{4}\big (\cos (\theta _{\tau , 1}-\theta _{\tau ,2}+\vartheta +\alpha )+\cos (\theta _{\tau , 2}-\theta _{\tau ,1}+\vartheta +\alpha )\big ) \end{aligned}$$

(27)

$$\begin{aligned} {\tilde{G}}^{(2)}_\sigma (\vartheta )&= g(\vartheta )+K\left( 1-\frac{1}{N}\right) K_\sigma \cos (\vartheta +\alpha ). \end{aligned}$$

(28)

For $K_1 = 1$, $K_2=-1$, $K_3=-1+\delta$, $K_4=-1-\delta$, we obtain the oscillator dynamics where the phase of oscillator k in each population $\sigma =1,\ldots ,4$ evolves according to

$$\begin{aligned}&\begin{aligned} {\dot{\theta }}_{1,k}&= \omega +{\tilde{G}}^{(2)}_1(\theta _{1,3-k}-\theta _{1,k}) +K{\tilde{G}}^{(4)}(\theta _{4},\theta _{1,3-k}-\theta _{1,k})\\&\quad \quad -\,K{\tilde{G}}^{(4)}(\theta _{2},\theta _{1,3-k}-\theta _{1,k}) +K{\tilde{G}}^{(4)}(\theta _{3},\theta _{1,3-k}-\theta _{1,k}), \end{aligned} \end{aligned}$$

(29a)

$$\begin{aligned}&\begin{aligned} {\dot{\theta }}_{2,k}&= \omega +{\tilde{G}}^{(2)}_2(\theta _{2,3-k}-\theta _{2,k}) -K{\tilde{G}}^{(4)}(\theta _{4},\theta _{2,3-k}-\theta _{2,k}) \\&\quad \quad +\,K{\tilde{G}}^{(4)}(\theta _{1},\theta _{2,3-k}-\theta _{2,k}) -K{\tilde{G}}^{(4)}(\theta _{3},\theta _{2,3-k}-\theta _{2,k}), \end{aligned}\end{aligned}$$

(29b)

$$\begin{aligned}&\begin{aligned} {\dot{\theta }}_{3,k}&= \omega +{\tilde{G}}^{(2)}_3(\theta _{3,3-k}-\theta _{3,k}) -K{\tilde{G}}^{(4)}(\theta _{4},\theta _{3,3-k}-\theta _{3,k}) \\&\qquad -\,K{\tilde{G}}^{(4)}(\theta _{1},\theta _{3,3-k}-\theta _{3,k}) +K(1+\delta ){\tilde{G}}^{(4)}(\theta _{2},\theta _{3,3-k}-\theta _{3,k}), \end{aligned}\end{aligned}$$

(29c)

$$\begin{aligned}&\begin{aligned} {\dot{\theta }}_{4,k}&= \omega +{\tilde{G}}^{(2)}_4(\theta _{4,3-k}-\theta _{4,k}) -K{\tilde{G}}^{(4)}(\theta _{1},\theta _{4,3-k}-\theta _{4,k}) \\&\qquad +\,K(1-\delta ){\tilde{G}}^{(4)}(\theta _{2},\theta _{4,3-k}-\theta _{4,k}) -K{\tilde{G}}^{(4)}(\theta _{3},\theta _{4,3-k}-\theta _{4,k}). \end{aligned} \end{aligned}$$

(29d)

If $\delta =0$, these equations relate to the system of four interacting populations in Bick (2018) as discussed in Appendix A. The vector field is $({\mathbf {S}}_N\times {\mathbf {T}})^M$-equivariant: The symmetric group ${\mathbf {S}}_N$ acts by permuting oscillators within populations and ${\mathbf {T}}^{M}$ by a phase shift in each population. If $\delta =0$, the system is $({\mathbf {S}}_N\times {\mathbf {T}})^M\rtimes {\mathbb {Z}}_2$ equivariant where ${\mathbb {Z}}_2=\langle (34)\rangle$ acts by permuting populations three and four. If $\delta \ne 0$, then there is a parameter symmetry $(\delta , \theta _3, \theta _4)\mapsto (-\delta , \theta _4, \theta _3)$. Again, we consider the dynamics on the reduced phase space ${\mathbf {T}}^{M(N-1)}={\mathbf {T}}^4$ of phase differences of the oscillators in each population. As above, we have the equilibria ${\mathrm{S}\mathrm{S}\mathrm{S}\mathrm{S}}= (0, 0, 0, 0)$, ${\mathrm{D}\mathrm{S}\mathrm{S}\mathrm{S}}= (\pi , 0, 0, 0)$, etc., on the reduced phase space ${\mathbf {T}}^4$.

Fig. 1

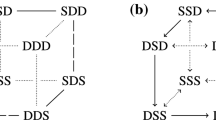
A heteroclinic network ${{\mathbf {\mathsf{{N}}}} }_2$ arises in $M=4$ coupled populations of $N=2$ oscillators. The types of arrowhead (>, $\gg$, $\ggg$) indicate the eigenvalues for $\alpha =\frac{\pi }{2}$ and $\delta =0$: $\lambda ^{\ggg }=-4K-4r< \lambda ^{\gg }=-2K-4r< \lambda ^{>}=-4r< 0 < 2K-4r$. The $\psi _k$ along an arrow indicates the phase difference that corresponds to the invariant subspace

Theorem 4.1

The system of coupled phase oscillator populations (29) supports a robust heteroclinic network ${{\mathbf {\mathsf{{N}}}} }_2$—sketched in Figs. 1 and 2—between relative equilibria with localized frequency synchrony.

Proof

First, suppose that $\delta =0$. The dynamics on the invariant subspaces ${\psi _1\psi _2\psi _3\mathrm{S}}$ and ${\psi _1\psi _2\mathrm{S}\psi _4}$ reduce to (11). Hence by Lemma 3.1, the coupled phase oscillator populations (29) have a heteroclinic network with two quasi-simple cycles ${\hat{{{\mathbf {\mathsf{{C}}}} }}}_2\subset {\psi _1\psi _2\psi _3\mathrm{S}}$ and ${\check{{{\mathbf {\mathsf{{C}}}} }}}_2\subset {\psi _1\psi _2\mathrm{S}\psi _4}$. Having $\delta \ne 0$ constitutes an equivariant perturbation that maintains the $({\mathbf {S}}_N\times {\mathbf {T}})^M$ symmetry, with respect to which both cycles are robust. $\square$

The eigenvalues of the linearization at the equilibria can be evaluated explicitly. For example, linearizing the reduced vector field at ${\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}$ yields eigenvalues

$$\begin{aligned} \lambda ^{\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}_1&= -2K\sin (\alpha )-2\cos (\alpha )+4r\cos (2\alpha ), \end{aligned}$$

(30a)

$$\begin{aligned} \lambda ^{\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}_2&= 2\cos (\alpha )+4r\cos (2\alpha ),\end{aligned}$$

(30b)

$$\begin{aligned} \lambda ^{\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}_3&= 2K(1+\delta )\sin (\alpha )-2\cos (\alpha )+4r\cos (2\alpha ),\end{aligned}$$

(30c)

$$\begin{aligned} \lambda ^{\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}_4&= 2K(1-\delta )\sin (\alpha )-2\cos (\alpha )+4r\cos (2\alpha ), \end{aligned}$$

(30d)

where $\lambda ^{\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}_\sigma$ determines linear stability of ${\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}$ with respect to perturbations of the phase differences $\psi _\sigma$. As above, this gives explicit bounds for parameter values which support the heteroclinic network—where linear stability of the equilibria now also depends on $\delta$—and conditions to linearize the flow around the heteroclinic network (cf. Lemma 3.3).

Fig. 2

The heteroclinic network ${{\mathbf {\mathsf{{N}}}} }_2$ shown in Fig. 1 is constituted by the heteroclinic cycles ${\hat{{{\mathbf {\mathsf{{C}}}} }}}_2\subset {\psi _1\psi _2\psi _3\mathrm{S}}$ and ${\check{{{\mathbf {\mathsf{{C}}}} }}}_2\subset {\psi _1\psi _2\mathrm{S}\psi _4}$. The stability indices along the saddle connections are denoted by ${\hat{{\mathfrak {s}}}}_q$ and ${\check{{\mathfrak {s}}}}_q$, respectively

Note that there are other equilibria that are not part of either cycle in the heteroclinic network. For example, on ${\mathrm{S}\mathrm{S}\mathrm{S}\mathrm{S}}$ all populations are phase synchronized and its stability is governed by the (quadruple) eigenvalue $\lambda ^{\mathrm{S}\mathrm{S}\mathrm{S}\mathrm{S}}_\sigma = 4r\cos (2\alpha )-2\cos (\alpha )$, independent of the parameters $K$, $\delta$. We typically consider a phase-lag parameter $\alpha$ with $|\alpha -\frac{\pi }{2}|$ sufficiently small (cf. Sect. 3.1), in which case we have that ${\mathrm{S}\mathrm{S}\mathrm{S}\mathrm{S}}$ is linearly stable for $r>0$ sufficiently large. Moreover, note that if $\delta =0$, we have $\lambda ^{\mathrm{S}\mathrm{S}\mathrm{S}\mathrm{S}}= \lambda ^{\mathrm{D}\mathrm{D}\mathrm{S}\mathrm{S}}_3$; then ${\mathrm{S}\mathrm{S}\mathrm{S}\mathrm{S}}$ is linearly stable if the transverse eigenvalues within the corresponding subspace of each cycle are negative; cf. Sect. 3.2.

4.2 Stability of the Cycles

Note that by construction, the saddle ${\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}$ has a two-dimensional unstable manifold. Hence, neither cycle can be asymptotically stable for $\left| \delta \right|$ and $\left| \alpha -\frac{\pi }{2}\right|$ sufficiently small. Since the cycles are quasi-simple, we can determine their stability by looking at the corresponding transition matrices. Because of the parameter symmetry, we restrict ourselves to the cycle ${\hat{{{\mathbf {\mathsf{{C}}}} }}}_2\subset {\psi _1\psi _2\psi _3\mathrm{S}}$ without loss of generality and just write ${{\mathbf {\mathsf{{C}}}} }$ and ${\mathfrak {s}}_q$ for the remainder of this subsection.

Within the invariant subspace ${\psi _1\psi _2\psi _3\mathrm{S}}$, we have one contracting, expanding, and transverse direction with local coordinates denoted by v, w, z as above. In addition, there is another transverse direction—denoted by $z^\perp$ in local coordinates—which is mapped to itself under the global map. The second transverse eigenvalues (those transverse to ${\psi _1\psi _2\psi _3\mathrm{S}}$) evaluate to

$$\begin{aligned} t^\perp _{\mathrm{D}\mathrm{S}\mathrm{S}\mathrm{S}}&= -2K\sin (\alpha )-2\cos (\alpha )+4r\cos (2\alpha ), \end{aligned}$$

(31a)

$$\begin{aligned} t^\perp _{\mathrm{D}\mathrm{D}\mathrm{S}\mathrm{S}}&= -2K\delta \sin (\alpha )-2\cos (\alpha )+4r\cos (2\alpha ),\end{aligned}$$

(31b)

$$\begin{aligned} t^\perp _{\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}&= 2K(1-\delta )\sin (\alpha )-2\cos (\alpha )+4r\cos (2\alpha ),\end{aligned}$$

(31c)

$$\begin{aligned} t^\perp _{\mathrm{S}\mathrm{D}\mathrm{D}\mathrm{S}}&= -2K\delta \sin (\alpha )-2\cos (\alpha )+4r\cos (2\alpha ),\end{aligned}$$

(31d)

$$\begin{aligned} t^\perp _{\mathrm{S}\mathrm{S}\mathrm{D}\mathrm{S}}&= -2K\sin (\alpha )-2\cos (\alpha )+4r\cos (2\alpha ),\end{aligned}$$

(31e)

$$\begin{aligned} t^\perp _{\mathrm{D}\mathrm{S}\mathrm{D}\mathrm{S}}&= -4K\sin (\alpha )-2\cos (\alpha )+4r\cos (2\alpha ). \end{aligned}$$

(31f)

There are two possibilities for transverse bifurcations when $\delta$ changes. If $\delta >0$, there is a transverse bifurcation at $t^\perp _{\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}= 0$. But since $t^\perp _{\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}= e_{\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}$, the other cycle of the network then ceases to exist. If $\delta <0$, there is a possibility of two simultaneous transverse bifurcations when $t^\perp _{\mathrm{D}\mathrm{D}\mathrm{S}\mathrm{S}}= t^\perp _{\mathrm{S}\mathrm{D}\mathrm{D}\mathrm{S}}= 0$. Write $b^\perp _q = -t^\perp _q/e_q$. Again, the global maps are permutations of the local coordinate axes and the return map evaluates to

$$\begin{aligned}h_q(w,z,z^\perp ) = (B_q w^{b_{q}}z, D_q w^{a_q}, E_q w^{b_{q}^\perp }z^\perp )\end{aligned}$$

where $B_q, D_q, E_q$ are constants.

In logarithmic coordinates $(\eta , \xi , \xi ^\perp )$, this gives the transition matrix

$$\begin{aligned} {{{\textsf {\textit{M}}}}}_q&= \left( \begin{array}{ccc}b_{q} &{}\quad 1 &{}\quad 0 \\ a_q &{}\quad 0 &{}\quad 0 \\ b_{q}^\perp &{}\quad 0 &{}\quad 1\end{array}\right) \end{aligned}$$

(32)

that governs the stability of the cycle. Note that the upper left $2 \times 2$ submatrix is the same as the transition matrix (21). In order to simplify notation, we write $\xi _1 \ \widehat{=} \ {\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}$ and $\xi _2,\ldots , \xi _6$ for the subsequent equilibria of ${{\mathbf {\mathsf{{C}}}} }$. Assuming that we are in a parameter region where the network exists, see Theorem 4.1, we can now make the following statement about the stability of its subcycles.

Theorem 4.2

Assume that the cycle ${{\mathbf {\mathsf{{C}}}} }$ is asymptotically stable⁵ within the three-dimensional subspace it is contained in and $\left| \delta \right|$ sufficiently small. Then we have the following dichotomy.

• (i) If the transition matrix product ${{{\textsf {\textit{M}}}}}^{(2)}$ satisfies the eigenvector condition (C3), then ${{\mathbf {\mathsf{{C}}}} }$ is f.a.s. and its stability indices ${\mathfrak {s}}_q$, $q=1,\ldots ,6$, (with respect to the dynamics in ${\mathbf {T}}^{M}$) are given by

  $$\begin{aligned} {\mathfrak {s}}_q&= F^{\mathrm{ind}}(\mu _q,\nu _q,1)>-\infty , \end{aligned}$$

  where $\mu _q=b_q\mu _{q+1}+a_q\nu _{q+1}+b_q^\perp ,\ \nu _q=\mu _{q+1}$ for $q=2,\ldots ,6$ and $\mu _1=b_1^\perp ,\ \nu _1=0$.

• (ii) If ${{{\textsf {\textit{M}}}}}^{(2)}$ does not satisfy condition (C3), then ${{\mathbf {\mathsf{{C}}}} }$ is completely unstable.

Proof

Since $t_1^\perp >0$ is the only positive transverse eigenvalue of an equilibrium in ${{\mathbf {\mathsf{{C}}}} }$, the transition matrix ${{{\textsf {\textit{M}}}}}_1$ is the only one with a negative entry, $b_1^\perp <0$. By Proposition 2.7 the stability of ${{\mathbf {\mathsf{{C}}}} }$ depends on whether or not all ${{{\textsf {\textit{M}}}}}^{(q)}$ satisfy conditions (C1)–(C3) in Sect. 2. Statement (ii) follows immediately by Proposition 2.7(a).

For (i), we want to apply Proposition 2.7(b). By Garrido-da-Silva and Castro (2019, Lemma 3.6), it suffices to show that ${{{\textsf {\textit{M}}}}}^{(2)}$ satisfies conditions (C1) and (C2), because then all ${{{\textsf {\textit{M}}}}}^{(q)}$ satisfy (C1)–(C3). We calculate

$$\begin{aligned} {{{\textsf {\textit{M}}}}}^{(2)}={{{\textsf {\textit{M}}}}}_1{{{\textsf {\textit{M}}}}}_6 \cdots {{{\textsf {\textit{M}}}}}_2= \left( \begin{array}{c@{\quad }c@{\quad }c}* &{} * &{} 0 \\ * &{} * &{} 0 \\ b_{1}^\perp \mu +\nu &{} b_{1}^\perp {\tilde{\mu }}+{\tilde{\nu }} &{} 1\end{array}\right) , \end{aligned}$$

where $\mu ,\nu ,{\tilde{\mu }},{\tilde{\nu }}>0$. For a moment, suppose that $\delta =0$. Due to the symmetry of the system in the subspace ${\psi _1\psi _2\psi _3\mathrm{S}}$, the upper left $2 \times 2$ submatrix is the third power of the matrix ${{{\textsf {\textit{M}}}}}$ in (24) and we can use the calculations from Sect. 3.3. Note that ${{{\textsf {\textit{M}}}}}^{(2)}$ has an eigenvalue $\lambda =1$ with eigenvector (0, 0, 1). Its other two eigenvalues are the third powers of those of ${{{\textsf {\textit{M}}}}}$, call them $\lambda _1>\lambda _2$, by a slight abuse of notation. Then $\lambda ^{\max }=\lambda _1>1$ under the assumptions of this theorem, so conditions (C1) and (C2) are satisfied. Proposition 2.7(b) applies, and ${{\mathbf {\mathsf{{C}}}} }$ is f.a.s.. Since eigenvectors and eigenvalues vary continuously in $\delta$, the same is true for $\left| \delta \right|$ sufficiently small.

In order to derive expressions for the stability indices, we have to find the arguments $\beta ^{(l)} \in {\mathbb {R}}^3$ of the function $F^\text {ind}$ from Proposition 2.7. As is shown in Garrido-da-Silva and Castro (2019), this becomes simpler if for all $q=1,\ldots ,6$ we have

$$\begin{aligned} U^{-\infty }\big ({{{\textsf {\textit{M}}}}}^{(q)}\big ):=\left\{ \, x \in {\mathbb {R}}^3_-\,\left| \;\lim \limits _{k \rightarrow \infty } \left( {{{\textsf {\textit{M}}}}}^{{(q)}}\right) ^kx= -\infty \right. \right\} ={\mathbb {R}}^3_-, \end{aligned}$$

(33)

where ${\mathbb {R}}^3_-=\left\{ \, (x_1,x_2,x_3)\,\left| \;x_1,x_2,x_3<0\right. \right\}$ and the convergence is demanded in every component. Clearly, this asymptotic behavior is controlled by the eigenvectors of ${{{\textsf {\textit{M}}}}}^{(q)}$. Consider first the case $q=2$. Under our assumptions, all components of the eigenvector corresponding to the largest eigenvalue $\lambda ^{\max }>1$ have the same sign. Another eigenvector is (0, 0, 1). From Sect. 3.3, we know that the first two components of the remaining eigenvector have opposite signs. It follows that any $x\in {\mathbb {R}}^3_-$ written in the eigenbasis of ${{{\textsf {\textit{M}}}}}^{(2)}$ must have a nonzero coefficient for the largest eigenvector. Therefore, $x\in U^{-\infty }\big ({{{\textsf {\textit{M}}}}}^{(2)}\big )$ and (33) holds. For $q \ne 2$, note that all ${{{\textsf {\textit{M}}}}}^{(q)}$ are similar, hence they have the same eigenvalues. Their eigenvectors are obtained by multiplying those of ${{{\textsf {\textit{M}}}}}^{(2)}$ by ${{{\textsf {\textit{M}}}}}_2, {{{\textsf {\textit{M}}}}}_3{{{\textsf {\textit{M}}}}}_2,\ldots ,{{{\textsf {\textit{M}}}}}_6{{{\textsf {\textit{M}}}}}_5{{{\textsf {\textit{M}}}}}_4{{{\textsf {\textit{M}}}}}_3{{{\textsf {\textit{M}}}}}_2$, respectively. This involves only matrices with nonnegative entries and thus does not affect our conclusions using the signs of the entries of the eigenvectors. Therefore, (33) holds for all $q=1,\ldots ,6$.

Since (33) is satisfied, the only arguments $\beta ^{(l)} \in {\mathbb {R}}^3$ that must be considered for $F^\text {ind}$ in the calculation of ${\mathfrak {s}}_q$ are the rows of the (products of) transition matrices ${{{\textsf {\textit{M}}}}}_q,{{{\textsf {\textit{M}}}}}_{q+1}{{{\textsf {\textit{M}}}}}_q,{{{\textsf {\textit{M}}}}}_{q+2}{{{\textsf {\textit{M}}}}}_{q+1}{{{\textsf {\textit{M}}}}}_q$ and so on. Among these, we only need to take rows into account where at least one entry is negative; if there are none, the respective index is equal to $+\infty$. Negative entries can only occur when ${{{\textsf {\textit{M}}}}}_1$ is involved in the product, and then only in the last row. So for ${\mathfrak {s}}_q$ the last row of ${{{\textsf {\textit{M}}}}}_1{{{\textsf {\textit{M}}}}}_6\cdots {{{\textsf {\textit{M}}}}}_q$ must be considered. Since ${{{\textsf {\textit{M}}}}}_2$ has no negative entries and its third column is (0, 0, 1), the first two entries in the last row of ${{{\textsf {\textit{M}}}}}_2{{{\textsf {\textit{M}}}}}_1{{{\textsf {\textit{M}}}}}_6\cdots {{{\textsf {\textit{M}}}}}_q$ are greater than the respective entries of ${{{\textsf {\textit{M}}}}}_1{{{\textsf {\textit{M}}}}}_6\cdots {{{\textsf {\textit{M}}}}}_q$, yielding a greater value for $F^{\text {ind}}$. The same goes for ${{{\textsf {\textit{M}}}}}_3{{{\textsf {\textit{M}}}}}_2{{{\textsf {\textit{M}}}}}_1{{{\textsf {\textit{M}}}}}_6\cdots {{{\textsf {\textit{M}}}}}_q$ and so on. Thus, ${\mathfrak {s}}_q$ is indeed obtained by plugging the last row of ${{{\textsf {\textit{M}}}}}_1{{{\textsf {\textit{M}}}}}_6\cdots {{{\textsf {\textit{M}}}}}_q$ into $F^\text {ind}$. We get

$$\begin{aligned} {\mathfrak {s}}_1&=F^{\text {ind}}(\hbox {last row of}\ {{{\textsf {\textit{M}}}}}_1),\\ {\mathfrak {s}}_2&=F^{\text {ind}}(\hbox {last row of}\ {{{\textsf {\textit{M}}}}}_1{{{\textsf {\textit{M}}}}}_6{{{\textsf {\textit{M}}}}}_5{{{\textsf {\textit{M}}}}}_4{{{\textsf {\textit{M}}}}}_3{{{\textsf {\textit{M}}}}}_2),\\ {\mathfrak {s}}_3&=F^{\text {ind}}(\hbox {last row of}\ {{{\textsf {\textit{M}}}}}_1{{{\textsf {\textit{M}}}}}_6{{{\textsf {\textit{M}}}}}_5{{{\textsf {\textit{M}}}}}_4{{{\textsf {\textit{M}}}}}_3),\\ {\mathfrak {s}}_4&=F^{\text {ind}}(\hbox {last row of}\ {{{\textsf {\textit{M}}}}}_1{{{\textsf {\textit{M}}}}}_6{{{\textsf {\textit{M}}}}}_5{{{\textsf {\textit{M}}}}}_4),\\ {\mathfrak {s}}_5&=F^{\text {ind}}(\hbox {last row of}\ {{{\textsf {\textit{M}}}}}_1{{{\textsf {\textit{M}}}}}_6{{{\textsf {\textit{M}}}}}_5),\\ {\mathfrak {s}}_6&=F^{\text {ind}}(\hbox {last row of}\ {{{\textsf {\textit{M}}}}}_1{{{\textsf {\textit{M}}}}}_6). \end{aligned}$$

The lower right entry of all these matrices is 1, so for all $q=1,\ldots ,6$ we can write ${\mathfrak {s}}_q=F^\text {ind}(\mu _q,\nu _q,1)>-\infty$. Since the last row of ${{{\textsf {\textit{M}}}}}_1$ is $(b_1^\perp ,0,1)$, we have $\mu _1=b_1^\perp$ and $\nu _1=0$ as claimed. The recursive relations now follow immediately from (32). $\square$

We conclude this section with a few remarks on our results. We first recall some facts about the stability index and nonasymptotic attraction properties (that hold under some mild assumptions, see Lohse 2015 for details) that are helpful to put the remarks into perspective: A cycle is e.a.s. if and only if the stability indices along all its connections are positive. This means that the cycle attracts “a lot of” initial conditions in its neighborhood and thus is expected to be observable in experiments. When an index is even equal to $+\infty$, the cycle attracts everything except for possibly a set of measure zero near the respective connection.

By contrast, being f.a.s. is a weaker property: An f.a.s. cycle still attracts a positive measure set of initial conditions—however, this set may be very small in the sense that its proportion of a neighborhood of the cycle may shrink to zero when the neighborhood becomes small. Therefore, without additional information, it is hard to say whether or not an f.a.s. cycle may be detected experimentally. Such information can be provided through stability indices: An f.a.s. cycle may possess connections with positive (even $+\infty$) and negative (even $-\infty$) indices at the same time—only if initial conditions are chosen close to a connection with positive index is the cycle likely to be observed. With this in mind, we now comment on some aspects of Theorem 4.2.

Remark 4.3

Consider condition (C3). Let $u^\text {max}=(u^\text {max}_1, u^\text {max}_2 ,u^\text {max}_3)$ be the eigenvector of ${{{\textsf {\textit{M}}}}}^{(2)}$ associated with $\lambda ^{\max }$. For $\delta =0$, note that $(u^\text {max}_1, u^\text {max}_2)$ is an eigenvector of ${{{\textsf {\textit{M}}}}}$ associated with its largest eigenvalue, so both of its components have the same sign. Let ${{\,\mathrm{sgn}\,}}$ denote the sign function. To fulfill (C3), we need ${{\,\mathrm{sgn}\,}}(u^\text {max}_3)={{\,\mathrm{sgn}\,}}(u^\text {max}_{1/2})$. A straightforward calculation yields

$$\begin{aligned} u^\text {max}_3=\frac{(b_{1}^\perp \mu +\nu )u^\text {max}_1+ (b_{1}^\perp {\tilde{\mu }}+{\tilde{\nu }})u^\text {max}_2}{\lambda ^{\max }-1}=\frac{\mu _2u^\text {max}_1 + \nu _2u^\text {max}_2}{\lambda ^{\max }-1}, \end{aligned}$$

so it is sufficient to have $\mu _2, \nu _2>0$. This is stronger than assuming (C3), and as soon as it is satisfied, we have ${\mathfrak {s}}_2=F^\text {ind}(\mu _2,\nu _2,1)=+\infty$. Thus, in that case the cycle is strongly attracting along the connection $[{\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}\rightarrow {\mathrm{S}\mathrm{D}\mathrm{D}\mathrm{S}}]$. However, the cycle is not necessarily e.a.s., since the other stability indices are independent of ${\mathfrak {s}}_2$ and might be negative.

By contrast, the indices ${\mathfrak {s}}_1$ and ${\mathfrak {s}}_6$ are always finite because $F^\text {ind}$ has at least one positive and at least one negative argument through $b_1^\perp$. This makes sense since they are indices along connections shared with the other cycle in the network, while ${\mathfrak {s}}_2$ belongs to the trajectory that is furthest away from the common ones (in terms of following connections in the direction of the flow). For the other indices ${\mathfrak {s}}_3,{\mathfrak {s}}_4,{\mathfrak {s}}_5$, there is not necessarily a negative argument, so they could be equal to $+\infty$. From the recursive relations between the $\mu _q$ and $\nu _q$, we see that ${\mathfrak {s}}_q=+\infty$ implies ${\mathfrak {s}}_{q-1}=+\infty$ for $q\in \left\{ 3,4,5\right\}$, which is plausible given the architecture of the heteroclinic network.

Remark 4.4

Since ${\mathfrak {s}}_q>-\infty$ for all q, we have shown that under the assumptions of Theorem 4.2 the cycle ${{\mathbf {\mathsf{{C}}}} }$ is not only f.a.s., but indeed attracts a positive measure set of initial conditions along every single one of its connections. Straightforward constraints on $\mu _q, \nu _q$ given through the definition of $F^\text {ind}$ determine the signs of all ${\mathfrak {s}}_q$ and thus yield necessary and sufficient conditions for ${{\mathbf {\mathsf{{C}}}} }$ to be e.a.s.. A simple example for such a necessary condition is $b_1^{\perp }>-1$, so that ${\mathfrak {s}}_1>0$. This is the same as $e_{{\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}}>t_{{\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}}^\perp$ and in terms of the network parameters amounts to $\delta >0$, cf. Fig. 3.

Similar conditions for the other ${\mathfrak {s}}_q$ become increasingly cumbersome to write down explicitly and we gain little insight from them. Instead, we evaluated the stability indices (of both cycles) numerically. Two cases are illustrated in Fig. 3. We conjecture that there is an open parameter region where the assumptions of Theorem 4.2 are satisfied and the network is e.a.s. (though not asymptotically stable) due to both cycles being maximally stable—one of them e.a.s. and the other one with positive stability indices everywhere except for the connections shared by both cycles. We comment further on this below.

4.2.1 Relationship to the Kirk–Silber Heteroclinic Network

The connection structure of our heteroclinic cycle/network resembles that of the Kirk–Silber network (Kirk and Silber 1994) illustrated in Fig. 4. From the perspective of the heteroclinic network, one may view the network ${{\mathbf {\mathsf{{N}}}} }_2$ in Theorem 4.1 as a Kirk–Silber heteroclinic network with an additional equilibrium in each connection. However, the cycles in the Kirk–Silber network are of type B, while the stability properties of ${{\mathbf {\mathsf{{N}}}} }_2$ rather resemble type C cycles, see Sect. 3.2. We now comment on the similarities and differences between the possible stability configurations for both networks. We find that some stability features of the network in Kirk and Silber (1994) are universal in the sense that similar conclusions hold even for a more complicated network such as the one investigated here.

Fig. 3

Stability indices of the heteroclinic cycles ${\hat{{{\mathbf {\mathsf{{C}}}} }}}_2$ and ${\check{{{\mathbf {\mathsf{{C}}}} }}}_2$ as in Fig. 2 for $(\alpha ,K,r)=(\frac{\pi }{2}, 0.2, 0.01)$. The symbol ‘$+$’ for a stability index denotes ‘positive and finite’ and ‘−’ denotes ‘negative and finite’

First, note that the equivalent of Remark 4.3 also holds for the Kirk–Silber network, where both cycles contain $\xi _2$, but the connection $[\xi _2\rightarrow \xi _3]$ belongs to only one of them. In this sense, the connection $[\xi _2\rightarrow \xi _3]$ in the Kirk–Silber network corresponds to $[{\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}\rightarrow {\mathrm{S}\mathrm{D}\mathrm{D}\mathrm{S}}]$ in ${{\mathbf {\mathsf{{N}}}} }_2$, where ${\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}$ belongs to both cycles but ${\mathrm{S}\mathrm{D}\mathrm{D}\mathrm{S}}$ does not. The stability index ${\tilde{{\mathfrak {s}}}}_{23}$ along $[\xi _2\rightarrow \xi _3]$ is always equal to $+\infty$ under assumptions corresponding to the ones we make in Theorem 4.2, in particular if each cycle is asymptotically stable within its respective subspace, cf. Castro and Lohse (2014, Subsection 5.1).

Second, all stability indices along common connections in the Kirk–Silber network are finite which is the same for ${{\mathbf {\mathsf{{N}}}} }_2$ as shown in Theorem 4.2 and Remark 4.3. In the Kirk–Silber network, this applies only to $[\xi _1\rightarrow \xi _2]$. The last observation in Remark 4.3 means that $\tilde{{\mathfrak {s}}}_{31}=+ \infty$ implies $\tilde{{\mathfrak {s}}}_{23}= + \infty$ in the Kirk-Silber case. Note that this is not true anymore if one drops the assumption that all eigenvalues transverse to the network are negative, see Castro and Lohse (2014, Figure 8) where ${\tilde{{\mathfrak {s}}}}_{31}$ is finite but ${\tilde{{\mathfrak {s}}}}_{23}=+\infty$. We do not address this case for our network here—in this sense our study corresponds to Kirk and Silber (1994) rather than Castro and Lohse (2014).

Fig. 4

The Kirk–Silber network (Kirk and Silber 1994) is formed of two heteroclinic cycles. The stability indices along connections in the cycle containing the equilibria $(\xi _1, \xi _2, \xi _3)$ carry a tilde, those with respect to $(\xi _1, \xi _2, \xi _4)$ do not

Third, conditions for the Kirk–Silber network to be f.a.s. or e.a.s. can be stated explicitly, see in particular Kirk and Silber (1994, Lemma 3) or Castro and Lohse (2014, Subsection 5.1) for a formulation in terms of stability indices. For ${{\mathbf {\mathsf{{N}}}} }_2$, the situation is more complex due to the higher number of connections and equilibria in the network as indicated in Theorem 4.2 and Remark 4.4 and an exhaustive description of all these seems hardly worthwhile.

4.3 Stability of the Heteroclinic Network

Even if the stability of all cycles that constitute a heteroclinic network is known, it is hard to make general conclusions about the stability of the network as a whole. For “simple” cases, like the Kirk–Silber network, a comprehensive study can be found in Castro and Lohse (2014). Based on the results in the previous section, one can draw several conclusions. If one cycle of ${{\mathbf {\mathsf{{N}}}} }_2$ is f.a.s.—conditions are given in Theorem 4.2—then the network itself is f.a.s. Moreover, if one cycle, say ${\hat{{{\mathbf {\mathsf{{C}}}} }}}_2$, is e.a.s. and the heteroclinic trajectories in ${\check{{{\mathbf {\mathsf{{C}}}} }}}_2$ that are not contained in ${\hat{{{\mathbf {\mathsf{{C}}}} }}}_2$ have positive stability indices, then the network is e.a.s.—this is the case in Fig. 3(b).

The geometry of the two-dimensional manifold $W^\text {u}({\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}})\subset \mathrm{S}\mathrm{D}\psi _3\psi _4$ gives insight into the dynamics near the heteroclinic network ${{\mathbf {\mathsf{{N}}}} }_2$. For simplicity, we focus on the case $\alpha =\frac{\pi }{2}$. By (29), the dynamics of the phase differences on $\mathrm{S}\mathrm{D}\psi _3\psi _4$ are given by

$$\begin{aligned} {\dot{\psi }}_3&= \sin (\psi _3)\left( K\cos (\psi _4) -4r\cos (\psi _3) +K(1+2\delta ) \right) , \end{aligned}$$

(34a)

$$\begin{aligned} {\dot{\psi }}_4&= \sin (\psi _4)\left( K\cos (\psi _3) -4r\cos (\psi _4) +K(1-2\delta ) \right) . \end{aligned}$$

(34b)

Note that if $\left| \delta \right| K< 2\left| r\right|$ there is a (saddle) equilibrium $\xi ^{\mathrm{S}\mathrm{D}\psi _3\mathrm{D}}\in \mathrm{S}\mathrm{D}\psi _3\mathrm{D}$ with $\psi _3 = \arccos (\delta K/2r)\in (0, \pi )$. For the same condition, there is an analogous equilibrium $\xi ^{\mathrm{S}\mathrm{D}\mathrm{D}\psi _4}\in \mathrm{S}\mathrm{D}\mathrm{D}\psi _4$ with $\psi _4 = \arccos (-\delta K/2r)\in (0, \pi )$. The stable manifolds of these saddle equilibria now organize the dynamics on $\mathrm{S}\mathrm{D}\psi _3\psi _4$.

Fig. 5

The two-dimensional unstable manifold $W^\text {u}({\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}})\subset \mathrm{S}\mathrm{D}\psi _3\psi _4$ of ${\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}$ (bottom left circle) not only contains points (shaded) which are in the stable manifold of ${\mathrm{D}\mathrm{S}\mathrm{D}\mathrm{S}}$ (top left circle) and ${\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{D}}$ (bottom right circle) but also points in the stable manifold of $\mathrm{S}\mathrm{D}\mathrm{D}\mathrm{D}$ (top right circle). The stable manifolds of the additional equilibria $\xi ^{\mathrm{S}\mathrm{D}\psi _3\mathrm{D}}$ and $\xi ^{\mathrm{S}\mathrm{D}\mathrm{D}\psi _4}$ (black squares) separate the initial conditions. The other parameters are $(\alpha ,K,r)=(\frac{\pi }{2}, 0.2, 0.01)$

Proposition 4.5

For the heteroclinic network ${{\mathbf {\mathsf{{N}}}} }_2$ in Theorem 4.1 with $|\alpha - \frac{\pi }{2}|$ and $|\delta |$ sufficiently small, and an open interval of r, there is robustly an open wedge of initial conditions on $W^\text {u}({\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}})$ such that the trajectories converge to an equilibrium which is not contained in either cycle constituting ${{\mathbf {\mathsf{{N}}}} }_2$.

Proof

We first give conditions on the parameters that ensure that there are no asymptotically stable sets in the invariant set $(0,\pi )^2\subset \mathrm{S}\mathrm{D}\psi _3\psi _4$. It suffices to show that there are no equilibria in $(0,\pi )^2$. By direct calculation, one can verify that for $\alpha =\frac{\pi }{2}$, $\delta =0$ any equilibrium in $(0,\pi )^2$ must lie in $\left\{ \psi :=\psi _3=\psi _4\right\} \subset (0,\pi )^2$. The dynamics of $\psi$ are given by ${\dot{\psi }}=(K-4r)\cos (\psi )+K$. Hence, there are no equilibria if $0<r<K/2$ given $K>0$; these are exactly the conditions for there to be an asymptotically stable heteroclinic cycle in each subspace by Lemma 3.1 and Theorem 3.5.

Now $W^\text {s}(\xi ^{\mathrm{S}\mathrm{D}\psi _3\mathrm{D}})$, $W^\text {s}(\xi ^{\mathrm{S}\mathrm{D}\mathrm{D}\psi _4})$ are—as source–saddle connections—robust heteroclinic trajectories $[{\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}\rightarrow \xi ^{\mathrm{S}\mathrm{D}\psi _3\mathrm{D}}]$, $[{\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}\rightarrow \xi ^{\mathrm{S}\mathrm{D}\mathrm{D}\psi _4}]$. These separate $(0,\pi )^2$ into three distinct sets of initial conditions which completes the proof. $\square$

The dynamics on $(0, \pi )^2\subset \mathrm{S}\mathrm{D}\psi _3\psi _4$ are shown in Fig. 5. The stable manifolds of $\xi ^{\mathrm{S}\mathrm{D}\psi _3\mathrm{D}}$ and $\xi ^{\mathrm{S}\mathrm{D}\mathrm{D}\psi _4}$ subdivide $(0, \pi )^2$ robustly into three wedges with nonempty interior that lie in the stable manifolds of ${\mathrm{S}\mathrm{D}\mathrm{D}\mathrm{S}}$, ${\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{D}}$, and $\mathrm{S}\mathrm{D}\mathrm{D}\mathrm{D}$, respectively. In particular, this suggests that a significant part of trajectories passing by ${\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}$ will approach $\mathrm{S}\mathrm{D}\mathrm{D}\mathrm{D}$ which is not contained in either heteroclinic cycle of the network ${{\mathbf {\mathsf{{N}}}} }_2$.

Remark 4.6

Let ${{\mathbf {\mathsf{{N}}}} }$ be a heteroclinic network and let $\xi _q$, $p=1, \ldots , Q$, denote the equilibria of all its cycles. Abusing the ambiguity of Definition 2.1,⁶ we call ${{\mathbf {\mathsf{{N}}}} }$complete (Ashwin et al. 2018) or clean (Field 2017) if $W^\text {u}(\xi _p)\subset \bigcup _{q=1}^{Q}W^\text {s}(\xi _q)$ for all p and almost complete if the set $W^\text {u}(\xi _p)\cap \bigcup _{q=1}^{Q}W^\text {s}(\xi _q)$ is of full measure for all p and the Lebesgue measure for any volume form on $W^\text {u}(\xi _p)$; see also Bick (2019) for a detailed discussion in the context of coupled oscillator populations.

For ${{\mathbf {\mathsf{{N}}}} }_2$ to be almost complete for $\left| \delta \right|$ sufficiently small, the set $W^\text {u}({\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}})\cap (W^\text {s}({\mathrm{S}\mathrm{D}\mathrm{D}\mathrm{S}})\cup W^\text {s}({\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{D}}))$ would have to be of full (Lebesgue) measure in $\mathrm{S}\mathrm{D}\psi _3\psi _4$. However, Proposition 4.5 shows that there is a set of nonvanishing measure in $\mathrm{S}\mathrm{D}\psi _3\psi _4$ which lies in the stable manifold of $\mathrm{S}\mathrm{D}\mathrm{D}\mathrm{D}$, an equilibrium which is not in the network. Hence, ${{\mathbf {\mathsf{{N}}}} }_2$ cannot be almost complete (nor complete).

Fig. 6

The heteroclinic network ${{\mathbf {\mathsf{{N}}}} }_2$ induces transitions between invariant sets with localized frequency synchrony for $M=4$ populations of $N=2$ oscillators (29) with parameters $\alpha =\frac{\pi }{2}$, $K=0.3$, $r=0.005$, $\delta =0.1$. The top plot in each panel shows the oscillators’ phase evolution (shading; black corresponds to $\theta _{\sigma ,k}=\pi$ and white to $\theta _{\sigma ,k}=0$) in a co-rotating reference frame in which synchronized populations appear stationary. The bottom plot shows the average instantaneous frequencies of each population (colors; populations $\sigma =1,2$ in gray, $\sigma =3$ in blue, $\sigma =4$ in red). Panel a shows a trajectory that is attracted to the cycle ${\hat{{{\mathbf {\mathsf{{C}}}} }}}_2$ and Panel b shows a trajectory that is attracted to the cycle ${\check{{{\mathbf {\mathsf{{C}}}} }}}_2$. Since the network is not asymptotically stable, there are trajectories—see Panel c—which spend time close to the heteroclinic network before converging to the sink ${\mathrm{S}\mathrm{S}\mathrm{S}\mathrm{S}}$ (Color figure online)

4.4 Numerical Exploration

Solving the system of $M=4$ populations of $N=2$ oscillators (29) numerically shows transitions between dynamically invariant sets with localized frequency synchrony along the heteroclinic network ${{\mathbf {\mathsf{{N}}}} }_2$. Figure 6 shows the phase dynamics: There are initial conditions for which the trajectories are attracted to either cycle of ${{\mathbf {\mathsf{{N}}}} }_2$. Since the network is not asymptotically stable, there are trajectories that spend some time close to the heteroclinic network before converging to the asymptotically stable equilibrium ${\mathrm{S}\mathrm{S}\mathrm{S}\mathrm{S}}$. A full classification of the geometry close to the heteroclinic network as for the Kirk–Silber network (see, for example, Kirk and Silber 1994, Figure 5) is beyond the scope of this paper: On the one hand, the Kirk–Silber network only allows for limited ways of trajectories switching between the two disjoint cycles (Castro and Lohse 2016), so here one may expect more diverse configurations in our (higher-dimensional) setting. On the other hand, the particular geometry of our setting likely imposes additional constraints.

Switching between the cycles ${\hat{{{\mathbf {\mathsf{{C}}}} }}}_2$ and ${\check{{{\mathbf {\mathsf{{C}}}} }}}_2$ in ${{\mathbf {\mathsf{{N}}}} }_2$—similar to the dynamics in Bick (2018)—can be observed in the system (29) subject to additive noise. More specifically, for (29) written as ${\dot{\theta }}_{\sigma ,k}=\omega +Y_{\sigma ,k}(\theta )$—see (2)—and independent Wiener processes $W_{\sigma ,k}$, we solved the stochastic differential equation

$$\begin{aligned} {\dot{\theta }}_{\sigma ,k}=\omega +Y_{\sigma ,k}(\theta )+\eta W_{\sigma ,k} \end{aligned}$$

(35)

using XPP (Ermentrout 2002). As shown in Fig. 7, the solutions show transitions either along the heteroclinic trajectory $[{\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}\rightarrow {\mathrm{S}\mathrm{D}\mathrm{D}\mathrm{S}}]$ or $[{\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}\rightarrow {\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{D}}]$. While there are trajectories that will leave the neighborhood of ${{\mathbf {\mathsf{{N}}}} }_2$ eventually, sufficiently large noise can counteract this and push the trajectory back into the basin of attraction of one of the cycles.

Fig. 7

The phase dynamics of system (35) with additive noise of strength $\eta =10^{-7}$ explore the entire heteroclinic network ${{\mathbf {\mathsf{{N}}}} }_2$ for parameters $\alpha =\frac{\pi }{2}$, $r=0.005$, $K=0.3$, and $\delta =0.01$. Data are plotted as in Fig. 6

5 Discussion

Coupled populations of identical phase oscillators do not only support heteroclinic networks between sets with localized frequency synchrony but the stability properties of these networks can also be calculated explicitly. Rather than looking at dynamical systems with generic properties at the equilibria, we focus on a specific class of vector fields and obtain explicit expressions for the stability of a heteroclinic network—a feature of the global dynamics of the system—in terms of the coupling parameters. In particular, this does not exclude the possibility that stability properties depend nonmonotonously on the coupling parameters. The coupling parameters themselves can be related to physical parameters of interacting real-world oscillators, for example through phase reductions of neural oscillators (Hansel et al. 1993).

Our results motivate a number of further questions and extensions, in particular in the context of the companion paper (Bick 2019). First, we here restricted ourselves to the quotient system; this is possible by considering nongeneric interactions between oscillator populations. The question what the dynamics look like if the resulting symmetries are broken, will be addressed in future research. Second, what happens for coupled populations with $N>2$ oscillators? The existence conditions for cycles in Bick (2019) and the numerical results in Bick (2018) suggest existence of such a network, but stability conditions would rely on the explicit calculation of the stability indices (Podvigina and Ashwin 2011). In particular, the main tool used here, namely the results for quasi-simple cycles (Garrido-da-Silva and Castro 2019), ceases to apply since the unstable manifold of ${\mathrm{S}\mathrm{D}\mathrm{S}\mathrm{S}}$ would be of dimension four and contain points with different isotropy (Bick 2019).

How coupling structure shapes the global dynamics of a system of oscillators is a crucial question in many fields of application. Hence, our results may be of practical interest: In the neurosciences for example, some oscillators may fire at a higher frequency than others for some time before another neural population becomes more active (Tognoli and Scott Kelso 2014). The networks here mimic this effect to a certain extent: Trajectories which move along the heteroclinic network correspond to sequential speeding up and slowing down of oscillator populations. At the same time, large-scale synchrony is thought to relate to neural disfunction (Uhlhaas and Singer 2006). From this point of view, the (in)stability results of Sect. 4 appear interesting, since trajectories in numerical simulations may get “stuck” in the fully phase synchronized configuration ${\mathrm{S}\mathrm{S}\mathrm{S}\mathrm{S}}$. Hence, our results may eventually elucidate how to design networks that avoid transitions to a highly synchronized pathological state.

Appendix A. Phase Oscillator Populations with Nonpairwise Coupling

The dynamical equations (29) contain interaction terms that arise naturally in phase reductions of limit cycle oscillators. At the same time, they are related to interactions between oscillator populations through state-dependent phase shift which may be approximated by nonpairwise coupling as shown in Bick (2018); here we generalize these calculations to allow for arbitrary coupling topologies.

Consider a system of $M$ populations of $N$ phase oscillators where $\theta _{\sigma ,k}$ denotes the phase of oscillator k of population $\sigma$. Recall that the Kuramoto-order parameter

$$\begin{aligned}Z_\sigma = \frac{1}{N}\sum _{j=1}^N\exp (i\theta _{\sigma ,j}) \end{aligned}$$

encodes the level of synchrony of population $\sigma$. In particular, $R_\sigma =\left| Z_\sigma \right| =1$ if and only if all oscillators are phase synchronized. Now suppose that the phase of oscillator k in population $\sigma$ evolves according to

$$\begin{aligned} {\dot{\theta }}_{\sigma ,k} = \omega +\sum _{j\ne k} g(\theta _{\sigma ,j}-\theta _{\sigma ,k}+K\Delta \alpha _\sigma ) \end{aligned}$$

(36)

where the interaction is mediated through the coupling function

$$\begin{aligned} g(\vartheta ) = \sin (\vartheta +\alpha )-r\sin (a(\vartheta +\alpha )), \end{aligned}$$

(37)

$a\in {\mathbb {N}}$, and the phase shifts

$$\begin{aligned} \Delta \alpha _\sigma = \sum _{\tau \ne \sigma } K_{\sigma \tau }(1-R_\tau ^2) \end{aligned}$$

are linear combination of the (square of the) Kuramoto-order parameters. Here, $K\ge 0$ is the overall interaction strength and $K_{\sigma \tau }\ge 0$ determines the strength of interaction between populations $\sigma$ and $\tau$. Set $K_\sigma := \sum _{\tau =1}^MK_{\sigma \tau }$.

To approximate the dynamics, we expand the coupling function. We have

$$\begin{aligned} \begin{aligned} g(\vartheta +K\Delta \alpha _\sigma )&= g(\vartheta )+K\Delta \alpha _\sigma \cos (\vartheta +\alpha ) +O\!\left( Kr\right) +O\!(K^2). \end{aligned} \end{aligned}$$

(38)

Using trigonometric identities, we obtain

$$\begin{aligned}R_\tau ^2 = \frac{1}{N^2}\sum _{p,q=1}^N\cos (\theta _{\tau ,p}-\theta _{\tau ,q})\end{aligned}$$

which implies

$$\begin{aligned} R_\tau ^2\cos (\vartheta +\alpha )&= \frac{1}{N}\cos (\vartheta +\alpha ) +\frac{1}{N^2}\sum _{p\ne q}\cos (\theta _{\tau ,p}-\theta _{\tau ,q} + \vartheta +\alpha ). \end{aligned}$$

(39)

Now define the interaction functions

$$\begin{aligned} {\tilde{G}}^{(2)}(\vartheta )&= g(\vartheta ) +K\left( 1-\frac{1}{N}\right) K_\sigma \cos (\vartheta +\alpha ), \end{aligned}$$

(40)

$$\begin{aligned} {\tilde{G}}^{(4)}(\theta _\tau ; \vartheta )&= -\frac{1}{N^2}\sum _{p\ne q}\cos (\theta _{\tau ,p}-\theta _{\tau ,q} + \vartheta +\alpha ). \end{aligned}$$

(41)

Substituting (38) and (39) into (36) and dropping the $O\!\left( Kr\right)$, $O\big (K^2\big )$ terms yield

$$\begin{aligned} {\dot{\theta }}_{\sigma ,k}&= \omega + \sum _{j\ne k}\left( {\tilde{G}}^{(2)}(\theta _{\sigma ,j}-\theta _{\sigma ,k}) +K\sum _{\tau =1}^MK_{\sigma \tau }{\tilde{G}}^{(4)}(\theta _\tau ; \theta _{\sigma ,j}-\theta _{\sigma ,k}) \right) \end{aligned}$$

(42)

as an approximation for (36). Note that the interaction between different populations is through nonpairwise coupling terms: the arguments of the trigonometric functions in ${\tilde{G}}^{(4)}$ depend on four phase variables rather than just differences between pairs of phases.

The $M=3$ coupled populations of $N=2$ oscillators above are determined by the coupling matrix

$$\begin{aligned}(K_{\sigma \tau }) = \left( \begin{array}{ccc} 0 &{}\quad -1 &{}\quad 1\\ 1 &{}\quad 0 &{}\quad -1\\ -1 &{}\quad 1 &{}\quad 0 \end{array}\right) .\end{aligned}$$

Note that $K_\sigma = 0$ for all $\sigma$. Thus,

$$\begin{aligned} {\tilde{G}}^{(2)}(\vartheta )&= g(\vartheta )\\ {\tilde{G}}^{(4)}(\theta _\tau ; \vartheta )&= -\frac{1}{4}\big (\cos (\theta _{\tau , 1}-\theta _{\tau ,2}+\vartheta +\alpha )+\cos (\theta _{\tau , 2}-\theta _{\tau ,1}+\vartheta +\alpha )\big ) \end{aligned}$$

and (42) reduce to Eq. (11) in the main text above.

Now consider $M=4$ populations of $N=2$ oscillators with coupling matrix

$$\begin{aligned}(K_{\sigma \tau }) = \left( \begin{array}{cccc} 0 &{}\quad -1 &{}\quad 1 &{}\quad 1\\ 1 &{}\quad 0 &{}\quad -1 &{}\quad -1\\ -1 &{}\quad 1+\delta &{}\quad 0 &{}\quad -1\\ -1 &{}\quad 1-\delta &{}\quad -1 &{}\quad 0 \end{array}\right) \end{aligned}$$

where the parameter $\delta$ parametrizes the asymmetry between populations three and four. For $\delta =0$, the coupling corresponds to the phase shifts

$$\begin{aligned} \Delta \alpha _1&=-(1-R_{2}^2)+(1-R_{3}^2)+(1-R_{4}^2), \end{aligned}$$

(43a)

$$\begin{aligned} \Delta \alpha _2&=(1-R_{1}^2)-(1-R_{3}^2)-(1-R_{4}^2),\end{aligned}$$

(43b)

$$\begin{aligned} \Delta \alpha _3&=-(1-R_{1}^2)+(1-R_{2}^2)-(1-R_{4}^2),\end{aligned}$$

(43c)

$$\begin{aligned} \Delta \alpha _4&=-(1-R_{1}^2)+(1-R_{2}^2)-(1-R_{3}^2). \end{aligned}$$

(43d)

considered in Bick (2018). We have

$$\begin{aligned} {\tilde{G}}^{(4)}(\theta _\tau ; \vartheta )&= -\frac{1}{4}\big (\cos (\theta _{\tau , 1}-\theta _{\tau ,2}+\vartheta +\alpha )+\cos (\theta _{\tau , 2}-\theta _{\tau ,1}+\vartheta +\alpha )\big )\end{aligned}$$

(44)

$$\begin{aligned} {\tilde{G}}^{(2)}_\sigma (\vartheta )&= g(\vartheta )+K\left( 1-\frac{1}{N}\right) K_\sigma \cos (\vartheta +\alpha ) \end{aligned}$$

(45)

with $K_1 = 1$, $K_2=-1$, $K_3=-1+\delta$, $K_4=-1-\delta$. Hence, Eq. (29) can also be interpreted as a nonpairwise truncation (42) of the system (36) studied in Bick (2018).