Introduction

Cobalt-60 is a prominent element by-product of nuclear reactor operations that may be found in low-level radioactive waste streams. Cobalt-60 has a prolonged half-life of 5.27 years and a greater gamma-ray intensity emitter when the comparison with different gamma-ray supplies. Several applications exist for cobalt-60, including cosmetic sanitization, food irradiation, and medicinal and industrial applications[1], and its manufacturing necessitates effective separation from dissolved targets. Despite these critical applications for cobalt and its compounds, environmental responsibility and regulatory limits require that effluents from these sectors be thoroughly treated before being discharged to minimize environmental concerns and human health dangers. Cesium on the contrary side is a prominent by-product of fission and also the most common radioisotope detected in radioactive wastes, with more than 30 isotopes. The most stable is 133Cs, nonetheless, 134Cs and 137Cs are the most often seen fission products of uranium. Directly following the Fukushima nuclear power disaster in 2011, the two forms of radioactive cesium are the biggest releases of radiation. 137Cs (t1/2 = 30 years) have a substantially longer half-life and a larger energy release than 134Cs (t1/2 = 2.1 years) [2]. Crown ethers are multi-ether group-containing cyclic compounds that can also be modified with dibenzo, dicyclohexane, and other chemical compounds. Researchers have shown curiosity in employing gamma rays to create polymeric composite-supported crown ether in recent times. The following factors are beneficial in shedding some light on how to select the prepared material during the investigation, in which the initial report of crown ethers [3] gained tremendous consideration for alkaline earth cations because of their unusual coordinating capabilities. Extremely compounds have been created with various levels of substitution in addition to the simple crown ether [4]. Because of their distinguishable guest–host structures, crown ethers, as well as their derivative products, have an immense promise for metal separation since they can preferentially coordinate with metal ions through, ion–dipole, or other interconnections. This is very beneficial in adsorption and has been employed extensively [5]. Resulting directly are crown ether concept of environmental cobalt separation adsorbents too though. Even if a study of crown ether-based adsorbents and their shortcomings for cesium sorption would be helpful, it will prove inadequate if it does not also include their application as cesium ion adsorbents [6]. A substance P (NIPAm-Co-AA-DB18C-6) composite was prepared in this research, which is difficult to prepare by traditional techniques. Accordingly, a fundamental study was carried out to prepare and construct the method to obtain a final product in which the components are combined in a certain sequence and quantities with the respect did not add organic solvents to crown ether at all experiments and, accordingly, prepare this substance and sequence of addition was studied because it is the only way to reach and obtain homogenous solution ready to be polymerized using gamma radiation [7]. The objective of this work was to identify the optimum addition sequence between monomer and crown ether. In pursuit of this goal was focused on such characteristics as pH, monomers ratio, and crown ether concentration.

Materials and procedures

Before usage, N-Isopropylacrylamide (NIPAAm, Aldrich, 97%) was purified from n-hexane by recrystallization and drying in an oven under a vacuum. Acrylic acid (AA, 99%) was sold from Sigma–Aldrich. N,N′-Methylenebis(acrylamide) (BIS) was purchased from ACROS company, and the preparation method included the use of sodium hydroxide (NaOH, Merck), acetone (Merck), nitric acid (HNO3, Merck), and ethanol (Nasr, 99 percent). Distilled and deionized water was used for all processes including, solution preparation, and polymer purification. In addition, the cobalt chloride hexahydrate (CoCl2(H2O)6, Merck) and cesium nitrate (Alfa Aesar, Germany) were used as a carrier in the aqueous for 137Cs and 60Co radionuclides solution, and they are used in inactive experiments.

Synthesizing P(NIPAm-co-AA-DB18C-6) composite

Utilization of N-isopropyl acrylamide (NIPAm) copolymerized with acrylic acid (AA) combined with Dibenzo-18-crown-6 (DB18C-6) in the preparation of the polymeric composites is considered a great challenge to maximize the use of its distinctive features using gamma irradiation technique and ultrasonic homogenizer assistance [8]. The monomer mixture, which consisted of NIPAm1.2 and 0.5% AA with a total monomer concentration of 17 and 0.03 wt% BIS as the cross-linker, was dissolved in deionized water (100 ml) and homogenized for 15 min in a small beaker using an ice bath at 5 °C using an ultrasonic homogenizer mixture that was purged with N2 gas for roughly 1 h while stirring at room temperature. In addition, many different experimental conditions effects were investigated, and these included sequence of addition at different crown ether concentrations (1, 2, 3, and 4) wt% and different monomer concentrations [9, 10].

Characterization of sonicated fabric composite.

A dynamic light scattering device (Nicomp 380ZLS, SSNICOMP) with a scattering angle of 176.1 was analyzed to determine the particle size of its specific composite. The size of the particle core and surface structures, and also the kind of ions in the medium, all influence the measuring performance. The examination was conducted using Fourier transform infrared spectroscopy (FTIR), using a Nicolet 560 FTIR instrument, and the samples were combined with KBr and compacted into pellets. The instrument Japan-made JEM 100CS, Jeol, transmission electron microscope (TEM) model was used to examine the morphological and structure of composite material at a 100 kV acceleration voltage. To determine weight variations concerning temperature and time, thermogravimetric analysis (TGA) of polymers is used. Decomposition and oxidation reactions, in addition to physical processes like sublimation, evaporation, and desorption, where DTA is based on temperature difference, can culminate in weight changes of polymeric materials.

Radiometric analysis

For measuring the activity of 60Co and 137Cs, high-resolution NaI(Tl) scintillation detectors are used, USA, Model 802-3 × 3, Canberra, and the data processing software Activision 32 (ORTEC, USA) was used for 60Co and 137Cs determination in supernatant fluids at the energy of γ-photons: 60Co–1173.24 and 137Cs–1081.00 keV. Standardized 60Co solution of 2.181 MBq/mL and 137Cs solution of 1.097 MBq/mL were obtained from the second research reactor, Egyptian atomic energy [11].

Adsorption studies in binary metal system

Batch adsorption experiments were conducted in binary solutions of Co2+ and Cs+ spiked with 60Co and 137Cs and contained 100 mg/L of each ion. Using various quantities of NaOH or HCL, the pH was adjusted to the optimal. Metal solutions were prepared by dispersing CoCl2 and CsNO3 to suitable initial concentrations in deionized water. At 25 °C, the contents of the vials were shaken (120 rpm) for 24 h [12]. Analyzing the metal ion adsorption capabilities in the pH ranges of 1.0 to 8.0 (starting pH value) for both cobalt and cesium ions in binary metal systems at an initial metal ion concentration of 100 mg/L allowed the impact of pH values. The liquid phase was filtered out after each operation and quantified radiometrically. All of the tests were done twice. Mathematical average values are used unless so indicated. The percentage removal (%R) of Co2+ and Cs+ ions is calculated using the following equation [13].

$$\% R = \frac{{\left( {A_{o} - A_{t} } \right)}}{{A_{o} }} \times 100$$
(1)

where Ai and Ae are the initial and equilibrium activity of the investigated radioisotopes.

Adsorption selectivity and distribution

The distribution coefficient for Co (II) separation from the Cs(I)–Co(II) system was evaluated using a batch approach at 25 ± 1°C at various pH. With 10 mL of 100 mg/L Co(II) and Cs(I)ion solutions spiked with a combination of 60Co and 137Cs, 0.02 g of the resin was stirred. The research was carried out using a binary element system. The mixtures were centrifuged after 1 h of incubation (the time it took to reach equilibrium), and the pH solutions were calculated using a bench pH meter. To determine each metal ion's sorption concentration, a multichannel analyzer was employed. The distribution coefficients (Kdi) values for binary system were calculated using the following equations [14]:

$$K_{di} = \frac{{q_{ei} }}{{M^{+i} }}$$
(2)

Where the sorption capacities (qe) and equilibrium concentration [M] of both metals were obtained in binary mixtures with known initial concentrations. The separation factor is computed for the preferable absorption of metal ions in separating a mixture of two metal ions and can be defined by the following equation [15]:

$$\left( {\alpha_{B}^{A} } \right) =\frac{{K_{dCo} }}{{K_{dCs} }}= \frac{{q_{eCo} /\left[ {M^{2 + } } \right]}}{{q_{eCs} /\left[ {M^{ + } } \right]}}$$
(3)

where β is the distribution coefficient for each ion.

Desorption

First, 0.1 g of P(NIPAm-Co-AA-DB18C-6) was shaken with 20 ml (137Cs + 60Co) solution at a concentration of 100 mg/L. After saturation, the sorbent was centrifuged and dried at room temperature. After that, Cs and Co were desorbed using 0.2 M HNO3, and the desorbed solutions were analyzed radiometrically.

Dynamic sorption

Fixed-bed column studies were carried out using a glass column of 1.0 cm internal diameter and 10 cm length. Prior to packing in a glass column, 1 g of the P(NIPAm-Co-AA-DB18C-6) particles were soaked in appropriate amount of deionized water and agitated until complete swelling, and no air bubbles were detected in the solution to avoid entrapping of air bubbles inside particles. A piece of woollen was attached to the bottom of the column to serve as the exchanger substance’s support surface. The loading technique involved passing 50 ml of 100 ppm carrier to every metal ion at pH = 5 avoiding any precipitation for Co+2 ions. As well as a flow rate of 5 ml/min using a pressure adjustable peristaltic pump (Mini-Pump Variable Flow—Fisher Scientific, USA) across the column bed. Equivalent sample were collected, and the activities were measured radiometrically. Co2+ and Cs+ ion column capacities (mg/g) were measured directly and estimated using the following equation [16]:

$${\text{Capacity}} = \frac{{FC_{o} t_{1/2} }}{m}$$
(4)

where m is the amount of the column bed in (g), F is the flow rate (ml/min), Co is the starting concentration of the feed solution (mg/L), and t1/2 is the half breakthrough time (min).

Results and discussion

Characterization of prepared composite

Fourier transforms infrared (FTIR) spectroscopy

The synthesized polymeric composite P(NIPAm-Co-AA-DB18C-6) characterization was satisfactorily supported by the FTIR spectra presented in Fig. 1 and demonstrated that the distinct absorption bands at 3680 and 789 cm−1, correspondingly, belonged to DAB18C-6's hydroxyl (O–H) groups and free amide (N–H) stretch. The broadband at 1752 cm−1 exhibits the carboxylic group COOH's stretching band [17]. The absorption bands at cm−1, 1506 cm−1, 1452 cm−1, 1338 cm−1, and 1232 cm−1 indicate NH bending, CH2 bending, COOH bending, and C–O stretching [18]. The stretching vibration of C=O causes a strong band in the regions of 1581, while broad bands are generated in the areas of 3230 cm−1 by the stretching vibrations of O–H [19]. The existence of these absorption bands for the remaining functional groups of total monomers (NIPAm-Co-AA) in the composite spectrum demonstrates that polymerization and the amide function group enter the DB18C-6 backbone, which has occurred effectively [23].

Fig. 1
figure 1

FTIR of the P(NIPAm-Co-AA-DB18C-6) composite

Full size image

Scanning electron microscope (SEM)-EDX and mapping spectra

According to Fig. 2, the synthesized P(NIPAm-Co-AA-DB18C-6) composite’s morphological characteristics were examined using a scanning electron microscope, and the EDX-elemental analysis. The surface is inconsistent and rough, and the composition contains accessible pores [20, 21]. The presence of pores may have enhanced the probability of metal ion adsorption due to the greater effect of DB18C-6 ether cross-linking. The SEM images reflect the great effect of the added crown ether on the backbone polymer and lead to increased surface roughness. They also indicate that DB18C-6 layers have penetrated inside the prepared matrix, urging a noticeable change for the better. It is clear from the figure if compared to the literature [22]. The data obtained show that the apparent effect of the addition of crown ether is reflected in a change in the morphology and the surface area of the product has been increased.

Fig. 2
figure 2

SEM and EDX results of an electron micrograph of P(NIPAm-Co-AA-DB18C-6)

Full size image

Thermogravimetric analysis (TGA)

An additional kinetic model of the prepared polymer degradation is provided by thermogravimetric analysis (TGA) and differential thermal analysis (DTA), which have been carried out using a thermogravimetric analyzer or thermobalance and are depicted in Fig. 3. 10 °C/min of heat was applied to the produced polymer. Four stages of deterioration are present. Weight loss of 7.6% is seen in the first stage from (27 to 225 °C) with a maximum endothermic peak at 150 °C. This is because all surface and matrix-bound moisture, as well as all absorbed or coordinated water molecules, have been removed [12]. The weight loss in the second stage, from 225 to 265 degrees Celsius, is 33.7%, CO2 is released as a result of the dehydration of reactive monomer, with a maximum endothermic peaks at 254 °C. With a maximum endothermic peak at 420 °C, the third stage, which extends from 265 to 435 °C, exhibits a significant rate of weight loss of 37.0% and 1.6 gm. This might be caused by the depletion of volatile hydrocarbon that developed in the oxide state and the short-chain fragmentation produced by chain scission [13]. The fourth stage, which is the lowest level and occurs between 435 and 640 °C, is characterized by a loss weight of 4.07% and represents the result of the primary chain scission mechanism and final degradation to the oxidized form [14].

Fig. 3
figure 3

DTA and TGA analysis for the P(NIPAm-Co-AA-DB18C-6) composite.3.1.4 X-ray diffraction

Full size image

X-ray diffraction

Figure 4 illustrates the synthesis of reactionary monomers with di benzo 18 crown ether. XRD is a powerful technique for determining the phases of a crystalline substance. The crystalline phase of the synthesized P(NIPAm-Co-AA-DB18C-6) composite is demonstrated by two peaks at diffraction patterns of 10.0° and 20.5°. The information showed that the prepared composite had a considerable crystalline character.

Fig. 4
figure 4

XRD analysis for the P(NIPAm-Co-AA-DB18C-6) composite

Full size image

Dynamic light scattering (DLS)

The Stokes–Einstein equation in DLS is used to calculate the hydrodynamic radius of nanoparticles based upon its diffusion coefficient in a media, and the consequence is indeed the diameter of a sphere that has the same diffusion rate as the NCCs in the form of rods [23]. The prepared P(NIPAm-Co-AA-DB18C-6) composite's particle size and distribution were examined using a dynamic light scattering DLS, and the results are shown in Fig. 5. The (DLS) dynamic light scattering approach is described, with both a focus on bare facts and afterward methods for extracting quantitative details regarding size distribution and produced composite size were discussed. Figure 5 shows that the P(NIPAm-Co-AA-DB18C-6) composite has an average particle size of 878 nm and considerable particle size, having a PDI (polydispersity index) of 0.69. Even the interaction and contribution of di benzo18C-6 crown ether may have attributed to the produced composite's diminished size and size distribution, which causes Since the operation of the ultrasonic homogenizer, composite lesser droplets will still be produced [24].

Fig. 5
figure 5

Intensity distribution of the P(NIPAm-Co-AA-DB18C-6) composite in water measured by DLS

Full size image

Preparation conditions optimization

Performance of the sequence of addition on the polymerization process with different crown ether concentrations

The effect of additional sequences for the polymeric composite on conversion yield was investigated by comparing mixing for three different addition sequences. The first addition sequence was the addition of the total monomer at the same time to crown ether. This addition is referred to as total monomer first (Tm. F). The second addition sequence referred to as acrylic acid second (AA. S) adds the NIPAM to the crown ether before AA. The third addition sequence investigated was the simultaneous addition of AA to crown ether before NIPAM referred to as acrylic acid first (AA. F). In addition, some different experimental conditions effects were investigated, as these included different crown ether concentrations (1, 2, 3, 4 and 5) wt%. As illustrated in Fig. 6a, (AA. F) was the best addition sequence, as evidenced by both the homogenous solution matrix without settling of crown ether and no use of an organic solvent. Compared with the other experiments, it was the best result.

Fig. 6
figure 6

Addition sequence effect for determining crown ether concentration for a (AA.F) based on the b capacity and c conversion rate of P(NIPAm-Co-AA -DB18C-6)

Full size image

Performance of monomers concentration ratio on the polymerization process

Figure 7a, b illustrates the contribution of total monomer concentration based on the existing capacity of the prepared P (NIPAm-Co-AA-DB18C-6) composite that was studied toward Cu2+ ions for the studying process. The maximum Cu2+ capacity was obtained for total monomer concentration at 17 wt.%, specifically for each (NIPAM: AA) monomer, i.e., when conversion rates are highest, which was correlated to maximum sorption uptake percent, where the uptake reached 96%. The specific interaction of metal ions is mostly caused by the NH2 and COOH groups of NIPAM and AA in the composite structure because of the typical variation between Cu2+ ions and (NH2, COOH) groups. Figure 7A reveals that whenever the monomer concentrations increase, the capacity goes up too. Furthermore, as the concentration of NIPAM rises, specifically through the results shown in Fig. 7, which exhibited the behavior of the monomer, the capacity of the prepared composite increases as a result of the effective arrangement of the presented function groups regularly [25, 26].

Fig. 7
figure 7

Impact of the monomer concentration on A conversion yield and B capacity of DB18C-6 (NIPAm-Co-AA)

Full size image

Figure 7B shows that when the monomer concentrations increase, the percent conversion rises as well, with a steady-state occurring in the range of total monomer concentration of 17 wt%. The possibility of an association between the monomer network increases until it reaches a specified concentration (1.2:0.5) wt%. The highest and best-specified concentrations of bonding occurred between the monomer molecules and each other, which reversed highly cross-linking and percent conversion, reached 99.9%.

Sorption investigation

Zero-point charge

The pH value equivalent to levels of positive and negative charges are found mostly on the surface of a substance that is known as the point of zero charges, or pHPZC [27] as shown in Fig. 8. The adsorbent prefers to attract negative-charged ions due to its positive surface charge at pH values lower than that of the pHPZC (anionic species). The adsorbent possesses a negatively charged surface when its pH is higher than the pHPZC, which favors the sorption of positively charged ions (cationic species). The surface charge of the synthesized composite has indeed been calculated using the pHPZC (point of zero charges) method. Varying pH values, from 1.0 to 12.0, were investigated for this objective. The value of pHPZC was determined and confirmed to be 4 by graphing ΔpH (pH initial–pH final) against pH initial (Fig. 8). In the pH range of 1.0 to 4.0, where cobalt and cesium cation sorption was decreased as a result of the repulsion interaction between the synthesized polymer's surface positive charge and the cationic ions, and such number suggests that its surface is charged positively. Between pH 5.0 and 12.0, the surface of the composite becomes negatively charged, increasing the composite's sorption capacity toward Co(II) and Cs(I) species.

Fig. 8
figure 8

The value pHPZC for innovative polymeric composite

Full size image

Swelling

This section studies the swelling degree of the synthetic composite at various pH levels and is represented in Fig. 9 and shows that the composite shows a pH-independent swelling behavior at a pH range from1.0 to 5.0. This may be due to that the (NH2) and (COOH) groups are virtually exclusively in their protonated state. Consequently, an electro-osmotic effect occurs because the sorbent is ionized [28]. This allows water to penetrate the sorbent, causing the sorbent to swell. After that, the swelling degree percent increases gradually until reaching its maximum value at pH = 9; due to the synthetic polymer's significant loss of ionization and removal of the electro-osmotic action, the movement of water from inside the matrix and the swelling activity are terminated.

Fig. 9
figure 9

Swelling percent at different pH values

Full size image

Chemical stability

Chemical stability is a major concern for practical applications of polymeric composites in ionic sorption. The mechanical features of DB18-Crown-6 were enhanced by combining them into co-monomers, which also improved the physicochemical properties and thermal stability [29]. Multiple experiments, on the other hand, were carried out to investigate the screening for prospective chemical instability routes, in which several common structural properties are sensitive to chemical instability [29].

The study of durability in different circumstances includes two methodological approaches, qualitative and quantitative. In quantifiable information, the concentration of a substance is measured at several periods, whereas incubating below a set of circumstances is meant to resemble a stability test. The experiments below demonstrate how to compare the chemical permanence under physicochemical circumstances such as solution pH in the laboratory. The prepared composite is subjected to a variety of pH, in which pH 1–12, showing stability in the waste, [30] indicating stability in different pH values, are the most widely applied pH for stability in earlier phases of waste treatment. At a subsequent stage, a more detailed pH stability profile ensures that all instances are handled [31].

The crown ether composition and preparation process affect the chemical stability of composite-supported crown ether, which also influences crystal size and composition. Crown ether solubility is affected by modification in the crown ether structure by the use of composite. Compared with polymer materials, using crown ether causes an increase in solubility, while using the crown ether causes a decrease in solubility.

Static adsorption

Effect of pH

The pH of the liquid is usually a key analysis factor for the quantitative sorption of metal ions via liquid–solid interactions. Figure 10 shows how pH affects the percentage of Co(II) and Cs(I) removed within the pH range of 1.0–8.0, to avoid cobalt precipitation since its predominant species at pH 9 and higher are CoOH+ and Co(OH)2 [32]. Results indicate that, as the pH of solution increases, the cobalt (II) removal percent increases sharply until it reaches its maximum value (about 91.0%) at pH 6. On other side, removal percent of cesium(I) increases very slow and reaches its maximum value (about 41 %) at pH 8. The Co(II) species and the protonation of functional groups on composite molecular chains may be impacted by the pH value. To produce protonation at lower pH levels, the proton with a high concentration can react with the amine groups of n-isopropyl acrylamide and the carboxylic acid of acrylic acid monomers [33]. The main Co(II) species is shown to be free of Co2+ ions at pH values below 6.0, while species such as Co(OH)+, Co(OH)2, and Co(OH)3 begin to accumulate at pH values above 7.0. Therefore, pH levels of 6.0 were used in several tests to avoid the impacts of cobalt hydroxyl species. The groups of −NH2 on composite were more easily protonated into −NH3+ in very acidic circumstances. The sorption between composite and Co(II) was decreased due to the competing action of hydrogen ions. As a consequence, the composite would remove the little quantity of Co(II) at a very low pH level. As the pH level increased, the competing activity and repulsion force of hydrogen ions reduced. Thus, composite at a higher pH value may remove Co(II) efficiently. The findings, which are displayed in Fig. 8, reveal that the protonation of the composite was severe. As the initial pH value raised, the final pH value progressively exceeded the original pH value as the composite dose grew. This indicates that the composite’s protonation was reduced, and its ultimate pH value relied on the number of alkaline groups it contained. Additionally, the performance of the composite may be affected by its surface charge [34, 35]. Therefore, the optimum pH was taken at 6 to complete this study.

Fig. 10
figure 10

Effect of pH on the amount sorbed of Co2+ and Cs+ ions from aqueous solutions onto prepared polymeric composite

Full size image

Effect of contact time

The synthetic composite's sorption of Cs(I) and Co(II) ions was interpreted as the use of equilibration time. The sorption process depends on time, as illustrated in Fig. 11. The amount of adsorbed material qe increases with longer equilibration times, grew rapidly up to 30 min, then gradually, until, at around 150 min, a consistent value of 17 mg/g was achieved. The sorption process was unaffected by an increase in response time over the time desired. The occurrence of fissures at the sorption sites mostly on the surface of the nanoparticles might explain this finding [36]. The sorption was delayed as these sites were gradually saturated, and the kinetics method changed to be more reliant on how quickly molybdenum ions were moved from the bulk phase to the actual adsorption sites. Furthermore, the observed curve indicated that metal ions were likely to be monolayer filled on the adsorbent's surface. For all future observations, however, an equilibrium duration of 180 min was used to verify that equilibrium sorption was obtained.

Fig. 11
figure 11

Effect of contact time on the removal of Co(II) and Cs(I) by the synthetic composite

Full size image

Adsorption kinetics and their validity

Four nonlinear kinetic models [37,38,39,40] were examined to describe the mechanism of the adsorption and the rate-controlling step for Co(II) and Cs(I) ions adsorption by P(NIPAm-Co-AA -DB18C-6). These four kinetic models are pseudo-first-order models. Their nonlinear forms are given, respectively, by the following Eq. (5).

$$q_{t} = q_{e} \left[ {1 - \exp \left( { - k_{1} t} \right)} \right]$$
(5)
$$q_{t} = \left( {\frac{{K_{2} q_{e}^{2} t}}{{1 + K_{2} q_{e} t}}} \right)$$
(6)
$$q_{t} = \left( {\frac{1}{\beta }} \right)\ln \left( {\alpha \beta } \right) + \left( {\frac{1}{\beta }} \right)\ln \;t$$
(7)
$$q_{t} = K_{i} t^{0.5} + C$$
(8)

where K1 (min−1), K2 (g/mg.min), and Ki (mg/g.min−0.5) are the rate constants of PFO, PSO, and intra-particle diffusion models, respectively, (qt and qe) mg/g are the adsorbed quantity of the investigated ions at time t and calculated equilibrium adsorbed quantity, respectively, β is the adsorption constant (g/mg) and C is a constant value representing the boundary layer effect. Besides the correlation coefficient (R2) values, models validity was examined using Chi-square (χ2) and root-mean-square error (RMSE) tests [41] which can be given by the following equations:

$$\chi^{2} = \sum\limits_{n = 1}^{n} {\left( {\frac{{q_{\exp ,n} - q_{{{\text{calc}},n}} }}{{q_{\exp ,n} }}} \right)^{2} }$$
(9)
$${\text{RMSE}} = \sqrt {\frac{{\sum\nolimits_{n = 1}^{n} {\left( {q_{\exp ,n} - q_{{{\text{calc}},n}} } \right)^{2} } }}{n - 1}}$$
(10)

Fitted kinetic curves are represented in Fig. 12, and all parameters are collected in Table 1 from which we can conclude that pseudo-first-order and pseudo-second-order models show high values of R2 joined to the lower value of χ2 and RMSE values. On another side, the calculated qe values from the pseudo-first-order model (qcalc = 70.1 for 137Cs and 84.8 for 60Co) were found not close to the experimental values (qexp = 89.6 for 137Cs and 124.2 for 60Co). On the opposite side, qe calculated from the pseudo-second-order model (qe = 88.9 for 137Cs and 123.6 for 60Co) was found close to the experimental values implying that the adsorption process in a binary system can be described not only by physisorption but also by chemisorption. The values of Elovich parameters confirm the chemisorption adsorption since the values of the initial constant rate (α = 3.3 for 137Cs and 7.5 for 60Co) are greater than the values of desorption coefficient (β = 0.049 for 137Cs and 0.042 for 60Co). Intra-particle diffusion parameters show a low value of R2 (0.81 for Cs and 0.84 for Co) and high values of χ2 (12.3 for Cs and 14.6 for Co) and RMSE values (16.7 for Cs and 18.1 for Co) confirming that the pore diffusion was not rating controlling step for the adsorption of 137Cs and 60Co on P(NIPAm-Co-AA-DB18C-6) in a binary system. Moreover, the values of the intra-particle diffusion constant (C = 7.49 for Cs and 15.28 mg/g for Co) support the suggestion that the intra-particle diffusion was not the controlling step. This may be due to that, in the binary system, it is difficult to cross the surrounding layer around the adsorbent to reach the internal sites because the competition takes place between Cs and Co ions. Otherwise, ions in the two-component system limit the available surface sites and absorption capacity of the resin for each other [42].

Fig. 12
figure 12

Nonlinear kinetic model fitting of A pseudo-first-order, B pseudo-second-order, C Elovich, and D intra-particle diffusion for adsorption of 137Cs and 60Co using P(NIPAm-Co-AA-DB18C-6)

Full size image
Table 1 Calculated parameters of nonlinear kinetic models and their respective determination coefficients (R2, χ2, and RMSE) for the adsorption of 137Cs and 60Co using P(NIPAm-Co-AA -DB18C-6)
Full size table

Effect of initial concentration

Evaluating the sorption processes within an organization of the practically adsorbed species requires solid-state speciation of Co2+ and Cs+ ions with the produced composite. The characteristics of the adsorbent, as well as the composition of ionized radicals at different pH levels, influence the species of Co2+ and Cs+ ions on active sites of P(NIPAm-Co-AA-DB18C-6) composite. The obtained data are reported in Table 2, which reveals that the greatest sorption capacity for Co2+ and Cs+ ions was 108.0 and 82.0 mg/g, respectively. Due to the active sites belonging to crown ether produced in the polymeric composite besides the effective function groups, and hence, these findings illustrate why Co2+ was specifically removed over Cs+.

Table 2 Metal cations concentrations impact on separation factor
Full size table

Equilibrium isotherm models and their validity

At a specific temperature, there is an isotherm between the optimum adsorbate concentrations in the liquid phase and the equilibrium adsorption quantity in the solid matrix. We can predict the adsorption mechanism—physic sorption, chemosorption, and ion exchange—that took place here between sorbent and adsorbate based on this relationship. Six nonlinear isotherm models are used for binary systems: variable for two parameters (the Langmuir and Freundlich models) and four involving three parameters (the Khan, Sips, Hills, and Redlish-Peterson models)[43,44,45]. Their equations are given below, respectively:

Two parameters models:

$$q_{e} = \frac{{q_{L} K_{L} C_{e} }}{{1 + K_{L} C_{e} }}$$
(11)
$$q_{e} = K_{F} C_{e}^{1/n}$$
(12)

Three parameters models:

$$q_{e} = \frac{{q_{S} b_{K} C_{e} }}{{\left( {1 + b_{K} C_{e} } \right)^{{a_{K} }} }}$$
(13)
$$q_{e} = \frac{{q_{m} K_{S} C_{e} }}{{\left( {1 + a_{S} C_{e}^{n} } \right)}}$$
(14)
$$q_{e} = \frac{{q_{SH} C_{e}^{nH} }}{{\left( {K_{D} + C_{e}^{nH} } \right)^{{}} }}$$
(15)
$$q_{e} = \frac{{K_{RP} C_{e} }}{{\left( {1 + a_{RP} C_{e}^{b} } \right)}}$$
(16)

where qe (mg/g) and Ce (mg/L) are the equilibrium sorption amount and the equilibrium concentration of ions (mg/L), respectively, qL, qS, qm, and qSH are the theoretical maximum adsorption capacity (mg/g) for each model. KL (L/mg) is the Langmuir equilibrium constant, and KF and 1/n are Freundlich constant corresponding to adsorption capacity and the linearity index, respectively. bK is the Khan model constant and aK is its exponent, Ks and aS are Sips model constants, nH and KD are Hills model constants, KRP and aRP are Redlish–Peterson constants, and b is its exponent.

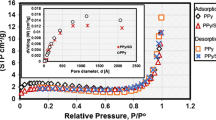
Figure 13 shows the different fits of Cs+ and Co2+ binary sorption data at the optimum conditions, on P(NIPAm-Co-AA-DB18C-6). From this figure, it is clear that three-parameter isotherm models (Khan, Sips, Hills, and Rdlish-Peterson) fitted well with the experimental values but two-parameter models (Langmuir and Freundlich) are not fitted at all. On another side, Table 3 contains all parameters associated with the models, based on the three error analysis methods (R2, χ2, and RMSE) coefficient values, two-parameter models were not suitable for adjusting the adsorption isotherms of Cs+ and Co2+ ions in a binary system using P(NIPAm-Co-AA-DB18C-6). The correlation coefficient (R2 = −0.68) gives the same negative values for Co2+ ion in both Langmuir and Freundlich models coupled with high values of χ2 (=1822.8 and 1820.3) for Langmuir and Freundlich, respectively. In the Khan model, aK is equal unity for both ions (aK = 0.97 and 0.99 for Cs+ and Co2+, respectively) indicating monolayer adsorption. The values of b in the Rdlish-Peterson model ensure that the adsorption is monolayer since its values are near to unity for both ions (b = 0.98 and 0.99 for Cs+ and Co2+, respectively). Finally, the correlation coefficient degree of the three-parameter isotherms follows the sequence: Khan > Rdlish-Peterson > Hills > Sips (Table 4).

Fig. 13
figure 13

Nonlinear isotherm model fitting of A Langmuir, B Freundlich, C Sips, D Hills, C Khan and F Redlish-Peterson for adsorption of 137Cs and 60Co using P(NIPAm-Co-AA-DB18C-6)

Full size image
Table 3 Calculated parameters of nonlinear isotherm models and their respective determination coefficients (R2, χ2 and RMSE) for the adsorption of 137Cs and 60Co using P(NIPAm-Co-AA-DB18C-6)
Full size table
Table 4 Comparison between capacities for different sorbents
Full size table

Application

Dynamic sorption–fixed-bed column

It is possible to describe fixed-bed continuous flow column adsorption as dynamic adsorption in which the influent continually enters and exits the column. It assists in describing the adsorbent's performance, illustrating the adsorbent-adsorbate system's behavior, ascertaining the kinetic column parameters, and forecasting breakthrough curves. The breakthrough point, also known as the moment at which the effluent concentration reaches the maximum permissible discharge concentration of a particular solution contamination, is indicated by the breakthrough curve.

The revolution curves for the Cs+–Co2+ system on the newly developed sorption solid are shown in Fig. 14A. Basically, the adsorbate is swiftly and completely absorbed mostly by adsorbent as the influent is supplied via the column in the initial stage, resulting in the absence of adsorbate in the effluent solution. Adsorbate concentration in the effluent (Ct) and the ratio of adsorbate concentration in the effluent to starting concentration (Ct/CO) are both zero at this stage. The adsorbent then progressively gets filled with adsorbate as the adsorption process continues, losing some of its effectiveness. Because the mass transfer zone (MTZ), which moves a unit length incrementally across the adsorbent, starts moving at about this point, it is possible to measure the concentration of the adsorbate within the effluent. After then, the adsorbent becomes saturated and depleted, adsorption stops, and the ratio of Ct to CO has become close to 1. Noting that the MTZ, also known as the primary sorption zone (PSZ), is the region between the breakthrough point selected arbitrarily) and the saturation point adsorbate concentration (closely imminent concentration of influent). The connection between fixed-bed adsorption and the breakthrough curve’s characteristics is also expressed using MTZ.

Fig. 14
figure 14

Column operation for A breakthrough curve B Elution curve of Cs +–Co2 + system using innovative sorbent

Full size image

Through the plotting of Ct/Co vs the effluent time (min), the breakthrough capacity for Co2+and Cs+ ions on the novel sorption solid was determined and also was observed to be 105.0 mg/g for Co2+, which would be nearer to the batch adsorption capacity =108.0 mg/g, and 67.0 mg g−1 for Cs+, which would be fewer than just that acquired from batch adsorption (82 mg/g). The inadequate equilibrium circumstances in column operation for Cs+ may be to blame for this behavior.

The elution profiles for the investigated cations are given in Fig. 14B. The elution of Co2+ and Cs+ is studied with different concentrations of nitric acid (0.1–1 M) as an eluent. It was observed that Co2+ and Cs+ ions were released using 0.1 M HNO3. Otherwise, Co2+ ions only were released using 0.5 and 1 M HNO3. This may be explained according to the selectivity order of investigated ions with the innovative sorbent.

Desorption studies

The whole removal of the radioactive elements applied in this study through using the composite has been investigated, and this is a significant stage to comprehending how the prepared material behaves, to ensure its effect and stability for repeated applications. To prove this, a study examined several concentrations and changed them to see whether the number of ions adsorbed on the composite could be reused pass or fail.

Figure 15 illustrates that the use of 0.2 M HNO3 solution has been reached to desorb the radioactive Co and Cs ions from the prepared composite. The metal ions were completely desorbed in less than 30 min. In 15 min, rapid desorption (almost 85 percent) was detected. Figure 8 depicts the results, and it is evident that desorption of Co ions reaches a maximum of 97 percent after 20 min, after that, there is no more desorption occurs. Within 30 min, Cs(I) desorption had came to a head. As a result of this study, the synthesized composite may be effectively regenerated, and it may be sometimes used regularly to remove metal ions from water-based solutions.

Fig. 15
figure 15

Desorption of metal ions

Full size image

Summary

In this work, great effort was devoted to investigating the selective adsorption behavior toward 60Co in binary solute systems. The originality of this work was the multi-stage synthesis and testing of the innovative material. Three different sequence additions were investigated adding the total monomer at the same time to crown ether, adding the NIPAM to crown ether before AA, and adding the AA to crown ether before NIPAM. Results indicated that the performance was optimized when the AA was added firstly to crown ether, in which the addition sequence influences socialization mood and prevented it from separating the matrix of the system. The adsorption and separation of cobalt-60 ions from radioactive liquid waste containing cesium-137 have been investigated to determine whether a newly synthesized adsorbent performs in batch operations and continued to be used for environmental waste. Kinetics studies employ pseudo-first-order, as well as pseudo-second-order, analyses at various contact times for Co(II) and Cs(I) ions onto P(NIPAm-Co-AA-DB18C-6) composite, and it is found that the second kinetic equation is superior to other ones for the description of kinetic data. Regarding equilibrium, Redlich-Peterson's isotherm model represented the adsorption process, and it is the best fit. In various solution media, the innovative polymeric composite has demonstrated its efficiency and chemical stabilities.