An investigation of the influence of extracellular matrix anisotropy and cell–matrix interactions on tissue architecture

Abstract

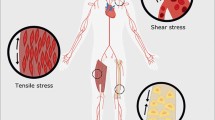
Mechanical interactions between cells and the fibrous extracellular matrix (ECM) in which they reside play a key role in tissue development. Mechanical cues from the environment (such as stress, strain and fibre orientation) regulate a range of cell behaviours, including proliferation, differentiation and motility. In turn, the ECM structure is affected by cells exerting forces on the matrix which result in deformation and fibre realignment. In this paper we develop a mathematical model to investigate this mechanical feedback between cells and the ECM. We consider a three-phase mixture of collagen, culture medium and cells, and formulate a system of partial differential equations which represents conservation of mass and momentum for each phase. This modelling framework takes into account the anisotropic mechanical properties of the collagen gel arising from its fibrous microstructure. We also propose a cell–collagen interaction force which depends upon fibre orientation and collagen density. We use a combination of numerical and analytical techniques to study the influence of cell–ECM interactions on pattern formation in tissues. Our results illustrate the wide range of structures which may be formed, and how those that emerge depend upon the importance of cell–ECM interactions.

Appendix A: Approximation of the cell force, \(\varvec{F}_c\)

In this appendix, we give details of the calculation that leads to the leading-order expression for the cell force given in Eq. (14). Note that we suppress time dependence within this section for notational convenience. We begin by using the fact that $\varvec{x}' = \varvec{x} + \eta \varvec{\xi }$, where $\eta \ll 1$, to expand the terms in Eq. (13) which are evaluated at $\varvec{x}'$ as follows:

$$\begin{aligned} \varvec{a}\left( \varvec{x}'\right)= & {} \varvec{a}(\varvec{x}) + \eta (\varvec{\xi } \cdot \nabla ) \varvec{a}\vert _{\varvec{ x}}+ O(\eta ^2),\end{aligned}$$

(31a)

$$\begin{aligned} \phi _n\left( \varvec{ x}'\right)= & {} \phi _n\left( \varvec{ x}\right) + \eta (\varvec{\xi } \cdot \nabla )\phi _n\vert _{\varvec{ x}} + O(\eta ^2),\end{aligned}$$

(31b)

$$\begin{aligned} \phi _c\left( \varvec{ x}'\right)= & {} \phi _c\left( \varvec{ x}\right) + \eta (\varvec{\xi } \cdot \nabla )\phi _c\vert _{\varvec{ x}} + O(\eta ^2), \end{aligned}$$

(31c)

where the notation $(\varvec{\xi } \cdot \nabla ) \varvec{a}\vert _{\varvec{ x}}$ is intended to emphasise the fact that the directional derivatives are evaluated at the point $\varvec{x}$.

On integration, the contribution of the leading-order terms in the integral is zero by symmetry. Proceeding to next order, we find

$$\begin{aligned} \varvec{F}_c(\varvec{x})= & {} \eta ^{N+2} \int _{{\varOmega }} F(|\varvec{\xi }|) \varvec{\xi }[\phi ^2_c (2 \phi _n (\varvec{a} \cdot \hat{\varvec{\xi }}) [( (\varvec{\xi } \cdot \nabla ) \varvec{a} ) \cdot \hat{\varvec{\xi }}]\nonumber \\&+\, (\varvec{a} \cdot \hat{\varvec{\xi }})^2 (\varvec{\xi } \cdot \nabla ) \phi _n )+ 2 \phi _n \phi _c (\varvec{a} \cdot \hat{\varvec{\xi }} )^2 ( \varvec{\xi } \cdot \nabla ) \phi _c]\,d^N \xi , \end{aligned}$$

(32)

where $\hat{\varvec{\xi }} = \varvec{\xi } / | \varvec{\xi }|$, and $\phi _n$, $\phi _c$ and $\varvec{a}$ are evaluated at $\varvec{x}$ (unless otherwise stated). In component form we have

$$\begin{aligned} F_{{c}_i}= & {} \eta ^{N+2} \int _{{\varOmega }} F(|\varvec{\xi }|) \xi _i \left[ \phi ^2_c \left( 2 \phi _n a_l \hat{\xi }_l \xi _k \frac{\partial a_j}{\partial x_k} \hat{\xi }_j + a_j \hat{\xi }_j a_l \hat{\xi }_l \xi _k \frac{\partial \phi _n}{\partial x_k} \right) \right. \nonumber \\&\left. +\, 2 \phi _n \phi _c a_l \hat{\xi }_l a_j \hat{\xi }_j \xi _k \frac{\partial \phi _c }{\partial x_k} \right] \, d^N \xi , \end{aligned}$$

(33)

or, equivalently

$$\begin{aligned} F_{{c}_i} = \eta ^{N+2} \int _{{\varOmega }} F(|\varvec{\xi }|) \frac{1}{|\varvec{\xi }|^2} \xi _i \xi _j \xi _k \xi _l T_{j k l} \, d^N \xi = A_{i j k l}(\varvec{\xi }) T_{j k l}(\varvec{x}), \end{aligned}$$

(34)

where $T_{j k l}$ is independent of $\varvec{\xi }$, and is given by

$$\begin{aligned} T_{j k l} (\varvec{x}) = \left( a_j \frac{\partial }{\partial x_k} (\phi _n \phi ^2_c) + 2 \phi _n \phi ^2_c \frac{\partial a_j}{\partial x_k} \right) a_l , \end{aligned}$$

(35)

and

$$\begin{aligned} A_{i j k l} = \int _{{\varOmega }}F(|\varvec{\xi }|) \frac{1}{|\xi |^2} \xi _i \xi _j \xi _k \xi _l\, d^N \xi . \end{aligned}$$

(36)

Since $A_{i j k l}$ is an isotropic integral, it must be of the form (Spain 1953)

$$\begin{aligned} A_{i j k l} = \lambda _1 \delta _{i j} \delta _{k l} + \lambda _2 \delta _{i k} \delta _{j l} + \lambda _3 \delta _{i l} \delta _{j k }. \end{aligned}$$

(37)

Furthermore, since $A_{i j k l} = A_{i k j l} = A_{i l j k}$, we deduce that

$$\begin{aligned} \lambda _1 = \lambda _2 = \lambda _3 = \lambda ^*. \end{aligned}$$

(38)

From Eqs. (36) and (37) we note that

$$\begin{aligned} A_{i i k l} = \int _{{\varOmega }} F(|\xi |) \xi _k \xi _l \, d^N \xi = \left( N +2 \right) \lambda ^* \delta _{k l} , \end{aligned}$$

(39)

and contracting over the remaining indices we obtain

$$\begin{aligned} N(N+2) \lambda ^* = \int _{{\varOmega }} F(|\xi |) |\xi |^2 \, d^N \xi . \end{aligned}$$

(40)

Hence, on substituting Eq. (37) into Eq. (34), and on using the well-known properties of the Kronecker delta and the fact $|\varvec{a}|=1$, we find

$$\begin{aligned} \varvec{F}_{c}(\varvec{x})= & {} \lambda [2 \phi _n \phi _c^2 (\varvec{a} \cdot \nabla ) \varvec{a} + \varvec{a} \phi _c^2 (\varvec{a} \cdot \nabla ) \phi _n +\phi _n \varvec{a} ( (\varvec{a} \cdot \nabla ) \phi ^2_c) ] \nonumber \\&+\, \lambda [\phi _c^2 \nabla \phi _n +\phi _n \nabla (\phi _c^2) ]\nonumber \\&+\,\lambda [2 \phi _n \phi _c^2 (\nabla \cdot \varvec{a}) \varvec{a} + \phi _c^2 \varvec{a} (\varvec{a} \cdot \nabla ) \phi _n + \phi _n \varvec{a} (\varvec{a} \cdot \nabla \phi ^2_c)], \end{aligned}$$

(41)

where we have assumed that $\lambda = \eta ^{N+2} \lambda ^* = O(1)$. A little algebra then yields

$$\begin{aligned} \varvec{F}_c(\varvec{x}) = 2 \lambda \left[ (\varvec{a} \cdot \nabla ) (\phi _n \phi _c^2 \varvec{a} ) + \phi _n \phi _c^2 \varvec{a} (\nabla \cdot \varvec{a}) +\frac{1}{2} \nabla (\phi _c^2 \phi _n )\right] . \end{aligned}$$

(42)