Fixation in large populations: a continuous view of a discrete problem

Abstract

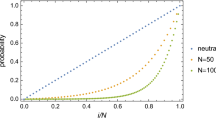
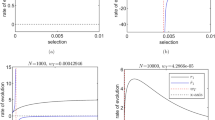
We study fixation in large, but finite, populations with two types, and dynamics governed by birth-death processes. By considering a restricted class of such processes, which includes many of the evolutionary processes usually discussed in the literature, we derive a continuous approximation for the probability of fixation that is valid beyond the weak-selection (WS) limit. Indeed, in the derivation three regimes naturally appear: selection-driven, balanced, and quasi-neutral—the latter two require WS, while the former can appear with or without WS. From the continuous approximations, we then obtain asymptotic approximations for evolutionary dynamics with at most one equilibrium, in the selection-driven regime, that does not preclude a weak-selection regime. As an application, we study the fixation pattern when the infinite population limit has an interior evolutionary stable strategy (ESS): (1) we show that the fixation pattern for the Hawk and Dove game satisfies what we term the one-half law: if the ESS is outside a small interval around ${1}/{2}$, the fixation is of dominance type; (2) we also show that, outside of the weak-selection regime, the long-term dynamics of large populations can have very little resemblance to the infinite population case; in addition, we also present results for the case of two equilibria, and show that even when there is weak-selection the long-term dynamics can be dramatically different from the one predicted by the replicator dynamics. Finally, we present continuous restatements valid for large populations of two classical concepts naturally defined in the discrete case: (1) the definition of an ${\textsc {ESS}}_N$ strategy; (2) the definition of a risk-dominant strategy. We then present three applications of these restatements: (1) we obtain an asymptotic definition valid in the quasi-neutral regime that recovers both the one-third law under linear fitness and the generalised one-third law for $d$-player games; (2) we extend the ideas behind the (generalised) one-third law outside the quasi-neutral regime and, as a generalisation, we introduce the concept of critical-frequency; (3) we recover the classification of risk-dominant strategies for $d$-player games.

Appendices

Appendix A: Proof of Theorem 1

First, observe that

$$\begin{aligned} \prod _{r\in [{1}/{N},s]_{N}}\frac{\varDelta ^-_N(r)}{\varDelta ^+_N(r)}=\exp \left( \sum _{r\in [{1}/{N},s]_{N}}\log \left( \frac{\varDelta ^-_N(r)}{\varDelta ^+_N(r)}\right) \right) =\exp \left( -\sum _{r\in [{1}/{N},s]_{N}}\varTheta _N(r)\right) . \end{aligned}$$

Now we observe that

$$\begin{aligned} \sum _{r\in [{1}/{N},s]_{N}}\varTheta _N(r)&=\Vert \varTheta _N\Vert _\infty \sum _{r\in [{1}/{N},s]_{N}}\frac{\varTheta _N(r)}{\Vert \varTheta _N\Vert _\infty }\\&=\Vert \varTheta _N\Vert _\infty \sum _{r\in [{1}/{N},s]_{N}}\left( \frac{\varTheta _N(r)}{\Vert \varTheta _N\Vert _\infty }-\theta (r)\right) +\kappa ^{-1}_N\sum _{r\in [{1}/{N},s]_{N}}\frac{\theta (r)}{N}. \end{aligned}$$

The last sum can be interpreted as a Riemann sum in two different ways: either as a right sum, or as a midpoint sum. The classical error bounds for the Riemann sums (Atkinson 1989; Stoer and Bulirsch 2002), are as follows:

$$\begin{aligned} \left\| \frac{\theta (x_0+{1}/{N})}{N}-\int _{x_0}^{x_0+{1}/{N}}\theta (r)\,{\mathrm {d}}r\right\| \le \frac{\theta '(c)}{2N^2},\quad c\in (x_0,x_0+{1}/{N}), \end{aligned}$$

for the right rule, and

$$\begin{aligned} \left\| \frac{\theta (x_0+{1}/{N})}{N}-\int _{x_0-\delta _N}^{x_0+\delta _N}\theta (r)\,{\mathrm {d}}r\right\| \le \frac{\theta ''(c)}{24N^3},\quad c\in (x_0-\delta _N,x_0+\delta _N), \end{aligned}$$

for the midpoint rule, where

$$\begin{aligned} \delta _N=\frac{1}{2N}. \end{aligned}$$

These bounds yield the following simple bounds:

$$\begin{aligned} \left\| \sum _{r\in [{1}/{N},s]_{N}}\frac{\theta (r)}{N}-\int _0^s\theta (r)\,{\mathrm {d}}r\right\| _\infty \le \frac{\Vert \theta '\Vert _\infty }{2N}; \end{aligned}$$

for the former, whereas, in the latter, we have

$$\begin{aligned} \left\| \sum _{r\in [{1}/{N},s]_{N}}\frac{\theta (r)}{N}-\int _{\delta _N}^{s+\delta _N}\theta (r)\,{\mathrm {d}}r\right\| _\infty \le \frac{\Vert \theta ''\Vert _\infty }{24N^2}. \end{aligned}$$

In addition, we also have that

$$\begin{aligned} \left\| \sum _{r\in [{1}/{N},s]_{N}}\left( \frac{\varTheta _N(r)}{\Vert \varTheta _N\Vert _\infty }-\theta (r)\right) \right\| _\infty \le N\epsilon _N. \end{aligned}$$

Combining these two results, we find that

$$\begin{aligned} \sum _{r\in \left[ {1}/{N},s-{1}/{N}\right] _N}\varTheta _N(r)=\kappa ^{-1}_N\int _{\delta _N}^{s-\delta _N}\theta (r)\,{\mathrm {d}}r + \kappa ^{-1}_N\epsilon _NR_1^0(s)+\kappa ^{-1}_NN^{-2}R_2^0(s), \end{aligned}$$

where

$$\begin{aligned} \kappa _N^{-1}\epsilon _NR_1^0(s)= & {} \Vert \varTheta _N\Vert _\infty \sum _{r\in [{1}/{N},s]_{N}}\left( \frac{\varTheta _N(r)}{\Vert \varTheta _N\Vert _\infty }-\theta (r)\right) \quad \text {and} \quad \kappa _N^{-1}N^{-2}R_2^0(s)\\= & {} \sum _{r\in [{1}/{N},s]_{N}}\frac{\theta (r)}{N}-\int _{\delta _N}^{s+\delta _N}\theta (r)\,{\mathrm {d}}r, \end{aligned}$$

and hence we have that $\Vert R_1^0\Vert _\infty$ and $\Vert R_2^0\Vert _\infty$ are bounded uniformly in $N$. Recalling that

$$\begin{aligned} {\fancyscript{F}}(s)=-\int _0^s\theta (r)\,{\mathrm {d}}r, \end{aligned}$$

we then have that

$$\begin{aligned} \sum _{r\in \left[ {1}/{N},s-{1}/{N}\right] _N}\varTheta _N(r)&= -\kappa ^{-1}_N{\fancyscript{F}}(s-\delta _N) +\underbrace{\kappa ^{-1}_N{\fancyscript{F}}(\delta _N)}_{{\fancyscript{C}}_N} + \underbrace{\kappa ^{-1}_N\epsilon _NR_1(s)+\kappa ^{-1}_NN^{-2}R_2(s)}_{{\fancyscript{G}}_N(s)} \\&=-\kappa ^{-1}_N{\fancyscript{F}}(s-\delta _N)+{\fancyscript{C}}_N+{\fancyscript{G}}_N(s). \end{aligned}$$

Thus

$$\begin{aligned}&\sum _{s\in [{1}/{N},x]_N}\prod _{r\in [{1}/{N},s-{1}/{N}]_N}\frac{\varDelta ^-_N(r)}{\varDelta ^+_N(r)}=\exp (-{\fancyscript{C}}_N)\sum _{s\in [{1}/{N},x]_N}\exp \left( \kappa _N^{-1}{\fancyscript{F}}(s-\delta _N)\right) \exp (-{\fancyscript{G}}_N(s))\\&\quad =\exp (-{\fancyscript{C}}_N)\exp (\kappa _N^{-1}{\fancyscript{F}}(\bar{s}))\sum _{s\in [{1}/{N},x]_N}\exp \left( \kappa _N^{-1}{\fancyscript{H}}(s-\delta _N)\right) \exp (-{\fancyscript{G}}_N(s)). \end{aligned}$$

where $\bar{s}$ is any point where the global maximum of ${\fancyscript{F}}$ is attained, and ${\fancyscript{H}}(s)={\fancyscript{F}}(s)-{\fancyscript{F}}(\bar{s})$.

Let

$$\begin{aligned} \varUpsilon _N=\kappa _N^{-1}\max \left\{ \Vert R_1^0\Vert _\infty \epsilon _N,\Vert R_2^0\Vert _\infty N^{-2}\right\} . \end{aligned}$$

Since $\Vert {\fancyscript{G}}_N\Vert _\infty \le \varUpsilon _N$, we can find $E_N(x)$, with $\Vert E_N(x)\Vert _\infty \le \varUpsilon _N$, such that

$$\begin{aligned}&\sum _{s\in [{1}/{N},x]_N}\prod _{r\in [{1}/{N},s-{1}/{N}]_N}\frac{\varDelta ^-_N(r)}{\varDelta ^+_N(r)}=\exp (-{\fancyscript{C}}_N)\exp (\kappa _N^{-1}{\fancyscript{F}}(\bar{s}))\\&\quad \times \sum _{s=[{1}/{N},x]_N}\exp \left( \kappa _N^{-1}{\fancyscript{H}}(s-\delta _N)\right) (1+E_N(x)). \end{aligned}$$

Therefore, we have

$$\begin{aligned}&\sum _{s\in [{1}/{N},x]_N}\prod _{r\in [{1}/{N},s-2\delta _N]_N}\frac{\varDelta ^-_N(r)}{\varDelta ^+_N(r)}\\&\quad =N\exp (-C_N)\exp \left( \kappa _N^{-1}{\fancyscript{F}}(\bar{s})\right) \sum _{s\in [{1}/{N},x]_N}\frac{1}{N}\exp \left( \kappa _N^{-1}{\fancyscript{H}}(s-\delta _N)\right) (1+E_N(x))\\&\quad =N\exp (-{\fancyscript{C}}_N)\exp \left( \kappa _N^{-1}{\fancyscript{F}}(\bar{s})\right) \left[ \int _{\delta _N}^{x+\delta _N}\exp \left( \kappa _N^{-1}{\fancyscript{H}}(s-\delta _N)\right) \,{\mathrm {d}}s + R_N(x)\right] (1+E_N(x))\\&\quad =N\exp (-{\fancyscript{C}}_N)\exp \left( \kappa _N^{-1}{\fancyscript{F}}(\bar{s})\right) \left[ \int _{0}^{x}\exp \left( \kappa _N^{-1}{\fancyscript{H}}(s)\right) \,{\mathrm {d}}s + R_N(x)\right] (1+E_N(x)) \end{aligned}$$

with

$$\begin{aligned} R_N(x)=\frac{\kappa _N^{-1}}{24N^3}\sum _{j=1}^m\exp \left( \kappa _N^{-1}{\fancyscript{H}}(\bar{s}_j)\right) \left( \kappa _N^{-1}\theta ^2(\bar{s}_j)-\theta '(\bar{s}_j)\right) , \end{aligned}$$

where $\bar{s}_j\in ({1}/{2N}+{(j-1)}/{N},{1}/{2N}+{j}/{N})$, and with $m=\lfloor xN\rfloor$.

If we write

$$\begin{aligned} I_N(x)=\int _{0}^{x}\exp (\kappa _N^{-1}{\fancyscript{H}}(s))\,{\mathrm {d}}s, \end{aligned}$$

then, by combining all the previous calculations, we obtain the following approximation:

$$\begin{aligned} \varPhi _N(x)&=\frac{I_N(x)+R_N(x)}{I_N(1)+R_N(1)}\times \frac{1+E_N(x)}{1+E_N(1)} =\frac{{I_N(x)}/{I_N(1)}+{R_N(x)}/{I_N(1)}}{1+{R_N(1)}/{I_N(1)}}\times \frac{1+E_N(x)}{1+E_N(1)}\\&=\frac{\phi _N(x)+{\fancyscript{Q}}_N(x)}{1+{\fancyscript{D}}_N}\times \frac{1+E_N(x)}{1+E_N(1)} \end{aligned}$$

where

$$\begin{aligned} {\fancyscript{D}}_N=\frac{R_N(1)}{I_N(1)}, \quad {\fancyscript{Q}}_N(x)=\frac{R_N(x)}{I_N(1)}, \end{aligned}$$

In addition, we have also used that

$$\begin{aligned} \phi _{N}(x)=\frac{I_N(x)}{I_N(1)}=d_N^{-1}\int _0^x\exp \left( \kappa _N^{-1}{\fancyscript{F}}(s)\right) \,{\mathrm {d}}s,\quad d_N=\int _0^1\exp \left( \kappa _N^{-1}{\fancyscript{F}}(s)\right) \,{\mathrm {d}}s. \end{aligned}$$

If $\kappa _N^{-1}$ has a finite limit as $N\rightarrow \infty$, then

$$\begin{aligned} \left| \kappa _N^{-1}\theta ^2(x)-\theta '(x) \right| \le C. \end{aligned}$$

Hence

$$\begin{aligned} |R_N(x)|\le \frac{Cm}{N^3}\le \frac{C}{N^2}. \end{aligned}$$

For $x>{1}/{N}$, since $I_N(x)>I_N({1}/{N})$, we have

$$\begin{aligned} |{\fancyscript{Q}}_N(x)|\le C\frac{{1}/{N^2}}{\exp (\kappa _N^{-1}{\fancyscript{H}}(0)){1}/{N}+{\mathrm {O}}\left( {1}/{N^2}\right) }\le \frac{C}{N}. \end{aligned}$$

This proves Eq. (4).

For the remaining results, we first observe that an asymptotic argument using Watson’s lemma along the lines discussed in Sect. 4 and Appendix B yields

$$\begin{aligned} \left| I_N(1)\right| = \left\{ \begin{array}{lr} C\kappa _N+{\mathrm {O}}\left( \kappa _N^2\right) ,&{}\text {if }{\fancyscript{F}}\text { is a boundary potential};\\ C\kappa _N^{1/2}+{\mathrm {O}}\left( \kappa _N\right) ,&{}\text {if }{\fancyscript{F}}\text { is an interior potential}. \end{array} \right. \end{aligned}$$

To bound $R_N(x)$ we will need the following Lemma:

Lemma 1

If $\kappa _N^{-1}$ is not bounded as $N\rightarrow \infty$, then we have

$$\begin{aligned} \left| R_N(x)\right| \le C \left\{ \begin{array}{lr} \frac{\kappa _N^{-1}}{N^2},&{}{\fancyscript{F}}\text { is a boundary potential;}\\ \frac{\kappa _N^{-1/2}}{N^2},&{}{\fancyscript{F}}\text { is an interior potential}. \end{array} \right. \end{aligned}$$

Thus, we immediately obtain combining the asymptotic estimations together with the Lemma that:

$$\begin{aligned} \left| {\fancyscript{D}}_N\right| ,\left| {\fancyscript{Q}}_N(x)\right| \le \left\{ \begin{array}{lr} C\frac{\kappa _N^{-2}}{N^2},&{}\text {if }{\fancyscript{F}}\text { is a boundary potential};\\ C\frac{\kappa _N^{-1}}{N^2},&{}\text {if }{\fancyscript{F}}\text { is an interior potential}. \end{array} \right. \end{aligned}$$

Notice also that if $\varPhi _N(x)$ is exponentially small then we must have ${\fancyscript{F}}(s)<0$, $s\in (0,x)$. Hence we also have that $\phi _N(x)$ is exponentially small and also $R_N(x)$ is exponentially small. This proves Eq. (3).

To prove Eq. (5), notice that if $\kappa _N^{-1}$ is not bounded, and if $\phi _N(x)={1}/{N}$, then

$$\begin{aligned} I_N(x)=\frac{1}{N}\left\{ \begin{array}{lr} \kappa _N,&{} \text {if }{\fancyscript{F}}\text { is a boundary potential};\\ \kappa _N^{1/2},&{}\text {if }{\fancyscript{F}}\text { is an interior potential}. \end{array} \right. \end{aligned}$$

Hence

$$\begin{aligned} |\tilde{{\fancyscript{Q}}}_N(x)|\le \left\{ \begin{array}{lr} \frac{\kappa _N^{-2}}{N},&{} \text {if }{\fancyscript{F}}\text { is a boundary potential};\\ \frac{\kappa _N^{-1}}{N},&{}\text {if }{\fancyscript{F}}\text { is an interior potential}. \end{array} \right. \end{aligned}$$

Thus the continuous approximation can correctly identify the neutral boundary, provided $\kappa _N={\mathrm {O}}\left( N^{\alpha }\right)$, with $\alpha <{1}/{2}$, if ${\fancyscript{F}}$ is a boundary potential, or that evolution is in the moderate selection regime, if ${\fancyscript{F}}$ is an interior potential.

Proof

(Proof of the Lemma) We now observe that

$$\begin{aligned} R_N(x)&=\frac{\kappa _N^{-1}}{24N^3}\sum _{j=1}^m\exp \left( \kappa _N^{-1}{\fancyscript{H}}(\bar{s}_j)\right) \left( \kappa _N^{-1}\theta ^2(\bar{s}_j)-\theta '(\bar{s}_j)\right) \\&=\frac{\kappa _N^{-1}}{24N^2}\left[ \int _0^x\exp \left( \kappa _N^{-1}{\fancyscript{H}}(s)\right) \left( \kappa _N^{-1}\theta ^2(s)-\theta '(s)\right) \,{\mathrm {d}}s + {\fancyscript{R}}_N(x)\right] \\&=\frac{\kappa _N^{-1}}{24N^2}\left[ \exp \left( \kappa _N^{-1}{\fancyscript{H}}(0)\right) \theta (0)-\exp \left( \kappa _N^{-1}{\fancyscript{H}}(x)\right) \theta (x)+ {\fancyscript{R}}_N(x)\right] , \end{aligned}$$

where

$$\begin{aligned} {\fancyscript{R}}_N(x)=\frac{\kappa _N^{-1}}{2N^2}\sum _{j=1}^m\exp \left( \kappa _N^{-1}{\fancyscript{H}}(\hat{s}_j)\right) \left( -\kappa _N^{-1}\theta ^3(\hat{s}_j)+3\theta (\hat{s}_j)\theta '(\hat{s}_j)-\kappa _N\theta ''(\hat{s}_j)\right) , \end{aligned}$$

with $\hat{s}_j\in ({1}/{2N}+{(j-1)}/{N},{1}/{2N}+{j}/{N})$.

If $\kappa _N^{-1}$ is bounded then, we can bound

$$\begin{aligned} \left\| \exp \left( \kappa _N^{-1}{\fancyscript{H}}(x)\right) \left( -\kappa _N^{-1}\theta ^3(x)+3\theta (x)\theta '(x)-\kappa _N\theta ''(x)\right) \right\| _\infty <C,\quad \text {independent of }N. \end{aligned}$$

Hence, we have that

$$\begin{aligned} |{\fancyscript{R}}_N(x)|\le \frac{C}{N}. \end{aligned}$$

Otherwise, if $\kappa _N^{-1}$ is not bounded, we have the following bounds:

$$\begin{aligned} \left| {{\fancyscript{R}}}_{N}(x)\right| \le \left\{ \begin{array}{lr} C\frac{\kappa _N^{-1}}{N^2},&{}\text {if }{\fancyscript{F}}\text { is a boundary potential};\\ C\frac{\kappa _N^{-1/2}}{N},&{}\text {if }{\fancyscript{F}}\text { is an interior potential}. \end{array} \right. \end{aligned}$$

Indeed, if ${\fancyscript{F}}$ is a boundary potential, then we have either that ${\fancyscript{H}}(0)=0$ or that ${\fancyscript{H}}(1)=0$. We we will treat the former, the latter being similar. In this case, let $s^*$ be the smallest interior global minimum, if it exists, or $s^*=1$ if there is no interior global minimum. Then there exists $\tilde{K}$ and $0<\tilde{x}={m}/{N}<s^*$, such that

$$\begin{aligned} \tilde{K}s\le -{\fancyscript{H}}(s),\quad s\in [0,\tilde{x}]. \end{aligned}$$

Then

$$\begin{aligned}&\left| \sum _{j=0}^m\exp \left( \kappa _N^{-1}{\fancyscript{H}}(\hat{s}_j)\right) \left( -\kappa _N^{-1}\theta ^3(\hat{s}_j)+3\theta (\hat{s}_j)\theta '(\hat{s}_j)-\kappa _N\theta ''(\hat{s}_j)\right) \right| \\&\quad \le \kappa _N^{-1}M'\sum _{j=0}^m\exp (-\kappa _N^{-1}\tilde{K}\bar{s}_j)\\&\quad \le \kappa _N^{-1}M'\int _0^\infty \exp (-\kappa _N^{-1}\tilde{K}s)\,{\mathrm {d}}s\\&\quad = \tilde{C}_{-1},\quad \tilde{C}_{-1}={\mathrm {ord}}(1). \end{aligned}$$

If ${\fancyscript{F}}$ is an interior potential, let us write $x^*$ for any of its interior maxima. Recall that, in this case, we have $\theta (x^*)=0$ and $\theta '(x^*)>0$. Let

$$\begin{aligned} J(x)=\exp \left( \kappa _N^{-1}{\fancyscript{H}}(x)\right) \left[ -\kappa _N^{-1}\theta ^3(x)+3\theta (x)\theta '(x)-\kappa _N\theta ''(x)\right] ,\quad x\in [0,1]. \end{aligned}$$

We claim that $\Vert J\Vert _\infty ={\mathrm {O}}\left( \kappa _N^{1/2}\right)$. To see this, let

$$\begin{aligned} \tilde{J}(x)=\exp \left( \kappa _N^{-1}{\fancyscript{H}}(x)\right) \left[ -\kappa _N^{-1}\theta ^3(x)+3\theta (x)\theta '(x)\right] \end{aligned}$$

and compute

$$\begin{aligned} \tilde{J}'(x)=\exp \left( \kappa _N^{-1}{\fancyscript{H}}(x)\right) \left[ \kappa _N^{-2}\theta ^4(x)-6\kappa _N^{-1}\theta ^2(x)\theta '(x)+3\left( {\theta '}^2(x)+\theta (x)\theta ''(x)\right) \right] . \end{aligned}$$

Then $\tilde{J}'(x)=0$ is equivalent to

$$\begin{aligned} \theta ^4(x)-6\kappa _N\theta ^2(x)\theta '(x)+3\kappa _N^{2}\left( {\theta '}^2(x)+\theta (x)\theta ''(x)\right) =0. \end{aligned}$$

Firstly, we observe that we are only interested in solutions close to $x^*$, since $\tilde{J}$ is exponentially small otherwise. An analysis of the magnitude of the terms in the previous equation, suggests that if $\bar{x}$ is a solution, then $|\theta (\bar{x})|={\mathrm {O}}\left( \kappa _N^{1/2}\right)$. Since this problem is a regular perturbation—but where we can not apply the implicit function theorem—we write

$$\begin{aligned} \bar{x}=x^*+\kappa _N^{1/2}x_1+{\mathrm {O}}\left( \kappa _N\right) \end{aligned}$$

which yields the following equation for $x_1$:

$$\begin{aligned} \left( \theta '(x^*)\right) ^4x_1^4-6\left( \theta '(x^*)\right) ^3x_1^2+3\left( \theta '(x^*)\right) ^2=0. \end{aligned}$$

The solutions are

$$\begin{aligned} x_1=\pm \left( \theta '(x^*)\right) ^{-1/2}\sqrt{3\pm \sqrt{6}}. \end{aligned}$$

and it can be easily verified that two of these solutions correspond to local minima of $\tilde{J}$ that are close to $x^*$, while the two other correspond to local maxima. In any case, a direct computation yields

$$\begin{aligned} {\fancyscript{H}}(\bar{x})&={\fancyscript{H}}(x^*)+{\fancyscript{H}}'(x^*)\kappa _N^{1/2}x_1+\frac{\kappa _N}{2}{\fancyscript{H}}''(x^*)x_1^2+{\mathrm {O}}\left( \kappa _N^{3/2}\right) \\&=0-\theta (x^*)\kappa _N^{1/2}x_1-\frac{\kappa _N}{2}\theta '(x^*)x_1^2+{\mathrm {O}}\left( \kappa _N^{3/2}\right) \\&=-\frac{\kappa _N}{2}\left( 3\pm \sqrt{6}\right) +{\mathrm {O}}\left( \kappa _N^{3/2}\right) . \end{aligned}$$

Hence

$$\begin{aligned} \exp \left( \kappa _N^{-1}{\fancyscript{H}}(\bar{x})\right) \!=\!\exp \left( \!-\!\frac{\left( 3\pm \sqrt{6}\right) }{2}\!+\!{\mathrm {O}}\left( \kappa _N^{1/2}\right) \right) . \end{aligned}$$

Also

$$\begin{aligned} -\kappa _N^{-1}\theta ^3(\bar{x})\!+\!3\theta (\bar{x})\theta '(\bar{x})\!&=\!-\kappa _N^{-1}\left( \left( \theta '(x^*)\right) ^3\kappa _N^{3/2}x_1^3\!+\!{\mathrm {O}}\left( \kappa _N^2\right) \right) \!+\!3\kappa _N^{1/2}x_1\theta '(x^*)^2+{\mathrm {O}}\left( \kappa _N\right) \\&=\kappa _N^{1/2}\left[ -\left( \theta '(x^*)\right) ^3x_1^3+3x_1\theta '(x^*)^2\right] +{\mathrm {O}}\left( \kappa _N\right) \\&=\kappa _N^{1/2}\left[ 3\left( \theta '(x^*)\right) ^{3/2}\left( 3\pm \sqrt{6}\right) ^{1/2}-\left( \theta '(x^*)\right) ^{3/2} \left( 3\pm \sqrt{6}\right) ^{3/2} \right] \\&\quad +{\mathrm {O}}\left( \kappa _N\right) \\&=\kappa _N^{1/2}\left( \theta '(x^*)\right) ^{3/2}\left[ 3\left( 3\pm \sqrt{6}\right) ^{1/2}- \left( 3\pm \sqrt{6}\right) ^{3/2} \right] +{\mathrm {O}}\left( \kappa _N\right) ,\\&=\mp \sqrt{6}\left( 3\pm \sqrt{6}\right) ^{1/2}\theta '(x^*)^{3/2}\kappa _N^{1/2}+{\mathrm {O}}\left( \kappa _N\right) . \end{aligned}$$

Therefore, we have

$$\begin{aligned} |\tilde{J}(\bar{x})|={\mathrm {O}}\left( \kappa _N^{1/2}\right) \end{aligned}$$

and hence we conclude that

$$\begin{aligned} \Vert \tilde{J}\Vert _\infty \le C\kappa _N^{1/2}. \end{aligned}$$

Since we can easily bound

$$\begin{aligned} \Vert \exp \left( \kappa _N^{-1}{\fancyscript{H}}\right) \kappa _N\theta ''\Vert _\infty <C\kappa _N, \end{aligned}$$

we can conclude that

$$\begin{aligned} \Vert J\Vert _\infty \le \Vert \tilde{J}\Vert _\infty + \Vert \exp \left( \kappa _N^{-1}{\fancyscript{H}}\right) \kappa _N\theta ''\Vert _\infty \le C_1\kappa _N^{1/2}+C_2\kappa _N\le C\kappa _N^{1/2}. \end{aligned}$$

This yields the bounds on ${\fancyscript{R}}_N$. We now proceed to estimate

$$\begin{aligned} R_N(x)=\frac{\kappa _N^{-1}}{24N^2}\left[ \exp \left( \kappa _N^{-1}{\fancyscript{H}}(0)\right) \theta (0)-\exp \left( \kappa _N^{-1}{\fancyscript{H}}(x)\right) \theta (x)+ {\fancyscript{R}}_N(x)\right] . \end{aligned}$$

If ${\fancyscript{F}}$ is a boundary potential, we have that either ${\fancyscript{H}}(0)=0$ or ${\fancyscript{H}}(1)=0$, and hence

$$\begin{aligned} |R_N(x)|\le C\frac{\kappa _N^{-1}}{24N^2}. \end{aligned}$$

If ${\fancyscript{F}}$ is an interior potential, let us write

$$\begin{aligned} L(x)=\exp \left( \kappa _N^{-1}{\fancyscript{H}}(0)\right) \theta (0)-\exp \left( \kappa _N^{-1}{\fancyscript{H}}(x)\right) \theta (x). \end{aligned}$$

Then

$$\begin{aligned} L'(x)=\exp \left( \kappa _N^{-1}{\fancyscript{H}}(x)\right) \left[ \kappa _N^{-1}\theta ^2(x)-\theta '(x)\right] \end{aligned}$$

Now notice that a solution $L'(x)=0$ is given by $\bar{x}=x^*+\kappa _N^{1/2} x_1$. Direct substitution in $L$ then yields

$$\begin{aligned} \Vert L\Vert _\infty \le C\kappa _N^{1/2}. \end{aligned}$$

Hence, we obtain that

$$\begin{aligned} |R_N(x)|\le C\frac{\kappa _N^{-1/2}}{N^2}. \end{aligned}$$

Appendix B: Proof of the asymptotic results

Write Eq. (3) as

$$\begin{aligned} \phi _\kappa (x)=\frac{I(x)}{I(1)},\qquad I(x)=\int _{0}^{x}\exp \left( \kappa ^{-1}{\fancyscript{F}}(s)\right) \,{\mathrm {d}}s. \end{aligned}$$

1.1 B.1: Dominance

For dominance of ${\mathbb {A}}$, we have $\theta (x)>0$ in unit interval, and hence the argument of the exponential has a maximum at $s=0$. Let $s=\kappa z$. Then, using Laplace’s method (Hinch 1991; Bender and Orszag 1999), we find

$$\begin{aligned} I(x)&=\kappa \int _0^{x/\kappa }\exp \left( \kappa ^{-1}{\fancyscript{F}}(\kappa z )\right) \,{\mathrm {d}}z\\&=\frac{\kappa }{\theta (0)}\left( 1-\exp \left( \frac{-\theta (0)x}{\kappa }\right) \right) +{\mathrm {O}}\left( \kappa ^2\right) . \end{aligned}$$

Hence, we have

$$\begin{aligned} \phi _\kappa (x)=1-\exp \left( -\frac{\theta (0)x}{\kappa }\right) +{\mathrm {O}}\left( \kappa \right) . \end{aligned}$$

(17)

For dominance of ${\mathbb {B}}$, recall that we have $\theta (x)<0$ throughout $[0,1]$. Hence. the argument in exponential will then have a maximum at $s=1$. Thus, we write $s=1-\kappa z$ and, analogously as before, we find

$$\begin{aligned} I(x)=-\frac{\kappa \exp (\kappa ^{-1}{\fancyscript{F}}(1))}{\theta (1)}\left[ \exp \left( \frac{\theta (1)(1-x)}{\kappa }\right) -\exp \left( \frac{\theta (1)}{\kappa }\right) +{\mathrm {O}}\left( \kappa \right) \right] . \end{aligned}$$

Hence, we find

$$\begin{aligned} \phi _\kappa (x)=\exp \left( \frac{\theta (1)(1-x)}{\kappa }\right) +{\mathrm {O}}\left( \kappa \right) . \end{aligned}$$

(18)

1.2 B.2: Coexistence

In the case of coexistence, the fitness potential has a minimum at $x=x^*$; hence we have no contribution from the interior. On the other hand, $\theta$ is positive near $s=0$ and negative near $s=1$. Hence, the argument in the exponential has a maximum at both $s=0$ and $s=1$. Hence combining the previous calculations we find

$$\begin{aligned} I(x)= & {} \frac{\kappa }{\theta (0)}\left( 1-\exp \left( \frac{-\theta (0)x}{\kappa }\right) \right) \nonumber \\&-\frac{\kappa \exp (\kappa ^{-1}{\fancyscript{F}}(1)}{\theta (1)}\left[ \exp \left( \frac{\theta (1)(1\!-\!x)}{\kappa }\right) \!-\!\exp \left( \frac{\theta (1)}{\kappa }\right) \!+\!{\mathrm {O}}\left( \kappa \right) \right] . \end{aligned}$$

(19)

If ${\fancyscript{F}}(1)\ll -\kappa$, then the second term of (19) is exponentially small, and hence we obtain once again (17). On the other hand, if ${\fancyscript{F}}(1)\gg \kappa$, the second term is then exponentially large, and in this case we obtain (18).

Otherwise, if ${\fancyscript{F}}(1)\sim \kappa$, let

$$\begin{aligned} C=\exp ({\fancyscript{F}}(1)/\kappa )\quad \text {and}\quad \gamma =\frac{|\theta (1)|}{\theta (0)}. \end{aligned}$$

We now have that (19) becomes

$$\begin{aligned} I(x)=\frac{\kappa }{\theta (0)}\left( 1-\exp \left( \frac{-\theta (0)x}{\kappa }\right) \right) +\frac{\kappa C}{|\theta (1)|}\exp \left( \frac{\theta (1)(1-x)}{\kappa }\right) +{\mathrm {O}}\left( \kappa ^2\right) . \end{aligned}$$

Also, we have

$$\begin{aligned} I(1)=\kappa \frac{|\theta (1)|+\theta (0)C}{\theta (0)|\theta (1)|} +{\mathrm {O}}\left( \kappa ^2\right) . \end{aligned}$$

Therefore,

$$\begin{aligned} \phi _\kappa (x)=\frac{\gamma }{\gamma +C}\left( 1-\exp \left( \frac{-\theta (0)x}{\kappa }\right) \right) + \frac{C}{\gamma +C}\exp \left( \frac{\theta (1)(1-x)}{\kappa }\right) + {\mathrm {O}}\left( \kappa \right) . \end{aligned}$$

(20)

1.3 B.3: Coordination

For coordination, we have that the fitness potential has a maximum at $x=x^*$. Hence, we write

$$\begin{aligned} {\fancyscript{F}}(s)={\fancyscript{F}}(x^*)-\theta '(x^*)\frac{(s-x^*)^2}{2} +{\mathrm {O}}\left( (s-x^*)^3\right) . \end{aligned}$$

Then, if we write

$$\begin{aligned} z=\sqrt{\frac{\theta '(x^*)}{\kappa }}(s-x^*), \end{aligned}$$

Hence we have that

Therefore, we find that

$$\begin{aligned} \phi _\kappa (x)=\frac{{\fancyscript{N}}\left( \sqrt{\frac{\theta '(x^*)}{\kappa }}(x-x^*)\right) - {\fancyscript{N}}\left( -\sqrt{\frac{\theta '(x^*)}{\kappa }}xs\right) }{{\fancyscript{N}}\left( \sqrt{\frac{\theta '(x^*)}{\kappa }}(1-x^*)\right) - {\fancyscript{N}}\left( -\sqrt{\frac{\theta '(x^*)}{\kappa }}x^*\right) } +{\mathrm {O}}\left( \sqrt{\kappa }\right) . \end{aligned}$$

Appendix C: Proof of Theorem 5

As before, we write

$$\begin{aligned} \phi _\kappa (x)=\frac{I_\kappa (x)}{I_\kappa (1)},\qquad I_\kappa (x)=\int _0^x\exp ({\fancyscript{F}}(s)/\kappa )\,{\mathrm {d}}s. \end{aligned}$$

Write

$$\begin{aligned} \exp \left( {\fancyscript{F}}(s)/\kappa \right) =1+\kappa ^{-1}{\fancyscript{F}}(s)+\kappa ^{-2}{\fancyscript{F}}(s)^2\sum _{l=0}^\infty \frac{1}{\kappa ^{l}(l+2)!}{\fancyscript{F}}(s)^{l} \end{aligned}$$

and integrate to obtain:

$$\begin{aligned} I_\kappa (x)=x+\kappa ^{-1}\int _0^x{\fancyscript{F}}(s)\,{\mathrm {d}}s+\kappa ^{-2}H(x;\kappa ), \end{aligned}$$

where

$$\begin{aligned} H(x;\kappa )=\int _0^x{\fancyscript{F}}(s)^2\sum _{l=0}^\infty \frac{1}{\kappa ^l(l+2)!}{\fancyscript{F}}(s)^l\,{\mathrm {d}}s, \end{aligned}$$

which is order one. Notice that this will be also true for its derivatives.

Since $H$ is $C^3$ and $H(0,\kappa )=\partial _xH(0,\kappa )=\partial _x^2H(0,\kappa )=0$, we can invoke Hadamard Lemma, cf. Bruce and Giblin (1992), and write

$$\begin{aligned} H(x;\kappa )=x^3{\mathfrak {H}}(x;\kappa ), \end{aligned}$$

with ${\fancyscript{H}}$ being $C^2$.

Hence, we have

$$\begin{aligned} \phi _\kappa (x)=x-\kappa ^{-1}\left[ x\int _0^1{\fancyscript{F}}(s)\,{\mathrm {d}}s-\int _0^x{\fancyscript{F}}(s)\,{\mathrm {d}}s\right] + \kappa ^{-2}R(x;\kappa )+ {\mathrm {O}}\left( \kappa ^{-3}\right) , \end{aligned}$$

where,

$$\begin{aligned} R(x;\kappa )=x\left[ \int _0^1{\fancyscript{F}}(s)\,{\mathrm {d}}s\right] ^2-x{\mathfrak {H}}(1;\kappa )+x^3{\mathfrak {H}}(x;\kappa )-\int _0^x{\fancyscript{F}}(s)\,{\mathrm {d}}s\int _0^1{\fancyscript{F}}(s)\,{\mathrm {d}}s. \end{aligned}$$

Since $R(0;\kappa )=0$, a further application of Hadamard Lemma yields

$$\begin{aligned} R(x;\kappa )=x{\mathfrak {R}}(x;\kappa ), \end{aligned}$$

with ${\mathfrak {R}}$ being $C^2$.

Finally, observe that integration by parts imply that

$$\begin{aligned} \int _0^x{\fancyscript{F}}(s)\,{\mathrm {d}}s= -\int _0^x{\fancyscript{F}}(s)\frac{{\mathrm {d}}}{{\mathrm {d}}s}\left[ (x-s)\right] \,{\mathrm {d}}s=\int _0^x(x-s){\fancyscript{F}}'(s)\,{\mathrm {d}}s=-\int _0^x(x-s)\theta (s)\,{\mathrm {d}}s. \end{aligned}$$