The effect of competition on the neutral intraspecific diversity of invasive species

Abstract

This paper deals with the effect of interspecific competition on the dynamics of neutral genetic diversity in a range-expanding population. The spread of an invasive species in an environment already hosting a resident competitor is described by a traveling wave solution with minimal speed, $u(t,x)=U(x - c^* \, t)$, of a diffusive Lotka–Volterra competition model. The description of the dynamics of neutral genetic fractions in this wave is based on a decomposition of the wave into several components, as proposed by Roques et al. (Proc Natl Acad Sci USA 109(23):8828–8833, 2012). Our analytical results reveal that the wave can be either the pulled type, corresponding to strong erosion of the diversity, or the pushed type, corresponding to maintenance of the initial diversity. The pulled/pushed nature of the wave depends on the linear or nonlinear nature of the speed $c^*$. Our results show that, for sufficiently strong competition, the speed is nonlinear, and therefore all of the genetic diversity in the invasive population is maintained. Conversely, in the absence of competition, or when competition is mild, the speed is linear, which means that only the furthest forward fraction in the initial invasive population eventually remains in the colonization front. Our numerical results also show that the sufficient conditions of Lewis et al. (J Math Biol 45(3):219–233, 2002) and Huang (J Dyn Differ Equ 22(2):285–297, 2010) for the linearity of the speed $c^*$ can still be improved, and they show that nonlinear speeds occur across a wide region of the parameter space, providing a counterpoint to recent analytical results suggesting that nonlinear speeds only occur in certain limiting cases.

Appendix A: numerical computations, technical aspects

Our computations have been carried out with the softwares Comsol Multiphysics$^{\copyright }$ (Figs. 1, 2) and freefem++ (Hecht 2012) (Figs. 3, 4). In both cases, a finite element method was used, with a uniform discretization space (step $\delta _x=0.1$). In Comsol Multiphysics$^{\copyright }$, we used the time-dependent solver with default parameter values (second order basis elements and modified Newton method with damping factor for the treatment of the nonlinearity). In freefem++ we used piecewise linear and continuous basis functions with a backward Euler method and an adaptive time step. The nonlinearity has been treated with a Newton-Raphson algorithm applied to the variational formulations of the corresponding equations with a criterion of convergence equal to $10^{-10}$.

For the computations of the results presented in Figs. 1, 2, 3, we considered the problem (2.1) in a moving frame by setting $\tilde{u}(t,x)=u(t,x+\tilde{c} \, t)$ and $\tilde{v}(t,x)=v(t,x+\tilde{c} \, t),$ for some constant $\tilde{c}\ge c_0.$ The functions $\tilde{u}$ and $\tilde{v}$ satisfy the following system:

$$\begin{aligned} \left\{ \begin{array}{lc} \partial _t \tilde{u} = d\partial _{xx}\tilde{u}+ \tilde{c} \, \partial _{x} \tilde{u}+ \tilde{u}(1-\tilde{u}-a_1\,\tilde{v}), &{}\quad t >0, x \in \mathbb R,\\ \partial _t \tilde{v} = \partial _{xx} \tilde{v} +\tilde{c} \, \partial _{x} \tilde{v} + r\, \tilde{v}(1-a_2\,\tilde{u}-\tilde{v}) , &{}\quad t >0, x \in \mathbb R, \\ \tilde{u}(0,x)=u(0,x), &{}\quad x \in \mathbb R,\\ \tilde{v}(0,x)=v(0,x), &{}\quad x \in \mathbb R. \end{array} \right. \end{aligned}$$

(6.1)

Convergence towards a traveling wave (Fig. 1 ) The result presented in Fig. 1 was obtained by solving the Cauchy problem (5.1) with $\tilde{c} =c_0$, in the bounded interval $(-50,150),$ with the boundary conditions $u(t,-50)=v(t,150)=1,$ $u(t,150)=v(t,-50)=0,$ and with a compactly supported initial condition $u_0(x)=1\!\!1_{(-50,50)}$ and $v_0(x)=1-u_0(x)$.

Asymptotic behavior of $U(x)$ as $x\rightarrow +\infty$ (Fig. 2 ) Again, the Cauchy problem (5.1) was solved in the bounded interval $(-50,150),$ with the boundary conditions $u(t,-50)=v(t,150)=1,$ $u(t,150)=v(t,-50)=0,$ and with a compactly supported initial condition $u_0(x)=1\!\!1_{(-50,0)}$ and $v_0(x)=1-u_0(x)$. For the computation of $c^*,$ we looked for $\tilde{c}\ge c_0$ such that the level sets of $\tilde{u}(t,x)$ and $\tilde{v}(t,x)$ moved with a null speed after a sufficiently large time $T=500+T_0,$ where $T_0\ge 0.$ The speed of the level sets of $\tilde{u}(t,x)$ was considered as being $0$ at time $T_0$ if it was smaller than $10^{-5}$ per time unit. The speed $c^*$ was then approached by setting $c^*=\tilde{c}.$ With this speed, $\tilde{u}(t,x)$ (resp. $\tilde{v}(t,x)$) keeps an almost stationary profile for $t\ge T$ (i.e., the profile moves with a speed smaller than $10^{-5}$), corresponding to an approximation of the wave profile $U$ (resp. $V$). The values of $\lambda _1^{\pm }$ are given by formula (2.8).

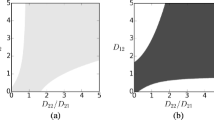
Linear vs nonlinear nature of the speed $c^*$ (Fig. 3 ) Both Figs. 3a and b have been built from $5\cdot 10^4$ computations of the speed $c^*,$ with couples of parameters $(a_1,d)$ randomly drawn with a uniform distribution in $(0,1)\times (0.01,1.5)$. The computation of $c^*$ was performed following the procedure described in the above paragraph.

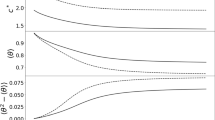
Inside dynamics of the waves (Fig. 4 ) The system (3.2) was approached on a bounded interval $(-50,150),$ with the boundary conditions $u(t,-50)=v(t,150)=1,$ $u(t,150)=v(t,-50)=0,$ $\mu ^1(t,-50)=1,$ $\mu ^i(t,-50)=0$ for $i=2,\ldots ,6$ and $\mu ^i(t,150)=0$ for $i=1,\ldots ,6.$ The initial conditions $u(0,x)=U(x)$ and $v(0,x)=V(x)$ were approached as described above (paragraph “Asymptotic behavior”).