Introduction

In recent decades, increasingly frequent periods of drought, together with an increasing water demand for uses other than agriculture, have led to the need to modernize irrigation systems in arid and semi-arid areas. These improvements have evolved, enhancing the efficiency of irrigation systems; however, they have increased energy costs (Sánchez-Escobar et al. 2018; Willaarts et al. 2020), jeopardizing the viability of farms. Traditionally, the energy employed for this purpose has been obtained from non-renewable sources, fundamentally fossil fuels (Santra 2020; Willaarts et al. 2020), which have a significant environmental impact and are currently experiencing high cost increases each year.

The abundant availability of sunlight in many countries of the Mediterranean basin facilitates the use of photovoltaic (PV) energy to supply electricity to pumping facilities needed to irrigate many of the crops grown in these areas (Carrêlo 2014; López-Luque et al. 2015; García-Tejero and Durán Zuazo 2018; Todde et al. 2019; Hajjali et al. 2022). For its part, the increase in photovoltaic generation capacity in Spain (Zafrilla et al. 2019) and the reduction in the cost of solar panels have made their replacement of non-renewable energies increasingly attractive (Branker et al. 2011). The growing interest in this technology in areas without access to grid electricity in developing countries with a lot of sunshine is evident in the review by Wazed et al. (2018). Moreover, with the economic benefits and the possibility of installing photovoltaic energy in areas where it is difficult to access conventional energy (Bakelli et al. 2011; Tiwari et al. 2020; Verma et al. 2020), the environmental benefits obtained should also be highlighted. For each kWh generated in this manner, 0.264 kg of CO2 is prevented from being released into the atmosphere (Syngros et al. 2017).

The large number of studies that have been published on the use of photovoltaic energy in irrigation pumping shows the great interest that this type of application has increased (Hamidat et al. 2003; Hamidat and Benyoucef 2009; López-Luque et al. 2015; Paredes-Sánchez et al. 2015; Mérida García et al. 2018, 2019, 2020; Zafrilla et al. 2019; Santra 2020; Senthil Kumar et al. 2020).

However, much remains to be done in optimizing irrigation systems, as shown in the review of isolated photovoltaic pumping systems by Gevorkov et al. (2023). His paper emphasizes factors affecting system efficiency, performance evaluation, optimization of operation, and the potential for integrating these systems with modern control techniques. Some authors have proposed improving the management of the irrigation network by grouping the hydrants to bring the operating point of the pumping equipment closer to the optimum performance level (Jiménez-Bello et al. 2010, 2011, 2015; Córcoles et al. 2015; Picazo et al. 2018). Considering hybrid systems (photovoltaic–wind), Chandel et al. (2017), Hajjali, et al. (2022) and Li et al. (2017) also analyzed the different factors affecting the performance of the photovoltaic pumping system in to improve overall energy production efficiency. Other studies have focused on optimizing the management of irrigation systems by combining photovoltaic panels and batteries (Reges et al. 2016; Yahyaoui et al. 2016). Following the same line, Bhattacharjee et al. (2016) proposed an optimized energy management method in which, during cloudy periods when photovoltaic energy is insufficient, it would be supplemented by energy stored in a battery. Mosethe et al. (2023), also for rural systems and expanding energy supply alternatives, compared PV, wind, diesel generators and batteries; in this work, a weighting of functional or economic criteria of the supply alternatives is even considered for an adequate adaptation of the design process. Under a different approach, numerous works seek to optimize the control elements of solar panels; in these cases, it is intended that the system works at its maximum power point tracking (MPPT) (Karmouni et al. 2022; Ahmed and Demirci 2022; Hilali et al. 2022; Errouha et al. 2022). Carrillo-Cobo et al. (2014) defined the sector size that best fits the variable production of photovoltaic energy to reduce dependence on the electricity grid. Merida-García et al. (2018) proposed a model that integrates the coordinated operation of solar energy production, the pumping station and the irrigation network into a single algorithm of a soil–water-plant model that satisfies the crop´s irrigation requirements. In this direction, Okakwu et al. (2022) compared the photovoltaic power to operate the pump and the water requirements of different crops.

In isolated direct pumping photovoltaic systems, Gasque et al. (2020) theoretically demonstrated that using two equal half-size pumps working in parallel instead of a single pump allows pumping to be started and stopped at lower irradiance levels. They also proposed a pumping strategy that optimizes the use of the available energy. Furthermore, Gasque et al. (2021) validated the suitability of this strategy for distributing the power generated by a photovoltaic pumping system equipped with two identical pumps working in parallel.

Although these works show the interest in using several pumps in parallel instead of a single larger pump, a method for determining the most appropriate number of pumps to be placed in parallel has yet to be established, as well as its consequences for the size of the photovoltaic generator necessary to cover a specific demand.

The main goal of this paper is to determine, for a case study of pumping water between two tanks, the most suitable number of pumps from a technical and economic point of view that may be connected in parallel, as well as to set the optimal size of the needed photovoltaic generator. In addition, the effect of the size of the photovoltaic generator on the pumped volume under each of the studied configurations is discussed.

Materials and methodology

Case study

The proposed methodology is applied to study a pumping installation under the responsibility of the Sector 4 Water Users Association near Picassent (Valencian Community, Spain), in the East of the Iberian Peninsula. The Tous-La Ribera Reservoir supplies this area via an open-air trapezoidal cross-section channel called Júcar-Turia Canal.

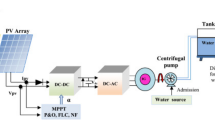
The studied installation pumps water from a 15,000 m3 capacity tank for which the water surface is 142 m above sea level, near the “Sagrada Familia” pumping station (coordinates 39°23′13.06"N, 0°31′12.65"W), to a tank with a capacity of 1680 m3 and a water surface at 165.3 m above sea level (actual geometric height, 23.3 m), located by the “San Rafael” pumping station (coordinates 39°22′51.46"N, 0°31′59.43"W). The “San Rafael” tank supplies, via gravity, an irrigation area of 48.93 ha. Water is pumped from one tank to another through a 1400 m-long PVC-U pipeline DN 400 PN 6 (Internal Diameter 380.4 mm). An installation scheme is shown in Fig. 1.

Fig. 1
figure 1

Diagram of the photovoltaic pumping system considered in this study

Full size image

The power scheme consists of a single PV generator connected to a grid-type inverter responsible for the Maximum Power Point Tracking drivers (MPPT) and adjusting the power produced to that demanded by the pumps which operate with a starter. Therefore, starters turn on the number of pumps that, at a nominal rotation speed, consume the available power. This configuration is used to compare all hypotheses under the same condition.

Water requirements are based on the predominant local fruit crop (citrus) during its entire growth cycle, assuming a canopy cover of more than 70%. The crop and climate data necessary to establish irrigation needs is obtained from the Agroclimatic Information System for Irrigation (SIAR in Spanish) corresponding to the Picassent agroclimatic station (www.siar.es).

Pumps (SP UGP serial pump with ISM ML motors, Zamudio, Spain) from the Indar trade brand (https://www.ingeteam.com) are considered in this study. The same brand manufacturer as the pre-existing pump used in the baseline hypothesis was selected for all pumps. The operational simulations were undertaken according to this manufacturer´s models. The selection of the pumps, with different operating points depending on the number of pumps studied, is made based on the maximum efficiency that the pump models can provide.

In this study, eight cases or hypotheses were considered. The baseline hypothesis (hypothesis 1) has a single pump necessary to meet the hydraulic requirements of the described system. Two pumps are considered in hypothesis 2, 3 in the third hypothesis, etc. When all pumps in one of the hypotheses operate, the pumped flow equals the flow rate pumped by the baseline hypothesis.

Table 1 shows the flow pumped to the corresponding Hm, the operating point efficiency and the power required for each pump in each hypothesis. The results shown in this study were validated using the Epanet hydraulic simulation software (Rossman 2000).

Table 1 Hypothesis, number of pumps, individual flow (m3h−1 pump−1), total driven flow (m3h−1), Total Dynamic Head (m), ηmp (%) of each pump and required power (Pb, kW) for the pumps in operation
Full size table

The minimum Hm obtained was 23.3 m with a flow rate of 35 m3h−1 and occurred in hypothesis 8 when only one pump was in operation, while the maximum Hm of 25.1 m occurred in all the hypotheses when the pumped flow was 280 m3h−1.

When considering hypotheses 1, 3, 5 and 8, the costs of the pumps, based on the manufacturer's listed prices in the year 2019, were € 6800 Ud−1, € 3400 Ud−1, € 2100 Ud−1 and € 1875 Ud−1, respectively. Alternatively, the cost of each PV panel in 2019 was € 124.2 Ud−1.


The baseline PV generator consists of 170 panels of 320 Wp each. The Power Factor (Fp) relating the installed power to the required power is defined as:

$$Fp = \frac{{N_{{\text{paneles }}} \cdot PP_{p} }}{{P_{{b_{i} }} }}$$
(1)

where Npanels is the number of panels, PPp is the peak power for each panel and \({P}_{{b}_{i}}\) is the power required by the number of pumps in each hypothesis.

To study the effect of the size of the PV generator on the operation of the installation, different Fp ratios were considered, from 1 to 2 (increasing at intervals of 0.1), 2.5, 3, 4, 5 and 10. In addition, different Fp ratios were studied under several of the hypotheses; one pump (Fp: 1.78), three pumps (Fp: 1.69), five pumps (Fp: 1.65) and finally, under the hypothesis of eight pumps (Fp: 1.45).

Volume per week Vweek was determined for all power factors as explained in Sect. “Hydraulic Model and Photovoltaic Generator” and compared to the volumes required to supply the relevant irrigated area. The lowest Fp in which the discharged volume was greater than the volume required in the period of maximum needs was chosen.

Selection of the optimal number of pumps

This methodology aimed to determine the most effective number of pumps operating in parallel, as well as the minimum power of the photovoltaic generator that guarantees the necessary water supply. The methodology is divided into five parts, as follows:

  1. 1.

    The flow rate and head required by the pumping installation were determined. The baseline hypothesis (hypothesis 1) considers a single pump selected. Subsequent hypotheses, formed by the incremental increase of pumps from 2 to Npumps, are then considered. The maximum number of pumps in parallel is one after which the formed system operates with a hydraulic efficiency above a certain threshold, namely 60%, considering a standard value following the work of Abadia et al. (2008).

    The pump flow rate (Qpump, m3h−1) was determined for each pump in each hypothesis, as well as the head loss due to friction (hf, m) and localized singularities (hs, m). The pump head (Hm, m) for each hypothesis was determined.

  2. 2.

    Generator peak power determination is based on the method of the most unfavorable month (MUMi).

    The generated power was determined hourly as a function of the incident solar radiation on the capture plane, corrected by the temperature effect of the photovoltaic cell for each day (Tcel, oC). The hourly power of the photovoltaic generator (Pint, W) determines the net power for each hour and day (Pnet, W), considering the generator’s efficiency.

  3. 3.

    The pumping hypotheses were formulated with different Npumps operating in parallel. This process was carried out as follows:

    The first hypothesis was formed by a pump that provides the required flow at the necessary pressure (Q, Hm). The second hypothesis consisted of two equal pumps in parallel, the third by three and so on until the eight pumps of the eighth hypothesis. When all the pumps of each hypothesis work, the same point of operation is reached as with hypothesis 1. However, when only one pump works, the pumped flow rate is about 1/Npumps of each hypothesis.

    The pumps were selected based on the Q and Hm required, and the efficiency of each pump (η) was determined for each hypothesis. After that, the power required for each number of pumps working within each hypothesis (\({P}_{{b}_{i}}\), W) was calculated.

    The pumped volumes were calculated on an hourly basis throughout the year by considering the number of hours in which the available power (APh, h) is sufficient to operate the maximum possible number of pumps within each hypothesis; that is when the net power (Pnet) is higher than the power required by the pumps \({P}_{{b}_{i}}\). Considering that each hypothesis will always work the higher possible number of pumps conditioned by the available power (APh) to maximize the volume discharged.

    Finally, the daily pumped volumes (Vday, m3day−1) were calculated by multiplying the operating hours of each pump by the flow rate of each pump and adding up the flow of all the pumps working in each hypothesis (Qpump, m3h−1).

  4. 4.

    The same calculation was carried out considering different PV generator sizes for each hypothesis.

  5. 5.

    The optimum number of pumps (Npumps) based on economic criteria was determined with the lowest pumped water ratio to the pumping station's economic cost. Figure 2 shows a methodology scheme to select the optimal NPumps for a photovoltaic pumping station. The total cost was calculated by combining the costs of both the pumps and the solar panels in each hypothesis as follows:

    $${\text{Min}} \left( {\frac{V}{{PC_{h} \times N_{{{\text{Pumps}}}} + PVC_{h} \times N_{{{\text{Panels}}}} }}} \right) \left( {m^{3} {\EUR^{ - 1} }} \right)$$
    (2)

    where V is the annual pumped volume (m3), PCh is the cost of the pump model in each hypothesis (€ Ud−1), PVCh is the cost of the photovoltaic panel (€ Ud−1) and Npanels is the number of photovoltaic panels needed in each hypothesis to supply the required volume. This ratio remains proportional to the pumped volume across all the hypotheses independent of the number of years considered.

    Fig. 2
    figure 2

    Flow chart of the methodology to select the optimal number of pumps in parallel (NPumps)for a photovoltaic pumping station

    Full size image

Hydraulic model and photovoltaic generator

Selection of the photovoltaic generator and the hydraulic pump


The most unfavorable month (MUM) had the highest quotient in Eq. (3):

$${\text{MUM}}_{i} = \frac{{{\text{HE}}_{i} }}{{G{\text{max}}_{i} }}$$
(3)

here HEi is the monthly average daily required energy (kWh) and Gmaxi is the monthly average of daily available solar radiation (kWh). Gmaxi is obtained from the irradiance data of a typical meteorological year (TMY) at the installation´s location, provided by the Photovoltaic Geographic Information System (PVGIS) of the European Commission´s science and knowledge service (https://ec.europa.eu/jrc/en/pvgis). These values were used to design and select the pump of the baseline hypothesis.


HEi was determined, for each month of the year, using Eq. (4):

$${\text{HE}}_{i} = \mathop \sum \limits_{i = 1}^{{{\text{md}}}} \frac{{\rho \cdot g \cdot Hm \cdot V_{{{\text{day}}}} }}{3600}$$
(4)

where ρ is the density of water (kg.m−3), g is gravity acceleration (9.81 m s−2), Hm is the pump head (m), Vday is the daily volume of pumped water (m3 day−1) and md is the number of days per month for each month of the year.


The crop water requirement, CWRday (mm day−1), was determined using Eq. (5):

$${\text{CWR}}_{{{\text{day}}}} = ETo \cdot Kc \cdot fc_{{{\text{month}}}}$$
(5)

where ETo is the reference evapotranspiration (mm day−1), Kc is the crop coefficient for citrus fruit with percentages of canopy cover greater than 70% (local adaptation for the Mediterranean region’s conditions (Castel 2000) and fcmonth is the monthly correction factor proposed for citrus fruits.

Moreover, the monthly volume of water required was determined by adding the daily volume needed to pump Vday (m3 day−1) throughout the month. This was determined using Eq. (7):

$$V_{{{\text{day}}}} = 10^{ - 3} \cdot CWR_{{{\text{day}}}} \cdot {\text{Area}}$$
(6)
$$V_{{{\text{month}}}} = \mathop \sum \limits_{i = 1}^{{{\text{md}}}} V_{{{\text{day}}}}$$
(7)

Taking into consideration the discharge characteristics, the head (Hm) that the pumping system should achieve was determined as follows:

$$Hm = \left( {Z_{2} - Z_{1} } \right) + hf + hs$$
(8)
$$hf = 10.674 \cdot \frac{{Q^{1.852} }}{{C^{1.852} \cdot D^{4.871} }} \cdot L$$
(9)

where (Z2—Z1) is the difference between tank elevation (m), hf is the pressure loss due to friction calculated according to the Hazen-Williams equation (m) (Eq. 9), hs is the localized singular loss of pressure, in this case, 30% of hf (m) is considered, Q is the determined flow rate for each hypothesis (m3 s−1), C the coefficient of roughness (150), D the internal diameter (m) and L is the length of the discharge pipe (m).

The design flow rate (Q, m−3 s−1) was determined for the most unfavorable month, considering that the pumping time (PH) coincides with the peak sun hours (PSH) for each month. PSH was calculated by averaging the daily irradiances of each month (kWh∙m−2∙day−1). PH was determined by adding the hours in which the power required by the number of pumps in each hypothesis was less than the generated power.

$$Q = \frac{{V_{{{\text{day}}}} }}{{{\text{PH}}}}$$
(10)

Based on the hydraulic energy HEi for the most unfavorable month, the electric energy (EE) (Eq. 11), the necessary peak power (Pp) (Eq. 12) and finally, the number of panels (Npanels) (Eq. 13) were determined using the following equations:

$${\text{EE}} = \frac{{{\text{HE}}_{i} }}{{ \eta_{mp} }}(W)$$
(11)
$$P_{p} = \frac{{{\text{EE}}}}{{{\text{EES}} \cdot {\text{PSH}}}}(W)$$
(12)
$$N_{{{\text{panels}}}} = \frac{{Pp_{{{\text{panels}}}} }}{{ Pp_{{{\text{panels}}}} }}$$
(13)

where ηmp, the efficiency of the motor pump, EES, is the system’s energy efficiency.

To calculate the number of solar panels (Eq. 13), a panel of 320 Wp, an EES = 0.4 and a motor-pump efficiency of ηmb = 0.8 were considered. These efficiency and performance values are commonly used in technical projects. They are in the range of those obtained experimentally (ESS between 10 and 45%) in smaller installations (2.2 kW) by Hamidat and Beyoucef (2009). They are also similar to those considered (EES = 0.5) in other studies of comparable hydraulic characteristics (Monis et al. 2020).

Net generator power


The power supplied by the generator throughout the year 2019 was determined on an hourly basis every day during the study period, taking radiation and temperature into account. The meteorological data were obtained from the IVIA Picassent agroclimatic station, which is part of SIAR. Cell temperature (Tcel) was determined using Markvart and Castaner’s (2003) expression:

$$T_{{{\text{cel}}}} = T + \frac{{\left( {NOCT - 20} \right) \cdot G}}{800}$$
(14)

where T is Temperature in degrees Celsius, NOCT is the nominal operating temperature of the photovoltaic cell (45 °C in this case) and G is the irradiance (W m−2).


The PV system consisted of 170 panels with 72 six-inch polycrystalline cells with a power of 320 Wp for each panel. The available instantaneous photovoltaic power was determined by the equation:

$$P_{{{\text{int}}}} = P_{p} \cdot \frac{G}{1000} \cdot \left( {1 + \frac{{\alpha_{p} }}{100} \cdot \left( {T_{{{\text{cel}}}} - 25} \right)} \right)$$
(15)

where Pp is the solar panel’s peak power, G is the irradiance (W m−2) throughout the year 2019, αp is the Pp to temperature variation coefficient (%  °C−1) and Tcel is the temperature of the photovoltaic cell.

Finally, the net power (Pnet) that pumps can use was determined by considering the efficiencies of the inverter and the motor.

$$P_{{{\text{net}}}} = P_{{\text{int}}} \cdot \eta_{fc} \cdot \eta_{mp}$$
(16)

ηfc is the efficiency of the inverter, which is considered to be 0.9, and ηmp is the efficiency of the motor-pump, already considered to be 0.8.

Pumping hypothesis

The useful volume in the tanks is sufficient to provide irrigation water for one day in the month of maximum irrigation needs. The design flow rate (Q, m−3 s−1) was determined by multiplying the crop evapotranspiration (ETc) by the study area and dividing by the hours of the day in which the irradiance is sufficient for the pumping system to operate in the month of maximum needs.

The pumping system must be able to raise the flow to the required head (Hm, m), for which the power generated must be greater than the power demanded. In an installation where solar radiation is the only energy source, the available power is variable over time. For much of that time, the PV power is insufficient to raise the flow to the required height. It is possible, however, that at certain times PV power would be enough to operate a lower-rated pump. This way, solar energy can be used more efficiently by running several smaller pumps in parallel instead of a larger single pump.

As already mentioned, to study the effect of increasing the number of pumps in parallel on the pumped flow, eight hypotheses were proposed to be studied. The baseline hypothesis with a single pump and hypotheses 2 to N with a successively incremental number of pumps. The first hypothesis considers the case of a single pump needing to raise a Q to a Hm. The second hypothesis considers the case of two pumps operating in parallel, needing to raise water to the same height, each pump raising half the flow. Similarly, the third hypothesis employs three pumps, each producing a third of the flow, and so on, until reaching the eighth hypothesis in which up to N pumps operate.


In each hypothesis, depending on the power that the PV generator can provide, the pumps become operational up to the maximum permitted in each hypothesis, provided that the sum of the power demanded by the working pumps remains lower than the maximum that the PV generator can provide. Thus, when the power that the solar panels can supply is higher than that required by two pumps, the second pump switches on so that the flow is then supplied by those 2 pumps, and so on successively until the maximum number of pumps within each hypothesis is reached. Therefore, the APh for each of the pumps in each hypothesis is determined depending on whether the PV power generated allows the different pumps in each hypothesis to become connected. The subsequent total discharge flow is the sum of the flow discharged by the individual pumps in each hypothesis. The flow rate and head of each pump within each hypothesis is calculated according to Eq. 17.

$$Q_{{{\text{pump}}}} = \frac{{Q_{IP} }}{N}$$
(17)

where Qpump is the flow rate supplied by each pump (m3h−1), QIP is the flow rate that should be supplied if a single pump was installed (280 m3h−1) and N is the number of pumps being considered in each of the hypotheses (from 1 to 8).


As the discharge flow varies, pressure is lost due to friction, and consequently, each pump´s head and efficiency are modified and, in turn, the power required by them (\({P}_{{b}_{i}}\), W).

$$P_{{b_{i} }} = \frac{1}{{ \eta_{i} }} \cdot \gamma \cdot Q_{i } \cdot Hm_{i}$$
(18)

where ηi is the pumping efficiency for each pump in each hypothesis, γ is the specific weight of the water (Nm−3), Qi is the sum of the flow rate of each working pump in each hypothesis (m3s−1) and Hmi is the head required for the set of pumps in each hypothesis (m).

The weekly volume pumped (Vweek) is calculated from the weekly hours when the energy supplied by the photovoltaic system is greater than the energy required by each of the pumps in operation in each of the hypotheses, and these hours are multiplied by the flow of each pump Qpump using the following equation:

$$V_{{{\text{week}}}} = \sum\nolimits_{{i = 1}}^{7} {\left( {IWh_{{{\text{Pump}}}} \cdot Q_{{{\text{Pumpi}}}} } \right)}$$
(19)

Vweek being the volume in m3 per week, IWhpumpi is the weekly hours in which the power supplied to the number of pumps of each hypothesis is higher than is required and Qpumpi is the flow rate supplied by the operating pumps in each hypothesis (m3h−1).

Once the weekly volumes during the entire year are determined, they are added together to obtain the annual volume supplied by each hypothesis (from 1 to 8 pumps), from which the differences concerning the baseline hypothesis (1 pump) can be determined.

Selection of the number of pumps by economic criteria

In this section, the installation cost of each of the hypotheses was evaluated, as well as the volume pumped (m3) for each euro invested when installing each.

The economic study was limited to the cost of the pumps and the solar panels without considering other costs involved, such as the construction of the building that houses the facilities, the land on which the solar panels are installed, the metalwork carried out, the supports for the photovoltaic panels or the electrical wiring necessary. In addition, maintenance and operation costs have yet to be considered since they are very conditioned by other project considerations. On the other hand, as the pump system is considered isolated from the electrical grid, possible income due to surplus energy is not accounted for either. The assumptions considered are contemplated in Eq. 2.

Results and discussion

Design results

The volume of water needed to cover the water needs of a citrus crop with coverage greater than 70% in the most unfavorable month (august) is 3.43 mm day−1, which means a daily water volume of 1680 m3 for the entire irrigated area (489,306 m2) is required. With the pump selected (baseline hypothesis) and the necessary pressure requirements (280 m3 h−1, 25.1 m), six PSH are needed to drive the required volume, which fits with the average daily radiation in August (6.43 kWh m−2 day−1).

Table 1 summarizes the results of the eight hypotheses being considered. The first one is the baseline hypothesis.

This study was limited to eight pumps in parallel, considering that with this number, we would cover the range in which the optimal number would be found, as indeed happened and is discussed below.

Table 1 shows that within the hypotheses, the flow rate (Total Q) and design pressure (Hm) are reached when each hypothesis's pumps are in operation. The pressure needed to pump a lower flow rate is also lower than expected because the energy losses decrease, as occurs when, within a hypothesis, the maximum number of pumps does not work. It should be noted that the greater the number of pumps a hypothesis has, the lower their performance (e.g., η = 78.5% vs. 65% in hypotheses 8 and 1, respectively), which was also expected since the performance of the pumps decreases with size. These performance values are reasonable values for pumps with these characteristics. They are consistent with the lowest values (η = 33.5%) obtained in experimental studies with smaller pumps (1.5 kW) in direct photovoltaic water pumping systems (Orts-Grau et al. 2021; Gasque et al. 2022).

Energy requirements for the different hypotheses

A PV hypothesis of 54.4 kWp of peak power (170 panels × 320 Wp panel−1) was used as the baseline generator. The power required by the single pump of the first hypothesis was 30.5 kW, which means oversizing the PV generator concerning the motor-pump group power equal to Fp = 1.78, and is within the typical values in direct photovoltaic water pumping systems (between 1.4 and 1.9).

Figure 1a shows the power required (Eq. 16) for each operating pump in each hypothesis (Pb column in Table 1). As previously commented, the necessary energy to pump the same volume of water increases slightly as the hypotheses involving a greater number of pumps are successively contemplated, in line with decreased performance when involving smaller pumps. These results can be extrapolated to other cases and trade brands, given that their performances are comparable.

In addition, as observed in Fig. 3a, the number of operating points increases as the number of pumps increases, indicating that it is easier to adapt the energy supplied by the generator to the energy required. For example, there is only one operating point in the baseline hypothesis, so it is impossible to start pumping until the energy supplied by the generator reaches the energy required. In contrast, in the second hypothesis (two pumps in parallel), one of the pumps starts operating when the PV power is around half the power required to start the single pump of the first hypothesis. Subsequently, the second pump starts when the PV power eventually reaches the level required in the first hypothesis for its only pump to work. Hence, in hypothesis 2, by the time the second pump starts operating, the first has already been pumping water.

Fig. 3
figure 3

Power requirements per pump for the eight hypotheses (a) and flow rate pumped (b) by the pumps (m3h−1) compared to the number of pumps in operation in each of the hypotheses (from 1 to 8 pumps)

Full size image

As the number of pumps increases with each successive hypothesis, the power required by each one decreases, so the energy supplied by the irradiance can be used more efficiently. Although, when all the pumps of the different hypotheses are in operation, the sum of their separate powers is greater than the power required by the single pump of the first hypothesis (Fig. 3a) while supplying the same flow rate (Fig. 3b). As the number of pumps increases within each hypothesis, each pump´s flow rate decreases (Fig. 3b) inversely proportional to the number of pumps.

Figure 4 shows the points of each hypothesis and the number of pumps along the pumping resistance curve. All hypotheses have at least one operating point in common when all the pumps of each hypothesis are in operation, pumping 280 m3h−1 at Hm of 25.1 m. As the supplied power increases due to the increasing irradiance, more pumps begin to operate in each of the hypotheses, causing the operating points of the parallel pumps to move along the resistance curve. Consequently, the head and pumping flow increase until the baseline parameters (Hm of 25.1 m and a Q of 280 m3 h−1) are reached.

Fig. 4
figure 4

Operating points of the different hypotheses depending on the number of pumps running over the resistance curve of the installation (Hm [m], Q [m3h−1])

Full size image

The variation in the power requirements of each hypothesis is related to three factors. The most important is the number of pumps in operation (Fig. 3a). The second factor is the flow rate since, as it increases, so does pressure loss due to friction, and consequently, an increase in the required head is observed (Fig. 4). Finally, the efficiency of the pumps; the lower the efficiency, the greater the energy requirement (Eq. 18). As shown in Fig. 5, although the head height and flow rate are the same when all the pumps of each of the hypotheses are in operation (Q = 280 m3h−1), the energy required (kW) increases with the number of pumps. This occurs because smaller pumps have lower efficiency; therefore, for the same head and flow rate, the smaller the pumps used, the more power required.

Fig. 5
figure 5

Power requirements (kW) versus the pumped flow rate (m3h−1) regarding the number of pumps in operation for each hypothesis (from 1 to 8 pumps)

Full size image

Pumped volumes

Comparison of the volume pumped by each hypothesis

Figure 6 shows the evolution of the weekly volume pumped throughout 2019 for each of the hypotheses contemplated. It highlights that the baseline pumped volume (hypothesis 1 pump) is significantly lower than the rest of the hypotheses throughout the year.

Fig. 6
figure 6

Pumped volume (m3) per week during the year 2019

Full size image

The greater the number of pumps in each hypothesis, the greater the volume pumped, although the gains decreased as the number of pumps increased. Even though each pump discharges less volume than in the previous hypothesis (Eq. 17), the hours of available energy (energy supplied-energy required) are greater, and hence also the volume pumped (m3). As the number of pumps increased when moving to the following hypothesis, the increment in pumped volume decreased. For the five pump hypothesis, the gain in the annual volume discharged with respect to the baseline hypothesis (one pump) was 27%. However, beyond the five pump hypothesis, the gain diminished and became asymptotic, showing that the most suitable pumping configuration, in this case, corresponds to the hypothesis of five pumps in parallel (Fig. 7). The procedure required using the minimum number of pumps necessary to reach stabilization of the trend. In this case, we used eight pumps as a safety (it is a high number) to show that it tends to stabilize the pumped volume. We reached the same conclusions considering six, seven or any greater number of pumps.

Fig. 7
figure 7

Percentage gain in volume pumped with the two to eight pump hypotheses versus the reference hypothesis of one pump and gain trend line

Full size image

Variation of the discharged volume depends on the PV generator

To study the influence of PV generator size on the annual pumped volume (V), different generator sizes (indicated in Sect. “Case Study”) were considered for the hypotheses with one, three, five and eight pumps.

Figure 8 shows the volume pumped (m3 year−1) obtained by increasing the size of the PV generator for each of the hypotheses with one, three, five and eight pumps in parallel. As expected, increasing the power of the PV generator also increased the volume pumped in all the hypotheses, and for a given PV generator power, the volume pumped was greater with a higher the number of pumps in the hypothesis. However, these increases were minor as the number of pumps running in parallel increased. Changing from the hypothesis of five to eight pumps operating in parallel, the gain was substantially reduced, which confirms that the best outcome for this case study is the installation of five pumps in parallel.

Fig. 8
figure 8

Pumped volume (m3) versus kWp of the photovoltaic generator for different power factors (0.1–2 [increasing in intervals of 0.1], 2.5, 3, 4, 5 and 10), which relates installed power and required power

Full size image

Variation in discharged volume relative to the size of the PV generator

The effect of the relative size of the photovoltaic generator on the pumped volume was studied in this section using the power factors (Fp). Figure 9 shows the weekly pumped volumes, Vweek (m3), obtained with hypotheses 1, 3, 5, and 8 and with the generator sizes necessary to pump all the water required throughout all weeks of the year, together with the weekly volume necessary. Fp’s of 1.78, 1.1, 1 and 1 were required to pump the needed weekly volumes for hypotheses of one, three, five and eight pumps, respectively (Fig. 9). The required size of the photovoltaic generator decreased as the hypothesis had a greater number of pumps, the same tendency shown in Fig. 7 and deduced from Fig. 8. Moreover, it was also observed that as the number of pumps increased, the differences in the necessary Fp were gradually reduced. In fact, from three to five pumps (Fp: 1.0 and 32.9 kWp, respectively), Fp was reduced by 0.1 (43.8% less compared to the hypothesis with a single pump); and from five to eight pumps (Fp: 1.0 and 37.5 kWp, respectively) Fp was not reduced compared with the hypothesis of five pumps (43.8% less compared to the single pump hypothesis). Therefore, it can be stated that, in this case, more than five pumps do not present reductions in the minimum photovoltaic power required to achieve the needed pumped volumes.

Fig. 9
figure 9

Volume pumped weekly (m3) with the hypotheses of one, three, five, and eight pumps with power factors of 1.78, 1.1, 1 and 1, respectively, to pump the required weekly water, compared to the weekly volume required by the irrigation zone

Full size image

Use of irradiance

As we have already seen, the greater the number of pumps in a hypothesis, the greater the annual volume pumped. This is because smaller pumps require less power to pump, and consequently, the number of daily hours with enough power available increases.

Figure 10 shows the hourly evolution of energy available in summer and winter together with the energy required (horizontal lines) for the operation of the pumps in the baseline (top) and in the second hypothesis (bottom). When the hypothesis of a single pump as applied, the number of daily hours of pumping was 4:40 h in winter and 10:42 h in summer; in both seasons, 280 m3 h−1 was pumped. In contrast, in the hypothesis with two pumps in parallel, one can pump 140 m3 h−1 with lower required power, adding 1.57 h of pumping in the summer and 2.13 h in the winter. Although the flow rate was half that driven during this additional time when both pumps operate, the daily volume pumped was greater than with the single pump hypothesis.

Fig. 10
figure 10

Hourly evolution (hours in Coordinated Universal Time system) of energy available in summer (06/23/2019) and winter (12/24/2019) together with the energy required (horizontal lines) to operate the pumps in the hypotheses with one pump (top) and two pumps (bottom). The operating time of each pump in each hypothesis is indicated, as well as the gain in pumping time between the hypothesis of one pump with respect to that of two pumps

Full size image

Due to this increase in pumping hours, the daily pumped volume increased for one or more of the pumps involved in the hypotheses with several pumps in parallel. However, as noted previously, as the number of pumps increased, the gain in the volume discharged decreased in comparison to the previous hypothesis.

The variation in pumping hours is determined by the different irradiances required, which depends on the number of pumps in each hypothesis. Table 2 compares the minimum power requirements for the hypothesis with one pump to that of the five pump hypothesis.

Table 2 Required power and pumping irradiance threshold for the hypotheses with one and five pumps considering a generator peak power of 54.4 kW (power factor of 1.78)
Full size table

For the hypothesis with one pump, the minimum power required to start pumping was 30.5 kW, which means an irradiance threshold of 336.6 Wm−2 for the most unfavorable month (July). However, for pumping to begin in the hypothesis with five pumps in parallel, only 6.1 kW was required, which means an irradiance threshold of 66.0 Wm−2 (19.6% of that with the first hypothesis) Furthermore, as the irradiance increased throughout the day, a greater number of pumps were connected until reaching the maximum required power of 32.9 kW, which is equivalent to a threshold irradiance of 364.5 Wm−2 with a peak power generator of 54.4 kW. These values are consistent with those obtained experimentally (Orts-Grau et al. 2021) during seven completely sunny days operating in comparable conditions (301.30 ± 12.30 W m−2).

Selection of the number of pumps economic criteria

The last step, indicated in Sect. “Selection of the optimal number of pumps” (Fig. 2), was to select the hypothesis that fulfilling the objective implies a lower economic cost. The economic cost of each hypothesis was determined by adding the pumps' cost to the PV panels' cost. The cost of the pumps was calculated by multiplying the price of the pump by the number of pumps to be installed in each hypothesis. Similarly, the cost of the PV panels was determined by multiplying the price of a PV panel by the minimum number of PV panels necessary to supply the volume to be pumped in each of the Fp’s considered. Fp: 1.78 (one pump), Fp: 1.1 (three pumps), Fp: 1 (five pumps) and Fp: 1 (eight pumps).

The installation cost, depending on the number of pumps (N), fits the following equation:

$${\text{Cost}} \left( \EUR \right) = - 10.311 N^{3} + 559.17 N^{2} - 4439.1 N + 31804$$
(20)

To set a comparative ratio, the annual pumped volume was divided by the economic cost of the pumping station. This ratio will remain proportional with respect to the pumped volume, independent of the number of years considered or the amortization period of the pumping station.

As is shown in Fig. 9, increasing the number of pumps can decrease the number of photovoltaic panels needed to supply a specific pumped volume.

In this case, the annual cost per cubic meter fits the following equation:

$${\text{Cost}} \left( {m^{3} \EUR^{ - 1} } \right) = 0.041 N^{3} - 1.3979 N^{2} + 10.618 N + 14.613$$
(21)

In Fig. 11, both functions are represented, showing that the optimal solution is to install five pumps in parallel.

Fig. 11
figure 11

Cost of the pumps and photovoltaic panels that supply them for hypotheses 1, 3, 5 and 8, depending on the number of pumps and annual volume driven per cost of pumps and PV panels of each hypothesis

Full size image

As would be expected, increasing the number of pumps and reducing the necessary number of PV panels resulted in a reduction in the installation costs. However, the slope of the cost curve began to increase from the point where the hypothesis of five pumps in operation was considered. This is due to two factors: i) as the power of the pumps decreases, the price difference between the pumps is reduced, even though the number of pumps increases and ii) as the number of pumps increases, their power and efficiency decrease. Although the Fp and the size of the PV generator required are also reduced, the decrease in generator cost of the five-pump scenario to the eight-pump scenario is negligible compared to the significant increase in pump cost.

Up to eight pumps working in parallel was selected as the maximum number of pumps. The number of pumps was increased until the slope of the m3€−1 curve shown in Fig. 11 was negative. This function has a maximum at the fifth pump. Also, the gain shown in Fig. 7 increased up to pump five. This gain remained constant from pump five to pump eight.

Thus, according to the economic criterion, the most favorable option for this scenario is installing five pumps in parallel. Similarly, Eq. 2 shows that the highest ratio between pumping volume and total economic investment is given by five pumps.

Although the procedure proposed in this article is robust, to be generalized, it is essential to reduce uncertainties using data corresponding to the location and characteristics of the installation in which it intends to be applied. Meteorological data, the geometric and hydraulic characteristics of the installation, the price and characteristics of the pumps, the price, position and orientation of the solar panels, the price and characteristics of the electronic elements, etc., must correspond to the installation in which the study intends to be carried out.

Finally, it must be considered that the cost calculation was limited to the cost of the pumps and the photovoltaic panels. Hence, future research must develop a function that includes all the expenses and income PV installation can generate. Also, the use of frequency speed drivers in one or more of the pumps should be studied technically and taken into consideration in the economic criteria.

This methodology presents advantages such as a greater volume of water being promoted with a lower number of PV panels and a reduction in costs. Additionally, with having a greater number of pumps installed, greater service safety is achieved since even when one of the pumps does not work, the flow can continue to be propelled by the rest of the pumps. The main disadvantage may be that a greater number of pumps increases installation complexity.

Although, a starter is considered to drive each pump in this work, it is technically possible to install a variable speed drive (VSD) per pump connected to a single photovoltaic generator or a VSD to drive one of the pumps while the others are commanded with a starter. Any of these configurations would make it possible to take even better advantage of solar radiation, given that a VSD adjusts the frequency and voltage supplied to the pump to consume the power that the generator can produce, pumping more water. Studying the advantages of these configurations is an open avenue for future studies. However, the difficulty of managing the operating point of the generator and the distribution of power between the different pumps is still not well resolved and is another possible improvement for development.

Conclusions

This paper studied a particular case of an isolated photovoltaic installation for pumping water between two tanks, splitting the total pump power needed among several smaller pumps in the required photovoltaic power generator to meet water pumping requirements and reduce the total installation cost.

The results show that the volume pumped increased with the number of available pumps in parallel while decreasing the size of the photovoltaic generator needed. However, the gain in the pumped volume decreased with each additional pump, and the initial decrease in total costs was followed by a subsequent increase because the increment in the cost of the pumps was greater than the decrease in the cost of the necessary photovoltaic generator.

In the case analyzed, significant increases in pumped volume were not achieved with more than five pumps in parallel, nor were reductions in the size of the generator needed, while the total cost of installation increased significantly by increasing the number of pumps above five.

Compared to the installation of a single pump (baseline hypothesis), with the installation of five pumps in parallel it was possible to pump up to 27% more water throughout the year, with a reduction of 44.1% of the necessary peak power of the generator and a 13.3% reduction in the cost of the installation compared to the baseline hypothesis.

The procedure used to determine the number of pumps to install in parallel to pump water between two tanks to minimize the size of the photovoltaic generator while guaranteeing the pumping requirements is easily generalizable for isolated photovoltaic water pumping systems.