Introduction

Minerals contain microstructures and much of what minerals can tell us about past geological processes, and about their own intrinsic properties, is related to microstructures. This balances the importance of microstructures with the actual crystallographic structure. Through the enormous progress in nanotechnology over the past decade, our perspective of materials in general and minerals in particular has shifted towards a much better understanding of microstructures. Microstructures cover a huge range of length scales from coarse twinning (mm scale), fine twins (typically on a micrometer scale) and tweed structures with repetition scales between 10 and 100 nm. On an even smaller scale we have structural disruptions, like kinks and domain wall bendings, so-called wobbles, inside these microstructures (Salje et al. 2017a; He et al. 2018; Wang et al. 2018; Nataf et al. 2020). These small disruptions appear as shifts of atomic positions and are typically measured on a pm scale (e.g. Van Aert et al. 2012 for the perovskite structure). The smallest range is reflected by electron microscopists who often use the term ‘nanoscopy’ to emphasise that the relevant scales for domains do not end at some micrometres. The range of length scales often covers some nine decades, which has led, in the field of correlated systems, to the hypothesis of ‘scale invariance’ indicating that certain aspects of microstructural physics are applicable over the full range of length scales.

A second development relates to the time scales on which microstructures change. Such changes are either induced by external forcing, like stress, electric or magnetic fields, oxygen fugacities, etc., or during creep experiments without external forcing (Salje et al. 2018). Geological processes do not always act on ‘geological’ time scales of longer than 103 years but they can also be very fast. Structural changes during radiation damage, for example, take only ca. 5 femto-seconds (10–15 s) and the propagation of a twin wall requires times between 10–8 s and 10–3 s in many cases. The fundamental question is then: what determines the origin of time scales? In this paper we argue that for avalanche processes there is not a ‘typical’ time scale but, instead, a large dynamic range of time scales.

Microstructures often evolve in a non-smooth manner. The shift of a domain boundary is virtually never continuous but occurs in a stop-and-go fashion. Cracks do not progress along straight trajectories but wobble, bifurcate and form complex patterns on an atomistic length scale. The appropriate description of such processes lies in the concept of avalanches. Their discovery, which was sometimes ignored in mineralogy, is probably the most important progress in the design and application of high-tech devices and covers a novel branch of scientific endeavour, referred to a ‘avalanche science’ with several books published in this field (e.g. Salje et al. 2017b). Historically, its importance stems from the intrinsic properties of microstructures, like holes, inclusions, twin boundaries, dislocation lines, twin junctions and so on. We know today that a transistor, as an example, does not need bulk materials to operate but is often localized in tiny areas inside twin boundaries or near junctions between boundaries. The same holds for ferroic memories and memristive conductors (Salje et al. 2017a; He et al. 2019; Bak et al. 2020; Lu et al. 2020a; Zhang et al. 2020; Salje 2021) where only a few atoms near domain boundaries move. The diameters or thicknesses of these functional regions are a few inter-atomic distances (Lu et al. 2019, 2020b; McCartan et al. 2020). Emerging properties such as ferroic memory elements are based inside twin boundaries while the surrounding crystal matrix is simply there to keep domain walls in place (Salje et al. 2016c; Salje 2020). Predesigned domain wall structures are constructed in the field of ‘domain boundary engineering’, which has become a very powerful approach in many recent applications (Salje 2010). We will allude to its relevance in mineral physics in this paper.

Most examples in this review are taken from the field of mineral physics. If the reader wishes to pursue the topic further for other minerals, we recommend consulting Salje and Dahmen (2014) as a reference paper which includes the major ideas of physical avalanche systems.

Avalanches

Crackling noise is encountered when a material is subjected to external forces with jerky responses spanning over a wide range of sizes and energies. The Barkhausen effect of pinned domain walls (Harrison et al. 2002; Robinson et al. 2002; Roberts et al. 2017, 2019) during magnetization processes (Durin and Zapperi 2006), martensitic transitions (Vives et al. 1994; Gallardo et al. 2010), plastic deformation in solids (Csikor et al. 2007; Weiss et al. 2007; Salje et al. 2009; Puchberger et al. 2017, 2018), or materials failure (Zapperi et al. 1997; Aue and De Hosson 1998) is well documented. Upon variation of an external field, avalanches show a spectacular absence of time and length scales. Crackling noise is often related to critical behaviour of avalanches, which stem from intrinsic inhomogeneities or by jamming of microstructures (Salje et al. 2011a). In all these cases one finds that the internal structures of the domain boundaries or the domain patterns display a high degree of complexity—very much in contrast to the early perception of Barkhausen noise (Barkhausen 1919; Tebble et al. 1950).

Crackling noise avalanches, like the well-known snow avalanches, are collective motions, which follow well-defined statistical rules while their exact time-dependent behaviour of any part of the avalanche remains unknown. Collapse avalanches have been thoroughly analysed in porous minerals, like SiO2 based glass (Vycor) (Salje et al. 2011b), goethite (Salje et al. 2013), porous alumina (Castillo-Villa et al. 2013) and berlinite (Nataf et al. 2014b), to name just a few prototypic examples. Their statistical characteristics share many similarities with seismicity such as the Earth crust failure due to stresses originated from plate tectonics (Davidsen et al. 2007; Kawamura et al. 2012). These similarities go beyond the avalanche statistics and include the statistics of aftershocks and waiting times of acoustic emission or earthquakes (Baró et al. 2013). More specifically, it is shown that the Gutenberg–Richter law, the modified Omori’s law, the law of aftershock productivity and the universal scaling law for the waiting time distribution typically used in statistical seismology hold for all avalanches, often in a broad range of at least six decades of jerk energies with exponents similar to those obtained in earthquakes. Similar results were found in other collapsing minerals.

The following fundamental parameters are essential for our further discussions.

Amplitude A

The amplitude A(t) is a function of time t and captures the evolution of the conjugate parameter to the external force. In many cases, the force originates from the external stress (or strain), so that the amplitude parameter is the strain (or stress) in the sample due to the hole collapses. The time evolution of the amplitude is typically initiated by an incubation period where A(t) increases exponentially leading to the maximum amplitude, called Amax. It then decays with a long tail of strain signals until the avalanche terminates. Amplitudes can display very complex evolution patterns, in particular when several avalanches coincide. Sometimes they develop ‘eternal’ avalanches, which never fully end but just diminish and resurge. The obvious analogy to disease spreading mechanisms highlights the close similarity between these two areas of research.

Duration D

The duration is the time period over which an avalanche survives. Experimental time scales typically extend from a few microseconds to many milliseconds.

Energy E

The energy is the time integral over the local squared amplitude A(t)2, integrated over the full duration of the avalanche:

$$E = \int_{o}^{D} {A^{2} \cdot } {\text{dt}}$$

This means that for avalanches which represent a short δ-function excitation at the time tmax, A(t) = Amax δ (t–tmax) will always display a scaling E ~ Amax2. This is not true for long and smooth A(t) functions. Various scalings E ~ AX with 2 < x < 3 are discussed in literature (Casals et al. 2019, 2020, 2021a, b; McFaul et al. 2020).

Size S

The size of the amplitude indicates the number of particles that move during the avalanche. While this parameter appears intuitive in geometrical terms like a ‘patch’ of transformed material, this is not correct. If areas transform, they can do so in compact regions where every atom takes part in the transformation. They can also transform by selecting some of these atoms, forming some ‘sponge-like’ areas. The fractal dimension of these transformed areas becomes then paramount and while ‘size’ is popular in the general description of avalanches, the meaning of such ‘size’ parameter can be surprisingly complex. It is, therefore, recommended to explore the scaling of size with the amplitude or energy as a more fundamental parameter. As an example, if the movement relates to low-dimensional dynamical patterns, the relationship is linear S ~ A while in magnetic systems with high fractal dimensions we find S ~ A2. This already highlights that model calculations are often required to determine this S(A) scaling and that scaling depends sensitively on the fractal dimension of the domain patterns (Casals et al. 2019, 2021a; Nataf et al. 2020; Xu et al. 2020).

Waiting time or inter-event time tw

The two names are used interchangeably. They denote the time between avalanches, i.e. the time the system needs to recover after an avalanche has happened. In neural networks, these inter-event times are the ‘sleeping periods’ after high neural activity. Their probability distributions are typically power laws with two different, approximate exponents for short and long times, P(tw) ~ tw−1 and P(tw) ~ tw−2, respectively. Note that in these scaling relationships the negative sign in the exponent is often included in the equation so that the term ‘exponent’ often means the value after the minus sign. These exponents represent the results in the simplest mean field (ML) theory (Salje and Dahmen 2014). Similar values have been observed experimentally and deviations from ML predictions are analysed in terms of specific physical models (Christensen et al. 1996; Corral and Paczuski 1999; Navas-Portella et al. 2016).

In addition, there is a multitude of secondary scaling laws, in particular those describing aftershock activities (Baró et al. 2013, 2018; Nataf et al. 2014a) and inter-correlations of times (Baró et al. 2016a, 2018) with several important practical extensions for mineral behaviour, as described in (Jiang et al. 2017).

Acoustic emission (AE) spectroscopy

During 100 years of research many experimental methods were developed to quantify avalanches. They range from magnetic measurements to electrical depolarization currents in ferroelectrics and optical observations of crack patterns and the determination of fractal dimensions (Lung and Zhang 1989; Xie and Sanderson 1995; Lhotel et al. 2008; McHugh et al. 2009). Some experiments are conducted under in vivo conditions where the actual changes of domain structures are determined; others are post-mortem analyses where, e.g. the fractal dimension of cracks are measured (Chen et al. 2020). All methods have advantages and disadvantages and evolved with the purpose of the specific research. Over the past decade the emphasis has moved towards a deeper understanding of avalanche science rather than a more general determination of stabilities of minerals in geomechanics. With this movement came the desire to measure the main avalanche parameters, as listed above, with the highest possible accuracy. The current method of choice is in this case the acoustic emission (AE) spectroscopy. The acoustic waves emitted by a sample during changing fields is detected by piezoelectric receivers and analysed using straightforward amplification devices. A simple summary is found in (Chen et al. 2019; Xie et al. 2019).

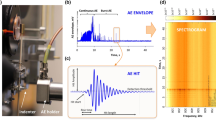
Figure 1 shows schematic representation of the composition of an avalanche signal in acoustic emission experiments. The size of the sample and the detector is some 5 mm, the detector covers often a large part of the sample. During local switching, an avalanche emits a strain signal which propagates through the sample and is eventually measured by the detector. During the propagation, the signal generates the ringing of the sample and is modified by elastic wave reflections on surfaces, scattering on lattice imperfections. The profile of a source delta function would generate T(t), the so-called transfer function. The measured AE profile AAE(t) is the convolution of the source function with the transfer function. (Modified from Casals et al. 2021a, b).

Fig. 1
figure 1

Schematic representation of the composition of an avalanche signal in acoustic emission experiments

Full size image

While AE spectroscopy is probably the best way to detect avalanches under in-vivo conditions, it has a serious drawback. The measured AE spectrum, i.e. the macroscopic jerk spectrum of a sample, is not exactly the initial avalanche distribution V(t) nor does it reproduce exactly the predictions of theory. There are two main reasons. First, the measured AE spectrum is modified by the transfer function by the travelling sound waves. This modification is most notorious if the time and frequency scales of the initial avalanche formation (some microseconds in many cases) differs greatly from the inverse frequency of the sample ringing and hence the transfer time scale. Ringing times are typically between several microseconds and some milliseconds. This time scale depends on the sample size (decreasing transfer time with decreasing sample size) and the nature of the initial avalanche. Crack propagation and dislocation dynamics are fairly similar in their local duration D while ferroelectric and ferroelastic domain movements are often much slower. Nevertheless, the energy probability function is hardly affected by these modifications and there is a large amount of literature which elucidates some of the intricacies of AE spectroscopy (Chi-Cong and Weiss 2020; Vu et al. 2020; Yang et al. 2020). The avalanche duration is not easily determined while the rise time R during the incubation period often correctly represents the avalanche formation and propagation much better. It is close to the atomic rise time and is less polluted by the effect of the transfer function (Salje et al. 2017a; Casals et al. 2021a, b).

Porous collapse

Minerals are often lighter than their chemical composition would suggest. Defect chemistry traditionally points to vacancies as a reason for the weight loss. This is not always the case. In fact, vacancies are simply the smallest version of holes and cavities in mineral structures. Holes can also be envisaged as empty inclusions, so that much what is known about holes can be extended to other inclusions. Holes are also structural elements in porous materials, which are widely used as filters, fillers, low thermal conduction materials and so on. Porous materials are particularly important due to their relevance in the collapse forecast of both natural and artificial structures such as mines (Jiang et al. 2016), buildings (Salje 2015), or bones (Baró et al. 2016b). It has been shown that when mining materials are subjected to a compressive stress, failure can be heralded by a significant precursor activity (Salje et al. 2011b; Jiang et al. 2017). In the precursor regime, the response of the system to the applied compressive stress is not smooth as classically expected for elastoplastic materials, but instead occurs as a sequence of avalanches. Typical minerals where pores were induced by burning carbon inclusions are shales (Baró et al. 2016a), porous quartz (Nataf et al. 2014a), berlinite (Nataf et al. 2014b), corundum (Castillo-Villa et al. 2013) and goethite (Salje et al. 2013). Avalanche behaviour was found in all these materials, and the energy exponents varied between 1.33 and 2 with another common value at 1.66. These values coincide with the predictions of mean field theory, MF, as described in Salje and Dahmen (2014).

A prototype of porous materials is the tuff-like Vycor, which is a porous material based on SiO2 with holes covering a very wide range of diameters. The smallest hole diameter is ca. 5 nm. Understanding holes requires to understand their strain fields. Vacancies (and other inclusions) exert large strain fields, which were summarized in Markenscoff et al. (2015). Depending on the underlying symmetry of the mineral structure, they are either dipolar or quadrupolar in symmetry, but rarely monopolar. Defects with isotropic forces do not interact because each defect changes the volume of the sample and, if the sample is unbounded, such volume-change generates no energy. This situation changes dramatically when the sample size is bound by external forces. Interaction energies in general decay as 1/rn in space with n = 3 or 5 for dipoles and quadrupoles. While n = 5 restricts interactions to close neighbour holes, n = 3 has a more invasive characteristic: it produces ‘non-local’ forces. One defect in the sample changes the shape of the entire sample and two holes will always interact (Peyla and Misbah 2003). In case of surfaces, such as the inner surfaces of holes, the interaction is even more long-ranging with n = 2 dipole–dipole interactions and n = 3 for dipole–quadrupole interactions (Kukta et al. 2002). Such effects have been widely investigated and it was shown that in particular dipolar strain fields lead to characteristic microstructures such as tweed and very high densities of twin boundaries (Bratkovsky et al. 1994; Marais et al. 1994). When the strain fields are strong enough, i.e. when they exceed the Griffith strength, cracks will occur around holes (Fig. 2).

Fig. 2
figure 2

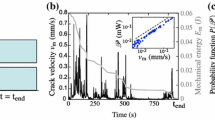
Sample height (a), the square of its time derivative (b), AE activity (c), amplitude (d), duration (e), and energy (f) of AE signals recorded during the compression experiment of the sample of porous SiO2 (Gelsile 2.6). The vertical scales are logarithmic in (b), (c), (e), and (f) [after Nataf et al. (2014a)]

Full size image

Cracks and hole–hole interactions have in common that they do not form simple microstructures. Like cracks in scattered window glass, they form complex patterns where the crack propagation does not follow linear trajectories but progress by junctions, bifurcations, spirals and specific patterns, like Turing patterns (Scott 2020). Similarly, strain fields of a multitude of cavities form patterns of great complexity (and beauty). These patterns are virtually always fractal, even when the holes are man-made in a periodic fashion (Whyte et al. 2014). Any simple description for such patterns for cracks and clouds of holes (Salje et al. 2016a; Kustov et al. 2018, 2020) remains on a rather coarse length scale because the knowledge of any finer details still exceeds our current ability to understand patterns. Local configurations matter greatly for the macroscopic properties of the mineral. One particularly impressive property is that such disordered patterns are always piezoelectric and are often polar even when the crystal structure is centro-symmetric (Lu et al. 2019, 2020b).

We now explore what happens when stress is applied to a porous sample and refer to the extended literature for samples with crack propagation (here the crack propagation in granite is a particularly nice example how AE and avalanche physics helped to determine the thermal stability of minerals (Xie et al. 2019)). When stress is imposed, a hole will eventually collapse. This collapse emits strain waves that further destroy interacting holes. As the interactions are mainly non-local, many other holes are affected. This leads to a collective collapse of holes which progresses over very short time scales. After this collapse is terminated, another primary hole may collapse and destroy another group of secondary holes which survived previous collapses, and so on. Each such event is seen macroscopically as a ‘jerk’ of the mineral. During jerks, the number of collapsing holes varies widely. As a jerk emits strain waves, namely sound waves at some frequency in the approximate range between 0.5 kHz and 100 MHz, the process is aptly described as ‘crackling noise’ (Sethna et al. 2001). The association with the crackling noise of a wood fire (namely the bursting of water inclusions in wood) is correct because it follows the same time sequence as the porous collapse and, as will be argued, many other statistical properties.

The AE during the uniaxial compression experiments of SiO2-Vycor with 40% porosity is shown as an example in Fig. 3. Vycor was loaded at a constant compression rate R for three different experiments at R = 0.2, 1.6 and 12.2 kPa/s. The external forces in most avalanche experiments are changed with extremely slow rates (one experiment can often last 3 days) in order to have little time overlap between events. Compression is applied without lateral confinement until the shrinkage of the samples is above 20%, leading to multifragmentation. Simultaneous recording of acoustic emission (AE) is performed by using a detector coupled to the upper compression plate. The signal is then preamplified (60 dB), band filtered (between 20 kHz and 2 MHz) and analysed by a multi-channel analyser. An AE avalanche event starts at the time ti when the preamplified signal V(t) crosses a fixed threshold of 26 dB and finish when the signal remains below a threshold for more than 200 μs. The energy Ei associated with each event i is computed as the integral of V2(t) for the duration of the event divided by a reference resistance. More details of the experiment can be found in Salje et al. (2011b).

Fig. 3
figure 3

a Example of the outcome of a compression experiment of SiO2-Vycor at a rate R = 1.6 kPa/s, showing the change in the specimen’s height h versus time (proportional to stress) and the energy of the AE avalanches, on a logarithmic scale. b Time evolution of the AE activity rate and of the total number N of events. [after Baró et al. (2013)]

Full size image

Figure 3a shows an example of the raw data of Vycor under compression for an experiment with R = 1.6 kPa/s. The jerky evolution of the specimen’s height is apparent, as well as the broad range of values of the event energy detected at the transducer. Another view of this intermittent dynamics is provided in Fig. 3b by the AE activity rate r(t) (counting events every 60 s) and the cumulative number of events, \(N(t) = \int_{o}^{t} {r(t)} \cdot {\text{dt}}\). Despite an apparent correlation between the most energetic events and large changes in height, one observes also regions with high acoustic activity not associated with noticeable sample shrinkage. The simple shape change of a mineral is not necessarily a good measure for the associated noise emission. Figure 4 shows the histograms that estimate the probability densities of the energies (Salje et al. 2011b; Baró and Vives 2012), considering time windows of 3 × 103 s. The distributions show a power-law behaviour \(P(E) \propto E^{ - \varepsilon }\), with an exponent near ε = 1.39 ± 0.07, which is stable for the whole experiment. This remarkably stationary energy dissipation varies greatly for other minerals. A greater heterogeneity of the sample will lead to strongly non-stationary behaviour because different parts of the sample will collapse at different stresses.

Fig. 4
figure 4

Distribution of avalanche energies of SiO2-Vycor during the full experiment with R = 1.6 kPa/s and during seven different subperiods. The line shows the behaviour corresponding to εψ = 1.39. The inset shows the maximum-likelihood exponent ε as a function of a lower threshold Emin for the three experiments. [after Baró et al. (2013)]

Full size image

The next step in a typical AE analysis is the computation of the number of aftershocks (AS) in order to compare with Omori’s law for avalanches (also in Earthquakes). We define as mainshocks (MS) all the events with energies in a certain predefined energy interval. After each MS we study the sequence of subsequent events until an event with an energy larger than the energy of the MS is found. This terminates the AS sequence. Then we divide the timeline from the MS towards the future in intervals, for which we count the number of AS in each interval. Averages of the different sequences corresponding to all MS in the same energy range are performed, normalizing each interval by the number of sequences that reached such a time distance. The results compiled in Fig. 5a, b show the tendency to follow Omori’s law in Vycor, in some cases for up to 6 decades, compared with Sornette and Ouillon (2005). Foreshocks, obtained in an analogous way, show a similar behaviour, with a slightly smaller value of p.

Fig. 5
figure 5

a Distribution of waiting times for different values of Emin and the compression rate R. b The same data under rescaling, including also the results of the ETAS model and earthquakes from Southern-California (Bak et al. 2002; Corral 2004) for the period Jan 1984–Jun 2011. The similarity of the scaling over some 10 decades demonstrates the close similarity of aftershock time scales between AE events and Earth Quakes. (Baró et al. 2013)

Full size image

One of the most intricate examples of collapsing holes, which mix with sliding dislocations, is described in Ho-doped Mg metal. The microstructure is shown in Fig. 6.

Fig. 6
figure 6

TEM figure shows Ho granule with surrounding dislocations (a) and dislocations in Mg matrix (b) in the sample after compression. (Chen et al. 2019)

Full size image

The AE spectrum is dominated by a separation of signals which correspond to the hole collapse and sliding dislocations. Their respective fingerprints are very different and relate to their individual signal strengths. Porous collapse generates very strong AE signals while dislocation movements create more but weaker signals. This allows a separation of the two processes even though they almost always coincide temporarily. The porous collapse follows approximately the predictions of mean-field behaviour of short, independent avalanches (ε = 1.4, τ’ = 1.82, α = 2.56, x = 1.93, χ = 1.95) (mean field scaling) (Salje and Dahmen 2014). The resulting microstructure is highly fractal. The exponents for dislocation movement are greater (ε = 1.92, τ’ = 2.44, α = 3.0, x = 1.7, χ = 1.42). Here another theory is approximately correct (the so-called force integrated mean-field predictions) where the progression of avalanches involves full structural relaxations of the mineral between individual avalanches (Salje and Dahmen 2014). The Omori scaling is similar for both mechanisms. This study by (Chen et al. 2019) represents the most advanced study of a real-life, complex microstructural change in any material (here an alloy, the same is envisaged for minerals) with more than 2 million AE events experimentally observed.

Moving twin boundaries

The observation that many minerals are twinned is as old as mineralogy itself. So why became the investigation of twins, or more precisely of boundaries between twins, so popular during the past decade? There are two aspects to clarify. First, we know almost nothing about the detailed structure of boundaries between growth twins and research in this field has hardly started. Boundaries between ferroelastic twins, on the other hand, are much better understood (Janovec et al. 1994; George et al. 2003; Salje and Ding 2016; Schiaffino and Stengel 2017; Casals et al. 2018; Royo and Stengel 2019; Warwick et al. 2019; Zhao and Iniguez 2019) and virtually all previous work relates to ferroelastic materials (Salje 2012). The main result of ferroelastic twin walls is that two twins do not just join in the boundary without topological defects but that they generate a thin layer of materials which has a different crystal structure from the bulk material. In a first approach Landau, see, e.g. a text book (Salje 1993), assumed that the local structure in the boundary is simply the high symmetry, para-elastic structure. Starting from this assumption, the profile of a twin boundary can be derived from reasonable potentials as follows:

$${\text{Q = Q}}_{{0}} {\text{ tanh }}\left( {{{\text{x}} \mathord{\left/ {\vphantom {{\text{x}} {\text{W}}}} \right. \kern-\nulldelimiterspace} {\text{W}}}} \right),$$

where Q is the ferroelastic order parameter (proportional to the shear strain, i.e. the twin angle, in our case), Q0 is its bulk value and the tanh-functions describe the profile of the boundary. When the space coordinate x becomes zero in the middle of the boundary, the order parameter becomes zero and describes hence the paraelastic phase. Researchers argued since the 1990s that this restriction to one-order parameter is insufficient and that domain walls are much more complex (Conti et al. 2011; Houchmandzadeh et al. 1991, 1992a, b) involving the cooperation of several state parameters. This approach of order parameter coupling was first considered heretical but was then confirmed by more detailed first-principle approaches and MD simulations using simplified potentials (Salje et al. 2016b). The prediction of all these approaches was that new (~ ‘emerging’) properties exist in the domain walls which cannot be seen anywhere else in the structure (Morozovska et al. 2007, 2020a, b; Viehland and Salje 2014; Biancoli et al. 2015; Dziaugys et al. 2020). The first experimental confirmation was achieved by (Van Aert et al. 2012; Gonnissen et al. 2016) together with observation of polarity and enhanced conductivity of domain walls. This development has progressed to the point that domain walls are now perceived as the loci of the active devices while the bulk is there to hold the device in place. This perception is somewhat oversimplified, however. The domain walls can move under external forcing in the bulk so that we have now the unique opportunity to have a thin layer of a device, which can be shifted and positioned in a matrix. The full implications of this discovery are still not fully understood but it has certainly triggered a major research effort in domain boundary engineering (Salje 2010, 2020).

Much progress is expected from research on mineral structures over the coming years, not only in the discovery of novel twin boundaries based on growth phenomena, but also in the exploration of boundary mobilities. Mineral physics follows metallurgy where such studies are more advanced. Martensites and many alloys were investigated using AE spectroscopy to identify how twin boundaries move (Salje et al. 2011a). The result of these studies is that the movements are a mix of avalanches and smooth behaviour. A first breakthrough was the quantitative observation of the dynamics of domain switching. After observations of jerk-like switching, similar to Barkhausen noise (Shur et al. 2002) and the measurement of jerky propagation of needle domains under stress in ferroelastics (Harrison and Salje 2010) and the investigation of acoustic noise in martensites (Salje et al. 2011a), a full set of dynamical switching parameters in BaTiO3 and some other ferroelectric materials were measured (Salje et al. 2019; Xu et al. 2020). In most studies, the switching currents constituted a first indicator for avalanche switching dynamics (Casals et al. 2020; Tan et al. 2019). The time resolution of more detailed investigations was greatly improved by using the acoustic emission (AE) technique to measure the switching energy, amplitude, time sequence, aftershock probability and correlations (Salje et al. 2019). The results of these experiments show that switching proceeds by avalanches of correlated domain wall movements. Several full sets of avalanche parameters were determined (Salje and Dahmen 2014; Salje et al. 2019). In addition, much milder, smoother domain propagation (Zhang et al. 2020) coexists. This schism is captured by the notion that we observe ‘wild’ and ‘mild’ processes where wild means that spiky energy emission, so-called ‘jerks’, dominate the domain wall movements (Weiss et al. 2015, 2019; Yang et al. 2020; Salje 2020, 2021).

The mild movements still constitute avalanches in the description of (Salje and Dahmen 2014). Coexistence of mild and wild movements is well known for restructuring processes in many materials under external forcing, like ice (Weiss 2019), martensites (Chen et al. 2019), dislocation (Pan et al. 2019) and in crack propagation (Bonamy et al. 2008; Laurson et al. 2010). Mild processes are much more difficult to observe than spiky jerks (Casals et al. 2019) where the optical observation of domain wall movements proved particularly useful (Casals et al. 2020). Mild movements produce very little strain although they are potentially visible in AE at very low noise level. A second development relates to the current in domain walls and associated chemical changes. Ever since the discovery of superconductivity in domain walls (Aird and Salje 1998) and subsequent studies of highly conducting walls (Seidel et al. 2010), the concept of domain wall electronics was developed rapidly and was reviewed by Catalan et al. (2012) and Evans et al. (2020).

An important step forward was the idea that domain wall transport includes chemical changes during electronic conduction. This impacts on the origin of memristor properties of ferroelastic domain walls (Bibes and Barthelemy 2008; Garcia et al. 2009). In fact, networks of ferroelectric domains have similar properties as arrays of memristors (Chanthbouala et al. 2012). A typical nanostructure is a needle domain approaching a perpendicular wall, leading to the formation of a junction between domain walls or tweed microstructures (Salje and Parlinski 1991; Hayward et al. 1998a, b; Hayward and Salje 1999; Salje and Ding 2016). If the walls are superconducting, the connection between the two walls’ orientations constitutes a Josephson junction. An additional effect is that the current provokes chemical changes in the walls or in the needle domain itself. Such modifications may lead to a percolation criticality when the needle touches an orthogonal wall, an interface or the surface of the sample (Novak et al. 2002; Zhao et al. 2019).

As an example, we now consider a perovskite structure, BaTiO3, which is not only ferroelastic but also ferroelectric. The relevant domain boundaries are twin walls. They can be shifted by electric fields and by external stress. In this example we use the electric field as driving field. The experiment takes typically one night to increase and decrease the field six times (blue line in Fig. 7). The moving twin walls progress in avalanches and emit AE signals. The AE spectrum is seen in Fig. 7.

Fig. 7
figure 7

Jerk spectrum of acoustic noise of BaTiO3 during domain switching (red signals). The noise is measured as time evolution of the energy of AE signals. The electric field (blue line) is ramped between − 1000 and 1000 V with a rate of 0.5 V/s (right axis). In total six loops (from 1000 to − 1000 V back to 1000 V) were measured. The scale for the jerk energy (in attojoule) is logarithmic and stretches over five decades (Salje et al. 2019)

Full size image

The energy of the jerks that constitute the avalanche is power law distributed with an overall exponent ε = 1.65 (Fig. 8). All other avalanche parameters have been evaluated by Salje et al. (2019) and were confirmed by optical microscopy by Casals et al. (2021a).

Fig. 8
figure 8

The probability distribution function (binned data, top panel) shows a power-law distribution. The maximum likelihood graph (bottom panel) is used to determine the energy exponent. The energy exponent is 1.65 as average over all loops (Salje et al. 2019)

Full size image

Bio-mineralisation

To discuss avalanches in bio-minerals we choose microbially induced calcite precipitation (MICP), which is a common process in bio-geotechnical engineering. Laboratory tests have demonstrated that MICP treatment of granular soils improves their strength by three orders of magnitude (DeJong et al. 2006, 2010, 2014; Whiffin et al. 2007; Al Qabany and Soga 2013; Chu et al. 2013) and increases the small-strain stiffness (Montoya and DeJong 2015; Feng and Montoya 2016). Current in-situ applications of MICP treatment include large-scale ground improvements (DeJong et al. 2014; Gomez et al. 2017; Nassar et al. 2018) and the protection and consolidation of heritage buildings and sculptures (Jroundi et al. 2017). The treatment time (few hours–several days) and the spatial distribution are controlled according to engineering requirements by adjusting the metabolic activity of the bacteria (Chekroun et al. 2004; DeJong et al. 2010; Achal et al. 2015). The resulting cemented soil exhibits significant improvement of strength and stiffness, which is hard to produce by other means (Terzis and Laloui 2018).

In order to test the MICP material, uniaxial compression was applied to calcareous sand grains, sands without cementation and bio-cemented sand samples treated by MICP. The sand composition was mainly aragonite and Mg-bearing calcite, the carbonate component was above 97%. The microstructure is characterized by accumulated insoluble MICP calcite bridging sand grains. The SEM image of a bio-cemented sand sample shows that sand particles are bridged by microbial induced calcite (Xiao et al. 2018, 2019). Uniaxial compression force was applied with a rate of 0.1 mm/min.

Stress–strain relationships and AE spectra for calcareous sand grains and a bio-cemented sand sample are shown in Fig. 9. The compressive strength of sands is very weak and cannot be detected by conventional loading systems. The AE parameters such as energies E, amplitudes A and waiting time δ were extracted from the AE spectra. The strain–stress curve of sand grains is almost stationary besides the initial incubation time in the elastic compression regime. This is not the case for the bio-cemented sand sample where we see no incubation time. Instead, we observe silent intervals with no AE activity (Fig. 9b) during the course of the compression experiment. The inserts in Fig. 9a, b show the samples after testing.

Fig. 9
figure 9

a, b compression stress–strain curve and AE energy spectrum for grain and bio-cemented sand sample; the inserts show the sample after failure; and c AE energy spectrum of sand. Note the yield behaviour in a while crack propagation in b is interrupted by ‘silent’ episodes (Wang et al. 2021)

Full size image

The probability distribution function (PDF) of avalanche energies is shown in Fig. 10a. It follows a power law P(E) ~ E−ε. Figure 10a shows the distribution of AE energy from grains, bio-cemented sand samples and sands with ε-exponents of 1.37, 1.46 and 1.7, respectively. To investigate the exponents in more detail, we use the maximum likelihood method (Fig. 10b) [see Salje et al. (2017c) for detail]. The horizontal dashed lines indicate the PDF slopes and hence the exponents. The ML curves of bio-cemented sand samples show increases with increasing Emin indicating that the AE signals are damped by absorption or scattering of the acoustic signals (Salje et al. 2017c).

Fig. 10
figure 10

a Distribution of AE energies, b shows the ML-fitted exponent as a function of a lower threshold Emin for the three experiments during the full experiment. c ML-fitted exponent in different time windows (Wang et al. 2021)

Full size image

Grains show excellent plateaus with ε = 1.4 remarkably close to the theoretical MF result 4/3. The energy exponent for sands is 1.7, which is near another MF prediction value of 5/3. MICP ceramics show an overall energy exponent 1.46. The most important observation is that in MICP ceramics, but not in sand or gains, different time windows show variable values (Fig. 10c) between 1.35 and 1.6. These avalanches are a combination of the AE energies of sands and grains with variable proportions. This observation allows us to conclude that the collapse mechanism is the breaking of the bio-mineralized bridges between the hard grains. This process starts at very low stress and is not visible by the macroscopic shape change. Compression leads to a ‘rubble’ of grains mixed with larger bio-mineralized segments. The grains are constrained by neighbours, which hinders their rotations. This makes the materials harder for compression than sand. Once the sample is compressed further it transforms back to sand with a dusting of MICP particles.

Conclusion

Changes of microstructures often progress in a wild, non-smooth manner. Experimental evidence rules out simple catastrophic events, like one big step when a twin wall moves. Instead, we find universal behaviour with multitudes of small ‘jerks’ which can cut down the big step into millions of small steps. This phenomenon appears in many systems, and only three of them were briefly reviewed here. The overall behaviour of the totality of the jerks follows very strict rules. These rules are the same as what is theoretically expected for avalanches, which establishes a close link between avalanches and microstructural evolution. As the probability to find a ‘jerk’ with an energy E follows a power law with well-defined exponents, which appear to be universal for many systems. The power law is important because it is ‘scale invariant’. To illustrate the scale invariance, let us consider the energy probability P(E) = E−ε. Consider an energy interval between E and 2E; then the probabilities are between E−ε and (2E)−ε. We now scale the energy by a factor x. The interval is now from xE to 2xE and the probabilities change to (x E)−ε and 2−ε (x E)−ε. The common numerical prefactor x−ε is irrelevant for the functional form, which remains exactly the same as before. This proves that the power-law distributions are scale invariant. Note that this is a special property of the power law and that other functions are not scale invariant. Furthermore, combinations of power laws are not power laws and hence not scale invariant.

The scale invariance in avalanches is not restricted to energies but holds equally for the amplitudes, durations and, with some modification, for waiting times. In practical terms, anything we see in a space (or time) interval is exactly the same as in any other. The limits are given by cut-offs, such as the atomic diameter or the sample size, but the region between these cut-offs can reach many orders of magnitude. AE allows us to estimate this range and we find that 6–8 orders of magnitude of energy are not uncommon for microstructural changes. The question on which length scale do structural changes happen is hence ill-posed: there is a large interval of length scales and wherever we situate our experiment we will see the same change.

This powerful approach is important for minerals where defects and lattice imperfections favour avalanches. The induced behaviour is then independent of these obstacles and significant similarities are found in a multitude of different minerals. For reasons alluded to in the introduction, the full power of this method has been used to solve several problems in solid-state physics and metallurgy, but much less in mineral physics. There is a wide range of mineralogical research waiting to be done in future.