Heat–Viscoelastic Plate Interaction via Bending Moment and Shear Forces Operators: Analyticity, Spectral Analysis, Exponential Decay

Abstract

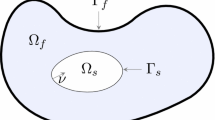
We consider a heat–plate interaction model where the 2-dimensional plate is subject to viscoelastic (strong) damping. Coupling occurs at the interface between the two media, where each component evolves through differential operators. In this paper, we apply “high” boundary interface conditions, which involve the two classical boundary operators of a physical plate: the bending moment operator $B_1$ and the shear forces operator $B_2$. We prove three main results: analyticity of the corresponding contraction semigroup on the natural energy space; sharp location of the spectrum of its generator, which does not have compact resolvent, and has the point $\lambda =-\,1$ in its continuous spectrum; exponential decay of the semigroup with sharp decay rate. Here analyticity cannot follow by perturbation.

Appendices

Appendix A: The Adjoint Operator ${\mathcal {A}^*}$

Step 1 Here we establish Theorem 2.1 by identifying the adjoint operator ${\mathcal {A}}^*$. Let $[v_1,v_2,h]\in {\mathcal {D}}({\mathcal {A}})$ described in (2.6)–(2.9), and let $[\widehat{v}_1,\widehat{v}_2,\widehat{h}]\in {\mathcal {D}}({\mathcal {A}}^*)$ described in (2.14) and (2.17). Recalling ${\mathcal {A}}$ in (2.6) and the topology of $\mathbf{H}$ in (2.4), we compute

$$\begin{aligned}&\left( {\mathcal {A}}\begin{bmatrix} v_1\\v_2\\h\end{bmatrix},\begin{bmatrix} \widehat{v}_1\\ \widehat{v}_2\\ \widehat{h} \end{bmatrix}\right) _{\mathbf{H}} = \left( \begin{bmatrix} 0&I&0\\De^2-I&-\Delta ^2&0\\ 0&0&\Delta \end{bmatrix}\begin{bmatrix} v_1\\v_2\\h\end{bmatrix},\begin{bmatrix} \widehat{v}_1\\ \widehat{v}_2 \\ \widehat{h}\end{bmatrix}\right) _{\mathbf{H}} \nonumber \\&\quad = \left( \begin{bmatrix} v_2\\ -\Delta ^2(v_1+v_2) - v_1\\ \Delta h\end{bmatrix},\begin{bmatrix} \widehat{v}_1\\ \widehat{v}_2\\ \widehat{h}\end{bmatrix} \right) _{\mathbf{H}} \end{aligned}$$

(A.1)

$$\begin{aligned}&=(\Delta v_2,\Delta \widehat{v}_1) + (v_2,\widehat{v}_1) - (\Delta ^2(v_1+v_2),\widehat{v}_2) - (v_1,\widehat{v}_2) +(\Delta h,\widehat{h}) \end{aligned}$$

(A.2)

$$\begin{aligned}&=(\Delta v_2,\Delta \widehat{v}_1) + (v_2,\widehat{v}_1) -(\Delta (v_1+v_2),\Delta \widehat{v}_2)-\left( \frac{\partial \Delta (v_1+v_2)}{\partial \nu },\widehat{v}_2\right) _{\Gamma _{s}}\nonumber \\&\qquad +\left( \Delta (v_1+v_2),\frac{\partial \widehat{v}_2}{\partial \nu }\right) _{\Gamma _{s}} \nonumber \\&\qquad - (v_1,\widehat{v}_2) +(h,\Delta \widehat{h})-\left( \frac{\partial h}{\partial \nu },\widehat{h}\right) _{\Gamma _{s}}+\left( h,\frac{\partial \widehat{h}}{\partial \nu }\right) _{\Gamma _{s}}. \end{aligned}$$

(A.3)

In going from (A.2) to (A.3), we have used Green’s second theorem for the third and fifth terms in (A.2), along with $h|_{\Gamma _{f}}=0$ by (2.8) and $\widehat{h}|_{\Gamma _{f}}=0$ by (2.17). We next recall $\displaystyle \Delta (v_1+v_2)=-(1-\mu )B_1v_2$ on $\Gamma _{s}$ by (2.9b) along with $\frac{\partial \Delta (v_1+v_2)}{\partial \nu }=-(1-\mu )B_2v_2 + v_2 - \frac{\partial h}{\partial \nu }$ on $\Gamma _{s}$ by (2.9c). We re-write (A.3) as

$$\begin{aligned}&\hbox {RHS of }(A.3)= (\Delta v_2,\Delta (\widehat{v}_1-\widehat{v}_2))-(\Delta v_1,\Delta \widehat{v}_2) - (v_1,\widehat{v}_2) + (v_2,\widehat{v}_1) \nonumber \\&\qquad +\,(1-\mu )\left( B_2v_2,\widehat{v}_2)\right) _{\Gamma _{s}} - (v_2,\widehat{v}_2)_{\Gamma _{s}} +\left( \frac{\partial h}{\partial \nu },\widehat{v}_2\right) _{\Gamma _{s}} \nonumber \\&\qquad -\,(1-\mu )\left( B_1v_2,\frac{\partial \widehat{v}_2}{\partial \nu })\right) _{\Gamma _{s}} + (h,\Delta \widehat{h}) - \left( \frac{\partial h}{\partial \nu },\widehat{h}\right) _{\Gamma _{s}} + \left( h, \frac{\partial \widehat{h}}{\partial \nu }\right) _{\Gamma _{s}}. \qquad \quad \end{aligned}$$

(A.4)

Step 2 Applying now Green’s second theorem to the first term in (A.4), we obtain as $v_2 = h$ on $\Gamma _{s}$ by (2.8):

(A.5)

where the cancellation occurs since $\widehat{h}=\widehat{v}_2$ on $\Gamma _{s}$ by (2.17). Next, we recall by (2.16b) and (2.16c) that

$$\begin{aligned} \Delta (\widehat{v}_1 - \widehat{v}_2) = (1-\mu ) B_1 \widehat{v}_2 \ \hbox { on } \ \Gamma _{s}\quad \hbox { and } \quad \frac{\partial \Delta (\widehat{v}_1 - \widehat{v}_2) }{\partial \nu } + \widehat{v}_2 - \frac{\partial \widehat{h}}{\partial \nu } = (1-\mu ) B_2 \widehat{v}_2 \ \hbox { on } \Gamma _{s}. \end{aligned}$$

(A.6)

We obtain recalling the topology (2.4):

$$\begin{aligned} \begin{aligned} \hbox {RHS of }(\mathrm{A.3}) =&\left( \begin{bmatrix} v_1\\v_2\\h \end{bmatrix}, \begin{bmatrix} -\widehat{v}_2\\ \Delta ^2(\widehat{v}_1 - \widehat{v}_2) + \widehat{v}_1 \\ \Delta \widehat{h}\end{bmatrix}\right) \\&- (1-\mu )\left[ \left( B_1v_2,\frac{\partial \widehat{v}_2}{\partial \nu })\right) _{\Gamma _{s}} - (B_2 v_2, \widehat{v}_2)_{\Gamma _{s}} \right] \\&+ (1-\mu )\left[ \left( \frac{\partial v_2}{\partial \nu },B_1\widehat{v}_2)\right) _{\Gamma _{s}} - (v_2, B_2 \widehat{v}_2)_{\Gamma _{s}} \right] . \end{aligned} \end{aligned}$$

(A.7)

Step 3 We now invoke the following fundamental result.

Lemma A.1

[28, Corollary 3C.3, p. 301] Let $f, g \in H^2(\Omega _{s})$. Then

$$\begin{aligned} \int _{\Gamma _{s}} \left[ (B_1 f) \frac{\partial g}{\partial \nu } - (B_2 f) g \right] \,d\Gamma _{s}&= \int _{\Gamma _{s}} \left[ (B_1 g) \frac{\partial f}{\partial \nu } - (B_2 g) f \right] \,d\Gamma _{s}\nonumber \\&= \int _{\Omega _{s}} \big [ 2(f_{xy} g_{xy} - f_{xx} g_{yy} - f_{yy} g_{xx} \big ]\,d\Omega _{s} \end{aligned}$$

(A.8)

Applying the above Lemma with $f=v_2, g = \widehat{v}_2 \in H^2(\Omega _{s})$, we obtain

$$\begin{aligned} \left( B_1 v_2,\frac{\partial \widehat{v}_2}{\partial \nu })\right) _{\Gamma _{s}} - (B_2 v_2, \widehat{v}_2)_{\Gamma _{s}} = \left( B_1 \widehat{v}_2,\frac{\partial v_2}{\partial \nu })\right) _{\Gamma _{s}} - (B_2 \widehat{v}_2, v_2)_{\Gamma _{s}}. \end{aligned}$$

(A.9)

Thus (A.9) used in (A.7) produces a cancellation of the boundary terms and yields

$$\begin{aligned}&\left( {\mathcal {A}}\begin{bmatrix} v_1\\v_2\\h \end{bmatrix}, \begin{bmatrix} \widehat{v}_1\\ \widehat{v}_2\\ \widehat{h}\end{bmatrix}\right) _{\mathbf{H}} = (\Delta v_1,\Delta (-\widehat{v}_2))+(v_1,(-\widehat{v}_2))+\left( v_2,\Delta ^2(\widehat{v}_1-\widehat{v}_2)\right) +(v_2,\widehat{v}_1)\nonumber \\&\qquad +(h,\Delta \widehat{h})\nonumber \\&\quad = \left( \begin{bmatrix} v_1\\ v_2\\h \end{bmatrix},\begin{bmatrix} -\widehat{v}_2 \\ \Delta ^2(\widehat{v}_1-\widehat{v}_2) + \widehat{v}_1 \\ \Delta \widehat{h}\end{bmatrix}\right) _{\mathbf{H}} = \left( \begin{bmatrix} v_1\\ v_2\\h\end{bmatrix}, \begin{bmatrix} 0&-I&0\\ \Delta ^2+I&-\Delta ^2&0\\ 0&0&\Delta \end{bmatrix} \begin{bmatrix} \widehat{v}_1\\ \widehat{v}_2\\ \widehat{h}\end{bmatrix}\right) _{\mathbf{H}}\nonumber \\ \end{aligned}$$

(A.10)

for $[v_1,v_2,h]\in {\mathcal {D}}({\mathcal {A}})$ in (2.6)–(2.9) and $[\widehat{v}_1,\widehat{v}_2,\widehat{h}]\in {\mathcal {D}}({\mathcal {A}}^*)$ in (2.14) and (2.17). Theorem 2.1 is proved.

Appendix B: Proof of Theorem 2.5 for Problem (2.34)

(i) (Compare with Sect. 3.1) The proof is based on the following alternative Green formula [28, Proposition C.12, p. 310], which introduces the positive bilinear form $a(\cdot ,\cdot )$ in the first place.

$$\begin{aligned} (\Delta ^2 f,g)_{\Omega _{s}}= & {} a(f,g) + \int _{\Omega _{s}}\left[ \frac{\partial \Delta f}{\partial \nu } + (1-\mu ) B_2 f\right] g\, d\Omega _{s}\nonumber \\&- \int _{\Gamma _{s}}\left[ \Delta f + (1-\mu ) B_1 f\right] \frac{\partial g}{\partial \nu } \, d\Gamma _{s}\end{aligned}$$

(B.1)

with a(f, g) defined in (2.35). Next, for $[v_1,v_2,h] \in {\mathcal {D}}(\widetilde{{\mathcal {A}}})$, we compute via (2.36) and (2.37) and the Green formula (B.1):

$$\begin{aligned} \left( \widetilde{{\mathcal {A}}} \begin{bmatrix} v_1\\v_2\\h \end{bmatrix}, \begin{bmatrix} v_1\\v_2\\h \end{bmatrix} \right) _{\widetilde{\mathbf{H}}}&= \left( \begin{bmatrix} v_2\\ - \Delta ^2(v_1+v_2)\\ \Delta h \end{bmatrix}, \begin{bmatrix} v_1\\v_2\\h \end{bmatrix} \right) _{\widetilde{\mathbf{H}}} \end{aligned}$$

(B.2)

$$\begin{aligned}&= a(v_2,v_1) - (\Delta ^2(v_1 + v_2),v_2) + (\Delta h, h) \end{aligned}$$

(B.3)

$$\begin{aligned} \hbox {(by }(\mathrm{B.1})) \qquad&= a(v_2,v_1) - a(v_1+v_2,v_2) \nonumber \\&\qquad - \left( \dfrac{\partial \Delta (v_1 + v_2)}{\partial \nu } + (1-\mu )B_2 (v_1 + v_2), v_2 \right) _{\Gamma _{s}} \nonumber \\&\qquad + \left( \Delta (v_1 + v_2) + (1-\mu )B_1 (v_1 + v_2), \dfrac{\partial v_2}{\partial \nu } \right) _{\Gamma _{s}} \nonumber \\&\qquad - \left( \dfrac{\partial h}{\partial \nu }, h \right) _{\Gamma _{s}} - \Vert \nabla h\Vert ^2 \end{aligned}$$

(B.4)

since $h|_{\Gamma _{f}} = 0$ in $\widetilde{{\mathcal {A}}}$, see (2.34e). Next, the B.C. of $\widetilde{{\mathcal {A}}}$ include also (see (2.34c), (2.34d))

$$\begin{aligned} \Delta (v_1 + v_2) + (1-\mu )B_1 (v_1 + v_2)&= -\dfrac{\partial v_2}{\partial \nu } \quad \hbox {on } \Gamma _{s} \end{aligned}$$

(B.5)

$$\begin{aligned} \dfrac{\partial \Delta (v_1 + v_2)}{\partial \nu } + (1-\mu )B_2 (v_1 + v_2)&= v_2 - \dfrac{\partial h}{\partial \nu } \quad \hbox {on } \Gamma _{s} \end{aligned}$$

(B.6)

The (B.4) becomes via (B.5), (B.6), as well as $a(v_1+v_2, v_2) = a(v_1, v_2) + a(v_2, v_2)$:

(B.7)

(B.8)

recalling $h = v_2$ on $\Gamma _{s}$ by (2.34e). Since $\hbox {Re}\{a(v_2,v_1) - a(v_1,v_2)\}=0$, then (B.8) yields

$$\begin{aligned} \hbox {Re}\left( \widetilde{{\mathcal {A}}} \begin{bmatrix} v_1\\v_2\\h \end{bmatrix}, \begin{bmatrix} v_1\\v_2\\h \end{bmatrix} \right) _{\widetilde{\mathbf{H}}}= & {} -a(v_2,v_2) - \Vert \nabla h\Vert ^2 - \Vert v_2\Vert _{\Gamma _{s}}^2 \nonumber \\&- \left\| \dfrac{\partial v_2}{\partial \nu } \right\| ^2_{\Gamma _{s}} \le 0, \quad [v_1,v_2,h] \in {\mathcal {D}}(\widetilde{{\mathcal {A}}}) \end{aligned}$$

(B.9)

and Part (i) of Theorem 2.5 is established.

(ii) Let $x^*=[v_1^*,v_2^*,h^*]\in \widetilde{\mathbf{H}}$, we seek to solve $\tilde{{\mathcal {A}}}x=x^*$ for $x=[v_1,v_2,h]\in {\mathcal {D}}(\tilde{{\mathcal {A}}})$, with bounded inverse. From (2.37) we have as in (3.14)

$$\begin{aligned} \tilde{{\mathcal {A}}}\begin{bmatrix} v_1\\v_2\\h\end{bmatrix}=\begin{bmatrix} v_2\\ -\Delta ^2(v_1+v_2)\\ \Delta h\end{bmatrix}=\begin{bmatrix} v_1^*\\v_2^*\\ h^*\end{bmatrix},\quad v_2=v_1^*\in H^2(\Omega _{s}) \end{aligned}$$

(B.10)

We have

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta h=h^*\in L_2(\Omega _f)\\ h|_{\Gamma _{f}}=0,\ h|_{\Gamma _{s}}=v_2|_{\Gamma _{s}}=v_1^*|_{\Gamma _{s}}\in H^{3/2}(\Gamma _{s}) \end{array}\right. },\quad h=A_D^{-1} h^*+\widetilde{D_f}\Big (v_1^*|_{\Gamma _{s}}\Big )\in H^2(\Omega _{f}).\nonumber \\ \end{aligned}$$

(B.11)

The novelty is that now the equation of (B.10) has different B.C., as in (2.38a)-(2.38b), so that now

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta ^2(v_1+v_1^*)=-v_2^*\in L_2(\Omega _s)\\ \Big [\Delta (v_1+v_1^*)+(1-\mu )B_1(v_1+v_1^*)\Big ]=-\dfrac{\partial v_1^*}{\partial \mu }\in H^{1/2}(\Gamma _{s})\\ \Big [\dfrac{\partial \Delta (v_1+v_1^*)}{\partial \nu }+(1-\mu )B_2(v_1+v_1^*)\Big ]_{\Gamma _{s}}=\Big [v_1^*-\dfrac{\partial h}{\partial \nu }\Big ]_{\Gamma _{s}}\in H^{1/2}(\Gamma _{s}). \end{array}\right. } \end{aligned}$$

(B.12)

Then recalling the operator $\mathbb {A}$ in (2.11) and the Green maps $G_1$ and $G_2$ from (2.13), we obtain via (B.12)

$$\begin{aligned} v_1+v_1^*=-\mathbb {A}^{-1}v_2^*-G_1\Big (\frac{\partial v_1^*}{\partial \nu }\Big |_{\Gamma _{s}}\Big )-G_2\Big [v_1^*-\frac{\partial h}{\partial \nu }\Big ]_{\Gamma _{s}} \in H^3(\Omega _{s}). \end{aligned}$$

(B.13)

So that, ultimately $v_2\in H^2(\Omega _{s})$, as required, recalling the regularity properties of $G_1$, $G_2$ in (2.13), so that $\displaystyle G_2\Big ([v_1^*-\dfrac{\partial h}{\partial \nu }\Big ]_{\Gamma _{s}}\in H^{1/2+7/2}(\Omega _{s})=H^4(\Omega _{s})$, and $G_1\Big (\frac{\partial v^*}{\partial \nu }\Big |_{\Gamma _{s}}\Big )\in H^{1/2+5/2}(\Omega _{s})=H^3(\Omega _{s})$. In (B.13), $\dfrac{\partial h}{\partial \nu }|_{\Gamma _{s}}$ is explicitly obtained from (B.11) in terms of the data $\{v_1^*,h^*\}$. Then (B.10), (B.11), (B.13) allow one to obtain an explicit formula of ${\mathcal {A}}^{-1}$.

Appendix C: Explicit Expression of ${\mathcal {A}}^{-1}$

We now establish directly that, in fact, $0\in \rho ({\mathcal {A}})$, the resolvent set of ${\mathcal {A}}$ and in fact obtain the explicit expression for ${\mathcal {A}}^{-1}$, as a bounded operator on ${\mathcal {L}}(\mathbf{H})$. Let $[v_1^*,v_2^*,h^*]\in \mathbf{H}$, we seek to solve ${\mathcal {A}}[v_1,v_2,h]=[v_1^*,v_2^*,h^*]$, or via (2.6),

The third equation yields the following elliptic problem in $\Omega _{f}$:

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta h=h^*\in L_2(\Omega _f)\\ h|_{\Gamma _{f}}=0,\ \ h|_{\Gamma _{s}}=v_2|_{\Gamma _{s}}=v_1^*|_{\Gamma _{s}}\in H^{3/2}(\Gamma _{s}) \end{array}\right. };\ \ \ h=A^{-1}_D h^*+\widetilde{D}_fv_1^*\in H^2(\Omega _{f}),\nonumber \\ \end{aligned}$$

(C.2)

where $A_Df=\Delta f$, ${\mathcal {D}}(A_D)=H^2(\Omega _{f})\cap H^1_0(\Omega _{f})$ while $\widetilde{D}_f$ in the following Dirichlet map in $\Omega _{f}$

$$\begin{aligned}&\widetilde{D}_f:\ \ \ \widetilde{D}_fg=\psi \Leftrightarrow \{ \Delta \psi =0\ \hbox {in}\ \Omega _{f}, \psi =g\ \hbox {on}\ \Gamma _{s},\nonumber \\&\quad \psi =0\ \hbox {on}\ \Gamma _{f}\};\ \ \widetilde{D}_f: \ H^r(\Gamma _{s})\rightarrow H^{r+1/2}(\Omega _{f}) \end{aligned}$$

(C.3)

Eqt (C.1b), along with $v_2=v_1^*$ in (C.1a) and the B.C. in (2.9a)–(2.9c) yield

With $v_1^*\in H^2(\Omega _{s})$ and $\dfrac{\partial h}{\partial \nu }\Big |_{\Gamma _{s}}\in H^{1/2}(\Gamma _{s})$ by (C.2), we have

$$\begin{aligned}&v_1^*|_{\Gamma _{s}}\in H^{3/2}(\Omega _{s});\ \dfrac{\partial ^2 v_1^*}{\partial \tau ^2}\Big |_{\Gamma _{s}}\in H^{-1/2}(\Gamma _{s});\ \dfrac{\partial v_1^* }{\partial \nu }\Big |_{\Gamma _{s}}\nonumber \\&\quad \in H^{1/2}(\Gamma _{s});\ \frac{\partial ^2}{\partial \tau ^2}\frac{\partial v_1^*}{\partial \nu }\Big |_{\Gamma _{s}}\in H^{-3/2}(\Gamma _{s}) \end{aligned}$$

(C.5)

and hence recalling (2.2a) and (2.2b), in (C.4b), (C.4c):

$$\begin{aligned} g_1= & {} -(1-\mu )B_1(v_1^*)=-(1-\mu )\Big \{-\dfrac{\partial ^2 v_1^*}{\partial \tau ^2}-c(\eta )\dfrac{\partial v_1^*}{\partial \nu }\Big \}_{\Gamma _{s}}\in H^{-1/2}(\Gamma _{s})\qquad \end{aligned}$$

(C.6)

$$\begin{aligned} g_2= & {} \Big [-(1-\mu )B_2(v_1^*)+v_1^*-\dfrac{\partial h}{\partial \nu }\Big ]_{\Gamma _{s}}\nonumber \\= & {} -(1-\mu )\Big \{\dfrac{\partial ^2}{\partial \tau ^2}\dfrac{\partial v_1^*}{\partial \nu }-\frac{\partial (div \nu )}{\partial \tau }\dfrac{\partial v_1^*}{\partial \tau }\Big \}_{\Gamma _{s}}\in H^{-3/2}(\Gamma _{s}) \end{aligned}$$

(C.7)

We rewrite problem (C.4) as

The operator

$$\begin{aligned} Q\psi =\Delta ^2\psi +\psi ,\ \ {\mathcal {D}}(Q)=\left\{ \psi \in H^4(\Omega _{s}):\ \Delta \psi |_{\Gamma _{s}}=\dfrac{\partial \Delta \psi }{\partial \nu }\Big |_{\Gamma _{s}}=0\right\} \end{aligned}$$

(C.9)

is non-negative self-adjoint, via Green’s second Theorem

$$\begin{aligned}&(Q\psi ,\tilde{\psi })=(\Delta ^2\psi ,\tilde{\psi })+(\psi ,\tilde{\psi })=(\psi ,\Delta ^2\tilde{\psi })+(\psi ,\tilde{\psi }),\ \ \ \psi ,\tilde{\psi }\in {\mathcal {D}}(Q)\qquad \quad \end{aligned}$$

(C.10)

$$\begin{aligned}&(Q\psi ,\psi )=\Vert \Delta \psi \Vert ^2+\Vert \psi \Vert ^2\ge 0,\ \ \ \psi \in {\mathcal {D}}(Q) \end{aligned}$$

(C.11)

so that $Q\psi =0$ implies $\psi \equiv 0$. The unique solution of problem (C.8) is

$$\begin{aligned}&\phi =v_1+v_1^*=Q^{-1}f+G_1g_1+G_2g_2\in H^2(\Omega _{s}) \end{aligned}$$

(C.12)

$$\begin{aligned}&Q^{-1}f\in H^4(\Omega _{s}),\quad G_1g_1\in H^{-1/2+5/2}(\Omega _{s}),\quad G_2g_2H^{-3/2+7/2}(\Omega _{s})\qquad \quad \end{aligned}$$

(C.13)

and hence $v_1\in H^2(\Omega _{s})$ as desired. In conclusion: the formulas

$$\begin{aligned} v_1 =&-v_1^*+Q^{-1}[v_1^*-v_2^*]+G_1[-(1-\mu )B_1(v_1^*)|_{\Gamma _{s}}]\nonumber \\&+G_2[-(1-\mu )B_2(v_1^*)+v_1^*]-\dfrac{\partial }{\partial \nu }[A_D^{-1}h^*+\widetilde{D}_f v_1^*]\in H^2(\Omega _{s}) \end{aligned}$$

(C.14)

$$\begin{aligned} v_2&=v_1^*\in H^2(\Omega _{s}); \quad h=A_D^{-}h^*+\widetilde{D}_fv_1^*\in H^2(\Omega _{f}) \end{aligned}$$

(C.15)

provide the explicit expression for the map ${\mathcal {A}}^{-1}:\ [v_1^*,v_2^*,h^*]\in \mathbf{H}\rightarrow {\mathcal {D}}({\mathcal {A}})$.