A Heat–Viscoelastic Structure Interaction Model with Neumann and Dirichlet Boundary Control at the Interface: Optimal Regularity, Control Theoretic Implications

Abstract

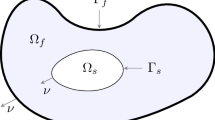
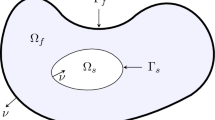
We consider a heat–structure interaction model where the structure is subject to viscoelastic (strong) damping, and where a (boundary) control acts at the interface between the two media in Neumann-type or Dirichlet-type conditions. For the boundary (interface) homogeneous case, the free dynamics generates a s.c. contraction semigroup which, moreover, is analytic on the energy space and exponentially stable here Lasiecka et al. (Pure Appl Anal, to appear). If ${\mathcal {A}}$ is the free dynamics operator, and ${\mathcal {B}}_N$ is the (unbounded) control operator in the case of Neumann control acting at the interface, it is shown that ${\mathcal {A}}^{-\frac{1}{2}}{\mathcal {B}}_N$ is a bounded operator from the interface measured in the $\mathbf{L}^2$-norm to the energy space. We reduce this problem to finding a characterization, or at least a suitable subspace, of the domain of the square root $(-{\mathcal {A}})^{1/2}$, i.e., ${\mathcal {D}}((-{\mathcal {A}})^{1/2})$, where ${\mathcal {A}}$ has highly coupled boundary conditions at the interface. To this end, here we prove that ${\mathcal {D}}((-{\mathcal {A}})^{\frac{1}{2}})\equiv {\mathcal {D}}((-{\mathcal {A}}^*)^{\frac{1}{2}})\equiv V$, with the space V explicitly characterized also in terms of the surviving boundary conditions. Thus, this physical model provides an example of a matrix-valued operator with highly coupled boundary conditions at the interface, where the so called Kato problem has a positive answer. (The well-known sufficient condition Lions in J Math Soc JAPAN 14(2):233–241, 1962, Theorem 6.1 is not applicable.) After this result, some critical consequences follow for the model under study. We explicitly note here three of them: (i) optimal (parabolic-type) boundary $\rightarrow$ interior regularity with boundary control at the interface; (ii) optimal boundary control theory for the corresponding quadratic cost problem; (iii) min–max game theory problem with control/disturbance acting at the interface. On the other hand, if ${\mathcal {B}}_D$ is the (unbounded) control operator in the case of Dirichlet control acting at the interface, it is then shown here that ${\mathcal {A}}^{-1}{\mathcal {B}}_D$ is a bounded operator from the interface measured this time in the $\mathbf{H}^{\frac{1}{2}}$-norm to the energy space. Similar consequences follow.