Abstract
This paper considers the structure consisting of the set of all words over a given alphabet together with the subword relation, regular predicates, and constants for every word. We are interested in the counting extension of first-order logic by threshold counting quantifiers. The main result shows that the two-variable fragment of this logic can be decided in twofold exponential alternating time with linearly many alternations (and therefore in particular in twofold exponential space as announced in the conference version (Kuske and Schwarz, in: MFCS’20, Leibniz International Proceedings in Informatics (LIPIcs) vol. 170, pp 56:1–56:13. Schloss Dagstuhl - Leibniz-Zentrum für Informatik, 2020) of this paper) provided the regular predicates are restricted to piecewise testable ones. This result improves prior insights by Karandikar and Schnoebelen by extending the logic and saving one exponent in the space bound. Its proof consists of two main parts: First, we provide a quantifier elimination procedure that results in a formula with constants of bounded length (this generalises the procedure by Karandikar and Schnoebelen for first-order logic). From this, it follows that quantification in formulas can be restricted to words of bounded length, i.e., the second part of the proof is an adaptation of the method by Ferrante and Rackoff to counting logic and deviates significantly from the path of reasoning by Karandikar and Schnoebelen.
Similar content being viewed by others
1 Introduction
The subword relation is one of the simplest nontrivial examples of a well-quasi-ordering [5] and can be used in the verification of infinite state systems [4]. It can be understood as embeddability of one word into another. This embeddability relation has been considered for other classes of structures like trees, posets, semilattices, lattices, graphs, Mazurkiewicz traces, etc. [7, 8, 12, 13, 15, 23, 24].
Many of these papers study logical aspects of the embeddability relation. Regarding the subword relation, the literature provides a rather sharp description of the border between decidable and undecidable fragments of first-order logic: For the subword order alone, the \(\exists ^*\)-theory is decidable [14] and the \(\exists ^*\forall ^*\)-theory is undecidable [9]. For the subword order together with regular predicates, the two-variable theory is decidable [9] (this holds even for the two-variable fragment of the logic \(\mathrm {C}{+}\mathrm {MOD}\), i.e., the extension of first-order logic by threshold- and modulo-counting quantifiers [16]) and the three-variable theory [9] as well as the \(\exists ^*\)-theory are undecidable [6] (these two undecidabilities already hold if we only consider singleton predicates, i.e., constants). Recently, Baumann et al. [1] strengthened the last undecidability result by showing that all semi-decidable languages can be defined by an existential formula using constants (even more, a language belongs to the \(n^{th}\) existential level of the arithmetical hierarchy if, and only if, it can be defined by a \(\varSigma _n\)-formula).
We next sketch the decision procedure for the 2-variable fragment of the first-order theory of the subword relation together with regular predicates from [9]. Let \(\varphi (x)\) be a formula with a single free variable. It may contain regular predicates that are given in any familiar formalism. Then, the crucial insight from [9] is that the set of words satisfying \(\varphi (x)\) can be obtained from the regular predicates by a fixed set of rational transductions and Boolean operations. Hence, one can inductively build the minimal deterministic finite automaton (henceforth dfa) accepting this set. The only known upper bound for the size of this minimal dfa is non-elementary since any quantification requires to apply one of the rational transductions to the language of a minimal dfa (which leads to a nondeterministic finite automaton, i.e., nfa) and then to determinise and minimise this nfa. The crucial insight from the follow-up paper [10] by the same authors is that the size of these minimal dfas is at most triply exponential if, instead of regular predicates, one allows constants, only (alternatively: singleton predicates). Since determinisation and minimisation of an nfa can be done in space polynomial in the resulting minimal dfa (and logarithmic in the nfa), the above construction can be carried out in threefold exponential spaceFootnote 1 which is also an upper bound for the said theory (the best lower bound we know so far is PSPACE [9]). This bound on the size of the minimal dfas is possible since all defined languages are piecewise testable [20]. A useful complexity measure for piecewise testable languages is their height. The new and innovative contribution of the proof from [10] are bounds for the height of the upwards closure \(L{\mathord {\uparrow }}\), the downwards closure \(L{\mathord {\downarrow }}\), and the incomparability set \(L{\mathord {\parallel }}\) of a piecewise testable language L; these new bounds are polynomial in the height of L (assuming a fixed alphabet).Footnote 2
We improve this 3EXPSPACE upper bound for the theory in three aspects:
-
1.
We prove an upper bound of twofold exponential alternating time with linearly many alternations (which implies an upper bound of twofold exponential space, i.e., the result we announced in the conference version of this paper [11]).
-
2.
We allow piecewise testable predicates given by so-called pt-nfas [17, 18] (which are more succinct than minimal dfas). Further, the upper bound is measured in the depth of these pt-nfas as opposed to their size.
Remark
Any piecewise testable predicate can be defined in the one-variable fragment of first-order logic. Consequently, these predicates do not increase the expressive power. Since a pt-nfa of depth k accepts a piecewise testable language of height k, the naive translation of a pt-nfa into a formula yields a formula of size exponential in the depth of the pt-nfa. As to whether this size increase is necessary seems not to be known.
-
3.
We extend the two-variable fragment of first-order logic by threshold counting quantifiers \(\exists ^{\geqslant t}\) (from [16], we know that this theory is decidable, even with regular predicates).
Following and extending the ideas from [10], we first prove new results on the height of piecewise testable languages. Namely, we extend the above mentioned results about \(L{\mathord {\uparrow }}\), \(L{\mathord {\downarrow }}\), and \(L{\mathord {\parallel }}\) to, e.g., \(L{\mathord {\uparrow }}_{\geqslant t}\), the set of words that have at least t subwords in L (and similarly for \(L{\mathord {\downarrow }}^{\geqslant t}\) and \(L{\mathord {\parallel }}^{\geqslant t}\)). These considerations can be found in Sect. 3.
From these results, it follows that a language L defined by a formula (that uses threshold counting quantifiers and piecewise testable predicates given by pt-nfas) is piecewise testable of height at most doubly exponential in the size of the formula (Theorem 4.3).
Remark
Consequently, L can be defined by a quantifier-free first-order formula. It follows that also the addition of counting quantifiers \(\exists ^{\geqslant t}\) does not increase the expressive power of the logic. But the use of counting quantifiers allows to write exponentially more succinct formulas (Theorem 4.5).
So far, this parallels the development in [10] where the corresponding result was shown for first-order logic. But at this point, instead of building automata (as done in [10]), we follow another path of argument, that is an adaptation of Ferrante and Rackoff’s method [3].
The language-theoretic considerations imply that any formula is equivalent to a quantifier-free formula that uses constants of doubly exponential length and no piecewise testable predicates (Corollary 4.4). From this, we derive that quantification in formulas can be restricted to words of doubly exponential length. This implies that the two-variable fragment of the threshold counting extension of first-order logic becomes decidable in twofold exponential alternating time with linearly many alternations (allowing piecewise testable predicates in the formula given by pt-nfas).
2 Definitions and main results
Throughout this paper, we fix an alphabet \(\varSigma \). We denote by \(\varSigma ^*\) the set of (finite) words over \(\varSigma \). A word \(u\in \varSigma ^*\) is a subword of \(v\in \varSigma ^*\) if \(u=u_1u_2\dots u_n\) and \(v=v_0u_1v_1u_2v_2\cdots u_nv_n\) for some \(n\in {{\mathbb {N}}}\) and \(u_i,v_i\in \varSigma ^*\). We write \(u\sqsubseteq v\) for this fact and alternatively say that v is a superword of u. Finally, we write \(u{\mathord {\parallel }}v\) if neither u is a subword of v nor vice versa; we say that u and v are incomparable. Note that for any two distinct words u and v, we have precisely one of the three relations \(u\sqsubseteq v\), \(u\sqsupseteq v\), or \(u{\mathord {\parallel }}v\).
Let \(L\subseteq \varSigma ^*\) be a language. Its upwards closure is the language \(L{\mathord {\uparrow }}= \{v\in \varSigma ^*\mid \exists u\in L:u\sqsubseteq v\}\) of all words v that have some subword u in L. Dually, the downwards closure of L is the language \(L{\mathord {\downarrow }}= \{u\in \varSigma ^*\mid \exists v\in L:u\sqsubseteq v\}\) of all words u that have some superword v in L. Finally, the incomparability set of L is the language \(L{\mathord {\parallel }}= \{u\in \varSigma ^*\mid \exists v\in L:u{\mathord {\parallel }}v\}\) of all words u that have some incomparable word v in L.
Note that, for any language L, we have \(L\subseteq L{\mathord {\uparrow }}\cap L{\mathord {\downarrow }}\), i.e., these two sets need not be disjoint. For, e.g., \(L=\{aa,bb\}^*\), we even get \(L{\mathord {\uparrow }}=L{\mathord {\downarrow }}=L{\mathord {\parallel }}=\varSigma ^*\) provided \(\varSigma =\{a,b\}\).
2.1 Piecewise testable languages and the main result for language theorists
The length of a word \(u\in \varSigma ^*\) is denoted |u|, \(\varSigma ^{\leqslant n}\) denotes the set of words of length \(\leqslant n\). We next define Simon’s congruences \(\sim _n\) that play an important role in our considerations.
Definition
Let \(u,v\in \varSigma ^*\) and \(n\in {{\mathbb {N}}}\). Then, u and v are n-equivalent (denoted \(u\sim _n v\)) if they have the same subwords of length \(\leqslant n\). We denote by \([u]_n\) the equivalence class containing the word u wrt. the equivalence relation \(\sim _n\).
A language \(L\subseteq \varSigma ^*\) is piecewise testable if there exists \(n\in {{\mathbb {N}}}\) such that L is a union of languages \([u]_n\) for some words \(u\in \varSigma ^*\) (which is equivalent to saying that L is closed under \(\sim _n\)). The minimal such n is called the height of L. We write \({\mathrm {PT}}(n)\) for the class of piecewise testable languages of height \(\leqslant n\). Note that \({\mathrm {PT}}(n)\subseteq {\mathrm {PT}}(n+1)\), and that both \(\emptyset \) and \(\varSigma ^*\) are of height 0. Since the set of equivalence classes \([u]_n\) forms a partition of \(\varSigma ^*\), the class \({\mathrm {PT}}(n)\) is closed under Boolean operations. Since \(\varSigma ^{\leqslant n}\) is finite, there are only finitely many equivalence classes of \(\sim _n\). Hence, for any \(n\in {{\mathbb {N}}}\), there are only finitely many languages \(L\subseteq \varSigma ^*\) in \({\mathrm {PT}}(n)\).
Let \(L\subseteq \varSigma ^*\) be piecewise testable. Then, the upwards closure \(L{\mathord {\uparrow }}\), the downwards closure \(L{\mathord {\downarrow }}\) and the incomparability set \(L{\mathord {\parallel }}\) are all piecewise testable of height polynomial in that of L (the degree of the polynomial is the size of the alphabet \(\varSigma \)) [10]. We will extend these results to the following more general operations.
Let \(L\subseteq \varSigma ^*\) be some language and \(t\in {{\mathbb {N}}}\) some threshold. Then
denotes the set of words v that have \(\geqslant t\) subwords in L. In particular, \(L{\mathord {\uparrow }}_{\geqslant 0}=\varSigma ^*\) and \(L{\mathord {\uparrow }}_{\geqslant 1}\) is the usual upwards closure \(L{\mathord {\uparrow }}\) of L. Note that any language \(L{\mathord {\uparrow }}_{\geqslant t}\) is upwards closed (i.e., satisfies \(\bigl (L{\mathord {\uparrow }}_{\geqslant t}\bigr ){\mathord {\uparrow }}=L{\mathord {\uparrow }}_{\geqslant t}\)) and therefore piecewise testable.
Dually, the set
consists of all words u that have \(\geqslant t\) superwords in L; the above remarks on \(L{\mathord {\uparrow }}_{\geqslant t}\) apply mutatis mutandis.
Let
contain all words u that are incomparable with \(\geqslant t\) words from L.
We will also write, e.g., \(L{\mathord {\parallel }}^{<t}\) for the complement of \(L{\mathord {\parallel }}^{\geqslant t}\), i.e., for the set of words that are incomparable with at most \(t-1\) words from L.
The function \(g_{|\varSigma |}\) that will bound the height of the resulting languages \(L{\mathord {\uparrow }}_{\geqslant t}\), etc. is defined as follows: Let \(n\in {{\mathbb {N}}}\). Then, \(\sim _n\) has only finitely many equivalence classes. Let \(g_{|\varSigma |}(n)\) be minimal such that every equivalence class \([x]_n\) contains some word of length \(\leqslant g_{|\varSigma |}(n)\). Then, \(n\leqslant g_{|\varSigma |}(n)\leqslant g_{|\varSigma |}(n+1)\) for all \(n\in {{\mathbb {N}}}\). From [10, Thm. 3.7 & Eq. (3.12)], we know that \(g_{|\varSigma |}(n)\leqslant (n+2)^{|\varSigma |}\).
The main result for language theorists now reads as follows (for the proof, see Sect. 3): it generalises [10, Theorems 4.4, 5.5, and 6.1] from \(t=1\) to general thresholds.
Theorem 2.1
Let \(\varSigma \) be some alphabet, \(n,t\in {{\mathbb {N}}}\), and \(L\subseteq \varSigma ^*\) be a piecewise testable language of height \(\leqslant n\). Then, the following hold:
-
1.
\(L{\mathord {\uparrow }}_{\geqslant t}\) is piecewise testable of height \(\leqslant g_{|\varSigma |}(n)+t-1\).
-
2.
\(L{\mathord {\downarrow }}^{\geqslant t}\) is piecewise testable of height \(\leqslant (|\varSigma |+1)\cdot \bigl (g_{|\varSigma |}(n)+1\bigr )\) (note that this upper bound does not depend on t).
-
3.
\(L{\mathord {\parallel }}^{\geqslant t}\) is piecewise testable of height \(\leqslant g_{|\varSigma |}(n)+t\).
Before we turn to a consequence in logic, we shortly recall some results on the relation of nondeterministic finite automata (abbreviated nfa) and piecewise testable languages.
There are different characterisations of piecewise testable languages using nfas; we only rely on one by Masopust and Thomazo [17, 18] (see following remark for missing definition). They define a class of nondeterministic finite automata, called pt-nfa and prove the following:
-
A language is piecewise testable iff it is accepted by some pt-nfa [18, Thm. 25].
-
Further, the depth \(||{\mathcal {A}}||\) of a pt-nfa (i.e., the maximal length of a simple path) bounds the height of the accepted language [17, Thm. 8].
Remark
The concrete definition of a pt-nfa is of no importance for this paper; we only recall it for the convenience of the interested reader.
An nfa is a tuple \({\mathcal {A}}=(Q,I,T,F)\) such that Q is a finite set, \(I,F\subseteq Q\), and \(T\subseteq Q\times \varSigma \times Q\). For \(p,q\in Q\) and \(\varGamma \subseteq \varSigma \), we write \(p\xrightarrow {\varGamma ^*}q\) whenever there exists a word over \(\varGamma \) that labels some path from p to q. The depth of the nfa \({\mathcal {A}}\) is the maximal length of a simple path. The language \(L({\mathcal {A}})\) of the nfa \({\mathcal {A}}\) is the set of words over \(\varSigma \) that label some path from some element of I to some element of F.
Let \({\mathcal {A}}=(Q,I,T,F)\) be an nfa. For \(r\in Q\), we write \(\varSigma _r\) for the set of letters \(a\in \varSigma \) with \((r,a,r)\in T\). The nfa \({\mathcal {A}}\) is a pt-nfa [17, Def. 3] if the following hold:
-
The reachability relation is a partial order (i.e., \(p\xrightarrow {\varSigma ^*} q\xrightarrow {\varSigma ^*} p\) implies \(p=q\)). (An nfa satisfying this property is called acyclic.)
-
For all \(p,q\in Q\), \(p\xrightarrow {\varSigma _p^*}q\) implies \(p=q\).
-
For all \(p,q,r\in Q\), \(p\xrightarrow {\varSigma _r^*}q,r\) implies \(q\xrightarrow {\varSigma _r^*}r\).
2.2 The logic \(\mathrm {C}^2\) and the main result for logicians
Let \({\mathrm {NFA}}\) be the set of all nfas over the alphabet \(\varSigma \) (to make this a set as opposed to a class, we require that states of these nfas belong to \({{\mathbb {N}}}\)). Consider the structure
whose universe is the set of words, whose only binary relation is the subword relation, that has a unary relation \(L({\mathcal {A}})\) for each nfa \({\mathcal {A}}\in {\mathrm {NFA}}\) and a constant for every word over \(\varSigma \).
We can make statements about this structure using some variant of classical first-order logic. To control the use of nfas in these formulas, let \({\mathrm {A}}\subseteq {\mathrm {NFA}}\) be a set of nfas (e.g., \({\mathrm {A}}={\mathrm {NFA}}\), \({\mathrm {A}}=\emptyset \), or \({\mathrm {A}}={\mathrm {ptNFA}}\subseteq {\mathrm {NFA}}\) which is the set of pt-nfas). Then, formulas from \(\mathrm {C}^2_{\mathrm {A}}\) are defined by the following syntax:
where \(c,d\in \{x,y\}\cup \varSigma ^*\) are variables from \(\{x,y\}\) or words over \(\varSigma \), \({\mathcal {A}}\in {\mathrm {A}}\) is some nfa over \(\varSigma \), \(t\in {{\mathbb {N}}}\), and \(z\in \{x,y\}\) is a variable. Note that we allow only the variables x and y. The semantics of these formulas is defined in the obvious way with the understanding that \(\exists ^{\geqslant t}x\,\varphi \) holds if there are t mutually distinct words that all make the formula \(\varphi \) true. Consequently, \(\exists ^{\geqslant 1}\) is the usual existential quantifier and \(\exists ^{\geqslant 0}x\,\varphi \) is always true. Let \(\mathrm {FO}_{\mathrm {A}}^2\) denote the subset of \(\mathrm {C}^2_{\mathrm {A}}\) that only uses the quantifier \(\exists ^{\geqslant 1}\), i.e., the classical first-order quantifier.
For arbitrary structures, the introduction of threshold counting quantifiers \(\exists ^{\geqslant t}\) in conjunction with the restriction to two variables extends the expressive power. Later, we will see that in our context, the logics \(\mathrm {C}^2_{\mathrm {ptNFA}}\) and \(\mathrm {FO}^2_\emptyset \) are equally expressive by Corollary 4.4, but \(\mathrm {C}^2_{\mathrm {ptNFA}}\) is exponentially more succinct than \(\mathrm {FO}^2_\emptyset \) by Theorem 4.5.
As a side remark, we prove that constants of length \(\leqslant 2\) suffice for the whole expressive power.
Theorem 2.2
Let \({\mathrm {A}}\subseteq {\mathrm {NFA}}\). For every formula \(\varphi \in \mathrm {C}^2_{\mathrm {A}}\), there exists an equivalent formula \(\psi \in \mathrm {C}^2_{\mathrm {A}}\) that uses constants of length \(\leqslant 2\), only. The same applies to the logic \(\mathrm {FO}^2_{\mathrm {A}}\).
Proof
We show that, for every word \(w\in \varSigma ^*\), there exists a formula \(\uplambda _w(x)\in \mathrm {FO}^2_\emptyset \) using at most constants of length \(\leqslant 2\) such that w is the only word satisfying \(\uplambda _w(x)\).
Before we start the construction of \(\uplambda _w(x)\), consider the following inductively defined formula \(\alpha _n(z)\) (where z is any variable from \(\{x,y\}\) and \(z'\) is the other variable):
Then, \({\mathcal {S}}\models \alpha _n(u)\) iff \(|u|\geqslant n\).
We now come to the construction of \(\uplambda _w(x)\) by induction on the length of w. If \(|w|\leqslant 2\), we simply set \(\uplambda _w(x)=w\).
Now let \(n=|w|>2\) and define \(m=\lfloor \nicefrac {n}{2}\rfloor +1<n\). Define \(S_w=\{u\in \varSigma ^{\leqslant m}\mid u\sqsubseteq w\}\). Then, \(\uplambda _w(x)\) is the following formula:
The first two conjuncts express \(|x|=n\), i.e., the length of x equals that of w. By the induction hypothesis, \(\uplambda _u(y)\) expresses \(y=u\). Consequently, the latter two conjuncts are equivalent to \(x\sim _m w\).
In other words, \({\mathcal {S}}\models \uplambda _w(v)\) iff \(|v|=|w|\) and \(v\sim _m w\). But this is equivalent to \(v=w\) [22, Thm. 6.2.16]. \(\square \)
The size of a formula is defined with the understanding that the size \(|{\mathcal {A}}|\) of an nfa \({\mathcal {A}}\) is its number of states, the size of a variable is 1, the size of a word is its length, and the size of the quantifier \(\exists ^{\geqslant t}\) is the length \(|\mathrm {bin}(t)|\) of the binary encoding of t.
Besides the size, we also define the norm \(||\varphi ||\) of a formula \(\varphi \) from \(\mathrm {C}^2_{\mathrm {ptNFA}}\) (recall that \(||{\mathcal {A}}||\) denotes the depth of the pt-nfa \({\mathcal {A}}\)):
Note that this norm \(||\varphi ||\) forms a mixture between the size of a formula and its quantifier depth: It depends on the maximal size of constants and simple paths in automata appearing in \(\varphi \) as well as on the quantifier depth (where the quantifier \(\exists ^{\geqslant t}\), that intuitively corresponds to a sequence of t quantifiers, contributes only \(\lceil \log (t)\rceil \) to the norm). In particular, \(||\varphi ||\) bounds the length of constants and the depth of pt-nfas occurring in \(\varphi \). Note further that the norm \(||\varphi ||\) of any formula \(\varphi \) is at most its size \(|\varphi |\), i.e., \(||\varphi ||\leqslant |\varphi |\).
From Theorem 2.1, we infer in Sect. 4 that all definable languages are piecewise testable of bounded height (Theorem 4.3). This allows to derive a quantifier elimination result that reads as follows:
Corollary
4.4. Let \(c=2\cdot |\varSigma |\). Every \(\mathrm {C}^2_{\mathrm {ptNFA}}\)-formula \(\varphi \) is equivalent to some quantifier- and automata-free formula \(\psi \in \mathrm {FO}^2_\emptyset \) with \(||\psi ||< 2^{c^{2||\varphi ||}}\).
Karandikar and Schnoebelen [10] showed that any non-empty piecewise testable language of height n has elements of length polynomial in n. Based on Corollary 4.4, we can therefore restrict quantification in a formula \(\varphi \) to words of bounded length, implying our main result for logicians.
Theorem
5.3. The \(\mathrm {C}^2_{\mathrm {ptNFA}}\)-theory of \({\mathcal {S}}\) belongs to \(\mathsf {STA}\bigl (*,2^{2^{\mathrm {poly}(n)}},O(n)\bigr )\), i.e., can be decided in doubly exponential alternating time with linearly many alternations.
Recall that, by [2], \(\mathsf {STA}(s,t,a)\) is the class of all languages, for which membership can be decided by an alternating Turing machine whose space, time, and alternations are bounded by the functions s, t, and a, respectively. Typically, \(*\) is used to denote that no restriction is placed on a specific resource. Thus, \(\mathsf {STA}\) is a combined complexity measure that is particularly useful when describing the complexity of logical theories (see, e.g., [2, 3]).
3 Closure of the class of piecewise testable languages
The purpose of this section is to prove Theorem 2.1, i.e., our main result for language theorists.
3.1 Notions and results used in the proof
A set of words L is convex if \(u,w\in L\) and \(u\sqsubseteq v\sqsubseteq w\) imply \(v\in L\). It is a chain if it is linearly ordered by the subword order and if it is infinite. Since the subword order is well-founded, any chain is isomorphic to \(({\mathbb {N}},\leqslant )\).
Lemma 3.1
(compiled in [10]) Let \(u,v\in \varSigma ^*\), \(a\in \varSigma \), and \(n\in {{\mathbb {N}}}\).
-
1.
The equivalence class \([u]_n\) is convex.
-
2.
If \(u\sim _n v\), then there exists \(w\in [u]_n\) with \(u,v\sqsubseteq w\).
-
3.
If \(uv\sim _n uav\), then \(uv\sim _n ua^\ell v\) for all \(\ell \in {{\mathbb {N}}}\).
-
4.
The equivalence class \([u]_n\) is infinite or a singleton.
Proof
(cited from [10]) (1) is by combining the definition of \(\sim _n\) with the observation \(\{u\}{\mathord {\downarrow }}\subseteq \{v\}{\mathord {\downarrow }}\) provided \(u\sqsubseteq v\). (2) is [21, Lemma 6] (cf. [22, Thm. 6.2.6] for an alternative proof). (3) is in the proof of [22, Cor. 6.2.8]. Finally, (4) follows from (1), (2), and (3). \(\square \)
An example of a singleton equivalence class is \([u]_{|u|+1}\) for any \(u\in \varSigma ^*\); if u contains two distinct letters, then even \([u]_{|u|}=\{u\}\) (but \([aa]_2=aaa^*\)).
For a set \(L\subseteq \varSigma ^*\) of words, let \(\min (L)\) denote the set of words \(v\in L\) that have no proper subword in L. Since the subword relation is well-founded, any word from L is a superword of some word from \(\min (L)\), i.e., \(L\subseteq \min (L){\mathord {\uparrow }}\).
Imre Simon found a description of the set of minimal elements of an equivalence class \([u]_n\) that uses the following concept. For a set \(B\subseteq \varSigma \), let \(\mathrm {Perm}(B)\subseteq \varSigma ^*\) denote the set of permutations of B seen as words, i.e., \(\mathrm {Perm}(\emptyset )=\{\varepsilon \}\) and \(\mathrm {Perm}(B)=\bigcup _{b\in B}b\,\mathrm {Perm}\bigl (B\setminus \{b\}\bigr )\) for \(B\ne \emptyset \). For sets \(B_i\subseteq \varSigma \), define \(\mathrm {Perm}(B_1,B_2,\dots ,B_k)=\mathrm {Perm}(B_1)\,\mathrm {Perm}(B_2)\,\ldots \,\mathrm {Perm}(B_k)\). For instance, \(\mathrm {Perm}\bigl (\{a\},\{b\},\{c\}\bigr )=\{abc\}\) while \(\mathrm {Perm}\bigl (\{a,b\},\{c\}\bigr )=\{abc,bac\}\) for all letters \(a,b,c\in \varSigma \). For \(k=0\), we set \(\mathrm {Perm}\bigl (\bigr )=\{\varepsilon \}\).
Theorem 3.2
([20], cf. [22, Thm. 6.2.9]) Let \(n\in {{\mathbb {N}}}\) and \(u\in \varSigma ^*\). Then, there exist \(k\in {{\mathbb {N}}}\) and \(B_1,B_2,\dots ,B_k\subseteq \varSigma \) with \(\min \bigl ([u]_n\bigr )=\mathrm {Perm}(B_1,B_2,\dots ,B_k)\).
Deleting all empty sets from the tuple \((B_1,B_2,\dots ,B_k)\) makes the above presentation of \(\min \bigl ([u]_n\bigr )\) unique. The theorem implies in particular that all words from \(\min \bigl ([u]_n\bigr )\) have the same Parikh image. Further, they all have the same length \(\sum _{1\leqslant i\leqslant k}|B_i|\) which is \(\leqslant g_{|\varSigma |}(n)\) (by the very definition of that function) and therefore \(\leqslant (n+2)^{|\varSigma |}\) (by [10, Thm. 3.7 and Eq. (3.12)]).
Theorem 3.3
Let \(\varSigma \) be an alphabet, \(w\in \varSigma ^*\), and \(n\in {{\mathbb {N}}}\). Then, there exists a word \(v\sim _n w\) with \(|v|\leqslant g_{|\varSigma |}(n)\) and \(v\sqsubseteq w\).
Proof
The definition of the function \(g_{|\varSigma |}\) implies the existence of some word \(u'\sim _n w\) with \(|u'|\leqslant g_{|\varSigma |}(n)\). Since the subword order is well-founded, there exist words \(u,v\in \min ([w]_n)\) with \(u\sqsubseteq u'\) and \(v\sqsubseteq w\). Now Theorem 3.2 implies \(|v|=|u|\leqslant |u'|\leqslant g_{|\varSigma |}(n)\). \(\square \)
3.2 Upward closures
The following result verifies the first claim of Theorem 2.1.Footnote 3
Proposition 3.4
Let \(L\in {\mathrm {PT}}(n)\) be a piecewise testable language of height \(\leqslant n\) and \(t\in {{\mathbb {N}}}\). Then, the language \(L{\mathord {\uparrow }}_{\geqslant t}\) is piecewise testable of height \(\leqslant g_{|\varSigma |}(n)+t-1\).
Proof
Let \(z\in L{\mathord {\uparrow }}_{\geqslant t}\) and \(z'\sim _{g_{|\varSigma |}(n)+t-1}z\). Then, there exists a t-elements set \(Y\subseteq L\) with \(y \sqsubseteq z\) for all \(y\in Y\). Choosing the elements of Y as short as possible, we can assume \(Y{\mathord {\downarrow }}\cap L=Y\).
Now let \(y\in Y\). By Theorem 3.3, there is a word x with \(x\sim _n y\), \(x\sqsubseteq y\), and \(|x|\leqslant g_{|\varSigma |}(n)\).
Since x is a subword of y, there are more than \(|y|-|x|\) words \(x'\) with \(x\sqsubseteq x'\sqsubseteq y\). Since the equivalence class \([y]_n\) is convex, any such word \(x'\) satisfies \(x'\sim _n y\) and therefore \(x'\in L\). Consequently,
But this implies \(|y|\leqslant g_{|\varSigma |}(n)+t-1\).
So far, we proved that all words from Y have length at most \(g_{|\varSigma |}(n)+t-1\). Since they all are subwords of \(z\sim _{g_{|\varSigma |}(n)+t-1} z'\), we obtain \(y\sqsubseteq z'\) for all \(y\in Y\). From \(|Y|=t\) and \(Y\subseteq L\), we derive \(z'\in L{\mathord {\uparrow }}_{\geqslant t}\), i.e., \(L{\mathord {\uparrow }}_{\geqslant t}\) is closed under \(\sim _{g_{|\varSigma |}(n)+t-1}\). \(\square \)
3.3 Downward closures
To verify the second claim of Theorem 2.1, we first prove that only singleton equivalence classes \([x]_n\) have maximal elements. We will use this lemma in the following proof when showing that \([x]_n{\mathord {\downarrow }}^{\geqslant t}=[x]_n{\mathord {\downarrow }}\) if the equivalence class \([x]_n\) is not a singleton.
Lemma 3.5
Let \(n\in {{\mathbb {N}}}\) and \(x,y\in \varSigma ^*\) be distinct with \(x\sim _n y\). Then, there exists \(z\in \varSigma ^*\) with \(y\sim _n z\), \(y\sqsubseteq z\), and \(y\ne z\).
Proof
Since \([x]_n=[y]_n\) is not a singleton, it is infinite by Lemma 3.1(4), thus contains in particular a word w of length \(|w|>|y|\). By Lemma 3.1(2), there exists a \(z\in [y]_n\) with \(y,w\sqsubseteq z\), implying \(|z|\geqslant |w|\), and therefore \(z\ne y\). \(\square \)
Proposition 3.6
Let \(L\in {\mathrm {PT}}(n)\) be a language over \(\varSigma \) and \(t\in {{\mathbb {N}}}\). Then, the language \(L{\mathord {\downarrow }}^{\geqslant t}\) belongs to \({\mathrm {PT}}\bigl ((|\varSigma |+1)\cdot (g_{|\varSigma |}(n)+1)\bigr )\).
Proof
Since \(L\in {\mathrm {PT}}(n)\) and since \(\sim _n\) has finite index, there are finitely many words \(x_1,\dots ,x_m\) with \(L=\bigcup _{1\leqslant i\leqslant m}[x_i]_n\) and \(x_i\not \sim _n x_j\) for all \(1\leqslant i<j\leqslant m\). By the definition of the function \(g_{|\varSigma |}\), we can assume \(|x_i|\leqslant g_{|\varSigma |}(n)\) for all \(1\leqslant i\leqslant m\).
Set
such that in particular \(L=F\cup I\).
We first show
For the inclusion “\(\subseteq \)”, let \(x\in L{\mathord {\downarrow }}^{\geqslant t}\setminus F{\mathord {\downarrow }}^{\geqslant t}\). Then, x has t superwords in \(L=F\cup I\), but at most \(t-1\) many in F. Hence, it has at least one superword in I, i.e., \(x\in I{\mathord {\downarrow }}\). For the converse inclusion, note that \(F{\mathord {\downarrow }}^{\geqslant t}\subseteq L{\mathord {\downarrow }}^{\geqslant t}\) is trivial since \(F\subseteq L\). So let \(x\in I{\mathord {\downarrow }}\). Then, there exists \(y\in I\) with \(x\sqsubseteq y\). Since \(y\in I\), the equivalence class \([y]_n\subseteq I\) is infinite and therefore contains no maximal element by Lemma 3.5. Hence, there are infinitely many (and therefore in particular \(\geqslant t\)) superwords of \(y\sqsupseteq x\) in \(I\subseteq L\). Consequently, \(x\in L{\mathord {\downarrow }}^{\geqslant t}\).
Note that the height of I is \(\leqslant n\) since it is a union of equivalence classes of \(\sim _n\). Consequently, the height of \(I{\mathord {\downarrow }}\) is \(\leqslant (|\varSigma |+1)\cdot \bigl (g_{|\varSigma |}(n)+1\bigr )\) by [10, Thm. 5.5].
Since every finite equivalence class \([x_j]_n\) is a singleton, we obtain
implying that all words from F and therefore from \(F{\mathord {\downarrow }}^{\geqslant t}\) have length at most \(g_{|\varSigma |}(n)\). Hence, \(F{\mathord {\downarrow }}^{\geqslant t}\) is finite and thus of height \(\leqslant g_{|\varSigma |}(n)+1\leqslant (|\varSigma |+1)\cdot \bigl (g_{|\varSigma |}(n)+1\bigr )\).
We showed that both, \(F{\mathord {\downarrow }}^{\geqslant t}\) and \(I{\mathord {\downarrow }}\), are closed under \(\sim _{(|\varSigma |+1)\cdot (g_{|\varSigma |}(n)+1)}\); hence, the same holds for their union \(L{\mathord {\downarrow }}^{\geqslant t}\). \(\square \)
3.4 Incomparability set
There are three types of equivalence classes \([x]_n\): the singletons, the chains (i.e., infinite languages ordered linearly by the subword order), and the infinite ones which are no chains. Note that by Lemma 3.1(4) this is a complete characterization of the equivalence classes. Propositions 3.7, 3.9, and 3.14, respectively, bound the heights of \([x]_n{\mathord {\parallel }}^{\geqslant t}\) for these three types of equivalence classes and collectively verify Theorem 2.1(3).
Proposition 3.7
Let \(n,t\in {{\mathbb {N}}}\) and \(x\in \varSigma ^*\) such that \(L=[x]_n\) is a singleton. Then, \(L{\mathord {\parallel }}^{\geqslant t}\in {\mathrm {PT}}\bigl (g_{|\varSigma |}(n)\bigr )\).
Proof
If \(t\geqslant 2\), then \(L{\mathord {\parallel }}^{\geqslant t}=\emptyset \) since L is a singleton. If \(t=0\), then \(L{\mathord {\parallel }}^{\geqslant t}=\varSigma ^*\). Note that both these languages belong to \({\mathrm {PT}}(0)\subseteq {\mathrm {PT}}\bigl (g_{|\varSigma |}(n)\bigr )\).
Finally, consider the case \(t=1\). Then, \(L{\mathord {\parallel }}^{\geqslant t}=\varSigma ^*\setminus (L{\mathord {\uparrow }}\cup L{\mathord {\downarrow }})\) since L is a singleton.
Note that \(L{\mathord {\uparrow }}\cup L{\mathord {\downarrow }}=L{\mathord {\uparrow }}\cup \bigl (L{\mathord {\downarrow }}\setminus \{x\}\bigr )\) since \(x\in L{\mathord {\uparrow }}\). The height of the former language is \(\leqslant |x|\). The latter is finite, and all its elements have length \(<|x|\); hence, the height of that language is \(\leqslant |x|\) as well. Thus, the height of \(L{\mathord {\uparrow }}\cup L{\mathord {\downarrow }}\) is \(\leqslant |x|\) and the same applies to its complement \(L{\mathord {\parallel }}^{\geqslant t}\). Since \(L=[x]_n\) is a singleton, the definition of the function \(g_{|\varSigma |}\) implies \(|x|\leqslant g_{|\varSigma |}(n)\). \(\square \)
Next, we consider the case that \([x]_n\) is a chain and bound the height of \([x]_n{\mathord {\parallel }}^{\geqslant t}\). The following lemma provides the central argument that will also be used later.
Lemma 3.8
Let \(t\geqslant 1\) and let C be the convex chain  . Then, \(C{\mathord {\parallel }}^{<t}=C\cup \{x_{t-1}\}{\mathord {\downarrow }}\).
. Then, \(C{\mathord {\parallel }}^{<t}=C\cup \{x_{t-1}\}{\mathord {\downarrow }}\).
Note that, provided \(x_0\ne \varepsilon \), the chain C is not maximal since it can be extended to the left.
Proof
We first demonstrate the inclusion “\(\supseteq \)”. Since any two elements of C are comparable, we clearly have \(C{\mathord {\parallel }}^{<t}\supseteq C\). Further, any subword of \(x_{t-1}\) is a subword of all words \(x_{t-1+i}\) for \(i\in {{\mathbb {N}}}\) and therefore at most incomparable with the \(t-1\) words \(x_0\), \(x_1\), ..., \(x_{t-2}\) from C.
For the converse inclusion, let \(y\in C{\mathord {\parallel }}^{<t}\). Then, y is comparable with infinitely many words from C. Since C has only finitely many words that are shorter than y, there is \(\ell \in {{\mathbb {N}}}\) with \(y\sqsubseteq x_\ell \). Let \(\ell \in {{\mathbb {N}}}\) be minimal with this property. We distinguish three cases of the relation between \(x_0\) and y:
-
If \(y\sqsubseteq x_0\), then \(y\in \{x_{t-1}\}{\mathord {\downarrow }}\).
-
If \(y\parallel x_0\), then \(x_0,x_1,\ldots ,x_{\ell -1}\parallel y\) since \(\ell \) was chosen minimal with \(y\sqsubseteq x_\ell \) and \(x_0\sqsubseteq x_1\sqsubseteq \cdots \sqsubseteq x_{l-1}\) is a chain. From \(y\in C{\mathord {\parallel }}^{<t}\), we obtain \(\ell <t\) and therefore \(y\sqsubseteq x_\ell \sqsubseteq x_{t-1}\).
-
If \(y\sqsupseteq x_0\), we have \(x_0\sqsubseteq y\sqsubseteq x_\ell \) and therefore \(y\in C\) since C is convex.
Thus, in any case, \(y\in C\cup \{x_{t-1}\}{\mathord {\downarrow }}\). \(\square \)
Proposition 3.9
Let \(n,t\in {{\mathbb {N}}}\) and \(x\in \varSigma ^*\) such that \(C=[x]_n\) is a chain. Then, \(C{\mathord {\parallel }}^{\geqslant t}\in {\mathrm {PT}}\bigl (g_{|\varSigma |}(n)+t\bigr )\).
Proof
If \(t=0\), then \(C{\mathord {\parallel }}^{\geqslant t}=\varSigma ^*\in {\mathrm {PT}}(0)\). It therefore suffices to consider the case \(t>0\).
We list the elements of the chain C in increasing order:

Since \(C=[x]_n\) is a chain, it is a convex chain by Lemma 3.1(1) such that \(|x_i|=|x_0|+i\) holds for all \(i\geqslant 0\). From Lemma 3.8, we obtain
Since \(\{x_{t-1}\}{\mathord {\downarrow }}\) is finite, its height is \(\leqslant |x_{t-1}|+1=|x_0|+t-1+1\leqslant g_{|\varSigma |}(n)+t\). The height of C is \(\leqslant n\leqslant g_{|\varSigma |}(n)\) by assumption; thus, the height of \(C{\mathord {\parallel }}^{<t}\) is \(\leqslant g_{|\varSigma |}(n)+t\). But then the same bound applies to the height of \(C{\mathord {\parallel }}^{\geqslant t}=\varSigma ^*\setminus C{\mathord {\parallel }}^{<t}\). \(\square \)
It remains to prove a similar statement for infinite equivalence classes \([x]_n\) that are not a chain. The proof of the case \(t=1\) from [10] first shows that \([x]_n\) contains at least two elements of every length \(>|x|\). Consequently, every word of length \(>|x|\) is incomparable with some word from \([x]_n\), i.e., \([x]_n{\mathord {\parallel }}^{\geqslant 1}\) is cofinite and therefore piecewise testable.
Our proof for \(t>1\) shows that the set of pairs of words of equal length can be grouped into two convex chains, i.e., the equivalence class \([x]_n\) contains two convex chains that intersect, at most, in \(\min \bigl ([x]_n\bigr )\) (Lemma 3.13). Then, we apply Lemma 3.8. But first, we need some insight into convex chains which is the topic of the following considerations.
Lemma 3.10
Let \(x,y\in \varSigma ^*\) and \(a\in \varSigma \). Then, \(xa^*y\) is a convex chain.
Proof
Let \(x'\) be the longest prefix of x not ending with a (i.e., \(x'\in \varSigma ^*\setminus \varSigma ^*a\) and \(x\in x'a^*\)) and \(y'\) the longest suffix of y not beginning with a. Then, \(x a^* y \subseteq x'a^*y'\) is convex in \((x'a^*y',\sqsubseteq )\) and we prove the stronger claim that the latter set is a convex chain.
To simplify notation, suppose \(x\in \varSigma ^*\setminus \varSigma ^*a\) and \(y\in \varSigma ^*\setminus a\varSigma ^*\).
Clearly, \(xa^*y\) is a chain in \((\varSigma ^*,\sqsubseteq )\).
Let \(w\in \varSigma ^*\) and \(i,\ell \in {{\mathbb {N}}}\) with \(xa^iy\sqsubseteq w\sqsubseteq xa^\ell y\). We have to show that w belongs to \(xa^*y\). Note that \(xy\sqsubseteq w\) since \(xy\sqsubseteq xa^iy\sqsubseteq w\). Let \(w_1\) be the prefix of length |x| of w, \(w_3\) be the suffix of length |y| of w, and \(w_2\) be the unique word with \(w=w_1w_2w_3\). Since w is a subword of \(xa^\ell y\), dropping the first |x| letters in both w and \(xa^\ell y\) preserves the subword relation. The same holds when dropping the last |y| letters, hence \(w_2\sqsubseteq a^\ell \), i.e. \(w_2\in a^*\). By similar reasoning for \(xy\sqsubseteq w_1w_2w_3\), we can conclude that \(x\sqsubseteq w_1w_2\). Since \(w_2\in a^*\), but x does not end on a, x has to be a subword of \(w_1\) and thus \(x=w_1\), as both words are of the same length. Symmetrically, we can show \(y=w_3\). Consequently, we have \(w\in xa^*y\). \(\square \)
The third item of the following lemma implies, together with Theorem 3.2, that the maximal a-prefixes of two words from \(\min \bigl ([x]_n\bigr )\) differ in length by at most one.
Lemma 3.11
Let \(B_1,B_2,\dots ,B_k\subseteq \varSigma \) be non-empty, \(a\in \varSigma \) and \(u,v\in \varSigma ^*\).
-
(1)
If \(au\in \mathrm {Perm}(B_1,\dots ,B_k)\), then \(a\in B_1\) and \(u\in \mathrm {Perm}\bigl (B_1\setminus \{a\},B_2,\dots ,B_k\bigr )\).
-
(2)
If \(aau\in \mathrm {Perm}(B_1,\dots ,B_k)\), then \(B_1=\{a\}\).
-
(3)
If \(u,v\notin a\varSigma ^*\) and \(m,n\in {{\mathbb {N}}}\) with \(a^m u,a^n v\in \mathrm {Perm}(B_1,\dots ,B_k)\), then \(|m-n|\leqslant 1\).
Proof
Since \(B_1\ne \emptyset \), the first claim follows from
Now assume \(aau\in \mathrm {Perm}(B_1,\dots ,B_k)\). Then, by the above, \(a\in B_1\) and the word au belongs to the set \(\mathrm {Perm}\bigl (B_1\setminus \{a\},B_2,\dots ,B_k\bigr )\). If, towards a contradiction, \(B_1\ne \{a\}\), then \(B_1\setminus \{a\}\ne \emptyset \). Hence, by the first claim again, \(a\in B_1\setminus \{a\}\), a contradiction. Thus, indeed, \(B_1=\{a\}\).
Towards a contradiction, assume \(u,v\notin a\varSigma ^*\), \(|m-n|>1\), and \(a^m u,a^n v\in \mathrm {Perm}(B_1,\dots ,B_k)\). Without loss of generality, we may assume \(m\geqslant n+2\). By the second claim, we get \(B_1=\{a\}\) from \(m\geqslant n+2\geqslant 2\). Hence,
By induction, we obtain \(a^{m-n}u,v\in \mathrm {Perm}(B_{n+1},\dots ,B_k)\). Since \(m-n\geqslant 2\), the second claim implies \(B_{n+1}=\{a\}\) and therefore \(v\in a\varSigma ^*\). But this contradicts our choice of v. \(\square \)
Lemma 3.12
Let \({\overline{B}}\) be a tuple of finite nonempty sets of letters, \(x_1,x_2,y_1,y_2\in \varSigma ^*\) be words with \(x_1x_2, y_1y_2\in \mathrm {Perm}({\overline{B}})\), and \(a,b\in \varSigma \) letters with \(x_1ax_2\ne y_1by_2\).
Then, \(x_1 a^* x_2\) and \(y_1 b^* y_2\) are convex chains that intersect, at most, in \(x_1x_2\).
Proof
Without loss of generality, we assume \(|x_1|\leqslant |y_1|\). Since \(|x_1x_2| = |y_1y_2|\), we get \(|x_2|\geqslant |y_2|\). By Lemma 3.10, \(C_1=x_1 a^* x_2\) and \(C_2=y_1 b^* y_2\) form convex chains.
It remains to be shown that their intersection is contained in \(\{x_1x_2\}=\{y_1y_2\}\). So let \(v\in C_1\cap C_2\). Then, there exist non-negative integers \(\ell \) and m with \(v=x_1 a^\ell x_2 = y_1 b^m y_2\). Since the words \(x_1x_2\) and \(y_1y_2\) are of equal length, we have \(\ell =m\). If \(\ell =0\), then \(v=x_1 a^0 x_2=y_1 b^0 y_2\) is in \(\{x_1x_2\}\) and we are done. Thus, we may assume \(\ell >0\).
Since \(x_1x_2\) and \(y_1y_2\) both belong to \(\mathrm {Perm}({\overline{B}})\), we get \(|x_1x_2|_a=|y_1y_1|_a\), implying \(0 < \ell = |a^\ell |_a = |x_1 a^\ell x_2|_a - |x_1x_2|_a = |y_1 b^\ell y_2|_a - |y_1y_2|_a = |b^\ell |_a\) and therefore \(a=b\).
Since \(x_1\) and \(y_1\) both are prefixes of \(x_1 a^\ell x_2\) with \(|x_1|\leqslant |y_1|\), the word \(x_1\) is a prefix of \(y_1\), i.e., there is a word \(x_1'\) with \(y_1=x_1 x_1'\). Symmetrically, we get a word \(y_2'\) with \(x_2=y_2' y_2\). From \(x_1x_1' a^\ell y_2 = y_1a^\ell y_2 = x_1 a^\ell x_2 = x_1 a^\ell y_2'y_2\), we conclude \(x_1'a^\ell = a^\ell y_2'\) (and therefore in particular \(|x_1'|=|y_2'|\)). Aiming at a contradiction, assume \(|x_1'|=|y_2'|\leqslant \ell \). Then, \(x_1'\) is a prefix of \(a^\ell \) and similarly \(y_2'\) a suffix of \(a^\ell \), hence \(x_1'=y_2'=a^k\) for some nonnegative integer \(k\in {{\mathbb {N}}}\). But then \(y_1 b y_2 = y_1 a y_2 = x_1 a^k a y_2 = x_1 a a^k y_2 = x_1 a x_2\), as opposed to our assumption. Consequently \(|x_1'|=|y_2'|>\ell \), implying that there exists \(k\in {{\mathbb {N}}}\) and a word \(w\in \varSigma ^*\setminus a\varSigma ^*\) such that \(x_1'=a^\ell a^k w\) and \(y_2'= a^k w a^\ell \). If \(w=\varepsilon \), then \(x_1'=y_2'=a^{k+\ell }\) and therefore (as above) \(y_1 b y_2 = y_1 a y_2 = x_1 a^{k+\ell } a y_2 = x_1 a a^{k+\ell } y_2 = x_1 a x_2\), as opposed to our assumption. Hence, \(w= cw'\) for some letter \(c\ne a\) and some word \(w'\in \varSigma ^*\).
Note that
Applying Lemma 3.11(1), we obtain a tuple \({\overline{C}}\) of non-empty subsets of \(\varSigma \) with \(a^k cw' a^\ell y_2,a^{\ell +k} cw'y_2\in \mathrm {Perm}({\overline{C}})\).
Since \(c\ne a\), Lemma 3.11(3) implies \(|\ell +k-k|\leqslant 1\), i.e., \(\ell \leqslant 1\). But \(\ell =1\) is impossible since \(x_1 a x_2 \ne y_1 a y_2\). Hence, \(\ell =0\) and therefore \(v=x_1x_2\).
Recall that we considered an arbitrary word \(v\in C_1\cap C_2\) and derived \(v\in \{x_1x_2\}\). Hence, indeed, \(C_1\cap C_2\subseteq \{x_1x_2\}\). \(\square \)
Note that, in the lemma above, the two words \(x_1x_2\) and \(y_1y_2\) have the same Parikh image. However, replacing the requirement \(x_1x_2,y_1y_2\in \mathrm {Perm}({\overline{B}})\) by this weaker property does not suffice for the claim of the lemma: consider \(x_1=aac\), \(y_2=caa\), \(x_2=y_1=\varepsilon \), and \(a=b\). Then, \(x_1x_2=aac\) and \(y_1y_2=caa\) satisfy the modified prerequisites, but \(x_1a^*x_2=aaca^*\) and \(y_1b^*y_2=b^*caa=a^*caa\) are two convex chains that intersect in aacaa.
Lemma 3.13
Let \(u\in \varSigma ^*\) and \(n\in {{\mathbb {N}}}\) such that \([u]_n\) is infinite but not a single chain. Then, \([u]_n\) contains two convex chains \(C_1\) and \(C_2\) with \(C_1\cap C_2\subseteq \min \bigl ([u]_n\bigr )\) and \(C_i\cap \min \bigl ([u]_n\bigr )\ne \emptyset \) for \(i\in \{1,2\}\).
Proof
Since \([u]_n\) is infinite but not a single chain, [10, Lemma 6.2 and 6.3] implies that there are words \(x_1,x_2,y_1,y_2\in \varSigma ^*\) and letters \(a,b\in \varSigma \) such that \(x_1x_2,y_1y_2\in \min \bigl ([u]_n\bigr )\), \(x_1 a x_2,y_1 b y_2\in [u]_n\), and \(x_1 a x_2\ne y_1 b y_2\).
By Theorem 3.2, there exists a tuple \({\overline{B}}\) of nonempty subsets of \(\varSigma \) such that \(x_1x_2,y_1y_2\in \min \bigl ([u]_n\bigr )\subseteq \mathrm {Perm}({\overline{B}})\). By Lemma 3.12, \(x_1a^*x_2\) and \(y_1b^*y_2\) are convex chains whose intersection is contained in \(\{x_1x_2\}\). By Lemma 3.1(3) they are both subsets of \([u]_n\), obviously containing elements from \(\min \bigl ([u]_n\bigr )\). \(\square \)
Now we can handle the remaining equivalence classes, i.e., bound the height of \([x]_n{\mathord {\parallel }}^{\geqslant t}\) provided \([x]_n\) is infinite but not a chain.
Proposition 3.14
Let \(n,t\in {{\mathbb {N}}}\) and \(x\in \varSigma ^*\) such that \(L=[x]_n\) is infinite but not a chain. Then, \(L{\mathord {\parallel }}^{\geqslant t}\in {\mathrm {PT}}\bigl (g_{|\varSigma |}(n)+t\bigr )\).
Proof
If \(t=0\), then \(L{\mathord {\parallel }}^{\geqslant t}=\varSigma ^*\in {\mathrm {PT}}(0)\). Hence, it remains to consider the case \(t>0\).
By Lemma 3.13, there exist two convex chains \(C_1,C_2\subseteq L\) such that \(C_1\cap C_2\subseteq \min (L)\) and \(C_i\cap \min (L)\ne \emptyset \) for \(i\in \{1,2\}\). We prove that
Let \(v\in \varSigma ^*\) with \(|v|\geqslant g_{|\varSigma |}(n)+t>g_{|\varSigma |}(n)\). Then, by Theorem 3.2 and the definition of the function \(g_{|\varSigma |}\), \(v\notin \min (L)\) implying \(v\notin C_1\cap C_2\), without loss of generality, we assume \(v\notin C_1\). Since \(C_1\cap \min (L)\ne \emptyset \), the chain \(C_1\) contains some word of length \(\leqslant g_{|\varSigma |}(n)\). Consequently, its word \(x_{t-1}\) number \(t-1\) satisfies \(|x_{t-1}|<g_{|\varSigma |}(n)+t\leqslant |v|\), i.e., v cannot be a subword of \(x_{t-1}\). Now Lemma 3.8 implies \(v\notin C_1{\mathord {\parallel }}^{<t}\). From \(C_1\subseteq L\), we now obtain \(v\in C_1{\mathord {\parallel }}^{\geqslant t}\subseteq L{\mathord {\parallel }}^{\geqslant t}\). Consequently, \(v\notin L{\mathord {\parallel }}^{<t}\) which proves the above claim.
Since all words in \(L{\mathord {\parallel }}^{<t}\) are “short”, we obtain \(L{\mathord {\parallel }}^{<t}\in {\mathrm {PT}}\bigl (g_{|\varSigma |}(n)+t\bigr )\) and the same holds for the complement \(L{\mathord {\parallel }}^{\geqslant t}\) of this set. \(\square \)
We can now put the above three propositions together to verify the last claim of Theorem 2.1.
Proposition 3.15
Let \(L\in {\mathrm {PT}}(n)\) be a language over \(\varSigma \) and \(t\in {{\mathbb {N}}}\). Then, \(L{\mathord {\parallel }}^{\geqslant t}\in {\mathrm {PT}}\bigl (g_{|\varSigma |}(n)+t\bigr )\).
Proof
Since L is of height \(\leqslant n\), there is a finite set of words \(\{x_1,\dots ,x_m\}\) with \(x_i\not \sim _n x_j\) for all \(1\leqslant i<j\leqslant m\) such that L is the union of the equivalence classes \([x_i]_n\). Since equivalence classes are disjoint, we obtain
where the union is taken over all functions \(g:\{1,2,\dots ,m\}\rightarrow \{0,1,\dots ,t\}\) with \(\sum _{1\leqslant i\leqslant m}g(i)=t\). The previous propositions show that any of the languages \([x_i]_n{\mathord {\parallel }}^{\geqslant s}\) is piecewise testable of height \(\leqslant g_{|\varSigma |}(n)+t\). Since the class \({\mathrm {PT}}\bigl (g_{|\varSigma |}(n)+t\bigr )\) is closed under Boolean operations, the claim follows. \(\square \)
4 Expressive power and quantifier elimination
Having completed the language-theoretic part of this paper, we now come to its consequences in logic, i.e., we consider the threshold counting logic \(\mathrm {C}^2_{{\mathrm {ptNFA}}}\) that has two variables x and y, unary predicates for each piecewise testable language (represented by some pt-nfa), the subword order, a constant for every word, and threshold quantifiers of the form \(\exists ^{\geqslant t}\) for \(t\in {{\mathbb {N}}}\). The central result, Theorem 4.3, states that every language definable in this logic is piecewise testable of height bounded in terms of the norm of the defining formula. But first a simple result on the expressive power of quantifier-free formulas.
Lemma 4.1
Let \(n\in {{\mathbb {N}}}\).
-
(1)
Any language \(L\in {\mathrm {PT}}(n)\) is defined by some quantifier- and automata-free formula \(\varphi (x)\in \mathrm {FO}^2_\emptyset \) with \(||\varphi ||\leqslant n\).
-
(2)
If \(\varphi (x)\in \mathrm {FO}^2_{\mathrm {ptNFA}}\) is a quantifier-free formula with \(||\varphi ||\leqslant n\), then it defines a language from \({\mathrm {PT}}(n+1)\).
Proof
-
(1)
Since \(L\in {\mathrm {PT}}(n)\), it is a finite union of equivalence classes \([v]_n\) for \(v\in \varSigma ^*\). Such an equivalence class \([v]_n\) can be defined by the formula
$$\begin{aligned} \varphi (x)=\bigwedge _{\begin{array}{c} u\sqsubseteq v\\ |u|\leqslant n \end{array}}u\sqsubseteq x \wedge \bigwedge _{\begin{array}{c} u\not \sqsubseteq v\\ |u|\leqslant n \end{array}}\lnot (u\sqsubseteq x)\,. \end{aligned}$$Since \(\varphi \) uses constants of length \(\leqslant n\), only, we have \(||\varphi ||\leqslant n\).
-
(2)
Now let \(\varphi (x)\in \mathrm {FO}^2_{\mathrm {ptNFA}}\) be a quantifier-free formula with \(||\varphi (x)||\leqslant n\). First, suppose \(x\in L({\mathcal {A}})\) is a subformula of \(\varphi (x)\). Then, the depth of the pt-nfa \({\mathcal {A}}\) is \(\leqslant n\). Hence, by [17, Thm. 8], \(L({\mathcal {A}})\in {\mathrm {PT}}(n)\). By the first statement, any subformula \(x\in L({\mathcal {A}})\) can be replaced by a quantifier- and automata-free formula \(\uplambda (x)\in \mathrm {FO}^2_\emptyset \) with \(||\uplambda (x)||\leqslant n\). Consequently, we can assume that \(\varphi (x)\) is automata-free, i.e., belongs to \(\mathrm {FO}^2_\emptyset \). Now replace subformulas of the form \(x\sqsubseteq v\) (with v a word) by
$$\begin{aligned} \bigvee _{u\sqsubseteq v}x=u\,, \end{aligned}$$such that the formula \(\varphi (x)\) becomes a Boolean combination of formulas \(u\sqsubseteq x\) and \(u=x\) with constants u of length \(\leqslant n\). Note that \(\{u\}{\mathord {\uparrow }}\) is of height \(\leqslant |u|\) and \(\{u\}\) is of height \(\leqslant |u|+1\). Hence, \(\varphi (x)\) defines a Boolean combination of languages from \({\mathrm {PT}}(n+1)\), i.e., a language from \({\mathrm {PT}}(n+1)\). \(\square \)
Remark
The above lemma shows that quantifier- and automata-free formulas of norm \(\leqslant n\) suffice to describe all piecewise testable languages of height \(\leqslant n\), but any such formula is only guaranteed to define a piecewise testable language of height \(\leqslant n+1\). The bounds are tight as the following two examples demonstrate (with \(\varSigma =\{a\}\)):
-
(1)
The language \(\{aaa\}a^*\) belongs to \({\mathrm {PT}}(3)\), but cannot be defined by a formula of norm \(\leqslant 2\).
-
(2)
The formula \(x=aaa\) of norm 3 defines the language \(\{aaa\}\) from \({\mathrm {PT}}(4)\setminus {\mathrm {PT}}(3)\).
Note that all heights appearing in Theorem 2.1 are bounded by \((|\varSigma |+1)\cdot \bigl (g_{|\varSigma |}(n)+m\bigr )\). We now bound this function by a polynomial.
Lemma 4.2
Let \(c=2\cdot |\varSigma |\) and let \(m,n\in {{\mathbb {N}}}\). Then, \((|\varSigma |+1)\cdot \bigl (g_{|\varSigma |}(n)+m\bigr )<(m+n+2)^c\).
Proof
If \(|\varSigma |=1\), we get
If \(|\varSigma |\geqslant 2\), we obtain
\(\square \)
Theorem 4.3
Let \(c=2\cdot |\varSigma |\) and \(\varphi (x)\in \mathrm {C}^2_{\mathrm {ptNFA}}\). Then, the language \(L_\varphi =\bigl \{u\in \varSigma ^*\mid {\mathcal {S}}\models \varphi (u)\bigr \}\) is piecewise testable of height \(<2^{c^{2||\varphi ||}}\).
Proof
We prove the claim by induction on the construction of the formula \(\varphi \).
First suppose \(\varphi (x)\) is quantifier-free. Then, by Lemma 4.1(2), the language \(L_\varphi \) is piecewise testable of height \(\leqslant ||\varphi ||+1 <2^{c^{2||\varphi ||}}\) since \(c\geqslant 2\). If the formula \(\varphi \) is a Boolean combination of formulas, the claim follows by induction since the doubly exponential function is monotone.
Now let \(\varphi (x)=\exists ^{\geqslant t}y:\varphi '(x,y)\). Our first goal is to express the formula \(\varphi (x)\) as a Boolean combination of formulas \(\alpha (x)\) with \(||\alpha ||\leqslant ||\varphi '||\) and \(\exists ^{\geqslant s}y:\bigl (x\theta y\wedge \gamma (y)\bigr )\) with \(s\leqslant t\),  , and \(||\gamma ||\leqslant ||\varphi '||\).
, and \(||\gamma ||\leqslant ||\varphi '||\).
There exists a finite set A of formulas of the following form such that \(\varphi '(x,y)\) is a Boolean combination of formulas from A:
-
formulas where at most x or y, but not both, are free
-
atomic formulas \(x\sqsubseteq y\), \(x=y\), and \(y\sqsubseteq x\)
Note that all formulas \(\alpha \) from A satisfy \(||\alpha ||\leqslant ||\varphi '||\) since they are subformulas of \(\varphi '(x,y)\).
For \(B\subseteq A\) set
Then, there is a set \({\mathcal {B}}\) of subsets of A such that \(\varphi '(x,y)\) is equivalent to
Since any pair of words can satisfy at most one formula \(\delta _B(x,y)\), the formula \(\varphi (x)=\exists ^{\geqslant t}y:\varphi '(x,y)\) is equivalent to
where the disjunction extends over all tuples \((t_B)_{B\in {\mathcal {B}}}\) of natural numbers from \(\{0,1,\dots ,t\}\) that sum up to t.
So far, we expressed the formula \(\varphi (x)\) as a Boolean combination of formulas \(\exists ^{\geqslant s}y:\delta (x,y)\) with \(s\leqslant t\) and \(\delta (x,y)\) a conjunction of possibly negated formulas from A. Note that any such formula is equivalent to the disjunction over all formulas

where the disjunction extends over all tuples \((s_1,s_2,s_3,s_4)\) of natural numbers from \(\{0,1,\dots ,s\}\) that sum up to s.
So far, we expressed the formula \(\varphi (x)\) as a Boolean combination of formulas \(\exists ^{\geqslant s}y:\bigl (x\theta y\wedge \delta (x,y)\bigr )\) with \(s\leqslant t\), \(\delta (x,y)\) a conjunction of possibly negated formulas from A, and  .
.
We now consider one such formula. Since \(\delta (x,y)\) is a conjunction of possibly negated formulas from A, we can write it as \(\alpha (x)\wedge \beta (x,y)\wedge \gamma (y)\) with \(||\alpha ||,||\gamma ||\leqslant ||\varphi '||\) and \(\beta (x,y)\) a conjunction of formulas of the form \(x\sqsubseteq y\), \(x\sqsupseteq y\), and their negations. Depending on whether \(x\theta y\) is consistent with \(\beta (x,y)\) or not, the formula \(\exists ^{\geqslant s}y:\bigl (x\theta y\wedge \delta (x,y)\bigr )\) is equivalent to \(\bot \) or to
Thus, we reached our first goal: we expressed the formula \(\varphi (x)\) as a Boolean combination
-
(1)
of formulas \(\alpha (x)\) with \(||\alpha ||\leqslant ||\varphi '||\) and
-
(2)
of formulas \(\exists ^{\geqslant s}y:\bigl (x\theta y\wedge \gamma (y)\bigr )\) with \(s\leqslant t\),
 , and \(||\gamma ||\leqslant ||\varphi '||\).
, and \(||\gamma ||\leqslant ||\varphi '||\).
Since the class \({\mathrm {PT}}(n)\) is closed under Boolean operations, it suffices to show that any such formula defines a piecewise testable language of height \(< 2^{c^{2||\varphi ||}}\). By the induction hypothesis, this is clear for formulas from (1) since \(||\varphi '||\leqslant ||\varphi ||\).
Our second and final goal is to show that it also holds for formulas from (2). So let \(s\leqslant t\),  , and \(\gamma (y)\) be a formula with \(||\gamma ||\leqslant ||\varphi '||\) and consider the formula \(\exists ^{\geqslant s}y:\bigl (x\theta y\wedge \gamma (y)\bigr )\).
, and \(\gamma (y)\) be a formula with \(||\gamma ||\leqslant ||\varphi '||\) and consider the formula \(\exists ^{\geqslant s}y:\bigl (x\theta y\wedge \gamma (y)\bigr )\).
We consider the language
that, by the induction hypothesis, is piecewise testable of height \(< 2^{c^{2||\varphi '||}}\). Now we have to consider the four possible values of \(\theta \) separately.
-
1.
Let
 . Then, the formula
. Then, the formula  is equivalent to $$\begin{aligned}&\gamma (x)\wedge \exists ^{\geqslant s+1}y:\bigl (x\sqsubseteq y\wedge \gamma (y)\bigr )\\ \vee&\lnot \gamma (x)\wedge \exists ^{\geqslant s}y:\bigl (x\sqsubseteq y\wedge \gamma (y)\bigr )\,. \end{aligned}$$
is equivalent to $$\begin{aligned}&\gamma (x)\wedge \exists ^{\geqslant s+1}y:\bigl (x\sqsubseteq y\wedge \gamma (y)\bigr )\\ \vee&\lnot \gamma (x)\wedge \exists ^{\geqslant s}y:\bigl (x\sqsubseteq y\wedge \gamma (y)\bigr )\,. \end{aligned}$$Consequently, the set of words satisfying
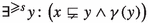 equals $$\begin{aligned} (L\cap L{\mathord {\downarrow }}^{\geqslant s+1})\cup (L{\mathord {\downarrow }}^{\geqslant s}\setminus L)\,. \end{aligned}$$
equals $$\begin{aligned} (L\cap L{\mathord {\downarrow }}^{\geqslant s+1})\cup (L{\mathord {\downarrow }}^{\geqslant s}\setminus L)\,. \end{aligned}$$From Theorem 2.1(2), we obtain
$$\begin{aligned} L{\mathord {\downarrow }}^{\geqslant s+1},L{\mathord {\downarrow }}^{\geqslant s}\in {\mathrm {PT}}\Bigl (\bigl (|\varSigma |+1\bigr )\cdot \bigl (g_{|\varSigma |}(2^{c^{2||\varphi '||}})+1\bigr )\Bigr )\,. \end{aligned}$$Note that
$$\begin{aligned} \bigl (|\varSigma |+1\bigr )\cdot \bigl (g_{|\varSigma |}(2^{c^{2||\varphi '|||}})+1\bigr )&< (2^{c^{2||\varphi '||}}+3)^c&\text {by Lemma}~4.2\\&< (2^{c^{2||\varphi '||}}+2^{c^{2||\varphi '||}})^c&\text {since }c\geqslant 2,||\varphi '||\geqslant 1\\&=(2\cdot 2^{c^{2||\varphi '||}})^c\\&<(2^{c^{|\mathrm {bin}(s)|}} \cdot 2^{c^{2||\varphi '||}})^c\\&=(2^{c^{|\mathrm {bin}(s)|}+c^{2||\varphi '||}})^c\\&\leqslant (2^{c^{|\mathrm {bin}(s)|+2||\varphi '||}})^c&\text {since }c\geqslant 2,|\mathrm {bin}(s)|,||\varphi '||\geqslant 1\\&= 2^{c^{1+|\mathrm {bin}(s)|+2||\varphi '||}}\\&\leqslant 2^{c^{2||\varphi ||}} \end{aligned}$$where the last inequality holds since \(||\varphi ||=|\mathrm {bin}(t)|+||\varphi '||\), \(|\mathrm {bin}(s)|\geqslant 1\), and \(s\leqslant t\). It follows that \(L{\mathord {\downarrow }}^{\geqslant s+1}\) and \(L{\mathord {\downarrow }}^{\geqslant s}\) both are piecewise-testable of height \(<2^{c^{2||\varphi ||}}\). Since this also holds for the language L and since \({\mathrm {PT}}(2^{c^{2||\varphi ||}}-1)\) is closed under Boolean combinations, this settles the case
 .
. -
2.
Now let
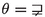 . Similarly to above, the set of words satisfying
. Similarly to above, the set of words satisfying  is a Boolean combination of the languages L, \(L{\mathord {\uparrow }}_{\geqslant s+1}\), and \(L{\mathord {\uparrow }}_{\geqslant s}\). By Theorem 2.1(1), the latter two languages both belong to $$\begin{aligned} {\mathrm {PT}}\bigl (g_{|\varSigma |}(2^{c^{2||\varphi '||}})+s\bigr )\,. \end{aligned}$$
is a Boolean combination of the languages L, \(L{\mathord {\uparrow }}_{\geqslant s+1}\), and \(L{\mathord {\uparrow }}_{\geqslant s}\). By Theorem 2.1(1), the latter two languages both belong to $$\begin{aligned} {\mathrm {PT}}\bigl (g_{|\varSigma |}(2^{c^{2||\varphi '||}})+s\bigr )\,. \end{aligned}$$Note that
$$\begin{aligned} g_{|\varSigma |}(2^{c^{2||\varphi '||}})\geqslant 2^{c^{2||\varphi '||}} \geqslant 16>4 \end{aligned}$$since \(c\geqslant 2\) and \(||\varphi '||\geqslant 1\). It follows that
$$\begin{aligned} g_{|\varSigma |}(2^{c^{2||\varphi '||}})+s&< g_{|\varSigma |}(2^{c^{2||\varphi '||}})+s+g_{|\varSigma |}(2^{c^{2||\varphi '||}})-4&\text {since }g_{|\varSigma |}(2^{c^{2||\varphi '||}})>4\\&\leqslant 2\cdot \bigl (g_{|\varSigma |}(2^{c^{2||\varphi '||}})+s-2\bigr )\\&\leqslant \bigl (|\varSigma |+1\bigr )\cdot \bigl (g_{|\varSigma |}(2^{c^{2||\varphi '||}})+s-2\bigr )&\text {since }|\varSigma |\geqslant 1\\&< (2^{c^{2||\varphi '||}}+s)^c&\text {by Lemma}~4.2\\&\leqslant (2^{c^{2||\varphi '||}}+2^{c^{|\mathrm {bin}(s)|}})^c&\text {since }c\geqslant 2\\&\leqslant (2^{c^{|\mathrm {bin}(s)|+2||\varphi '||}})^c\\&\leqslant 2^{c^{2||\varphi ||}} \end{aligned}$$where the last equality follows from \(||\varphi ||=|\mathrm {bin}(t)|+||\varphi '||\) and \(s\leqslant t\). Thus, we showed that \(L{\mathord {\uparrow }}_{\geqslant s+1}\) and \(L{\mathord {\uparrow }}_{\geqslant s}\) both are of height \(<2^{c^{2||\varphi ||}}\). Since this also holds for the language L and since \({\mathrm {PT}}\bigl (2^{c^{2||\varphi ||}}-1\bigr )\) is closed under Boolean operations, this settles the case
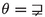 .
. -
3.
Next consider the case \(\theta ={\parallel }\). By Theorem 2.1(3), the set of words satisfying \(\exists ^{\geqslant s}y:(x\parallel y\wedge \gamma (y))=L{\mathord {\parallel }}^{\geqslant s}\) belongs to \({\mathrm {PT}}(g_{|\varSigma |}(2^{c^{2||\varphi '||}})+s)\). The claim follows from \(g_{|\varSigma |}(2^{c^{2||\varphi '||}})+s<2^{c^{2||\varphi ||}}\) as we verified in the previous case.
-
4.
It remains to consider the (trivial) case that \(\theta \) is equality. Then, the set of words satisfying \(\exists ^{\geqslant s}y:\bigl (x=y\wedge \gamma (y)\bigr )\) equals
-
\(\varSigma ^*\in {\mathrm {PT}}(0)\) if \(s=0\),
-
\(L\in {\mathrm {PT}}(2^{c^{2||\varphi '||}}-1)\) if \(s=1\), and
-
\(\emptyset \in {\mathrm {PT}}(0)\) if \(s>1\).
Consequently, it is always of height \(<2^{c^{2||\varphi ||}}\).
-
Thus, we reached our second and final goal.
In summary, we proved that the set of words satisfying \(\varphi (x)\) is a Boolean combination of piecewise testable languages of height \(< 2^{c^{2||\varphi ||}}\) and therefore belongs to this class as well.
This finishes the inductive proof of the theorem. \(\square \)
Since piecewise testable languages of bounded height can be defined by quantifier-free formulas from \(\mathrm {FO}^2_\emptyset \), we obtain the following quantifier-elimination result (that, differently from the theorem above, applies also to formulas with two free variables).
Corollary 4.4
Let \(c=2\cdot |\varSigma |\). Every \(\mathrm {C}^2_{\mathrm {ptNFA}}\)-formula \(\varphi \) is equivalent to some quantifier- and automata-free formula \(\psi \in \mathrm {FO}^2_\emptyset \) with \(||\psi ||< 2^{c^{2||\varphi ||}}\).
For first-order formulas \(\varphi \), this result can be found in [10, Cor. 7.4 & Thm. 7.5].
Proof
Let \(\varphi (x,y)\) be some formula from \(\mathrm {C}^2_{\mathrm {ptNFA}}\). As in the previous proof, it is a Boolean combination of formulas with a single free variable of norm \(\leqslant ||\varphi ||\) and of the formulas \(x\sqsubseteq y\), \(x=y\), and \(x\sqsupseteq y\). By Theorem 4.3, any formula \(\alpha (x)\) with a single free variable defines a piecewise testable language L of height \(< 2^{c^{2||\varphi ||}}\). By Lemma 4.1(1), this language can be defined by a quantifier- and automata-free formula \(\alpha '(x)\) from \(\mathrm {FO}^2_\emptyset \) with \(||\alpha '||< 2^{c^{2||\varphi ||}}\). Replacing, in the Boolean combination \(\varphi (x,y)\), all occurrences of \(\alpha (x)\) with \(\alpha '(x)\), we obtain a quantifier- and automata-free formula \(\psi (x,y)\) that is equivalent to \(\varphi (x,y)\) and satisfies \(||\psi ||<2^{c^{2||\varphi ||}}\). \(\square \)
Note that the above corollary implies in particular that the logics \(\mathrm {C}^2_{\mathrm {ptNFA}}\) and \(\mathrm {FO}^2_\emptyset \) are equally expressive (a description of this expressive power in terms of subword-piecewise testable relations can be found in [10, Thm. 7.2(ii)]). It bounds the norm of the resulting formula \(\psi \) in terms of the norm of \(\varphi \) (which, in turn, is bounded by the size of \(\varphi \)). Since \(\psi \) is automata- and quantifier-free, its norm equals the maximal length of a constant appearing in \(\psi \), i.e., all words in \(\psi \) are of length at most doubly exponential in \(|\varphi |\). Hence, the number of distinct atomic formulas in \(\psi \) is at most triply exponential. It follows that the size of \(\psi \) is at most fivefold exponential in the norm (and therefore the size) of \(\varphi \).
This explosion of size is not surprising since, in \(\psi \), we are not allowed to use quantification (let alone threshold counting quantification) nor piecewise testable predicates. The following result shows that disallowing threshold counting quantification alone already results in an exponential increase in formula size.
Theorem 4.5
For \(\varSigma =\{a\}\), the logic \(\mathrm {C}^2_\emptyset \) is exponentially more succinct than \(\mathrm {FO}^2_\emptyset \). More precisely, there is a sequence \(\bigl (\varphi _n(x)\bigr )_{n\in {{\mathbb {N}}}}\) of formulas in \(\mathrm {C}^2_\emptyset \) of size O(n) such that, for every sequence of equivalent formulas \(\bigl (\psi _n(x)\bigr )_{n\in {{\mathbb {N}}}}\) from \(\mathrm {FO}^2_\emptyset \), \(\psi _n\) is of size \(\varOmega (2^n)\).
We do not know whether the same result holds for non-singleton alphabets.
Proof
Let \(\varSigma =\{a\}\). For \(n\in {{\mathbb {N}}}\) consider the formula
Note that \(|\varphi _n|=O(n)\) since the thresholds \(2^n\) and \(2^n+1\) are encoded in binary. Furthermore, \(a^{2^n-1}\) is the only word satisfying this formula.
Now let \(\psi _n(x)\) be a formula from \(\mathrm {FO}^2_\emptyset \) that is equivalent to \(\varphi _n(x)\). First note that \(a^m\sqsubseteq z\) (where z is any variable) is equivalent to the formula
(where \(z'\) is the other variable). Thus, replacing all subformulas \(a^m\sqsubseteq z\) and \(z\sqsubseteq a^m\) by \(\alpha _m(z)\) and \(\lnot \alpha _{m+1}(z)\), respectively, we eliminate all constants from \(\psi _n(x)\). This replacement results in a linear increase in formula size, only (note that the size of the word \(a^m\) is m). So, from now on, we can assume that \(\psi _n(x)\) is constant-free.
Now, let \(\psi (x)\) be any constant-free formula from \(\mathrm {FO}^2_\emptyset \) of quantifier-rank d and let \(k,\ell \in {{\mathbb {N}}}\) with \(k,\ell \geqslant d\). Then, by induction on d, one can show that \({\mathcal {S}}\models \psi (a^k)\iff {\mathcal {S}}\models \psi (a^\ell )\).
Since \(a^{2^n-1}\) is the only word satisfying \(\psi _n(x)\), the quantifier-rank of \(\psi _n(x)\) is \(\geqslant 2^n-1\). Hence, the size of \(\psi _n(x)\) is exponential in n. \(\square \)
5 Complexity of the \(\mathrm {C}^2_{\mathrm {ptNFA}}\)-theory
We now adapt the technique by Ferrante and Rackoff from first-order logic to its extension by threshold counting quantifiers to derive our upper complexity bound from Corollary 4.4.Footnote 4 Central to this proof is the following lemma expressing that quantification in formulas can be restricted to words of bounded length. This property is the core of the method by Ferrante and Rackoff [3].
Lemma 5.1
Let \(\varphi (x)=\exists ^{\geqslant t}y:\psi (x,y)\) be a formula from \(\mathrm {C}^2_{\mathrm {ptNFA}}\). Let \(c=2\cdot |\varSigma |\), \(N\in {{\mathbb {N}}}\) with \(2^{c^{2||\varphi ||}}\leqslant N\), and \(u\in \varSigma ^*\) with \(|u|<N\). Then, \({\mathcal {S}}\models \varphi (u)\) iff there are t words v of length \(< N^{2c}\) such that \({\mathcal {S}}\models \psi (u,v)\).
Proof
We have to show that, whenever \(\varphi (u)\) holds, then there are t short words v such that \(\psi (u,v)\) holds (the other implication is trivial).
So assume there are at least t words in the language \(L:=\bigl \{v\in \varSigma ^*\mid {\mathcal {S}}\models \psi (u,v)\bigr \}\).
By Corollary 4.4, there exists a quantifier- and automata-free formula \(\psi '(x,y)\in \mathrm {FO}^2_\emptyset \) equivalent to \(\psi (x,y)\) such that \(||\psi '||<2^{c^{2||\psi ||}}< 2^{c^{2||\varphi ||}}\leqslant N\). Since \(|u|<N\), also the norm of the quantifier- and automata-free formula \(\psi '(u,y)\) is \(<N\). Note that L is defined by this formula. Hence, by Lemma 4.1(2), L is piecewise testable of height \(\leqslant N\). Since L contains at least t words, the definition of the function \(g_{|\varSigma |}\) together with the convexity of all equivalence classes implies that L contains mutually distinct words \(v_1,\dots ,v_t\) of length \(<g_{|\varSigma |}(N)+t\leqslant (N+t+2)^c\) (by Lemma 4.2). We have \(|\mathrm {bin}(t)|\leqslant ||\varphi ||\) which implies \(t\leqslant N\). Hence, \((N+t+2)^c\leqslant (2N+2)^c\) which is smaller than \(N^{2c}\) since \(N\geqslant 16\). Thus, we have \(|v_i|<N^{2c}\) for all \(1\leqslant i\leqslant t\). Consequently, we found t “short” witnesses for \(\psi (u,y)\). \(\square \)
Proposition 5.2
There is an alternating algorithm that, on input of a formula \(\varphi (x,y)\in \mathrm {C}^2_{\mathrm {ptNFA}}\) and words u and v, decides whether \({\mathcal {S}}\models \varphi (u,v)\). This alternating algorithm runs in time doubly exponential in \(\bigl |\bigl |\varphi (u,v)\bigr |\bigr |\) and uses \(O\bigl (|\varphi |\bigr )\) alternations.
Proof
Before we come to the actual proof, we explain the idea underlying our approach. First, from \(\varphi \), u, v, and N, we could compute a propositional formula (whose atomic propositional formulas are atomic formulas from \(\mathrm {C}^2_{\mathrm {ptNFA}}\)) that is equivalent to \(\varphi (u,v)\). This is possible since, by the previous lemma, we can restrict quantification in \(\varphi \) to words of bounded length. To serve as the basis of an alternating algorithm, we need in addition that the propositional formula is in negation normal form (i.e., at most atomic formulas are negated).
However, this approach has the following two problems.
First, the length bound from Lemma 5.1 is doubly exponential. Hence, the propositional formula for \(\exists ^{\geqslant 1} y:\psi (u,y)\) is the disjunction over all formulas \(\psi (u,v)\) with v a word of doubly exponential length. But computing this formula requires triply exponential time. The solution to this first problem is that the propositional formula is not calculated explicitly. Instead, its evaluation is simulated by a procedure that takes, as arguments, a formula \(\alpha (x,y)\), two words \(w_x\) and \(w_y\), and a natural number N and returns the truth value of \(\alpha (w_x,w_y)\) if all quantifications are bounded by values that depend on N.
Since we do not compute the propositional formula, we cannot compute its negation normal form afterwards. Nor can we transform the \(\mathrm {C}^2_{\mathrm {ptNFA}}\)-formula into negation normal form since this logic does not allow universal quantifiers. This problem is solved by considering not just one procedure as above, but two (one for formulas \(\alpha \) occurring positively, one for negative occurrences).
Formally (and now the actual proof starts), we use the following recursive procedures \(\mathsf {check}_\mathsf {P}\) and \(\mathsf {check}_\mathsf {N}\) whose parameters are
-
a \(\mathrm {C}^2_{\mathrm {ptNFA}}\)-formula \(\alpha (x,y)\),
-
two words \(w_x\) and \(w_y\), and
-
a natural number N.
-
(1)
If \(\alpha \) is an atomic formula, then decide whether \(\alpha (w_x,w_y)\) holds. This can be done by a nondeterministic algorithm in time linear in \(|w_x|+|w_y|+|\alpha |\). If so, the procedure \(\mathsf {check}_\mathsf {P}\) returns true and false otherwise. The procedure \(\mathsf {check}_\mathsf {N}\) returns the negation of these values.
-
(2)
If \(\alpha =\beta \vee \gamma \), then a call of \(\mathsf {check}_\mathsf {P}(\alpha ,w_x,w_y,N)\) returns true iff at least one of \(\mathsf {check}_\mathsf {P}(\beta ,w_x,w_y,N)\) and \(\mathsf {check}_\mathsf {P}(\gamma ,w_x,w_y,N)\) returns true. Dually, \(\mathsf {check}_\mathsf {N}(\alpha ,w_x,w_y,N)\) returns true iff both, \(\mathsf {check}_\mathsf {N}(\beta ,w_x,w_y,N)\) and \(\mathsf {check}_\mathsf {N}(\gamma ,w_x,w_y,N)\), return true.
-
(3)
If \(\alpha =\lnot \beta \), then \(\mathsf {check}_\mathsf {P}(\alpha ,w_x,w_y,N)\) returns true iff \(\mathsf {check}_\mathsf {N}(\beta ,w_x,w_y,N)\) returns true and dually for \(\mathsf {check}_\mathsf {N}(\alpha ,w_x,w_y,N)\).
-
(4)
Let \(\alpha =\exists ^{\geqslant t}y:\psi (x,y)\). Then, \(\mathsf {check}_\mathsf {P}(\alpha ,w_x,w_y,N)\) returns true iff, for some set T of t words of length \(<N^{2c}\), the call of \(\mathsf {check}_\mathsf {P}(\psi ,w_x,w_y',N^{2c})\) returns true for all words \(w_y'\in T\). Thus, the evaluation of \(\mathsf {check}_\mathsf {P}\) consists of two phases: an existential phase (in which a set T is guessed, i.e. the computation branches into a sub-computation for each choice of T), followed by a universal phase (in which for each sub-computation, i.e. for each choice of T, it is checked whether T is a set of t solutions). Dually, \(\mathsf {check}_\mathsf {N}(\alpha ,w_x,w_y,N)\) returns true iff, for some set T of \(t-1\) words of length \(<N^{2c}\), the call of \(\mathsf {check}_\mathsf {N}(\psi ,w_x,w_y',N^{2c})\) returns true for all words \(w_y'\) of length \(<N^{2c}\) that do not belong to T. As before, the call of \(\mathsf {check}_\mathsf {N}(\alpha ,w_x,w_y,N)\) too consists of an existential phase followed by a universal phase (considering, instead of the guessed set T, its complement wrt. the set of words of length \(<N^{2c}\)).
Now let \(\varphi (x,y)\) be a formula from \(C^2_{\mathrm {ptNFA}}\), \(u,v\in \varSigma ^*\), and \(N_0\in {{\mathbb {N}}}\) with \(|u|,|v|<N_0\) and \(2^{c^{2||\varphi ||}}\leqslant N_0\). By induction on the size of \(\varphi \) and using Lemma 5.1, one obtains that \({\mathcal {S}}\models \varphi (u,v)\) iff \(\mathsf {check}_\mathsf {P}(\varphi ,u,v,N_0)\) returns true iff \(\mathsf {check}_\mathsf {N}(\varphi ,u,v,N_0)\) returns false.
Now let \(\psi =\varphi (u,v)\). Then, \({\mathcal {S}}\models \varphi (u,v)\) iff \(\mathsf {check}_\mathsf {P}(\psi ,\varepsilon ,\varepsilon ,2^{c^{2||\psi ||}})\) returns true.
We now analyse the runtime of an execution of a call of \(\mathsf {check}_\mathsf {P}(\psi ,\varepsilon ,\varepsilon ,2^{c^{2||\psi ||}})\). First, the value of the parameter N is bounded by
where \(d\leqslant ||\psi ||\) is the quantifier depth of \(\psi \). Consequently, the recursive execution considers only words of this doubly exponential length. Further, when handling a quantifier \(\exists ^{\geqslant t}\), it considers a set of at most t words of this doubly exponential length. Since t is at most exponential in the size of \(\psi \), the alternating algorithm runs in at most doubly exponential time.
Further note that the execution alternates between universal and existential states only linearly often. \(\square \)
Since \(||\varphi ||\leqslant |\varphi |\), we immediately obtain
Theorem 5.3
The \(\mathrm {C}^2_{\mathrm {ptNFA}}\)-theory of \({\mathcal {S}}\) belongs to \(\mathsf {STA}\bigl (*,2^{2^{\mathrm {poly}(n)}},O(n)\bigr )\), i.e., can be decided in doubly exponential alternating time with linearly many alternations.
6 Summary and open question
We considered the extension of first-order logic by threshold-counting quantifiers over the subword order with piecewise testable predicates and constants. We showed that the 2-variable fragment of this theory is decidable using doubly exponential space, more precisely, it belongs to \(\mathsf {STA}\bigl (*,2^{2^{\mathrm {poly}(n)}},O(n)\bigr )\). This extends a result from [10] in two aspects: first, we add threshold counting quantifiers and piecewise testable predicates to first-order logic and, secondly, we improve their upper bound by one exponent (if only considering the space bound). Our proof relies on two independent aspects: the consideration of the height of definable languages (which is a direct continuation from [10]) and an adaptation of Ferrante and Rackoff’s method [3].
The work done in this paper can be continued in the following directions:
-
Addition of further binary relations: Let \({\mathcal {C}}\) be some collection of binary relations on \(\varSigma ^*\) such that Boolean combinations of relations from \({\mathcal {C}}\cup \{\sqsubseteq \}\) are effectively rational. This holds, e.g., if \({\mathcal {C}}\) consists of the prefix relation, the relation “have equal length”, the cover relation as well as powers thereof (e.g., the relation “\(u\sqsubseteq v\) and \(|v|-|u|=k\)” for fixed \(k\in {{\mathbb {N}}}\)). Then, the proof of [9, Thm. 5.5] can be extended to show the following result: The \(\mathrm {FO}^2_{\mathrm {NFA}}\)-theory of the extension of the structure \({\mathcal {S}}\) with the binary relations from \({\mathcal {C}}\) is decidable. If the Boolean combinations are even effectively unambiguous rational, then the \(\mathrm {C}^2_{\mathrm {NFA}}\)-theory becomes decidable using the arguments from [16] (where the result is demonstrated in case \({\mathcal {C}}\) contains the cover relation, only). It is not clear for which sets \({\mathcal {C}}\) the \(\mathrm {C}^2_{\mathrm {ptNFA}}\)-theory becomes decidable in elementary space (which is the case for \({\mathcal {C}}=\emptyset \) as demonstrated in this paper). The same question applies already for the \(\mathrm {FO}^2_\emptyset \)-theory.
-
Addition of regular predicates: By [16], the \(\mathrm {C}^2_{\mathrm {NFA}}\)-theory is decidable, but the only known algorithm is non-elementary. On the other hand, the \(\mathrm {C}^2_{\mathrm {ptNFA}}\)-theory is decidable using elementary space. It is not clear whether there are other classes of nfas \({\mathrm {A}}\subseteq {\mathrm {NFA}}\) such that the \(\mathrm {C}^2_{\mathrm {A}}\)- or \(\mathrm {FO}^2_{\mathrm {A}}\)-theory are decidable in elementary space.
Notes
The operation \({\mathord {\uparrow }}_{\geqslant t}\) for \(t\geqslant 2\) is not idempotent and therefore not a closure operator. For convenience, we stick to this name.
References
Baumann, P., Ganardi, M., Thinniyam, R. S., Zetzsche, G.: Existential definability over the subword ordering. In: STACS’22, volume 219 of LIPIcs, pp. 7:1–7:15. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2022)
Berman, L.: The complexitiy of logical theories. Theoret. Comput. Sci. 11, 71–77 (1980)
Ferrante, J., Rackoff, Ch.: The Computational Complexity of Logical Theories Lecture Notes in Mathematics, vol. 718. Springer, Berlin (1979)
Finkel, A., Schnoebelen, Ph.: Well-structured transition systems everywhere! Theoret. Comput. Sci. 256, 63–92 (2001)
Higman, G.: Ordering by divisibility in abstract algebras. Proc. Lond. Math. Soc. 2, 326–336 (1952)
Halfon, S., Schnoebelen, Ph., Zetzsche, G.: Decidability, complexity, and expressiveness of first-order logic over the subword ordering. In: LICS’17, pp. 1–12. IEEE Computer Society (2017)
Ježek, J., McKenzie, R.: Definability in substructure orderings. I: finite semilattices. Algebra Univers 61(1), 59–75 (2009)
Kudinov, O.V., Selivanov, V.L.: Undecidability in the homomorphic quasiorder of finite labelled forests. J. Log. Comput. 17(6), 1135–1151 (2007)
Karandikar, P., Schnoebelen, Ph.: Decidability in the logic of subsequences and supersequences. In: FSTTCS’15, Leibniz International Proceedings in Informatics (LIPIcs) vol. 45, pp. 84–97. Leibniz-Zentrum für Informatik (2015)
Karandikar, P., Schnoebelen, Ph.: The height of piecewise-testable languages and the complexity of the logic of subwords. Log. Methods Comput. Sci. 15(2) (2019)
Kuske, D., Schwarz, Ch.: Complexity of counting first-order logic for the subword order. In: MFCS’20, Leibniz International Proceedings in Informatics (LIPIcs) vol. 170, pp. 56:1–56:13. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2020)
Kudinov, O.V., Selivanov, V.L., Yartseva, L.V.: Definability in the subword order. In: CiE’10, Lecture Notes in Computer Science, vol. 6158, pp. 246–255. Springer (2010)
Kudinov, O.V., Selivanov, V.L., Zhukov, A.V.: Definability in the h-quasiorder of labeled forests. Ann. Pure Appl. Logic 159(3), 318–332 (2009)
Kuske, D.: Theories of orders on the set of words. Theoret. Inf. Appl. 40, 53–74 (2006)
Kuske, D.: The subtrace order and counting first-order logic. In: CSR’20, Lecture Notes in Computer Science, vol. 12159, pp. 289–302. Springer (2020)
Kuske, D., Zetzsche, G.: Languages ordered by the subword order. In: FoSSaCS’19, Lecture Notes in Computer Science, vol. 11425, pp. 348–364. Springer (2019)
Masopust, T.: Piecewise testable languages and nondeterministic automata. In: MFCS’16, Leibniz International Proceedings in Informatics (LIPIcs) vol. 58, pp. 67:1–67:14. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2016)
Masopust, T., Thomazo, M.: On Boolean combinations forming piecewise testable languages. Theoret. Comput. Sci. 682, 165–179 (2017)
Schnoebelen, Ph.: Personal communication, February (2020)
Simon, I.: Hierarchies of events with dot-depth one. Ph.D. thesis, University of Waterloo (1972)
Simon, I.: Piecewise testable events. In: Automata Theory and Formal Languages, Lecture Notes in Comp. Science vol. 33, pp. 214–222. Springer (1975)
Sakarovitch, J., Simon, I.: Subwords. In: Combinatorics on Words, chapter 6, pp. 105–144. Addison-Wesley, Boston (1983)
Thinniyam, R.S.: Definability of recursive predicates in the induced subgraph order. In: 7th Indian Conference on Logic and Its Applications (ICLA’17), Lecture Notes in Computer Science, vol. 10119, pp. 211–223. Springer (2017)
Thinniyam, R.S.: Defining recursive predicates in graph orders. Log. Methods Comput. Sci. 14(3) (2018)
Acknowledgements
We thank the reviewer for the thorough reading and commenting of the submitted version; these remarks led to several simplification of proofs and also improved the readability.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kuske, D., Schwarz, C. Alternating complexity of counting first-order logic for the subword order. Acta Informatica 60, 79–100 (2023). https://doi.org/10.1007/s00236-022-00424-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00236-022-00424-2



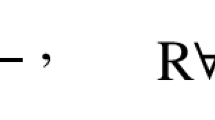
 , and
, and  . Then, the formula
. Then, the formula  is equivalent to
is equivalent to 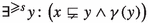 equals
equals  .
.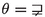 . Similarly to above, the set of words satisfying
. Similarly to above, the set of words satisfying  is a Boolean combination of the languages L,
is a Boolean combination of the languages L, 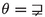 .
.