The Lawson number of a semitopological semilattice

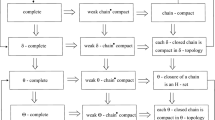
Abstract

For a Hausdorff topologized semilattice X its Lawson number $\bar{\Lambda }(X)$ is the smallest cardinal $\kappa$ such that for any distinct points $x,y\in X$ there exists a family $\mathcal U$ of closed neighborhoods of x in X such that $|\mathcal U|\le \kappa$ and $\bigcap \mathcal U$ is a subsemilattice of X that does not contain y. It follows that $\bar{\Lambda }(X)\le \bar{\psi }(X)$, where $\bar{\psi }(X)$ is the smallest cardinal $\kappa$ such that for any point $x\in X$ there exists a family $\mathcal U$ of closed neighborhoods of x in X such that $|\mathcal U|\le \kappa$ and $\bigcap \mathcal U=\{x\}$. We prove that a compact Hausdorff semitopological semilattice X is Lawson (i.e., has a base of the topology consisting of subsemilattices) if and only if $\bar{\Lambda }(X)=1$. Each Hausdorff topological semilattice X has Lawson number $\bar{\Lambda }(X)\le \omega$. On the other hand, for any infinite cardinal $\lambda$ we construct a Hausdorff zero-dimensional semitopological semilattice X such that $|X|=\lambda$ and $\bar{\Lambda }(X)=\bar{\psi }(X)=\mathrm {cf}(\lambda )$. A topologized semilattice X is called (i) $\omega$-Lawson if $\bar{\Lambda }(X)\le \omega$; (ii) complete if each non-empty chain $C\subseteq X$ has $\inf C\in {\overline{C}}$ and $\sup C\in {\overline{C}}$. We prove that for any complete subsemilattice X of an $\omega$-Lawson semitopological semilattice Y, the partial order $\le _X=\{(x,y)\in X\times X:xy=x\}$ of X is closed in $Y\times Y$ and hence X is closed in Y. This implies that for any continuous homomorphism $h:X\rightarrow Y$ from a complete topologized semilattice X to an $\omega$-Lawson semitopological semilattice Y the image h(X) is closed in Y.

1 Introduction

In this paper we introduce a new cardinal invariant $\bar{\Lambda }(X)$ of a Hausdorff topologized semilattice X, called the Lawson number of X. This was motivated by studying the closedness properties of complete topologized semilattices, see [1,2,3,4,5,6]. It turns out that complete semitopological semilattices share many common properties with compact topological semilattices, in particular their continuous homomorphic images in Hausdorff topological semilattices are closed.

A semilattice is any commutative semigroup of idempotents (an element x of a semigroup is called an idempotent if $xx=x$).

Each semilattice X carries the natural partial order $\le _X$ defined by $x\le _X y$ iff $xy=x=yx$. Many properties of semilattices are defined in the language of the natural partial order. In particular, for any point $x\in X$ we can consider its upper and lower sets

$$\begin{aligned} {\uparrow }x:=\{y\in X:xy=x\}\text { \ and \ }{\downarrow }x:=\{y\in X:xy=y\} \end{aligned}$$

in the partially ordered set $(X,\le _X)$.

A subset C of a semilattice X is called a chain if $xy\in \{x,y\}$ for any $x,y\in C$. A semilattice X is called chain-finite if each chain in X is finite. A semilattice is called linear if it is a chain in itself.

A semilattice endowed with a topology is called a topologized semilattice. A topologized semilattice X is called a (semi )topological semilattice if the semigroup operation $X\times X\rightarrow X$, $(x,y)\mapsto xy$, is (separately) continuous.

In [16] Stepp proved that for any homomorphism $h:X\rightarrow Y$ from a chain-finite semilattice to a Hausdorff topological semilattice Y, the image h(X) is closed in Y. In [1], the first authors improved this result of Stepp proving the following theorem.

Theorem 1

(Banakh, Bardyla) For any homomorphism $h:X\rightarrow Y$ from a chain-finite semilattice to a Hausdorff semitopological semilattice Y, the image h[X] is closed in Y.

Topological generalizations of the notion of chain-finiteness are the notions of chain-compactness and completeness, discussed in [5].

A topologized semilattice X is called

• chain-compact if each closed chain in X is compact;

• complete if each non-empty chain $C\subseteq X$ has $\inf C\in {\overline{C}}$ and $\sup C\in {\overline{C}}$.

Here ${\overline{C}}$ stands for the closure of C in X. Chain-compact and complete topologized semilattices appeared to be very helpful in studying the closedness properties of topologized semilattices, see [1,2,3,4,5,6, 11]. By Theorem 3.1 [1], a Hausdorff semitopological semilattice is chain-compact if and only if it is complete (see also Theorem 4.3 [5] for generalization of this characterization to topologized posets). In [1] the first two authors proved the following closedness property of complete topologized semilattices.

Theorem 2

(Banakh, Bardyla) For any continuous homomorphism $h:X\rightarrow Y$ from a complete topologized semilattice X to a Hausdorff topological semilattice Y, the image h[X] is closed in Y.

Theorems 1 and 2 motivate the following (still) open problem.

Problem 1

Assume that $h:X\rightarrow Y$ is a continuous homomorphism from a complete topologized semilattice X to a Hausdorff semitopological semilattice Y. Is h[X] closed in Y?

In [4] the first two authors gave the following partial answer to Problem 1.

Theorem 3

(Banakh, Bardyla) For any continuous homomorphism $h:X\rightarrow Y$ from a complete topologized semilattice X to a sequential Hausdorff semitopological semilattice Y, the image h[X] is closed in Y.

Another partial result to Problem 1 was given in [6].

Theorem 4

(Banakh, Bardyla, Ravsky) For any continuous homomorphism $h:X\rightarrow Y$ from a complete topologized semilattice X to a functionally Hausdorff semitopological semilattice Y, the image h[X] is closed in Y.

Let us recall that a topological space X is functionally Hausdorff if for any distinct points $x,y\in X$ there exists a continuous map $f:X\rightarrow {\mathbb R}$ such that $f(x)\ne f(y)$.

In fact, in [6] Theorem 4 was derived from the following closedness property of the partial order of a complete subsemilattice of a functionally Hausdorff semitopological semilattice.

Theorem 5

(Banakh, Bardyla, Ravsky) For any complete subsemilattice X of a functionally Hausdorff semitopological semilattice Y, the partial order $\le _X$ of X is a closed subset of $Y\times Y$.

In this paper we shall show that the answer to Problem 1 is affirmative under the additional condition that the semitopological semilattice Y is $\omega$-Lawson. We shall also prove a counterpart of Theorem 5 for complete subsemilattices of $\omega$-Lawson semitopological semilattices.

We define a topologized semilattice X to be $\omega$-Lawson if for any distinct points $x,y\in X$ there exists a countable family $\mathcal U$ of closed neighborhoods of x such that $\bigcap \mathcal U$ is a subsemilattice of X that does not contain y. A topologized semilattice X is $\omega$-Lawson if and only if it is Hausdorff and has at most countable Lawson number $\bar{\Lambda }(X)$.

The Lawson number $\bar{\Lambda }(X)$ of a Hausdorff topologized semilattice X is defined as the smallest cardinal $\kappa$ such that for any distinct points $x,y\in X$ there exists a family $\mathcal U$ of closed neighborhoods of x such that $|\mathcal U|\le \kappa$ and $\bigcap \mathcal U$ is a subsemilattice of X that does not contain y.

The Lawson number will be studied in more details in Sect. 2. In that section we shall prove that every Hausdorff topological semilattice X has $\bar{\Lambda }(X)\le \omega$. On the other hand, for any infinite cardinal $\lambda$ we shall construct a Hausdorff zero-dimensional semitopological semilattice X of cardinality $|X|=\lambda$ and Lawson number $\bar{\Lambda }(X)=\mathrm {cf}(\lambda )$. In Sect. 4 we prove the main result of this paper:

Theorem 6

For any complete subsemilattice X of an $\omega$-Lawson semitopological semilattice Y, the natural partial order $\le _X$ of X is a closed subset of $Y\times Y$. Consequently, X is closed in Y.

Remark 1

By [7] (and [8]), there exists a metrizable (Lawson) semitopological semilattice X whose partial order $\le _X$ is not closed in $X\times X$.

Since the completeness is preserved by continuous homomorphisms into Hausdorff semitopological semilattices (see Lemma 1), Theorem 6 implies the following corollary giving a partial answer to Problem 1.

Corollary 1

For any continuous homomorphism $h:X\rightarrow Y$ from a complete topologized semilattice to an $\omega$-Lawson semitopological semilattice Y the image h[X] is closed in Y.

Problem 2

Let X be a complete subsemilattice of an $\omega _1$-Lawson semitopological semilattice Y. Is X closed in Y? Is the natural partial order $\le _X$ of X closed in $X\times X$?

2 The Lawson number of a Hausdorff topologized semilattice

In this section we study the Lawson number of a topologized semilattice in more details. We start with recalling the principal definition.

Definition 1

The Lawson number $\bar{\Lambda }(X)$ of a Hausdorff topologized semilattice X is the smallest cardinal $\kappa$ such that for any distinct points $x,y\in X$ there exists a family $\mathcal U$ of closed neighborhoods of x such that $|\mathcal U|\le \kappa$ and the intersection $\bigcap \mathcal U$ is a subsemilattice of X that does not contain y.

For any Hausdorff topologized semilattice X the Lawson number $\bar{\Lambda }(X)$ is well-defined and does not exceed the closed pseudocharacter $\bar{\psi }(X)$ of X, defined as the smallest cardinal $\kappa$ such that for any point $x\in X$ there exists a family $\mathcal U$ of closed neighborhoods of x such that $|\mathcal U|\le \kappa$ and $\bigcap \mathcal U=\{x\}$. Therefore, $\bar{\Lambda }(X)\le \bar{\psi }(X)$ for any Hausdorff topologized semilattice X.

Observe that a topologized semilattice X is $\omega$-Lawson if and only if X is Hausdorff and has $\bar{\Lambda }(X)\le \omega$.

Definition 2

A topologized semilattice X is defined to be $\kappa$-Lawson for a cardinal $\kappa$ if X is Hausdorff and $\bar{\Lambda }(X)\le \kappa$.

The Lawson number admits the following simple characterization.

Proposition 1

The Lawson number of a Hausdorff topologized semilattice X is equal to the smallest cardinal $\kappa$ such that for any distinct points $x,y\in X$ there exist a closed subsemilattice L in X and a family $\mathcal V$ of closed neighborhoods of x such that $|\mathcal V|\le \kappa$ and $\bigcap \mathcal V\subseteq L\subseteq X\setminus \{y\}$.

Proof

We should prove that $\bar{\Lambda }(X)=\Lambda (X)$ where $\Lambda (X)$ is the smallest cardinal $\kappa$ such that for any distinct points $x,y\in X$ there exist a closed subsemilattice L in X and a family $\mathcal V$ of closed neighborhoods of x such that $|\mathcal V|\le \kappa$ and $\bigcap \mathcal V\subseteq L\subseteq X\setminus \{y\}$.

To see that $\Lambda (X)\le \bar{\Lambda }(X)$, for any distinct points $x,y\in X$ use the definition of $\bar{\Lambda }(X)$ and find a family $\mathcal U$ of closed neighborhoods of x such that $|\mathcal U|\le \bar{\Lambda }(X)$ and $L:=\bigcap \mathcal U$ is a closed subsemilattice of X that does not contain y. Then $\bigcap \mathcal U=L\subseteq X\setminus \{y\}$, witnessing that $\Lambda (X)\le \bar{\Lambda }(X)$.

To see that $\bar{\Lambda }(X)\le \Lambda (X)$, for any distinct points $x,y\in X$ use the definition of $\Lambda (X)$ and find a closed subsemilattice L of X and a family $\mathcal V$ of closed neighborhoods of x such that $|\mathcal V|\le \Lambda (X)$ and $\bigcap \mathcal V\subseteq L\subseteq X\setminus \{y\}$. Then $\mathcal U:=\{V\cup L:V\in \mathcal V\}$ is a family of closed neighborhoods of x such that $|\mathcal U|\le |\mathcal V|\le \Lambda (X)$ and $\bigcap \mathcal U=(\bigcap \mathcal V)\cup L=L$ is a closed subsemilattice of X that does not contain y and witnesses that $\bar{\Lambda }(X)\le \bar{\Lambda }(X)$. $\square$

The notion of a 1-Lawson semilattice extends the well-known notion of a Lawson semilattice (or else a topologized semilattice with small subsemilattices), introduced and studied by Lawson [13] (see also [10], Chapter 2]). Following [10], p. 12], we define a topologized semilattice X to be

• Lawson if it has a base of the topology consisting of open subsemilattices;

• a V-semilattice if for any points $x\in X$ and $y\in X\setminus {\uparrow }x$ there exists a point $v\in X\setminus {\downarrow } y$ such that ${\uparrow }v$ is a neighborhood of x in X;

• $\mathbb I$-separated if for any distinct points $x,y\in X$ there exists a continuous homomorphism $f:X\rightarrow \mathbb I$ such that $f(x)\ne f(y)$.

Here by $\mathbb I$ we denote the unit interval [0, 1] endowed with the semilattice operation $\min$.

Proposition 2

For a Hausdorff semitopological semilattice X, consider the following conditions:

• 1. X is 1-Lawson;

• 2. X is Lawson;

• 3. X is a V-semilattice;

• 4. X is $\mathbb I$-separated.

Any of the conditions (2),(3),(4) implies (1). If the space X is compact, then the conditions (1)–(4) are equivalent.

Proof

To prove that X is 1-Lawson, fix any distinct points $x,y\in X$. We need to find a closed subsemilattice L in X that contains x in its interior but does not contain y.

$(2)\Rightarrow (1)$ Assume that X is Lawson. Since X is Hausdorff, there exists a closed neighborhood $N_x\subseteq X$ of x such that $y\notin N_x$. Since X is Lawson, there exists an open subsemilattice $V\subseteq X$ such that $x\in V\subseteq N_x$. Since X is a semitopological semilattice, the closure ${\overline{V}}$ of the semilattice V is a closed subsemilattice that contains x in its interior but does not contain y. Therefore, the semilattice X is 1-Lawson.

$(3)\Rightarrow (1)$ Assume that X is a V-semilattice. If $x\notin {\downarrow }y$, then $y\notin {\uparrow }x$ and there exists an element $v\in X\setminus {\downarrow }y$ such that the upper set ${\uparrow }v$ contains x in its interior. Since X is a Hausdorff semitopological semilattice the upper set ${\uparrow }v=\{z\in X:zv=v\}$ is closed. Then the closed subsemilattice ${\uparrow }v$ is a neighborhood of x that does not contain y. If $x\in {\downarrow }y$, then $x\notin {\uparrow }y$. Since X is a V-semilattice, there exists an element $u\in X\setminus {\downarrow }x$ such that the upper set ${\uparrow }u$ contains y in its interior. Observe that the complement $U:=X\setminus {\uparrow }u$ is an open subsemilattice of X, containing x. Then ${\overline{U}}$ is a closed subsemilattice of X, which is a neighborhood of x that does not contain y.

$(4)\Rightarrow (1)$ Assuming that X is $\mathbb I$-separated, we can find a continuous homomorphism $f:X\rightarrow \mathbb I$ such that $f(x)\ne f(y)$. Choose any closed neighborhood $N\subset \mathbb I$ of f(x) such that $f(y)\notin N$. Then $f^{-1}(N)$ is a closed subsemilattice in X that contains x in its interior but does not contain y.

Now assume that X is compact. In this case the conditions (1)–(4) are equivalent by Theorem 7.1 in [2]. In fact, the equivalence of the conditions (2) and (4) is a classical result of Lawson [13, 14]. $\square$

Example 1

The topological semilattice $\mathbb Z^\omega$ with the Tychonoff product topology and coordinatewise operation of minimum is Lawson and $\mathbb I$-separated but not a V-semilattice.

By [10, Example 2.21], there exists a metrizable compact topological semilattice, which is not Lawson and hence is not 1-Lawson. However, such a semilattice necessarily is $\omega$-Lawson as shown by the following simple proposition.

Proposition 3

Each Hausdorff topological semilattice X is $\omega$-Lawson.

Proof

Given two distinct points $x,y\in X$, choose a decreasing sequence $(U_n)_{n\in \omega }$ of open neighborhoods of x such that $y\notin \overline{U_0}$ and $U_{n}\cdot U_n\subseteq U_{n-1}$ and hence $\overline{U_n}\cdot \overline{U_n}\subseteq \overline{U_{n-1}}$ for all $n\in \mathbb N$. The choice of $U_0$ is possible by the Hausdorff property of X, and the choice of the neighborhoods $U_n$ is possible by the continuity of the semilattice operation at (x, x). It follows that the intersection $\bigcap _{n\in \omega }\overline{U_n}$ is a closed subsemilattice of X containing x but not y. $\square$

Corollary 2

Each compact Hausdorff semitopological semilattice is $\omega$-Lawson.

Proof

By [14], each compact Hausdorff semitopological semilattice is a topological semilattice and by Proposition 3, is $\omega$-Lawson. $\square$

Let us also notice the following trivial (but useful) fact.

Proposition 4

Each (Hausdorff) linear topologized semilattice X is Lawson (and 1-Lawson).

Let us recall that a topological space X is Urysohn if any distinct points in X have disjoint closed neighborhoods. It is clear that each Urysohn space is Hausdorff.

We define a topological space X to be $\kappa$-Urysohn for a cardinal $\kappa$ if for any distinct points $x,y\in X$ there are families $\mathcal U_x$ and $\mathcal U_y$ of open sets on X such that $\max \{|\mathcal U_x|,|\mathcal U_y|\}\le \kappa$, $x\in \bigcap \mathcal U_x$, $y\in \bigcap \mathcal U_y$ and the sets $\bigcap _{U\in \mathcal U_x}{\overline{U}}$ and $\bigcap _{V\in \mathcal U_y}{\overline{V}}$ are disjoint.

It is easy to see that a topological space is Urysohn if and only if it is 1-Urysohn.

Example 2

For every infinite cardinal $\kappa$, there exists a Hausdorff Lawson topological semilattice, which is not $\kappa$-Urysohn.

Proof

Take any ordinal $\lambda$ of cofinality $\mathrm {cf}(\lambda )>\kappa$ (for example, put $\lambda :=\kappa ^+$). Consider the set $L=\{x_\alpha \}_{\alpha \le \lambda }\cup \{z\}\cup \{y_\alpha \}_{\alpha \le \lambda }$ of pairwise distinct points endowed with the linear order in which $x_\alpha<x_\beta<z<y_\beta <y_\alpha$ for any ordinals $\alpha <\beta \le \lambda$. Let ${\ddot{L}}:=L\setminus \{x_{\lambda },y_{\lambda }\}$. On the set

$$\begin{aligned} X=({\ddot{L}}\times [0,\lambda ))\cup (\{x_{\lambda },y_{\lambda }\}\times \{\lambda \}) \end{aligned}$$

consider the semilattice operation

$$\begin{aligned} (x,\alpha )\cdot (y,\beta ):={\left\{ \begin{array}{ll} (\min \{x,y\},\min \{\alpha ,\beta \})&{}\hbox { if}\ \alpha ,\beta<\lambda ;\\ (\min \{x,z\},\alpha ),&{}\hbox { if}\ \alpha<\lambda =\beta ;\\ (\min \{z,y\},\beta ),&{}\hbox { if}\ \beta <\lambda =\alpha ;\\ (\min \{x,y\},\lambda ),&{}\hbox { if}\ \alpha =\lambda =\beta . \end{array}\right. } \end{aligned}$$

Endow X with the topology $\tau$ consisting of all sets $U\subseteq X$ satisfying the following three conditions:

• if $(z,\alpha )\in U$ for some $\alpha \in [0,\lambda )$, then $\{(x_\gamma ,\alpha ),(y_\gamma ,\alpha ):\beta<\gamma <\lambda \}\subseteq U$ for some $\beta \in [0,\lambda )$;

• if $(x_{\lambda },\lambda )\in U$, then $\{(x_\beta ,\gamma ):\beta ,\gamma \in [\alpha ,\lambda )\}\subseteq U$ for some $\alpha \in [0,\lambda )$;

• if $(y_{\lambda },\lambda )\in U$, then $\{(y_\beta ,\gamma ):\beta ,\gamma \in [\alpha ,\lambda )\}\subseteq U$ for some $\alpha \in [0,\lambda )$.

Taking into account that $\mathrm {cf}(\lambda )>\kappa$, we can show that $(X,\tau )$ is a required Hausdorff Lawson topological semilattice which is not $\kappa$-Urysohn. $\square$

Now we construct Hausdorff zero-dimensional semitopological semilattices having an arbitrarily large Lawson number. We recall that a topological space is zero-dimensional if it has a base of the topology consisting of open-and-closed sets.

Example 3

For any infinite cardinal $\lambda$ there exists a Hausdorff zero-dimensional semitopological semilattice X such that $|X|=\lambda$ and $\bar{\Lambda }(X)=\bar{\psi }(X)=\mathrm {cf}(\lambda )$.

Proof

Consider the set

$$\begin{aligned} X:=\{A\subseteq \lambda :A=\lambda \quad \text {or}\, \,A \ \text {is finite}\} \end{aligned}$$

endowed with the semilattice operation of union. This semilattice has cardinality $|X|=\lambda$. Here we identify the cardinal $\lambda$ with the set $[0,\lambda )$ of all ordinals smaller than $\lambda$.

Now the trick is to introduce an appropriate topology on the semilattice X. For this we define several kinds of sets in $\lambda$.

A finite subset $A\subseteq \lambda$ is defined to be sparse if $|A\cap [\alpha ,\alpha +\omega )|\le 1$ for any ordinal $\alpha \in \lambda$.

For a set $A\in X$ and an ordinal $\alpha \in \lambda$ consider the set

$$\begin{aligned} S[A;\alpha ]:=\{B\in X:{B\cap [0,\alpha )=A\cap [0,\alpha ) \text { and } B\cap [\alpha ,\lambda ) \text { is sparse}}\}, \end{aligned}$$

and observe that $\lambda \notin S[A;\alpha ]$.

Let $\alpha \in \lambda$ be an ordinal, n be a finite ordinal and $\varepsilon$ be a positive real number. A subset $A\subset \lambda$ is called $(\alpha ,n,\varepsilon )$-fat if there exists a limsit ordinal $\beta \in [\alpha ,\lambda )$ and a finite ordinal $m>n$ such that

• (i) the set $A\cap [\beta +\omega ,\lambda )$ is sparse;

• (ii) $[\beta ,\beta +\omega )\cap A=[\beta ,\beta +m]$;

• (iii) the set $[0,\beta )\cap A$ is finite and has cardinality $<\varepsilon \cdot m$.

The conditions (i),(ii) ensure that the ordinal $\beta$ is unique.

Consider the subset

$$\begin{aligned} F[\alpha ,n,\varepsilon ]:=\{\lambda \}\cup \{A\in X:A \text { is } (\alpha ,n,\varepsilon )\text {-fat}\} \end{aligned}$$

of X.

Now we define a topology $\tau$ on the semilattice X. This topology consists of the sets $U\subseteq X$ satisfying the following two conditions:

• (a) for any finite subset $A\in U$ of $\lambda$ there exists an ordinal $\alpha \in \lambda$ such that $A\in S[A,\alpha ]\subseteq U$;

• (b) if $\lambda \in U$, then there exist ordinals $\alpha \in \lambda$, $k\in \omega$, and a positive real number $\varepsilon$ such that $F[\alpha ,k,\varepsilon ]\subseteq U$.

It is easy to see that $\tau$ is a well-defined topology on X. Now we show that this topology is Hausdorff and zero-dimensional. Subsets $U\in \tau$ of X will be called $\tau$-open. $\square$

Claim 1

For any element $A\in X$ and ordinal $\alpha \in \lambda$ the set $S[A;\alpha ]$ is open in $(X,\tau )$.

Proof

To see that $S[A;\alpha ]$ is open, take any element $B\in S[A;\alpha ]$ and observe that $B\cap [0,\alpha )=A\cap [0,\alpha )$ and $B\cap [\alpha ,\lambda )$ is sparse. Then $B\in S[B;\alpha ]\subseteq S[A;\alpha ]\subseteq X\setminus \{\lambda \}$ and the set $S[A;\alpha ]$ is open by the definition of the topology $\tau$. $\square$

Claim 2

For any ordinals $\alpha \in \lambda$, $n\in \omega$ and a positive real number $\varepsilon$, the set $F[\alpha ,n,\varepsilon ]$ is open and closed in $(X,\tau )$.

Proof

Given any element $A\in F[\alpha ,n,\varepsilon ]\setminus \{\lambda \}$, find a unique limit ordinal $\beta \ge \alpha$ witnessing that A is $(\alpha ,n,\varepsilon )$-fat. Then $S[A;\beta +\omega ]\subseteq F[\alpha ,n,\varepsilon ]$, witnessing that the set $F[\alpha ,n,\varepsilon ]$ is open in $(X,\tau )$.

To see that this set is closed in $(X,\tau )$, choose any set $A\in X\setminus F[\alpha ,n,\varepsilon ]$. It follows that A is a finite subset of $\lambda$, which is not $(\alpha ,n,\varepsilon )$-fat. Let $\beta$ be the smallest limit ordinal such that the intersection $A\cap [\beta +\omega ,\lambda )$ is sparse. Let $m\in \omega$ be the smallest finite ordinal such that $A\cap [\beta ,\beta +\omega )\subseteq [\beta ,\beta +m]$. Since A is not $(\alpha ,n,\varepsilon )$-fat, one of the following conditions holds:

• 1. $\beta <\alpha$;

• 2. $m\le n$;

• 3. $\beta \ge \alpha$ and $m>n$ but $[\beta ,\beta +m]\not \subseteq A$;

• 4. $\beta \ge \alpha$, $m>n$, $[\beta ,\beta +m]\subseteq A$ but $|A\cap [0,\beta )|\ge \varepsilon \cdot m$.

In all these cases $S[A;\beta +\omega ]$ is a $\tau$-open neighborhood of A such that $S[A;\beta +\omega ]\cap F[\alpha ,n,\varepsilon ]=\emptyset$. $\square$

Claim 3

For any finite set $A\in X$ of $\lambda$ and any ordinal $\alpha \in \lambda$, the set $S[A;\alpha ]$ is closed in $(X,\tau )$.

Proof

Take any element $B\in X\setminus S[A;\alpha ]$. If $B=\lambda$, then $F[\alpha ,1,1]$ is a neighborhood of B, disjoint with $S[A;\alpha ]$.

If $B\ne \lambda$, then $B\notin S[A;\alpha ]$ implies that either $B\cap [\alpha ,\lambda )$ is not sparse or $B\cap [\alpha ,\lambda )$ is sparse but $B\cap [0,\alpha )\ne A\cap [0,\alpha )$. In the latter case $S[B;\alpha ]$ is a $\tau$-open neighborhood of B, disjoint with $S[A;\alpha ]$. So, we assume that $B\cap [\alpha ,\lambda )$ is not sparse. In this case we can choose any ordinal $\beta \in \lambda$ with $B\subset [0,\beta )$ and observe that $S[B,\beta ]$ is a $\tau$-open neighborhood of B such that $S[B;\beta ]\cap S[A;\alpha ]=\emptyset$. $\square$

Claim 4

The topology $\tau$ is Hausdorff.

Proof

Take any distinct elements $A,B\in X$. If A and B are finite subsets of X, then we can find an ordinal $\alpha \in \lambda$ such that $A\cup B\subseteq [0,\alpha )$ and observe that $S[A;\alpha ]$ and $S[B;\alpha ]$ are disjoint $\tau$-open neighborhoods of the elements A and B, respectively.

If $B=\lambda$, then A is a finite set, contained in $[0,\alpha )$ for some ordinal $\alpha \in \lambda$. In this case $S[A;\alpha ]$ and $F[\alpha ,1,1]$ are disjoint $\tau$-open neighborhoods of A and B, respectively,

The case $A=\lambda$ can be considered by analogy. $\square$

Claims 1–4 show that the topology $\tau$ is Hausdorff and zero-dimensional.

Claim 5

The topologized semilattice $(X,\tau )$ is semitopological.

Proof

Given any element $a\in X$, we should prove that the shift $s_a:X\rightarrow X$, $s_a:x\mapsto ax$, is continuous. If $a=\lambda$, then $s_a(X)=\{\lambda \}$ is a singleton, so the continuity of $s_a$ is trivial. So, we assume that a is a finite subset of $\lambda$. To check the continuity of the shift $s_a$ at a point $x\in X$, fix any neighborhood $O_{ax}\in \tau$ of the point $ax=x\cup a$.

If $x\ne \lambda$, then $ax\ne \lambda$ and by the definition of the topology $\tau$, there exists an ordinal $\alpha \in \lambda$ such that $ax\in S[ax;\alpha ]\subseteq O_{ax}$. Replacing $\alpha$ by a larger ordinal, we can assume that $ax\subseteq [0,\alpha )$. Then $O_x:=S[x;\alpha ]$ is a $\tau$-open neighborhood of x such that $s_a(O_x)\subseteq S[ax;\alpha ]\subseteq O_{ax}$.

If $x=\lambda$, then $ax=\lambda$ and by the definition of the topology $\tau$, there exist $\alpha \in \lambda$, $k\in \omega$ and $\varepsilon >0$ such that $F[\alpha ,k,\varepsilon ]\subseteq O_{ax}$. Replacing $\alpha$ by a larger ordinal, we can assume that $a\subset [0,\alpha )$. Replacing k by a larger number, we can assume that $|a|\le \frac{1}{2}\varepsilon k$. In this case $O_x:=F[\alpha ,k,\frac{1}{2}\varepsilon ]$ is a $\tau$-open neighborhood of $x=\lambda$ such that $s_a(O_x)\subseteq F[\alpha ,k,\varepsilon ]\subseteq O_{ax}$. $\square$

Claim 6

Let $\mathcal U\subseteq \tau$ be a family of open sets and L be a $\tau$-closed subsemilattice in X such that $|\mathcal U|<\mathrm {cf}(\lambda )$ and $\emptyset \ne \bigcap \mathcal U\subseteq L$. Then $\lambda \in L$.

Proof

Fix any element $x\in \bigcap \mathcal U$. If $x=\lambda$, then $\lambda =x\in \bigcap \mathcal U\subseteq L$ and we are done. So, we assume that x is a finite subset of $\lambda$. Since the set L is $\tau$-closed, the inclusion $\lambda \in L$ will follow as soon as we show that each neighborhood $O_\lambda \in \tau$ of $\lambda$ meets the set L. By Claim 2, there exist ordinals $\alpha \in \lambda$, $k\in \omega$ and a positive real number $\varepsilon$ such that $F[\alpha ,k,\varepsilon ]\subseteq O_\lambda$.

By Claim 1 and $|\mathcal U|\le \kappa <\mathrm {cf}(\lambda )$, there exists a limit ordinal $\beta \in [\alpha ,\lambda )$ such that $x\in [0,\beta )$ and $x\in S[x;\beta ]\subseteq \bigcap \mathcal U\subseteq L$. Choose a finite ordinal $n> k$ such that $|x|<\varepsilon n$. Observe that for every ordinal $\gamma \in [\beta ,\beta +n]$ the set $x\cup \{\gamma \}$ belongs to the semilattice $L\supseteq S[x;\beta ]$. Since L is a subsemilattice, the $(\beta ,k,\varepsilon )$-fat set $x\cup [\beta ,\beta +n]$ belongs to $L\cap F[\beta ,k,\varepsilon ]\subseteq L\cap O_\lambda$. $\square$

Claim 7

The semitopological semilattice $(X,\tau )$ has $\bar{\Lambda }(X,\tau )=\bar{\psi }(X,\tau )=\mathrm {cf}(\lambda )$.

Proof

Claim 6 implies that $\mathrm {cf}(\lambda )\le \bar{\Lambda }(X,\tau )$. Since $\bar{\Lambda }(X,\tau )\le \bar{\psi }(X,\tau )$, it remains to prove that $\bar{\psi }(X,\tau )\le \mathrm {cf}(\lambda )$.

Choose a cofinal subset $C\subseteq \lambda$ of cardinality $|C|=\mathrm {cf}(\lambda )$. To see that $\bar{\psi }(X,\tau )\le \mathrm {cf}(\lambda )$, take any $A\in X$. If A is a finite subset of $\lambda$, then $A\subseteq [0,\alpha )$ for some ordinal $\alpha \in \lambda$. Then $\{A\}=\bigcap _{\alpha \le \gamma \in C}S[A;\gamma ]$. If $A=\lambda$, then $\{A\}=\{\lambda \}=\bigcap _{\gamma \in C}F[\gamma ;1,1]$. In both cases the singleton $\{A\}$ is the intersection of $\mathrm {cf}(\lambda )$ many closed neighborhoods of A, witnessing that $\bar{\psi }(X,\tau )\le \mathrm {cf}(\lambda )$. $\square$

3 Complete topologized semilattices

In this section we recall some known properties and characterizations of complete topologized semilattices.

By a poset we understand a set endowed with a partial order. A topologized poset is a poset endowed with a topology. So, each topologized semilattice is a topologized poset.

A subset D of a poset $(X,\le )$ is called

• a chain if any elements $x,y\in D$ are comparable in the sense that $x\le y$ or $y\le x$;

• up-directed if for any $x,y\in D$ there exists $z\in D$ such that $x\le z$ and $y\le z$;

• down-directed if for any $x,y\in D$ there exists $z\in D$ such that $z\le x$ and $z\le y$.

It is clear that each chain in a poset is both up-directed and down-directed.

A topologized poset X is defined to be

• up-complete if any nonempty up-directed subset $U\subseteq X$ has the least upper bound $\sup U\in {\overline{U}}$ in X;

• down-complete if any nonempty down-directed subset $D\subseteq X$ has the greatest lower bound $\inf D\in {\overline{D}}$ in X.

The proof of the following classical characterization can be found in [9, 12, 15] or [5], 2.2].

Proposition 5

For a topologized poset X the following conditions are equivalent:

• 1. X is up-complete;

• 2. Each non-empty chain $C\subseteq X$ has the least upper bound $\sup C\in {\overline{C}}$ in X.

Proposition 5 implies the following useful characterization of completeness in topologized semilattices.

Corollary 3

A topologized semilattice X is complete if and only if it is up-complete and down-complete.

This corollary implies that each closed subsemilattice of a complete topologized semilattice has the smallest element.

A topologized semilattice Y is called $\uparrow$-closed if for every $y\in Y$ the upper set ${\uparrow }y=\{x\in Y:xy=y\}$ is closed in Y. It is easy to see that each $T_1$ semitopological semilattice is ${\uparrow }$-closed.

The following lemma (that can be derived from Corollary 3) is proved in [5], Lemma 5.3].

Lemma 1

Let $h:X\rightarrow Y$ be a continuous surjective homomorphism between topologized semilattices. If X is complete and Y is $\uparrow$-closed, then the topologized semilattice Y is complete.

4 Proof of Theorem 6 and Corollary 1

The proof of Theorem 6 is based on the following lemma.

Lemma 2

Let X be a complete subsemilattice of a semitopological semilattice Y. Let a pair $(x,y)\in Y\times Y$ belong to the closure of the natural partial order $\le _X$ of X in $Y\times Y$, and let $\{U_n\}_{n\in \omega }$, $\{V_n\}_{n\in \omega }$ be sequences of closed neighborhoods of the points x and y in Y, respectively. Then there exist points $x'\in X\cap \bigcap _{n\in \omega }U_n$ and $y'\in X\cap \bigcap _{n\in \omega }V_n$ such that $x'\le y'$.

Proof

Replacing each set $U_n$ by $\bigcap _{i\le n}U_i$, we can assume that $U_{n+1}\subseteq U_n$ for all $n\in \omega$. By the same reason, we can assume that the sequence $(V_n)_{n\in \omega }$ is decreasing. For every $n\in \omega$ denote by $U_n^\circ$ and $V_n^\circ$ the interiors of the sets $U_n$ and $V_n$ in Y.

By induction we shall construct sequences $(x_n)_{n\in \omega }$ and $(y_n)_{n\in \omega }$ of points of X such that for every $n\in \omega$ the following conditions are satisfied:

$(1_{n})$:

$x_n\le y_n$;

$(2_{n})$:

$\{x_i\cdots x_n,x_i\cdots x_nx\}\subseteq U_i^\circ$ for all $i\le n$;

$(3_{n})$:

$\{y_i\cdots y_n,y_i\cdots y_ny\}\subseteq V_i^\circ$ for all $i\le n$.

To choose the initial points $x_0,y_0$, use the separate continuity of the semilattice operation and find neighborhoods $U'_0\subseteq U_0^\circ$ and $V'_0\subseteq V_0^\circ$ of x and y in Y such that $U'_0x\subseteq U_0^\circ$ and $V'_0y\subseteq V_0^\circ$. By our assumption, there are points $x_0\in X\cap U'_0$ and $y_0\in X\cap V'_0$ such that $x_0\le y_0$. The choice of the neighborhoods $U'_0$ and $V'_0$ ensures that the conditions $(2_0)$ and $(3_0)$ are satisfied.

Now assume that for some $n\in \mathbb N$ points $x_0,\dots ,x_{n-1}$ and $y_0,\dots ,y_{n-1}$ of X are chosen so that the conditions $(1_{n-1})$–$(3_{n-1})$ are satisfied. The condition $(2_{n-1})$ implies that for every $i\le n$ we have the inclusion $x_i\cdots x_{n-1}xx=x_i\cdots x_{n-1}x\in U_i^\circ$ (if $i=n$, then we understand that $x_i\cdots x_{n-1}x=x$). Using the continuity of the shift $s_x:Y\rightarrow Y$, $s_x:z\mapsto xz$, we can find a neighborhood $U_{n}'\subseteq Y$ of x such that $x_i\cdots x_{n-1}\cdot (U_n'\cup U_n'x)\subseteq U_i^\circ$ for every $i\le n$. By analogy, we can find a neighborhood $V_n'\subseteq Y$ of y such that $y_i\cdots y_{n-1}\cdot (V_n'\cup V_n'y)\subseteq V_i^\circ$ for every $i\le n$. By our assumption, there are points $x_n\in X\cap U_n'$ and $y_n\in X\cap V_n'$ such that $x_n\le y_n$. The choice of the neighborhoods $U'_0$ and $V'_0$ ensures that the conditions $(2_n)$ and $(3_n)$ are satisfied. This completes the inductive step.

Now for every $i\in \omega$ consider the chain $C_i=\{x_i\cdots x_n:n\ge i\}\subseteq U_i^\circ$ in X. By the completeness of X, this chain has $\inf C_i\in X\cap \overline{C_i}\subseteq X\cap \overline{U_i^\circ }\subseteq X\cap U_i$. Observing that $\inf C_i\le x_ix_{i+1}\cdots x_n\le x_{i+1}\cdots x_n$ for all $i>n$, we see that $\inf C_i$ is a lower bound of the chain $C_{i+1}$ and hence $\inf C_i\le \inf C_{i+1}$. By the completeness of X, for every $i\in \omega$ the chain $D_i:=\{\inf C_j:j\ge i\}\subseteq U_i$ has $\sup D_i\in X\cap \overline{D_i}\subseteq X\cap U_i$. Since the sequence $(\inf C_i)_{i\in \omega }$ is increasing, we get $\sup D_0=\sup D_i\in X\cap U_i$ for all $i\in \omega$. Consequently, $\sup D_0\in X\cap \bigcap _{i\in \omega }U_i$.

By analogy, for every $k\in \omega$ consider the chain $E_i=\{y_i\cdots y_n:n\ge i\}\subseteq V_i^\circ$ in X. By the completeness of X, this chain has $\inf E_i\in X\cap \overline{E_i}\subseteq X\cap \overline{V_i^\circ }\subseteq X\cap V_i$. By the completeness of X, for every $i\in \omega$ the chain $F_i:=\{\inf E_j:j\ge i\}\subseteq V_i$ has $\sup F_i\in X\cap \overline{F_i}\subseteq X\cap \overline{V_i}=X\cap V_i$. Since the sequence $(\inf E_i)_{i\in \omega }$ is increasing, we get $\sup F_0=\sup F_i\in X\cap V_i$ for all $i\in \omega$. Consequently, $\sup F_0\in X\cap \bigcap _{i\in \omega }V_i$.

To finish the proof of Lemma 2, it suffices to show that $\sup D_0\le \sup F_0$. The inductive conditions $(1_n)$, $n\in \omega$, imply that $\inf C_i\le \inf E_i$ for all $i\in \omega$ and $\sup D_0=\sup \{\inf C_i:i\in \omega \}\le \sup \{\inf E_i:i\in \omega \}=\sup F_0$. $\square$

The following two lemmas imply Theorem 6.

Lemma 3

Let Y be an $\omega$-Lawson semitopological semilattice. For any complete subsemilattice $X\subseteq Y$ the natural partial order $\le _X$ of X is closed in $Y\times Y$.

Proof

By Corollary 3, the complete semitopological semilattice X is both up-complete and down-complete. To show that the partial order $\le _X:=\{(x,y)\in X\times X:x\le y\}$ is closed in $Y\times Y$, take any pair $(y_1,y_2)$ in the closure of the set $\le _X$ in $Y\times Y$. For every $i\in \{1,2\}$, let ${\mathfrak {U}}_i$ be the set of all countable families $\mathcal U$ of closed neighborhoods of $y_i$ in Y such that $\bigcap \mathcal U$ is a subsemilattice of Y. By Lemma 2, for any $\mathcal U_1\in {\mathfrak {U}}_1$ and $\mathcal U_2\in {\mathfrak {U}}_2$ there are points $x_1\in X\cap \bigcap \mathcal U_1$ and $x_2\in X\cap \bigcap \mathcal U_2$ such that $x_1\le x_2$. In particular, the closed subsemilattice $X\cap \bigcap \mathcal U_1$ is not empty and has the smallest element $\inf (X\cap \bigcap \mathcal U_1)\in X$ (by the down-completeness of X). Denote this smallest element by $x(\mathcal U_1)$. It follows that $x(\mathcal U_1):=\inf (X\cap \bigcap \mathcal U_1)\le x_1\le x_2$. Consequently, the closed subsemilattice $({\uparrow }x(\mathcal U_1))\cap (X\cap \bigcap \mathcal U_2)\ni x_2$ is not empty and has the smallest element (by down-completeness of X), which will be denoted by $y(\mathcal U_1,\mathcal U_2)$. Observe that $x(\mathcal U_1)\in X\cap \bigcap \mathcal U_1$, $y(\mathcal U_1,\mathcal U_2)\in X\cap \bigcap \mathcal U_2$ and $x(\mathcal U_1)\le y(\mathcal U_1,\mathcal U_2)$. For any families $\mathcal U_1\in {\mathfrak {U}}_1$ and $\mathcal U_2,\mathcal U_2'\in {\mathfrak {U}}_2$ with $\mathcal U_2\subseteq \mathcal U_2'$ we have $y(\mathcal U_1,\mathcal U_2)\le y(\mathcal U_1,\mathcal U_2')$. Therefore, the set $\{y(\mathcal U_1,\mathcal U_2):\mathcal U_2\in {\mathfrak {U}}_2\}\subseteq X$ is up-directed and by the up-completeness of X, it has the smallest upper bound in X, which will be denoted by $y(\mathcal U_1)$. It follows that $x(\mathcal U_1)\le y(\mathcal U_1)$. We claim that $y(\mathcal U_1)=y_2$. In the opposite case we can use the $\omega$-Lawson property of Y and choose a countable family $\mathcal U_2'\in {\mathfrak {U}}_2$ such that $y(\mathcal U_1)\notin \bigcap \mathcal U_2'$. Taking into account that the set $\{y(\mathcal U_1,\mathcal U_2\cap \mathcal U_2'):\mathcal U_2\in {\mathfrak {U}}_2\}$ is cofinal in $\{y(\mathcal U_1,\mathcal U_2):\mathcal U_2\in {\mathfrak {U}}_2\}$, we conclude that

$$\begin{aligned} y(\mathcal U_1)=\sup \{y(\mathcal U_1,\mathcal U_2):\mathcal U_2\in {\mathfrak {U}}_2\}=\sup \{y(\mathcal U_1,\mathcal U_2\cap \mathcal U_2'): \mathcal U_2\in {\mathfrak {U}}_2\}\in {\textstyle \bigcap }\mathcal U_2', \end{aligned}$$

which contradicts the choice of the family $\mathcal U'_2$. This contradiction shows that $y_2=y(\mathcal U_1)\in X$. Now we see that $x(\mathcal U_1)\le y(\mathcal U_1)=y_2$ for every $\mathcal U_1\in {\mathfrak {U}}_1$. By the up-completeness of the semitopological semilattice X, the up-directed subset $\{x(\mathcal U_1):\mathcal U_1\in {\mathfrak {U}}_1\}$ has the smallest upper bound $x\in X$. It follows from $x(\mathcal U_1)\le y_2$ for all $\mathcal U_1\in {\mathfrak {U}}_1$ that $x\le y_2$.

It remains to check that $x=y_1$. In the opposite case, using the $\omega$-Lawson property of X, we can find a countable family $\mathcal U_1'\in {\mathfrak {U}}_1$ such that $x\notin \bigcap \mathcal U_1'$. Taking into account that the family $\{x(\mathcal U_1\cap \mathcal U_1'):\mathcal U_1\in {\mathfrak {U}}_1\}$ is cofinal in $\{x(\mathcal U_1):\mathcal U_1\in {\mathfrak {U}}_1\}$, we conclude that

$$\begin{aligned} x=\sup \{x(\mathcal U_1):\mathcal U_1\in {\mathfrak {U}}_1\}= \sup \{x(\mathcal U_1\cap \mathcal U_1'):\mathcal U_1\in {\mathfrak {U}}_1\}\in {\textstyle \bigcap }\mathcal U_1', \end{aligned}$$

which contradicts the choice of $\mathcal U_1'$. This contradiction shows that $y_1=x\in X$. Therefore we obtain that $(y_1,y_2)\in X\times X$ and $y_1=x\le y_2$, which means that $(y_1,y_2)\in \;\le _X$. $\square$

Lemma 4

Each complete subsemilattice X of an $\omega$-Lawson semitopological semilattice Y is closed in Y.

Proof

By Lemma 3, the partial order $\le _X:=\{(x,y)\in X\times X:xy=x\}$ is a closed subset of $Y\times Y$. By Corollary 3, the complete semilattice X has the smallest element $\min X\in X$. Consider the continuous map $f:Y\rightarrow Y\times Y$, $f:y\mapsto (\min X,y)$, and observe that $X=f^{-1}(\le _X)$ is a closed subset of X, being the preimage of the closed set $\le _X$ under the continuous map f. $\square$

Finally, we prove Corollary 1.

Lemma 5

For every continuous homomorphism $h:X\rightarrow Y$ from a complete topologized semilattice X to an $\omega$-Lawson semitopological semilattice Y, the image h[X] is closed in Y.

Proof

Observe that the $\omega$-Lawson property of Y implies that the semitopological semilattice Y is Hausdorff and hence ${\uparrow }$-closed. By Lemma 1, the semitopological semilattice h[X] of Y is complete and by Lemma 4, h[X] is closed in Y. $\square$