1 Introduction

A fundamental insight in tropical geometry is that the tropicalization of a classical variety is the underlying set of a polyhedral complex in \({\mathbb R}^n\) whose top-dimensional cells are equipped with multiplicities, or weights, such that certain balancing conditions are satisfied for the top-dimensional cells meeting at a common face of codimension 1. This understanding has led to the definition of a tropical variety as a (finite and rational) polyhedral complex in \({\mathbb R}^n\) together with weights for its top-dimensional cells such that the mentioned balancing conditions are satisfied.

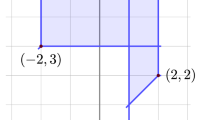
Instead of entering into the technical details of the balancing condition, we give an impression of its nature in terms of the following illustration of a plane tropical curve.

While every plane tropical curve is realizable, i.e. it arises as the tropicalization of a classical curve, is is not true that all tropical varieties are realizable, which makes it hard to justify that the definition of a tropical variety captures the ‘correct’ class of objects. Note that we cannot restrict to the subclass of realizable tropical varieties if we want to include Bergman fans of matroids as a particularly simple class of tropical linear spaces.

However, there are other disturbing artefacts about tropical varieties: for one, the structure of a polyhedral complex is not intrinsic to a tropicalization, but depends on choices; secondly, the balancing condition makes only sense for equidimensional tropical varieties.

We add a third artefact in this note: Bergman fans satisfy certain balancing conditions for cells of arbitrary positive codimension.

Before we address the potential implications of our result on tropical geometry at the end of the introduction, we give an impression of our main result, which extends in fact to the more ample class of tropical manifolds, as explained in the following.

Fig. 1
figure 1

A tropical curve in \({\mathbb R}^2\) and the balancing conditions for its vertices

Full size image

1.1 Tropical manifolds

A tropical manifold is a topological space X together with a cover by open subsets \(U_i\) and an open embedding of each \(U_i\) into the Bergman fan of a matroid, which are called the charts of X. We avoid a precise definition in this text since it is technical and not necessary for our purposes; instead we refer the interested reader to [1, section 1.6] and [2, section 3.1].

Since the polyhedral structure of X is defined by its charts, balancing conditions for X stem from balancing conditions for Bergman fans.

1.2 Example: locally tropical convex tropical varieties

Before we turn to Bergman fans, let us mention an important example of a tropical manifold, namely tropical varieties in \({\mathbb R}^n\) that are locally tropically convex.

To explain, a subset X in \({\mathbb R}^n\) is tropically convex if for all \(x,y\in X\) and \(a,b\in {\mathbb R}\), the tropical linear combination \(z=(a\odot x)\oplus (b\odot y)\) (with coordinates \(z_i=\min \{a+x_i,b+y_i\}\)) is contained in X. A subset X in \({\mathbb R}^n\) is locally tropically convex if every point of X has an open tropically convex neighbourhood. By [3, Prop. 3.3], a tropical variety X is locally tropically convex if and only if for every point p of X, the (underlying set of the) star \({{\,\mathrm{Star}\,}}_X(p)\) at p is the (underlying set of the) Bergman fan of a matroid. Since p has an open neighbourhood \(U_p\) that embeds as an open subset of \({{\,\mathrm{Star}\,}}(p)\), this shows that X is a tropical manifold with respect to these embeddings.

Note that locally tropical convex tropical varieties form a well-understood class of tropical varieties: A tropical variety is locally tropically convex if and only if it is tropically convex as a set ([3, Thm. 1.2]), and tropical linear spaces are tropically convex ([3, Prop. 2.14]). In fact, the only discrepancy between tropical linear spaces and tropically convex tropical varieties lies in the possibility of higher weights: by [3, Thm. 1.1], the underlying set of a tropically convex tropical variety is equal to the underlying set of a tropical linear space. For more details, cf. [3] and [4].

1.3 A preview on higher balancing

It is well-known that the Bergman fan of a matroid is a tropical variety, which means that it satisfies the balancing condition for all top-dimensional cones containing a given cone of codimension 1 (with respect to a constant weight function). In this text, we show that a Bergman fan satisfies balancing conditions for polyhedra of any codimension. These higher balancing conditions require a distinction of the cones of a Bergman fan according to their ‘types’, which is a finer invariant than the dimension. The formulation of the higher balancing conditions requires some preparatory definitions and can be found in Theorem 2.

1.4 A remark on the relevance of higher balancing

Locally tropically convex tropical varieties are blessed with the property that they look locally like a Bergman fan, and therefore inherit a canonical polyhedral structure that satisfies higher balancing conditions with respect to a constant weight function. Other types of tropical varieties do not come with such an intrinsic structure, but one needs additional information in order to extend the weight function to polyhedra of higher codimension.

Tentative calculations show that in good cases a finite tropical basis for the tropical variety provides enough structure to define a polyhedral structure of the tropical variety together with a weight function for which higher balancing holds; see [5, section 12.2] for a definition of the weight function. In particular, this works well for hypersurfaces with one defining equation, which is in nature similar to Lemma 3.6 in [6]. We have hopes to extend this to all tropicalizations of classical varieties. It might also apply to tropical prevarieties that are defined by tropical ideals in the sense of [7], which have recently been proven to be balanced in codimension 1; see [8].

To conclude, we see higher balancing as an indication for that there might be interesting information about the tropicalizations of classical varieties that has not been used so far. Our hope is that this additional information finds a satisfactory explanation in terms of tropical scheme theory, as developed in [5, 9] and [10]. In particular, we would like to propose the following question as a guiding problem for further developments in tropical scheme theory.

Question

For which subschemes of the tropical torus (i.e. ideals in the semiring of tropical Laurent polynomials) can we make sense of higher balancing?

2 The Bergman fan of a matroid

Matroids are combinatorial objects that capture the notion of linear independence beyond the framework of linear algebra. A tantalizing property of matroids is that they can be defined in many different ‘cryptomorphic’ ways, which reflects the fundamental importance of the concept of a matroid.

In this note, we focus on the incarnation of a matroid in terms of its family of flats. To explain, a matroid M on a ground set E is a family \({\mathcal F}\) of subsets F of E, called flats, that satisfies the following axioms:

  1. (1)

    E is a flat;

  2. (2)

    if F and \(F'\) are flats, then \(F\cap F'\) is a flat;

  3. (3)

    if F is a flat and \(e\in E-F\), then there is exactly one flat \(F'\) that contains \(F\cup \{e\}\) and such that \(F\subsetneq F''\subset F'\) implies \(F''=F'\) for every other flat \(F''\).

The family \({\mathcal F}\) is partially ordered by inclusion and forms a ranked lattice: its bottom element is \(\emptyset \) and its top element is E; the rank of a flat \(F\in {\mathcal F}\) is

$$\begin{aligned} rk\, F \ = \ \max \{\, l \,\mid \, \text {there is a chain }\emptyset \subsetneq F_1 \subsetneq \dotsc \subsetneq F_l=F \text { of length }l \, \}. \end{aligned}$$

Note that all maximal chains \(\emptyset \subsetneq F_1 \subsetneq \dotsc \subsetneq F_l=F\) have the same length \(l=rk\, F\).

The Bergman complex of a matroid was introduced by Sturmfels in [11]. Subsequently the related notion of the Bergman fan of a matroid was introduced by Ardila and Klivans in [12]. We will review this theory in the following. For a pleasant introduction, cf. section 2.2 of [13].

Let M be a matroid with ground set E. The Bergman fan of M is the fan B(M) in \({\mathbb R}^E\) whose cones are defined as follows. Let \(\{e_i\}_{i\in E}\) be the standard basis of \({\mathbb R}^E\). For a subset F of E, we define \(e_F=\sum _{i\in F}e_i\). A flag of flats is a tuple \({\mathcal F}=(F_0,\dotsc ,F_d)\) of flats \(F_i\) of M such that

$$\begin{aligned} \emptyset \, = \, F_0 \ \subsetneq \ F_1 \ \subsetneq \ \cdots \ \subsetneq \ F_d \, = \, E. \end{aligned}$$

The cone of \({\mathcal F}\) is defined as

$$\begin{aligned} {\mathfrak c}_{\mathcal F}= & {} \sum _{i=0}^{d-1} {\mathbb R}^+ \cdot e_{F_i} + {\mathbb R}\cdot e_E \\= & {} \ \bigg \{ \, \sum _{i=0}^{d} \lambda _ie_{F_i} \, \bigg | \, \lambda _i\in {\mathbb R}^+\text { for }i=1,\dotsc ,d-1\text { and }\lambda _d\in {\mathbb R}\, \bigg \} \end{aligned}$$

where \({\mathbb R}^+\) are the nonnegative reals.

By definition, \({\mathfrak c}_{\mathcal F}\) is a rational cone of dimension d (in the sense of toric geometry, cf. [14]). The maximal linear subspace contained in \({\mathfrak c}_{\mathcal F}\) is the line spanned by \(e_E\). Let \(|{\mathcal F}|=\{F_0,\dotsc ,F_d\}\). We have an inclusion \({\mathfrak c}_{{\mathcal F}'} \subset {\mathfrak c}_{{\mathcal F}}\) if and only if \(|{\mathcal F}'|\subset |{\mathcal F}|\). In this case \({\mathfrak c}_{{\mathcal F}'}\) is a face of \({\mathfrak c}_{\mathcal F}\), and every face of \({\mathfrak c}_{\mathcal F}\) is of the form \({\mathfrak c}_{{\mathcal F}'}\) for some flag of flats \({\mathcal F}'\). In particular, every cone \({\mathfrak c}_{\mathcal F}\) contains \({\mathfrak c}_{(\emptyset ,E)}={\mathbb R}\cdot e_E\) as its unique 1-dimensional face. Given two flags of flats \({\mathcal F}\) and \({\mathcal F}'\), the intersection of the associated cones is \({\mathfrak c}_{\mathcal F}\cap {\mathfrak c}_{{\mathcal F}'}={\mathfrak c}_{{\mathcal F}''}\) where \({\mathcal F}''\) is the flag of flats with \(|{\mathcal F}''|=|{\mathcal F}|\cap |{\mathcal F}'|\). This shows that B(M) is an equidimensional polyhedral complex whose dimension is equal to the rank \(rk\, M\) of M.

Note that some authors (e.g. Hampe in [3]) define the Bergman fan of M as the image of B(M) in \({\mathbb R}^E/{\mathbb R}\cdot e_E\). This image is indeed a fan in the sense of toric geometry since all cones become strictly convex. Concerning balancing conditions, it does not make any essential difference, which version of the Bergman fan one uses. For our purposes, we find it more convenient to follow the definition of this paper.

Note further that the matroid M is determined by its Bergman fan B(M) since a subset F of E is a flat if and only if \(e_F\) is contained in the underlying set of B(M), which is the union \(|B(M)|=\bigcup {\mathfrak c}_{\mathcal F}\) of all cones \({\mathfrak c}_{\mathcal F}\) of B(M).

Let \({\mathcal F}=(F_0,\dotsc ,F_d)\) be a flag of flats. The type of \({\mathcal F}\) is the tuple \((rk\, F_0,\dotsc ,rk\, F_d)\), which is a tuple of strictly increasing integers with \(rk\, F_0=0\) and \(rk\, F_d=rk\, M\).

3 Balancing in codimension 1

The Bergman fan of a matroid is a tropical variety in the sense that it is balanced at cones of codimension 1 with respect to a constant weight function on the top-dimensional cones. This balancing condition was first considered in Speyer’s thesis [15], and can be formulated as follows for Bergman fans. For details on matroid theory, we refer to [16].

Let M be a matroid with ground set E. Given flats F and \(F'\), we write \(F\le F'\) if \(F\subset F'\) and \(F<F'\) if \(F\subsetneq F'\). We say that \(F'\) covers F, and write \(F<:F'\), if \(F\le F'\) and \(rk\, F'=rk\, F+1\), i.e. if there exists no flat strictly in between F and \(F'\).

Proposition 1

Consider a flag of flats \({\mathcal F}=(F_0,\dotsc ,F_d)\) of length \(d=rk\, M-1\), i.e. the type of \({\mathcal F}\) is \((0,1,\dotsc ,i,i+2,\dotsc ,r)\) for some \(i\in \{0,\dotsc , r-2\}\) where \(r=rk\, M\). Then

$$\begin{aligned} \sum _{F_{i}<:F'<:F_{i+1}} e_{F'} \quad \in \quad {\mathfrak c}_{\mathcal F}. \end{aligned}$$

Proof

In the following, we reproduce the short argument from Huh’s thesis ([13, Prop. 16]). As a first step, we consider the restriction \(M'=M\vert _{F_{i+1}}\) of M to \(F_{i+1}\), which results from M by deleting \(E-F_{i+1}\). The ground set of \(M'\) is \(E'=F_{i+1}\) and its flats are precisely those flats of M that are contained in \(F_{i+1}\). The matroid axiom for flats, applied to \(F_{i}\) as a flat of \(M'\), states that

$$\begin{aligned} F_{i+1}\,-\,F_{i} \ = \ \coprod _{F_{i}<:F'<:F_{i+1}} F' \,-\, F_{i}. \end{aligned}$$

Therefore

$$\begin{aligned} e_{F_{i+1}}-e_{F_{i}} \ = \ \sum _{F_{i}<:F'<:F_{i+1}} (e_{F'} - e_{F_{i}}) \end{aligned}$$

and thus

$$\begin{aligned} \sum _{F_{i}<:F'<:F_{i+1}} e_{F'} \ = \ e_{F_{i+1}}+(m-1)e_{F_{i}} \quad \in \quad {\mathfrak c}_{{\mathcal F}} \end{aligned}$$

where \(m\ge 1\) is the number of flats \(F'\) with \(F_{i}<:F'<:F_{i+1}\). \(\square \)

4 Higher balancing

We are prepared to state and prove the main result of this text.

Theorem 2

Let M be a matroid with ground set E and \({\mathcal F}=(F_0,\dotsc ,F_d)\) a flag of flats of type \((r_0,\dotsc ,r_d)\). Let i and k be integers such that \(0\le i\le d-1\) and \(1\le k\le r_{i+1}-r_{i}\). Then

$$\begin{aligned}&\sum _{F^{(0)}<:\cdots<:F^{(k)}\le F_{i+1}} \quad (e_{F^{(k)}}-e_{F^{(k-1)}})\\&\quad + \sum _{l=1}^{k-1} (-1)^{k-l} \quad \sum _{F^{(0)}<:\cdots<:F^{(l)}< F_{i+1}} \quad (e_{F_{i+1}}-e_{F^{(l-1)}}) \\&\quad + \quad (-1)^k (e_{F_{i+1}}-e_{F_{i}}) \quad = \quad 0 \end{aligned}$$

where \(F^{(0)}=F_{i}\) is fixed and \(F^{(1)},\dotsc ,F^{(k)}\) vary over all possible flats. We call this relation the (i, k)-balancing condition at \({\mathfrak c}_{\mathcal F}\).

Proof

We prove the result by induction on k. For the sake of presentation, we will show that the first sum in the balancing condition equals the inverse of the other terms.

The case \(k=1\) follows by the same argument that we have used to prove Proposition 1 where we note that the proof did not make any use of the assumptions that \({\mathcal F}\) is of length \(d=rk\, M-1\) and that \(r_{i+1}-r_i=2\). Therefore, we derive that

$$\begin{aligned} \sum _{F^{(0)}<:F^{(1)}\le F_{i+1}} \quad (e_{F^{(1)}}-e_{F^{(0)}}) = e_{F_{i+1}}-e_{F_{i}} = -\Big [ (-1)^k(e_{F_{i+1}}-e_{F_{i}})\Big ], \end{aligned}$$

where we use that \((-1)^k=-1\) and that there is no middle term of the form “\(\sum _{l=1}^{k-1}\dotsc \)” since \(k-1<1\).

If \(k>1\), then we can split the sequences \(F^{(0)}<:\cdots <:F^{(k)}\le F_{i+1}\) into \(F^{(0)}<:F^{(1)}\) and \(F^{(1)}<:\cdots <:F^{(k)}\le F_{i+1}\), which yields an equality

$$\begin{aligned}&\sum _{F^{(0)}<:\cdots<:F^{(k)}\le F_{i+1}} \quad (e_{F^{(k)}}-e_{F^{(k-1)}})\\&\quad =\sum _{F^{(0)}<:F^{(1)}< F_{i+1}} \left[ \sum _{F^{(1)}<:\cdots <:F^{(k)}\le F_{i+1}} \quad (e_{F^{(k)}}-e_{F^{(k-1)}}) \right] . \end{aligned}$$

Applying the inductive hypothesis to the sum inside the brackets transforms this expression into

$$\begin{aligned}&-\sum _{F^{(0)}<:F^{(1)}< F_{i+1}} \left[ \sum _{l=1}^{k-2} (-1)^{(k-1)-l} \quad \sum _{F^{(1)}<:\cdots<:F^{(l+1)}< F_{i+1}} \quad (e_{F_{i+1}}-e_{F^{(l)}}) \right. \\&\quad \left. + (-1)^{k-1} (e_{F_{i+1}}-e_{F^{(1)}}) \right] . \end{aligned}$$

Merging the outer sum over \(F^{(0)}<:F^{(1)}<F_{i+1}\) with the inner terms and replacing l by \(l-1\) yields

$$\begin{aligned}&-\Bigg [ \sum _{l=2}^{k-1} (-1)^{k-l} \quad \sum _{F^{(0)}<:\cdots<:F^{(l)}<F_{i+1}}\quad (e_{F_{i+1}}-e_{F^{(l-1)}})\\&\quad + (-1)^{k-1} \quad \sum _{F^{(0)}<:F^{(1)}< F_{i+1}} \quad (e_{F_{i+1}}-e_{F^{(1)}})\Bigg ]. \end{aligned}$$

We can apply the case \(k=1\) to the sum on the right hand side and get

$$\begin{aligned}&(-1)^{k-1} \quad \sum _{F^{(0)}<:F^{(1)}< F_{i+1}} \quad (e_{F_{i+1}}-e_{F^{(1)}}) \\&\quad = (-1)^{k-1} \quad \sum _{F^{(0)}<:F^{(1)}< F_{i+1}} \quad (e_{F_{i+1}}-e_{F^{(0)}}) + (-1)^k (e_{F_{i+1}}-e_{F_{i}}). \end{aligned}$$

Substituting this term in the expression above produces the desired outcome

$$\begin{aligned} -\left[ \sum _{l=1}^{k-1} (-1)^{k-l} \quad \sum _{F^{(0)}<:\cdots<:F^{(l)}<F_{i+1}}\quad (e_{F_{i+1}}-e_{F^{(l-1)}}) + (-1)^{k} (e_{F_{i+1}}-e_{F_{i}})\right] . \end{aligned}$$

\(\square \)

5 Geometric interpretation of higher balancing

Let \({\mathcal F}=(F_0,\dotsc ,F_d)\) be a flag of flats in M of type \((r_0,\dotsc ,r_d)\). The cases of (i, k)-balancing for \(k=r_{i+1}-r_i\) are degenerate and we will discuss them below. For now we assume that \(k<r_{i+1}-r_i\) and write \(F<F'\) for \(F\subsetneq F'\).

To begin with, we observe that the flags \(F^{(0)}<:\cdots<:F^{(l)}< F_{i+1}\) that occur as indices of the sums in the (i, k)-balancing condition can be identified with the cones \({\mathfrak c}_{{\mathcal F}'}\) with

$$\begin{aligned} {\mathcal F}'=(F_0,\dotsc ,F_{i},F^{(1)},\dotsc ,F^{(l)},F_{i+1},\dotsc ,F_d). \end{aligned}$$

Thus we can interpret the sum as varying over all cones in B(M) of type

$$\begin{aligned} (r_0,\dotsc ,r_{i},r_{i}+1,\dotsc ,r_{i}+l,r_{i+1},\dotsc ,r_d) \end{aligned}$$

that contain \({\mathfrak c}_{\mathcal F}\).

Therefore the (i, 1)-balancing condition

$$\begin{aligned} \sum _{F_{i}<:F^{(1)}\le F_{i+1}} \quad (e_{F^{(1)}}-e_{F_{i}}) - (e_{F_{i+1}}-e_{F_{i}}) = 0 \end{aligned}$$

can be rewritten as

$$\begin{aligned} \sum _{\begin{array}{c} {\mathcal F}'=(F_0',\dotsc ,F_{d+1}')\text { of type }\\ (r_0,\dotsc ,r_{i},r_{i}+1,r_{i+1},\dotsc ,r_d)\\ \text {such that }{\mathfrak c}_{\mathcal F}\subset {\mathfrak c}_{{\mathcal F}'} \end{array}} e_{F_{i+1}'} = e_{F_{i+1}} + (m-1) e_{F_{i}} \in {\mathfrak c}_{\mathcal F}\end{aligned}$$

where \(m\ge 1\) is the number of flags \({\mathcal F}'\) of type \((r_0,\dotsc ,r_{i},r_{i}+1,r_{i+1},\dotsc ,r_d)\) such that \({\mathfrak c}_{\mathcal F}\subset {\mathfrak c}_{{\mathcal F}'}\). Note that \(e_{{\mathcal F}'}\) is a primitive vector for \({\mathfrak c}_{{\mathcal F}'}\) modulo \({\mathfrak c}_{\mathcal F}\), which is a ray. In particular, this recovers the usual balancing condition for tropical varieties in the case that \({\mathfrak c}_{\mathcal F}\) is of dimension \(rk\, M-1\).

For \(k>1\), a geometric interpretation of (i, k)-balancing involves different ‘types’ of ‘primitive vectors’, one for each ray of \({\mathfrak c}_{{\mathcal F}'}\) that is not contained in \({\mathfrak c}_{{\mathcal F}}\). Without spelling out the obvious formula, the (i, k)-balancing condition states that a certain linear combination of primitive vectors of (the rays of) cones containing \({\mathfrak c}_{\mathcal F}\), ordered by their types, is contained in the linear subspace spanned by \({\mathfrak c}_{\mathcal F}\).

Balancing in the degenerate case \(k=r_{i+1}-r_i=1\) yields the trivial relation

$$\begin{aligned} (e_{F_{i+1}}-e_F)-(e_{F_{i+1}}-e_F) \ = \ 0. \end{aligned}$$

If \(k=r_{i+1}-r_i>1\), then (i, k)-balancing results from \((i,k-1)\)-balancing after a trivial rearrangement of terms, which brings, however, the relation into a more symmetric shape. In particular, (i, k)-balancing implies that

$$\begin{aligned} \sum _{l=2}^k \quad (-1)^k \sum _{F_i<:F^{(1)}<:\cdots <:F^{(l)}\le F_{i+1}} e_{F^{(l-1)}} \end{aligned}$$

is contained in the linear subspace spanned by \({\mathfrak c}_{{\mathcal F}}\).

6 Relation to CSM-balancing

Lopez de Medrano, Rincón and Shaw introduce in [17] the k-th Chern-Schwartz-MacPherson cycle \({{\,\mathrm{csm}\,}}_k(M)\) of a matroid M for \(k=0,\dotsc ,rk\, M\), which is the k-skeleton of the Bergman fan of the matroid together with certain weights on its k-dimensional cones. A fundamental insight is that the Chern-Schwartz-MacPherson cycles are tropical varieties; see [17, Thm. 2.14]. We refer to this result by CSM-balancing for short.

We can reinterpret this result as follows. We can endow all cones \({\mathfrak c}_{\mathcal F}\) of the Bergman fan B(M) of M with certain weights \(\mu _{\mathcal F}\) such that for every cone \({\mathfrak c}_{\mathcal F}\) of dimension \(k<rk\, M\),

$$\begin{aligned} \sum _{\begin{array}{c} {\mathfrak c}_{{\mathcal F}}\subset {\mathfrak c}_{{\mathcal F}'}\\ \dim {\mathfrak c}_{{\mathcal F}'}=k+1 \end{array}} \mu _{{\mathcal F}'} \ e_{{\mathcal F}'} \end{aligned}$$

lies in the subspace spanned by \({\mathfrak c}_{\mathcal F}\) where \(e_{{\mathcal F}'}\) is a primitive vector of \({\mathfrak c}_{{\mathcal F}'}\) modulo \({\mathfrak c}_{\mathcal F}\).

It is possible to express the weights \(\mu _{{\mathcal F}'}\) as a linear combination of the number of cones containing \({\mathcal F}'\) (ordered by their types), which indicates a relation to higher balancing in the sense of this paper. We were able to verify that CSM-balancing can be traced back to certain linear combinations of the relations that occur in Theorem 2 up to codimension 3, i.e. for \(rk\, M-k-1\le 3\). We strongly suspect that CSM-balancing can be deduced from higher balancing in general. A proof of this conjecture would be desirable.

7 Example

As an example, we consider the uniform matroid \(M=U_{3,4}\) of rank 3 with ground set \(E=\{1,2,3,4\}\). Its lattice of flats is as follows.

figure a

The different types of cones of the Bergman fan B(M) of M are described in the following table where we fix an identification \(E=\{i,j,k,l\}\).

type

typical flag \({\mathcal F}\)

\((x_1,\dotsc ,x_4)\) in \({\mathfrak c}_{\mathcal F}\) iff.

dimension

number of cones

(0, 3)

\((\emptyset ,E)\)

\(x_i=x_j=x_k=x_l\)

1

1

(0, 1, 3)

\((\emptyset ,\{i\},E)\)

\(x_i\ge x_j= x_k= x_l\)

2

4

(0, 2, 3)

\((\emptyset ,\{i,j\},E)\)

\(x_i= x_j\ge x_k= x_l\)

2

6

(0, 1, 2, 3)

\((\emptyset ,\{i\},\{i,j\},E)\)

\(x_i\ge x_j\ge x_k= x_l\)

3

12

We find non-trivial balancing conditions (i.e. \(k<r_{i+1}-r_i\)) at all cones of positive codimension, i.e. at cones of types (0, 1, 3), (0, 2, 3) and (0, 3). These balancing conditions are, up to permuting \(E=\{i,j,k,l\}\), as follows.

$$\begin{aligned} \begin{array}{ll} (1,1)\hbox {-balancing at} {\mathfrak c}_{(\emptyset ,\{i\},E)}: &{} \displaystyle \sum _{\{i\}<:\{i,n\}<E} \quad (e_{\{i,n\}}-e_i) \ - \ (e_E-e_i) \ = \ 0 \\ (0,1)\hbox {-balancing at} {\mathfrak c}_{(\emptyset ,\{i,j\},E)}: &{} \displaystyle \sum _{\emptyset<:\{m\}<\{i,j\}} \quad (e_{m}-e_\emptyset ) \ - \ (e_{\{i,j\}}-e_\emptyset ) \ = \ 0 \\ (0,1)\hbox {-balancing at} {\mathfrak c}_{(\emptyset ,E)}: &{} \displaystyle \sum _{\emptyset<:\{m\}<E} \quad (e_{m}-e_\emptyset ) \ - \ (e_E-e_\emptyset ) \ = \ 0 \\ (0,2)\hbox {-balancing at} {\mathfrak c}_{(\emptyset ,E)}: &{} \displaystyle \quad \sum _{\emptyset<:\{m\}<:\{m,n\}<E} \quad (e_{\{m,n\}}-e_m)- \sum _{\emptyset<:\{m\}<E} \\ &{}\qquad (e_{E}-e_\emptyset ) \ + \ (e_E-e_\emptyset ) \ = \ 0\\ \end{array} \end{aligned}$$

Note that the first two conditions are balancing conditions in codimension 1, i.e. they are the ‘classical’ balancing conditions for tropical varieties. In particular note that these classical balancing conditions are divided into two different types.