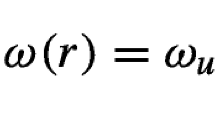On the existence of the Green function for elliptic systems in divergence form

Abstract

We study the existence of the Green function for an elliptic system in divergence form $-\nabla \cdot a\nabla$ in ${\mathbb {R}}^d$, with $d>2$. The tensor field $a=a(x)$ is only assumed to be bounded and $\lambda$-coercive. For almost every point $y \in {\mathbb {R}}^d$, the existence of a Green’s function $G(\cdot , y)$ centered in y has been proven in Conlon et al. (Calc Var PDEs 56(6), (2017))[2]. In this paper we show that the set of points $y \in {\mathbb {R}}^d$ for which $G( \cdot , y)$ does not exist has zero p-capacity, for an exponent $p >2$ depending only on the dimension d and the ellipticity ratio of a.

This paper is an extension of [2] and further investigates the existence of a Green’s function for the second-order elliptic operator $-\nabla \cdot a \nabla$ in ${\mathbb {R}}^d$, with $d> 2$. We focus on the case of systems of m equations, namely when a is a measurable tensor field $a : {\mathbb {R}}^d\rightarrow {\mathcal {L}}({\mathbb {R}}^{m \times d} ; {\mathbb {R}}^{m \times d})$, with m being any positive integer. We stress that in this paper we do only assume that a is bounded and $\lambda$-coercive, i.e. that there exists $\lambda >0$ such that

$$\begin{aligned} \begin{aligned}&\forall \zeta \in C^\infty _0( {\mathbb {R}}^d; {\mathbb {R}}^m)\ \ \ \int \nabla \zeta (x) \cdot a(x) \nabla \zeta (x) \, \text {d} x\geqslant \lambda \int |\nabla \zeta (x)|^2 \, \text {d} x,\\&\forall x\in {\mathbb {R}}^d,\ \forall \ \xi \in {\mathbb {R}}^{m\times d} \ \ \ |a(x)\xi |\leqslant |\xi | . \end{aligned} \end{aligned}$$

(0.1)

In [2], Conlon and the authors show that a Green’s function $G(\cdot , y)$ centered in y exists for every coefficient field a satisfying (0.1) and for (Lebesgue-)almost every point $y\in {\mathbb {R}}^d$. In this paper, we improve this result by showing that the exceptional set $\Sigma$ of points $y\in {\mathbb {R}}^d$ for which $G(a; \cdot , y)$ does not exist has p-capacity zero [4, Definition 4.10], for an exponent $p > 2$ depending only on the dimension d and the ellipticity ratio $\lambda$. This, in particular, implies that for every coefficient field a that is $\lambda$-coercive and bounded, the Hausdorff dimension of $\Sigma$ is strictly smaller than $d-2$ [4, Theorem 4.17].

The result of [2] crucially relies on the idea of studying the Green function as a map $G = G(\cdot , \cdot )$ in both variables $x, y \in {\mathbb {R}}^d$. This yields optimal estimates for the $L^2$-norm in y and x of G, $\nabla _x G$ and $\nabla _x \nabla _y G$ both away from the diagonal $\{ x = y \}$ and close to it. By the standard properties of Lebesgue-integrable functions, these estimates allow to give a pointwise meaning in y to $G( \cdot , y)$, up to a set of Lebesgue-measure zero. The main idea behind the result of this paper is to exploit the integrability of the mixed derivatives $\nabla _y \nabla _x G$ and extend the set of Lebesgue points y where $G( \cdot , y)$ is well-defined up to the set $\Sigma$ having zero p-capacity.

We remark that in the case of elliptic systems the set $\Sigma$ may indeed be non-trivial. There are, indeed, coefficient fields a satisfying (0.1) for which one may construct unbounded a-harmonic vector fields. From this, and by means of representation formulas, it follows that the points where such vector fields are unbounded cannot be Lebesgue points for $G( \cdot , y)$. A classical example of a discontinuous a-harmonic vector field is due to De Giorgi [3]: For any dimension $d> 2$, the vector field $u : {\mathbb {R}}^d\rightarrow {\mathbb {R}}^d$

$$\begin{aligned} u(x)=\frac{x}{|x|^{\gamma }}, \ \ \ \gamma :=\frac{\text {d}}{2}\biggl (1-\frac{1}{\sqrt{(2\text {d}-2)^2+1}}\biggr )> 1 \end{aligned}$$

(0.2)

solves $-\nabla \cdot a_0 \nabla u = 0$ in ${\mathbb {R}}^d$, with $a_0$ satisfying (0.1) and being smooth everywhere outside of the origin. We remark that the coefficient $a_0$ is not only $\lambda$-coercive as in (0.1), but also strongly elliptic: For almost every $x \in {\mathbb {R}}^d$ and every matrix $\xi \in {\mathbb {R}}^{d \times d}$, it satisfies $\xi \cdot a_0(x) \xi \geqslant \lambda |\xi |^2$, with $\lambda$ depending on d.

In the case $d=3$, the previous example implies that the exceptional set $\Sigma$ for $a_0$ contains at least the origin. For higher dimensions $d \geqslant 3$, the trivial extension of the vector field u for $d=3$ is itself ${\bar{a}}_0$-harmonic if

$$\begin{aligned} {\bar{a}}_0:=\begin{pmatrix} a_0 &{}\quad 0 \\ 0 &{}\quad \mathop {I} \end{pmatrix}. \end{aligned}$$

This implies, in particular, that $\Sigma$ for ${\bar{a}}_0$ has Hausdorff dimension at least $d-3$.

The previous counterexample also implies that for (locally) a-harmonic vector fields one may only aim at statements on their partial regularity as, for instance, their continuity outside of a singular set. We remark that there exist examples of discontinuous a-harmonic vector fields with discontinuity much larger than (0.2): we refer, for instance, to the paper by Soucek [10], which exhibits an a-harmonic vector field discontinuous on a dense countable set, and the one by John et al. [6], in which, for every countable union of closed sets (i.e. $F_\sigma$-set), an a-harmonic vector field discontinuous there is constructed.

Without using the equation, the fact that a-harmonic functions are locally in $H^1$ immediately implies that they are 2-quasicontinuous. This means that there exist sets, of arbitrarily small 2-capacity, outside of which the function considered is continuous [4, Definition 4.11]. This argument is oblivious to the difference between scalar and vectorial functions. Using the equation and appealing to Meyers’ [9] or Gehring’s [5] estimates, this notion of continuity may be upgraded from 2-quasicontinuity to p-quasicontinuity, for an exponent $p>2$. The result of this paper provides an analogous statement for the solution operator for $-\nabla \cdot a \nabla$. By means of representation formulas, indeed, we prove that for any family ${\mathcal {F}}$ of locally a-harmonic functions that are uniformly bounded in the $H^1_{loc}$-norm, there exist common sets of arbitrarily small p-capacity outside of which ${\mathcal {F}}$ is equicontinuous (see Corollary 1). These sets are universal in the sense that they depend only on the coefficient a and on the dimension d, but not on the family ${\mathcal {F}}$.

Notation and previous results For notational convenience, as in [2] we assume that a is symmetric, i.e. that for almost every $x\in {\mathbb {R}}^d$, the tensor $a(x) \in {\mathcal {L}}({\mathbb {R}}^{m \times d} ; {\mathbb {R}}^{m \times d})$ is symmetric. Throughout this paper the expression “almost every” is meant with respect to the Lebesgue measure and all the PDEs considered are assumed to hold only in the distributional sense.

We denote by $W^{1,p}({\mathbb {R}}^d, {\mathbb {R}}^m)$, $p \geqslant 1$ the Sobolev spaces of functions in ${\mathbb {R}}^d$ taking values in ${\mathbb {R}}^m$; if $m =1$, we use the usual notation $W^{1,p}({\mathbb {R}}^d)$. The same criteria are employed for all the other standard functions spaces used in the paper. If we represent the elements of the product space ${\mathbb {R}}^d \times {\mathbb {R}}^d$ by (x, y), we use the notation $W^{1,q}_x({\mathbb {R}}^d)$ to specify in the lower index the differentiation and integration variable. Similarly, we write $\nabla _x, \nabla _{y}$ or $\nabla _{x,y}$ when the gradient is taken with respect to x, y or both variables (x, y), respectively. We write $\gtrsim$ and $\lesssim$ for $\geqslant C$ and $\leqslant C$ with a constant C depending only on the dimension d, the ellipticity ratio $\lambda$ and the dimension of the target space m.

For an open (not necessarily bounded) set $D \subseteq {\mathbb {R}}^d$, we may define the space

$$\begin{aligned} Y^{1,2}(D ; {\mathbb {R}}^{m}) := \bigl \{ u \in L^{\frac{2d}{d-2}}(D ; {\mathbb {R}}^{m}) \, : \, \nabla u \in L^2(D ; {\mathbb {R}}^{m \times d}) \bigr \}, \end{aligned}$$

and equip it with the norm $\Vert u\Vert _{Y^{1,2}(D ; {\mathbb {R}}^{m})}:= \Vert u \Vert _{L^{\frac{2d}{d-2}}(D; {\mathbb {R}}^{m})} + \Vert \nabla u \Vert _{L^2(D ; {\mathbb {R}}^{m \times d})}$. The main theorem of [2, Theorem 1] provides the existence of a map

$$\begin{aligned} \begin{aligned} G&: {\mathbb {R}}^d\times {\mathbb {R}}^d\rightarrow {\mathbb {R}}^{m \times m} \end{aligned} \end{aligned}$$

(0.3)

such that for all $1\leqslant q < \frac{d}{d-1}$

$$\begin{aligned} G \in W^{1, q}_{loc}({\mathbb {R}}^d\times {\mathbb {R}}^d; {\mathbb {R}}^{m \times m}) \end{aligned}$$

(0.4)

and for almost every $y \in {\mathbb {R}}^d$, the tensor field $G( \cdot , y ) \in Y_x^{1,2}(\{ |x-y| > 1 \} ; {\mathbb {R}}^{m\times m})$ and satisfies

$$\begin{aligned} -\nabla _x \cdot a(\cdot ) \nabla _x G(\cdot , y) = \delta ( \cdot - y) \quad \text {in}\ { {\mathbb {R}}^d.} \end{aligned}$$

(0.5)

Furthermore, for every $R > 0$, $z\in {\mathbb {R}}^d$ and $\alpha > \frac{d}{2} -1$ it holds

$$\begin{aligned} \int _{|y-z|< R}\int _{|x-z|< R} |x-y|^{2\alpha } |\nabla _{x,y} G(x, y)|^2 dx \, \text {d} y&\lesssim _\alpha R^{2+ 2\alpha }, \end{aligned}$$

(0.6)

$$\begin{aligned} \int _{|y-z|< R}\int _{|x-z|> 2R} |\nabla _x G(x, y)|^2 dx \, \text {d} y&\lesssim R^2, \end{aligned}$$

(0.7)

$$\begin{aligned} \int _{|y-z|< R}\int _{|x-z|> 2R} |\nabla _y\nabla _x G(x, y)|^2 dx \, \text {d} y&\lesssim 1 . \end{aligned}$$

(0.8)

Here, the notation $\lesssim _\alpha$ means that the constant depends also on the exponent $\alpha$.

We stress that [2, Theorem 1] does not state that for almost every $y \in {\mathbb {R}}^d$, the tensor field $G( \, \cdot \, , y ) \in Y_x^{1,2}(\{ |x-y| > 1 \} ; {\mathbb {R}}^{m\times m})$. However, this property is an immediate consequence of [2, Inequality (15) in Theorem 1], together with Sobolev’s inequality in the exterior domain $\{ |x- y | > 1 \}$. Sobolev’s inequality holds since, by [2, Equation (8) in Section 2], the tensor field $G(\cdot , y)$ vanishes at infinity for almost every $y\in {\mathbb {R}}^d$.

We also remark that in this paper we restrict ourselves to the case $d > 2$ as in dimension $d=2$ the map G does not exist. We refer to [2] for further details and for an existence result for G if ${\mathbb {R}}^2$ is replaced by any domain $D \subseteq {\mathbb {R}}^2$ having at least a bounded direction [2, Theorem 1, (b)].

1 Main result

Theorem 1

Recall $d > 2$. Let a be symmetric and satisfy assumptions (0.1). Let $G : {\mathbb {R}}^d \times {\mathbb {R}}^d \rightarrow {\mathbb {R}}^{m \times m}$ be the Green function in the sense of [2] and constructed there. Then, there exists a (measurable) set $\Sigma = \Sigma (a) \subseteq {\mathbb {R}}^d$ with the following properties:

• (a) There exists an exponent $p= p(d, \lambda ) > 2$ such that

  $$\begin{aligned} \text {{p-}cap}\bigl ( \Sigma \bigr ) = 0. \end{aligned}$$

• (b) There exists an exponent $q=q(d, \lambda ) >1$ such that for every $y \in {\mathbb {R}}^d\backslash \Sigma$ and for all $R >0$

  $$\begin{aligned} \fint _{|z- y| < \delta } G( \cdot , z) \, d z \rightharpoonup G^*( \cdot , y) \quad {\text {as}}\ {\delta \downarrow 0} \end{aligned}$$

  in $W^{1, q}_{ x}(\{ |x-y| < R \} ; {\mathbb {R}}^{m\times m}) \cap Y^{1,2}_x(\{ | x- y | > R \}; {\mathbb {R}}^{m\times m})$.

• (c) The representative $G^*( \cdot , y)$ solves Eq. (0.5) for every $y \in {\mathbb {R}}^d\backslash \Sigma$. Furthermore, there exists an exponent $\alpha < \frac{d}{2}$ such that

  $$\begin{aligned} \int \min \{ |x-y|^{2\alpha } , 1 \} |\nabla _x G^*( x, y)|^2 \, \text {d} x< + \infty .\end{aligned}$$

In addition, as a corollary we have:

Corollary 1

Let the coefficient field a and the exponent $p > 2$ be as in Theorem 1. Consider

$$\begin{aligned} {\mathcal {F}}:=\biggl \{ u \, :\, \ u\ {\text {is}}\ {\text {a}}{-}{\text {harmonic}}\ {\text {in}}\ \{ |x|< 4\}, \int _{|x| < 4} |\nabla \text {u}|^2 \leqslant 1 \ \ \biggr \}. \end{aligned}$$

Then for every $\varepsilon > 0$ there exists an open set $U^\varepsilon \subseteq \{|x| < 1\}$ having

$$\begin{aligned} \text {{p-}cap}(U^{\varepsilon }) < \varepsilon \end{aligned}$$

such that ${\mathcal {F}}$ is equicontinuous in $\{|x| < 1\}\backslash U^\varepsilon$ and the modulus of continuity is uniform in $\{|x| < 1\}\backslash U^\varepsilon$.

2 Proofs

For the sake of simplicity, throughout this section we use a scalar notation and language by pretending that a is a field of $d\times d$ matrices and that the Green function is scalar. For a detailed discussion about this abuse of notation, we refer to [2, Section 2]. Moreover, for a function $f \in L^1_{loc}({\mathbb {R}}^d)$, we introduce the notation

$$\begin{aligned} {\mathcal {M}}f(y)&:= \sup _{\delta > 0} \fint _{|{{\tilde{y}}}-y|< \delta } | f({{\tilde{y}}})| \, d{{\tilde{y}}}, \end{aligned}$$

(2.9)

$$\begin{aligned} {\mathcal {M}}_0 f(y)&:= \limsup _{\delta \downarrow 0}\fint _{|{{\tilde{y}}} -y|< \delta } |f({{\tilde{y}}})| \, d{{\tilde{y}}}. \end{aligned}$$

(2.10)

Before giving the proof of Theorem 1, we recall some further properties of $G(\cdot , \cdot )$ obtained in [2] which will be used in our proofs:

• [2, Definition (11) and Theorem 1]: For every $R >0$, $z\in {\mathbb {R}}^{d}$ and almost every $y \in {\mathbb {R}}^d$ such that $|y- z| < R$,

  $$\begin{aligned} -\nabla _x \cdot a(\cdot ) \nabla _x \nabla _{y} G(\cdot , y) = 0 \quad \hbox {in}\ \{|x- z| > \hbox {2R} \} \end{aligned}$$

  (2.11)

  and $\nabla _y G(\cdot , y) \in Y^{1, 2}_x(\{|x- z| > 2R \}, {\mathbb {R}}^d)$.

• [2, Property (87)]: For almost every $(x, y) \in {\mathbb {R}}^d\times {\mathbb {R}}^d$

  $$\begin{aligned} G( x, y) = G(y, x). \end{aligned}$$

  (2.12)

• [2, Remark 2]: For every $g \in L^2({\mathbb {R}}^d; {\mathbb {R}}^d)$ and every $f \in L^2({\mathbb {R}}^d)$ having compact support, the solution $u \in Y^{1,2}({\mathbb {R}}^d)$ to

  $$\begin{aligned} -\nabla \cdot a \nabla u = \nabla \cdot g +f \quad \text {in}\ { {\mathbb {R}}^d} \end{aligned}$$

  may be written as the identity (up to a set of Lebesgue-measure zero)

  $$\begin{aligned} u(\cdot ) = - \int g(y) \cdot \nabla _y G( \cdot , y) \, \text {d} y+ \int f(y) G(\cdot , y) \, \text {d} y. \end{aligned}$$

  (2.13)

Proof of Theorem 1

We divide the proof into five steps: in Step 1 we give a formulation of the standard Gehring’s estimate tailored to our needs. It allows to upgrade estimate (0.8) into an $L^2$-estimate in x and $L^{{\bar{p}}}$ in y, for the Gehring exponent ${\bar{p}} > 2$. Steps 2-4 contain the main capacitary estimates for the exceptional set $\Sigma$, which is closely related to the set of points $y \in {\mathbb {R}}^d$ where $G( \cdot , y)$ and $\nabla _x G( \cdot , y)$ have infinite $W^{1,q}_{x}(\{|x-y| < 1 \})$- or $Y^{1,2}_x( \{ |x- y | > 1 \})$-norms. These estimates on the capacity of $\Sigma$ crucially rely on the upgraded version of (0.8) and are combined with a maximal function estimate for Sobolev functions. Finally, in Step 5 we argue how to construct the representative $G^*( \cdot , y)$ away from the singularity set $\Sigma$.

Step 1. Gehring’s estimate   Let $u \in H^1(\{ |x| < 2R\})$ be a solution to

$$\begin{aligned} - \nabla \cdot a \nabla u = \nabla \cdot g \quad \text {in}\ { \{ |x| < 2R \}.} \end{aligned}$$

(2.14)

Then, there exists an exponent ${\bar{p}}={\bar{p}}(d, \lambda ) > 2$ such that

$$\begin{aligned} \left( \fint _{|x|< R} |\nabla u(x)|^{{\bar{p}}} \, \text {d} x\right) ^{\frac{1 }{{\bar{p}}}} \lesssim \left( \fint _{|x|< 2R} |\nabla u(x)|^2 \, \text {d} x\right) ^{\frac{1}{2}} + \left( \fint _{|x| < 2R} | g(x)|^{{\bar{p}}} \, \text {d} x\right) ^{\frac{1}{ {\bar{p}}}}. \end{aligned}$$

(2.15)

This is a standard result in elliptic regularity theory and we refer to [5, Chapter V, Theorem 2.1] for its proof.¹ We pick a (smooth) cut-off function $\eta$ for $\{|x| < R \}$ in $\{ |x| < 2R \}$. Since we may assume ${{\bar{p}}} \leqslant \frac{2d}{d-2}$, the Poincaré-Sobolev inequality yields

$$\begin{aligned} \left( \fint _{|x|< 2R} |\eta (x) u(x)|^{{\bar{p}}} \, \text {d} x\right) ^{\frac{1}{{\bar{p}}}} \leqslant R \left( \fint _{|x| < 2R} |\nabla (\eta (x) u(x))|^2 \, \text {d} x\right) ^{\frac{1}{2}}, \end{aligned}$$

it follows that

$$\begin{aligned}&R^{-1}\left( \fint _{|x|< R} | u(x)|^{{\bar{p}} }\, \text {d} x\right) ^{\frac{1}{{\bar{p}}}} + \left( \fint _{|x|< R} |\nabla u(x)|^{{\bar{p}}} \, \text {d} x\right) ^{\frac{ 1}{ {\bar{p}}}} \nonumber \\&\quad \lesssim R^{-1}\left( \fint _{|x|< 2R} | u(x)|^2 \, \text {d} x\right) ^{\frac{1}{2}}+ \left( \fint _{|x|< 2R} |\nabla u(x)|^2 \, \text {d} x\right) ^{\frac{1}{2}} + \left( \fint _{|x| < 2R} | g(x)|^{{\bar{p}}} \, \text {d} x\right) ^{\frac{1}{{\bar{p}}}}. \end{aligned}$$

(2.16)

Step 2. Capacity estimates: First reduction   Recall the definition (2.10) of ${\mathcal {M}}_0$ which we always think as acting on the y-variable. Let $p \geqslant 1$. We claim that if for an exponent $0< \alpha =\alpha (d, \lambda ) < \frac{d}{2}$ and every $R> 0$, $z \in {\mathbb {R}}^d$

$$\begin{aligned} \begin{aligned} \text {{p-}cap}\biggl \{ \, |y -z|< 1 \, :\, {\mathcal {M}}_0 \biggl ( \int _{|x-y|< R} |x-y|^{2\alpha } |G( x, y)|^2 \, \text {d} x\biggr )^{\textstyle \frac{1}{2}}= +\infty \biggr \}&= 0,\\ \text {{p-}cap}\biggl \{ \, |y -z|< 1 \, :\, {\mathcal {M}}_0 \biggl ( \int _{|x-y| < R} |x-y|^{2\alpha } |\nabla _x G(x, y)|^2 \, \text {d} x\biggr )^{\textstyle \frac{1}{2}}= +\infty \biggr \}&= 0, \end{aligned} \end{aligned}$$

(2.17)

then we may also find an exponent $q= q(d, \lambda ) > 1$ such that for every $R> 0$

$$\begin{aligned} \text {{p-}cap}\biggl \{ y \in {\mathbb {R}}^d\, :\, {\mathcal {M}}_{0} \Vert G(\cdot , y) \Vert _{W^{1,q}_x(\{ |x-y| < R \} ) } = +\infty \biggr \} = 0 . \end{aligned}$$

(2.18)

Similarly, if for every $R> 0$ and $z \in {\mathbb {R}}^d$ it holds

$$\begin{aligned} \begin{aligned} \text {{p-}cap}\biggl \{ \, |y -z|< 1 \, :\, {\mathcal {M}}_0 \biggl ( \int _{|x-y|> R} |G( x, y)|^{\frac{2d}{d-2}} \, \text {d} x\biggr )^{\frac{d-2}{2d}} = +\infty \biggr \}&= 0,\\ \text {{p-}cap}\biggl \{ \, |y -z|< 1 \, :\, {\mathcal {M}}_0 \biggl ( \int _{|x-y| > R} |\nabla _x G( x, y)|^2 \, \text {d} x\biggr )^{\textstyle \frac{1}{2}}= +\infty \biggr \}&= 0, \end{aligned} \end{aligned}$$

(2.19)

then for every $R> 0$

$$\begin{aligned} \text {{p-}cap}\biggl \{ y \in {\mathbb {R}}^d\, :\, {\mathcal {M}}_{0} \Vert G(\cdot , y)\Vert _{Y^{1,2}_x(\{|x-y| > R \})} = +\infty \biggr \} = 0. \end{aligned}$$

(2.20)

Since we may cover the whole space ${\mathbb {R}}^d$ with a countable number of unit balls, the subadditivity of the capacity and (2.19) immediately imply (2.20). Analogously, the subadditivity of the capacity and (2.17) yield that for each $R > 0$

$$\begin{aligned} \begin{aligned} \text {{p-}cap}\biggl \{ y \in {\mathbb {R}}^d\, :\, {\mathcal {M}}_0 \bigl ( \int _{|x-y| < R} |x-y|^{2\alpha } (|G(x, y)|^2 + |\nabla _x G(x, y)|^2 )\, \text {d} x\bigr )^{\textstyle \frac{1}{2}}= +\infty \biggr \} = 0. \end{aligned}\nonumber \\ \end{aligned}$$

(2.21)

Since for $\alpha < \frac{d}{2}$, Hölder’s inequality implies that there exists $1< q =q(\alpha ) < 2$ such that for any u

$$\begin{aligned} \int _{|x-y|< R} |u(x)|^q \, \text {d} x&\lesssim _R \biggl ( \int _{|x-y| < R} |x-y|^{2\alpha }|u(x)|^2 \, \text {d} x\biggr )^{\frac{q}{2}}, \end{aligned}$$

estimate (2.18) is implied by this inequality together with identity (2.21) and the monotonicity of the capacity.

Step 3. Capacity estimates: Second reduction   Let $2< p < {\bar{p}}$ be fixed, with ${\bar{p}}$ as in Step 1. We now argue that in order to prove (2.17) and (2.19) with this choice of exponent p, it suffices to show that for every $R > 0$, $z \in {\mathbb {R}}^d$, and all $\lambda > 0$

$$\begin{aligned} \begin{aligned} \text {{p-}cap}\biggl \{ |y-z|< \frac{R}{2} \, :\, {\mathcal {M}}_0\biggl ( \int _{ |x-y|> 8R } |\nabla _{x}G( x, y)|^2 \, \text {d} x\biggr )^{\frac{{\bar{p}}}{2p}}> \lambda \biggr \}&\lesssim \lambda ^{-p} R^{-\frac{ d{\bar{p}}}{ 2} + d + ({\bar{p}} - p)}, \\ \text {{p-}cap}\biggl \{ |y-z| < \frac{R}{2} \, :\, {\mathcal {M}}_0\biggl ( \int _{ |x-y|> 8R } |G( x, y)|^{\frac{2d}{d-2}} \, \text {d} x\biggr )^{\frac{d-2}{2d}}> \lambda \biggr \}&\lesssim \lambda ^{-p} R^{-\frac{ dp}{ 2} + d}. \end{aligned} \end{aligned}$$

(2.22)

Without loss of generality, we argue (2.17) and (2.19) in the case $z=0$ and for $R=1$. We begin by observing that, since $p \leqslant {\bar{p}}$, definition (2.10) for ${\mathcal {M}}_0$ together with Jensen’s inequality yield that for every $y \in {\mathbb {R}}^d$

$$\begin{aligned} {\mathcal {M}}_0\biggl ( \int _{ |x-y|> 8R } |\nabla _{x}G( x, y)|^2 \, \text {d} x\biggr )^{\frac{{\bar{p}}}{2p}} \geqslant \biggl ( {\mathcal {M}}_0\biggl ( \int _{ |x-y| > 8R } |\nabla _{x}G( x, y)|^2 \, \text {d} x\biggr )^{\frac{1}{2}}\biggr )^{\frac{{\bar{p}}}{p}}. \end{aligned}$$

This and the first inequality in (2.22) imply, after relabelling the parameter $\lambda ^{\frac{p}{{\bar{p}}}}$ as $\lambda$, that for every $R > 0$ and $\lambda > 0$ it holds

$$\begin{aligned} \text {{p-}cap}\biggl \{ |y-z| < \frac{R}{2} \, :\, {\mathcal {M}}_0\biggl ( \int _{ |x-y|> 8R } |\nabla _{x}G( x, y)|^2 \, \text {d} x\biggr )^{\frac{1}{2}}> \lambda \biggr \} \lesssim \lambda ^{-{\bar{p}}} R^{-\frac{ d {\bar{p}}}{ 2} + d + ({\bar{p}} - p)}. \end{aligned}$$

(2.23)

For any $0 < R \leqslant 1$ fixed, we may cover the set $\{|y| < 1\}$ by $N \lesssim R^{-d}$ balls of radius R; Hence, (2.23) and the second estimate in (2.22) yield that for all $\lambda > 0$

$$\begin{aligned} \text {{p-}cap}\biggl \{ |y| < 1 \, :\, {\mathcal {M}}_0\biggl (\int _{ |x-y|> 8R } |G( x, y)|^{\frac{2d}{d-2}} \, \text {d} x\biggr )^{\frac{d-2}{2d}} > \lambda \biggr \} \lesssim \lambda ^{- p} R^{-\frac{ d p}{ 2} } \end{aligned}$$

(2.24)

and

$$\begin{aligned} \text {{p-}cap}\biggl \{ |y| < 1 \, :\, {\mathcal {M}}_0\biggl (\int _{ |x-y|> 8R } |\nabla _{x}G( x, y)|^2 \, \text {d} x\biggr )^{\frac{1}{2}} > \lambda \biggr \} \lesssim \lambda ^{-\bar{p}} R^{-\frac{ d {\bar{p}}}{ 2} + ({\bar{p}} - p)}. \end{aligned}$$

(2.25)

Inequalities (2.19) immediately follow from these estimates if we choose $R=\frac{1}{8}$ and send $\lambda \uparrow +\infty$.

We now derive (2.17) for $\nabla _x G$ from (2.25). We begin by smuggling $R^\alpha$ into the left-hand side of (2.25) and redefining $R^\alpha \lambda$ as $\lambda$ so that

$$\begin{aligned} \text {{p-}cap}\biggl \{ |y| < 1 \, :\, {\mathcal {M}}_0 \biggl ( R^{2\alpha } \int _{ |x-y|> 8R}|\nabla _x G(x,y)|^2 \, \text {d} x\biggr )^{\textstyle \frac{1}{2}}> \lambda \biggr \} \lesssim \lambda ^{-{\bar{p}}} R^{-\frac{ d p}{ 2} + ({\bar{p}} - p) +\alpha {\bar{p}}}. \end{aligned}$$

Since

$$\begin{aligned} \int _{8R< |x-y|< 16R}|x-y|^{2\alpha } |\nabla _x G(x,y)|^2 \, \text {d} x\lesssim R^{2\alpha }\int _{ |x-y|> 8R} |\nabla _x G(x,y)|^2 \, \text {d} x,\end{aligned}$$

we conclude that also

$$\begin{aligned}&\text {{p-}cap}\biggl \{ |y|< 1 \, :\, {\mathcal {M}}_0 \biggl ( \int _{8R< |x-y|< 16R}|x-y|^{2\alpha }|\nabla _x G(x,y)|^2 \, \text {d} x\biggr )^{\textstyle \frac{1}{2}}> \lambda \biggr \} \lesssim \lambda ^{-{\bar{p}}}\nonumber \\&\quad R^{-\frac{ d {\bar{p}}}{ 2} + (\bar{p} - p)+ {\bar{p}} \alpha }. \end{aligned}$$

(2.26)

We now define

$$\begin{aligned} A&:= \biggl \{ |y|< 1 \, :\, {\mathcal {M}}_0 \biggl ( \int _{|x-y|< 1}|x-y|^{2\alpha }|\nabla _x G(x,y)|^2 \, \text {d} x\biggr )^{\textstyle \frac{1}{2}}> \lambda \biggr \} \end{aligned}$$

(2.27)

and, given a sequence of weights

$$\begin{aligned} \{&\omega _n \}_{n\in {\mathbb {N}}} \subseteq {\mathbb {R}}_+ \ \ \text { such that} \sum _\text { n} \omega _\text { n} \leqslant 1, \end{aligned}$$

(2.28)

the sets

$$\begin{aligned} A_n:= \biggl \{ |y|< 1 \, :\, {\mathcal {M}}_0 \biggl (&\int _{ 2^{-n}< |x-y|< 2^{-n+1}} |x-y|^{2\alpha }|\nabla _x G(x,y)|^2 \, \text {d} x\biggr )^{\textstyle \frac{1}{2}}> \omega _n \lambda \biggr \} \end{aligned}$$

(2.29)

for $n \in {\mathbb {N}}$. We claim that

$$\begin{aligned} A \subseteq \bigcup _n A_n. \end{aligned}$$

(2.30)

This can be easily seen by proving the complementary statement $\bigcap _n A_n^c \subseteq A^c$: Indeed, if

$$\begin{aligned} {\mathcal {M}}_0 \biggl ( \int _{ 2^{-n}< |x-y|< 2^{-n+1}}|x-y|^{2\alpha }|\nabla _x G(x,y)|^2 \, \text {d} x\biggr )^{\textstyle \frac{1}{2}}\leqslant \omega _n \lambda \ \ \ \ \text { for all}\ { n\in {\mathbb {N}},}\end{aligned}$$

then the inclusion of the sequence spaces $\ell ^1 \subseteq \ell ^2$, the subadditivity of the operator ${\mathcal {M}}_0$, and assumption (2.28) yield

$$\begin{aligned} {\mathcal {M}}_0 \biggl (&\int _{|x-y|< 1}|x-y|^{2\alpha }|\nabla _x G(x,y)|^2 \, \text {d} x\biggr )^{\textstyle \frac{1}{2}}\\&\leqslant \sum _{n\in {\mathbb {N}}}{\mathcal {M}}_0 \biggl ( \int _{ 2^{-n}< |x-y|< 2^{-n+1}}|x-y|^{2\alpha }|\nabla _x G(x,y)|^2 \, \text {d} x\biggr )^{\textstyle \frac{1}{2}}\leqslant \lambda \sum _{n\in {\mathbb {N}}} \omega _n {\mathop {\leqslant }\limits ^{(2.28)}} \lambda . \end{aligned}$$

We thus established (2.30).

By (2.30), we get

$$\begin{aligned} \text {{p-}cap}( A ) \leqslant \sum _n \text {{p-}cap}( A_n ), \end{aligned}$$

and, recalling definition (2.29), we use estimate (2.26) with $\lambda$ and R substituted by $\omega _n\lambda$ and $2^{-(n+3)}$ to bound

$$\begin{aligned} \text {{p-}cap}( A ) \lesssim \lambda ^{-{\bar{p}}}\sum _n \omega _n^{-{\bar{p}}} 2^{-n(-\frac{ d {\bar{p}}}{ 2} + ({\bar{p}} - p)+ {\bar{p}} \alpha )}. \end{aligned}$$

Choosing in (2.28) $\omega _n= \frac{6}{(\pi n)^2}$, the sum on the right-hand side converges provided that $\alpha > \frac{d}{2} - \frac{{\bar{p}} -p}{{\bar{p}}}$ . Since we assumed $p < {\bar{p}}$, there exists $\alpha < \frac{d}{2}$ such that

$$\begin{aligned} \text {{p-}cap}( A ) \lesssim \lambda ^{-{\bar{p}}}. \end{aligned}$$

By definition (2.27), sending $\lambda \uparrow +\infty$, we recover (2.17) for $\nabla _x G$.

The argument for G in (2.17) follows along the same lines as the one for $\nabla _xG$, as we shall argue now. In fact, since by Hölder’s inequality with exponents $\frac{d}{d-2}$ and $\frac{d}{2}$ we may bound

$$\begin{aligned} \biggl ( \int _{ 8R< |x-y| < 16R } |G( x, y)|^2 \, \text {d} x\biggr )^{\frac{1}{2}} \lesssim R \biggl ( \int _{ |x-y| > 8R } |G( x, y)|^{\frac{2d}{d-2}} \, \text {d} x\biggr )^{\frac{d-2}{2d}}, \end{aligned}$$

inequality (2.24) yields

$$\begin{aligned} \text {{p-}cap}\biggl \{ |y-z|< 1 \, :\, R^{-1} {\mathcal {M}}_0\biggl ( \int _{ 8R< |x-y| < 16R } |G( x, y)|^2 \, \text {d} x\biggr )^{\textstyle \frac{1}{2}}> \lambda \biggr \} \lesssim \lambda ^{- p} R^{-\frac{ d p}{ 2} }, \end{aligned}$$

and thus also

$$\begin{aligned} \text {{p-}cap}\biggl \{ |y-z|< 1 \, :\, {\mathcal {M}}_0\biggl ( \int _{ 8R< |x-y| < 16R } |G( x, y)|^2 \, \text {d} x\biggr )^{\textstyle \frac{1}{2}}> \lambda \biggr \} \lesssim \lambda ^{- p} R^{-\frac{ d p}{ 2} + p}. \end{aligned}$$

From this inequality we conclude (2.17) for G as we did in the case of $\nabla _x G$ from (2.25). This concludes the proof of Step 3.

Step 4. Maximal function estimate We now prove (2.22) and begin with the first estimate. Without loss of generality, we focus on the case $z=0$. For any $R > 0$ and $y \in {\mathbb {R}}^d$, let

$$\begin{aligned} F_R(y) := \biggl ( \int _{ |x| > 4R } |\nabla _{x}G( x, y)|^2 \, \text {d} x\biggr )^{\frac{{\bar{p}}}{2p}}. \end{aligned}$$

(2.31)

We first claim that it suffices to show that for every $R > 0$

$$\begin{aligned} \int _{|y| < R} \bigl (R^{-p} |F_R(y)|^p + |\nabla F_R(y)|^p\bigr ) \, \text {d} y\lesssim R^{-\frac{d{\bar{p}}}{2} + d + ({\bar{p}} - p)}. \end{aligned}$$

(2.32)

Indeed, if $\eta _R$ is a smooth cut-off function for $\{|y| < \frac{R}{2}\}$ in $\{|y| < R\}$, then by (2.32) the product $\eta _{R} F_R$ satisfies

$$\begin{aligned} \Vert \eta _{R}F_R \Vert _{W^{1,p}({\mathbb {R}}^d)}^p {\mathop {\lesssim }\limits ^{(2.32)}} R^{-\frac{d{\bar{p}}}{2} + d + ({\bar{p}} - p)}. \end{aligned}$$

We thus apply the maximal function estimate [7, Inequality (3.1)] to $\eta _{R}F_R$ and infer that

$$\begin{aligned} \text {{p-}cap}\biggl \{ |y| < R \, :\, {\mathcal {M}}(\eta _{R} F_R)(y) > \lambda \biggr \} \lesssim \lambda ^{-p} R^{-\frac{d{\bar{p}}}{2} + d + ({\bar{p}} - p)}, \end{aligned}$$

where ${\mathcal {M}}$ is defined in (2.9). Since by the assumption on $\eta _{R}$ and the definitions (2.9) and (2.10) we have

$$\begin{aligned} {\mathcal {M}}_0 F_R \leqslant {\mathcal {M}}(\eta _{R}F_R) \quad \text { on}\ \{|y| < {\frac{\text { R}}{2}}\}, \end{aligned}$$

we infer that

$$\begin{aligned} \text {{p-}cap}\biggl \{ |y| < {\frac{R}{2}} \, :\, {\mathcal {M}}_0 F_R(y) > \lambda \biggr \} \lesssim \lambda ^{-p} R^{-\frac{d{\bar{p}}}{2} + d + ({\bar{p}} - p)}. \end{aligned}$$

(2.33)

Furthermore, since $|y| < \frac{R}{2}$ implies $\{ |x-y|> 8R \} \subseteq \{ |x| > 4R \}$ so that

$$\begin{aligned} \left( \int _{ |x-y| > 8R } |\nabla _{x}G( x, y)|^2 \, \, \text {d} x\right) ^{\frac{{\bar{p}}}{ 2p}} \leqslant F_R(y), \end{aligned}$$

we conclude (2.22) for $\nabla _x G$ from (2.33).

To complete the argument for the first line in (2.22) it remains to prove (2.32): The main ingredient for this are inequalities (0.7) and (0.8) which, by redefining R as 2R and setting $z=0$, we rewrite as

$$\begin{aligned} \int _{|x | > 4R} \int _{|y| < 2R } \bigl ( R^{-2}| \nabla _x G(x, y)|^2 + | \nabla _y\nabla _x G(x, y)|^2 \bigr ) \, \text {d} y\, \text {d} x\lesssim 1. \end{aligned}$$

(2.34)

By (2.12) and (2.11) the vector field $\nabla _x G( x, \cdot )$ satisfies for almost every x with $|x | > 4R$ the equation

$$\begin{aligned} -\nabla _y \cdot a(y) \nabla _y \nabla _x G(x, y) = 0 \quad \text {in}\ { \{ |y| < 2 R\}.} \end{aligned}$$

We thus apply (2.16) of Step 1 so that (2.34) turns into

$$\begin{aligned} \int _{|x| > 4R} \biggl ( \int _{|y| < R } R^{-{\bar{p}}}| \nabla _x G(x, y)|^{{\bar{p}}} + | \nabla _y\nabla _x G(x, y)|^{{\bar{p}}} \, \text {d} y\biggl )^{\frac{ 2 }{{\bar{p}}}} \, \text {d} x&\lesssim R^{-d + \frac{2 d}{ \bar{p}}}. \end{aligned}$$

Since ${\bar{p}} \geqslant 2$, by Minkowski’s inequality this in turn yields

$$\begin{aligned} \int _{|y| < R }\biggl (\int _{|x| > 4R} | \nabla _y\nabla _x G(x, y)|^{2} \, \text {d} x\biggl )^{\frac{{\bar{p}} }{2}} \, \text {d} y&\lesssim R^{-\frac{d{\bar{p}}}{2} + d}, \end{aligned}$$

(2.35)

$$\begin{aligned} \int _{|y| < R } \biggl (\int _{|x| > 4R}| \nabla _x G(x, y)|^{2} \, \text {d} x\biggr )^{\frac{{\bar{p}}}{2}} \, \text {d} y&\lesssim R^{-\frac{d{\bar{p}}}{2} + d + {\bar{p}}}. \end{aligned}$$

(2.36)

Differentiating (2.31) in y, the chain rule and Cauchy–Schwarz’s inequality yield

$$\begin{aligned} |\nabla F_R(y)| \lesssim \biggl ( \int _{|x|> 4R} |\nabla _x G(x, y)|^2 {\mathrm {d}}x \biggr )^{\frac{{\bar{p}}-p}{2p}} \biggl (\int _{|x| > 4R} |\nabla _x\nabla _y G(x,y)|^2 {\mathrm {d}}x\biggr )^{\frac{1}{2}}\nonumber \\ \end{aligned}$$

(2.37)

By Hölder’s inequality with exponents $\frac{{\bar{p}}}{{\bar{p}} - p}$ and $\frac{{\bar{p}}}{p} > 1$,

$$\begin{aligned}&\int _{ |y|< R} |\nabla F_R(y)|^p \, \text {d} y\\&\quad \leqslant \biggl ( \int _{ |y|< R } \bigl ( \int _{|x|> 4R} |\nabla _x G(x, y)|^2 {\mathrm {d}}x \bigr )^{\frac{{\bar{p}}}{2}} \, \text {d} y\biggr )^{1- \frac{p}{{\bar{p}}}} \\&\qquad \times \biggl ( \int _{ |y| < R } \bigl (\int _{|x| > 4R} |\nabla _y\nabla _x G(x,y)|^2 \, \text {d} x\bigr )^{\frac{{\bar{p}}}{ 2}} \, \text {d} y\biggr )^{\frac{p}{{\bar{p}}}}.\nonumber \end{aligned}$$

Inserting (2.35) and (2.36), this implies (2.32) for $\nabla F_R$. The $F_R$-part of (2.32) is immediate from (2.36), which in view of (2.31), assumes the desired form of

$$\begin{aligned} \int _{ |y| < R } | F_R(y)|^p \, \text {d} y\lesssim R^{-\frac{d{\overline{p}}}{2}+d+{\overline{p}}}. \end{aligned}$$

This concludes the proof of (2.32) and thus of the first estimate of (2.22).

The second estimate in (2.22) follows by a similar argument. We define for $R>0$ and $y\in {\mathbb {R}}^d$

$$\begin{aligned} {{\tilde{F}}}_R(y) : = \biggl ( \int _{ |x| > 8R} |G(x,y)|^{\frac{2d}{d-2}} \, \text {d} x\biggr )^{\frac{d-2}{2d}} \end{aligned}$$

(2.38)

and presently argue that

$$\begin{aligned} \int _{|y| < R} \bigl (R^{-p} |{{\tilde{F}}}_R(y)|^p + |\nabla \tilde{F}_R(y)|^p\bigr ) \, \text {d} y\lesssim R^{-\frac{d p}{2} + d}. \end{aligned}$$

(2.39)

This is the analogue of (2.32) for $F_R$ in (2.31): we pass to the second inequality in (2.22) from (2.39) as is done above to show the first inequality in (2.22) from (2.32).

We prove (2.39) as follows: Similarly to (2.37), we differentiate ${{\tilde{F}}}_R$ in the y-variable, apply Hölder’s inequality, this time with exponents $\frac{2d}{d+2}$ and $\frac{2d}{d-2}$, and bound

$$\begin{aligned} |\nabla {{\tilde{F}}}_R(y)| \leqslant \biggl ( \int _{ |x| > 8R} |\nabla _yG(x,y)|^{\frac{2d}{d-2} }\, \text {d} x\biggr )^{\frac{d-2}{2d}}. \end{aligned}$$

(2.40)

Since for almost every $y \in {\mathbb {R}}^d$ we have that

$$\begin{aligned} G( \cdot , y) \in Y^{1,2}_x(\{ |x- y|> 1\}), \ \ \nabla _y G(\cdot , y) \in Y^{1,2}_x(\{|x- y|>1 ; {\mathbb {R}}^d) \end{aligned}$$

[see the line above (0.5) and the one below (2.11)], definition (2.38), estimate (2.40) and Sobolev’s inequality in the exterior domain $\{ |x| > 8R \}$ imply that

$$\begin{aligned} \int _{|y|< R}|{{\tilde{F}}}_R(y)|^p \, \text {d} y&\lesssim \int _{|y|< R} \biggl ( \int _{ |x|> 8R} |\nabla _x G(x,y)|^{2}\, \text {d} x\biggr )^{\frac{p}{2}} \, \text {d} y,\\ \int _{|y|< R} |\nabla {{\tilde{F}}}_R(y)|^p \, \text {d} y&\lesssim \int _{|y| < R} \biggl ( \int _{ |x| > 8R} |\nabla _x\nabla _yG(x,y)|^{2}\, \text {d} x\biggr )^{\frac{p}{2}} \, \text {d} y. \end{aligned}$$

Another application of Hölder’s inequality in $\{|y| < R \}$ with exponents $\frac{{\bar{p}}}{p}$ and $\frac{{\bar{p}}}{{\bar{p}} -p}$ further yields

$$\begin{aligned} \int _{|y|< R}|\tilde{F}_R(y)|^p \, \text {d} y\lesssim R^{d(1- \frac{p}{\bar{p}})} \biggl ( \int _{|y|< R} \bigl ( \int _{|x|> 8R} |\nabla _x G(x,y)|^2 \, \text {d} x\bigr )^{\frac{\bar{p} }{2}} \, \text {d} y\biggr )^{\frac{p}{\bar{p}}} {\mathop {\lesssim }\limits ^{(2.36)}} R^{-\frac{dp}{2} + d +p},\\ \int _{|y|< R}|\nabla \tilde{F}_R(y)|^p \, \text {d} y\lesssim R^{d(1- \frac{p}{\bar{p}})} \biggl ( \int _{|y| < R}\bigl ( \int _{|x|> 8R} |\nabla _x \nabla _y G(x,y)|^2 \, \text {d} x\bigr )^{\frac{\bar{p} }{2}} \, \text {d} y\biggr )^{\frac{p}{\bar{p}}}{\mathop {\lesssim }\limits ^{(2.35)}} R^{-\frac{dp}{2} + d}, \end{aligned}$$

i.e. estimate (2.39). The proof of Step 4 is complete.

Step 5. Construction of $G^*(a; \cdot , \cdot )$   Wrapping up Steps 2–4, we have that G and $\nabla _x G$ satisfy (2.22) and therefore also (2.19) and (2.17) and (2.18) and (2.20) with an exponent p that may be chosen strictly bigger than 2. Equipped with these estimates, we now proceed to prove the existence of $G^*( \cdot , y)$ for y outside an exceptional set $\Sigma$ satisfying (a) in the statement of Theorem 1.

For a test function $\zeta \in C^\infty _0({\mathbb {R}}^d)$, we consider the function

$$\begin{aligned} u(y)= \int \zeta (x) G(x, y) \, \text {d} x. \end{aligned}$$

By the representation formula (2.13), $u\in Y^{1,2}({\mathbb {R}}^d)$ and solves

$$\begin{aligned} -\nabla \cdot a\nabla u = \zeta \quad \text {in}\ { {\mathbb {R}}^d.} \end{aligned}$$

(2.41)

Since $\zeta \in C^\infty _0({\mathbb {R}}^d)$, Gehring’s estimate (2.16) implies in particular that $u \in W^{1,p}_{loc}({\mathbb {R}}^d)$. By Lebesgue’s theorem for Sobolev functions [8, Theorem 2.55], we infer that the limit

$$\begin{aligned} \lim _{\delta \downarrow 0}&\fint _{|{{\tilde{y}}} -y|< \delta }u(\tilde{y}) \, d{{\tilde{y}}}= \lim _{\delta \downarrow 0} \fint _{|{{\tilde{y}}} -y| < \delta } \int \zeta (x) G( x, {{\tilde{y}}}) \, \text {d} x\, d{{\tilde{y}}} \end{aligned}$$

exists as an element of ${\mathbb {R}}^m$ for all $y \in {\mathbb {R}}^d$ outside a set of zero p-capacity. Select a countable subset $\{ \zeta _n \}_{n \in {\mathbb {N}}} \subseteq C^\infty _0( {\mathbb {R}}^d)$ dense with respect to the $C^1$-topology. Hence, there exists a set ${\tilde{\Sigma }}$ with $\text {{p-}cap}( {\tilde{\Sigma }})=0$ such that

$$\begin{aligned} \forall \, \text {y} \in {\mathbb {R}}^d\backslash {\tilde{\Sigma }}, \, \forall \text {n}\in {\mathbb {N}}\ \ \lim _{\delta \downarrow 0} \fint _{|{{\tilde{y}}} -y| < \delta } \int \zeta _n(x) G(x, {{\tilde{y}}})\, \text {d} x\, d{{\tilde{y}}} \ \ \ \text {exists.} \end{aligned}$$

(2.42)

Let $\Sigma _1$ and $\Sigma _2$ be the p-capacity zero sets of (2.18), (2.20) in Step 2 and define

$$\begin{aligned} \Sigma := {\tilde{\Sigma }} \cup \Sigma _1 \cup \Sigma _2. \end{aligned}$$

With this definition, $\Sigma$ satisfies (a) of Theorem 1. By (2.19) and (2.17) of Step 2, we remark that for every $y \notin \Sigma$, it also holds

$$\begin{aligned} {\mathcal {M}}_0\left( \int \min \{ |x- y|^{2\alpha }, 1\} |\nabla _x G(x, y)|^2 \, \text {d} x\right) < +\infty , \end{aligned}$$

(2.43)

for the exponent $\alpha < \frac{d}{2}$ of Step 2. By Jensen’s inequality, for every $R > 0$ and $y \in {\mathbb {R}}^d$ we have

$$\begin{aligned} \limsup _{\delta \downarrow 0}\bigl \Vert \fint _{|{{\tilde{y}}}-y|< \delta } G( \cdot , {{\tilde{y}}}) \, d{{\tilde{y}}}&\bigr \Vert _{W^{1,q}_x(\{|x -y|< R\} )}\leqslant {\mathcal {M}}_0 \Vert G( \cdot , y)\Vert _{W^{1,q}_x(\{|x-y|< R \})},\\ \limsup _{\delta \downarrow 0}\bigl \Vert \fint _{|{{\tilde{y}}}-y| < \delta } G( \cdot , {{\tilde{y}}}) \, d{{\tilde{y}}}&\bigr \Vert _{Y^{1,2}_x(\{|x -y|> R\} )}\leqslant {\mathcal {M}}_0 \Vert G( \cdot , y)\Vert _{Y^{1,2}_x(\{|x-y| > R \} )} \end{aligned}$$

so that by (2.18) and (2.20) and weak compactness, we infer that for every $y\in {\mathbb {R}}^d\backslash \Sigma$ there exists a subsequence $\delta _k \downarrow 0$ (a priori depending on y) and a limit $G^*( \cdot , y)$ such that for all $R >0$

$$\begin{aligned} \fint _{|{{\tilde{y}}} -y| < \delta _k} G( \cdot , {{\tilde{y}}})\, d{{\tilde{y}}} \rightharpoonup G^*( \cdot , y) \end{aligned}$$

(2.44)

in $W^{1,q}_{x}(\{|x - y| < R \}) \cap Y^{1,2}_x(\{ |x -y | > R \})$. Moreover, inequality (2.43) and weak lower-semicontinuity also yield

$$\begin{aligned} \int \min \{ |x-y|^{2\alpha } , 1\} |{\nabla _x} {G^*}( x, y)|^2 \, \text {d} x< +\infty . \end{aligned}$$

(2.45)

We now show that (2.44) holds for the entire family $\delta \downarrow 0$: Let us assume that this were not the case, i.e. that there exist two sequences $\{ \delta _k^{(1)}\}_k, \{\delta _k^{(2)}\}_{k}$ along which we obtain two different limits $G^{(1)}(\cdot , y), G^{(2)}(\cdot , y)$ in (2.44). Appealing to (2.42), to Fubini’s theorem to exchange the order of the integrals, and to (2.44) we infer that for every $n\in {\mathbb {N}}$

$$\begin{aligned} \int \zeta _n(x) G^{(1)}( x, y) \, \text {d} x= \int \zeta _n(x) G^{(2)}( x, y) \, \text {d} x. \end{aligned}$$

Since the subset $\{ \zeta _n \}_{n\in {\mathbb {N}}}$ is chosen to be dense, we conclude that $G^{(1)}(x, y) = G^{(2)}(x, y)$ for almost every $x \in {\mathbb {R}}^d$.

For every point y outside $\Sigma$, we thus constructed $G^*( \cdot , y)$ which, by (2.44) and (2.45), satisfies (b) and the last inequality in (c) of Theorem 1. To conclude the proof of Theorem 1, it thus remains to show that $G^*( \cdot , y)$ solves Eq. (0.5). Since $G( \cdot , {{\tilde{y}}})$ solves Eq. (0.5) for almost every ${{\tilde{y}}} \in {\mathbb {R}}^d$, for every $\zeta \in C^\infty _0({\mathbb {R}}^d)$, $y \in {\mathbb {R}}^d$ and $\delta > 0$ we have

$$\begin{aligned} \fint _{|{{\tilde{y}}} - y|< \delta } \int \nabla \zeta (x) \cdot a(x)\nabla _x G(x, {{\tilde{y}}}) \, \text {d} x{\mathrm {d}}{{\tilde{y}}} =\fint _{|{{\tilde{y}}}- y| < \delta } \zeta ({{\tilde{y}}}) {\mathrm {d}}{{\tilde{y}}}, \end{aligned}$$

so that, by Fubini’s theorem,

$$\begin{aligned} \int \nabla \zeta (x) \cdot a(x) \fint _{|{{\tilde{y}}}- y|< \delta }\nabla _x G(x,{{\tilde{y}}}){\mathrm {d}}{{\tilde{y}}} \, \text {d} x= \fint _{|{{\tilde{y}}}- y| < \delta } \zeta ({{\tilde{y}}}) {\mathrm {d}}{{\tilde{y}}}. \end{aligned}$$

(2.46)

Taking the limit $\delta \downarrow 0$, the assumption on $\zeta$, the boundedness (0.1) of a and (2.44) yield that for all $y \in {\mathbb {R}}^d\backslash \Sigma$ it holds

$$\begin{aligned} \int \nabla \zeta (x) \cdot a(x) \nabla _x G^*(x, y) \, \text {d} x= \zeta ( y). \end{aligned}$$

(2.47)

Since $\zeta \in C^\infty _0({\mathbb {R}}^d)$ is arbitrary, we conclude that $G^*( \cdot , y)$ solves Eq. (0.5).

$\square$

Proof of Corollary 1

Let $\Sigma$ be as in the statement of Theorem 1 and $\eta$ be a smooth cut-off function for $\{|x| < 4 \}$ in $\{|x | < 2 \}$. With no loss of generality we may assume that each u satisfies $\int _{|x| < 4} u= 0$. The function $\eta u$ solves

$$\begin{aligned} -\nabla \cdot a \nabla (\eta u) = \nabla \cdot g + f \quad \text {in}\ {{\mathbb {R}}^d} \end{aligned}$$

(2.48)

with

$$\begin{aligned} g := -u a \nabla \eta , \ \ \ f:= -\nabla \eta \cdot a \nabla u.\end{aligned}$$

Both g and f are supported in $\{ 2< |x| < 4 \}$ and by the definition of $\eta$, the second inequality in (0.1), the bound on the Dirichlet energy of u and Poincaré’s inequality, they satisfy

$$\begin{aligned} \int |g(x)|^2 \, \text {d} x+ \int |f(x)|^2 \, \text {d} x\lesssim 1. \end{aligned}$$

(2.49)

Furthermore, the representation formula (2.13), (2.12) and Theorem 1 imply that for every $y \notin \Sigma$ with $|y|< 2$ we may define as representative

$$\begin{aligned} u( y) = - \int _{2< |x|<4 } g(x) \cdot \nabla _x G^*( x , y)\, \text {d} x+ \int _{2< |x| < 4 } f(x) G^*( x, y) \, \text {d} x. \end{aligned}$$

To make our notation leaner, we define

$$\begin{aligned} v(y):= \int g(x) \cdot \nabla _x G^*( x, y) \, \text {d} x, \ \ \ w(y):= \int f(x) G^*( x,y) \, \text {d} x\end{aligned}$$

(2.50)

and prove the statement of the corollary for v. The function w may be treated analogously.

We adapt the proof of [4, Theorem 4.19] to show that there exist a sequence of sets $\{ B_j \}_{j \in {\mathbb {N}}} \subseteq \{ |y| < 1\}$ having

$$\begin{aligned} \text {{p-}cap}\bigl \{ B_j \bigr \} \lesssim \frac{1}{2^{j}} \end{aligned}$$

(2.51)

and moduli of continuity $\omega _j : {\mathbb {R}}_+ \rightarrow {\mathbb {R}}_+$ such that the following holds: For every v constructed as in (2.50), there exists a sequence $\{ v_j \}_{j \in {\mathbb {N}}}$ satisfying for all $j \in {\mathbb {N}}$

$$\begin{aligned} \sup _{\{|y|< 1\} \backslash B_j} |v(y) - v_j(y)| < \frac{1}{2^j} \end{aligned}$$

(2.52)

and

$$\begin{aligned} |v_j(y) - v_j({{\tilde{y}}})| \leqslant \omega _j( |y - {{\tilde{y}}}|) \ \ \ \ \forall y, {{\tilde{y}}} \ \text {s.t.} \ |y |< 1, |{{\tilde{y}}}|< 1. \end{aligned}$$

(2.53)

From this, the corollary follows easily: For each $\varepsilon > 0$ fixed, let $j_0 \in {\mathbb {N}}$ such that

$$\begin{aligned} \text {{p-}cap}\left\{ \bigcup _{j \geqslant j_0}B_j \right\} {\mathop {< }\limits ^{(2.51)}}\frac{\varepsilon }{2}. \end{aligned}$$

By definition of capacity (see, for instance, [4, Theorem 4.15 (i)]) we may find an open set $U^\varepsilon \supset \bigcup _{j \geqslant j_0}B_j$ having $\text {{p-}cap}(U^\varepsilon ) < \varepsilon$. We prove that on $\{ |y| < 1\}\backslash U^\varepsilon$, the vector fields v in (2.50) are equicontinuous and that the continuity is uniform in $\{ |y| < 1\}\backslash U^\varepsilon$. More precisely, this means proving that for each $\kappa >0$, there exists $\delta =\delta (\kappa ) > 0$ such that for all v as in (2.50) and all $y, {{\tilde{y}}} \notin U^\varepsilon$ and such that $|y| < 1$, $|{{\tilde{y}}}| < 1$ and $|y - {{\tilde{y}}}| < \delta$ we may bound

$$\begin{aligned} |v(y)- v({{\tilde{y}}}) |< \kappa . \end{aligned}$$

By the triangle inequality, (2.52) and the definition of $U^\varepsilon$, we know indeed that if we fix $j \geqslant j_0$ such that $2^{-j} < \frac{\kappa }{3}$, then

$$\begin{aligned} |v(y) - v({{\tilde{y}}})|&\leqslant |v(y) - v_{j}(y)| + |v({{\tilde{y}}}) - v_{j}({{\tilde{y}}})| + |v^j({{\tilde{y}}}) - v_{j}(y)|\\&\leqslant \frac{2}{3}\kappa + |v_j({{\tilde{y}}}) - v_{j}(y)|\\&{\mathop {\leqslant }\limits ^{(2.53)}} \frac{2}{3}\kappa + \omega _j(|y -{{\tilde{y}}}|). \end{aligned}$$

It thus remains to pick $\delta$ such that the last term on the right-hand-side is smaller than $\frac{\kappa }{3}$. This concludes the statement of the corollary.

We now show (2.51), (2.52) and (2.53). Let $p> 2$ is as in Theorem 1. It is easy to see that (2.35) obtained in the proof of Theorem 1 holds also with the sets $\{ |y| < R \}$ and $\{ |x| > 4R \}$ replaced by $\{ |y -z | < R \}$ and $\{ |x -z | > 4R \}$, for any $z \in {\mathbb {R}}^d$ and $R>0$. Hence, by a simple covering argument, we obtain that

$$\begin{aligned} \int _{|y|< \frac{3}{2}}\bigl ( \int _{2< |x| < 4} |\nabla _x \nabla _y G^*( x,y)|^2 \, \text {d} x\bigr )^{\frac{p}{2}} \, \text {d} y\lesssim 1. \end{aligned}$$

Similarly, this time using (2.36), we have that

$$\begin{aligned} \int _{|y|< \frac{3}{2}}\bigl ( \int _{2< |x| < 4}&|\nabla _x G^*( x,y)|^2 \, \text {d} x\bigr )^{\frac{p}{2}} \, \text {d} y\lesssim 1. \end{aligned}$$

By standard approximation arguments adapted to Banach-valued functions (see e.g. [1, Corollary 1.4.37]), we may find a sequence $\{F_j \}_{j\in {\mathbb {N}}}$ of continuous maps

$$\begin{aligned} F_j: \bigl \{ |y|< \frac{3}{2} \bigr \} \rightarrow L^2 \bigl (\{ 2< |x| < 4 \} ; {\mathbb {R}}^{d} \bigr ) \end{aligned}$$

such that for each $j \in {\mathbb {N}}$ we have

$$\begin{aligned} \begin{aligned} \int _{|y|< \frac{3}{2}} \bigl ( \int _{2<|x|< 4}&|\nabla _x G^*( x,y) - F_j(x,y)|^2 \, \text {d} x\bigr )^{\frac{p}{2}} \, \text {d} y\\&+ \int _{|y|< \frac{3}{2}} \bigl ( \int _{2<|x| < 4} |\nabla _y \nabla _x G^*( x,y) - \nabla _y F_j(x,y)|^2 \, \text {d} x\bigr )^{\frac{p}{2}} \, \text {d} y\\&\leqslant \frac{1}{2^{(p+1)j}}. \end{aligned}\nonumber \\ \end{aligned}$$

(2.54)

Let $\Sigma$ be the exceptional set of Theorem 1 and let ${\mathcal {M}}_0$ be the maximal function operator (see (2.10)). We claim that

$$\begin{aligned} \begin{aligned} B_j:= \biggl \{ |y|< 1 \, :\, \ \ {\mathcal {M}}_0\bigl ( \int _{2< |x| < 4} | \nabla _x G^*(a; x, y) - F_j(x, y)|^2&\, \text {d} x\bigr )^{\frac{1}{2}} > \frac{1}{2^j}\biggr \} \cup \Sigma \end{aligned}\nonumber \\ \end{aligned}$$

(2.55)

and $\omega _j$ such that for all $R> 0$

$$\begin{aligned} \omega _j(R) := \sup \biggl \{ \biggl (\int _{2< |x|< 4} | F_j(x,y) - F_j(x, {{\tilde{y}}})|^2 \, \text {d} x\biggr )^{\frac{1}{2}} \, | \, |y| \leqslant 1, \, |{{\tilde{y}}}| \leqslant 1, \, |y - {{\tilde{y}}}| < R \biggr \},\nonumber \\ \end{aligned}$$

(2.56)

satisfy (2.51), (2.52) and (2.53) provided that for every v we choose as approximating sequence

$$\begin{aligned} v_j(y):= \int g(x) \cdot F_j(x,y) \, \text {d} x. \end{aligned}$$

(2.57)

Here, g is the vector field in the definition (2.50) of v. We stress that, since each $F_j$ is continuous in $\{|y| \leqslant 1\}$ with values in $L^2 \bigl (\{ 2< |x| < 4 \} ; {\mathbb {R}}^{d} \bigr )$, the above function is a well-defined modulus of continuity by the Heine-Cantor theorem. Furthermore, appealing to Cauchy–Schwarz’s inequality, (2.49) and (2.56), definition (2.57) immediately imply that $\{ v_j \}_{j \in {\mathbb {N}}}$ satisfy (2.53).

It remains to show (2.51) and (2.52): since by Theorem 1 we have $\text {{p-}cap}( \Sigma )=0$, we may argue for $B_j$ as done for (2.22) and obtain that

$$\begin{aligned} \begin{aligned} \text {{p-}cap}(B_j)&\lesssim 2^{pj } \int _{|y|< \frac{3}{2}} \left( \int _{2< |x|< 4} | \nabla _x G^*( x,y) - F_j(x,y)|^2 \, \text {d} x\right) ^{\frac{p}{2}} \, \text {d} y\\&\quad + 2^{pj } \int _{|y|< \frac{3}{2}} \left( \int _{2< |x| < 4} |\nabla _y \nabla _x G^*( x,y) - \nabla _y F_j(x,y)|^2 \, \text {d} x\right) ^{\frac{p}{2}} \, \text {d} y\\&\quad {\mathop {\lesssim }\limits ^{(2.54)}} 2^{-j}, \end{aligned}\nonumber \\ \end{aligned}$$

(2.58)

i.e. inequality (2.51). It remains to show that $\{ v_j \}_{j\in {\mathbb {N}}}$ defined in (2.57) satisfies (2.52): For every $y \notin B_j \cup \Sigma$ with $|y|< 1$, we use the definition (2.50) of v and (b) of Theorem 1 to rewrite

$$\begin{aligned} |v_j(y) - v(y) | = \limsup _{r\downarrow 0} | v_j(y) - \fint _{|{{\tilde{y}}} - y| < r} v({{\tilde{y}}})\, {\mathrm {d}}{{\tilde{y}}}|. \end{aligned}$$

By the triangle inequality, we bound

$$\begin{aligned} |v_j(y) - v(y) |&\leqslant \limsup _{r\downarrow 0} | v_j(y) - \fint _{|{{\tilde{y}}} - y|< r} v_j({{\tilde{y}}})\, {\mathrm {d}}{{\tilde{y}}}| \\&\quad + \limsup _{r\downarrow 0} |\fint _{|{{\tilde{y}}} - y| < r}( v({{\tilde{y}}}) -v_j({{\tilde{y}}})) \, {\mathrm {d}}{{\tilde{y}}}| . \end{aligned}$$

By (2.53), the first limit supremum on the right-hand side is zero. Hence, we have that

$$\begin{aligned} \begin{aligned} | v_j(y) - v(y) |\leqslant \limsup _{r\downarrow 0} \fint _{|{{\tilde{y}}} - y| < r} | v_j({{\tilde{y}}}) - v({{\tilde{y}}})|\, {\mathrm {d}}{{\tilde{y}}}. \end{aligned} \end{aligned}$$

(2.59)

Furthermore, the definitions of v and $v_j$, Cauchy-Schwarz’s inequality and the definition of $B_j$ together with (2.49) allow us to bound

$$\begin{aligned}&\limsup _{r \downarrow 0}\fint _{|{{\tilde{y}}} - y|< r } | v_j({{\tilde{y}}}) -v({{\tilde{y}}})| {\mathrm {d}}{{\tilde{y}}}\\&\quad \lesssim \limsup _{r \downarrow 0} \fint _{|{{\tilde{y}}} -y|< r}\bigl ( \int _{2< |x| < 4} | \nabla _x G^*( x,{{\tilde{y}}}) - F_j(x,{{\tilde{y}}})|^2 \, \text {d} x\bigr )^{\frac{1}{2}} {\mathrm {d}}{{\tilde{y}}} \lesssim 2^{-j}. \end{aligned}$$

Inserting this into (2.59) we conclude (2.52). The proof of Corollary 1 is complete.

$\square$