Lower Bounds Against Sparse Symmetric Functions of ACC Circuits: Expanding the Reach of #SAT Algorithms

Abstract

We continue the program of proving circuit lower bounds via circuit satisfiability algorithms. So far, this program has yielded several concrete results, proving that functions in $\mathsf {Quasi}\text {-}\mathsf {NP} = \mathsf {NTIME}[n^{(\log n)^{O(1)}}]$ and other complexity classes do not have small circuits (in the worst case and/or on average) from various circuit classes $\mathcal { C}$, by showing that $\mathcal { C}$ admits non-trivial satisfiability and/or # SAT algorithms which beat exhaustive search by a minor amount. In this paper, we present a new strong lower bound consequence of having a non-trivial # SAT algorithm for a circuit class ${\mathcal C}$. Say that a symmetric Boolean function f(x₁,…,x_n) is sparse if it outputs 1 on O(1) values of ${\sum }_{i} x_{i}$. We show that for every sparse f, and for all “typical” $\mathcal { C}$, faster # SAT algorithms for $\mathcal { C}$ circuits imply lower bounds against the circuit class $f \circ \mathcal { C}$, which may be stronger than $\mathcal { C}$ itself. In particular:

• # SAT algorithms for n^k-size $\mathcal { C}$-circuits running in 2ⁿ/n^k time (for all k) imply NEXP does not have $(f \circ \mathcal { C})$-circuits of polynomial size.

• # SAT algorithms for $2^{n^{{\varepsilon }}}$-size $\mathcal { C}$-circuits running in $2^{n-n^{{\varepsilon }}}$ time (for some ε > 0) imply Quasi-NP does not have $(f \circ \mathcal { C})$-circuits of polynomial size.

Applying # SAT algorithms from the literature, one immediate corollary of our results is that Quasi-NP does not have EMAJ ∘ ACC⁰ ∘ THR circuits of polynomial size, where EMAJ is the “exact majority” function, improving previous lower bounds against ACC⁰ [Williams JACM’14] and ACC⁰ ∘THR [Williams STOC’14], [Murray-Williams STOC’18]. This is the first nontrivial lower bound against such a circuit class.

1 Introduction

Currently, our knowledge of algorithms vastly exceeds our knowledge of lower bounds. Is it possible to bridge this gap, and use the existence of powerful algorithms to give lower bounds for hard functions? Over the last decade, the program of proving lower bounds via algorithms has been positively addressing this question. A line of work starting with Kabanets and Impagliazzo [16] has shown how deterministic subexponential-time algorithms for polynomial identity testing would imply lower bounds against arithmetic circuits. Starting around 2010 [22, 23], it was shown that even slightly nontrivial algorithms could imply Boolean circuit lower bounds. For example, a circuit satisfiability algorithm running in O(2ⁿ/n^k) time (for all k) on n^k-size circuits with n inputs would already suffice to yield the (infamously open) lower bound NEXP⊄P/poly. A generic connection was found between non-trivial SAT algorithms and circuit lower bounds:

Theorem 1 (22, 23, Informal)

Let $\mathcal {C}$ be a circuit class closed under AND, projections, and compositions.¹ Suppose for all k there is an algorithm A such that, for every $\mathcal {C}$-circuit of n^k size, A determines its satisfiability in O(2ⁿ/n^k) time. Then NEXP does not have polynomial-size $\mathcal {C}$-circuits.

To illustrate Theorem 1 with two examples, when $\mathcal {C}$ is the class of general fan-in 2 circuits, Theorem 1 says that non-trivial Circuit SAT algorithms imply NEXP⊄P/poly; when $\mathcal {C}$ is the class of Boolean formulas, it says non-trivial Formula-SAT algorithms imply NEXP⊄NC¹. Both are major open questions in circuit complexity. Theorem 1 and related results have been applied to prove several concrete circuit lower bounds: super-polynomial lower bounds against ACC⁰ [23], ACC⁰ ∘THR [25], quadratic lower bounds against depth-two symmetric and threshold circuits [1, 19], and average-case lower bounds as well [5, 6].

Recently, the algorithms-to-lower-bounds connection has been extended to show a trade-off between the running time of the SAT algorithm on large circuits, and the complexity of the hard function in the lower bound [17]. In particular, it is even possible to obtain some circuit lower bounds against NP with this algorithmic approach [7, 24]. Let us state a form of the connection that is suitable for the results of this paper.

Theorem 2 (17, Informal)

Let $\mathcal {C}$ be a class of circuits closed under unbounded AND and negation. Suppose there is an algorithm A and ε > 0 such that, for every $\mathcal {C}$-circuit C of $2^{n^{{\varepsilon }}}$ size, A solves satisfiability for C in $O(2^{n-n^{{\varepsilon }}})$ time. Then Quasi-NP does not have polynomial-size $\mathcal {C}$-circuits.²

In fact, Theorem 2 holds even if A only distinguishes between unsatisfiable circuits from those with at least 2^n− 1 satisfying assignments; we call this easier problem GAP-UNSAT.

Intuitively, the aforementioned results show that, as circuit satisfiability algorithms improve in running time and scope, they imply stronger lower bounds. In all known results, to prove a lower bound against $\mathcal {C}$, one must design a SAT algorithm for a circuit class that is at least as powerful as $\mathcal { C}$. Inspecting the proofs of the above theorems carefully, it is not hard to show that, even if $\mathcal {C}$ did not satisfy the desired closure properties, it would suffice to give a SAT algorithm for a slightly more powerful class than $\mathcal {C}$. For example, in Theorem 2, a SAT algorithm running in $O(2^{n-n^{{\varepsilon }}})$ time for $2^{n^{{\varepsilon }}}$-size AND of OR₃ of (possibly negated) $\mathcal {C}$ circuits³ (on n inputs, of $2^{n^{{\varepsilon }}}$ size) would still imply $\mathcal {C}$-circuit lower bounds for Quasi-NP functions. Our key point is that these proof methods require a SAT algorithm for a potentially more powerful circuit class than the class for which we can conclude a lower bound. Is this an artifact of our proof method, or is it inherent?

Proving lower bounds against more powerful classes from SAT algorithms? We feel it is natural to conjecture that a SAT algorithm for a circuit class $\mathcal {C}$ implies a lower bound against a class that is more powerful than $\mathcal {C}$, because checking satisfiability is itself a very powerful ability. Intuitively, a SAT algorithm for $\mathcal {C}$ on n-input circuits running in o(2ⁿ) time is computing a uniform OR of 2ⁿ $\mathcal {C}$-circuits evaluated on fixed inputs, in o(2ⁿ) time. (Recall that a “uniform” circuit informally means that any gate of the circuit can be efficiently computed by an algorithm.) Given an algorithm to decide the outputs of uniform ORs of $\mathcal {C}$-circuits more efficiently than their actual circuit size, perhaps this may be used to obtain a lower bound against $\mathsf {OR} \circ \mathcal { C}$ circuits.

Similarly, a # SAT algorithm for $\mathcal {C}$ on n-input circuits can be used to compute the output of any circuit of the form $f(C(x_{1}),\ldots ,C(x_{2^{n}}))$ where f is a uniform symmetric Boolean function, C is a $\mathcal {C}$-circuit with n inputs, and $x_{1},\ldots ,x_{2^{n}}$ is an enumeration of all n-bit strings. Should we therefore expect to prove lower bounds on symmetric functions of $\mathcal {C}$-circuits, using a # SAT algorithm? This question is particularly significant because in many of the concrete lower bounds proved via this program [17, 23, 25], non-trivial # SAT algorithms were actually obtained, not just SAT algorithms. So our question amounts to asking: how strong of a circuit lower bound can we prove, given the #SAT algorithms we already have? We use SYM to denote the class of Boolean symmetric functions. Informally, we conjecture the following.

Conjecture 1 (Stronger Lower Bounds from # SAT, Informal)

Non-trivial # SAT algorithms for circuit classes $\mathcal {C}$ imply size lower bounds against $\mathsf {SYM} \circ \mathcal {C}$ circuits. In particular, all statements in Theorem 1 and Theorem 2 hold when the SAT algorithm is replaced by a # SAT algorithm, and the lower bound consequence for $\mathcal {C}$ is replaced by $\mathsf {SYM} \circ \mathcal {C}$.

(We keep the statement of Conjecture 1 informal, because we would be happy with many formal versions of it.) If Conjecture 1 is true, then existing # SAT algorithms would already imply super-polynomial lower bounds against SYM ∘ACC⁰ ∘THR circuits, a class that contains depth-two symmetric circuits (for which no lower bounds greater than n² are presently known) [1, 19].

More intuition for Conjecture 1 can be seen from a recent paper of the second author, who showed how # SAT algorithms for a circuit class $\mathcal {C}$ can imply lower bounds on (real-valued) linear combinations of $\mathcal {C}$-circuits [24]. For example, known # SAT algorithms for ACC⁰ circuits imply Quasi-NP problems cannot be computed via polynomial-size linear combinations of polynomial-size ACC⁰ ∘THR circuits. However, the linear combination representation is rather constrained: the linear combination is required to always output 0 or 1. Applying PCPs of proximity, Chen and Williams [7] showed that the lower bound of [24] can be extended to “approximate” linear combinations of $\mathcal {C}$-circuits, where the linear combination does not have to be exactly 0 or 1, but must be closer to the correct value than to the incorrect one, within an additive constant factor. These results show, in principle, how a # SAT algorithm for a circuit class $\mathcal {C}$ can imply lower bounds against a stronger class of representations than $\mathcal {C}$.

1.1 Conjecture 1 Holds for Sparse Symmetric Functions

In this paper, we take a concrete step towards realizing Conjecture 1, by proving it for “sparse” symmetric functions. We say a symmetric Boolean function f(x₁,…,x_n) is k-sparse if f is 1 on at most k values of ${\sum }_{i} x_{i}$. The 1-sparse symmetric functions can realize the exact threshold (ETHR with polynomial weights) or exact majority (EMAJ) functions, which have been studied for years in both circuit complexity (e.g. [3, 12,13,14,15]) and structural complexity theory, where the corresponding complexity class (computing an exact majority over all computation paths) is known as C₌P [21].

Theorem 3

Let $\mathcal {C}$ be closed under⁴AND₂, negation, and suppose the all-ones and parity function⁵ are in $\mathcal {C}$. Let f = {f_n} be a family of k-sparse symmetric functions for some k = O(1).

• If there is a # SAT algorithm for n^k-size $\mathcal {C}$-circuits running in 2ⁿ/n^k time (for all k), then NEXP does not have $(f \circ \mathcal {C})$-circuits of polynomial size.

• If there is a # SAT algorithm for $2^{n^{{\varepsilon }}}$-size $\mathcal {C}$-circuits running in $2^{n-n^{{\varepsilon }}}$ time (for some ε > 0), then Quasi-NP does not have $(f \circ \mathcal {C})$-circuits of polynomial size.

Applying known # SAT algorithms for AC⁰[m] ∘THR circuits from [25], we obtain the first non-trivial lower bound for the class EMAJ ∘ACC⁰ ∘THR.

Corollary 1

There exists an e such that $\mathsf {NTIME}[n^{\log ^{e} n}]$ does not have polynomial size EMAJ ∘ACC⁰ ∘THR circuits.

Since the publication of the conference version of this work [20], some further progress on Conjecture 1 has been made. Notably, Chen-Ren [8] have proved lower bounds against the larger circuit class MAJ ∘ACC⁰ ∘THR. However, Conjecture 1 remains open.

1.2 Intuition

Here we briefly explain the new ideas that lead to our new circuit lower bounds.

As in prior work [7, 24], the high-level idea is to show that if (for example) Quasi-NP has polynomial-size $\mathsf {EMAJ} \circ \mathcal {C}$ circuits, and there is a # SAT algorithm for $\mathcal { C}$ circuits, then we can design a nondeterministic algorithm for verifying GAP Circuit Unsatisfiability (GAP-UNSAT) on generic (unrestricted) circuits that beats exhaustive search. In GAP-UNSAT, we are given a generic circuit and are promised that it is either unsatisfiable, or at least half of its possible assignments are satisfying, and we need to nondeterministically prove the unsatisfiable case. (Note this is a much weaker problem than SAT.) As shown in [17, 22, 23], combining a nondeterministic algorithm for GAP-UNSAT with the hypothesis that Quasi-NP has polynomial-size circuits, we can derive that nondeterministic time $n^{\log ^{c} n}$ can be simulated in time $o(n^{\log ^{c} n})$, contradicting the nondeterministic time hierarchy theorem.

Our key idea is to use probabilistically checkable proofs (PCPs) in a new way to exploit the power of a # SAT algorithm. First, let’s observe a task that a # SAT algorithm for $\mathcal {C}$ can compute on an $\mathsf {EMAJ} \circ \mathcal {C}$ circuit. Suppose our $\mathsf {EMAJ} \circ \mathcal {C}$ circuit has the form

$$B(x) = \left[\sum\limits_{i=1}^{t} C_{i}(x) = s\right],$$

where each C_i(x) is a Boolean $\mathcal {C}$-circuit on n inputs, s is a threshold value, and B outputs 1 if and only if the sum of the C_i’s equals s.⁶ Consider the expression

$$ \begin{array}{@{}rcl@{}} E(x) := \left( \sum\limits_{i=1}^{t} C_{i}(x) - s\right)^{2}. \end{array} $$

(1)

Treated as a function, E(x) outputs integers; E(a) = 0 when B(a) = 1, and otherwise E(a) ∈ [1,(t + s)²]. Hence the quantity

$$ \begin{array}{@{}rcl@{}} \sum\limits_{a \in \{0,1\}^{n}} E(a) \end{array} $$

(2)

is a (t + s)² multiplicative approximation to the number of unsatisfying assignments to B. We claim that this quantity can be computed faster than exhaustive search using a faster # SAT algorithm. To see this, using distributivity, we can rewrite (1) as

$$E(x) = \sum\limits_{(i,j) \in [t]^{2}} (C_{i} \wedge C_{j})(x) - 2 s \sum\limits_{i=1}^{t} C_{i}(x) + s^{2}.$$

Assuming $\mathcal {C}$ is closed under conjunction, each C_i ∧ C_j is also a $\mathcal {C}$-circuit, and we can compute

$$ \sum\limits_{a \in \{0,1\}^{n}} E(a) = \sum\limits_{(i,j) \in [t]^{2}} \left( \sum\limits_{a \in \{0,1\}^{n}}(C_{i} \wedge C_{j})(a)\right) - 2 s \sum\limits_{i=1}^{t} \left( \sum\limits_{a \in \{0,1\}^{n}} C_{i}(a)\right) + s^{2} \cdot 2^{n}$$

by making O(t²) calls to a # SAT algorithm for $\mathcal {C}$-circuits. Thus we can compute (2) using a # SAT algorithm.

How is computing (2) useful? This is where PCPs enter the story. It seems we cannot use (2) to directly solve SAT for B. (If we could, we could apply existing results such as [23] which yield lower bounds from SAT algorithms, and obtain our desired lower bound for $\mathsf {EMAJ} \circ \mathcal {C}$.) But as we mentioned earlier, we can use (2) to obtain a multiplicative approximation to the number of assignments that falsify B. In particular, each satisfying assignment to B is counted zero times in (2), and each falsifying assignment is counted between 1 and (less than) (t + s)² times. We want to exploit this, and obtain a faster GAP-UNSAT algorithm. We do this using the following series of steps:

• 1. We start with a generic circuit which is a GAP-UNSAT instance.

• 2. We use an efficient hitting set construction [11] to increase the gap of GAP-UNSAT, resulting in a new circuit D(x) which is either UNSAT or has at least 2ⁿ − o(2ⁿ) satisfying assignments where |x| = n (Section 2.1).

• 3. Next (Lemma 3) we reduce the GAP-UNSAT instance D to a graph G_D. For every assignment x to D, there is a corresponding partial assignment π_x to the vertices of G_D. We denote the resulting graph after applying the partial assignment π_x to G_D by G_D(π_x). Each G_D(π_x) can be thought of as a implicitly created instance of Independent Set, one for each x ∈{0,1}ⁿ. Our reduction guarantees that for all x such that D(x) = 0, G_D(π_x) has a large independent set, and for all x such that D(x) = 1, G_D(π_x) only has small independent sets. We expand on this step at the end of the current subsection.

Returning to the assumption that Quasi-NP has small $\mathsf {EMAJ} \circ \mathcal {C}$ circuits, and applying an easy witness lemma [17], it follows (Lemma 10) that the solution to the implicitly created Independent Set instances can be encoded by a single $\mathsf {EMAJ} \circ \mathcal {C}$ circuit i.e. there exists a small $\mathsf {EMAJ} \circ \mathcal {C}$ circuit whose truth table is the solutions to the Independent Set instances. It turns out that the constraints of an Independent Set problem are easily verifiable if the values of vertices is encoded by a $\mathsf {EMAJ} \circ \mathcal {C}$ circuit. (This is why we chose to reduce to Independent Set.)

We can now obtain a non-deterministic GAP-UNSAT algorithm using the above reductions as follows (done formally in the proof of Theorem 7). We will start with the GAP-UNSAT instance circuit D, which is either has “no satisfying assignment” or “most assignments satisfying”. In the “no satisfying assignment” case, for all x the reduced Independent Set instance G_D(π_x) has a large independent set. Counting the sum of independent sets in G_D(π_x) over all x gives a high value. In contrast, in the “most assignments are satisfying” case, for most x the reduced Independent Set instance G_D(π_x) has a small independent set and G_D(π_x) has a large independent set for only very few x. Hence in this case counting the sum of independent sets in G_D(π_x) over all x yields a low value. The difference between the high value and low value is large enough that even an approximate count of these values is enough to distinguish them. As the solutions to the Independent Set instances are encoded by a $\mathsf {EMAJ} \circ \mathcal {C}$, we can non-deterministically guess this circuit, and show that we can “efficiently” calculate an approximation to the sum of independent sets over all x by using expression (2). This completes our algorithm to solve the given GAP-UNSAT instance.

We now expand further on Step 3 of our reduction, mentioned above. This step has three sub-steps.

• a. We start by applying a PCP of Proximity and an error correcting code to D (Lemma 4), yielding a 3-SAT instance.

• b. We amplify the gap of the 3-SAT instance (Lemma 7) using derandomized serial repetition [9]. This results in a k-SAT instance with a large gap.

• c. Finally, we apply the FGLSS (short for Feige, Goldwasser, Lovász, Safra and Szegedy [10]) reduction (Lemma 9) to the k-SAT instance, obtaining the graph G_D.

In each of these sub-steps, we are implicitly creating 2ⁿ instances, one for each assignment x to the n variables of the circuit D. These instances are implicitly created via partial assignments as in Step 3. Hence we need the guarantees of serial repetition and FGLSS to hold for all of these implicitly created instances. As such a guarantee is not provided by the original statements of serial repetition and FGLSS, we cannot directly apply them in our argument. Therefore we have to study the behavior of these reductions with respect to partial assignments. While for these two reductions, we are able to prove that they behave “nicely” with respect to partial assignments, it is entirely unclear that this is true for other PCP reductions such as alphabet reduction, parallel repetition, and so on.

Our approach is very general; to handle k-sparse symmetric functions, we can simply modify the function E accordingly.

1.3 Organization

In Section 2, we set up our notation and introduce some useful lemmas from prior work. We also show how to amplify the gap of the GAP-UNSAT problem using hitting set constructions (Theorem 6). In Section 3 we give a reduction from Circuit SAT to “Generalized” Independent Set. Section 4 applies this reduction to prove lower bounds against $\mathsf {EMAJ}\circ \mathcal {C}$ assuming #SAT algorithms for $\mathcal {C}$ with running time $2^{n-n^{{\varepsilon }}}$. Section 4.1 uses this result to prove lower bounds against EMAJ ∘ACC⁰ ∘THR. Section 5 generalizes these results to $f \circ \mathcal {C}$ lower bounds, where f is a sparse symmetric function. In Section 6 we give lower bounds against $\mathsf {EMAJ} \circ \mathcal {C}$, assuming #SAT algorithms for $\mathcal {C}$ with running time 2ⁿ/n^ω(1).

2 Preliminaries

We assume general familiarity with basic concepts in circuit complexity and computational complexity [2]. In particular we assume familiarity with AC⁰, ACC⁰, P_/poly, NEXP, and so on. k-CSP refers to a constraint satisfaction problem (CSP) which is a conjunction of constraints where each constraint only depends on k variables. k-SAT refers to the subset of k-CSPs where every constraint is a disjunction over variables (or their negations). We will refer to the constraints of k-CSP and k-SAT as “clauses”. We will restrict our attention to Boolean k-CSP and k-SAT.

Circuit Notation

Here we define notation for the relevant circuit classes. By SIZE(h(n)) we denote arbitrary circuits with size at most O(h(n)). By $\text {SIZE}_{\mathcal {C}}(h(n))$ we denote circuits from circuit class $\mathcal {C}$ with size at most O(h(n)). By size(D) we refer to the size of the circuit D. We will consider Boolean circuits as well as circuits with integer outputs. By (-)$\mathcal {C}$-circuit we refer to a circuit which is either a $\mathcal {C}$-circuit or − 1 times a $\mathcal {C}$-circuit. By a poly(n)-uniform circuit we mean a circuit which can be constructed in poly(n) time given n as input in unary.

Definition 1

An $\mathsf {EMAJ}\circ \mathcal {C}$ circuit (a.k.a. “exact majority of $\mathcal {C}$ circuit”) has the general form EMAJ(C₁(x),C₂(x),…,C_t(x),u), where u is a positive integer, x are the input variables, $C_{i} \in \mathcal {C}$, and the gate EMAJ(y₁,…,y_t,u) outputs 1 if and only if exactly u of the y_i’s output 1.

Definition 2

A $\mathsf {SUM}^{\geq 0} \circ \mathcal {C}$ circuit (“positive sum of $\mathcal {C}$ circuits”) has the form

$$\mathsf{SUM}^{\geq 0}(C_{1}(x), C_{2}(x), \ldots, C_{t}(x)) = \sum\limits_{i \in [t]} C_{i}(x)$$

where C_i is a (-)$\mathcal {C}$-circuit, i.e., either a $\mathcal {C}$-circuit or − 1 times a $\mathcal {C}$-circuit. Furthermore, we are promised that ${\sum }_{i \in [t]} C_{i}(x) \geq 0$ over all x ∈{0,1}ⁿ.

For circuits C₁,…,C_t, we say $f : \{0,1\}^{n} \rightarrow \{0,1\}$ is represented by the positive-sum circuit SUM^≥ 0(C₁(x),C₂(x),…,C_t(x)) if for all x, f(x) = 1 when ${\sum }_{i \in [t]} C_{i}(x) > 0$, and f(x) = 0 when ${\sum }_{i \in [t]} C_{i}(x) = 0$.

Definition 3

A circuit class $\mathcal {C}$ is typical if there is a k ≥ 1 such that the following hold:

• Closure under negation. For every $\mathcal {C}$ circuit C, there is a $\mathcal {C}$-circuit $C^{\prime }$ computing the negation of C where $\text {size}(C^{\prime }) \leq \text {size}(C)^{k}$. Moreover, given C of size s, $C^{\prime }$ can be constructed in poly(s) time.

• Closure under AND₂. For all $\mathcal {C}$ circuits C₁ and C₂, there is a $\mathcal {C}$-circuit $C^{\prime }$ computing the AND of C₁ and C₂ where $\text {size}(C^{\prime }) \leq \text {poly}(\text {size}(C_{1})+\text {size}(C_{2}))$. Moreover, given C₁,C₂ each of size ≤ s, $C^{\prime }$ can be constructed in poly(s) time.

• Contains all-ones. The function $\textbf {1}_{n} : \{0,1\}^{n} \rightarrow \{0,1\}$ which maps all n bit strings to 1 has a $\mathcal {C}$-circuit of size O(n^k).

The vast majority of circuit classes that are studied (AC⁰, ACC⁰, TC⁰, NC¹, P_/poly) are typical.⁷ Our next lemma shows that the negation of an exact-majority of $\mathcal {C}$ can be represented as a “positive-sum” of $\mathcal {C}$, if $\mathcal {C}$ is typical.

Lemma 1

Let $\mathcal {C}$ be typical. If a function f has a $\mathsf {EMAJ}\circ \mathcal {C}$ circuit D of size s, then ¬f can be represented by a $\mathsf {SUM}^{\geq 0} \circ \mathcal {C}$ circuit $D^{\prime }$ of size poly(s). Moreover, a description of the circuit $D^{\prime }$ can be obtained from a description of D in polynomial time.

Proof

Suppose f is computable by the $\mathsf {EMAJ} \circ \mathcal {C}$ circuit

$$D = \mathsf{EMAJ}(D_{1}, D_{2}, \ldots, D_{t}, u),$$

where u ∈{0,1,…,t}. Consider the expression

$$E(x) := (\mathsf{SUM}(D_{1}, D_{2}, \ldots, D_{t})-u)^{2}.$$

Note that E(x) = 0 when D(x) = 1, and E(x) > 0 when D(x) = 0. So to prove the lemma, it suffices to show that E can be written as a $\mathsf {SUM}^{\geq 0} \circ \mathcal {C}$ circuit. Expanding the expression E,

$$ \begin{array}{@{}rcl@{}} E(x) &=& \mathsf{SUM}(D_{1}, D_{2}, \ldots, D_{t})^{2} - 2u \cdot \mathsf{SUM}(D_{1}, D_{2}, \ldots, D_{t}) + u^{2}\\ &=& \sum\limits_{(i,j) \in [t]^{2}} (D_{i} \wedge D_{j}) - \sum\limits_{j=1}^{2u} \sum\limits_{i=1}^{t} D_{i} + u^{2}. \end{array} $$

By Definition 3 $\mathsf {AND}_{2} \circ ~\mathcal {C} = \mathcal {C}$ hence each D_i ∧ D_j is a circuit from $\mathcal {C}$ of size poly(s). Since the all-ones function is in $\mathcal {C}$, the function x↦u² also has a $\mathsf {SUM} \circ \mathcal {C}$ circuit of size O(t²). Therefore there are circuits $D^{\prime }_{i} \in \mathcal {C}$ and $t^{\prime } \leq O(t^{2})$ such that by defining $D^{\prime } := \mathsf {SUM}^{\geq 0}(D^{\prime }_{1},\ldots ,D^{\prime }_{t^{\prime }})$ we have $D^{\prime }(x) = E(x)$ for all x.

Error-Correcting Codes

We will need an efficient construction of binary error correcting codes with constant rate and constant relative distance.

Theorem 4 (Theorem 19 in 18, Linear Codes)

There exists a universal constant γ ∈ (0,1) such that for all sufficiently large n, there are linear functions $ENC^{n} : (\mathbb {F}_{2})^{n} \rightarrow (\mathbb {F}_{2})^{O(n)}$ such that for all x≠y with |x| = |y| = n, the Hamming distance between ENCⁿ(x) and ENCⁿ(y) is at least γn. Furthermore, ENCⁿ can be computed in O(n) time.

In what follows, we generally drop the superscript n for notational brevity. Letting ${\text {ENC}^{n}_{i}}(x)$ denote the i th bit of ENCⁿ(x) (for i = 1,…,cn), note that ${\text {ENC}^{n}_{i}}(x)$ is a parity function on a subset of the bits of x.

2.1 Weak GAP-UNSAT Algorithms are Sufficient for Lower Bounds

Murray and Williams [17] showed that GAP-UNSAT algorithms, i.e., algorithms which distinguish between unsatisfiable circuits and circuits with ≥ 2^n− 1 satisfying assignments, suffice for proving circuit lower bounds. For our results, it is necessary to strengthen the “gap”, which can be done using known hitting set constructions. Intuitively, these constructions say that if a Boolean function f is 1 with ≥ 1/2 probability then it is easy to find arguments which satisfy f.

Lemma 2 (Corollary C.5 in 11, Hitting Set Construction)

There is a constant ψ > 0 and a $\text {poly}(n, \log {g})$ time algorithm S which, given a (uniform random) string r of $n+\psi \cdot \log {g}$ bits where n and g are integers, S outputs $t=O(\log g)$ strings $x_{1}, x_{2}, \ldots , x_{t} \in \{0,1\}^{n}$ such that for every $f : \{0,1\}^{n} \rightarrow \{0,1\}$ with ${\sum }_{x} f(x) \geq 2^{n-1}$, $\Pr _{r}[\mathsf {OR}_{i=1}^{t} f(x_{i}) = 1] \geq 1-1/g$.

We will use the following “algorithms to lower bounds” connections as black box:

Theorem 5 (Theorem 1.5 in 17, GAP-UNSAT Algorithms Imply Lower Bounds)

Suppose for some constant ε ∈ (0,1) there is a non-deterministic algorithm A that for all $2^{n^{{\varepsilon }}}$-size circuits C on n inputs, A(C) runs in $2^{n-n^{{\varepsilon }}}$ time, outputs YES on all unsatisfiable C, and outputs NO on all C that have at least 2^n− 1 satisfying assignments. Then for all k, there is a c ≥ 1 such that $\mathsf {NTIME}[2^{\log ^{ck^{4}/{\varepsilon }} n}] \not \subset \text {SIZE}(2^{\log ^{k} n})$.

Applying Lemma 2 to Theorem 5, we observe that the circuit lower bound consequence can be obtained from a significantly weaker-looking hypothesis. This weaker hypothesis will be useful for our lower bound results.

Theorem 6

Suppose for some constant ε ∈ (0,1/2) there is an algorithm A that for all $2^{n^{{\varepsilon }}}$-size circuits C on n inputs, A(C) runs in 2ⁿ/g(n)^ω(1) time, outputs YES on all unsatisfiable C, and outputs NO on all C that have at least 2ⁿ(1 − 1/g(n)) satisfying assignments, for $g(n) = 2^{n^{2{\varepsilon }}}$. Then for all k, there is a c ≥ 1 such that $\mathsf {NTIME}[2^{\log ^{ck^{4}/{\varepsilon }} n}] \not \subset \text {SIZE}(2^{\log ^{k} n})$.

Proof

We show that we can construct a strong GAP-UNSAT algorithm $A^{\prime }$ (as in assumption of Theorem 5) from a weak GAP-UNSAT algorithm (as in the assumption of this Theorem). To this end, an input circuit $D^{\prime }$ of $A^{\prime }$ is converted into an input circuit D of A by amplifying the satisfying assignments. Our starting point is Theorem 5 ([17]): we are given an m-input, $2^{m^{\delta }}$-size circuit $D^{\prime }$ that is either UNSAT or has at least 2^m− 1 satisfying assignments, and we wish to distinguish between the two cases with a $2^{m-m^{\delta }}$-time algorithm. We set δ = ε/2. First, we amplify the gap between the cases. We create a new circuit D with n inputs, where n satisfies

$$n = m + \psi \cdot \log{g(n)},$$

and ψ > 0 is the constant from Lemma 2. (Note that, since g(n) ≤ 2^o(n), such an n can be found in subexponential time.) The circuit D has the following form:

• D treats its n bits of input as a string of randomness r and computes $t=O(\log g(n))$ strings $x_{1}, x_{2}, \ldots , x_{t} \in \{0,1\}^{m}$ by simulating algorithm “S” in Lemma 2 with a $\text {poly}(m, \log g(n))$-size circuit.

• It computes $\{D^{\prime }(x_{i})\}_{i}$.

• The output is the $\mathsf {OR}(D^{\prime }(x_{1}), D^{\prime }(x_{2}), \ldots , D^{\prime }(x_{t}))$.

Note the total size of circuit D is $\text {poly}(m,\log g(n)) + O(\log g(n))\cdot \text {size}(D^{\prime }) = \text {poly}(n) + O(n^{2{\varepsilon }}) \cdot 2^{m^{\delta }} < 2^{n^{2\delta }} = 2^{n^{{\varepsilon }}}$ as ε = 2δ. Clearly, if $D^{\prime }$ is unsatisfiable, then D is also unsatisfiable. By Lemma 2, if $D^{\prime }$ has 2^m− 1 satisfying assignments, then D has at least 2ⁿ(1 − 1/g(n)) satisfying assignments. As $\text {size}(D) \leq 2^{n^{{\varepsilon }}}$, by our assumption we can distinguish the case that D is unsatisfiable from the case that D has at least 2ⁿ(1 − 1/g(n)) satisfying assignments, with an algorithm running in time 2ⁿ/g(n)^ω(1). This yields an algorithm for distinguishing the original circuit $D^{\prime }$ on m inputs and $2^{m^{\delta }}$ size, running in time

$$2^{n}/g(n)^{\omega(1)} = 2^{m}g(n)^{O(1)}/g(n)^{\omega(1)} = 2^{m}/g(n)^{\omega(1)} \!\leq\! 2^{m}2^{-n^{2{\varepsilon}}} \leq2^{m}2^{-n^{\delta}} \leq 2^{m-m^{\delta}},$$

since $g(n) = 2^{n^{2{\varepsilon }}}$ and ε = 2δ. By Theorem 5, this implies that for all k, there is a c ≥ 1 such that $\mathsf {NTIME}[2^{\log ^{ck^{4}/\delta } n}] \not \subset \text {SIZE}(2^{\log ^{k} n})$. As, ε = 2δ we get that $\mathsf {NTIME}[2^{\log ^{2ck^{4}/{\varepsilon }} n}] \not \subset \text {SIZE}(2^{\log ^{k} n})$. But as the constant 2 can be absorbed in the constant c, we get that for all k, there is a c ≥ 1 such that $\mathsf {NTIME}[2^{\log ^{ck^{4}/{\varepsilon }} n}] \not \subset \text {SIZE}(2^{\log ^{k} n})$.

3 From Circuit SAT to Independent Set

The goal of this section is to give the main PCP reduction (Lemma 3) we will use in our new algorithm-to-lower-bound theorem. First we need a definition of “generalized” independent set instances, where some vertices have already been “assigned” in or out of the independent set.

Definition 4

Let G = (V,E) be a graph. Let π : V →{0,1,⋆} be a partial Boolean assignment to V. We define G(π) to be a graph with the label function π on its vertices (where each vertex gets the label 0, or 1, or no label). We construe G(π) as an generalized independent set instance, in which any valid independent set (vertex assignment) must be consistent with π: any independent set must contain all vertices labeled 1, and no vertices labeled 0.

Our main technical lemma is the following.

Lemma 3

Let k be a function of n. There is a poly(m,2^k)-time reduction such that, given a circuit D on X with ${\lvert }{X}{\rvert } = n$ bits and of size m > n, the reduction outputs a generalized independent set instance on a graph G_D = (V_D,E_D) such that:

• Each vertex v ∈ V_D is associated with a set of pairs S_v of the form $\{(i, b)\} \subseteq [O(n)] \times \{0, 1\}$. The sets {S_v} are produced as part of the reduction.

• Each assignment x to X defines a partial assignment π_x to V_D such that

  $$\pi_{x}(v) = \begin{cases} 0 & ~\text{if} ~~ \exists (i, b) \in S_{v} \text{~such that~} ENC_{i}(x) \neq b\\ \star & ~\text{otherwise}, \end{cases}$$

  where ENC is the error-correcting code from Theorem 4.

Further, G_D satisfies that:

• If D(x) = 0, the maximum independent set in G_D(π_x) has size α, and given x, it can be found in time poly(m,2^k).

• If D(x) = 1, then the maximum independent set in G_D(π_x) has size at most α/2^k.

where α is an integer produced as part of the reduction.

The remainder of this section is devoted to the proof of Lemma 3. We will prove Lemma 4, 7, and 9 each of which describes a reduction, combining them sequentially will give us Lemma 3.

Let us set up some notation for variable assignments to a formula. Let F be a SAT instance on a variable set Z, and let τ : Z →{0,1,⋆} be a partial assignment to Z. Define F(τ) to be the formula obtained by setting the variables in F according to τ. Note that we do not perform further reduction rules on the clauses in F(τ): for each clause in F that becomes false (or true) under τ, there is a clause in F(τ) which is always false (true).

For every subsequence Y of variables from Z, and every vector y ∈{0,1}^{|Y |}, we define F(Y = y) to be the formula F in which the i^th variable in Y is assigned y_i, and variables in Z ∖ Y left unassigned.

Next, we state a probabilistically checkable proof (PCP) transformation of Chen and Williams [7] which will be the first step in the reduction in Lemma 3. In the following, we say that a CNF formula $F^{\prime }$ is at most δ-satisfiable if no assignment to its free variables satisfies more than a δ-fraction of the clauses in $F^{\prime }$.

Lemma 4 (PCPs of Proximity+Error Correcting Codes(PCPP+ECC), 7)

Let ENC : {0,1}ⁿ →{0,1}^O(n) be the linear encoding function from Theorem 4, where (for all i) the i^th bit of output ENC_i(x) satisfies $\text {ENC}_{i}(x) = \oplus _{j \in U_{i}} x_{j}$ for some set U_i.

There is a polynomial-time transformation and constant δ < 1 which, given a circuit D on n inputs of size m ≥ n, outputs a 3-SAT instance F on a variable set Y ∪ Z, where ${\lvert }{Y}{\rvert } = O(n)$, ${\lvert }{Z}{\rvert } \leq \text {poly}(m)$, and the following hold for all x ∈{0,1}ⁿ:

• If D(x) = 0 then F(Y = ENC(x)) on variable set Z has a satisfying assignment z_x. Furthermore, there is a poly(m)-time algorithm that given x outputs z_x.

• If D(x) = 1 then F(Y = ENC(x)) is at most δ-satisfiable, i.e., no assignment to the Z variables in F(Y = ENC(x)) satisfies more than a δ-fraction of the clauses.

Serial repetition [9] is a basic operation on Boolean constraint satisfaction problems (CSPs) and PCPs. Recall that a CSP is a collection of logical constraints over variables that take values from a finite domain (here, we will only consider Boolean domain). A k-CSP is a CSP in which every constraint is k-ary, in that each constraint is a function of at most k variables. In serial repetition, a new CSP is created from an old one, where the new CSP constraints are ANDs (conjunctions) of a fixed number of randomly sampled clauses from the old CSP. In derandomized serial repetition, the choices of which old constraints are used to create the new constraints are purely deterministic. Serial repetition is usually done for the purpose of reducing the soundness parameter, i.e., reducing the fraction of satisfiable clauses in the NO case. We will prove that the guarantees of derandomized serial repetition hold for partial assignments where some but not all variables are assigned (Lemma 7). This will be the second step in the reduction in Lemma 3.

We begin by stating the standard formulation of derandomized serial repetition.

Lemma 5 (Corollary 2.5 in 9, Derandomized Serial Repetition)

Let Ψ₁,Ψ₂,…,Ψ_m be a sequence of m circuits over a set of variables Y. Let β and μ be two positive real values. Then there exists a sequence of t = m ⋅poly(1/β) new circuits ${\varPsi }^{\prime }_{1}, {\varPsi }^{\prime }_{2},\ldots , {\varPsi }^{\prime }_{t}$ such that

• 1. Each new circuit ${\varPsi }^{\prime }_{i}$ is the AND of s old circuits Ψ_i with $s = O(\log (1/\beta )/\mu )$. In particular, every assignment to the variables Y that satisfies all of the old circuits also satisfies all of the new circuits.

• 2. Every assignment to the variables Y that causes μm of the old circuits to reject also causes (1 − β)t of the new circuits to reject.

• 3. On input Ψ₁,Ψ₂,…,Ψ_m,β,μ, the new sequence ${\varPsi }^{\prime }_{1}, {\varPsi }^{\prime }_{2},\ldots , {\varPsi }^{\prime }_{t}$ can be constructed uniformly in polynomial time (in the input and output lengths).

We will use the following slightly modified form of the above reduction. The below reduction works for all alphabet sizes, though we will only be looking at Boolean CSPs, in which case the k-CSP is analogous to the k-SAT problem. For simplicity, we use “clauses” to refer to the constraints of a k-CSP.

Lemma 6

There is a polynomial-time algorithm which, given a constant δ ∈ (0,1) and an m-clause 3-SAT instance F on a variable set Y with |Y | = n, outputs an O(k)-CSP formula $F^{\prime }$ on the same n variables with t = m ⋅ 2^O(k) clauses such that:

• 1. If y ∈{0,1}ⁿ satisfies F, then y satisfies $F^{\prime }$.

• 2. If F is ≤ δ-satisfiable then $F^{\prime }$ is ≤ (1/2^k)-satisfiable.

• 3. Each clause of $F^{\prime }$ is an AND of O(k) clauses of F, moreover, there is a fixed polynomial time computable mapping $p : [t] \to \binom {m}{O(k)}$ such that the i^th clause of $F^{\prime }$ is the AND of the clauses of F whose indices in the set $p(i) \in \binom {m}{O(k)}$.

Proof

This lemma follows from Lemma 5. In particular it follows by setting Ψ_i to be the clauses in the 3-SAT instance, β = 1/2^k and μ = 1 − δ. As δ is some fixed constant, the resulting ${\varPsi }^{\prime }_{i}$ are ANDs of $s = O(\log (1/\beta )/\mu ) = O(k/(1-\delta )) = O(k)$ clauses of the 3-SAT. Hence each ${\varPsi }^{\prime }_{i}$ can be thought of as a constraint of 3 ⋅ O(k) = O(k) variables and $\{{\varPsi }^{\prime }_{i}\}_{i=1}^{t}$ can be together thought of as a O(k)-CSP with t = m ⋅poly(1/β) = m ⋅ 2^O(k) clauses. All the stated properties of the reduction directly follow from the properties of Lemma 5.

We now prove a stronger version of derandomized serial repetition, in which there are soundness guarantees for partial Boolean assignments. The proof directly follows from the guarantees of Lemma 6 above.

Lemma 7 (Serial Repetition with Partial Assignments)

Let k be a function of n. There is a polynomial-time algorithm that, for all constants δ < 1, given an m-clause 3-SAT instance F on a variable set Y ∪ Z with |Y ∪ Z| = n, outputs an O(k)-CSP formula $F^{\prime }$ on the same n variables with m ⋅ 2^O(k) clauses such that:

• 1. If the assignment Y = y,Z = z satisfies F then y,z satisfies $F^{\prime }$.

• 2. If F(Y = y) is at most δ-satisfiable, then $F^{\prime }(Y = y)$ is at most 1/2^k-satisfiable.

• 3. Each clause of $F^{\prime }$ is an AND of O(k) clauses of F, moreover, there is a fixed polynomial time computable mapping $p : [t] \to \binom {m}{O(k)}$ such that the i^th clause of $F^{\prime }$ is the AND of the clauses of F whose indices in the set $p(i) \in \binom {m}{O(k)}$.

Proof

We prove that the standard serial repetition from Lemma 6 suffices.

Property 1 and 3 directly follow from Property 1 and 3 in Lemma 6. We turn to verifying Property 2. Let F(Y = y) be ≤ δ-satisfiable. Given $y \in \{0, 1\}^{{\lvert }{Y}{\rvert }}$, define F_y = F(Y = y), where all clauses that become FALSE or TRUE under Y = y remain in F_y as clauses with no variables. Let $F^{\prime }_{y}$ be the O(k)-CSP formula obtained by applying serial repetition to F_y from Lemma 7. By Property 3, of Lemma 6, the formula $F^{\prime }(Y = y)$ obtained by first applying serial repetition and then setting Y = y, is the same as the formula $F^{\prime }_{y}$ obtained by setting Y = y, and then applying serial repetition (Lemma 6).

By assumption, F_y is at most δ-satisfiable, by Property 2 of Lemma 6, $F^{\prime }_{y}$ is at most (1/2^k)-satisfiable. Since $F^{\prime }(Y = y) = F^{\prime }_{y}$, it follows that $F^{\prime }(Y = y)$ is at most (1/2^k)-satisfiable.

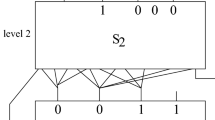
The well-known FGLSS reduction [10] maps a CSP Φ to a graph G_Φ such that the MAX-SAT value of Φ equals to the size of the maximum independent set in G_Φ. We will prove that the guarantees of the FGLSS reduction hold for partial assignments (Lemma 9), this reduction will be the third step in the reduction in Lemma 3. We start by stating the standard FGLSS reduction.

Lemma 8 (Theorem 3 in 10, FGLSS)

There is a poly(n,m,2^k) time reduction that given an m-clause n-variable k-CSP instance F, outputs a graph G_F = (V_F,E_F) such that the size of the maximum independent set in G_F equals the maximum number of clauses satisfiable in F.

We note that a stronger version of the FGLSS reduction [10] holds with guarantees for partial assignments.

Lemma 9 (FGLSS with partial assignments)

Given a Boolean k-CSP instance F on variable set Y,Z with ${\lvert }{Y}{\rvert }+{\lvert }{Z}{\rvert } = n$ and m clauses, there is a poly(n,m,2^k) time reduction that given F, outputs a graph G_F = (V_F,E_F). Each vertex v ∈ V_F is associated with a set $S_{v} \subseteq [{\lvert }Y{\rvert }] \times \{0, 1\}$. For each assignment to the Y variables τ : Y →{0,1}, define the partial assignment π_τ to V_F:

$$\pi_{\tau}(v) = \begin{cases} 0 & ~\text{if} ~~ \exists (i, b) \in S_{v} \text{~such that~} \tau(Y_{i}) \neq b\\ \star & ~\text{otherwise.}, \end{cases}$$

Then the maximum independent set in the generalized independent set instance G_F(π_τ) equals the maximum number of clauses satisfiable in F(τ). Furthermore, there is a poly(n,m,2^k)-time algorithm that given τ and an assignment to F(τ) satisfying α clauses, outputs an independent set of size α in the graph G_F(π_τ).

The proof is analogous to the proof of the standard FGLSS reduction (Lemma 8). We include a proof for completeness. Let w be a clause of F and let w_i denote the i^th variable in w. Let ℓ denote a satisfying assignment to w in which ℓ_i denotes the assignment to w_i. For every w,ℓ pair, we create a vertex v_w,ℓ in V_F, and set $S_{v_{w, \ell }} = \{(w_{i}, \ell _{i}) \mid 1 \leq i \leq k\}$. As F is a k-CSP instance, there are at most poly(m,2^k) vertices. For u,v ∈ V_F add (u,v) to E_F iff assignments S_u and S_v contradict each other i.e. ∃x,b ∈{0,1} s.t. (x,b) ∈ S_u and (x,1 − b) ∈ S_v. Note that this means that there is always an edge between two vertices associated with a particular clause, but different satisfying assignments. That is, the set of all vertices associated a particular clause form a clique in G_F.

Let τ : Y →{0,1} be such that F(τ) has an assignment satisfying α clauses, and let x : Y ∪ Z →{0,1} be a assignment to all variables (consistent with τ) satisfying α clauses. We will give an independent set in G_F(π_τ) of size α. For each clause w of F satisfied by x and satisfying assignment ℓ to w (derived from x) we put v_w,ℓ in a set $I_{x} \subseteq V_{F}$. Note that ${\lvert }{I_{x}}{\rvert } = \alpha$ since there are α satisfied clauses, and I_x is an independent set because each pair of vertices u,v ∈ I_x are derived from the same assignment x, so S_u and S_v cannot contradict each other. Furthermore, our choice of I_x does not contradict π_τ (as defined in the statement of Lemma) as all partial assignments corresponding to vertices set to 0 by π_τ contradict τ and hence contradict x, while we only chose vertices consistent with x. Hence the maximum number of clauses satisfied in F(τ) is at most the maximum independent set size in G_F(π_τ). From the above it is clear that this independent set is also constructible in time poly(n,m,2^k), given the assignment x.

Now taking an independent set I in G_F(π_τ) of size α, we give an assignment to F(τ) satisfying α clauses. Recall that, the set of vertices corresponding to a particular clause form a clique, so only one vertex from the set can be in a independent set. Hence the independent set I with α vertices must have vertices associated with α different clauses of F. For a vertex u associated with (w,ℓ), the partial assignment S_u satisfies w. The partial assignment S_u is also consistent with τ, as otherwise vertex u would have already been set to 0 by π_τ. For two vertices u,v in I the partial assignments from S_v and S_u do not contradict, as otherwise (u,v) would be an edge in G_F. Hence we can join all partial assignments S_v for the vertices v in I to obtain a partial assignment satisfying α clauses in F(τ). Thus the maximum independent set size in G_F(π_τ) is at most the maximum number of clauses satisfied in F(τ). This completes the proof.

We next present the proof of Lemma 3 which just follows by combining Lemma 4, 7, and 9 sequentially.

Proof Proof of Lemma 3

The proof follows by applying Lemma 4, 7 and 9 sequentially.

Step 1: Convert D to 3-SAT Start with a circuit D with input variables X (${\lvert }X{\rvert } = n$) and size m > n. Applying Lemma 4, (PCPP+ECC), we transform D into a 3-SAT instance F with poly(m) clauses on the variable set Y ∪ Z, where ${\lvert }Y{\rvert } \leq \text {poly}(n)$, ${\lvert }Z{\rvert } \leq \text {poly}(m)$, and the following hold for all x ∈{0,1}ⁿ:

• (a) If D(x) = 0, then the formula F(Y = ENC(x)) on variable set Z has a satisfying assignment z_x. Furthermore, there is a poly(m)-time algorithm that given x, outputs z_x.

• (b) if D(x) = 1, then there is no assignment to the Z variables in F(Y = ENC(x)) satisfying more than a δ-fraction of the clauses, for a universal constant δ ∈ (0,1).

(Recall ENC : {0,1}ⁿ →{0,1}^O(n) is the linear error-correcting encoding function from Theorem 4.)

Step 2: Reduce 3-SAT to O(k)-CSP Now apply Lemma 7 to F. This yields a O(k)-CSP $F^{\prime }$ on the variable set Y ∪ Z variables with α = poly(m) ⋅ 2^O(k) clauses, such that:

• 1. If Y,Z = y,z satisfies F then y,z satisfies $F^{\prime }$.

• 2. If F(Y = y) is at most δ-satisfiable then $F^{\prime }(Y = y)$ is at most (1/2^k)-satisfiable.

Step 3: Reduce O(k)-CSP to a graph Finally, apply Lemma 9 to $F^{\prime }$, to get graph $G_{F^{\prime }}$. The size of the graph $G_{F^{\prime }}$ is poly(n + m,poly(m) ⋅ 2^O(k),2^O(k)) ≤poly(m,2^k) since m > n. Lemma 9 gives us the following condition on the graph $G_{F^{\prime }}$:

• (i) If Y,Z = y,z satisfies $F^{\prime }$ then $G_{F^{\prime }}(\pi _{Y=y})$ has an independent set of size α. Furthermore, there is a poly(m,2^k)-time algorithm that given y,z outputs an independent set of size α in the graph $G_{F^{\prime }}(\pi _{Y = y})$.

• (ii) If $F^{\prime }(Y = y)$ is at most (1/2^k)-satisfiable then all independent sets in $G_{F^{\prime }}(\pi _{Y = y})$ have size ≤ α/2^k.

We consider partial assignments τ which assign Y to ENC(x) for some x. As τ is fixed by fixing x, we rename π_τ to π_x. Combining (a)+ 1+(i) and (b)+ 2+(ii) we have:

• If D(x) = 0 then $G_{F^{\prime }}(\pi _{x})$ has an independent set I_x of size α. Furthermore, there is a poly(m,2^k)-time algorithm that given x outputs I_x.

• if D(x) = 1 then all independent sets in $G_{F^{\prime }}(\pi _{x})$ have size ≤ α/2^k.

where α is the number of clauses in $F^{\prime }$. This completes the proof.

4 Main Result

We now turn to the proof of the main lower bound result, Theorem 3. We first prove the result for $\mathsf {EMAJ} \circ \mathcal {C}$; in Section 5, we sketch how to extend to $f \circ \mathcal {C}$ for sparse symmetric f. Below, we prove $\mathsf {EMAJ} \circ \mathcal {C}$ lower bounds for Quasi-NP functions, when there are $2^{n-n^{{\varepsilon }}}$ time algorithms for #SAT on $\mathcal {C}$ circuits of size $2^{n^{{\varepsilon }}}$. For the other parts of Theorem 3 (on #SAT algorithms with running time 2ⁿ/n^ω(1)), see Section 6.

We note here that in Theorem 3 we claimed polynomial size lower bounds against $\mathsf {EMAJ} \circ \mathcal {C}$, but in fact we obtain quasi-polynomial size lower bounds below.

Theorem 7

Suppose $\mathcal {C}$ is typical and the parity function has poly(n)-uniform, poly(n)-sized $\mathcal {C}$ circuits. Further suppose that for some ε ∈ (0,1) there is a #SAT algorithm running in time $2^{n-n^{{\varepsilon }}}$ for all circuits from class $\mathcal {C}$ of size at most $2^{n^{{\varepsilon }}}$. Then for every k, Quasi-NP does not have $\mathsf {EMAJ} \circ \mathcal {C}$ circuits of size $O(n^{\log ^{k} n})$.

Define ${\mathscr{H}}$ to be $\mathsf {EMAJ} \circ \mathcal {C}$. Let us assume that for a fixed k > 0, Quasi-NP has ${\mathscr{H}}$ circuits of size $O(n^{\log ^{k} n})$ which implies $\mathsf {Quasi}\text {-}\mathsf {NP} \subset \text {SIZE}(n^{\log ^{k} n})$ for general circuits. By Theorem 6, we obtain a contradiction if, for some constant δ ∈ (0,1) and $g(n) = 2^{n^{2\delta }}$, we can construct a 2ⁿ/g(n)^ω(1) time nondeterministic algorithm that given a circuit D with n inputs and size $m \leq h(n) := 2^{n^{\delta }}$ can distinguish between:

• 1. YES case: D has no satisfying assignments.

• 2. NO case: D has at least $2^{n}\left (1-1/g(n)\right )$ satisfying assignments.

Under the hypothesis, we will give such an algorithm for δ = ε/4. Using Lemma 3, we reduce the circuit D to an independent set instance G_D (with $k = \log {h(n)}$) on n₂ ≤poly(m,2^O(k)) ≤poly(m,h(n)^O(1)) ≤poly(h(n)) vertices. As described in Lemma 3, we also find sets of pairs S_i for every vertex i ∈ [n₂]. Let π_x be the partial assignment which assigns a vertex i to 0 if there exist $(j^{\prime }, b) \in S_{i}$ such that $\text {ENC}_{j^{\prime }}(x) \neq b$ and leaves i unassigned otherwise. By Lemma 3, G_D has the following properties:

This means it suffices for us to distinguish between the following two cases:

• 1. If D(x) = 0, then there is an independent set of size α in G_D(π_x). Furthermore, given x we can find this independent set in poly(h(n)) time.

• 2. If D(x) = 1, then all independent sets have size at most α/h(n) in G_D(π_x).

• 1. YES case: For all x, G_D(π_x) has an independent set of size α.

• 2. NO case: For at most 2ⁿ/g(n) values of x,G_D(π_x) has an independent set of size α/h(n).

Guessing a Succinct Witness Circuit

As guaranteed by Lemma 3, given an x such that D(x) = 0, we can find the assignment A(x) to G_D which is consistent with π_x and represents an independent set of size α, in poly(h(n)) time. Let A(x,i) denote the assignment to the i^th vertex in A(x). Given x and vertex i ∈ [n₂], we can produce ¬A(x,i) in time poly(h(n)).

Lemma 10

Under the hypothesis, there is a ${\mathscr{H}} = \mathsf {EMAJ} \circ \mathcal {C}$ circuit U of size h(n)^o(1) with (x,i) as input representing ¬A(x,i).

Under the hypothesis, for some constant k, we have $\mathsf {Quasi}\text {-}\mathsf {NP} \subseteq \text {SIZE}_{{\mathscr{H}}}(n^{\log ^{k} n})$. Specifically, for $p(n) = n^{\log ^{k+1} n}$ we have $\mathsf {NTIME}[p(n)] \subseteq \text {SIZE}_{{\mathscr{H}}}(p(n)^{1/\log n}) \subseteq \text {SIZE}_{{\mathscr{H}}}(p(n)^{o(1)})$. As $h(n) = 2^{n^{{\varepsilon }}} \gg p(n)$, a standard padding argument implies $\mathsf {NTIME}[\text {poly}(h(n))] \subseteq \text {SIZE}_{{\mathscr{H}}}((\text {poly}(h(n)))^{o(1)}) = \text {SIZE}_{{\mathscr{H}}}(h(n)^{o(1)})$. Since ¬A(x,i) is computable in poly(h(n)) time, we have that ¬A(x,i) can be represented by a h(n)^o(1)-sized ${\mathscr{H}} = \mathsf {EMAJ} \circ \mathcal {C}$ circuit.

Our nondeterministic algorithm for GAP-UNSAT begins by guessing U guaranteed by Lemma 10 which is supposed to represent ¬A. Then by the reduction in Lemma 1, we can convert U to a $\mathsf {SUM}^{\geq 0} \circ \mathcal {C}$ circuit R for A(x,i) of size poly(h(n)^o(1)) = h(n)^o(1). Note that if our guess for U is correct, i.e., U = ¬A, then R represents A.

Let the subcircuits of R be R₁,R₂,…,R_t for t ≤ h(n)^o(1), so that $R(x) = {\sum }_{j \in [t]} R_{j}$, where R_j is a (-)$\mathcal {C}$-circuit, i.e., either a $\mathcal {C}$-circuit or − 1 times a $\mathcal {C}$-circuit. The number of inputs to R_j is $n^{\prime } = {\lvert }x{\rvert }+\log {n_{2}}=n+O(\log h(n))$, and the size of R_j is h(n)^o(1).

Note that R(x,i) = 0 represents that the i^th vertex is not in the independent set of G_D in a solution corresponding to x, while R(x,i) > 0 represents that it is in the independent set of G_D in a solution corresponding to x. For all x and i, we have 0 ≤ R(x,i) ≤ t ≤ h(n)^o(1).

Verifying that R Encodes Valid Independent Sets

We can verify that the circuit R produces an independent set on all x by checking each edge over all x. To check the edge between vertices i₁ and i₂ we need to verify that at most one of them is in the independent set, that is, for all x, we check that R(x,i₁) ⋅ R(x,i₂) = 0. As R(x,i) is at least 0 we can just verify

$$\sum\limits_{x \in \{0, 1\}^{n}} R(x, i_{1}) \cdot R(x, i_{2}) = 0.$$

Since $R(x, i) = {\sum }_{j \in [t]} R_{j}(x, i)$, it suffices to verify that

$$\sum\limits_{x \in \{0, 1\}^{n}} \sum\limits_{j_{1}, j_{2} \in [t]} R_{j_{1}}(x, i_{1}) \cdot R_{j_{2}}(x, i_{2}) = 0.$$

Let $R_{j_{1}, j_{2}}(x, i_{1}, i_{2}) = R_{j_{1}}(x, i_{1}) \cdot R_{j_{2}}(x, i_{2})$. Since $\mathcal {C}$ is closed under AND, $R_{j_{1}, j_{2}}$ also has a poly(h(n)^o(1)) = h(n)^o(1) sized (-)$\mathcal {C}$ circuit. Exchanging the order of summations, it suffices for us to verify

$$\sum\limits_{j_{1}, j_{2} \in [t]} \left( \sum\limits_{x \in \{0, 1\}^{n}} R_{j_{1}, j_{2}}(x, i_{1}, i_{2})\right) = 0.$$

For fixed i₁,i₂,j₁,j₂ the number of inputs to $R_{j_{1}, j_{2}}$ is ${\lvert }x{\rvert }=n$, and its size is at most $h(n)^{o(1)} \leq 2^{n^{{\varepsilon }}}$. Hence, for fixed i₁,i₂,j₁,j₂, we can compute ${\sum }_{x} R_{j_{1}, j_{2}}(x, i_{1}, i_{2})$ using the #SAT algorithm from our assumption, in time $2^{n-n^{{\varepsilon }}}$. Summing over all j₁,j₂ pairs only adds another multiplicative factor of t² = h(n)^o(1). This allows us to verify that the edge (i₁,i₂) is satisfied by R. Checking all edges of G_D only adds another multiplicative factor of poly(h(n)). Hence the total running time for verifying that R encodes valid independent sets on all x is still $2^{n-n^{{\varepsilon }}}\text {poly}(h(n))$.

Verifying Consistency of the Independent Set Produced by R with π _x (for all x)

As we care about the sizes of independent sets in G_D(π_x) over all x we need to check if the assignment derived by R is consistent with π_x. As π_x only assigns vertices to 0, we need to verify that all vertices assigned to 0 in π_x are in fact assigned to 0 by the assignment given by R(x,⋅). From Lemma 3, we know that π_x assigns a vertex i to 0 if for some $(j^{\prime }, b) \in S_{i}$, $\text {ENC}_{j^{\prime }}(x) \neq b$. To check this condition we need to verify that R(x,i) = 0 when there is a $(j^{\prime }, b) \in S_{i}$, $\text {ENC}_{j^{\prime }}(x) \neq b$. This is equivalent to checking $(\text {ENC}_{j^{\prime }}(x) \oplus b) \cdot R(x, i) = 0$ for all $x, i, (j^{\prime }, b) \in S_{i}$. Since $(\text {ENC}_{j^{\prime }}(x) \oplus b) \cdot R(x, i) \geq 0$ we can just check that

$$\sum\limits_{x \in \{0, 1\}^{n}} (\text{ENC}_{j^{\prime}}(x) \oplus b) \cdot R(x, i) = 0$$

for all $i, (j^{\prime }, b) \in S_{i}$. Since $R(x, i) = {\sum }_{j \in [t]} R_{j}(x, i)$ we can equivalently verify that

$$\sum\limits_{x \in \{0, 1\}^{n}} \sum\limits_{j \in [t]} (\text{ENC}_{j^{\prime}}(x) \oplus b) \cdot R_{j}(x, i) = 0$$

for all $i, (j^{\prime }, b) \in S_{i}$. Note that $R_{j^{\prime }}(x, i)$ has a h(n)^o(1) sized $\mathcal {C}$ circuit. By our assumption, (ENC_j(x) ⊕ b) has a poly(n)-uniform, poly(n)-sized $\mathcal {C}$-circuit. Hence $(\text {ENC}_{j}(x) \oplus b) \cdot R_{j^{\prime }}(x, i)$ has a poly(n,h(n)^o(1)) ≤ h(n)^o(1)-sized $\mathcal {C}$ circuit as we are given that $\mathcal {C}$ is typical. Moreover, we can construct the $\mathcal {C}$-circuit for $(\text {ENC}_{j}(x) \oplus b) \cdot R_{j^{\prime }}(x, i)$ in ≤ h(n)^o(1) time as we have already guessed $R_{j^{\prime }}$ and the circuit for ENC_j is poly(n)-uniform.

For fixed $(i, j, j^{\prime })$, $(\text {ENC}_{j^{\prime }}(x) \oplus b) \cdot R_{j}(x, i) \in \mathcal {C}$ has ${\lvert }x{\rvert } = n$ inputs and size $h(n)^{o(1)} < 2^{n^{{\varepsilon }}}$. Hence we can use the #SAT algorithm from the assumption to calculate ${\sum }_{x \in \{0, 1\}^{n}} (\text {ENC}_{j^{\prime }}(x) \oplus b) \cdot R_{j}(x, i)$ in time $2^{n-n^{{\varepsilon }}}$. Summing over all j ∈ [t] introduces another multiplicative factor of h(n)^o(1). This allows us to verify the desired condition for a fixed $i, (j^{\prime }, b) \in S_{i}$. To check it for all $i, (j^{\prime }, b) \in S_{i}$ (recall ${\lvert }{S_{i}}{\rvert } \leq O(n)$ by Theorem 4) only introduces another multiplicative factor of poly(h(n)) ⋅ O(n) ≤poly(h(n)) in time. Therefore the total running time for verifying consistency with respect to π_x (for all x) is $2^{n-n^{{\varepsilon }}}\text {poly}(h(n))$.

Distinguishing Between the YES and NO Cases

As we now know that R represents an independent set, and that R is consistent with π_x, We need to distinguish between:

• 1. YES case: For all x, R(x,⋅) represents an independent set of size α.

• 2. NO case: For at most 2ⁿ/g(n) values of x,R(x,⋅) represents an independent set of size ≥ α/h(n).

Lemma 11

For all x such that R(x,⋅) represents an independent set of size a, we have $a \leq {\sum }_{i \in [n_{2}]} R(x, i) \leq at$.

For every vertex i in the independent set, 1 ≤ R(x,i) ≤ t. For all vertices i not in the independent set, R(x,i) = 0. Hence $a \leq {\sum }_{i \in [n_{2}]} R(x, i) \leq at$.

To distinguish between the YES and NO cases, we now compute

$$ \begin{array}{@{}rcl@{}} \sum\limits_{x \in \{0, 1\}^{n}} \sum\limits_{i \in [n_{2}]} R(x, i) \end{array} $$

(3)

This allows us to distinguish between the YES case and NO cases as follows.

• 1. YES case: For all x ∈{0,1}ⁿ, the independent set is at least of size α. Hence by Lemma 11, the sum is ${\sum }_{x \in \{0, 1\}^{n}} {\sum }_{i \in [n_{2}]} R(x, i) \geq 2^{n}\alpha$.

• 2. NO case: For at least 2ⁿ(1 − 1/g(n)) values of x, we have an independent set of size at most α/h(n). By Lemma 11, for such x, ${\sum }_{i \in [n_{2}]} R(x, i) \leq t\alpha /h(n)$. For the rest of the 2ⁿ/g(n) values of x the independent set is at most all vertices in the graph G_D. By Lemma 11, for such values of x, ${\sum }_{i \in [n_{2}]} R(x, i) \leq tn_{2} = \text {poly}(h(n))$. Hence

  $$ \begin{array}{@{}rcl@{}} \sum\limits_{x \in \{0, 1\}^{n}} \sum\limits_{i \in [n_{2}]} R(x, i) &\leq& (2^{n}/g(n)) \cdot \text{poly}(h(n))+ 2^{n}t\alpha/h(n)\\ &\leq& o(2^{n})+2^{n}t\alpha/h(n)~ [\text{Since } h(n) = g(n)^{o(1)}]\\ &\leq& o(2^{n})+o(2^{n}\alpha)~ [\text{Since } t = h(n)^{o(1)}]\\ &<& 2^{n} \alpha~ [\text{Since } \alpha > 1] \end{array} $$

All that remains is how to compute (3). As $R(x, i) = {\sum }_{j \in [t]} R_{j}(x, i)$, we can compute

$$\sum\limits_{x \in \{0, 1\}^{n}} \sum\limits_{i \in [n_{2}]} \sum\limits_{j \in [t]} R_{j}(x, i) = \sum\limits_{j \in [t]} \sum\limits_{i \in [n_{2}]} \left( \sum\limits_{x \in \{0, 1\}^{n}} R_{j}(x, i) \right)$$

For a fixed i,j, $R_{j}(x, i) \in \mathcal {C}$ has ${\lvert }x{\rvert } = n$ inputs and size $\leq \text {poly}(h(n)^{o(1)}) = h(n)^{o(1)} < 2^{n^{{\varepsilon }}}$. Hence we can use the assumed #SAT algorithm to calculate ${\sum }_{x \in \{0, 1\}^{n}} R_{j}(x, i)$ in time $2^{n-n^{{\varepsilon }}}$. Summing over all j ∈ [t],i ∈ [n₂] only introduces another h(n)^o(1)poly(h(n)) = poly(h(n)) multiplicative factor. Thus the running time for distinguishing the two cases is at most $2^{n-n^{{\varepsilon }}}\text {poly}(h(n))$.

In total our running time is bounded by $2^{n-n^{{\varepsilon }}}\text {poly}(h(n)) = 2^{n-n^{4\delta }+O(n^{\delta })} \leq 2^{n-n^{3\delta }} = 2^{n}/g(n)^{\omega (1)}$ as $g(n) = 2^{n^{2\delta }}$ and ε = 4δ. By Theorem 6, this gives us a contradiction which completes our proof.

The above theorem when combined with known #SAT algorithms for ACC⁰ ∘THR gives the following Quasi-NP lower bound for EMAJ ∘ACC⁰ ∘THR.

4.1 E M A J ∘A C C ⁰ ∘T H R Lower Bound

We will apply a known # SAT algorithm for ACC ∘THR circuits.

Theorem 8

[25] For every pair of constants d,m, there exists a constant ε ∈ (0,1) such that #SAT can be solved in time $2^{n-n^{{\varepsilon }}}$ time for AC⁰[m] ∘THR circuits of depth d and size $2^{n^{{\varepsilon }}}$.

Theorem 9

For all constants k,d and m, Quasi-NP does not have $n^{\log ^{k} n}$-size EMAJ ∘AC⁰[m] ∘THR circuits of depth d.

Proof

We prove a lower bound for circuits of the type EMAJ ∘AC⁰[2m] ∘THR and note that $\mathsf {EMAJ} \circ \mathsf {AC}^{0}[m] \circ \mathsf {THR} \subseteq \mathsf {EMAJ} \circ \mathsf {AC}^{0}[2m] \circ \mathsf {THR}$ as MOD_m gates can be simulated by MOD_2m gates by repeating every input gate twice. We first observe that AC⁰[2m] ∘THR is indeed typical, and ENC(x) can be computed by poly(n)-uniform, poly(n)-size AC⁰[2m]. To see this, note that the parity function can be easily represented in AC⁰[2m] for all m by repeating each input gate m times and then applying the MOD_2m gate.

By Theorem 8, we know that for all constants d,m there is an ε ∈ (0,1) and a #SAT algorithm running in time $2^{n-n^{{\varepsilon }}}$ for all circuits from class AC⁰[2m] ∘THR of size $\leq 2^{n^{{\varepsilon }}}$ and depth d.

The above properties imply that AC⁰[2m] ∘THR satisfies the preconditions of Theorem 7 and hence Quasi-NP does not have $n^{\log ^{k} n}$-size EMAJ ∘AC⁰[2m] ∘THR circuits of depth d.

The above theorem can be rewritten as: For constants k,d and m, there is an e ≥ 1 such that $\mathsf {NTIME}[n^{\log ^{e} n}]$ does not have $n^{\log ^{k} n}$-size EMAJ ∘AC⁰[m] ∘THR circuits of depth d, where e depends on k,d and m. Using a trick (as in [17]) this dependence can be removed, which proves Corollary 1.

Proof Proof of Corollary 1

Assume for contradiction that for all e, every language in $\mathsf {NTIME}[n^{\log ^{e} n}]$ has poly-sized EMAJ ∘ACC⁰ ∘THR circuits. This implies that CIRCUIT EVALUATION problem (which is in P) has poly-sized EMAJ ∘AC⁰[m₀] ∘THR circuits of a fixed constant depth d₀ and fixed constant m₀. By plugging in a description of any circuit of size s in CIRCUIT EVALUATION, it follows that every circuit of size s has an equivalent poly(s)-sized EMAJ ∘AC⁰[m₀] ∘THR circuit of depth d₀. Therefore our assumption implies that for all e, $\mathsf {NTIME}[n^{\log ^{e} n}]$ has poly-sized EMAJ ∘AC⁰[2m₀] ∘THR circuit of depth d₀. This contradicts Theorem 9, which completes the proof.

5 Extension to All Sparse Symmetric Functions

Our lower bounds extend to circuit classes of the form $f \circ \mathcal {C}$ where f denotes a family of symmetric functions that only take the value 1 on a small number of slices of the hypercube. Formally, let $f : \{0,1\}^{n} \rightarrow \{0,1\}$ be a symmetric function, and let $g : \{0,1,\ldots ,n\} \rightarrow \{0,1\}$ be its “spectrum” function, where for all x, $f(x) = g({\sum }_{i} x_{i})$ (here, x_i denotes the i-th bit of x). For k ∈{0,1,…,n}, we say that a symmetric function f is k-sparse if |g^− 1(1)| = k. For example, the all-zeroes function is 0-sparse, the all-ones function is n-sparse, and the EMAJ function is 1-sparse.

Theorem 10

Let k < n/2. Every k-sparse symmetric function $f : \{0,1\}^{n} \rightarrow \{0,1\}$ can be represented as an exact majority of n^O(k) ANDs/ORs on k inputs.

Proof

Given a k-sparse f and its spectrum function g, consider the polynomial expression

$$E(x) := \prod\limits_{v \in g^{-1}(1)}\left( \sum\limits_{i} x_{i} - v\right).$$

Then E(x) = 0 whenever f(x) = 1, and E(x)≠ 0 otherwise. Expanding E into a sum of products, we can write E as a multilinear n-variate polynomial of degree at most k, with integer coefficients of magnitude at most n^O(k) (since each v ≤ n). Each monomial with a positive weight s can be viewed as the sum of s ANDs. Each monomial with negative weight − s can be viewed as a sum of a constant plus s ORs (using De Morgan’s laws), where the ORs take in negated x_i’s as inputs. We can therefore write f as the EMAJ of n^O(k) distinct ANDs/ORs on up to k inputs (or their negations).

The above theorem immediately implies that for every k-sparse symmetric function f_m, every circuit with f_m at the output gate can be rewritten as a circuit with an EMAJ of fan-in at most m^O(k) at the output gate (and ANDs/ORs of fan-in up to k below that).

Corollary 2

For every fixed k, and every k-sparse symmetric function family f = {f_n}, Quasi-NP does not have polynomial-size f ∘ACC⁰ ∘THR circuits.

6 NEXP Lower Bounds

In this section, we show how circuit lower bounds for NEXP would follow from weaker algorithmic assumptions. The proof follows the same basic pattern as the proof of lower bound for Quasi-NP in Theorem 7.

6.1 NEXP Lower Bounds

We start with stating the analogue of Theorem 5.

Theorem 11

[23] Suppose for some constant ε ∈ (0,1) there is an algorithm A that for all poly(n)-size circuits C on n inputs, A(C) runs in 2ⁿ/n^ω(1) time, outputs YES on all unsatisfiable C, and outputs NO on all C that have at least 2^n− 1 satisfying assignments. Then $\mathsf {NTIME}[2^{n}] \not \subset \mathsf {P}_{\textsf {/poly}}$.

Next we prove the analogue of Theorem 6 by the same proof technique.

Theorem 12

Suppose there is an algorithm A that for all poly(n)-sized circuits C on n inputs, A(C) runs in 2ⁿ/g(n)^ω(1) time, outputs YES on all unsatisfiable C, and outputs NO on all C that have at least 2ⁿ(1 − 1/g(n)) satisfying assignments, for some time-constructible g(n) satisfying n^ω(1) ≤ g(n) ≤ 2^o(n). Then $\mathsf {NTIME}[2^{n}] \not \subset \mathsf {P}_{\textsf {/poly}}$.

Proof

Our starting point is Theorem 11 [23]: we are given an m-input, poly(m)-size circuit $D^{\prime }$ that is either UNSAT or has at least 2^m− 1 satisfying assignments, and we wish to distinguish between the two cases with a 2^m/m^ω(1)-time algorithm. First, we amplify the gap between the cases. We create a new circuit D with n inputs, where n satisfies

$$n = m + \psi \cdot \log{g(n)},$$

and ψ > 0 is the constant from Lemma 2. (Note that, since g(n) is time constructible and g(n) ≤ 2^o(n), such an n can be found in subexponential time.) The circuit D has the following form:

• D treats its n bits of input as a string of randomness r and computes $t=O(\log g(n))$ strings $x_{1}, x_{2}, \ldots , x_{t} \in \{0,1\}^{m}$ by simulating algorithm “S” in Lemma 2 with a $\text {poly}(m, \log g(n))$-size circuit.

• It computes $\{D^{\prime }(x_{i})\}_{i}$.

• The output is the $\mathsf {OR}(D^{\prime }(x_{1}), D^{\prime }(x_{2}), \ldots , D^{\prime }(x_{t}))$.

Note the total size of our circuit D is $\text {poly}(m,\log g(n)) + O(\log g(n))\cdot \text {size}(D^{\prime }) = \text {poly}(m) = \text {poly}(n)$. Clearly, if $D^{\prime }$ is unsatisfiable, then D is also unsatisfiable. By Lemma 2, if $D^{\prime }$ has 2^m− 1 satisfying assignments, then D has at least 2ⁿ(1 − 1/g(n)) satisfying assignments. As size(D) ≤poly(n), by our assumption we can distinguish the case that D is unsatisfiable from the case that D has at least 2ⁿ(1 − 1/g(n)) satisfying assignments, with an algorithm running in time 2ⁿ/g(n)^ω(1). This yields an algorithm for distinguishing the original circuit $D^{\prime }$ on m inputs and poly(m) size, running in time

$$2^{n}/g(n)^{\omega(1)} = 2^{m}g(n)^{O(1)}/g(n)^{\omega(1)} = 2^{m}/g(n)^{\omega(1)} \leq 2^{m}/n^{\omega(1)} \leq 2^{m}/m^{\omega(1)}$$

since n > m,g(n) = n^ω(1). By Theorem 11, this implies that $\mathsf {NTIME}[2^{n}] \not \subset \mathsf {P}_{\textsf {/poly}}$.

Now we prove the main result of this section, which proves that #SAT algorithms for poly(n)-sized $\mathcal {C}$-circuits running in time 2ⁿ/n^ω(1) imply $\mathsf {EMAJ}\circ \mathcal {C}$ lower bounds.

Theorem 13

Suppose $\mathcal {C}$ is typical, and the parity function has poly(n)-uniform, poly(n)-sized $\mathcal {C}$ circuits. Then for every k, NTIME[2ⁿ] does not have $\mathsf {EMAJ} \circ \mathcal {C}$ circuits of size poly(n), if there is a #SAT algorithm running in time 2ⁿ/w(n) for all poly(n)-sized circuits from class $\mathcal {C}$, where w(n) = n^ω(1).

Let us assume NTIME[2ⁿ] has poly(n)-sized ${\mathscr{H}} = \mathsf {EMAJ} \circ \mathcal {C}$ circuits, which implies $\mathsf {NTIME}[2^{n}] \subset \mathsf {P}_{\textsf {/poly}}$. By Theorem 12, we will derive a contradiction if we can construct a 2ⁿ/g(n)^ω(1) time nondeterministic algorithm that, given a circuit D with n inputs and size m ≤poly(n), can distinguish between:

• 1. YES case: D is unsatisfiable.

• 2. NO case: D has at least $2^{n}\left (1-1/g(n)\right )$ satisfying assignments.

Under the hypothesis, we will give such an algorithm for every g(n) satisfying n^ω(1) ≤ g(n) ≤ w(n)^o(1). Note that as g(n) ≤ w(n)^o(1) we also have g(n) = 2^o(n). Let h(n) be a function such that n^ω(1) ≤ h(n) ≤ g(n)^o(1). Using Lemma 3 we reduce D to independent set instance on G_D (with $k = \log {h(n)}$) over n₂ ≤poly(m,2^O(k)) ≤poly(m,h(n)) ≤poly(h(n)) vertices and edges as h(n) ≥ n^ω(1) and m ≤poly(n). As described in Lemma 3, we also find sets of pairs S_i for every vertex i ∈ [n₂]. Let π_x be the partial assignment which assigns a vertex i to 0 if there exist $(j^{\prime }, b) \in S_{i}$ such that $\text {ENC}_{j^{\prime }}(x) \neq b$ and leaves i unassigned otherwise. By Lemma 3, G_D has the following properties:

• 1. If D(x) = 0 then there is an independent set of size α in G_D(π_x). Further given x we can find this assignment in poly(h(n)) time.

• 2. If D(x) = 1 then all independent sets have size ≤ α/h(n) in G_D(π_x).

This means we need to distinguish between the following two cases:

• 1. YES case: For all x, G_D(π_x) has an independent set of size α.

• 2. NO case: For at most 2ⁿ/g(n) values of x,G_D(π_x) has an independent set of size ≥ α/h(n).

Guessing a Succinct Witness Circuit

As guaranteed by Lemma 3, given an x such that D(x) = 0, we can find the assignment A(x) to G_D which is consistent with π_x and represents an independent set of size α, in poly(h(n)) time. Let A(x,i) denote the assignment to the i^th vertex in A(x). Given x and vertex i ∈ [n₂] we can produce ¬A(x,i) in time poly(h(n)).

Lemma 12

Under the hypothesis, there exists a poly(n)-sized $\mathsf {EMAJ}\circ \mathcal {C}$ circuit U with (x,i) as input representing A(x,i).

Proof

Under the hypothesis, NTIME[2ⁿ] has poly-sized $\mathsf {EMAJ} \circ \mathcal {C}$ circuits. Given x and vertex i ∈ [n₂] in time poly(h(n)) ≤ 2^o(n) we can produce ¬A(x,i). It follows that given x and i ∈ [n₂] we can also produce ¬A(x,i) by a $\text {poly}(n+\log n_{2}) = \text {poly}(n+O(\log h(n))) = \text {poly}(n)$ $\mathsf {EMAJ} \circ \mathcal {C}$ circuit with (x,i) as input.

Our nondeterministic algorithm for GAP-UNSAT begins by guessing U guaranteed by Lemma 12 which is supposed to represent ¬A. Then by the reduction in Lemma 1, we can convert U to a $\mathsf {SUM}^{\geq 0} \circ \mathcal {C}$ circuit R for A(x,i) of size poly(n). Note that if our guess for U is correct, i.e., U = ¬A, then R represents A.

Let the subcircuits of R be R₁,R₂,…,R_t, i.e., $R(x) = {\sum }_{j \in [t]} R_{j}$ where R_j is a (-)$\mathcal {C}$-circuit and t ≤poly(n). The number of inputs to R_j is $n^{\prime } = {\lvert }x{\rvert }+\log {n_{2}}=n+O(\log h(n))$, and the size of R_j is poly(n).

Note that R(x,i) = 0 represents that the i^th vertex is not in the independent set in a solution corresponding to x, while R(x,i) > 0 represents that the i^th vertex is in the independent set in a solution corresponding to x. For all x,i, 0 ≤ R(x,i) ≤ t ≤poly(n).

Verifying that R Encodes Valid Independent Sets

As in Section 4, we need to verify that

$$\sum\limits_{x} R(x, i_{1}) \cdot R(x, i_{2}) = 0.$$

Since $R(x, i) = {\sum }_{j \in [t]} R_{j}(x, i)$, it suffices to verify that

$$\sum\limits_{x} \sum\limits_{j_{1}, j_{2} \in [t]} R_{j_{1}}(x, i_{1}) \cdot R_{j_{2}}(x, i_{2}) = 0$$

Let $R_{j_{1}, j_{2}}(x, i_{1}, i_{2}) = R_{j_{1}}(x, i_{1}) \cdot R_{j_{2}}(x, i_{2})$. Since $\mathcal {C}$ is closed under AND, $R_{j_{1}, j_{2}}$ also has a poly(n) sized (-)$\mathcal {C}$ circuit. Swapping the order of summations, we find that we need to verify

$$\sum\limits_{j_{1}, j_{2} \in [t]} \sum\limits_{x} R_{j_{1}, j_{2}}(x, i_{1}, i_{2}) = 0.$$

For a fixed j₁,j₂, the number of inputs to $R_{j_{1}, j_{2}}$ is ${\lvert }x{\rvert }=n$, and its size is at most poly(n). Hence for a fixed pair of j₁,j₂, we can compute ${\sum }_{x} R_{j_{1}, j_{2}}(x, i_{1}, i_{2})$ using the #SAT algorithm from our assumption, in time 2ⁿ/w(n). Summing over all j₁,j₂ pairs only adds another multiplicative factor of t² = poly(n). This allows us to verify that the edge (i₁,i₂) is satisfied by R.

Checking all edges only adds another multiplicative factor of poly(h(n)). Hence the total running time for verifying that R encodes valid independent sets is still 2ⁿpoly(h(n))/w(n).

Verifying Consistency of the Independent Set Produced by R with π _x (for all x)

As in Section 4, we need to check that

$$\sum\limits_{x \in \{0, 1\}^{n}} \sum\limits_{j \in [t]} (\text{ENC}_{j^{\prime}}(x) \oplus b)R_{j}(x, i) = 0$$

for all $i, (j^{\prime }, b) \in S_{i}$. Note that $R_{j^{\prime }}(x, i)$ has a poly(n)-sized $\mathcal {C}$ circuit. By our assumption, (ENC_j(x) ⊕ b) has a poly(n)-uniform, poly(n)-sized $\mathcal {C}$-circuit. Hence $(\text {ENC}_{j}(x) \oplus b) \cdot R_{j^{\prime }}(x, i)$ has a poly(n)-sized $\mathcal {C}$-circuit as we are given that $\mathcal {C}$ is typical. Moreover, we can construct the $\mathcal {C}$-circuit for $(\text {ENC}_{j}(x) \oplus b) \cdot R_{j^{\prime }}(x, i)$ in poly(n) time as we have already guessed $R_{j^{\prime }}$ and the circuit for ENC_j is poly(n)-uniform.

For fixed $(i, j, j^{\prime })$, $(\text {ENC}_{j^{\prime }}(x) \oplus b) \cdot R_{j}(x, i) \in \mathcal {C}$ has ${\lvert }x{\rvert } = n$ inputs and size at most poly(n). Hence we can use the #SAT algorithm from our assumption to calculate ${\sum }_{x \in \{0, 1\}^{n}} (\text {ENC}_{j^{\prime }}(x) \oplus b)R_{j}(x, i)$, in time 2ⁿ/w(n). Summing over all j ∈ [t] adds another multiplicative factor of poly(n). This allows us to verify the condition for a fixed i and $(j^{\prime }, b) \in S_{i}$.

Enumerating over all $i, (j^{\prime }, b) \in S_{i}$ (${\lvert }{S_{i}}{\rvert } \leq O(n)$ by Theorem 4) only adds another multiplicative factor of poly(h(n)) ⋅ O(n) ≤poly(h(n)) in time. The total running time for verifying consistency with respect to π_x (for all x) is 2ⁿpoly(h(n))/w(n).

Distinguishing Between the YES and NO Cases

As we now know that R represents an independent set, and that R is consistent with π_x, we need to distinguish between:

• 1. YES case: For all x, R(x,⋅) represents an independent set of size α.

• 2. NO case: For at most 2ⁿ/g(n) values of x,R(x,⋅) represents an independent set of size ≥ α/h(n).

We next state an analogous Lemma to Lemma 11. We omit the proof as it is exactly the same.

Lemma 13

For all x such that R(x,⋅) represents an independent set of size a, we have $a \leq {\sum }_{i \in [n_{2}]} R(x, i) \leq at$.

To distinguish between the YES and NO cases, we now compute

$$\sum\limits_{x \in \{0, 1\}^{n}} \sum\limits_{i \in [n_{2}]} R(x, i).$$

We can then distinguish between the YES case and NO case, as follows.

• 1. YES case: For at least 2ⁿ(1 − 1/g(n)) values of x, we have an independent set of size at most α/h(n). By Lemma 13, for such x, ${\sum }_{i \in [n_{2}]} R(x, i) \leq t\alpha /h(n)$. For the rest of the 2ⁿ/g(n) values of x, the independent is at most all vertices in the graph G_D. By Lemma 13, for such values of x, ${\sum }_{i \in [n_{2}]} R(x, i) \leq tn_{2} = \text {poly}(h(n))$. Hence

  $$ \begin{array}{@{}rcl@{}} \sum\limits_{x \in \{0, 1\}^{n}} \sum\limits_{i \in [n_{2}]} R(x, i) &\leq& (2^{n}/g(n)) \cdot \text{poly}(h(n))+ 2^{n}t\alpha/h(n)\\ &\leq& o(2^{n})+2^{n}t\alpha/h(n)~ [\text{As } h(n) = g(n)^{o(1)}]\\ &\leq& o(2^{n})+o(2^{n}\alpha)~ [\text{As } t = h(n)^{o(1)}]\\ &<& 2^{n} \alpha ~[\text{As } \alpha > 1] \end{array} $$

• 2. NO case: For all x ∈{0,1}ⁿ, the independent set is at least of size α. Hence by Lemma 13, the sum is ${\sum }_{x \in \{0, 1\}^{n}} {\sum }_{i \in [n_{2}]} R(x, i) > 2^{n}\alpha$.

All that remains is to determine how to compute ${\sum }_{x \in \{0, 1\}^{n}} {\sum }_{i \in [n_{2}]} R(x, i)$. Since $R(x, i) = {\sum }_{j \in [t]} R_{j}(x, i)$, we can compute

$$\sum\limits_{x \in \{0, 1\}^{n}} \sum\limits_{i \in [n_{2}]} \sum\limits_{j \in [t]} R_{j}(x, i) = \sum\limits_{j \in [t]} \sum\limits_{i \in [n_{2}]} \left( \sum\limits_{x \in \{0, 1\}^{n}} R_{j}(x, i)\right).$$

For a fixed i,j, $R_{j}(x, i) \in \mathcal {C}$ has ${\lvert }x{\rvert } = n$ inputs and size poly(n). Hence we can use the #SAT algorithm from the assumption to calculate ${\sum }_{x \in \{0, 1\}^{n}} R_{j}(x, i)$ in time 2ⁿ/w(n). Doing the summation for all j ∈ [t],i ∈ [n₂] adds another h(n)^o(1)poly(h(n)) = poly(h(n)) multiplicative factor. The running time for distinguishing the YES case and NO case is at most 2ⁿpoly(h(n))/w(n).

In total, our running time is 2ⁿpoly(h(n))/w(n) = 2ⁿ/g(n)^ω(1). By Theorem 12, this yields a contradiction which completes the proof.