Marked Length Spectral determination of analytic chaotic billiards with axial symmetries

Abstract

We consider billiards obtained by removing from the plane finitely many strictly convex analytic obstacles satisfying the non-eclipse condition. The restriction of the dynamics to the set of non-escaping orbits is conjugated to a subshift, which provides a natural labeling of periodic orbits. We show that under suitable symmetry and genericity assumptions, the Marked Length Spectrum determines the geometry of the billiard table.

Appendix A: The Marked Lyapunov Spectrum

In this appendix we collect some rather technical results that are needed for this paper. Some of these results have been stated in the paper [5] in more general settings, but not all proofs appear to be complete. In this work we only need results in the (much simpler) situation in which the scatterers are symmetric: we therefore state and prove such results here, in order for the arguments in this paper to be complete.

Theorem A.1

The Lyapunov exponent of any palindromic periodic orbit in any billiard table in $\mathbf{B}(m)$ is a $\mathcal{MLS}$-invariant.

Lemma A.2

Let $(\bar{s}_{0},\ldots ,\bar{s}_{p-1})$ denote the collision points of a palindromic periodic orbit of (least) period $p = 2q$, so that $\bar{s}_{i} = \bar{s}_{p-i}$ for any $0 < i < p$. For $k \geq 1$, define $L_{k}\colon (s_{0},s_{1},\ldots ,s_{k}) \mapsto \sum _{j = 0}^{k-1}h(s_{j},s_{j+1})$. Then

$$\begin{aligned} L_{q}(s_{0},\ldots ,s_{q}) - L_{q}(\bar{s}_{0},\ldots ,\bar{s}_{q}) &= Q_{q}(s_{0}- \bar{s}_{0},\ldots , s_{q}-\bar{s}_{q}) + R_{q}, \end{aligned}$$

where $Q_{q}$ is a positive definite quadratic form and $R_{q}$ is a remainder term that satisfies the estimate:

$$\begin{aligned} R_{q} = O(\|(s_{0}-\bar{s}_{0},\ldots , s_{q}-\bar{s}_{q})\|^{3}). \end{aligned}$$

Proof

Since $(\bar{s}_{0},\ldots ,\bar{s}_{p-1})$ is palindromic, $L_{q}(s_{0},\ldots ,s_{q})$ has a critical point (in fact, a minimum) at $(\bar{s}_{0},\ldots ,\bar{s}_{q})$; recall in fact that the periodic orbit has necessarily orthogonal collisions at the points $s_{0}$ and $s_{q}$. This amounts to say that $\partial _{j}L_{q}(\bar{s}_{0},\ldots ,\bar{s}_{q}) = 0$ for any $j = 0,\ldots ,q$. Hence the lemma follows from Taylor’s formula, provided that we show that the Hessian of $L_{q}$ at $(\bar{s}_{0},\ldots ,\bar{s}_{q})$ is positive definite. □

From the definition of $L_{q}$, we have $\partial _{0} L_{q}=\partial _{0} h(s_{0},s_{1})$, $\partial _{i} L_{q}=\partial _{1} h(s_{i-1},s_{i})+\partial _{0} h(s_{i},s_{i+1})$, for $0< i< q$, and $\partial _{q} L_{q}=\partial _{1} h(s_{q-1},s_{q})$. It follows that $\partial _{ij}L_{q} = 0$ if $|i-j| > 1$; in other terms, the Hessian of $L_{q}$ is a tridiagonal (symmetric) matrix. For notational convenience, let $h^{ij} = h(\bar{s}_{i},\bar{s}_{j})$; let $\bar{\varphi}_{j}\in [-\frac {\pi }{2},\frac {\pi }{2}]$ denote the angle formed by the outgoing trajectory at the $j$-th collision point and the unit normal vector to the domain at $\bar{s}_{j}$; finally, let $\mathcal{K}_{j}$ denote reciprocal of the radius of curvature at the point $\bar{s}_{j}$. Recall that by convention $\mathcal{K}_{j} > 0$ for any $j$.

A direct computation shows that the diagonal terms are given by:

$$\begin{aligned} \partial _{00} L_{q} &= \frac{1}{h^{01}}\cos ^{2}\bar{\varphi}_{0}+ \mathcal{K}_{0}\cos \bar{\varphi}_{0}, \\ \partial _{jj} L_{q} &= \left [\frac{1}{h^{j-1 j}}+ \frac{1}{h^{j j+1}}\right ]\cos ^{2}\bar{\varphi}_{j}+2\mathcal{K}_{j}\cos \bar{\varphi}_{j}\text{ for } 0 < j < q, \\ \partial _{qq} L_{q} &= \frac{1}{h^{q-1q}}\cos ^{2}\bar{\varphi}_{q}+ \mathcal{K}_{q}\cos \bar{\varphi}_{q}, \end{aligned}$$

while the off-diagonal terms are given by:

$$\begin{aligned} \partial _{jj+1}L_{q} &= \frac{1}{h^{jj+1}}\cos \bar{\varphi}_{j}\cos \bar{\varphi}_{j+1}. \end{aligned}$$

Using the above expressions it is simple to prove the following lemma.

Lemma A.3

For $0 \leq k\leq q$, let $f_{k}$ denote the determinant of the $(k+1)\times (k+1)$ top-left minor of $(\partial _{ij}L_{q})_{i,j}$. Then $f_{k} > 0$ for all $0 \leq k\leq q$.

By Sylvester’s criterion, the above lemma implies that all eigenvalues of $(\partial _{ij}L_{q})_{i,j}$ are positive, which completes the proof of Lemma A.2. □

Proof of Lemma A.3

We will in fact prove a slightly stronger statement which holds for $0 \leq k < q$, namely:

$$\begin{aligned} f_{k} > f_{k-1}\frac{\cos ^{2}\bar{\varphi}_{k}}{h^{k k+1}}, \end{aligned}$$

(A.1)

with the convention $f_{-1} = 1$. The proof will follow by induction. Since the matrix is tridiagonal, it is known that the determinants $f_{k}$ can be expressed by the following recursive relation:

$$\begin{aligned} f_{k} = \partial _{kk}L_{q}f_{k-1}-(\partial _{k-1k}L_{q})^{2}f_{k-2}, \end{aligned}$$

with the convention $f_{-2} = 0$ (recall that $f_{-1} = 1$).

The base case is $f_{0} = \partial _{00}L_{q}$, for which (A.1) immediately holds. Assuming by inductive hypothesis that (A.1) holds for $k-1$, let us prove it for $k$. The recursive relation yields, for $k < q$:

$$\begin{aligned} &f_{k}-f_{k-1}\frac {\cos ^{2}\bar{\varphi}_{k}}{h^{kk+1}} \\ &= f_{k-1} \left (\partial _{kk}L_{q}-\frac{\cos ^{2}\bar{\varphi}_{k}}{h^{kk+1}} \right ) -(\partial _{k-1k}L_{q})^{2}f_{k-2} = \\ &= f_{k-1}\left (\frac{\cos ^{2}\bar{\varphi}_{k}}{h^{k-1k}}+2 \mathcal{K}_{k}\cos \bar{\varphi}_{k}\right ) -\left ( \frac{\cos \bar{\varphi}_{k-1}\cos \bar{\varphi}_{k}}{h^{k-1 k}}\right )^{2}f_{k-2} > \\ &> f_{k-2}\frac{\cos ^{2}\bar{\varphi}_{k-1}}{h^{k-1k}} \frac{\cos ^{2}\bar{\varphi}_{k}}{h^{k-1k}} +2f_{k-1}\mathcal{K}_{k} \cos \bar{\varphi}_{k}-\left ( \frac{\cos \bar{\varphi}_{k-1}\cos \bar{\varphi}_{k}}{h^{k-1k}}\right )^{2}f_{k-2} > \\ &> 2f_{k-1}\mathcal{K}_{k}\cos{\bar{\varphi}_{k}} > 0. \end{aligned}$$

This shows the statement for up to $k = q-1$; an analogous computation then shows that also

$$ f_{q}>\frac{1}{h^{q-1 q}}\mathcal{K}_{q} \cos \bar{\varphi}_{q} \cos ^{2} \bar{\varphi}_{q-1}> 0, $$

which concludes the proof of our lemma. □

Lemma A.4

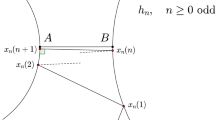
Let $\sigma = (\sigma _{0}\cdots \sigma _{q-1})$ with $\sigma _{i} = \sigma _{q-i}$ encode a palindromic periodic orbit of period $q$ and Lyapunov exponent $\mathrm{LE}(\sigma )=-\frac{1}{q}\log \lambda$, $\lambda =\lambda (\sigma )$ being the contracting eigenvalue of $D\mathcal{F}^{q}$ at $\sigma$; let $\tau$ (of length $p$) be so that both $\sigma \tau$ and $\tau \sigma$ are admissible. Let $h_{n}(\sigma ,\tau )$ denote the periodic orbit encoded by $(\tau \sigma ^{n})$ of period $p+nq$. There exist $C_{0}(\sigma ,\tau )\in {\mathbb{R}}$ and $C_{1}(\sigma ,\tau )\neq 0$ so that:

$$\begin{aligned} \mathcal {L}(h_{n}(\sigma ,\tau )) - n\mathcal {L}(\sigma )&= C_{0}(\sigma ,\tau ) +C_{1}(\sigma ,\tau )\lambda ^{n} +o(\lambda ^{n}). \end{aligned}$$

(A.2)

Proof

The existence of $C_{0}(\sigma ,\tau )$ follows by the same arguments used in the definition of $\mathcal{L}^{\infty}$ (see also Proposition 3.1). Obtaining the remaining terms follows step-by-step by the proof of Proposition 6.1, where it is proved in the special case $\sigma = (12)$ and $\tau = (32)$, and obtains an explicit expression for the coefficient $C_{1}((12),(32))$, which we do not need in this lemma. It is omitted in the interest of keeping the length of this paper under control. The important point is that the coefficient $C_{1}(\sigma ,\tau )$ does not vanish, which comes from the fact that the quadratic form in Lemma A.2 is positive definite. □

Proof of Theorem A.1

Using Lemma A.4, and taking the limit of (A.2) for $n\to \infty$, we conclude that $C_{0}(\sigma ,\tau )$ is a $\mathcal{MLS}$-invariant, since the left hand side is spectrally determined. Hence, again by (A.2), and as $C_{1}(\sigma ,\tau )\neq 0$, we gather:

$$\begin{aligned} \lambda = \lim _{n\to \infty} \frac{1}{n}\log |\mathcal {L}(h_{n}( \sigma ,\tau ))- n\mathcal {L}(\sigma ) - C_{0}(\sigma ,\tau )|. \end{aligned}$$

Since the right hand side is spectrally determined, we conclude that $\lambda$ is $\mathcal{MLS}$-invariant. Similar considerations show that $C_{1}(\sigma ,\tau )$ is also $\mathcal{MLS}$-invariant. □

Theorem A.1 has the following immediate corollary:

Theorem A.5

Let $\mathcal{D}\in \mathbf{B}_{\mathrm{sym}}(m)$; consider the 2-periodic orbit encoded by the word $\sigma = (12)$ and let $R=\mathcal{K}^{-1}$ be the (common) curvature radius at the collision points of the orbit. Then $R$ is a $\mathcal{MLS}$-invariant.

Proof

By Theorem A.1, the Lyapunov exponent $\mathrm{LE}(\sigma )$ of the 2-periodic orbit is a $\mathcal{MLS}$-invariant. Hence, ${\mathcal{MLS}}(D)$ determines the eigenvalues of the linearization of the square of the billiard map $D\mathcal {F}^{2}$ at the collision points of the 2-periodic orbit; by (2.2) we have

$$\begin{aligned} D\mathcal{F}^{2}_{(0,0)} = \left ( \textstyle\begin{array}{c@{\quad}c} \mathscr{L}\mathcal {K}+1& \mathscr{L} \\ \mathscr{L}\mathcal {K}^{2} + 2\mathcal {K}& \mathscr{L} \mathcal {K}+1 \end{array}\displaystyle \right )^{2}, \end{aligned}$$

where $\mathscr{L}:=\frac {1}{2} \mathcal {L}((12))$. In particular, we have that $\lambda ^{1/2}+\lambda ^{-1/2} = 2(\mathscr{L}\mathcal {K}+1)$; since it is of course spectrally determined, we conclude that $R=\mathcal {K}^{-1}$ is $\mathcal{MLS}$-invariant. □

Remark A.6

Theorem A.1 also holds for non-palindromic orbits. It must be noted that in the general case there is no analog of Lemma A.3, since there is no sub-orbit contained in a periodic orbit that is a length minimizer (otherwise we would have an orthogonal collision, which would force the orbit to be palindromic). Because of this, one needs to show an additional cancellation for $\Sigma ^{1}_{n}$ and $\Sigma ^{2}_{n}$; the proofs are marginally more involved but, in the interest of keeping this paper short but self-contained, we have only stated the result in the palindromic case.