Abstract
For a smooth variety Y over a perfect field of positive characteristic, the sheaf \(D_Y\) of crystalline differential operators on Y (also called the sheaf of PD-differential operators) is known to be an Azumaya algebra over \(T^*_{Y'},\) the cotangent space of the Frobenius twist \(Y'\) of Y. Thus to a sheaf of modules M over \(D_Y\) one can assign a closed subvariety of \(T^*_{Y'},\) called the p-support, namely the support of M seen as a sheaf on \(T^*_{Y'}.\) We study here the family of p-supports assigned to the reductions modulo primes p of a holonomic \(\mathcal {D}\)-module. We prove that the Azumaya algebra of differential operators splits on the regular locus of the p-support and that the p-support is a Lagrangian subvariety of the cotangent space, for p large enough. The latter was conjectured by Kontsevich. Our approach also provides a new proof of the involutivity of the singular support of a holonomic \(\mathcal {D}\)-module, by reduction modulo p.
We’re sorry, something doesn't seem to be working properly.
Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.
Avoid common mistakes on your manuscript.
1 Introduction
Let Y be a smooth variety over a perfect field. We may consider two sheaves of differential operators on Y : on the one hand the sheaf \(D^{(\infty )}_Y\) constructed by Grothendieck in EGA IV and on the other the sheaf \(D_Y\) of crystalline differential operators, also called the sheaf of PD-differential operators, see e.g. [6] and [4]. These sheaves coincide if the base field is of characteristic zero but they are very different if it is of positive characteristic. For example, \(D^{(\infty )}_Y\) is typically a centerless sheaf of non-Noetherian rings. But \(D_Y\) has a large center canonically identified with the symmetric algebra of the tangent sheaf of the Frobenius twist \(Y'\) of Y. And it is an Azumaya algebra over it, by [6].
Thus to a coherent sheaf of modules M over \(D_Y\) one can assign a closed subvariety of the cotangent space \(T^*_{Y'}\) called the p-support, see Definition 2.1.4. Namely it is the support of M seen as a sheaf on \(T^*_{Y'}.\) One might hope that the p-support is analogous to the classical notion of singular support of a say complex \(\mathcal {D}\)-module. The results of this paper confirm this hope. Note however that without further restrictions on M, the p-support is arbitrary. Indeed every closed subvariety Z of \(T^*_{Y'}\) is the p-support of the quotient of \(D_Y\) by the corresponding ideal \(I_Z\) of its center.
We consider here the reductions of a holonomic \(\mathcal {D}\)-module modulo large primes. That is to say, let S be an integral scheme dominant and of finite type over \({\text {Spec}}{\mathbb {Z}},\) for example the spectrum of the ring of integers of a number field, let X be a smooth S-scheme of relative dimension n. Then for \(\mu \) the generic point of S and for any closed point s of S, the generic fiber \(X_\mu \) is a smooth variety over a field of characteristic zero while the fiber \(X_s\) is a smooth variety over a field of positive characteristic. Let \(D_{X/S}\) be the sheaf of relative crystalline differential operators and let M be a coherent left \(D_{X/S}\)-module. Suppose that the generic fiber \(M_\mu \) of M is a nonzero holonomic \(D_{X_\mu }\)-module. For every closed point s of S, we let \(M_s\) be the fiber of M over s. Our main results are:
-
(a)
(Theorem 3.1.1) There is an open dense subset \(U\subset S\) such that for all closed points s of U, the p-suppport of \(M_s\) is equidimensional of dimension n.
-
(b)
(Theorem 4.3.3) Suppose that \(X= \mathbb {A}^n_S\) with coordinates \(\{x_1, \dots , x_n\}.\) For all closed points s of S of characteristic p, consider the embedding of the twisted cotangent space \(T^*_{X_s'}\) in \(\mathbb {P}^{2n}_{k(s)}\) associated to the Rees ring of the filtration of \(k(s)[x_1^p, \dots , x_n^p, \partial _1^p, \dots , \partial _n^p]\) by the degree of k(s)-polynomials in the variables \(\{x_1^p, \dots , x_n^p, \partial _1^p, \dots , \partial _n^p\},\) each of which is of degree 1 (see Definition 4.2.1 and Proposition 4.3.1). Then there is a dense open subset \(U \subset S\) such that, for all closed points s of S and for every generic point z of an irreducible component of the p-support of \(M_s\) of closure \(\overline{\{z\}}\) in \(\mathbb {P}^{2n}_{k(s)},\) one has
$$\begin{aligned} \deg (\overline{\{z\}})\le e(M_\mu ), \ \mathrm {rk}_z(M_s)\le e(M_\mu )p^n, \end{aligned}$$where \(e(M_\mu )\) is the multiplicity of \(M_\mu \) for the Bernstein filtration of the Weyl algebra \(A_n(k(\mu ))\) (see Definition 4.1.4), \(\mathrm {rk}_z(M_s):=\dim _{k(z)}({(F_*M_s)}_z\otimes k(z))\) and \(\deg (\overline{\{z\}})\) is the degree of the reduced closure of the image of z in \(\mathbb {P}^{2n}_{k(s)}.\)
-
(c)
(Theorem 5.1.4) There is an open dense subset \(U\subset S\) such that for all closed points s of U, the Azumaya algebra \(F_*D_{X_s}\) splits on the regular locus of the p-support of \(M_s,\) where \(X_s \xrightarrow {F} X_s'\) is the Frobenius.
-
(d)
(Theorem 2.2.1) There is an open dense subset \(U\subset S\) such that for all closed points s of U, the p-support of \(M_s\) is a Lagrangian subvariety of \(T^*_{X_s'}.\)
Finally as a corollary of (d), which may be seen as the main result of the paper, we give a new proof that the singular support of a holonomic \(\mathcal {D}\)-module is a Lagrangian subvariety of the cotangent space, by reduction modulo p, see Corollary 6.3.1.
The statements (a) and (d) are the first essential steps in a comprehensive program of study of the geometry of the p-supports of a holonomic \(\mathcal {D}\)-module as p varies, outlined by Kontsevich in [29].
The geometry of the p-supports of a given module is very rich indeed. They need neither be conical nor come by reduction modulo p from an invariant defined over \({\text {Spec}}{\mathbb {Z}},\) and are closely related to the p-curvatures of the \(\mathcal {D}\)-module. Let us illustrate this with a couple examples:
-
(1)
Let \(S={\text {Spec}}{\mathbb {Z}},\)\(X=\mathbb {A}^n_{S}\) and let M be the finitely generated left \(D_{X/S}\)-module corresponding to the integrable connection \(\nabla =d+dg\) on \(\mathcal {O}_X,\) where g is a global section of \(\mathcal {O}_X.\) From the identity \((\partial _i+\partial g/\partial x_i)^p=(\partial _i)^p+(\partial g/\partial x_i)^p\) in \(A_n(\mathbb {Z}/p\mathbb {Z})\) [27, 5.2.4] follows that the p-support of \(\mathbb {Z}/p\mathbb {Z}\otimes _{\mathbb {Z}}M\)\(\subset T^*_{(\mathbb {A}^{n}_{\mathbb {Z}/p\mathbb {Z}})'}=T^*_{\mathbb {A}^n_{\mathbb {Z}/p\mathbb {Z}}}\) is the graph of dg modulo p. Thus the p-supports are not necessarily conical.
-
(2)
Let \(\mathbb {Z}[\lambda ]\) be the subring of \(\mathbb {C}\) generated by \(\lambda \in \mathbb {C}\) and \(S= {\text {Spec}}\mathbb {Z}[\lambda ].\) Let \(X={\text {Spec}}\mathbb {Z}[\lambda ][x,x^{-1}]=\mathbb {A}^1_S-\{0\}\subset \mathbb {A}^1_S={\text {Spec}}\mathbb {Z}[\lambda ][x].\) Consider the finitely generated left \(D_{X/S}\)-module M corresponding to the integrable S-connection \(\nabla =d+\lambda ~dx/x\) on \(\mathcal {O}_X.\) The identity \((x\partial )^p=x^p\partial ^p+x\partial \) in \(A_1(\mathbb {Z}/p\mathbb {Z})\) [22, Lemma 1] implies that for each closed point s of S of positive characteristic p, the p-support of \(M_s,\)p-supp(\(M_s\)) \(\subset T^*_{X'_s}\subset T^*_{\mathbb {A}^{1'}_{k(s)}}=T^*_{\mathbb {A}^1_{k(s)}}\) is given by the equation \(xy=\lambda ^p-\lambda \) (\(\mathrm {mod}\)p), where y is the global section of \(\mathcal {O}_{T^*_{\mathbb {A}^1_{k(s)}}}\) corresponding to dx. Thus if \(\lambda \) is not rational, then the p-supports depend nontrivially on p.
1.1 Survey of the proofs
Let us now comment on the proofs of (a)–(d) above. This will also serve as a description of the contents of the paper.
Since pure coherent sheaves have equidimensional supports, we prove (a) by showing that \(F_*M_s\) is a pure coherent sheaf of dimension n on \(T^*_{X'_s},\) for all closed points s of a dense open subset \(S_1\) of S. For which we use the following criterion, see Theorem 3.2.3: \(\forall l\ne n\) and \(\forall s\in S_1,\)
The vanishing of \(\mathcal {E} xt ^l_{D_{X_s}}(\mathcal {E} xt ^l_{D_{X_s}}(M_s, D_{X_s}), D_{X_s}), \forall l\ne n\) follows from the well-known duality property of holonomic \(D_{X_\mu }\)-modules by specialization of \(M_\mu \) (Proposition 3.3.4). One then checks the criterion using that \(F_*D_{X_s}\) is an Azumaya algebra on \(T^*_{X'_s}\) (Proposition 3.3.5). This concludes the proof of (a). Note that we also prove along the way that if Y is a smooth variety over a perfect field of positive characteristic, then the dimensions of a coherent \(D_Y\)-module as a \(D_Y\)-module and as a coherent module over the center of \(D_Y\) are equal (Proposition 3.3.5).
We show in Sect. 2.4 that the proof of the main theorem (d) reduces to \(X/S = \mathbb {A}^n_S/S.\) In this case we prove that for all closed points s of a dense open subset \(S_2\) of \(S_1,\) each irreducible component of the p-support \(p\text {-}supp(M_s)\) of \(M_s\) contains a dense smooth open subset U which is a certain specialization of the complement Y of a divisor with normal crossings D in a smooth projective variety over a field of characteristic zero. More precisely there are an irreducible scheme H of generic point \(\gamma \) of characteristic zero, a smooth H-scheme \(\Upsilon \) and a closed point \(h\in H\) such that \(\Upsilon _h=U\) and \(\Upsilon _\gamma =Y.\) Moreover we show that there is a differential 1-form \(\nu \) on Y such that \(d\nu \) has logarithmic poles along D and the restriction of the symplectic form to U is the specialization at h of \(d\nu .\) But by Hodge theory ([13, Corollaire 3.2.14]) such a \(d\nu \) has to vanish. Finally by our choice of \(\Upsilon \) this implies that the symplectic form vanishes on U. Thus the symplectic form vanishes on a dense open subset of the p-support and since the p-support is equidimensional of dimension n by (a), it is a Lagrangian subvariety of \(T^*_{(\mathbb {A}_{k(s)}^{n})'}.\)
Let us now give more details of how this is achieved. The starting point of the proof are the estimates of (b). We verify them as follows. Let \(\Gamma \) be a good filtration of M, see Definition 3.3.1. Then for all closed points s of a dense open subset \(S_3\) of \(S_2,\)\(\Gamma \) specializes to a good filtration \(\Gamma _s\) of \(M_s\) such that its Hilbert polynomial is equal to that of the good filtration \(\Gamma _\mu \) of the (characteristic zero) \(D_{X_\mu }\)-module \(M_\mu \) (Lemma 4.1.5). In particular, the degree of this Hilbert polynomial is the dimension m of the singular support of \(M_\mu \) and its leading coefficient is \(m!e(M_\mu ).\) We then show that to a good filtration \(\Gamma _s\) of \(M_s\) is associated a good filtration \(p\Gamma _s\) of \(M_s\) as a module over the center of \(A_n(k(s))\) with the Bernstein filtration (Lemma 4.2.6). The Hilbert polynomial of \(p\Gamma _s\) is of degree m and its leading coefficient is \(m!e(M_\mu )p^m\) (Proposition 4.2.7). Thus the coherent sheaf on \(\mathbb {P}_{k(s)}^{2n}\) corresponding to the Rees module of \(p\Gamma _s\) is of dimension m and degree \(e(M_\mu )p^m.\) It then follows from intersection theory that \(\Sigma _z \mathrm {rk}_z(M_s)\deg (\overline{\{z\}}) \le e(M_\mu )p^m,\) where the sum is over the generic points of the (top-dimensional) irreducible components of the p-support of \(M_s\) (Proposition 4.3.2). This gives the estimate of the ranks since \(m = n\) by assumption that \(M_\mu \) is holonomic. But \(F_*M_s\) is a module over an Azumaya algebra of rank \(p^{2n},\) thus by Morita theory the ranks \(\mathrm {rk}_z(M_s)\) are divisible by \(p^n.\) This gives the estimate of the degrees and concludes the proof of (b). Note that it also proves an estimate of the number of irreducible components of \(p\text {-}supp(M_s),\) namely \(\le e(M_\mu ).\) Let us remark that if we relaxed the holonomicity assumption on \(M_\mu \) we would obtain an estimate \(\le e(M_\mu )p^{m-n}\) of the degrees of the top-dimensional irreducible components and it is only in the holonomic case \(m=n\) that we get a bound independent of the prime p. This is crucial in what follows.
We consider an open embedding \(T_{\mathbb {A}_{S_3}^n}^* \hookrightarrow \mathbb {P}_{S_3}^{2n}\) which specializes at every closed point s of \(S_3\) to the open embedding of \(T^*_{({\mathbb {A}_{k(s)}^{n}})'}= T^*_{\mathbb {A}_{k(s)}^n}\) in \(\mathbb {P}^{2n}_{k(s)}\) from (b). Let \(\mathcal {H}\) be the Hilbert scheme of closed subschemes of \(\mathbb {P}_{S_3}^{2n}\) of dimension n and degree \(\le e(M_\mu ).\) Provided the estimate of the degrees of the irreducible components of the p-support of (b), all of dimension n by (a), we see that for all closed points \(s\in S_3,\) the closure in \(\mathbb {P}^{2n}_{k(s)}\) of each irreducible component of \(p\text {-}supp(M_s)\) corresponds to a closed point of \(\mathcal {H}.\) This allows us to use \(\mathcal {H}\) to show that there is an integer \(N_1>0\) such that for \(S_4= S_3[\frac{1}{N_1}]\) the following is satisfied. For each irreducible component Z of \(p\text {-}supp(M_s)\) for s a closed point of \(S_4,\) there is an open embedding  where \(U\subset Z\) is a dense smooth open subset and \(\overline{U}\) is a smooth projective variety over k(s) such that the complement of j is a divisor with normal crossings D. Indeed let \(\mathcal {Z}_{\mathcal {H}} \subset \mathbb {P}_{\mathcal {H}}^{2n}\) be the universal closed subscheme. By the resolution of singularities in characteristic zero, neglecting finitely many positive characteristics \(\{p_1,\dots , p_r\}\) with \(p_1\dots p_r = N_1,\) we have a finite partition of the open subset of the Hilbert scheme \(\mathcal {H}[\frac{1}{N_1}]\) into irreducible subschemes generically of characteristic zero \((\mathcal {H}_i)\) and above each \(\mathcal {H}_i\) an open embedding \(\mathcal {Y}\hookrightarrow \overline{\mathcal {Y}}\) with complement \(\Delta \) a divisor with normal crossings relative to \(\mathcal {H}_i,\) where \(\mathcal {Y}\) is the smooth locus of the intersection \(\mathcal {Z}_{\mathcal {H}}|_{\mathcal {H}_i}\cap T_{\mathbb {A}_{\mathcal {H}_i}^n}^*\subset \mathbb {P}_{\mathcal {H}_i}^{2n}\) and \(\overline{\mathcal {Y}}\) is a smooth projective \(\mathcal {H}_i\)-scheme (Proposition 6.1.4). Let z be the closed point of the Hilbert scheme \(\mathcal {H}\) corresponding to the closure in \(\mathbb {P}_{k(s)}^{2n}\) of the irreducible component Z of \(p\text {-}supp(M_s)\) and suppose that \(z\in \mathcal {H}_i.\) Then we set
where \(U\subset Z\) is a dense smooth open subset and \(\overline{U}\) is a smooth projective variety over k(s) such that the complement of j is a divisor with normal crossings D. Indeed let \(\mathcal {Z}_{\mathcal {H}} \subset \mathbb {P}_{\mathcal {H}}^{2n}\) be the universal closed subscheme. By the resolution of singularities in characteristic zero, neglecting finitely many positive characteristics \(\{p_1,\dots , p_r\}\) with \(p_1\dots p_r = N_1,\) we have a finite partition of the open subset of the Hilbert scheme \(\mathcal {H}[\frac{1}{N_1}]\) into irreducible subschemes generically of characteristic zero \((\mathcal {H}_i)\) and above each \(\mathcal {H}_i\) an open embedding \(\mathcal {Y}\hookrightarrow \overline{\mathcal {Y}}\) with complement \(\Delta \) a divisor with normal crossings relative to \(\mathcal {H}_i,\) where \(\mathcal {Y}\) is the smooth locus of the intersection \(\mathcal {Z}_{\mathcal {H}}|_{\mathcal {H}_i}\cap T_{\mathbb {A}_{\mathcal {H}_i}^n}^*\subset \mathbb {P}_{\mathcal {H}_i}^{2n}\) and \(\overline{\mathcal {Y}}\) is a smooth projective \(\mathcal {H}_i\)-scheme (Proposition 6.1.4). Let z be the closed point of the Hilbert scheme \(\mathcal {H}\) corresponding to the closure in \(\mathbb {P}_{k(s)}^{2n}\) of the irreducible component Z of \(p\text {-}supp(M_s)\) and suppose that \(z\in \mathcal {H}_i.\) Then we set  where \(\mu _i\) is the generic point of \(\mathcal {H}_i\) and \(\theta _{\mathcal {H}}\) is the canonical 1-form on \(T_{\mathbb {A}_{\mathcal {H}}^n}^*.\)
where \(\mu _i\) is the generic point of \(\mathcal {H}_i\) and \(\theta _{\mathcal {H}}\) is the canonical 1-form on \(T_{\mathbb {A}_{\mathcal {H}}^n}^*.\)
We have that the restriction \(\omega |_U\) to U of the symplectic form \(\omega \) on \(T^*_{({\mathbb {A}_{k(s)}^{n}})'}\) is equal to the restriction of the exterior derivative \(d\theta _{\mathcal {H}}\) to the fiber \(\mathcal {Y}_z.\) Moreover the partition of \(\mathcal {H}\) into \((\mathcal {H}_i)\) is such that if \((d\theta _{\mathcal {H}}|_{\mathcal {Y}})_{\mu _i}=0,\) then \(d\theta _{\mathcal {H}}|_{\mathcal {Y}}=0\) and if there is a closed point z of \(\mathcal {H}_i\) such that \((d\theta _{\mathcal {H}}|_{\mathcal {Y}})_z\) has logarithmic poles along \(\Delta _z,\) then \((d\theta _{\mathcal {H}}|_{\mathcal {Y}})_{\mu _i}\) has logarithmic poles along \(\Delta _{\mu _i}\) (Proposition 6.1.4). Thus to prove the main theorem (d) it is enough to show that there exists a dense open subset \(S_5\subset S_4\) such that for all closed points \(s\in S_5\) and for each irreducible component Z of \(p\text {-}supp(M_s),\) the restriction of the symplectic form \(\omega |_U\) has logarithmic poles along D, where U and D are constructed above. To do so we first show that \(\theta _{\mathcal {H}}|_U\) is locally in the image of the p-curvature operator \(W^*-C_U,\) see Definition 5.2.2. And then that if a 1-form \(\eta \) is locally in the image of the p-curvature operator (and has poles along D of order at most \(p-1,\) which \(\theta _{\mathcal {H}}|_U\) has for all large enough characteristic p), then it has logarithmic poles along D (Proposition 6.2.2).
The proof that \(\theta _{\mathcal {H}}|_U\) is locally in the image of the p-curvature operator goes as follows. There is a morphism \(\Omega _U^1 \xrightarrow {\phi _U} Br(U)\) with values in the Brauer group (arising from the p-curvature exact sequence, see Definition 5.2.4) such that \(\phi _U(\theta _{\mathcal {H}}|_U)\) is the class of the Azumaya algebra \(F_*D_{\mathbb {A}_{k(s)}^n}|_U\) (Proposition 5.2.9) and the kernel of \(\phi _U\) is the space of 1-forms locally in the image of the p-curvature operator (Proposition 5.2.7). We thus are left to show that \(F_*D_{\mathbb {A}_{k(s)}^n}\) splits on the regular locus of each irreducible component of \(p\text {-}supp(M_s).\) This amounts to the splitting of the central simple algebra \(\mathcal {A}_z:= (F_*D_{\mathbb {A}_{k(s)}^n})_z\otimes k(z)\) for each irreducible component Z of \(p\text {-}supp(M_s)\) of generic point z. Note that this is equivalent to (c) in the case \(X/S= \mathbb {A}_S^n/S.\) (From which the general case follows, see the proof of Theorem 5.1.4.) But by the estimate of the ranks in (b) we have that this central simple algebra has a representation of dimension \(\le e(M_\mu )p^n\) and thus that \(e[\mathcal {A}_z]=0\) for some \(e\le e(M_\mu )\) (Lemma 5.1.1). Moreover \(\mathcal {A}_z\) is of rank \(p^{2n},\) thus \(p^n[\mathcal {A}_z]=0.\) Hence for p large enough, since e and \(p^n\) are coprime, we have \([\mathcal {A}_z]=0.\) We thus see that there exists an integer \(N_2>0\) such that \(S_5=S_4[\frac{1}{N_2}]\) has the required properties. This concludes the proofs of (c) and (d).
Let us mention that provided (a)–(c), one may also prove (d) by adapting the arguments of [15], as explained in [33]. Our original approach presented here has, among other things, the advantage of being independent of [15], providing in particular a new, more geometric insight into the classical involutivity theorem.
Note finally that for the reader’s convenience we have included an “Appendix” on the (algebraic) symplectic geometry of the cotangent space.
1.2 Conventions
Schemes are assumed to be Noetherian, positive characteristics to be nonzero and morphisms of algebras to preserve the identity element. For X / S a scheme, \(s\in S\) and \({\text {Spec}}k(s) \xrightarrow {i} S\) the corresponding point, we let \(X_s/{\text {Spec}}k(s)\) be the fiber of X / S at s, that is the base-change of X / S by i. If M is a coherent left \(D_{X/S}\)-module, we denote by \(M_s\) the left \(D_{X_s/{\text {Spec}}k(s)}\)-module \(k(s)\otimes _{\mathcal {O}_S}M,\) the restriction of M to the fiber \(X_s/{\text {Spec}}k(s).\) When there is no risk of confusion, we denote the fiber by \(X_s\) (instead of \(X_s/{\text {Spec}}k(s)\)) and \(D_{X_s/{\text {Spec}}k(s)}\) by \(D_{X_s}.\) As a general rule, if there is no risk of confusion we omit the base scheme S from the notation if S is the spectrum of a field. Local coordinates of a smooth scheme X / S mean local étale relative coordinates in the neighborhood of a closed point of X. If Y is a scheme over a field k of positive characteristic, we denote \(Y'\) its base-change by the Frobenius endomorphism of k. A reduced scheme over a field is called a variety. As a rule we define notions and state results for left modules, we often omit to mention that they easily adapt to right modules.
2 Statement of the main result and general reductions in its proof
2.1 Preliminary definitions and notations
Let S be a scheme, X be a smooth S-scheme of relative dimension n and let \(T_{X/S}\) be the tangent sheaf.
Definition 2.1.1
The sheaf of crystalline differential operators \(D_{X/S}\) on X / S is the enveloping algebra \(U_{\mathcal {O}_X}(T_{X/S})\) of the Lie algebroid \((T_{X/S}, [-,-]),\) where \([-,-]\) is the Lie bracket on \(T_{X/S}.\)
Thus \(D_{X/S}\) is generated by the structure sheaf \(\mathcal {O}_X\) and the tangent sheaf \(T_{X/S}\), subject to relations \(f.\partial =f\partial ,\ \partial .f-f.\partial =\partial (f)\) and \(\partial .\partial '-\partial '.\partial =[\partial ,\partial '],\) for all f (resp. \(\partial , \partial '\)) local sections of \(\mathcal {O}_X\) (resp. \(T_{X/S}\)). Note that the formation of \(D_{X/S}\) commutes with base-change \(S'\rightarrow S.\) Moreover if S is the spectrum of a field of characteristic 0, then \(D_{X/S}\) is the usual sheaf of algebraic differential operators on X. When S is the spectrum of a field, we often omit the base S from the notations.
We now briefly discuss the coherence of \(D_{X/S}.\) Left multiplication by \(\mathcal {O}_X\) makes \(D_{X/S}\) into an \(\mathcal {O}_X\)-module and one sees in local coordinates that \(D_{X/S}\) is quasi-coherent. Further using local coordinates, one easily checks the following:
Proposition 2.1.2
The sheaf of rings \(D_{X/S}\) has a natural filtration \(D_{X/S}= \bigcup _{m\ge 0} D_{X/S,\le m}\), defined by \(D_{X/S,\le 0}:=\mathcal {O}_X\) and \(D_{X/S,\le m+1}:=T_{X/S}. D_{X/S, \le m}+D_{X/S,\le m}\), whose associated graded sheaf of rings \(grD_{X/S}\) is canonically isomorphic to \(\mathcal {O}_{T^*_{X/S}}\), the structure sheaf of the cotangent space of X / S.
Therefore by [2, Corollaires 2.2.5 and 3.1.2], \(D_{X/S}\) is a sheaf of coherent Noetherian rings. By [2, Proposition 3.1.3], coherent \(D_{X/S}\)-modules have the following properties:
Proposition 2.1.3
-
(1)
A left \(D_{X/S}\)-module is coherent if and only if it is quasi-coherent as an \(\mathcal {O}_X\)-module and its module of sections over any open of an affine covering is a finitely generated left module over the ring of sections of \(D_{X/S}.\)
-
(2)
Assume that X is affine. Then the functor of global sections is an equivalence from the category of coherent left \(D_{X/S}\)-modules to the category of finitely generated left modules over the global sections of \(D_{X/S}.\)
Let Y be a smooth variety of pure dimension n over a perfect field k of positive characteristic p. We denote the relative Frobenius morphism by \(Y \xrightarrow {F} Y'.\) Let \(D_Y:= D_{Y/{\text {Spec}}(k)}\) and \(T_Y:= T_{Y/{\text {Spec}}(k)}.\) Recall that by [6, Lemma 1.3.2], the \(\mathcal {O}_{Y'}\)-linear map \(T_{Y'} \xrightarrow {c'} F_*D_Y\) sending \(\partial \) to \(\partial ^p-\partial ^{[p]},\) where \(\partial \) is a local section of \(T_{Y'}\) and \(\partial ^{[p]}\) is its p-th power in \(T_{Y'},\) lands in the center and induces an isomorphism
with \(Z(D_Y)\) the center of \(D_Y.\) We will thus consider \(F_*D_Y\) as an \(\mathcal {O}_{T^*_{Y'}}\)-algebra. Furthermore, by [6, Theorem 2.2.3], \(F_*D_Y\) is an Azumaya algebra over \(T^*_{Y'}.\) In particular, it is a coherent sheaf on \(T^*_{Y'}.\) Hence if M be a coherent left \(D_Y\)-module, then \(F_*M\) is a coherent \(\mathcal {O}_{T^*_{Y'}}\)-module.
We now introduce our main object of study:
Definition 2.1.4
Let M be a coherent left \(D_Y\)-module. The p-support of M is the support of the coherent \(\mathcal {O}_{T^*_{Y'}}\)-module \(\mathcal {M}\) deduced from the direct image \(F_*M,\) using the isomorphism c. It is a closed subset p-supp(M) of \(T^*_{Y'}\), which we endow with its reduced subscheme structure.
Remark 2.1.5
Note that the p-support commutes with étale localization on Y.
Remark 2.1.6
The schematic support of \(\mathcal {M}\) is a not necessarily reduced subscheme of \(T^*_{Y'},\) refining the p-support of M. We do not explore this notion further here.
2.2 The statement
If X is an S-scheme, M a left \(D_{X/S}\)-module and s a point of S, we denote by \(X_s\) the fiber of X at s and by \(M_s\) the left \(D_{X_s}\)-module deduced from M by base-change. We refer to the “Appendix” for the definitions of symplectic form \(\omega \) on the cotangent space (Definition A.0.4) and Lagrangian subvariety (Definition A.0.5). Our main result is the following:
Theorem 2.2.1
Let S be an integral scheme dominant and of finite type over \(\mathbb {Z},\) of generic point \(\mu .\) Let X be a smooth S-scheme of relative dimension n and let M be a coherent left \(D_{X/S}\)-module. Suppose that \(M_\mu \) is a nonzero holonomic left \(D_{X_\mu }\)-module, then there is a dense open subset U of S such that the p-support of \(M_u\) is a Lagrangian subvariety of \((T^*_{X'_u},\omega _{X'_u}),\) for all closed points u of U.
The proof occupies most of the paper and is concluded in Sect. 6.3.
2.3 First reductions
Here we carry out some standard reductions. It is also convenient to consider the case of the fiber of M at the generic point \(\mu \) of S being zero. We put these into two remarks:
Remark 2.3.1
The conclusion of Theorem 2.2.1 depends on S only up to restricting to a dense open subset, and so do its hypotheses. Moreover, the assertion is Zariski-local (even étale-local) on X. Indeed Lagrangianity is local and so is the p-support, as in Remark 2.1.5. And the hypotheses are stable by restriction to open coverings. Hence to prove the main theorem we may further assume that S is affine, regular and that X is regular, affine and integral.
Remark 2.3.2
If the fiber of M at the generic point \(\mu \) of S is zero, then there is a dense open subset U of S such that \(M|_{U}=0.\)
Proof
Indeed one may assume that X and S are affine and thus consider a left module over the ring of global sections of \(D_{X/S}.\) By the hypotheses, this module has a finite generating family \(\{m_1,\ldots ,m_l\}\) and each \(m_i\) is annihilated by a nonzero global section \(r_i\) of \(\mathcal {O}_S.\) Since \(\mathcal {O}_S\) acts through the center of \(D_{X/S},\) the open subset of S determined by the product of these global sections fulfills the statement. \(\square \)
2.4 Reduction to \(\mathbb {A}^n\)
Here we show that the proof of the main theorem reduces to \(X/S=\mathbb {A}^n_S.\) To do so we use the direct image of \(D_{X/S}\)-modules and the general result on the dimension of p-supports (Theorem 3.1.1), proved independently below.
Proposition 2.4.1
To prove Theorem 2.2.1, it is sufficient to suppose that \(X/S=\mathbb {A}^n_S.\)
Proof
By Remark 2.3.1, one may suppose that X / S is smooth of relative dimension n and that X and S are affine. Hence there is a closed immersion \(X \overset{f}{\hookrightarrow }\mathbb {A}^m_S\) over S, for some \(m\ge 0.\)
Let M be a left \(D_{X/S}\)-module as in the statement of Theorem 2.2.1 and let \(f_+M\) be its direct image, see [3, 2.4.1] for the definition. It is easy to see that one has the classical description of the transfer bimodule, as in [9, (4) p. 259]. Hence the latter is flat over \(D_{X/S}.\) In particular, the direct image \(f_+M\) is supported in degree 0 and \(H^0f_+M\) is a coherent left \(D_{\mathbb {A}^m_S/S}\)-module. Furthermore, it follows directly from the definition that the formation of the transfer bimodule commutes with base-change \(S'\rightarrow S.\) Hence \(H^0f_+\) commutes with base-change \(S'\rightarrow S.\) Thus the generic fiber \((H^0f_+M)_\mu = H^0{f_\mu }_+M_\mu \) is nonzero and is holonomic by preservation of holonomicity under direct images, where \(\mu \) is the generic point of S and \(X_\mu \overset{f_\mu }{\hookrightarrow }\mathbb {A}^m_{k(\mu )}\) is the induced closed immersion. Finally, for all closed points \(s\in S,\) it is also an immediate consequence of the description of the transfer bimodule as in [9, (4) p. 259] that
where \(f_s'\) is the base-change of \(f_s\) by the Frobenius and we have used the notation of the “Appendix” for the maps in the cotangent diagram of \(f_s'.\)
Thus by Lemma A.0.6, to prove that the symplectic form vanishes on the regular locus of \(p\text {-}supp(M_s)\) it is enough to prove the corresponding symplectic form vanishes on the regular locus of \(p\textit{-supp}(H^0{f_s}_+M_s).\) This concludes the proof of the proposition since the part of the theorem concerning dimensions is Theorem 3.1.1, proved independently below. \(\square \)
3 Dimension of the p-supports
As outlined in the introduction, the main theorem splits into an assertion about the dimension of the p-support and one about the vanishing of the symplectic form on the regular locus of the p-support. We start by considering the former.
3.1 Statement
Theorem 3.1.1
Let S be an integral scheme dominant and of finite type over \(\mathbb {Z},\) of generic point \(\mu .\) Let X be a smooth S-scheme of relative dimension n and let M be a coherent left \(D_{X/S}\)-module. Suppose that \(M_\mu \) is a nonzero holonomic left \(D_{X_\mu }\)-module, then there is a dense open subset U of S such that the p-support of the fiber of M at each closed point u of U is equidimensional of dimension \(n = \dim X.\)
The proof is contained in the Sect. 3.3. In view of Remark 2.3.1, we may and shall assume that S and X are regular, integral and affine.
3.2 Pure coherent sheaves
Recall that the (co)dimension of a coherent sheaf is the (co)dimension of its support and let us call a coherent sheaf equidimensional if its support is equidimensional. There is a strengthening of equidimensionality which has a very convenient interpretation in terms of duality theory. Namely, let Y be an affine scheme.
Definition 3.2.1
A coherent sheaf on Y is pure if all its nonzero coherent subsheaves are of the same dimension.
It is easily seen to imply equidimensionality:
Proposition 3.2.2
A coherent sheaf \(\mathcal {F}\) on Y is pure if and only if all its associated points \(y \in Ass(\mathcal {F})\) are of the same dimension. In particular, a pure coherent sheaf on Y is equidimensional.
Proof
By [18, Proposition 3.1.2] a prime ideal \(\mathfrak {p}\) corresponding to an associated point of \(\mathcal {F}\) is associated to the module of global sections of \(\mathcal {F}.\) Thus \(\mathfrak {p}\) is the annihilator of a global section of \(\mathcal {F}.\) The only if part immediately follows.
Suppose that the dimension of every associated point of \(\mathcal {F}\) is d and let \(\mathcal {F}'\subset \mathcal {F}\) be a nonzero coherent subsheaf. Then the dimension of \(\mathcal {F}'\) is d. Indeed the associated points of \(\mathcal {F}'\) contain the generic points of its support, by [18, Corollaire 3.1.4], and are associated to \(\mathcal {F}\) by [18, Proposition 3.1.7 (i)]. This concludes the proof of the proposition. \(\square \)
Here is the interpretation in terms of duality theory.
Theorem 3.2.3
Suppose that Y is regular and equidimensional. A coherent sheaf \(\mathcal {F}\) on Y is pure if and only if there is a nonnegative integer c such that
for all \(l \ne c\). If \(\mathcal {F}\) is nonzero, then c is its codimension.
Proof
This is well-known. We refer to the literature. Our definition of purity is equivalent to [8, A:IV 2.5.] by [9, V, 2.2.3]. The theorem is then [8, A:IV 2.6], since a regular local ring is Auslander regular by [8, A:IV 3.4]. \(\square \)
3.3 Equidimensionality of the p-supports
Here we prove Theorem 3.1.1. In particular, we use Remark 2.3.1 and suppose that X / S is smooth of relative dimension n with S and X regular, affine and integral. We start by recalling the notion of good filtration on a coherent \(D_{X/S}\)-module. Recall the filtration on \(D_{X/S}\) from Proposition 2.1.2.
Definition 3.3.1
A good filtration on a coherent left \(D_{X/S}\)-module is a filtration by coherent \(\mathcal {O}_X\)-submodules, compatible with the filtration on \(D_{X/S},\) which is bounded below and such that the associated graded module over \(grD_{X/S} \cong \mathcal {O}_{T^*_{X/S}}\) is coherent.
Note that coherent left \(D_{X/S}\)-modules admit good filtrations by [3, 5.2.3 (iv)].
We next give a lemma guaranteeing the freeness on S of a module whose associated graded is free. The proof of the last part of the lemma was kindly provided by Michel Van den Bergh.
Lemma 3.3.2
Let M be a left module over a ring R and let \(\{M_i\}_{i\in \mathbb {Z}}\) be an exhaustive increasing filtration of M by left R-submodules. Suppose that there is \(i_0 \in \mathbb {Z}\) such that \(M_{i_0}=0\) and, \(\forall i > i_0,\) the left R-module \(M_i/M_{i-1}\) is flat, then M is flat. Suppose further that \(\forall i, M_i/M_{i-1}\) is free, then M is free.
Proof
By hypothesis, \(M_{i_0+1} \cong M_{i_0+1}/(M_{i_0}=0)\) is flat. Moreover, \(\forall i \ge i_0+1, M_i/M_{i-1}\) is flat. So, since extensions of flat modules are flat ([11, §2 n\(^\mathrm{o}\)5 Proposition 5]), \(\forall i \ge i_0+1, M_i\) is flat. Thus M is a union of flat submodules. Hence it is flat by [11, §2 n\(^\mathrm{o}\)3 Proposition 2(ii)]. This proves the first assertion.
Suppose that the \(M_i/M_{i-1}\) are free. Then the union, over all \(i \ge i_0+1,\) of an arbitrary lift to \(M_i\) of a basis of \(M_i/M_{i-1}\) is a basis of M. Thus M is free. This finishes the proof of the lemma. \(\square \)
The following lemma is standard for \(\mathcal {O}\)-modules. Considering the associated graded allows us to deduce a version for \(D_{X/S}\)-modules.
Lemma 3.3.3
Let M be a coherent left \(D_{X/S}\)-module. Then there is a dense open subset U of S such that \(\forall l\ge 0\) and \(\forall s \in U\), the canonical map
is an isomorphism, where the subscript s denotes the restriction to the fiber.
Proof
First of all, there are only finitely many degrees l to consider. Namely, by [8, A:IV 4.5], both target and domain of the above morphism are zero for \(l > \dim T^*_{X/S} \ge \dim T^*_{X_s}.\) Indeed, \(T^*_{X/S}\) and \(T^*_{X_s}\) are the respective spectra of the rings \(grD_{X/S}\) and \(grD_{X_s},\) which are both regular. Thus guaranteeing the vanishing of \(\mathcal {E} xt ^l\) for \(l > \dim T^*_{X/S}.\) Hence it suffices to prove that, \(\forall l,\) there is an open U as in the statement.
We thus want to prove a \(D_{X/S}\)-module version of [18, Corollaire 9.4.3]. But the proof of the latter adapts to \(D_{X/S}\)-modules by considering the associated graded to good filtrations. Indeed, coherent left \(D_{X/S}\)-modules form an abelian category and the proof of [18, Proposition 9.4.2] carries through, using [25, Proposition A.17] and Lemma 3.3.2 to conclude. \(\square \)
We now obtain that the following well-known consequence of holonomicity spreads from the generic fiber to a neighborhood.
Proposition 3.3.4
Let M be a coherent left \(D_{X/S}\)-module. Suppose that \(M_\mu \) is a holonomic left \(D_{X_\mu }\)-module, for \(\mu \) the generic point of S. Then there is a dense open subset U of S such that for all \(l \ne n\) and all \(s \in U\),
Proof
By Lemma 3.3.3 and [9, VI 1.12], \(\forall l \ne n,\) the fiber of \(\mathcal {E} xt ^l_{D_{X/S}}(M,D_{X/S})\) at the generic point of S vanishes. Hence by Remark 2.3.2 and Lemma 3.3.3, \(\forall l \ne n,\) there is a dense open subset \(U_l\) of S such that for all \(s \in U_l,\)\(\mathcal {E} xt ^l_{D_{X_s}}(M_s,D_{X_s})=0.\) Since by the proof of 3.3.3 there are only finitely many such degrees l to consider, \(U:=\bigcap _lU_l\) fulfills the proposition. \(\square \)
Then we use the Azumaya property of the ring of differential operators in positive characteristic ([6, Theorem 2.2.3]) to transfer purity from a \(D_{X/S}\)-module to its associated coherent sheaf on the twisted cotangent space.
Proposition 3.3.5
Let Y be a smooth equidimensional scheme over a field k of positive characteristic p, let \(Y \xrightarrow {F} Y'\) be the relative Frobenius and let M be a coherent left \(D_Y\)-module. Then, \(\forall l\ge 0,\)
where \(\mathcal {M}:=F_*M\) is endowed with an action of \(\mathcal {O}_{T^*_{Y'}}\) as in Definition 2.1.4.
Proof
Since F is affine, \(\mathcal {E} xt ^l_{D_Y}(M,D_Y)=0\) if and only if
Set \(\mathcal {D}_Y:={F}_*D_Y,\) we thus have \(\mathcal {E} xt ^l_{{F}_*D_Y}({F}_*M,{F}_*D_Y)= \mathcal {E} xt ^l_{\mathcal {D}_Y}(\mathcal {M},\mathcal {D}_Y).\) Let us show that
Indeed, both \(\mathcal {E} xt ^l_{\mathcal {D}_Y}(\mathcal {M},\mathcal {D}_Y)\) and \(\mathcal {E} xt ^l_{\mathcal {O}_{T^*_{Y'}}}(\mathcal {M},\mathcal {O}_{T^*_{Y'}}),\) are quasi-coherent sheaves on \(T^*_{Y'}.\) Hence their respective vanishings may be checked on a flat covering \(\mathcal {U} \xrightarrow {\pi } T^*_{Y'}\) of \(T^*_{Y'}\). Since \(\mathcal {D}_Y\) is an Azumaya algebra over \(\mathcal {O}_{T^*_{Y'}}\) by [6, Theorem 2.2.3], this covering may be chosen to split \(\mathcal {D}_Y.\) That is \((\mathcal {D}_Y)_\mathcal {U}:=\pi ^*\mathcal {D}_Y \simeq M_r(\mathcal {O}_{\mathcal {U}})\), the sheaf of \(r\times r\) matrices with coefficients in \(\mathcal {O}_{\mathcal {U}}.\)
As is well-known in Morita theory, tensoring with the \((M_r(\mathcal {O}_{\mathcal {U}}),\mathcal {O}_{\mathcal {U}})\)-bimodule \(\mathcal {O}^r_{\mathcal {U}}\) induces an equivalence between the category of coherent \(\mathcal {O}_{\mathcal {U}}\)-modules and the category of coherent left \(M_r(\mathcal {O}_{\mathcal {U}})\)-modules. Note that the coherent sheaf \((\mathcal {O}^r_{\mathcal {U}})^\vee \) is sent to \(\mathcal {O}^r_{\mathcal {U}} \otimes _{\mathcal {O}_{\mathcal {U}}}(\mathcal {O}^r_{\mathcal {U}})^\vee \cong M_r(\mathcal {O}_{\mathcal {U}})\) by this equivalence. Let \(\mathcal {F}\) be a coherent sheaf such that \(\mathcal {M}_\mathcal {U}:=\pi ^*\mathcal {M}\simeq \mathcal {O}^r_{\mathcal {U}} \otimes _{\mathcal {O}_{\mathcal {U}}}\mathcal {F}\) as coherent left \((\mathcal {D}_Y)_\mathcal {U} \simeq M_r(\mathcal {O}_{\mathcal {U}})\)-modules. Then, by localization and the above Morita equivalence,
if and only if, by commutation with finite direct sums, \(\mathcal {E} xt ^l_{\mathcal {O}_{\mathcal {U}}}(\mathcal {F},\mathcal {O}_{\mathcal {U}})\text { vanishes},\) if and only if
using again commutation with finite direct sums and localization. This concludes the proof of the proposition. \(\square \)
We can now prove the theorem.
Proof
(of Theorem 3.1.1) Note that if the fiber of M at the generic point of S is nonzero then M is nonzero. Therefore, by generic freeness [14, Theorem 14.4] applied to the associated graded to a good filtration on M and Lemma 3.3.2, there is a dense open subset W of S on which M is faithfully flat. Hence \(\forall s\in W, M_s\ne 0\) and thus \(F_*M_s\ne 0.\) Since M is holonomic on the generic fiber of S, there is a dense open subset U of W such that \(\forall l\ne n\) and \(\forall s\in U, \mathcal {E} xt ^l_{D_{X_s}}(M_s,D_{X_s})=0,\) by Proposition 3.3.4. Which, by Proposition 3.3.5, is equivalent to, \(\forall l\ne n\) and \(\forall s\in U, \mathcal {E} xt ^l_{\mathcal {O}_{T^*_{X'_s}}}(F_*{M_s},\mathcal {O}_{T^*_{X'_s}})=0.\) In particular, \(\forall l\ne n\) and \(\forall s\in U,\)
This implies by Theorem 3.2.3 that \(\forall s\in U, F_*{M_s}\) is a pure nonzero coherent \(\mathcal {O}_{T^*_{X'_s}}\)-module of dimension n. Hence it is equidimensional of dimension n by Proposition 3.2.2. This proves the theorem. \(\square \)
Remark 3.3.6
The purity of the coherent \(\mathcal {O}_{T^*_{X'_s}}\)-module \(F_*M_s\) guarantees furthermore that it has no embedded associated points.
4 Degrees and ranks estimates
We now consider \(D_{\mathbb {A}^n_S/S}\)-modules. In addition to the filtration by the order of differential operators (Proposition 2.1.2), \(D_{\mathbb {A}^n_S/S}\) is endowed with the Bernstein filtration. The latter has the property that each summand of its associated graded ring is a finitely generated module over \(\mathcal {O}(S).\) For a \(D_{\mathbb {A}^n_S/S}\)-module M whose generic fiber is holonomic, we use the Bernstein filtration to estimate the degree (for a suitable projective embedding) of the p-support \(p\textit{-supp}(M_s)\) as well as the rank of \(F_*M_s\) at the generic point of an irreducible component of its support \(p\textit{-supp}(M_s),\) for s a closed point in a dense open subset of S, see Theorem 4.3.3.
4.1 Bernstein filtration
Let S be an affine scheme and let R be its ring of global sections. If we fix coordinates \(\{x_1, \dots , x_n\}\) on \(\mathbb {A}^n_S,\) then the ring of global sections of \(D_{\mathbb {A}^n_S/S}\) is isomorphic to the n-th Weyl algebra \(A_n(R)\) over R,
Definition 4.1.1
The Bernstein filtration\(\mathcal {B}\) of \(A_n(R)\) is the filtration by the total order in x and \(\partial .\) Namely \(\forall l \in \mathbb {Z},\)\(\mathcal {B}_lA_n(R):=\bigoplus _{|\alpha |+|\beta |\le l} R x^{\alpha }\partial ^{\beta },\) where \(\alpha , \beta \in \mathbb {Z}_{\ge 0}^n\) are multi-indices and we have used the standard notation \(x^\alpha := x_1^{\alpha _1}\dots x_n^{\alpha _n}, \partial ^\beta := \partial _1^{\beta _1}\dots \partial _n^{\beta _n}\) and for a multi-index \(\alpha \in \mathbb {Z}_{\ge 0}^n, |\alpha |:= \alpha _1+\dots +\alpha _n.\)
Remark 4.1.2
Note that the associated graded ring \(gr^{\mathcal {B}}A_n(R)\) is the R-algebra of polynomials in the variables \(\{x_1,\ldots ,x_n,\)\(y_1,\ldots ,y_n\},\) graded by the order of polynomials. Where, \(\forall 1\le i\le n, x_i\) (resp. \(y_i\)) is the class of \(x_i\) (resp. \(\partial _i\)) \(\in \mathcal {B}_1A_n(R)/\mathcal {B}_0A_n(R).\) In particular, \(\forall l \in \mathbb {Z}, \mathcal {B}_lA_n(R)/\mathcal {B}_{l-1}A_n(R)\) is a finitely generated free R-module.
We will use the notion of good filtration on a \(A_n(R)\)-module.
Definition 4.1.3
A filtration \(\Gamma \) of a left \(A_n(R)\)-module M is an increasing exhaustive filtration of M, indexed by \(\mathbb {Z}\) and compatible with \(\mathcal {B}.\) It is said to be a good filtration if it is bounded below and the associated graded module \(gr^{\Gamma }M\) is finitely generated over the algebra \(gr^{\mathcal {B}}A_n(R)\).
It is easy to see that finitely generated left \(A_n(R)\)-modules have good filtrations, see e.g. [7, Ch.1 Proposition 2.7]. Note that if \(\Gamma \) is a good filtration of M, then \(\forall l\in \mathbb {Z}, \Gamma _lM/\Gamma _{l-1}M\) (and hence \(\Gamma _lM\)) is a finitely generated R-module.
Suppose that R is a field K. Then a left \(A_n(K)\)-module has well-defined degree and multiplicity. Indeed, let M be a finitely generated left \(A_n(K)\)-module and let \(\Gamma \) be a good filtration on M. Then for l large enough, the function \(l\mapsto \dim _K\Gamma _lM\) coincides with a polynomial \(\mathcal {H}_{M,\Gamma } \in \mathbb {Q}[t]\) ([7, Ch.1 Corollary 3.3]).
Definition 4.1.4
Let d (resp. \(a_d\)) be the degree (resp. the leading coefficient) of \(\mathcal {H}_{M,\Gamma }.\) Then \(d!a_d\) is a nonnegative integer. The nonnegative integers \(d(M):=d\) and \(e(M):=d!a_d\) are independent of \(\Gamma \) and called the dimension and multiplicity of M, respectively ([7, p. 8]).
Now we look at the behavior of these invariants in a family.
Lemma 4.1.5
Suppose that R is a domain and let M be a finitely generated left \(A_n(R)\)-module. Then there is a dense open subset U of \(S:={\text {Spec}}(R)\) such that the functions \(s\mapsto d(M_s)\) and \(s\mapsto e(M_s)\) are constant on U.
Proof
Let \(\Gamma \) be a good filtration on M. Then by generic freeness ([14, Theorem 14.4]), there is a dense open subset U of S such that \(\forall l\in \mathbb {Z}, (\Gamma _lM/\Gamma _{l-1}M)|_U\) is free over \(\mathcal {O}(U).\) In particular, \(\forall l\in \mathbb {Z}, (\Gamma _lM/\Gamma _{l-1}M)|_U\) is a flat \(\mathcal {O}(U)\)-module. Hence, \(\forall l\in \mathbb {Z}\) and \(\forall s\in U, (\Gamma _lM/\Gamma _{l-1}M)_s\cong (\Gamma _lM)_s/(\Gamma _{l-1}M)_s\) and \((\Gamma )_s\) is a good filtration on \(M_s\). The lemma follows since, \(\forall s\in U\) and \(\forall l\in \mathbb {Z}, \dim _{k(s)}(\Gamma _lM)_s=\sum _{i=-\infty }^{i=l} \dim _{k(s)}(\Gamma _iM)_s/(\Gamma _{i-1}M)_s\) and
is the rank of the free module \(\mathcal {O}(U)\)-module \(\Gamma _lM/\Gamma _{l-1}M|_U.\) Hence \(\mathcal {H}_{M_s,\Gamma _s}\) is constant on U. \(\square \)
4.2 On the filtrations of the center
Let K be a field of positive characteristic p. With the notation of Sect. 4.1, the center \(ZA_n(K)\) of \(A_n(K)\) is the algebra of polynomials \(K[x_1^p,\ldots ,x_n^p,\partial _1^p,\ldots ,\partial _n^p].\)
Definition 4.2.1
Let \(\mathcal {C}\) be the filtration on \(ZA_n(K)\) derived from the grading \(| \bullet |\) of polynomials, where \(|x_i^p|= |\partial _j^p|= 1.\)
We would like to compare \(\mathcal {C}\) with the Bernstein filtration and to do so we will use the classical construction of the Rees ring associated to a filtered ring.
Definition 4.2.2
-
(1)
The Rees ring of the filtered ring \((ZA_n(K),\mathcal {C})\) is the graded ring \(R_n(\mathcal {C}):=\bigoplus \nolimits _{i\in \mathbb {N}} \mathcal {C}_iZA_n(K).\)
-
(2)
Let G be an increasing \(\mathcal {C}\)-compatible filtration of a \(ZA_n(K)\)-module M. Then the Rees module associated with G is \(\mathcal {R}(M,G):=\bigoplus \nolimits _{i\in \mathbb {Z}} G_iM.\) It is a naturally an \(R_n(\mathcal {C})\)-module.
We recall elementary properties of the Rees ring in the following lemma.
Lemma 4.2.3
-
(1)
The graded algebra morphism
$$\begin{aligned}&K[t_0,x_1^p,\ldots ,x_n^p,\partial _1^p,\ldots ,\partial _n^p] \rightarrow R_n(\mathcal {C}):=\bigoplus \limits _{i\in \mathbb {N}} \mathcal {C}_iK[x_1^p,\ldots ,x_n^p,\partial _1^p,\ldots ,\partial _n^p] \\&\quad t_0\mapsto 1, x_i^p \mapsto x_i^p, \partial _j^p \mapsto \partial _j^p \end{aligned}$$with \(t_0\) in degree 1, is an isomorphism.
-
(2)
Using the same notation for \(t_0\) and its image under the isomorphism of (1), the natural map \(R_n(\mathcal {C})/t_0R_n(\mathcal {C}) \rightarrow gr^{\mathcal {C}}ZA_n(K)\) is an isomorphism of graded algebras.
-
(3)
There is a unique morphism \(R_n(\mathcal {C})_{t_0}\rightarrow ZA_n(K),\) sending \(t_0\) to 1 and extending the inclusions \(\mathcal {C}_iK[x_1^p,\ldots ,x_n^p,\partial _1^p,\ldots ,\partial _n^p] \subset ZA_n(K).\) Its restriction to \(R_n(\mathcal {C})_{(t_0)},\) the subring of degree 0 elements of the graded ring \(R_n(\mathcal {C})_{t_0},\) is an isomorphism \(R_n(\mathcal {C})_{(t_0)}\widetilde{\rightarrow } ZA_n(K).\)
We will use good filtrations of \(ZA_n(K)\)-modules.
Definition 4.2.4
A filtration G of a \(ZA_n(K)\)-module M as in the definition 4.2.2 is said to be good if the associated Rees module \(\mathcal {R}(M,G)\) is a finitely generated \(R_n(\mathcal {C})\)-module.
This implies in particular that G is bounded below. Moreover, one easily sees that a filtration G on M is good if and only if G is bounded below and the associated graded module \(gr^GM\) is finitely generated over \(gr^{\mathcal {C}}ZA_n(K)\) ([8, A:III 1.29]).
Let M be a left \(A_n(K)\)-module and let \(r_*M\) be the module M considered as a \(ZA_n(K)\)-module. We now introduce a \(\mathcal {C}\)-filtration of \(r_*M\) associated with a \(\mathcal {B}\)-filtration of M.
Definition 4.2.5
Let \(\Gamma \) be a filtration of the left \(A_n(K)\)-module M. The \(\mathcal {C}\)-filtration \(p\Gamma \) of \(r_*M\) is given by \((p\Gamma )_lr_*M:=\Gamma _{pl}M,\) for all integers l.
We now want to relate properties of \(p\Gamma \) to those of \(\Gamma .\)
Lemma 4.2.6
Let \(\Gamma \) be a good filtration of the left \(A_n(K)\)-module M, then \(p\Gamma \) is a good filtration of \(r_*M.\)
Proof
It is clear from the definition that the filtration \(p\Gamma \) is bounded below, since \(\Gamma \) is.
Let us show that the \(gr^{\mathcal {C}}ZA_n(K)\)-module \(gr^{p\Gamma }r_*M\) is finitely generated. In order to do so, we consider the filtration \(\Phi \) of the center induced by the Bernstein filtration. Thus, \(\forall l\in \mathbb {Z}, \Phi _lZA_n(K):=ZA_n(K)\cap \mathcal {B}_lA_n(K).\) In particular, \(x_i^p\) and \(\partial _j^p\) are of degree p for the filtration \(\Phi ,\) for all i, j. Let \(\Phi (\Gamma )\) be the \(\Phi \)-filtration on \(r_*M\) defined by \(\Phi (\Gamma )_lr_*M:=\Gamma _{pm}M\), where pm is the greatest integer multiple of p such that \(pm\le l\). Note that there is a K-module isomorphism \(gr^{p\Gamma }r_*M\rightarrow gr^{\Phi (\Gamma )}r_*M\) defined by
It is \(\rho \)-linear, where \(\rho \) is the isomorphism of K-algebras \(gr^{\mathcal {C}}ZA_n(K)\rightarrow gr^\Phi ZA_n(K)\) satisfying
Hence \(gr^{p\Gamma }r_*M\) is finitely generated over \(gr^{\mathcal {C}}ZA_n(K)\) if and only if \(gr^{\Phi (\Gamma )}r_*M\) is finitely generated over \(gr^\Phi ZA_n(K)\). Let us show the latter.
Consider the finite exhaustive filtration of \(gr^{\Phi (\Gamma )}r_*M\) by graded \(gr^\Phi ZA_n(K)\)-submodules,
It is defined as follows, \(\forall 0\le i\le p, \forall l\in \mathbb {Z},\) let pm the greatest integer multiple of p such that \(pm\le l.\) Then \((gr^{\Phi (\Gamma )}r_*M)_i \cap \Phi (\Gamma )_lr_*M/\Phi (\Gamma )_{l-1}r_*M\) is the image of the map \(\Gamma _{p(m-1)+i}M \rightarrow \Phi (\Gamma )_lr_*M/\Phi (\Gamma )_{l-1}r_*M\) induced by the inclusion \(\Gamma _{p(m-1)+i}M \subset \Gamma _{pm}M=:\Phi (\Gamma )_lr_*M.\) Let \(gr(gr^{\Phi (\Gamma )}r_*M):= \bigoplus \nolimits _{i=1}^{i=p}(gr^{\Phi (\Gamma )}r_*M)_i/(gr^{\Phi (\Gamma )}r_*M)_{i-1}\) be the associated graded \(gr^\Phi ZA_n(K)\)-module. Note furthermore that the module \(gr^{\Gamma }M\) seen as a module over \(gr^\Phi ZA_n(K) \hookrightarrow gr^{\mathcal {B}}A_n(K)\) decomposes into a direct sum of graded \(gr^\Phi ZA_n(K)\)-submodules \(\bigoplus \nolimits _{i=1}^{i=p}(gr^{\Gamma }M)_i,\) where \((gr^{\Gamma }M)_i :=\bigoplus _{l\in \mathbb {Z}}gr_{pl+i}^{\Gamma }M.\) Let \(F_*gr^{\Gamma }M\) be the graded \(gr^\Phi ZA_n(K)\)-module \(\bigoplus \nolimits _{i=1}^{i=p}(gr^{\Gamma }M)_i[i-p],\) where \([\bullet ]\) denotes the degree shift. Then, \(\forall 1\le i\le p,\) there is an isomorphism of graded \(gr^\Phi ZA_n(K)\)-modules
Indeed in degree \(l\in \mathbb {Z},\) with pm the greatest integer multiple of p such that \(pm\le l,\) it is induced by the quotient map \(\Gamma _{p(m-1)+i}M \rightarrow gr_{p(m-1)+i}^{\Gamma }M,\) the latter being equal to \(((gr^{\Gamma }M)_i)_{p(m-1)+i} = ((gr^{\Gamma }M)_i[i-p])_{pm},\) where the outermost index refers to the homogeneous component of a graded \(gr^\Phi ZA_n(K)\)-module. These finally assemble into an isomorphism of graded \(gr^\Phi ZA_n(K)\)-modules
We conclude by noting that the \(gr^\Phi ZA_n(K)\)-module \(F_*gr^{\Gamma }M\) is finitely generated. Indeed, by hypothesis, the \(gr^{\mathcal {B}}A_n(K)\)-module \(gr^{\Gamma }M\) is finitely generated. Hence it is finitely generated as a \(gr^\Phi ZA_n(K)\)-module since \(gr^{\mathcal {B}}A_n(K)\cong K[x_1,\ldots ,x_n,y_1,\ldots ,y_n]\) is a finitely generated module over \(K[x_1^p,\ldots ,x_n^p,y_1^p,\ldots ,y_n^p] \cong gr^\Phi ZA_n(K).\) Thus \(F_*gr^{\Gamma }M\) is a finitely generated \(gr^\Phi ZA_n(K)\)-module as direct summands of a finitely generated module are finitely generated. So, by the above isomorphism, the \(gr^\Phi ZA_n(K)\)-module \(gr(gr^{\Phi (\Gamma )}r_*M)\) is finitely generated. Consequently the finite exhaustive filtration of \(gr^{\Phi (\Gamma )}r_*M\) has finitely generated subquotients and hence \(gr^{\Phi (\Gamma )}r_*M\) is a finitely generated \(gr^\Phi ZA_n(K)\)-module. This finishes the proof of the lemma. \(\square \)
Let M be a left \(A_n(K)\)-module and let \(\Gamma \) be a good filtration of M. By the above Lemma 4.2.6, the Rees module of \((r_*M,p\Gamma )\) is a finitely generated graded module over the Rees ring \(R_n(\mathcal {C})\simeq K[t_0,x_1^p,\ldots ,x_n^p,\partial _1^p,\ldots ,\partial _n^p].\) Thus it has a Hilbert polynomial \(\mathcal {H}_{\mathcal {R}(r_*M,p\Gamma )}.\) In the following proposition, we express \(\mathcal {H}_{\mathcal {R}(r_*M,p\Gamma )}\) in terms of the Hilbert polynomial \(\mathcal {H}_{M,\Gamma }\) of \((M,\Gamma ).\)
Proposition 4.2.7
Let M be a left \(A_n(K)\)-module and let \(\Gamma \) be a good filtration of M. The Hilbert polynomial \(\mathcal {H}_{\mathcal {R}(r_*M,p\Gamma )}(t)\) of the Rees module of \((r_*M,p\Gamma )\) is \(\mathcal {H}_{M,\Gamma }(pt).\) In particular, the degree of \(\mathcal {H}_{\mathcal {R}(r_*M,p\Gamma )}\) is the dimension d(M) of M and its leading coefficient times d(M)! is \(e(M)p^{d(M)},\) where e(M) is the multiplicity of M.
Proof
For l large enough, on the one hand the Hilbert polynomial \(\mathcal {H}_{M,\Gamma }(l)\) coincides with the function \(l\mapsto \dim _K\Gamma _lM\) and on the other \(\mathcal {H}_{\mathcal {R}(r_*M,p\Gamma )}(l)\) coincides with \(l\mapsto \dim _K(p\Gamma )_lM=\dim _K\Gamma _{pl}M.\) The proposition immediately follows. \(\square \)
4.3 Conclusion
Here we obtain the estimates mentioned at the beginning of the section.
First, we would like to recall a well-known geometric interpretation of the Rees ring and module. We use the notations of [17, §2] for projective schemes.
Proposition 4.3.1
Using the notations of Lemma 4.2.3, we have

where j is an open embedding and i is its closed complement, and
-
(a)
\(D_+(t_0)\cong {\text {Spec}}(ZA_n(K))\)
-
(b)
\(V_+(t_0)\cong Proj(gr^{\mathcal {C}}ZA_n(K))\)
Proof
-
(a)
By definition, \(D_+(t_0)= {\text {Spec}}(R_n(\mathcal {C})_{(t_0)}).\) Hence (a) follows immediately from (3) of Lemma 4.2.3.
-
(b)
By definition, \(V_+(t_0)= Proj(R_n(\mathcal {C})/t_0R_n(\mathcal {C})).\) Hence (b) follows from (2) of Lemma 4.2.3. \(\square \)
Making these identifications, let G be a good filtration on a finitely generated \((ZA_n(K),\mathcal {C})\)-module M. Then the coherent sheaf \(\widetilde{\mathcal {R}(M,G)}\) on \(Proj(R_n(\mathcal {C}))\) extends the coherent sheaf \(\widetilde{M}\) on \({\text {Spec}}(ZA_n(K))\) and its restriction to the complement \(Proj(gr^{\mathcal {C}}ZA_n(K))\) of \({\text {Spec}}(ZA_n(K))\) is isomorphic to \(\widetilde{gr^GM}\). Finally, one easily sees that the support of \(\widetilde{\mathcal {R}(M,G)}\) is the closure of \(supp(\widetilde{M})\) in \(Proj(R_n(\mathcal {C}))\). Note that here
The leading coefficient of the Hilbert polynomial of \(\widetilde{\mathcal {R}(M,G)}\) is related to the top-dimensional irreducible components of its support through the following:
Proposition 4.3.2
Let \(Y \overset{i}{\hookrightarrow }\mathbb {P}^{m}_K\) be a closed subscheme and let \(\mathcal {F}\) be a coherent sheaf of dimension d on Y. Let the degree of \(\mathcal {F}\) with respect to i be \(\mu (\mathcal {F}):=d!a_d\) where \(a_d\) is the leading coefficient of the Hilbert polynomial of \(\mathcal {F}\) with respect to i. Then
where the sum is over the generic points of the d-dimensional irreducible components of \(supp(\mathcal {F})\), \(\mathrm {rk}_z(\mathcal {F}):=\dim _{k(z)}(\mathcal {F}_z\otimes k(z))\) and \(\deg (\overline{\{z\}})\) is the degree of \(\overline{\{z\}}^{red}\) with respect to i.
Proof
By [28, Lemma B.4] and [18, Proposition 5.3.1], \(\mu (\mathcal {F})=\Sigma _z \lg _{\mathcal {O}_{Y,z}}(\mathcal {F}_z) \mu (\mathcal {O}_{\overline{\{z\}}^{red}}),\) where \(\lg \) denotes the length, summing over the generic points of the d-dimensional irreducible components of \(supp(\mathcal {F}).\) Let z be as above, then by additivity of the length under short exact sequences \(\lg _{\mathcal {O}_{Y,z}}(\mathcal {F}_z)\ge \lg _{k(z)}(\mathcal {F}_z\otimes k(z))=\dim _{k(z)}(\mathcal {F}_z\otimes k(z))=:\mathrm {rk}_z(\mathcal {F}).\) The proposition follows as \(\deg (\overline{\{z\}}):=\mu (\mathcal {O}_{\overline{\{z\}}^{red}}).\)\(\square \)
Theorem 4.3.3
Let S be an integral scheme dominant and of finite type over \(\mathbb {Z}\) and let M be a coherent left \(D_{\mathbb {A}^n_S/S}\)-module. Let \(\mu \) be the generic point of S. Suppose that \(M_{\mu }\) is a nonzero holonomic left \(D_{\mathbb {A}^n_{k(\mu )}}\)-module. Then there is a dense open subset U of S such that for each closed point \(u\in U\) and each z generic point of an irreducible component of p-supp(\(M_u\))
where \(e(M_\mu )\) is the multiplicity for the Bernstein filtration of \(M_{\mu },\)\(\deg (\overline{\{z\}})\) is the degree of the reduced closure of the image of z in \(\mathbb {P}^{2n}_{k(u)}\) by the open immersion of the Rees construction and \(\mathrm {rk}_z(M_u):=\dim _{k(z)}((F_*{M_u})_z\otimes k(z)).\)
Proof
The proof reduces to the case of an integral and affine \(S = {\text {Spec}}(R)\). We may thus consider that M is a finitely generated left \(A_n(R)\)-module. By Lemma 4.1.5, there is a dense open subset \(U_e\) of S such that for each closed point \(u\in U_e\), \(d(M_u)=n\) and \(e(M_u)=e(M_\mu ).\)
Let \(u\in U_e\) with \(p = char(k(u))\) and let \(\Gamma \) be a good filtration on the left \(A_n(k(u))\)-module \(M_u\). By Proposition 4.2.7, \(\widetilde{\mathcal {R}(M_u,p\Gamma )}\) is of dimension n and \(\mu (\widetilde{\mathcal {R}(M_u,p\Gamma )})=e(M_\mu )p^n\). Moreover \(supp(\widetilde{\mathcal {R}(M_u,p\Gamma )})\) is the closure \(\overline{p \text {-}supp(M_u)}\) of p-\(supp(M_u),\) in which p-\(supp(M_u)=\overline{p \text {-}supp(M_u)}\cap {\text {Spec}}(ZA_n(K))\) is open. Hence Proposition 4.3.2 implies that \(\Sigma _z \mathrm {rk}_z(M_u)\deg (\overline{\{z\}})\le e(M_\mu )p^n,\) where the sum is over the generic points of the n-dimensional irreducible components of p-supp(\(M_u\)).
By the equidimensionality of the p-supports (Theorem 3.1.1), there is a dense open subset \(U\subset U_e\) such that for all closed points u of U, all the irreducible components of p-\(supp(M_u)\) are of dimension n. Hence we deduce that, for each z generic point of an irreducible component of p-supp(\(M_u\)), \(\mathrm {rk}_z(M_u)\deg (\overline{\{z\}})\le e(M_\mu )p^n\). This implies the second estimate of the theorem.
Finally, let u be a closed point in U of characteristic p. By [6, Theorem 2.2.3], \(F_*M_u\) is a left module over an Azumaya algebra of rank \(p^{2n}.\) Hence \((F_*M_u)_z\otimes \overline{k(z)}\) is by [19, Théorème 5.1 (i)] a left module over the algebra of \(p^n\times p^n\) matrices \(M_{p^n}(\overline{k(z)}),\) where \(\overline{k(z)}\) is an algebraic closure of k(z). Therefore by Morita theory there is a finite dimensional \(\overline{k(z)}\)-vector space V such that \((F_*M_u)_z\otimes \overline{k(z)} \simeq \overline{k(z)}^{p^n} \otimes _{\overline{k(z)}}V,\) where \(\overline{k(z)}^{p^n}\) is the standard left \(M_{p^n}(\overline{k(z)})\)-module. In particular \(\mathrm {rk}_z(M_u):=\dim _{k(z)}((F_*M_u)_z\otimes k(z))=\dim _{\overline{k(z)}}((F_*M_u))_z\otimes \overline{k(z)})\) is divisible by \(p^n.\) The first estimate of the theorem follows. \(\square \)
Remark 4.3.4
The first estimate was conjectured in [29, Conjecture 1].
5 The Brauer group and differential forms
Here we prove, in a first part, that the Azumaya algebra of differential operators splits on the regular locus of the p-support of a holonomic \(\mathcal {D}\)-module, for p large enough. See Theorem 5.1.4.
In a second part, we recollect some facts of differential calculus in positive characteristic. In particular, we consider the p-curvature exact sequence and a map arising from it which sends 1-forms to the Brauer group. The image of the canonical form is the class of the Azumaya algebra of differential operators. In view of the first part of the section and for later use in the proof of our main theorem, we describe its kernel.
5.1 Splittings of Azumaya algebras on the support of their modules
Let Y be a scheme and let \(\mathcal {A}\) be an Azumaya algebra on Y. Since \(\mathcal {A}\) is a coherent \(\mathcal {O}_Y\)-module, it is a coherent Noetherian ring and a left \(\mathcal {A}\)-module is coherent if and only if it is coherent as an \(\mathcal {O}_Y\)-module. Recall that an Azumaya algebra \(\mathcal {A}\) is said to split on Y if its class \([\mathcal {A}]\) in the Brauer group Br(Y) of Y is trivial.
Let M be a coherent left \(\mathcal {A}\)-module and let z be the generic point of an irreducible component of the support of the coherent \(\mathcal {O}_Y\)-module M. The next proposition shows that the rank \(\mathrm {rk}_z(M)\) of M at z constrains the order of \([\mathcal {A}|_{(\overline{\{z\}}^{red})^{reg}}]\) in \(Br((\overline{\{z\}}^{red})^{reg}).\)
We first prove a lemma.
Lemma 5.1.1
Let Y be a scheme and let \(\mathcal {A}\) be an Azumaya algebra of rank \(r^2\) on Y. Suppose that \(\mathcal {A}\) acts on the left on a locally free sheaf \(\mathcal {V}\) of rank v. Then r divides \(v=lr\) and \(l[\mathcal {A}]=0\) in Br(Y).
Proof
By hypothesis there is a morphism of \(\mathcal {O}_Y\)-algebras \(\mathcal {A} \rightarrow \mathcal {E}nd_{\mathcal {O}_Y}(\mathcal {V}),\) sending 1 to 1. It is injective by [16, Proposition 0.5.5.4] since the fiber of \(\mathcal {A}\) at each point of Y is a simple algebra by [19, Théorème 5.1 (i)]. Therefore one may view \(\mathcal {A}\) as a subalgebra of \(\mathcal {E}nd_{\mathcal {O}_Y}(\mathcal {V})\) and in particular consider the commutant \(\mathcal {C}_{\mathcal {E}nd_{\mathcal {O}_Y}(\mathcal {V})}(\mathcal {A})\) of \(\mathcal {A}\) in \(\mathcal {E}nd_{\mathcal {O}_Y}(\mathcal {V}),\) which is a coherent subalgebra of \(\mathcal {E}nd_{\mathcal {O}_Y}(\mathcal {V}).\) By [1, Theorem 3.3], the natural morphism of \(\mathcal {O}_Y\)-algebras \(\mathcal {A}\otimes _{\mathcal {O}_Y}\mathcal {C}_{\mathcal {E}nd_{\mathcal {O}_Y}(\mathcal {V})}(\mathcal {A})\rightarrow \mathcal {E}nd_{\mathcal {O}_Y}(\mathcal {V})\) is an isomorphism and \(\mathcal {C}_{\mathcal {E}nd_{\mathcal {O}_Y}(\mathcal {V})}(\mathcal {A})\) is an Azumaya algebra on Y. Hence by the behaviour of ranks under tensor products, \(\mathcal {C}_{\mathcal {E}nd_{\mathcal {O}_Y}(\mathcal {V})}(\mathcal {A})\) is of constant rank \(l^2,\) such that \(v=lr\). By definition of the Brauer group \(0=[\mathcal {E}nd_{\mathcal {O}_Y}(\mathcal {V})]=[\mathcal {A}]+[\mathcal {C}_{\mathcal {E}nd_{\mathcal {O}_Y}(\mathcal {V})}(\mathcal {A})]\) in Br(Y). The lemma follows since for each Azumaya algebra \(\mathcal {B}\) of rank \(n^2\) on Y, \(n[\mathcal {B}]=0\) in Br(Y) [19, §2] giving \(0=l[\mathcal {A}]+l[\mathcal {C}_{\mathcal {E}nd_{\mathcal {O}_Y}(\mathcal {V})}(\mathcal {A})]=l[\mathcal {A}].\)\(\square \)
Proposition 5.1.2
Suppose that Y is of finite type over a field K. Let \(\mathcal {A}\) be an Azumaya algebra of rank \(r^2\) on Y, let M be a coherent left \(\mathcal {A}\)-module and let z be the generic point of an irreducible component \(\overline{\{z\}}\) of supp(M). Then r divides \(\mathrm {rk}_z(M)=l_z(M)r\) and
in \(Br((\overline{\{z\}}^{red})^{reg}).\)
Proof
Since the vector space \(M_z\otimes k(z)\) is of dimension \(\mathrm {rk}_z(M)\) and acted upon on the left by the rank \(r^2\) Azumaya algebra \(\mathcal {A}_z\otimes k(z),\) Lemma 5.1.1 implies that \(\mathrm {rk}_z(M)=l_z(M)r\) and \(l_z(M)[\mathcal {A}_z\otimes k(z)]=0\) in Br(k(z)). Moreover the restriction of \(\mathcal {A}\) to the regular locus of the irreducible component satisfies \(\mathcal {A}_z\otimes k(z)\cong (\mathcal {A}|_{\overline{\{z\}}^{red}})_z\otimes k(z) \cong (\mathcal {A}|_{(\overline{\{z\}}^{red})^{reg}})_z\otimes k(z).\) The proposition then follows from the canonical embedding \(Br((\overline{\{z\}}^{red})^{reg}) \hookrightarrow Br(k(z)),\) see [30, IV Corollary 2.6]. \(\square \)
The following combines Proposition 5.1.2 with the second estimate of Theorem 4.3.3.
Theorem 5.1.3
Let S be an integral scheme dominant and of finite type over \(\mathbb {Z}\) and let M be a coherent left \(D_{\mathbb {A}^n_S/S}\)-module. Let \(\mu \) be the generic point of S. Suppose that \(M_{\mu }\) is a nonzero holonomic left \(D_{\mathbb {A}^n_{k(\mu )}}\)-module. Then there is a dense open subset U of S such that for each closed point \(u\in U\) and each z generic point of an irreducible component of p-supp(\(M_u\)), the Azumaya algebra \(F_*D_{\mathbb {A}^n_{k(u)}}\) on \(T^*_{(\mathbb {A}^n_{k(u)})'}\) splits on \((\overline{\{z\}}^{red})^{reg}.\)
Proof
By Theorem 4.3.3 and using its notations, there is a dense open subset \(U_b\) of S such that for each closed point \(u\in U_b\) and each z generic point of an irreducible component of p-supp(\(M_u\)), \(\mathrm {rk}_z(M_u) \le e(M_\mu )p^n\) where p is the characteristic of the residue field k(u). Thus using Proposition 5.1.2 and its notations, we have \(l_z(M_u)\le e(M_\mu )\) and \(l_z(M_u)[F_*D_{\mathbb {A}^n_{k(u)}}|_{(\overline{\{z\}}^{red})^{reg}}]=0\) in \(Br((\overline{\{z\}}^{red})^{reg}).\) Note that by definition \(l_z(M_u)\ne 0\) and hence for \(u \in U\) the open dense subset of \(U_b\) defined by inverting all the primes \(\le e(M_\mu )\), \(l_z(M_u)\) and \(p^n\) are coprime, that is there are integers a and b such that \(1=al_z(M_u)+bp^n.\) Since \(F_*D_{\mathbb {A}^n_{k(u)}}\) is of rank \(p^{2n}\), \(p^n[F_*D_{\mathbb {A}^n_{k(u)}}|_{(\overline{\{z\}}^{red})^{reg}}]=0\) by [19, §2] and the theorem follows from \([F_*D_{\mathbb {A}^n_{k(u)}}|_{(\overline{\{z\}}^{red})^{reg}}] =1[F_*D_{\mathbb {A}^n_{k(u)}}|_{(\overline{\{z\}}^{red})^{reg}}] \)
\(\square \)
As a corollary, we have the following.
Theorem 5.1.4
Let S be an integral scheme dominant and of finite type over \(\mathbb {Z}\), let X be a smooth S-scheme of relative dimension n and let M be a coherent left \(D_{X/S}\)-module. Suppose that the fiber of M at the generic point \(\mu \) of S is a holonomic left \(D_{X_\mu }\)-module. Then there is a dense open subset U of S such that for each closed point u of U, the Azumaya algebra \(F_*D_{X_u}\) on \(T^*_{X'_u}\) splits on the regular locus of the p-support \(p\text {-}supp(M_u)^{reg}.\)
Proof
If \(M_\mu = 0,\) the theorem is trivial by Remark 2.3.2. We thus suppose that \(M_\mu \) does not vanish.
By the canonical injection of the Brauer group for the Zariski site (i.e. the classes of Azumaya algebras which are Zariski-locally isomorphic to an algebra of matrices) into the Zariski cohomology \(H^2(Y,\mathcal {O}_Y^\times )\) ([19, (2.1)]), the case \(i=2\) of Lemma 5.1.5 below implies that on a regular (Noetherian) scheme for an Azumaya algebra to be split is a Zariski-local condition.
Therefore by Remark 2.3.1, one may further assume that S and X are regular integral and affine and in particular that there is a closed immersion \(X \overset{f}{\hookrightarrow }\mathbb {A}^m_S\) over S.
Let us specialize to a closed point u of positive characteristic p of S. Since \(f'_d\) is smooth by Lemma A.0.2, the description of \(p\text {-}supp(H^0(f_u)_+M_u)\) given in the proof of Proposition 2.4.1, of which we use the notations, implies that \(p\textit{-supp}(H^0(f_u)_+M_u)^{reg}= ({f_u'})_{\pi }\circ ({f_u'})_d^{-1}(p\text {-}supp(M_u)^{reg}).\)
By [5, Proposition 3.7], \({f'_d}^*(F_*D_{X_u})\) splits on \({f'_d}^{-1}(p\text {-}supp(M_u)^{reg})\) if \(F_*D_{\mathbb {A}^m_{k(u)}}\) splits on the regular locus of \(p\textit{-supp}(H^0(f_u)_+M_u).\) Moreover the pullback of Brauer classes \({f'_d}^*\) induces an injective morphism of Brauer groups \(Br(p\text {-}supp(M_u)^{reg}) \hookrightarrow Br({f'_d}^{-1}(p\text {-}supp(M_u)^{reg})).\) Indeed \(f'_d\) Zariski-locally admits a section by Lemma A.0.2 and, on the regular locus, being split is Zariski-local as we explained above. So \(F_*D_{X_u}\) splits on the regular locus of \(p\text {-}supp(M_u)\) if \(F_*D_{\mathbb {A}^m_{k(u)}}\) splits on \(p\textit{-supp}(H^0(f_u)_+M_u)^{reg}.\)
Finally, an Azumaya algebra splits on a regular Noetherian scheme if and only if it splits on its irreducible components. Thus the theorem follows from Theorem 5.1.3. \(\square \)
Lemma 5.1.5
Let Y be a noetherian scheme. If Y is locally factorial, i.e. its local rings are UFD, then the Zariski cohomology \(H^i(Y,\mathcal {O}_Y^\times )=0,\) for all \(i\ge 2.\)
Proof
By definition of the sheaf \(\mathcal {D}iv_Y\) of Cartier divisors there is an exact sequence of abelian sheaves \(0\rightarrow \mathcal {O}_Y^\times \rightarrow \mathcal {K}_Y^\times \rightarrow \mathcal {D}iv_Y\rightarrow 0\) on Y, where \(\mathcal {K}_Y\) is the sheaf of meromorphic functions and \(\mathcal {O}_Y^\times \rightarrow \mathcal {K}_Y^\times \) is the natural injection. If Y is locally factorial then it is the sum of its (finitely many) irreducible components, each of which is integral, by [16, Proposition 4.5.5]. Hence if \(Y_i \overset{f_i}{\hookrightarrow }Y\) is the open immersion of the i-th irreducible component, then \(\mathcal {K}_Y^\times \cong \Pi _i {f_i}_*\mathcal {K}_{Y_i}^\times .\) Moreover \(\mathcal {K}_{Y_i}^\times \) is isomorphic to the constant sheaf associated to \(k(y_i)^\times \) for \(y_i\) the generic point of \(Y_i.\) In particular \(\mathcal {K}_Y^\times \) is flasque. Since \(\mathcal {D}iv_Y\) is flasque by [18, Corollaire 21.6.11], \(\mathcal {K}_Y^\times \rightarrow \mathcal {D}iv_Y\) is a flasque right resolution of \(\mathcal {O}_Y^\times ,\) vanishing in degrees \(\ge 2.\) The result follows as sheaf cohomology may be computed using flasque resolutions. \(\square \)
5.2 The Brauer group via the p-curvature exact sequence
Let Y be a smooth scheme over a perfect field K of positive characteristic p. Let \(Y \xrightarrow {F} Y'\) be the relative Frobenius morphism and let \(Y'\xrightarrow {W}Y\) be the projection. We denote by \(\bigoplus _{i\in \mathbb {Z}} \Omega ^{i}_{Y'} \xrightarrow {C_Y^{-1}} \bigoplus _{i\in \mathbb {Z}} \mathcal {H}^{i}(F_*\Omega ^{\bullet }_Y)\) the Cartier isomorphism, see [27, Theorem 7.2].
Definition 5.2.1
The Cartier operator is the composed morphism
where \(Z^i(F_*\Omega ^\bullet _Y):= \ker (F_*\Omega ^i_Y \xrightarrow {F_*d} F_*\Omega ^{i+1}_Y)\) is the sheaf of closed i-forms and \(\pi \) is the quotient morphism.
Recall that there is an exact sequence of étale sheaves on \(Y'\):
where \(dlog(y):= dy/y\) for all local sections y of \(\mathbb {G}_{\,m/Y}\) and \(W^{\star }\) is induced by the pullback on forms, see [24, Corollaire 0.2.1.18].
Definition 5.2.2
The exact sequence (5.2.1) is the p-curvature exact sequence and the morphism \(F_*Z^1(\Omega ^{\bullet }_Y) \xrightarrow {W^{\star }-C_Y} \Omega ^{1}_{Y'}\) is the p-curvature operator.
The p-curvature exact sequence (5.2.1) decomposes into two short exact sequences of étale sheaves on \(Y':\)
Composing the coboundary morphisms of the corresponding étale cohomology long exact sequences, one deduces a morphism:
Proposition 5.2.3
The morphism \(H^0(Y',\Omega ^{1}_{Y'}) \xrightarrow {\Psi _Y} H^2(Y',\mathbb {G}_{\,m/Y'})\) factors uniquely through the canonical embedding \(Br(Y')_p\hookrightarrow H^2(Y',\mathbb {G}_{\,m/Y'}),\) where \(Br(Y')_p\) is the kernel of multiplication by p in \(Br(Y').\)
Proof
This is well-known. By construction \(\Psi _Y\) factors through
the end maps being the natural ones. Moreover by [23, Proposition 2.1], the image of \(\ker H^2(F^*)\hookrightarrow H^2(Y',\mathbb {G}_{\,m/Y'})\) is the kernel \(H^2(Y',\mathbb {G}_{\,m/Y'})_p\) of multiplication by p, the latter being the image of the canonical embedding \(Br(Y')_p\hookrightarrow H^2(Y',\mathbb {G}_{\,m/Y'}).\)\(\square \)
Definition 5.2.4
The morphism deduced from Proposition 5.2.3 is denoted \(H^0(Y',\Omega ^{1}_{Y'}) \xrightarrow {\phi _Y} Br(Y')_p.\)
Remark 5.2.5
Here is another description of \(\phi _Y,\) from [31, Remark 4.3]:
Let \(\alpha \in H^0(Y',\Omega ^{1}_{Y'}),\) then \(\phi _Y(\alpha )=[s_{\alpha }^*(F_*D_{Y})] \in Br(Y'),\) where \(Y' \overset{s_{\alpha }}{\rightarrow }T^*_{Y'}\) is the section of \(T^*_{Y'}/Y'\) corresponding to \(\alpha .\)
The morphism \(\phi _Y\) depends functorially on Y:
Lemma 5.2.6
Let \(Z\xrightarrow {f} Y\) be a K-morphism of smooth K-schemes, \(Z'\xrightarrow {f'} Y'\) its base-change by Frobenius and let \(\alpha \in H^0(Y',\Omega ^1_{Y'}).\) Then \(f'^*\phi _Y(\alpha )=\phi _Z((f'^*)^{ad}\alpha ),\) where \(f'^*\) on the left (resp. on the right) is the pullback of classes in the Brauer group (resp. pullback of forms) by \(f'\).
Proof
Set \(\mathcal {D}_Y:= F_*D_{Y}\) and \(\mathcal {D}_Z:= F_*D_{Z}.\) With the notations of the “Appendix”, we have: By Remark 5.2.5, \(\phi _Z((f'^*)^{ad}\alpha )=[s_{(f'^*)^{ad}\alpha }^*(\mathcal {D}_Z)].\) And \([s_{(f'^*)^{ad}\alpha }^*(\mathcal {D}_Z)]=[(f'_d \circ (Z\times _Ys_{\alpha }))^*(\mathcal {D}_Z)],\) since \(s_{(f'^*)^{ad}\alpha }=f'_d \circ Z\times _Ys_{\alpha },\) by Remark A.0.1. Moreover by [5, Proposition 3.7], \([{f'_d}^*(\mathcal {D}_Z)]=[{f'_{\pi }}^*(\mathcal {D}_Y)].\) Hence \([(f'_d \circ (Z\times _Ys_{\alpha }))^*(\mathcal {D}_Z)]=[(Z\times _Ys_{\alpha })^*{f'_d}^*(\mathcal {D}_Z)] =[(Z\times _Ys_{\alpha })^*{f'_{\pi }}^*(\mathcal {D}_Y)] =[(f'_{\pi } \circ (Z\times _Ys_{\alpha }))^*(\mathcal {D}_Y)]=[(s_{\alpha }\circ f')^*(\mathcal {D}_Y)],\) using the equality \(f'_{\pi } \circ (Z\times _Ys_{\alpha }) = s_{\alpha }\circ f'.\) Finally by Remark 5.2.5, the last term is equal to \(f'^*\phi _Y(\alpha ),\) as stated. \(\square \)
By construction \(\phi _Y\) factors through \({\text {coker}}H^0(W^{\star }-C_{Y})\) and we denote the resulting map by \({\text {coker}}H^0(W^{\star }-C_{Y}) \xrightarrow {\overline{\phi _Y}} Br(Y')_p.\) The following proposition provides information on the kernel of \(\phi _Y.\)
Proposition 5.2.7
Suppose further that Y is affine. Then there is an exact sequence, commuting with restriction to affine open subsets:
Proof
This is a special case of [23, Corollary 1.7]. \(\square \)
Let us now specialize to the case \(Y=T^*_X,\) with X is a smooth K-scheme. Let \(X \xrightarrow {F_X} X'\) be the Frobenius morphism and \(X' \xrightarrow {W_X} X\) the projection.
Remark 5.2.8
The pullback of forms \(W_X^*\Omega ^1_X \xrightarrow {W_X^*}\Omega ^1_{X'}\) is an isomorphism and induces an isomorphism \({T^*_X}'\tilde{\rightarrow } T^*_{X'}.\) We use this isomorphism to identify \({T^*_X}'\) and \(T^*_{X'}.\)
We have the following description of the Brauer class of the algebra of differential operators in terms of \(\phi :\)
Proposition 5.2.9
Let \(\theta _{X'}\) be the canonical 1-form on \(T^*_{X'},\) see Definition A.0.3. Then \(\phi _{T^*_X}(\theta _{X'})\) is the class of the algebra of differential operators \({F_X}_*D_X\) in the Brauer group \(Br(T^*_{X'}).\)
Proof
This follows from [31, Propositions 4.4 and 4.2]. (See also [5, Proposition 3.11].) \(\square \)
6 Lagrangianity
In this section, we complete the proof of Theorem 2.2.1.
6.1 Nice compactification of the p-supports
Here for p large enough, we show the existence of normal-crossings compactifications of the regular locus of the p-supports which are well-behaved as p varies. The poles of the canonical form at infinity of this nice compactification have nice properties. This will allow us to transfer characteristic zero results to p-supports.
6.1.1 Poles
To fix notations, we first recall some definitions. Let S be a scheme, let \(\overline{Y}\) be a smooth S-scheme and let \(D\subset \overline{Y}\) be a divisor with normal crossings relative to S, defined by the invertible ideal sheaf I. Denote by  the affine open embedding complement to D. For an \(\mathcal {O}_{\overline{Y}}\)-module \(\mathcal {F}\) and \(n\in \mathbb {Z},\) we let \(\mathcal {F}(nD)\) denote \(\mathcal {F}\otimes _{\mathcal {O}_{\overline{Y}}}\mathcal {I}^{\otimes _{\mathcal {O}_{\overline{Y}}}(-n)}.\) We have \(j_*\Omega ^m_{Y/S}= \bigcup _{n\ge 0}\Omega ^m_{\overline{Y}/S}(nD),\) where \(\Omega ^m_{Y/S}\) is the sheaf of relative differential forms of degree m on Y / S. Note that if S is the spectrum of a field and when there is no risk of confusion, we will (and have already) commit the abuse of notation to denote \(\Omega ^m_{Y/S}\) by \(\Omega ^m_{Y}.\)
the affine open embedding complement to D. For an \(\mathcal {O}_{\overline{Y}}\)-module \(\mathcal {F}\) and \(n\in \mathbb {Z},\) we let \(\mathcal {F}(nD)\) denote \(\mathcal {F}\otimes _{\mathcal {O}_{\overline{Y}}}\mathcal {I}^{\otimes _{\mathcal {O}_{\overline{Y}}}(-n)}.\) We have \(j_*\Omega ^m_{Y/S}= \bigcup _{n\ge 0}\Omega ^m_{\overline{Y}/S}(nD),\) where \(\Omega ^m_{Y/S}\) is the sheaf of relative differential forms of degree m on Y / S. Note that if S is the spectrum of a field and when there is no risk of confusion, we will (and have already) commit the abuse of notation to denote \(\Omega ^m_{Y/S}\) by \(\Omega ^m_{Y}.\)
Definition 6.1.1
A local section of \(j_*{\Omega }^m_{Y/S}\) which is in \({\Omega }^m_{\overline{Y}/S}(nD)\) is said to have poles of order at most n along D.
We denote the logarithmic de Rham complex by \((\Omega ^{\bullet }_{\overline{Y}/S}(logD), d),\) see [12, II §3]. It is a subcomplex of \(j_*(\Omega ^{\bullet }_{Y/S}, d_{Y/S}).\)
Definition 6.1.2
A local section of \(j_*\Omega ^m_{Y/S}\) which is in \(\Omega ^m_{\overline{Y}/S}(logD)\) is said to have logarithmic poles along D.
6.1.2 Hilbert scheme
Let us fix coordinates \(\{x_1, \dots , x_n\}\) on \(\mathbb {A}^n_{\mathbb {Z}}.\) They induce by base-change coordinates \(\{x_1, \dots , x_n\}\) on \(\mathbb {A}^n_S\) and \(\{x_1, \dots , x_n, y_1, \dots , y_n\}\) on its relative cotangent space \(T^*_{\mathbb {A}^n_S},\) for any scheme S. We thus have a filtration of \(\mathcal {O}_{T^*_{\mathbb {A}^n_S}}\) by the order in \(\{x_1, \dots , x_n, y_1, \dots , y_n\}\) and an open embedding \(T^*_{\mathbb {A}^n_S} \hookrightarrow \mathbb {P}^{2n}_S,\) by the Rees construction (Proposition 4.3.1). If S is the spectrum of a field K of positive characteristic, we also deduce identifications of the base-change by Frobenius \((\mathbb {A}^n_K)' = \mathbb {A}^n_K\) and \(T^*_{(\mathbb {A}^n_K)'}= T^*_{\mathbb {A}^n_K}.\) This embedding is the same as that considered on page 20.
Let \(P\in \mathbb {Q}[X]\) be a rational polynomial and let \(\mathcal {H}:= \mathcal {H}ilb^P_{\mathbb {P}^{2n}_{\mathbb {Z}}}\) be the Hilbert scheme of \(\mathbb {P}^{2n}_{\mathbb {Z}}\) of index P, see [20, p. 17]. We let \(\mathcal {Z}_{\mathcal {H}} \subset \mathbb {P}^{2n}_{\mathbb {Z}}\times _{{\text {Spec}}(\mathbb {Z})}\mathcal {H}\) be the associated universal flat closed subscheme. The following definition is convenient:
Definition 6.1.3
A (locally closed) subscheme  is nice if
is nice if
-
(1)
\(\mathcal {S}\) is irreducible and generically of characteristic 0,
-
(2)
Let \(\mathcal {Z}\) be the restriction \(\mathcal {Z}_{\mathcal {H}}\times _{\mathcal {H}}\mathcal {S}\) of \(\mathcal {Z}_{\mathcal {H}}\) to \(\mathcal {S}.\) There exists an open \(U\subset \mathcal {Z}^{red}\) surjecting onto \(\mathcal {S}\) and an open immersion
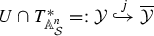 such that \(\overline{\mathcal {Y}}\) is a smooth projective \(\mathcal {S}\)-scheme and the complement \(\Delta \) of j is a divisor with normal crossings relative to \(\mathcal {S},\)
such that \(\overline{\mathcal {Y}}\) is a smooth projective \(\mathcal {S}\)-scheme and the complement \(\Delta \) of j is a divisor with normal crossings relative to \(\mathcal {S},\) -
(3)
Let \(\mu \) be the generic point of \(\mathcal {S}.\) Then \((d\theta _{\mathbb {A}^n_{\mathcal {S}}}|_\mathcal {Y})= 0\) if and only if \((d\theta _{\mathbb {A}^n_{\mathcal {S}}}|_\mathcal {Y})_\mu =0,\)
-
(4)
The restriction \(d\theta _{\mathbb {A}^n_{\mathcal {S}}}|_\mathcal {Y}\) of the symplectic form \(d\theta _{\mathbb {A}^n_{\mathcal {S}}}\) to \(\mathcal {Y}\) has logarithmic poles along \(\Delta \) if and only if there exists a closed point \(s\in \mathcal {S}\) such that the fiber \((d\theta _{\mathbb {A}^n_{\mathcal {S}}}|_\mathcal {Y})_s\) has logarithmic poles along \(\Delta _s.\)
We may now state and prove the existence of compactification result.
Proposition 6.1.4
There exists a positive integer N such that \(\mathcal {H}[\frac{1}{N}]\) has a finite partition into nice subschemes.
Proof
Let \(X\hookrightarrow \mathcal {H}\) be a subscheme. Denote P(X) the property that there exists an integer \(N_X>0\) such that \(X[\frac{1}{N_X}]\) is empty or admits a partition into nice subschemes of \(\mathcal {H}.\) We have P(X) if and only if \(P(X^{red})\) holds. Let us prove P(X) holds for all reduced closed subschemes X of \(\mathcal {H},\) by Noetherian induction.
Let \(S\hookrightarrow \mathcal {H}\) be a reduced subscheme. By Noetherian induction, we assume P(T) holds for all reduced closed subschemes T of S, distinct from S. Clearly there is an integer \(N>0\) such that the irreducible components of \(S[\frac{1}{N}]\) have all generic points of characteristic zero. If \(S[\frac{1}{N}]\) is empty then we have P(S). We thus from now on assume that \(S[\frac{1}{N}]\) is not empty.
Let \(z\in S[1/N]\) be the generic point of an irreducible component and let \(\mathcal {Z}_z\) be the fiber of \((\mathcal {Z}_{\mathcal {H}}\times _{\mathcal {H}}S[1/N])^{red}\) at z. Then \(\mathcal {Z}_z\subset \mathbb {P}^{2n}_{k(z)}\) is a scheme of finite type over the field of characteristic zero k(z). It is reduced by [18, Proposition 8.7.2 a)] and hence contains an open dense smooth subset \(U\subset \mathcal {Z}_z.\) By the resolution of singularities in characteristic zero, there is an open immersion \(Y \overset{j}{\hookrightarrow }\overline{Y}\) of the quasi-projective variety \(Y:=U\cap T^*_{\mathbb {A}^n_{k(z)}}\subset \mathbb {P}^{2n}_{k(z)}\) into a smooth projective scheme \(\overline{Y}\) over k(z) which is the complement of a divisor D with normal crossings relative to k(z). Hence by [18, Théorème 8.10.5 and Proposition 17.7.8], there are an open affine neighborhood \(\mathcal {T}\) of z, a non-empty smooth open subset \(\mathcal {U}\subset (\mathcal {Z}_{\mathcal {H}}\times _{\mathcal {H}}\mathcal {T})^{red}\) and an open \(\mathcal {T}\)-immersion \(\mathcal {U}\cap T^*_{\mathbb {A}^n_\mathcal {T}}=:\mathcal {Y} \overset{j}{\hookrightarrow }\overline{\mathcal {Y}}\) into a smooth projective \(\mathcal {T}\)-scheme which is the complement of a divisor \(\mathcal {D}\) with normal crossings relative to \(\mathcal {T}.\) Moreover, since smooth morphisms are open, \(\mathcal {T}\) may be chosen such that \(\mathcal {U}\) surjects on \(\mathcal {T}.\) Finally by [16, Proposition 2.1.9 (ii)] it can also be chosen to be integral and hence irreducible, since S is reduced.
Let \(\theta \) be the restriction to \(\mathcal {Y}\) of the canonical form \(\theta _{\mathbb {A}^n_{\mathcal {T}}/\mathcal {T}}\) on \(T^*_{\mathbb {A}^n_{\mathcal {T}}}.\) If \(d\theta \) vanishes on the generic fiber \(\mathcal {Y}_z,\) then there is a dense open subset \(V\subset \mathcal {T}\) above which \(d\theta \) vanishes. If \(d\theta \) does not vanish on the generic fiber of \(\mathcal {Y},\) then we set \(V =\mathcal {T}.\)
Finally, there is a dense open subset \(W\subset V\) such that \(d\theta |_{\mathcal {Y}|_W}\) has logarithmic poles along \(\mathcal {D}|_W\) as soon as there is a fiber on which it has logarithmic poles. Indeed there is a closed subset \(\mathcal {L}\) of V such that for all closed points \(v \in V,\)\(d\theta |_{\mathcal {Y}_v}\) has logarithmic poles along \(\mathcal {D}_v\) if and only if \(v\in \mathcal {L}.\) We prove it as follows. There is an integer \(m>0\) such that \(d\theta |_{\mathcal {Y}}\) is a section of the locally free \(\mathcal {O}_{\overline{\mathcal {Y}}}\)-module \({\Omega }^2_{\overline{\mathcal {Y}}/V}(m\mathcal {D}).\) Let us locally choose a basis \(\{b_1, \dots , b_j\}\) of \({\Omega }^2_{\overline{\mathcal {Y}}/V}(m\mathcal {D})\) extending a basis \(\{b_1, \dots , b_l\}\) of \({\Omega }^2_{\overline{\mathcal {Y}}/V}(log\mathcal {D}) \subset {\Omega }^2_{\overline{\mathcal {Y}}/V}(m\mathcal {D})\) such that for each closed point \(v\in V,\) the restriction \(\{b_1|_{\mathcal {Y}_v}, \dots , b_j|_{\mathcal {Y}_v}\}\) is a basis of \({\Omega }^2_{\overline{\mathcal {Y}}_v}(m\mathcal {D}_v)\) extending a basis \(\{b_1|_{\mathcal {Y}_v}, \dots , b_l|_{\mathcal {Y}_v}\}\) of \({\Omega }^2_{\overline{\mathcal {Y}}_v}(log\mathcal {D}_v).\) That such a basis exists follows from the case of \((\mathbb {A}^d_V, \{x_1\dots x_r = 0\}),\) which is immediate. Locally we thus have \(d\theta |_{\mathcal {Y}}= \Sigma _{i=1}^{i=j} \alpha _ib_i\) for some unique sections \(\alpha _1, \dots , \alpha _j\) of \(\mathcal {O}_{\overline{\mathcal {Y}}}.\) Moreover its restriction \(d\theta |_{\mathcal {Y}_v}\) has logarithmic poles along \(\mathcal {D}_v\) if and only if the restrictions \(\alpha _{l+1}|_{\overline{\mathcal {Y}}_v}, \dots , \alpha _j|_{\overline{\mathcal {Y}}_v}\) vanish. Let \(O \subset \overline{\mathcal {Y}}\) be the open complement of the closed subset of \(\overline{\mathcal {Y}}\) locally given by \(\{\alpha _{l+1}=\dots =\alpha _j=0\}.\) For each closed point \(v\in V,\) we thus have that \(d\theta |_{\mathcal {Y}_v}\) has logarithmic poles along \(\mathcal {D}_v\) if and only if \(O\cap \overline{\mathcal {Y}}_v\) is empty, that is \(v\not \in \pi (O),\) where \(\pi \) is the structure map \(\overline{\mathcal {Y}}\rightarrow V.\) But \(\pi (O)\) is open since \(\pi \) is smooth and thus open. We have that \(\mathcal {L}\) is the complement of \(\pi (O).\) If \(\mathcal {L}\subsetneq V,\) then we let W be the open complement \(V\setminus \mathcal {L}.\) Otherwise we set \(W=V.\)
Thus we have found a nice non-empty open subset \(W\subseteq S.\) Since by Noetherian induction we have \(P(S\setminus W),\) it follows immediately that we have P(S). This concludes the proof of the proposition. \(\square \)
6.2 Action of the p-curvature operator on the order of poles
Let \(\eta \) be a 1-form in the image of the p-curvature operator. Here we will show that if \(\eta \) has poles of small order (i.e. \(\le p-1\)), then its exterior derivative \(d\eta \) has at most simple poles and hence has logarithmic poles. The following definition is convenient.
Definition 6.2.1
Let D be a divisor in a smooth variety X over a field K. Etale coordinates \(\{x_1, \dots , x_n\}: V_x \rightarrow \mathbb {A}^n_K\) in the neighbourhood \(V_x\) of a point \(x\in X\) are D-good, or good if there is no risk of confusion, if there is \(0\le r\le n\) such that \(D\cap V_x=\{x_1\dots x_r =0\}.\)
Thus \(D\subset X\) has normal crossings if and only if X has an étale covering \(\pi \) admitting \(\pi ^{-1}(D)\)-good étale coordinates in the neighbourhood of each of its points.
Throughout this subsection, \(\overline{Y}\) will denote a smooth variety over a perfect field K of positive characteristic p and \(D\subset \overline{Y}\) a normal crossings divisor of open complement  As above, we use ’ to denote the base-change by the Frobenius automorphism of K. Recall Definition 5.2.2 of the p-curvature operator \(F_*Z^1(\Omega ^{\bullet }_Y) \xrightarrow {W^{\star }-C_Y} \Omega ^{1}_{Y'}.\) Here is the main result of the subsection:
As above, we use ’ to denote the base-change by the Frobenius automorphism of K. Recall Definition 5.2.2 of the p-curvature operator \(F_*Z^1(\Omega ^{\bullet }_Y) \xrightarrow {W^{\star }-C_Y} \Omega ^{1}_{Y'}.\) Here is the main result of the subsection:
Proposition 6.2.2
Let \(\mathcal {I}m(W^{\star }-C_Y)\) be the image of abelian sheaves for the Zariski topology and let \(\mathcal {I}\) be the intersection of the subsheaves \({\Omega }^1_{\overline{Y}'}((p-1)D')\) and \(j'_*\mathcal {I}m(W^{\star }-C_Y)\) of \(j'_*\Omega ^{2}_{Y'}.\) Then \(d(\mathcal {I}) \subset \Omega ^2_{\overline{Y}'}(logD').\)
Proof
The assertion is étale local on \(\overline{Y}.\) Hence by definition of divisor with normal crossings, we may and do assume that there are good étale coordinates in the neighbourhood of every point of \(\overline{Y}.\) In this situation, let us prove that \(\mathcal {I}\subseteq j'_*B^1\Omega ^\bullet _{Y'} + \Omega ^1_{\overline{Y}'}(log D'),\) with \(B^1\Omega ^\bullet _{Y'}\) the exact 1-forms. This immediately implies the proposition.
Let \(\eta \) be a local section of \(\mathcal {I}.\) By Lemma 6.2.4, we may assume that locally, there is a local section \(\rho \in j'_*F_*Z^1(\Omega ^{\bullet }_Y)\) such that \(\eta = j'_*(W^{\star }-C_Y)\rho .\) Moreover, by \(p^{-1}\)-linearity of the Cartier operator \(C_Y,\) see [24, Lemme 0.2.5.4], \(\rho \) has poles of order at most \(p-1\) along D.
Hence by Lemma 6.2.3, \(\rho \) is locally a sum of an exact form and a closed form with logarithmic poles along D. The proposition follows since, by [27, (7.2.4) of Theorem 7.2], the Cartier operator \(C_Y\) preserves forms with logarithmic poles. \(\square \)
Lemma 6.2.3
Suppose that there are D-good étale coordinates in the neighbourhood of each point of \(\overline{Y}.\) Then there is an inclusion of quasi-coherent subsheaves of \(j'_*F_*\Omega ^1_Y\):
where \(B^1(F_*\Omega ^\bullet _Y):= \mathrm {Im}(F_*\mathcal {O}_Y \xrightarrow {F_*d} F_*\Omega ^1_Y)\) and \(Z^1(F_*\Omega ^\bullet _{\overline{Y}}(log D)):= \ker (F_*\Omega ^1_{\overline{Y}}(log D)\xrightarrow {F_*d}F_*\Omega ^2_{\overline{Y}}(log D)).\)
Proof
The assertion being local, we may assume that we have global good étale coordinates \(\overline{Y}\xrightarrow {\{y_1,\dots , y_n\}} \mathbb {A}^n_K.\) Moreover it is clear that the lemma reduces to \(\overline{Y}= \mathbb {A}^n_K\) by pullback. So we may assume that \((\overline{Y}, D)= (\mathbb {A}^n_K, \{y_1\dots y_r =0\})\) for some \(0\le r\le n,\) where \(\{y_1,\dots , y_n\}\) are coordinates on \(\mathbb {A}^n_K.\)
The coordinates induce a splitting of the canonical short exact sequence \(0\rightarrow B^1(F_*\Omega ^{\bullet }_Y)\rightarrow Z^1(F_*\Omega ^{\bullet }_Y)\xrightarrow {C_Y}{\Omega }^1_{Y'} \rightarrow 0\) by \({\Omega }^1_{Y'}\xrightarrow {\delta } Z^1(F_*\Omega ^{\bullet }_Y),\) sending a local section \(\sum \nolimits _{i=1}^{n} a_idy_i\) to \(\delta (\sum \nolimits _{i=1}^{n} a_idy_i)= \sum \nolimits _{i=1}^{n} a_i^py_i^{p-1}dy_i,\) where we have identified \(\mathbb {A}^n_K\) and its base-change by Frobenius using the coordinates. Applying \(j'_*\) we get that a local section \(\rho \) of \(j'_*Z^1(F_*\Omega ^\bullet _Y)\) may uniquely be written as a sum \(\rho = \rho _b+\rho _c,\) where \(\rho _b\) is a local section of \(j'_*B^1(F_*\Omega ^\bullet _Y),\) and \(\rho _c= \sum \nolimits _{i=1}^{n} a_i^py_i^{p-1}dy_i,\) with \(\{a_1, \dots , a_n\}\) uniquely determined local sections of \(j'_*\mathcal {O}_{Y'}.\)
Let us show that if \(\rho \) is a local section of \(j'_*Z^1(F_*\Omega ^\bullet _Y) \cap F_*\Omega ^1_{\overline{Y}}((p-1)D),\) then \(\rho _c\) is a local section of \(Z^1(F_*\Omega ^\bullet _{\overline{Y}}(log D)).\) This implies the lemma. First one sees immediately by a computation in coordinates that if \(\rho _c\) has poles of order at most \(p-1,\) then it actually has poles of order at most 1. Thus it has logarithmic poles along D, since it is closed.
We conclude the proof by showing that if \(\rho \) has poles of order at most \(p-1,\) then so does \(\rho _c\) (and hence \(\rho _b\)). Set \(h:= y_1\dots y_r.\) We claim that \((h^n\rho )_c= h^n\rho _c,\) for all \(n\ge 0,\) where the multiplication by \(h^n\) denotes here the action on \(\Omega ^1_Y.\) Since for all local sections \(\xi \) of \(j'_*Z^1(F_*\Omega ^\bullet _Y), \xi _c= j'_*\delta \circ j'_*C_Y(\xi )\) and \(j'_*\delta \circ j'_*C_Y\) preserves regular forms (i.e. forms having poles of order at most 0 along D), the claim indeed implies the assertion. But the claim is easily checked by adjoining to the domain \(\mathcal {O}(Y)\) all the p-th roots of its elements. Indeed the composition of the \(p^{-1}\)-linear morphism \(j'_*C_Y\) and the p-linear morphism \(j'_*\delta \) is linear. \(\square \)
Lemma 6.2.4
Let \(\overline{X}\) be a smooth variety over a perfect field K of positive characteristic p and let \(D\subset \overline{X}\) be a normal crossings divisor of open complement  Then the canonical inclusion \(\mathcal {I}m(j'_*(W^{\star }-C_X)) \hookrightarrow j'_*\mathcal {I}m(W^{\star }-C_X)\) is an isomorphism.
Then the canonical inclusion \(\mathcal {I}m(j'_*(W^{\star }-C_X)) \hookrightarrow j'_*\mathcal {I}m(W^{\star }-C_X)\) is an isomorphism.
Proof
The p-curvature exact sequence of abelian sheaves on \(X'\) for the Zariski topology \(0\rightarrow \mathcal {O}_{X'}^\times \xrightarrow {F^*} F_*\mathcal {O}_X^\times \xrightarrow {F_*dlog} Z^1(F_*\Omega ^{\bullet }_X) \xrightarrow {W^{\star }-C_X} \Omega ^{1}_{X'},\) see [24, Corollaire 0.2.1.18], breaks into two short exact sequences: \(0\rightarrow {\text {coker}}F^* \xrightarrow {F_*dlog} Z^1(F_*\Omega ^{\bullet }_X) \xrightarrow {W^{\star }-C_X} \mathcal {I}m(W^{\star }-C_X) \rightarrow 0\) and \(0\rightarrow \mathcal {O}_{X'}^\times \xrightarrow {F^*} F_*\mathcal {O}_X^\times \rightarrow {\text {coker}}F^* \rightarrow 0.\) The long exact sequence for \(Rj'_*\) of the former:
implies that the lemma follows from the vanishing of \(R^1j'_*{\text {coker}}F^*.\)
This in turn would follow from the vanishing of \(R^1j'_*(F_*\mathcal {O}_X^\times )\) and \(R^2j'_*\mathcal {O}_{X'}^\times ,\) by the long exact sequence for \(Rj'_*\) of the other short exact sequence:
But the direct image \(F_*\) preserves flasque sheaves and is exact, since F is a homeomorphism. Hence by [21, III Corollary 8.3], \(R^qF_*(G)=0\) for all abelian sheaves G and all \(q>0.\) Thus \(R^1j'_*(F_*\mathcal {O}_X^\times ) \cong R^1(j'_*\circ F_*)(\mathcal {O}_X^\times )=R^1(F_* \circ j_*)(\mathcal {O}_X^\times ) \cong F_*R^1j_*(\mathcal {O}_X^\times ).\) We have therefore shown that the Lemma is implied by the vanishing of \(R^1j_*(\mathcal {O}_X^\times )\) and \(R^2j'_*\mathcal {O}_{X'}^\times .\) This follows from Lemma 6.2.5 below, since smooth schemes are locally factorial. \(\square \)
Lemma 6.2.5
Let \(U \overset{j}{\hookrightarrow }Y\) be an open immersion. Suppose that Y is a locally factorial Noetherian scheme. Then \(R^qj_*(\mathcal {O}_U^\times )=0,\) for all \(q>0.\)
Proof
By [21, Proposition 8.1 of Chapter III], \(R^qj_*(\mathcal {O}_U^\times )\) is the abelian sheaf associated to the presheaf \(V \mapsto H^q(U\cap V,\mathcal {O}_{U\cap V}^\times ),\) for all V open in Y. But by Lemma 5.1.5, \(H^q(U\cap V,\mathcal {O}_{U\cap V}^\times )=0\) for all \(q\ge 2.\) Thus \(R^qj_*(\mathcal {O}_U^\times )=0,\) for all \(q\ge 2.\)
For \(q=1,\)\(R^1j_*(\mathcal {O}_U^\times )\) is the abelian sheaf associated to the presheaf of Picard groups: \(V \mapsto Pic(U\cap V),\) for all V open in Y. Let \(\mathcal {L}_{U\cap V} \in Pic(U\cap V).\) By [18, Corollaire 21.6.11], it extends to an invertible sheaf \(\mathcal {L}_V \in Pic(V).\) Hence \(\mathcal {L}_{U\cap V}\) is trivial on the restriction to U of an open covering of V trivializing \(\mathcal {L}_V.\) Thus the corresponding section of the associated sheaf \(R^1j_*(\mathcal {O}_U^\times )\) vanishes locally, hence is 0. This implies that \(R^1j_*(\mathcal {O}_U^\times )\) vanishes. \(\square \)
6.3 Conclusion
We now combine most of the results above to prove our main theorem.
Proof of Theorem 2.2.1
By Theorem 3.1.1, there is a dense open subset \(U_1\) of S such that p-supp\((M_u)\) is equidimensional of dimension n, for all closed points u of \(U_1.\)
By Proposition 2.4.1, we may assume that \(X/S=\mathbb {A}^n_S/S.\) Thus by Theorem 5.1.3, there is a dense open subset \(U_2\) of \(U_1\) such that the Azumaya algebra \(F_*D_{\mathbb {A}^n_{k(u)}}\) splits on the regular locus of each irreducible component of the p-support of \(M_u,\) for every closed point u of \(U_2.\) Let \(\theta _u= \theta _{(\mathbb {A}^n_{k(u)})'/{\text {Spec}}k(u)}\) be the canonical form on \(T^*_{(\mathbb {A}^n_{k(u)})'}.\) Then the restriction of \(\theta _u\) to the regular locus \(Z_u^{reg}\) of an irreducible component \(Z_u\) of p-supp\((M_u)\) is in the image of the p-curvature operator \(\mathcal {I}m(W^{\star }-C_{Z_u^{reg}}),\) where we have identified \(Z_u^{reg}\) with \({Z_u^{reg}}',\) as k(u) is perfect. This follows from the description of \(\ker \overline{\phi _Y}\) in Proposition 5.2.7, since \(\phi _{T^*_{\mathbb {A}^{n}_{k(u)}}}(\theta _u)\) is the class of \(F_*D_{\mathbb {A}^n_{k(u)}}\) in the Brauer group by Proposition 5.2.9 and \(\phi _Y\) is commutes with the pullback by Lemma 5.2.6.
By Theorem 4.3.3 and using its notations, there are a dense open subset \(U_3\) of \(U_2\) and an integer \(e>0\) such that for all closed points u of \(U_3,\) the degree of each irreducible component \(Z_u\) of the p-support of \(M_u\) is not larger than e. Hence the Hilbert polynomial of \(Z_u\) belongs to a finite set \(\{P_1, \dots , P_r\},\) independent of u. Indeed the Hilbert polynomial of \(Z_u\) is the same as that of \(Z_u \times _{{\text {Spec}}k(u)}{\text {Spec}}\overline{k(u)}\) for an algebraic closure \(\overline{k(u)}\) of the residue field k(u). We can then conclude using Chow coordinates, see [20, Lemme 2.4 and Théorème 2.1(b)]. Moreover by Proposition 6.1.4, there is an integer \(N>0\) such that the localization \(\coprod _{i=1}^{i=r}\mathcal {H}ilb^{P_i}_{\mathbb {P}^{2n}_{\mathbb {Z}}}[\frac{1}{N}]\) of the Hilbert scheme of index \(\{P_1, \dots , P_r\}\) has a finite partition into nice subschemes, see Definition 6.1.3. Hence, in particular, there are a dense open subset \(U_4\) of \(U_3\) and an integer \(N'>0\) satisfying the following. For all closed points u of \(U_4,\) each irreducible component \(Z_u\) of the p-support of \(M_u\) has a smooth dense open subset \(Y_u\subset Z_u\) embedding as an open into a smooth projective variety  with complement a divisor \(D_u\) with normal crossings. Moreover the restriction of the canonical form \(\theta _u|_{Y_u}\) has poles of order at most \(N'\) along \(D_u.\)
with complement a divisor \(D_u\) with normal crossings. Moreover the restriction of the canonical form \(\theta _u|_{Y_u}\) has poles of order at most \(N'\) along \(D_u.\)
Hence by further inverting a positive integer, there exists an open dense subset \(U_5\) of \(U_4\) such that for all closed points u of \(U_5, \theta _u|_{Y_u}\) has poles of order at most \(p_u-1\) along \(D_u,\) where \(p_u\) is the characteristic of k(u). Thus since \(\theta _u|_{Y_u}\) is in the image of the p-curvature operator, Proposition 6.2.2 implies that its exterior derivative \(d\theta _u|_{Y_u}\) has logarithmic poles along \(D_u.\)
By construction of \(\overline{Y_u}\) there are an irreducible \(U_5\)-scheme H generically of characteristic zero, a smooth projective H-scheme \(\overline{Y}\) and a divisor \(\Delta \) of \(\overline{Y}\) with normal crossings relative to H such that the complement \(Y:= \overline{Y}-\Delta \) is identified with an open in \(T^*_{\mathbb {A}^n_H}.\) And if we denote by  the open embedding, there is a closed point t of H such that \(j_u\) (resp. \(\theta _u|_{Y_u}\)) is the specialization of j (resp. \(\theta _{\mathbb {A}^n_H/H}|_Y\)) at t. By point (4) of the definition of nice subscheme, the above implies that \(d\theta _{\mathbb {A}^n_H/H}|_Y\) has logarithmic poles along \(\Delta .\) Hence so does its restriction \(d\theta _{\mathbb {A}^n_{k(\gamma )}}|_{Y_{\gamma }}\) to the fiber at the generic point \(\gamma \) of H. Clearly, being globally exact, the class of the symplectic form \(d\theta _{\mathbb {A}^n_{k(\gamma )}}|_{Y_{\gamma }}\) vanishes in the hypercohomology of the de Rham complex \(({j_{\gamma }}_*\Omega _{Y_{\gamma }}^\bullet , {j_{\gamma }}_*d).\) But since the residue field of \(\gamma \) is of characteristic zero, the canonical inclusion of complexes \(\Omega _{\overline{Y_{\gamma }}}(log \Delta _{\gamma }) \subset {j_{\gamma }}_*\Omega _{Y_{\gamma }}^\bullet \) is a quasi-isomorphism by [13, Proposition 3.1.8]. Hence the class of \(d\theta _{\mathbb {A}^n_{k(\gamma )}}|_{Y_{\gamma }}\) vanishes in the hypercohomology of the logarithmic de Rham complex, as well. Thus by the degeneracy at \(E_1\) of the logarithmic Hodge to de Rham spectral sequence ([13, Corollaire 3.2.13 (ii) and Corollaire 3.2.14]), \(d\theta _{\mathbb {A}^n_{k(\gamma )}}|_{Y_{\gamma }}=0.\) Therefore by point (3) of the definition of nice subscheme, \(d\theta _{\mathbb {A}^n_H/H}|_Y=0.\) It follows directly that for all closed points u of \(U_5, d\theta _u|_{Y_u}=0.\) This concludes the proof of the theorem. \(\square \)
the open embedding, there is a closed point t of H such that \(j_u\) (resp. \(\theta _u|_{Y_u}\)) is the specialization of j (resp. \(\theta _{\mathbb {A}^n_H/H}|_Y\)) at t. By point (4) of the definition of nice subscheme, the above implies that \(d\theta _{\mathbb {A}^n_H/H}|_Y\) has logarithmic poles along \(\Delta .\) Hence so does its restriction \(d\theta _{\mathbb {A}^n_{k(\gamma )}}|_{Y_{\gamma }}\) to the fiber at the generic point \(\gamma \) of H. Clearly, being globally exact, the class of the symplectic form \(d\theta _{\mathbb {A}^n_{k(\gamma )}}|_{Y_{\gamma }}\) vanishes in the hypercohomology of the de Rham complex \(({j_{\gamma }}_*\Omega _{Y_{\gamma }}^\bullet , {j_{\gamma }}_*d).\) But since the residue field of \(\gamma \) is of characteristic zero, the canonical inclusion of complexes \(\Omega _{\overline{Y_{\gamma }}}(log \Delta _{\gamma }) \subset {j_{\gamma }}_*\Omega _{Y_{\gamma }}^\bullet \) is a quasi-isomorphism by [13, Proposition 3.1.8]. Hence the class of \(d\theta _{\mathbb {A}^n_{k(\gamma )}}|_{Y_{\gamma }}\) vanishes in the hypercohomology of the logarithmic de Rham complex, as well. Thus by the degeneracy at \(E_1\) of the logarithmic Hodge to de Rham spectral sequence ([13, Corollaire 3.2.13 (ii) and Corollaire 3.2.14]), \(d\theta _{\mathbb {A}^n_{k(\gamma )}}|_{Y_{\gamma }}=0.\) Therefore by point (3) of the definition of nice subscheme, \(d\theta _{\mathbb {A}^n_H/H}|_Y=0.\) It follows directly that for all closed points u of \(U_5, d\theta _u|_{Y_u}=0.\) This concludes the proof of the theorem. \(\square \)
Let us explain how our results imply the involutivity of the singular support of a holonomic \(\mathcal {D}\)-module M. The latter is an important special case of the involutivity of the singular support of an arbitrary nonzero coherent \(\mathcal {D}\)-module, which was originally proved in [26]. A purely algebraic proof was later given in [15].
Corollary 6.3.1
Let Y be a smooth variety over a field L of characteristic zero and let M be a nonzero holonomic left \(\mathcal {D}_Y\)-module. Then the singular support of M is a Lagrangian subvariety of \((T^*_Y, \omega _Y).\)
Proof
The corollary immediately reduces to an equidimensional and affine Y. One proves that the singular support is equidimensional of dimension \(\dim Y\) by the methods of Sect. 3, purely in characteristic zero, see e.g. [8, A:IV Theorem 5.2].
Let us now show that the symplectic form \(\omega _Y\) vanishes on the regular locus of the singular support SS(M). Consider a spreading out (X, N) of (Y, M). Namely, there are a finitely generated subring \(A\subset L,\) a smooth affine scheme X over \(S:={\text {Spec}}(A)\) and a coherent left \(D_{X/S}\)-module N such that, for \(\mu \) the generic point of S, there are compatible isomorphisms \(L\otimes _{k(\mu )}X_\mu \cong Y\) and \(L\otimes _{k(\mu )}N_\mu \cong M.\) Let us define the closed subset \(SS(N)\subset T^*_{X/S}\) to be the support of the associated graded \(gr^\Gamma N,\) where \(\Gamma \) is a good filtration of N, see Definition 3.3.1. As usual the subset SS(N) does not depend on the choice of good filtration of N. We claim that there is a dense open subset \(S^*\) of S such that, for all closed points u of \(S^*,\) the symplectic form \(\omega _{X_u}\) vanishes on the regular locus of the fiber \(SS(N)_u\) of SS(N). Since \(SS(M)= L\otimes _{k(\mu )}{SS(N)}_\mu ,\) the corollary follows from the claim.
By generic freeness of \(gr^\Gamma N\) on S, there is a dense open subset \(S_1\) of S such that the fiber \(\Gamma _u\) of \(\Gamma \) is a good filtration and \(SS(N)_u=SS(N_u),\) for all closed points u of \(S_1.\) Moreover it is clear that Lemma 4.2.6 and its proof generalize to the Bernstein filtration replaced by the filtration by the order of differential operators, and \(\mathbb {A}^n_{k(u)}\) replaced by \(X_u.\) Thus (4.2.1) gives an isomorphism of \(gr^\Phi Z(D_{X_u})\)-modules \(gr(gr^{\Phi (\Gamma _u)} r_*N_u) \simeq F_*gr^{\Gamma _u} N_u,\) where \(\Phi \) is the filtration induced by the order of differential operators on the center \(Z(D_{X_u})\) of \(D_{X_u}\) and we have used the notations of the proof of Lemma 4.2.6. In addition, we have that the symplectic form \(\omega _{X_u}\) vanishes on the regular locus of the support of \(gr^{\Gamma _u} N_u\) if and only if \(\omega _{X'_u}\) vanishes on the regular locus of the support of \(F_*gr^{\Gamma _u} N_u.\) Indeed these regular loci and symplectic forms are mapped to one another by the projection map \(T^*_{X'_u}\rightarrow T^*_{X_u},\) which is an isomorphism since k(u) is perfect. Hence the symplectic form \(\omega _{X_u}\) vanishes on the regular locus of the support of \(gr^{\Gamma _u} N_u\) if and only if \(\omega _{X'_u}\) vanishes on the regular locus \(T_u^{reg}\) of the support \(T_u\) of \(gr^{\Phi (\Gamma _u)} r_*N_u.\)
But using the Rees module with respect to \(\Phi ,\) we see that \(T_u\) is the reduced scheme associated to the fiber at the origin of a flat \(\mathbb {A}^1\)-scheme of generic fiber isomorphic to the p-support of \(N_u.\) And by Theorem 2.2.1, there is a dense open subset \(S_2\) of \(S_1\) such that the p-support of \(N_u\) is Lagrangian, for all closed points u of \(S_2.\) Thus the claim would follow if the reduced scheme associated to the fiber at the origin of a flat \(\mathbb {A}^1\)-scheme of Lagrangian generic fiber was Lagrangian. This is not in general true in positive characteristic. In our case however, the proof reduces to the case \(X_u = \mathbb {A}^n\) and we may use Theorem 4.3.3. Hence there is a dense open subset \(S_3\) of \(S_2\) such that for all closed \(u\in S_3,\) the generic fiber of the \(\mathbb {A}^1\)-scheme is Lagrangian and of degree bounded independently of \(u\in S_3\) (for the projective embedding of Theorem 4.3.3). We may thus use the Hilbert scheme to conclude that there is an integer \(l>0\) such that for all \(u\in S^*:= S_3[\frac{1}{l}],\) the assertion that the reduced scheme associated to the fiber at the origin of the above \(\mathbb {A}^1\)-scheme is Lagrangian, follows from the case of characteristic zero. But the latter is a special case of Lemma 6.3.2 below, applied to the symplectic form. This concludes the proof of the claim and thus of the corollary. \(\square \)
Lemma 6.3.2
Let S be an integral scheme over a field L of characteristic 0. Let \(\mathfrak {M}\) be a smooth S-scheme, let \(Z \subset \mathfrak {M}\) be a subscheme which is a reduced, flat and surjective S-scheme of relative dimension d, and let \(\alpha \) be a relative differential form on \(\mathfrak {M}\) over S. Assume that the restriction of \(\alpha \) to the smooth locus of the generic fibre of Z vanishes and that S is the spectrum of a Dedekind ring. Then the restriction of \(\alpha \) to the smooth locus of the reduced scheme associated to every closed fibre of Z vanishes.
Proof
We will reduce the proof to the case of a smooth Z, which is immediate. Indeed if Z is smooth over S, the points s of the base S such that the restriction of \(\alpha \) vanishes on the fibre \(Z_s\) form a closed subset \(V_\alpha \subset S.\) Since the generic point of S belongs to \(V_\alpha \) by hypothesis, we have \(V_\alpha =S,\) which is what we wanted to prove.
By the Reduced Fibre Theorem [32, Theorem 09IL], there is an integral affine scheme T and a finite surjective morphism \(T \xrightarrow {\phi } S,\) such that if we denote by \(Z_T\) the base-change of Z with respect to \(\phi ,\) and \(Y \xrightarrow {\nu } Z_T\) the normalization, then the smooth locus U of Y over T is dense in all the fibres of Y over T. Note that since the normalization morphism is finite and surjective, Y is a T-scheme of relative dimension d. Let \(Z_T \xrightarrow {\beta } Z\) be the projection morphism. For each \(s\in S,\) we have morphisms between the reduced schemes associated to the fibres  such that \((\nu _s)_{red}\) and \((\beta _s)_{red}\) are finite and surjective. Thus, in particular, the composition \(\psi := (\beta _s)_{red} \circ (\nu _s)_{red} \circ j\) is dominant.
such that \((\nu _s)_{red}\) and \((\beta _s)_{red}\) are finite and surjective. Thus, in particular, the composition \(\psi := (\beta _s)_{red} \circ (\nu _s)_{red} \circ j\) is dominant.
We will use the following claim: Let \(\mathcal {Y} \xrightarrow {g} \mathcal {Z}\) be a finite morphism between schemes of pure dimension d. If V is a dense open subset of \(\mathcal {Z},\) then \(g^{-1}(V)\) is a dense open subset of \(\mathcal {Y}.\) Indeed if the open complement W of the closure \(\overline{g^{-1}(V)}\) of \(g^{-1}(V)\) in \(\mathcal {Y}\) is not empty then it is of dimension d. But it maps to the complement of V in \(\mathcal {Z},\) which is of dimension \(<d.\) This is not possible since g is finite. Thus W is empty and \(g^{-1}(V)\) is a dense open subset of \(\mathcal {Y}.\)
By generic smoothness on the target applied to \(\psi ,\) there is a dense open subset \(\mathcal {U}\) of \((Z_s)_{red}\) such that the restriction of \(\psi \) to \(\mathcal {U}\) is smooth. Moreover, by the claim applied to \( (\beta _s)_{red} \circ (\nu _s)_{red},\) we have that the inverse image \(\psi ^{-1}(\mathcal {U} \cap (Z_s)_{red}^{sm})\) of the dense open subset \(\mathcal {U} \cap (Z_s)_{red}^{sm}\) of the smooth locus \((Z_s)_{red}^{sm}\) of \((Z_s)_{red}\) is dense in \(U_{\phi ^{-1}(s)}.\) Thus the restriction of \(\alpha \) to \((Z_s)_{red}^{sm}\) vanishes if and only if its restriction to \(U_{\phi ^{-1}(s)}\) vanishes. Hence the lemma follows from the smooth case, applied to U and the restriction of \(\alpha \) to U. \(\square \)
References
Auslander, M., Goldman, O.: The Brauer group of a commutative ring. Trans. AMS 97, 367–409 (1960)
Berthelot, P.: \({\cal{D}}\)-modules arithmétiques I. Opérateurs différentiels de niveau fini. Ann. sc. de l’ENS 29(2), 185–272 (1996)
Berthelot, P.: Introduction à la théorie arithmétique des \(\cal{D}\)-modules, Cohomologies p-adiques et applications arithmétiques II. Astérisque 279, 1–80 (2002)
Berthelot, P., Ogus, A.: Notes on Crystalline Cohomology. Princeton University Press, Princeton (1978)
Bezrukavnikov, R., Braverman, A.: Geometric Langlands correspondence for \(\cal{D}\)-modules in prime characteristic: the \(GL(n)\) case. Pure Appl. Math. Q. 3(1), 153–179 (2007)
Bezrukavnikov, R., Mirkovic, I., Rumynin, D.: Localization of modules for a semisimple Lie algebra in prime characteristic (with an Appendix by R. Bezrukavnikov and S. Riche: Computation for \({\mathfrak{sl}}\) (3)). Ann. Math. (2) 167(3), 945–991 (2008)
Björk, J.-E.: Rings of Differential Operators. North-Holland Mathematical Library, vol. 21. North-Holland Publishing Co, Amsterdam (1979)
Björk, J.-E.: Analytic \(\cal{D}\)-Modules and Applications. Mathematics and its Applications, vol. 247. Kluwer Academic Publishers Group, Dordrecht (1993)
Borel, A., et al.: Algebraic \(D\)-Modules. Perspectives in Math, vol. 2. Academic Press, Cambridge (1987)
Bourbaki, N.: Algèbre, chapitre III in Algèbre, Chapitres 1 à 3. Hermann, Paris (1970)
Bourbaki, N.: Algèbre commutative, chapitre I in Algèbre commutative, Chapitres 1 à 4. Nouveau tirage, Masson, Paris (1985)
Deligne, P.: Equations différentielles à points singuliers réguliers. LNM 163. Springer, Berlin, Heidelberg, New York (1970)
Deligne, P.: Théorie de Hodge, II. Publ. Math. de l’IHES 40, 5–57 (1971)
Eisenbud, D.: Commutative algebra. With a view toward algebraic geometry. GTM 150. Springer, Berlin (1995)
Gabber, O.: The integrability of the characteristic variety. Am. J. Math. 103(3), 445–468 (1981)
Grothendieck, A., Dieudonné, J.: EGA I. Grundlehren der math. Wissenschaften, vol. 166. Springer, Berlin (1971)
Grothendieck, A.: EGA II (rédigé avec la collaboration de Jean Dieudonné) Étude globale élémentaire de quelques classes de morphismes. Publ. Math. IHES No. 8 (1961)
Grothendieck, A.: EGA IV (rédigé avec la collaboration de Jean Dieudonné) Étude locale des schémas et des morphismes de schémas. Publ. Math. IHES No. 20, 24, 28, 32 (1964–1967)
Grothendieck, A., Le groupe de Brauer I.: Algèbres d’Azumaya et interprétations diverses in Dix Exposés sur la Cohomologie des Schémas, p. 46-66. North-Holland, Amsterdam; Masson, Paris (1968)
Grothendieck, A.: Séminaire Bourbaki. Techniques de construction et théorèmes d’existence en géométrie algébrique IV : les schémas de Hilbert 221 (1960–1961)
Hartshorne, R.: Algebraic Geometry. Springer, Berlin (1977). GTM 52
Hochschild, G.: Simple algebras with purely inseparable splitting fields of exponent 1. Trans. AMS 79, 477–489 (1955)
Hoobler, R.: Cohomology of purely inseparable Galois coverings. J. Reine Angew. Math. 266, 183–199 (1974)
Illusie, L.: Complexe de de Rham-Witt et cohomologie cristalline. Ann. sc. de l’ENS 12(4), 501–661 (1979)
Kashiwara, M.: D-modules and Microlocal Calculus. Translations of Mathematical Monographs, vol. 217. American Mathematical Society (2003)
Kashiwara, M., Kawai, T., Sato, M.: Microfunctions and Pseudo-Differential Equations. LNM 287, p. 264–529. Springer, Berlin (1973)
Katz, N.: Nilpotent connections and the monodromy theorem: applications of a result of Turrittin. Publ. Math. de l’IHES 39, 175–232 (1970)
Kleiman, S.: The Picard scheme. Fundamental algebraic geometry. AMS Math. Surv. Monogr. 123, 235–321 (2005)
Kontsevich, M.: Holonomic \(\cal{D}\)-modules and positive characteristic. Jpn. J. Math. 4(1), 1–25 (2009)
Milne, J.: Étale Cohomology. Princeton Mathematical Series, vol. 33. Princeton University Press, Princeton (1980)
Ogus, A., Vologodsky, V.: Nonabelian Hodge theory in characteristic \(p\). Publ. Math. de l’IHES 106, 1–138 (2007)
The Stacks project. https://stacks.math.columbia.edu. Accessed 6 Sept 2018
Van den Bergh, M.: On involutivity of \(p\)-support. Int. Math. Res. Not. IMRN 15, 6295–6304 (2015)
Acknowledgements
This paper is a streamlined version of my 2010 Orsay PhD thesis, made under the direction of Maxim Kontsevich. This work owes him a lot. In fact, the systematic use of the Azumaya property excepted, all the main characters involved here were present in [29]. He also suggested that “the restriction of the canonical form to the p-support should have logarithmic poles”. It is my pleasure to thank him here. I have also had wonderful conversations on questions related to this work with Joseph Bernstein, for which I am very grateful. The influence of Ofer Gabber on the general topics discussed here is obvious. He also provided me with very useful references. Many thanks go to him. I would like to thank Pierre Berthelot for his comments on a previous version of this manuscript. The feedback and support from Konstantin Ardakov, Sam Raskin, Simon Riche and Olivier Schiffmann has been quite useful at various stages of the completion of this project. A special thanks goes to them. Finally I am grateful to the referees for their many useful remarks. The author was partially supported by EPSRC grant EP/L005190/1.
Author information
Authors and Affiliations
Corresponding author
Appendix A: Symplectic geometry of the cotangent space
Appendix A: Symplectic geometry of the cotangent space
Let S be a scheme and let Y be a smooth S-scheme of relative dimension n. Recall that the cotangent space of Y / S is the Y-scheme \(T^*_{Y/S} \xrightarrow {p_Y} Y:= V((\Omega ^1_{Y/S})^*)={\text {Spec}}_Y(Sym_{\mathcal {O}_Y}(\Omega ^1_{Y/S})^*)\) and hence that the sheaf of germs of Y-sections of \(T^*_{Y/S}/Y\) is canonically identified with \(\Omega ^1_{Y/S},\) see [17, (1.7.9)]. Moreover \(T^*_{Y/S}\) is a smooth Y-scheme of relative dimension n by [18, Proposition 17.3.8], smooth of relative dimension 2n as an S-scheme. We use the notation \(T^*_Y\) (instead of \(T^*_{Y/S}\)) when there is no risk of confusion, for example when S is the spectrum of a field. For \(f:X\rightarrow Y\) a S-morphism of smooth S-schemes, the pullback of differentials \(\Omega ^1_{X/S}\xleftarrow {f^*} f^*\Omega ^1_{Y/S}\) ([18, 16.4.3.6]) gives rise to the X-morphism \(T^*_{X/S} \xleftarrow {(f)_d} X\times _Y T^*_{Y/S}\) called the cotangent map. It is part of the cotangent diagram of \(f:\)

where \((f)_\pi \) is the canonical projection.
Remark A.0.1
Let \(U\subset Y\) be an open subset, it follows directly from the definitions that if \(s_{\alpha }\) is the section of \(T^*_{Y/S}/U\) corresponding to \(\alpha \in \Gamma (U,\Omega ^1_{Y/S}),\) then \((f)_d \circ (X\times _Ys_{\alpha })\) corresponds to \((f^*)^{ad}\alpha \in \Gamma (f^{-1}(U),\Omega ^1_{X/S}),\) where \(f_*\Omega ^1_{X/S}\xleftarrow {(f^*)^{ad}} \Omega ^1_{Y/S}\) is adjoint to \(f^*.\)
We have the
Lemma A.0.2
If \(f:X\rightarrow Y\) is an immersion (resp. a closed immersion) then \((f)_d\) is smooth and surjective and \((f)_\pi \) is an immersion (resp. a closed immersion). Moreover \((f)_d\) admits a section locally on X.
Proof
The morphism \((f)_d\) is smooth and surjective by [18, Proposition 17.2.5], [17, Proposition 1.7.11 (iii)], [18, Proposition 17.3.8] and stability under base-change of surjective smooth morphisms. We have that \((f)_\pi \) is an immersion (resp. a closed immersion) by [16, Proposition 4.3.1 (i)]. Finally, local sections of the locally split “conormal” short exact sequence of [18, Proposition 17.2.5] induce local sections of \((f)_d,\) by [17, Proposition 1.7.11 (i)]. \(\square \)
Definition A.0.3
The canonical global S-relative 1-form \(\theta _{Y/S}\) on the cotangent space of Y / S is the relative 1-form corresponding to the section
of the cotangent space \(T^*_{T^*_{Y/S}/S} \xrightarrow {p_{T^*_{Y/S}}} T^*_{Y/S}\), where \(\Delta _{T^*_{Y/S}/Y}\) is the diagonal of \(T^*_{Y/S} \xrightarrow {p_Y} Y\).
Let \(\{y_1,\ldots ,y_n\}\) be local étale coordinates on Y. In terms of the associated local étale coordinates \(\{y_1,\ldots ,y_n;\xi _1,\ldots ,\xi _n\}\) on \(T^*_{Y/S}\), where \(\{\xi _1,\ldots ,\xi _n\}\) are dual to \(\{dy_1,\ldots ,dy_n\}\), \(\theta _{Y/S}=\sum _{i=1}^{i=n}\xi _idy_i\). Note that the formation of the canonical form commutes with base-change \(S'\rightarrow S\) and is compatible with the cotangent diagram, the latter in the sense that \((f)_\pi ^*\theta _{Y/S}=(f)_d^*\theta _{X/S}\).
If S is the spectrum of a field k, then we omit the base S from the notations. Let Q be a smooth k-scheme of pure dimension n.
Definition A.0.4
The nondegenerate global exact 2-form \(\omega _Q:=d\theta _Q\) on \(T^*_Q\) is called the symplectic form.
Definition A.0.5
A subvariety \(X \overset{i}{\hookrightarrow }T^*_Q\) is said to be a Lagrangian subvariety of \((T^*_Q,\omega _Q)\) if it contains a dense open \(U\subset X\) on which the symplectic form vanishes, \((i^*\omega _Q)|U=0\) and if at each of its points x it is of dimension \(n=dim_xQ\).
Let us finally note the
Lemma A.0.6
Let \(f:X\rightarrow Y\) be an immersion of smooth k-schemes and let \(Z_Y \overset{i}{\hookrightarrow }T^*_Y\) and \(Z_X \overset{j}{\hookrightarrow }T^*_X\) be reduced subschemes. Suppose that \((f)_\pi ^{-1}Z_Y=(f)_d^{-1}Z_X\) and that \((f)_\pi ^{-1}Z_Y \xrightarrow {(f)_\pi }Z_Y\) is surjective. Then \(\omega _Y\) vanishes on a dense open subset of \(Z_Y\) if and only if \(\omega _X\) vanishes on a dense open subset of \(Z_X\).
Proof
Note that by Lemma A.0.2, \((f)_d|_{Z_X}\) is smooth and surjective and \((f)_\pi |_{Z_Y}\) is an immersion. Since by hypothesis \((f)_\pi |_{Z_Y}\) is surjective, it is a nilimmersion. Hence, \(Z_Y\) being reduced, an isomorphism. Moreover by [18, Proposition 17.2.3 (ii)], [10, §7 n\(^\mathrm{o}\)2 Proposition 4] and flatness of smooth morphisms, the pullback of forms \((f)_d^*:\Omega ^2_{Z_X,z} \rightarrow \Omega ^2_{(f)_d^{-1}Z_X,\tilde{z}}\) is injective for all \(z=(f)_d(\tilde{z})\). Since \((f)_\pi ^*\omega _Y=(f)_d^*\omega _X\) as \((f)_\pi ^*\theta _Y=(f)_d^*\theta _X,\) and \(((f)_d|_{Z_X})\circ ((f)_\pi |_{Z_Y})^{-1}\) as well as \(((f)_\pi |_{Z_Y})\circ ((f)_d|_{Z_X})^{-1}\) preserve open dense subsets, the lemma follows. \(\square \)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bitoun, T. On the p-supports of a holonomic \(\mathcal {D}\)-module. Invent. math. 215, 779–818 (2019). https://doi.org/10.1007/s00222-018-0837-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-018-0837-6


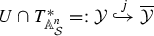 such that
such that