Parabolic John–Nirenberg spaces with time lag

Abstract

We introduce a parabolic version of the so-called John–Nirenberg space that is a generalization of functions of parabolic bounded mean oscillation. Parabolic John–Nirenberg inequalities, which give weak type estimates for the oscillation of a function, are shown in the setting of the parabolic geometry with a time lag. Our arguments are based on a parabolic Calderón–Zygmund decomposition and a good lambda estimate. Chaining arguments are applied to change the time lag in the parabolic John–Nirenberg inequality.

1 Introduction

Functions of bounded mean oscillation ${{\,\mathrm{\textrm{BMO}}\,}}$ and their generalization, the so-called John–Nirenberg space denoted by $JN_q$ with $1<q<\infty$, were introduced by John and Nirenberg in [6]. Let $\Omega$ be a domain in $\mathbb {R}^n$. A function $f\in L_{\textrm{loc}}^1(\Omega )$ belongs to the John–Nirenberg space $JN_q(\Omega )$, $1<q<\infty$, if

where the supremum is taken over countable collections $\{Q_i\}_{i\in {\mathbb {N}}}$ of pairwise disjoint subcubes of $\Omega$. A particularly useful result for ${{\,\mathrm{\textrm{BMO}}\,}}$ is the John–Nirenberg lemma which gives an exponential decay estimate for the mean oscillation of a function in ${{\,\mathrm{\textrm{BMO}}\,}}$. Moreover, the John–Nirenberg lemma for $JN_q$ gives a weak type estimate for the oscillation of a function in $JN_q$ implying that the John–Nirenberg space is a subset of weak $L^q$. The corresponding time-dependent theory was initiated by Moser in [16, 17] to study the regularity of parabolic partial differential equations, and parabolic ${{\,\mathrm{\textrm{BMO}}\,}}$ was explicitly defined by Fabes and Garofalo in [5]. The proof of the parabolic John–Nirenberg lemma requires genuinely new ideas compared to the time independent case. The theory of parabolic ${{\,\mathrm{\textrm{BMO}}\,}}$ has been further studied in [1, 7, 9,10,11, 19]. See also [14] for the one-dimensional case.

The purpose of this paper is to introduce and study a parabolic version of the John–Nirenberg space in the parabolic geometry with a time lag $0<\gamma <1$. This geometry is motivated by certain parabolic nonlinear partial differential equations, see [1, 7, 9,10,11, 19]. Let $\Omega _T = \Omega \times (0,T)$ be a space-time cylinder in $\mathbb {R}^{n+1}$. A function $f\in L_{\textrm{loc}}^1(\Omega _T)$ belongs to the parabolic John–Nirenberg space $PJN_q^+(\Omega _T)$, $1<q<\infty$, if

where the supremum is taken over countable collections $\{R_i\}_{i\in {\mathbb {N}}}$ of pairwise disjoint space-time subrectangles of $\Omega _T$. Here $R_i$ is a parabolic rectangle in the parabolic p-geometry with $1< p<\infty$ and $0<\gamma <1$ is the time lag, see Sect. 2 for notation. In a similar way to the standard setting, this space is a generalization of parabolic ${{\,\mathrm{\textrm{BMO}}\,}}$ in a sense that parabolic $JN_q$ contains parabolic ${{\,\mathrm{\textrm{BMO}}\,}}$, and parabolic ${{\,\mathrm{\textrm{BMO}}\,}}$ is obtained as the limit of parabolic John–Nirenberg spaces as $q\rightarrow \infty$. A one-sided John–Nirenberg space has been considered by Berkovits [2] in the case $p=1$, but the geometry is not related to nonlinear parabolic partial differential equations. For recent developments in the theory of John–Nirenberg spaces in the standard setting, we refer to [3, 4, 8, 12, 13, 15, 18, 21,22,23,24].

Our main results are parabolic John–Nirenberg inequalities for parabolic $JN_q$. The main challenges are the time lag between the two mean oscillations in the definition and the parabolic geometry. The proof of the parabolic John–Nirenberg inequality in Theorem 3.1 is based on a parabolic Calderón–Zygmund decomposition and a good lambda inequality. Theorem 4.1 shows that by applying suitable parabolic chaining arguments we may improve the obtained John–Nirenberg lemma by changing the time lag. This allows us to conclude that the parabolic John–Nirenberg space is independent of the size of the time lag, see Corollary 4.2. For more about chaining techniques in the parabolic geometry, see [7, 19, 20].

2 Definition and properties of parabolic John–Nirenberg spaces

The underlying space throughout is $\mathbb {R}^{n+1}=\{(x,t):x=(x_1,\dots ,x_n)\in {\mathbb {R}}^n,t\in {\mathbb {R}}\}$. Unless otherwise stated, constants are positive and the dependencies on parameters are indicated in the brackets. The Lebesgue measure of a measurable subset A of $\mathbb {R}^{n+1}$ is denoted by $|A|$. A cube Q is a bounded interval in ${\mathbb {R}}^n$, with edges parallel to the coordinate axes and equally long, that is, $Q=Q(x,L)=\{y \in \mathbb R^n: |y_i-x_i|\le L,\,i=1,\dots ,n\}$ with $x\in \mathbb R^n$ and $L>0$. The point x is the center of the cube and L is the edge length of the cube. Instead of Euclidean cubes, we work with the following collection of parabolic rectangles in $\mathbb {R}^{n+1}$.

Definition 2.1

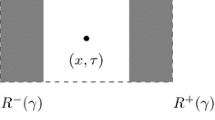
Let $1<p<\infty$, $x\in {\mathbb {R}}^n$, $L>0$ and $t \in \mathbb {R}$. A parabolic rectangle centered at (x, t) with edge length L is

$$\begin{aligned} R = R(x,t,L) = Q(x,L) \times (t-L^p, t+L^p) \end{aligned}$$

and its upper and its lower parts are respectively

$$\begin{aligned} R^+(\gamma ) = Q(x,L) \times (t+\gamma L^p, t+L^p) \quad \text {and}\quad R^-(\gamma ) = Q(x,L) \times (t - L^p, t - \gamma L^p), \end{aligned}$$

where $-1< \gamma < 1$ is called the time lag.

Note that $R^-(\gamma )$ is the reflection of $R^+(\gamma )$ with respect to the time slice $\mathbb {R}^n \times \{t\}$. The spatial edge length of a parabolic rectangle R is denoted by $l_x(R)=L$ and the time length by $l_t(R)=2L^p$. For short, we write $R^\pm$ for $R^{\pm }(0)$. The top of a rectangle $R = R(x,t,L)$ is $Q(x,L) \times \{t+L^p\}$ and the bottom is $Q(x,L) \times \{t-L^p\}$. The $\lambda$-dilate of R with $\lambda >0$ is denoted by $\lambda R = R(x,t,\lambda L)$.

The integral average of $f \in L^1(A)$ in measurable set $A\subset \mathbb {R}^{n+1}$, with $0<|A|<\infty$, is denoted by

The positive and the negative parts of a function f are denoted, respectively, by

$$\begin{aligned} f_+ = \max \{ f, 0 \} \quad \text {and}\quad f_- = - \min \{ f, 0 \}. \end{aligned}$$

Let $\Omega \subset \mathbb {R}^{n}$ be an open set and $T>0$. A space-time cylinder is denoted by $\Omega _T=\Omega \times (0,T)$. It is possible to consider space-time cylinders $\Omega \times (t_1,t_2)$ with $t_1<t_2$, but we focus on $\Omega _T$.

We recall the definition of the parabolic ${{\,\mathrm{\textrm{BMO}}\,}}$. The differentials $\, d x\, d t$ in integrals are omitted in the sequel.

Definition 2.2

Let $\Omega \subset \mathbb {R}^{n}$ be a domain, $T>0$, $0 \le \gamma < 1$ and $0< r < \infty$. A function $f \in L_{\textrm{loc}}^r(\Omega _T)$ belongs to ${{\,\mathrm{\textrm{PBMO}}\,}}_{\gamma ,r}^{+}(\Omega _T)$ if

If the condition above holds with the time axis reversed, then $f \in {{\,\mathrm{\textrm{PBMO}}\,}}_{\gamma ,r}^{-}(\Omega _T)$.

This section discusses basic properties of the parabolic John–Nirenberg space. We begin with the definition.

Definition 2.3

Let $\Omega \subset \mathbb {R}^{n}$ be a domain, $T>0$, $0 \le \gamma < 1$, $1< q < \infty$ and $0< r < q$. A function $f \in L_{\textrm{loc}}^r(\Omega _T)$ belongs to $PJN_{q,\gamma ,r}^{+}(\Omega _T)$ if

where the supremum is taken over countable collections $\{R_i\}_{i\in {\mathbb {N}}}$ of pairwise disjoint parabolic subrectangles of $\Omega _T$. If the condition above holds with the time axis reversed, then $f \in PJN_{q,\gamma ,r}^{-}(\Omega _T)$.

We shall write $PJN_{q}^{+}$ and $\Vert f \Vert$ whenever parameters are clear from the context or are not of importance. Observe that $f \in L_{\textrm{loc}}^r(\Omega _T)$ belongs to $PJN_{q,\gamma ,r}^{+}(\Omega _T)$ if and only if for every collection $\{R_i\}_{i\in \mathbb {N}}$ of parabolic rectangles there exist constants $c_i\in {\mathbb {R}}$, that may depend on $R_i$, with

where $M\in {\mathbb {R}}$ is a constant that is independent of $\{R_i\}_{i\in \mathbb {N}}$.

The next lemma shows that for every parabolic rectangle R, there exists a constant $c_R$, depending on R, for which the infimum in the definition above is attained. In the sequel, this minimal constant is denoted by $c_R$. The proof is analogous to that of the parabolic ${{\,\mathrm{\textrm{BMO}}\,}}$ in [9], and thus is omitted here.

Lemma 2.4

Let $\Omega _T \subset \mathbb {R}^{n+1}$ be a space-time cylinder, $0 \le \gamma < 1$, $1< q < \infty$ and $0<r<q$. Assume that $f\in PJN_{q,\gamma ,r}^{+}(\Omega _T)$. Then for every parabolic rectangle $R\subset \Omega _T$, there exists a constant $c_R\in {\mathbb {R}}$, that may depend on R, such that

In particular, it holds that

We list some properties of the parabolic John–Nirenberg space below. In particular, $PJN_{q}^{+}$ is closed under addition and scaling by a positive constant. On the other hand, multiplication by negative constants reverses the time direction. The proof is similar to that of the parabolic ${{\,\mathrm{\textrm{BMO}}\,}}$ in [9], and thus is omitted here.

Lemma 2.5

Let $0 \le \gamma < 1$, $1< q < \infty$ and $0<r<q$. Assume that f and g belong to $PJN_{q,\gamma ,r}^{+}(\Omega _T)$ and let $PJN_{q}^\pm =PJN_{q,\gamma ,r}^\pm (\Omega _T)$. Then the following properties hold.

• (i)
  $$\begin{aligned} \Vert f+a \Vert _{PJN_{q}^{+}} = \Vert f \Vert _{PJN_{q}^{+}},\, a \in \mathbb {R}. \end{aligned}$$
• (ii)
  $$\begin{aligned} \Vert f+g \Vert _{PJN_{q}^{+}} \le \max \{ 2^{\frac{1}{r}-1} , 2^{1-\frac{1}{r}} \} \Bigl ( \Vert f \Vert _{PJN_{q}^{+}} + \Vert g \Vert _{PJN_{q}^{+}} \Bigr ). \end{aligned}$$
• (iii)
  $$\begin{aligned} \Vert af \Vert _{PJN_{q}^{+}} = {\left\{ \begin{array}{ll} \displaystyle a \Vert f \Vert _{PJN_{q}^{+}}, &{}\quad a \ge 0, \\ \displaystyle -a \Vert f \Vert _{PJN_{q}^{-}}, &{}\quad a < 0. \end{array}\right. } \end{aligned}$$
• (iv)
  $$\begin{aligned} \Vert \max \{f,g\} \Vert _{PJN_{q}^{+}}&\le \max \{1, 2^{\frac{1}{r} -1 }\} \Bigl ( \Vert f \Vert _{PJN_{q}^{+}} + \Vert g \Vert _{PJN_{q}^{+}} \Bigr ), \\ \Vert \min \{f,g\} \Vert _{PJN_{q}^{+}}&\le \max \{1, 2^{\frac{1}{r} -1 }\} \Bigl ( \Vert f \Vert _{PJN_{q}^{+}} + \Vert g \Vert _{PJN_{q}^{+}} \Bigr ). \end{aligned}$$

Remark 2.6

For $1\le r<q$, the constants in (ii) and (iv) can be avoided by considering the norm

which is an equivalent norm with our definition. However, the current definition will be convenient in the proof of the John–Nirenberg lemma below.

Properties (i) and (iv) of Lemma 2.5 imply that every $PJN_{q,\gamma ,r}^{+}$ function can be approximated pointwise by bounded $PJN_{q,\gamma ,r}^{+}$ functions.

Remark 2.7

If $f\in {{\,\mathrm{\textrm{PBMO}}\,}}_{\gamma ,r}^{+}(\Omega _T)$ with $|\Omega _T |< \infty$, then $f \in PJN_{q,\gamma ,r}^{+}(\Omega _T)$ for every $1<q<\infty$. More precisely, we have

$$\begin{aligned} \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(\Omega _T)} \le |\Omega _T |^\frac{1}{q} \Vert f \Vert _{{{\,\mathrm{\textrm{PBMO}}\,}}_{\gamma ,r}^{+}(\Omega _T)}, \end{aligned}$$

which follows from

The parabolic John–Nirenberg space is a generalization of the parabolic BMO in the sense that a function is in PBMO$^+_{\gamma ,r}$ if and only if the $PJN_{q,\gamma ,r}^{+}$ norm of the function is uniformly bounded as q tends to infinity.

Proposition 2.8

Let $\Omega _T\subset \mathbb {R}^{n+1}$ be of finite measure, $0 \le \gamma < 1$ and $0<r<\infty$. Assume that $f \in L_{\textrm{loc}}^r(\Omega _T)$. Then

$$\begin{aligned} \lim _{q \rightarrow \infty } \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(\Omega _T)} = \Vert f \Vert _{{{\,\mathrm{\textrm{PBMO}}\,}}_{\gamma ,r}^{+}(\Omega _T)}. \end{aligned}$$

Proof

We may assume that $|\Omega _T |>0$. Let $\{R_i\}_i$ be a collection of pairwise disjoint parabolic subrectangles of $\Omega _T$. Recall that if $|\Omega _T |< \infty$, then $\Vert \cdot \Vert _{L^q(\Omega _T)} \rightarrow \Vert \cdot \Vert _{L^\infty (\Omega _T)}$ as $q\rightarrow \infty$. It follows that

as $q\rightarrow \infty$. Hence, we have

We can interchange the order of taking the supremum and the limit since

is an increasing function of q which can be seen by Hölder’s inequality. Thus, we conclude that

$$\begin{aligned} \lim _{q\rightarrow \infty } \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(\Omega _T)} = \Vert f \Vert _{{{\,\mathrm{\textrm{PBMO}}\,}}_{\gamma ,r}^{+}(\Omega _T)}. \end{aligned}$$

$\square$

3 Parabolic John–Nirenberg inequality

This section discusses a John–Nirenberg inequality for parabolic John–Nirenberg spaces. The argument is based on a parabolic Calderón–Zygmund decomposition and applies a parabolic sharp maximal function to obtain a good lambda estimate. For short, we suppress the variables (x, t) in the notation and, for example, write

$$\begin{aligned} R^{+}(\alpha )\cap \{(f-c_{R})_+> \lambda \} =\{(x,t)\in R^{+}(\alpha ):(f(x,t)-c_{R})_+ > \lambda \} \end{aligned}$$

in the sequel.

Theorem 3.1

Let $R \subset \mathbb {R}^{n+1}$ be a parabolic rectangle, $0 \le \gamma < 1$, $\gamma< \alpha < 1$, $1< q < \infty$ and $0 < r \le 1$. Assume that $f \in PJN_{q,\gamma ,r}^{+}(R)$. Then there exist constants $c_R\in {\mathbb {R}}$ and $C=C(n,p,q,r,\gamma ,\alpha )$ such that

$$\begin{aligned} |R^{+}(\alpha ) \cap \{ (f-c_{R})_+ > \lambda \} |\le C \frac{ \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(R)}^q}{\lambda ^q} \end{aligned}$$

and

$$\begin{aligned} |R^{-}(\alpha ) \cap \{ (f-c_{R})_- > \lambda \} |\le C \frac{ \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(R)}^q}{\lambda ^q} \end{aligned}$$

for every $\lambda >0$.

Proof

The beginning of the proof is similar to the John–Nirenberg lemma for parabolic BMO in [9]. However, the rest of the proof uses several new ideas when dealing with weak type estimates for parabolic $JN_q$ compared to the exponential decay estimate for parabolic ${{\,\mathrm{\textrm{BMO}}\,}}$. Let $R_0=R=R(x_0,t_0,L) = Q(x_0,L) \times (t_0-L^p, t_0+L^p)$. By considering the function $f(x+x_0,t+t_0)$, we may assume that the center of $R_0$ is the origin, that is, $R_0 = Q(0,L) \times (-L^p, L^p)$. By (i) of Lemma 2.5, we may assume that $c_{R_0} = 0$. We note that it is sufficient to prove the first inequality of the theorem since the second inequality follows from the first one by applying it to the function $-f(x,-t)$.

Let $\Vert f \Vert = \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(R_0)}$. We claim that

$$\begin{aligned} |R^{+}_0(\alpha )\cap \{f_+ > \lambda \} |\le C \frac{ \Vert f \Vert ^q}{\lambda ^q} \end{aligned}$$

for every $\lambda >0$. Let m be the smallest integer with $3 + \alpha \le 2^{pm+1} (\alpha - \gamma )$, that is,

$$\begin{aligned} \frac{1}{p} \log _2 \biggl ( \frac{3+ \alpha }{2 (\alpha - \gamma )} \biggr ) \le m < \frac{1}{p} \log _2 \biggl ( \frac{3+ \alpha }{2 (\alpha - \gamma )} \biggr ) + 1. \end{aligned}$$

Let $S^+_0 = R^+_0(\alpha ) = Q(0,L) \times (\alpha L^p,L^p)$. The time length of $S^+_0$ is $l_t(S^+_0) = (1-\alpha )L^p$. We partition $S^+_0$ by dividing each spatial edge $[-L,L]$ into $2^m$ equally long intervals. If

$$\begin{aligned} \frac{l_t(S_{0}^+)}{\lfloor 2^{pm} \rfloor } < \frac{(1-\alpha )L^p}{2^{pm}}, \end{aligned}$$

we divide the time interval of $S^+_0$ into $\lfloor 2^{pm} \rfloor$ equally long intervals. Otherwise, we divide the time interval of $S^+_0$ into $\lceil 2^{pm} \rceil$ equally long intervals. Here $\lfloor \cdot \rfloor$ and $\lceil \cdot \rceil$ are the floor and ceiling functions, respectively. We obtain subrectangles $S^+_1$ of $S^+_0$ with spatial edge length $l_x(S^+_1)=l_x(S^+_0)/2^m = L / 2^m$ and time length either

$$\begin{aligned} l_t(S^+_1)=\frac{l_t(S^+_0)}{\lfloor 2^{pm} \rfloor } =\frac{(1-\alpha )L^p}{\lfloor 2^{pm} \rfloor } \quad \text {or}\quad l_t(S^+_1)=\frac{(1-\alpha )L^p}{\lceil 2^{pm} \rceil }. \end{aligned}$$

For every $S^+_1$, there exists a unique rectangle $R_1$ with spatial edge length $l_x = L / 2^{m}$ and time length $l_t = 2\,L^p / 2^{mp}$ such that $R_1$ has the same top as $S^+_1$. We select those rectangles $S^+_1$ for which $\lambda < c_{R_1}$ and denote the obtained collection by $\{ S^+_{1,j} \}_j$. If $\lambda \ge c_{R_1}$, we subdivide $S^+_1$ in the same manner as above and select all those subrectangles $S^+_2$ for which $\lambda < c_{R_2}$ to obtain family $\{ S^+_{2,j} \}_j$. We continue this selection process recursively. At the ith step, we partition unselected rectangles $S^+_{i-1}$ by dividing each spatial edge into $2^m$ equally long intervals. If

$$\begin{aligned} \frac{l_t(S_{i-1}^+)}{\lfloor 2^{pm} \rfloor } < \frac{(1-\alpha )L^p}{2^{pmi}}, \end{aligned}$$

(3.1)

we divide the time interval of $S^+_{i-1}$ into $\lfloor 2^{pm} \rfloor$ equally long intervals. If

$$\begin{aligned} \frac{l_t(S_{i-1}^+)}{\lfloor 2^{pm} \rfloor } \ge \frac{(1-\alpha )L^p}{2^{pmi}}, \end{aligned}$$

(3.2)

we divide the time interval of $S^+_{i-1}$ into $\lceil 2^{pm} \rceil$ equally long intervals. We obtain subrectangles $S^+_i$. For every $S^+_i$, there exists a unique rectangle $R_i$ with spatial edge length $l_x = L / 2^{mi}$ and time length $l_t = 2\,L^p / 2^{pmi}$ such that $R_i$ has the same top as $S^+_i$. Select those $S^+_i$ for which $\lambda < c_{R_i}$ and denote the obtained collection by $\{ S^+_{i,j} \}_j$. If $\lambda \ge c_{R_i}$, we continue the selection process in $S^+_i$. In this manner we obtain a collection $\{S^+_{i,j} \}_{i,j}$ of pairwise disjoint rectangles.

Observe that if (3.1) holds, then we have

$$\begin{aligned} l_t(S_i^+) = \frac{l_t(S^+_{i-1})}{\lfloor 2^{pm} \rfloor } < \frac{(1-\alpha )L^p}{2^{pmi}}. \end{aligned}$$

On the other hand, if (3.2) holds, then

$$\begin{aligned} l_t(S_i^+) = \frac{l_t(S^+_{i-1})}{\lceil 2^{pm} \rceil } \le \frac{l_t(S^+_{i-1})}{2^{pm}} \le \dots \le \frac{(1-\alpha )L^p}{2^{pmi}}. \end{aligned}$$

This gives an upper bound

$$\begin{aligned} l_t(S_i^+) \le \frac{(1-\alpha )L^p}{2^{pmi}} \end{aligned}$$

for every $S_i^+$.

Suppose that (3.2) is satisfied at the ith step. Then we have a lower bound for the time length of $S_i^+$, because

$$\begin{aligned} l_t(S^+_i) = \frac{l_t(S_{i-1}^+)}{\lceil 2^{pm} \rceil } \ge \frac{\lfloor 2^{pm} \rfloor }{\lceil 2^{pm} \rceil } \frac{(1-\alpha )L^p}{2^{pmi}} \ge \frac{1}{2} \frac{(1-\alpha )L^p}{2^{pmi}}. \end{aligned}$$

On the other hand, if (3.1) is satisfied, then

$$\begin{aligned} l_t(S^+_i) = \frac{l_t(S_{i-1}^+)}{\lfloor 2^{pm} \rfloor } \ge \frac{l_t(S_{i-1}^+)}{ 2^{pm}}. \end{aligned}$$

In this case, (3.2) has been satisfied at an earlier step $i'$ with $i'< i$. We obtain

$$\begin{aligned} l_t(S^+_i) \ge \frac{l_t(S_{i-1}^+)}{ 2^{pm}} \ge \dots \ge \frac{l_t(S_{i'}^+)}{ 2^{pm(i-i')}} \ge \frac{1}{2} \frac{(1-\alpha )L^p}{ 2^{pmi}} \end{aligned}$$

by using the lower bound for $S_{i'}^+$. Thus, we have

$$\begin{aligned} \frac{1}{2} \frac{(1-\alpha )L^p}{2^{pmi}} \le l_t(S^+_i) \le \frac{(1-\alpha )L^p}{2^{pmi}} \end{aligned}$$

for every $S^+_i$. By using the lower bound for the time length of $S^+_i$ and the choice of m, we observe that

$$\begin{aligned} l_t(R_i) - l_t(S^+_i)&\le \frac{2 L^p}{2^{pmi}} - \frac{1}{2} \frac{(1-\alpha )L^p}{2^{pmi}} = \frac{1}{2} \frac{L^p}{2^{pmi}} (3+ \alpha ) \\&\le \frac{(\alpha -\gamma ) L^p}{2^{pm(i-1)}} = \frac{(1-\gamma )L^p}{2^{pm(i-1)}} - \frac{(1-\alpha )L^p}{2^{pm(i-1)}} \\&\le l_t(R^+_{i-1}(\gamma )) - l_t(S^+_{i-1}) . \end{aligned}$$

This implies

$$\begin{aligned} R_{i} \subset R^+_{i-1}(\gamma ) \end{aligned}$$

(3.3)

for a fixed rectangle $S^+_{i-1}$ and for every subrectangle $S^+_{i} \subset S^+_{i-1}$. By the construction of the subrectangles $S^+_i$, we have

$$\begin{aligned} 2^{nm} \lfloor 2^{pm} \rfloor |S^+_i |\le |S^+_{i-1} |\le 2^{nm} \lceil 2^{pm} \rceil |S^+_i |\end{aligned}$$

(3.4)

and

$$\begin{aligned} \frac{1}{2} \frac{1-\alpha }{1-\gamma } |R^+_i(\gamma ) |\le |S^+_i |\le \frac{1-\alpha }{1-\gamma } |R^+_i(\gamma ) |. \end{aligned}$$

(3.5)

We have a collection $\{ S^+_{i,j} \}_{i,j}$ of pairwise disjoint rectangles. However, the rectangles in the corresponding collection $\{ S^-_{i,j} \}_{i,j}$ may overlap. Thus, we replace it by a subfamily $\{ \widetilde{S}^-_{i,j} \}_{i,j}$ of pairwise disjoint rectangles, which is constructed in the following way. At the first step, choose $\{ S^-_{1,j} \}_{j}$ and denote it by $\{ \widetilde{S}^-_{1,j} \}_j$. Then consider the collection $\{ S^-_{2,j} \}_{j}$ where each $S^-_{2,j}$ either intersects some $\widetilde{S}^-_{1,j}$ or does not intersect any $\widetilde{S}^-_{1,j}$. Select the rectangles $S^-_{2,j}$ that do not intersect any $\widetilde{S}^-_{1,j}$, and denote the obtained collection by $\{ \widetilde{S}^-_{2,j} \}_j$. At the ith step, choose those $S^-_{i,j}$ that do not intersect any previously selected $\widetilde{S}^-_{i',j}$, $i' < i$. Hence, we obtain a collection $\{ \widetilde{S}^-_{i,j} \}_{i,j}$ of pairwise disjoint rectangles. Observe that for every $S^-_{i,j}$ there exists $\widetilde{S}^-_{i',j}$ with $i' \le i$ such that

$$\begin{aligned} \text {pr}_x(S^-_{i,j}) \subset \text {pr}_x(\widetilde{S}^-_{i',j}) \quad \text {and} \quad \text {pr}_t(S^-_{i,j}) \subset 3 \text {pr}_t(\widetilde{S}^-_{i',j}). \end{aligned}$$

(3.6)

Here pr$_x$ denotes the projection to ${\mathbb {R}}^n$ and pr$_t$ denotes the projection to the time axis.

Rename $\{ S^+_{i,j} \}_{i,j}$ and $\{ \widetilde{S}^-_{i,j} \}_{i,j}$ as $\{ S^+_{i} \}_{i}$ and $\{ \widetilde{S}^-_{j} \}_j$, respectively. Let $S(\lambda ) = \bigcup _i S^+_i$. Note that $S^+_i$ is spatially contained in $S^-_i$, that is, $\text{ pr}_x (S^+_i)\subset \text{ pr}_x (S^-_i)$. In the time direction, we have

$$\begin{aligned} \text {pr}_t(S^+_i) \subset \text {pr}_t(R_i) \subset \frac{7 + \alpha }{1-\alpha } \text {pr}_t(S^-_i), \end{aligned}$$

(3.7)

because

$$\begin{aligned} \biggl ( \frac{7 + \alpha }{1-\alpha } + 1 \biggr ) \frac{l_t(S^-_i)}{2} \ge \frac{8}{1-\alpha } \frac{(1-\alpha )L^p}{2^{pmi+2}} = \frac{2L^p}{2^{pmi}} = l_t(R_i). \end{aligned}$$

Therefore, by (3.6) and (3.7), it holds that

$$\begin{aligned} |S(\lambda ) |= \Big |\bigcup _i S^+_i \Big |\le c_1 \sum _j |\widetilde{S}^-_j |\quad \text {with}\quad c_1 = 3\frac{7+\alpha }{1-\alpha }. \end{aligned}$$

(3.8)

Let $\lambda> \delta > 0$ and consider the collection $\{S^+_k\}_k$ for $\delta$. Define $\mathcal {J}_k = \{ j \in \mathbb {N}: \widetilde{S}^+_j \subset S^+_k \}$. Since each $S^+_i$ is contained in some $S^+_k$, we get the partition

$$\begin{aligned} \bigcup _j \widetilde{S}^-_j = \bigcup _k \bigcup _{j\in \mathcal {J}_k} \widetilde{S}^-_j. \end{aligned}$$

Fix $k \in \mathbb {N}$. We have $\widetilde{S}^+_j \subset S^+_k$ for every $j \in \mathcal {J}_k$, where $S^+_k$ was obtained by subdividing a previous $S^+_{k^-}$ for which $a_{R_{k^-}} \le \delta$. Hence, it holds that $\widetilde{S}^-_j \subset R_k$ for every $j \in \mathcal {J}_k$. From (3.3), it follows that $\widetilde{S}^-_j \subset R^+_{k^-}(\gamma )$ for every $j \in \mathcal {J}_k$. We have

for every $j \in \mathcal {J}_k$. Let $\mathcal {M}_k = \{j\in \mathcal {J}_k: I_j \le II_j \}$ and

$$\begin{aligned} \mathcal {K} = \biggl \{ k \in \mathbb {N}: |R^+_{k^-}(\gamma ) |\le A \Bigl |\bigcup _{j \in \mathcal {M}_k} \widetilde{S}^-_j \Bigr |\biggr \}, \end{aligned}$$

where $A>1$ will be specified later. Then for $j \in \mathcal {M}_k$ we have

By summing over $j \in \mathcal {M}_k$, we obtain

$$\begin{aligned} (\lambda ^r - \delta ^r) \sum _{j \in \mathcal {M}_k} |\widetilde{S}^-_j |< \sum _{j \in \mathcal {M}_k} 2 \int _{\widetilde{S}^-_j} (f - a_{R_{k^-}})^r_+ \le 2 \int _{R^+_{k^-}(\gamma )} (f - a_{R_{k^-}})^r_+ . \end{aligned}$$

Thus, if $k \in \mathcal {K}$, we observe that

for every $(x,t) \in R_{k^-}$, where $M^\sharp f$ is the parabolic sharp maximal function defined by

It holds that

$$\begin{aligned} M^\sharp f(x,t) > \frac{1}{2A} (\lambda ^r - \delta ^r) \end{aligned}$$

for every $(x,t) \in \bigcup _{k \in \mathcal {K}} R_{k^-}$. Thus, we obtain

$$\begin{aligned} \Bigl |\bigcup _{k \in \mathcal {K}} \bigcup _{j\in \mathcal {M}_k} \widetilde{S}^-_j \Bigr |\le \Bigl |\bigcup _{k \in \mathcal {K}} R^+_{k^-}(\gamma ) \Bigr |\le \Bigl |\bigcup _{k \in \mathcal {K}} R_{k^-} \Bigr |\le \bigr |R_0 \cap \{ M^\sharp f > \tfrac{1}{2A} (\lambda ^r - \delta ^r) \} \bigl |. \end{aligned}$$

For every $(x,t) \in R_0 \cap \{ M^\sharp f(x,t) > \frac{1}{2A} (\lambda ^r - \delta ^r) \}$, there exists $R_{(x,t)} \subset R_0$ such that $(x,t) \in R_{(x,t)}$ and

By a similar argument to the Vitali covering theorem, we obtain a countable collection $\{R_i\}_i$ of pairwise disjoint parabolic rectangles such that

$$\begin{aligned} \big \{ (x,t) \in R_0: M^\sharp f(x,t) > \tfrac{1}{2A} (\lambda ^r - \delta ^r) \big \} \subset \bigcup _{l=1}^\infty 5 R_l. \end{aligned}$$

Then we have

where $c_2 = 5^{n+p} 2^{\frac{q}{r}+2} c_1 / (1-\gamma )$. On the other hand, if $k \notin \mathcal {K}$, we have

$$\begin{aligned} \Bigl |\bigcup _{j \in \mathcal {M}_k} \widetilde{S}^-_j \Bigr |\le \frac{1}{A} |R^+_{k^-}(\gamma ) |. \end{aligned}$$

Summing over all indices $k \notin \mathcal {K}$ and applying (3.4) together with (3.5), we conclude that

$$\begin{aligned} \sum _{k \notin \mathcal {K}} \sum _{j \in \mathcal {M}_k} |\widetilde{S}^-_j |&\le \frac{1}{A} \sum _{k \notin \mathcal {K}} |R^+_{k^-}(\gamma ) |\le \frac{2}{A} \frac{1-\gamma }{1-\alpha } \sum _{k \notin \mathcal {K}} |S^+_{k^-} |\\&\le \frac{2}{A} \frac{1-\gamma }{1-\alpha } 2^{nm} \lceil 2^{pm} \rceil \sum _{k \notin \mathcal {K}} |S^+_k |\le \frac{c_3}{Ac_1} |S(\delta ) |, \end{aligned}$$

where

$$\begin{aligned} 2^{nm} \lceil 2^{pm} \rceil&\le 2^{nm} 2^{pm+1} \le 2^{1+(n+p) \bigl ( \frac{1}{p} \log _2\bigl ( \frac{3+\alpha }{2(\alpha - \gamma )}\bigr ) + 1 \bigr ) } \\&= 2^{1+n+p} \biggl ( \frac{3+\alpha }{2(\alpha - \gamma )}\biggr )^{1 + \frac{n}{p}} = \frac{1}{2c_1} \frac{1-\alpha }{1-\gamma } c_3 . \end{aligned}$$

By combining the cases $k\in \mathcal {K}$ and $k \notin \mathcal {K}$, we obtain

$$\begin{aligned} c_1 \sum _{k} \sum _{j \in \mathcal {M}_k} |\widetilde{S}^-_j |&= c_1 \sum _{k \in \mathcal {K}} \sum _{j \in \mathcal {M}_k} |\widetilde{S}^-_j |+ c_1 \sum _{k \notin \mathcal {K}} \sum _{j \in \mathcal {M}_k} |\widetilde{S}^-_j |\\&\le \frac{c_2 A^\frac{q}{r}}{2} \frac{ \Vert f \Vert ^q}{(\lambda ^r - \delta ^r)^\frac{q}{r}} + \frac{c_3}{A} |S(\delta ) |. \end{aligned}$$

It is left to consider the case $j \notin \mathcal {M}_k$. Using (3.5), we have

for every $(x,t) \in R_{j}$ and thus for every $(x,t) \in \bigcup _{k} \bigcup _{j\notin \mathcal {M}_k} R_{j}$. Then arguing as before, we obtain

$$\begin{aligned} \Big |\bigcup _{k} \bigcup _{j\notin \mathcal {M}_k} \widetilde{S}^-_j \Big |&\le \Big |\bigcup _{k} \bigcup _{j\notin \mathcal {M}_k} R_j \Big |\le \bigl |R_0 \cap \{ M^\sharp f > \tfrac{1}{4} \tfrac{1-\alpha }{1-\gamma } (\lambda ^r - \delta ^r) \} \bigr |\\&\le \frac{c_4}{2c_1} \frac{ \Vert f \Vert ^q}{(\lambda ^r - \delta ^r)^\frac{q}{r}} , \end{aligned}$$

where $c_4 = c_2 ( 2(1-\gamma )/(1-\alpha ))^{\frac{q}{r}}$. By using (3.8) and combining the cases $j \in \mathcal {M}_k$ and $j \notin \mathcal {M}_k$, we conclude that

$$\begin{aligned} |S(\lambda ) |&\le c_1 \sum _j |\widetilde{S}^-_j |= c_1 \sum _{k} \sum _{j \in \mathcal {M}_k} |\widetilde{S}^-_j |+ c_1 \sum _{k} \sum _{j \notin \mathcal {M}_k} |\widetilde{S}^-_j |\\&\le A^\frac{q}{r} c_4 \frac{ \Vert f \Vert ^q}{(\lambda ^r - \delta ^r)^\frac{q}{r}} + \frac{c_3}{A} |S(\delta ) |. \end{aligned}$$

By choosing $A = 2^{\frac{q}{r}+1} c_3$ and replacing $\lambda$ and $\delta$ by $2^\frac{1}{r} \lambda$ and $\lambda$, respectively, we have

$$\begin{aligned} |S( 2^\frac{1}{r} \lambda ) |\le A^\frac{q}{r} c_4 \frac{ \Vert f \Vert ^q}{ \lambda ^q} + \frac{c_3}{A} |S(\lambda ) |. \end{aligned}$$

(3.9)

Let

$$\begin{aligned} \lambda _0 = \frac{ \Vert f \Vert }{|R_0^+(\alpha ) |^\frac{1}{q}}. \end{aligned}$$

For $0 < \lambda \le \lambda _0$, we have

$$\begin{aligned} |R^{+}_0(\alpha ) \cap \{ f(x,t)_+ > \lambda \} |\le |R_0^+(\alpha ) |= \frac{ \Vert f \Vert ^q}{\lambda _0^q} \le \frac{ \Vert f \Vert ^q}{\lambda ^q}. \end{aligned}$$

Assume then that $\lambda > \lambda _0$. There exists an integer $N \in \mathbb {N}$ such that $2^\frac{N}{r} \lambda _0 \le \lambda < 2^\frac{N+1}{r} \lambda _0$. We claim that

$$\begin{aligned} |S(2^\frac{K}{r} \lambda _0) |\le c_5 \frac{ \Vert f \Vert ^q}{(2^{\frac{K}{r}} \lambda _0)^q} \end{aligned}$$

for every $K=0,1,\dots ,N$, where $c_5 = 2^{\frac{q}{r}+1} A^\frac{q}{r} c_4$. We prove the claim by induction. First, note that the claim holds for $K=0$, because

$$\begin{aligned} |S(\lambda _0) |\le |R_0^+(\alpha ) |= \frac{ \Vert f \Vert ^q}{\lambda _0^q} \le c_5 \frac{ \Vert f \Vert ^q}{\lambda _0^q}. \end{aligned}$$

Then assume that the claim holds for $K \in \{0,1,\dots ,N-1\}$, that is,

$$\begin{aligned} |S(2^\frac{K}{r} \lambda _0) |\le c_5 \frac{ \Vert f \Vert ^q}{(2^\frac{K}{r} \lambda _0)^q}. \end{aligned}$$

We show that this implies the claim for $K+1$. By using (3.9) for $2^\frac{K}{r} \lambda _0$ we observe that

$$\begin{aligned} |S( 2^\frac{K+1}{r} \lambda _0 ) |&\le A^\frac{q}{r} c_4 \frac{ \Vert f \Vert ^q}{ (2^\frac{K}{r} \lambda _0)^q} + \frac{c_3}{A} |S(2^\frac{K}{r} \lambda _0) |\le A^\frac{q}{r} c_4 \frac{ \Vert f \Vert ^q}{ (2^\frac{K}{r} \lambda _0)^q} + \frac{c_3}{A} c_5 \frac{ \Vert f \Vert ^q}{(2^\frac{K}{r} \lambda _0)^q} \\&= 2^\frac{q}{r} \biggl ( A^\frac{q}{r} c_4 + \frac{c_3}{A} c_5 \biggr ) \frac{ \Vert f \Vert ^q}{(2^\frac{K+1}{r} \lambda _0)^q} = c_5 \frac{ \Vert f \Vert ^q}{(2^\frac{K+1}{r} \lambda _0)^q} . \end{aligned}$$

Therefore, the claim holds for $K+1$.

If $(x,t) \in S^+_0 \setminus S(\lambda )$, then there exists a sequence $\{S^+_l\}_{l\in {\mathbb {N}}}$ of subrectangles containing (x, t) such that $c_{R_l} \le \lambda$ and $|S^+_l |\rightarrow 0$ as $l \rightarrow \infty$. Then by (3.5) and Lemma 2.4 it holds that

The Lebesgue differentiation theorem [9, Lemma 2.3] implies that $f(x,t)^r_+ \le \lambda ^r$ for almost every $(x,t) \in S^+_0 {\setminus } S(\lambda )$. It follows that

$$\begin{aligned} \{ (x,t) \in S^+_0: f(x,t)_+ > \lambda \} \subset S(\lambda ) \end{aligned}$$

up to a set of measure zero. We conclude that

$$\begin{aligned} |S^+_0 \cap \{ f_+ > \lambda \} |&\le |S(\lambda ) |\le |S(2^\frac{N}{r} \lambda _0) |\le c_5 \frac{ \Vert f \Vert ^q}{(2^{\frac{N}{r}} \lambda _0)^q} \\&= 2^\frac{q}{r} c_5 \frac{ \Vert f \Vert ^q}{(2^{\frac{N+1}{r}} \lambda _0)^q} \le C \frac{ \Vert f \Vert ^q}{\lambda ^q} , \end{aligned}$$

where $C = 2^\frac{q}{r} c_5$. This completes the proof. $\square$

4 Chaining arguments and the time lag

Weak type estimates in Theorem 3.1 together with chaining arguments enable us to change the time lag in the parabolic John–Nirenberg inequality.

Theorem 4.1

Let $R \subset \mathbb {R}^{n+1}$ be a parabolic rectangle, $0< \gamma <1$, $-1 < \rho \le \gamma$, $-\rho < \sigma \le \gamma$, $1<q<\infty$ and $0< r \le 1$. Assume that $f \in PJN_{q,\gamma ,r}^{+}(R)$. Then there exist constants $c \in \mathbb {R}$ and $C=C(n,p,q,r,\gamma ,\rho ,\sigma )$ such that

$$\begin{aligned} |R^{+}(\rho ) \cap \{ (f-c)_+ > \lambda \} |\le C \frac{ \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(R)}^q}{\lambda ^q} \end{aligned}$$

and

$$\begin{aligned} |R^{-}(\sigma ) \cap \{ (f-c)_- > \lambda \} |\le C \frac{ \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(R)}^q}{\lambda ^q} \end{aligned}$$

for every $\lambda >0$.

Proof

The beginning of the proof is similar to [9, Theorem 4.1]. Let $R_0 = R$ and $\Vert f \Vert = \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(R_0)}$. Without loss of generality, we may assume that the center of $R_0$ is the origin. Since $f \in PJN_{q,\gamma ,r}^{+}(R_0)$, Theorem 3.1 holds for any parabolic subrectangle of $R_0$ and for any $\gamma< \alpha <1$. Let m be the smallest integer with

$$\begin{aligned} m \ge \log _2 \biggl ( \frac{1+\alpha }{1-\alpha } \biggr ) + \frac{1}{p-1} \biggl ( 2 + \log _2 \frac{1+\alpha }{\rho +\sigma } \biggr ) + 2. \end{aligned}$$

Then there exists $0 \le \varepsilon < 1$ such that

$$\begin{aligned} m = \log _2 \biggl ( \frac{1+\alpha }{1-\alpha } \biggr ) + \frac{1}{p-1} \biggl ( 2 + \log _2 \frac{1+\alpha }{\rho +\sigma } \biggr ) + 2 + \varepsilon . \end{aligned}$$

We partition $R^+_0(\rho ) = Q(0, L) \times (\rho L^p, L^p)$ by dividing each of its spatial edges into $2^m$ equally long intervals and the time interval into $\lceil (1-\rho )2^{mp}/(1-\alpha )\rceil$ equally long intervals. Denote the obtained rectangles by $U^+_{i,j}$ with $i \in \{1,\dots ,2^{mn}\}$ and $j \in \{1,\dots ,\lceil (1-\rho )2^{mp}/(1-\alpha )\rceil \}$. The spatial edge length of $U^+_{i,j}$ is $l = l_x(U^+_{i,j}) =L/2^m$ and the time length is

$$\begin{aligned} l_t(U^+_{i,j}) = \frac{(1-\rho )L^p}{\lceil (1-\rho )2^{mp}/(1-\alpha )\rceil }. \end{aligned}$$

For every $U^+_{i,j}$, there exists a unique rectangle $R_{i,j}$ that has the same top as $U^+_{i,j}$. Our aim is to construct a chain from each $U^+_{i,j}$ to a central rectangle which is of the same form as $R_{i,j}$ and is contained in $R_0$. This central rectangle will be specified later. First, we construct a chain with respect to the spatial variable. Fix $U^+_{i,j}$. Let $P_0 = R_{i,j}$ and

$$\begin{aligned} P_0^+ = R^+_{i,j}(\alpha ) = Q_i \times (t_j - (1-\alpha )l^p, t_j). \end{aligned}$$

We construct a chain of cubes from $Q_i$ to the central cube Q(0, l). Let $Q'_0 = Q_i = Q(x_i, l)$ and set

$$\begin{aligned} Q'_k = Q'_{k-1} - \frac{x_i}{|x_i|} \frac{\theta l}{2} \quad \text {for every} \ k \in \{0,\dots ,N_i\}, \end{aligned}$$

where $1 \le \theta \le \sqrt{n}$ depends on the angle between $x_i$ and the spatial axes and is chosen such that the center of $Q'_k$ is on the boundary of $Q'_{k-1}$. We have

$$\begin{aligned} \frac{1}{2^n} \le \frac{|Q'_k \cap Q'_{k-1} |}{|Q'_k |} \le \frac{1}{2} \quad \text {for every} \ k \in \{0,\dots ,N_i\}, \end{aligned}$$

and $|x_i| = \frac{\theta }{2} (L - bl)$, where $b \in \{1, \dots , 2^m\}$ depends on the distance of $Q_i$ to the center of $Q_0 = Q(0,L)$. The number of cubes in the spatial chain $\{Q'_k\}_{k=0}^{N_i}$ is

$$\begin{aligned} N_i + 1 = \frac{|x_i|}{\frac{\theta }{2} l} + 1 = \frac{L}{l} - b + 1. \end{aligned}$$

Next, we also take the time variable into consideration in the construction of the chain. Let

$$\begin{aligned} P^+_k = Q'_k \times ( t_j - (1-\alpha )l^p - k(1+\alpha )l^p, t_j - k(1+\alpha )l^p ) \end{aligned}$$

and $P^-_k = P^+_k - (0, (1+\alpha )l^p)$, for every $k \in \{ 0, \dots , N_i \}$, be the upper and the lower parts of a parabolic rectangle respectively. These will form a chain of parabolic rectangles from $U^+_{i,j}$ to the eventual central rectangle. Observe that every rectangle $P_{N_i}$ coincides spatially for all pairs (i, j). Consider $j=1$ and such i that the boundary of $Q_i$ intersects the boundary of $Q_0$. For such a cube $Q_i$, we have $b=1$, and thus $N = N_i = \frac{L}{l} - 1$. In the time variable, we travel from $t_1$ the distance

$$\begin{aligned} (N+1)(1+\alpha )l^p + (1-\alpha )l^p = (1+\alpha ) L l^{p-1} + (1-\alpha ) l^p. \end{aligned}$$

We show that the lower part of the final rectangle $P^-_N$ is contained in $R_0$. To this end, we subtract the time length of $U^+_{i,1}$ from the distance above and observe that it is less than half of the time length of $R_0 {\setminus }(R_0^+(\rho ) \cup R_0^-(\sigma ))$. This follows from the computation

$$\begin{aligned}&(1+\alpha ) L l^{p-1} + (1-\alpha ) l^p - \frac{(1-\rho )L^p}{\lceil (1-\rho )2^{mp}/(1-\alpha )\rceil }\\&\qquad = \biggl ( \frac{1+\alpha }{2^{m(p-1)}} + \frac{1-\alpha }{2^{mp}} - \frac{1-\rho }{\lceil (1-\rho )2^{mp}/(1-\alpha ) \rceil } \biggr ) L^p \\&\qquad \le \Biggl ( \frac{1+\alpha }{2^{m(p-1)}} + \frac{1-\alpha }{2^{mp}} - \frac{1-\rho }{2\frac{(1-\rho )2^{mp}}{1-\alpha }} \Biggr ) L^p \\&\qquad = \biggl ( \frac{1+\alpha }{2^{m(p-1)}} + \frac{1-\alpha }{2^{mp+1}} \biggr ) L^p \le 2 \frac{1+\alpha }{2^{m(p-1)}} L^p \le \frac{\rho +\sigma }{2} L^p , \end{aligned}$$

because

$$\begin{aligned} m \ge \frac{1}{p-1} \biggl ( 2 + \log _2 \frac{1+\alpha }{\rho +\sigma } \biggr ). \end{aligned}$$

This implies that $P^-_N \subset R_0^+(\rho - (\rho +\sigma )/2)$. Denote this rectangle $P_N$ by $\mathfrak {R} = \mathfrak {R}_\rho$. This is the central rectangle where all chains will eventually end.

Let $j=1$ and assume that i is arbitrary. We extend the chain $\{P_k\}_{k=0}^{N_i}$ by $N - N_i$ rectangles into the negative time direction such that the final rectangle coincides with the central rectangle $\mathfrak {R}$. More precisely, we consider $Q'_{k+1} = Q'_{N_i}$,

$$\begin{aligned} P^+_{k+1} = P^+_{k} - (0, (1+\alpha )l^p) \quad \text {and}\quad P^-_{k+1} = P^+_{k+1} - (0, (1+\alpha )l^p) \end{aligned}$$

for $k \in \{N_i, \dots , N-1\}$. For every $j \in \{2,\dots ,\lceil (1-\rho )2^{mp}/(1-\alpha )\rceil \}$, we consider a similar extension of the chain. The final rectangles of the chains coincide for fixed j and for every i. Moreover, every chain is of the same length $N+1$, and it holds that

$$\begin{aligned} \frac{1}{2^n} \le \eta = \frac{|P_k^+ \cap P_{k-1}^- |}{|P_k^+ |} \le 1. \end{aligned}$$

Then we consider an index $j \in \{2,\dots ,\lceil (1-\rho )2^{mp}/(1-\alpha )\rceil \}$ related to the time variable. The time distance between the current ends of the chains for pairs (i, j) and (i, 1) is

$$\begin{aligned} (j-1) \frac{(1-\rho ) L^p}{\lceil (1-\rho )2^{mp}/(1-\alpha )\rceil }. \end{aligned}$$

Our objective is to have the final rectangle of the continued chain for (i, j) to coincide with the end of the chain for (i, 1), namely, with the central rectangle $\mathfrak {R}$. To achieve this, we modify $2^{m-1}$ intersections of $P^+_k$ and $P^-_{k+1}$ by shifting $P_k$ and also add a chain of $M_j$ rectangles traveling to the negative time direction into the chain $\{P_k\}_{k=0}^{N}$. We shift every $P_k, k \in \{ 1, \dots , 2^{m-1} \}$, by a $\beta _j$-portion of their temporal length more than the previous rectangle was shifted, that is, we move each $P_k$ into the negative time direction a distance of $k \beta _j (1-\alpha ) l^p$. The values of $M_j \in \mathbb {N}$ and $0\le \beta _j <1$ will be chosen later. In other words, for every $k \in \{ 1, \dots , 2^{m-1} \}$, we modify the definitions of $P^+_k$ by

$$\begin{aligned} P^+_k = Q'_k \times ( t_j - (1-\alpha )l^p - k( 1+\alpha + \beta _j (1-\alpha )) l^p, t_j - k( 1+\alpha + \beta _j (1-\alpha )) l^p), \end{aligned}$$

and then add $M_j$ rectangles defined by

$$\begin{aligned} P^+_{k+1} = P^+_{k} - (0, (1+\alpha )l^p) \quad \text {and}\quad P^-_{k+1} = P^+_{k+1} - (0, (1+\alpha )l^p) \end{aligned}$$

for every $k \in \{N,\dots , N+M_j-1\}$. Note that there exists $1 \le \tau < 2$ such that

$$\begin{aligned} \tau \frac{(1-\rho )2^{mp}}{1-\alpha } =\Bigg \lceil \frac{(1-\rho )2^{mp}}{(1-\alpha )}\Bigg \rceil . \end{aligned}$$

We would like to find such $0\le \beta _j <1$ and $M_j \in \mathbb {N}$ that

$$\begin{aligned} (j-1) \frac{(1-\rho ) L^p}{\lceil (1-\rho )2^{mp}/(1-\alpha )\rceil } - M_j \frac{(1+\alpha ) L^p}{2^{mp}} = 2^{m-1} \beta _j \frac{(1-\alpha ) L^p}{2^{mp}}, \end{aligned}$$

which is equivalent with

$$\begin{aligned} (j-1)\tau ^{-1} (1-\alpha ) - M_j (1+\alpha ) = 2^{m-1} \beta _j (1-\alpha ). \end{aligned}$$

With this choice all final rectangles coincide. Choose $M_j \in \mathbb {N}$ such that

$$\begin{aligned} M_j (1+\alpha ) \le (j-1) \tau ^{-1} (1-\alpha ) < (M_j + 1)(1+\alpha ), \end{aligned}$$

that is,

$$\begin{aligned} 0 \le \xi = (j-1) \tau ^{-1} (1-\alpha ) - M_j (1+\alpha ) < 1+\alpha \end{aligned}$$

and

$$\begin{aligned} \frac{(j-1)(1-\alpha )}{2 (1+\alpha )} -1 \le \frac{(j-1)(1-\alpha )}{\tau (1+\alpha )} -1 < M_j \le \frac{(j-1)(1-\alpha )}{\tau (1+\alpha )} \le \frac{(j-1)(1-\alpha )}{1+\alpha }. \end{aligned}$$

By choosing $0\le \beta _j <1$ such that

$$\begin{aligned} \xi = 2^{m-1} \beta _j (1-\alpha ) = 2^{\frac{2}{p-1} + 1 + \varepsilon } \biggl ( \frac{1+\alpha }{\rho +\sigma } \biggr )^\frac{1}{p-1} \beta _j (1+\alpha ), \end{aligned}$$

we have

$$\begin{aligned} \beta _j = 2^{-\frac{2}{p-1} - 1 - \varepsilon } \biggl ( \frac{\rho +\sigma }{1+\alpha } \biggr )^\frac{1}{p-1} \frac{\xi }{1+\alpha }. \end{aligned}$$

Observe that $0\le \beta _j \le \frac{1}{2}$ for every j. For measures of the intersections of the modified rectangles, it holds that

$$\begin{aligned} \frac{1}{2^{n+1}} \le \frac{|P_k^+ \cap P_{k-1}^- |}{|P_k^+ |} = \eta (1-\beta _j) \le 1 \end{aligned}$$

for every $k \in \{ 1, \dots , 2^{m-1} \}$, and thus

$$\begin{aligned} \frac{1}{2^{n+1}} \le \tilde{\eta }_j = \frac{|P_k^+ \cap P_{k-1}^- |}{|P_k^+ |} \le 1 \end{aligned}$$

for every $k \in \{1,\dots , N+M_j\}$. Fix $U^+_{i,j}$. We conclude that

where in the last inequality we used that $P_k$ are pairwise disjoint separately for even k and for odd k. We have

$$\begin{aligned} N+1+M_j&= \frac{L}{l}+M_j \le 2^m + (j-1) \frac{1-\alpha }{1+\alpha } \\&\le 2^m + \frac{(1-\rho )2^{mp}}{1-\alpha } \frac{1-\alpha }{1+\alpha } \le 2^m + 2^{mp+1} \le 2^{mp+2} \\&\le 2^{\frac{2p}{p-1} + 3p +2} \biggl ( \frac{1+\alpha }{\rho +\sigma } \biggr )^\frac{p}{p-1} \biggl ( \frac{1+\alpha }{1-\alpha } \biggr )^p \end{aligned}$$

for every j. Hence, we obtain

$$\begin{aligned}&(c_{R_{i,j}} - c_{\mathfrak {R}} )_+ \le B \frac{ \Vert f \Vert }{|P_0^+ |^\frac{1}{q}} \quad \text{ with }\quad \\&\quad B = 2^{ \frac{1}{q} + (n+1)\frac{1}{r} } \biggl ( 2^{\frac{2p}{p-1} + 3p +2 } \biggl ( \frac{1+\alpha }{\rho +\sigma } \biggr )^\frac{p}{p-1} \biggl ( \frac{1+\alpha }{1-\alpha } \biggr )^p\biggr )^{\frac{1}{r}-\frac{1}{q}}. \end{aligned}$$

We observe that

$$\begin{aligned}&|R^{+}_0(\rho ) \cap \{ (f-c_{\mathfrak {R}})_+> \lambda \} |\\&\qquad \le \sum _{i,j} |R^+_{i,j}(\alpha ) \cap \{ (f-c_{\mathfrak {R}})_+> \lambda \} |\\&\qquad \le \sum _{i,j} |R^+_{i,j}(\alpha ) \cap \{ (f-c_{R_{i,j}})_+> \tfrac{\lambda }{2} \} |+ \sum _{i,j} |R^+_{i,j}(\alpha ) \cap \{ (c_{R_{i,j}}-c_{\mathfrak {R}})_+ > \tfrac{\lambda }{2} \} |. \end{aligned}$$

The first sum of the right-hand side can be estimated by Theorem 3.1 as follows

$$\begin{aligned} \sum _{i,j} |R^+_{i,j}(\alpha ) \cap \{ (f-c_{R_{i,j}})_+ > \tfrac{\lambda }{2} \} |&\le \sum _{i,j} 2^q C \frac{ \Vert f \Vert ^q_{PJN^+_{q,\gamma ,r}(R_{i,j})}}{\lambda ^q} \\&\le 2^q C \Bigg \lceil \frac{l_t(R_{i,j})}{l_t(U^+_{i,j})} \Bigg \rceil \frac{ \Vert f \Vert ^q_{PJN^+_{q,\gamma ,r}(R_0)}}{\lambda ^q} \\&\le 2^q C \Bigg \lceil \frac{4}{1-\alpha } \Bigg \rceil \frac{ \Vert f \Vert ^q_{PJN^+_{q,\gamma ,r}(R_0)}}{\lambda ^q} \\&\le \frac{2^{q+3} C}{1-\alpha } \frac{ \Vert f \Vert ^q_{PJN^+_{q,\gamma ,r}(R_0)}}{\lambda ^q} . \end{aligned}$$

To estimate the second sum above, assume that $\lambda \ge 2 B \Vert f \Vert / |P_0^+ |^\frac{1}{q}$. This implies that

$$\begin{aligned} |R^+_{i,j}(\alpha ) \cap \{ (c_{R_{i,j}}-c_{\mathfrak {R}})_+> \tfrac{\lambda }{2} \} |&\le |R^+_{i,j}(\alpha ) \cap \{ B \Vert f \Vert / |P_0^+ |^\frac{1}{q} > \tfrac{\lambda }{2} \} |= 0 \end{aligned}$$

for every i, j. Thus,

$$\begin{aligned} |R^{+}_0(\rho ) \cap \{ (f-c_{\mathfrak {R}})_+ > \lambda \} |\le \frac{2^{q+3} C}{1-\alpha } \frac{ \Vert f \Vert ^q}{\lambda ^q} \end{aligned}$$

for every $\lambda \ge 2 B \Vert f \Vert / |P_0^+ |^\frac{1}{q}$. For $0<\lambda < 2 B \Vert f \Vert / |P_0^+ |^\frac{1}{q}$, we have

$$\begin{aligned}&|R^{+}_0(\rho ) \cap \{ (f-c_{\mathfrak {R}})_+ > \lambda \} |\\&\qquad \le |R^+_0(\rho ) |= 2^{(n+p)m} \frac{1-\rho }{1-\alpha } |P^+_0 |\\&\qquad \le 2^{(n+p)(\frac{2}{p-1} + 3 )} \biggl ( \frac{1+\alpha }{\rho +\sigma } \biggr )^\frac{n+p}{p-1} \biggl ( \frac{1+\alpha }{1-\alpha } \biggr )^{n+p} \frac{1-\rho }{1-\alpha } 2^q B^q \frac{ \Vert f \Vert ^q}{\lambda ^q} . \end{aligned}$$

We can apply a similar chaining argument in the reverse time direction for $R_0^-(\sigma )$ with the exception that we also extend (and modify if needed) every chain such that the central rectangle $\mathfrak {R}_\sigma$ coincides with $\mathfrak {R}=\mathfrak {R}_\rho$. A rough upper bound for the number of rectangles needed for the additional extension is given by

$$\begin{aligned} \Bigg \lceil \frac{(\rho +\sigma )L^p}{(1+\alpha )l^p} \Bigg \rceil = \Bigg \lceil \frac{\rho +\sigma }{1+\alpha } 2^{mp} \Bigg \rceil \le 2^{mp+1}. \end{aligned}$$

Thus, the constant B above is $2^{\frac{1}{r} - \frac{1}{q} }$ times larger in this case. This proves the second inequality of the theorem. $\square$

The next corollary of Theorem 4.1 tells that the spaces $PJN_{q,\gamma ,r}^{+}$ coincide for every $0< \gamma <1$ and $0<r<q$.

Corollary 4.2

Let $\Omega _T \subset \mathbb {R}^{n+1}$ be a space-time cylinder, $0<\rho \le \gamma < 1$, $1< q < \infty$ and $0<r \le s<q <\infty$. Then there exist constants $c_1=c_1(n,p,q,r,s,\gamma ,\rho )$ and $c_2=c_2(n,p,q,r,s,\gamma ,\rho )$ such that

$$\begin{aligned} c_1 \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(\Omega _T)} \le \Vert f \Vert _{PJN_{q,\rho ,s}^{+}(\Omega _T)} \le c_2 \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(\Omega _T)}. \end{aligned}$$

Proof

Let $\{R_i\}_{i\in {\mathbb {N}}}$ be a collection of pairwise disjoint parabolic subrectangles of $\Omega _T$. By Hölder’s inequality, we have

where $c_0 = \max \{1, 2^{\frac{1}{r}-1} \} \max \{1, 2^{1 -\frac{1}{s}} \}$. We observe that

By summing over $i\in \mathbb {N}$ and taking supremum over all collections of pairwise disjoint parabolic rectangles, we arrive at

$$\begin{aligned} \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(\Omega _T)} \le c_0 \biggl ( \frac{1-\rho }{1-\gamma } \biggr )^{\frac{1}{s}-\frac{1}{q}} \Vert f \Vert _{PJN_{q,\rho ,s}^{+}(\Omega _T)}. \end{aligned}$$

To show the second inequality, we make the restriction $0 < r \le 1$ so that we can apply Theorem 4.1. This is not an issue because after establishing the second inequality for $0 < r \le 1$ we can use the first inequality to obtain the whole range $0 < r \le s$. Cavalieri’s principle and Theorem 4.1 imply that

$$\begin{aligned} \int _{R_i^+(\rho )} (f-c)_+^s&= s \int _0^\infty \lambda ^{s-1} |R_i^{+}(\rho ) \cap \{ (f-c)_+ > \lambda \} |\, d \lambda \\&\le s \int _{|R_i^{+}(\rho )|^{-\frac{1}{q}} \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(R_i)} }^\infty C \lambda ^{s-q-1} \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(R_i)}^q \, d \lambda \\ {}&\qquad + s \int _0^{|R_i^{+}(\rho )|^{-\frac{1}{q}} \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(R_i)}} \lambda ^{s-1} |R_i^{+}(\rho )| \, d \lambda \\&= \frac{Cs}{q-s} |R_i^{+}(\rho )|^{1-\frac{s}{q}} \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(R_i)}^s + |R_i^{+}(\rho )|^{1-\frac{s}{q}} \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(R_i)}^s \\&\le \frac{Cq}{q-s} |R_i^{+}(\rho )|^{1-\frac{s}{q}} \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(R_i)}^s . \end{aligned}$$

Similarly, we obtain

$$\begin{aligned} \int _{R_i^-(\rho )} (f-c)_-^s \le \frac{Cq}{q-s} |R_i^{+}(\rho )|^{1-\frac{s}{q}} \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(R_i)}^s. \end{aligned}$$

These estimates imply that

Thus, we conclude that

$$\begin{aligned} \Vert f \Vert _{PJN_{q,\rho ,s}^{+}(\Omega _T)} \le \biggl ( \frac{2Cq}{q-s} \biggr )^\frac{1}{s} \Vert f \Vert _{PJN_{q,\gamma ,r}^{+}(\Omega _T)}. \end{aligned}$$

$\square$