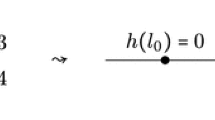Abstract
In this paper we introduce a refined multiplicity for rational tropical curves in arbitrary dimension, which generalizes the refined multiplicity introduced by Block and Göttsche (Compositio Mathematica 152(1): 115–151, 2016). We then prove an invariance statement for the count of rational tropical curves in several enumerative problems using this new refined multiplicity. This leads to the definition of Block–Göttsche polynomials in any dimension.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Enumerative geometry, classical and tropical
Tropical enumerative geometry takes its roots in the founding paper [16] by Mikhalkin. He there proved a correspondence theorem that allows one to compute several classical geometric invariants for toric surfaces, namely Gromov–Witten type invariants and Welschinger invariants whenever defined, through the solving of some associated enumerative problem in planar tropical geometry. Other approaches to the correspondence theorem were later provided by Shustin [21] and Tyomkin [23] along with a generalization for rational curves in higher dimensional toric varieties by Nishinou and Siebert [19]. Some progress has even been made in the non-toric case, for instance in the case of abelian surfaces by Nishinou [18].
In each situation, the spirit of the tropical approach is the same: the goal is to make a count of algebraic curves satisfying some constraints and which is known to be invariant when the constraints vary in some family, e.g. a count of curves passing through some points and which does not depend on the choice of the points as long as it is generic. One then degenerates the constraints to the so-called tropical limit, where the classical enumerative problem becomes a tropical enumerative problem. The desired curve count might then be recovered by counting the tropical curves solution to this new problem with a suitable multiplicities depending on the problem.
Example 1.1
Explicitly, in the case of rational curves in the projective plane \({\mathbb {C}}P^2\), one of these enumerative problems consists in finding the degree d rational curves passing through a chosen configuration of \(3d-1\) points chosen in \({\mathbb {C}}P^2\). The result does not depend on the chosen points if their choice is generic, and is known as \(N_d\), a Gromov–Witten invariant of \({\mathbb {C}}P^2\).
Over the real numbers, Welschinger showed in [26] that if the configuration of \(3d-1\) points is chosen invariant by conjugation and the curves are counted with a suitable sign, the count only depends on d and the number s of pairs of complex conjugated points. It is denoted by \(W_{d,s}\). In particular \(W_{d,0}\) corresponds to the signed count of real rational curves passing through a generic configuration of \(3d-1\) real points. \(\square \)
We keep in mind the case of degree d rational curves in the pursue of this introduction. To the tropical limit, the enumerative problems leading to the definition of \(N_d\) and \(W_{d,0}\) degenerate to the following tropical enumerative problem: finding degree d rational tropical curves passing through a chosen configuration of \(3d-1\) points. For a definition of tropical curves, see Sect. 2, but for the reading of the introduction, one only needs to know that they are some finite graphs inside an affine space \({\mathbb {R}}^r\), and that they have some infinite edges whose slopes form the degree of the curve. According to [16], to recover both invariants \(N_d\) and \(W_{d,0}\), it suffices to count tropical curves \(\Gamma \) passing through a generic choice of \(3d-1\) points with different multiplicities \(m_\Gamma ^{\mathbb {C}}\) and \(m_\Gamma ^{\mathbb {R}}\), defined as follows: there exists a natural vertex multiplicity \(m_V\), and one then sets
Both multiplicities are a product over the vertices of the tropical curve. The count with \(m^{\mathbb {C}}_\Gamma \) gives \(N_d\) and the count with \(m_\Gamma ^{\mathbb {R}}\) gives \(W_{d,0}\). In [3], Block and Göttsche introduced a refined multiplicity for tropical curves, which is also a product over the vertices of the tropical curve:
This multiplicity is a Laurent polynomial in one variable q, which specializes to \(m_\Gamma ^{\mathbb {C}}\) and \(m_\Gamma ^{\mathbb {R}}\) when q goes respectively to 1 and \(-1\). The count of tropical solutions using this refined multiplicity was proven to also lead to an invariant by Itenberg and Mikhalkin [13]. The classical meaning of these tropically defined invariants remains quite mysterious. Conjecturally [11], they relate to the computation of the \(\chi _{-y}\)-genera of the relative Hilbert schemes of some linear systems of curves. Some attempts in this direction have been made by Nicaise et al. [18].
Another lead to understand these invariants was provided by Mikhalkin [17]. Though his approach is valid for curves in a general toric surface, we still consider the degree d rational curves in the case of the projective plane, and a configuration \({\mathcal {P}}\) of \(3d-1\) points which are this time chosen on the coordinate axis of the projective plane. Mikhalkin introduced a signed count for the oriented real rational curves passing through \(\pm p\) for each \(p\in {\mathcal {P}}\). This count is refined according to the value of a so called quantum index, which is defined more generally for each oriented real curve of type I. He then proved that the result of the count only depends on the number of pairs of complex conjugated points on each axis. If the points are all chosen real, he relates the refined count to the tropical invariant obtained solving the analog tropical enumerative problem, and using Block–Göttsche multiplicities. The tropical analog problem is finding degree d rational tropical curves whose infinite edges are contained in some fixed lines. The result was extended by the author in [7] and [6] in case there are complex conjugated points.
Since, many other tropical enumerative problems have been shown to support a refinement, i.e. the existence of a non-trivial polynomial multiplicity such that the count of solution using this multiplicity does not depend on the chosen constraints. See for instance [2, 20] or [10]. However, in every of these situations, the new refined multiplicity of a tropical curve is a product over its vertices, just as is the complex multiplicity. In higher dimension, the complex multiplicity is also not necessarily a product over the vertices. This a priori prevents anyone to find a simple multiplicity which is a product over the vertices and leads to an invariant. Finding a refined multiplicity which is not a product over the vertices seems even more complicated. Here, we show an in-between approach, providing a multiplicity which is up to sign a product over the vertices. The definition of this sign, which is at the center of the proof, carries the “non-vertex” information.
Remark 1.2
Notice that it might happen even in the planar setting that the complex multiplicity of a tropical curve is not a product over its vertices, as shown by Mandel and Ruddat [15]. This occurs when dealing with tropical curves which are not trivalent, for instance, imposing that the curves meets some line at one of its vertices. \(\square \)
1.2 Moment problem and refined invariance
A natural generalization of the tropical enumerative problem considered by Mikhalkin [17] is the following, which we call \(\omega \)-problem. Let N be a lattice of rank r and M its dual lattice. From now on, \(N_{\mathbb {R}}=N\otimes _{\mathbb {Z}}{\mathbb {R}}\) will be our workspace for tropical curves and every enumerative problem. We consider tropical curves of degree \(\Delta \), which is a multiset of vectors in N of total sum 0, and not containing the zero vector. Let \(\omega \) be a 2-form on N, and for each \(n_e\in \Delta \), fix a hyperplane \({\mathcal {H}}_e\) with slope \(\ker \iota _{n_e}\omega \). We look for degree \(\Delta \) rational tropical curves such that the unbounded end directed by \(n_e\) is contained in \({\mathcal {H}}_e\). As this is not enough to ensure having a finite number of solutions, we add the condition that a chosen unbounded end \(e_0\) is contained in a fixed plane \(D\subset N_{\mathbb {R}}\) transverse to \({\mathcal {H}}_{e_0}\).
Remark 1.3
In the planar case, there is only one possible choice of non-zero 2-form \(\omega \) up to multiplication by a scalar, and no need to choose a plane D. For each choice of \(\Delta \), the \(\omega \)-problems coincide with the enumerative problem considered by Mikhalkin [17]. \(\square \)
Such an enumerative problem where tropical curves have constraints imposed on their unbounded ends by a 2-form also appear in the work of Mandel [14]. In his paper, the author deals with the refinement of some classical invariants appearing in the balancing of some scattering diagrams, thus expanding to higher dimension the refined approach of Filippini and Stoppa [8] to the tropical vertex group considered by Gross et al. [12].
The tropical solutions to the \(\omega \)-problem are trivalent, and are counted with the following multiplicity:
where \(a_V\) and \(b_V\) are two among the three outgoing slopes at the vertex V, chosen such that \(\omega (a_V,b_V)>0\). The space \(K_\omega \) is the space generated by the \(a_V\wedge b_V\) in the kernel of \(\omega :a\wedge b\in \Lambda ^2 N\mapsto \omega (a,b)\in {\mathbb {Z}}\). Implicitly in the notation, the exponents of the variable q are taken modulo \(K_\omega \). For a generic choice of \(\omega \), one has \(K_\omega =0\) and there is no quotient. This multiplicity is a product over the vertices of the curve, and can be seen as a Laurent polynomial in several variables, whose number depends on the rank of the quotient lattice \(\Lambda ^2 N/K_\omega \). This multiplicity also appears in [22] to prove a local invariance statement in a similar but different setting. One recovers the refined multiplicity from Mandel [14] by evaluating the 2-form \(\omega \) on the exponents, and divising by a suitable power of \(q-q^{-1}\). However, and surprisingly, such an evaluation is not necessary to get an invariance statement.
Remark 1.4
Getting back to the planar case, denoting by \(\mathrm {det}\) the 2-form, and identifying \(\Lambda ^2 N={\mathbb {Z}}\det \) with \({\mathbb {Z}}\), the refined multiplicity \(B_\Gamma ^{K_\mathrm {det}}\) is given by
It is thus equal to the refined multiplicity of Block–Göttsche up to a factor \(q-q^{-1}\) at each vertex and a dilatation by 2 in the exponents. It comes from the fact that \(q^m-q^{-m}\) is always divisible by \(q-q^{-1}\), but in the general case, there is no such canonical choice to divide all vertex multiplicities. \(\square \)
We have the following invariance statement, asserting that the curve count does not depend on the choice of the hyperplanes \({\mathcal {H}}_e\) nor the choice of D.
Theorem
3.14 The count of solutions to the \(\omega \)-problem using the refined multiplicity \(B_\Gamma ^{K_\omega }\) does not depend on the choice of \({\mathcal {H}}_e\) and D as long as it is generic. It only depends on the choice of \(\omega \) and the unbounded end \(e_0\).
In particular the curve count does not depend on the choice of D, including the choice of its slope. The obtained invariant is denoted by \({\mathcal {B}}_\Delta ^{\omega ,e_0}\). Thus, we get a family of invariants \({\mathcal {B}}_\Delta ^{\omega ,e_0}\in {\mathbb {Z}}[\Lambda ^2 N/K_\omega ]\). Furthermore, we prove that this map is continuous in the following sense. The map \(\omega \mapsto K_\omega \) is constant on the cones of some fan \(\Omega _\Delta \) in \(\Lambda ^2 M_{\mathbb {R}}\). Denoting \(K_\sigma \) the value on some cone \(\sigma \) of \(\Omega _\Delta \), for \(\tau \prec \sigma \), one has \(K_\sigma \subset K_\tau \), leading to a projection \(p_\sigma ^\tau :{\mathbb {Z}}[\Lambda ^2 N/K_\sigma ]\rightarrow {\mathbb {Z}}[\Lambda ^2 N/K_\tau ]\). We then have the following theorem.
Theorem
5.3 The function \(\omega \mapsto {\mathcal {B}}_\Delta ^{\omega ,e_0}\) is constant on the interior of the cones of \(\Omega _\Delta \), and for \(\tau \prec \sigma \), the value on \(\tau \) is the image of the value on \(\sigma \) under the projection \(p_\sigma ^\tau \).
1.3 Main results
Theorem 3.14 is an invariance result with little improvement compared to already known tropical refined invariants since its proof relies on the fact that for the \(\omega \)-problem, the complex multiplicity of a tropical curve is still a product over its vertices, just as in the planar case. To some extent, it might even be seen as a particular case of the balancing of scaterring diagrams done by Mandel [14]. However, this especially simple observation can then be used to provide an invariance statement in a larger class of enumerative problems for which the complex multiplicity is no longer a product over the vertices.
Consider rational tropical curves of degree \(\Delta \) in \(N_{\mathbb {R}}\), and for each \(n_e\in \Delta \), choose \(L_e\) a sublattice of \(N/\langle n_e \rangle \) such that \(\sum _e \mathrm {cork}L_e=|\Delta |+r-3\). Let \({\mathcal {L}}_e\) be a affine subspace of \(N_{\mathbb {R}}/\langle n_e \rangle \) with slope \(L_e\). We look for rational tropical curves of degree \(\Delta \) such that image of the unbounded end e in \(N_{\mathbb {R}}/\langle n_e \rangle \) lies in \({\mathcal {L}}_e\). The dimension count ensures that if the \({\mathcal {L}}_e\) are chosen generically, there is a finite number of solutions. Now, let \(\omega \) be a 2-form such that
where \(m^{{\mathbb {C}},(L_e)}\) denotes the complex multiplicity in the hereby considered enumerative problem, while \(m_\Gamma ^{{\mathbb {C}},\omega ,e_0}\) denotes the complex multiplicity in the \(\omega \)-problem associated to \(\omega \). See Sect. 2.5 for a proper definition of the complex multiplicity. The choice \(\omega =0\) always suits the hypothesis, but provides a trivial result. However, in many cases, it is possible to choose a non-trivial \(\omega \), see Example 4.4. Under this technical hypothesis, we have the following invariance result.
Theorem
4.5 There exists signs \(\varepsilon _\Gamma \) only depending on the combinatorial type of \(\Gamma \) and the constraints \((L_e)\) such that the count of solutions with multiplicity \(\varepsilon _\Gamma B_\Gamma ^{K_\omega }\) only depends on the choice of the slopes \(L_e\) and not the affine subspaces \({\mathcal {L}}_e\).
The obtained invariant is denoted by \({\mathcal {B}}_\Delta ^{K_\omega }(L_e)\). The proof of the existence of the signs \(\varepsilon _\Gamma \) is combined with the proof of invariance since the signs are in fact chosen so that the count of solutions remains invariant. Moreover, the signs \(\varepsilon _\Gamma \) can be interpreted as orientations on the cones of the moduli space of tropical curves. With this interpretation, the multiplicities leading to invariant counts can be viewed as cycles in the star complex of the moduli space. The star complex of a fan \({\mathcal {F}}\) is the CW-complex \(\left( {\mathcal {F}}\backslash \{0\}\right) /{\mathbb {R}}_+^*\). It can be seen as the space over which \({\mathcal {F}}\) is the cone. Such an interpretation may lead to further interesting invariants.
The idea that drives the proof is that with an additional technical assumption, a multiplicity that leads to an invariant in a specific enumerative problem may be used to get a new invariant in another enumerative problem.
We also prove a statement of continuity of the invariants \({\mathcal {B}}_\Delta ^{K_\omega }(L_e)\) in terms of the slopes \((L_e)\). See Theorem 5.5.
Finally, we prove some enhancements of the main Theorem 4.5 by imposing conditions on marked points and not only unbounded ends, and study the possibility of replacing the affine constraints by tropical cycles.
1.4 Motivations
The study of the aforementioned tropical enumerative problems using the proposed refined multiplicity is justified by their connection to a family of classical enumerative problems, through the use of a correspondence theorem. We now make this connection explicit.
In the planar case, the classical counterpart to the tropical enumerative problems are as follows: let \({\mathbb {C}}\Delta \) be a toric surface endowed with its canonical real structure, the problem consists in finding the real rational curves in \({\mathbb {C}}\Delta \) with fixed intersection with the toric boundary of \({\mathbb {C}}\Delta \). This intersection comprises real points and pairs of complex conjugated points. This is the problem studied by Mikhalkin [17]. The general case takes place in a toric variety \({\mathbb {C}}\Delta \), and consists in finding the real rational curves whose intersection points with the toric boundary belong to some chosen orbits of subtori of the toric variety.
As mentioned above, in the planar case, Mikhalkin proved that there exists a refined signed count of the solutions to each classical enumerative problem that leads to an invariant. The refinement is provided by the value of quantum index, which up to a shift corresponds to the log-area of the oriented curves solutions to the problem. Recall that the log-area defined by the integral of the volume form of \(N_{\mathbb {R}}\simeq {\mathbb {R}}^2\) pull-backed by the logarithmic map \(\mathrm {Log}:N\otimes {\mathbb {C}}^*\subset {\mathbb {C}}\Delta \longrightarrow N_{\mathbb {R}}\). For more details, see [6, 17]. Preferably to the Block–Göttsche multiplicity \(m_\Gamma ^{BG}\), the refined multiplicity \(B_\Gamma ^{K_\mathrm {det}}=\prod _V (q^{m_V}-q^{-m_V})\) is the one involved in the correspondence result of Mikhalkin [17] that relates the tropical refined invariant to the classical refined invariant. As a matter of fact, denoting by \({\mathcal {N}}_\Delta \) the classical refined invariant introduced in the same paper in case all intersection points are real, one has
In other terms, the multiplicity furnished by the correspondence theorem to count a tropical solution \(\Gamma \), which corresponds to the signed refined number of solutions to the classical enumerative problem which tropicalize to \(\Gamma \), is \(B_\Gamma ^{K_\mathrm {det}}\). This is no surprise since through the use of the correspondence theorem, the product over the vertices of the quantity \(q^{a_V\wedge b_V}-q^{-a_V\wedge b_V}\) carries a deep connection to the set of all families of real oriented curves tropicalizing to \(\Gamma \). This connection stays in higher dimension.
In higher dimension, although some signed counts for real curves are known, for instance by Welschinger [25], there are at the time of writing no generalization for the refined signed count of Mikhalkin. A desirable generalization would be to make a signed count of the solutions to the aforementioned classical enumerative problem according to the value of a quantum class for which we now sketch a definition. For a toric variety \({\mathbb {C}}\Delta \) with dense torus \(N\otimes {\mathbb {C}}^*\), one still has a logarithmic map \(\mathrm {Log}:N\otimes {\mathbb {C}}^*\longrightarrow N_{\mathbb {R}}\). However, there is no canonical choice of a 2-form to pull-back in order to measure the area of an oriented curve (except maybe \(\omega \) in the case of the \(\omega \)-problem). For an oriented real curve \(\varphi :S\dashrightarrow {\mathbb {C}}\Delta \), the map that associates to a 2-form \(\varpi \in \Lambda ^2 M_{\mathbb {R}}\) the log-area \(\int _{\varphi (S)}\mathrm {Log}^*\varpi \) of the curve under \(\varpi \) is linear, and up to a shift corresponds to an element of \(\mathrm {Hom}(\Lambda ^2 M,{\mathbb {Z}})\simeq \Lambda ^2 N\). This element is called the quantum class and is introduced in [5], to which we refer for more details. It is a generalization in higher dimension of the quantum index introduced by Mikhalkin [17] and shares many common properties with it. In particular it can be computed close to the tropical limit as a sum over the vertices of the limit tropical curve. The refined multiplicity of a tropical curve thus appears as a signed count of the solutions close to the tropical limit, refined by the value of their quantum class.
The existence of tropical invariants in the tropical enumerative problems considered in the paper proves the existence of a refined signed count of classical curves close to the tropical limit using this quantum class. Moreover, it suggests the existence of classical refined invariants generalizing the refined invariants from [17] in the general case. As the definition of the signs in the classical setting is currently unknown, this paper only deals with the tropical side of the invariants, and will hopefully be connected to some classical refined invariant in a future work.
1.5 Plan of the paper
In the second section we gather the notions about tropical curves, their moduli spaces and the definition of the various involved multiplicities. The proofs for the computation of the complex multiplicities and the invariance statement it leads to are postponed to the appendices. Next, we introduce the \(\omega \)-problem, a specific kind of enumerative problem in higher dimension for which we prove an invariance statement. This result is used in the fourth section to provide a new invariance result in the case of larger class of tropical enumerative problems. In the fifth section we study the first properties of the new refined invariants, more precisely their dependence on the constraints of the enumerative problems, and their possible enhancements. Last but not least, we give some examples.
2 Tropical forest
2.1 Abstract tropical curves
Let \({\overline{\Gamma }}\) be a finite connected graph without bivalent vertices. Let \({\overline{\Gamma }}_\infty ^0\) be the set of 1-valent vertices of \({\overline{\Gamma }}\), and \(\Gamma ={\overline{\Gamma }}\backslash {\overline{\Gamma }}^0_\infty \). We denote by \(\Gamma ^0\) the set of vertices of \(\Gamma \), and by \(\Gamma ^1\) the set of edges of \(\Gamma \). The non-compact edges resulting from the eviction of 1-valent vertices are called unbounded ends. The set of unbounded ends is denoted by \(\Gamma ^1_\infty \), while its complement, the set of bounded edges, is denoted by \(\Gamma _b^1\). An element of \(\Gamma ^1_\infty \) is usually denoted by e. Let \(l:\gamma \in \Gamma _b^1\mapsto |\gamma |\in {\mathbb {R}}_+^*=]0;+\infty [\) be a function, called length function. It endows \(\Gamma \) with the structure of a metric graph by declaring that a bounded edge \(\gamma \) is isometric to \([0;|\gamma |]\), and an unbounded end is isometric to \([0;+\infty [\).
Definition 2.1
Such a metric graph \(\Gamma \) is called an abstract tropical curve.
An isomorphism between two abstract tropical curves \(\Gamma \) and \(\Gamma '\) is an isometry \(\Gamma \rightarrow \Gamma '\). In particular an automorphism of \(\Gamma \) does not necessarily respect the labeling of the unbounded ends since it only respects the metric. Therefore, an automorphism of \(\Gamma \) induces a permutation of the set \(\Gamma ^1_\infty \) of unbounded ends.
An abstract tropical curve is said to be rational if the first betti number \(b_1(\Gamma )\) of the underlying graph, also called genus of the graph, is equal to 0. In graph theory, it is also called a tree.
2.2 Parametrized tropical curves
Let N be a lattice of rank \(r\geqslant 2\), and \(M=\mathrm {Hom}(N,{\mathbb {Z}})\) be the dual lattice, which has the same rank. We denote by \(N_{\mathbb {R}}=N\otimes _{\mathbb {Z}}{\mathbb {R}}\) the associated vector space, isomorphic to \({\mathbb {R}}^r\). We now consider tropical curves inside \(N_{\mathbb {R}}\).
Definition 2.2
A parametrized tropical curve in \(N_{\mathbb {R}}\) is a pair \((\Gamma ,h)\), where \(\Gamma \) is an abstract tropical curve and \(h:\Gamma \rightarrow N_{\mathbb {R}}\) is a map such that:
-
the restriction of h to each edge of \(\Gamma \) is affine with slope in N,
-
at each vertex \(V\in \Gamma ^0\), one has the balancing condition: let \(e_1,\dots ,e_k\), be the edges adjacent to V, and let \(u_1,\dots ,u_k\in N\) be the outgoing slope of h on them respectively, then one has
$$\begin{aligned} \sum _1^k u_i=0\in N. \end{aligned}$$
Two parametrized tropical curves \((\Gamma ,h)\) and \((\Gamma ',h')\) are isomorphic if there exists an isometry \(\varphi :\Gamma \rightarrow \Gamma '\) such that \(h=h'\circ \varphi \). A parametrized tropical curve is rational if the underlying abstract tropical curve is itself rational.
For a parametrized tropical curve \(h:\Gamma \rightarrow N_{\mathbb {R}}\), the set of slopes of h on the unbounded ends is called the degree of the curve and is usually denoted by \(\Delta \). It is a multiset of elements of N, and due to balancing condition, one has
An abstract tropical curve \(\Gamma \) is said to be trivalent if every vertex \(V\in \Gamma ^0\) is adjacent to precisely three edges. Let \(h:\Gamma \rightarrow N_{\mathbb {R}}\) be a parametrized tropical curve with \(\Gamma \) trivalent. For a vertex V, let \(a_V,b_V,c_V\) be the outgoing slopes of h, satisfying \(a_V+b_V+c_V=0\). Then we define the associated bivector
defined up to sign.
If a tropical curve \(\Gamma \) is not trivalent, we define the overvalence of the graph to be
where \(\mathrm {val}(V)\) is the valency of a vertex. The overvalence measures the default of trivalency of the graph.
Remark 2.3
If N is of rank 2, i.e. \(r=2\), then \(\pi _V\) is a multiple of a generator of \(\Lambda ^2 N\), which is a lattice of rank 1. The absolute value of the scalar is called vertex multiplicity. \(\square \)
2.3 Moduli space of rational tropical curves
We now focus on the structure of the moduli spaces of rational tropical curves, both abstract and parametrized. These spaces serve as parameter spaces for tropical curves. They are the domain of some suitable composed evaluation maps allowing us to work conveniently with the enumerative problems considered in the following sections.
Definition 2.4
Let \(\Gamma \) be an abstract rational tropical curve. The combinatorial type of \(\Gamma \), denoted by \(\mathrm {Comb}(\Gamma )\) is the homeomorphism type of the underlying graph, i.e. the labeled graph without the metric.
Conversely, to give a graph a tropical structure, one just needs to assign a length to the bounded edges of the graph. If the curve is trivalent, there are precisely \(|\Gamma _\infty ^1|-3\) bounded edges. Otherwise, there are \(|\Gamma _\infty ^1|-3-\mathrm {ov}(\Gamma )\) bounded edges, where \(\mathrm {ov}(\Gamma )\) is the overvalence of the graph. The set of tropical curves having the same combinatorial type is then parametrized by \({\mathbb {R}}_+^{|\Gamma _\infty ^1|-3-\mathrm {ov}(\Gamma )}\), where the coordinates are given by the lengths of the bounded edges.
For a given combinatorial type \(\mathrm {Comb}(\Gamma )\), the boundary of the orthant \({\mathbb {R}}_+^{|\Gamma _\infty ^1|-3-\mathrm {ov}(\Gamma )}\) corresponds to tropical curves for which at least one edge has length 0. Those tropical curves can be identified with curves whose underlying graph has been suitably modified: edges with zero length are deleted and their extremities are merged together. These identifications allow us to glue together the cones corresponding to the finitely many combinatorial types of graphs. One obtains the moduli space \({\mathcal {M}}_{0,|\Gamma _\infty ^1|}\) of rational curves with \(|\Gamma _\infty ^1|\) marked points which has thus the structure of a fan.
The space \({\mathcal {M}}_{0,m}\) is a simplicial fan of pure dimension \(m-3\). The top-dimensional cones parametrize curves whose underlying graph is trivalent. Codimension 1 cones, which are called facets, correspond to combinatorial types whose underlying graph is trivalent except for one vertex which is quadrivalent. Each facet belongs to exactly three faces, which correspond to the three possible smoothings of the quadrivalent vertex into a pair of trivalent vertices.
Given an abstract rational tropical curve \(\Gamma \), and a degree \(\Delta \subset N\) assigning a slope \(n_e\in N\) to each unbounded end of \(\Gamma \), there is a unique way up to translation to define a map \(h:\Gamma \rightarrow N_{\mathbb {R}}\) which makes \((\Gamma ,h)\) into a parametrized tropical curve of degree \(\Delta \): the slope of the unbounded ends is fixed by the degree, and the slope of interior edges is fixed by the balancing condition. The translation is fixed by the position of a vertex in \(\Gamma \). This observation gives a bijection between the moduli space \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\) of parametrized rational tropical curves of degree \(\Delta \) in \(N_{\mathbb {R}}\) and \({\mathcal {M}}_{0,|\Delta |}\times N_{\mathbb {R}}\), where the bijection is given by the projection to the underlying graph and the position of a chosen vertex, for instance the vertex adjacent to a fixed unbounded end \(e_0\).
The cones of the moduli space \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\) are of the form \({\mathbb {R}}_+^{|\Delta |-3}\times N_{\mathbb {R}}\), whose tangent space contains the lattice \({\mathbb {Z}}^{|\Delta |-3}\times N\).
Remark 2.5
The multiset \(\Delta \) is allowed to contain the 0 vector. Unbounded ends on which the map h has zero slope are sometimes called marked points because their image inside \(N_{\mathbb {R}}\) is a point. \(\square \)
Remark 2.6
Notice that by abuse of notation, the set of unbounded ends of parametrized tropical curves in \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\) are canonically identified since they are labeled. Thus, one can speak about \(\Gamma _\infty ^1\) without having to specify a curve \(\Gamma \). The degree \(\Delta \) is then a map \(e\in \Gamma _\infty ^1\mapsto n_e\in N\). \(\square \)
The set of combinatorial types of parametrized tropical curves of degree \(\Delta \) is denoted \({\mathcal {C}}_\Delta \), where the \({\mathcal {C}}\) stands both for combinatorial and for cones. Among them, the set of top-dimensional combinatorial types is denoted by \({\mathcal {C}}_\Delta ^\mathrm {top}\). Otherwise, the set of cones of a given dimension is denoted by \({\mathcal {C}}_\Delta ^{(k)}\). A combinatorial type is usually denoted by the letter C, whose notation is also used to denote the associated cone in the moduli space \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\). Moreover, for a given parametrized tropical curve \(h:\Gamma \rightarrow N_{\mathbb {R}}\), we sometimes forget the h in the notation, and use the same notation \(\Gamma \) for the curve and the combinatorial type \(\mathrm {Comb}(\Gamma )\) that it belongs to.
At some point, we need to orient the cones of the moduli space \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\), which means find an orientation for the underlying lattice \({\mathbb {Z}}^{|\Delta |-3}\times N\) of each cone \(C\in {\mathcal {C}}_\Delta ^\mathrm {top}\), or similarly, its linear span. If \(C\in {\mathcal {C}}_\Delta ^\mathrm {top}\) is a combinatorial type, associated to an orthant of the moduli space \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\) and denoted by the same letter, we denote by \({{\mathfrak {o}}}{{\mathfrak {r}}}(C)\) an orientation of the linear span of the cone. If W is a facet adjacent to C, W belongs to the boundary of C. Then, as the normal bundle of W in C is canonically oriented, an orientation \({{\mathfrak {o}}}{{\mathfrak {r}}}(C)\) induces an orientation of the tangent bundle to W, which is denoted by \(\partial _W{{\mathfrak {o}}}{{\mathfrak {r}}}(C)\). Notice that a reversing of the orientation of C also reverses the induced orientation on W.
2.4 Evaluation map
For each unbounded end \(e\in \Gamma ^1_\infty \), let \(n_e\) be the slope assigned by the degree \(\Delta \). One has a well-defined evaluation map on the moduli space \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\), which sends a parametrized tropical curve to the image of the unbounded end inside the quotient \(N_{\mathbb {R}}/\langle n_e\rangle \), where \(\langle n_e\rangle \) denotes the saturation of the sublattice spanned by \(n_e\). If the slope is 0, this quotient is just \(N_{\mathbb {R}}\) itself and the image is a point, justifying the name marked point. Otherwise, the image corresponds to the line that contains the image of the unbounded end under h. Putting all these maps together, we get the evaluation map:
where \(p_e\) is any point chosen in \(e\in \Gamma ^1_\infty \).
By definition, the evaluation map is linear on every cone of \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\simeq {\mathcal {M}}_{0,|\Delta |}\times N_{\mathbb {R}}\) but is not necessarily injective on top-dimensional cones. For instance, it is not the case when some bounded edge has zero slope, or when the combinatorial type contains a flat vertex, which is a vertex whose adjacent edges are contained in a line.
2.5 Complex multiplicity of tropical curves
One main feature of tropical enumerative geometry is to count tropical curves solution to a given enumerative problem \({\mathcal {P}}\), which means finding the curves which are subject to some constraints. It is often necessary to use suitable multiplicities m to get a count that does not depend on the choice of the constraints when those vary in some family. Such a count using multiplicity m is said to lead to an invariant for the problem \({\mathcal {P}}\). Here, we describe the main multiplicities that are of interest to us, procrastinating the proper introduction to the associated enumerative problems.
Remark 2.7
In some particular enumerative problems, some multiplicities leading to an invariant are provided through the use of some correspondence theorems, such as Mikhalkin’s [16], Shustin’s [21], Nishinou and Siebert’s [19] or Tyomkin’s [24]. The use of these multiplicities leads to tropical invariants which have the value of some classical invariants, e.g. Gromov–Witten invariants, Welschinger invariants, or refined invariants introduced by Mikhalkin [17]. Such a relation to classical invariants is not systematic although is sometimes suspected, as it is the case for refined invariants introduced by Block and Göttsche [3]. \(\square \)
In this section, we recall the definition of the complex multiplicity, which is the multiplicity that comes from the correspondence theorem [16] in the planar case, or [19] in the higher dimensional case. Let \(\Gamma \) be a parametrized tropical curve of degree \(\Delta \subset N\). For each unbounded end e, let \(L_e\) be a full sublattice of \(N/\langle n_e\rangle \), meaning that the quotient is without torsion. In order to simplify the notation, we denote by \(Q_e\) the quotient of \(N/\langle n_e\rangle \) by \(L_e\), which is a lattice of rank \(\mathrm {rk}\ N/\langle n_e\rangle - \mathrm {rk}\ L_e=\mathrm {cork}\ L_e\). We denote by \(Q_e^{\mathbb {R}}=Q_e\otimes _{\mathbb {Z}}{\mathbb {R}}\) the associated vector space. We assume that \(\sum _{e\in \Gamma ^1_\infty } \mathrm {cork}L_e\) is equal to the dimension of \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\), which is \(|\Delta |+r-3\). We then compose the evaluation map with the quotient maps \(N_{\mathbb {R}}/\langle n_e\rangle \rightarrow Q_e\), getting what we call a composed evaluation map:
For a combinatorial type \(C\in {\mathcal {C}}_\Delta ^\mathrm {top}\), we denote by \(\mathrm {ev}^{(L_e)}_C\) the restriction to the orthant of the combinatorial type C, which is linear. Due to the assumption on the ranks of the lattices, both spaces have the same dimension.
Definition 2.8
We set the complex multiplicity to be
where the domain is endowed with a basis of the lattice \({\mathbb {Z}}^{|\Delta |-3}\times N\), and the codomain a basis of the lattice \(\prod _e Q_e\).
Remark 2.9
One other way to describe the complex multiplicity is as follows: consider the sublattice \(\prod _e L_e\subset \prod _e N/\langle n_e\rangle \), which is a full sublattice of codimension \(|\Delta |+r-3\) by assumption. Let \(\alpha _{(L_e)}\in \Lambda ^{|\Delta |+r-3}\left( \prod _e N/\langle n_e\rangle \right) ^*\) be its Plücker vector obtain as follows: take the wedge product of a basis of the dual orthogonal of \(\prod _e L_e\). Then the pull-back of \(\alpha _{(L_e)}\) by the evaluation map \(\mathrm {ev}_C\) restricted to a cone C is a top-dimensional form. Thus, it is a scalar multiple of the determinant form on the lattice of the orthant. The absolute value of the scalar factor is the multiplicity.
It also follows from standard tropical intersection theory (see [1]) that the complex multiplicity corresponds to the index of the lattice spanned by \(\mathrm {ev}_C({\mathbb {Z}}^{|\Delta +r-3}\times N)\) and \(\prod _e L_e\) inside \(\prod _e N/\langle n_e\rangle \), which are of complementary dimension if \(\mathrm {ev}\) is injective on the cone relative to the combinatorial type. If not, the complex multiplicity is 0. \(\square \)
The complex multiplicity can be computed in the hereby described fancy way. This can be seen as a particular case of a result of Mandel and Ruddat [15], which we restate in our setting for sake of completeness. To keep a general setting, here and only here, we consider tropical curves \((\Gamma ,h)\) that are not necessarily trivalent. Nevertheless, for such a curve and an evaluation map
the complex multiplicity is still defined as the determinant of \(\mathrm {ev}^{(L_e)}\) restricted to the cone of the combinatorial type, provided that it has the same dimension as the target space. We assume it is the case.
For each primitive sublattice \(L\subset N\) of corank l, there is an orthogonal dual primitive sublattice \(L^\perp \subset M\) of rank l, and an associated Plücker vector \(\rho \in \Lambda ^l M\) defined up to sign. This polyvector is defined as follows: let \(m_1,\dots ,m_l\) be a basis of \(L^\perp \). Then, one has
This polyvector does not depend on the chosen basis up to sign. Hence, given a parametrized rational tropical curve \(h:\Gamma \rightarrow N_{\mathbb {R}}\), one has a polyvector \(\rho _e\) associated to each of the unbounded ends e of the curve: the Plücker vector associated to the full sublattice spanned by \(n_e\) and \(L_e\).
We choose one vertex of \(\Gamma \) to be the sink of the curve and orient every edge toward it. We then cut the branches of the tropical curve with the following rule: let V be a vertex different from the sink, with incoming unbounded ends directed by \(n_1,\dots ,n_s\), and respective polyvectors \(\rho _1,\dots ,\rho _s\), and a unique outgoing bounded edge, thus directed by \(n_1+\cdots +n_s\). The polyvector associated to the outgoing edge of V is
Recall that \(\iota _n\), for \(n\in N\), denotes the interior product by n. Geometrically, the polyvector associated to an edge and to an unbounded end is a multiple of the Plücker vector associated to the space described by the edge when it moves. This means the following:
-
For an unbounded end \(e\in \Gamma ^1_\infty \) associated to a sublattice \(L_e\), the unbounded end can move in the direction \(L_e\), thus describe the space with slope spanned by \(n_e\) and \(L_e\).
-
At a vertex V with incoming edges having respective polyvectors \(\rho _1,\dots ,\rho _s\). Assume by induction that the incoming edges move in an affine space directed by a vector subspace whose Plücker vector is \(\rho _i\) respectively. Then, the vertex moves in the intersection of all these subspaces. Therefore, the affine subspace has Plücker vector \(\rho _1\wedge \cdots \wedge \rho _s\).
-
Finally, for the outgoing edge of V, it moves in an affine space equal to the affine space where V lives, enlarged by the direction of the edge: \(n_1+\cdots +n_s\). Hence, the polyvector is obtained by making the interior product with \(n_1+\cdots +n_s\).
At the sink, let \(\rho _1,\dots ,\rho _s\) be the polyvectors associated to the incoming adjacent edges. Because of the assumption on dimensions, we have
Thus, it is an integer multiple of a generator of \(\Lambda ^r M\). The absolute value of the proportionality constant, obtained by evaluating on a basis of N, is the desired determinant. The proof that it does not depend on the choice of the sink and that it computes the determinant is proved in the appendix.
Theorem
6.8 The value obtained by the preceding algorithm is equal to the complex multiplicity \(m_\Gamma ^{\mathbb {C}}\).
2.6 Refined multiplicities of a trivalent tropical curve
To finish this section about tropical curves, we define the refined multiplicities that we use in the following sections. Let \({\mathcal {V}}_\Delta \) be the set of types of trivalent vertices that occur in some combinatorial type of \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\). A trivalent vertex is determined by the slopes of the three outgoing edges. Using the balancing condition, the type of a vertex is fully determined by the partition of \(\Delta \) into three subsets that it induces. Hence, \({\mathcal {V}}_\Delta \) is finite.
Let \(\omega _0\) be a 2-form such that for any \(V\in {\mathcal {V}}_\Delta \) with \(\pi _V\ne 0\), \(\omega _0(\pi _V)\ne 0\). This condition means that for any non-flat vertex, the restriction of \(\omega _0\) to the plane spanned by the outgoing edges is non-zero. The refined multiplicity is defined as follows.
Definition 2.10
The refined multiplicity of a parametrized tropical curve \(h:\Gamma \rightarrow N_{\mathbb {R}}\) is
where the bivector \(\pi _V\) of V is chosen such that \(\omega _0(\pi _V)>0\). If the curve contains some flat vertex W, then \(\pi _W=0\) and then \(B^0_\Gamma =0\).
The refined multiplicity is a Laurent polynomial in several variables. The number of indeterminates is equal to the rank of \(\Lambda ^2 N\), which is \(\begin{pmatrix}{r}\\ {2}\\ \end{pmatrix}\). It depends up to sign on the choice of \(\omega _0\), but the pair \(\{\pm B_\Gamma ^0\}\) does not depend on the choice of \(\omega _0\).
Let \(K\subset \Lambda ^2 N\) be a sublattice. Then we can compose the definition of \(B^0_\Gamma \) with the projection \(p_K:{\mathbb {Z}}[\Lambda ^2 N]\longrightarrow {\mathbb {Z}}[\Lambda ^2 N/K]\) to get a slightly less refined multiplicity.
Definition 2.11
For a sublattice \(K\subset \Lambda ^2 N\), let \(B_\Gamma ^{K}=p_K(B^0_\Gamma )\), obtained by reducing the exponents modulo K.
Notice that this notation is consistent with the notation for \(B_\Gamma ^0\), which corresponds to the choice \(K=\{0\}\). Although the relation \(p_K(B^0_\Gamma )=B^K_\Gamma \) shows that \(B^0_\Gamma \) determines the other refined multiplicities, the use of these multiplicities is necessary since the multiplicity \(B_\Gamma ^0\) might fail to provide an invariant, while some \(B_\Gamma ^K\) might do so.
Remark 2.12
If N is of rank 2, then \(\Lambda ^2 N\simeq {\mathbb {Z}}\), and the choice of a generator of \(\Lambda ^2 N\) identifies \({\mathbb {Z}}[\Lambda ^2 N]\) with \({\mathbb {Z}}[q,q^{-1}]\). Up to a division by \((q-q^{-1})^{|\Delta |-2}\), we recover the definition of the refined multiplicity proposed by Block and Göttsche [3]. \(\square \)
Remark 2.13
The refined multiplicity depends up to a sign on the choice of \(\omega _0\). In every occurrence of the refined multiplicity, the choice of \(\omega _0\) is fixed in a non-ambiguous way so it does not bring up any problem. \(\square \)
3 \(\omega \)-problem and first refinement
Before turning to more general enumerative problems and providing them with a refined way to count the solutions, we present a family of enumerative problems, called \(\omega \)-problems, where it is slightly easier to show the existence of an associated refined invariant, i.e. a refined way to count the solutions of the problem leading to a result independent of the constraints.
In the planar case, meaning that \(r=2\), one can consider the classic enumerative problem of finding degree \(\Delta \) rational tropical curves passing through \(|\Delta |-1\) points. In that case, the complex multiplicities of rational tropical curves split as a product over the vertices of the curve. This fact, which is specific to the two-dimensional case and fails in arbitrary dimension, is used to prove invariance with the refined multiplicity of Block–Göttsche [3], see [13]. The \(\omega \)-problems also share this property of the complex multiplicity splitting into a product over the vertices of the curve.
Remark 3.1
In the planar case, the \(\omega \)-problem amounts to find rational tropical curves passing through \(|\Delta |-1\) points when these points are located on the toric divisors, meaning that the unbounded ends are contained in fixed lines of the same slope. \(\square \)
3.1 Enumerative problem
Let \(\Delta \subset N\) be a tropical degree consisting only of non-zero vectors, and let \(\omega \in \Lambda ^2 M\) be a 2-form chosen such that \(\omega (n_e,-)\ne 0\) for every \(n_e\in \Delta \). Before getting to the enumerative problem, let us define what we mean by moment.
Definition 3.2
For a parametrized tropical curve \(h:\Gamma \rightarrow N_{\mathbb {R}}\) of degree \(\Delta \), the moment \(\mu _\omega (e)\) of an unbounded end \(e\in \Gamma ^1_\infty \) with respect to \(\omega \) is defined as follows: let \(n_e\) be the slope of h on e and let p be any point in h(e),
This definition may be extended to the bounded edge of \(\Gamma \) if an orientation is specified. Geometrically, the moment corresponds to the position of the affine space \({\mathcal {H}}_e\) of slope \(H_e=\ker \iota _{n_e}\omega \) that contains the image of the unbounded end e. Using the balancing condition at each vertex of the curve, one easily proves the following proposition.
Proposition 3.3
For \(h:\Gamma \rightarrow N_{\mathbb {R}}\) a parametrized tropical curve, one has
meaning that the family \(\mu \) of moments of the curve belongs to \({\mathfrak {M}}=\{\mu :\ \sum _e\mu _e=0\}\subset {\mathbb {R}}^{\Delta }\).
Remark 3.4
This fact generalizes the planar Menelaus relation noticed by Mikhalkin [17]. That is why we also call it tropical Menelaus relation. \(\square \)
We now state the \(\omega \)-problem. Consider the global moment map
The moment map, which has image in \({\mathfrak {M}}\) due to the tropical Menelaus relation, is a specific case of composed evaluation map, where one chooses \(L_e=H_e\).
Problem 3.5
Let \(\mu \in {\mathcal {H}}\). How many parametrized rational tropical curves of degree \(\Delta \) satisfy \(\mathrm {mom}(\Gamma ,h)=\mu \)? In other words, for each \(e\in \Gamma ^1_\infty \backslash \{e_0\}\), fix \({\mathcal {H}}_e\) an affine hyperplane with slope \(H_e\). How many parametrized rational tropical curves of degree \(\Delta \) satisfy \(h(e)\subset {\mathcal {H}}_e\)?
Unfortunately, the codomain has dimension \(|\Delta |-1\), while the domain has dimension \(|\Delta |+r-3\). Therefore, unless \(r=2\), this is not enough to ensure a finite number of solutions. We then add the following condition: let \(e_0\in \Gamma _\infty ^1\) be a specific unbounded end and let \(\delta \in N/\langle n_{e_0}\rangle \) be a primitive vector such that \(\omega (n_{e_0},\delta )\ne 0\) and D be a line with slope \(\delta \). We add the condition that \(h(e_0)\in D\subset N_{\mathbb {R}}/\langle n_{e_0}\rangle \), getting to the \(\omega \)-problem denoted by \({\mathcal {P}}(\omega ,e_0)\).
Problem 3.6
Let \(\mu \in {\mathcal {H}}\) and D be a line with slope \(\delta \) inside \(N_{\mathbb {R}}/\langle n_{e_0}\rangle \). How many parametrized rational tropical curves of degree \(\Delta \) satisfy \(\mathrm {mom}(\Gamma ,h)=\mu \) and \(h(e_0)\in D\)?
Remark 3.7
The condition \(h(e_0)\in D\) means that the image of the unbounded end \(e_0\) is contained in a plane. \(\square \)
We denote the associated composed evaluation map as follows:
where the \({\mathbb {R}}\) terms correspond to the evaluation of the moments of the unbounded ends different from \(e_0\).
Remark 3.8
We omit \(\delta \) from the notation \({\mathcal {P}}(\omega ,e_0)\), since, as proven in Theorem 3.14, the solutions do not depend on \(\delta \). \(\square \)
Remark 3.9
There are other ways to impose further constraints on the curves to get a finite number of tropical curves:
-
The problem depends on the chosen end \(e_0\).
-
The constraint could have been split into two constraints on two different unbounded ends.
-
One could have impose constraints on one or several new marked points on the curve.
Some of these possibilities are studied later on in Sect. 5. \(\square \)
3.2 Count of solutions and complex invariance statement
We now get to the invariance statement for the count of solutions to \({\mathcal {P}}(\omega ,e_0)\) using first the complex multiplicity, meaning that the count does not depend on the choice of \((\mu ,D)\) as long as it is generic. The invariance of the count using complex multiplicity has already been proven in various ways: by hand showing the local invariance around walls, using tropical intersection theory, or using the invariance in the complex setting and some correspondence theorem. In any case, the statement is a particular case of a more general statement which is proved in the appendix. Yet, as the invariance with the complex multiplicity is a key ingredient in the proof of invariance using refined multiplicity, we give here the main steps of what could be called the pedestrian proof.
Proposition 3.10
For a generic choice of \(\mu \) and D, there are finitely many tropical curves solution to \({\mathcal {P}}(\omega ,e_0)\). Moreover, such curves are trivalent.
Proof
The set of top-dimensional combinatorial types \({\mathcal {C}}_\Delta ^\mathrm {top}\) decomposes between the types on which the composed evaluation map \(\mathrm {ev}^{\omega ,e_0}\) is non-injective, and the ones where it is bijective. The image of the cones where the composed evaluation map is non-injective is nowhere dense inside the codomain since \(\mathrm {ev}^{\omega ,e_0}\) is linear and non-surjective either. The same applies for the image of the cones which are not top-dimensional. Therefore, if \((\mu ,D)\) is chosen outside the image of these cones, the only cones that may provide a solution are top-dimensional ones where the evaluation map is injective. Such a solution, if it exists, is unique. As there are finitely many combinatorial types, the conclusion follows. \(\square \)
Remark 3.11
This fact can also be proven using tropical intersection theory: for a generic choice of constraints, the spaces \(\mathrm {ev}({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}}))\) and \(D\times \prod _{e\ne e_0} {\mathcal {H}}_e\) intersect transversally inside \(\prod _e N_{\mathbb {R}}/\langle n_e \rangle \) and intersection points belong to the interior of top-dimensional faces. The conclusion follows along with the invariance of the count using complex multiplicity. \(\square \)
We now compute the complex multiplicities of the solutions.
Lemma 3.12
For each trivalent solution \(h:\Gamma \rightarrow N_{\mathbb {R}}\) to the \(\omega \)-problem, the complex multiplicity takes the following form:
Proof
We use the algorithm to compute the complex multiplicity by choosing as sink the vertex adjacent to the unbounded end \(e_0\). Then, the recursion uses the following identity:
Hence, the computation reduces to the case there is just one vertex. Noticing that the constraint on \(e_0\) is associated to the polyvector \(\iota _\delta \iota _{n_{e_0}}\Omega \), where \(\Omega \) is a generator of \(\Lambda ^r M\), we have
\(\square \)
To conclude, for a generic choice \((\mu ,D)\), let
be the count of solutions to \({\mathcal {P}}(\omega ,e_0)\) using the complex multiplicity. This count is well-defined since the solutions \(\Gamma \) are trivalent. Then one has the following invariance statement.
Proposition 3.13
The value of the count \(N^{\mathbb {C}}_\Delta (\mu ,D)\) does not depend on the choice of \(\mu \) nor the choice of D as long as these choices are generic. It only depends on the choice of \(\omega \) and the slope \(\delta \) of D.
The proof follows from tropical intersection theory, or from the computations done in the appendix.
3.3 Refined invariance statement
We conclude this section by showing an invariance statement for the same enumerative problem 3.6, using this time the refined multiplicities \(B^{K_\omega }\) introduced in Sect. 2.6.
Let \(K_\omega =\langle \pi _V:\omega (\pi _V)=0\rangle _{V\in {\mathcal {V}}_\Delta }\subset \Lambda ^2 N\) be the space spanned by the vertices spanning a plane where \(\omega \) restricts to 0. If \(\omega \) is chosen generically with respect to \(\Delta \), then \(K_\omega =0\). Otherwise, the 2-form \(\omega \) might take value 0 on some vertex V occurring in a rational tropical curve of degree \(\Delta \). We use the refined multiplicity \(B_\Gamma ^{K_\omega }\) of a tropical curve, which is
The 2-vector \(\pi _V\) is chosen so that \(\omega (\pi _V)>0\). If \(\omega (\pi _V)=0\), then \(\pi _V\in K_\omega \) and the multiplicity is equal to 0 since the exponents are taken modulo \(K_\omega \). Then, for a generic choice \((\mu ,D)\), let
Theorem 3.14
The refined count \({\mathcal {B}}_\Delta (\mu ,D)\) does not depend on the choice of \(\mu \) and D as long as it is generic. Neither does it depend on the slope \(\delta \) of D. It only depends on the choice of \(\omega \) and the choice of the unbounded end \(e_0\) with the additional constraint. It is denoted by \({\mathcal {B}}_\Delta ^{\omega ,e_0}\).
Proof
We already know that the count of solutions with complex multiplicity \(m^{{\mathbb {C}},\omega ,e_0}\) leads to an invariant. This means that the repartition of the solutions around a wall matches the invariance of the count with complex multiplicities. Recall that here, a wall is a tropical curve with a unique quadrivalent vertex. Therefore, we need to check for each wall that the count with refined multiplicities is also invariant.
We check the local invariance around the wall corresponding to a quadrivalent vertex of the tropical curve. Let \(a_1,a_2,a_3,a_4\) be the slopes of the outer edges, with index taken in \({\mathbb {Z}}/4{\mathbb {Z}}\). Up to a relabeling, we assume that \(\omega (a_i,a_{i+1})>0\) for every i: the vectors span a 3-dimensional subspace, and \(\omega \) restricted to the subspace is either 0 or has a non-trivial kernel. Thus, we can can quotient by the kernel and restrict to the planar case. In the planar case, the 2-form induces an orientation, and we can choose \(a_1,a_2,a_3,a_4\) in the counterclock-wise order. Then, for each i, \(\omega (a_i,a_{i+1})>0\), otherwise \(\omega (a_i,a_{i+1}),\omega (a_i,a_{i+2}),\omega (a_i,a_{i+3})\) would all be negative and their sum could not be 0, contradicting the balancing condition. If some value is equal to 0, the proof remains unchanged. Moreover, we assume that \(\omega (a_2,a_3)>\omega (a_1,a_2)\). The invariance of the complex count amounts to the following relation:
and the repartition of combinatorial types around the wall is given by the sign of each term. It means up to sign that one is positive and is on one side of the wall, and the two other ones are negative, on the other side of the wall. Hence, we just need to study the signs of each term to know which curve is on which side. We know that \(\omega (a_1,a_2)\) and \(\omega (a_1+a_2,a_3)=\omega (a_3,a_4)\) are positive. Therefore, their product, which is the term of 12//34, is also positive. We know that \(\omega (a_2,a_3)\) is positive, but \(\omega (a_2+a_3,a_1)=-\omega (a_4,a_1)\) is negative. Therefore, their product is negative and 14//23 is on the other side of the wall. It means that the combinatorial types 12//34 and 14//23 are on opposite sides of the wall. We need to determine on which side the type 13//24 is, and that is given by the sign of the middle term. As by assumption \(\omega (a_2,a_1+a_3)=\omega (a_2,a_3)-\omega (a_1,a_2)>0\), it is determined by the sign of \(\omega (a_1,a_3)\).
-
If \(\omega (a_1,a_3)>0\), then 12//34 and 13//24 are on the same side, and the invariance for refined multiplicities is dealt with the identity
$$\begin{aligned}&(q^{a_2\wedge a_3}-q^{a_3\wedge a_2})(q^{a_1\wedge (a_2+a_3)}-q^{(a_2+a_3)\wedge a_1}) \\&\quad = (q^{a_1\wedge a_2}-q^{a_2\wedge a_1})(q^{(a_1+a_2)\wedge a_3}-q^{a_3\wedge (a_1+a_2)}) \\&\qquad + (q^{a_1\wedge a_3}-q^{a_3\wedge a_1})(q^{a_2\wedge (a_1+a_3)}-q^{(a_1+a_3)\wedge a_2}), \end{aligned}$$ -
and if \(\omega (a_1,a_3)<0\), then 14//23 and 13//24 are on the same side and then the invariance for refined multiplicities is true since
$$\begin{aligned}&(q^{a_2\wedge a_3}-q^{a_3\wedge a_2})(q^{a_1\wedge (a_2+a_3)}-q^{(a_2+a_3)\wedge a_1}) \\&\quad + (q^{a_3\wedge a_1}-q^{a_1\wedge a_3})(q^{a_2\wedge (a_1+a_3)}-q^{(a_1+a_3)\wedge a_2})\\&\quad = (q^{a_1\wedge a_2}-q^{a_2\wedge a_1})(q^{(a_1+a_2)\wedge a_3}-q^{a_3\wedge (a_1+a_2)}). \end{aligned}$$
This completes the proof if each complex multiplicity is non-zero. If the multiplicity of some side of the wall is 0, it does not provide any solution to the enumerative problem for generic values, and one needs to cancel its refined multiplicity, which might not be 0 if one chooses the refined multiplicity \(B^0_\Gamma \). If some combinatorial type has complex multiplicity 0, it means that for some W among the two displayed vertices, \(\omega (\pi _W)=0\). The same relations between refined multiplicity lead to the invariance provided that one mods out the exponent by \(\pi _W\), which sends the refined multiplicity to 0. One just obtains that the curves on the two remaining sides of the wall have the same multiplicity.
The result also does not depend on \(\delta \) since the refined multiplicity does not depend on \(\delta \), and the set of solutions for a given choice of \((\mu ,D)\) only depends on \(\mu \) and the intersection point of D with the hyperplane \({\mathcal {H}}_{e_0}\). \(\square \)
Remark 3.15
We have proven a refined invariance statement for every \(\omega \) such that for every \(n\in \Delta \), \(\iota _n\omega \ne 0\). For every \(\omega \) not taking the value 0 on \({\mathcal {V}}_\Delta \), we have a refined invariant in \({\mathbb {Z}}[\Lambda ^2 N]\). If for some V one has \(\omega (\pi _V)=0\), the space of the exponents where the refined invariant takes value is reduced by \(\pi _V\). \(\square \)
4 Refined count for rational tropical curves
We now use the refined invariance proven in the setting of the \(\omega \)-problem to prove a refined invariance for a larger class of enumerative problems, where the constraints we ask a tropical curve to satisfy do not necessarily come from the choice of a 2-form \(\omega \).
4.1 New enumerative problems
Let \(\Delta \subset N\) be a tropical degree without any zero vector. For each \(n_e\in \Delta \), let \(L_e\) be a saturated sublattice of \(N/\langle n_e \rangle \), and let \({\mathcal {L}}_e\) be an affine subspace of \(N_{\mathbb {R}}/\langle n_e\rangle \) with slope \(L_e\). A full sublattice means that the quotient is without torsion. Assume that \(\sum _e \mathrm {cork}L_e=|\Delta |+r-3\).
Problem 4.1
How many rational tropical curves \(h:\Gamma \rightarrow N_{\mathbb {R}}\) of degree \(\Delta \) satisfy for each unbounded end \(e\in \Gamma _\infty ^1\), \(h(e)\in {\mathcal {L}}_e\)?
In other words, using previous notations, solving this enumerative problem means finding the preimages of a generic point for the following composed evaluation map
The enumerative problem is referred as \({\mathcal {P}}(L_e)\), and is related to an analogous complex enumerative problem through the use of a correspondence theorem. The count with the complex multiplicity \(m^{{\mathbb {C}},(L_e)}_\Gamma \) is already known to lead to an invariant. The result is recalled here is proven in the appendix.
Theorem
6.10 For a generic choice of \(({\mathcal {L}}_e)\), the count \(N_\Delta ^{\mathbb {C}}({\mathcal {L}}_e)=\sum _{\Gamma :h(e)\in {\mathcal {L}}_e}m_\Gamma ^{{\mathbb {C}},(L_e)}\) does not depend on the choice of \(({\mathcal {L}}_e)\). It only depends on the choice of \(\Delta \) and \((L_e)\).
Furthermore, the result of this count is equal to the complex invariant provided by the analogous complex problem. However, the involved complex multiplicity \(m^{{\mathbb {C}},(L_e)}\) does not in general split into a product over the vertices of the curve. Nevertheless, we prove that for a suitable choice of K and up to a change of sign, the refined multiplicity \(B_\Gamma ^K\), which is a product over the vertices, does lead to a invariant. Meanwhile, let us describe the combinatorial types that have complex multiplicity 0.
Lemma 4.2
A parametrized tropical curve \(h:\Gamma \rightarrow N_{\mathbb {R}}\) with complex multiplicity 0 falls into at least one of the following categories:
-
(i)
The curve has a contracted bounded edge, i.e. it is reducible.
-
(ii)
The curve has a flat vertex, i.e. \(\pi _V=0\) for some V.
-
(iii)
For some bounded edge \(\gamma \in \Gamma ^1_b\), the ranks of the constraints are improperly distributed: let \(A\sqcup B\) be the partition of \(\Gamma _\infty ^1\) induced by \(\gamma \), then
$$\begin{aligned} \sum _{e\in A} \mathrm {cork}\ L_e>r+|A|-2 \text { or }\sum _{e\in B} \mathrm {cork}\ L_e>r+|B|-2. \end{aligned}$$ -
(iv)
The curve has no flat vertex or contracted edge, the ranks of constraints are properly distributed but non-generic.
Proof
In the first two cases, the multiplicity is zero since the evaluation map is non-injective, so neither is the composed evaluation map. Let us focus on the third case and assume there is a bounded edge \(\gamma \in \Gamma ^1_b\) such that the constraints are improperly distributed. Out of symmetry, let assume that \(\sum _{e\in A} \mathrm {cork}\ L_e>r+|A|-2\) and the sink used to compute the multiplicity is in the B part of the curve. The recursive formula \(\rho =\iota _{n+n'}(\rho _1\wedge \rho _2)\) used to compute the complex multiplicity shows that the polyvector \(\rho _\gamma \) obtained applying the algorithm is the interior product with a polyvector belonging to \(\Lambda ^{\sum _A\mathrm {cork}L_e -|A|+2}M\). By assumption, this space is 0 since the weight is strictly bigger than r, and so is the multiplicity.
By disjunction, the last case contains indeed the remaining cases. Using the Plücker embedding, the space of corank l sublattices of a given lattice N is \(\Lambda ^l M\). As \(\mathrm {Hom}(N/\langle n_e \rangle ,{\mathbb {Z}})\simeq \langle n_e \rangle ^\perp \subset M\), the complex multiplicity can be seen as a multilinear form on the space \(\prod _e \Lambda ^{\mathrm {cork}L_e}\langle n_e \rangle ^\perp \) of possible slopes for the lattices \(L_e\), once their dimensions are fixed. The assumption ensures that the multilinear form itself is non-zero, but it might still take the zero value on some specific choice of slopes. This is avoided if the slopes are chosen generically. \(\square \)
4.2 Main results
For a choice of slope constraints \((L_e)\), let \(\omega \in \Lambda ^2 M\) be a 2-form satisfying the following property: for every top-dimensional combinatorial type \(\Gamma \),
In particular, if for some combinatorial type \(\Gamma \) which is not of type (i) or (ii) one has \(m^{{\mathbb {C}},(L_e)}_\Gamma =0\), then \(K_\omega \ne \{0\}\). Such a \(\omega \) is often not unique and in some cases might even be 0. However, the choice of \(\omega \) does not really matter, only the space \(K_\omega \) matters. See Corollary 4.9 for a precise statement.
Remark 4.3
It is an interesting question to decide whether there exists a non-trivial \(\omega \) satisfying these requirements. These conditions need only be checked on combinatorial types having neither contracted edges nor flat vertices. Nevertheless, to prove the interest of the results, we provide a wide class of examples which admit such an \(\omega \). \(\square \)
Example 4.4
Choose the boundary constraints on every unbounded end to be at least codimension 1 and having generic slope, and let \(\omega \) be a 2-form such that \(K_\omega =\{0\}\), meaning that the only combinatorial types with complex multiplicity relative to \(\omega \) equal to 0 are the curves with a flat vertex or a contracted edge. Then, we prove that the complex multiplicity relative to \((L_e)\) is never 0 unless there is a flat vertex or contracted edge.
According to the classification of Lemma 4.2, we can only be in the case (iii). Thus, we show that the dimensions are properly distributed. Let \(\gamma \in \Gamma ^1_b\) be an edge and \(A\sqcup B=\Gamma _\infty ^1\) the associated partition. Then by assumption,
Moreover, one has \(\sum _{e}\mathrm {cork}L_e=|\Delta |+r-3\). Thus,
and as each term on the left-hand side is positive, neither can be bigger than \(r-2\). Hence, constraints are properly distributed. \(\square \)
We now get to the main result. We use the refined multiplicity \(B_\Gamma ^{K_\omega }\), where the bivectors \(\pi _V\) are chosen such that \(\omega (\pi _V)>0\). If \(\omega (\pi _V)=0\), then \(B_\Gamma ^{K_\omega }=0\) and the sign does not matter.
Theorem 4.5
There exists a collection of signs \(\varepsilon _\Gamma \) indexed by the combinatorial types \({\mathcal {C}}_\Delta ^\mathrm {top}\) such that the following refined count
does not depend on the choice of the constraints \({\mathcal {L}}_e\) as long as it is generic. It only depends on the choice of \(L_e\).
Remark 4.6
It might happen that for some combinatorial type \(m_\Gamma ^{{\mathbb {C}},(L_e)}\ne 0\) and still \(B_\Gamma ^{K_\omega }=0\), but not the other way around. \(\square \)
The construction of the collection of signs is given in the proofs. They can be obtained as follows. Let C be a top-dimensional combinatorial type in \({\mathcal {C}}_\Delta ^\mathrm {top}\) with non-zero complex multiplicity \(m_C^{{\mathbb {C}},(L_e)}\). We have two evaluation maps restricted to the cone C:
Let us assume that the maps are invertible, otherwise the definition of the sign does not matter since \(B_C^{K_\omega }=0\). Let us choose once and for all an orientation of the codomains, i.e. not depending on the chosen combinatorial type \(\Gamma \). For any orientation on \(C={\mathbb {R}}_{+}^{|\Delta |-3}\times N_{\mathbb {R}}\), if the maps both preserve the orientation or both reverse it, the sign is \(+\). If one of them preserves the orientation and the other reverses it, the sign is –. The signs \(\varepsilon _C\) are thus defined up to a global sign depending on the choice of the identification between the codomains of both evaluation maps.
In other words, if one identifies the codomains with \({\mathbb {R}}^{|\Delta |+r-3}\) and one chooses an orientation on it, the sign \(\varepsilon _C\) compares the orientations on C which are induced by both composed evaluation maps.
4.3 Proofs of invariance
We give two different proofs of the result. Both proofs use a trick that might be of an interest in other situations as well: without giving too much context, given two tropical enumerative problems \({\mathcal {P}}\) and \({\mathcal {P}}'\) for tropical curves having the same walls, assuming some additional condition on the combinatorial types not providing any solution, it is possible to use a multiplicity m leading to an invariant in \({\mathcal {P}}\) to get an invariant in \({\mathcal {P}}'\), eventually twisting the multiplicity m with a sign. In our case, we use the invariance with respect to the refined multiplicity \(B^{K_\omega }\) in the \(\omega \)-problem \({\mathcal {P}}(\omega ,e_0)\) to get an invariance in the problem \({\mathcal {P}}(L_e)\).
First proof of Theorem 4.5
The first way of proving the existence of the signs is choosing the sign of one combinatorial type and spreading the signs so that one has local invariance around the walls, which are here the curves with a quadrivalent vertex. Then, one just has to check that the signs are well-defined.
Let \({\mathcal {W}}_\Delta \) be the set of walls, i.e. combinatorial types of curves with a quadrivalent vertex. Consider the graph on \({\mathcal {C}}_\Delta ^\mathrm {top}\) where the two combinatorial types C and \(C'\) are adjacent if they are adjacent to a common wall \(W\in {\mathcal {W}}_\Delta \). We consider the subgraph \({\mathcal {G}}_\mathrm {reg}\subset {\mathcal {C}}_\Delta ^\mathrm {top}\) only containing the combinatorial types with non-zero multiplicity \(B_C^{K_\omega }\), and thus non-zero complex multiplicity \(m_C^{{\mathbb {C}},(L_e)}\), along with the edges between them. This graph might not be connected anymore. For a given connected component, let \(C_0\) be a fixed combinatorial type, thus having non-zero complex multiplicity \(m_{C_0}^{{\mathbb {C}},(L_e)}\). Let \(\varepsilon _{C_0}=1\). For a given wall \(W\in {\mathcal {W}}_\Delta \), we write the local invariance relation for \(B^{K_\omega }\) around W in the following way:
where \(\eta _C^W\) are equal to \(\pm 1\), and depend on the repartition of the sides of the wall in the enumerative problem \({\mathcal {P}}(\omega ,e_0)\). The triple \((\eta ^W_{C_1},\eta ^W_{C_2},\eta ^W_{C_3})\) is defined up to global change of sign. If for a given combinatorial type C one has \(B_C^{K_\omega }=0\), the signs \(\eta _C^\bullet \) are not uniquely defined but their definition is unimportant. Now, for a combinatorial type \(C\in {\mathcal {G}}_\mathrm {reg}\subset {\mathcal {C}}_\Delta ^\mathrm {top}\), let
be a path going from \(C_0\) to C in \({\mathcal {G}}_\mathrm {reg}\), where \(W_i\in {\mathcal {W}}_\Delta \) is a wall adjacent to both combinatorial types \(C_i\) and \(C_{i+1}\). Now, we use the following rule to define the signs \(\varepsilon _{C_i}\): let \(C'_i\in {\mathcal {C}}_\Delta ^\mathrm {top}\) be the last combinatorial type adjacent to \(W_i\), so that the adjacent combinatorial types are \(C_i\), \(C_{i+1}\) and \(C'_i\). We are in one of the following situations:
-
The combinatorial types \(C_i\) and \(C_{i+1}\) are on the same side of the wall, so that the invariance relation for the complex multiplicity \(m^{{\mathbb {C}},(L_e)}\) writes itself
$$\begin{aligned} m_{C_i}^{{\mathbb {C}},(L_e)}+m_{C_{i+1}}^{{\mathbb {C}},(L_e)}=m_{C'_i}^{{\mathbb {C}},(L_e)}. \end{aligned}$$We write the invariance relation for \(B^{K_\omega }\) mimicking the previous relation, and multiply it so that the coefficient of \(m^{K_\omega }_{C_i}\) is \(\varepsilon _{C_i}\), leading to
$$\begin{aligned} \varepsilon _{C_i}m_{C_i}^{K_\omega } + \varepsilon _{C_i}\frac{\eta ^{W_i}_{C_{i+1}}}{\eta ^{W_i}_{C_i}}m_{C_{i+1}}^{K_\omega } =-\varepsilon _{C_i}\frac{\eta ^{W_i}_{C'_i}}{\eta ^{W_i}_{C_i}}m_{C'_i}^{K_\omega }. \end{aligned}$$Thus, we choose
$$\begin{aligned} \varepsilon _{C_{i+1}}=\varepsilon _{C_i}\frac{\eta ^{W_i}_{C_{i+1}}}{\eta ^{W_i}_{C_i}}. \end{aligned}$$ -
If \(C_i\) and \(C_{i+1}\) are on different sides of the walls, the invariance for the complex multiplicity writes itself
$$\begin{aligned} m_{C_i}^{{\mathbb {C}},(L_e)}+m_{C'_i}^{{\mathbb {C}},(L_e)}=m_{C_{i+1}}^{{\mathbb {C}},(L_e)} \text { or }m_{C_i}^{{\mathbb {C}},(L_e)}=m_{C_{i+1}}^{{\mathbb {C}},(L_e)}+m_{C'_i}^{{\mathbb {C}},(L_e)}. \end{aligned}$$We then proceed similarly and choose
$$\begin{aligned} \varepsilon _{C_{i+1}}=-\varepsilon _{C_i}\frac{\eta ^{W_i}_{C_{i+1}}}{\eta ^{W_i}_{C_i}}. \end{aligned}$$ -
If \(m^{{\mathbb {C}},(L_e)}_{C'_i}=0\), \(C_i\) and \(C_{i+1}\) are on different sides of the wall, and the combinatorial type \(C'_i\) never provides any solution to the enumerative problem for a generic value. As by assumption \(B^{K_\omega }_{C'_i}\) is also 0, the previous case still works.
For each connected component of \({\mathcal {G}}_\mathrm {reg}\), the choice of a sign on one combinatorial type \(C_0\) thus propagates to define a sign for every other combinatorial type in the connected component. The rule to propagate the sign from one side of the wall to another might be reformulated in the following closed way. Fix an orientation on the codomain of the composed evaluation map \(\mathrm {ev}^{(L_e)}\). Let \({{\mathfrak {o}}}{{\mathfrak {r}}}(C)\) be the orientation of C induced \(\mathrm {ev}^{(L_e)}_C\). For a combinatorial type on which the composed evaluation map is not invertible, the orientation is chosen at random and does not matter. Then, two combinatorial types \(C_i\) and \(C_{i+1}\) stand on the same side of the wall \(W_i\) if and only if the induced orientations \(\partial _{W_i}{{\mathfrak {o}}}{{\mathfrak {r}}}(C_i)\) and \(\partial _{W_i}{{\mathfrak {o}}}{{\mathfrak {r}}}(C_{i+1})\) on \(W_i\) coincide. Thus, we can use the closed formula
We now check that the signs are well-defined, meaning that the definition of \(\varepsilon _C\) does not depend on the chosen path between \(C_0\) and C. Notice that the rule of propagation is reversible: the sign of \(C_i\) determines the sign of \(C_{i+1}\) in the same way that the sign of \(C_{i+1}\) determines the sign \(C_i\). Thus, we only have consider a loop from \(C_0\) to itself, and prove that the sign obtained by the propagation rule is equal to the original sign \(\varepsilon _{C_0}=+1\). Let
be such a loop inside a connected component of \({\mathcal {G}}_\mathrm {reg}\). Then, the iteration of the rule of signs gives the following sign on \(C_0\):
and needs to be equal to 1. This can be written as a condition on the signs \(\eta \):
Splitting the right-hand side product and reindexing its numerator, we get to
Each triple \((\eta ^W_{C_1},\eta ^W_{C_2},\eta ^W_{C_3})\) is defined up to sign. Notice that the above condition does not depend on the choice of this sign. Neither does it depend on the \(\eta _C^\bullet \) for C with \(B_C^{K_\omega }=0\) since the loop stays inside a component of \({\mathcal {G}}_\mathrm {reg}\). As each factor of the right-hand side is unchanged if the orientation of a combinatorial type \(C_i\) is reversed, then the condition does not depend on the orientations of each C. Therefore, the rule to propagate signs depends on the orientations \({{\mathfrak {o}}}{{\mathfrak {r}}}(C)\) chosen on the combinatorial types, but the condition to ensure that these signs are uniquely defined only depends on the \(\eta _C^W\), not on the chosen orientations. Thus, we can choose any orientation to check the formula, for instance, the orientation induced by the composed evaluation map \(\mathrm {ev}^{\omega ,e_0}\), related to \({\mathcal {P}}(\omega ,e_0)\).
As the refined multiplicity \(B^{K_\omega }\) is known to give an invariant in the problem \({\mathcal {P}}(\omega ,e_0)\), the local invariance around a wall \(W_i\) gives by definition \(\eta _C^W=\frac{\partial _W{{\mathfrak {o}}}{{\mathfrak {r}}}_\omega (C)}{{{\mathfrak {o}}}{{\mathfrak {r}}}(W)}\), for a fixed orientation \({{\mathfrak {o}}}{{\mathfrak {r}}}(W)\) of W. Thus,
It implies that the relation is verified, which concludes the proof since by construction the local invariance is satisfied at each wall. \(\square \)
Remark 4.7
We could have noticed from the start that the \(\eta _C^W\) are given by the formula \(\frac{\partial _W{{\mathfrak {o}}}{{\mathfrak {r}}}_\omega (C)}{{{\mathfrak {o}}}{{\mathfrak {r}}}(W)}\) and conclude that the necessary relation to guarantee that signs were well-defined is satisfied. However, this wouldn’t emphasize the fact the condition solely depends on the signs in front of the multiplicities in the dependence relations given by the walls. \(\square \)
This first proof gives the existence of the signs but fails to provide a useful definition, which is given in the following second proof, whose idea consists in interpreting the multiplicities leading to an invariant as cycles on the moduli space \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\).
Second proof of Theorem 4.5
Consider the orientation \({{\mathfrak {o}}}{{\mathfrak {r}}}(C)\) of \(C\in {\mathcal {C}}_\Delta ^\mathrm {top}\) induced by the composed evaluation map \(\mathrm {ev}^{(L_e)}\) and a fixed orientation of its codomain. If the restriction to a given combinatorial type is not invertible, the chosen orientation does not matter. We then consider the following top dimensional chain
Technically, this is a chain in the star complex of the fan \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\), obtained as the quotient of \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\backslash \{0\}\) by \({\mathbb {R}}_+^*\). The fan \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\) is the cone over its star complex, which is a compact CW-complex. Again, by abuse of notation, we write \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\) to avoid further notations which are not essential to the proof, denoting the cells of the star complex by their associated cone in \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\). Choosing an arbitrary orientation \({{\mathfrak {o}}}{{\mathfrak {r}}}(W)\) of every wall, the boundary of \(\Xi \) is
where \(C_1,C_2\) and \(C_3\) are the sides adjacent to the wall W, and the sign \(\eta ^W_{C_i}=\frac{\partial _W{{\mathfrak {o}}}{{\mathfrak {r}}}(C)}{{{\mathfrak {o}}}{{\mathfrak {r}}}(W)}\) is given by the boundary map. Then, the local invariance relation needed to show that multiplicities \(m^{(L_e)}\) lead to an invariant for the enumerative problem \({\mathcal {P}}(L_e)\) is equivalent to the fact that \(\Xi \) is a cycle, i.e. \(\partial \Xi =0\). Conversely, any \(m=(m_C)_C\) such that
provides an invariant for the enumerative problem \({\mathcal {P}}(L_e)\). The first relation ensures the local invariance statement while the second condition ensures that combinatorial types which do not provide any solution do not interfere in the local invariance.
Now, let \({{\mathfrak {o}}}{{\mathfrak {r}}}_\omega (C)\) be the orientation of C induced by the composed evaluation map \(\mathrm {ev}^{\omega ,e_0}\). Then, as the refined multiplicity \(B^{K_\omega }\) provides an invariance in the enumerative problem \({\mathcal {P}}(\omega ,e_0)\), one has
Thus, twisting the signs, one gets
As by assumption \(m_C^{{\mathbb {C}},(L_e)}=0\Rightarrow B_C^{K_\omega }=0\), the choice \(\varepsilon _C=\frac{{{\mathfrak {o}}}{{\mathfrak {r}}}_\omega (C)}{{{\mathfrak {o}}}{{\mathfrak {r}}}(C)}\) gives an invariant in the enumerative problem \({\mathcal {P}}(L_e)\) and concludes the proof. \(\square \)
Remark 4.8
The second proof allows one to view the multiplicities leading to an invariant as some homology class in \(H_\mathrm {top}\left( \mathrm {Star}({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})),R\right) \) with values in some ring R, \({\mathbb {Z}}\) or \({\mathbb {Z}}[\Lambda ^2 N]\) for instance. \(\square \)
The second proof gives an explicit description of signs that provide invariance using the \(\omega \). However, the first proof provides all possible signs: one choice of signs for each connected component of the graph \({\mathcal {G}}_\mathrm {reg}\) (Recall that \({\mathcal {G}}_\mathrm {reg}\) is the graph of combinatorial types whose multiplicity is non-zero). It would be interesting to know whether this graph is always connected or not. If the graph was not connected, the sum of multiplicities of curves solution to an enumerative problem and whose combinatorial type belongs to a given component of \({\mathcal {G}}_\mathrm {reg}\) would lead to refined invariants of a new kind. Thus, we have the following proposition that follows from the first proof of Theorem 4.5.
Corollary 4.9
Let c be the number of connected components of \({\mathcal {G}}_\mathrm {reg}\). Up to a global change of signs, one has \(2^{c-1}\) choices of signs that provide invariance. In particular, if \({\mathcal {G}}_\mathrm {reg}\) is connected, the choice is unique and signs do not depend on the choice of \(\omega \).
In other words, the choice of \(\omega \) has only an influence on the number of combinatorial types whose refined multiplicity vanishes: for some of them it always has to be 0 (those for which \(m_\Gamma ^{{\mathbb {C}},(L_e)}=0\)), but some other might also have a vanishing refined multiplicity (for instance if \(\omega =0\)). The choice of \(\omega \) has an influence on this last part. This only depends on \(K_\omega \).
5 First properties and possible enhancements of refined invariants
We now focus on some properties of these new refined invariants, including their relation to the complex multiplicities. We then provide some directions to enlarge and improve the family of refined invariants.
5.1 Relation to the complex multiplicities
In the case of the \(\omega \)-problem \({\mathcal {P}}(\omega ,e_0)\), we first prove a connection between the refined multiplicity and the complex multiplicity. In the general setting, to some extent with prove the non-existence of such a relation. The goal of this section is to find a way to recover \(m^{{\mathbb {C}}}_\Gamma \) from \(B_\Gamma ^K\).
Let us first consider the planar setting, i.e. \(r=2\), and let \(\mathrm {det}\) be a generator of \(\Lambda ^2 M\). Recall that the refined multiplicity of Block–Göttsche is defined as follows: for a trivalent parametrized tropical curve \(h:\Gamma \rightarrow N_{\mathbb {R}}\),
where \(\pi _V\) is chosen so that \(\mathrm {det}(\pi _V)>0\). This refined multiplicity is related to our choice of refined multiplicity through the relation
where \(\varphi _\mathrm {det}:{\mathbb {Z}}[\Lambda ^2 N]\rightarrow {\mathbb {Z}}[q^{\pm 1/2}]\) is the morphisms that evaluates \(\mathrm {det}/2\) on the exponents. As \(m^{BG}_\Gamma \xrightarrow {q\rightarrow 1}\prod _V\mathrm {det}(\pi _V)=m^{{\mathbb {C}}}_\Gamma \), the refined multiplicity determines the complex multiplicity in the planar case, and so the refined invariant \({\mathcal {B}}_\Delta ^{\omega ,e_0}\) determines the complex invariant \(N_\Delta ^{\omega ,e_0}\).
Getting back to the general case, this limit relation extends to any dimension, and thus proves that the refined multiplicity determines the complex multiplicity in the \(\omega \)-problem \({\mathcal {P}}(\omega ,e_0)\) for any \(\omega \), which is stated in the following proposition.
Proposition 5.1
For any choice of \(\omega \), one has \((q-q^{-1})^{2-|\Delta |}\varphi _\omega (B_\Gamma ^{K_\omega })\xrightarrow {q\rightarrow 1}m^{{\mathbb {C}},\omega ,e_0}_\Gamma \), and thus
In the general case of the enumerative problem \({\mathcal {P}}(L_e)\), the question remains to know whether the complex multiplicity can be recovered using the refined multiplicity and some clever function involving the constraints. Due to the finite number of refined multiplicities for a fixed degree \(\Delta \), the complex multiplicity cannot be determined solely with the refined multiplicity.
Remark 5.2
It is possible to find tropical curves satisfying constraints of the same slope, and with the same refined multiplicity but different complex multiplicities, preventing from finding a simple relation between the refined multiplicity and the complex multiplicity. Indeed, for each combinatorial type, the algorithm from Sect. 2.5 expresses the complex multiplicity as a multilinear function depending on the Plücker vectors of the constraints. If two unbounded ends point in the same direction, the corresponding function has no reason to be the same when you switch the constraints imposed on these unbounded ends, and the complex multiplicity depends on the repartition of the constraints. Meanwhile, the refined multiplicity only depends on the combinatorial type. \(\square \)
5.2 Regularity of the invariants
For a fixed degree \(\Delta \), the invariants \({\mathcal {B}}_\Delta ^{\omega ,e_0}\) and \({\mathcal {B}}_\Delta ^{K}(L_e)\) form a large family of invariants depending on \(\omega \) for the first family, and \((L_e)\) for the second. The 2-form \(\omega \) varies on the space \(\Lambda ^2 M\otimes {\mathbb {R}}\), while \((L_e)\) varies in \(\prod _e \Lambda ^{l_e}\langle n_e \rangle ^\perp \), where \(l_e=\mathrm {cork}L_e\). In this section we study the dependence of these invariants in their respective parameter spaces.
The following theorem adresses the case of the invariants \({\mathcal {B}}_\Delta ^{\omega ,e_0}\). First, let us introduce the fan structure \(\Omega _\Delta \) on \(\Lambda ^2M_{\mathbb {R}}\), which is induced by the linear forms \(\omega \mapsto \omega (\pi _V)\), for every \(V\in {\mathcal {V}}_\Delta \). Notice that the function \(\omega \mapsto K_\omega =\langle \pi _V:\omega (\pi _V)=0 \rangle _{V\in {\mathcal {V}}_\Delta }\) is constant on the cones of the subdivision, and thus denoted by \(K_\sigma \) for a given cone \(\sigma \) of \(\Omega _\Delta \). Furthermore, if \(\tau \prec \sigma \) are cones, then \(K_\sigma \subset K_\tau \). The top-dimensional cones are those for which \(K_\sigma =\{0\}\). Remember that \({\mathcal {B}}_\Delta ^{\omega ,e_0}\) is defined whenever \(\Delta \cap \{n:\iota _n\omega =0\}=\emptyset \). The set of \(\omega \) not satisfying this assumption is some subfan of \(\Omega _\Delta \), where one can set \({\mathcal {B}}_\Delta ^{\omega ,e_0}=0\).
Theorem 5.3
-
The function \(\omega \mapsto {\mathcal {B}}_\Delta ^{\omega ,e_0}\) is constant on the interior of the cones of \(\Omega _\Delta \) where it is defined.
-
If \(\tau \prec \sigma \) and \(\tau \) are cones of \(\Omega _\Delta \), with values \({\mathcal {B}}(\sigma )\) and \({\mathcal {B}}(\tau )\), then \({\mathcal {B}}(\tau )\) is the image of \({\mathcal {B}}(\sigma )\) under the projection \({\mathbb {Z}}[\Lambda ^2N/K_\sigma ]\rightarrow {\mathbb {Z}}[\Lambda ^2N/K_\tau ]\).
Proof
Let \(\omega _0\) be a fixed 2-form where \({\mathcal {B}}_\Delta \) is defined. Let \(C\in {\mathcal {C}}_\Delta ^\mathrm {top}\) be a combinatorial type with non-zero multiplicity \(m_C^{{\mathbb {C}},\omega _0,e_0}\) and \(\Gamma _0\) be a curve belonging to the interior of C. We consider \(\mathrm {ev}^{\omega ,e_0}\) as a function of both \(\omega \) and \(\Gamma \in C\). This way, the partial differential \(\frac{\partial \mathrm {ev}^{\omega ,e_0}}{\partial \Gamma }\) at \((\omega _0,\Gamma _0)\) is the usual differential of \(\mathrm {ev}^{\omega _0,e_0}\). Recall that \(\mathrm {ev}^{\omega _0,e_0}\) is linear on C. Therefore, the differential is invertible since its determinant is equal to the complex multiplicity \(m_{\Gamma _0}^{{\mathbb {C}},\omega _0,e_0}\), which is non-zero by assumption. Thus, the Implicit Function Theorem ensures that at the neighborhood \((\omega _0,\Gamma _0)\), the equation \(\mathrm {ev}^{\omega ,e_0}(\Gamma )=\mathrm {ev}^{\omega _0,e_0}(\Gamma _0)\) in \((\omega ,\Gamma )\) solves with \(\Gamma \) being a function \(\Gamma (\omega )\), with \(\Gamma (\omega _0)=\Gamma _0\).
For a generic value \((\mu ,D)\), at \(\omega _0\), one has
For the combinatorial types that contribute a solution in the above sum, the previous fact using implicit functions theorem shows that they still provide a solution when \(\omega \) moves in the neighborhood of \(\omega _0\). For the same reasons, combinatorial types where the composed evaluation map is invertible but which do not provide a solution continue not to provide a solution. The remaining combinatorial types never provide a solution for \({\mathcal {P}}(\omega _0,e_0)\), but might start to do so for some \({\mathcal {P}}(\omega ,e_0)\). However, their multiplicity \(B_\Gamma ^{K_{\omega _0}}\) is 0. Moreover, the function
is constant in a neighborhood of \(\omega _0\): if the value is 0, it stays zero since some \(\pi _V\) belongs to \(K_{\omega _0}\), otherwise the conditions \(\omega (\pi _V)>0\) remains valid for \(\omega \) in a neighborhood of \(\omega _0\). In particular, for \(\omega \) belonging to the same cone of \(\Omega _\Delta \), since then one has \(K_\omega =K_{\omega _0}\), the multiplicity stays the same, and \(\omega \mapsto {\mathcal {B}}_\Delta ^{\omega ,e_0}\) is locally constant for \(\omega \) in the neighborhood of \(\omega _0\) and in the same cone. The first statement follows since cones are connected.
If \(\omega \) is still in the neighborhood of \(\omega _0\) but does not belong to the same cone of \(\Omega _\Delta \), then the same observation applies. And \({\mathcal {B}}_\Delta ^{\omega ,e_0}={\mathcal {B}}_\Delta ^{\omega _0,e_0}\in {\mathbb {Z}}[\Lambda ^2N/K_{\omega _0}]\) which means that \({\mathcal {B}}_\Delta ^{\omega _0,e_0}\) is the image of \({\mathcal {B}}_\Delta ^{\omega ,e_0}\) under the map that projects the exponents \({\mathbb {Z}}[\Lambda ^2N/K_{\omega }]\rightarrow {\mathbb {Z}}[\Lambda ^2N/K_{\omega _0}]\), thus proving the second statement. \(\square \)
Remark 5.4
Clearly, the \(\omega \)-problem \({\mathcal {P}}(\omega ,e_0)\) depends on \(\omega \) only up to multiplication by a scalar. The fan \(\Omega _\Delta \) induces a subdivision on the projective space \({\mathbb {P}}(\Lambda ^2 M_{\mathbb {R}})\), which is a hyperplane arrangement. Then, \([\omega ]\mapsto {\mathcal {B}}_\Delta ^{\omega ,e_0}\) is a function constant on the cells of the subdivision and satisfying the compatibility condition when going from a cell to one of its faces. On the cells where \({\mathcal {B}}_\Delta ^{\omega ,e_0}\) is not defined, the map can be extended by 0. This choice is natural since for such 2-forms, the composed evaluation map is never surjective, and there is an invariant which has value 0. \(\square \)
For the general enumerative problem \({\mathcal {P}}(L_e)\), the same reasoning applies. Let \((L_e^0)\) be a specific set of slope constraints. Let \(l_e=\mathrm {cork}L_e^0\), so that the tuple \((L_e)\) varies in \({\mathbb {L}}=\prod _e\Lambda ^{l_e}\langle n_e \rangle ^\perp \).
Theorem 5.5
Let \((L_e^0)\in {\mathbb {L}}\) be a specific set of slopes constraints. Let \(\omega \) be a 2-form satisfying
leading to an invariant \({\mathcal {B}}_\Delta ^{K_\omega }(L_e^0)\in {\mathbb {Z}}[\Lambda ^2 N/K_\omega ]\). Then \(\omega \) also satisfies the condition for \((L_e)\) in a neighborhood of \((L_e^0)\), and the function \((L_e)\mapsto {\mathcal {B}}_\Delta ^{K_\omega }(L_e)\) is constant in a neighborhood of \((L_e^0)\).
Proof
The condition
can be restated as
Furthermore, for each combinatorial type \(C\in {\mathcal {C}}_\Delta ^\mathrm {top}\), the complex multiplicity seen as a function \((L_e)\mapsto m_C^{{\mathbb {C}},(L_e)}\) is continuous on \({\mathbb {L}}\). Thus, in a neighborhood of \((L_e^0)\), one still has \(m_C^{{\mathbb {C}},(L_e)}\ne 0\). Thus, the 2-form \(\omega \) also satisfies the condition for \((L_e)\) and thus provides an invariant in \({\mathbb {Z}}[\Lambda ^2 N/K_\omega ]\). The implicit functions theorem provides the local invariance in the same way as for the \(\omega \)-problem case: combinatorial types where the complex multiplicity is non-zero provide or not a solution for a specific value of the constraints, and we apply the implicit functions theorem, and combinatorial type where the complex multiplicity vanishes might provide a solution for \((L_e)\) in a neighborhood of \((L_e^0)\) but their multiplicity \(B_C^{K_\omega }\) is 0 by assumption. \(\square \)
5.3 Tropical cycles constraints
We now try to enlarge the scope of the refined invariance theorems by generalizing the family of enumerative problems \({\mathcal {P}}(L_e)\) considered in Theorem 4.5. A possible generalization would be to replace the affine constraints in \(N_{\mathbb {R}}/\langle n_e \rangle \) by tropical cycles of the same dimension. Let \((\Xi _e)\) be a family of tropical cycles \(\Xi _e\subset N_{\mathbb {R}}/\langle n_e \rangle \) such that \(\sum _e\mathrm {codim}\Xi _e=|\Delta |+r-3\).
Problem 5.6
The problem referred as \({\mathcal {P}}(\Xi _e)\) is counting rational tropical curves of degree \(\Delta \) which intersect \(\Xi _e\) for every \(e\in \Gamma _\infty ^1\).
The dimension count ensures that if the cycles \(\Xi _e\) are chosen generically, there is a finite number of solutions. In this situation, general theory still provides a complex multiplicity which leads to an invariant. However, the proof of Theorem 4.5 for the refined invariance fails in this context for the following reasons.
-
First, in the case of affine constraints, each tropical curve \(h:\Gamma \rightarrow N_{\mathbb {R}}\) determines uniquely the constraints that it satisfies: \({\mathcal {L}}_e\) is the affine space with slope \(L_e\) passing through \(h(e)\in N_{\mathbb {R}}/\langle n_e \rangle \). This can be reprased as the existence of the composed evaluation map \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\rightarrow \prod _e Q_e^{\mathbb {R}}\), where \(Q_e^{\mathbb {R}}\) is a moduli space for the affine subspaces \({\mathcal {L}}_e\) of slope \(L_e\). The proof of invariance then consists in showing that this map has a well-defined degree for various multiplicities. This is not the case for tropical cycle constraints \((\Xi _e)\) since they vary in a wider moduli space: there is no composed evaluation map anymore. Thus, there is no suitable definitions of the “walls” inside \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\) that could lead to an analogous proof.
-
Then, if one tries instead to mimic the invariance proof for the complex multiplicity, whether it uses tropical intersection theory or not, we have to check invariance around one new kind of wall: where the intersection point between one tropical curve \(\Gamma \) solution to the enumerative problem and one of the constraints \(\Xi _e\) belongs to a facet of \(\Xi _e\). This intersection is not generic among the choices of \(\Xi _e\), and the invariance for the complex multiplicity is provided by the balancing condition of \(\Xi _e\), which would express as \(\rho _1+\rho _2+\rho _3=0\) for the Plücker vectors of the adjacent facets of \(\Xi _e\). However, at this wall, two solutions on one side of the wall become one on the other side, but the combinatorial types of the solutions are the same. This prevents any local invariance using a multiplicity solely depending on the combinatorial type of the curve, such as \(B_\Gamma ^K\).
-
Despite the impossibility of the multiplicity \(B_\Gamma ^K\) to provide a local refined invariant, there might exists a clever way to find another refined multiplicity leading to an invariant. However, such a multiplicity would not have the close relationship that \(B_\Gamma ^0\) shares with the count of real curves tropicalizing to \(\Gamma \) through the correspondence theorem.
Nevertheless, we can prove refined invariance in the following particular case. Let \(\Xi _{e_0}\subset N_{\mathbb {R}}/\langle e_0 \rangle \) be a tropical cycle of dimension 1, i.e. a tropical curve, and \(\omega \in \Lambda ^2M\) be a 2-form. We consider the following variant of the \(\omega \)-problem.
Problem 5.7
How many rational tropical curves \(h:\Gamma \rightarrow N_{\mathbb {R}}\) of degree \(\Delta \) have fixed family of moments \(\mu _\omega \) and satisfy \(h(e_0)\in \Xi _{e_0}\)?
We count the solutions to the problem with multiplicity \(|\omega (n_{e_0},\delta )|B_\Gamma ^{K_\omega }\), where \(\delta \) is the slope of \(\Xi _{e_0}\) at the intersection point with \(\Gamma \):
We have the following invariance result.
Theorem 5.8
For a generic choice of \((\mu _\omega ,\Xi _{e_0})\), the count does not depend on the choice of \(\mu _\omega \) nor the choice of \(\Xi _{e_0}\). It only depends on \(\omega \) and the degree of \(\Xi _{e_0}\). Moreover, its value is
where \(\omega \cdot \Xi _{e_0}\) is the intersection index between \(\Xi _{e_0}\) and an affine hyperplane of slope \(H_{e_0}\).
Proof
The proof is immediate because due to Theorem 3.14, for each intersection point between \({\mathcal {H}}_{e_0}\) and \(\Xi _{e_0}\), the refined count is \(|\omega (n_{e_0},\delta )|{\mathcal {B}}_\Delta ^{\omega ,e_0}\), the result follows by definition of the intersection index. \(\square \)
5.4 Constraints on marked points
The other main direction to generalize the refined invariance theorems by staying in the realm of cycle constraints would be to allow the constraints to live in the main strata \(N_{\mathbb {R}}\). This would mean to allow unbounded ends with slope 0 and impose cycle constraints on them.
The first problem that occurs is that the \(\omega \)-problem, which is at the core of the proof of invariance, does not allow unbounded ends to have slope 0. If we are to go by the same proof as for Theorem 4.5, the first step is then to find a suitable enumerative problem that does so. For instance, the following variant of the \(\omega \)-problem. The idea is to add marked points that do not add any constraints for the curves.
Let \(\varphi _1,\dots ,\varphi _p\in M\) be p non-zero linear forms, and let \({\mathcal {H}}_i\subset N_{\mathbb {R}}\) be affine hyperplanes with respective slope \(\ker \varphi _i\). Let \(\omega \) be a 2-form, \(\mu \in {\mathfrak {M}}\) a family of moments and \(D\subset N_{\mathbb {R}}/\langle e_0 \rangle \), all chosen generically. We consider the following enumerative problem \({\mathcal {P}}\left( \omega ,e_0,(\varphi _i)\right) \). We consider curves of degree \(\Delta \sqcup \{0^p\}\), which means that curves have now p new unbounded ends of slope 0, which are called marked points and are denoted by \(i\in [\![1;p]\!]\).
Problem 5.9
\({\mathcal {P}}\left( \omega ,e_0,(\varphi _i)\right) \) How many parametrized rational tropical curves \(h:\Gamma \rightarrow N_{\mathbb {R}}\) of degree \(\Delta \sqcup \{0^p\}\) satisfy \(\mathrm {mom}(\Gamma )=\mu \), \(h(e_0)\in D\), and \(h(i)\in {\mathcal {H}}_i\) ?
Remark 5.10
The new additional conditions are kind of void for the following reason. Forgetting the marked points, each solution of \({\mathcal {P}}\left( \omega ,e_0,(\varphi _i)\right) \) gives a solution of the usual \(\omega \)-problem \({\mathcal {P}}(\omega ,e_0)\). Conversely, every solution to \({\mathcal {P}}\left( \omega ,e_0,(\varphi _i)\right) \) is obtained from a solution to the standard \(\omega \)-problem \({\mathcal {P}}(\omega ,e_0)\) by choosing intersection points with the hyperplanes \({\mathcal {H}}_i\). Such points always exist. Therefore, the solutions are morally the same solutions as for the \(\omega \)-problem. The new marked points on the curve just have to be chosen at the intersection points between the solutions to the \(\omega \)-problem and \({\mathcal {H}}_i\).
\(\square \)
Standard intersection theory ensures that the count of solutions with complex multiplicity yields an invariant. Using the algorithm to compute the complex multiplicity of a solution \(h:\Gamma \rightarrow N_{\mathbb {R}}\), one sees that the vertex corresponding to the marked point i just contributes a factor \(|\varphi _i(\delta _i^\Gamma )|\), where \(\delta _i^\Gamma \) is the slope of \(\Gamma \) at the marked point. Hence, the complex multiplicity tales the following form:
Using Remark 5.10, one obtains that by adding all the multiplicities over the curves solutions to problem 5.9,
where \(\varphi _i\cdot \Delta =\sum _{n\in \Delta :\varphi _i(n)>0}\varphi _i(n)\) denotes the intersection index between a curve of degree \(\Delta \) and a hyperplane of slope \(\ker \varphi _i\). The combinatorial types where \(\varphi _i(\delta _i^C)\) have thus zero complex multiplicity. They were previously part of the fourth type. They do not occur if \((\varphi _i)\) are chosen generically with respect to \(\Delta \).
We now get to the refined count of this enhanced \(\omega \)-problem.
Proposition 5.11
The count of solutions to problem \({\mathcal {P}}\left( \omega ,e_0,(\varphi _i)\right) \) with refined multiplicity \(\prod _i|\varphi _i(\delta _i^\Gamma )| B_\Gamma ^{K_\omega }\) yields an invariant which is equal to \(\left( \prod _i\varphi _i\cdot \Delta \right) {\mathcal {B}}_\Delta ^{\omega ,e_0}\).
Proof
The proof uses Remark 5.10 which describes solutions to problem 5.9 in terms of solutions to the usual moment problem. The direct computations yields the result. \(\square \)
We can then proceed, applying the same trick as in the proof of Theorem 4.5, to get a new invariance result. Let \(L_e\subset N/\langle n_e \rangle \) for \(e\in \Gamma _\infty ^1\) and \(L_i\subset N\) for \(i\in [\![1;p]\!]\) be saturated sublattices such that
Let \({\mathcal {L}}_e\), \({\mathcal {L}}_i\) be affine subspaces of respective slopes \(L_e,L_i\). There is no relation between \(\varphi _i\) and \(L_i\). The first are involved in the toy problem for which we have an easy invariance, and the second are the constraints in the new following enumerative problem:
Problem 5.12
How many rational curves of degree \(\Delta \sqcup \{0^p\}\) satisfy \(h(e)\in {\mathcal {L}}_e\) and \(h(i)\in {\mathcal {L}}_i\) ?
Remark 5.13
The infinite constraints associated to the \({\mathcal {L}}_e\) can be forgotten by taking \(L_e=N/\langle n_e \rangle \). \(\square \)
Standard intersection theory yields that the use of the complex multiplicity \(m_C^{{\mathbb {C}},(L_e),(L_i)}\) leads to an invariant. Meanwhile, the use of refined multiplicity gives an invariant as follows. Let \(\omega ,\varphi _i\) be such that
Theorem 5.14
There exists signs \(\varepsilon _\Gamma \) such that the refined count of solutions to problem 5.12 using multiplicity \(\varepsilon _C\prod _i|\varphi _i(\delta _i^C)| B_C^{K_\omega }\) leads to an invariant.
Proof
The proof is identical to the proof of Theorem 4.5. \(\square \)
Remark 5.15
One gets many new invariants depending on the choice of the linear forms \(\varphi _i\). Clearly, the invariants are 1-homogeneous in the linear forms \(\varphi _i\). Yet, it would be interesting to study the various obtained invariants. \(\square \)
As before, there is a subtle condition for the existence of refined invariants, which is the existence of \(\omega ,(\varphi _i)\). To see that this generalization is still of an interest, notice that the class of enumerative problems for which constraints on the unbounded ends and marked points are of codimension at least 1 provide a family of examples for which a generic choice of \(\omega \) and \(\varphi _i\) satisfy the assumption, leading to refined invariants in \({\mathbb {Z}}[\Lambda ^2 N]\).
As in the case of tropical cycle constraints, the appearance of factors \(\prod _i|\varphi _i(\delta _i^C)|\) makes the new multiplicity lose its relationship to the real curves tropicalizing to the tropical curve.
6 Examples of refined invariants
We now give a few examples, limited for the two following computational technicalities: first, we do not have yet a way of solving efficiently either of the enumerative problems \({\mathcal {P}}(\omega ,e_0)\) and \({\mathcal {P}}(L_e)\), secondly, in the case of \({\mathcal {P}}(L_e)\), finding a 2-form \(\omega \) satisfying the assumptions might be difficult.
Example 6.1
First, assume that \(\omega =\varphi \wedge \psi \) is a generic 2-form of rank 1, where \(\varphi ,\psi \in M\). Then, the 2-form has a \((r-2)\)-dimensional kernel \(\ker \omega =\ker \varphi \cap \ker \psi \) which is contained in every \(\ker \iota _{n_e}\omega \). Therefore, the translate of a curve \(h:\Gamma \rightarrow N_{\mathbb {R}}\) by a vector in \(\ker \omega \) has the same moments. Hence, solving the \(\omega \)-problem in \(N_{\mathbb {R}}\) can be done by solving the \(\omega \)-problem in \(N_{\mathbb {R}}/\ker \omega \) and then lifting the solutions to \(N_{\mathbb {R}}\): a solution \(h:\Gamma \rightarrow N_{\mathbb {R}}\) to \({\mathcal {P}}(\omega ,e_0)\) gives a solution to \({\mathcal {P}}({\overline{\omega }})\) to the \(\omega \)-problem in \(N_{\mathbb {R}}/\ker \omega \) by composing with the quotient map \(N_{\mathbb {R}}\rightarrow N_{\mathbb {R}}/\ker \omega \), which is endowed with the quotient form \({\overline{\omega }}\). Conversely, any solution in the quotient can be lifted uniquely to a solution in \(N_{\mathbb {R}}\) such that \(h(e_0)\) belongs to the line D chosen for the enumerative problem. Therefore, we reduce to the planar case and the computation can be done using the recursive formula from [4]. In particular, as the solutions are determined uniquely up to translation by a solution in the quotient, for such 2-forms, the value of \({\mathcal {B}}_\Delta ^{\omega ,e_0}\) does not depend on the choice of \(e_0\). \(\square \)
In all the following examples, we now consider tropical lines in \({\mathbb {R}}^4\), i.e. curves of degree \(\Delta =\{e_1,e_2,e_3,e_4,e_5\}\), where \((e_1,e_2,e_3,e_4)\) is the canonical basis of \({\mathbb {Z}}^4\) and \(e_5=-\sum _1^4 e_i\). Up to a change of basis of the lattice \(N={\mathbb {Z}}^4\) and maybe a change of lattice, this includes all cases of degree \(\Delta \) of cardinal 5 which span a 4-dimensional space. The moduli space \({\mathcal {M}}(\Delta ,{\mathbb {R}}^4)\) is of dimension 6, in bijection with \({\mathcal {M}}_{0,5}\times {\mathbb {R}}^4\). The moduli space \({\mathcal {M}}_{0,5}\) is the cone over the Petersen graph. It has 15 cones of dimension 2 corresponding to the 15 top-dimensional combinatorial types, and 10 rays, which are the walls of our enumerative problem. This small number of possibilities allows one to solve the enumerative problems by brute force using a computer, providing us with the following examples, which we use to illustrate the various results of the paper more than to provide useful values. We identify \({\mathbb {Z}}[\Lambda ^2{\mathbb {Z}}^4]\) with \({\mathbb {Z}}[q_{ij}^{\pm 1}]_{1\leqslant i<j\leqslant 4}\) through its canonical basis: \(q_{ij}=q^{e_i\wedge e_j}\).
Example 6.2
Let us start with a simple example. We consider the \(\omega \)-problem with the generic 2-form whose matrix in the canonical basis is given by
The genericity means that the 2-form does not vanish any \(\pi _V\) for \(V\in {\mathcal {V}}_\Delta \). The \(\omega \)-problem \({\mathcal {P}}(\omega _1,e_1)\) with chosen unbounded end directed by \(e_1\) gives
\(\square \)
Example 6.3
Similarly, we now consider the 2-form whose matrix is
For different choices of the unbounded end with the plane constraint, one has
In particular, we see that in general the value of the invariant \({\mathcal {B}}_\Delta ^{\omega ,e_0}\) depends on the choice of \(e_0\) since in that case the invariants \({\mathcal {B}}_\Delta ^{\omega _2,e_1}\) and \({\mathcal {B}}_\Delta ^{\omega _2,e_2}\) are different: the last row of their expression are differents. \(\square \)
Example 6.4
We now look at the 2-form \(\omega _0\) given by
This 2-form is non-generic since it has value zero at the vertex formed by the meeting of the unbounded ends directed by \(e_1\) and \(e_2\). The invariant lives in \({\mathbb {Z}}[\Lambda ^2{\mathbb {Z}}^4/\langle e_1\wedge e_2 \rangle ]\), which is identified with \({\mathbb {Z}}[q_{ij}]_{(i,j)\ne (1,2)}\). One gets
There are two ways to deform slightly the 2-form \(\omega _0\), getting the following 2-forms:
In fact, \(\omega _0\) belongs to a facet of the fan \(\Omega _\Delta \), and \(\omega _\pm \) belongs to each of the adjacent maximal cones. They have the following invariants:
In particular, one can see that although \({\mathcal {B}}_\Delta ^{\omega _+,e_1}\ne {\mathcal {B}}_\Delta ^{\omega _-,e_1}\), they both project to \({\mathcal {B}}_\Delta ^{\omega _0,e_1}\) by the quotient map \({\mathbb {Z}}[\Lambda ^2{\mathbb {Z}}^4]\rightarrow {\mathbb {Z}}[\Lambda ^2{\mathbb {Z}}^4/\langle e_1\wedge e_2 \rangle ]\), which in our notations is identified with the map \({\mathbb {Z}}[q_{ij}]\xrightarrow {q_{12}=1}{\mathbb {Z}}[q_{ij}]_{(i,j)\ne (1,2)}\): for \({\mathcal {B}}_\Delta ^{\omega _+,e_1}\) it is immediate, and for \({\mathcal {B}}_\Delta ^{\omega _-,e_1}\), the first two rows give the value of \({\mathcal {B}}_\Delta ^{\omega _0,e_1}\) while the last rows cancels when \(q_{12}\) goes to 1. \(\square \)
Example 6.5
We now give an example of refined invariant in the general case. We consider the enumerative problem with the following constraints:
-
The unbounded end directed by \(e_1\) lies in an affine subspace of slope
$$\begin{aligned} L_{e_1}=\ker \begin{pmatrix} 0 &{} 3780 &{} -315 &{} -2543 \\ \end{pmatrix}\cap \ker \begin{pmatrix} 0 &{} -6958 &{} 7243 &{} 3904 \\ \end{pmatrix}. \end{aligned}$$ -
The unbounded end directed by \(e_2\) lies in an affine hyperplane of slope
$$L_{e_2}=\ker \begin{pmatrix} -25 &{} 0 &{} -16 &{} -72 \\ \end{pmatrix}.$$ -
The unbounded end directed by \(e_3\) lies in an affine hyperplane of slope
$$L_{e_3}=\ker \begin{pmatrix} -4387 &{} 564 &{} 0 &{} 2857 \\ \end{pmatrix}.$$ -
\(e_4\) lies in an affine hyperplane of slope directed by \(L_{e_4}=\ker \begin{pmatrix} -720 &{} -843 &{} -718 &{} 0 \\ \end{pmatrix}\).
-
\(e_5\) lies in an affine hyperplane of slope directed by \(L_{e_5}=\ker \begin{pmatrix} -1091 &{} -562 &{} 653 &{} 1000 \\ \end{pmatrix}\).
These particular constraints are in the family of problems described in example 4.4. Thus, a generic choice of \(\omega \) satisfies the condition of Theorem 4.5. We choose
The rule of sign and computation of the invariants then gives
\(\square \)
Example 6.6
Last, we give an example where a generic choice of \(\omega \) does not satisfy the assumption \(m_\Gamma ^{{\mathbb {C}},(L_e)}=0\Rightarrow m_\Gamma ^{{\mathbb {C}},\omega ,e_0}=0\). We consider the enumerative problem of lines passing through two points which are located on the unbounded ends directed by \(e_1\) and \(e_5\). Notice that by standard geometry, there is always exactly one line passing through two points. Hence, the complex multiplicity can only be 0 or 1. Furhermore, a combinatorial type can provide at most one solution.
The combinatorial type where some of the unbounded ends directed by \(e_2\), \(e_3\) and \(e_4\) are adjacent to a common vertex have complex multiplicity 0. One can check that the other combinatorial types, of the form 1i//j//k5 have complex multiplicity 1. This notation denotes the combinatorial type where unbounded ends directed by \(e_1\) and \(e_i\) are adjacent to the same vertex, as well as \(e_k\) and \(e_5\). In order to apply Theorem 4.5, we can choose a 2-form \(\omega \) that vanishes on \(e_2\wedge e_3\), \(e_2\wedge e_4\) and \(e_3\wedge e_4\). For instance, take

One has \(K_{\omega _4}=\langle e_2\wedge e_3,e_2\wedge e_4,e_3\wedge e_4 \rangle \). Thus, the invariant lives in \({\mathbb {Z}}[\Lambda ^2{\mathbb {Z}}^4/K_{\omega _4}]\simeq {\mathbb {Z}}[q_{12},q_{13},q_{14}]\). The invariance stated in Theorem 4.5 means that every tropical line with non-zero complex multiplicity has the same refined multiplicity. For instance,

Recall that the term of each product are obtained as \(q^{\pi _V}-q^{-\pi _V}\) where \(\omega _4(\pi _V)>0\). For instance, for the midle vertex of the combinatorial type 13//2//45, one has \(\omega _4((e_1+e_3)\wedge e_2)=1>0\), thus,
\(\square \)
Data Availability Statement
I do not have any data to point.
References
Allermann, L., Rau, J.: First steps in tropical intersection theory. Mathematische Zeitschrift 264(3), 633–670 (2010)
Blechman, L., Shustin, E.: Refined descendant invariants of toric surfaces. Discrete Comput. Geom. 62(1), 180–208 (2019)
Block, F., Göttsche, L.: Refined curve counting with tropical geometry. Compos. Math. 152(1), 115–151 (2016)
Blomme, T.: A Caporaso-Harris type formula for relative refined invariants (2019). arXiv preprint arXiv:1912.06453
Blomme, T.: Computation of refined enumerative invariants in real and tropical geometry. PhD Thesis (2020)
Blomme, T.: Computation of refined toric invariants ii (2020). arXiv preprint arXiv:2007.02275
Blomme, T.: A tropical computation of refined toric invariants (2020). arXiv preprint arXiv:2001.09305
Filippini, S.A., Stoppa, J.: Block–Göttsche invariants from wall-crossing (2012). arXiv preprint arXiv:1212.4976
Gathmann, A., Markwig, H.: Kontsevich’s formula and the wdvv equations in tropical geometry. Adv. Math. 217(2), 537–560 (2008)
Göttsche, L., Schroeter, F.: Refined broccoli invariants. J. Algebra. Geom. 28(1), 1–41 (2019)
Göttsche, L., Shende, V.: Refined curve counting on complex surfaces. Geom. Topol. 18(4), 2245–2307 (2014)
Gross, M., Pandharipande, R., Siebert, B., et al.: The tropical vertex. Duke Math. J. 153(2), 297–362 (2010)
Itenberg, I., Mikhalkin, G.: On Block–Göttsche multiplicities for planar tropical curves. Int. Math. Res. Not. 2013(23), 5289–5320 (2013)
Mandel, T.: Scattering diagrams, theta functions, and refined tropical curve counts (2015). arXiv preprint arXiv:1503.06183
Mandel, T., Ruddat, H.: Tropical quantum field theory, mirror polyvector fields, and multiplicities of tropical curves (2019). arXiv preprint arXiv:1902.07183,
Mikhalkin, G.: Enumerative tropical algebraic geometry in R\(^2\). J. Am. Math. Soc. 18(2), 313–377 (2005)
Mikhalkin, G.: Quantum indices and refined enumeration of real plane curves. Acta Math. 219(1), 135–180 (2017)
Nicaise, J., Payne, S., Schroeter, F.: Tropical refined curve counting via motivic integration. Geom. Topol. 22(6), 3175–3234 (2018)
Nishinou, T., Siebert, B.: Toric degenerations of toric varieties and tropical curves. Duke Math. J. 135(1), 1–51 (2006)
Schroeter, F., Shustin, E.: Refined elliptic tropical enumerative invariants. Israel J. Math. 225(2), 817–869 (2018)
Shustin, E.: A tropical approach to enumerative geometry. St. Petersb. Math. J. 17(2), 343–375 (2006)
Shustin, E.: On refined count of rational tropical curves (2018). arXiv preprint arXiv:1812.08038
Tyomkin, I.: Tropical geometry and correspondence theorems via toric stacks. Math. Ann. 353(3), 945–995 (2012)
Tyomkin, I.: Enumeration of rational curves with cross-ratio constraints. Adv. Math. 305, 1356–1383 (2017)
Welschinger, J.-Y.: Enumerative invariants of stongly semipositive real symplectic six-manifolds (2005). arXiv preprint arXiv: math/0509121
Welschinger, J.-Y.: Invariants of real symplectic 4-manifolds and lower bounds in real enumerative geometry. Invent. Math. 162(1), 195–234 (2005)
Funding
Open Access funding provided by Université de Genève.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Jean-Yves Welschinger.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix: Computation of the complex multiplicity
We here prove that the algorithm described in Sect. 2.5 computes the complex multiplicity. This result also appears in a paper of Mandel and Ruddat [15] in a slightly different context. We include a proof in our setting for the sake of completeness.
Lemma 6.7
The result of the algorithm does not depend on the chosen sink.
Proof
We prove that the obtained value does not change if we replace the sink V by one of its neighbors. Let V be a vertex, W one of its neighbors, and E the edge between them, directed by n. Let \(\rho _1,\dots ,\rho _s\) be the polyvectors of the edges adjacent to V different from E, and \(\rho '_1,\dots ,\rho '_{s'}\) the polyvectors associated to the edges adjacent to W different from E. The computation leads to the two following results:
-
If V is the sink, we get
$$\begin{aligned} \rho _1\wedge \cdots \wedge \rho _s\wedge \iota _n(\rho '_1\wedge \cdots \wedge \rho '_{s'}). \end{aligned}$$ -
If W is the sink, we get
$$\begin{aligned} \iota _n(\rho _1\wedge \cdots \wedge \rho _s)\wedge \rho '_1\wedge \cdots \wedge \rho '_{s'}. \end{aligned}$$
Therefore, the equality (up to sign) comes from the fact that \(\rho _1\wedge \cdots \wedge \rho _s\wedge \rho '_1\wedge \cdots \wedge \rho '_{s'}\) is 0 since it is in \(\Lambda ^{r+1}M=\{0\}\), and that \(\iota _n\) is a derivation on \(\Lambda ^\bullet M\). \(\square \)
Theorem 6.8
The value obtained by the algorithm from Sect. 2.5 is equal to the complex multiplicity \(m_\Gamma ^{\mathbb {C}}\).
Proof
We proceed by induction on the number of vertices of the curve \(\Gamma \), and cut the branches one by one.
-
If the curve has just one vertex, let \(\rho _i=m_{i1}\wedge \cdots \wedge m_{ir_i}\) be the polyvectors associated to the lattices \(L_i\) for the s unbounded edges of the curve. The evaluation matrix of \(\mathrm {ev}^{(L_e)}\), denoted by [f], has the following form:
$$\begin{aligned} {[}\mathrm {ev}^{(L_e)}]=\begin{pmatrix} m_{11}\\ \vdots \\ m_{1r_1} \\ \vdots \\ m_{sr_s}\\ \end{pmatrix}. \end{aligned}$$Therefore, we have
$$\begin{aligned} \mathrm {det}\ \mathrm {ev}^{(L_e)}=m_{11}\wedge \cdots \wedge m_{1r_1}\wedge \cdots \wedge m_{sr_s}=\rho _1\wedge \cdots \wedge \rho _s. \end{aligned}$$ -
If \(\Gamma \) has more than one vertex, let V be a vertex adjacent to a unique neighbor vertex W. Let \(\rho _1,\dots ,\rho _s\) be the polyvectors associated to the ends adjacent to V. We keep the same notations \(\rho _i=m_{i1}\wedge \cdots \wedge m_{ir_i}\). We choose a basis of the cone associated to the combinatorial type of \(\Gamma \) consisting of the canonical basis of \({\mathbb {R}}_{\geqslant 0}^{m-3-\mathrm {ov}(\Gamma )}\), and the \(N_{\mathbb {R}}\) factor corresponding to the position of W. Then, the matrix of \(\mathrm {ev}^{(L_e)}\) has the following form:
$$\begin{aligned}{}[\mathrm {ev}^{(L_e)}]=\begin{pmatrix} * &{} \cdots &{} * &{} * &{} \cdots &{} * &{} 0 \\ \vdots &{} \ddots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ * &{} \cdots &{} * &{} * &{} \cdots &{} * &{} 0 \\ &{} m_{11} &{} &{} 0 &{} \cdots &{} 0 &{} \langle m_{11},n\rangle \\ &{} \vdots &{} &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ &{} m_{sr_s} &{} &{} 0 &{} \cdots &{} 0 &{} \langle m_{sr_s},n\rangle \\ \end{pmatrix}, \end{aligned}$$where the first columns correspond to the evaluation of the vertex W, the last column to the evaluation corresponding to the edge between V and W, and n is its slope. We expand the determinant with respect to the last column. We get the following result:
$$\begin{aligned} \mathrm {det}\ \mathrm {ev}^{(L_e)}=\sum _{i=1}^s\sum _{j=1}^{r_i} (-1)^\bullet \langle m_{ij},n\rangle \left| \begin{matrix} * &{} \cdots &{} * &{} * &{} \cdots &{} * \\ \vdots &{} \ddots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ * &{} \cdots &{} * &{} * &{} \cdots &{} * \\ &{} m_{11} &{} &{} 0 &{} \cdots &{} 0 \\ &{} \vdots &{} &{} \vdots &{} \ddots &{} \vdots \\ &{} {\hat{m}}_{ij} &{} &{} 0 &{} \cdots &{} 0 \\ &{} \vdots &{} &{} \vdots &{} \ddots &{} \vdots \\ &{} m_{sr_s} &{} &{} 0 &{} \cdots &{} 0 \\ \end{matrix} \right| . \end{aligned}$$Each determinant in the sum is the determinant of the evaluation matrix \(\mathrm {ev}^{(L_e)}\) for a tropical curve where the vertex V is deleted and the edge between V and W replaced by an unbounded end, associated with a constraint having polyvector \((-1)^\bullet \langle m_{ij}, n\rangle m_{11}\wedge \cdots \wedge {\hat{m}}_{ij}\wedge \cdots \wedge m_{sr_s}\). The sum of these vectors is precisely \(\iota _n(\rho _1\wedge \cdots \wedge \rho _s)\).
The result follows by induction. \(\square \)
Appendix: Invariance for the complex multiplicity
We consider parametrized rational tropical curves of degree \(\Delta \) in \(N_{\mathbb {R}}\). We allow vectors of \(\Delta \) to be 0, so that the unbounded ends associated to these vectors are marked points on the curves. For each unbounded end e, let \(L_e\) be a primitive sublattice of \(N/\langle n_e\rangle \), and let \(l_e\) be its corank. We denote by \(L_e^{\mathbb {R}}=L_e\otimes {\mathbb {R}}\). Notice that if e corresponds to a marked point, \(L_e\) is a sublattice of N. Let \({\mathcal {L}}_e\) be a generic affine space in \(N_{\mathbb {R}}/\langle n_i\rangle \) with slope \(L_e^{\mathbb {R}}\). This amounts to the choice of a point \(\lambda _e\) in \(N_{\mathbb {R}}/\left( \langle n_e\rangle \oplus L_e^{\mathbb {R}}\right) \). We prove the invariance of the solutions to problem \({\mathcal {P}}(L_e)\) using the complex multiplicity \(m^{{\mathbb {C}},(L_e)}\).
Lemma 6.9
For a generic choice of \((\lambda _e)\), there is a finite number of solutions to \({\mathcal {P}}(L_e)\). Moreover, these solutions are trivalent.
Proof
There is a finite number of cones in the moduli space \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\). Moreover, on each cone, i.e. each combinatorial type, \(\mathrm {ev}^{(L_e)}\) is linear. If the restriction of \(\mathrm {ev}^{(L_e)}\) to this cone is injective, the combinatorial type contributes at most one solution.
The point \((\lambda _e)\) can always be chosen outside the image of the non top-dimensional cones, since these lie in proper subspaces of \(\prod _e Q_e^{\mathbb {R}}\). For a combinatorial type of top-dimension, as by assumption its dimension is equal to the dimension of \(\prod _e Q_e^{\mathbb {R}}\), if \(\mathrm {ev}^{(L_e)}\) is not injective, it is not surjective either, and its image is thus contained in a proper subspace. Finally, a choice of \((\lambda _e)\) outside the image of the non top-dimensional cones and the cones where \(\mathrm {ev}^{(L_e)}\) is not injective is called generic.
For such a choice of \((\lambda _e)\), there is a finite number of solutions, and the corresponding curves are trivalent since they belong to top dimensional cones of \({\mathcal {M}}_0(\Delta ,N_{\mathbb {R}})\). \(\square \)
Now, let \((\lambda _e)\) be chosen generically. We set
Notice that if the subspaces \({\mathcal {L}}_e\) are chosen generically, there is no curve with zero multiplicity that contributes to the sum, otherwise \(\mathrm {ev}^{(L_e)}\) is neither injective nor surjective on the cone corresponding to the combinatorial type of the curve, and thus \((\lambda _e)\) has been chosen away from its image.
Theorem 6.10
The value of \(N_\Delta ({\mathcal {L}}_e)\) only depends on the slopes \(L_e\) of the affine subspaces and not on the specific choice of the subspaces as long as it is generic.
This invariant is thus denoted by \(N_\Delta (L_e)\). Using Theorem 5.1 from [24], it coincides with the complex count.
Proof
As many proofs of tropical invariance, the proof goes by the study of local invariance at the walls of the tropical moduli space. The proof is similar to Proposition 4.4 in [9]. We proceed in two steps: first, we show that the sum of the determinants of the composed evaluation maps around a wall is zero, and then we show that the sign of these determinants characterizes the existence of solutions, thus proving the local invariance.
-
We consider the wall associated to a quadrivalent vertex in the tropical curve. Let the adjacent edges be denoted by the indices 1, 2, 3, 4. The three adjacent combinatorial types are determined by the splitting of the quadrivalent vertex into two trivalent vertices. These possibilities are denoted by 12//34, 13//24 and 14//23. The cone in the moduli space \({\mathcal {M}}_0(N_{\mathbb {R}},\Delta )\) corresponding to each combinatorial type is the quadrant of the vector space \(N_{\mathbb {R}}\times {\mathbb {R}}^{m-4}\times {\mathbb {R}}\), consisting of the points with positive coordinates on the \({\mathbb {R}}\) entries, where the \(N_{\mathbb {R}}\) factor corresponds to the vertex V adjacent to the edge 1, the \({\mathbb {R}}^{m-4}\) has canonical basis indexed by the edges of the curve with the quadrivalent vertex, which are common to all curves in the adjacent combinatorial types, and the \({\mathbb {R}}\) factor corresponds to the length of the edge resulting from the splitting of the quadrivalent vertex. Let \(v_j\) be a directing vector of the edge j, oriented outward the quadrivalent vertex. For each marked point or unbounded end i, associated to a constraint \(L_i\), let \(m_{i1},\dots ,m_{ir_i}\) be linear forms defining the sublattice \(L_i\): \(L_i=\bigcap _{j=1}^{r_i}\ker m_{ij}\). Then, for the combinatorial type 12//34, the matrix of the composed evaluation map \(\mathrm {ev}^{(L_e)}\) takes the following form:
$$\begin{aligned} \begin{array}{c|c|c|c|c|c|c|c} 12//34 &{} N_{\mathbb {R}}&{} {\mathbb {R}}^{m-8} &{} 1 &{} 2 &{} 3 &{} 4 &{} {\mathbb {R}}\\ \hline \text {behind }1 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} \langle m_{ij},v_1\rangle &{} 0 &{} 0 &{} 0 &{} 0 \\ \text {behind }2 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} 0 &{} \langle m_{ij},v_2\rangle &{} 0 &{} 0 &{} 0 \\ \text {behind }3 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} 0 &{} 0 &{} \langle m_{ij},v_3\rangle &{} 0 &{} \langle m_{ij},v_1+v_2\rangle \\ \text {behind }4 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} 0 &{} 0 &{} 0 &{} \langle m_{ij},v_4\rangle &{} \langle m_{ij},v_1+v_2\rangle \\ \end{array}. \end{aligned}$$The columns are separated according to the decomposition of the moduli space as \(N_{\mathbb {R}}\times {\mathbb {R}}^{m-4}\times {\mathbb {R}}\). Moreover, we separate the coordinates corresponding to the lengths of the edges 1, 2, 3, 4, assuming they are bounded edges. The rows are separated according to which of the four edges 1, 2, 3, 4 is on the shortest path between the vertex V and the unbounded end or marked point i. For each unbounded end or marked point i, we evaluate the linear forms \((m_{ij})_j\). For each edge e directed by v, the evaluation for the unbounded end or marked point i is \(\langle m_{ij},v\rangle \) if the edge e is part of the shortest path between V and unbounded end or marked point i, otherwise it is 0. This fact allows us to complete the middle entries of the matrix. The same rule apply for the entries of the last columns. The matrices for the combinatorial types 13//24 and 14//23 are respectively
$$\begin{aligned}&\begin{array}{c|c|c|c|c|c|c|c} 13//24 &{} N_{\mathbb {R}}&{} {\mathbb {R}}^{m-8} &{} 1 &{} 2 &{} 3 &{} 4 &{} {\mathbb {R}}\\ \hline \text {behind }1 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} \langle m_{ij},v_1\rangle &{} 0 &{} 0 &{} 0 &{} 0 \\ \text {behind }2 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} 0 &{} \langle m_{ij},v_2\rangle &{} 0 &{} 0 &{} \langle m_{ij},v_1+v_3\rangle \\ \text {behind }3 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} 0 &{} 0 &{} \langle m_{ij},v_3\rangle &{} 0 &{} 0 \\ \text {behind }4 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} 0 &{} 0 &{} 0 &{} \langle m_{ij},v_4\rangle &{} \langle m_{ij},v_1+v_3\rangle \\ \end{array},\\&\begin{array}{c|c|c|c|c|c|c|c} 14//23 &{} N_{\mathbb {R}}&{} {\mathbb {R}}^{m-8} &{} 1 &{} 2 &{} 3 &{} 4 &{} {\mathbb {R}}\\ \hline \text {behind }1 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} \langle m_{ij},v_1\rangle &{} 0 &{} 0 &{} 0 &{} 0 \\ \text {behind }2 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} 0 &{} \langle m_{ij},v_2\rangle &{} 0 &{} 0 &{} \langle m_{ij},v_1+v_4\rangle \\ \text {behind }3 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} 0 &{} 0 &{} \langle m_{ij},v_3\rangle &{} 0 &{} \langle m_{ij},v_1+v_4\rangle \\ \text {behind }4 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} 0 &{} 0 &{} 0 &{} \langle m_{ij},v_4\rangle &{} 0 \\ \end{array}. \end{aligned}$$We make the sum of the three determinants for the three adjacent combinatorial types, and use the linearity with respect to the last column, since all the other columns are equal. We get
$$\begin{aligned} \begin{array}{c|c|c|c|c|c|c|c} &{} N_{\mathbb {R}}&{} {\mathbb {R}}^{m-8} &{} 1 &{} 2 &{} 3 &{} 4 &{} {\mathbb {R}}\\ \hline \text {behind }1 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} \langle m_{ij},v_1\rangle &{} 0 &{} 0 &{} 0 &{} 0 \\ \text {behind }2 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} 0 &{} \langle m_{ij},v_2\rangle &{} 0 &{} 0 &{} \langle m_{ij},2v_1+v_3+v_4\rangle \\ \text {behind }3 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} 0 &{} 0 &{} \langle m_{ij},v_3\rangle &{} 0 &{} \langle m_{ij},2v_1+v_2+v_4\rangle \\ \text {behind }4 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} 0 &{} 0 &{} 0 &{} \langle m_{ij},v_4\rangle &{} \langle m_{ij},2v_1+v_2+v_3\rangle \\ \end{array}. \end{aligned}$$Using a combination of the columns corresponding to \(N_{\mathbb {R}}\) applied to \(v_1\), and the balancing condition \(v_1+v_2+v_3+v_4=0\), we get
$$\begin{aligned} \begin{array}{c|c|c|c|c|c|c|c} &{} N_{\mathbb {R}}&{} {\mathbb {R}}^{m-8} &{} 1 &{} 2 &{} 3 &{} 4 &{} {\mathbb {R}}\\ \hline \text {behind }1 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} \langle m_{ij},v_1\rangle &{} 0 &{} 0 &{} 0 &{} \langle m_{ij},v_1\rangle \\ \text {behind }2 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} 0 &{} \langle m_{ij},v_2\rangle &{} 0 &{} 0 &{} \langle m_{ij},v_2\rangle \\ \text {behind }3 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} 0 &{} 0 &{} \langle m_{ij},v_3\rangle &{} 0 &{} \langle m_{ij},v_3\rangle \\ \text {behind }4 &{} m_{ij} &{} 0 \text { or } \langle m_{ij},v\rangle &{} 0 &{} 0 &{} 0 &{} \langle m_{ij},v_4\rangle &{} \langle m_{ij},v_4\rangle \\ \end{array}. \end{aligned}$$Now, we see that the last column is the sum of the columns indexed 1, 2, 3, 4. Thus, the sum of the determinants is 0. If some of the edges 1, 2, 3, 4 was unbounded, the columns with the corresponding indices would not appear, but for the linear forms \(m_{ij}\) that would be evaluated on the corresponding unbounded end, one would already have \(\langle m_{ij},v_i\rangle =0\) and the result is unchanged. Finally, one has
$$\begin{aligned} \mathrm {det} A_{12//34}+\mathrm {det} A_{13//24}+\mathrm {det} A_{14//23}=0. \end{aligned}$$ -
We now use the previous statement to prove the invariance of the count. We denote by \({\mathcal {L}}\) the tuple \(({\mathcal {L}}_e)\). Let \({\mathcal {L}}(t)\) be a generic path between two generic configurations \({\mathcal {L}}(0)\) and \({\mathcal {L}}(1)\), i.e. a path in \(\prod _e Q_e^{\mathbb {R}}\). Outside a finite set of values of t, the configuration \({\mathcal {L}}(t)\) is generic and \(N_\Delta ({\mathcal {L}}(t))\) is given by a sum over some combinatorial types with non-zero multiplicity. More precisely, on each combinatorial type with non-zero multiplicity, the composed evaluation map \(\mathrm {ev}^{(L_e)}\) is a linear map associated with a matrix A. If the coordinates on the combinatorial type are denoted by (V, l), the equation can be formally solved: \((V,l)=A^{-1}{\mathcal {L}}\), and this provide a true solution of \(\mathrm {ev}^{(L_e)}(\Gamma ,h)={\mathcal {L}}\) if the coordinates of l are non-negative. As the multiplicity only depends on the combinatorial type, the value of \(N_\Delta ({\mathcal {L}}(t))\) is locally constant at generic \({\mathcal {L}}(t)\), thus, we only need to show invariance around the special values t where \({\mathcal {L}}(t)\) is not generic. Let \(t^*\) be such a value. At least one of the curves of \((\mathrm {ev}^{(L_e)})^{-1}(t^*)\) has a quadrivalent vertex, and it deforms into the adjacent combinatorial types when t moves slightly around \(t^*\). Let \(A_{12//34}\), \(A_{13//24}\) and \(A_{14//23}\) be the matrices of \(\mathrm {ev}^{(L_e)}\) on the three adjacent combinatorial types. On each combinatorial type, we can solve uniquely \(A_\star (V,l)={\mathcal {L}}(t)\): \((V,l)=A_\star ^{-1}\lambda (t)\), where \(\star \) is one of the three adjacent combinatorial types, and we get a true solution if all the coordinates of l are non-negative. This is the case for all the edges except the edge that appears with the splitting of the quadrivalent vertex. Using Cramer’s rule to solve \(A_\star (V,l)={\mathcal {L}}(t)\), the length of the new edge is equal to \(\frac{\mathrm {det}{\tilde{A}}_\star }{\mathrm {det} A_\star }\), where \({\tilde{A}}_\star \) is the matrix \(A_\star \) with the last column (the one that corresponds to the length of the new edge) being replaced with \({\mathcal {L}}\in \prod _i Q_e^{\mathbb {R}}\). As the matrices \(A_{12//34}\), \(A_{13//24}\) and \(A_{14//23}\) only differ in their last column, the numerators are all equal, and the sign of the length of the new edge is thus determined by the sign of \(\mathrm {det} A_\star \). Finally, the sign of the determinant determines which combinatorial type provide a true solution, and the local invariance follows from the relation
$$\begin{aligned} \mathrm {det} A_{12//34}+\mathrm {det} A_{13//24}+\mathrm {det} A_{14//23}=0. \end{aligned}$$
\(\square \)
Remark 6.11
The invariance also follows from general results of tropical intersection theory [1]. Had we worked with more general tropical cycles \(\Xi _e\), the proof with intersection theory would also work, but in that case, we would have more walls to study. These walls correspond to the cases where the parametrized tropical curves do not intersect the cycles \(\Xi _e\) in their top-dimensional faces. The invariance would then result from the balancing condition for the cycles \(\Xi _e\). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Blomme, T. Refined count for rational tropical curves in arbitrary dimension. Math. Ann. 382, 1199–1244 (2022). https://doi.org/10.1007/s00208-021-02287-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-021-02287-3