Higher connectivity of tropicalizations

Abstract

We show that the tropicalization of an irreducible d-dimensional variety over a field of characteristic 0 is $(d-\ell )$-connected through codimension one, where $\ell$ is the dimension of the lineality space of the tropicalization. From this we obtain a higher connectivity result for skeleta of rational polytopes. We also prove a tropical analogue of the Bertini Theorem: the intersection of the tropicalization of an irreducible variety with a generic hyperplane is again the tropicalization of an irreducible variety.

1 Introduction

The tropicalization of a d-dimensional irreducible subvariety of the algebraic torus $(K^*)^n$, where K is a field, is the support of a pure, d-dimensional polyhedral complex in $\mathbb R^n$. Being pure means that all inclusion-maximal faces have the same dimension. The facets and ridges of a pure, d-dimensional polyhedral complex are the faces of dimensions d and $d-1$ respectively. A fundamental result in tropical geometry is that the tropicalization of an irreducible variety is connected through codimension one: given any two facets there is a path between them that goes through facets and ridges only [6, 7, 15, Theorem 3.5.1].

In this paper we show the stronger result that the tropicalization of an irreducible variety remains connected through codimension one even after we remove some closed facets. A pure polyhedral complex is k-connected through codimension one if removing any $k-1$ closed facets leaves it connected through codimension one. In other words, the facet-ridge incidence hypergraph, whose vertices are facets of the polyhedral complex and whose hyperedges are the ridges, remains connected after any $k-1$ vertices and their incident hyperedges are removed. A hypergraph is connected if there is a path from any vertex to any other vertex where each step connects two vertices in the same hyperedge.

Theorem 1

Let K be a field of characteristic 0 that is either algebraically closed, complete, or real closed with convex valuation ring. Let X be a d-dimensional irreducible subvariety of $(K^*)^n$. Let $\Sigma$ be a pure d-dimensional rational polyhedral complex with support $|\Sigma |={{\,\textrm{trop}\,}}(X)$. Write $\ell$ for the dimension of the lineality space of $\Sigma$. Then $\Sigma$ is $(d-\ell )$-connected through codimension one. In other words, its facet-ridge hypergraph is $(d-\ell )$-connected.

The hypotheses on the field, except for the characteristic assumption, come from the case $d=1$, which is [7, Theorem 1]. The characteristic assumption comes from the toric Bertini theorem. The lineality space depends on the choice of polyhedral complex structure $\Sigma$ on the tropical variety, as does the facet-ridge hypergraph. However the result holds for any choice of polyhedral structure, whether or not the lineality space is the largest possible one; see Example 4.

This result is sharp. In a d-dimensional polyhedral fan with $\ell$-dimensional lineality space, a simplicial facet has $d-\ell$ ridges as its boundary, so we can remove $d-\ell$ neighboring facets to isolate the simplicial facet.

Theorem 1 can be considered a generalization of Balinski’s Theorem, which says that the edge graph of a d-dimensional polytope is d-connected [4]. Any complete fan is the tropicalization of the algebraic torus $(K^*)^n$, which is irreducible. If $\Sigma$ is the (complete) normal fan of a full dimensional polytope P in $\mathbb R^d$, then, since Theorem 1 holds for any such fan $\Sigma$, it can be translated as: removing $d-1$ vertices and their incident edges from the edge graph of the polytope P does not disconnect this graph. This is precisely Balinski’s Theorem.

A new polyhedral consequence of Theorem 1 is the following necessary condition for a k-dimensional rational fan in ${\mathbb {R}}^n$ to be the k-skeleton of the normal fan of a polytope.

Corollary 2

The k-dimensional skeleton of the normal fan of a rational full-dimensional polytope is k-connected through codimension one.

Proof

The k-skeleton of the normal fan of a rational full-dimensional polytope $P \subset {\mathbb {R}}^n$ is the tropicalization of an irreducible variety, as it is the tropicalization of any sufficiently general complete intersection of $n-k$ polynomials with Newton polytope P [15, Corollary 4.6.11], [23]. $\square$

When the incidence hypergraph is replaced by the graph in which each hyperedge is replaced by the clique joining the vertices of the hyperedge, even higher connectivity holds [3, 20]. However, as noted above, the hypergraph version of the statement cannot be strengthened.

The connectedness result also gives a new obstruction for the realizability of a polyhedral complex as the tropicalization of an irreducible variety, as we will now demonstrate with a simple example.

Example 3

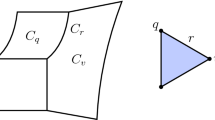
Consider the two-dimensional fan in $\mathbb R^5$ that is the union of two standard tropical planes living in ${{\,\textrm{span}\,}}\{{\textbf {e}}_1,{\textbf {e}}_2,{\textbf {e}}_3\}$ and ${{\,\textrm{span}\,}}\{{\textbf {e}}_1,{\textbf {e}}_4,{\textbf {e}}_5\}$ respectively, meeting along the ray spanned by ${\textbf {e}}_1$, where ${\textbf {e}}_1,\dots ,{\textbf {e}}_5$ is the standard basis for ${\mathbb {R}}^5$. See Figure 1. Each node in the figure represents a ray and each edge represents a two-dimensional cone of the fan. The ray spanned by ${\textbf {e}}_1$ is the only intersection of these two tropical planes. Removing a closed maximal cone containing ${\textbf {e}}_1$ disconnects the fan, so the fan is not 2-connected. It is therefore not the tropicalization of an irreducible variety over characteristic 0.

Fig. 1

The two-dimensional tropical variety from Example 3 depicted here is not 2-connected since removing any facet containing $e_1$ disconnects it. So it is not the tropicalization of an irreducible variety

The connectivity depends on the choice of polyhedral structure, and in particular on the choice of lineality space.

Example 4

Let X be the subvariety of $(K^*)^3$ defined by $x_1+x_2+1=0$. The tropicalization ${{\,\textrm{trop}\,}}(X)$ is the support of the two-dimensional fan with lineality space ${{\,\textrm{span}\,}}({\textbf {e}}_3)$, and three cones generated by ${\textbf {e}}_1$, ${\textbf {e}}_2$, and $-{\textbf {e}}_1-{\textbf {e}}_2$ in addition to the lineality space. With that choice of polyhedral complex, the facet-ridge hypergraph has three vertices and one hyperedge containing all vertices, which is connected but not 2-connected. An alternate polyhedral structure is given by subdividing each cone using the hyperplane $x_3=0$, to obtain a fan with trivial lineality space and six maximal cones: ${{\,\textrm{pos}\,}}({\textbf {e}}_1,{\textbf {e}}_3), {{\,\textrm{pos}\,}}({\textbf {e}}_1,-{\textbf {e}}_3), {{\,\textrm{pos}\,}}({\textbf {e}}_2,{\textbf {e}}_3), {{\,\textrm{pos}\,}}({\textbf {e}}_2,-{\textbf {e}}_3)$, ${{\,\textrm{pos}\,}}(-{\textbf {e}}_1-{\textbf {e}}_2,{\textbf {e}}_3),$ and ${{\,\textrm{pos}\,}}(-{\textbf {e}}_1-{\textbf {e}}_2,-{\textbf {e}}_3)$. The facet-ridge hypergraph now has six vertices, two hyperedges with three vertices each, and three hyperedges with two vertices each. This is 2-connected.

The fact that tropicalizations of irreducible varieties are connected through codimension one plays a crucial role in algorithms to compute tropical varieties, as implemented in [12], following algorithms originally outlined in [6]. It would be interesting to exploit this higher connectivity algorithmically. As the space of phylogenetic trees can be realized as the tropicalization of an irreducible variety (the complement of the type-A hyperplane arrangement) [2], it would be interesting to explore this connection. It would also be interesting to understand the extent to which d-connectivity is a combinatorial notion. In that direction, in Proposition 14 we show that the fine fan structure on the Bergman fan of a matroid of rank $d+1$ is d-connected. Such Bergman fans play the role of building blocks for abstract tropical varieties.

The proof of Theorem 1 involves aspects of both algebraic and polyhedral geometry. In Sect. 2 we prove the following tropical version of Bertini’s Theorem.

Theorem 5

(Tropical Bertini Theorem). Let $X \subseteq (K^*)^n$ be an irreducible d-dimensional variety, with $d \ge 2$, over an algebraically closed valued field K of characteristic 0 with ${\mathbb {Q}}$ contained in the value group. The space of rational affine hyperplanes in ${\mathbb {R}}^n$ can be identified with $\mathbb P^{n}_{{\mathbb {Q}}}$. The set of hyperplanes H for which the intersection ${{\,\textrm{trop}\,}}(X) \cap H$ is the tropicalization of an irreducible variety is dense in the Euclidean topology on ${\mathbb {P}}^n_{{\mathbb {Q}}}$.

This gives an affirmative answer to Question 9 of [7] in characteristic zero, which asks, for an irreducible variety X, whether there always exists an affine hyperplane whose intersection with ${{\,\textrm{trop}\,}}(X)$ is proper and connected through codimension one.

In Sect. 3 we prove the connectivity theorem using the tropical Bertini theorem and induction on dimension. Proposition 14 on Bergman fans is proved in Sect. 4, and we state some open problems in Sect. 5.

After this paper was posted on the ArXiv, [11] gave a purely combinatorial proof of Corollary 2, removing the rationality assumption, and [10] removed the characteristic p assumption from the tropical Bertini theorem, and thus, by Remark 11, from Theorem 1.

2 Proof of the tropical Bertini theorem

Let K be a (possibly trivially) valued field. The tropicalization of a variety $X \subset (K^*)^n$ is the set ${{\,\textrm{trop}\,}}(X) = \overline{{{\,\textrm{val}\,}}(X(L))} \subseteq {\mathbb {R}}^n$, where L is any nontrivially valued algebraically closed field extension of K, and the closure is taken in the Euclidean topology. For example, the tropicalization of a subtorus of $(K^*)^n$ is a usual linear subspace of $\mathbb R^n$ defined over $\mathbb Q$. Taking field extensions does not change the tropicalization.

The Tropical Bertini Theorem (Theorem 5) says that most intersections of the tropicalization of an irreducible variety and a hyperplane are again the tropicalization of an irreducible variety.

Example 6

Let $X = V \left( x_1-x_2^2x_3^2 \right) \subseteq \mathbb (K^*)^3$. The intersection of X with the subtorus defined by $x_1^{a_1} x_2^{2a_2} x_3^{2 a_3} = 1$ is not irreducible for any tuple of integers $(a_1,a_2,a_3) \notin \mathbb Z(1,-1,-1)$, so it is not the case that the intersection of X with a “generic” subtorus is irreducible. However the tropicalization of the statement is true.

Remark 7

If a polyhedral complex is the tropicalization of an irreducible variety, then so is its image under any invertible linear transformation over $\mathbb Q$. To see this, first note that for any nonzero rational number r, the scaling $r \cdot {{\,\textrm{trop}\,}}(X)$ is achieved by scaling the valuation of the coefficient field. This means that we may scale the image to assume that the linear transformation is given by an integer matrix. Changing basis over $\mathbb Z$ for the source or target corresponds to an automorphism of the respective torus, so we only need to consider diagonal linear transformations. Finally, note that if $X \subset (K^*)^n$ is irreducible, so is its image under the map $(x_1,\dots ,x_n) \mapsto (x_1^{c_1},x_2^{c_2}, \dots , x_n^{c_n})$ for any integers $c_1,\dots ,c_n$.

The key idea for the proof of Theorem 5 is the following subtorus analogue of Bertini’s Theorem due to [9, 24]. We also make crucial use of some modifications due to [1]. Following [1] we will say that a map $\pi : X \rightarrow (K^*)^d$ satisfies the property PB (pullback) if the pullback $\lambda ^*X := X \times _{(K^*)^d} (K^*)^d$ of X along $\pi$ and $\lambda$ is irreducible for every isogeny $\lambda$ of $(K^*)^d$. An isogeny of $(K^*)^d$ is a surjective group homomorphism with finite kernel, so can be represented by a $d \times d$ rank d matrix with integer entries.

Theorem 8

(Toric Bertini Theorem. Fuchs, Mantova, Zannier, Theorem 1.5 of [9]). Let X be an irreducible quasiprojective variety of dimension d over an algebraically closed field of characteristic zero, and let $\pi : X \rightarrow (K^*)^d$ be a dominant map that is finite onto its image, satisfying property PB. Then there is a finite union ${\mathcal {E}}$ of proper subtori of $(K^*)^d$ such that, for every subtorus $T \subset (K^*)^d$ not contained in ${\mathcal {E}}$ and every point $p \in (K^*)^d$, the preimage $\pi ^{-1}(p \cdot T)$ is an irreducible subvariety of X.

We also make use of the following lemma, which is a special case of [18, Proposition 4].

Lemma 9

Let X be a d-dimensional subvariety of $(K^*)^n$, and let $\pi : (K^*)^n \rightarrow (K^*)^d$ be a morphism. If the linear map ${{\,\textrm{trop}\,}}(\pi ) :{\mathbb {R}}^n \rightarrow {\mathbb {R}}^d$ is injective on every maximal face of ${{\,\textrm{trop}\,}}(X)$, then the restriction $\pi |_X :X \rightarrow (K^*)^d$ is a finite morphism.

Proof of Lemma 9

The tropicalization ${{\,\textrm{trop}\,}}(X)_{\textrm {triv}}$ of X with respect to the trivial valuation is the recession fan of ${{\,\textrm{trop}\,}}(X)$, so the hypothesis that ${{\,\textrm{trop}\,}}(\pi )$ is injective on every maximal face of ${{\,\textrm{trop}\,}}(X)$ implies that the same is true for ${{\,\textrm{trop}\,}}(X)_{\textrm {triv}}$. When K is given the trivial valuation, the “tilted group ring” $R[M]^{\textbf {0}}$ of [17, §2.4] is just the Laurent polynomial ring K[M], so for $v = {\textbf {0}}$, the scheme $T'_{\phi (v)}$ of [18, Proposition 4] is $(K^*)^d$. The preimage of ${\textbf {0}} \in {\mathbb {R}}^d$ under the map ${{\,\textrm{trop}\,}}(X)_{\textrm {triv}} \rightarrow {\mathbb {R}}^d$ is just ${\textbf {0}}$, so the scheme ${\mathcal {X}}_{{\textbf {0}}}$ of [18] is just X. Proposition 4 of [18] then states that the morphism ${\mathcal {X}}_{{\textbf {0}}} \rightarrow (K^*)^d$ is finite, which proves the lemma. $\square$

Proof of Theorem 5

Fix a rational polyhedral complex $\Sigma$ with support ${{\,\textrm{trop}\,}}(X)$. Choose a linear map $P :{\mathbb {R}}^n \rightarrow {\mathbb {R}}^d$, given by a $d \times n$ integer matrix, that is injective on every maximal face of ${{\,\textrm{trop}\,}}(X)$. The kernel of such a map is an $(n-d)$-dimensional subspace of ${\mathbb {Q}}^n$, and the set of such subspaces is dense in the analytic topology on the Grassmannian ${{\,\textrm{Gr}\,}}(n-d,n)$. We will show that there is a dense open set in the space of rational affine hyperplanes ${\overline{H}}$ in ${\mathbb {R}}^d$ for which $P^{-1}({\overline{H}}) \cap {{\,\textrm{trop}\,}}(X)$ is the tropicalization of an irreducible variety. The set of $H = P^{-1}({\overline{H}})$ for all such P is dense in $\mathbb P^{n}_{{\mathbb {Q}}}$, proving the Theorem.

Let $\pi : (K^*)^n \rightarrow (K^*)^d$ be the morphism of tori corresponding to P. By Remark 7 we can change coordinates to assume that the linear map $P : \mathbb R^n \rightarrow \mathbb R^d$ is the coordinate projection onto the first d coordinates. Thus $\pi$ is also a coordinate projection from $(K^*)^n$ onto the first d coordinates. By Lemma 9 the morphism $\pi |_X$ is finite.

In order to apply Theorem 8, we would like $\pi |_X$ to have property PB. If $\pi |_X$ does not have property PB, then there is an isogeny $\mu : (K^*)^d \rightarrow (K^*)^d$ such that $\mu ^* X$ is not irreducible. Let $I \subseteq K \left[ x_1^{\pm 1},\dots ,x_n^{\pm 1}\right]$ be the ideal of X, and let $\mu$ be given by

$$\begin{aligned}\mu ^* :K \left[ z_1^{\pm 1},\dots ,z_d^{\pm 1}\right] \rightarrow K \left[ z_1^{\pm 1},\dots ,z_d^{\pm 1}\right] \text { with }\mu ^{*}(z_i) = z^{\alpha _i}.\end{aligned}$$

Since $\pi$ is assumed to be the projection onto the first d coordinates, the coordinate ring of the pullback $\mu ^* X$ is

$$\begin{aligned}K \left[ x_1^{\pm 1},\dots ,x_n^{\pm 1},z_1^{\pm 1},\dots ,z_d^{\pm 1}\right] / (I + \langle x_i - z^{\alpha _i} : 1 \le i \le d \rangle ).\end{aligned}$$

This is isomorphic to

$$\begin{aligned} K \left[ x_{d+1}^{\pm 1},\ldots ,x_n^{\pm 1},z_1^{\pm 1},\ldots ,z_d^{\pm 1}\right] /J\end{aligned}$$

where J is obtained from I by substituting $z^{\alpha }_i$ for $x_i$ for $i=1,\dots ,d$. Write $\rho :(K^*)^n \rightarrow (K^*)^d$ for the map corresponding to the inclusion $K \left[ z_1^{\pm 1},\ldots ,z_d^{\pm 1}\right] \rightarrow K \left[ x_{d+1}^{\pm 1},\ldots ,x_n^{\pm 1},z_1^{\pm 1},\ldots ,z_d^{\pm 1} \right]$.

Write Z for the reduced structure on $\mu ^*X$, which is described by the radical of the ideal J. We have the following diagram:

(1)

The components of Z have dimension at least $\dim (X)$, by the Principal Ideal Theorem (see for example [8, Theorem 10.2]). Since the pullback $\mu ' :\mu ^*X \rightarrow X$ of the finite morphism $\mu$ is finite, this morphism is also proper, so the image of every irreducible component is closed. As X is irreducible, there must thus be a component Y that maps surjectively to X.

The group $\ker (\mu )$ acts on Z via $(t,x) \mapsto (\zeta \cdot t, x)$ for $\zeta \in \ker (\mu )$. This group acts transitively on the fibers of $\mu$, so the orbit of Y is all of Z. We also have that Y is not fixed by this action, as otherwise it would be the reduced structure on the only irreducible component of $\mu ^*X$, contradicting the assumption that $\mu ^*X$ is reducible. This means that the map $\mu '|_Y$ has degree less than $\deg (\mu )$.

If $\mu$ is chosen so that $\rho |_Y$ has minimal degree, then $\rho |_Y$ must have property PB. Otherwise we can repeat the above argument with Y and $\rho$ in the place of X and $\pi$ to further reduce the degree since

$$\begin{aligned} \deg (\rho |_Y) = \deg (\rho |_Y)\deg (\mu )/\deg (\mu ) = \deg (\pi |_X) \deg (\mu '|_Y)/\deg (\mu ) < \deg (\pi |_X).\end{aligned}$$

The isogeny $\mu : (K^*)^d \rightarrow (K^*)^d$ has a natural tropicalization ${{\,\textrm{trop}\,}}(\mu ) : \mathbb R^d \rightarrow \mathbb R^d$ such that ${{\,\textrm{trop}\,}}\circ \mu = {{\,\textrm{trop}\,}}(\mu ) \circ {{\,\textrm{trop}\,}}$ as maps from $(K^*)^d$ to $\mathbb R^d$. Then Diagram (1) tropicalizes as

(2)

where ${{\,\textrm{trop}\,}}(\mu ')$ maps ${{\,\textrm{trop}\,}}(Y)$ to ${{\,\textrm{trop}\,}}(X)$.

Since ${{\,\textrm{trop}\,}}(\mu )$ and ${{\,\textrm{trop}\,}}(\mu ')$ are invertible linear maps, the assumption that P is injective on every maximal face of ${{\,\textrm{trop}\,}}(X)$ implies that ${{\,\textrm{trop}\,}}(\rho )$ is also injective on every maximal face of ${{\,\textrm{trop}\,}}(Y)$. Therefore $\rho |_Y$ is a finite morphism by Lemma 9. We can now apply Theorem 8 to $\rho |_Y :Y \rightarrow (K^*)^d$. Let ${\mathcal {E}}$ be the exceptional set in the theorem, which is a union of finitely many proper subtori. Then ${{\,\textrm{trop}\,}}({\mathcal {E}})$ is the union of finitely many proper linear subspaces of ${\mathbb {R}}^d$. The affine rational hyperplanes that are not parallel to any subspace in ${{\,\textrm{trop}\,}}({\mathcal {E}})$ form a dense open subset of ${\mathbb {P}}^d_\mathbb Q$. Let ${\overline{H}}$ be one such generic hyperplane. Let $T \subseteq (K^*)^d$ be the torus such that ${{\,\textrm{trop}\,}}(T)$ is a hyperplane parallel to ${\overline{H}}$. For any $s \in (K^*)^d$ with ${{\,\textrm{val}\,}}(s) \in {\overline{H}}$, we have ${{\,\textrm{trop}\,}}(s \cdot T) = {\overline{H}}$. By Theorem 8, $\rho |_Y^{-1}(s \cdot T) \subset Y$ is irreducible.

Let H be the hyperplane in $\mathbb R^n$ defined by $H := ({{\,\textrm{trop}\,}}\rho )^{-1}({\overline{H}})$. Since $\rho$ is a monomial map from $(K^*)^n \rightarrow (K^*)^d$, we have $H = {{\,\textrm{trop}\,}}(\rho ^{-1}(s \cdot T))$. The intersection $H \cap {{\,\textrm{trop}\,}}(Y)$ is transverse because ${{\,\textrm{trop}\,}}(\rho )$ is injective on every maximal face of ${{\,\textrm{trop}\,}}(Y)$. Thus the Transverse Intersection Lemma [16, Theorem 1.1], [6, Lemma 15], [15, Theorem 3.4.12] implies that

$$\begin{aligned}H \cap {{\,\textrm{trop}\,}}(Y) = {{\,\textrm{trop}\,}}(\rho ^{-1}(s \cdot T) \cap Y) = {{\,\textrm{trop}\,}}(\rho |_Y^{-1}(s \cdot T)) .\end{aligned}$$

Thus $H \cap {{\,\textrm{trop}\,}}(Y)$ is the tropicalization of the irreducible variety $\rho |_Y^{-1}(s \cdot T)$. It follows from Remark 7 that the same is true for ${{\,\textrm{trop}\,}}(\mu ')(H) \cap \Sigma = {{\,\textrm{trop}\,}}(\pi )^{-1}({{\,\textrm{trop}\,}}(\mu )({\overline{H}}))$. As the set of ${{\,\textrm{trop}\,}}(\mu )({\overline{H}})$ where ${\overline{H}}$ is not parallel to any subspace in ${{\,\textrm{trop}\,}}({\mathcal {E}})$ is dense and open in ${\mathbb {P}}^d_{{\mathbb {Q}}}$, the result follows. $\square$

Example 10

We illustrate the key constructions of the proof on the variety from Example 6: $X = V \left( x_1-x_2^2x_3^2 \right) \subseteq \mathbb (K^*)^3$. The tropicalization is ${{\,\textrm{trop}\,}}(X) = \{{\textbf {w}} \in {\mathbb {R}}^3 : w_1 =2w_2+2w_3 \}$. The projection of ${{\,\textrm{trop}\,}}(X)$ to the first two coordinates is a bijection, so the tropicalization of the projection $\pi :\mathbb (K^*)^3 \rightarrow \mathbb (K^*)^2, (x_1,x_2,x_3) \mapsto (x_1, x_2)$ satisfies the condition of the first paragraph of the proof.

Consider the isogeny $\mu : (K^*)^2 \rightarrow (K^*)^2$ given by $\mu (z_1,z_2) = \left( z_1^4,z_2 \right)$. The coordinate ring of the pullback $\mu ^* X$ is

$$\begin{aligned}&K \left[ x_1^{\pm 1},x_2^{\pm 1},x_3^{\pm 1},z_1^{\pm 1},z_2^{\pm 2}\right] /\langle x_1-x_2^2x_3^2, x_1-z_1^4,x_2-z_2 \rangle \\&\quad \cong K \left[ x_3^{\pm 1},z_1^{\pm 1},z_2^{\pm 1}\right] /\langle z_1^4-z_2^2x_3^2 \rangle ,\end{aligned}$$

so the ideal J of the proof is $\langle z_1^4-z_2^2x_3^2 \rangle \subseteq K \left[ z_1^{\pm 1},z_2^{\pm 1},x_3^{\pm 1}\right]$. Note that V(J) is not irreducible, so $\pi$ does not have property PB. It is, however, radical, so defines the subscheme Z. The map $\mu ' :Z \rightarrow X$ given by $\mu ' :(z_1,z_2,x_3) \mapsto \left( z_1^4,z_2,x_3 \right)$ has degree 4.

One component of Z is given by $Y = V \left( z_1^2-z_2x_3 \right)$. This maps surjectively to X via the map $\mu '$, and $\mu '|_Y$ has degree 2. The kernel of $\mu$ is the multiplicative abelian group $\{(1,1),(-1,1),(i,1),(-i,1)\}$.

We now check that the projection of Y onto the first two coordinates has property PB. For every isogeny $\lambda$ on $(K^*)^2$, given by $\lambda (t_1, t_2)= \left( t_1^{a_1} t_2^{a_2}, t_1^{b_1}t_2^{b_2} \right)$, the coordinate ring of the pullback $\lambda ^* Y$ is

$$\begin{aligned}&K \left[ z_1^{\pm 1}, z_2^{\pm 1}, x_3^{\pm 1}, t_1^{\pm 1}, t_2^{\pm 1}\right] / \langle z_1^2 - z_2 x_3, z_1 - t_1^{a_1} t_2^{a_2}, z_2 - t_1^{b_1}t_2^{b_2} \rangle \\&\quad \cong K \left[ x_3^{\pm 1}, t_1^{\pm 1}, t_2^{\pm 1}\right] / \langle t_1^{2a_1} t_2^{2a_2} - t_1^{b_1}t_2^{b_2} x_3 \rangle \end{aligned}$$

The binomial $t_1^{2a_1} t_2^{2a_2} - t_1^{b_1}t_2^{b_2} x_3$ is irreducible in the Laurent polynomial ring, so the pullback is irreducible.

Remark 11

The results in the paper [9] are stated over ${\mathbb {C}}$. The proofs there rely on resolution of singularities and on some facts from Galois theory that are simpler in characteristic zero, but all go through in the case that the field is algebraically closed of characteristic zero. The Tropical Bertini Theorem (Theorem 5) is the only place where the characteristic zero assumption is used in the proof of the higher connectivity result in Theorem 1.

3 Proof of the connectivity theorem

We now prove the main result of this paper: Theorem 1.

Let X be a d-dimensional irreducible subvariety of $(K^*)^n$, where K is a field of characteristic zero that is either algebraically closed, complete, or real closed with convex valuation ring. Fix a polyhedral complex $\Sigma$ with support $|\Sigma |$ equal to ${{\,\textrm{trop}\,}}(X)$, such that the normal fan of every facet of $\Sigma$ is a rational polyhedral fan.

Suppose $\Sigma$ has an $\ell$-dimensional lineality space V. The rationality assumption implies that V is a rational subspace of ${\mathbb {R}}^n$, so it determines an $\ell$-dimensional subtorus $T'$ of $(K^*)^n$, with ${{\,\textrm{trop}\,}}(T')=V$. We claim that $T'$ acts on X. If $T'$ did not act on X, then the orbit of X under $T'$ would have dimension greater than d, and its tropicalization would also have dimension greater than d. On the other hand, the tropicalization of this orbit is $\Sigma + V = \Sigma$, which has dimension d. Therefore $T'$ must act on X. Since the action of $T'$ on $(K^*)^n$ is free, the restriction to X is also free. Let ${\widetilde{X}} = X/T' \subseteq (K^*)^n/T' \cong (K^*)^{n-\ell }$ be the quotient. Then ${\widetilde{X}}$ is irreducible of dimension $d-\ell$, ${{\,\textrm{trop}\,}}({\widetilde{X}})= \Sigma /V$ is the quotient of ${{\,\textrm{trop}\,}}(X)$ by its lineality space, and $\Sigma$ and $\Sigma /V$ have the same connectivity. Therefore we may reduce to the case when the lineality space is trivial and $\ell =0$. Since ${{\,\textrm{trop}\,}}(X)$ is connected, the triviality of the lineality space implies that every face of ${{\,\textrm{trop}\,}}(X)$ is pointed, meaning that it does not contain an affine line.

By [7, Proposition 4] we may replace the field K by its algebraic closure, and X by any irreducible component of the extension $X_{{\overline{K}}}$ without changing the tropicalization. We henceforth assume that K is algebraically closed, and X is geometrically irreducible. We may thus pass to a further field extension if necessary to assume that the valuation on K is nontrivial, and ${\mathbb {Q}}$ is contained in the value group.

We may also assume that ${{\,\textrm{trop}\,}}(X)$ does not live in any proper subspace in ${\mathbb {R}}^n$. Otherwise X lives in a translate of a subtorus of $(K^*)^n$ by [13, Corollary 14], and the result for the translate of X in the subtorus implies the result for X.

We will first prove the result when the tropical variety is all of $\mathbb R^d$, with an arbitrary polyhedral complex structure but trivial lineality space. It suffices to show that for any $d \ge 1$ removing $d-1$ closed pointed convex sets $C_1,\dots ,C_{d-1}$ from $\mathbb R^d$ does not disconnect $\mathbb R^d$. Indeed, in our context this would imply that there was a path between any two points in the interior of facets. If this path passed through a codimension two cell, none of the neighborhood of this cell would have been removed, so we can deform the path to only pass through facets and codimension-one cells.

To show connectedness, identify $\mathbb R^d$ with the hyperplane defined by $x_1 = 1$ in $\mathbb R^{d+1}$. Let $S^d$ be a sphere around the origin in $\mathbb R^{d+1}$. Let $\widetilde{C_i}$ be the closure of $\textrm {cone}(\{1\} \times C_i) \cap S^d$, and let $H = \{x \in S^d \mid x_1 \le 0\}$ be the lower hemisphere. Then $S^d {\setminus } (H \cup \widetilde{C_1} \cup \cdots \cup \widetilde{C_{d-1}})$ is homeomorphic to $\mathbb R^d {\setminus } (C_1\cup \cdots \cup C_{d-1})$.

By Alexander duality, $S^d {\setminus } (H \cup \widetilde{C_1} \cup \cdots \cup \widetilde{C_{d-1}})$ is connected if and only if $H \cup \widetilde{C_1} \cup \cdots \cup \widetilde{C_{d-1}}$ does not have homology in dimension $d-1$. Since the $C_i$s are pointed and convex, the intersection of any collection of $\widetilde{C_i}$s is contractible. The intersection of any of them with the lower hemisphere is also contractible. By the Nerve Theorem for regular cell complexes [5, Theorem 10.6] the union $H \cup \widetilde{C_1} \cup \cdots \cup \widetilde{C_{d-1}}$ has the same homology as its nerve complex. But the nerve complex is a simplicial complex on d vertices, so it cannot have homology in dimension $d-1$. This completes the proof when the tropical variety is all of $\mathbb R^n$.

We assume from now on that $|\Sigma | \ne \mathbb R^n$. We proceed by induction on the dimension d of $\Sigma$. The base case $d=1$ is the statement that the tropicalization of an irreducible curve is connected (see [7] or [15, Proposition 6.6.22]); this result does not depend on the choice of polyhedral complex structure on ${{\,\textrm{trop}\,}}(X)$. The hypothesis on the field K is used here.

Now let $d \ge 2$ and assume that the assertion in the theorem is true for smaller dimensions. Let ${\mathcal {G}}$ be any collection of $d-1$ facets of $\Sigma$. For any two facets P, Q of $\Sigma {\setminus } \mathcal G$ we need to show that after removing the closed facets in ${\mathcal {G}}$, there is still a path from P and Q through ridges and facets only.

Let F be any facet in $\mathcal G$. We define an equivalence relation $\sim _F$ on the facets of $\Sigma {\setminus } F$ as the transitive closure of the following relation: $P \sim _F Q$ if there exists a hyperplane H with $H \cap F = \varnothing$, which meets both P and Q in their relative interior.

The theorem then follows from the following two claims.

Claim 12

For facets P, Q of $\Sigma$ which are not in $\mathcal G$, if $P \sim _F Q$, then there is a facet-ridge path between P and Q that avoids $\mathcal G$.

Claim 13

The equivalence relation $\sim _F$ has only one equivalence class. $\square$

Proof of Claim 12

Suppose that $P \sim _F Q$. We first observe that there is a rational hyperplane H such that

• (a) H does not meet F but meets the relative interiors of both P and Q,

• (b) H does not contain any vertex of $\Sigma$, and

• (c) $H \cap \Sigma$ is the tropicalization of an irreducible variety.

The assumption that $P \sim _F Q$ implies the existence of some hyperplane H not intersecting F but meeting the relative interiors of P and Q. Since $\dim (\Sigma )\ge 2$, H can be perturbed to be rational, and satisfy (a) and (b). Moreover further small perturbation will preserve (a) and (b). By Theorem 5 the hyperplanes satisfying (c) are dense in ${\mathbb {P}}^{n}_{{\mathbb {Q}}}$. Thus there exists a rational hyperplane H satisfying (a),(b), and (c).

Let Z be an irreducible variety such that ${{\,\textrm{trop}\,}}(Z) = H \cap \Sigma$. By induction on dimension, ${{\,\textrm{trop}\,}}(Z)$ is $(d-1)$-connected through codimension one. The condition (b) above implies that every facet of ${{\,\textrm{trop}\,}}(Z)$ is the intersection of a facet of $\Sigma$ with H, and every ridge of ${{\,\textrm{trop}\,}}(Z)$ is the intersection of a ridge of $\Sigma$ with H. This gives a natural inclusion of the facet-ridge hypergraph of ${{\,\textrm{trop}\,}}(Z)$ into the facet-ridge hypergraph G of $\Sigma$. By construction the resulting sub-hypergraph $G'$ of G contains the vertices corresponding to P and Q, but not the vertex corresponding to F or any of its incident hyperedges. While $G'$ may contain some of the vertices corresponding to ${\mathcal {G}} {\setminus } \{F\}$, since $G'$ is $(d-1)$-connected, $G'$ with ${\mathcal {G}} {\setminus } \{F\}$ and their incident hyperedges removed is still connected, so there is a path between the vertices corresponding to P and Q. There is thus a path between P and Q in G not passing through the vertices corresponding to any element of ${\mathcal {G}}$. $\square$

Proof of Claim 13

Let $P^\circ$ denote the relative interior of P. For any two facets P, Q of $\Sigma {\setminus } {\mathcal {G}}$, we claim that if there is a line L which intersects $P^\circ$ and $Q^\circ$ but does not intersect F, then $P \sim _F Q$. To see this, take a linear projection onto $\mathbb R^{n-1}$ such that the image of the line L is a point ${\overline{L}}$ and the image of F is a convex polyhedron ${\overline{F}}$. Since L does not meet F, we have ${\overline{L}} \notin {\overline{F}}$. Let ${\overline{V}}$ be a hyperplane through ${\overline{L}}$ which does not meet ${\overline{F}}$. The preimage of ${\overline{V}}$ in $\mathbb R^n$ is the desired hyperplane through $P^\circ$ and $Q^\circ$ which does not meet F. Thus $P \sim _F Q$.

Recall that we are assuming that $\Sigma$ is not full dimensional. Fix $F \in {\mathcal {G}}$. Let H be an affine hyperplane containing F. Let P, Q be two facets of $\Sigma {\setminus } {\mathcal {G}}$. If there are points $p \in P^\circ {\setminus } H$ and $q \in Q^\circ \cap H$, then the line through p and q meets H only at q, so it does not intersect F, so $P \sim _F Q$ as shown above. In fact, we can weaken the condition: if $p \in P {\setminus } H$ and $q \in (Q \cap H) {\setminus } \mathcal G$, then we perturb the line through p and q to get a line through $P^\circ$ and $Q^\circ$ which does not intersect F, because F is closed, so we still have $P \sim _F Q$.

If there are facets P, Q in $\Sigma$ such that $(P {\setminus } H) \setminus \mathcal G\ne \emptyset$ and $(Q \cap H) {\setminus } \mathcal G\ne \emptyset$, then every facet of $\Sigma {\setminus } \mathcal G$ not contained in H is equivalent to Q under $\sim _F$: every facet of $\Sigma {\setminus } \mathcal G$ contained in H is equivalent to P under $\sim _F$, and $P \sim _F Q$, so Claim 13 follows by transitive closure. In other words, it suffices to show that there is a hyperplane $H \supset F$ so that $(\Sigma {\setminus } H) \setminus \mathcal G\ne \emptyset$ and $(\Sigma \cap H) {\setminus } \mathcal G\ne \emptyset$.

We are assuming that $\Sigma$ is not contained in any affine subspace. Let $\sigma$ be a facet of $\Sigma$ which is not contained in H for some hyperplane H containing F. Since $\sigma$ is a d-dimensional pointed polyhedron, it is incident to at least d distinct ridges $\tau _1,\dots ,\tau _d$ of $\Sigma$. By the balancing condition at $\tau _i$ there is at least one other facet $\sigma _i$ containing $\tau _i$. If $\tau _i \not \subset H$, then $\sigma _i \not \subset H$. If $\tau _i \subset H$, then we can choose $\sigma _i$ to be on the other side of H from $\sigma$ by the balancing condition. Thus we have found d distinct facets $\sigma _1,\dots ,\sigma _d$, none of which is in H, so at least one of these is not in $\mathcal G$. Therefore $(\Sigma {\setminus } H) \setminus \mathcal G\ne \emptyset$ for any hyperplane H containing F.

If $\Sigma$ has codimension greater than one, then take any point $x \in \Sigma {\setminus } \mathcal G$ and let H be a hyperplane containing x and F. Then $x \in (\Sigma \cap H) {\setminus } \mathcal G\ne \emptyset$.

It thus remains to show this in the case that $\Sigma \subset \mathbb R^n$ is a balanced pointed polyhedral complex of dimension $d = n-1$. We will show the following by induction on r: if V is an r-dimensional affine subspace of $\mathbb R^n$ such that $\Sigma \cap V \ne \emptyset$, then $\Sigma \cap V$ is not contained in the union of $r-1$ facets of $\Sigma$. The case of $r=1$ is trivial. Suppose V is an affine subspace of dimension $r \ge 2$ such that $\Sigma \cap V \ne \emptyset$. We first claim that $\Sigma \cap V$ is not contained in a single facet of $\Sigma$. This is immediate if V contains $\Sigma$, as a pure positive-dimensional balanced polyhedral complex with trivial lineality space has more than one facet. If $\Sigma \not \subseteq V$, then since $\Sigma \cap V \ne \emptyset$, we have that $\Sigma \cap V$ contains the stable intersection of $\Sigma$ and V by [14, Lemma 2.6]. This stable intersection is a balanced polyhedral complex of positive dimension by [14, Theorem 2.13], so not contained in a single pointed facet of $\Sigma$. If $\Sigma \cap V$ is contained in the union of $r-1$ facets of $\Sigma$, then we choose one of these facets $\sigma$, a point $x \in \Sigma \cap V {\setminus } \sigma$, and an affine subspace $V' \subset V$ of dimension $r-1$ that contains x but does not intersect $\sigma$. Then $\Sigma \cap V'$ is contained in the union of $r-2$ facets of $\Sigma$, contradicting the induction hypothesis. Applying this for $r=d$, we see that for any hyperplane H, $\Sigma \cap H$ is not contained in the union of the $d-1$ facets in $\mathcal G$, so $(\Sigma \cap H){\setminus } \mathcal G\ne \emptyset$. $\square$

4 Bergman fans

The trivial valuation tropical variety of a linear space that is given as the row span of a matrix A depends only on the vector matroid on the columns of A. This tropical variety is called the Bergman fan of the matroid. Bergman fans are defined also for matroids that are not representable over any field. The Bergman fan of a rank r matroid is an r-dimensional polyhedral fan whose lineality space contains ${\textbf {1}} = (1,1,\dots ,1)$. In [2] Ardila and Klivans gave two fan structures to a Bergman fan: the coarse subdivision is derived from the matroid polytope, and the fine subdivision is a cone over a geometric realization of the order complex of its lattice of flats. The rays of the fine subdivision are the 0/1 indicator vectors of flats of the matroids and the cones correspond to chains of flats ordered by inclusion. We will now show that the fine subdivision of the Bergman fan of any matroid M, representable or not, is ${{\,\textrm{rk}\,}}(M)-1$ connected.

Proposition 14

Let M be a matroid of rank $d+1$ on the ground set $\{0,\dots , n\}$, and let $\Sigma$ be the fine subdivision on the Bergman fan ${{\,\textrm{trop}\,}}(M)$ in ${\mathbb {R}}^n \cong {\mathbb {R}}^{n+1}/{\mathbb {R}} {\textbf {1}}$. The facet-ridge hypergraph of $\Sigma$ is d-connected.

Proof

The Bergman fan of M with the fine subdivision is a d-dimensional pointed fan in ${\mathbb {R}}^n \cong {\mathbb {R}}^{n+1}/{\mathbb {R}} {\textbf {1}}$. The proof is by induction on the rank, $d+1$, of the matroid. When $d=1$, $\Sigma$ is a one-dimensional fan, with all facets (rays) meeting at the origin, so the fan is connected. We now assume $d>1$.

Fix a collection ${\mathcal {G}}$ of $d-1$ facets of $\Sigma$. The facets in ${\mathcal {G}}$ are labeled by maximal chains of flats in M, so every facet contains exactly one rank-one flat. The rank-one flat in each chain is a parallel class of elements of M. There are at least $d+1$ parallel classes because M has rank $d+1$. Since every rank-one flat is in a facet, there are at least $d+1$ facets, so we can fix two other facets $\sigma _1, \sigma _2 \not \in {\mathcal {G}}$. Since $|{\mathcal {G}}|=d-1$, there is an element $i \in \{0,\dots ,n\}$ which is not in any of the rank-one flats of cones in ${\mathcal {G}}$. We write $M_1$ and $M_2$ for the initial matroids corresponding to vectors in the relative interior of $\sigma _1$ and $\sigma _2$ respectively. As these cones are in ${{\,\textrm{trop}\,}}(M)$, both these matroids are loop-free, so there are bases $B_1, B_2$ containing i in $M_1,M_2$ respectively.

An ordering of a basis $B = (b_1,b_2,\dots ,b_{d+1})$ determines a chain of flats

$$\begin{aligned} {{\,\textrm{cl}\,}}(b_1) \subsetneq {{\,\textrm{cl}\,}}(b_1,b_2) \subsetneq \cdots \subsetneq {{\,\textrm{cl}\,}}(b_1,b_2, \dots , b_{d+1}) = \{0,1,\dots ,n\}\end{aligned}$$

in M, where the closure ${{\,\textrm{cl}\,}}(S)$ denotes the minimal flat containing S. Therefore for every basis B of M there are at least d! cones of $\Sigma$ with i in their rank-one flat, and with B as a basis of the corresponding initial matroid.

Choose facets $\sigma '_1, \sigma '_2$ of $\Sigma$ such that $B_1$ and $B_2$ respectively are bases of the corresponding initial matroid and i is in their rank-one flat. Thus $\sigma '_1, \sigma '_2$ are not in ${\mathcal {G}}$,

By [19, Theorem 2.6] the collection of cones in $\Sigma$ for which B is a basis of the corresponding initial matroid is homeomorphic to ${\mathbb {R}}^d$, and thus is d-connected. This means that there is a facet-ridge path between $\sigma _1$ and $\sigma '_1$, and between $\sigma _2$ and $\sigma '_2$, after the closed facets in ${\mathcal {G}}$ are removed.

It remains to show that $\sigma '_1$ and $\sigma '_2$ are connected. By construction $\sigma '_1$ and $\sigma '_2$ have the same rank-one flat $F_i$ containing i. The flats containing $F_i$ (or i) are in natural inclusion-preserving bijection with the flats of the contraction M/i. Therefore the star of $\Sigma$ at the ray corresponding to $F_i$ is the Bergman fan of the contraction M/i. Since M/i has rank d, by induction its Bergman fan with the fine subdivision is $(d-1)$-connected, so the star of $F_i$ in $\Sigma$ is $(d-1)$-connected.

By assumption, no element of ${\mathcal {G}}$ has rank-one flat $F_i$, so there are no elements of ${\mathcal {G}}$ in this star. Thus there is a ridge path in the star of $F_i$ between $\sigma '_1$ and $\sigma '_2$ avoiding ${\mathcal {G}}$, which completes the proof. $\square$

5 Open Problems

• Bergman fans and tropical linear spaces: Is any (nonrealizable) Bergman fan $r-\ell$ connected through codimension one with the coarse fan structure? Any fan structure? Here r and $\ell$ denote the dimension of the Bergman fan and the dimension of the lineality space respectively. Similarly for (nonrealizable) tropical linear spaces of valuated matroids as defined in [21].

• Connectivity, irreducibility, and algebraic matroids: An irreducible variety X in $K^n$ gives a matroid on ground set $\{1,2,\dots ,n\}$ where the rank of a subset $S \subset \{1,2,\dots ,n\}$ is the dimension of the projection of X onto the S-coordinates. This is called the algebraic matroid of X, and tropicalization preserves algebraic matroids [22]. In general it is not known which balanced polyhedral complexes give matroids this way. Does the higher connectivity imply that a balanced polyhedral complex gives an algebraic matroid? If the balanced complex is tropically irreducible, in the sense that it is not a union of two proper balanced weighted rational polyhedral complexes, does the complex have a higher connectivity or give an algebraic matroid?