Classifying simply connected wandering domains

Abstract

While the dynamics of transcendental entire functions in periodic Fatou components and in multiply connected wandering domains are well understood, the dynamics in simply connected wandering domains have so far eluded classification. We give a detailed classification of the dynamics in such wandering domains in terms of the hyperbolic distances between iterates and also in terms of the behaviour of orbits in relation to the boundaries of the wandering domains. In establishing these classifications, we obtain new results of wider interest concerning non-autonomous forward dynamical systems of holomorphic self maps of the unit disk. We also develop a new general technique for constructing examples of bounded, simply connected wandering domains with prescribed internal dynamics, and a criterion to ensure that the resulting boundaries are Jordan curves. Using this technique, based on approximation theory, we show that all of the nine possible types of simply connected wandering domain resulting from our classifications are indeed realizable.

1 Introduction

We consider dynamical systems defined by the iteration of holomorphic maps $f:{{\mathbb {C}}}\rightarrow {{\mathbb {C}}}$ on the complex plane, and particularly transcendental ones, that is, those with an essential singularity at infinity. The complex plane, seen as the phase space of the system, splits into two completely invariant subsets: the Fatou set, or those points in a neighbourhood of which the iterates $\{f^n\}$ form a normal family, and its complement, the Julia set. The Fatou set is open and consists typically of infinitely many connected components called Fatou components. Fatou components map from one to another and this leads to dynamics on the set of these components.

In this setting, periodic Fatou components were completely classified a century ago by Fatou, in terms of the possible limit functions of the family of iterates; see, for example, [10]. Indeed, if U is a periodic Fatou component of period $p\ge 1$, then U can only be one of the following: a domain on which the iterates $\{f^{pn}|_U\}_n$ converge to an attracting or parabolic fixed point of $f^p$ (known as an attracting or parabolic component, respectively); or a domain on which the iterates $\{f^{pn}|_U\}_n$ converge to infinity locally uniformly (known as a Baker domain); or a topological disk on which $f^p$ is conjugate to a rigid irrational rotation (known as a Siegel disk).

If a Fatou component U is neither periodic, nor preperiodic (that is, eventually periodic), then $f^i(U)\cap f^j(U)=\emptyset$ for all $i,j\ge 0$, $i\ne j$ and U is called a wandering domain. On a wandering domain all limit functions must be constant [28]. Those for which the only limit function is the point at infinity are called escaping, while the rest are either oscillating (if infinity is a limit function and some other finite value also) or dynamically bounded (if all limit functions are points in the plane). A major open problem in transcendental dynamics is whether dynamically bounded wandering domains exist at all. We believe that any progress towards solving this problem will require a deeper knowledge of the dynamics inside (and around) wandering domains, our main motivation for the work in this paper.

An essential role in the theory of holomorphic dynamics is played by the singular values, that is, those points for which not all inverse branches are locally well defined. In transcendental dynamics, these can be critical values (images under f of zeros of $f'$), asymptotic values or accumulations thereof.

For a wide class of functions known as finite type maps (those maps with a finite number of singular values), every Fatou component is periodic or preperiodic. Indeed, the absence of wandering domains for polynomials (actually for rational maps) [39] and for transcendental entire functions of finite type [22, 31] was a major breakthrough in the theory of complex dynamics, and meant that the possible types of dynamical behaviours of all such maps within the Fatou set was fully classified. The result about the absence of wandering domains for the class of transcendental maps of finite type was particularly striking because in the 1970s Baker [1] had constructed a transcendental entire function which had a nested sequence of multiply connected Fatou components, each mapping to the next and whose orbits escaped to infinity, showing that wandering domains can indeed exist. While the wandering domains in Baker’s example were multiply connected, since then a wide variety of examples of simply connected wandering domains have been given; see, for example, [2, p. 564, p. 567], [18, p. 222], [22, Examples 1 and 2], [26, Sect. 4.3], [32, p. 106] and [39, p. 414]. But it is only more recently that wandering domains have emerged as a major focus of attention, as the least understood of all the different types of Fatou components.

Indeed, several important advances have been made in recent years. For example, (oscillating) wandering domains have been constructed for functions in the Eremenko–Lyubich class $\mathcal {B}$ (those maps with a bounded sets of singular values) [14, 27, 34], a landmark result because escaping wandering domains have been shown not to exist for maps in this class [22]. We also mention the recent construction by Bishop [15] of an entire function with Julia set of Hausdorff dimension 1, solving a long standing problem in transcendental dynamics. This function has multiply connected wandering domains and also exhibits other remarkable properties; for example, all the boundary components of its wandering domains are Jordan curves.

Moreover, a detailed description of the dynamics of entire functions within multiply connected wandering domains was obtained in [13]. Perhaps surprisingly it turns out that in these wandering domains all orbits behave in essentially the same manner, eventually landing in and remaining in a sequence of very large nested round annuli. This detailed description has proved crucial in establishing results about classes of commuting transcendental entire functions [9].

Surprisingly, however, very little is known about the full range of possible behaviours of the orbits inside simply connected wandering domains, relative to the components themselves. This behaviour is connected to the relation between the postsingular set P(f) (that is, the union of the forward orbits of the singular values) and the wandering domains, another major open problem in the subject. Indeed, recent results in [3, 35] establish that if U is a wandering domain and $U_n$ is the Fatou component containing $f^n(U)$ for $n\in {{\mathbb {N}}}$, then for every $z\in U$, there exists a sequence $p_n\in P(f)$ such that ${\text {dist}}(p_n, U_n) / {\text {dist}}(f^n(z),\partial U_n) \rightarrow 0$ as $n\rightarrow \infty$. Hence the understanding of the possible dynamics of orbits inside wandering domains may throw some light on the possible relations between the postsingular set and the wandering domains, both issues being potentially relevant in any future attempt to eliminate dynamically bounded wandering domains.

One of the challenges is that several different types of behaviour are known to exist. Let us elaborate a bit further on this observation. Consider any holomorphic self-map of ${{\mathbb {C}}}\setminus \{0\}$, or an entire map $F:{{\mathbb {C}}}\rightarrow {{\mathbb {C}}}$ for which $z=0$ is either an omitted value or has itself as its only preimage; for example, $F_\lambda (z)=\lambda z^d \exp (z)$ with $d\in {{\mathbb {N}}}$, $\lambda \in {{\mathbb {C}}}\setminus \{0\}$. Such a map F can be lifted by the exponential map to a transcendental entire function $f:{{\mathbb {C}}}\rightarrow {{\mathbb {C}}}$ satisfying $\exp (f(z)) = F(\exp (z))$. Observe that f is not uniquely defined, since any map of the form $f_k(z)=f(z)+2k\pi i$ for $k\in {{\mathbb {Z}}}$ will have the same property. Now notice that if F had, say, an attracting component U (not containing $z=0$), then any logarithm of U, say ${\widetilde{U}}$, would be a wandering domain for $f_k$ (for an appropriate choice of k). Nevertheless, the orbits of points in ${\widetilde{U}}$ would still “remember” that they were lifted from an attracting component, in the sense that the iterates of any given point would be successively closer to the orbit of ${\widetilde{p}}{:}{=}\log p \in {\widetilde{U}}$, where p is the fixed point of F in U. Likewise, if U had been, for example, a Siegel disk, the iterates of points in the successive images of ${\widetilde{U}}$ would “rotate” around a centre point (actually orbit), again the iterates of ${\widetilde{p}}$. See Fig. 1, and also Fig. 4 in Sect. 3.3 for a lift of a parabolic component.

Fig. 1

Left: Dynamical plane of $F(w)= \lambda w^2e^{-w}$ with $\lambda =e^{2-\rho }/(2-\rho )$ and $\rho =e^{\pi i (1-\sqrt{5})}$. There is a (bounded) super-attracting component centred at $w=0$ (white) and a Siegel disk centred at $w_0=2-\lambda$ (gray). Right: Dynamical plane of $f(z)=2 z - e^z + \log \lambda$ satisfying $\exp (f(z))=F(\exp (z))$. The super-attracting component lifts to a Baker domain (white), while the Siegel disk lifts to infinitely many orbits of wandering domains on which f is univalent (gray). See [11, 24, 26] for details. The range is $[-9,9]\times [-9,9]$ (color figure online)

With this lifting procedure, one can construct examples of simply connected escaping wandering domains exhibiting the three different types of internal dynamics that correspond to the possible dynamics inside a periodic component: attracting, parabolic or rotation-like. Thus we already have a contrast with multiply connected wandering domains, where only one type of dynamical behaviour is possible, as noted above. These observations suggest a very natural question: How special are the three examples above in the general world of wandering domains; in other words, is there a classification of wandering domains in the spirit of Fatou’s classification of periodic Fatou components or is any orbit behaviour realizable? Let us note that, due to the lack of periodicity, the dynamics of f on a sequence of wandering domains can be thought of as a non-autonomous system (at every iterate we apply a “different” map), and such systems are a priori difficult to study because they may exhibit a wide range of behaviours. This might be an indication that such a classification may not exist. On the other hand, the successful description of the dynamics in multiply connected wandering domains obtained in [13] is encouraging.

The dynamics of points which belong to wandering domains can be seen from two perspectives. While points have to move together with the wandering domain which contains them (in the way that passengers on a cruise ship must follow the ship’s trajectory), on the one hand they may or may not cluster together as they move along (as happens when lifting an attracting component but not when lifting a Siegel disk), and on the other hand orbits may stay away from the boundaries of their domains (as happens when lifting an attracting basin but not when lifting a parabolic basin).

Our results will address both of those points of view. More precisely we give a complete and precise description of the possible dynamics of orbits inside the wandering components in terms of both the contraction properties with respect to the hyperbolic metric, and the distance of orbits to the boundary of the wandering components (Theorems  A,  B and  C). This provides a wandering version of the Fatou Classification Theorem of periodic components, a cornerstone of holomorphic dynamics. Moreover, we show that all of the possible cases exist by proving a new general and potentially very useful tool (Theorem  D) to establish the existence of wandering components for a given map. Finally, we prove that under certain conditions the wandering domains have Jordan curve boundaries. Our proof includes a novel result (Theorem 7.5) on the Euclidean lengths of vertical geodesics of annuli, using a new technique involving the classical Féjer–Riesz Inequality, which is of independent interest.

Statement of results

The most natural intrinsic quantity that we have to hand—intrinsic in that it does not depend on the embedding of the wandering domains in the plane—are the hyperbolic distances between pairs of corresponding points of two orbits, and so our approach will be to evaluate how hyperbolic distances between such pairs of points evolve under iteration.

Let us recall that a domain $U\subset {{\mathbb {C}}}$ is hyperbolic if its boundary (in ${{\mathbb {C}}}$) contains at least two points. For a hyperbolic domain U, let $\rho _U(z)$ denote the hyperbolic density at $z\in U$ and for $z,z'\in U$ let ${\text {dist}}_U(z,z')$ denote the hyperbolic distance in U between z and $z'$. Also recall that if U, V are hyperbolic domains, and $f:U\rightarrow V$ is a holomorphic map, then the Schwarz–Pick Lemma ensures that f is a contraction for the hyperbolic distance. Hence, if $U\subset {{\mathbb {C}}}$ is a wandering domain of a transcendental entire function f and we define $U_n$, as above, to be the Fatou component containing $f^n(U)$, for $n\in {{\mathbb {N}}}$, we have that, given any two points $z,z' \in U$, the sequence of hyperbolic distances

$$\begin{aligned} {\text {dist}}_{U_n}(f^n(z), f^n(z')) \end{aligned}$$

is decreasing and therefore converges to a value that we denote by

$$\begin{aligned} c(z,z')=c_{U}(z,z'){:}{=}\lim _{n\rightarrow \infty }{\text {dist}}_{U_n}(f^n(z), f^n(z')) \ge 0. \end{aligned}$$

Our first classification result shows that whether or not $c(z,z')$ is zero does not actually depend on the chosen pair $(z,z')$, provided that the two points have distinct orbits. We also give a criterion to discriminate between these cases based on the concept of hyperbolic distortion [8, Sect. 5,11].

Definition 1.1

(Hyperbolic distortion) If $f:U\rightarrow V$ is a holomorphic map between two hyperbolic domains U and V, then the hyperbolic distortion of f at z is

$$\begin{aligned} \Vert Df(z)\Vert _U^V{:}{=}\lim _{z'\rightarrow z}\frac{{\text {dist}}_V(f(z'),f(z))}{{\text {dist}}_U(z',z)}, \end{aligned}$$

and it equals the modulus of the hyperbolic derivative of f at z, given by $\rho _V(f(z)) f'(z)/\rho _U(z)$.

Theorem A

(First classification theorem) Let U be a simply connected wandering domain of a transcendental entire function f and let $U_n$ be the Fatou component containing $f^n(U)$, for $n \ge 0$. Define the countable set of pairs

$$\begin{aligned} E=\{(z,z')\in U\times U : f^k(z)=f^k(z') \text { for some } k\in {{\mathbb {N}}}\}. \end{aligned}$$

Then, exactly one of the following holds.

• (1) ${\text {dist}}_{U_n}(f^n(z), f^n(z'))\underset{n\rightarrow \infty }{\longrightarrow }c(z,z')= 0$ for all $z,z'\in U$, and we say that U is (hyperbolically) contracting;

• (2) ${\text {dist}}_{U_n}(f^n(z), f^n(z'))\underset{n\rightarrow \infty }{\longrightarrow }c(z,z') >0$ and ${\text {dist}}_{U_n}(f^n(z), f^n(z')) \ne c(z,z')$ for all $(z,z')\in (U \times U) \setminus E$, $n \in {{\mathbb {N}}}$, and we say that U is (hyperbolically) semi-contracting; or

• (3) there exists $N>0$ such that for all $n\ge N$, ${\text {dist}}_{U_n}(f^n(z), f^n(z')) = c(z,z') >0$ for all $(z,z') \in (U \times U) \setminus E$, and we say that U is (hyperbolically) eventually isometric.

Moreover for $z \in U$ and $n\in {{\mathbb {N}}}$ let $\lambda _n(z)$ be the hyperbolic distortion $\Vert Df(f^{n-1}(z))\Vert _{U_{n-1}}^{U_{n}}$. Then

• U is contracting if and only if $\sum _{n=1}^{\infty } (1-\lambda _n(z))=\infty$;

• U is eventually isometric if and only if $\lambda _n(z) = 1$, for n sufficiently large.

Note that, by the Schwarz–Pick Lemma, U is eventually isometric if and only if $f:U_n\rightarrow U_{n+1}$ is univalent for large n and so a wandering domain obtained by lifting a Siegel disk is always eventually isometric. In contrast, we show that lifting an attracting or parabolic component results in a contracting wandering domain. To distinguish between these two cases, we refine the classification of contracting wandering domains according to the rate of contraction.

Definition 1.2

(Rate of contraction) Let U be a simply connected wandering domain of a transcendental entire function f and $U_n$ be the Fatou component containing $f^n(U)$, for $n \ge 0$. We say that U is strongly contracting if there exists $c\in (0,1)$ such that

$$\begin{aligned} {\text {dist}}_{U_n}(f^n(z),f^n(z'))=O(c^n), \quad \text {for } z,z' \in U. \end{aligned}$$

We say that U is super-contracting if it satisfies the stronger condition that

$$\begin{aligned} \lim _{n \rightarrow \infty } ({\text {dist}}_{U_n}(f^n(z),f^n(z')))^{1/n} = 0, \quad \text {for } z,z' \in U. \end{aligned}$$

It is easy to see that the lift of an attracting component is strongly contracting, and we prove in Sect. 3 that the lift of a parabolic component is contracting but not strongly contracting. We do this by a careful analysis of the behaviour of the hyperbolic distance between pairs of points in two orbits in any parabolic component; see Theorem 3.4.

A special case of super-contracting wandering domains is given by wandering domains which contain an orbit consisting of critical points. An example of such a domain which does not arise from a lifting procedure is given in Theorem F.

Next, we give sufficient criteria for a wandering domain to be strongly contracting or super-contracting in terms of the long term average values of the hyperbolic distortion along the orbit of a point $z_0 \in U$. We also show that this quantity is independent of the point $z_0$.

Theorem B

Let U be a simply connected wandering domain of a transcendental entire function f and let $U_n$ be the Fatou component containing $f^n(U)$, for $n \ge 0$. Fix a point $z_0 \in U$ and, for $z \in U$ and $n \in {{\mathbb {N}}}$, let $\lambda _n(z) = \Vert Df(f^{n-1}(z))\Vert _{U_{n-1}}^{U_{n}}$. Then the following hold:

• (a) If $\limsup _{n \rightarrow \infty } \frac{1}{n}\sum _{k=1}^{n} \lambda _k(z_0)<1$, then U is strongly contracting.

• (b) If $\lim _{n \rightarrow \infty } \frac{1}{n}\sum _{k=1}^{n} \lambda _k(z_0)=0$, then U is super-contracting.

• (c) If $z \in U$, then $\limsup _{n \rightarrow \infty } \frac{1}{n}\sum _{k=1}^{n} \lambda _k(z) = \limsup _{n \rightarrow \infty } \frac{1}{n}\sum _{k=1}^{n} \lambda _k(z_0)$.

Once the behaviour of orbits in relation to each other within simply connected wandering domains is well understood, we turn to the question of how these orbits interact with the boundaries of the wandering domains. The concept of orbits ‘approaching the boundary’ is in itself delicate to define since it depends on the shape of the sets $U_n$, which may become highly distorted (think for example of the ratio of the diameter of the domains to their conformal radius, which may tend to infinity). There are alternative candidates for the definition of convergence to the boundary (see Sect. 4), but in this paper we use the following definition based on Euclidean distance, denoted by ${\text {dist}}(.,.)$.

Definition 1.3

(Boundary convergence) Let U be a simply connected wandering domain of a transcendental entire function f and let $U_n$ be the Fatou component containing $f^n(U)$, for $n \ge 0$. We say that the orbit of $z\in U$ converges to the boundary (of $U_n$) if and only if ${\text {dist}}(f^{n}(z),\partial U_{n})\rightarrow 0$ as $n \rightarrow \infty$.

We show that, with this definition, the following trichotomy holds.

Theorem C

(Second classification theorem) Let U be a simply connected wandering domain of a transcendental entire function f and let $U_n$ be the Fatou component containing $f^n(U)$, for $n \ge 0$. Then exactly one of the following holds:

• (a) $\liminf _{n\rightarrow \infty } {\text {dist}}(f^{n}(z),\partial U_{n})>0$ for all $z\in U$, that is, all orbits stay away from the boundary;

• (b) there exists a subsequence $n_k\rightarrow \infty$ for which ${\text {dist}}(f^{n_k}(z),\partial U_{n_k})\rightarrow 0$ for all $z\in U$, while for a different subsequence $m_k\rightarrow \infty$ we have that

  $$\begin{aligned} \liminf _{k \rightarrow \infty } {\text {dist}}(f^{m_k}(z),\partial U_{m_k})>0, \quad \text {for }z\in U; \end{aligned}$$

• (c) ${\text {dist}}(f^{n}(z),\partial U_{n})\rightarrow 0$ for all $z\in U$, that is, all orbits converge to the boundary.

We remark that we actually prove a stronger version of Theorem  C (see Theorem 4.2), which takes into account different definitions of converging to the boundary.

Construction of examples

Theorems  A and  C combine to give nine different dynamical types of simply connected wandering domains. A natural question to ask is whether all of these can be realized. As far as we know, the existing examples of simply connected wandering domains in the literature belong to one of the following three cases: contracting and converging to the boundary (e.g. lifts of parabolic components); contracting and staying away from the boundary (e.g. lifts of attracting components); isometric and staying away from the boundary (e.g. lifts of Siegel disks). We will use approximation theory (see Sect. 5) to construct examples of each of the nine possibilities. In fact, we present a new general technique to construct bounded simply connected wandering domains (see Theorem 5.3) which allows us to keep good control on the internal dynamics, as well as on the degree of the resulting maps from one Fatou component to the next. As a key step we prove the following general result to show the existence of bounded simply connected wandering domains. Its statement uses the following terminology.

Definition 1.4

We say that a curve $\sigma$ surrounds a set B if and only if B is contained in a bounded complementary component of $\sigma$. Also, for a Jordan curve $\eta$ we denote by ${\text {int}}\eta$ the bounded component of ${{\mathbb {C}}}\setminus \eta$ and by ${\text {ext}}\eta$ the unbounded component of ${{\mathbb {C}}}\setminus \eta$.

We can now state our result; see Fig. 5 in Sect. 5 for an illustration of the setup in Theorem D.

Theorem D

(Existence criteria for wandering domains) Let f be a transcendental entire function and suppose that there exist Jordan curves $\gamma _n$ and $\Gamma _n$, $n\ge 0$, a bounded domain D, a subsequence $n_k\rightarrow \infty$ and compact sets $L_k$ (associated with $\Gamma _{n_k}$) such that

• (a) $\Gamma _n$ surrounds $\gamma _n$, for $n \ge 0$;

• (b) for every $k,n, m\ge 0$, $m\ne n$ the sets $L_k, \overline{D}, \Gamma _m$ are in ${\text {ext}}\Gamma _n$;

• (c) $\gamma _{n+1}$ surrounds $f(\gamma _n)$, for $n \ge 0$;

• (d) $f(\Gamma _n)$ surrounds $\Gamma _{n+1}$, for $n \ge 0$;

• (e) $f({\overline{D}} \cup \bigcup _{k\ge 0} L_k)\subset D$;

• (f) $\max \{{\text {dist}}(z,L_{k}): z \in \Gamma _{n_k}\} = o({\text {dist}}(\gamma _{n_k}, \Gamma _{n_k}))\;\text { as}\; k \rightarrow \infty .$

Then there exists an orbit of simply connected wandering domains $U_n$ such that $\overline{{\text {int}} \gamma _n} \subset U_n \subset {\text {int}}\Gamma _n$, for $n \ge 0$.

Moreover, if there exists $z_n \in {\text {int}}\gamma _n$ such that both $f(\gamma _n)$ and $f(\Gamma _n)$ wind $d_n$ times around $f(z_n),$ then $f:U_n \rightarrow U_{n+1}$ has degree $d_n$, for $n \ge 0$.

We use Theorem D to construct examples of each of the nine possible types, and also to construct simply connected wandering domains that contain any prescribed (finite) number of orbits consisting of critical points. A wandering domain U will be called k-super-attracting if there exist critical points $z_1, \ldots , z_k \in U$, such that $f^{n}(z_1), \ldots , f^n(z_k)$ are critical points of f, for all $n \in {{\mathbb {N}}}$.

Theorem E

(All types are realizable) (a) For each of the nine possible types of simply connected wandering domains arising from Theorems A and  C, there exists a transcendental entire function with a bounded, simply connected escaping wandering domain of that type.

(b) For each $k\in {{\mathbb {N}}}$, there exists a transcendental entire function f having a bounded, simply connected escaping wandering domain U which is k-super-attracting.

Note that our examples in part (b) of Theorem E are super-contracting wandering domains that are not lifts of super-attracting components.

The bounded, simply connected wandering domains, $(U_n)$ say, constructed in Theorem E all have a shape that tends to the shape of a Euclidean disk as $n \rightarrow \infty$, but in fact the construction can easily be modified to give wandering domains with different limiting shapes.

Finally, we show that our methods can be adapted to construct simply connected wandering domains bounded by Jordan curves. Theorem E is proved by obtaining entire functions that approximate sequences of translates of Blaschke products associated with sequences of Jordan curves with the properties given in Theorem D, and we show that, if these Blaschke products are in a certain sense uniformly expanding and have uniformly bounded degree, then the resulting wandering domains have Jordan curve boundaries.

Further questions and developments

Our results suggest numerous further questions. For example, in view of the results in [3, 35], mentioned earlier, it is natural to ask if there is a relationship between the different types of wandering domains in our classifications and the behaviour of the postsingular set of f near or in these wandering domains. Another question is the relationship between the classification of the internal behaviour in simply connected wandering domains and the behaviour of boundary orbits; we investigate this question in forthcoming work.

Since this paper was written there have been several developments. First, in [23] the methods of this paper were used to construct examples of oscillating simply connected wandering domains of the six types that are possible under the classifications given in Theorems A and C of this paper. More recently, Boc Thaler [16] showed that many bounded simply connected domains, including all Jordan domains, can be realised as a wandering domain (either escaping or oscillating) of some transcendental entire function.

Structure of the paper

The first part of the paper (Sects.  2,  3 and  4) is devoted to studying the possible behaviours of orbits in simply connected wandering domains, proving Theorems A, B and C. We begin in Sect. 2 by setting up related non-autonomous dynamical systems of self maps of the unit disk. We prove several results in this general setting which may be of wider interest. In Sect. 3 we use our results from Sect. 2 to prove Theorems A and B. We prove Theorem C in Sect. 4.

The second part of the paper (Sects. 5,  6 and  7) is devoted to the construction of examples. In Sect. 5 we give the proof of Theorem D and develop a new general technique for constructing bounded wandering domains. In Sect. 6 we use this technique to construct examples of every possible behaviour classified in the first part of the paper, proving Theorem E. Finally, in Sect. 7 we show that, under certain conditions, our new construction technique gives simply connected wandering domains that are Jordan domains.

2 Non-autonomous dynamical systems of self maps of the unit disk

In this section we prove several results in the general setting of non-autonomous forward dynamical systems of holomorphic self maps of the unit disk fixing the origin. These results may be of wider interest with applications outside holomorphic dynamics. In the next section, we apply them to the case of transcendental entire functions with simply connected wandering domains in order to prove Theorem  A and Theorem B.

Our proofs are based on hyperbolic distances in the unit disk and we make frequent use of the fact that

$$\begin{aligned} {\text {dist}}_{{{\mathbb {D}}}}(w,0) = \int _{0}^{|w|} \frac{2\,dt}{1-t^2} = \log \left( \frac{1 + |w|}{1 - |w|}\right) , \quad \text {for } w \in {{\mathbb {D}}}. \end{aligned}$$

(2.1)

In our first result, we characterize when the limits of such systems of holomorphic self maps of the unit disk are identically equal to zero, in terms of the values of the derivatives of the maps at 0. In particular, unless $|g_n'(0)|\rightarrow 1$ as $n\rightarrow \infty$, the limit of the maps $G_n$ is always zero.

Theorem 2.1

(Criterion for converging to zero) For each $n \in {{\mathbb {N}}}$, let $g_n: {{\mathbb {D}}}\rightarrow {{\mathbb {D}}}$ be holomorphic with $g_n(0) = 0$ and $|g_n'(0)| = \lambda _n$, and let $G_n = g_{n}\circ \cdots \circ g_1$.

• (a) If $\sum _{n=1}^{\infty }(1 - \lambda _n) = \infty$, then $G_n(w) \rightarrow 0$ as $n \rightarrow \infty$, for all $w \in {{\mathbb {D}}}$.

• (b) If $\sum _{n=1}^{\infty }(1 - \lambda _n) < \infty$, then $G_n(w) \nrightarrow 0$ as $n \rightarrow \infty$, for all $w \in {{\mathbb {D}}}$ for which $G_n(w) \ne 0$ for all $n \in {{\mathbb {N}}}$.

Proof

We begin with ideas used by Beardon and Carne [5]. First, it follows from the hyperbolic triangle inequality and hyperbolic contraction that, if $\psi : {{\mathbb {D}}}\rightarrow {{\mathbb {D}}}$ is holomorphic, then for all $w\in {{\mathbb {D}}}$ we have

$$\begin{aligned} {\text {dist}}_{{{\mathbb {D}}}}(0,\psi (w))\le & {} {\text {dist}}_{{{\mathbb {D}}}}(0,\psi (0))+{\text {dist}}_{{{\mathbb {D}}}}(\psi (0),\psi (w))\nonumber \\\le & {} {\text {dist}}_{{{\mathbb {D}}}}(0,\psi (0))+{\text {dist}}_{{{\mathbb {D}}}}(0,w), \end{aligned}$$

(2.2)

and, similarly,

$$\begin{aligned} {\text {dist}}_{{{\mathbb {D}}}}(0,\psi (0))\le {\text {dist}}_{{{\mathbb {D}}}}(0,\psi (w))+{\text {dist}}_{{{\mathbb {D}}}}(0,w), \text { for all } w\in {{\mathbb {D}}}. \end{aligned}$$

(2.3)

We also use the fact that

$$\begin{aligned} \sum _{n=1}^{\infty }(1 - \lambda _n) = \infty \iff \lambda _{m+n}\cdots \lambda _{m+1} \rightarrow 0 \text { as } n \rightarrow \infty , \quad \text {for all } m \in {{\mathbb {N}}}. \end{aligned}$$

(2.4)

In the case when $\lambda _n \ne 0$, for all n, and the right-hand side is $\lambda _{n}\cdots \lambda _{1} \rightarrow 0 \text { as } n \rightarrow \infty$, this statement is a standard property of infinite products proved by taking logarithms. Here it is possible that some or all of the terms $\lambda _n$ are zero, so the right-hand side of (2.4) takes account of these possibilities.

Now take $w_0 \in {{\mathbb {D}}}$ and, for simplicity, denote $G_n(w_0)$ by $w_n$, for $n \in {{\mathbb {N}}}$.

To prove part (a), we assume that $\lambda _{m+n}\cdots \lambda _{m+1} \rightarrow 0$ as $n \rightarrow \infty$, for all $m \in {{\mathbb {N}}}$, and deduce that $w_n \rightarrow 0$ as $n\rightarrow \infty$. Suppose that $w_n \nrightarrow 0$ as $n\rightarrow \infty$. Since $w_n = g_n(w_{n-1})$, we deduce by Schwarz’s Lemma that $|w_n| \le |w_{n-1}|$, and hence that $|w_n|$ decreases to some $d>0$ as $n \rightarrow \infty$.

First choose $m \in {{\mathbb {N}}}$ so large that $|w_m|$ is sufficiently close to d to ensure that

$$\begin{aligned} {\text {dist}}_{{{\mathbb {D}}}}(0,w_{n+m}/w_m) > {\text {dist}}_{{{\mathbb {D}}}}(0,w_m), \quad \text {for } n \in {{\mathbb {N}}}. \end{aligned}$$

(2.5)

Next we fix $n \in {{\mathbb {N}}}$ and define the holomorphic map

$$\begin{aligned} \psi (w) = (g_{m+n} \circ \cdots \circ g_{m+1}(w))/w, \quad \text {for } w \in {{\mathbb {D}}}\setminus \{0\}, \end{aligned}$$

with

$$\begin{aligned} \psi (0) = (g_{m+n} \circ \cdots \circ g_{m+1})'(0) = \lambda _{m+n} \cdots \lambda _{m+1}. \end{aligned}$$

Applying (2.2) to the function $\psi$ at the point $w=w_m$ gives

$$\begin{aligned} {\text {dist}}_{{{\mathbb {D}}}}(0,w_{n+m}/w_m)= & {} {\text {dist}}_{{{\mathbb {D}}}}(0,\psi (w_m))\\\le & {} {\text {dist}}_{{{\mathbb {D}}}}(0,\psi (0)) + {\text {dist}}_{{{\mathbb {D}}}}(0,w_m)\\= & {} {\text {dist}}_{{{\mathbb {D}}}}(0,\lambda _{m+n} \cdots \lambda _{m+1}) + {\text {dist}}_{{{\mathbb {D}}}}(0,w_m). \end{aligned}$$

Since we have assumed that $\lambda _{m+n}\cdots \lambda _{m+1} \rightarrow 0$ as $n \rightarrow \infty$, we obtain a contradiction to (2.5), showing that $w_n \rightarrow 0$ as $n \rightarrow \infty$.

To prove part (b), we assume that, for some $m_0 \in {{\mathbb {N}}}$, $\lambda _{m_0+n}\cdots \lambda _{m_0+1} \rightarrow \lambda > 0$ as $n \rightarrow \infty$, and deduce that whenever $w_n \ne 0$, for all $n \in {{\mathbb {N}}}$, we have $w_n \nrightarrow 0$ as $n \rightarrow \infty$. Suppose that $w_n \rightarrow 0$ as $n\rightarrow \infty$.

First choose m so large that $m \ge m_0$ and

$$\begin{aligned} {\text {dist}}_{{{\mathbb {D}}}}(0,w_m) < {\text {dist}}_{{{\mathbb {D}}}}(0,\lambda ), \end{aligned}$$

(2.6)

and note that, for such m,

$$\begin{aligned} \lambda _{m+n}\cdots \lambda _{m+1} \ge \lambda _{m+n}\cdots \lambda _{m_0+1} = \lambda _{m_0 + (m-m_0)+n}\cdots \lambda _{m_0+1} \ge \lambda , \quad \text {for } n \in {{\mathbb {N}}}. \nonumber \\ \end{aligned}$$

(2.7)

Next we fix $n \in {{\mathbb {N}}}$ and apply (2.3) with $\psi$ defined as earlier and $w=w_m$ to give

$$\begin{aligned} {\text {dist}}_{{{\mathbb {D}}}}(0,\lambda _{m+n}\cdots \lambda _{m+1}) \le {\text {dist}}_{{{\mathbb {D}}}}(0,w_{m+n}/w_m) + {\text {dist}}_{{{\mathbb {D}}}}(0,w_m). \end{aligned}$$

Letting $n \rightarrow \infty$, we obtain a contradiction to (2.6) in view of (2.7) and hence to the supposition that $w_n \rightarrow 0$ as $n \rightarrow \infty$. This completes the proof. $\square$

The following corollary to Theorem 2.1 shows that if the hyperbolic distance between two distinct orbits converges to zero, then the same occurs for every pair of orbits.

Corollary 2.2

For $n \in {{\mathbb {N}}}$, let $g_n: {{\mathbb {D}}}\rightarrow {{\mathbb {D}}}$ be holomorphic and let $G_n = g_{n}\circ \cdots \circ g_1$. If there exist $w_0,w_0' \in {{\mathbb {D}}}$ such that $G_n(w_0') \ne G_n(w_0)$ for all $n \in {{\mathbb {N}}}$ and ${\text {dist}}_{{{\mathbb {D}}}}(G_n(w_0'),G_n(w_0)) \rightarrow 0$ as $n \rightarrow \infty$, then

$$\begin{aligned} {\text {dist}}_{{{\mathbb {D}}}}(G_n(w),G_n(w_0)) \rightarrow 0 \text { as } n \rightarrow \infty , \quad \text {for all } w \in {{\mathbb {D}}}. \end{aligned}$$

Proof

For each $n \in {{\mathbb {N}}}$, let $w_n = g_n(w_{n-1})$ and, for $n \ge 0$, let $M_n:{{\mathbb {D}}}\rightarrow {{\mathbb {D}}}$ be a Möbius map satisfying $M_n(w_n)=0$. Then, for each $n \in {{\mathbb {N}}}$, the map $h_n=M_n \circ g_n \circ M_{n-1}^{-1}$ is a holomorphic self map of the unit disk and $h_n(0)=0$. For $n \in {{\mathbb {N}}}$, let $H_n {:}{=} h_{n}\circ \cdots \circ h_1$ and notice that $H_n(0)=0$. Since Möbius maps are isometries and $H_n = M_n \circ G_n \circ M_0^{-1}$, for $n \in {{\mathbb {N}}}$, we have

$$\begin{aligned} {\text {dist}}_{{{\mathbb {D}}}}(0, H_n(M_0(w_0')))&= {\text {dist}}_{{{\mathbb {D}}}}(H_n(0), H_n(M_0(w_0'))) \\&= {\text {dist}}_{{{\mathbb {D}}}}(M_n\circ G_n\circ M_0^{-1}(0),M_n\circ G_n\circ M_0^{-1}\circ M_0 (w_0'))\\&= {\text {dist}}_{{{\mathbb {D}}}}(M_n\circ G_n(w_0),M_n\circ G_n(w_0'))\\&= {\text {dist}}_{{{\mathbb {D}}}}(G_n(w_0),G_n(w_0')) \rightarrow 0 \quad \text {as } n \rightarrow \infty , \end{aligned}$$

and hence $H_n(M_0(w_0')) \rightarrow 0$ as $n \rightarrow \infty$. Since $H_n(M_0(w_0')) = M_n(G_n(w_0')) \ne 0$, for each $n \in {{\mathbb {N}}}$, we deduce that when Theorem 2.1 is applied to $H_n {:}{=} h_{n}\circ \cdots \circ h_1$ the conclusion of part (b) of that theorem does not hold. Therefore, $H_n(w') \rightarrow 0$ as $n \rightarrow \infty$ for all $w' \in {{\mathbb {D}}}$. The result now follows since

$$\begin{aligned} {\text {dist}}_{{{\mathbb {D}}}}(G_n(w),G_n(w_0))= & {} {\text {dist}}_{{{\mathbb {D}}}}(H_n(M_0(w)),H_n(0)) \\= & {} {\text {dist}}_{{{\mathbb {D}}}}(H_n(M_0(w)),0), \quad \text {for } w \in {{\mathbb {D}}}. \end{aligned}$$

$\square$

Theorem 2.1 and Corollary 2.2 will be used in the proof of Theorem  A (see Sect. 3.1).

We now prove several results giving estimates for the rate at which limits tend to zero in the case when the limit in Theorem 2.1 is identically equal to zero. The results proven in the remainder of this section will be used in Sect. 3.2 to prove Theorem  B, that is, the subclassification of contracting wandering domains.

We use the following result which includes a generalization of Schwarz’s Lemma.

Lemma 2.3

(Variation of Schwarz’s Lemma) Let $\psi :{{\mathbb {D}}}\rightarrow {{\mathbb {D}}}$ be holomorphic. Then

$$\begin{aligned} \frac{|\psi (0)|-|w|}{1-|\psi (0)||w|}\le |\psi (w)|\le \frac{|\psi (0)|+|w|}{1+|\psi (0)||w|}, \quad \text { for } w \in {{\mathbb {D}}}. \end{aligned}$$

Proof

The right-hand inequality arises from (2.2) and is given in [5, p.217]. We prove the left-hand inequality using similar methods. First note that it follows from (2.3) that

$$\begin{aligned} {\text {dist}}_{{{\mathbb {D}}}}(0,\psi (w))\ge {\text {dist}}_{{{\mathbb {D}}}}(0,\psi (0))-{\text {dist}}_{{{\mathbb {D}}}}(0,w), \end{aligned}$$

that is,

$$\begin{aligned} \log \frac{1+|\psi (w)|}{1-|\psi (w)|}\ge \log \frac{1+|\psi (0)|}{1-|\psi (0)|}-\log \frac{1+|w|}{1-|w|}. \end{aligned}$$

By the monotonicity of the logarithm, this is equivalent to the following inequality:

$$\begin{aligned} \frac{1+|\psi (w)|}{1-|\psi (w)|}\ge \left( \frac{1+|\psi (0)|}{1-|\psi (0)|}\right) \left( \frac{1-|w|}{1+|w|}\right) , \end{aligned}$$

which gives

$$\begin{aligned} |\psi (w)| \ge \frac{\left( \frac{1+|\psi (0)|}{1-|\psi (0)|}\right) \left( \frac{1-|w|}{1+|w|}\right) -1}{\left( \frac{1+|\psi (0)|}{1-|\psi (0)|}\right) \left( \frac{1-|w|}{1+|w|}\right) +1}=\frac{|\psi (0)|-|w|}{1-|\psi (0)||w|}, \end{aligned}$$

as claimed. $\square$

We make frequent use of the following corollary of Lemma 2.3.

Corollary 2.4

Let $g:{{\mathbb {D}}}\rightarrow {{\mathbb {D}}}$ be holomorphic with $g(0) = 0$ and $|g'(0)| = \lambda$. Then, for all $w \in {{\mathbb {D}}}$,

$$\begin{aligned} |w| \left( \frac{\lambda - |w|}{1 - \lambda |w|} \right) \le |g(w)| \le |w| \left( \frac{\lambda + |w|}{1 + \lambda |w|} \right) \end{aligned}$$

Proof

The result follows by applying Lemma 2.3 to the holomorphic map $\psi :{{\mathbb {D}}}\rightarrow {{\mathbb {D}}}$ defined by

$$\begin{aligned} \psi (w) = g(w)/w, \quad \text {for } w \in {{\mathbb {D}}}\setminus \{0\}, \end{aligned}$$

with $\psi (0) = g'(0)$. $\square$

We first use Corollary 2.4 to prove the following result giving rather precise upper and lower estimates of the rate at which the sequences $|G_n(w)|$ in Theorem 2.1 decrease, expressed in terms of the derivatives $|g'_n(0)|$. This result can be used to give a more direct proof of Theorem 2.1; see the remark after the proof of Theorem 2.5.

Theorem 2.5

For each $n \in {{\mathbb {N}}}$, let $g_n: {{\mathbb {D}}}\rightarrow {{\mathbb {D}}}$ be holomorphic with $g_n(0) = 0$ and $|g_n'(0)| = \lambda _n = 1 - \mu _n$, and let $G_n = g_{n}\circ \cdots \circ g_1$. If $w\in {{\mathbb {D}}}$ and $w_n=G_n(w)$, $n\in {{\mathbb {N}}}$, then

• (a)
  $$\begin{aligned} |w_n| \le |w| \prod _{k=1}^n (1 - c_w\mu _k), \quad \text {where } c_w = (1-|w|)/2; \end{aligned}$$

  (2.8)

• (b) if $|w| \le \lambda _k$, for $1 \le k \le n$, then

  $$\begin{aligned} |w_n| \ge |w| \prod _{k=1}^n (1-d_w\mu _k), \quad \text {where } d_w = \frac{1+|w|}{1-|w|}. \end{aligned}$$

  (2.9)

Proof

Set $w_0=w$. We begin the proof of part (a) by noting that it follows from Corollary 2.4 that, for $k \ge 0$ and $w \in {{\mathbb {D}}}$,

$$\begin{aligned} |w_{k+1}|= & {} |g_{k+1}(w_k)| \le |w_k| \frac{\lambda _{k+1} + |w_k|}{1 + \lambda _{k+1} |w_k|}\\= & {} |w_k| \left( 1 - \frac{\mu _{k+1}( 1- |w_k|)}{1 + \lambda _{k+1} |w_k|} \right) \\\le & {} |w_k| \left( 1-\frac{ \mu _{k+1}(1-|w_k|)}{2}\right) \\\le & {} |w_k|(1-c_w\mu _{k+1}), \end{aligned}$$

where the second inequality follows because $\lambda _{k+1} |G_k(w)|<1$ and the last inequality follows because $|w_k|=|G_k(w)| \le |w|$ by Schwarz’s Lemma. The result of (2.8) now follows and this completes the proof of part (a).

We now prove part (b). Using Corollary 2.4 again,

$$\begin{aligned} |w_{k+1}| = |g_{k+1}(w_{k})| \ge |w_{k}| \left( \frac{\lambda _{k+1} - |w_k|}{1 - \lambda _{k+1} |w_k|} \right) . \end{aligned}$$

(2.10)

Now we use the elementary calculus estimate that

$$\begin{aligned} \frac{\lambda -r}{1-\lambda r} \ge 1-\left( \frac{1+r}{1-r}\right) (1-\lambda ),\quad \text {for }0<r<\lambda \le 1, \end{aligned}$$

to deduce from (2.10) that, for $k \ge 0$, if $|w|\le \lambda _{k+1}$, then

$$\begin{aligned} |w_{k+1}| \ge |w_k|\left( 1-\left( \frac{1+|w_k|}{1-|w_k|}\right) \mu _{k+1}\right) \ge |w_k|\left( 1-\left( \frac{1+|w|}{1-|w|}\right) \mu _{k+1}\right) , \end{aligned}$$

using the fact that $|w_k|=|G_k(w)| \le |w|$ again. The result of (2.9) now follows and this completes the proof of part (b). $\square$

Remark

Theorem 2.5 can be used to give a proof of Theorem 2.1. To do so, it is first necessary to use Hurwitz’ Theorem in order to show that either $G_n(w) \rightarrow 0$ as $n \rightarrow \infty$ for all $w \in {{\mathbb {D}}}$ or $G_n(w) \rightarrow 0$ as $n \rightarrow \infty$ only for those points $w \in {{\mathbb {D}}}$ for which $G_n(w) = 0$ eventually.

We now prove another result giving upper estimates for the rate at which the sequences $|G_n(w)|$ decrease, this time expressed in terms of the average of the derivatives $|g_n'(0)|$. The proof of this result is also based on Corollary 2.4.

Theorem 2.6

For each $n \in {{\mathbb {N}}}$, let $g_n: {{\mathbb {D}}}\rightarrow {{\mathbb {D}}}$ be holomorphic with $g_n(0) = 0$ and $|g_n'(0)| = \lambda _n = 1 - \mu _n$, and let $G_n = g_{n}\circ \cdots \circ g_1$. Then, for all $n \in {{\mathbb {N}}}$, if $w_0 \in {{\mathbb {D}}}$ and $w_n = G_n(w_0)$, for $n \in {{\mathbb {N}}}$,

$$\begin{aligned} |w_n| \le \left( \frac{1}{n}\sum _{k=1}^n \lambda _k + \frac{1}{n} \sum _{k=0}^{n-1} |w_k|\right) ^n. \end{aligned}$$

(2.11)

Hence

• (a) if

  $$\begin{aligned} \limsup _{n \rightarrow \infty } \frac{1}{n} \sum _{k=1}^n \lambda _k = a < 1, \end{aligned}$$

  then, for any $c\in (a,1),$ we have

  $$\begin{aligned} |G_n(w)| = O(c^n)\;\text { as } n \rightarrow \infty , \quad \text {for } w \in {{\mathbb {D}}}; \end{aligned}$$

• (b) if

  $$\begin{aligned} \lim _{n \rightarrow \infty } \frac{1}{n} \sum _{k=1}^n \lambda _k = 0, \end{aligned}$$

  then

  $$\begin{aligned} |G_n(w)|^{1/n} \rightarrow 0 \;\text { as } n \rightarrow \infty , \quad \text {for } w \in {{\mathbb {D}}}. \end{aligned}$$

Proof

By using Corollary 2.4, and then applying the fact that the geometric mean of n positive numbers is at most equal to their arithmetic mean, we see that, for $w_0 \in {{\mathbb {D}}}$ and $n \in {{\mathbb {N}}}$,

$$\begin{aligned} |w_n|\le & {} |w_0| \left( \frac{\lambda _{n}+|w_{n-1}|}{1+\lambda _{n}|w_{n-1}|}\right) \cdots \left( \frac{\lambda _{1}+|w_{0}|}{1+\lambda _{1}|w_{0}|}\right) \\\le & {} |w_0|((\lambda _{n}+|w_{n-1}|)\cdots (\lambda _{1}+|w_{0}|)) \\\le & {} |w_0| \left( \frac{1}{n}((\lambda _{n}+|w_{n-1}|) + \cdots + (\lambda _{1}+|w_{0}|))\right) ^n \\= & {} |w_0| \left( \frac{1}{n} \sum _{k=1}^{n}\lambda _k+ \frac{1}{n} \sum _{k=0}^{n-1}|w_k|\right) ^n. \end{aligned}$$

This proves (2.11).

Next, if $\limsup _{n \rightarrow \infty } \frac{1}{n} \sum _{k=1}^n \lambda _k = a < 1$, then $\sum _{k=1}^{\infty }(1-\lambda _k) = \infty$ and so it follows from Theorem 2.1 that $w_n \rightarrow 0$ as $n \rightarrow \infty$ and hence that $\frac{1}{n} \sum _{k=0}^{n-1}|w_k| \rightarrow 0$ as $n \rightarrow \infty$. So, in this case, it follows from (2.11) that

$$\begin{aligned} |G_n(w_0)|^{1/n} = |w_n|^{1/n} \le a + o(1) \; \text { as } n \rightarrow \infty . \end{aligned}$$

The results of parts (a) and (b) now follow. $\square$

Theorems 2.5 (a) and 2.6 give uniform upper estimates on the rate that $|G_n(w)|$ tends to 0, in the situation where $\sum _{n=1}^{\infty } (1-\lambda _n)=\infty$. It is natural to ask whether we can demonstrate such a uniform rate if we know the rate at which $|G_n(w)|$ tends to 0 on some subset of ${{\mathbb {D}}}$. It is clear that we cannot deduce any uniform rate at which $G_n(w)\rightarrow 0$ from information about the behaviour of $G_n$ at a single point $w_0\in {{\mathbb {D}}}$, since we may have $G_n(w_0)=0$, for example. However, if we have an upper bound for $|G_n(w)|$ on some circle $\{w:|w|=r_0\}$, where $0<r_0<1$, then we can obtain an upper bound for $|G_n(w)|$ for all $w\in {{\mathbb {D}}}$ by applying the following simple proposition.

Proposition 2.7

(Hadamard convexity) Let $f:{{\mathbb {D}}}\rightarrow {{\mathbb {D}}}$ be holomorphic and satisfy

$$\begin{aligned} |f(w)|\le a, \quad \text {for } |w|\le r_0, \end{aligned}$$

where $0<a\le r_0<1$. Then,

$$\begin{aligned} |f(w)|\le a^{\frac{\log r }{\log r_0}} \quad \text {for } |w|\le r, \end{aligned}$$

for all r such that $r_0\le r < 1$.

Proof

For $0\le r<1$, let

$$\begin{aligned} M(r)=M(r,f){:}{=}\sup _{|z|=r}|f(z)| \end{aligned}$$

denote the maximum modulus function and put

$$\begin{aligned} \varphi (t)=\log M(e^t), \quad \text {for } -\infty< t < 0. \end{aligned}$$

Then $\varphi$ is convex by Hadamard’s Three Circles Theorem [40, page 172], negative and increasing, and by hypothesis $\varphi (\log r_0) \le \log a$ and $\varphi (t)\le 0$ for $t<0$. Hence

$$\begin{aligned} \varphi (t)\le \left( \frac{\log a}{\log r_0} \right) t, \quad \text {for } \log r_0 \le t < 0; \end{aligned}$$

that is,

$$\begin{aligned} \log M(r) \le \left( \frac{\log a}{\log r_0} \right) \log r, \quad \text {for } r_0\le r < 1, \end{aligned}$$

and hence

$$\begin{aligned} M(r)\le a^{\frac{\log r }{\log r_0}}, \quad \text {for } r_0\le r < 1, \end{aligned}$$

as required. $\square$

Remark

In Proposition 2.7, the circle $\{w : |w| = r_0\}$ can be replaced by any subset of ${{\mathbb {D}}}$ of positive logarithmic capacity, using a more delicate argument involving Green potentials in ${{\mathbb {D}}}$. We omit the details.

3 Contraction trichotomy: Proof of Theorems A and B

This section is devoted to a classification of simply connected wandering domains based on hyperbolic distances between orbits of points. More precisely we prove Theorems  A and  B and we also show that lifts of parabolic components are contracting yet not strongly contracting; (see Theorem 3.4).

The proofs are based on the results from Sect. 2 concerning self maps of the unit disk. We first show how the hyperbolic distances between orbits of points in the wandering domain compare with the distances between related orbits of points in the unit disk. We also compare the hyperbolic distortion along an orbit of a point in the wandering domain with the derivatives of the related maps of the unit disk.

Let f be a transcendental entire function with a simply connected wandering domain U and let $U_n$ be the Fatou component containing $f^n(U_0)$, for $n \ge 0$. Note that each of the domains $U_n$ is simply connected; indeed, if some $U_n$ is multiply connected, then by [2, Theorem 3.1], all the Fatou components are bounded, so f is a proper map between Fatou components and the claim follows from the Riemann–Hurwitz formula. Although $U_n = f^n(U_0)$ if $U_0$ is bounded, this is not necessarily true in the case that $U_0$ is unbounded when $U_n \setminus f^n(U)$ may contain one point; see for example [33].

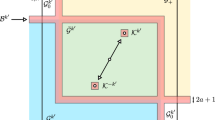
We prove Theorems A and B by considering a sequence $(g_n)$ of holomorphic self maps of the unit disk associated to f and $U_n$ in the following way. Fix a point $z_0 \in U_0$ and, for each $n \ge 0$, choose $\varphi _n: U_n \rightarrow {{\mathbb {D}}}$ to be a Riemann map such that $\varphi _n(f^n(z_0)) = 0$. Then, for $n\in {{\mathbb {N}}}$, consider the holomorphic maps $g_n:{{\mathbb {D}}}\rightarrow {{\mathbb {D}}}$ defined as

$$\begin{aligned} g_n = \varphi _n \circ f \circ \varphi _{n-1}^{-1}, \end{aligned}$$

and the composite maps $G_n:{{\mathbb {D}}}\rightarrow {{\mathbb {D}}}$ defined as

$$\begin{aligned} G_n = g_{n}\circ \cdots \circ g_1 = \varphi _n \circ f^n \circ \varphi _0^{-1}. \end{aligned}$$

Because of the choice of normalization for the Riemann maps we have that $g_n(0)=G_n(0)=0$. This setup is illustrated in Fig. 2. Each of the maps $g_n$ and $G_n$ is an inner function, but we do not use this fact in this paper.

Fig. 2

Self maps of the unit disk arising from an orbit of wandering domains

Before stating the next theorem, we recall that if $f:U\rightarrow V$ is a holomorphic map between two hyperbolic domains U and V, then the hyperbolic distortion of f at z is defined to be

$$\begin{aligned} \Vert Df(z)\Vert _U^V{:}{=}\lim _{z'\rightarrow z}\frac{{\text {dist}}_V(f(z'),f(z))}{{\text {dist}}_U(z',z)}. \end{aligned}$$

Lemma 3.1

Let U be a simply connected wandering domain of a transcendental entire function f and let $U_n$ be the Fatou component containing $f^n(U)$, for $n \ge 0$. Let $z_0\in U$ and let $g_n, G_n$ be as defined above.

• (a) If $z \in U$ and $\varphi _0(z) = w$, then

  $$\begin{aligned} {\text {dist}}_{U_n}(f^n(z),f^n(z_0)) = \log \left( \frac{1 + |G_n(w)|}{1 - |G_n(w)|}\right) , \quad \text {for } n \in {{\mathbb {N}}}. \end{aligned}$$

• (b) For each $n \in {{\mathbb {N}}}$,

  $$\begin{aligned} \lambda _n(z_0){:}{=}\Vert Df(f^{n-1}(z_0))\Vert _{U_{n-1}}^{U_{n}}=|g_n'(0)|. \end{aligned}$$

Proof

• (a) Let $n\in {{\mathbb {N}}}$. Since $G_n = \varphi _n \circ f^n \circ \varphi _0^{-1}$ and $\varphi _n$ is conformal, if $z \in U$ and $\varphi _0(z) = w,$ then

  $$\begin{aligned} {\text {dist}}_{U_n}(f^n(z),f^n(z_0))= & {} {\text {dist}}_{{{\mathbb {D}}}}(G_n(w),G_n(0)) = {\text {dist}}_{{{\mathbb {D}}}}(G_n(w),0) \\= & {} \log \left( \frac{1 + |G_n(w)|}{1 - |G_n(w)|}\right) , \end{aligned}$$

  where the last equality follows from (2.1).

• (b) Let $n\in {{\mathbb {N}}}$. Since $g_n = \varphi _n \circ f \circ \varphi _{n-1}^{-1}$ and $\varphi _n$ is conformal we have

  $$\begin{aligned} \Vert Dg_n(0)\Vert _{{\mathbb {D}}}^{{\mathbb {D}}}=\Vert Df(f^{n-1}(z_0))\Vert _{U_{n-1}}^{U_{n}}=\lambda _n(z_0). \end{aligned}$$

  Since $g_n(0) = 0$, it follows from (2.1) that

  $$\begin{aligned} \Vert Dg_n(0)\Vert _{{\mathbb {D}}}^{{\mathbb {D}}}= & {} \lim _{w\rightarrow 0}\frac{{\text {dist}}_{{\mathbb {D}}}(g_n(w), g_n(0))}{{\text {dist}}_{{\mathbb {D}}}(w,0)} = \lim _{w\rightarrow 0}\frac{{\text {dist}}_{{\mathbb {D}}}(g_n(w), 0)}{{\text {dist}}_{{\mathbb {D}}}(w,0)}\\= & {} \lim _{w \rightarrow 0} \frac{\log \left( \frac{1 + |g_n(w)|}{1 - |g_n(w)|}\right) }{\log \left( \frac{1 + |w|}{1 - |w|}\right) }\\= & {} \lim _{w \rightarrow 0} \frac{2|g_n(w)|}{2|w|} = |g_n'(0)|, \end{aligned}$$

  by using the Taylor expansion for the logarithm. $\square$

3.1 Proof of Theorem  A

We now use the results of Sect. 2 together with Lemma 3.1 to prove Theorem  A, that is, the classification of simply connected wandering domains according to the behaviour of the hyperbolic distances between orbits of points.

Let U be a simply connected wandering domain of a transcendental entire function f and let $U_n$ be the Fatou component containing $f^n(U)$, for $n \ge 0$. Also, let

$$\begin{aligned} E=\{(z,z')\in U\times U : f^k(z)=f^k(z') \text { for some }\, k\in {{\mathbb {N}}}\}. \end{aligned}$$

Let $z_0\in U_0$ and let $\varphi _n, g_n,G_n$ be as defined at the beginning of this section.

First we suppose that there exists $z_0' \in U_0$ with

$$\begin{aligned} (z_0',z_0) \notin E \quad \text {and } {\text {dist}}_{U_n}(f^n(z_0'), f^n(z_0))\underset{n\rightarrow \infty }{\longrightarrow }0. \end{aligned}$$

(3.1)

Let $w_0' = \varphi _0(z_0')$. By (3.1) and Lemma 3.1 (a), we have that $G_n(w_0') \underset{n\rightarrow \infty }{\longrightarrow }0$ and $G_n(w_0') \ne 0$ for all $n\in {{\mathbb {N}}}$. Hence by Theorem 2.1 (b) we have that $\sum _{n=1}^{\infty }(1-\lambda _n) = \infty$, where $\lambda _n = |g_n'(0)|$, and therefore that $G_n(w)\underset{n\rightarrow \infty }{\longrightarrow }0$, for all $w \in {{\mathbb {D}}}$, by Theorem 2.1 (a). By Lemma 3.1 (a) again, ${\text {dist}}_{U_n}(f^n(z), f^n(z_0))\underset{n\rightarrow \infty }{\longrightarrow }0$, for all $z \in U_0$. We conclude that ${\text {dist}}_{U_n}(f^n(z), f^n(z'))\underset{n\rightarrow \infty }{\longrightarrow }0$, for all $z,z' \in U_0$, by the triangle inequality, which is case (1).

We have shown that (3.1) implies that $\sum _{n=1}^{\infty }(1-\lambda _n) = \infty$ and that this implies that $U_0$ is contracting. Thus $U_0$ is contracting if and only if $\sum _{n=1}^{\infty }(1-\lambda _n) = \infty$, where

$$\begin{aligned} \lambda _n = |g_n'(0)| = \Vert Df(f^{n-1}(z_0))\Vert _{U_{n-1}}^{U_{n}}=\lambda _n(z_0),\;\text { for }n\in {{\mathbb {N}}}, \end{aligned}$$

by Lemma 3.1 (b).

Now suppose that there exist $z,z' \in U_0$ and $N \in {{\mathbb {N}}}$ with

$$\begin{aligned} {\text {dist}}_{U_n} (f^n(z),f^n(z')) = c(z,z') > 0, \quad \text { for all } n \ge N. \end{aligned}$$

(3.2)

Then, by the Schwarz–Pick Lemma, $f:U_n \rightarrow U_{n+1}$ is an isometry, for all $n \ge N$, and so for every pair $z,z'\in U_0$ we have that

$$\begin{aligned} {\text {dist}}_{U_n} (f^n(z),f^n(z')) = {\text {dist}}_{U_N} (f^N(z),f^N(z')), \quad \text {for } n \ge N. \end{aligned}$$

Thus, if $(z,z') \in (U \times U) \setminus E$ we have that ${\text {dist}}_{U_n} (f^n(z),f^n(z')) = c(z,z') > 0$ for all $n \ge N$ and that $U_0$ is eventually isometric, which is case (3). In this case, $\lambda _n(z) = 1$ for all $z\in U_0$ and for $n \ge N$, by the Schwarz–Pick Lemma, as required.

Finally, we show that case (2) is the only other possibility. It follows from the above proof that, if there exists $z_0' \in U_0$ for which neither (3.1) nor (3.2) holds, then the only possibility is that neither of these conditions hold for any $z \in U_0$; that is, $U_0$ is semi-contracting, which is case (2). This completes the proof of Theorem  A.

3.2 Subclassification of contracting wandering domains: Proof of Theorem B

In this subsection we prove Theorem  B, which gives sufficient conditions for a simply connected wandering domain to be strongly contracting or super-contracting. We prove parts (a) and (b) by using the results of Sect. 2 together with Lemma 3.1.

Let U be a simply connected wandering domain of a transcendental entire function f and let $U_n$ denote the Fatou component containing $f^n(U)$, for $n \ge 0$. Let $z_0\in U_0$ and let $g_n,G_n$ be as defined in the beginning of this section.

Also, for $n \in {{\mathbb {N}}}$, we let $\lambda _n =\lambda _n(z_0) = \Vert Df(f^{n-1}(z_0))\Vert _{U_{n-1}}^{U_{n}}$ and note from Lemma 3.1 (b) that $\lambda _n = |g_n'(0)|$.

To prove part (a), observe that if $\lim \sup _{n \rightarrow \infty } \frac{1}{n}\sum _{k=1}^n \lambda _k = a < 1$, then it follows from Theorem 2.6 (a) that

$$\begin{aligned} |G_n(w)| = O(c^n) \;\text { as }n\rightarrow \infty , \quad \text {for } w \in {{\mathbb {D}}}, \; c \in (a,1). \end{aligned}$$

So, by Lemma 3.1 (a), if we take $z \in U_0$ and put $w = \varphi _0(z)$, then

$$\begin{aligned} {\text {dist}}_{U_n}(f^n(z), f^n(z_0)) = O(c^n)\;\text { as }n\rightarrow \infty , \quad \text {for } c\in (a,1). \end{aligned}$$

This proves part (a) of Theorem  B.

To prove part (b), we note that, if $\lim _{n \rightarrow \infty } \frac{1}{n}\sum _{k=1}^n \lambda _k = 0$, then, from Theorem 2.6 (b),

$$\begin{aligned} \left( {\text {dist}}_{U_n}(f^n(z), f^n(z_0))\right) ^{1/n} \rightarrow 0 \quad \text {as } n\rightarrow \infty , \end{aligned}$$

and hence $U_0$ is super-contracting.

To prove part (c) we need to show that, for $n \in {{\mathbb {N}}}$, $z \in U_0$,

$$\begin{aligned} \lim \sup _{n \rightarrow \infty } \frac{1}{n}\sum _{k=1}^n \lambda _k(z) = \lim \sup _{n \rightarrow \infty } \frac{1}{n}\sum _{k=1}^n \lambda _k, \quad \text {for } z \in U_0. \end{aligned}$$

(3.3)

(Recall that $\lambda _k = \lambda _k(z_0)$.) We begin by supposing that $\lim \sup _{n \rightarrow \infty } \frac{1}{n}\sum _{k=1}^n \lambda _k = a < 1$ and fix $c \in (a,1)$ and $z \in U_0$. From part (a) above, there exists $C > 0$ such that

$$\begin{aligned} {\text {dist}}_{U_k}(f^k(z), f^k(z_0)) \le C c^k, \quad \text {for } k \in {{\mathbb {N}}}. \end{aligned}$$

(3.4)

We now use the following result of Beardon and Minda to obtain a bound on the difference between $\lambda _k(z)$ and $\lambda _k$.

Lemma 3.2

[8, Theorem 11.2] Let U, V be hyperbolic domains and let $f:U\rightarrow V$ be holomorphic. Then

$$\begin{aligned} {\text {dist}}_{{{\mathbb {D}}}}(\Vert Df(z)\Vert _U^V, \Vert Df(w)\Vert _U^V) \le 2 {\text {dist}}_{U}(z,w), \quad \text {for all } z,w \in U. \end{aligned}$$

It follows from Lemma 3.2 together with (3.4) that, under our supposition,

$$\begin{aligned} {\text {dist}}_{{{\mathbb {D}}}}(\lambda _k(z), \lambda _k) \le 2C c^k, \quad \text {for } k \in {{\mathbb {N}}}. \end{aligned}$$

Since

$$\begin{aligned} {\text {dist}}_{{{\mathbb {D}}}}(\lambda _k(z), \lambda _k) = \left| \int _{\lambda _k}^{\lambda _k(z)} \frac{2\,dt}{1-t^2}\right| \ge \left| \int _{\lambda _k}^{\lambda _k(z)} 2\,dt\right| = 2|\lambda _k(z) - \lambda _k|, \end{aligned}$$

it follows that

$$\begin{aligned} |\lambda _k(z) - \lambda _k| \le C c^k, \quad \text {for } k \in {{\mathbb {N}}}. \end{aligned}$$

So, if $\lim \sup _{n \rightarrow \infty } \frac{1}{n}\sum _{k=1}^n \lambda _k = a < 1$, then

$$\begin{aligned} \lim \sup _{n \rightarrow \infty } \frac{1}{n}\sum _{k=1}^n \lambda _k(z)\le & {} \lim \sup _{n \rightarrow \infty } \frac{1}{n}\sum _{k=1}^n \lambda _k + \lim \sup _{n \rightarrow \infty } \frac{C}{n}\sum _{k=1}^n c^k\\= & {} \lim \sup _{n \rightarrow \infty } \frac{1}{n}\sum _{k=1}^n \lambda _k = a. \end{aligned}$$

Since the roles of $z_0$ and z are interchangeable, we have shown that (3.3) holds whenever $\lim \sup _{n \rightarrow \infty } \frac{1}{n}\sum _{k=1}^n \lambda _k < 1$. The only remaining case is that

$$\begin{aligned} \lim \sup _{n \rightarrow \infty } \frac{1}{n}\sum _{k=1}^n \lambda _k(z) = 1 = \lim \sup _{n \rightarrow \infty } \frac{1}{n}\sum _{k=1}^n \lambda _k. \end{aligned}$$

This completes the proof of Theorem  B.

3.3 Rate of contraction in parabolic components

It is clear that if a wandering domain U is the lift of an attracting component V, then U is strongly contracting and, if V is super-attracting, then U is super-contracting. We end this section by showing that if a wandering domain U occurs as a lift of a parabolic component, then U is contracting but not strongly contracting. We need the following lemma; see [38, p. 157], for example.

Lemma 3.3

If G is a simply connected domain, not the whole complex plane, then for $z,w \in G$,

$$\begin{aligned} {\text {dist}}_G(z,w)\ge \frac{1}{2}\log \left( 1+ \frac{|z-w |}{\min \{{\text {dist}}(z,\partial G), {\text {dist}}(w,\partial G)\}}\right) . \end{aligned}$$

We have the following general result about the contraction rate in a parabolic component. The estimates in this result are fairly easy to obtain for hyperbolic distances within a parabolic petal, by using Fatou coordinates, but more delicate arguments seem to be needed within a parabolic component. These estimates may be known, but we are not aware of a reference.

Theorem 3.4

Let V be an invariant parabolic component of a meromorphic function f. Then, for all $z_0, z_0' \in V$, either $f^m(z_0)=f^m(z'_0)$ for some $m\in {{\mathbb {N}}}$ or there exist positive constants k and K depending on $z_0$, $z'_0$ and p, the number of petals, such that

$$\begin{aligned} \frac{k}{n} \le {\text {dist}}_V(f^n(z_0),f^n(z'_0))\le \frac{K}{n},\;\text { for }n\in {{\mathbb {N}}}. \end{aligned}$$

(3.5)

Proof

Without loss of generality we assume that 0 is the parabolic fixed point in $\partial V$ and let p be the number of petals of f at 0. The following proof uses detailed estimates from the discussion of Abel’s functional equation in [7, pages 110–122] and we start by summarising this discussion, mainly using the notation from [7].

First, the function f is conformally conjugate near 0 to an analytic function of the form

$$\begin{aligned} F(z)=z-z^{p+1}+O(z^{2p+1}) \quad \text {as }z \rightarrow 0. \end{aligned}$$

Substituting $w=z^{-p}$, $z=w^{-1/p}$, where $w^{-1/p}$ denotes the principal root, we obtain

$$\begin{aligned} g(w)=1/\left( F(w^{-1/p})\right) ^p = w+p+A/w+O(1/w^{1+1/p}) \quad \text {as }w \rightarrow \infty , \end{aligned}$$

for some constant A, from which it follows that there exists a parabola-shaped domain of the form $\Pi =\{u+iv:v^2>4K(K-u)\}$, $K>0$, that is forward invariant under g. For $w\in \Pi$, we have

$$\begin{aligned} g^n(w) = np+\frac{A}{p}\log n+u_n(w), \quad \text {for } n\in {{\mathbb {N}}}, \end{aligned}$$

(3.6)

where the functions $u_n$ are holomorphic in $\Pi$ and converge locally uniformly on $\Pi$ to a univalent function u, which satisfies $u(g(w))=u(w)+p$, a form of Abel’s functional equation.

Now let P denote the petal-shaped domain that corresponds to $\Pi$ under the mapping $w\mapsto w^{-1/p}$ and which is symmetric with respect to the positive real axis, subtending an angle of $2\pi /p$ at 0. Then P is invariant under F. Let $w_0, w'_0\in \Pi$ be distinct points and let $z_0 = w_0^{-1/p}$, $z'_0 = (w'_0)^{-1/p}$ be the corresponding points in P; see Fig. 3.

Fig. 3

Conjugate orbits: on the left two orbits in P under F and on the right the corresponding orbits in $\Pi$ under g (in this figure, $p=3$)

It follows from the above properties of the functions $u_n$ and the univalence of u that

$$\begin{aligned} g^n(w'_0)-g^n(w_0) = u_n(w'_0)-u_n(w_0) \rightarrow u(w'_0)-u(w_0) \ne 0 \;\text { as } n\rightarrow \infty . \end{aligned}$$

(3.7)

On substituting $z=w^{-1/p}$ we find that $z_n=F^n(z_0)$ and $z'_n= F^n(z'_0)$ both approach 0 tangentially to the positive real axis through P. Moreover, by (3.6),

$$\begin{aligned} |z_n|=|g^n(w_0)|^{-1/p}=\frac{1}{\left| np+\frac{A}{p}\log n+u_n(w_0)\right| ^{1/p}}\sim \frac{1}{(np)^{1/p}} \;\text { as}\;n\rightarrow \infty ,\nonumber \\ \end{aligned}$$

(3.8)

and

$$\begin{aligned} |z'_n|=|g^n(w'_0)|^{-1/p}=\frac{1}{\left| np+\frac{A}{p}\log n+u_n(w'_0)\right| ^{1/p}}\sim \frac{1}{(np)^{1/p}} \;\text { as}\;n\rightarrow \infty .\nonumber \\ \end{aligned}$$

(3.9)

Also, by (3.6),

$$\begin{aligned} g^n(w)^{-1/p}=\frac{1}{(np)^{1/p}}\left( 1-\frac{1}{p}\left( \frac{A\log n}{np^2}-\frac{u_n(w)}{np}\right) +O\left( \left( \frac{\log n}{n}\right) ^2\right) \right) \;\text { as}\;n\rightarrow \infty , \end{aligned}$$

so, by (3.7), (3.8) and (3.9),

$$\begin{aligned} |z_n-z_n'|=|g^n(w_0)^{-1/p}-g^n(w'_0)^{-1/p}|\sim \frac{|u(w_0)-u(w'_0)|}{p(np)^{1+1/p}}\;\text { as}\;n\rightarrow \infty .\nonumber \\ \end{aligned}$$

(3.10)

Since F is conformally conjugate to f near 0, we deduce that the estimates (3.8), (3.9) and (3.10) continue to hold if we redefine $z_n=f^n(z_0)$ and $z'_n=f^n(z'_0)$, for $n \in {{\mathbb {N}}}$, where $z_0$ and $z'_0$ are redefined to be the corresponding points in the invariant parabolic component V for f. Without loss of generality, we may suppose that orbits under f in V also approach 0 tangentially to the positive real axis. Note that V is one of p distinct invariant parabolic components for f at 0, each containing an invariant petal-shaped domain subtending an angle of $2\pi /p$ at 0.

Therefore, by Lemma 3.3 and the fact that ${\text {dist}}(z,\partial V)\le |z|$, for $z\in V$, together with (3.8), (3.9) and (3.10), we have

$$\begin{aligned} {\text {dist}}_{V}(z_n,z_n')\ge & {} \frac{1}{2} \log \left( 1+ \frac{|z_n-z_n'|}{\min \{{\text {dist}}(z_n,\partial V), {\text {dist}}(z_n',\partial V)\}}\right) \\\ge & {} \frac{1}{2} \log \left( 1+ \frac{|z_n-z_n'|}{\min \{|z_n|, |z_n'|\}}\right) \\\ge & {} k \frac{1/n^{1+1/p}}{1/n^{1/p}}=\frac{k}{n},\;\text { for } n\in {{\mathbb {N}}}, \end{aligned}$$

for some positive constant k depending on $z_0$, $z'_0$ and p.

Finally, for $n \in {{\mathbb {N}}}$, let $\gamma _n$ denote the line segment joining $z_n$ to $z_n'$. Then, in view of the fact that $z_n$ and $z'_n$ approach 0 tangentially to the positive real axis, the line segment $\gamma _n$, for n sufficiently large, lies in the invariant petal-shaped domain in V. Also, for n sufficiently large, we have

$$\begin{aligned} \min \{{\text {dist}}(z_n,\partial V), {\text {dist}}(z_n',\partial V)\} \ge \frac{1}{2} \sin (\pi /p) |z_n|. \end{aligned}$$

Therefore, by the standard hyperbolic density estimate in a simply connected domain (see, for example, [17, page 13]), (3.8), (3.9), and the triangle inequality, we have

$$\begin{aligned} {\text {dist}}_{V}(z_n,z_n')\le & {} \int _{\gamma _n} \rho _{V}(z)\,|dz| \\\le & {} \int _{\gamma _n} \frac{2}{{\text {dist}}(z,\partial V)}\,|dz| \\\le & {} \frac{2|z_n-z_n'|}{\min \{{\text {dist}}(z_n,\partial V), {\text {dist}}(z_n',\partial V)\}-\tfrac{1}{2}|z_n-z'_n|}\\\le & {} K \frac{1/n^{1+1/p}}{1/n^{1/p}}=\frac{K}{n}, \end{aligned}$$

for some positive constant K depending on $z_0$, $z'_0$ and p, and n sufficiently large.

Finally, we note that, for all pairs of points $z_0, z'_0 \in V$ with disjoint orbits, we have $f^n(z_0), f^n(z'_0)\in V$ for n sufficiently large. This completes the proof. $\square$

Remark

Using a more careful analysis of the size of the hyperbolic density in V near the points $z_n$ and $z'_n$ we can show that the estimate (3.5) in Theorem 3.4 can be replaced by

$$\begin{aligned} {\text {dist}}_V(f^n(z_0),f^n(z'_0))\sim \frac{c}{n}\;\text { as }n\rightarrow \infty , \end{aligned}$$

for some positive constant c depending on $z_0$, $z'_0$ and p. The proof uses results about the behaviour of any Riemann map from a sector of angle $2\pi /p$ onto V which maps 0 to 0, justified by using standard results about angular derivatives of conformal mappings at boundary points.

By conformality and Definition 1.2, we have the following corollary of Theorem 3.4.

Corollary 3.5

Let U be a simply connected wandering domain that is the lift of an invariant parabolic component V and let $U_n$ be the Fatou component containing $f^n(U)$, for $n \ge 0$. Then, for all $z_0, z'_0\in U$, either $f^m(z_0)=f^m(z'_0)$ for some $m\in {{\mathbb {N}}}$ or there exist positive constants k and K depending on $z_0$ and $z'_0$ such that

$$\begin{aligned} \frac{k}{n} \le {\text {dist}}_{U_n}(f^{n}(z_{0}),f^{n}(z'_{0}))\le \frac{K}{n}, \quad \text {for } n \in {{\mathbb {N}}}. \end{aligned}$$

In particular, U is contracting but not strongly contracting.

Fig. 4

Left: Dynamical plane of F in Example 2. The super-attracting basin of $w=0$ is shown in light blue, while in gray we see the parabolic basin of $w=1$. Right: Dynamical plane of f. In blue the Baker domain (lift of the superattracting basin). In black the parabolic invariant basin at $z=0$. In gray the wandering domains. The range is $[-9,9]\times [-9,9]$ (color figure online)

Here are two examples of simply connected wandering domains, obtained by lifting parabolic components, which are contracting but not strongly contracting.

Example 1

Consider the entire functions

$$\begin{aligned} f(z)=z+e^{-z}+2\pi i, \quad g(z)=z+e^{-z} \quad \text {and}\quad F(w)=we^{-w}. \end{aligned}$$

Then both f and g are obtained by lifting F under the exponential function $w=e^{-z}$. Since F has an invariant parabolic component associated with the fixed point at 0, the function g has congruent unbounded invariant Baker domains $U_n$, $n\in {{\mathbb {Z}}}$, such that $U_n\subset \{z:(2n-1)\pi<{\text {Im}}(z)<(2n+1)\pi \}$; see [19, 25]. Since $J(f)=J(g)$, by [12], the components $U_n$ form a sequence of simply connected wandering domains which, by Corollary 3.5, are contracting but not strongly contracting.

Example 2

As another example, consider

$$\begin{aligned} f(z)=2z + 1 - e^{z} \quad \text {and}\quad F(w)=e\,w^2e^{-w}, \end{aligned}$$

which belongs to the same family (that is, $F_{\lambda ,d}(w)=\lambda \,w^d e^{-w}$, $\lambda \in {{\mathbb {C}}}, d\in {{\mathbb {N}}}$) as the example in Fig. 1, both closely related to an example of Bergweiler [11]. In this case, f is a lift of F under $w=e^{z}$, and F has an invariant parabolic component associated with the fixed point at 1 which lifts to congruent, bounded, simply connected Fatou components, $V_n$, $n\in {{\mathbb {Z}}}$, say, of f such that $0\in \partial V_0$ and

$$\begin{aligned} V_n=V_0+2n\pi i,\;\text { for } n\in {{\mathbb {Z}}},\quad \text {and}\quad f(V_n)=V_{2n},\;\text { for } n\in {{\mathbb {Z}}}. \end{aligned}$$

From this it follows that $V_{2n}$, $n\ge 1$, is a sequence of bounded, escaping, simply connected wandering domains which, by Corollary 3.5, are contracting but not strongly contracting (see Fig. 4).

4 Convergence to the boundary: Proof of Theorem  C

In this section we give the proof of Theorem  C, the classification of simply connected wandering domains in terms of whether orbits of points converge to the boundary. Recall that the Euclidean distance of a point z from the boundary of a hyperbolic domain U is closely related to the hyperbolic density $\rho _U(z)$ of the point in the domain. Indeed, if U is a simply connected wandering domain of a transcendental entire function f, $U_n$ is the Fatou component containing $f^n(U)$, for $n \ge 0$, and $z \in U_0$, then by standard estimates [17, page 13]

$$\begin{aligned} \hbox {dist}(f^n(z), \partial U_n) \rightarrow 0 \iff \rho _{U_n}(f^n(z)) \rightarrow \infty . \end{aligned}$$

We prove Theorem  C by considering the hyperbolic densities $\rho _{U_n}(f^n(z))$. In fact, we show that a trichotomy as in Theorem  C occurs if we consider the quantities $a_n\rho _{U_n}(f^n(z))$, for any sequence $a_n$ and not just for $a_n = 1$. As we mentioned in the introduction, the issue of convergence to the boundary is somehow delicate in that it is tightly related to the shape of the wandering domains, and there may be situations where it is more appropriate to use an alternative definition involving different sequences $a_n$. For example, if the domains $U_n$ are shrinking then it may make sense to say that $z_n$ converges to the boundary if $a_n \rho _{U_n}(f^n(z)) \rightarrow \infty$ as $n \rightarrow \infty$ where

$$\begin{aligned} a_n=\sup _D \{{\text {diam}}D : D\; \text {is a disk contained in}\;U_n\}. \end{aligned}$$

In order to prove Theorem  C we need the following lemma, which can be thought of as a Harnack inequality for hyperbolic density in a simply connected domain; see [6, Lemma 6.2] for a similar type of result (with a different proof) for hyperbolic density in the unit disk.

Lemma 4.1

(Estimate of hyperbolic quantities) Let $U \subset {\mathbb {C}}$ be a simply connected domain. Then, for all $z,z'\in U$,

$$\begin{aligned} \exp (-2{\text {dist}}_U(z,z'))\le \frac{\rho _U(z')}{\rho _U(z)} \le \exp (2{\text {dist}}_U(z,z')). \end{aligned}$$

Proof

Let $z,z' \in U$ and let $\varphi :{{\mathbb {D}}}\rightarrow U$ be a Riemann map with $\varphi (0)=z$ and $\varphi (r)=z'$, for some $r \in [0,1)$. By conformal invariance of the hyperbolic metric, together with (2.1),

$$\begin{aligned} {\text {dist}}_U(z,z')={\text {dist}}_{{{\mathbb {D}}}}(0,r)=\log \frac{1+r}{1-r}, \end{aligned}$$

and, by the definition of the hyperbolic density on U,

$$\begin{aligned} \rho _U(z)&= {\rho _{{\mathbb {D}}}(0)}/{|\varphi '(0)|}= {2}/{|\varphi '(0)|}\\ \rho _U(z')&=\rho _{{\mathbb {D}}}(r)/|\varphi '(r)|=\frac{2}{1-r^2}\bigg / |\varphi '(r)|. \end{aligned}$$

Also, by a standard distortion theorem for conformal maps [36, p. 9],

$$\begin{aligned} \frac{1-r}{(1+r)^3}\le \frac{|\varphi '(r)|}{|\varphi '(0)|}\le \frac{1+r}{(1-r)^3}. \end{aligned}$$

Putting everything together we obtain the lower bound,

$$\begin{aligned} \frac{\rho _U(z')}{\rho _U(z)}=\frac{1}{1-r^2}\frac{|\varphi '(0)|}{|\varphi '(r)|}\ge \frac{(1-r)^2}{(1+r)^2} = \exp (-2{\text {dist}}_U(z,z')), \end{aligned}$$

and the upper bound follows by symmetry. $\square$

Remark

It is easy to check that the inequalities in Lemma 4.1 are sharp in the case when U is ${\mathbb {C}}\setminus (-\infty ,0]$ and the points $z,z'$ lie on the positive real axis.

We now prove the main result of this section.

Theorem 4.2

Let U be a simply connected wandering domain of a transcendental entire function f, let $U_n$ be the Fatou component containing $f^n(U)$, for $n \ge 0$, and let $(a_n)$ be a real positive sequence.

• (a) If there is a subsequence $n_k\rightarrow \infty$ and a point $z\in U_0$ such that $a_{n_k} \rho _{U_{n_k}}(f^{n_k}(z))\rightarrow \infty$, then the same is true for all other points in $U_0$.

• (b) If there is a subsequence $m_k\rightarrow \infty$ and a point $z\in U_0$ such that $a_{m_k} \rho _{U_{m_k}}(f^{m_k}(z))$ is bounded, then the same is true for all other points in $U_0$.

Proof

• (a) Suppose that $a_{n_k} \rho _{U_{n_k}}(f^{n_k}(z))\rightarrow \infty$ as $k \rightarrow \infty$ and let $z' \in U_0$ with $z'\ne z$. By the contraction property of the hyperbolic metric, we have that

  $$\begin{aligned} {\text {dist}}_{U_n}(f^{n}(z),f^{n}(z')) \le {\text {dist}}_{U_0}( z,z')=:C, \quad \text { for } n \in {{\mathbb {N}}}. \end{aligned}$$

  By Lemma 4.1, $\rho _{U_n}(f^n(z')) \ge e^{-2C} \rho _{U_n}(f^n(z))$, for $n \in {{\mathbb {N}}}$. Hence

  $$\begin{aligned} a_{n_k} \rho _{U_{n_k}}(f^{n_k}(z'))\ge e^{-2C} a_{n_k} \rho _{U_{n_k}}(f^{n_k}(z))\rightarrow \infty \quad \text {as } k \rightarrow \infty \end{aligned}$$

• (b) Now suppose that $a_{m_k} \rho _{U_{m_k}}(f^{m_k}(z)) \le M$, for $k \in {{\mathbb {N}}}$, and let $z' \in U_0$ with $z'\ne z$. Again, by the contraction property of the hyperbolic metric, we have that

  $$\begin{aligned} {\text {dist}}_{U_{m_k}}(f^{m_k}(z),f^{m_k}(z')) \le {\text {dist}}_{U_0}( z,z')=:C. \end{aligned}$$

  Now, applying Lemma 4.1 and interchanging z and $z'$, we obtain that

  $$\begin{aligned} \rho _{U_{m_k}} (f^{m_k}(z')) \le e^{2C} \rho _{U_{m_k}}(f^{m_k}(z)), \end{aligned}$$

  which implies that

  $$\begin{aligned} a_{m_k} \rho _{U_{m_k}}(f^{m_k}(z'))\le e^{2C} a_{m_k} \rho _{U_{m_k}}(f^{m_k}(z)) \le M e^{2C}, \end{aligned}$$

  so $a_{m_k} \rho _{U_{m_k}}(f^{m_k}(z'))$ is bounded, for $k \in {{\mathbb {N}}}$. $\square$

The result of Theorem C follows from Theorem 4.2, by taking $a_n = 1$, for $n \ge 0$.

5 Constructing wandering domains

We begin this section with the proof of Theorem  D, which we then use together with an extension of Runge’s Approximation Theorem to prove Theorem 5.3. This result enables us to construct bounded simply connected wandering domains in which various different dynamical behaviours can be specified and is the main tool that we use to construct examples in Sect. 6.

5.1 Proof of Theorem  D

Let f be a transcendental entire function and let $\gamma _n$, $\Gamma _n$, $n_k$, $L_k$, and D be as in Theorem D; see Fig. 5. It follows from properties (a) and (b) of Theorem  D that for each $n,m\in {{\mathbb {N}}}$ with $n\ne m$ the curve $\gamma _n$ is in ${\text {ext}}\gamma _m$ and so, by property (c) and Montel’s theorem, there exist Fatou components $U_n$ such that

$$\begin{aligned} \overline{{\text {int}}\gamma _n} \subset U_n, \;\text {for}\;n \ge 0. \end{aligned}$$

(5.1)

Notice that, a priori, the components $U_n$ need not be different from each other. One of our goals is to show that they are indeed different, by proving that $U_n \subset {\text {int}}\Gamma _n$, for $n\ge 0$.

Fig. 5

Sketch of the setup of the proof of Theorem  D

By property (e), the domain D must contain an attracting fixed point and so it is contained in an attracting Fatou component, say V. It then follows by property (e) that for all $k \ge 0$ the set $L_k$ is contained in a union of Fatou components, $V_k$ say, that maps into V. As above, notice that the $V_k$’s may all be the same component. Since for every n we have that $\overline{D}\subset {\text {ext}}{\Gamma _n}$ while $\gamma _n\subset {\text {int}}{\Gamma _n}$, we deduce that $U_0$ is not in the grand orbit of V and hence that $\bigcup _{n\ge 0} U_n \cap \bigcup _{k\ge 0}V_k=\emptyset$. Therefore

$$\begin{aligned} {\text {dist}} (z',\partial U_{{n}_{k}})< \delta _k {:}{=}\max \{ {\text {dist}}(z ,L_k) : z \in \Gamma _{n_k}\},\;\text { for all}\; z' \in \Gamma _{n_k} \cap U_{{n}_{k}}. \end{aligned}$$

(5.2)

Note that $U_n$ is simply connected for $n \ge 0$. Indeed, if $U_n$ is multiply connected for some $n \ge 0$, then it is a wandering domain and by [13, Theorem 1.2] there exists $N>0$ such that $f^k({\text {int}}\gamma _n)$ contains an annulus $A(r_k,R_k)$ for all $k\ge N$ with $R_k/r_k \rightarrow \infty$ as $k \rightarrow \infty$. It follows by property (c) that $A(r_k,R_k)$ is contained in ${\text {int}} \gamma _{n+k}$ and this contradicts property (b). So $U_n$ must be simply connected for $n \ge 0$.

We now show that $U_n \subset {\text {int}}\Gamma _n$, for $n \ge 0$, using proof by contradiction. If there exists $m \ge 0$ for which $U_m$ is not a subset of ${\text {int}}\;\Gamma _m$, then it follows from (5.1) and property (a) that $U_m \cap \Gamma _m \ne \emptyset$ and so we can take $z_m \in {\text {int}}\gamma _m$ and $z_m'\in U_m \cap \Gamma _m$, and join them by a compact curve $C_m \subset (U_m \cap {\text {int}}\;\Gamma _m)$.

Then, by properties (c) and (d), we can choose simple curves $C_n$, $n \ge m$, such that $C_n \subset f^{n-m}(C_m) \subset (U_n \cap {\text {int}}\;\Gamma _n)$ and also $C_n$ joins $z_n{:}{=}f^{n-m}(z_m) {\in {\text {int}}\gamma _{n}}$ to a point $z_n' \in \Gamma _n \cap f^{n-m}(C_m) \subset U_n$, while $C_n$ lies in $\overline{{\text {int}} \Gamma _n}$. Such a curve $C_n$ must also intersect $\gamma _n$. Then, on the one hand, since $C_n \subset f^{n-m}(C_m)$ and $f^{n-m}:U_m \rightarrow U_n$ is a hyperbolic contraction, we have that

$$\begin{aligned} {\text {length}}_{U_n} C_n \le {\text {length}}_{U_n} f^{n-m}(C_m) \le {\text {length}}_{U_m} C_m < \infty , \end{aligned}$$

(5.3)

for all $n\ge m$. On the other hand, by Lemma 3.3 and (5.2), for $n_k \ge m$, we have

$$\begin{aligned} {\text {length}}_{U_{n_k}} C_{n_k}&\ge {\text {dist}}_{U_{n_k}} (z_{n_k},z_{n_k}')\\&\ge \frac{1}{2} \log \left( 1+ \frac{|z_{n_k}-z_{n_k}'|}{\min \{{\text {dist}}(z_{n_k}, \partial U_{n_k}), {\text {dist}}(z_{n_k}', \partial U_{n_k})\}}\right) \\&\ge \frac{1}{2} \log \left( 1+ \frac{|z_{n_k}-z_{n_k}'|}{{\text {dist}}(z_{n_k}', \partial U_{n_k})}\right) \\&\ge \frac{1}{2} \log \left( 1+ \frac{{\text {dist}}(\gamma _{n_k}, \Gamma _{n_k})}{\delta _k}\right) . \end{aligned}$$

By property (f), this quantity tends to infinity as $k\rightarrow \infty$, which contradicts (5.3), so $U_m \subset {\text {int}}\Gamma _m$ and hence $U_m$ is a bounded wandering domain by property (b).

Finally, suppose that, for some $n \ge 0$, there exists $z_n \in {\text {int}}\gamma _n$ such that both $f(\gamma _n)$ and $f(\Gamma _n)$ wind $d_n$ times round $f(z_n)$. Since $f(\Gamma _n)$ winds $d_n$ times around $f(z_n)$, we deduce that f takes the value $f(z_n)$ exactly $d_n$ times in ${\text {int}}\Gamma _n$. Similarly, f takes the value $f(z_n)$ exactly $d_n$ times in ${\text {int}}\gamma _n$. Hence f takes the value $f(z_n)$ exactly $d_n$ times in $U_n$. Since $U_n$ is a bounded Fatou component, $f:U_n \rightarrow U_{n+1}$ is a proper map; since the above argument holds for a neighbourhood of $f(z_n)$, we deduce that the degree of f on $U_n$ is equal to $d_n$.

5.2 Main construction result

In the proof of our main construction result, Theorem 5.3 below, we use the following extension of the main lemma in [21], which is a strong version of the well-known Runge’s Approximation Theorem.

Lemma 5.1

(Approximating on infinitely many compact sets) Let $(E_n)$ be a sequence of compact subsets of ${\mathbb {C}}$ with the following properties:

• (i) ${\mathbb {C}}\setminus E_n$ is connected, for $n \ge 0$;

• (ii) $E_n \cap E_m = \emptyset$, for $n \ne m$;

• (iii) $\min \{|z|: z \in E_n\} \rightarrow \infty$ as $n \rightarrow \infty$.

Suppose $\psi$ is holomorphic on $E = \bigcup _{n=0}^{\infty } E_n$ and $j\in {{\mathbb {N}}}$. For $n \ge 0$, let $\varepsilon _n > 0$ and let $z_{n,i} \in E_n$, $1 \le i \le j$. Then there exists an entire function f satisfying, for $n \ge 0$,

$$\begin{aligned}&|f(z)-\psi (z)|<\varepsilon _n, \quad \text {for } z\in E_n; \end{aligned}$$

(5.4)

$$\begin{aligned}&f(z_{n,i})=\psi (z_{n,i}), \quad f'(z_{n,i}) = \psi '(z_{n,i}),\;\text { for } 1\le i\le j. \end{aligned}$$

(5.5)

The main lemma in [21] allows for one point $z_n$ in every compact set at which f and $f'$ can be specified, but its proof can easily be modified to hold for finitely many points in every $E_n$, as stated above.

The following lemma will also be used in the proof of Theorem 5.3.

Lemma 5.2

(Hyperbolic distance on disks) Suppose that $0<s<r<1<R$ and set

$$\begin{aligned} c(s,R)= \frac{1-s^2}{R-s^2/R},\quad D_r=D(0,r) \quad \text {and}\quad D_R=D(0,R). \end{aligned}$$

If $|z|,|w|\le s$, then

$$\begin{aligned} {\text {dist}}_{D_R}(z,w)= {\text {dist}}_{{\mathbb {D}}}({z}/{R},{w}/{R})\ge c(s,R){\text {dist}}_{{\mathbb {D}}}(z,w), \end{aligned}$$

(5.6)

and

$$\begin{aligned} {\text {dist}}_{D_r}(z,w)= {\text {dist}}_{{\mathbb {D}}}({z}/{r},{w}/{r})\le \frac{1}{c(s/r,1/r)}{\text {dist}}_{{\mathbb {D}}}(z,w). \end{aligned}$$

(5.7)

Also, $0<c(s,R)<1$ and if the variables s, r and R satisfy in addition

$$\begin{aligned} 1-r=o(1-s)\;\text { as } s\rightarrow 1\quad \text {and}\quad R-1=O(1-r)\;\text { as } r\rightarrow 1, \end{aligned}$$

(5.8)

then

$$\begin{aligned} c(s,R)\rightarrow 1\;\text { as}\;s \rightarrow 1, \end{aligned}$$

(5.9)

and

$$\begin{aligned} c\left( s/r,1/r \right) \rightarrow 1\;\text { as}\;s \rightarrow 1. \end{aligned}$$

(5.10)

Proof

Suppose that $0<s<r<1<R$ and take $z,w \in {\mathbb {D}}$ with $|z|,|w|\le s$. Let $\gamma$ be the hyperbolic geodesic in ${\mathbb {D}}$ joining z/R to w/R. Then

$$\begin{aligned} {\text {dist}}_{{\mathbb {D}}}({z}/{R},{w}/{R})= \int _{\gamma }\frac{2\,|dt|}{1-|t|^2}. \end{aligned}$$

Now substitute $\zeta = Rt$, $t \in {\mathbb {D}}$, so $|d\zeta |=R|dt|.$ Also let $R\gamma {:}{=} \{Rz: z \in \gamma \}$. Since $R>1$, we have

$$\begin{aligned} {\text {dist}}_{{\mathbb {D}}}({z}/{R},{w}/{R})= \frac{1}{R}\int _{R\gamma }\frac{2\,|d\zeta |}{1-|\zeta |^2/R^2}= R\int _{R\gamma }\frac{2\,|d\zeta |}{R^2-|\zeta |^2}. \end{aligned}$$

Now for $\zeta \in R\gamma$ we have $|\zeta |\le s$, so

$$\begin{aligned} \frac{R^2-|\zeta |^2}{1-|\zeta |^2} \le \frac{{ R^2-s^2}}{1-s^2}, \quad \text {for }\zeta \in R\gamma . \end{aligned}$$

Hence

$$\begin{aligned} {\text {dist}}_{{\mathbb {D}}}({z}/{R},{w}/{R})= R\int _{R\gamma }\frac{2\,|d\zeta |}{R^2-|\zeta |^2} \ge \frac{R(1-s^2)}{R^2-s^2} \int _{R\gamma }\frac{2\,|d\zeta |}{1-|\zeta |^2}\ge c(s,R){\text {dist}}_{{\mathbb {D}}}(z,w), \end{aligned}$$

since

$$\begin{aligned} {\text {dist}}_{{\mathbb {D}}}(z,w)= \min \left\{ \int _{\gamma '}\frac{2\,|d\zeta |}{1-|\zeta |^2}:\;\text {for all paths}\;\gamma '\;\text {joining}\;z\;\text {to}\;w\;\text {in}\; {\mathbb {D}}\right\} . \end{aligned}$$

This proves (5.6).

Next,

$$\begin{aligned} {\text {dist}}_{D_r}(z,w)={\text {dist}}_{{\mathbb {D}}}({z}/{r},{w}/{r})\;\;\text {and}\;\; \left| \frac{z}{r}\right| ,\left| \frac{w}{r}\right| \le \frac{s}{r}<1. \end{aligned}$$

Hence, by (5.6), with s, r and R replaced by s/r, 1 and 1/r, respectively, and z, w replaced by z/r and w/r, respectively, we obtain

$$\begin{aligned} {\text {dist}}_{{\mathbb {D}}}({z}/{r},{w}/{r}) \le \frac{1}{c(s/r,1/r)}{\text {dist}}_{D_{1/r}}({z}/{r},{w}/{r})= \frac{1}{c(s/r,1/r)}{\text {dist}}_{{\mathbb {D}}}(z,w). \end{aligned}$$

This proves (5.7).

It is clear that $0<c(s,R)<1$ since $0<s<1<R$. Finally, suppose that (5.8) holds. Then $R-1=O(1-r)=o(1-s)$ as $s\rightarrow 1$ and hence

$$\begin{aligned} c(s,R)=\frac{R(1-s)(1+s)}{(R-s)(R+s)}= \frac{R(1-s)}{1-s+o(1-s)}\,\frac{1+s}{R+s}\rightarrow 1\;\text { as } s\rightarrow 1, \end{aligned}$$

and

$$\begin{aligned} c(s/r,1/r)= \frac{(r-s)(1+s/r)}{(1-s)(1+s)}= \frac{1-s + o(1-s)}{1-s}\,\frac{1+s/r}{1+s} \rightarrow 1\;\text { as } s\rightarrow 1, \end{aligned}$$

which give (5.9) and (5.10). $\square$

We now give our main construction result, which we use in Sect. 6 to construct examples. In these examples, we shall prescribe the orbits of at most two points $z_1,z_2 \in D(0,r_0)$, although the result below allows us to prescribe the orbits of any finite number of points in $D(0,r_0)$.

Theorem 5.3

(Main construction) Let $b_{n}$, $n\in {{\mathbb {N}}}$, be a sequence of Blaschke products of corresponding degrees $d_n \ge 1$ and let $T_n$, $n\ge 0$, be the sequence of translations $z \mapsto z+4n$ and $D_n$, $n\ge 0$, be the sequence of disks $D_n= \{z: |z-4n|<1\}$. Suppose also that $j\in {{\mathbb {N}}}$ and $z_i \in D_0$, $1\le i\le j$. Then there exists a transcendental entire function f having an orbit of bounded, simply connected, escaping, wandering domains $U_n$ such that, for $n\ge 0$,

• (i) $\overline{\Delta _n'}{:}{=}\overline{D(4n,r_n)} \subset U_n \subset D(4n, R_n){=}{:}\Delta _n$, for some sequences $(r_n)$ and $(R_n)$ such that $0<r_n<1<R_n$ and $r_n, R_n \rightarrow 1$ as $n \rightarrow \infty$;

• (ii) $f_{n+1}{:}{=} T_{n+1} \circ b_{n+1} \circ T_{n}^{-1}$ is holomorphic on $\overline{\Delta _n},$ and $|f(z)-f_{n+1}(z)|\rightarrow 0$ uniformly on $\overline{\Delta _n}$ as $n \rightarrow \infty$;

• (iii) $f^n(z_i)=F_{n}(z_i)$ and $f'((f^n)(z_i))= f'_{n+1}(F_{n}(z_i)),\;1 \le i\le j$, where $F_n=f_n\circ \cdots \circ {f_1}$;

• (iv) $f:U_{n} \rightarrow U_{n+1}$ has degree $d_{n+1}.$

Finally, if $z, z' \in \overline{D(0,r_0)}$, then we have

$$\begin{aligned} k_n{\text {dist}}_{D_{n}}(f^{n}(z), f^{n}(z')) \le {\text {dist}}_{U_{n}}(f^{n}(z), f^{n}(z'))\le K_n {\text {dist}}_{D_{n}}(f^{n}(z), f^{n}(z')),\nonumber \\ \end{aligned}$$

(5.11)

for some sequences $(k_n)$ and $(K_n)$ such that $0<k_n<1<K_n$ and $k_n,K_n \rightarrow 1$ as $n \rightarrow \infty$.

Fig. 6

Sketch of the setup of Theorem 5.3. In green, the disks $D_n$ centred at 4n. In blue, the boundaries of the disks of radii $r_n$ and $R_n$ in between which lie the boundaries of the wandering domains. In red, the curves $L_n$ introduced in the proof (color figure online)

Proof

For $n \ge 0$, let

$$\begin{aligned} b_n(z) = e^{i \theta _n} \prod _{j=1}^{d_n}\frac{z+a_{n,j}}{1+\overline{a_{n,j}}z}, \end{aligned}$$

where $a_{n,j} \in {\mathbb {D}}$ are not necessarily different from each other, and $\theta _n \in [0, 2\pi )$.

We first define the increasing sequence $(r_n)$ and the decreasing sequence $(R_n)$ inductively. These sequences determine the following circles which play a key role in the proof (see Fig. 6):

$$\begin{aligned} \gamma _n =\{z:|z-4n|=r_n\} \quad \text {and} \quad \Gamma _n=\{z:|z-4n|=R_n\}. \end{aligned}$$

(5.12)

First, take $R_0\in (1,3/2)$ such that $R_0< {1}/{\max _j\{|a_{1,j}|\}}\}$, which ensures that $b_1$ is holomorphic inside $\Gamma _0$ and in a neighborhood of $\Gamma _0$, and take $r_0\in (1/2,1)$ such that $r_0>\max _i|z_i|$ and also such that $b_{1}(z)=w$ has exactly $d_{1}$ solutions in $D(0,r_0)$ for $w \in D(0,1/2)$. Now assume that $r_k, R_k$ have been chosen for $k=0,\cdots ,n-1$, for some $n \in {{\mathbb {N}}}$. We choose $r_{n}$ and $R_{n}$ so that the following statements all hold:

$$\begin{aligned}&0<1-r_{n} \le \min \left\{ \frac{1-r_{n-1}}{2}, {{\text {dist}}(f_{n}(\gamma _{n-1}), \partial D_{n})^2} \right\} ;\end{aligned}$$

(5.13)

$$\begin{aligned}&f_{n+1}(\gamma _{n})\;\text { winds exactly }\, d_{n+1}\, {\mathrm{times~round }} D(4n,1/2); \end{aligned}$$

(5.14)

$$\begin{aligned}&0<R_{n}-1 \le \nonumber \\&\quad \min \left\{ \frac{R_{n-1}-1}{2}, {1-r_{n}}, \frac{1}{2} {\text {dist}}(f_{n}(\Gamma _{n-1}), \partial D_{ n}), \frac{1}{\max _j\{|a_{n+1,j}|\}}- 1 \right\} .\nonumber \\ \end{aligned}$$

(5.15)

These properties prescribe the values $r_n$ and $R_n$, and hence the circles $\gamma _n$ and $\Gamma _n$. In particular, by (5.13) and (5.15), the sequence $(r_n)$ increases to 1 and the sequence $(R_n)$ decreases to 1, and the maps $f_{n+1}$, $n \ge 0$, defined in property (ii), satisfy

$$\begin{aligned}&\gamma _{n+1}\;\text { surrounds}\;f_{n+1}(\gamma _n), \end{aligned}$$

(5.16)

$$\begin{aligned}&f_{n+1}(\Gamma _n)\;\text { surrounds}\; \Gamma _{n+1}. \end{aligned}$$

(5.17)

Our aim is to use Lemma 5.1 to approximate all the maps $f_n$ by a single entire function f such that, for $n \ge 0$, $\gamma _{n+1}$ surrounds $f(\gamma _n)$ and $f(\Gamma _n)$ surrounds $\Gamma _{n+1}$.

We first define

$$\begin{aligned} \delta _n= R_n-r_n,\quad \text {for } n \ge 0, \end{aligned}$$

(5.18)

and observe that $\delta _n \rightarrow 0$ as $n \rightarrow \infty$.

We then define $L_n$, $n\ge 0$, to be the curve

$$\begin{aligned} L_n{:}{=}\{z:|z-4n|=R_n+\delta _n^2/2,\;|{\text {arg}}(z)| \le \pi - \delta _n^2\}, \end{aligned}$$

(5.19)

so

$$\begin{aligned} \max \{{\text {dist}}(z,L_n): z \in \Gamma _n\} \le 2\delta _n^2, \quad \text {for } n \ge 0, \end{aligned}$$

(5.20)

and define the error quantities

$$\begin{aligned} \varepsilon _n= \min \left\{ \frac{1}{4} {\text {dist}}(f_n(\gamma _{n-1}), \partial D_{n}), \frac{1}{4} {\text {dist}}(f_n(\Gamma _{n-1}), \partial D_{n}), \delta _n/4 \right\} >0, \end{aligned}$$

(5.21)

for $n\ge 1$. Since $0<\varepsilon _n \le \delta _n/4$, we have that $\varepsilon _n< \delta _0/4<1/4$, $n \ge 1$, and $\varepsilon _n \rightarrow 0$ as $n \rightarrow \infty$.

We now apply Lemma 5.1 to the sets $E_0=\overline{D(-4,1)}$ and $E_{2k+1} = L_{k}$, $E_{2k+2}=\overline{\Delta _{k}}$, for $k \ge 0$, with the function $\psi$ defined by

$$\begin{aligned} \psi (z)=\left\{ \begin{array}{ll} -4,&{}\quad \text {if }\;z \in \overline{D(-4,1)},\\ -4,&{}\quad \text {if } \; z \in L_n, \; n \ge 0,\\ f_{n+1}(z),&{}\quad \text {if }\;z \in \overline{\Delta _n}, \; n \ge 0. \end{array}\right. \end{aligned}$$

Lemma 5.1 allows us to choose finitely many points $z_{n,i}$, $1\le i \le j$, in each set $E_n$ where we do the approximation. The choice of these points in $\overline{D(-4,1)} \cup \bigcup _{k=0}^{\infty } L_k$ plays no role in our argument. In $E_2=\overline{\Delta _0}$ we choose $z_{2,i}=z_i \in D_0$, $1\le i \le j$, and in $E_{2k+2} = \overline{\Delta _{k}}$, $k \ge 1$, we choose $z_{2k+2,i} = F_k(z_i)$, $1\le i\le j$, where $F_k=f_k\circ \cdots \circ {f_1}$.

It then follows from Lemma 5.1 that there exists an entire function f such that, for $n \ge 0$,

$$\begin{aligned}&|f(z)-f_{n+1}(z)| < \varepsilon _{n+1},\,\, \text { for }\, z \in \overline{\Delta _n}; \end{aligned}$$

(5.22)

$$\begin{aligned}&|f(z)+4| \le 1/2,\, \text { for }\, z\in L_n; \end{aligned}$$

(5.23)

$$\begin{aligned}&|f(z)+4| \le 1/2, \ \ \text { for } \, z \in \overline{D(-4,1)}; \end{aligned}$$

(5.24)

$$\begin{aligned}&f^n(z_i)=F_n(z_i),\ \ \text { for } \ \ 1\le i\le j; \end{aligned}$$

(5.25)

$$\begin{aligned}&f'((f^n)(z_i))= f'(F_n(z_i))=f_{n+1}'(F_n(z_i)), \ \ \text { for } 1\le i\le j. \end{aligned}$$

(5.26)

It follows from (5.13), (5.15), (5.22) and (5.21) that, for $n \ge 0$,

$$\begin{aligned}&\gamma _{n+1}\;\text {surrounds}\; f(\gamma _n) \;\text { (which surrounds the point } 4(n+1)); \end{aligned}$$

(5.27)

$$\begin{aligned}&f(\Gamma _n)\;\text {surrounds}\;\Gamma _{n+1}. \end{aligned}$$

(5.28)

We now apply Theorem  D to the Jordan curves $\gamma _n$, $\Gamma _n$, $n \ge 0$, the compact curves $L_n$, $n \ge 0$, and the bounded domain $D = D(-4,1)\subset E_0$, noting that these sets satisfy the required hypotheses. Indeed, the hypotheses (a) and (b) are clearly true, (c) follows from (5.27), (d) follows from (5.28), (e) holds by (5.23) and (5.24), and (f) holds by (5.18) and (5.20).

Part (i) of our result now follows from Theorem  D, part (ii) is true by construction, and part (iii) follows from (5.25) and (5.26). We now show that part (iv) holds.

By (5.21) and (5.22), we can write $f(z)=f_{n+1}(z)+e_{n+1}(z)$ for some holomorphic map $e_{n+1}(z)$ which satisfies $|e_{n+1}(z)| < 1/4$, for $z\in \overline{\Delta _n}$.

By (5.14), we have

$$\begin{aligned} |f_{n+1}(z)-4(n+1)|\ge 1/2,\;\text { for } z\in \gamma _n=\partial \Delta _n'. \end{aligned}$$

It follows from this together with the fact that $|e_{n+1}(z)| < 1/4$, for $z\in \overline{\Delta _n}$ and (5.14) that

$$\begin{aligned} |f(z)-4(n+1)|\ge 1/4,\;\text { for } z\in \gamma _n, \end{aligned}$$

(5.29)

and $f(\gamma _n)$ winds exactly $d_{n+1}$ times around $4(n+1)$, so f takes the value $4(n+1)$ exactly $d_{n+1}$ times in $\Delta _n'$. Similarly, by (5.14), (5.21) and (5.22), $f(\Gamma _n)$ winds exactly $d_{n+1}$ times around $4(n+1)$, so f takes the value $4(n+1)$ exactly $d_{n+1}$ times in $\Delta _n$. Therefore, by the final statement of Theorem D, $f:U_n \rightarrow U_{n+1}$ has degree $d_{n+1}$.

It remains to prove the double inequality (5.11), which compares the hyperbolic distances in $U_n$ between points of two orbits under f with the corresponding hyperbolic distances in the disks $D_n$. To do this, we let $s_n{:}{=} 1-\tfrac{3}{4}{\text {dist}}(f_n(\gamma _{n-1}), \partial D_n)$, for $n\ge 1$, and note that, if $z,z' \in \overline{D(0,r_0)}$, then

$$\begin{aligned} f^n(z), f^n(z')\in \overline{D(4n, s_n)}\subset \Delta _n', \;\text { for } n\in {{\mathbb {N}}}, \end{aligned}$$

by (5.16), (5.21) and (5.22).

Now $1-r_n =o(1-s_n)$ as $n\rightarrow \infty$, by (5.13), and $R_n-1 \le 1-r_n$, by (5.15), so the properties (5.8) hold for the sequences $(s_n)$, $(r_n)$ and $(R_n)$. Also,

$$\begin{aligned} {\text {dist}}_{\Delta _{n}}(f^n(z),f^n(z'))\le {\text {dist}}_{U_{n}}(f^n(z),f^n(z'))\le {\text {dist}}_{\Delta _{n}'}(f^n(z),f^n(z')), \end{aligned}$$

since $\Delta _n'\subset D_n \subset \Delta _n$. Therefore, we deduce from Lemma 5.2 that

$$\begin{aligned} c(s_n,R_n){\text {dist}}_{D_n}(f^n(z),f^n(z'))\le & {} {\text {dist}}_{U_{n}}(f^n(z),f^n(z'))\\\le & {} \frac{1}{c(s_n/r_n,1/r_n)}{\text {dist}}_{D_n}(f^n(z),f^n(z')) \end{aligned}$$

and

$$\begin{aligned} c(s_n,R_n) \rightarrow 1\;\text { as } n \rightarrow \infty ,\quad c(s_n/r_n,1/r_n) \rightarrow 1\;\text { as } n \rightarrow \infty , \end{aligned}$$

which gives (5.11). $\square$

6 Examples: Proof of Theorem  E

In this section we construct the examples described in Theorem E. In every case we use Theorem 5.3 and the notation there. Hence $(b_{n})$ denotes the sequence of Blaschke products of degree $d_n \ge 1$; $(T_n)$ the sequence of real translations $z \mapsto z+4n$; and $(D_n)$ the sequence of disks $D_n= \{z: |z-4n|<1\},$ $n \ge 0$. Moreover, for $n \in {{\mathbb {N}}}$, we set $B_n=b_n\circ \cdots \circ b_{1}$, $f_n=T_{n} \circ b_n \circ T_{n-1}^{-1},$ and $F_n=f_n \circ \cdots \circ f_{1}$, so $F_n = T_{n} \circ B_n$; see Fig. 7.

Fig. 7

The maps $f_n, B_n, T_n$

6.1 Preliminary lemmas

We first prove two lemmas that will be used in the constructions.

Lemma 6.1

Let f be a transcendental entire function with an orbit of bounded, simply connected, wandering domains $U_n$, $n\ge 0$, arising from Theorem 5.3, with Blaschke products $b_n$ and associated functions $B_n$ and $F_n$ such that $f^n(0) = F_n(0)$, for $n \in {{\mathbb {N}}}$. Then, we have the following cases.

• (a) If $B_n(0) \rightarrow 0$ as $n \rightarrow \infty$, then, for all $z\in U_0$,

  $$\begin{aligned} \liminf _{n\rightarrow \infty } {\text {dist}}(f^{n}(z),\partial U_{n})>0, \end{aligned}$$

  that is, all orbits stay away from the boundary.

• (b) If there exists a subsequence $n_k\rightarrow \infty$ with $B_{n_k}(0) \rightarrow 1$ and a different subsequence $m_k\rightarrow \infty$ with $B_{m_k}(0) \rightarrow 0$, then ${\text {dist}}(f^{n_k}(z),\partial U_{n_k})\rightarrow 0$ for all $z\in U_0$, while

  $$\begin{aligned} \liminf _{k \rightarrow \infty } {\text {dist}}(f^{m_k}(z),\partial U_{m_k})>0, \quad \text {for all }z\in U_0. \end{aligned}$$

• (c) If $B_n(0) \rightarrow 1$ as $n \rightarrow \infty$, then ${\text {dist}}(f^{n}(z),\partial U_{n})\rightarrow 0$ for all $z\in U_0$, that is, all orbits converge to the boundary.

Proof

It follows from Theorem  C that all points in a simply connected wandering domain have the same limiting behaviour in relation to the boundary and so, in each case, it is sufficient to find just one point whose orbit behaves as required. We choose this point to be $0 \in U_0$.

If $B_n(0) \rightarrow 0$ as $n \rightarrow \infty$ then

$$\begin{aligned} f^n(0) - 4n = F_n(0) - 4n \rightarrow 0 \quad \text {as } n \rightarrow \infty \end{aligned}$$

and so, by Theorem 5.3 part (i), we have

$$\begin{aligned} \liminf _{n\rightarrow \infty } {\text {dist}}(f^{n}(0),\partial U_{n}) = 1>0, \end{aligned}$$

which is sufficient to prove part (a).

If $B_n(0) \rightarrow 1$ as $n \rightarrow \infty$ then

$$\begin{aligned} f^n(0) - (4n + 1) = F_n(0) - (4n+1) \rightarrow 0 \; \text { as } n \rightarrow \infty \end{aligned}$$

and so, by Theorem 5.3 part (i), we have

$$\begin{aligned} {\text {dist}}(f^{n}(0),\partial U_{n}) \rightarrow 0\;\text { as } n\rightarrow \infty , \end{aligned}$$

which is sufficient to prove part (c).

The proof of part (b) follows in a similar way. $\square$

In some of our constructions we use the following properties about a specific family of Blaschke products of degree 2.

Lemma 6.2

Let $b(z)=\left( \frac{z+a}{1+az}\right) ^2,$ where $1/3\le a<1$, and let $0<r<s<1$. Then

• (a) the function b has a fixed point at 1, which is attracting if $a>1/3$ and parabolic if $a=1/3$, and $b^n(r) \rightarrow 1$ as $n \rightarrow \infty$ for all $a\ge 1/3$;

• (b) ${\text {dist}}_{\mathbb {{{\mathbb {D}}}}}(b^n(r),b^n(s)) \nrightarrow 0$ as $n \rightarrow \infty$ if $a>1/3;$

• (c) ${\text {dist}}_{\mathbb {{{\mathbb {D}}}}}(b^n(r),b^{n+1}(r)) = O(1/n)$ as $n \rightarrow \infty$ if $a=1/3$.

Proof

The proof of part (a) is straightforward.

For part (b) note first that

$$\begin{aligned} {\text {dist}}_{{\mathbb {D}}}(b^n(r),b^{n}(s))= \int _{b^n(r)}^{b^n(s)} \frac{2\,dt}{1-t^2} \ge \int _{b^n(r)}^{b^n(s)} \frac{dt}{1-{t}} = \log \frac{1 - b^n(r)}{1-b^n(s)}. \end{aligned}$$

(6.1)

Also, since 1 is an attracting fixed point of b when $a>1/3$, there exist $\lambda \in (0,1)$ and $d>c>0$ such that $1-b^n(r) \sim d\lambda ^n$ and $1-b^n(s) \sim c\lambda ^n$ as $n\rightarrow \infty$. Hence, by (6.1),

$$\begin{aligned} \lim _{n\rightarrow \infty }{\text {dist}}_{{\mathbb {D}}}((b^n(r),{b^{n}(s)}) \ge \log \frac{d}{c} >0. \end{aligned}$$

For part (c), we need only note that 1 is a parabolic fixed point of the function b in this case and that ${{\mathbb {D}}}$ is an associated Fatou component of b, so the required estimate follows from Theorem 3.4 by taking $V={{\mathbb {D}}}$, $z_0=r$ and $z'_0=b(r)$. $\square$

6.2 The nine types of simply connected wandering domains

We now prove part (a) of Theorem  E by constructing examples corresponding to each of the nine cases given in Theorems  A and C. The following maps will play key roles in the constructions:

$$\begin{aligned} b(z)= & {} \left( \frac{z+a}{1+az}\right) ^2, \;\text { for } 1/3\le a<1,\nonumber \\ \mu _n(z)= & {} \frac{z+a_n}{1+a_nz} \quad \text {and} \quad \widetilde{\mu }_n(z)= \frac{z-a_n^2}{1-a_n^2z}, \quad \text {for } n \in {{\mathbb {N}}}, \end{aligned}$$

(6.2)

where $a_n \in (0,1)$ is an arbitrary sequence satisfying $a_n \rightarrow 1$ as $n \rightarrow \infty$.

Examples 1, 2 and 3, which follow, correspond to the three cases of Theorem A. Within each of them we give three functions, corresponding to the three cases of Theorem C.

Example 1

(Three contracting wandering domains) For each of the cases (a), (b) and (c) of Theorem  C, there exists a transcendental entire function f having an orbit of bounded, simply connected, escaping contracting wandering domains $U_n$, $n\ge 0$, with the stated behaviour:

• (a) for all $z\in U_0$,

  $$\begin{aligned} \liminf _{n\rightarrow \infty } {\text {dist}}(f^{n}(z),\partial U_{n})>0, \end{aligned}$$

  that is, all orbits stay away from the boundary;

• (b) there exists a subsequence $n_k\rightarrow \infty$ for which ${\text {dist}}(f^{n_k}(z),\partial U_{n_k})\rightarrow 0$ for all $z\in U$, while for a different subsequence $m_k\rightarrow \infty$ we have that

  $$\begin{aligned}\liminf _{k \rightarrow \infty } {\text {dist}}(f^{m_k}(z),\partial U_{m_k})>0, \quad \text {for }z\in U_0;\end{aligned}$$

• (c) ${\text {dist}}(f^{n}(z),\partial U_{n})\rightarrow 0$ for all $z\in U_0$, that is, all orbits converge to the boundary.

Proof

(a) Let $b_n(z)=z^2$, for $n\in {{\mathbb {N}}}$, and apply Theorem 5.3 with the points $z_1 = 0$ and $z_2=1/2$. For $n \in {{\mathbb {N}}}$, we have

$$\begin{aligned} {\text {dist}}_{D_{{n}}}(f^n(0),f^n(1/2))= & {} {\text {dist}}_{{\mathbb {D}}}(F_n(0),F_n(1/2))\\= & {} {\text {dist}}_{{\mathbb {D}}}(B_n(0),B_n(1/2))\\= & {} {\text {dist}}_{{\mathbb {D}}}(0,1/2^{2^n}) \rightarrow 0 \;\text { as}\;n\rightarrow \infty . \end{aligned}$$

It follows from (5.11) that

$$\begin{aligned} {\text {dist}}_{U_{n}}(f^n(0),f^n(1/2)) \rightarrow 0\;\text {as}\;n\rightarrow \infty . \end{aligned}$$

By Theorem  A, this is sufficient to show that $U_0$ is contracting. Since $B_n(0) = 0$, for $n \in {{\mathbb {N}}}$, the result now follows from case (a) of Lemma 6.1.

(b) In this case, for $n\in {{\mathbb {N}}}$, we let

$$\begin{aligned} b_n(z)= {\left\{ \begin{array}{ll} z^2 &{} \text {if } n=3k-2, k\ge 1,\\ \mu _k(z), &{} \text {if } n=3k-1, k\ge 1,\\ \mu _k^{-1}(z), &{} \text {if }n=3k, k\ge 1, \end{array}\right. } \end{aligned}$$

where $\mu _k$ is as defined in (6.2). As in case (a), we apply Theorem 5.3 with $z_1 = 0$ and $z_2=1/2$. For $k \in {{\mathbb {N}}}$, we have

$$\begin{aligned} {\text {dist}}_{D_{3k}}(f^{3k}(0),f^{3k}(1/2))= & {} {\text {dist}}_{{\mathbb {D}}}(F_{3k}(0),F_{3k}(1/2))\\= & {} {\text {dist}}_{{\mathbb {D}}}(B_{3k}(0),B_{3k}(1/2))\\= & {} {\text {dist}}_{{\mathbb {D}}}(0,1/2^{2^ k}) \rightarrow 0 \;\text { as}\;k\rightarrow \infty . \end{aligned}$$

As in case (a), this is sufficient to show that $U_0$ is contracting. Since $B_{3k}(0) = 0$, for $k \in {{\mathbb {N}}}$, and $B_{3k-1}(0)=a_{3k-1} \rightarrow 1$ as $k \rightarrow \infty$, the conclusion now follows from case (b) of Lemma 6.1.

(c) In this case we let $b_n(z)=b(z) =\left( \frac{z+1/3}{1+z/3}\right) ^2$, for $n \in {\mathbb {N}}$, and we apply Theorem 5.3 with $z_1 = 0$ and $z_2 = b(0)$. For $n \in {{\mathbb {N}}}$, we have

$$\begin{aligned} {\text {dist}}_{D_{n}}(f^n(0),f^n(b(0)))= & {} {\text {dist}}_{{{\mathbb {D}}}}(F_n(0),F_n(b(0)))\\= & {} {\text {dist}}_{{{\mathbb {D}}}}(B_n(0),B_n(b(0)))\\= & {} {\text {dist}}_{{{\mathbb {D}}}}(b^n(0),b^{n+1}(0)) \rightarrow 0 \;\text {as}\;n\rightarrow \infty , \end{aligned}$$

by Lemma 6.2(c). As before, this is sufficient to show that $U_0$ is contracting. It also follows from Lemma 6.2(a) that $B_n(0) = b^n(0) \rightarrow 1$ as $n \rightarrow \infty$ and the result now follows from case (c) of Lemma 6.1$\square$

Remark

Cases (a) and (b) of Example 1 are in fact super-contracting (see Definition 1.2).

Example 2

(Three semi-contracting wandering domains) For each of the cases (a), (b) and (c) of Theorem  C, there exists a transcendental entire function f having an orbit of bounded, simply connected, escaping, semi-contracting, wandering domains $U_n$, $n\ge 0$, with the stated behaviour.

Proof

(a) In this case we let $b_n(z) = \widetilde{\mu }_n ((\mu _n(z))^2)$, for $n \in {{\mathbb {N}}}$, where $\mu _n$ and $\widetilde{\mu }_n$ are as defined in (6.2). We apply Theorem 5.3 with the points $z_1 = 0$ and $z_2=1/2$.

A calculation shows that, for $n \in {{\mathbb {N}}}$, we have $b_n(0) = 0$ and $b_n'(0)= \frac{2a_n}{1+a_n^2}\rightarrow 1$ as $n \rightarrow \infty$. Hence we can choose $(a_n)$ so that, in addition,

$$\begin{aligned} \sum _{n=1}^{\infty } (1-b_n'(0)) <\infty . \end{aligned}$$

(6.3)

It follows from Theorem 2.1(b) that $B_n(1/2) \nrightarrow 0$ as $n \rightarrow \infty$. Thus

$$\begin{aligned} {\text {dist}}_{D_{{n}}}(f^n(0),f^n(1/2))= & {} {\text {dist}}_{{\mathbb {D}}}(F_n(0),F_n(1/2))\\= & {} {\text {dist}}_{{\mathbb {D}}}(B_n(0),B_n(1/2))\\= & {} {\text {dist}}_{{\mathbb {D}}}(0,B_n(1/2)) \nrightarrow 0 \;\text {as}\;n\rightarrow \infty . \end{aligned}$$

It follows from (5.11) that

$$\begin{aligned} {\text {dist}}_{U_{n}}(f^n(0),f^n(1/2)) \nrightarrow 0\;\text { as}\;n\rightarrow \infty , \end{aligned}$$

and so $U_0$ is not contracting. Also, for $n \in {{\mathbb {N}}}$, the Blaschke product $b_n$ has degree 2 and so, by Theorem 5.3 part (iv), $f: U_{n-1}\rightarrow U_n$ has degree 2. Thus $U_0$ is not eventually isometric and so it follows from Theorem  A that $U_0$ is semi-contracting.

Since $B_n(0) = 0$, for $n \in {{\mathbb {N}}}$, the result now follows from case (a) of Lemma 6.1.

(b) In this case, for $n \in {{\mathbb {N}}}$, we let

$$\begin{aligned} b_n(z)= {\left\{ \begin{array}{ll} \mu _k(z), &{} \text {if } n=3k-2, k\ge 1,\\ z^2, &{} \text {if } n=3k-1, k\ge 1,\\ \widetilde{\mu }_k(z), &{} \text {if } n=3k, k\ge 1, \end{array}\right. } \end{aligned}$$

where $\mu _k$ and $\widetilde{\mu }_k$ are as defined in (6.2). Note the similarity to case (a), where each Blaschke product $b_n$ was defined to be the composite of the three maps above.

As in case (a), we apply Theorem 5.3 with $z_1 = 0$ and $z_2=1/2$. Using similar arguments to those used in part (a), we can choose $(a_n)$ such that

$$\begin{aligned} {\text {dist}}_{U_{3k}}(f^{3k}(0),f^{3k}(1/2)) \nrightarrow 0\;\text { as}\;k\rightarrow \infty , \end{aligned}$$

and so $U_0$ is not contracting. Also, for $k \in {{\mathbb {N}}}$, the Blaschke product $b_{3k-1}$ has degree 2 and so, by Theorem 5.3 part (iv), $f: U_{3k-2}\rightarrow U_{3k-1}$ has degree 2. Thus $U_0$ is not eventually isometric and so it follows from Theorem  A that $U_0$ is semi-contracting.

Since $B_{3k}(0) = 0$, for $k \in {{\mathbb {N}}}$, and $B_{3k-2}(0)=a_{3k-2} \rightarrow 1$ as $k \rightarrow \infty$, the conclusion now follows from case (b) of Lemma 6.1.

(c) In this case we choose $a > 1/3$ and let $b_n(z)=b(z) = \left( \frac{z+a}{1+az}\right) ^2$, for $n \in {\mathbb {N}}$. As in Example 1(c), we apply Theorem 5.3 with $z_1 = 0$ and $z_2 = b(0)$. For $n \in {{\mathbb {N}}}$, we have

$$\begin{aligned} {\text {dist}}_{D_{n}}(f^n(0),f^n(b(0)))&= {\text {dist}}_{{\mathbb {D}}}(F_n(0),F_n(b(0)))\\&= {\text {dist}}_{{{\mathbb {D}}}}(B_n(0),B_n(b(0)))\\&= {\text {dist}}_{{{\mathbb {D}}}}(b^n(0),b^{n+1}(0)) \nrightarrow 0 \;\text { as}\;n\rightarrow \infty , \end{aligned}$$

by Lemma 6.2(b). Arguing as above, this is sufficient to show that $U_0$ is not contracting. Also, for $n \in {{\mathbb {N}}}$, the Blaschke product $b_n$ has degree 2 and so, as above, it follows that $U_0$ is not eventually isometric. Hence, by Theorem A, it is semi-contracting.

It also follows from Lemma 6.2(a) that $B_n(0) = b^n(0) \rightarrow 1$ as $n \rightarrow \infty$ and the result now follows from case (c) of Lemma 6.1. $\square$

Example 3

(Three eventually isometric wandering domains) For each of the cases (a), (b) and (c) of Theorem C, there exists a transcendental entire function f having an orbit of bounded, simply connected, escaping, eventually isometric, wandering domains $U_n$, $n\ge 0$, with the stated behaviour.

Proof

(a) In this case we let $b_n(z)=z$, for $n \in {{\mathbb {N}}}$, and apply Theorem 5.3 with $z_1 = 0$. For $n \in {{\mathbb {N}}}$, the map $b_n$ is univalent and so, by Theorem 5.3 part (iv), $f: U_{n-1}\rightarrow U_n$ is also univalent. Thus $U_0$ is eventually isometric.

Since $B_n(0) = 0$, for $n \in {{\mathbb {N}}}$, the result now follows from case (a) of Lemma 6.1.

(b) In this case, for $n \in {{\mathbb {N}}}$, we let

$$\begin{aligned} b_n(z)= {\left\{ \begin{array}{ll} \mu _k(z), &{} \text {if }\, n=2k-1, k\ge 1,\\ \mu _k^{-1}(z), &{} \text {if }\, n=2k, k\ge 1, \end{array}\right. } \end{aligned}$$

where $\mu _k$ is as defined in (6.2). We apply Theorem 5.3 with $z_1 = 0$. For $n \in {{\mathbb {N}}}$, the map $b_n$ is univalent and so, as in case (a), $U_0$ is eventually isometric.

Since $B_{2k}(0) = 0$, for $k \in {{\mathbb {N}}}$, and $B_{2k-1}(0)=a_{2k-1} \rightarrow 1$ as $k \rightarrow \infty$, the conclusion now follows from case (b) of Lemma 6.1.

(c) In this case, for $n \in {{\mathbb {N}}}$, we let $b_n(z) = \frac{z + 1/2}{1 + z/2}$. As in cases (a) and (b), we apply Theorem 5.3 with $z_1 = 0$ and, since the map $b_n$ is univalent, for $n \in {{\mathbb {N}}}$, we deduce that $U_0$ is eventually isometric. Since $b_n(x) > x$, for $x \in [0,1)$, we deduce that $B_n(0) \rightarrow 1$ as $n \rightarrow \infty$. The conclusion now follows from case (c) of Lemma 6.1. $\square$

6.3 $2-$super-attracting wandering domains

We prove part (b) of Theorem E by giving an example of a transcendental entire function with an orbit of wandering domains $(U_n)$ containing two orbits consisting of critical points. The case of finitely many critical orbits is completely analogous.

We choose the sequence of Blaschke products $(b_n)$. We let

$$\begin{aligned} b_1(z)= z^2 \frac{z+a_1}{1+a_1z}, \end{aligned}$$

with $a_1<0$ chosen so that 1/2 is a critical point, and, for $n \in {{\mathbb {N}}}$ define $b_{n}$ inductively by setting

$$\begin{aligned} b_{n+1}(z)= z^2 \frac{z+a_{n+1}}{1+a_{n+1}z}, \end{aligned}$$

with $a_{n+1}\in (-1,1)$ chosen so that $b_n\circ b_{n-1}\circ \cdots \circ b_1(1/2)$ is a critical point of $b_{n+1}$. In this way we construct a sequence of Blaschke products $(b_n)$ of degree 3 such that, for $n \in {{\mathbb {N}}}$, we have $b_n(0)=0$ and the two critical points of $b_n$ are $0, B_{n-1}(1/2)$.

We now apply Theorem 5.3 with $z_1 = 0$ and $z_2 = 1/2$. We deduce that there exists a transcendental entire function f which has a sequence of bounded, simply connected, escaping, wandering domains $(U_n)$ such that, for $n \ge 0$, $f^n(0) = F_n(0) = 4n$, $f^n(1/2)= F_n(1/2)$ and $f'(f^n(0)) = f'(f^n(1/2))=0$. Hence, there are two points in $U_0$, namely 0 and 1/2, whose orbits under f consist of critical points of f.

Remark

It follows from Theorem B that these wandering domains are super-contracting and so, in particular, ${\text {dist}}_{U_n}(f^n(0),f^n(1/2)) \rightarrow 0$ as $n \rightarrow \infty$.

7 Wandering domains whose boundaries are Jordan curves

In this section we prove that, if the Blaschke products in Theorem 5.3 satisfy certain conditions, then the boundaries of the resulting wandering domains are Jordan curves. Apart from wandering domains arising from lifting constructions, as far as we are aware these are the first examples of simply connected wandering domains for which it is possible to obtain information concerning the boundary. Examples of multiply connected wandering domains for which it is known that connected components of the boundary are Jordan curves can be found in [15] and in [4].

In order for the boundaries of the resulting wandering domains to be Jordan curves, we need the Blaschke products in Theorem 5.3 to be uniformly expanding in the following precise sense.

Definition 7.1

(Uniformly expanding Blaschke products) Let $b_n$, $n\in {{\mathbb {N}}}$, be a sequence of Blaschke products. We say that the Blaschke products in the sequence $(b_n)$ are uniformly expanding if there exists $\xi >1$ and an $\varepsilon$-neighborhood $U_\varepsilon$ of the unit circle such that, for all $n\in {{\mathbb {N}}}$,

• 1. $b_n$ is holomorphic in $U_\varepsilon$, that is, $b_n$ has no poles in $U_\varepsilon$;

• 2. $|b_n'|\ge \xi$ on $U_\varepsilon$.

Note that the second condition implies that the functions $b_n$ have no critical points in $U_\varepsilon$.

Our aim for this section is to prove the following theorem.

Theorem 7.2

Let $b_n$, $n\in {{\mathbb {N}}}$, be a sequence of uniformly expanding Blaschke products such that $\max _n\{\mathrm{deg}\, b_n\} < \infty$ and let $U_n$, $n\ge 0$, be the resulting orbit of wandering domains given by Theorem 5.3. Then, for $n \ge 0$, the boundary of the wandering domain $U_n$ is a Jordan curve.

The proof of Theorem 7.2 follows in outline the proof that the Julia sets of certain quadratic polynomials are Jordan curves (see [7, Section 9.9], for example) but with very significant changes and novel arguments due to the fact that we are dealing with a lack of uniformity arising from the associated non-autonomous system of maps.

The proof has three steps:

• 1. For each $n \in {{\mathbb {N}}}$, we let $A_n$ be the annulus bounded by the circles $\gamma _n$ and $\Gamma _n$, which were defined in (5.12) and played a key role in the proof of Theorem 5.3. We consider the annulus $\breve{A}_n$ lying in $A_n$ between $\gamma _n$ and a component of $f^{-1}(A_{n+1})$ and show that the vertical geodesics of $\breve{A}_n$ have uniformly bounded Euclidean length.

• 2. We then use pullbacks under $f^{-n}$ of these vertical geodesics together with the uniformly expanding property of the functions $b_n$ (and hence of f on the annuli $A_n$) to induce a continuous map $\sigma$ from $\gamma _0$ to a closed curve $\sigma (\gamma _0)$, and a continuous map $\Sigma$ from $\Gamma _0$ to a closed curve $\Sigma (\Gamma _0)$.

• 3. Finally, we show that $\partial U_0$, which lies between $\sigma (\gamma _0)$ and $\Sigma (\Gamma _0)$, is a Jordan curve.

The first step in the proof relies on a general geometric result of independent interest about the Euclidean lengths of vertical geodesics of annuli, which we prove using the Fejér–Riesz inequality. We prove this and other preliminary geometric results in Sect. 7.1, and then give the proof of Theorem 7.2 in Sect. 7.2.

7.1 Preliminary results

We begin with a result about pre-images of annuli bounded by Jordan curves. Related results appear in [15, Lemma 11.1] and [37, Lemma 5].

In this lemma, we denote the inner boundary component of a topological annulus A by $\partial A_{\mathrm{inn}}$ and the outer boundary component by $\partial A_{\mathrm{out}}$. As usual, when we say that f is holomorphic on $\overline{A}$ we mean that f is holomorphic on a neighborhood of $\overline{A}$.

Lemma 7.3

Let A and B be annuli with Jordan curve boundary components, both surrounding 0, and let f be holomorphic on ${\overline{A}}$, with f and $f'$ non-zero on ${\overline{A}}$. Suppose that

$$\begin{aligned} \partial B_{\mathrm{inn}}\;\text { surrounds }\; f(\partial A_{\mathrm{inn}})\quad \text {and}\quad f(\partial A_{\mathrm{out}})\; \text { surrounds }\; \partial B_{\mathrm{out}}. \end{aligned}$$

(7.1)

Then A contains a unique component ${\widehat{A}}$ of $f^{-1}(B)$, which is an annulus that surrounds 0 with Jordan curve boundary components that satisfy

$$\begin{aligned} f(\partial {\widehat{A}}_{\mathrm{inn}})= \partial B_{\mathrm{inn}}\quad \text {and} \quad f(\partial {\widehat{A}}_{\mathrm{out}})= \partial B_{\mathrm{out}}. \end{aligned}$$

(7.2)

Proof

Since $f(\partial A) \cap B= \emptyset$ we deduce that every connected component H of $f^{-1}(B)$ which intersects A is in fact contained in A. Since $f(\partial A)$ intersects both components of $B^c$, we deduce that $f(A) \supset B$ and that there exists at least one component $\widehat{A}$ of $f^{-1}(B)$ that is contained in A. We now claim that $\widehat{A}$ is doubly connected, surrounds 0, and that there are no other preimage components of B in A.

Let H be any preimage component of B which is contained in A. By the Riemann–Hurwitz formula H is at least doubly connected. Let X be a bounded complementary component of H. Since $f:H\rightarrow B$ is proper, f(X) is the bounded complementary component of B, hence $0\in f(X)$. If X does not contain 0, then $X\subset A$, on which f cannot take the value 0 by assumption, giving a contradiction. Hence every preimage component H of B in A is doubly connected and surrounds 0. Now suppose that there are two such components. Then one of them is contained in the bounded complementary component of the other, and hence maps to the bounded complementary component of B, again a contradiction since it is a preimage component of B.

Since the boundary components of B are Jordan curves, the fact that $f:\widehat{A}\rightarrow B$ is proper, together with the fact that $f'\ne 0$ on ${\overline{A}}$, implies that the boundaries of $\widehat{A}$ are also Jordan curves, and also implies (7.2). $\square$

The main result in this subsection concerns the notion of a vertical foliation of an annulus which we now define.

Definition 7.4

(Vertical foliations) Let A be an open annulus and consider the straight annulus ${{\mathbb {A}}}_{\rho }=\{z:\rho<|z|<1\}$ such that $\varphi :{{\mathbb {A}}}_{\rho }\rightarrow A$ is a biholomorphism. The vertical foliation ${{\mathcal {F}}}_A$ of A consists of the image curves under $\varphi$ of the radial segments connecting the two circles which form the boundary of ${{\mathbb {A}}}_\rho$. Each of these image curves is a hyperbolic geodesic which we refer to as a vertical geodesic.

We can now state the main result of this subsection, which concerns the Euclidean lengths, denoted by $\ell _{\mathrm{Eucl}}(\cdot )$, of geodesics in vertical foliations of annuli. The proof uses the Fejér–Riesz inequality (stated below); similar reasoning using instead the Gehring–Hayman theorem (see [30] or [36, Chapter 4]) is possible.

Theorem 7.5

Let A be an annulus for which both boundary components are analytic Jordan curves with length at most S, and such that the bounded component of ${{\mathbb {C}}}\setminus A$ contains a disk of radius $r>0$. Then there exists $M=M(S,r)>0$ such that

$$\begin{aligned} {\ell _{{\text {Eucl}}}}(\gamma )\le M,\ \ \ \text { for all } \gamma \in {{\mathcal {F}}}_A. \end{aligned}$$

We prove Theorem 7.5 using the following technical lemma.

Lemma 7.6

Let A be an annulus for which both boundary components are analytic Jordan curves with length at most S, and consider the straight annulus ${{\mathbb {A}}}_{\rho }=\{z:\rho<|z|<1\}$ such that $\varphi :{{\mathbb {A}}}_{\rho }\rightarrow A$ is a biholomorphism. For $\theta \in [0,2\pi ]$, let $\sigma _\theta {:}{=}\varphi (\{r e^{i\theta }: \rho<r<1\})$ and $\ell (\theta ){:}{=}{\ell _{{\text {Eucl}}}}(\sigma _\theta )$.

Then the Lebesgue measure of the set of $\theta$ such that $\ell (\theta )<\frac{2S}{\rho }(1-\rho )$ is at least $2\pi -\frac{1}{2}$.

Proof

Consider the integral

$$\begin{aligned} I= \int _{\rho }^1\int _{0}^{2\pi }|\varphi '(re^{i\theta })|\,d\theta \, dr. \end{aligned}$$

The function

$$\begin{aligned} I(r){:}{=}\int _{0}^{2\pi }|\varphi '(re^{i\theta })|\,d\theta ,\quad \rho \le r\le 1, \end{aligned}$$

is a convex function of $\log r$ since $|\varphi '|$ can be extended to be subharmonic in a neighbourhood of $\overline{{{\mathbb {A}}}_{\rho }}$, so $I(r)\le \max \{I(\rho ), I(1)\}$, for $\rho \le r\le 1$. Then

$$\begin{aligned} \rho I(\rho )&= \int _{0}^{2\pi }\rho |\varphi '(\rho e^{i\theta })|\,d\theta = {\ell _{{\text {Eucl}}}}(\partial A_{\mathrm{inn}})\le S, \\ I(1)&= \int _{0}^{2\pi }|\varphi '(e^{i\theta })|\,d\theta ={\ell _{{\text {Eucl}}}}(\partial A_{\mathrm{out}})\le S. \end{aligned}$$

Hence $I(r)\le S/\rho$, for $\rho \le r\le 1$, so

$$\begin{aligned} I=\int _\rho ^1 I(r)\,dr\le \frac{S}{\rho }(1-\rho ). \end{aligned}$$

Changing the order of integration we obtain

$$\begin{aligned} I=\int _{0}^{2\pi } \left( \int _{\rho }^1 |\varphi '(re^{i\theta }| \,dr\right) \,d\theta =\int _{0}^{2\pi } \ell (\theta )\,d\theta \le \frac{S}{\rho }(1-\rho ). \end{aligned}$$

Hence the Lebesgue measure of the set $\{\theta \in [0,2\pi ]: \ell (\theta )> \frac{2S}{\rho }(1-\rho )\}$ is at most 1/2. $\square$

In particular, Lemma 7.6 shows that the annulus A has many vertical geodesics whose Euclidean length is at most $2S(1-\rho )/\rho$.

Next, we state the following classical result (see [29] and [20, Theorem 3.13]) about the space $H^p$, $p>0$, of functions g holomorphic in ${{\mathbb {D}}}$ such that

$$\begin{aligned} \sup _{0\le r< 1}\left\{ \int _0^{2\pi }|g(re^{i\theta })|^p\,d\theta \right\} <\infty . \end{aligned}$$

Lemma 7.7

(Fejér–Riesz inequality) If $g\in H^p$, then

$$\begin{aligned} \int _{-1}^1|g(x)|^p\, dx \le \frac{1}{2}\int _0^{2\pi }|g(e^{i\theta })|^p\,d\theta . \end{aligned}$$

We can now give a proof of Theorem 7.5.

Proof of Theorem 7.5

Since the result remains true under a translation, we can assume that ${{\mathbb {C}}}\setminus A$ contains a disk of radius r centred at 0.

We first claim that there exists $L=L(S,r)$ and a vertical geodesic $\sigma \in {{\mathcal {F}}}_A$ such that ${\ell _{{\text {Eucl}}}}(\sigma )\le L$. Since ${{\mathbb {C}}}\setminus A$ contains a disk of radius r centred at 0, and the outer boundary has length at most S, the modulus of A is bounded from above by a constant depending only on S and r. The claim then follows by Lemma 7.6, since $\rho$ is bounded from below by a positive constant depending only on S and r.

Now let $\log A$ be a lift of $A\setminus \sigma$ under the exponential map, using a suitable branch of the logarithm. Observe that $\log A$ is simply connected and that vertical geodesics in A lift to geodesic cross cuts in $\log A$. For any vertical geodesic $\gamma \in {{\mathcal {F}}}_A$ consider its lift $\log \gamma$ in $\log A$. Let $\psi :{{\mathbb {D}}}\rightarrow \log A$ be a biholomorphism such that $\psi (\{z: -1< {\text {Re}}z < 1\})=\log \gamma$. This can be done by mapping 0 to a point in $\log \gamma$, observing that geodesics are mapped to geodesics, and pre-composing with a rotation if necessary. By applying the Fejér–Riesz inequality (Lemma 7.7) with $p=1$ and $g=\psi '$, we obtain

$$\begin{aligned} {\ell _{{\text {Eucl}}}}(\log \gamma )\le \frac{1}{2}{\ell _{{\text {Eucl}}}}(\partial \log A). \end{aligned}$$

(7.3)

So it remains to show that ${\ell _{{\text {Eucl}}}}(\partial \log A)$ is bounded by a uniform constant and that the resulting bound on ${\ell _{{\text {Eucl}}}}(\log \gamma )$ can be translated into a bound for ${\ell _{{\text {Eucl}}}}(\gamma )$. We do this by studying the distortion of lengths of curves under the lift via the exponential. Let $t\mapsto z(t)$ for $t\in [0,1]$ be a parametrization of a curve C in $\overline{A}$ and let $\log C$ be its lift in $\overline{\log A}$. Then $t\mapsto \log (z(t))$ for $t\in [0,1]$ is a parametrization of the curve $\log C$, so

$$\begin{aligned} {\ell _{{\text {Eucl}}}}(C)=\int _{0}^{1} |z'(t)|\,dt \quad \text {and}\quad {\ell _{{\text {Eucl}}}}(\log C)=\int _{0}^{1} \left| \frac{z'(t)}{z(t)}\right| dt. \end{aligned}$$

Since A is contained in the straight annulus ${{\mathbb {A}}}(r,S/2)$ (this follows from considering the extremal case for $\partial A_{\mathrm{out}}$), we have that $r\le |z(t)|\le S/2$, so

$$\begin{aligned} \frac{2}{S}{\ell _{{\text {Eucl}}}}(C)\le {\ell _{{\text {Eucl}}}}(\log C)\le \frac{1}{r}{\ell _{{\text {Eucl}}}}(C). \end{aligned}$$

(7.4)

It follows that ${\ell _{{\text {Eucl}}}}(\log \sigma )\le \frac{1}{r}{\ell _{{\text {Eucl}}}}(\sigma )\le \frac{L}{r}$ and that if $\alpha =\partial A_{\mathrm{inn}}$ and $\beta =\partial A_{\mathrm{out}}$ are the inner and outer boundary components, respectively, of A, then we have

$$\begin{aligned} {\ell _{{\text {Eucl}}}}(\log \alpha )+{\ell _{{\text {Eucl}}}}(\log \beta )\le \frac{1}{r}({\ell _{{\text {Eucl}}}}(\alpha )+{\ell _{{\text {Eucl}}}}(\beta ))\le \frac{2S}{r}. \end{aligned}$$

So

$$\begin{aligned} {\ell _{{\text {Eucl}}}}(\partial \log A) = 2{\ell _{{\text {Eucl}}}}(\log \sigma ) + {\ell _{{\text {Eucl}}}}(\log \alpha )+{\ell _{{\text {Eucl}}}}(\log \beta ) \le \frac{2L}{r} + \frac{2S}{r}. \end{aligned}$$

It now follows from (7.3) and (7.4) that, for any vertical geodesic $\gamma \in {{\mathcal {F}}}_A$, we have

$$\begin{aligned} {\ell _{{\text {Eucl}}}}(\gamma )\le \frac{S}{2} {\ell _{{\text {Eucl}}}}(\log \gamma )\le \frac{S(L+S)}{2r}. \end{aligned}$$

This concludes the proof of Theorem 7.5. $\square$

7.2 Proof of Theorem 7.2

Let $b_n$, $n\in {{\mathbb {N}}}$, be a sequence of uniformly expanding Blaschke products of degree at most d and let f be the transcendental entire function with an associated orbit of wandering domains $(U_n)$ arising from Theorem 5.3. We will show that the boundary of $U_0$ is a Jordan curve.

For each $n \ge 0$, we let $A_n$ be the annulus bounded by the circles $\gamma _n$ and $\Gamma _n$ which were defined in (5.12) in the proof of Theorem 5.3. By the uniform expansivity condition on the functions $b_n$ and the fact that $\max \{|f(z)-f_n(z)|: z\in A_n\}\rightarrow 0$ as $n\rightarrow \infty$ (see (5.22)), we deduce using Cauchy’s estimate that there exists $\eta > 1$ such that, for sufficiently large $n \in {{\mathbb {N}}}$,

$$\begin{aligned} |f'|\ge \eta >1\, \text { on a neighborhood of}\, A_n; \end{aligned}$$

(7.5)

in particular, f has no critical points in a neighborhood of $A_n$ for such n. Relabeling the $U_n$ if necessary, we can assume that the above conditions hold for any $n\ge 0$. (Note that if $\partial U_n$ is a Jordan curve, for some $n \ge 1$, then $\partial U_{0}$ is also a Jordan curve, since $f^n$ is a proper map between the bounded domains $U_{0}$ and $U_n$ which extends analytically to $\partial U_0$.)

Step 1 For each $n \ge 0$, we let ${\widehat{A}}_n$ denote the pre-image component of $A_{n+1}$ under f in $A_n$, given by Lemma 7.3, with inner and outer boundary components ${\widehat{\gamma }}_n$ and ${\widehat{\Gamma }}_n$, say, respectively. Then let $\breve{A}_n$ denote the annulus lying between $\gamma _n$ and ${\widehat{\gamma }}_n$ (see Fig. 8). Our first claim is that there exists $M=M(\eta ,d)>0$ such that, for $n\ge 0$, each geodesic in the vertical foliation ${{\mathcal {F}}}_n$ of the annulus ${\breve{A}}_n$ has Euclidean length at most M.

We start by showing that each Jordan curve ${\widehat{\gamma }}_n$ has length which is uniformly bounded by $3\pi d/\eta$. Indeed, we can parametrize ${\widehat{\gamma }}_n:[t_0,t_1]\cup [t_1,t_2]\cup \cdots \cup [t_{d-1},t_d]\rightarrow {{\mathbb {C}}}$, where $t_0<t_1<\cdots <t_d$, with ${\widehat{\gamma }}_n(t_0)={\widehat{\gamma }}_n(t_d)$, in such a way that f is univalent on ${\widehat{\gamma }}_n(t_i, t_{i+1})$, $0\le i<d-1$. This can be done because the degree of $b_n$ (and hence of f on $\breve{A}_n$, for n sufficiently large) is bounded above by d, and ${\widehat{\gamma }}_n$ is a Jordan curve. Notice that $f({\widehat{\gamma }}_n[t_i,t_{i+1}])\subseteq \gamma _{n+1}$. For n large, we have, by (7.5),

$$\begin{aligned} 2\pi \ge {\ell _{{\text {Eucl}}}}(\gamma _{n+1})&\ge \frac{1}{d}\left( \int _{t_0}^{t_1} |f'({\widehat{\gamma }}_n(t))||{\widehat{\gamma }}_n'(t)|\,dt+\cdots + \int _{t_{d-1}}^{t_d}|f'({\widehat{\gamma }}_n(t))||{\widehat{\gamma }}_n'(t)|\,dt\right) \\&\ge \frac{\eta }{d} \int _{t_0}^{t_d}|{\widehat{\gamma }}_n'(t)|\,dt=\frac{\eta }{d} {\ell _{{\text {Eucl}}}}({\widehat{\gamma }}_n). \end{aligned}$$

(The second inequality becomes an equality if $f:{\widehat{\gamma }}_n[t_i,t_{i+1}]\rightarrow \gamma _{n+1}$ is surjective for every i.) Since, by construction, the bounded component of ${{\mathbb {C}}}\setminus {\widehat{A}}_n$ contains the circle $\gamma _n=\{z:|z|=r_n\}$ and $r_n \ge 1/2$ for $n\ge 0$, the annulus $\breve{A}_n$ satisfies the hypotheses of Theorem 7.5, giving the claim.

Fig. 8

Sketch of the setup in Step 1

Step 2 For $n\in {{\mathbb {N}}}$, let $\widetilde{\Gamma }_n$, $\widetilde{\gamma }_n$ be those pre-images under $f^n$ of $\Gamma _n,\gamma _n$, respectively, that are contained in $A_0$ and are such that $\widetilde{\Gamma }_n$ surrounds $\widetilde{\Gamma }_{n+1}$ for every n, while $\widetilde{\gamma }_n$ is surrounded by $\widetilde{\gamma }_{n+1}$ for every n. The existence of $\widetilde{\gamma }_n$ and $\widetilde{\Gamma }_n$, and the fact that they are Jordan curves, follows by applying inductively Lemma 7.3, since there are no critical points in $A_n$ for any n by the uniform expansivity condition.

We now concentrate on the family of Jordan curves $\widetilde{\gamma }_n$ and construct a continuous map $\sigma$ from $\gamma _0$ to the limit of the $\widetilde{\gamma }_n$, defined in an appropriate way.

Fix $z_0\in \gamma _0$. Let $\sigma _0(z_0)$ be the (unique) geodesic in ${{\mathcal {F}}}_0$ which connects $z_0$ to some point $z_1\in \widetilde{\gamma }_1$, and let us parametrize it as a curve $\sigma _0(z_0,t)$, $t\in [0,1]$, with $\sigma _0(z_0,0)=z_0$, $\sigma _0(z_0,1)=z_1$. Consider $f(z_1)\in \gamma _1$, and the geodesic $\omega _1\in {{\mathcal {F}}}_1$ which connects $f(z_1)$ to some point $z_2'$ say in $f^{-1}(\gamma _2)$. Notice that the definition of ${{\mathcal {F}}}_1$ automatically specifies the connected component of $f^{-1}(\gamma _2)$ to which $z'_2$ belongs. The preimage of $\omega _1$ under f which contains $z_1$ is an arc that can be parametrized as $\sigma _1 (z_0,t)$, $t\in [1,2]$, connecting $z_1$ to some point $z_2\in f^{-1}(z'_2)\cap \widetilde{\gamma }_2$. Proceeding in this way, for each n we can construct a point $z_n$ and a curve $\sigma _n (z_0,t)$, $t\in [n,n+1]$, connecting $z_n$ to $z_{n+1}$. This can be repeated for any starting point $z\in \gamma _0$ to construct a continuous injective curve

$$\begin{aligned} \sigma (z,t):\gamma _0\times [0,\infty )\rightarrow A_0, \end{aligned}$$

such that $\sigma (z,n)\in \widetilde{\gamma }_n$ and, for each $z\in \gamma _0$ and each $j\le n$, $n \in {{\mathbb {N}}}$, we have $f^j(\sigma (z,[n,n+1]))\subset A_j$ and $f^n(\sigma (z,[n,n+1]))$ is a geodesic in ${{\mathcal {F}}}_n$.

Recalling from Step 1 that the Euclidean length of elements in ${{\mathcal {F}}}_n$ is bounded uniformly in n by a constant $M=M(\eta ,d)>0$, and using the expansivity estimate (7.5) on f, we obtain

$$\begin{aligned} {\ell _{{\text {Eucl}}}}( \sigma (z,[n,n+1]))\le \frac{1}{\eta ^n}M,\;\text { for } z\in \gamma _0, n\in {{\mathbb {N}}}. \end{aligned}$$

It follows that the functions $\sigma (z,t)$, $z\in \gamma _0$, are uniformly Cauchy and so converge uniformly as $t\rightarrow \infty$, to a continuous function, say $\sigma (z), z\in \gamma _0$. Hence $\sigma (\gamma _0)$ is a closed curve. Note, however, that we have not shown that $\sigma$ is a Jordan curve, since the map $z\mapsto \sigma (z)$ has not been shown to be injective. Note that ${\widetilde{\gamma }}_n,$ $n \ge 0$ and $\sigma (z,t),$ $z\in \gamma _0, t\in [0,\infty ),$ are all in $U_0$, so the closed curve $\sigma (\gamma _0)\subset \overline{U_0}$.

We can construct analogous maps $\Sigma (z,t):\Gamma _0\times [0,\infty )\rightarrow A_0$ and $\Sigma : \Gamma _0\rightarrow \Sigma (\Gamma _0)$ and obtain a closed curve $\Sigma (\Gamma _0)$ as a uniform limit using the Jordan curves ${\widetilde{\Gamma }}_n$ in a similar manner, noting that ${\widetilde{\Gamma }}_n,$ $n \ge 0$ and $\Sigma (z,t),$ $z\in \Gamma _0, t\in [0,\infty ),$ are all in the exterior of $U_0$, so the closed curve $\Sigma (\Gamma _0)$ does not meet $U_0$.

Step 3 The final step is to show that $\partial U_0$ is indeed a Jordan curve. To show this, the first statement we need to prove is that

$$\begin{aligned} \partial U_0 \subset \sigma (\gamma _0). \end{aligned}$$

(7.6)

Let $C_n$, $c_n$ denote the bounded complementary components of the Jordan curves $\widetilde{\Gamma }_n$, $\widetilde{\gamma }_n$, respectively. Then $(C_n)$ and $(c_n)$ each form a sequence of nested topological disks which are respectively decreasing and increasing, because for each n we have that $f(\Gamma _n)$ surrounds $\Gamma _{n+1}$ and $f(\gamma _n)$ is surrounded by $\gamma _{n+1}$. Note that for each n, the annulus $\widetilde{A}_n{{:}{=}}C_n\setminus \overline{c_n}$ contains $\partial U_0$. This is because, for $n \ge 0$, we have $\Gamma _n$ surrounds $U_n$ and $\gamma _n\subset U_n$.

Suppose now that $\partial U_0 \not \subset \sigma (\gamma _0)$, and let $\zeta \in \partial U_0 \setminus \sigma (\gamma _0)$. Then for some $r>0$ the disk $D(\zeta ,r)$ does not meet the closed curve $\sigma (\gamma _0)$, so there is some open disk $D(\zeta ',r')\subset D(\zeta ,r)\cap U_0$. Hence $D(\zeta ',r')\subset \widetilde{A}_n$, for all $n\in {{\mathbb {N}}}$, and by construction $f^n(D(\zeta ',r'))\subset A_n$ for every n. Now, the maximal radii of the Euclidean disks contained in the annuli $A_n$ are bounded, and indeed converge to 0 as $n\rightarrow \infty$, by construction of the $A_n$. For large n, this contradicts the fact that, since $|({f^n})'(\zeta ')|\ge \eta ^n$, the image $f^n (D(\zeta ',r'))$ contains a disk of radius at least $Br' \eta ^n$, where $B>0$ is Bloch’s constant. This proves (7.6).

The idea now is to show that a parametrization of $\partial U_0$ as a Jordan curve can be obtained from the parametrization $\sigma : \gamma _0 \rightarrow \sigma (\gamma _0)$ of the closed curve $\sigma (\gamma _0)$ by removing those parts of the parametrization (if any) which correspond to points of $\sigma (\gamma _0)$ that lie in $U_0$.

First, it follows from (7.6) that all points of $\partial U_0$ are accessible from within $U_0$. Moreover, there are no points of $\partial U_0$ that are accessible from within $U_0$ in more than one homotopically inequivalent way. This follows by the blowing-up property of the Julia set of f (see for example, [10, Lemma 4 and the following discussion]), because the $U_n, n \ge 0,$ are simply connected wandering domains whose union omits large open subsets of ${\mathbb {C}}$.

To complete the proof, we use a technique from [7, p. 233]. Since $\partial U_0$ is a closed subset of $\sigma (\gamma _0)$, the set $E=\{z\in \gamma _0: \sigma (\zeta ) \in \partial U_0\}$ is closed, and its complement is an at most countable union of open arcs. By identifying such complementary open arcs of E with their endpoints, we can specify an equivalence relation $\sim$ on $\gamma _0$ whose equivalence classes correspond bijectively to points of $\partial U_0$. Moreover, this bijection from the quotient space $\gamma _0/\!\!\sim$ to $\partial U_0$ is clearly continuous, and hence a homeomorphism, and the quotient space $\gamma _0/\!\!\sim$ is homeomorphic to $\gamma _0$. Therefore $\partial U_0$ is a Jordan curve.

This completes the proof of Theorem 7.2.