Semicontinuity of Gauss maps and the Schottky problem

Abstract

We show that the degree of Gauss maps on abelian varieties is semicontinuous in families, and we study its jump loci. As an application we obtain that in the case of theta divisors this degree answers the Schottky problem. Our proof computes the degree of Gauss maps by specialization of Lagrangian cycles on the cotangent bundle. We also get similar results for the intersection cohomology of varieties with a finite morphism to an abelian variety; it follows that many components of Andreotti–Mayer loci, including the Schottky locus, are part of the stratification of the moduli space of ppav’s defined by the topological type of the theta divisor.

1 Introduction

The Gauss map of a hypersurface in projective space is the rational map that sends any smooth point of the hypersurface to its normal direction in the dual projective space. The analogous notion of Gauss maps for subvarieties of abelian varieties appears already in Andreotti’s proof of the Torelli theorem [2]. In contrast to the case of projective hypersurfaces, the Gauss map for any ample divisor on an abelian variety is generically finite of degree $>1$, and its degree is related to the singularities of the divisor. We show that this degree is lower semicontinuous in families, and we study its jump loci. As an application we get that in the moduli space of principally polarized abelian varieties, the degree of the Gauss map refines the Andreotti–Mayer stratification and answers the Schottky problem as conjectured in [11]. We work over an algebraically closed field k with $\mathrm {char}(k)=0$. In Sect. 7 we obtain similar results for the intersection cohomology of complex varieties with a finite morphism to an abelian variety. In particular, many Andreotti–Mayer loci such as the Schottky locus are determined over the complex numbers already by the topological type of the theta divisor.

1.1 Gauss maps and their jump loci

Let A be an abelian variety over k. By translations we may identify its tangent spaces at all points, hence the cotangent bundle $T^\vee A = A\times V$ is trivial with fiber $V=H^0(A, \Omega ^1_A)$. The Gauss map of a reduced effective divisor $D\subset A$ is the rational map

$$\begin{aligned} \gamma _D: \quad D \;\dashrightarrow \; \mathbb {P}V \end{aligned}$$

that sends a smooth point of the divisor to its conormal direction at that point; it coincides with the rational map given by the linear series $\mathbb {P}V^\vee = |{\mathscr {O}}_D(D)|$. For an irreducible divisor this is a generically finite dominant map iff the divisor is ample, which happens iff the divisor is not stable under translations by any positive dimensional abelian subvariety [32, cor. II.11, lem. II.9]. Even in the generically finite case the Gauss map can have positive dimensional fibers [4].

For algebraic families of generically finite maps the generic degree always defines a constructible stratification of the parameter space, but in general it can jump in both directions (see Example 4.2). Our first semicontinuity result says that for Gauss maps on abelian varieties this does not happen:

Theorem 1.1

Let $A \rightarrow S$ be an abelian scheme over a variety S, and let $D\subset A$ be a relatively ample divisor which is flat over S. Let $D_s\subset A_s$ denote their fibers over $s\in S$, and let $\gamma _{D_s}$ be the corresponding Gauss map. Then for each $d\in {\mathbb N}$ the subsets

$$\begin{aligned} S_d \;=\; \bigl \{ s\in S \mid \deg (\gamma _{D_s}) \le d \bigr \} \;\subseteq \; S \end{aligned}$$

are closed in the Zariski topology.

The above result does not show where the degree actually jumps. Let us say that an irreducible subvariety of an abelian variety is negligible if it is stable under translations by a positive dimensional abelian subvariety. Simple abelian varieties have no negligible subvarieties other than themselves. More generally, by [1, th. 3] an irreducible closed subvariety of an abelian variety is negligible iff it is not of general type. Our second result says that in the setting of Theorem 1.1 the degree of the Gauss map jumps whenever a new component of general type appears in the singular locus $\mathrm {Sing}(D_s)$. To make this precise we specify a curve along which we move inside the parameter space:

Theorem 1.2

Let $S'\subset S$ be a curve, and fix a point $0\in S'(k)$. If $\mathrm {Sing}(D_0)$ has an irreducible component which is of general type and not contained in the Zariski closure of $\bigcup _{s\in S'{\setminus } \{0\}} \mathrm {Sing}(D_s)$, then

$$\begin{aligned} \deg (\gamma _{D_0}) < \deg (\gamma _{D_s}) \end{aligned}$$

for all $s\in S'(k) {\setminus } \{0\}$ in some Zariski open neighborhood of the point 0.

The above in particular applies if all components of the singular locus are of general type and $\dim (\mathrm {Sing}(D_0))>\dim (\mathrm {Sing}(D_{s}))$ for all $s\ne 0$. This last condition is motivated by the case of theta divisors and the Schottky problem.

1.2 Application to the Schottky problem

Let ${\mathscr {A}}_g$ be the moduli space of principally polarized abelian varieties of dimension g. Inside it, consider for $d\in {\mathbb N}$ the Gauss loci

$$\begin{aligned} {\mathscr {G}}_d \;=\; \{ (A, \Theta ) \in {\mathscr {A}}_g \mid \deg (\gamma _\Theta ) \le d\} \end{aligned}$$

as in [11, sect. 4] The above results show that these loci are closed (Corollary 6.1) and refine the Andreotti–Mayer stratification (Corollary 6.3). Thus the Gauss loci provide a solution for the Schottky problem to characterize the closure of the locus of Jacobians in the moduli space of principally polarized abelian varieties:

Corollary 1.3

Inside ${\mathscr {A}}_g$ we have:

• (a) The locus of Jacobians is a component of ${\mathscr {G}}_{d}$ for $d=\left( {\begin{array}{c}2g-2\\ g-1\end{array}}\right)$.

• (b) The locus of hyperelliptic Jacobians is a is a component of ${\mathscr {G}}_{d}$ for $d=2^{g-1}$.

The above corollary is shown in Sect. 6 together with an analogous statement for Prym varieties. It confirms a conjecture by the first author, Grushevsky and Sernesi [11, Conjecture 1.6] who verified it for $g\le 4$ by an explicit description of the Gauss loci. As pointed out in loc. cit., this is only a weak solution to the Schottky problem: In general the Gauss loci in the above corollary have more than one irreducible component and the Jacobian locus is only one of them. The theory of ${\mathscr {D}}$-modules allows to refine the degree of the Gauss map to representation theoretic invariants that might distinguish the Jacobian locus [26].

1.3 The degree of conormal varieties

For the proof of Theorems 1.1 and 1.2 we interpret the degree of the Gauss map as an intersection number of Lagrangian cycles on the cotangent bundle of the abelian variety and apply specialization for such cycles [19, 34], which we can do because $\mathrm {char}(k)=0$. To explain how this works, let us forget about abelian varieties for a moment and fix any ambient smooth variety W over k. The conormal variety to a subvariety $X\subset W$ is defined as the closure

$$\begin{aligned} \Lambda _X \;=\; \overline{ \{ (x,\xi ) \mid x\in \mathrm {Sm}(X), \;\xi \in T_x^\vee (W), \; \xi \perp T_x (X) \}} \;\subset \; T^\vee (W) \end{aligned}$$

of the conormal bundle to the smooth locus $\mathrm {Sm}(X)$, where the closure is taken in the total space of the cotangent bundle of the ambient smooth variety. This conormal variety always has pure dimension $n=\dim (W)$, in fact it is Lagrangian with respect to the natural symplectic structure on the cotangent bundle. It is also conic, i.e. stable under the natural action of the multiplicative group on the fibers of the cotangent bundle. Conversely, any closed conic Lagrangian subvariety of the cotangent bundle arises like this [23, Lemma 3]. So the map $X\mapsto \Lambda _X$ induces an isomorphism

$$\begin{aligned} {\mathscr {Z}}(W) = \{ \text {cycles on}\,W\} \;{\mathop {\longrightarrow }\limits ^{\sim }}\; {\mathscr {L}}(W) = \{ \text {conic Lagrangian cycles on}\,T^\vee W\}, \end{aligned}$$

where by a conic Lagrangian cycle we mean a ${\mathbb Z}$-linear combination of closed conic Lagrangian subvarieties. In the case of projective varieties we can talk about the degree of conormal varieties:

Definition 1.4

If W is projective, the degree homomorphism on conic Lagrangian cycles is the map

$$\begin{aligned} \deg : \quad {\mathscr {L}}(W) \;\longrightarrow \; \mathrm {CH}^n(T^\vee (W)) \;{\mathop {\longrightarrow }\limits ^{i^*}}\; \mathrm {CH}^n(W) \;\twoheadrightarrow \; {\mathbb Z}\end{aligned}$$

which is given by the intersection number with the zero section $i: W \hookrightarrow T^\vee (W)$.

Example 1.5

Over the complex numbers the above degree can be computed as follows. For any constructible function $F: W\rightarrow {\mathbb Z}$ consider the topological Euler characteristic

$$\begin{aligned} \chi _\mathrm {top}(W, F) \;=\; \sum _{n\in {\mathbb Z}} \, n\cdot \chi _\mathrm {top}(F^{-1}(n)), \end{aligned}$$

where $\chi _\mathrm {top}(F^{-1}(n))$ denotes the alternating sum of the Betti numbers of $F^{-1}(n)$. In the theory of characteristic classes of singular varieties this definition is applied to a particular constructible function $\mathrm {Eu}_X: W \rightarrow {\mathbb Z}$, the local Euler obstruction of a subvariety $X\subseteq W$ [29, Sect. 3]. Outside of the singular locus $\mathrm {Sing}(X)\subseteq X$ it has the form

$$\begin{aligned} \mathrm {Eu}_X(p) \;=\; {\left\{ \begin{array}{ll} 0 &{} \text {for}\,p\in W{\setminus } X, \\ 1 &{} \text {for}\,p\in \mathrm {Sm}(X), \end{array}\right. } \end{aligned}$$

but its values on the singular locus depend on the singularities: For instance, if X is a curve, $\mathrm {Eu}_X(p)$ is the multiplicity of that curve at p. In general, the degree of conormal varieties in Definition 1.4 can be expressed as an Euler characteristic by the formula

$$\begin{aligned} \deg (\Lambda _X) \;=\; (-1)^{\dim (X)} \cdot \chi _\mathrm {top}(X, \mathrm {Eu}_X), \end{aligned}$$

see [34, Lemme 1.2.1] [17, Prop. 6.1(b)]. The right hand side can be computed easily as soon as we know the local Euler obstruction. For a smooth rational curve X we get $\deg (\Lambda _X)=-2$ while a nodal or cuspidal cubic has $\deg (\Lambda _X)=-3$. Note that a cuspidal cubic is homeomorphic to a smooth rational curve, so the degree of conormal varieties is not a topological invariant. Moreover, it can be negative.

1.4 Proof of the semicontinuity theorems

Of course there are no rational curves in abelian varieties, and in the case of abelian varieties the degree behaves much better. By [37, Th. 1] we have the following result (see Sect. 5):

Proposition 1.6

If $W=A$ is an abelian variety, then

• $\deg (\Lambda _X)\ge 0$ for any $X\subset A$,

• $\deg (\Lambda _X)>0$ if and only if X is of general type,

• $\deg (\Lambda _X)=\deg (\gamma _X)$ for divisors $X\subset A$ with Gauss map $\gamma _X$.

This easily implies Theorem 1.1 when combined with the principle of Lagrangian specialization which we recall in sect. 2: For any flat family of subvarieties in a smooth ambient 1-parameter family, the limit of their conormal varieties is an effective conic Lagrangian cycle whose support contains the conormal variety to the central fiber as a component, and the total degree of the limit cycle equals the degree of a general fiber. The same argument shows that our semicontinuity result holds not only for divisors but for subvarieties of any codimension:

Theorem 1.7

Let $A \rightarrow S$ be an abelian scheme over a variety S, and let $X\subset A$ be an arbitrary family of subvarieties which is flat over S. Then for each $d\in {\mathbb N}$ the subsets $S_d = \bigl \{ s\in S \mid \deg (\Lambda _{X_s}) \le d \bigr \} \subseteq S$ are closed in the Zariski topology.

It remains to prove Theorem 1.2. Given the interpretation for the degree of Gauss maps in Proposition 1.6, the proof has nothing to do with abelian varieties: In Sect. 3 we show that for any flat family of divisors on a smooth 1-parameter variety, the specialization of their conormal varieties contains an extra component whenever the singular locus of the fiber jumps. While the final criterion is phrased only for divisors, we formulate our arguments as far as possible for subvarieties in arbitrary codimension to get beyond Theorem 1.2 (see Example 3.6). This is important even if one only wants to study singularities of divisors: In the theory of Chern classes for singular varieties one attaches to any subvariety $X\subset A$ a characteristic cycle of the form

$$\begin{aligned} \Lambda \;=\; \Lambda _X + \sum _Z m_Z \Lambda _Z \end{aligned}$$

where Z runs through certain strata in $\mathrm {Sing}(X)$ [23, 34], and the topologically meaningful invariant that appears in generalizations of the Gauss-Bonnet index formula is the total degree $\deg (\Lambda )$ involving all the strata.

1.5 A topological view on jump loci

In Sect. 7, which is not used in the rest of the paper, we deduce from our previous results a general semicontinuity theorem for the intersection cohomology of varieties over the complex numbers. Recall that for a complex variety X, the intersection cohomology $\mathrm {IH}^\bullet (X)$ only depends on its homeomorphism type in the Euclidean topology; it coincides with Betti cohomology in the smooth case but is better behaved in general [6, 20, 21, 24, 30]. We denote by

$$\begin{aligned} \chi _\mathrm {IC}(X) \;=\; \sum _{i\ge 0} \; (-1)^{i+\dim (X)} \dim \mathrm {IH}^i(X) \end{aligned}$$

the Euler characteristic of the intersection cohomology. This Euler characteristic is usually not semicontinuous in families, it can jump in both directions. But for families of finite branched covers of subvarieties in complex abelian varieties this does not happen (see Lemma 7.6 and Corollary 7.7):

Theorem 1.8

Let $f: X \rightarrow S$ be a family of varieties such that each fiber $X_s$ is generically reduced and admits a finite morphism to an abelian variety. Then for each $d\in {\mathbb N}_0$ the loci

$$\begin{aligned} S_d \;:=\; \{ s\in S \mid \chi _{\mathrm {IC}}(X_s) \le d \} \;\subseteq \; S \end{aligned}$$

are closed in the Zariski topology.

This puts our results in a topological context, since the intersection cohomology of a complex variety only depends on its homeomorphism type. For instance, it follows from the above that a singular theta divisor cannot be homeomorphic to a smooth one (recall that there are examples of normal varieties which are singular but homemorphic to smooth varieties, such as those by Brieskorn [9, 10]). In Corollary 7.9 we will see that the Jacobian locus appears in the stratification of ${\mathscr {A}}_g$ by the intersection cohomology of the theta divisor, so we obtain:

Corollary 1.9

The locus of Jacobian varieties in ${\mathscr {A}}_g$ is an irreducible component of the closure of the locus of all ppav’s whose theta divisor is homeomorphic to a theta divisor on a Jacobian variety.

It seems an interesting problem to study the topology of theta divisors on abelian varieties in more detail.

2 Lagrangian specialization

For convenience we include in this section a self-contained review of some basic facts about the specialization of Lagrangian cycles, which was introduced in relation with Chern–MacPherson classes [34] and nearby cycles for ${\mathscr {D}}$-modules and perverse sheaves [19]. We work in a relative setting over a smooth curve S. The family of our ambient spaces is given by a smooth dominant morphism of varieties $f:W\rightarrow S$ where $\dim (W)=n+1$. Let $X\subset W$ be a reduced closed subvariety. The relative smooth locus

$$\begin{aligned} \mathrm {Sm}(X/S) \;=\; \{ \, x\in \mathrm {Sm}(X) \mid \; \text {the restriction}\, f|_X: X\rightarrow S\hbox { is smooth at }x \,\} \end{aligned}$$

is nonempty iff $\dim f(X)>0$, in which case $X\rightarrow S$ is flat and $\mathrm {Sm}(X/S)\subset X$ is an open dense subset because $\mathrm {char}(k)=0$. Any $x\in \mathrm {Sm}(X/S)$ is a smooth point of the fiber $X_{s} = f^{-1}(s)\cap X$ over the image point $s=f(x)$. Hence inside the total space

$$\begin{aligned} T^\vee (W/S) \;=\; T^\vee (W)/f^{-1}T^\vee (S) \end{aligned}$$

of the relative cotangent bundle, we define the relative conormal variety to X as the closure

$$\begin{aligned} \Lambda _{X/S} = \overline{\{ (x,\xi ) \in T^\vee (W/S) \mid x\in \mathrm {Sm}(X/S), \; \xi \perp T_x (X_{f(x)}) \}} \;\subset \; T^\vee (W/S). \end{aligned}$$

Remark 2.1

In [8] the relative conormal variety is instead defined as the closure inside the absolute cotangent bundle. This notion of relative conormal variety is obtained from ours by base change via the quotient map $T^\vee (W) \twoheadrightarrow T^\vee (W/S)$, i.e. we have

$$\begin{aligned} T^\vee (W) \times _{T^\vee (W/S)} \Lambda _{X/S} \;=\; \overline{ \{ (x,\xi ) \in T^\vee (W) \mid x\in \mathrm {Sm}(X/S), \; \xi \perp T_x X_{f(x)} \}}. \end{aligned}$$

Indeed, both sides are irreducible closed subvarieties of $T^\vee ( W)|_X$. For the right hand side this holds by definition, for the left hand side it follows from the fact that $\Lambda _{X/S}\subset T^\vee (X/S)$ is an irreducible closed subvariety and $T^\vee W\rightarrow T^\vee (X/S)$ is a fibration with irreducible fibers. So it suffices to show that both sides agree over some open dense $U \subset X$. We can assume X is flat over S and take $U=\mathrm {Sm}(X/S)$, in which case the claim becomes obvious.

Lemma 2.2

If X is flat and irreducible over S, then so is $\Lambda _{X/S}$.

Proof

$\Lambda _{X/S}$ is defined as the schematic closure of a locally closed subscheme V of the relative cotangent bundle $T^\vee (A/S)$. The subscheme V is the total space of a vector bundle over a smooth variety, so it is a smooth variety as well. Its schematic closure is integral, and a morphism from an integral scheme to a smooth curve is flat iff it is dominant [22, chapter III, Prop. 9.7]. $\square$

Relative conormal varieties can be seen as families of conormal varieties. In what follows we denote by

$$\begin{aligned} {\mathscr {L}}(W/S) \;=\; \bigoplus _{X\subset W} {\mathbb Z}\cdot \Lambda _{X/S} \end{aligned}$$

the free abelian group on relative conormal varieties to closed subvarieties $X\subset W$ that are flat over S. By the specialization of $\Lambda \in {\mathscr {L}}(W/S)$ at $s\in S(k)$ we mean the cycle

$$\begin{aligned} {\mathrm {sp}}_s(\Lambda ) \;=\; \bigl [ \Lambda \cdot f^{-1}(s) \bigr ] \end{aligned}$$

which underlies the schematic fiber of the morphism $\Lambda _{X/S} \rightarrow S$ at s. This is again a conic Lagrangian cycle by the following classical result, see [18, prop. (a), p. 179] or in an analytic setup [28, Sect. 1.2]:

Lemma 2.3

(Principle of Lagrangian specialization). The specialization at s gives a homomorphism

$$ {\mathrm {sp}}_s: \quad {\mathscr {L}}(W/S) \;\longrightarrow \; {\mathscr {L}}(W_s) $$

sending effective cycles to effective cycles. On Chow groups it induces the Gysin map in the bottom row of the following commutative diagram:

For any closed subvariety $X\subset W$ which is flat over S, there is a finite subset $\Sigma \subset S$ such that

$$\begin{aligned} {\mathrm {sp}}_s(\Lambda _{X/S}) \;=\; {\left\{ \begin{array}{ll} \Lambda _{X_s} &{} \textit{for}\,\,\, s\in S{\setminus } \Sigma , \\ m_{X_s}\Lambda _{X_s} + \sum _{Z\subset \mathrm {Sing}(X_s)} m_{Z}\Lambda _Z &{} \textit{for} \,\,\, s\in \Sigma , \end{array}\right. } \end{aligned}$$

where $m_{X_s}, m_{Z} > 0$ and the sum runs over finitely many subvarieties $Z\subset \mathrm {Sing}(X_s)$.

Proof

Note that $T^\vee (W_s)$ is an effective Cartier divisor in $T^\vee (W)$. It intersects properly any relative conormal variety to a subvariety which is flat over S. Hence it is clear that the specialization induces on Chow groups the Gysin map defined in [17, Sect. 2.6] and sends effective cycles to effective cycles.

Now take an irreducible subvariety $X\subset W$ which is flat over S. By Lemma 2.2 the morphism $\Lambda _{X/S} \rightarrow S$ is flat and hence all its fibers are pure dimensional of the same dimension. Furthermore the action of the multiplicative group preserves the fibers of $T^{\vee }(W/S)\rightarrow S$ and so the fibers of $\Lambda _{X/S}\rightarrow S$ are unions of conic subvarieties. As the canonical relative symplectic form on $T^{\vee }(W/S)$ restricts to the canonical symplectic form on $T^{\vee }(W_s)$ for every s, we conclude that the fibers of $\Lambda _{X/S}\rightarrow S$ are also Lagrangian and hence a union of conormal varieties, since the conic Lagrangian subvarieties of the cotangent bundle are precisely the conormal varieties [23, Lemma 3]. The coefficients are non-negative as the specialization of effective cycles is effective. Hence ${\mathrm {sp}}_s(\Lambda _{X/S})$ is a sum of conormal varieties, and since under the morphism $T^\vee (A_s) \rightarrow A_s$ its support surjects onto $X_s$, we conclude that one of the appearing components must be $\Lambda _{X_s}$.

As $\Lambda _{X/S}$ is irreducible and we work over a field of characteristic zero, there exists a Zariski open dense subset of S over which the fibers of the morphism $\Lambda _{X/S}\rightarrow S$ are reduced and irreducible. We conclude that for s in this Zariski open dense subset of S we have ${\mathrm {sp}}_s(\Lambda _{X/S})=\Lambda _{X_s}$. Moreover, the specialization cannot have any further components over the relative smooth locus $\mathrm {Sm}(X/S)\subseteq X$, since on that locus also the morphism $\Lambda _{X/S}\rightarrow S$ restricts to a smooth morphism. $\square$

We have the following consequence of flatness:

Proposition 2.4

Let $X\subset W$ be a closed subvariety which is flat over S, then the degree

$$\begin{aligned} d = \deg ({\mathrm {sp}}_s(\Lambda _{X/S})) \quad \hbox {is~independent~of~s}\in S(k). \end{aligned}$$

Proof

The cycle class of the specialization ${\mathrm {sp}}_s(\Lambda _{X/S})$ is the image of $[\Lambda _{X/S}]$ under the Gysin map in Lemma 2.3, and its degree is defined as the intersection number of this image with the zero section $X=\mathcal {X} \hookrightarrow \mathcal {W} = T^\vee (W/S)$. As $\mathcal {X}$ and $\mathcal {W}$ are flat over S and $\mathcal {X} \hookrightarrow \mathcal {W}$ is a regular embedding, the degree is therefore constant by [17, Th. 10.2] applied to the relative conormal variety $\mathcal {V}=\Lambda _{X/S}$. Note that $\mathcal {V}\hookrightarrow \mathcal {W}$ is not required to be a regular embedding; in order to apply loc. cit. we only need that its base change to $\mathcal {X}$ is proper over S, which is true. $\square$

Remark 2.5

For $\mathrm {char}(k)>0$ the specialization of a family of conormal varieties need not be a sum of conormal varieties, see [25, p. 215]. Similarly, for $\mathrm {char}(k)=0$ we need $\dim (S)=1$, otherwise we would have to restrict the class of morphisms as in [33]. For instance, for $S={\mathbb C}^2\ni s=(0,0)$ we have $i_s^{-1}(\Lambda _{X/S}) = T^\vee (W/S)|_{X_s}$ for the subvariety $X = \{ ((x,y,z), (x^2 - y^2 z, y)) \mid (x,y,z)\in {\mathbb C}^3 \} \subset W = {\mathbb C}^3 \times S.$

3 Jump loci for the degree

Let $f: W\rightarrow S$ be a smooth dominant morphism from a smooth variety to a smooth curve as above. For any S-flat subvariety $X\subset W$ and $s\in S(k)$ we have seen that ${\mathrm {sp}}_s(\Lambda _{X/S}) - \Lambda _{X_s} \ge 0,$ where the inequality means that the cycle on the left hand side is effective or zero. It is natural to ask for which $s\in S(k)$ the above inequality is strict. In the notation of Lemma 2.3 this happens iff $m_Z > 0$ for some $Z\subseteq \mathrm {Sing}(X_s)$. The following provides a sufficient criterion for this to happen for families of divisors:

Proposition 3.1

Assume $d=\mathrm {codim}(X, W)=1$. If $\mathrm {Sing}(X/S)$ has an irreducible component which is contained in the fiber over some point $s\in S(k)$, then for this component $Z\subset X_s$ we have

$$\begin{aligned} {\mathrm {sp}}_s(\Lambda _{X/S})-\Lambda _{X_s} \; \ge \; \Lambda _Z. \end{aligned}$$

We divide the proof in several steps. Most of the argument works in arbitrary codimension d, so for the moment we do not yet assume $d=1$. It will be enough to prove the claim over some open dense subset of W metting Z. Fixing a general point $p\in Z(k)$ and working locally near that point, we can assume that

• $Z=\mathrm {Sing}(X/S)$ (equality as a scheme),

• $T^\vee (W/S) \simeq W\times V$ is the trivial bundle with fiber $V=T^\vee _p(W_s)$,

• $X\subset W$ is cut out by a regular sequence $f_1, \ldots , f_d \in H^0(W,\mathcal {O}_W)$.

By the first item each $x\in (X{\setminus } Z)(k)$ is a smooth point of $X_t$ for $t=f(x)$. Fixing a trivialization as in the second item, we can furthermore identify the conormal space to $X_t\subset W_t$ at x with a subspace in $V= T^\vee _x(W_t)$ of codimension d. Consider the relative Gauss map

$$\begin{aligned} X{\setminus } Z \;\longrightarrow \; \hbox {Gr}(d, V ) \end{aligned}$$

which sends each point to the corresponding conormal space. This is a rational map whose locus of indeterminacy is precisely Z. Let $\gamma _X:\hat{X} \rightarrow \hbox {Gr}(d,V)$ denote its resolution of indeterminacy which is obtained by blowing up the base locus $Z\subset X$ as in [17, Sect. 4.4]:

We want to control the image of the exceptional divisor $E_X=\pi _X^{-1}(Z) \subset \hat{X}$ under the map

$$\begin{aligned} \alpha _X \;=\; (\pi _X, \gamma _X): \; \hat{X} \,\rightarrow \, X\times \hbox {Gr}(d, V) \,\subset \, W \times \hbox {Gr}(d, V) \;=\; \hbox {Gr}(d,T^\vee (W/S)). \end{aligned}$$

Lemma 3.2

The morphism $\alpha _X$ is a closed embedding.

Proof

By assumption $X\subset W$ is cut out by a regular sequence $f_1, \dots , f_d$. The same then holds for each fiber $X_t \subset W_t$. Hence it follows that the relative singular locus $\mathrm {Sing}(X/S)$ is cut out as a closed subscheme of W by $f_1, \dots , f_d$ and by the $d\times d$ minors

$$\begin{aligned} J(i_1, \dots , i_d) \;:=\; \det \begin{pmatrix} \partial _{i_1} (f_1) &{} \cdots &{} \partial _{i_1}(f_d) \\ \vdots &{} \ddots &{} \vdots \\ \partial _{i_d} (f_1) &{} \cdots &{} \partial _{i_d}(f_d) \end{pmatrix} \end{aligned}$$

with $1\le i_1< \cdots < i_d \le n$, where we fix an arbitrary basis $\partial _1, \ldots , \partial _n \in V^\vee$ for the fiber of the relative tangent bundle and regard the basis vectors as relative derivations for the smooth morphism $W\rightarrow S$.

Now let $\iota :X\times \hbox {Gr}(d, V)\hookrightarrow X\times \mathbb {P}(\Lambda ^d V )$ be the Plücker embedding of the Grassmannian as a closed subvariety of projective space. We want to show that the composite

$$\begin{aligned} \beta _X \;:=\; \iota \circ \alpha _X: \quad \hat{X} \;\longrightarrow \; X \times \hbox {Gr}(d, V) \longrightarrow X \times \mathbb {P}(\textstyle \bigwedge ^d V) \end{aligned}$$

is a closed embedding. For this let $I\unlhd \mathcal {O}_X$ be the ideal sheaf of $Z\subset X$. Then we have

$$\begin{aligned} \hat{X} \;=\; {\mathrm {Proj}}_X R_I \quad \text {for the graded Rees algebra} \quad R_I \;:=\; \bigoplus _{n\ge 0} \; I^n \cdot t^n \;\subset \; {\mathscr {O}}_X[t], \end{aligned}$$

where t is a dummy variable to keep track of degrees. The homomorphism

$$\begin{aligned} \beta _X^* :\quad \mathcal {O}_X\otimes \mathrm {Sym}^\bullet \left( \bigwedge ^{d}V^{\vee } \right) \;\longrightarrow \;\; R_I \;=\; \bigoplus _{n\ge 0} \; I^n \cdot t^n \end{aligned}$$

of graded $\mathcal {O}_X$-algebras satisfies

$$\begin{aligned} \beta _X^*(1\otimes (\partial _{i_1}\wedge \cdots \wedge \partial _{i_d})) \;=\; J(i_1, \dots , i_d)|_X \cdot t \;\in \; I\cdot t \end{aligned}$$

for $1\le i_1< \cdots < i_k\le n$. But we have seen above that the $\mathcal {O}_X$-module I is generated by the minors on the right hand side. Hence it follows that $\beta _X^*$ is an epimorphism in all degrees and so $\beta _X$ is a closed immersion. $\square$

Remark 3.3

If $d=1$, then $\hbox {Gr}(d, V)=\mathbb {P}V$ and the closed embedding $\alpha _X$ induces an isomorphism

$$\begin{aligned} \alpha _X: \quad \hat{X} \;{\mathop {\longrightarrow }\limits ^{\sim }} \; \mathbb {P}\Lambda _{X/S}. \end{aligned}$$

Indeed, the blowup $\hat{X}$ is again reduced and irreducible by [22, II.7.16]. Via $\alpha _X$ it is therefore an integral closed subscheme of $W\times \mathbb {P}V$ and as such it can be recovered as the Zariski closure of its restriction over the open dense subset $S{\setminus } \{s\}\subset S$, where it coincides with $\mathbb {P}\Lambda _{X/S}\subset W\times \mathbb {P}V$ by definition.

In particular, one may look at the scheme-theoretic fiber of $\hat{X}$ over $s\in S(k)$ to compute the multiplicities in ${\mathrm {sp}}_s(\Lambda _{X/S})$. For $d>1$ the situation becomes more complicated, so in what follows we restrict ourselves to set-theoretic arguments. To pass back to conormal varieties we look at the projection $\hbox {Fl}(d, 1, V) \longrightarrow \hbox {Gr}(d, V)$ from the partial flag variety. This projection is a smooth equidimensional morphism of relative dimension $d-1$. On the fiber product $Y = \hat{X} \times _{\hbox {Gr}(d, V)} \hbox {Fl}(d,1,V)$ consider the morphism

$$\begin{aligned} \alpha _Y = (\pi _Y, \gamma _Y): \quad Y \;\longrightarrow \; X\times \mathbb {P}V \end{aligned}$$

where $\pi _Y: Y\rightarrow \hat{X} \rightarrow X$ and $\gamma _Y: Y\rightarrow \hbox {Fl}(d,1,V)\rightarrow \mathbb {P}V$ are the natural composite maps. Taking the preimage of the previous exceptional divisor $E_X\subset \hat{X}$ we get the following lower bound on the specialization:

Lemma 3.4

The preimage $E_Y = \pi _Y^{-1}(Z)\subset Y$ has dimension $\dim (E_Y) = n$ and satisfies

$$\begin{aligned} \alpha _Y(E_Y) \;\subset \; \mathbb {P}(\mathrm {Supp}({\mathrm {sp}}_s(\Lambda _{X/S}))). \end{aligned}$$

Proof

The statement about the dimension holds because $\dim (Y)=n=\dim (V)$ and since the subvariety $E_Y\subset Y$ is a divisor, being the preimage of the exceptional divisor $E_X\subset \hat{X}$ under the fibration $Y\rightarrow \hat{X}$. To understand why the image $\gamma _Y(E_Y)$ is contained in the specialization, recall that $f: X\rightarrow S$ is smooth over the open subset $S^* = S{\setminus } \{s\}$. The identifications

$$\begin{aligned} Y^* \;:=\; S^* \times _S Y \;\simeq \; S^*\times _S \mathbb {P}\Lambda _{X/S} \;\subset \; S^* \times \mathbb {P}T^\vee (W/S) \end{aligned}$$

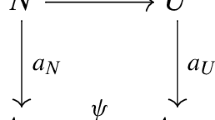
give the following Cartesian diagram where the vertical arrows are open embeddings and the top horizontal arrow is a closed immersion:

Now $\hat{X}$ is irreducible as a blowup of an irreducible variety. So Y is irreducible as well, hence equal to the Zariski closure of its nonempty open subset $Y^* \subset Y$. But then

$$\begin{aligned} {\mathbb P}({\mathrm {sp}}_s(\Lambda _{X/S}))&\;=\; \bigl ( \text {closure of} \; S^*\times _S {\mathbb P}\Lambda _{X/S} \; \text {in} \; \mathbb {P}T^\vee (W/S) \bigr )_s \\&\;=\; \bigl ( \text {closure of the image of}\,Y^*\hbox { in }\mathbb {P}T^\vee (W/S) \bigr )_s \;\supseteq \; \alpha _Y(Y_s) \end{aligned}$$

and we are done because by construction we have $E_Y \subseteq Y_s$. $\square$

Corollary 3.5

If $\alpha _Y: E_Y \rightarrow X\times \mathbb {P}V$ is generically finite onto its image, then we have

$$\begin{aligned} \Lambda _Z \; \subset \; \mathrm {Supp}({\mathrm {sp}}_s(\Lambda _{X/S})). \end{aligned}$$

Proof

Each irreducible component of $\mathbb {P}(\mathrm {Supp}({\mathrm {sp}}_s(\Lambda _{X/S})))$ is the projectivization of some conormal variety. Each of them has dimension $n-1$, so Lemma 3.4 and our generic finiteness assumption imply that $\alpha _Y(E_Y)$ must appear as one of the components. But then this component is $\Lambda _Z$ because it maps onto $Z\subset X$. $\square$

Note that by Lemma 3.2 the morphism $Y\rightarrow X\times \hbox {Fl}(d,1,V)$ is a closed immersion and hence generically finite onto its image. So Corollary 3.5 finishes the proof of Proposition 3.1 since for codimension $d=1$ the morphism $\hbox {Fl}(d,1,V)\rightarrow \mathbb {P}V$ is an isomorphism. This is the only point where we use $d=1$. For higher codimension the morphism $\alpha _Y: E_Y\rightarrow X\times \mathbb {P}V$ is not always a closed embedding, as the following example shows, but it may still be generically finite onto its image as needed for Corollary 3.5:

Example 3.6

Let $W={\mathrm {Spec}}\, k[x,y,z,s] \rightarrow S = {\mathrm {Spec}}\, k[s]$, and consider the family of subvarieties

$$\begin{aligned} X \;=\; \{ f = g = 0 \} \subset W \quad \text {for} \quad {\left\{ \begin{array}{ll} f \;=\; x^2 + y^2 + s, \\ g \;=\; x^2 + z^2 - s. \end{array}\right. } \end{aligned}$$

Here $Z=\mathrm {Sing}(X/S)\subset X$ is a fat point with ideal sheaf $I=(xy,xz,yz)\unlhd {\mathscr {O}}_X$ and looking at the minors of the Jacobian matrix we see that the relative Gauss map is given in Plücker coordinates on the Grassmannian $\hbox {Gr}(2, V)={\mathrm {Proj}}\, k[w_1, w_2, w_3]$ by

$$\begin{aligned} \gamma _X: \quad X{\setminus } Z \;\longrightarrow \; \hbox {Gr}(2, V) = \mathbb {P}^2, \quad (x,y,z,s) \;\mapsto \; [w_1:w_2:w_3] = [yz:xz:-xy]. \end{aligned}$$

Note that the right hand side does not involve the parameter s. Furthermore, we have $(2x^2 + y^2 + z^2)|_X = (f + g)|_X = 0$ and hence the relative Gauss map $\gamma _X$ factors over

$$\begin{aligned} Q_X \;=\; \{ 2w_2^2 w_3^2 + w_1^2 w_3^2 + w_1^2 w_2^2 = 0 \} \;\subset \; \hbox {Gr}(2, V). \end{aligned}$$

Write $\mathbb {P}V = {\mathrm {Proj}}\; k[v_1, v_2, v_3]$ for the dual coordinates $v_i$ where the flag variety is given by

$$\begin{aligned} \hbox {Fl}(2,1,V) \;=\; \{ v_1w_1 + v_2w_2 + v_3w_3 = 0 \} \;\subset \; \hbox {Gr}(2, V)\times \mathbb {P}V \end{aligned}$$

then for

$$\begin{aligned} Q_Y \;=\; \{ 2w_2^2 w_3^2 + w_1^2 w_3^2 + w_1^2 w_2^2 = v_1w_1 +v_2w_2 + v_3w_3 = 0 \} \;\subset \; \hbox {Gr}(2,V) \times \mathbb {P}V. \end{aligned}$$

we get the following diagram where the squares are Cartesian and the hooked arrows are closed immersions:

The composite of the arrows in the top row is the morphism $\alpha _Y: E_Y \rightarrow X\times \mathbb {P}V$ that we are interested in. The diagram shows that it is not a closed immersion, over $Z^\mathrm {red} = \{0\} \subset X$ we have the factorization

where $Q_Y \rightarrow \mathbb {P}V$ is an irreducible cover of generic degree four! However, since the left diagonal arrow is a closed immersion and hence birational for dimension reasons, the morphism $\alpha _Y: E_Y \rightarrow X\times \mathbb {P}V$ is generically finite over its image.

4 Generalities about families of rational maps

Before we apply the above to Gauss maps, let us recall some generalities about families of rational maps. Let $f:X\rightarrow S$ be a faithfully flat morphism of varieties of relative dimension n with irreducible fibers. Let ${\mathscr {L}}\in { Pic }(X)$ be a line bundle and ${\mathscr {V}}$ a rank $n+1$ vector subbundle of $f_*{\mathscr {L}}$. Then for each point $s\in S(k)$ we get a linear series ${\mathscr {V}}_s \subset H^0(X_s, {\mathscr {L}}_s)$ and we denote by $\phi _s:X_s \dashrightarrow \mathbb {P}{\mathscr {V}}_s$ the corresponding rational map. Note that since the source and the target of this map have the same dimension, the map is a generically finite cover iff it is dominant. So we consider the degree map

$$\begin{aligned} \deg : \quad S(k) \;\longrightarrow \; {\mathbb N}_0, \quad s\;\mapsto \;\deg (\phi _s), \end{aligned}$$

where we put $\deg (\phi _s)=0$ if $\phi _s$ is not dominant.

Lemma 4.1

The degree map $\deg$ is constructible.

Proof

By [17, Prop. 4.4] we can compute the degree in terms of Segre and Chern classes as

$$\begin{aligned} \deg (\phi _s) \;=\; \int _{X_s}c_1({\mathscr {L}}_s)^n-\int _{B_s}c({\mathscr {L}}_s)^n\cap s(B_s,X_s) \end{aligned}$$

where $B_s\subset X_s$ denotes the base locus of the linear series $\mathcal {V}_s\subset H^0(X_s, {\mathscr {L}}_s)$. We can put together all these fiberwise base loci into a relative base locus and consider the flattening stratification of this relative base locus. This is a stratification of S such that on each stratum the above intersection number is constant, hence the function $\deg$ is constructible. $\square$

However, in general the degree is neither upper nor lower semi-continuous, as the following variation of [11, Ex. 2.3] shows:

Example 4.2

Let S be a smooth affine curve with two marked points $s_\pm \in S(k)$ and fix positive integers $n_\pm \le n < 27$. Let $p_j: S\longrightarrow \mathbb {P}^3$ for $j=1,\dots , n$ be such that

• for $t\ne s_\pm$ the points $p_j(t)$ are in general position,

• for $t=s_\pm$ they consist of $n_\pm$ general points on a given line $\ell$ and $n-n_\pm$ points in general position not on that line.

For $t\in S(k)$ let $f_t:\mathbb {P}^3\dashrightarrow \mathbb {P}^3$ be the generically finite rational map defined by a linear system of four generic cubics passing trough the $p_j(t)$. By loc. cit. its degree is

$$\begin{aligned} \deg (f_t) \;=\; {\left\{ \begin{array}{ll} 27 - n &{} \text {for}\,t\ne s_\pm , \\ 20 - (n-n_\pm ) &{} \text {for}\,t=t_\pm \hbox { and }n_\pm \ge \max \{4, n-20 \}, \end{array}\right. } \end{aligned}$$

since in the second case the indeterminacy locus of $f_\pm$ consists of the chosen line $\ell$ together with the remaining $n-n_\pm$ points. So the degree is a constructible function as predicted by Lemma 4.1. However, taking for example $(n,n_+,n_-)=(20,10,4)$ we obtain an example where the generic value of the degree is seven, jumps up to ten at one point and down to four at another point. Hence in the same family the degree can both decrease and increase under specialization.

5 Gauss maps on abelian varieties

We now apply the above to an abelian scheme $f: A\rightarrow S$, so in this section we take $W=A$. Let $X\subset A$ be a closed subvariety which is flat over S. For $s\in S(k)$ we have the Gauss map

$$\begin{aligned} \gamma _{X_s}: \quad {\mathbb P}\Lambda _{X_s} \;\longrightarrow \;{\mathbb P}V \end{aligned}$$

where $V=H^0(A_s, \Omega _{A_s}^1)$. If this map is dominant, then for dimension reasons it is a generically finite cover and we denote by $\deg (\gamma _{X_s})$ its generic degree. If the map is not dominant we put $\deg (\gamma _{X_s})=0$; this occurs iff the subvariety $X_s\subset A_s$ arises by pull-back from some smaller dimensional abelian quotient variety [37, Th. 1], which by [1, Th. 3] happens iff $X_s$ is not of general type. The degree of the above Gauss map is related to the degree of conormal varieties as follows:

Lemma 5.1

We have $\deg (\Lambda _{X_s})=\deg (\gamma _{X_s})$.

Proof

The degree of our Gauss map $\gamma _{X_s}: {\mathbb P}\Lambda _{X_s} \rightarrow {\mathbb P}V$ coincides with the degree considered by Franecki and Kapranov terms of tangent rather than cotangent spaces in [16, Sect. 2]: Up to the duality $\hbox {Gr}(d, V)\simeq \hbox {Gr}(g-d, V^\vee )$ they study the map $p\circ q$ defined by the diagram

where $\widetilde{X}_s = \mathrm {Sm}(X_s) \times _{G(d,V)} F(d,g-1, V)$. By construction $\widetilde{X}_s \subset {\mathbb P}\Lambda _{X_s}$ is an open subset of the conormal variety, and their map $p\circ q$ is the restriction of our Gauss map to this open subset. Hence the claim follows from [16, Prop. 2.2]. $\square$

In particular $\deg (\Lambda _{X_s}) \ge 0$. Together with the preservation of the total degree under Lagrangian specialization this leads to our first semicontinuity result:

Corollary 5.2

The map $S(k) \rightarrow {\mathbb N}_0, s\mapsto \deg (\gamma _{X_s})$ is lower semicontinuous.

Proof

By Lemma 4.1, we know that the map is constructible. We have to show that its values decrease under specialization. For this we may assume that S is a curve, and after base change to its normalization we may assume this curve to be smooth. Let d be the value from Proposition 2.4. With notations as in Lemma 2.3 then

$$\begin{aligned} \deg (\Lambda _{X_s}) \;=\; {\left\{ \begin{array}{ll} d &{} \text {if}\,s\notin \Sigma , \\ d - \delta (s) &{} \text {if}\,s\in \Sigma , \end{array}\right. } \end{aligned}$$

where $\delta (s) = \sum _{Z\subset X_s} m_Z\cdot \deg (\Lambda _Z)$ with multiplicities $m_Z \ge 0$. Now in the case of abelian varieties the occuring degrees coincide with the degrees of the corresponding Gauss maps by Lemma 5.1. In particular, since the degrees of Gauss maps are obviously nonnegative, we have $\deg (\gamma _Z)\ge 0$ and therefore $\delta (s) \ge 0$, which proves that the degree of the Gauss map is constant on an open dense subset and can only drop on the finitely many points of the complement. $\square$

To see where the function in the previous corollary actually jumps, recall that a subvariety $Z\subset A_s$ has Gauss degree $\deg (\gamma _Z)=0$ iff it is not of general type. Thus we obtain the following sufficient jumping criterion:

Corollary 5.3

Suppose $\dim (S)=1$. Let $X\subset A$ be a divisor which is flat over S and let $0\in S(k)$ be a point such that $\mathrm {Sing}(X_0)$ has an irreducible component Z which is of general type and not contained in the closure of $\bigcup _{t\ne 0}\mathrm {Sing}(X_t)$. Then there is an open dense subset $U\subset S$ such that

$$\begin{aligned} \deg (\gamma _{X_t}) -\deg (\gamma _{X_0}) \;\ge \; \deg (\gamma _Z) \;>\; 0 \quad f\!or ~~all \quad t\;\in \; U(k) {\setminus } \{0\}. \end{aligned}$$

Proof

The first inequality follows from Proposition 3.1, the second from our assumption that the subvariety $Z\subset A_0$ is of general type. $\square$

6 Application to the Schottky problem

The moduli space ${\mathscr {A}}_g$ of principally polarized abelian varieties of dimension g over the field k admits the finite filtration $\cdots \subseteq {\mathscr {G}}_d \subseteq {\mathscr {G}}_{d-1} \subset \cdots \subseteq {\mathscr {G}}_{g!} = {\mathscr {A}}_g$ by the Gauss loci

$$\begin{aligned} {\mathscr {G}}_d \;:= \; \{(A,\Theta )\in {\mathscr {A}}_g \, | \, \deg (\gamma _{\Theta }) \le d\} \;\subseteq \; {\mathscr {A}}_g. \end{aligned}$$

Our semicontinuity result implies:

Corollary 6.1

For any $d\in {\mathbb N}$ the Gauss loci ${\mathscr {G}}_d$ are closed in ${\mathscr {A}}_g$.

Proof

The moduli space ${\mathscr {A}}_g$ has a finite cover by a smooth quasi-projective variety over which there exists universal theta divisor. On this cover the Gauss maps fit together in a family of rational maps as in the setting of Sect. 4. The Gauss loci are the level sets of the degree map, and we have to show that this map is lower-semicontinuous. This follows from Corollary 5.2. $\square$

Using our sufficient criterion for jumps in the degree of Gauss maps, we can now show that the stratification by the Gauss loci refines the stratification by the Andreotti–Mayer loci

$$\begin{aligned} {\mathscr {N}}_c \;=\; \{ (A, \Theta ) \in {\mathscr {A}}_g \mid \dim \mathrm {Sing}(\Theta ) \ge c\} \end{aligned}$$

from [3]. Some care is needed because the singular locus of the theta divisor may have components which are negligible, i.e. not of general type:

Remark 6.2

There are indecomposable ppav’s $(A,\Theta )\in {\mathscr {A}}_g$ with a theta divisor for which $\mathrm {Sing}(\Theta )\subset A$ is negligible. This even happens for generic ppav’s on certain irreducible components of Andreotti–Mayer loci: For instance, for $g=5$ one can show that for a generic ppav on the component ${\mathscr {E}}_{5,1}\subset {\mathscr {N}}_1$ from [13, Thm. 4.1(ii)] the singular locus $\mathrm {Sing}(\Theta )$ is an elliptic curve.

A more detailed discussion will be given in a forthcoming work by Constantin Podelski. In any case negligible components can only appear on decomposable abelian varieties, hence the following corollary of our jumping criterion covers all Andreotti–Mayer strata whose general point is a simple abelian variety:

Corollary 6.3

Let $c\in {\mathbb N}$, and let ${\mathscr {N}}\subset {\mathscr {N}}_c$ be an irreducible component whose general point is a ppav whose singular locus of the theta divisor has no negligible components. Then ${\mathscr {N}}$ is an irreducible component of ${\mathscr {G}}_d$ for some $d\in {\mathbb N}$.

Proof

Let $s \in {\mathscr {N}}(k)$ be a general point on the given component. Since the moduli space of ppav’s is a quasiprojective variety, we may pick an affine curve $S\subset {\mathscr {A}}_g$ such that $S\cap {\mathscr {N}}_c = \{s\}$ and S meets ${\mathscr {N}}$ transversely. After passing to a finite cover we may assume that there exists an abelian scheme $f: A\rightarrow S$ and a universal theta divisor $\Theta \subset A$ over this curve, and by our choice of the curve we have

$$\begin{aligned} \dim \mathrm {Sing}(\Theta _t) < \dim \mathrm {Sing}(\Theta _{s}) \quad \text {for all}\,t\ne s. \end{aligned}$$

Hence $\mathrm {Sing}(\Theta _s)$ has an irreducible component not in the closure of $\bigcup _{t\ne s} \mathrm {Sing}(\Theta _t)$ and so

$$\begin{aligned} \deg (\gamma _{\Theta _t}) \;>\; \deg (\gamma _{\Theta _s}) \quad \text {for all}\,t\ne s \end{aligned}$$

by Corollary 5.3. Varying s in an open subset of the component ${\mathscr {N}}$ and varying S among all curves meeting this component transversely in the chosen point, we get that some nonempty open subset of ${\mathscr {N}}$ is also an open subset of a Gauss locus ${\mathscr {G}}_d$ for some $d\in {\mathbb N}$. Hence the result follows by passing the the closure, since both the Andreotti–Mayer loci and the Gauss loci are closed in ${\mathscr {A}}_g$. $\square$

As an application we get that the stratification by the degree of the Gauss map gives a solution to the Schottky problem as conjectured in [11], where for the Prym version we denote by D(g) the degree of the varieties of quadrics in ${\mathbb P}^{g-1}$ of rank at most three:

Corollary 6.4

We have the following components of Gauss loci in ${\mathscr {A}}_g$:

• (a) The locus of Jacobians is a component of ${\mathscr {G}}_{d}$ for $d=\left( {\begin{array}{c}2g-2\\ g-1\end{array}}\right)$.

• (b) The locus of hyperelliptic Jacobians is a is a component of ${\mathscr {G}}_{d}$ for $d=2^{g-1}$.

• (c) The locus of Prym varieties is a is a component of ${\mathscr {G}}_d$ for $d=D(g)+2^{g-3}$.

Proof

The locus of Jacobians is a component of an Andreotti–Mayer locus by [3], and by [31, Proposition 3.4] a general Jacobian variety is a simple abelian variety and thus in particular has no negligible subvarieties other than itself. Furthermore, it is well-known that the degree of the Gauss map of a Jacobian is $d=\left( {\begin{array}{c}2g-2\\ g-1\end{array}}\right)$, see e.g. [2, proof of prop. 10]. Hence part (a) follows from corollary 6.3. If we replace Jacobians by hyperelliptic Jacobians, the above arguent works also in the hyperelliptic case, with the same references. For Prym varieties the argument is again the same but now one has to replace reference [3] with [14], and reference [2] with [36, Main Theorem]. In the last reference the reader can also find an explicit expression for the number D(g). $\square$

7 A topological view on jump loci

In this section we work over the complex numbers with the Euclidean topology. Let W be a smooth complex projective variety. For a closed subvariety $X\subset W$ the singular locus $\mathrm {Sing}(X)$ and the conormal degree $\deg (\Lambda _X)$ are not topological invariants of the subvariety, as Example 1.5 shows. But both are related to the intersection cohomology $\mathrm {IH}^\bullet (X)$ which only depends on the homeomorphism type of the subvariety in the Euclidean topology; see [6, 20, 21, 24, 30]. The Euler characteristic

$$\begin{aligned} \chi _\mathrm {IC}(X) \;=\; \sum _{i\ge 0} \; (-1)^{i+\dim (X)} \dim \mathrm {IH}^i(X) \end{aligned}$$

can be read off from a generalization of the Gauss-Bonnet theorem: The Kashiwara index formula [19, Th. 9.1] writes it as a degree in the sense of Definition 1.4. More precisely

$$\begin{aligned} \chi _{\mathrm {IC}}(X) \;=\; \deg (\hbox {CC}(\delta _X)), \end{aligned}$$

where $\delta _X\in \mathrm {Perv}(W)$ denotes the perverse intersection complex of $X\subseteq W$ [5, 12] and where the characteristic cycle $\hbox {CC}(\delta _X) \in {\mathscr {L}}(W)$ is an effective conic Lagrangian cycle which contains $\Lambda _X$ as a component of multiplicity one but may also have as components the conormal varieties to certain $Z\subseteq \mathrm {Sing}(X)$. Passing from conormal varieties to characteristic cycles restores topological invariance of the degree:

Example 7.1

In $W={\mathbb P}^2$ the conormal degree for a smooth rational curve differs from the one for a cuspical cubic, see Example 1.5. But this is compensated by a difference in

$$\begin{aligned} \hbox {CC}(\delta _X) \;=\; {\left\{ \begin{array}{ll} \Lambda _X &{} \text {if}\,X\hbox { is a smooth rational curve}, \\ \Lambda _X + \Lambda _{\{p\}} &{} \text {if}\,X\hbox { is a cuspidal cubic with cusp }p. \end{array}\right. } \end{aligned}$$

which in both cases gives the total degree $\deg (\hbox {CC}(\delta _X))=-2$.

In what follows we want to understand how for a morphism $X\rightarrow S$ of complex varieties the intersection cohomology Euler characteristic of the fibers varies. Basic stratification theory implies:

Lemma 7.2

The map $s\mapsto \chi _{\mathrm {IC}}(X_s)$ is constructible.

Proof

The homeomorphism invariance of intersection cohomology [21, Th. 4.1] shows that for a topologically locally trivial fibration over a connected base, all fibers have the same intersection cohomology. Any morphism of complex algebraic varieties restricts to a topologically locally trivial fibration over a Zariski open dense subset of the target [35, Cor. 5.1], so we are done by Noetherian induction. $\square$

In general the map in this lemma is neither upper nor lower semicontinuous, the jumps may go in both directions:

Example 7.3

Let $Q\subset {\mathbb P}^3$ be a quadric. Then by [30, Ex. 2.3.21 and Th. 2.4.6] we have

$$\begin{aligned} \chi _{\mathrm {IC}}(Q) \;=\; {\left\{ \begin{array}{ll} 4 &{} \text {if}\,Q\simeq {\mathbb P}^1 \times {\mathbb P}^1\hbox { is smooth}, \\ 3 &{} \text {if}\,Q\hbox { is a cone over a smooth rational curve}, \\ 6 &{} \text {if}\,Q\hbox { is a union of two projective planes}. \end{array}\right. } \end{aligned}$$

So for a family of quadrics whose general member is smooth, the number $\chi _{\mathrm {IC}}(Q)$ jumps down on nodal quadrics but jumps up on reducible quadrics.

Note that here the size of the jumps is precisely the Euler characteristic of the singular locus. This fits with the following sheaf-theoretic version of the Lagrangian specialization principle:

Theorem 7.4

Let $f: W\rightarrow S$ be a smooth proper family over a curve S, and let $X\subset W$ be a closed subvariety such that the morphism $f: X\rightarrow S$ is flat with generically reduced fibers. Then there exists $d\in {\mathbb Z}$ and a finite subset $\Sigma \subset S$ such that

$$\begin{aligned} \chi _{\mathrm {IC}}(X_s) \;=\; {\left\{ \begin{array}{ll} d &{} \text {for}\,s\in S{\setminus } \Sigma , \\ d - \deg (\Lambda (s)) &{} \text {for}\,s\in \Sigma , \end{array}\right. } \end{aligned}$$

where $\Lambda (s) = {\mathrm {sp}}_s(\hbox {CC}(\delta _X)) - \hbox {CC}(\delta _{X_s}) \in {\mathscr {L}}(W_s)$ is an effective cycle.

Proof

We interpret Lagrangian specialization via perverse sheaves. For $s\in S({\mathbb C})$ one has the functor of nearby cycles $\Psi _s: \mathrm {Perv}(W)\rightarrow \mathrm {Perv}(W_s)$, which is an exact functor with

$$\begin{aligned} \hbox {CC}(\Psi _s(P)) \;=\; {\mathrm {sp}}_s(\hbox {CC}(P)) \quad \text {for all} \quad P \;\in \; \mathrm {Perv}(W) \end{aligned}$$

by [19, Th. 5.5]. Here we abuse notation and view $\hbox {CC}(P)$ as an element of the group of relative conic Lagrangian cycles ${\mathscr {L}}(W/S)$ via Remark 2.1, discarding any component that is not flat over S. The last part of the specialization Lemma 2.3 has a sheaf-theoretic version: For any closed S-flat subvariety $X\subset W$ such that the map $f: X\rightarrow S$ has generically reduced fibers, there exists a finite subset $\Sigma \subset S$ such that the semisimplification $(\Psi _s(\delta _X))^{\mathrm{ss}}$ of the perverse sheaf $\Psi _s(\delta _X)$ has the form

$$\begin{aligned} (\Psi _s(\delta _X))^\mathrm{ss} \;\simeq \; {\left\{ \begin{array}{ll} \delta _{X_s} &{} \text {for}\,s\in S{\setminus } \Sigma , \\ \delta _{X_s} \oplus P(s) &{} \text {for}\,s\in \Sigma , \end{array}\right. } \end{aligned}$$

where $P(s)\in \mathrm {Perv}(X_s)$ is a perverse sheaf with support contained in $\mathrm {Sing}(X_s)$. So we get

$$\begin{aligned} {\mathrm {sp}}_s(\hbox {CC}(\delta _X)) \;=\; \hbox {CC}(\Psi _s(\delta _X)) \;=\; {\left\{ \begin{array}{ll} \hbox {CC}(\delta _{X_s}) &{} \text {for}\,s\in S{\setminus } \Sigma , \\ \hbox {CC}(\delta _{X_s}) + \Lambda (s) &{} \text {for}\,s\in \Sigma , \end{array}\right. } \end{aligned}$$

where $\Lambda (s) = \hbox {CC}(P(s))\in {\mathscr {L}}(W_s)$ is effective, being the characteristic cycle of a perverse sheaf. Hence the result follows by noting that if $f: W\rightarrow S$ is proper, then by Proposition 2.4 the degree $d=\deg ({\mathrm {sp}}_s(\hbox {CC}(\delta _X)))$ is independent of s. $\square$

In the case of abelian varieties the positivity of conormal degrees then gives an analog of Theorem 1.7. The same argument works for a much wider class of varieties, we only need the following positivity property:

Definition 7.5

A variety X satisfies the signed Euler characteristic property if we have

$$\begin{aligned} \chi (X, P) \;:=\; \sum _{i\in {\mathbb Z}} (-1)^i \dim \mathrm {H}^i(X, P) \;\ge \; 0 \quad \text {for all} \quad P\;\in \; \mathrm {Perv}(X). \end{aligned}$$

The terminology is borrowed from [15]. The above property holds for semiabelian varieties [16] and hence also for any finite cover of closed subvarieties of them:

Lemma 7.6

If a variety A has the signed Euler characteristic property, then so does any variety with a finite morphism to A. In particular, any variety with a finite morphism to a semiabelian variety has the signed Euler characteristic property.

Proof

If $f: X\rightarrow A$ is a finite morphism, then for any perverse sheaf $P\in \mathrm {Perv}(X)$ the direct image is a perverse sheaf $Rf_*(P)\in \mathrm {Perv}(A)$. If A has the signed Euler characteristic property, which holds for instance for abelian varieties [16], then we get $\chi (A, P)=\chi (A, Rf_*(P))\ge 0$. $\square$

The above theorem shows that for any family of such varieties the intersection cohomology Euler characteristic is semicontinuous:

Corollary 7.7

Let $f: W\rightarrow S$ be a smooth proper morphism to a variety S, and let $X\subset W$ be a closed subvariety such that $f: X\rightarrow S$ is flat and all its fibers are generically reduced and have the signed Euler characteristic property. Then for each $d\in {\mathbb N}$ the subsets $S_d = \bigl \{ s\in S \mid \chi _{\mathrm {IC}}(X_s) \le d \bigr \} \subseteq S$ are Zariski closed.

Proof

We must show that $\chi _{\mathrm {IC}}(X_s)$ cannot increase under specialization. For this we can assume S is a smooth curve. Then Theorem 7.4 applies, here $\chi (X_s, P(s))\ge 0$ since $X_s$ has the signed Euler characteristic property. $\square$

In deciding where the Euler characteristic actually jumps, we need to be more careful. Proposition 3.1 gives a way to see extra components in ${\mathrm {sp}}_s(\hbox {CC}(\delta _X))$ but does not guarantee that these enter in a new summand $\Lambda (s)$, a priori they could also appear in $\hbox {CC}(\delta _{X_s})$; however, this second case can only happen if $\hbox {CC}(\delta _{X_s})$ is reducible, which one can often exclude by a direct computation.

Let us illustrate this again with theta divisors. Corollary 7.7 says that for $d\in {\mathbb N}$ the loci

$$\begin{aligned} {\mathscr {X}}_d \;=\; \{ (A, \Theta ) \in {\mathscr {A}}_g \mid \chi _{\mathrm {IC}}(\Theta ) \le d\} \;\subseteq \; {\mathscr {A}}_g. \end{aligned}$$

are closed, and by the homeomorphism invariance of intersection cohomology they only depend on the topology of the theta divisor. This provides a topological view on Andreotti–Mayer loci, for instance:

Corollary 7.8

Let ${\mathscr {N}}\subset {\mathscr {N}}_c$ be an irreducible component of an Andreotti–Mayer locus such that a general point of this component is a ppav $(A, \Theta )$ with the property that

• $\hbox {CC}(\delta _\Theta )$ is irreducible, and

• $\mathrm {Sing}(\Theta )$ has no negligible components.

Then ${\mathscr {N}}$ is also an irreducible component of ${\mathscr {X}}_d$ for some $d\in {\mathbb N}$.

Proof

Use the same argument as in Corollary 6.3, together with the remark after the proof of Corollary 7.7. $\square$

This in particular applies to the locus of Jacobians. In the following corollary we do not mention hyperelliptic Jacobians because for them $\hbox {CC}(\delta _\Theta )$ is reducible, and we haven’t checked what happens for a generic Prym variety. However, we include the Andreotti–Mayer locus ${\mathscr {N}}_0 \subset {\mathscr {A}}_g$ of ppav’s with a singular theta divisor:

Corollary 7.9

Inside the moduli space ${\mathscr {A}}_g$ we have:

• (1) The locus ${\mathscr {N}}_0$ is equal to ${\mathscr {X}}_d$ for $d={\left\{ \begin{array}{ll} g!-1 &{} \text {if g is odd}, \\ g! - 2 &{} \text {if g is even}. \end{array}\right. }$

• (2) The locus of Jacobians is a component of ${\mathscr {X}}_{d}$ for $d=\left( {\begin{array}{c}2g-2\\ g-1\end{array}}\right)$.

Proof

(1) By definition ${\mathscr {A}}_g{\setminus } {\mathscr {N}}_0$ consists of all ppav’s $(A,\Theta )$ with a smooth theta divisor and for those we know that $\chi _{\mathrm {IC}}(\Theta )=g!$ because for a smooth variety intersection cohomology equals Betti cohomology. But at a generic point $(A, \Theta )$ of each of the two components of ${\mathscr {N}}_0$ the theta divisor has one respectively two nodes, and then

$$\begin{aligned} \chi _{\mathrm {IC}}(\delta _\Theta ) \;=\; {\left\{ \begin{array}{ll} g! - 2k &{} \text {if}\,g\hbox { is even}, \\ g! - k &{} \text {if}\,g\hbox { is odd}, \end{array}\right. } \end{aligned}$$

where $k\in \{1,2\}$ denotes the number of nodes [27, proof of prop. 4.2(2)]. Hence the claim follows by Corollary 7.7. Note that the degree of the classical Gauss map is $\deg (\Lambda _\Theta )=g! - 2k$ in both cases, but for odd g the cycle $\hbox {CC}(\delta _\Theta )=\Lambda _\Theta + \Lambda _{\mathrm {Sing}(\Theta )}$ is reducible and we cannot directly apply Corollary 7.8.

(2) For Jacobians of nonhyperelliptic curves we know that $\hbox {CC}(\delta _\Theta )=\Lambda _\Theta$ is irreducible by [7, Th. 3.3.1], so if we specialize to such a Jacobian, then any new component of the specialization must enter in $\Lambda (s)$. So the same argument as in the proof of Corollary 6.4 shows that the locus of Jacobians is a component of ${\mathscr {X}}_d$ where $d=\chi _{\mathrm {IC}}(\Theta )=\deg (\hbox {CC}(\delta _\Theta ))=\deg (\Lambda _\Theta )$ is the degree of the Gauss map for the theta divisor on a general Jacobian variety as in Corollary 6.4. $\square$

The above is still only a weak solution to the Schottky problem, though $\chi _{\mathrm {IC}}(\Theta )$ also appears as the dimension of an irreducible representation of a certain reductive group which gives more information [26, Sect. 4]. The following example for $g=4$ illustrates the difference between the various numerical invariants:

Example 7.10

Let $(A, \Theta ) \in {\mathscr {A}}_4$.

• If $\mathrm {Sing}(\Theta )$ consists of 8 nodes, then $\deg (\gamma _\Theta )=\chi _{\mathrm {IC}}(\delta _\Theta ) = 8$.

• If $\mathrm {Sing}(\Theta )$ consists of 5 nodes, then $\deg (\gamma _\Theta )=\chi _{\mathrm {IC}}(\delta _\Theta ) = 14$.

• If $(A, \Theta )$ is a hyperelliptic Jacobian, then $\deg (\gamma _\Theta )=8$ and $\chi _{\mathrm {IC}}(\delta _\Theta ) = 14$.

So there are non-homeomorphic theta divisors whose Gauss maps have the same degree. Are there also homeomorphic theta divisors with different Gauss degrees?