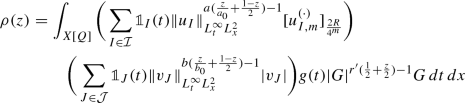Skip to main content
SpringerLink
Log in

Multi-scale bilinear restriction estimates for general phases

  • Published:
Mathematische Annalen Aims and scope Submit manuscript

Abstract

We prove (adjoint) bilinear restriction estimates for general phases at different scales in the full non-endpoint mixed norm range, and give bounds with a sharp and explicit dependence on the phases. These estimates have applications to high-low frequency interactions for solutions to partial differential equations, as well as to the linear restriction problem for surfaces with degenerate curvature. As a consequence, we obtain new bilinear restriction estimates for elliptic phases and wave/Klein–Gordon interactions in the full bilinear range, and give a refined Strichartz inequality for the Klein–Gordon equation. In addition, we extend these bilinear estimates to hold in adapted function spaces by using a transference type principle which holds for vector valued waves.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. This exploits the bound

    $$\begin{aligned} ( 1 + C 2^{-\frac{\alpha }{C}m}) \times ( 1 + C 2^{-\frac{\alpha }{C}(m-1)}) \times \cdots \times ( 1 + C) \lesssim 1\end{aligned}$$

    which follows by taking logs, and recalling the elementary estimate \(\log (1+x) \leqslant x\).

  2. Explicitly, in the region \(|\partial _1\Phi _1 - \partial _1 \Phi _2| \approx |\nabla \Phi _1 - \nabla \Phi _2|\), there exists a function \(\psi (\tau , \xi , \eta '):\mathbb {R}\times \mathbb {R}^n \times \mathbb {R}^{n-1} \rightarrow \mathbb {R}\) such that

    $$\begin{aligned} \Phi _1\big (\xi - (\psi , \eta ')\big ) + \Phi _2(\psi , \eta ') = \tau . \end{aligned}$$

    Thus we can write the surface as a graph \(\Sigma _2({\mathfrak {h}})= \{ (\psi (\eta '), \eta ') \in (h-\Lambda _1) \cap \Lambda _2\}\), and hence the surface measure is then \( d\sigma (\eta ) = \sqrt{1 + |\nabla _{\eta '} \psi |^2} d\eta ' = \frac{|\nabla \Phi _1 - \nabla \Phi _2| }{|\partial _1 \Phi _1 - \partial _1 \Phi _2|} d\eta '\).

  3. Since \(\chi _q\) has compact Fourier support, it can only have countable number of zeros. In particular, \(\chi _q>0\) almost everywhere.

  4. Just use the identities \(X[Q(t,x)] = X[Q(0)] + (t,x)\) and \(-X[Q(0)] = X[-Q(0)] = X[Q(0)]\).

  5. This is simply an application of complex interpolation. In more detail, we just repeat the proof of the Riesz–Thorin interpolation theorem, thus given a functions \(g \in L^2_t(\mathbb {R})\) and \(G \in L^\infty _t L^{r'}_x(\mathbb {R}^{1+n})\), we define the function \(\rho (z)\) for \(z\in \mathbb {C}\) as

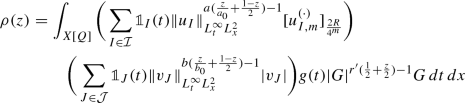
    where \(\frac{1}{a_0} = \frac{ \frac{1}{r} + \frac{1}{a}-1}{\frac{2}{r} -1}\) and \(\frac{1}{b_0} = \frac{ \frac{1}{r} + \frac{1}{b}-1}{\frac{2}{r} -1}\). It is easy to check that \(\rho \) is complex analytic when \(0\leqslant \mathfrak {R}(z)\leqslant 1\), is at most of exponential growth, and \(\rho (0)\) can be bounded by the \(L^2_{t,x}\) estimate, \(\rho (1)\) by the \(L^2_t L^1_x\) estimate. Hence interpolated bound follows from the Hadamard Three-Lines Theorem or Lindelöf’s Theorem.

References

  1. Bejenaru, I.: Optimal bilinear restriction estimates for general hypersurfaces and the role of the shape operator. Intern. Math. Res. Not. 23, 7109–7147 (2016)

    MATH  Google Scholar 

  2. Bourgain, J.: Refinements of Strichartz’ inequality and applications to \(2\)D-NLS with critical nonlinearity. Intern. Math. Res. Not. 5, 253–283 (1998)

    Article  MATH  Google Scholar 

  3. Buschenhenke, S., Müller, D., Vargas, A.: A Fourier restriction theorem for a two-dimensional surface of finite type. Anal. PDE 10(4), 817–891 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  4. Candy, T., Herr, S.: Conditional large initial data scattering results for the Dirac–Klein–Gordon system. Forum Math. Sigma 6, e9 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  5. Candy, T., Herr, S.: On the Majorana condition for nonlinear Dirac systems. Ann. Inst. H. Poincaré C, Anal. Non Linéaire 35, 1707–1717 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  6. Candy, T., Herr, S.: Transference of bilinear restriction estimates to quadratic variation norms and the Dirac–Klein–Gordon system. Anal. PDE 11(5), 1171–1240 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  7. Candy, T., Herr, S.: On the division problem for the wave maps equation. Ann. PDE 4(2), 17 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  8. Hadac, M., Herr, S., Koch, H.: Well-posedness and scattering for the KP-II equation in a critical space. Ann. Inst. H. Poincaré Anal. Non Linéaire 26(3), 917–941 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  9. Killip, R., Stovall, B., Visan, M.: Scattering for the cubic Klein–Gordon equation in two space dimensions. Trans. Am. Math. Soc. 364(3), 1571–1631 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  10. Koch, H., Tataru, D.: Dispersive estimates for principally normal pseudodifferential operators. Commun. Pure Appl. Math. 58(2), 217–284 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  11. Koch, H., Tataru, D.: A priori bounds for the 1d cubic NLS in negative sobolev spaces. Intern. Math. Res. Not. 9, rnm053 (2007)

    MathSciNet  MATH  Google Scholar 

  12. Lee, S.: Bilinear restriction estimates for surfaces with curvatures of different signs. Trans. Am. Math. Soc. 358(8), 3511–3533 (2006). (electronic)

    Article  MathSciNet  MATH  Google Scholar 

  13. Lee, S., Rogers, K.M., Vargas, A.: Sharp null form estimates for the wave equation in \({\mathbb{R}}^{3+1}\). Intern. Math. Res. Not. 18, rnn096 (2008)

    MATH  Google Scholar 

  14. Lee, S., Vargas, A.: Sharp null form estimates for the wave equation. Am. J. Math. 130(5), 1279–1326 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  15. Lee, S., Vargas, A.: Restriction estimates for some surfaces with vanishing curvatures. J. Funct. Anal. 258(9), 2884–2909 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  16. Moyua, A., Vargas, A., Vega, L.: Schrödinger maximal function and restriction properties of the Fourier transform. Intern. Math. Res. Not. 16, 793–815 (1996)

    Article  MATH  Google Scholar 

  17. Moyua, A., Vargas, A., Vega, L.: Restriction theorems and maximal operators related to oscillatory integrals in \(\mathbb{R}^3\). Duke Math J 96(3), 547–574 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  18. Ramos, J.: A refinement of the Strichartz inequality for the wave equation with applications. Adv. Math. 230(2), 649–698 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  19. Stein, E.M.: Harmonic analysis: real-variable methods, orthogonality, and oscillatory integrals, Princeton Mathematical Series, vol. 43, Princeton University Press, Princeton, NJ, 1993, With the assistance of Timothy S. Murphy, Monographs in Harmonic Analysis, III

  20. Sterbenz, J., Tataru, D.: Regularity of wave-maps in dimension \(2+1\). Commun. Math. Phys. 298(1), 231–264 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  21. Stovall, B.: Linear and bilinear restriction to certain rotationally symmetric hypersurfaces. Trans. Am. Math. Soc. 369(6), 4093–4117 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  22. Tao, T.: Endpoint bilinear restriction theorems for the cone, and some sharp null form estimates. Math. Z. 238(2), 215–268 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  23. Tao, T.: A sharp bilinear restrictions estimate for paraboloids. Geom. Funct. Anal. 13(6), 1359–1384 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  24. Tao, T., Vargas, A., Vega, L.: A bilinear approach to the restriction and Kakeya conjectures. J. Am. Math. Soc. 11(4), 967–1000 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  25. Tataru, D., Null form estimates for second order hyperbolic operators with rough coefficients, Harmonic analysis at Mount Holyoke (South Hadley, MA, : Contemp. Math., vol. 320, Amer. Math. Soc. Providence, RI 2003, 383–409 (2001)

  26. Temur, F.: An endline bilinear cone restriction estimate for mixed norms. Math. Z. 273(3–4), 1197–1214 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  27. Vargas, Ana: Restriction theorems for a surface with negative curvature. Math. Z. 249(1), 97–111 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  28. Wolff, T.: A sharp bilinear cone restriction estimate. Ann. Math. 2 153(3), 661–698 (2001)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The author would like to thank Sebastian Herr and the referee for a number of helpful comments and corrections.

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, University of Otago, Dunedin, 9054, New Zealand

    Timothy Candy

Authors
  1. Timothy Candy
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Timothy Candy.

Additional information

Communicated by Loukas Grafakos.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Financial support by the DFG through the CRC “Taming uncertainty and profiting from randomness and low regularity in analysis, stochastics and their applications” is acknowledged.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Candy, T. Multi-scale bilinear restriction estimates for general phases. Math. Ann. 375, 777–843 (2019). https://doi.org/10.1007/s00208-019-01841-4

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00208-019-01841-4

Search

Navigation