Introduction

Conventional generators are becoming undesirable in the power sector due to the negative effect of fossil fuel emissions on the environment which has led to several climate-related challenges such as increased temperatures and rainfall variabilities [1,2,3,4,5]. Thus, many countries around the world are now replacing their existing conventional generators with renewable energy (RE) sourced generators, in line with the Paris agreement, and the European green deal goal of zero carbon emission by 2050 as well as other RE policies geared at reducing greenhouse gases emissions [6,7,8,9].

Subsequently, about 627 GW of photovoltaic (PV) systems and 743 GW of wind turbines have already been integrated into the grid globally, with an expected increase of 45% by 2040 [10]. Thus, developed countries such as China, United States, Spain, India, Ireland, and Uruguay have already achieved high penetration of RE generators integrated into the grid [10].

On the other hand, synchronous generators (SGs) benefit the grid in numerous ways such as providing voltage and reactive power support, as well as provision of synchronous inertia, which is responsible for maintaining the grid’s frequency, particularly during times of system contingencies such as sudden loss of load or generator [10,11,12,13].

On the contrary, PV systems and modern variable speed wind turbines provide zero inertia to the grid because they lack rotating mass (for PV) and are decoupled from the grid through converters, hence they inherently cannot provide primary frequency response to the grid [14,15,16,17,18,19]. Furthermore, the increasing dominance of these variable RE generators in the power grid has led to the reduced overall system inertia of the grid, which causes grid stability challenges such as severe frequency nadir, voltage instability, fast rate of change of frequency (RoCoF), and increased harmonics [19,20,21]. For example, countries such as New Zealand, United States, United Kingdom, Cyprus, and Ireland with high penetration of RE sources have already reported cases of power disturbances due to large frequency nadir (47.5 Hz) and fast rate of change of frequency (0.73 Hz/s) which led to power interruption to a large number of customers [22].

Several methods have been proposed in the literature to mitigate frequency instability by primarily emulating the inertia response of SGs and induction machines through the use of RE sources and energy storage sources (ESS) with a suitable converter control strategy, this concept is called virtual inertia control [19, 23,24,25]. Other methods adopted to provide frequency stability include RE curtailment or deloaded operation of RE generators [26,27,28], use of synchronous condensers to provide synchronous inertia [22, 29,30,31], and load curtailment using incentive-based demand response schemes such as direct load control, and time-of-use rates [32,33,34].

Furthermore, optimization models have been used to proffer solutions to challenges arising from the increasing growth of RE generators in the grid. The authors in [35] developed a generation expansion planning (GEP) model solved as a mixed-integer linear programming (MILP) optimization problem to minimize investment cost and air pollution. Authors in [36,37,38,39] proposed a generation and transmission expansion planning model (GTEP) to minimize the investment and operational costs of new power plants. Authors in [40] and [41] developed a MILP model to minimize investment cost using the Tailored Benders decomposition algorithm in MATLAB and Nested Benders decomposition in Python. The studies, however, did not consider the frequency stability of the grid in planning. Furthermore, the authors in [42] carried out generation expansion planning for PV, thermal, and wind power plant to minimize the investment and operational costs. Fitiwi in [43] developed a linear AC optimal power flow model for generation expansion planning to minimize cost, voltage violations, and energy losses using the CPLEX solver in GAMS, this model was evaluated using the IEEE 23, 54, and 69 bus system. However, the study did not account for the inertia requirement of the grid for stability. Authors in [44] proposed a hybrid framework for GTEP to minimize planning cost while considering the resilience of the power system components. Furthermore, Kim in [45] proposed a probabilistic model for grid expansion planning using the Weibull distribution, considering wind energy uncertainties, while the authors in [46] proposed a model for optimal placement of battery energy storage system (BESS) in transmission expansion planning (TEP) using the Benders’ decomposition approach. More so, in [47], the authors proposed a generation, storage, and transmission expansion planning (GSTEP) model to minimize cost while meeting the load demand. In [48], an integrated multi-period model of transmission, generation, and storage expansion planning (TGSEP) model was proposed considering uncertainties from renewable energy sources (RES) and load demand. However, this model is limited as only BESS was considered as the energy storage system. In [49], a TEP model was proposed to minimize power outages and cost using the Benders decomposition algorithm, while the authors in [50] carried out a multi-period generation expansion planning for wind power plants using a differential evolution algorithm. Furthermore, the authors in [51] developed a scenario-based stochastic model for integrated electricity and gas networks expansion planning (IEGNEP) model considering N-1 contingency criteria, and system uncertainties from PV generation and electrical loads. More so, the authors in [52] and [53] analyzed the economic effect of carbon tax on power system expansion planning model by developing a MILP model to minimize carbon emission in the power system for a period of 10 years. Authors in [54] developed a scenario-based multi-objective model to minimize CO2 emission and cost of investment and operation in a distribution system expansion planning model (DSEP) considering system uncertainties. The authors in [55] also investigated the effect of climate changes on wind speed in GTEP for a 85 years planning period. Furthermore, the authors in [56] proposed a two-stage robust optimization approach to minimize investment cost in a distribution network, while considering N-1 generation contingency and demand response. The model was tested in a modified IEEE 123-bus test system.

The review of the literature reveals that no work has yet considered cost, emission, and the inertia requirement of the grid in joint generation and transmission expansion planning. This paper therefore aims to give foresight into inertia consideration in operational and joint generation and transmission expansion planning optimization model.

The specific objectives of this research are as follows:

  • To provide a synoptic review of the impact of increasing RE sources on the dynamics of the power grid.

  • To provide a review of virtual inertia topologies and strategies used in compensating system inertia in renewable energy sourced grid.

  • To give a concise review of the modeling characteristics of energy storage systems essential for providing additional inertia to the grid.

  • To provide a review on inertia estimation methods in power system.

The remaining part of this paper is organized as follows. “Frequency stability in power system” section highlights the transformation in grid composition and reviews the associated frequency instability challenges in the new grid. It further gives the modeling characteristics of energy storage systems suited for virtual inertia provision.  “The concept of inertia in power system ” section gives the description and mathematical formulation of system inertia. It further gives the various inertia estimation techniques in power system.  “Virtual inertia topology and strategy in modern power grid” section gives the types of virtual inertia control topologies and strategies highlighting their merits and demerits.  “Operational and expansion planning optimization in power system” section gives an overview of various techniques used in operational and expansion planning optimization models, while “Conclusion” section gives the conclusion of the research.

Frequency stability in power system

Frequency control techniques are used to ensure frequency is maintained within a specified limit after system contingency [33, 57]. During times of system contingency, the inertia inherent in the grid reacts first by providing an instant frequency response within 1–10 s after the disturbance, just before the controllers are triggered [58,59,60]. Figure 1 shows the timeline of frequency responses in power system. It is seen that a system with low inertia will experience larger frequency nadir compared with a system with high inertia system. More so, it is observed that primary frequency controllers are set to operate immediately after the inertia response has been provided, while the secondary frequency control or automatic generator control action takes place between 10 and 30 min after the contingency as occurred [58, 61].

Fig. 1
figure 1

Time-scale of frequency response during power system contingency [58]

Full size image

Dynamics and composition of renewable energy-sourced Grid

The dynamics and structural composition of the power grid are changing due to the increased penetration of RE generators into the grid. This in turn is responsible for the declining overall inertia of the grid. More so, the inertia obtained from RE sources is time-varying due to the stochastic nature of RE generators thus making the overall system inertia time-varying inertia [62]. These changes have led to technical challenges such as high-frequency deviations (spike and nadir), unwanted frequency oscillations, and high rate of change of frequency [63]. These frequency instabilities are undesirable in power system as they may lead to cascaded system failures. Figure 2 shows the transformation in the composition of the grid over the years, from synchronous generators dominant to renewable energy generators dominant.

Fig. 2
figure 2

Changes in the composition of the power grid

Full size image

Frequency mitigating strategies in Renewable energy sourced grid

Owing to the frequency-related challenges associated with renewable energy-sourced grid, countries such as Ireland and Australia have now pegged RE integration into the grid at a certain percentage (70%) to keep RoCoF below 0.5 Hz/s during contingencies, while others have revised their grid codes in line with the new dynamics of the grid [10]. The most commonly used method is by emulating the inertia of SGs and induction machines using RE sources, energy storage system with an appropriate converter control strategy [19, 24, 25]. Authors in [9, 13, 21, 64] also proposed the use of synchronous generators as spinning reserves, synchronous condensers, and rotating stabilizers to provide inertia to the grid during times of contingency, while RE generators remain the main source of power generation. Though this method provides the needed system inertia, it is however limited by its high cost of implementation and high carbon emission. Authors in [21, 22, 65] proposed the use of energy storage systems together with renewable energy sources in a hybrid combination such as PV-BESS, wind turbine-flywheel energy storage (FES), and PV-supercapacitor (SCES). Authors in [66] proposed a model comprising a hybrid combination of BESS and SCES to mitigate frequency fluctuation at the point of coupling of rooftop solar PV units.

Characteristics of energy storage systems

Energy storage systems are often used to provide stability in the grid by supplying energy to the grid during times of deficiency or absorbing energy from the grid during times of excess [80]. Good knowledge of the characteristics of the various types of energy storage systems used for providing additional inertia to the grid is important for proper modeling of the dynamics of the new grid. The unique characteristics of commonly used energy storage systems suited for inertia provision are discussed here.

Battery energy storage system

Battery energy storage system is one of the commonly used storage systems in modern power system. BESS can be modeled based on its characteristics such as the number of charge–discharge cycles, state of charge (SoC), depth of discharge (DoD), and charging and discharging rate [81,82,83,84] as seen in Table 1.

Table 1 Modeling features of BESS
Full size table

The charging and discharging equation of a battery can be given as in Eqs. (1) and (2), respectively.

$$E_{b}^{t} = E_{b}^{t - 1} + P_{b,c}^{t} .\eta_{b}^{c}$$
(1)
$$E_{b}^{t} = E_{b}^{t - 1} + P_{b,d}^{t} /\eta_{b}^{d}$$
(2)

where \(E_{b}^{t}\) and \(E_{b}^{t - 1}\) are the stored energy in the battery after and before charge, respectively. \(P_{b,c}^{t}\) is the charging power of battery, \(P_{b,d}^{t}\) is the discharging power of the battery, \(\eta_{b}^{c}\) and \(\eta_{b}^{d}\) are the charging and discharging efficiency of the battery, respectively.

The state of charge of a battery can then be estimated as in Eq. (3) [85].

$$SoC_{b,t} = SoC_{b,t - 1} + [P_{b,c}^{t} .\eta_{b}^{c} - P_{b,d}^{t} /\eta_{b}^{d} ]$$
(3)

where \(SoC_{b,t}\) and \(SoC_{b,t - 1}\) defines the present and previous state of charge of the battery, respectively.

The DoD of a battery indicates the battery’s discharge percentage relative to the total capacity of the battery. The DoD can be expressed in terms of the battery’s SoC as in Eq. (4).

$$DoD = 1 - SoC$$
(4)

Pumped hydro storage system

Pumped hydro energy storage (PHES) is an energy storage system that is often used in hybridized forms such as PV-PHES, WIND-PHES, WIND-PV-PHES, and HYDRO-PHES, which can provide synchronous inertia to the grid. Pumped hydro storage system comprises the pump, hydro-turbine, penstock, upper and lower reservoirs [93, 94]. PHES operates in generating mode during times of energy deficiencies and in the pumping mode during times of energy surplus. In the generating mode the water from the upper reservoir drives the hydro turbine to generate electricity, while in the pumping mode, water is transported from the lower to the upper reservoir for storage [95, 96].

PHES can be modeled based on its characteristics such as the size of its reservoirs, water flow rate, volume of water stored, type of pumps and turbines as seen in Table 2 and expressed in Eqs. (5, 6, 7, 8).

Table 2 Modeling characteristics of PHES
Full size table

During pumping mode, the electrical power used by the pump is expressed as in (5).

$$P_{out} = P_{input} \eta_{m}$$
(5)

where \(P_{input}\) defines the motor’s input power, and \(\eta_{m}\) the motor’s efficiency.

The flow rate QP of water in (m3/s) is expressed in Eq. (6):

$$Q_{p} = \frac{{P_{input} \eta_{p} }}{Hg\rho }$$
(6)

where \(\rho\) is the water density in (kg/m3), g is gravitational acceleration in (m/s2), H is the height difference between the two reservoirs in (m), and \(\eta_{p}\) is the pump efficiency.

During times of energy deficiency, the hydro turbine converts the potential energy \(P_{HT}\) of water in the upper reservoir to electrical power \(E_{HT}\) as expressed in Eqs. (7) and (8).

$$P_{HT} = Hg\rho Q_{p} \eta_{ht}$$
(7)
$$E_{HT} = Hg\rho V\eta_{ht}$$
(8)

where \(\eta_{ht}\) is the efficiency of the hydro turbine, and V is the volume of the upper reservoir in (m3).

Flywheel energy storage

Flywheel energy storage is an electro-mechanical storage system that offers numerous advantages such as environmental friendliness and reduced maintenance cost while providing synchronous inertia to the grid [97]. It is usually used in hybridized forms such as BESS-FES, and DIESEL-FES and can be modeled based on its mass and rotational speed [98,99,100,101].

Equations (9) and (10) give the expression of the kinetic energy stored and the moment of inertia in FES.

$$E = \frac{1}{2}J\omega^{2} = \frac{1}{2}k\pi \rho h(\omega^{2} )(r^{4} )$$
(9)
$$J = \frac{1}{2}mr^{2}$$
(10)

where E defines the kinetic energy of the flywheel in Joules, J defines the moment of inertia of the flywheel in (kg.m2), k defines the shape factor, \(\rho\) defines the density of rotor material in (Kg/m3), h defines the height of the rotor(m), \(\omega\) defines the angular velocity of the rotor in (rad/s), m defines the mass in kg of the cylindrical rotor, and r defines the radius of the cylindrical rotor in (m).

Supercapacitor storage system

Supercapacitor storage system is an efficient energy storage system often used in power systems and desired for providing virtual inertia in the grid through a control strategy. It can also be used in hybridized forms such as PV-SCES and WIND-SCES [102, 103].

SCES are desired in power system because of their winsome characteristics such as high efficiency and long life cycle. The energy stored in SCES is given as in Eq. (11). Equations (12–13) define the SoC and DoD of the SCES, respectively.

$$E = \frac{1}{2}CV^{2}$$
(11)

where C is the capacitance and V is the capacitor’s voltage.

$$SoC = \frac{{E_{inst} }}{{E_{rated} }} = \frac{{\frac{1}{2}CV_{inst}^{2} }}{{\frac{1}{2}CV_{rated}^{2} }}$$
(12)

where \(E_{inst}\) is the instantaneous energy capacity of the SCES, and \(E_{rated}\) is the rated energy capacity of the SCES.

$$DoD = \frac{{E_{disch\arg e} }}{{E_{rated} }} = \frac{{P_{load} .T}}{{\frac{1}{2}CV_{rated}^{2} }}$$
(13)

where Edischarge is the energy consumed by the load which is a function of the load power \(P_{load}\) and discharge duration T in seconds. Table 3 gives the summarized characteristics of various storage systems used in power system.

Table 3 Generic characteristics of energy storage systems [104,105,106,107,108,109]
Full size table

The concept of inertia in power system

In this section, a detailed mathematical representation of system inertia is given. Furthermore, a concise review of inertia estimation techniques is provided.

Analytical representation of inertia in power system

Inertia can be defined as the amount of kinetic energy stored in the rotor of synchronous generators which tends to resist changes in grid frequency, particularly during times of contingency. The inertia inherent in synchronous machines is called synchronous inertia, hence the moment of inertia of a synchronous generator can be defined as in Eq. (14).

$$E = \frac{1}{2}J\omega^{2} = S.H$$
(14)

where E defines the kinetic energy of the SGs in (MWs), J defines the moment of inertia in (Kg/m2), \(\omega\) defines the angular frequency in (rad/s), S defines the base apparent power in VA, and H is the inertia constant in seconds.

Also, from Eq. (14), H can be expressed as in Eq. (15):

$$H = \frac{E}{S} = \frac{{J\omega^{2} }}{2S}$$
(15)

Furthermore, the power imbalance can be represented using the swing equation as in Eq. (16):

$$P_{m} - P_{e} = P_{a} = \frac{dE}{{dt}} = J\omega \frac{d\omega }{{dt}}$$
(16)

Equation (16) can then be expressed in terms of torque as in Eq. (17):

$$\tau_{m} - \tau_{e} = \tau_{a} = J\frac{d\omega }{{dt}} = J\frac{{d^{2} \theta }}{{dt^{2} }}$$
(17)

where Pm defines the mechanical power developed in p.u, \(\tau_{m}\) defines the mechanical torque developed, \(\tau_{e}\) defines the electrical torque, Pe defines the electrical power output in p.u, and Pa defines the acceleration power in p.u,\(\theta\) defines the angular displacement of the rotor in rad, t is the time in seconds, f defines the supply frequency in (Hz), and df/dt is the RoCoF of the system.

From Eq. (16) and (17), we can obtain Eq. (18):

$$\frac{2H}{\omega } = \frac{J\omega }{S} = \frac{dt}{{d\omega }}\frac{{\left[ {P_{m} - P_{e} } \right]}}{1}$$
(18)

Rearranging Eq. (18) gives Eq. (19):

$$\frac{2H}{\omega }\frac{d\omega }{{dt}} = \frac{{\left[ {P_{m} - P_{e} } \right]}}{S}$$
(19)

Replacing the angular frequency with the supply frequency and making RoCoF and inertia constant H the subject, we have Eq. (20) and (21):

$$\frac{df}{{dt}} = \frac{{P_{a} }}{S}\frac{f}{2H} = RoCoF_{p.u} = \frac{{Pa_{p.u} }}{2H}$$
(20)

Equation (20) can be modified to give Eqs. (21) which is used for designing virtual inertia controllers [67].

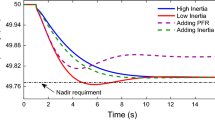
$$Pa_{p.u} = 2H_{VI} \frac{{df_{p.u} }}{dt} = K_{i} \frac{{df_{p.u} }}{dt}$$
(21)

where \(H_{VI}\) is the virtual inertia constant, \(Pa_{p.u}\) is the per unit change in power, \(K_{i}\) is the virtual inertia gain, and \(\frac{{df_{p.u} }}{dt}\) is the per unit rate of change of frequency.Equation (20) show the dependence of RoCoF (df/dt) on the power change \(P_{a}\), and the inertia constant (H). It further reveals that the inertia constant is inversely proportional to RoCoF, and so the higher the inertia constant the smaller the RoCoF and vice versa. Also, RoCoF is directly proportional to the acceleration power Pa, so the greater the power imbalance the greater the RoCoF. Therefore, a reliable and resilient power system can be achieved by having high system inertia values [68, 69]. Furthermore, Fig. 3 shows the variations of frequency nadir with increasing values of system inertia, and it is seen that the higher the system inertia, the lower the frequency nadir. In light of this, frequency instability in the modern power grid can primarily be mitigated by providing adequate inertia in the grid.

Fig. 3
figure 3

Effect of system inertia on RoCoF [10]

Full size image

Inertia in renewable energy-sourced power system

The effective inertia constant in the power system can be represented as the sum of the individual inertia of all connected SGs to the grid, aggregated as a single generator model. It can be expressed as in Eq. (29) [14, 40].

$$H_{eq} = \frac{{\sum\limits_{i = 1}^{N} {H_{i} S_{B,i} } }}{{S_{B} }}$$
(22)

where Heq is the aggregated synchronous inertia in the grid, SB is the base apparent power, SB,i is the individual generator apparent power, N is the total number of connected generators, and Hi is the inertia constant of each generator.

Similarly, since the modern power system comprises a hybrid combination of synchronous generators, ESS and RE generators, hence, the total inertia in the system will comprise of the synchronous inertia provided by the synchronous generators and the virtual inertia obtained from RE generators and energy storage systems. Therefore, the effective inertia Heq in a modern power grid can be expressed as in Eq. (23), [78, 111, 115].

$$H_{eq} = \frac{{\sum\limits_{i = 1}^{N} {H_{i} S_{B,i} + } \sum\limits_{j = 1}^{V} {H_{VI,j} S_{B,j} } }}{{S_{B} }}$$
(23)

where Hvi,j and SB,j are the virtual inertia constant in seconds and the rated apparent power in VA of the jth virtual machine, respectively. V and N define the number of the RE generators, and synchronous generators connected in the network, respectively. If Hvi,j is very small, then the effective inertia Heq in the grid will be substantially reduced, this explains why RE dominant power grid is associated with low inertia. Table 4 gives the average inertia values of different types of power generators. It is seen from Table 4 that the inertia constant from SGs ranges between 4 and 10 s, while the virtual inertia constant from ESS is between 2 and 4 s [74]. Therefore, it can be inferred from Eq. (23), that the aggregate inertia constant of modern power system should be between 4 and 10 s to ensure stability of the modern power grid.

Table 4 Summary of inertia values of different power generators
Full size table

Inertia estimation techniques in power system

Inertia estimation in power system is important to help power operators predict futuristic frequency deviation and make appropriate control decisions [40]. This sub-section gives a review of the various inertia estimation techniques in power system while highlighting their merits and demerits.

Inertia estimation techniques discussed here are classified based on the timing of estimation. Using this criterion three main approaches will be discussed; offline or post-mortem approach, online real-time approach, and forecast or predictive approach. The offline and online techniques are the most commonly used, while the predictive approach is still being advanced.

Offline or Post-mortem inertia estimation method

This is a post-mortem disturbance-based inertia estimation method driven by historical data of large disturbance events obtained using the phasor measurement units (PMUs). PMU is a measuring system installed at generator buses to monitor power system operating conditions such as voltage phasor, current phasor, active power, frequency deviation, harmonics, and power imbalance. The data obtained from the PMU is then used to estimate the system’s inertia at discrete time instances using an appropriate algorithm. The accuracy of this method depends on the precision of the measuring system and the algorithm used for inertia estimation. This approach is however limited by inaccurate frequency measurements due to oscillatory components, as well as distortions and noises in the system, subsequently, its accuracy can be improved by eliminating noise and other distortions in the system [40, 110].

Online inertia estimation approach

Unlike the offline method, the online estimation approach is a dynamic technique that uses real-time measurements from PMUs to give continuous and discrete inertia values of the power system. Examples of online inertia estimation techniques and models are dynamic regressor extension technique, autoregressive data-centered models, sliding discrete Fourier transform, and electro-mechanical oscillation modal extraction method [10].

Challenges of this estimation approach include (1) inaccurate estimation of the total system inertia (2) extended inertia estimation time (3) large computational burdens due to large dataset.

Inertia forecasting or prediction approach

Forecasting techniques are now being used for inertia estimation due to the time-varying nature of inertia from renewable energy generators. Several forecasting models are being developed for inertia estimation such as artificial neural network (ANN) based models, linear regression models, time series models, and probabilistic inertia forecasting models [13, 111]. However, this approach is still being advanced for inertia estimation due to the changing dynamics of the modern power system.

Other unclassified approaches used for inertia estimation are the system identification approach, and the zonal inertia estimation technique. The zonal inertia estimation approach sums up the inertia from each contributing zone to give the total system inertia [13]. The summarized characteristics of different inertia estimation schemes highlighting their merits and demerit are presented in Table 5.

Table 5 Inertia estimation techniques and their characteristics
Full size table

Virtual inertia topology and strategy in modern power grid

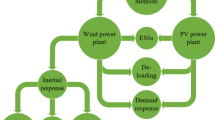
Virtual inertia control strategies help to provide artificial inertia to the grid through the use of RE sources, energy storage systems, and converters with appropriate control strategies [70]. The control strategies try to mimic the characteristics of SGs and induction machines to provide inertia virtually to the grid [71]. Figure 4 shows the virtual inertia control process in the modern grid, while Fig. 5 gives a broad classification of virtual inertia control topologies based on its modeling technique and solution method. Furthermore, Table 6 gives detailed characteristics, merits, and demerits of the different virtual inertia control topologies and strategies, while Table 7 compares key parameters among the control strategies.

Fig. 4
figure 4

Virtual inertia control system in the modern grid [10]

Full size image
Fig. 5
figure 5

Virtual inertia control classification

Full size image
Table 6 Overview of the characteristics of virtual inertia control strategy
Full size table
Table 7 Comparative analysis of virtual inertia control parameters
Full size table

Control equations of virtual inertia topology

The various types of inertia emulation topologies and strategies arise from the different mathematical models used to mimic the dynamics of SGs and induction machines. In this subsection, the mathematical equation which defines the different types of virtual inertia topology is given.

Swing equation-based topology

The swing equation-based topology is governed mathematically by Eq. (24) obtained by considering the damping coefficient in the conventional swing equation [40, 73].

$$P_{m} - P_{e} = J\omega_{{}} (\frac{{d\omega_{{}} }}{dt}) + D_{m} (\omega_{{}} - \omega_{ref} ) = 2H_{VI} \frac{{d\omega_{p.u} }}{dt} + D_{m} (\omega_{{}} - \omega_{ref} )$$
(24)

where \(P_{m}\) is the input power, \(P_{e}\) is the output power, \(J\) is the moment of inertia,\(\omega_{{}}\) is the angular frequency, \(\omega_{ref}\) is the reference angular frequency, and \(D_{m}\) is the damping factor. The control model of the swing equation-based synchronous power controller is given in Fig. 6 with gain K and time constant Td.

Fig. 6
figure 6

Transfer function block diagram of swing equation based synchronous power controller

Full size image

Frequency-power response topology

The control equation of the frequency-power response based topologies can be described by Eq. (25) [61, 73]:

$$P_{out} = K_{D} \Delta \omega + K_{i} \frac{d\Delta \omega }{{dt}}$$
(25)

where \(\frac{d\Delta \omega }{{dt}}\) is the rate of change of frequency,\(\Delta \omega\) is the change in angular frequency, K1 is the inertia constant, and KD is the damping constant. Figure 7 gives the control model of frequency-power response-based virtual synchronous generator.

Fig. 7
figure 7

Transfer function block diagram of frequency-power response-based virtual synchronous generator

Full size image

Droop control topology

The droop control based topology can be represented using Eq. (26) [73, 74].

$$P_{m} - P_{e} = \frac{1}{{D_{p} }}(\omega_{ref} - \omega ) + \frac{{T_{f} }}{{D_{p} }}.s.\omega$$
(26)

where \(\omega_{ref}\) is the reference angular frequency,\(\omega_{{}}\) is grid frequency,\(D_{p}\) is the active power droop,\(P_{m}\) is the reference active input power, \(P_{e}\) is the active output power, and \(T_{f}\) is the time constant of the low pass filter. Figure 8 shows the transfer functions block diagram of the droop control based topology.

Fig. 8
figure 8

Transfer function block diagram of droop control-based topology [74]

Full size image

Operational and expansion planning optimization in power system

An overview of power system optimization methods and techniques

The increasing complexity, changing dynamics, and the need to ensure grid stability have necessitated power system researchers to focus on advanced optimization techniques that have capabilities of handling the new grid peculiarities [14, 65, 116].

Power system optimization problems can be solved using several methods. These methods can be majorly classified as exact and approximate approaches. Exact approaches are also called mathematical or classical method while approximate method uses heuristics or meta-heuristics algorithms [38, 117]. These modeling approaches are the most suited to capture the dynamics and address specific challenges of the power grid with clearly defined objective functions, decision variables, and constraints.

Mathematical optimization models can be defined by the nature of the constraints which could be linear or nonlinear. Linear optimization problems are solved using linear programming(LP) and MILP techniques, while nonlinear programming (NLP), mixed-integer nonlinear programming (MINLP), and mixed-integer quadratic programming (MIQP) are used to solve nonlinear mathematical models [118, 119].

Furthermore, complex mathematical optimization models are now being solved using algebraic modeling languages such as General Algebraic Modeling System (GAMS), Advanced Interactive Multidimensional Modeling System (AIMMS), Grid Reliability and Adequacy Risk Evaluator (GRARE) software package, Python, PLEXOS, and Multi-Area Reliability Simulation (MARS) [125, 126].

On the other hand, heuristic and meta-heuristics optimization techniques are formulated based on the social behaviors of living organisms [108]. They have shorter processing times and achieve faster convergence, however, they do not guarantee optimal solutions, unlike mathematical techniques. Examples are genetic algorithm (GA), Benders decomposition, simulated annealing, Tabu search algorithm, differential evolution, binary fireworks algorithm, particle swarm optimization (PSO), nodal ant colony optimization, evolutionary programming (EP), etc. [120,121,122,123,124]. These algorithms can also be used in hybridized forms such as GA-PSO [127].

Several optimization models and expansion planning models have also been proposed to address the peculiarities of the modern renewable energy dominant grid as seen in Tables 8 and 9. Furthermore, to account for uncertainties arising from RE sources as well as variations in load demand, robust optimization models was developed in [38, 116, 120], while stochastic optimization models and risk assessment method were adopted in [116, 128,129,130,131]. Table 8 gives an overview of operational optimization models, and techniques used to address related power system problems.

Table 8 Review of operational optimization models in power system
Full size table
Table 9 Overview of expansion planning models in power system
Full size table

Expansion planning optimization model in power system

Expansion planning optimization models are gaining prominence in modern power system analysis due to the expected dominance of RE sources in the power grid and increasing energy demand. Expansion planning models are formulated as optimization problems with well-defined objectives and constraints [136,137,138,139]. Power system expansion planning models are mainly of three types; generation expansion planning (GEP), transmission expansion planning (TEP), and distribution expansion planning (DEP) [140, 146,147,148,149].

Generation expansion planning (GEP) problem determines the type of generators to be installed, optimal capacity of generators, location of generators, construction time of prospective generating units, and cost implications of new generators’ installations. Similarly, transmission expansion planning (TEP) problem determines the best choice for the installation of new transmission lines which aids power transfer within a planning horizon [36, 141].

The planning period for expansion could be static or dynamic (multi-period). In static expansion planning models, the decisions are made within a given target year, while dynamic expansion planning involves making decisions at different phases of the planning horizon, thus making use of a yearly representation of the investment decisions [43, 142]. Table 9 gives a summarized overview of various optimization techniques, methods, and solvers used in expansion planning models. It can be observed from Tables 7 and 8 that most optimization techniques and models only consider economic objective such as operational cost of generators, and technical objectives such as power flow, ramping limits, and voltage limits. Most models did not consider the inertia requirement of the grid which is important to ensure grid stability in renewable energy sourced power system.

Future research work

The review of the literature reveals that no study has yet considered cost, emission, and the inertia requirements of the grid in joint generation and transmission expansion planning. Therefore, in future, a new deterministic optimization model for generation and transmission expansion planning model will be developed to minimize cost and CO2 emission while maximizing the overall system inertia. Furthermore, the resilience of this new model during transient conditions will also be investigated.

Conclusion

This paper highlights the challenges associated with the modern power grid and further explains the role of inertia in ensuring frequency stability in the power grid. The following are the areas of discussion of this research: (1) A concise review of the modeling characterizes of different energy storage system used to provide inertia support to the grid. (2) Mathematical formulation of system inertia in power system. (3) overview of inertia estimation methods in power system. (4) Review of different virtual inertia control topologies and strategies highlighting their merit and demerit. (5) Review of optimization planning methods, techniques, and tools.

Findings of this study reveal the following: (1) adequate system inertia in the grid is important to mitigate frequency instability in the modern grid. (2) Disregarding inertia in power system operational and expansion planning optimization models could lead to sub-optimal optimization model. (3) Online inertia estimation technique is the most suited approach for inertia estimation in modern renewable energy-sourced grid due to the stochastic behavior of renewable energy sources. (4) Frequency-power response based topology such as VSG and VSYNC are preferred control strategies in renewable energy grid because they give better frequency stability.

In future, a new deterministic optimization model will be developed that will consider cost, CO2 emission, and the inertia requirement of the grid in planning. This model will help to increase the frequency stability of the modern power grid as well as reduce emission level.