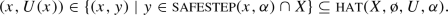Subgame perfection in recursive perfect information games

Abstract

We consider sequential multi-player games with perfect information and with deterministic transitions. The players receive a reward upon termination of the game, which depends on the state where the game was terminated. If the game does not terminate, then the rewards of the players are equal to zero. We prove that, for every game in this class, a subgame perfect $\varepsilon$-equilibrium exists, for all $\varepsilon > 0$. The proof is constructive and suggests a finite algorithm to calculate such an equilibrium.

1 Introduction

We study multi-player games where play proceeds from one state to another and where each transition is decided by one of the players. That is, each state is controlled by one of the players and it is the controlling player of a state who decides what the next state will be. We do not consider chance moves in our model and the number of states is finite. The players receive a (possibly negative) reward upon termination of the game. Termination is decided by the controlling player of the active state, who always has this option instead of moving to another state. The rewards to the players depend on the state where the game is terminated. Infinite play is a possibility in these games, as no player is forced to terminate the game (unless the structure of the game leaves him no other option). Infinite play is associated with a zero reward for all players.

Our games belong to the more general class of dynamic games with perfect information, which have numerous applications in economic theory, computer science, and other disciplines. One of the main goals in the literature has always been to identify conditions that guarantee the existence of a subgame perfect equilibrium, or at least of a subgame perfect $\varepsilon$-equilibrium for every positive error term $\varepsilon$. For our class of games, we prove the existence of a subgame perfect $\varepsilon$-equilibrium, for every $\varepsilon >0$. Our existence result extends several earlier results, where further restrictions were imposed on either the transition structure or the reward structure of the game. A subgame perfect $\varepsilon$-equilibrium, for every $\varepsilon >0$, was previously established in games with only nonnegative rewards (Flesch et al. 2010a), in free transition games (Kuipers et al. 2013), and in games where each player only controls one state (Kuipers et al. 2016). In the literature, we can also find sufficient conditions for other classes of games, such as in the classical papers by Fudenberg and Levine (1983) and Harris (1985), and more recently, in the papers by Solan and Vieille (2003), Flesch et al. (2010b), Purves and Sudderth (2011), Brihaye et al. (2013), Roux and Pauly (2014), Flesch and Predtetchinski (2016), Roux (2016), Mashiah-Yaakovi (2014), Cingiz et al. (2019) and Flesch et al. (2019). We further refer to the recent book by Alós-Ferrer and Ritzberger (2016), and the surveys by Jaśkiewicz and Nowak (2016) and Bruyère (2017).

In most economic models, payoffs are bounded and discounted, and this automatically guarantees continuity at infinity, a condition defined by Fudenberg and Levine (1983). For the topological meaning of continuity at infinity, we refer to Alós-Ferrer and Ritzberger (2016, 2017). Even though in our model payoffs are not discounted, our results have an implication for the discounted case. Indeed, the joint strategies that we construct are not only subgame perfect $\varepsilon$-equilibria in the undiscounted game, but also in the discounted game, provided that the discount factor is sufficiently close to 1 [cf. the notion of uniform $\varepsilon$-equilibrium, e.g., the survey by Jaśkiewicz and Nowak (2016)]. The strategy profile is thus independent of the discount factor, provided it is large enough, so the knowledge of the exact discount factor is not required.

The undiscounted game on its own is also interesting in the context of negotiations or delegation problems, when there is no specific deadline given for an agreement. An example of this can be found in the paper by Bloch (1996), where the negotiation process for coalition formation is modeled as a positive recursive game. A positive recursive model is limited to situations where any agreement is always better than no agreement, for all players. The generalization to recursive games that are not necessarily positive removes this limitation and allows for models, where some players may wish to sabotage certain outcomes.

The relevance of our paper, we think, mostly lies in the fact that we obtain insight in the structure of equilibria in perfect information games with deterministic transitions. Let us briefly discuss this. In general, one can distinguish two essentially different reasons why an error term may be needed for equilibrium play in a dynamic game. It could be that, in subgame perfect $\varepsilon$-equilibrium play, every action that is played with positive probability gives the player a reward that is very close or equal to his initially expected reward. Let us say that this is an error term of the first type. It could also be that, in subgame perfect $\varepsilon$-equilibrium play, a player must place a very small probability on an action that will lead to a substantially lower reward than initially expected. Let us say that this is an error term of the second type. For a game in our class, if an error term $\varepsilon$ is required, it is always of the second type, and the suboptimal action that is played with small probability invariably serves as a threat to one of the other players to make him follow the plan (Fig. 1).

Example 1

The following game was introduced in Solan and Vieille (2003). There are two players, player 1 and player 2, and two states, $s_1$ and $s_2$. Player 1 controls state $s_1$ and player 2 controls state $s_2$. In state $s_1$, player 1 has two actions: he can nominate state $s_2$, or terminate the game with reward $-1$ for himself and reward 2 for player 2. In state $s_2$, player 2 has two actions: he can nominate state $s_1$, or terminate the game with reward $-2$ for player 1 and reward 1 for himself. If no player ever terminates the game, then the reward is 0 for each player. This game can be represented as follows:

Fig. 1

Game where player 2 can threaten player 1 with termination of the game

Player 1 prefers that the game will never terminate, as he would then obtain reward 0, whereas he will obtain a negative reward, either $-1$ or $-2$, upon termination. Player 2 is interested in termination of the game. He can always force termination at state $s_2$ with reward 1 for himself, but he prefers that player 1 will terminate at state $s_1$, in which case he will obtain reward 2. Notice that, if the game terminates, then player 1 also prefers termination at state $s_1$ instead of $s_2$.

As Solan and Vieille (2003) show, this game has the following two important properties: There is no subgame perfect $\varepsilon$-equilibrium in pure strategies for small $\varepsilon >0$, and there is no subgame perfect 0-equilibrium, not even in randomized strategies.

Nevertheless, they show that the following stationary strategies constitute a subgame perfect $\varepsilon$-equilibrium for $\varepsilon \in (0,1)$: player 1 in state $s_1$ terminates with probability 1 (regardless the history), whereas player 2 in state $s_2$ nominates state $s_1$ with probability $1-\varepsilon$ and terminates with probability $\varepsilon$ (regardless the history).

Let us briefly argue that this strategy profile is indeed a subgame perfect $\varepsilon$-equilibrium. It is easy to see that player 2 cannot improve his reward by more than $\varepsilon$, as his expected reward, when starting in state $s_2$, is $(1-\varepsilon )\cdot 2+\varepsilon \cdot 1=2-\varepsilon$. Player 1 cannot improve his reward at all. Indeed, player 2’s strategy prescribes to always terminate with the same positive probability whenever the play is in state $s_2$, so player 2’s strategy makes sure that one of the players will eventually terminate. Intuitively, termination by player 2 with probability $\varepsilon$ can be seen as a threat against player 1, which retaliates any deviations by player 1. Note that the error term $\varepsilon$ is of the second type. We remark that all subgame perfect $\varepsilon$-equilibria in this game have this feature: player 2 threatens player 1 with termination at $s_2$. $\square$

It was shown by Flesch et al. (2010a), who studied perfect information games with positive recursive rewards and with chance moves, that, for their game model, a subgame perfect $\varepsilon$-equilibrium exists for every $\varepsilon > 0$. Here, the error term $\varepsilon$ is always of the first type and arises as the consequence of chance moves in the model. Indeed, they showed that, in the absence of chance moves, a subgame perfect equilibrium in pure strategies exists. When chance moves are eliminated from the model studied by Flesch et al. (2010a), we obtain a special case of the model we study here, with nonnegative rewards. Thus, the error term $\varepsilon$ is not needed when the rewards in our model are nonnegative. One can get some intuitive understanding for this by realizing that, when the rewards are all nonnegative, all players have an interest in termination of the game. By contrast, in the presence of negative rewards, some players may want to obstruct termination of the game when they foresee termination with a negative reward for them. This is when a threat, executed with small probability, is necessary to keep such players in check.

Another interesting feature is that subgame perfect $\varepsilon$-equilibrium play for a game in our class is mostly deterministic: At most once after each deviation will there be a stage where a small probability is placed on a threat action. In order to play such a strategy, a player needs to have two pieces of data in memory: (i) the most recent deviation from equilibrium play (if there was indeed a deviation) and (ii) whether a lottery took place after the most recent deviation to decide on the execution of a threat action, and if so, the outcome of the lottery.

Example 2

The following instructive game shows that, in order to obtain a subgame perfect $\varepsilon$-equilibrium, it may be necessary to make detours in the game, such that the same state must be visited twice, first on the way to reach a player who can execute a threat action, then to reach the player who should terminate the game (Fig. 2).

Fig. 2

Detours in a subgame perfect $\varepsilon$-equilibrium

This game is played by three players and has three states. The controlling player, the state, the possible actions of the controlling player and the rewards upon termination are represented similarly to Example 1. The rewards for players 1 and 2 in states $s_1$ and $s_2$ are exactly as in Example 1, i.e., $-1$ and 2 in state $s_1$ and $-2$ and 1 in state $s_2$. Player 3 can be seen as an additional player, who is not interested in terminating himself, as it gives him the worst possible reward $-1$.

One can verify that, for $\varepsilon \in (0,1)$, this game has the following subgame perfect $\varepsilon$-equilibrium that is very similar to the one in Example 1. Player 1 in state $s_1$ terminates with probability 1 (regardless the history). Player 2 in state $s_2$ nominates state $s_3$ with probability $1-\varepsilon$ and terminates with probability $\varepsilon$ (regardless the history). Player 3’s strategy is not stationary: if state $s_3$ is reached from state $s_1$ then player 3 nominates state $s_2$ with probability 1, whereas if state $s_3$ is reached from state $s_2$ then player 3 nominates state $s_1$ with probability 1.

In this strategy profile, if player 1 deviates by nominating state $s_3$, then instead of moving back to state $s_1$ directly, a detour is made via player 2, because player 2 is the only player who has a threat action against player 1. One can verify that such a detour, at least with a positive probability, is necessary to obtain a subgame perfect $\varepsilon$-equilibrium. This underlines the difficulty to construct subgame perfect $\varepsilon$-equilibria in our class of games. We remark that, in more complex games, a threat is sometimes not immediate termination by a player with small probability, but rather a complete sequence of actions that a player can start with small probability. $\square$

Interestingly, our analysis shows that just one computational effort suffices to find a subgame perfect $\varepsilon$-equilibrium for every $\varepsilon > 0$. The only difference between these equilibria is the probability with which a threat action should be executed. Examples 1 and 2 indicate how this works. The analysis in this paper suggests that it is unlikely that such a computation can be done efficiently: A naive implementation of the procedure we propose in this paper obviously requires super-exponential time. This is in contrast with the situation of nonnegative rewards, for which Flesch et al. (2010a) proved that a subgame perfect equilibrium can be computed in polynomial time.

Although the exact computation of a subgame perfect $\varepsilon$-equlibrium likely becomes intractable already for moderately sized problems, our results are probably useful for finding a good quality of solutions. As an illustration, let us see what happens if we introduce a discount factor $\beta \in (0,1)$ in the model to simplify the analysis. It follows from a result by Fink (1964) and Takahashi (1964) that the discounted model has a subgame perfect equilibrium in stationary strategies. For Example 1, we then have precisely one stationary equilibrium, which is also subgame perfect, and where both players should terminate the game with probability $\frac{1-\beta ^2}{\beta (2-\beta )}$ when they are active. This means that the game will terminate with probability 1, and when $\beta$ is close to 1, both states have a probability of approximately $\frac{1}{2}$ of termination. This totally ignores the fact that, given termination of the game, both players have an interest in termination at state 1.

Readers who are only interested in the construction of a subgame perfect $\varepsilon$-equilibrium for a game in our class and why it is indeed an equilibrium, can limit themselves to reading the first four sections of this paper. We formally introduce our model in Sect. 2, we introduce terminology and strategic concepts in Sect. 3, and we give a proof of our main result Sect. 4. The proof in Sect. 4 makes use of a fixed point theorem, which we prove in Sect. 5.

2 Formal model

Our class of games was informally introduced as consisting of games that potentially have infinite horizon, but where players only obtain a nonzero reward if one of them chooses to terminate. We formally introduce our class as always having infinite play. This is done by letting termination correspond to entering an absorbing state, after which the game continues, but is strategically over. We consider the class ${\mathcal {G}}$ of dynamic games given by

• (1) a non-empty set of players $N = \{1,\ldots , n\}$, where $n\in {{\mathbb {N}}}$,

• (2) a non-empty and finite set S of non-absorbing states and a set $S^*$ of absorbing states such that there is a one-to-one correspondence between states in S and $S^*$; the state in $S^*$ that corresponds to $t\in S$ is denoted by $t^*$,

• (3) for each state $t\in S\cup S^*$, an associated controlling player $i_t\in N$,

• (4) for each state $t \in S$, a set of actions $A(t) \subseteq \{t^*\} \cup (S{\setminus } \{t\})$ with $t^*\in A(t)$; for each state $t^*\in S$, we have $A(t^*) = \{t^*\}$,

• (5) for each state $t\in S$, an associated reward vector $r(t) \in {{\mathbb {R}}}^N$.

A game in ${\mathcal {G}}$ is to be played at stages in ${{\mathbb {N}}}$ in the following way. At any stage m one state is called active. If $t\in S$ is active, then player $i_t$ announces a state in A(t), and the announced state will be active at the next stage. If $t^*\in S^*$ becomes active, then the unique state $t^*\in A(t^*)$ will be active at the next stage and thus, $t^*$ will be active forever. The game is then strategically finished and the rewards to the players are according to r(t). The game starts with an initial state $s\in S$.

We assume complete information (i.e., the players know all the data of the game), full monitoring (i.e., the players observe the active state and the action chosen by the active player), and perfect recall (i.e., the players remember the entire sequence of active states and actions).

3 Strategic concepts

3.1 Basic concepts and terminology

It will be necessary to develop a rather extensive notation and terminology in this paper. Here, we introduce the basics.

Let us define the directed graph ${\mathbf {G}}$ by

$$\begin{aligned} {\mathbf {G}} = (S\cup S^*,\{(x, y) \mid x \in S \cup S^*\hbox { and } y \in A(x)\} ). \end{aligned}$$

This graph can obviously be interpreted as the graph on which the game is played. Whenever we refer to an ordered pair (x, y) as an edge, it is implicit that (x, y) is an edge of the directed graph ${\mathbf {G}}$, and hence that $y\in A(x)$.

Let us also have notation for the set of non-absorbing states that are controlled by one particular player. For every $i\in N$, we define

$$\begin{aligned} S^i = \{t\in S\mid i_t = i \}. \end{aligned}$$

Obviously, the sets $S^i$ form a partition of the set S of non-absorbing states.

Let us now introduce the basic concepts of this paper.

Plans: A plan is an infinite sequence of states $g = (t_m)_{m\in {{\mathbb {N}}}}$, such that $(t_m , t_{m+1} )$ is an edge for all $m \in {{\mathbb {N}}}$. A plan is interpreted as a prescription for play for a game with initial active state $t_1$. The set of non-absorbing states that become active during play if plan g is executed is denoted by ${\textsc {S}}(g)$, i.e.,

$$\begin{aligned} {\textsc {S}}(g) = \{t \in S \mid \exists m\in {{\mathbb {N}}}: t_m = t\}. \end{aligned}$$

Notice that, if the initial state of g is an element of $S^*$, then g is of the form $(t^*, t^*, \ldots )$, with $t^*\in S^*$. Such a plan will also be denoted as $(t^*)$. Also, if plan g contains a state in $S^*$, say $t^*$, and the initial state of g is an element of S, then we must have $t \in {\textsc {S}}(g)$ and there must be a stage M with $t_M = t$ and with $t_m = t^*$ for all $m > M$. This is interpreted as a prescription for player $i_t$ to announce his absorbing state $t^*$ at stage M . We say that the plan absorbs at t if this is the case. Otherwise, we say that the plan is non-absorbing. An absorbing plan, for example $(r,s,t,t^*,t^*,\ldots )$ will also be denoted as $(r,s,t,t^*)$. We denote by $\phi _i(g)$ the reward to player $i \in N$ when play is according to g, i.e., $\phi _i(g) = r_i(t)$ if g absorbs at t, and $\phi _i(g) = 0$ if g is non-absorbing. The initial state of plan g is denoted by ${\textsc {first}}(g)$.

Paths: A path (or history) is a finite sequence $p = (t_m)_{m=1}^k$ with $k \ge 1$, such that $(t_m , t_{m+1} )$ is an edge for all $m\in \{1,\ldots ,k-1\}$. The number $k-1$ is called the length of p. The initial state $t_1$ of p is denoted by ${\textsc {first}}(p)$ and the final state $t_k$ is denoted by ${\textsc {last}}(p)$. We will sometimes want to concatenate a number of paths to make a longer path or a plan, or we may want to concatenate a finite number of paths and a plan to make another plan. We allow concatenation if $p_1, p_2, \ldots , p_m$ are paths that satisfy ${\textsc {last}}(p_k) = {\textsc {first}}(p_{k+1})$ for all $k \in \{1,\ldots , m - 1\}$. The concatenation of these paths is denoted by $\langle p_1, p_2,\ldots , p_m\rangle$ and it represents the path that follows the prescription of $p_1$ from ${\textsc {first}}(p_1)$ to ${\textsc {last}}(p_1) = {\textsc {first}}(p_2)$, then follows the prescription of $p_2$ until ${\textsc {last}}(p_2) = {\textsc {first}}(p_3)$ is reached, and so on, until ${\textsc {last}}(p_m)$ is reached. Also, if g is a plan with ${\textsc {first}}(g) = {\textsc {last}}(p_m)$, then the plan that first follows the prescription of $\langle p_1, p_2,\ldots , p_m\rangle$ and then switches to g is denoted by $\langle p_1,\ldots , p_m,$g$\rangle$. Finally, if we have an infinite number of paths $p_1, p_2,\ldots$ with the property ${\textsc {last}}(p_k) = {\textsc {first}}(p_{k+1})$ for all $k\in {{\mathbb {N}}}$, then $\langle p_1, p_2, \ldots \rangle$ represents the path¹ or plan that subsequently follows the prescription of $p_1$, $p_2$, etc.

Strategies: A strategy $\pi ^i$ for player $i\in N$ is a decision rule that, for any path p with ${\textsc {last}}(p) \in S^i$, prescribes a probability distribution $\pi ^i(p)$ over the elements of $A({\textsc {last}}(p))$. We use the notation $\varPi ^i$ for the set of strategies for player i. A strategy $\pi ^i \in \varPi ^i$ is called pure if every prescription $\pi ^i(p)$ places probability 1 on one of the elements of $A({\textsc {last}}(p))$. We use the notation $\varPi$ for the set of joint strategies $\pi = (\pi ^i)_{i\in N}$ with $\pi ^i \in \varPi ^i$ for $i\in N$. A joint strategy $\pi = (\pi ^i)_{i\in N}$ is called pure if $\pi ^i$ is pure for all $i\in N$.

Expected rewards: Consider a joint strategy $\pi \in \varPi$ and a path p. Suppose that the game has developed along the path p and that state ${\textsc {last}}(p)$ is now active. Suppose further that all players, starting at ${\textsc {last}}(p)$, follow the joint strategy $\pi$, taking p as the history of the game. Denote the overall probability of absorption at t by ${{\mathbb {P}}}^{p,\pi }(t)$. In our model, where nonzero reward are only obtained in absorbing states, the expected reward for player $i\in N$ can then be expressed as

$$\begin{aligned} \psi ^p_{i}(\pi ) := \sum _{u\in S} {{\mathbb {P}}}^{p,\pi }(u) r_i(u). \end{aligned}$$

Equilibria: Consider a joint strategy $\pi \in \varPi$ and a game that has developed along the path p. The joint strategy $\pi =(\pi ^i)_{i\in N}\in \varPi$ is called a (Nash) $\varepsilon$-equilibrium for path p, for some $\varepsilon \ge 0$, if

$$\begin{aligned} \psi _i^p\left( \sigma ^i,(\pi ^j)_{j\in N {\setminus } \{i\}}\right) \le \psi _i^p\left( \pi \right) +\varepsilon \quad \quad \forall \sigma ^i\in \varPi ^i,\;\forall i\in N, \end{aligned}$$

which means that, given history p, no player i can gain more than $\varepsilon$ by a unilateral deviation from his proposed strategy $\pi ^i$ to an alternative strategy $\sigma ^i$. The joint strategy $\pi$ is called an $\varepsilon$-equilibrium for initial state $s\in S$ if $\pi$ is an $\varepsilon$-equilibrium for path (s). The joint strategy $\pi$ is called a subgame perfect $\varepsilon$-equilibrium if $\pi$ is an $\varepsilon$-equilibrium for every path p.

3.2 Strategic concepts and an update procedure

In this section, we introduce the strategic concepts that we need for the description of a subgame perfect $\varepsilon$-equilibrium. These concepts all involve the assignment of a real number to each of the non-absorbing states, represented by a real vector $\alpha \in {{\mathbb {R}}}^S$. One of the key concepts in the paper is that of an $\alpha$-viable plan. These are plans g where every player who controls a state $t\in S$ on g will receive a reward of at least $\alpha _t$ when plan g is executed. The vector $\alpha$ is chosen such that every plan that can possibly occur in a subgame perfect $\varepsilon$-equilibrium is surely contained in the set of $\alpha$-viable plans. Initially, the set of $\alpha$-viable plans may also contain plans that do not occur in any subgame perfect $\varepsilon$-equilibrium play for small enough $\varepsilon$. Our aim is to eliminate those plans by increasing one or more coordinates of $\alpha$ in an update procedure. The update procedure is repeated until no further increase in the coordinates of $\alpha$ is possible. The final vector $\alpha$ will then be used to construct a subgame perfect $\varepsilon$-equilibrium for every $\varepsilon >0$.

Viable plans: For $\alpha \in {{\mathbb {R}}}^S$, a plan g and a state $t \in S$, we say that t is $\alpha$-satisfied by g if $\phi _{i_t}(g) \ge \alpha _t$. We define ${\textsc {sat}}(g,\alpha ) = \{t \in S \mid t\hbox { is } \alpha \hbox {-satisfied by } g\}$. We say that plan g is $\alpha$-viable if ${\textsc {S}}(g) \subseteq {\textsc {sat}}(g,\alpha )$. This means that, if play is according to g, the controlling player of every non-absorbing state t that becomes active during play will receive a reward of at least $\alpha _t$. For every state $t \in S \cup S^*$, we denote the set of $\alpha$-viable plans g with ${\textsc {first}}(g) = t$ by ${\textsc {viable}}(t,\alpha )$. Notice that a plan of the form $g = (t^*, t^*, \ldots )$ with $t^*\in S^*$ is trivially $\alpha$-viable, since ${\textsc {S}}(g) = \varnothing$, and that the set ${\textsc {viable}}(t^*,\alpha )$ consists of only the plan $(t^*)$.

Compatible plans: Consider that a player $i\in N$ can influence play by choosing a specific action if play visits one of his states, say $t\in S$. Now, if every $\alpha$-viable plan after the selected action yields a strictly higher reward for player i than $\alpha _t$, then $\alpha _t$ can be increased without eliminating any plan that may occur in equilibrium. This idea formed the basis for the iterative procedure in Flesch et al. (2010b) and Kuipers et al. (2016). In those papers, it was sufficient to consider only one state at a time per iteration to eventually eliminate all non-equilibrium plans.

Fig. 3

A 1-player game

The approach fails for the trivial 1-player game in Fig. 3. Note that this game has one subgame perfect equilibrium, which is for the one player to never terminate the game. The values $\alpha _{1_A} = \alpha _{1_B} = 0$ correspond to this equilibrium. As an illustration, we set $\alpha _{1_A} = \alpha _{1_B} = -1$, which are the rewards of the game at termination. Then every plan is $\alpha$-viable. If player 1 specifies action $1_B \in A(1_A)$ for when state $1_A$ is visited, but does not specify a particular action for when $1_B$ is visited, then termination at $1_B$ is in accordance with the specification and $\alpha$-viable. An iterative procedure would reflect this by letting $\alpha$ unchanged and thus fail to eliminate any of the absorbing plans. Our iterative procedure should reflect the fact that player 1 is able to coordinate his actions in $1_A$ and $1_B$. We therefore consider that a player can select an action at multiple states simultaneously. This leads to the definition of compatible plans.

For $\alpha \in {{\mathbb {R}}}^S$ and $t,u\in S$, we say that state t is $\alpha$-safe at state u if $t \in {\textsc {sat}}($g$,\alpha )$ for all $g \in {\textsc {viable}}(u,\alpha )$. For $t^*\in S^*$, it will be convenient to say that $t^*$ is $\alpha$-safe at $t^*$. We define, for all $t \in S$,

$$\begin{aligned} {\textsc {safestep}}(t, \alpha ) = \{u \in A(t) \mid t\hbox { is } \alpha \hbox {-safe at } u\}. \end{aligned}$$

For $\alpha \in {{\mathbb {R}}}^S$ and a non-empty set $F\subseteq S$, we say that F is an $\alpha$-plateau if there exists $i\in N$ such that $i_t = i$ for all $t\in F$ and if $\alpha _s = \alpha _t$ for all $s,t\in F$. An $\alpha$-plateau that is maximal with respect to inclusion is called an $\alpha$-level.

For $\alpha \in {{\mathbb {R}}}^S$, we say that a function $U : F \rightarrow S \cup S^*$ is an $\alpha$-safe combination if the domain F of U is an $\alpha$-plateau and if we have $U(t)\in {\textsc {safestep}}(t,\alpha )$ for all $t \in F$. If the domain of an $\alpha$-safe combination ${\mathcal {U}}$ is not explicitly specified, then it will be denoted by F(U). We denote the set of all $\alpha$-safe combinations by ${\mathcal {U}}(\alpha )$ and the set of $\alpha$-safe combinations with given domain F by ${\mathcal {U}}(F,\alpha )$.

For a plan g and an $\alpha$-safe combination U, we now say that plan g is U-compatible if, for every state $t\in {\textsc {S}}(g) \cap F(U)$, the first occurrence of t on g is followed by U(t). A path p is U-compatible if, for every state $t\in {\textsc {S}}(g) \cap F(U)$, the first occurrence of t on p is followed by U(t) unless the first occurrence of t is at the end of p. For every $t\in S$ we denote the set of plans in ${\textsc {viable}}(t, \alpha )$ that are U-compatible by ${\textsc {viacomp}}(t, U, \alpha )$.

Now consider again the 1-player game in Fig. 3, where we set $\alpha$ by $\alpha _{1_A} = -1$ and $\alpha _{1_B} = -1$. We define U by $U(1_A) = 1_B$ and $U(1_B) = 1_A$. Notice that U is indeed an $\alpha$-safe combination. Also notice that the $\alpha$-viable plans $(1_A,1_A^*)$, $(1_A,1_B,1_B^*)$, $(1_B,1_B^*)$, and $(1_B,1_A,1_A^*)$ are not elements of ${\textsc {viacomp}}(t, U, \alpha )$. Nevertheless, there are still plans in ${\textsc {viacomp}}(t, U, \alpha )$ that should be eliminated if we wish to find the unique subgame perfect equilibrium associated with this example. The plans $(1_A,1_B,1_A, 1_A^*)$ and $(1_B,1_A,1_B,1_B^*)$ are examples of this. The set ${\textsc {viacomp}}(t, U, \alpha )$ thus only serves as a pre-selection of plans that are subject to further scrutiny to see if they can remain. For this, we introduce the concept of an admissible plan.

Admissible plans: Consider again the game depicted in Fig. 1, where we set $\alpha$ by $\alpha _{s_1} = -1$ and $\alpha _{s_2} = 2$. We define U by $U(s_1) = s_2$. Then U is an $\alpha$-safe combination, and the plan $(s_1,s_2,s_1,s_1^*)$ is an element of ${\textsc {viacomp}}(t, U, \alpha )$. Here, we do not wish to eliminate the plan, as it is a plan that can occur in equilibrium play. The reason this plan will be considered admissible is the fact that player 2, who controls state $s_2$ on the plan, can threaten player 1 with termination of the game at $s_2$. If player 1 does not follow the plan and nominates $s_2$ always when $s_1$ is active, then the threat will eventually become reality if player 2 places a small probability on executing the threat. So the intuition here is that player 1 has no possibility to force a better outcome than $(s_1,s_2,s_1,s_1^*)$. This is in contrast with the plan $(1_A,1_B,1_A,1_A^*)$ for the game in Fig. 3, where player 1 can easily force a non-absorbing plan without the possibility of retaliation. The formal criteria for admissibility distinguishes between these two situations and are given below.

Let $\alpha \in {{\mathbb {R}}}^S$, let $U\in {\mathcal {U}}(\alpha )$, and let $t\in F(U)$. For a plan $g\in {\textsc {viacomp}}(t, U, \alpha )$, we say that g is $(t, U, \alpha )$-admissible if it satisfies at least one of the following four conditions.

• AD-i $\alpha _t > 0$ or there exists a state x on g with $i_x = i_t$ and $\alpha _x > \alpha _t$ that appears on g before any state of F(U) has appeared for the second time;

• AD-ii g is non-absorbing;

• AD-iii each state of F(U) occurs at most once on g;

• AD-iv there exists a threat pair (x, v) for g. Here, x and v are a state and a plan respectively that satisfy the following properties:

  • (a) $x\in S$ and x appears on g before any state of F(U) has appeared for the second time on g,

  • (b) $i_{x} \ne i_t$,

  • (c) v is an $\alpha$-viable plan with ${\textsc {first}}(v)\in A(x)$,

  • (d) ${\textsc {first}}(v)$ differs from the state on g that follows the first occurrence of x on g,

  • (e) $x, t \notin {\textsc {sat}}(v, \alpha )$.

We denote the set of plans that are $(t, U, \alpha )$-admissible by ${\textsc {admiss}}(t, U, \alpha )$. We can gain some additional insight in the definition of a $(t,U,\alpha )$-admissible plan, by considering, for a plan $g\in {\textsc {viacomp}}(t, U, \alpha )$ an associated plan $g^U$. Plan $g^U$ is the plan where player $i_t$ chooses his selected actions defined by U always, and the other players keep their actions the same as in g. We may have $g^U = g$, for example when every state in F(U) appears at most once on g. The plans g and $g^U$ may also differ, which happens when at least one state of $t\in F(U)$ appears at least twice on g and t is not always followed by U(t). In the latter case $g^U$ is a non-absorbing plan, where a certain part of g is followed infinitely many times. We compare the plans g and $g^U$. If the comparison comes out in favor of $g^U$, then plan g can be discarded, i.e., plan g will not be considered admissible. Let us interpret the conditions for admissibility one by one in this way.

Condition AD-i: If $\alpha _t >0$ and the plan $g^U$ is non-absorbing, then $g^U$ gives a lower reward to $i_t$ than g does. If $\alpha _t >0$ and the plan $g^U$ is absorbing then $g^U = g$. In either case, g cannot be discarded in favor of $g^U$. If there exists x on the plan g with $i_x = i_t = i$ and $\alpha _x > \alpha _t$, then g is guaranteed to give a strictly higher reward than $\alpha _t$. Here, we keep g because this will not hinder an increase in $\alpha _t$. Also, it will be convenient to exclude this situation when we later consider plans that satisfy AD-iv, but not AD-i, AD-ii, or AD-iii.

Condition AD-ii: If g is non-absorbing, then both g and $g^U$ are non-absorbing, with the same reward 0. There is therefore no reason to discard g.

Condition AD-iii: If each state of F(U) appears at most once on g, then $g=g^U$.

Condition AD-iv: This describes a situation, where a player other than $i_t$, who controls a state x on the U-compatible plan g, has the possibility to switch from g to an $\alpha$-viable plan v with $t,x\notin {\textsc {sat}}(v,\alpha )$. Due to condition AD-iv-(a), state x is also on plan $g^U$. State x does not necessarily lie on the part of $g^U$ that is repeated, but to obtain intuition we assume that state x does lie on that part. Now imagine that the players are supposed to follow plan g, except for the player $i_x$, who is required to place a very small probability on the switch to v when state x is active. Then play will be according to g with very high probability if players indeed follow this prescription. If however player $i_t$ deviates by always playing U(s) for all $s\in F(U)$ when s is active, in an attempt to force play according to $g^U$, then this will eventually fail, since the switch to v will then be made with probability 1. Thus, the deviation by player $i_t$ is not profitable for him, since $t\notin {\textsc {sat}}(v,\alpha )$. The requirement $x\notin {\textsc {sat}}(v,\alpha )$ is there because player $i_x$ should not be tempted to increase the probability of a switch to v. These considerations are the motivation to call g admissible and to not discard g in favor of $g^U$.

An update procedure: Let $\alpha \in {{\mathbb {R}}}^S$ and let $U\in {\mathcal {U}}(\alpha )$. We define, for all $t\in F(U)$,

$$\begin{aligned} \beta (t, U, \alpha ) = \min \{\phi _{i_t}(g) \mid g \in {\textsc {admiss}}(t, U, \alpha )\}. \end{aligned}$$

We use the convention $\min \varnothing = \infty$, so that $\beta (t, U, \alpha )$ is well defined for all $t\in F(U)$.

We also define

$$\begin{aligned} \gamma (U,\alpha ) = \min \{\beta (t,U,\alpha )\mid t\in F(U)\}. \end{aligned}$$

Note that the plans in ${\textsc {admiss}}(t, U, \alpha )$ are all $\alpha$-viable, for every $t\in F(U)$. Thus, $\beta (t,U,\alpha ) \ge \alpha _t$ for all $t\in F(U)$, and hence also $\gamma (U,\alpha ) \ge \alpha _t$ for any representative $t\in F(U)$. One can interpret the number $\gamma (U,\alpha )$ as the worst possible reward for the player controlling the states of F(U) when play visits a state $t\in F(U)$ and if he selects action U(t) when this happens.

Now, we replace in $\alpha$ the number $\alpha _t$ by the number $\gamma (U, \alpha )$ at every coordinate t with $t \in F(U)$. Let us denote the updated vector by $\delta (U,\alpha )$.

The update procedure performs a simultaneous update on the states of a given $\alpha$-plateau. The idea is to repeat the procedure over and over until the updates do not change any $\alpha$-values, for any given $\alpha$-plateau.

Example 3

The example in Fig. 4 represents a game with 3 players and with 4 non-absorbing states.

Fig. 4

A game with 3 players and with 4 non-absorbing states

The game admits the following subgame perfect $\varepsilon$-equilibrium. When state $1_a$ is active, player 1 should nominate state 2, when state 2 is active, player 2 should nominate state $1_b$, and when state $1_b$ is active, player 1 should nominate state 3 with high probability and place a small probability on terminating the game. Finally, player 3 should terminate the game when state 3 is active. We will go through the process of updating to see how it all works.

Initialization: We choose $\alpha$ such that every plan in equilibrium play will surely be $\alpha$-viable. A good choice is to set $\alpha _t$ at the reward for player $i_t$ if play terminates at t. Thus, we set

$$\begin{aligned} \alpha _{1_a} = -2, \, \alpha _{2} = 1, \, \alpha _{1_b} = -1, \, \alpha _{3} = -1. \end{aligned}$$

Iteration 1: To obtain an overview of all $\alpha$-safe combinations, we determine the sets ${\textsc {safestep}}(t,\alpha )$ for all $t\in S$. The result can be seen in the picture below, where (x, y) is represented by a solid arrow if $y\in {\textsc {safestep}}(x,\alpha )$ and by a dashed arrow otherwise (Fig. 5).

Fig. 5

$\alpha$-safe combinations at the beginning of iteration 1

Note that an $\alpha$-safe combination U with $U(t) = t^*$ for all $t\in F(U)$ will not lead to an increase of any $\alpha$-value. Thus, there is only one $\alpha$-safe combination of interest, which is defined by $U(2) = 1_b$. For the update associated with this choice of U, it is important to see that the plans $(2,1_b,1_a,1_a^*)$ and $(2,1_b,1_a,2,2^*)$ are not $\alpha$-viable, and therefore not in ${\textsc {admiss}}(2,U,\alpha )$. Here, the set ${\textsc {admiss}}(2,U,\alpha )$ coincides with ${\textsc {viacomp}}(2,\alpha )$ and these sets consist of the plans that start at 2, then visit $1_b$, and terminate either at $1_b$ or at 3. Thus, $\beta (2,U,\alpha ) = \gamma (U,\alpha ) = 2$ and we update the value of $\alpha _2$ from 1 to 2. We proceed with

$$\begin{aligned} \alpha _{1_a} = -2, \, \alpha _{2} = 2, \, \alpha _{1_b} = -1, \, \alpha _{3} = -1. \end{aligned}$$

Iteration 2: We now have (Fig. 6)

Fig. 6

$\alpha$-safe combinations at the beginning of iteration 2

There is again one $\alpha$-safe combination of interest, defined by $U(1_a) = 2$. Here, the plan $(1_a,2,1_b,1_b^*)$ is $(1_a,U,\alpha )$-admissible due to condition AD-iii. It is also the plan that determines the number $\beta (1_a,U,\alpha ) = \gamma (U,\alpha )$. We thus have $\gamma (U,\alpha ) = -1$. We proceed with

$$\begin{aligned} \alpha _{1_a} = -1, \, \alpha _{2} = 2, \, \alpha _{1_b} = -1, \, \alpha _{3} = -1. \end{aligned}$$

Iteration 3: We now have (Fig. 7)

Fig. 7

$\alpha$-safe combinations at the beginning of iteration 3

Here, we have several $\alpha$-safe combinations to consider, all involving the states of player 1. The good choice is to define U by $U(1_a) = 2$ and $U(1_b) = 3$. Observe that all plans in ${\textsc {viacomp}}(1_a,U,\alpha )$ and ${\textsc {viacomp}}(1_b,U,\alpha )$ terminate at state 3, and that ${\textsc {admiss}}(t,U,\alpha ) = {\textsc {viacomp}}(t,U,\alpha )$ for $t = 1_a,1_b$. Thus, $\beta (1_a,U,\alpha ) = \beta (1_b,U,\alpha ) = 2$. The updated vector $\alpha$ is defined by

$$\begin{aligned} \alpha _{1_a} = 2, \, \alpha _{2} = 2, \, \alpha _{1_b} = 2, \, \alpha _{3} = -1. \end{aligned}$$

Iteration 4: Further attempts to update $\alpha$ do not lead to an increase in any of its coordinates. The current $\alpha$-values indicate that, under equilibrium play, the game will terminate at state 3 (with high probability) (Fig. 8).

Fig. 8

$\alpha$-safe combinations at the beginning of iteration 4

A final calculation will demonstrate how the subgame perfect $\varepsilon$-equilibrium should be played. Note that $1_a \in {\textsc {safestep}}(3,\alpha )$. We define the $\alpha$-safe combination U by $U(3) = 1_a$. Then the plan $(3,1_a,2,1_b,3,3^*)$ is an element of ${\textsc {viacomp}}(3,U,\alpha )$. Observe that this plan is also element of ${\textsc {admiss}}(3,U,\alpha )$ due to condition AD-iv: The threat pair is $(1_b,v)$ with $v = (1_b^*)$, which is also the threat pair needed in equilibrium play.

4 Construction of a subgame perfect $\varepsilon$-equilibrium

4.1 Introduction

For this section, we choose an arbitrary game G in the class ${\mathcal {G}}$. We also choose the parameter $\varepsilon > 0$. We keep G and $\varepsilon$ fixed throughout this section and we prove that the game G has a subgame perfect $\varepsilon$-equilibrium.

For the description of a subgame perfect $\varepsilon$-equilibrium for G, we will use the fact that a vector $\alpha ^*\in {{\mathbb {R}}}^S$ exists with the following properties:

F-i::

For every $t\in S$, we have ${\textsc {viable}}(t,\alpha ^*) \ne \varnothing$.

F-ii::

For every $U \in {\mathcal {U}}(\alpha ^*)$, we have $\delta (U, \alpha ^*) = \alpha ^*$.

The proof that such a vector indeed exists is delayed until Sect. 5. The properties F-i and F-ii essentially describe the existence of a fixed point for the update procedure from Sect. 3.

Property F-i can be used to formulate a (pure) joint strategy such that, for every state $t\in S$ that is visited during play, player $i_t$ can expect a reward of at least $\alpha _t^*$. This can be achieved by prescribing an $\alpha ^*$-viable plan that should be executed in its entirety with probability 1.

Property F-ii can be used to formulate a (pure) joint strategy such that, for every state $t\in S$ that is visited during play, player $i_t$ can expect a reward of at most $\alpha _t^*$ if he plays an action that is not prescribed by the joint strategy. This can be achieved by selecting a new $\alpha ^*$-viable plan to follow after a deviation. The following lemma shows that property F-ii makes the selection of such a new plan indeed possible.

Lemma 1

Let $t\in S$ and $u\in A(t)$.

• (i) If $u\in {\textsc {safestep}}(t,\alpha ^*)$, then there exists $g\in {\textsc {viable}}(u,\alpha ^*)$ with $\phi _{i_t}(g) = \alpha ^*_t$.

• (ii) If $u\notin {\textsc {safestep}}(t,\alpha ^*)$, then there exists $g\in {\textsc {viable}}(u,\alpha ^*)$ with $\phi _{i_t}(g) < \alpha ^*_t$.

Proof

Proof of (i): Let $t\in S$ and let $u\in {\textsc {safestep}}(t, \alpha ^*)$. Denote by U be the $\alpha ^*$-safe combination with domain $\{t\}$ and with $U(t) = u$. By property F-ii, we have

$$\begin{aligned} \beta (t,U,\alpha ^*) = \gamma (U,\alpha ^*) = \delta _t(U,\alpha ^*) = \alpha ^*_t. \end{aligned}$$

By definition of the number $\beta (t,U,\alpha ^*)$, there exists a plan $h\in {\textsc {admiss}}(t,U,\alpha ^*)$ with $\phi _{i_t}(h) = \beta (t,U,\alpha ^*)$. Thus, we have $\phi _{i_t}(h) = \alpha ^*_t$. The plan h is $\alpha ^*$-viable, since ${\textsc {admiss}}(t,U,\alpha ^*)$ is by definition a subset of ${\textsc {viable}}(t,\alpha ^*)$. The part of h that starts at the second state (i.e., at u) is the required plan $g\in {\textsc {viable}}(u,\alpha ^*)$ with $\phi _{i_t}(g) = \alpha ^*_t$.

Claim (ii) of the lemma follows by the definition of the set ${\textsc {safestep}}(t,\alpha ^*)$. $\square$

An informal description of a subgame perfect $\varepsilon$ -equilibrium. Consider a deterministic joint strategy, where initially, an $\alpha ^*$-viable plan is selected for the players to follow in its entirety. Only if a player deviates, a new $\alpha ^*$-viable plan is selected, such that the new plan minimizes the payoff to the deviating player. Note that a single deviation or even finitely many deviations do not profit a deviating player, by the result of Lemma 1. If $\alpha ^*\ge 0$, then infinitely many deviations do not help the deviating player either. Indeed, if $\alpha ^*\ge 0$, then the formulated joint strategy constitutes a subgame perfect 0-equilibrium. The situation is more complex when the vector $\alpha ^*$ has negative coordinates. The game of Example 1 is typical for this situation, where play according to a subgame perfect $\varepsilon$-equilibrium was achieved by placing a small probability on a non-credible threat. This way of playing a subgame perfect $\varepsilon$-equilibrium can be generalized to work for every game in our class. Specifically, at each stage of the game, the players are given a prescription of play that consists of a main plan g and possibly, depending on the properties of g, a threat pair (x, v) for g. If the prescription consists of only the main plan g, then the players are supposed to follow plan g. If the prescription consists of a main plan g together with a threat pair (x, v), then the players are supposed to follow plan g until the first occurrence of state x on g is reached. The controlling player of state x is then required to perform a lottery, where he places a high probability on the continuation of plan g and a small probability on the switch to plan v.

A joint strategy can now be formulated as follows. The game begins with an initial prescription, which could be any $\alpha ^*$-viable main plan g. A new prescription is selected when a player does not choose an action with positive probability according to the current prescription. Note that the lottery player may deviate from the prescription without instigating a new prescription, as long as he chooses a continuation of the main plan or a switch to the threat plan. A new prescription is chosen such that its main plan minimizes the reward of the deviating player among the available admissible plans. Note that a threat pair (x, v) can be part of the new prescription only if the main plan g is admissible due to condition AD-iv, as threat pairs are defined only for such plans. If this happens, then the execution of plan v is indeed a threat to the deviating player (who is identified as the player controlling the initial state of g), since this player strictly prefers g over v, by AD-iv-(e). Moreover, the execution of v is a non-credible threat, since player $i_x$, who must make the switch from g to v, also strictly prefers g over v, by AD-iv-(e). A non-credible threat makes sure that player $i_x$ cannot make a profit by increasing the probability of a switch to v.

Now, prescriptions consisting of a main plan with a threat pair are essentially there to make it impossible for a deviating player to deviate infinitely many times. Conceivably however, the deviating player may still establish infinite play when lotteries with a threat are prescribed as retaliation for his deviations. This would happen if the deviating player became active again and again after every deviation, before the lottery state is reached and before absorption takes place. By an appropriate choice of the prescriptions, we can however establish a bound on the number of times that a deviating player can avoid absorption or the execution of a lottery. This will ensure a lottery at more or less regular intervals and finally execution of the threat plan with probability 1 when a player keeps deviating.

In Sect. 4.2, we will establish a ranking of the states of each $\alpha ^*$-level. The ranking will be the tool to make sure that infinitely many deviations cannot occur. In Sect. 4.3, we give a description of a joint strategy $\pi _{\varepsilon }$, which is the detailed and complete version of the description given here. Then, in Sect. 4.4 we prove our main result, which is that $\pi _{\varepsilon }$ is a subgame perfect $\varepsilon$-equilibrium.

Let us choose $\alpha ^*\in {{\mathbb {R}}}^S$ such that it has properties F-i and F-ii and let us keep $\alpha ^*$ fixed for the remainder of this section.

4.2 A ranking of the states

Let $U\in {\mathcal {U}}(\alpha ^*)$. We will be interested in all admissible plans that can be associated with the $\alpha ^*$-safe combination U. We define therefore

$$\begin{aligned} {\textsc {admiss}}(U,\alpha ^*) = \cup _{t\in F(U)} {\textsc {admiss}}(t,U,\alpha ^*). \end{aligned}$$

For every $g\in {\textsc {admiss}}(U,\alpha ^*)$, we wish to identify the set of states on g, where the deviating player could sensibly deviate from g, to avoid a lottery or to avoid absorption at a state with negative reward for him. The following definition of the set D(g, U) simply lists the cases. We define, for $g\in {\textsc {admiss}}(U,\alpha ^*)$, the set D(g, U) by

• D-i $D(g,U) = \varnothing$ if g satisfies AD-i or AD-ii. (Here, infinitely many deviations do not profit the deviating player.)

• D-ii If g violates the conditions AD-i and AD-ii, but satisfies condition AD-iii, then we define $D(g,U) = {\textsc {S}}(g^-) \cap F(U)$, where $g^-$ is the part of g that starts at the second state of g. (Here, any deviation before absorption could be profitable, if it could be infinitely repeated.)

• D-iii In all other cases, i.e., if g violates the conditions AD-i, AD-ii, and AD-iii, but satisfies condition AD-iv, there exists a threat pair (x, v) for g. In this case, we choose state x as close as possible to the initial state of g, and we define D(g, U) as the set of states in F(U) that appear on g from the second state of g until the first occurrence of x on g. (Here, a deviation should really be before the lottery, as there are only finitely many opportunities available after the lottery.)

Notice that the first state of g can only be a member of D(g, U) if that state reappears on g. This is because we will interpret the first state of a plan in ${\textsc {admiss}}(U,\alpha ^*)$ as the state where a deviation just took place and the second state as the deviation.

Let $t\in S$ and $u\in A(t)$. Imagine that the choice for $u\in A(t)$ at state t is not according to the prescription and that $u\in {\textsc {safestep}}(t,\alpha ^*)$. Then, for the purpose of punishment, we choose $U\in {\mathcal {U}}(\alpha ^*)$ with $t\in F(U)$ and $U(t) = u$, and a plan g in ${\textsc {admiss}}(t,U,\alpha ^*)$ that minimizes the reward to player $i_t$. By property F-ii, the reward equals $\alpha ^*_t$. Ideally, we choose g such that also $D(g,U) = \varnothing$ holds. This may not always be possible, but we do have the following lemma.

Lemma 2

For every $U\in {\mathcal {U}}(\alpha ^*)$, there exists $g\in {\textsc {admiss}}(U,\alpha ^*)$ with $D(g,U) = \varnothing$ and with $\phi _{i}(g) = \alpha _t^*$, where i is the controlling player of the states in F(U) and t is any state in F(U).

Proof

Let $U\in {\mathcal {U}}(\alpha ^*)$. Because we have $\delta (U,\alpha ^*) = \alpha ^*$ by F-ii, there exists $s\in F(U)$ with $\beta (s,U,\alpha ^*) = \alpha _s^*$. Further, by the definition of the number $\beta (s,U,\alpha ^*)$, there exists a plan $h\in {\textsc {admiss}}(s,U,\alpha ^*)$ with $\phi _{i_s}(h) = \beta (s,U,\alpha ^*)$, hence with $\phi _{i_s}(h) =\alpha _s^*$. Now, if $D(h,U) = \varnothing$, then the claim of the lemma follows immediately by setting $t=s$ and $g=h$. We assume further that $D(h,U) \ne \varnothing$. This rules out the possibility that h satisfies AD-i or AD-ii. We distinguish between the two remaining possibilities.

Case 1: Assume that plan h satisfies AD-iii. Then each element of D(h, U) is visited exactly once on h. We define t as the state of D(h, U) that is visited last on h and we define g as the plan with ${\textsc {first}}(g) = t$ that follows the prescription of h from the unique occurrence of t on h. It is obvious that $g\in {\textsc {admiss}}(t,U,\alpha ^*)$ due to property AD-iii and that $D(g,U) = \varnothing$.

Case 2: Assume that plan h satisfies AD-iv but not AD-iii. Then there exists a threat pair (x, v) for h. By condition AD-iv, every element of D(h, U) is visited exactly once on h before the first occurrence of x on h. Define t as the state of D(h, U) visited last on h before x. Construct plan g with ${\textsc {first}}(g) = t$ as follows.

Follow plan h from the first occurrence of t on h until the next occurrence of a state in F(U), say r. If r is a state of F(U) that is visited for the first time during the construction of g and if the corresponding location of r on h is not the first occurrence of r on h, then we jump back to the first occurrence of r on h. From there, we follow h again. We proceed, jumping back to an earlier location on h every time a state of F(U) is visited for the first time during construction of g and if the corresponding location on h is not the first occurrence of that state on h.

The construction trivially results in a plan g with ${\textsc {S}}(g) \subseteq {\textsc {S}}(h)$. It is also clear that a jump back during the construction can occur only a finite number of times. The resulting plan g will therefore have its tail the same as h, which implies that $\phi (g) = \phi (h)$. It follows that ${\textsc {S}}(g) \subseteq {\textsc {S}}(h) \subseteq {\textsc {sat}}(h,\alpha ^*) = {\textsc {sat}}(g,\alpha ^*)$, proving that g is $\alpha ^*$-viable. Further, g is U-compatible, since at the first visit of a state in F(U) during construction of g, the action of that state’s first occurrence on h is copied to g. Thus, $g\in {\textsc {viacomp}}(s,U,\alpha ^*)$.

Notice that the construction of g starts at the first occurrence of t on h, after which the construction of g proceeds uninterrupted by jump backs until x is reached. Indeed, by the choice of t, there are no states of F(U) on h between t and x where such a jump back might occur. This demonstrates obviously that x appears on plan g, that the only element of F(U) appearing on g before x is t, and that t appears exactly once before x. Thus, the threat pair (x, v) for h can also serve as threat pair for plan g, and we may conclude that $g\in {\textsc {admiss}}(t,U,\alpha ^*)$ due to property AD-iv. Now, if g does not satisfy AD-iii, then definition D-iii applies, and we may conclude that D(g, U) consists of the states of $F(U){\setminus } \{t\}$ that appear before x on g. That is, we may conclude $D(g,U) = \varnothing$.

It remains to prove that AD-iii does not apply to g, i.e., that one of the states of F(U) appears more than once on g. By assumption, plan h does not satisfy AD-iii, so we have a state $r\in F(U)$ that appears more than once on h. At least one of the occurrences of r on h comes after the first occurrence of x on h, as all states of F(U) before x are different. It follows that state r appears on plan g, since obviously, all states on h that come after t are eventually visited during the construction of g. If the first appearance of r during the construction of g is upon arrival at the first location of r on h, then r will obviously reappear during the construction of g at a later stage, at the latest upon arrival at the second location of r on h. If the first appearance of r during the construction of g corresponds to the arrival at the second location of r on plan h, then a jump back to the first location on h will take place. Then too state r will reappear during the construction of g, as there will be another arrival at the second location of r on h. $\square$

The result of Lemma 2 does not guarantee that, for a given $t\in S$ and $u\in {\textsc {safestep}}(t,\alpha ^*)$, an appropriate $U\in {\mathcal {U}}(\alpha ^*)$ and $g\in {\textsc {admiss}}(t,U,\alpha ^*)$ exist that we consider ideal for punishment. However, the result is sufficient to prove that, for an arbitrary $\alpha ^*$-plateau F, there is at least one $t\in F$, such that for every $u\in {\textsc {safestep}}(t,\alpha ^*)$, an ideal pair $U\in {\mathcal {U}}(\alpha ^*)$ and $g\in {\textsc {admiss}}(t,U,\alpha ^*)$ for punishment exists.

Let F be an $\alpha ^*$-plateau and let $t\in F$. Say that t is tied to F if, for every $u\in {\textsc {safestep}}(t,\alpha ^*)$, there exists $U\in {\mathcal {U}}(F,\alpha ^*)$ with $U(t) = u$ and a plan $g\in {\textsc {admiss}}(t,U,\alpha ^*)$ with $\phi _{i_t}(g) = \alpha _t^*$ and $D(g,U) = \varnothing$. We define

$$\begin{aligned} {\textsc {tied}}(F) = \{t\in F\mid t \hbox { is tied to } F \}. \end{aligned}$$

Lemma 3

For every $\alpha ^*$-plateau F, the set ${\textsc {tied}}(F)$ is a non-empty subset of F.

Proof

Let F be an $\alpha ^*$-plateau and suppose that ${\textsc {tied}}(F) = \varnothing$. Then, for every $s\in F$, we can choose $u_s \in {\textsc {safestep}}(s,\alpha ^*)$ such that, for all $U\in {\mathcal {U}}(F,\alpha ^*)$ with $U(s) = u_s$, every plan $v\in {\textsc {admiss}}(s,U,\alpha ^*)$ satisfies $D(v,U) \ne \varnothing$ or $\phi _{i_s}(v) > \alpha _s^*$.

Now, define ${\widehat{U}}: F \rightarrow S\cup S^*$ by ${\widehat{U}}(s) = u_s$ for all $s\in F$. Then obviously ${\widehat{U}}\in {\mathcal {U}}(F,\alpha ^*)$. By Lemma 2, we can choose $t\in F$ and $g\in {\textsc {admiss}}(t,{\widehat{U}},\alpha ^*)$ such that $D(g,{\widehat{U}}) = \varnothing$ and $\phi _{i_t}(g) = \alpha _t^*$. On the other hand, by the fact that ${\widehat{U}}(t) = u_t$, every plan $v\in {\textsc {admiss}}(t,{\widehat{U}},\alpha ^*)$ satisfies $D(v,{\widehat{U}}) \ne \varnothing$ or $\phi _{i_t}(v) > \alpha ^*$. Contradiction. $\square$

Let us apply Lemma 3 to an $\alpha ^*$-level L. The fact that ${\textsc {tied}}(L)$ is non-empty shows that there exist states in L, where a deviation can always be retaliated by an ideal punishment plan, that is, a punishment plan which avoids all states of L, until absorption or until a lottery is executed. Let us apply Lemma 3 again, now to the set $L{\setminus } {\textsc {tied}}(L)$ (assuming that this set is non-empty). The lemma then shows that there is a non-empty subset of states of $L{\setminus } {\textsc {tied}}(L)$, where any deviation can be retaliated by a plan that may visit other states of L before absorption or lottery, but only those in ${\textsc {tied}}(L)$. So, after a deviation at a state in ${\textsc {tied}}(L{\setminus } {\textsc {tied}}(L))$, another deviation before absorption or lottery may be possible, but after the second deviation, there will be an ideal punishment plan in place. This suggests that an $\alpha ^*$-level L can be partitioned into a hierarchy of $\alpha ^*$-plateaus, where each plateau is given a rank indicating the maximum number of deviations to go before an ideal punishment plan is in place.

Let L be an $\alpha ^*$-level. We define

$$\begin{aligned} {\textsc {rank}}(1,L) = {\textsc {tied}}(L). \end{aligned}$$

Then, for $k > 1$, we define recursively

$$\begin{aligned} {\textsc {rank}}(k,L) = {\textsc {tied}}(L{\setminus } \cup _{\ell = 1}^{k-1} {\textsc {rank}}(\ell ,L)). \end{aligned}$$

We stop the recursive definitions when $\cup _{1}^{k} {\textsc {rank}}(\ell ,L) = L$. It follows by repeated application of Lemma 3 that the process will indeed terminate, say at iteration K, and that the sets ${\textsc {rank}}(k,L)$ for $k = 1, \ldots , K$ form a partition of L. We define the rank of a state $t\in L$ as the unique index k for which $t\in {\textsc {rank}}(k,L)$ and we denote its rank by ${\textsc {r}}(t)$.

We now demonstrate, for a state $t\in L$ and a deviation $u\in {\textsc {safestep}}(t,\alpha ^*)$, a punishment plan exists that, insofar it visits other states of L before absorption or lottery, it only visits those of rank strictly less than ${\textsc {r}}(t)$. The implication is that at state t, at most ${\textsc {r}}(t)$ deviations are possible (including the one at t) before absorption or a lottery will take place.

Lemma 4

Let L be an $\alpha ^*$-level, let $t\in L$, and let $F = \{x\in L\mid {\textsc {r}}(x) \ge {\textsc {r}}(t)\}$. Then, for all $u\in {\textsc {safestep}}(t,\alpha ^*)$, there exists $U\in {\mathcal {U}}(F,\alpha ^*)$ with $U(t) = u$, together with a plan $g\in {\textsc {admiss}}(t,U,\alpha ^*)$, such that $D(g,U) = \varnothing$ and $\phi _{i_t}(g) = \alpha _t^*$.

Proof

We have ${\textsc {rank}}({\textsc {r}}(t),L) = {\textsc {tied}}(L{\setminus } \cup _{\ell = 1}^{{\textsc {r}}(t) - 1} {\textsc {rank}}(\ell ,L))$ by the recursive definition, and we have $F = L{\setminus } \cup _{\ell = 1}^{{\textsc {r}}(t) - 1} {\textsc {rank}}(\ell ,L)$ by the definition of F. Thus, we have $t\in {\textsc {rank}}({\textsc {r}}(t),L) = {\textsc {tied}}(F)$. Now, let $u\in {\textsc {safestep}}(t,\alpha ^*)$. Then, by definition of the set ${\textsc {tied}}(F)$ and by the fact that t is an element of this set, there exists an $\alpha ^*$-safe combination $U\in {\mathcal {U}}(F,\alpha ^*)$ with $U(t) = u$ and a plan $g\in {\textsc {admiss}}(t,U,\alpha ^*)$ such that $D(g,U) = \varnothing$ and $\phi _{i_t}(g) = \alpha ^*_t$. $\square$

4.3 Description of the joint strategy $\pi _{\varepsilon }$

We will associate with each pair (t, u) with $t\in S$ and $u\in A(t)$ a main plan $g^{tu}$. In some cases, depending on the properties of the main plan $g^{tu}$, we may associate additionally a threat pair $(x^{tu},v^{tu})$ with (t, u). These plans and combinations of a plan and a threat pair will be used in prescription for play as outlined in Sect. 4.1.

Let $t\in S$ and $u\in A(t)$.

• Case 1: $\alpha _t^*\ge 0$. Then we choose $g^{tu} \in {\textsc {viable}}(u,\alpha ^*)$ with $\phi _{i_t}(g^{tu}) \le \alpha _t^*$. This is possible by Lemma 1. We do not choose a threat pair.

• Case 2: $\alpha _t^*< 0$ and $u\notin {\textsc {safestep}}(t,\alpha ^*)$. Then we choose $g^{tu} \in {\textsc {viable}}(u,\alpha ^*)$ with $\phi _{i_t}(g^{tu}) < \alpha _t^*$. This is possible by Lemma 1. We do not choose a threat pair.

• Case 3: $\alpha _t^*< 0$ and $u\in {\textsc {safestep}}(t,\alpha ^*)$. Then let L denote the $\alpha ^*$-level to which t belongs and let $F = \{x\in L\mid {\textsc {r}}(x) \ge {\textsc {r}}(t)\}$. By Lemma 4, there exists $U\in {\mathcal {U}}(F,\alpha ^*)$ with $U(t) = u$ and a plan $g^{tu}\in {\textsc {admiss}}(t,U,\alpha ^*)$ such that $\phi _{i_t}(g^{tu}) = \alpha _t^*$ and such that $D(g^{tu},U) = \varnothing$. If $g^{tu}$ is admissible due to condition AD-iv and not due to AD-i, AD-ii, or AD-iii then we choose additionally a threat pair $(x^{tu},v^{tu})$ for $g^{tu}$.

(The reader may note that the plan $g^{tu}$ starts at t in Case 3, and that it starts at u in Cases 1 and 2. This is inconsequential regarding its use as a prescription. In all three cases, if the prescription becomes current, the active state is already u when that happens.)

In Table 1, we listed the choices of the main plan $g^{tu}$ and the threat pair $(x^{tu},v^{tu})$ for the game of Example 3, for every (t, u).

Table 1 Main plan and threat pair after each possible deviation

With the above choices, we are set to formulate a joint strategy in the way that was already outlined in 4.1, by providing a prescription for play at every stage of the game. Here, we fill in the details.

The prescription for the players, at any stage, is given in two possible forms. A type I prescription consists of a main plan g alone. A type II prescription consists of a main plan g together with a threat pair (x, v). If the prescription is of type I, then the players are supposed to follow the main plan g in its entirety. If the prescription is of type II, then the players are supposed to follow the main plan g until the first occurrence of x on g. The player who controls x is then required to perform a lottery, where it is decided whether plan g is continued or whether a switch to plan v is made. A type II prescription will only be current until the lottery. After the lottery, a prescription of type II automatically reduces to a prescription of type I. It reduces to the main plan g if the lottery player chose continuation of g, or to the threat plan v if the lottery player decided to make the switch to v.

A renewal of the prescription becomes necessary if one of the players chooses an action with zero probability according to the current prescription. If this should happen, the new prescription becomes the one associated with the pair (t, u), where $t\in S$ is the state where the deviation took place, and $u\in A(t)$ is the state that was nominated.

To complete our description of a joint strategy, it remains to provide the specifics of the lotteries that may have to take place. This is where the parameter $\varepsilon$ plays a role. Let us determine an upper bound M on the absolute value of the expected reward to any player in the game G. We define

$$\begin{aligned} q_\varepsilon = \min \left( \frac{1}{2},\frac{\varepsilon }{4M}\right) . \end{aligned}$$

To play according to the joint strategy $\pi _\varepsilon$, a lottery player must always place probability $1-q_\varepsilon$ on continuation of the main plan and probability $q_\varepsilon$ on a switch to the threat plan.

4.4 Main result

Before we prove the claim that $\pi _{\varepsilon }$ is a subgame perfect $\varepsilon$-equilibrium for the game G, let us first establish a property of play when one player deviates while other players stick to $\pi _\epsilon$.

Lemma 5

Let p be an arbitrary path. Assume that play has developed along path p and that $t = {\textsc {last}}(p)$ is the current state. Suppose that player $i = i_t$ chooses an action that has probability 0 according to the prescription dictated by $\pi _{\varepsilon }$ at state t, and suppose that each player $j\in N{\setminus } \{i\}$ is going to use strategy $\pi _{\varepsilon }^j$ after p. Suppose further that player i becomes active again after his deviation at t, say at state s. (Player i may or may not be active between t and s.) Then $\alpha ^*_s \le \alpha ^*_t$. Moreover, if $\alpha ^*_s = \alpha ^*_t < 0$ and if no lottery took place during play from t to s, then ${\textsc {r}}(s) < {\textsc {r}}(t)$.

Proof

Say that player i violates the prescription at t with the action $u\in A(t)$. After this, the new prescription of $\pi _\varepsilon$ is given by the main plan $g^{tu}$, possibly together with the threat pair $(x^{tu}, v^{tu})$.

Let us first assume that all players acted according to prescription from u to s. For the claim $\alpha ^*_s \le \alpha ^*_t$, we distinguish between two cases.

Case 1: Assume that state s does not lie on plan $g^{tu}$. This is only possible if the main plan $g^{tu}$ is associated with a threat pair $(x^{tu},v^{tu})$, if state $x^{tu}$ was active before s, and if the lottery player chose the switch to plan $v^{tu}$. Thus, state s lies on plan $v^{tu}$. We then have $t\notin {\textsc {sat}}(v^{tu},\alpha ^*)$ by the properties of a threat plan (see AD-iv), and $s\in {\textsc {sat}}(v^{tu},\alpha ^*)$, because plan $v^{tu}$ is $\alpha ^*$-viable. It follows that $\alpha ^*_s < \alpha ^*_t$.

Case 2: Assume that state s lies on plan $g^{tu}$. We have $\phi _i(g^{tu}) \le \alpha ^*_t$ by the choice of plan $g^{tu}$. We also have $\phi _i(g^{tu}) \ge \alpha ^*_s$, since s lies on the $\alpha ^*$-viable plan $g^{tu}$. It follows that $\alpha ^*_s \le \alpha ^*_t$.

For the second claim of the lemma, assume that $\alpha ^*_s = \alpha ^*_t <0$ and that no lottery took place during play from t to s. Then $u\in {\textsc {safestep}}(t,\alpha ^*)$, as otherwise a plan $g^{tu}$ with $\phi _i(g^{tu}) < \alpha ^*_t$ would have been chosen, and we would have $\alpha ^*_t > \phi _i(g^{tu}) \ge \alpha ^*_s$.

We have $g^{tu}\in {\textsc {admiss}}(t,U,\alpha ^*)$, where U is an $\alpha ^*$-safe combination with $U(t) = u$ with domain $F = \{x\in L\mid {\textsc {r}}(x) \ge {\textsc {r}}(t)\}$, and where L denotes the $\alpha ^*$-level to which t belongs. Moreover, we have $D(g^{tu},U) = \varnothing$ and $\phi _{i}(g^{tu}) = \alpha _t^*$, by the choice of $g^{tu}$. We see that $g^{tu}$ does not satisfy AD-i as we assume $\alpha ^*_t < 0$. We also see that $g^{tu}$ does not satisfy AD-ii, since $\phi _{i}(g^{tu}) = \alpha _t^*< 0$ implies that $g^{tu}$ is absorbing. Thus, plan $g^{tu}$ satisfies AD-iii or AD-iv.

Notice that s and t must be different states. Indeed, if $g^{tu}$ satisfies AD-iii, this follows from the fact that all states of F on $g^{tu}$ are different. If $g^{tu}$ satisfies AD-iv, then state t is also different from s, by our assumption in the lemma that s comes before the lottery and the fact that, by AD-iv-(a), all states of F on $g^{tu}$ before $x^{tu}$ are different.

We now prove that $s\notin F$. Suppose to the contrary that $s\in F$, and hence that $s\in ({\textsc {S}}(g^{tu}) \cap F) {\setminus } \{t\}$. If $g^{tu}$ satisfies AD-iii, then it follows that $s\in ({\textsc {S}}(g^{tu}) \cap F) {\setminus } \{t\} = D(g^{tu},U)$. If $g^{tu}$ satisfies AD-iv, then it follows that s is a state in $({\textsc {S}}(g^{tu}) \cap F) {\setminus } \{t\}$ that comes before the lottery, hence that $s\in D(g^{tu},U)$. This contradicts that $g^{tu}$ has the property $D(g^{tu},U) = \varnothing$.

We proved that $s\notin F$, hence that $s\in L {\setminus } F = \{x\in L\mid {\textsc {r}}(x) < {\textsc {r}}(t)\}$. Thus, ${\textsc {r}}(s) < {\textsc {r}}(t)$.

Now assume that player i did not only deviate at state t, but that he deviated multiple times before s was reached. Then we apply the result for a single deviation multiple times, for each play between one deviation and the next. This then shows that the lemma also holds for multiple deviations. $\square$

Theorem 1

Joint strategy $\pi _\varepsilon$ is a subgame perfect $\varepsilon$-equilibrium for the game G.

Proof

Let p be an arbitrary path and let $i\in N$. Assume that play has developed along path p, that all players $j\in N{\setminus } \{i\}$ are going to use strategy $\pi ^j_\varepsilon$ after p, and that i is the only player who does not necessarily play according to $\pi _\varepsilon$. Let us denote the strategy of player i by $\sigma ^i$ and the resulting joint strategy by $\sigma$. We will prove that the reward to player i is at most $\varepsilon$ higher in expectation if, after p, play is according to $\sigma$, compared to i’s reward if play is according to $\pi _{\varepsilon }$: $\psi _i^p(\sigma ) \le \psi _i^p(\pi _\varepsilon ) + \varepsilon$.

Let us first provide a lower bound for the expected reward for i if play is according to the joint strategy $\pi _\varepsilon$. For this, we denote by $g^p$ the main plan from the prescription of $\pi _{\varepsilon }$, given to the players, when play has reached the last state of path p. If the prescription of $\pi _\varepsilon$ comes without a threat pair, then plan $g^p$ will be executed with probability 1, and the expected reward for player i equals $\phi _i(g^p)$. If the prescription consists of the main plan $g^p$ together with a threat pair $(x^p,v^p)$, then the expected reward for player i equals $(1-q_\varepsilon ) \phi _i(g^p) + q_\varepsilon \phi _i(v^p)$, as $g^p$ will be executed with probability $1- q_\varepsilon$ and $v^p$ with probability $q_\varepsilon$. In both cases, the number $\phi _i(g^p) - 2 q_\varepsilon M$ is a lower bound for the expected reward for player i under joint strategy $\pi _\varepsilon$, i.e.,

$$\begin{aligned} \psi _i^p(\pi _\varepsilon ) \ge \phi _i(g^p) - 2 q_\varepsilon M. \end{aligned}$$

(1)

Recall that, by definition of $q_\varepsilon$, we have $2 q_\varepsilon M \le \frac{1}{2} \varepsilon$. Thus, it will be sufficient to prove that the expected reward for player i under joint strategy $\sigma$ is bounded from above by $\phi _i(g^p) + 2 q_\varepsilon M$, i.e.,

$$\begin{aligned} \psi _i^p(\sigma ) \le \phi _i(g^p) + 2 q_\varepsilon M. \end{aligned}$$

(2)

We divide the proof in three cases, depending on the number of deviations by player i after p. For each case, we either bound the expected reward of the deviating player i from above by $\phi _i(g^p) + 2 q_\varepsilon M$, or we prove that the case has probability 0 of happening.

Case I: Player i does not deviate during play after history p under $\sigma$ . We distinguish three subcases.

(a): Assume that the prescription is given by the main plan $g^p$ without a threat pair. Then the expected reward to player i is equal to $\phi _i(g^p)$.

(b): Assume that the prescription is given by the main plan $g^p$ together with the threat pair $(x^p,v^p)$, and that player i is the controlling player of state $x^p$. Then it is still true that either plan $g^p$ or plan $v^p$ will be executed, because we assume no deviations. By the properties of a threat pair, we have $x^p\in {\textsc {sat}}(g^p,\alpha ^*)$ and $x^p\notin {\textsc {sat}}(v^p,\alpha ^*)$, hence $\phi _i(v^p) < \phi _i(g^p)$. Therefore, the expected reward for player i in this subcase is bounded from above by $\phi _i(g^p)$.

(c): Assume that the prescription is given by the main plan $g^p$ together with the threat pair $(x^p,v^p)$, and that player i is not the controlling player of state $x^p$. Then, like under strategy $\pi _{\varepsilon }$, plan $g^p$ will be executed with probability $1-q_\varepsilon$ and plan $v^p$ will be executed with probability $q_\varepsilon$. Here, player i may gain if $v^p$ is executed, but in expectation the gain will be small: The expected reward for i under $\sigma$ is $(1-q_\varepsilon ) \phi _i(g^p) + q_\varepsilon \phi _i(v^p) \le \phi _i(g^p) + 2 q_\varepsilon M$.

We see that (2) holds in each of the cases (a), (b), and (c).

Case II: Player i deviates at least once after history p under $\sigma$, but only finitely many times. Let us denote the state where player i makes his first deviation by $t\in S$ and the state where i makes his last deviation by $s\in S$. Let us further denote the chosen action by player i at state s by $u\in A(s)$. After the last deviation by player i, prescribed play according to $\pi _\varepsilon$ is given by the main plan $g^{su}$, possibly together with the threat pair $(x^{su},v^{su})$. Since no further deviations will take place, either plan $g^{su}$ or $v^{su}$ will be executed in its entirety. We have $\phi _{i}(g^{su}) \le \alpha _s^*$ and $\phi _{i}(v^{su}) < \alpha _s^*$ by the choices for $g^{su}$ and $v^{su}$. Therefore, the expected reward for player i is at most $\alpha _s^*$. By Lemma 5, we have $\alpha _s^*\le \alpha _t^*$, so we can bound the expected reward to player i from above by $\alpha _t^*$.

Let h denote the main plan in the prescription of $\pi _{\varepsilon }$ just before player i wants to make his first deviation at t. (We have $h = g^p$ or possibly $h=v^p$ if a lottery takes place before player i makes his first deviation.) Then $\phi _i(h) \ge \alpha ^*_t$, since t lies on h and since h is an $\alpha ^*$-viable plan. Thus, the reward to player i will be at least as good if he just follows the prescription of the main plan with probability 1, which is a strategy where he does not deviate. We have already seen in Case I that his reward is then bounded from above by $\phi _i(g^p) + 2q_\varepsilon M$.

Case III: Player i deviates infinitely many times after history p under $\sigma$ . We will prove that this case occurs with probability 0.

Let t denote the state where player i first deviates. First assume that $\alpha ^*_t \ge 0$. Infinitely many deviations by player i obviously implies infinite play along non-absorbing states. Therefore, the reward to player i will be zero if this happens. Let h denote the main plan in the prescription of $\pi _\varepsilon$ just before player i wants to make his first deviation at t. We have $\phi _i(h) \ge \alpha ^*_t$, since s lies on h and since h is $\alpha ^*$-viable. Thus, the reward to player i will be at least as good if he just follows the prescription of the main plan with probability 1, which is a strategy where he does not deviate. We have seen in Case I that his reward is then bounded from above by $\phi _i(g^p) + 2q_\varepsilon M$.

Now assume that $\alpha _t < 0$. By assuming that player i deviates infinitely many times, it is implied that infinitely many times a state in $S^i$ becomes active. The $\alpha ^*$-value of subsequent states in $S^i$ does not increase, by Lemma 5. Therefore, after a while, the $\alpha ^*$-value of the visited states in $S^i$ becomes a constant, say c. Then we have $c < 0$, since we assume $\alpha _t < 0$. Then, by Lemma 5, the rank of visited states in $S^i$ strictly decreases until a lottery is executed by a player $j\ne i$. Since the rank of a state can decrease only finitely many times, the execution of a lottery will happen infinitely many times. If at the lottery, where the prescription is given by say main plan h together with a threat pair (y, w), player $i_y$ chooses plan w, then player i will not be able to deviate again at a state with the constant $\alpha ^*$-value c. Thus, at every lottery the outcome must be continuation of the main plan. The probability of this happening is 0. $\square$

5 A fixed point theorem

There is one thing left to do, which is to prove that a vector $\alpha \in {{\mathbb {R}}}^S$ with properties F-i and F-ii exists. For this, we introduce, in Sect. 5.1, a non-empty set $\Omega \subseteq {{\mathbb {R}}}^S$ of semi-stable vectors, for which we prove that

$$\begin{aligned} \alpha \in \Omega \hbox { and } U\in {\mathcal {U}}(\alpha ) \Rightarrow {\textsc {admiss}}(t,U,\alpha ) \ne \varnothing \hbox { for all } t\in F(U). \end{aligned}$$

This implies that, for $\alpha \in \Omega$ and $U\in {\mathcal {U}}(\alpha )$, the updated vector $\delta (U,\alpha )$ is finite and satisfies $\delta (U,\alpha ) \ge \alpha$ (see Sect. 5.2). Now, if we could prove additionally that $\delta (U,\alpha ) \in \Omega$, then it would be an easy corollary to establish the existence of a fixed point in $\Omega$. However, as was demonstrated in Kuipers et al. (2016) by means of an example, for certain vectors $\alpha \in \Omega$ and $U\in {\mathcal {U}}(\alpha )$, we have $\delta (U,\alpha ) \notin \Omega$. This motivates the definition of a set $\Omega ^*\subseteq \Omega$ of stable vectors, in Sect. 5.3. The results derived in Sects. 5.1 and 5.2 for vectors of the set $\Omega$ hold for vectors of the set $\Omega ^*$ as well, as $\Omega ^*$ is by definition a subset of $\Omega$. The main effort in Sects. 5.3, 5.4, and 5.5 will therefore go into proving that, for all $\alpha \in \Omega ^*$ and all $U\in {\mathcal {U}}(\alpha )$, the vector $\delta (U,\alpha )$ is an element of $\Omega ^*$. The fixed point theorem is subsequently established in Sect. 5.6.

5.1 Semi-stable vectors and their properties

In this subsection, we present a condition for $\alpha \in {{\mathbb {R}}}^S$, which we call semi-stability. This condition guarantees the existence of a $(t,U,\alpha )$-admissible plan for all $U\in {\mathcal {U}}(\alpha )$ and all $t\in F(U)$, even with the additional property that, for every edge (x, y) of the plan, x is $\alpha$-safe at state y. For $\alpha \in {{\mathbb {R}}}^S$, let us therefore define the edge set

$$\begin{aligned} {\mathbf {A}}(\alpha ) = \{(x, y) \mid x \in S \cup S^*\hbox { and } y \in {\textsc {safestep}}(x,\alpha )\} \end{aligned}$$

and the graph

$$\begin{aligned} {\mathbf {G}}(\alpha ) = (S\cup S^*,{\mathbf {A}}(\alpha )). \end{aligned}$$

In the following, our aim is to impose an appropriate set of properties on the subsets of S, and then deduce the existence of a plan $g\in {\textsc {admiss}}(t,U,\alpha )$ in ${\mathbf {G}}(\alpha )$ for all $U\in {\mathcal {U}}(\alpha )$ and all $t\in F(U)$. For $\alpha \in {{\mathbb {R}}}^S$ and $X\subseteq S$, we define

$$\begin{aligned} \begin{array}{l} {\textsc {pos}}(X,\alpha ) = \{x\in X\mid \alpha _x > 0\}, \\ \\ {\textsc {esc}}(X,\alpha ) = \{x\in X\mid \exists y\in (S\cup S^*){\setminus } X: y\in {\textsc {safestep}}(x,\alpha )\}. \end{array} \end{aligned}$$

We also define

$$\begin{aligned} {\mathcal {C}} = \{X\subseteq S\mid A(x) \cap X \ne \varnothing \hbox { for all } x\in X\}, \end{aligned}$$

and for $\alpha \in {{\mathbb {R}}}^S$, we define

$$\begin{aligned} \begin{array}{l} {\mathcal {P}}(\alpha ) = \{X\subseteq S\mid {\textsc {pos}}(X,\alpha ) \ne \varnothing \}, \\ \\ {\mathcal {E}}(\alpha ) = \{X\subseteq S\mid {\textsc {esc}}(X,\alpha ) \cap {\textsc {pos}}(X,\alpha ) = \varnothing \}, \,\,\hbox {and} \\ \\ {\mathcal {X}}(\alpha ) = {\mathcal {P}}(\alpha ) \cap {\mathcal {E}}(\alpha ) \cap {\mathcal {C}}. \end{array} \end{aligned}$$

Now we provide some intuition for the set ${\mathcal {X}}(\alpha )$. Consider $U\in {\mathcal {U}}(\alpha )$ and $t\in F(U)$. Let us assume the existence of a plan in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {admiss}}(t,U,\alpha )$. To consider the critical case, let us assume that every such plan satisfies AD-iv, but not AD-i, AD-ii, or AD-iii. Choose such a plan, say g. Now, the crucial role is played by the states that are visited on g from the start at t to the point where a state in F(U) is visited for the second time. Let X denote the set of these states. Notice that there is indeed a second occurrence of a state in F(U), since g does not satisfy AD-iii, so X is well-defined. It is not difficult to argue from the assumptions that $X\in {\mathcal {X}}(\alpha )$. So, the set ${\mathcal {X}}(\alpha )$ contains all sets of states where AD-iv is crucial.

Let $X\subseteq S$ and let $e = (x,y)$ be an edge. We say that e is an $\alpha$-exit from X if $x\in X$, $y\in (S\cup S^*){\setminus } X$, and if, for all $v\in {\textsc {viable}}(y,\alpha )$,

$$\begin{aligned} {\textsc {esc}}(X,\alpha ) \subseteq {\textsc {sat}}(v,\alpha ) {\,\,\,\implies \,\,\,}x\in {\textsc {sat}}(v,\alpha ). \end{aligned}$$

(3)

The implication in (3) is trivially satisfied by the edge (x, y) if there exists $z\in {\textsc {esc}}(X,\alpha )$ with $i_z = i_x$ and $\alpha _z \ge \alpha _x$ (and in particular if $x\in {\textsc {esc}}(X,\alpha )$). To filter out such edges, we say that $e = (x,y)$ is a legitimate $\alpha$-exit from X if it is an $\alpha$-exit from X and if $\alpha _z < \alpha _x$ for all $z\in {\textsc {esc}}(X,\alpha )$ with $i_z = i_x$.

Legitimate $\alpha$-exits from X with $X\in {\mathcal {X}}(\alpha )$ are used to derive the existence of a threat pair for admissible plans that happen to visit all states of X. To see how, let (x, y) be a legitimate $\alpha$-exit from X. The fact that (x, y) is legitimate ensures that $y\notin {\textsc {safestep}}(x,\alpha )$, so it ensures the existence of $v\in {\textsc {viable}}(y,\alpha )$ with $x\notin {\textsc {sat}}(v,\alpha )$. From the fact that (x, y) is an $\alpha$-exit from X, we conclude that $t\in {\textsc {esc}}(X,\alpha )$ exists with $t\notin {\textsc {sat}}(v,\alpha )$. We see that (x, v)is a candidate to serve as a threat pair for an admissible plan g that starts at t and visits all states of X.

We say that $\alpha \in {{\mathbb {R}}}^S$ is semi-stable if the following two conditions hold:

• (i) for all $t\in S$, there exists a plan in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {viable}}(t,\alpha )$,

• (ii) for all $X\in {\mathcal {X}}(\alpha )$, there exists a legitimate $\alpha$-exit from X.

We denote the set of semi-stable vectors in ${{\mathbb {R}}}^S$ by $\Omega$. In Lemma 12 we prove that, for all $\alpha \in \Omega$, for all $U\in {\mathcal {U}}(\alpha )$, and for all $t\in F(U)$, a plan in ${\mathbf {G}}(\alpha )$ exists that is element of ${\textsc {admiss}}(t,U,\alpha )$. In Lemma 17 we prove that, for all $\alpha \in \Omega$ and for all $U\in {\mathcal {U}}(\alpha )$, the vector $\delta (U,\alpha )$ satisfies condition (i) of semi-stability.

Example 4

Let us return to Example 3 for an illustration of the definitions. For this example, we have ${\mathcal {C}} = \{ \{1_a,1_b,2\}, \{1_a,1_b,2,3\} \}$. Therefore, for any $\alpha \in {{\mathbb {R}}}^S$, the collection ${\mathcal {X}}(\alpha )$ contains at most two subsets of S. For each stage of the update procedure, we calculated the set ${\mathcal {X}}(\alpha )$ and the $\alpha$-exits, we check that conditions (i) and (ii) are satisfied, and we verify that Lemma 17 holds.

Initialization: We started the update procedure with

$$\begin{aligned} \alpha _{1_a} = -2, \, \alpha _{2} = 1, \, \alpha _{1_b} = -1, \, \alpha _{3} = -1. \end{aligned}$$

• The set ${\mathcal {X}}(\alpha )$: We have ${\mathcal {X}}(\alpha ) = \varnothing$, since $2\in {\textsc {esc}}(X,\alpha ) \cap {\textsc {pos}}(X,\alpha )$ for both $X=\{1_a,1_b,2\}$ and $X= \{1_a,1_b,2,3\}$.

• $\alpha$-exits: We do not check for $\alpha$-exits, since ${\mathcal {X}}(\alpha ) = \varnothing$.

• Condition (i) of semi-stability: For all $t\in S = \{1_a,1_b,2,3\}$, the plan $(t,t^*)$ is an $\alpha$-viable plan in ${\mathbf {G}}(\alpha )$.

• Condition (ii) of semi-stability: The vector $\alpha$ trivially satisfies condition (ii) of semi-stability, since ${\mathcal {X}}(\alpha ) = \varnothing$.

• Admissible plans in ${\mathbf {G}}(\alpha )$: For all $t\in S$ and U defined by $U(t) = t^*$, the plan $(t,t^*)$ is a plan in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {admiss}}(t,U,\alpha )$. For $t=2$ and U defined by $U(2) = 1_b$, the plan $(2,1_b,1_b^ *)$ will do.

Iteration 1: Recall that, after the first iteration, we obtained

$$\begin{aligned} \alpha _{1_a} = -2, \, \alpha _{2} = 2, \, \alpha _{1_b} = -1, \, \alpha _{3} = -1. \end{aligned}$$

• The set ${\mathcal {X}}(\alpha )$: We now have ${\mathcal {X}}(\alpha ) = {\mathcal {C}} = \{ \{1_a,1_b,2\}, \{1_a,1_b,2,3\} \}$.

• $\alpha$-exits: The edge $(2,2^*)$ is a legitimate $\alpha$-exit from both $\{1_a,1_b,2\}$ and $\{1_a,1_b,2,3\}$.

• Condition (i) of semi-stability: For $t\in \{1_a,1_b,3\}$, the plan $(t,t^*)$ is an $\alpha$-viable plan in ${\mathbf {G}}(\alpha )$. For $t=2$, we can take the plan $(2,1_b,1_b^*)$.

• Condition (ii) of semi-stability: Satisfied.

• Admissible plans in ${\mathbf {G}}(\alpha )$: For $t\in \{1_a,1_b,3\}$ and U defined by $U(t) = t^*$, the plan $(t,t^*)$ is a plan in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {admiss}}(t,U,\alpha )$. For $t=1_a$ and U defined by $U(1_a) = 2$, we take $(1_a,2,1_b,1_b^*)$. For $t=2$ and U defined by $U(2) = 1_b$, the plan $(2,1_b,1_b^ *)$ will do.

Iteration 2: After the second iteration 2, we have

$$\begin{aligned} \alpha _{1_a} = -1, \, \alpha _{2} = 2, \, \alpha _{1_b} = -1, \, \alpha _{3} = -1. \end{aligned}$$

• The set ${\mathcal {X}}(\alpha )$: We still have ${\mathcal {X}}(\alpha ) = {\mathcal {C}} = \{ \{1_a,1_b,2\}, \{1_a,1_b,2,3\} \}$.

• $\alpha$-exits: The edge $(2,2^*)$ is still a legitimate $\alpha$-exit from both $\{1_a,1_b,2\}$ and $\{1_a,1_b,2,3\}$. Also the edge $(1_a,1_a^*)$ is now an $\alpha$-exit from both sets. It is not legitimate though, since $1_b\in {\textsc {esc}}(X,\alpha )$, for each $X \in {\mathcal {X}}(\alpha )$.

• Condition (i) of semi-stability: For $t\in \{1_b,3\}$, the plan $(t,t^*)$ is an $\alpha$-viable plan in ${\mathbf {G}}(\alpha )$. For $t=1_a$, we can take the plan $(1_a,2,1_b,1_b^*)$. For $t=2$, we can take the plan $(2,1_b,1_b^*)$.

• Condition (ii) of semi-stability: Satisfied.

• Admissible plans in ${\mathbf {G}}(\alpha )$:

  • For U defined by $U(1_a) = 2$, the plan $(1_a,2,1_b,3,3^*)\in {\textsc {admiss}}(1_a,U,\alpha )$ is in ${\mathbf {G}}(\alpha )$.

  • For U defined by $U(1_b) = 1_b^*$, the plan $(1_b,1_b^*) \in {\textsc {admiss}}(1_b,U,\alpha )$ is in ${\mathbf {G}}(\alpha )$.

  • For U defined by $U(1_b) = 3$, the plan $(1_b,3,3^*) \in {\textsc {admiss}}(1_b,U,\alpha )$ is in ${\mathbf {G}}(\alpha )$.

  • For U defined by $U(1_b) = 1_a$, the plan $(1_b,1_a,2,1_b,1_b^*)\in {\textsc {admiss}}(1_b,U,\alpha )$ is in ${\mathbf {G}}(\alpha )$. This plan is admissible due to AD-iv and is related to the $\alpha$-exit $(2,2^*)$.

  • For U defined by $U(1_a) = 2$ and $U(1_b) = 1_b^*$, the plans $(1_a,2,1_b,1_b^*) \in {\textsc {admiss}}(1_a,U,\alpha )$ and $(1_b,1_b^*)\in {\textsc {admiss}}(1_b,U,\alpha )$ are both in ${\mathbf {G}}(\alpha )$.

  • For U defined by $U(1_a) = 2$ and $U(1_b) = 3$, the plans $(1_a,2,1_b,3,3^*) \in {\textsc {admiss}}(1_a,U,\alpha )$ and $(1_b,3,3^*)\in {\textsc {admiss}}(1_b,U,\alpha )$ are both in ${\mathbf {G}}(\alpha )$.

  • For U defined by $U(1_a) = 2$ and $U(1_b) = 1_a$, the plans $(1_b,1_a,2,1_b,1_b^*) \in {\textsc {admiss}}(1_b,U,\alpha )$ and $(1_a,2,1_b,1_a,2,1_b,1_b^*) \in {\textsc {admiss}}(1_a,U,\alpha )$ are both in ${\mathbf {G}}(\alpha )$. The plans are admissible due to AD-iv and are related to the $\alpha$-exit $(2,2^*)$.

  • For U defined by $U(2) = 1_b$, the plan $(2,1_b,1_b^*) \in {\textsc {admiss}}(2,U,\alpha )$ is in ${\mathbf {G}}(\alpha )$.

  • For U defined by $U(3) = 3^*$, the plan $(3,3^*) \in {\textsc {admiss}}(3,U,\alpha )$ is in ${\mathbf {G}}(\alpha )$.

Iteration 3: After the third iteration, we have

$$\begin{aligned} \alpha _{1_a} = 2, \, \alpha _{2} = 2, \, \alpha _{1_b} = 2, \, \alpha _{3} = -1. \end{aligned}$$

• The set ${\mathcal {X}}(\alpha )$: We still have ${\mathcal {X}}(\alpha ) = {\mathcal {C}}$.

• $\alpha$-exits: The edge $(2,2^*)$ is still a legitimate $\alpha$-exit from $\{1_a,1_b,2\}$. The edge $(2,2^*)$ is now not an $\alpha$-exit from $\{1_a,1_b,2,3\}$. Instead, the edge $(1_b,1_b^*)$ is a legitimate $\alpha$-exit from $\{1_a,1_b,2,3\}$.

• Condition (i) of semi-stability: For $t=1_a$, the plan $(1_a,2,1_b,3,3^*)$ is an $\alpha$-viable plan in ${\mathbf {G}}(\alpha )$. For $t=1_b$, we take the plan $(1_b,3,3^*)$. For $t=2$, we take the $(2,1_b,3,3^*)$. For $t=3$, we take $(3,3^*)$.

• Condition (ii) of semi-stability: Satisfied.

• Admissible plans in ${\mathbf {G}}(\alpha )$:

  • For U defined by $U(1_a) = 2$, the plan $(1_a,2,1_b,3,3^*)\in {\textsc {admiss}}(1_a,U,\alpha )$ is in ${\mathbf {G}}(\alpha )$.

  • For U defined by $U(1_b) = 3$, the plan $(1_b,3,3^*)\in {\textsc {admiss}}(1_b,U,\alpha )$ is in ${\mathbf {G}}(\alpha )$.

  • For U defined by $U(1_b) = 1_a$, the plan $(1_b,1_a,2,1_b,3,3^*)\in {\textsc {admiss}}(1_b,U,\alpha )$ is in ${\mathbf {G}}(\alpha )$. The plan is related to $(2,2^*)$, the $\alpha$-exit from $\{1_a,1_b,2\}$.

  • For U defined by $U(1_a) = 2$ and $U(1_b) = 3$, the plans $(1_a,2,1_b,3,3^*)\in {\textsc {admiss}}(1_a,U,\alpha )$ and $(1_b,3,3^*)\in {\textsc {admiss}}(1_b,U,\alpha )$ are both in ${\mathbf {G}}(\alpha )$.

  • For U defined by $U(1_a) = 2$ and $U(1_b) = 1_a$, the plans $(1_b,1_a,2,3,3^*)\in {\textsc {admiss}}(1_b,U,\alpha )$ and $(1_a,2,1_b,1_a,2,1_b,3,3^*)\in {\textsc {admiss}}(1_a,U,\alpha )$ are both in ${\mathbf {G}}(\alpha )$. The plans are related to the $\alpha$-exit $(2,2^*)$.

  • For U defined by $U(2) = 1_b$, the plan $(2,1_b,3,3^*)\in {\textsc {admiss}}(2,U,\alpha )$ is in ${\mathbf {G}}(\alpha )$.

  • For U defined by $U(3) = 3^*$, the plan $(3,3^*)\in {\textsc {admiss}}(3,U,\alpha )$ is in ${\mathbf {G}}(\alpha )$.

  • For U defined by $U(3) = 1_a$, the plan $(3,1_a,2,1_b,3,3^*)\in {\textsc {admiss}}(3,U,\alpha )$ is in ${\mathbf {G}}(\alpha )$. It is related to $(1_b,1_b^*)$, the $\alpha$-exit from $\{1_a,1_b,2,3\}$.

The set $\Omega$ of semi-stable vectors is non-empty. Indeed, let us define $\rho \in {{\mathbb {R}}}^S$ as the vector where, for all $t\in S$, the number $\rho _t$ is the reward to player $i_t$ when he decides to play his absorbing action $t^*$ at state t. In the following lemma, we show that $\rho \in \Omega$.

Lemma 6

Let $\rho$ be the vector defined by $\rho _t = r_{i_t}(t)$ for all $t\in S$. Then ${\mathcal {X}}(\rho ) = \varnothing$ and $\rho \in \Omega$.

Proof

Notice that, for all $t\in S$, the plan $(t,t^*)$ is a $\rho$-viable plan in ${\mathbf {G}}(\rho )$. This shows immediately that the vector $\rho$ satisfies condition (i) of semi-stability.

We now prove that ${\mathcal {X}}(\rho ) = \varnothing$. Notice that by proving this claim of the lemma, we also prove that condition (ii) of semi-stability holds trivially true for $\rho$, hence it finishes the proof.

Let $X\subseteq S$. If $X\notin {\mathcal {P}}(\rho )$ then trivially $X\notin {\mathcal {P}}(\rho )\cap {\mathcal {E}}(\rho )\cap {\mathcal {C}} = {\mathcal {X}}(\rho )$. If $X\in {\mathcal {P}}(\rho )$, then

$$\begin{aligned} {\textsc {pos}}(X,\rho ) \cap {\textsc {esc}}(X,\rho ) = {\textsc {pos}}(X,\rho ) \ne \varnothing , \end{aligned}$$

where the equality is by the fact that ${\textsc {esc}}(X,\rho ) = X$ and non-emptiness is by the fact that $X\in {\mathcal {P}}(\rho )$. This shows that $X\notin {\mathcal {E}}(\rho )$, hence $X\notin {\mathcal {X}}(\rho ) = {\mathcal {P}}(\rho )\cap {\mathcal {E}}(\rho )\cap {\mathcal {C}}$. This proves that indeed ${\mathcal {X}}(\rho ) = \varnothing$. $\square$

Lemma 7

Let $\alpha \in \Omega$. Then

• (i) for all $t\in S\cup S^*$, we have ${\textsc {safestep}}(t,\alpha ) \ne \varnothing$,

• (ii) for all $X\subseteq S$, we have ${\textsc {esc}}(X,\alpha ) = \varnothing {\,\,\,\implies \,\,\,}{\textsc {pos}}(X,\alpha ) = \varnothing$.

Proof

Proof of (i): For $t^*\in S^*$, we have ${\textsc {safestep}}(t^*,\alpha ) = \{t^*\}$ by convention, and for $t\in S$, the set ${\textsc {safestep}}(t,\alpha )$ is non-empty due to condition (i) of semi-stability.

Proof of (ii): Let $X\subseteq S$ and assume that ${\textsc {esc}}(X,\alpha ) = \varnothing$. Let $t\in X$. We will demonstrate that $\alpha _t\le 0$.

Choose a plan g in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {viable}}(t,\alpha )$, which is possible by condition (i) of semi-stability. Notice that there is no path in ${\mathbf {G}}(\alpha )$ from t to an element of $S^*$, as the existence of such a path would also imply the existence of an edge (x, y) in ${\mathbf {G}}(\alpha )$ with $x\in X$ and $y\in (S\cup S^*) {\setminus } X$, contradicting that ${\textsc {esc}}(X,\alpha ) = \varnothing$. Thus, plan g is a non-absorbing plan. As g is also $\alpha$-viable, it follows that $\alpha _t \le \phi _{i_t}(g) = 0$. $\square$

For any subgraph ${\mathbf {H}}$ of ${\mathbf {G}}$ and a subset X of the vertex set $V({\mathbf {H}})$ of ${\mathbf {H}}$, we say that X is an ergodic set of ${\mathbf {H}}$ if

• (i) for all $x,y\in X$, there exists a path p in ${\mathbf {H}}$ from x to y that has positive length and that lies entirely in X,

• (ii) for all $x\in X$ and $y\in V({\mathbf {H}}){\setminus } X$, there is no path in ${\mathbf {H}}$ from x to y.

The following lemma is an easy result in graph theory. It is stated without proof.

Lemma 8

Let ${\mathbf {H}} = (V({\mathbf {H}}),E(\mathbf{H }))$ be a directed graph, such that for every vertex $x\in V({\mathbf {H}})$, there exists $y\in V({\mathbf {H}})$ with $(x,y)\in E({\mathbf {H}})$. Then, for every $x\in V({\mathbf {H}})$, there is a path from x to an element of an ergodic set of ${\mathbf {H}}$.

Lemma 9

Let $\alpha \in \Omega$. Then

• (i) for all $t\in S$, there exists a path in ${\mathbf {G}}(\alpha )$ from t to an element in an ergodic set of ${\mathbf {G}}(\alpha )$,

• (ii) for all $t^*\in S^*$, the set $\{t^*\}$ is an ergodic set of the graph ${\mathbf {G}}(\alpha )$,

• (iii) an ergodic set of ${\mathbf {G}}(\alpha )$ is either a singleton from the set $S^*$ or a subset of S.

Proof

(i): The graph ${\mathbf {G}}(\alpha )$ satisfies the condition that every vertex has an outgoing edge by Lemma 7-(i). Therefore, Lemma 8 applies.

(ii): The edge $(t^*,t^*)$ is a path of positive length in ${\mathbf {G}}(\alpha )$ from $t^*$ to $t^*$, and there is no other outgoing edge from $t^*$ in ${\mathbf {G}}(\alpha )$. Thus, the set $\{t^*\}$ satisfies the conditions for an ergodic set.

(iii): This result follows from (ii) and the general fact that different ergodic sets in the same graph are always disjoint. $\square$

Lemma 10

Let $\alpha \in \Omega$, let p be a path in ${\mathbf {G}}(\alpha )$, and let g be an $\alpha$-viable plan such that ${\textsc {first}}(g) = {\textsc {last}}(p)$. Then the plan $\langle p,g\rangle$ is $\alpha$-viable.

Proof

Write $p = (z_j)_{j=1}^k$ with $k\ge 1$. Define, for all $j\in \{1,\ldots ,k\}$, the plan $g_j = \langle (z_j,\ldots ,z_k),g\rangle$. We prove by induction on j that all plans $g_j$ with $j\in \{1,\ldots , k\}$ are $\alpha$-viable. Trivially, the plan $g_k = g$ is $\alpha$-viable. Now assume that $g_{j+1}$ with $j<k$ is $\alpha$-viable. Then ${\textsc {S}}(g_j){\setminus } \{z_j\} \subseteq {\textsc {S}}(g_{j+1}) \subseteq {\textsc {sat}}(g_{j+1},\alpha ) = {\textsc {sat}}(g_j,\alpha )$. Thus, to prove that ${\textsc {S}}(g_j) \subseteq {\textsc {sat}}(g_j,\alpha )$, i.e., to prove that $g_j$ is $\alpha$-viable, it suffices to show that $z_j\in {\textsc {sat}}(g_j,\alpha )$.

We have $z_{j+1} \in {\textsc {safestep}}(z_j,\alpha )$, since p is a path in ${\mathbf {G}}(\alpha )$. It follows that $z_j\in {\textsc {sat}}(g_{j+1},\alpha )$, since $g_{j+1}$ is an $\alpha$-viable plan with ${\textsc {first}}(g_{j+1}) = z_{j+1}$. Because ${\textsc {sat}}(g_j,\alpha ) = {\textsc {sat}}(g_{j+1},\alpha )$, we indeed obtain $z_j\in {\textsc {sat}}(g_j,\alpha )$. $\square$

Lemma 11

Let $\alpha \in \Omega$. Then for all $t\in S$ and for all $U\in {\mathcal {U}}(\alpha )$, there exists a plan in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {viacomp}}(t,U,\alpha )$.

Proof

Let $t\in S$ and let $U\in {\mathcal {U}}(\alpha )$. Consider the set $\kappa$ of U-compatible paths in ${\mathbf {G}}(\alpha )$ with ${\textsc {first}}(p) = t$. The set $\kappa$ is non-empty as it contains the path (t) of length 0.

Among the paths in $\kappa$, we choose one, say p, for which the cardinality of the set $F(U) \cap {\textsc {S}}(p)$ is maximal. We denote ${\textsc {last}}(p)$ by s. We also choose r with $r\in {\textsc {safestep}}(s,\alpha )$, which is possible by Lemma 7-(ii). If $s\in F(U)$, then we further specify our choice of r and we choose $r = U(s)$. Note that the choice of r makes the edge (s, r) a U-compatible path. We complete our choices with a plan g in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {viable}}(r,\alpha )$, which is possible, since $\alpha$ satisfies condition (i) of semi-stability.

We will now prove the lemma by showing that the plan $h = \langle p,(s,r),g\rangle$ is a plan in ${\mathbf {G}}(\alpha )$ and an element of ${\textsc {viacomp}}(t,U,\alpha )$. Plan h is obviously a plan in ${\mathbf {G}}(\alpha )$ and it is an element of ${\textsc {viable}}(t,\alpha )$ by Lemma 10. To see that $h = \langle p,(s,r),g\rangle$ is U-compatible, we prove that $F(U) \cap {\textsc {S}}(g) \subseteq {\textsc {S}}(p)$. Suppose that this is not true. Then we choose $u\in F(U)$ that is on plan g and not on path p. If there is more than one candidate, we choose u as close to the beginning of g as possible. Let $g^\prime$ denote the path that follows g from start until the first occurrence of u.

We claim that the path $p^\prime = \langle p, (s,r),g^\prime \rangle$ is U-compatible. To prove the claim, consider a first occurrence of $x\in F(U)$ on $p^\prime$. If $x=u$, then we found the only occurrence of x on $p^\prime$ and it is at the end of $p^\prime$. We then have no condition to check for U-compatibility. If $x\in F(U) {\setminus } \{u\}$, then the first occurrence of x on $p^\prime$ is on path p, and not on $g^\prime$, by the choice of u. If the first occurrence of x is on p, not at the end, then x is followed by U(x), because p is a U-compatible path. If the first occurrence of x is at the end of path p, then $x=s$ and x is followed by $r = U(s) = U(x)$. Thus, $p^\prime$ is indeed U-compatible.

We proved that $p^\prime \in \kappa$. We obviously have $F(U) \cap {\textsc {S}}(p^\prime ) \supseteq F(U) \cap {\textsc {S}}(p)$. The inclusion is strict, because we have $u\in F(U) \cap {\textsc {S}}(p^\prime )$ and $u\notin F(U) \cap {\textsc {S}}(p)$. This contradicts the choice of p as an element of $\kappa$ that maximizes the cardinality of $F(U) \cap {\textsc {S}}(p)$. Thus, $F(U) \cap {\textsc {S}}(g) \subseteq {\textsc {S}}(p)$ as claimed.

We now see that, for any $u\in F(U)$ appearing on $h = \langle p,(s,r),g\rangle$, its first occurrence lies on path p. Then we also see that the first occurrence of u on h is followed by U(u), as required for a U-compatible plan. $\square$

The main result of this section concerns the existence of admissible plans.

Lemma 12

Let $\alpha \in \Omega$. Then for all $U\in {\mathcal {U}}(\alpha )$ and for all $t\in F(U)$, there exists a plan in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {admiss}}(t,U,\alpha )$.

Proof

Let $U\in {\mathcal {U}}(\alpha )$ and let $t\in F(U)$. By Lemma 11, there exists a plan in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {viacomp}}(t,U,\alpha )$. If among these plans one satisfies AD-i, AD-ii or AD-iii, we are done. Assume further that no such plan exists. We will demonstrate that a plan satisfying AD-iv exists.

Let us say that a U-compatible path p is strongly U-compatible if each element of F(U) appears at most once on p. Now define

$$\begin{aligned} X = \{x\in S\cup S^*\mid \hbox { a strongly } U\hbox {-compatible path in } {\mathbf {G}}(\alpha ) \hbox { from } t \hbox { to } x \hbox { exists} \}. \end{aligned}$$

The proof relies on the fact that $X\in {\mathcal {X}}(\alpha )$. This and more will be shown in the following.

I: Proof that $t\in X$ and $X\subseteq S$ : We have $t\in X$, since the path (t) of length 0 is a strongly U-compatible path from t to t.

To see that $X\subseteq S$, suppose to the contrary that $s^*\in X\cap S^*$ exists. Then let p be a strongly U-compatible path in ${\mathbf {G}}(\alpha )$ from t to $s^*$. The plan $g = (s^*, s^*, \ldots )$ is trivially in ${\mathbf {G}}(\alpha )$ and is trivially $\alpha$-viable. Now, the plan $\langle p,g\rangle$ is also trivially in ${\mathbf {G}}(\alpha )$, it is obviously U-compatible, and it is $\alpha$-viable by Lemma 10. Thus, $\langle p,g\rangle \in {\textsc {viacomp}}(t,U,\alpha )$. Now notice that plan $\langle p,g\rangle$ satisfies condition AD-iii, by the fact that p is a strongly U-compatible path and the fact that g contains no elements of F(U). This contradicts our assumption that there is no $(t,U,\alpha )$-admissible plan in ${\mathbf {G}}(\alpha )$ that satisfies AD-iii.

II: Proof that ${\textsc {esc}}(X,\alpha ) \subseteq F(U)$ : The set ${\textsc {esc}}(X,\alpha )$ is indeed defined, by the result of I. Suppose $x\in {\textsc {esc}}(X,\alpha ) {\setminus } F(U)$. We will prove a contradiction by showing that $y\in X$ for all $y\in {\textsc {safestep}}(x,\alpha )$. Let $y\in {\textsc {safestep}}(x,\alpha )$. Choose a strongly U-compatible path p in ${\mathbf {G}}(\alpha )$ from t to x. If y appears on path p, then obviously the part of p that goes from t to y is a strongly U-compatible path in ${\mathbf {G}}(\alpha )$ from t to y. Then it follows immediately that $y\in X$. Assume further that y does not appear on p. It suffices to prove that the path $q = \langle p,(x,y)\rangle$ is a strongly U-compatible path in ${\mathbf {G}}(\alpha )$ from t to y. The path q is a path in ${\mathbf {G}}(\alpha )$, since p is a path in ${\mathbf {G}}(\alpha )$ and the edge (x, y) is also an edge of ${\mathbf {G}}(\alpha )$. The path q is U-compatible, by the fact that p is U-compatible and by the fact that the additional edge (x, y) in q does not originate from a state in F(U). Further, the occurrence of y at the end of q cannot be the second occurrence of a state in F(U), since we assume that y does not appear on p. Thus, each state of F(U) appears at most once on q. So indeed, q is a strongly U-compatible path in ${\mathbf {G}}(\alpha )$ from t to y, and hence $y\in X$. Contradiction.

III: Proof that $U(x)\in {\textsc {safestep}}(x,\alpha ) \cap X$ for all $x\in F(U) \cap X$ : Let $x\in F(U) \cap X$. We have $U(x) \in {\textsc {safestep}}(x,\alpha )$ by definition of an $\alpha$-safe combination, so it remains to prove that $U(x) \in X$. Choose a strongly U-compatible path p in ${\mathbf {G}}(\alpha )$ from t to x. If U(x) appears on path p, then obviously the part of p that goes from t to U(x) is a strongly U-compatible path in ${\mathbf {G}}(\alpha )$ from t to U(x). Then it follows immediately that $U(x)\in {\textsc {safestep}}(x,\alpha ) \cap X$. Assume further that U(x) does not appear on p. It suffices to prove that the path $q = \langle p,(x,U(x))\rangle$ is a strongly U-compatible path in ${\mathbf {G}}(\alpha )$ from t to U(x). The path q is a path in ${\mathbf {G}}(\alpha )$, since p is a path in ${\mathbf {G}}(\alpha )$ and the edge (x, U(x)) is also an edge of ${\mathbf {G}}(\alpha )$. The path q is U-compatible, by the fact that p is U-compatible and by the fact that the (unique) occurrence of $x\in F(U)$ is followed by U(x) on q. Further, the occurrence of U(x) at the end of q cannot be the second occurrence of U(x), since we assume that U(x) does not appear on p. Thus, each state of F(U) appears at most once on q. Therefore, q is a strongly U-compatible path in ${\mathbf {G}}(\alpha )$ from t to U(x). This demonstrates that $U(x)\in X$.

IV: Proof that ${\textsc {safestep}}(x,\alpha ) \cap X \ne \varnothing$ for all $x\in X$ : Let $x\in X$. If $x\in F(U) \cap X$, then the fact that ${\textsc {safestep}}(x,\alpha ) \cap X$ is non-empty follows by the result of III. Assume further that $x\in X{\setminus } F(U)$. Then by the result of II, we have $x\in X{\setminus } {\textsc {esc}}(X,\alpha )$. Hence, ${\textsc {safestep}}(x,\alpha ) \subseteq X$. It follows that ${\textsc {safestep}}(x,\alpha ) \cap X = {\textsc {safestep}}(x,\alpha ) \ne \varnothing$, where non-emptiness is by Lemma 7-(i).

V: Proof that $X\in {\mathcal {C}}$ . For all $x\in X$, we have $A(x) \cap X \supseteq {\textsc {safestep}}(x,\alpha ) \cap X \ne \varnothing$. Here, the inclusion is trivial and non-emptiness is by the result of IV.

VI: Proof that $X\in {\mathcal {P}}(\alpha )$ : Suppose to the contrary that ${\textsc {pos}}(X,\alpha ) = \varnothing$. By the result of III, we have for all $x\in X$, an element $y\in X$ such that (x, y) is an edge of ${\mathbf {G}}(\alpha )$. Moreover, for every $x\in F(U) \cap X$ we may choose $y=U(x)$. Thus, it is possible to construct a non-absorbing U-compatible plan g with ${\textsc {first}}(g) = t$, with ${\textsc {S}}(g) \subseteq X$, and such that every edge of g is in the edge set of ${\mathbf {G}}(\alpha )$. Notice that $g\in {\textsc {viable}}(t,\alpha )$, by the assumption that ${\textsc {pos}}(X,\alpha ) = \varnothing$, and by the fact that a non-absorbing plan gives reward 0 to all players. Then g is a plan in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {admiss}}(t,U,\alpha )$ due to condition AD-ii. This contradicts our earlier assumption that no such plan exists.

VII: Proof that $X\in {\mathcal {E}}(\alpha )$ and that $\alpha _t\le 0$ : By Lemma 11, there is a plan in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {viacomp}}(t,U,\alpha )$. The assumption that this plan does not satisfy AD-i implies that $\alpha _t \le 0$. Then obviously $\alpha _s \le 0$ for all $s\in F(U)$. We may write this as $F(U) \cap {\textsc {pos}}(X,\alpha ) = \varnothing$. We have ${\textsc {esc}}(X,\alpha ) \subseteq F(U)$, by II. Thus, ${\textsc {esc}}(X,\alpha ) \cap {\textsc {pos}}(X,\alpha ) = \varnothing$.

VIII: Proof that, for all $x\in X$ with $i_x = i_t$, we have $\alpha _x \le \alpha _t$ : Suppose to the contrary that $x\in X$ with $i_x = i_t$ and $\alpha _x > \alpha _t$ exists. Then we choose a strongly U-compatible path in ${\mathbf {G}}(\alpha )$ from t to x, which is possible because $x\in X$. We also choose a plan g in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {viacomp}}(x,U,\alpha )$, which is possible by I and Lemma 11. Now, the plan $h = \langle p,g\rangle$ is obviously U-compatible, and it is $\alpha$-viable by Lemma 10. Thus, $h\in {\textsc {viacomp}}(t,U,\alpha )$. Observe that h satisfies condition AD-i of admissibility, due to the fact that x with $i_x = i_t$ and $\alpha _x > \alpha _t$ appears on plan h before an element of F(U) has appeared for the second time. Thus, $h\in {\textsc {admiss}}(t,U,\alpha )$ due to AD-i. Also, by construction, h is a plan in ${\mathbf {G}}(\alpha )$. This contradicts our assumption that there exists no plan in ${\mathbf {G}}(\alpha )$ that is $(t,U,\alpha )$-admissible due to AD-i, AD-ii or AD-iii.

IX: Construction of a plan in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {admiss}}(t,U,\alpha )$ : We have $X\in {\mathcal {X}}(\alpha )$ by V, VI and VII. Then, by condition (ii) of semi-stability, a legitimate $\alpha$-exit from X exists. Choose one and denote it by (x, y).

Since $x\in X$, there exists a strongly U-compatible path p in ${\mathbf {G}}(\alpha )$ from t to x. Also, there exists a plan g in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {viacomp}}(x,U,\alpha )$, by Lemma 11. We claim that $h = \langle p,g\rangle$ is a plan in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {admiss}}(t,U,\alpha )$.

Plan $h = \langle p,g \rangle$ is obviously in ${\mathbf {G}}(\alpha )$. The plan is U-compatible, because both p and g are U-compatible. The plan is $\alpha$-viable by Lemma 10. Thus, $h\in {\textsc {viacomp}}(t,U,\alpha )$. It now suffices to demonstrate that h satisfies AD-iv.

We have $x\in X{\setminus } {\textsc {esc}}(X,\alpha )$ because the $\alpha$-exit (x, y) is legitimate. Therefore $y\notin {\textsc {safestep}}(x,\alpha )$, and hence we can choose an $\alpha$-viable plan v with ${\textsc {first}}(v) = y$ and with $x\notin {\textsc {sat}}(v,\alpha )$. We will prove that (x, v) is a threat pair for h.

(a): The location of the first occurrence of x on h is such that each element of F(U) appears at most once on h before the first occurrence of x. Indeed, this follows from the fact that x lies on the strongly U-compatible path p.

(b): Proof that $i_x \ne i_t$: We have $X\subseteq S$ by I and ${\textsc {pos}}(X,\alpha ) \ne \varnothing$ by VI. Then ${\textsc {esc}}(X,\alpha ) \ne \varnothing$ by Lemma 7-(ii), so we can choose $s\in {\textsc {esc}}(X,\alpha )$. It follows by II that $s\in F(U)$, so we have $s\in F(U) \cap {\textsc {esc}}(X,\alpha )$ and $i_s = i_t$.

Now suppose that $i_x = i_t$. We then have $\alpha _x \le \alpha _t$ by the result of VIII. Since $s\in {\textsc {esc}}(X,\alpha )$ and since $i_x = i_t = i_s$, it follows by the definition of a legitimate $\alpha$-exit that $\alpha _x > \alpha _s$. Thus, $\alpha _s < \alpha _x \le \alpha _t$. This contradicts that $\alpha _s = \alpha _t$, as $s,t\in F(U)$.

(c): Plan v is obviously an $\alpha$-viable plan with ${\textsc {first}}(v) \in A(x)$.

(d): The state following x on plan h, say z, is not equal to state ${\textsc {first}}(v) = y$. Indeed, we have $z\in {\textsc {safestep}}(x,\alpha )$ because h is a plan in ${\mathbf {G}}(\alpha )$, and we have $y\notin {\textsc {safestep}}(x,\alpha )$.

(e): It remains to prove that $t\notin {\textsc {sat}}(v,\alpha )$. Suppose to the contrary that $t\in {\textsc {sat}}(v,\alpha )$. Then $F(U)\subseteq {\textsc {sat}}(v,\alpha )$, since $\alpha _s = \alpha _t$ for all $s\in F(U)$. It subsequently follows that ${\textsc {esc}}(X,\alpha ) \subseteq {\textsc {sat}}(v,\alpha )$, since ${\textsc {esc}}(X,\alpha ) \subseteq F(U)$, by the result of II. By definition of an $\alpha$-exit, we have,

$$\begin{aligned} {\textsc {esc}}(X,\alpha ) \subseteq {\textsc {sat}}(v,\alpha ) {\,\,\,\implies \,\,\,}x\in {\textsc {sat}}(v,\alpha ), \end{aligned}$$

so we conclude that $x\in {\textsc {sat}}(v,\alpha )$. This contradicts our choice of v such that $x\notin {\textsc {sat}}(v,\alpha )$. $\square$

5.2 Properties of an updated semi-stable vector

Let us continue with some fairly immediate consequences of Lemma 12.

Lemma 13

Let $\alpha \in \Omega$ and let $U\in {\mathcal {U}}(\alpha )$. Then $\alpha \le \delta (U,\alpha ) < \infty$.

Proof

Proof that $\delta (U,\alpha ) < \infty$: Choose $t\in F(U)$. The set ${\textsc {admiss}}(t,U,\alpha )$ is non-empty by Lemma 12. Thus, the number

$$\begin{aligned} \beta (t,U,\alpha ) = \min \{\phi _{i_t}(v) \mid v\in {\textsc {admiss}}(t,U,\alpha ) \} \end{aligned}$$

is finite and also the number $\gamma (U,\alpha ) = \min \{\beta (u,U,\alpha ) \mid u\in F(U) \}$ is finite. It follows that every coordinate of $\delta (U,\alpha )$ is finite.

Proof that $\alpha _u \le \delta _u(U,\alpha )$ for all $u\in S$: Choose $t\in F(U)$ such that $\beta (t,U,\alpha ) = \gamma (U,\alpha )$. We have $\alpha _t \le \phi _{i_t}(v)$ for all $v\in {\textsc {viable}}(t,\alpha )$. Then also $\alpha _t \le \phi _{i_t}(v)$ for all $v\in {\textsc {admiss}}(t,U,\alpha )$, since ${\textsc {admiss}}(t,U,\alpha ) \subseteq {\textsc {viable}}(t,\alpha )$. It follows that

$$\begin{aligned} \alpha _t \le \min \{ \phi _{i_t}(v) \mid v\in {\textsc {admiss}}(t,U,\alpha ) \} = \beta (t,U,\alpha ) = \gamma (U,\alpha ). \end{aligned}$$

Now, let $u\in S$. If $u\notin F(U)$, then we trivially have $\alpha _u = \delta _u(U,\alpha )$. If $u\in F(U)$, then $\alpha _u = \alpha _t \le \gamma (U,\alpha ) = \delta _u(U,\alpha )$. $\square$

Lemma 14

Let $\alpha \in \Omega$ and let $U\in {\mathcal {U}}(\alpha )$. Denote the vector $\delta (U,\alpha )$ by $\delta$. Then

• (i) ${\textsc {viable}}(t,\delta )\subseteq {\textsc {viable}}(t,\alpha )$ for all $t\in S$,

• (ii) ${\textsc {safestep}}(t,\delta ) \supseteq {\textsc {safestep}}(t,\alpha )$ for all $t\in S{\setminus } F(U)$,

• (iii) $U(t) \in {\textsc {safestep}}(t,\delta ) \subseteq {\textsc {safestep}}(t,\alpha )$ for all $t\in F(U)$,

• (iv) ${\textsc {esc}}(X,\delta ){\setminus } F(U) \supseteq {\textsc {esc}}(X,\alpha ){\setminus } F(U)$ for all $X\subseteq S$,

• (v) ${\textsc {esc}}(X,\delta ) \supseteq {\textsc {esc}}(X,\alpha )$ for all $X\subseteq S$ with $F(U) \cap X \subseteq {\textsc {esc}}(X,\delta )$.

Proof

Proof of (i): By Lemma 13 we have $\delta \ge \alpha$. Then, if a plan is $\delta$-viable, it is obviously also $\alpha$-viable.

Proof of (ii): Let $t\in S{\setminus } F(U)$ and let $u\in {\textsc {safestep}}(t,\alpha )$. We need to prove that $u\in {\textsc {safestep}}(t,\delta )$. Choose an arbitrary plan $g\in {\textsc {viable}}(u,\delta )$. Then $g\in {\textsc {viable}}(u,\alpha )$ by (i), and since $u\in {\textsc {safestep}}(t,\alpha )$, it follows that $t\in {\textsc {sat}}(g,\alpha )$. Since $t \notin F(U)$, we have $\alpha _t = \delta _t$, hence $t\in {\textsc {sat}}(g,\delta )$. So indeed, we have $u\in {\textsc {safestep}}(t,\delta )$.

Proof of (iii), part 1: Let $t\in F(U)$. To prove that $U(t)\in {\textsc {safestep}}(t,\delta )$, we must show that $t\in {\textsc {sat}}(g,\delta )$ for every $g\in {\textsc {viable}}(U(t),\delta )$. So, let $g\in {\textsc {viable}}(U(t),\delta )$.

Case 1: Assume that $F(U) \cap {\textsc {S}}(g) = \varnothing$. Plan g is $\alpha$-viable by the result of (i). Then plan $h = \langle (t,U(t)),g\rangle$ is $\alpha$-viable by Lemma 10 and the fact that $U(t) \in {\textsc {safestep}}(t,\alpha )$ (by definition of an $\alpha$-safe combination). It follows from the assumption $F(U) \cap {\textsc {S}}(g) = \varnothing$ that plan h is U-compatible and satisfies condition AD-iii. It follows that $h\in {\textsc {admiss}}(t,U,\alpha )$, and hence that $\phi _{i_t}(g) \ge \beta (t,U,\alpha ) \ge \delta _t$. Then indeed, $t\in {\textsc {sat}}(g,\delta )$.

Case 2: Assume that $F(U) \cap {\textsc {S}}(g) \ne \varnothing$, say $s\in F(U)$ is on plan g. Then it follows from the $\delta$-viability of g that $s\in {\textsc {sat}}(g,\delta )$. It subsequently follows that $t\in {\textsc {sat}}(g,\delta )$ from the fact that $\delta _t = \delta _s$.

Proof of (iii), part 2: Let $t\in F(U)$ and let $u\in {\textsc {safestep}}(t,\delta )$. We must show that $t\in {\textsc {sat}}(g,\alpha )$ for every $g\in {\textsc {viable}}(u,\alpha )$. So, let $g\in {\textsc {viable}}(u,\alpha )$.

Case 1: Assume that $F(U) \cap {\textsc {S}}(g) = \varnothing$. Then $g\in {\textsc {viable}}(u,\delta )$, since $\alpha _x = \delta _x$ for all $x\in {\textsc {S}}(g)$. It follows that $t\in {\textsc {sat}}(g,\delta )$ by the fact that $u\in {\textsc {safestep}}(t,\delta )$. Then also $t\in {\textsc {sat}}(g,\alpha )$ as $\alpha _t\le \delta _t$ by Lemma 13.

Case 2: Assume that $F(U) \cap {\textsc {S}}(g) \ne \varnothing$, say that $s\in F(U)$ is on plan g. Then it follows from the $\alpha$-viability of g that $s\in {\textsc {sat}}(g,\alpha )$. It subsequently follows that $t\in {\textsc {sat}}(g,\alpha )$ from the fact that $\alpha _t = \alpha _s$.

Proof of (iv): This follows immediately from (ii).

Proof of (v): Let $X\subseteq S$ be such that $F(U) \cap X \subseteq {\textsc {esc}}(X,\delta )$, and let $x\in {\textsc {esc}}(X,\alpha )$. If $x\in F(U)$, then $x\in {\textsc {esc}}(X,\delta )$ by assumption of (v). If $x\in X{\setminus } F(U)$, then $x\in {\textsc {esc}}(X,\delta )$ by the result of (iv). $\square$

Lemma 15

Let $\alpha \in \Omega$, let $U\in {\mathcal {U}}(\alpha )$, and let $t\in F(U)$. Then ${\textsc {admiss}}(t,U,\alpha ) \subseteq {\textsc {viable}}(t,\delta )$, where $\delta$ denotes the vector $\delta (U,\alpha )$.

Proof

Let $g\in {\textsc {admiss}}(t,U,\alpha )$. By definition of the vector $\delta$, we have $\delta _t \le \phi _{i_t}(g)$. For every state $x\in F(U)$ that appears on g, we then have $\delta _x = \delta _t \le \phi _{i_t}(g) = \phi _{i_x}(g)$. For every state $x\notin F(U)$ on g, we have $\delta _x = \alpha _x \le \phi _{i_x}(g)$, where the inequality follows, since $g\in {\textsc {admiss}}(t,U,\alpha ) \subseteq {\textsc {viable}}(t,\alpha )$. Thus, plan g is indeed $\delta$-viable.

$\square$

Lemma 16

Let $\alpha \in \Omega$, let $U\in {\mathcal {U}}(\alpha )$, and let $t\in F(U)$. If g is an absorbing plan in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {admiss}}(t,U,\alpha )$, then g is a plan in ${\mathbf {G}}(\delta )$, where $\delta$ denotes the vector $\delta (U,\alpha )$.

Proof

Let g be an absorbing plan in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {admiss}}(t,U,\alpha )$ and let (x, y) be an edge of g. We will prove that (x, y) is an edge of ${\mathbf {G}}(\delta )$. We distinguish four different cases.

Case 1: $x\in S^*$. In this case, we have $y=x$ and $(x,y) = (x,x)$ is trivially an edge of ${\mathbf {G}}(\delta )$.

Case 2: $x\in S{\setminus } F(U)$. Notice that $y\in {\textsc {safestep}}(x,\alpha )$, as (x, y) is an edge of ${\mathbf {G}}(\alpha )$. Then $y\in {\textsc {safestep}}(x,\delta )$ by Lemma 14-(ii). Thus, (x, y) is an edge of ${\mathbf {G}}(\delta )$.

Case 3: $x\in F(U)$ and $y=U(x)$. Then $y\in {\textsc {safestep}}(x,\delta )$ by Lemma 14-(iii), and hence (x, y) is an edge of ${\mathbf {G}}(\delta )$.

Case 4: $x\in F(U)$ and $y\ne U(x)$. Let $v\in {\textsc {viable}}(y,\delta )$. We need to prove that $x\in {\textsc {sat}}(v,\delta )$.

Let p denote the path that follows g from start t to the occurrence of x on g that corresponds with the edge (x, y). The path $\langle p,(x,y)\rangle$ is a part of g and is therefore a path in ${\mathbf {G}}(\alpha )$. The plan v is $\alpha$-viable by Lemma 14-(i). Therefore, the plan $h = \langle p,(x,y), v\rangle$ is $\alpha$-viable by Lemma 10.

Notice that the occurrence of x on g that corresponds with the edge (x, y) is not the first occurrence of x on g, as the first occurrence of x is followed by U(x) because $g\in {\textsc {admiss}}(t,U,\alpha )$. The path p contains the occurrence of x that corresponds with the edge (x, y), and hence p has at least two different occurrences of x.

We further distinguish between two subcases.

(4a): Assume that plan v is non-absorbing. Then plan $h = \langle p,(x,y), v\rangle$ is also non-absorbing. Since we demonstrated that h is $\alpha$-viable, it follows that $\alpha _z \le 0$ for all states z that lie on the path p. Now, path p contains a path of positive length from x to x, as it contains the first two occurrences of x on g. Denote this path by q and observe that the plan $(p,q,q,\ldots )$ is a non-absorbing U-compatible and $\alpha$-viable plan. Therefore, $(p,q,q,\ldots )$ is an element of ${\textsc {admiss}}(t,U,\alpha )$ by AD-ii. It follows that $\delta _x = \delta _t \le 0$. It also follows that $x\in {\textsc {sat}}(v,\delta )$.

(4b): Assume that plan v is absorbing. If one of the elements of F(U) is located on v, say s, then it is obvious that $s\in {\textsc {sat}}(v,\delta )$, hence that $x\in {\textsc {sat}}(v,\delta )$. We may therefore assume additionally that there are no elements of F(U) located on v. We claim that $h = \langle p,(x,y),v\rangle$ is an element of ${\textsc {admiss}}(t,U,\alpha )$.

The path $\langle p,(x,y)\rangle$ is part of g and is therefore a U-compatible path. The plan v does not contain any states of F(U), hence the plan $h = \langle p,(x,y),v\rangle$ is U-compatible. Since h is also $\alpha$-viable, we conclude that $h \in {\textsc {viacomp}}(t,U,\alpha )$.

If plan g is $(t,U,\alpha )$-admissible due to AD-i, then $\alpha _t > 0$ or there exists a state z on g with $i_z = i_t$ and $\alpha _z > \alpha _t$, located on g before any state of F(U) appears for the second time on g. In the former case, h is $(t,U,\alpha )$-admissible due to AD-i. In the latter case, notice that state z must be located on p, since there are at least two occurrences of $x\in F(U)$ located on p. We then see that plan h is also $(t,U,\alpha )$-admissible due to AD-i, since h has path p as its initial part.

Plan g is not $(t,U,\alpha )$-admissible due to AD-ii, because g is absorbing. Also, plan g is not $(t,U,\alpha )$-admissible due to AD-iii, because $x\in F(U)$ appears more than once on g.

If plan g is $(t,U,\alpha )$-admissible due to AD-iv, then there exists a threat pair for g, say (z, w), such that state z appears on g before any state of F(U) appears for the second time on g. State z must then be located on p, since there are at least two occurrences of $x\in F(U)$ located on p. We now see that plan h is also $(t,U,\alpha )$-admissible due to AD-iv, since plan h has path p as its initial part.

Thus, we have indeed $h\in {\textsc {admiss}}(t,U,\alpha )$. It follows that $\delta _x = \delta _t \le \phi _{i_t}(h) = \phi _{i_t}(v) = \phi _{i_x}(v)$, and hence $x\in {\textsc {sat}}(v,\delta )$. $\square$

We conclude this section with a proof that the vector $\delta (U,\alpha )$ satisfies condition (i) of semi-stability, for all $\alpha \in \Omega$ and all $U\in {\mathcal {U}}(\alpha )$.

Lemma 17

Let $\alpha \in \Omega$ and let $U\in {\mathcal {U}}(\alpha )$. Then for all $t\in S\cup S^*$, there exists a plan in ${\mathbf {G}}(\delta )$ that is element of ${\textsc {viable}}(t,\delta )$, where $\delta = \delta (U,\alpha )$.

Proof

Let $t\in S\cup S^*$. We distinguish between the cases $t\in F(U)$ and $t\notin F(U)$.

Case 1: Assume that $t\in F(U)$. Then we can choose a plan g in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {admiss}}(t,U,\alpha )$, by Lemma 12. We distinguish three subcases.

(1a): Plan g is absorbing. Then g is the required plan, as it is in ${\mathbf {G}}(\delta )$ by Lemma 16, and it is an element of ${\textsc {viable}}(t,\delta )$ by Lemma 15.

(1b): Plan g is a non-absorbing plan in ${\mathbf {G}}(\delta )$. Then g is the required plan in ${\mathbf {G}}(\delta )$ that is element of ${\textsc {viable}}(t,\delta )$, by Lemma 15.

(1c): Plan g is non-absorbing and not every edge of g is an edge of ${\mathbf {G}}(\delta )$. Then let (x, y) denote the first edge of g that is not of ${\mathbf {G}}(\delta )$.

We have $y\in {\textsc {safestep}}(x,\alpha )$, as (x, y) is an edge of ${\mathbf {G}}(\alpha )$ and we have $y\notin {\textsc {safestep}}(x,\delta )$, as (x, y) is not an edge of ${\mathbf {G}}(\delta )$. It follows that $x\in F(U)$ by Lemma 14-(ii). It also follows that $y\ne U(x)$ by Lemma 14-(iii). The fact that $x\in F(U)$ and $y\ne U(x)$ implies that x appears more that once on g and that the occurrence of x associated with the edge (x, y) is not the first occurrence, because g is a U-compatible plan. Now, let p denote the path with ${\textsc {first}}(p) = t$ and ${\textsc {last}}(p) = x$ that follows g from start to the occurrence of x on g that corresponds with the edge (x, y) of g. Let further q denote the path with ${\textsc {first}}(q) = {\textsc {last}}(q) = x$ that follows g from the first occurrence of x until the second occurrence. Then the plan $g^\prime = \langle p,q,q,\ldots )$ is a non-absorbing plan in ${\mathbf {G}}(\delta )$. Plan $g^\prime$ is also an element of ${\textsc {viable}}(t,\delta )$, since all states on the plan are states that also lie on the non-absorbing plan g. Thus, $g^\prime$ is the required plan.

Case 2: Assume that $t\notin F(U)$. Then we choose a plan g in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {viable}}(t,\alpha )$, which is possible by Lemma 11. If plan g does not contain any elements of F(U), then every edge of g is an edge of ${\mathbf {G}}(\delta )$ by Lemma 14-(ii). In that case, g is the required plan. We assume further that plan g has at least one state of F(U). Then let $x\in F(U)$ denote the first such state on g. Let p denote the path with ${\textsc {first}}(p) = t$ and ${\textsc {last}}(p) = x$ that follows g from start to the first occurrence of x. Notice that p is a path in ${\mathbf {G}}(\delta )$ by Lemma 14-(ii). We now choose a plan h in ${\mathbf {G}}(\delta )$ that is element of ${\textsc {viable}}(x,\delta )$, which is possible by the proof of Case 1. Then the plan $g^\prime = \langle p,h\rangle$ is a plan in ${\mathbf {G}}(\delta )$. The plan $g^\prime$ is also an element of ${\textsc {viable}}(t,\delta )$, which follows by Lemma 10 (applied to $\delta \in {{\mathbb {R}}}^S$). Thus, $g^\prime$ is the required plan. $\square$

We showed that, for all $\alpha \in \Omega$ and all $U\in {\mathcal {U}}(\alpha )$, the vector $\delta (U,\alpha )$ is finite and satisfies $\delta (U,\alpha ) \ge \alpha$ (see Lemma 13). The vector $\delta (U,\alpha )$ also satisfies condition (i) of semi-stability (see Lemma 17). If we could now prove that $\delta (U,\alpha )$ satisfies condition (ii) of semi-stability as well (and hence $\delta (U,\alpha ) \in \Omega$), then it would be an easy corollary to establish the existence of a fixed point in $\Omega$. However, for certain vectors $\alpha \in \Omega$ we have $\delta (U,\alpha ) \notin \Omega$, as was demonstrated in Kuipers et al. (2016) by means of an example. A similar example is given below in Fig. 9.

Example 5

For the game depicted in Fig. 9, one can verify that the vector $\alpha$ defined by

$$\begin{aligned} \alpha _{1} = 2, \, \alpha _{2} = -1, \, \alpha _{3_a} = -1, \, \alpha _{3_b} = -2, \, \alpha _{3_c} = -1, \end{aligned}$$

is an element of $\Omega$, and that $(3_a,3_b)$ is a legitimate $\alpha$-exit from $\{1,2,3_a\} \in {\mathcal {X}}(\alpha )$. Now, an update of state $3_b$ increases the value of $\alpha _{3_b}$ from $-2$ to $-1$. One can check that, for the updated vector $\alpha$, we still have $\{1,2,3_a\} \in {\mathcal {X}}(\alpha )$, but there is no longer a legitimate $\alpha$-exit from $\{1,2,3_a\}$. Thus, the updated $\alpha$ is not in $\Omega$. (If we now continue with an update of state $3_a$, then the value of $\alpha _{3_a}$ increases from $-1$ to 0. Finally, an update of state 2 increases the value of $\alpha _{2}$ from $-1$ to $\infty$, since we then have ${\textsc {admiss}}(2,U,\alpha ) = \varnothing$, where U is defined by $U(2) = 3_a$.) $\square$

Fig. 9

Exits and the update procedure

5.3 Stable vectors and exit sequences

The findings of Example 5 are the motivation for the definition of a set $\Omega ^*$ of stable vectors. The set $\Omega ^*$ is defined by replacing condition (ii) of semi-stability by a stronger condition and by keeping condition (i) the same. The strengthened condition (ii) requires the existence of a certain sequence of edges for every $X\in {\mathcal {X}}(\alpha )$, which contains a legitimate $\alpha$-exit from X, but also contains an edge (x, y) with $\alpha _x > 0$. The set $\Omega ^*$ is thus by definition a subset of $\Omega$. Therefore, all results derived in Sects. 5.1 and 5.2 for vectors of the set $\Omega$ hold for vectors of the set $\Omega ^*$ as well. The main effort in this section will therefore go into proving that, for all $\alpha \in \Omega ^*$ and all $U\in {\mathcal {U}}(\alpha )$, the vector $\delta (U,\alpha )$ satisfies condition (ii) of stability, and that hence $\delta (U,\alpha ) \in \Omega ^*$.

Let $\alpha \in \Omega$, $X\subseteq S$ and $Z\subseteq X$. We say that an edge (x, y) is an $(\alpha ,Z)$-exit from X if $x\in X$ and $y\in (S\cup S^*){\setminus } X$, and if, for all $v\in {\textsc {viable}}(y,\alpha )$,

$$\begin{aligned} Z \cup {\textsc {esc}}(X,\alpha ) \subseteq {\textsc {sat}}(v,\alpha ) {\,\,\,\implies \,\,\,}x\in {\textsc {sat}}(v,\alpha ). \end{aligned}$$

Note that an $(\alpha ,\varnothing )$-exit from X is simply an $\alpha$-exit from X. We say that a sequence of edges $\mathbf {e} = (x_j,y_j)_{j=1}^k$ is an $\alpha$-exit sequence from X if, for all $j\in \{1,\ldots ,k\}$, the edge $(x_j,y_j)$ is an $(\alpha ,\{x_1,\ldots ,x_{j-1}\})$-exit from X. For technical reasons, we allow $k=0$, i.e., the empty sequence will also be called an $\alpha$-exit sequence from X.

We say that an edge $(x,y) = (x_j, y_j)$ in the sequence $\mathbf {e}$ is legitimate if $\alpha _x > \alpha _z$ for every $z\in \{x_1, \ldots , x_{j-1} \} \cup {\textsc {esc}}(X,\alpha )$ with $i_z = i_x$. We say that the sequence $\mathbf {e}$ is legitimate if it is non-empty and if at least one of its edges is legitimate. We say that the edge (x, y) is positive if $x\in {\textsc {pos}}(X,\alpha )$. We say that the sequence $\mathbf {e}$ is positive if it is non-empty and if at least one of its edges is positive.

We now say that a vector $\alpha \in {{\mathbb {R}}}^S$ is stable if

• (i) for all $t\in S$, there exists a plan in ${\mathbf {G}}(\alpha )$ that is element of ${\textsc {viable}}(t,\alpha )$,

• (ii) for all $X\in {\mathcal {X}}(\alpha )$, there exists a positive $\alpha$-exit sequence from X.

We denote the set of stable vectors in ${{\mathbb {R}}}^S$ by $\Omega ^*$.

The motivation for these definitions can be explained by observing what goes ‘wrong’ in Example 5. In that example, we initially have a legitimate $\alpha$-exit (x, y) from a set $X\in {\mathcal {X}}(\alpha )$. After the update, which is an update of a state not in X, the set X is still in ${\mathcal {X}}(\alpha )$, but (x, y) is no longer a legitimate $\alpha$-exit from X, since now x is $\alpha$-safe at y. No other $\alpha$-exit comes in its place, so the updated vector is not in $\Omega$. The issue is solved when we have a positive $\alpha$-exit sequence from $X\in {\mathcal {X}}(\alpha )$. Then it is easy to prove that the sequence contains a legitimate $\alpha$-exit from X (see Lemma 18). After an update of a state not in X, essentially two things can happen. If, after the update, x is $\alpha$-safe at y, where (x, y) is a positive edge in the sequence, then X is no longer an element of ${\mathcal {X}}(\alpha )$, because we then have $x\in {\textsc {esc}}(X,\alpha ) \cap {\textsc {pos}}(X,\alpha )$. Otherwise, if x is not $\alpha$-safe at y after the update, then it is easy to prove that a positive $\alpha$-exit sequence from X remains, where (x, y) will be a positive edge in the sequence.

For an example of a positive $\alpha$-exit sequence, the reader can refer to Example 4. Here, we see that the edge $(2,2^*)$ is a legitimate $\alpha$-exit from the set $\{1_a,1_b,2,3\}$ after the first and the second iteration. This single edge then also forms a positive $\alpha$-exit sequence from $\{1_a,1_b,2,3\}$. After the third iteration, the edge $(1_b,1_b^*)$ is a legitimate $\alpha$-exit from $\{1_a,1_b,2,3\}$, and the sequence $((1_b,1_b^*),(2,2^*))$ is a positive $\alpha$-exit sequence from $\{1_a,1_b,2,3\}$.

The following lemma states some basic facts about exit sequences.

Lemma 18

Let $\alpha \in \Omega$ and let $X\subseteq S$.

• (i) If $\mathbf {e}$ is a non-empty $\alpha$-exit sequence from X, then its first edge is an $\alpha$-exit from X.

• (ii) If $\mathbf {e}$ is an $\alpha$-exit sequence from X, and if (x, y) is an edge of $\mathbf {e}$ that is not legitimate, then the sequence $\overline{\mathbf {e}}$ obtained from $\mathbf {e}$ by deleting the edge (x, y) is also an $\alpha$-exit sequence from X. Moreover, every edge that is legitimate in $\mathbf {e}$ is also legitimate in $\overline{\mathbf {e}}$.

• (iii) If a legitimate $\alpha$-exit sequence from X exists, then a legitimate $\alpha$-exit from X exists.

• (iv) If $\mathbf {e}$ and $\mathbf {f}$ are both $\alpha$-exit sequences from X, then the concatenation of these two sequences, denoted by $(\mathbf {e},\mathbf {f})$, is also an $\alpha$-exit sequence from X.

• (v) If $\mathbf {e}$ is a positive $\alpha$-exit sequence from X and if $X\in {\mathcal {X}}(\alpha )$, then the first positive edge of $\mathbf {e}$ is a legitimate edge.

• (vi) If $\mathbf {e} = (x_j,y_j)_{j=1}^k$ is an $\alpha$-exit sequence from X, and if $(x_h,y_h)$ and $(x_\ell ,y_\ell )$ with $h<\ell$ are such that $i_{x_h} = i_{x_\ell }$ and such that $(x_\ell ,y_\ell )$ is legitimate, then $\alpha _{x_h} < \alpha _{x_\ell }$.

Proof

Proof of (i): If $\mathbf {e}$ is a non-empty $\alpha$-exit sequence from X, then its first edge is by definition an $(\alpha ,\varnothing )$-exit from X. That is also the definition of an $\alpha$-exit from X.

Proof of (ii): Let $\mathbf {e} = (x_j,y_j)_{j=1}^k$ be an $\alpha$-exit sequence from X. Suppose that the edge $(x_h,y_h) = (x,y)$ is not legitimate. Then $z\in \{x_1, \ldots , x_{h-1}\} \cup {\textsc {esc}}(X,\alpha )$ exists with $i_z = i_x$ and $\alpha _z \ge \alpha _x$.

Now let $\overline{\mathbf {e}}$ denote the sequence obtained by deleting the edge (x, y) from $\mathbf {e}$. To see that $\overline{\mathbf {e}}$ is an $\alpha$-exit sequence from X, we need to check that $(x_j,y_j)$ is an $(\alpha , \{x_\ell \mid \ell <j, \ell \ne h\})$-exit from X, for all $j\in \{1,\ldots ,k\}$ with $j\ne h$.

Let $j\in \{1,\ldots ,k\} {\setminus } \{h\}$, let $g\in {\textsc {viable}}(y_j,\alpha )$ and assume that

$$\begin{aligned} \{x_\ell \mid \ell <j, \ell \ne h\} \cup {\textsc {esc}}(X,\alpha ) \subseteq {\textsc {sat}}(g,\alpha ). \end{aligned}$$

(4)

We need to prove that $x_j\in {\textsc {sat}}(g,\alpha )$.

If $j<h$, then assumption (4) is equivalent to

$$\begin{aligned} \{x_1, \ldots , x_{j-1} \} \cup {\textsc {esc}}(X,\alpha ) \subseteq {\textsc {sat}}(g,\alpha ). \end{aligned}$$

In this case $x_j\in {\textsc {sat}}(g,\alpha )$ follows immediately by the fact that $(x_j,y_j)$ is an $(\alpha ,\{x_1, \ldots , x_{j-1} \})$-exit from X.

Now consider the case $j>h$. Then $\{x_1, \ldots , x_{h-1}\} \subseteq \{x_\ell \mid \ell <j, \ell \ne h\}$. Since we have $z\in \{x_1, \ldots , x_{h-1}\} \cup {\textsc {esc}}(X,\alpha )$, it follows that $z\in \{x_\ell \mid \ell <j, \ell \ne h\} \cup {\textsc {esc}}(X,\alpha )$. Assumption (4) therefore implies that $z\in {\textsc {sat}}(g,\alpha )$. Then also $x_h = x\in {\textsc {sat}}(g,\alpha )$, because $\alpha _x \le \alpha _z$ and $i_x = i_z$. This result combined with assumption (4) implies

$$\begin{aligned} \{x_1, \ldots , x_{j-1} \} \cup {\textsc {esc}}(X,\alpha ) \subseteq {\textsc {sat}}(g,\alpha ). \end{aligned}$$

Now $x_j\in {\textsc {sat}}(g,\alpha )$ follows by the fact that $(x_j,y_j)$ is an $(\alpha ,\{x_1, \ldots , x_{j-1} \})$-exit from X.

We proved that $\overline{\mathbf {e}}$ is an $\alpha$-exit sequence from X. Now assume that the edge $(x_\ell ,y_\ell )$ is a legitimate edge of the sequence ${\mathbf {e}}$. We then have $\alpha _{x_\ell } > \alpha _z$ for all $z\in \{x_1, \ldots , x_{\ell - 1} \} \cup {\textsc {esc}}(X,\alpha )$ with $i_z = i_{x_\ell }$. Obviously, $\ell \ne h$, so the edge $(x_\ell ,y_\ell )$ is also an edge of the sequence $\overline{\mathbf {e}}$. Also obviously, $\alpha _{x_\ell } > \alpha _z$ for all $z\in (\{x_1, \ldots , x_{\ell - 1} \} {\setminus } \{x_h\}) \cup {\textsc {esc}}(X,\alpha )$ with $i_z = i_{x_\ell }$. Then $(x_\ell ,y_\ell )$ is a legitimate edge of the sequence $\overline{\mathbf {e}}$.

Proof of (iii): Let $\mathbf {e} = (x_j,y_j)_{j=1}^k$ be a legitimate $\alpha$-exit sequence from X. Let h be the smallest index such that the edge $(x_h,y_h)$ is legitimate. Denote by $\overline{\mathbf {e}}$ the edge-sequence obtained from $\mathbf {e}$ by deleting all edges $(x_j,y_j)$ from $\mathbf {e}$ with $j<h$. Then the edge-sequence $\overline{\mathbf {e}}$ is an $\alpha$-exit sequence from X, by (ii). The first edge of $\overline{\mathbf {e}}$ (i.e., $(x_h,y_h)$) is an $\alpha$-exit from X, by (i). Then obviously, it is a legitimate $\alpha$-exit from X.

Proof of (iv): Let $\mathbf {e} = (x_j,y_j)_{j=1}^k$ and $\mathbf {f} = (x_j,y_j)_{j=k+1}^\ell$ be two $\alpha$-exit sequences from X. To see that $(x_j,y_j)_{j=1}^\ell$ is an $\alpha$-exit sequence from X, let $j\in \{1,\ldots , \ell \}$, and let $v\in {\textsc {viable}}(y_j,\alpha )$ be such that $\{x_1,\ldots , x_{j-1}\} \cup {\textsc {esc}}(X,\alpha ) \subseteq {\textsc {sat}}(v,\alpha )$. We need to prove that $x_j\in {\textsc {sat}}(v,\alpha )$. If $j\le k$, this follows from the fact that $(x_j,y_j)$ is an $(\alpha ,\{x_1,\ldots ,x_{j-1}\})$-exit from X. If $j>k$, this follows from the fact that $(x_j,y_j)$ is an $(\alpha ,\{x_{k+1},\ldots ,x_{j-1}\})$–exit from X.

Proof of (v): Let $(x_j,y_j)_{j=1}^k$ be a positive $\alpha$-exit sequence from X with $X\in {\mathcal {X}}(\alpha )$ and let h denote the smallest index in $\{1,\ldots ,k\}$ with the property $x_h\in {\textsc {pos}}(X,\alpha )$. We need to prove that $(x_h,y_h)$ is a legitimate edge, i.e., we need to show that $\alpha _{x_h} > \alpha _z$ for all $z\in \{x_1,\ldots , x_{h-1} \} \cup {\textsc {esc}}(X,\alpha )$ with $i_z = i_{x_h}$. So let $z\in \{x_1,\ldots , x_{h-1} \} \cup {\textsc {esc}}(X,\alpha )$ with $i_z = i_{x_h}$. If $z\in \{x_1,\ldots , x_{h-1} \}$, then we have $\alpha _z \le 0$, as h is the smallest index with $\alpha _{x_h} > 0$. Then indeed $\alpha _{x_h} > 0 \ge \alpha _z$. Now assume that $z\in {\textsc {esc}}(X,\alpha )$. We then have $\alpha _z \le 0$, because ${\textsc {pos}}(X,\alpha ) \cap {\textsc {esc}}(X,\alpha ) = \varnothing$ by the fact that $X\in {\mathcal {X}}(\alpha ) \subseteq {\mathcal {E}}(\alpha )$. So indeed, $\alpha _{x_h} > 0 \ge \alpha _z$.

Proof of (vi): Let $\mathbf {e} = (x_j,y_j)_{j=1}^k$ be an $\alpha$-exit sequence from X. Suppose $(x_h,y_h)$ and $(x_\ell ,y_\ell )$ with $h<\ell$ are two edges with $i_{x_h} = i_{x_\ell }$ and with $\alpha _{x_h} \ge \alpha _{x_\ell }$. Then the edge $(x_\ell ,y_\ell )$ violates the conditions for a legitimate edge. $\square$

Lemma 19

We have $\rho \in \Omega ^*\subseteq \Omega$, where $\rho$ is the vector defined by $\rho _t = r_{i_t}(t)$ for all $t\in S$.

Proof

First we prove that $\rho \in \Omega ^*$. The vector $\rho$ is semi-stable by Lemma 6; hence, it satisfies condition (i) of semi-stability. Then the vector $\rho$ satisfies condition (i) of stability, as this is the same condition.

We have ${\mathcal {X}}(\rho ) = \varnothing$ by Lemma 6. Thus, the vector $\rho$ trivially satisfies condition (ii) of stability. It follows that $\rho \in \Omega ^*$.

Now we prove that $\Omega ^*\subseteq \Omega$. Let $\alpha \in \Omega ^*$. The vector $\alpha$ trivially satisfies condition (i) of semi-stability. To see that $\alpha$ satisfies condition (ii) of semi-stability, let $X\in {\mathcal {X}}(\alpha )$. Then a positive $\alpha$-exit sequence from X exists, as $\alpha$ satisfies condition (ii) of stability. The sequence is a legitimate $\alpha$-exit sequence from X, by Lemma 18-(v). Then a legitimate $\alpha$-exit from X exists, by Lemma 18-(iii). We see that $\alpha$ indeed satisfies condition (ii) of semi-stability. Thus $\alpha \in \Omega$. $\square$

Until further notice, we fix $\alpha \in \Omega ^*$ and $U\in {\mathcal {U}}(\alpha )$. We further denote the vector $\delta (U,\alpha )$ by $\delta$. The vector $\delta$ then satisfies condition (i) of stability by Lemma 17, as $\alpha \in \Omega ^*\subseteq \Omega$. The work needed to demonstrate that $\delta$ also satisfies condition (ii) of stability, and that hence $\delta \in \Omega ^*$, will be divided over two subsections as follows. We partition the set ${\mathcal {X}}(\delta )$ into two subsets:

$$\begin{aligned} \begin{array}{l} {\mathcal {V}}(U,\delta ) = \{X\in {\mathcal {X}}(\delta )\mid F(U)\cap X = \varnothing \hbox { or } F(U)\cap {\textsc {esc}}(X,\delta ) \ne \varnothing \}, \\ {\mathcal {W}}(U,\delta ) = \{X\in {\mathcal {X}}(\delta )\mid F(U) \cap X \ne \varnothing \hbox { and } F(U) \cap {\textsc {esc}}(X,\delta ) = \varnothing \}. \end{array} \end{aligned}$$

Note that the set ${\mathcal {V}}(U,\delta )$ contains the sets $X\in {\mathcal {X}}(\delta )$ for which the updated states are all outside of X, i.e., $F(U) \cap X = \varnothing$. Recall that this is the situation for which Example 5 demonstrated that the mere existence of a legitimate $\alpha$-exit does not guarantee the existence of a legitimate $\delta$-exit and which motivated us to consider the concept of a positive $\alpha$-exit sequence. The intuition which we developed for that situation translates into a relatively easy proof that a positive $\delta$-exit sequence from X exists, so that condition (ii) of stability indeed holds for these sets X: For every set $X\in {\mathcal {V}}(U,\delta )$, we will show that $X\in {\mathcal {X}}(\alpha )$ (Lemma 20) and that every $\alpha$-exit sequence from X is also a $\delta$-exit sequence from X (Lemma 21). Then, a positive $\delta$-exit sequence from X exists, since we know that a positive $\alpha$-exit sequence from X exists (Lemma 22). This is all handled in Sect. 5.4. We are then left to prove that a positive $\delta$-exit sequence from X exists for the sets $X\in {\mathcal {W}}(U,\delta )$. This turns out to be the difficult case. It is handled in Sect. 5.5.

In Sect. 5.4, we prove that, for all $X\in {\mathcal {V}}(U,\delta )$, there exists a positive $\delta$-exit sequence from X. In Sect. 5.5, we deal with the set ${\mathcal {W}}(U,\delta )$. The two results together then imply that $\delta$ satisfies condition (ii) of stability.

5.4 Existence of $\delta$-exit sequences: the easy case

Recall that $\alpha \in \Omega ^*$, $U\in {\mathcal {U}}(\alpha )$, and $\delta = \delta (U,\alpha )$ are fixed.

Our approach for demonstrating that every X in the set ${\mathcal {V}}(U,\delta )$ has a positive $\delta$-exit sequence from X is straightforward. We first prove that every member of ${\mathcal {V}}(U,\delta )$ is also present in ${\mathcal {X}}(\alpha )$. We then prove that, for all $X\in {\mathcal {V}}(U,\delta )$, every $\alpha$-exit sequence from X is a $\delta$-exit sequence from X.

Lemma 20

We have ${\mathcal {V}}(U,\delta ) \subseteq {\mathcal {X}}(\alpha )$.

Proof

Let $X\in {\mathcal {V}}(U,\delta )$.

We claim that $F(U) \cap {\textsc {pos}}(X,\delta ) = \varnothing$. This is obviously true if $F(U) \cap X = \varnothing$, so assume further that $F(U) \cap X \ne \varnothing$. Then, by definition of the set ${\mathcal {V}}(U,\delta )$, we have $F(U)\cap {\textsc {esc}}(X,\delta ) \ne \varnothing$; hence, we can choose $s\in F(U) \cap {\textsc {esc}}(X,\delta )$. We have ${\textsc {esc}}(X,\delta ) \cap {\textsc {pos}}(X,\delta ) = \varnothing$, by the fact that $X\in {\mathcal {V}}(U,\delta ) \subseteq {\mathcal {E}}(\delta )$. It follows that $s\notin {\textsc {pos}}(X,\delta )$, as we chose $s\in {\textsc {esc}}(X,\delta )$. That is, we have $\delta _s \le 0$. Then obviously, $\delta _t \le 0$ for all $t\in F(U)$ and the claim $F(U) \cap {\textsc {pos}}(X,\delta ) = \varnothing$ follows.

The fact that ${\textsc {pos}}(X,\delta )$ contains no elements of F(U) implies $\alpha _x \le \delta _x \le 0$ for all $x\in X\cap F(U)$. We also have $\alpha _x = \delta _x$ for all $x\in X{\setminus } F(U)$. It follows that ${\textsc {pos}}(X,\alpha ) = {\textsc {pos}}(X,\alpha ) {\setminus } F(U) = {\textsc {pos}}(X,\delta ) {\setminus } F(U) = {\textsc {pos}}(X,\delta )$. The set ${\textsc {pos}}(X,\delta )$ is non-empty by the fact that $X\in {\mathcal {V}}(U,\delta ) \subseteq {\mathcal {P}}(\delta )$. Thus, the set ${\textsc {pos}}(X,\alpha )$ is also non-empty, which demonstrates that $X\in {\mathcal {P}}(\alpha )$.

The fact that ${\textsc {pos}}(X,\alpha ) = {\textsc {pos}}(X,\alpha ) {\setminus } F(U)$ implies that

$$\begin{aligned} {\textsc {esc}}(X,\alpha ) \cap {\textsc {pos}}(X,\alpha ) = ({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \cap {\textsc {pos}}(X,\alpha ). \end{aligned}$$

It follows that

$$\begin{aligned} {\textsc {esc}}(X,\alpha ) \cap {\textsc {pos}}(X,\alpha )= & {} ({\textsc {esc}}(X,\alpha ) {\setminus } F(U) ) \cap {\textsc {pos}}(X,\alpha ) \\\subseteq & {} ({\textsc {esc}}(X,\delta ) {\setminus } F(U) ) \cap {\textsc {pos}}(X,\delta ) \\\subseteq & {} {\textsc {esc}}(X,\delta ) \cap {\textsc {pos}}(X,\delta ) \\= & {} \varnothing . \end{aligned}$$

Here, the first inclusion is by Lemma 14-(iv) and the fact that ${\textsc {pos}}(X,\alpha ) = {\textsc {pos}}(X,\delta )$. The final equality is by the fact that $X\in {\mathcal {V}}(U,\delta ) \subseteq {\mathcal {E}}(\delta )$. This demonstrates that $X\in {\mathcal {E}}(\alpha )$.

We have $X\in {\mathcal {C}}$ by the fact that $X\in {\mathcal {V}}(U,\delta ) \subseteq {\mathcal {C}}$. We proved $X\in {\mathcal {P}}(\alpha ) \cap {\mathcal {E}}(\alpha ) \cap {\mathcal {C}} = {\mathcal {X}}(\alpha )$. $\square$

Lemma 21

Let $X\in {\mathcal {V}}(U,\delta )$. Then every $\alpha$-exit sequence from X is a $\delta$-exit sequence from X.

Proof

Let $\mathbf {e} = (x_j,y_j)^k_{j=1}$ be an $\alpha$-exit sequence from X.

Let $j\in \{1,\ldots ,k\}$, let $g\in {\textsc {viable}}(y_j,\delta )$ and assume that

$$\begin{aligned} \{x_1,\ldots , x_{j-1}\} \cup {\textsc {esc}}(X,\delta ) \subseteq {\textsc {sat}}(g,\delta ). \end{aligned}$$

(5)

We need to prove that $x_j\in {\textsc {sat}}(g,\delta )$. We distinguish between two cases.

Case 1: $x_j\in F(U)$ . Then apparently $F(U)\cap X \ne \varnothing$, so we must have $F(U)\cap {\textsc {esc}}(X,\delta ) \ne \varnothing$, by the fact that $X\in {\mathcal {V}}(U,\delta )$. The fact that a representative of F(U), say t, exists in ${\textsc {esc}}(X,\delta )$ implies that $t\in {\textsc {sat}}(g,\delta )$, by Assumption (5). Then obviously also $x_j\in {\textsc {sat}}(g,\delta )$.

Case 2: $x_j \notin F(U)$ . We claim that

$$\begin{aligned} \{ x_1,\ldots , x_{j-1}\} \cup {\textsc {esc}}(X,\alpha ) \subseteq {\textsc {sat}}(g,\delta ). \end{aligned}$$

(6)

If $F(U) \cap X = \varnothing$, then ${\textsc {esc}}(X,\alpha ) \subseteq {\textsc {esc}}(X,\delta )$ by Lemma 14-(v), hence (6) holds by assumption (5). So assume $F(U) \cap X \ne \varnothing$. Then we have $F(U) \cap {\textsc {esc}}(X,\delta ) \ne \varnothing$, since $X\in {\mathcal {V}}(U,\delta )$. The fact that a representative of F(U) exists in the set ${\textsc {esc}}(X,\delta )$ makes clear that assumption (5) implies

$$\begin{aligned} \{ x_1,\ldots , x_{j-1}\} \cup {\textsc {esc}}(X,\delta ) \cup F(U) \subseteq {\textsc {sat}}(g,\delta ). \end{aligned}$$

(7)

We have ${\textsc {esc}}(X,\alpha ) \subseteq {\textsc {esc}}(X,\delta ) \cup F(U)$ by Lemma 14-(iv). Thus, Eq. (7) implies claim (6). We conclude that

$$\begin{aligned} \{x_1,\ldots , x_{j-1}\} \cup {\textsc {esc}}(X,\alpha ) \subseteq {\textsc {sat}}(g,\delta ) \subseteq {\textsc {sat}}(g,\alpha ), \end{aligned}$$

(8)

where the second inclusion is because we have $\alpha \le \delta$, by Lemma 13. We also have $g\in {\textsc {viable}}(y_j,\delta ) \subseteq {\textsc {viable}}(y_j,\alpha )$, which follows by Lemma 14-(i). Then $x_j \in {\textsc {sat}}(g,\alpha )$ follows by the fact that $(x_j,y_j)$ is an $(\alpha ,\{x_1,\ldots ,x_{j-1}\})$-exit from X. Since $x_j\notin F(U)$, we have $\alpha _{x_j} = \delta _{x_j}$, and we conclude that $x_j \in {\textsc {sat}}(g,\delta )$. $\square$

Lemma 22

Let $X\in {\mathcal {V}}(U,\delta )$. Then there exists a positive $\delta$-exit sequence from X.

Proof

We have $X\in {\mathcal {X}}(\alpha )$ by Lemma 20. Therefore, a positive $\alpha$-exit sequence from X exists. The sequence is a $\delta$-exit sequence from X by Lemma 21. The sequence has an edge (x, y) with $x\in {\textsc {pos}}(X,\alpha )$, because it is a positive $\alpha$-exit sequence. Then $x\in {\textsc {pos}}(X,\delta )$, as $\delta \ge \alpha$. The sequence is thus a positive $\delta$-exit sequence from X. $\square$

5.5 The existence of $\delta$-exit sequences: the difficult case

5.5.1 Introduction

Recall that $\alpha \in \Omega ^*$, $U\in {\mathcal {U}}(\alpha )$ and $\delta = \delta (U,\alpha )$ are still fixed. We still need to prove that a positive $\delta$-exit sequence from X exists for every X in the set ${\mathcal {W}}(U,\delta )$.

In this subsection, we will sometimes make use of additional notation. If $\mathbf {e} = (x_j,y_j)_{j=1}^k$ is a sequence of edges, we will use the notation $x_j(\mathbf {e}) = x_j$ and $y_j(\mathbf {e}) = y_j$ for $j\in \{1,\ldots ,k\}$. We will also use the notation $\mathbf {x}(\mathbf {e}) = \{x_1, \ldots , x_k\}$, $\mathbf {y}(\mathbf {e}) = \{y_1, \ldots , y_k\}$, and $k(\mathbf {e}) = k$. We will further use the notation for the empty sequence.

Let us give a quick overview of the approach we will take. We first define, for any $X\subseteq S$, a certain type of $\alpha$-exit sequences from X, called $\alpha$-exit sequences from X disregarding U, that do not involve the members of F(U) in any way. We order such sequences $\mathbf {e}$ by the cardinality of the set $\mathbf {x}(\mathbf {e})$, and we are interested in the sequences that are maximal in this sense.

It easily follows from the definition that every $\alpha$-exit sequence from X disregarding U is a $\delta$-exit sequence from X (see Lemma 24). Therefore, if an $\alpha$-exit sequence from X disregarding U exists that is positive, then we are done. Otherwise, a maximal sequence $\mathbf {e}^{*}$ can serve as the initial part of a positive $\delta$-exit sequence from X. The crucial result regarding the sequence $\mathbf {e}^{*}$, when non-positive, can be found in Lemma 32. It will imply that, for certain $t\in F(U) \cap X$ and for every $v\in {\textsc {viable}}(s,\delta )$ with $s\in A(t)$, we have

$$\begin{aligned} \{t\} \cup \mathbf {x}(\mathbf {e}^{*}) \cup {\textsc {esc}}(X,\delta ) \subseteq {\textsc {sat}}(v,\alpha ) {\,\,\,\implies \,\,\,}t\in {\textsc {sat}}(v,\delta ). \end{aligned}$$

The result hints at the fact that an edge of the form (t, s) with $t\in F(U)$ can be placed directly after the sequence $\mathbf {e}^{*}$ to make a $\delta$-exit sequence from X. The details of how to extend the sequence $\mathbf {e}^{*}$ with an appropriate edge (t, s) are handled in Lemma 33. The final details are then handled in Lemma 34: If $\delta _t > 0$, then $(\mathbf {e}^{*},(t,s))$ makes a positive $\delta$-sequence from X, and we are done. If $\delta _t \le 0$, then we show that $X\in {\mathcal {X}}(\alpha )$, so we can choose a positive $\alpha$-exit sequence from X, say $\mathbf {f}$. We then show that $(\mathbf {e}^{*},(t,s),\mathbf {f})$ is a positive $\delta$-exit sequence from X.

5.5.2 Exit sequences disregarding U, $\alpha$-caps and $\alpha$-hats

Let $X\subseteq S$, and let $\mathbf {e} = (x_j,y_j)_{j=1}^k$ be an $\alpha$-exit sequence from X. We will say that $\mathbf {e}$ is an $\alpha$-exit sequence from X disregarding U if $F(U) \cap \{x_1,\ldots ,x_k\} =\varnothing$, and if for all $j\in \{1,\ldots ,k\}$ and all $v\in {\textsc {viable}}(y_j,\alpha )$,

$$\begin{aligned} \{x_1,\ldots ,x_{j-1}\} \cup ({\textsc {esc}}(X,\alpha ) {\setminus } F(U) ) \subseteq {\textsc {sat}}(v,\alpha ) {\,\,\,\implies \,\,\,}x_j\in {\textsc {sat}}(v,\alpha ). \end{aligned}$$

Later in Sect. 5.5 we will need the fact that Lemma 18-(iv) is also valid for exit sequences from X disregarding U. This is expressed in the following lemma.

Lemma 23

Let $X\subseteq S$. If $\mathbf {e}$ and $\mathbf {f}$ are both $\alpha$-exit sequences from X disregarding U, then the concatenation of these two sequences, denoted by $(\mathbf {e},\mathbf {f})$, is also an $\alpha$-exit sequence from X disregarding U.

Proof

Let $\mathbf {e} = (x_j,y_j)_{j=1}^k$ and $\mathbf {f} = (x_j,y_j)_{j=k+1}^\ell$ be two $\alpha$-exit sequences from X disregarding U. We need to prove that $(x_j,y_j)_{j=1}^\ell$ is an $\alpha$-exit sequence from X disregarding U. To see this, let $j\in \{1,\ldots , \ell \}$ and let $v\in {\textsc {viable}}(y_j,\alpha )$ be such that $\{x_1,\ldots , x_{j-1}\} \cup ({\textsc {esc}}(X,\alpha ){\setminus } F(U)) \subseteq {\textsc {sat}}(v,\alpha )$. If $j\le k$, we use the fact that $\mathbf {e}$ is an $\alpha$-exit sequence from X disregarding U to deduce that $x_j\in {\textsc {sat}}(v,\alpha )$. If $j>k$, we use the fact that $\mathbf {f}$ is an $\alpha$-exit sequence from X disregarding U to deduce that $x_j\in {\textsc {sat}}(v,\alpha )$. $\square$

Later in Sect. 5.5 we will also use the fact that the claim of Lemma 21 is valid for exit sequences from X disregarding U and does not need the restriction $X\in {\mathcal {V}}(U,\delta )$. This is expressed in the following lemma.

Lemma 24

Let $X\subseteq S$. Then every $\alpha$-exit sequence from X disregarding U is a $\delta$-exit sequence from X.

Proof

Let $\mathbf {e} = (x_j,y_j)_{j=1}^k$ be an $\alpha$-exit sequence from X disregarding U. We will prove that $\mathbf {e}$ is a $\delta$-exit sequence from X.

The requirement $x_j \in X$ and $y_j \in (S\cup S^*) {\setminus } X$ for all $j\in \{1,\ldots ,k\}$ is obviously satisfied, because $\mathbf {e}$ is an $\alpha$-exit sequence from X. Now, let $j\in \{1,\ldots ,k\}$, let $g\in {\textsc {viable}}(y_j, \delta )$ and assume that

$$\begin{aligned} \{x_1,\ldots , x_{j-1}\} \cup {\textsc {esc}}(X,\delta ) \subseteq {\textsc {sat}}(g,\delta ). \end{aligned}$$

It remains to prove that $x_j \in {\textsc {sat}}(g,\delta )$.

We have ${\textsc {esc}}(X,\alpha ) {\setminus } F(U) \subseteq {\textsc {esc}}(X,\delta )$ by Lemma 14-(iv). Therefore,

$$\begin{aligned} \{x_1,\ldots , x_{j-1}\} \cup ({\textsc {esc}}(X,\alpha ){\setminus } F(U))\subseteq & {} \{x_1,\ldots , x_{j-1}\} \cup {\textsc {esc}}(X,\delta ) \\\subseteq & {} {\textsc {sat}}(g,\delta ) \\\subseteq & {} {\textsc {sat}}(g,\alpha ). \end{aligned}$$

Then $x_j \in {\textsc {sat}}(g,\alpha )$ follows by the fact that $\mathbf {e}$ is an $\alpha$-exit sequence from X disregarding U. We also have $x_j\notin F(U)$ by the fact that $F(U) \cap \{x_1, \ldots , x_k\} = \varnothing$. The combination $x_j \in {\textsc {sat}}(g,\alpha )$ and $x_j\notin F(U)$ implies that $x_j \in {\textsc {sat}}(g,\delta )$. $\square$

Let $X\subseteq S$ and let $\mathbf {e} = (x_j,y_j)_{j=1}^k$ be an $\alpha$-exit sequence from X disregarding U. It will be convenient to have terminology for an edge $e=(x,y)$ such that the concatenation $(\mathbf {e},e)$ fails to be an $\alpha$-exit sequence from X disregarding U only because $y\in X$. We say that (x, y) is an $\alpha$-cap for $(X,\mathbf {e},U)$ if $x\in X{\setminus } F(U)$ and $y\in X$, and if we have for all $v\in {\textsc {viable}}(y,\alpha )$ that

$$\begin{aligned} \{x_1,\ldots , x_k\} \cup ({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \subseteq {\textsc {sat}}(v,\alpha ) {\,\,\,\implies \,\,\,}x\in {\textsc {sat}}(v,\alpha ). \end{aligned}$$

We denote by ${\textsc {cap}}(X,\mathbf {e},U,\alpha )$ the set of $\alpha$-caps for $(X,\mathbf {e},U)$. Note that the set is well-defined, as is an $\alpha$-exit sequence from X disregarding U.

We also introduce terminology for an edge $e=(x,y)$ expressing that $(\mathbf {e},e)$ fails to be an $\alpha$-exit sequence from X disregarding U for the following two reasons: $x\in F(U) \cap X$ and $y\in X$. We say that (x, y) is an $\alpha$-hat for $(X,\mathbf {e},U)$ if $x\in F(U)\cap X$ and $y\in X$, and if we have for all $v\in {\textsc {viable}}(y,\alpha )$ that

$$\begin{aligned} \{x_1,\ldots , x_k\} \cup ({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \subseteq {\textsc {sat}}(v,\alpha ) {\,\,\,\implies \,\,\,}x\in {\textsc {sat}}(v,\alpha ). \end{aligned}$$

We denote by ${\textsc {hat}}(X,\mathbf {e},U,\alpha )$ the set of $\alpha$-hats for $(X,\mathbf {e},U)$. Note that the set is well-defined, as is an $\alpha$-exit sequence from X disregarding U.

Lemma 25

Let $X\in {\mathcal {C}}$. Then

• (i) for every $x \in X{\setminus } ({\textsc {esc}}(X,\alpha ) \cup F(U))$, we have

  

• (ii) for every $x \in {\textsc {esc}}(X,\alpha ) {\setminus } F(U)$, we have

  

• (iii) for every $x \in F(U) \cap X$, we have

  

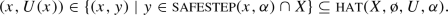
Proof

let $X\in {\mathcal {C}}$.

Proof of (i): Let $x \in X{\setminus } ({\textsc {esc}}(X,\alpha )\cup F(U))$. Non-emptiness of the set $\{(x,y)\mid y\in {\textsc {safestep}}(x,\alpha )\}$ follows directly from Lemma 7-(i).

Choose $y\in {\textsc {safestep}}(x,\alpha )$. We need to show that . The requirement $x\in X{\setminus } F(U)$ follows trivially from the fact that $x \in X{\setminus } ({\textsc {esc}}(X,\alpha )\cup F(U))$. We have ${\textsc {safestep}}(x,\alpha ) \subseteq X$, since $x\in X{\setminus } {\textsc {esc}}(X,\alpha )$. Therefore, the requirement $y\in X$ also follows. Now, let $v\in {\textsc {viable}}(y,\alpha )$ and assume that ${\textsc {esc}}(X,\alpha ) {\setminus } F(U) \subseteq {\textsc {sat}}(v,\alpha )$. The fact that $y\in {\textsc {safestep}}(x,\alpha )$ implies that $x\in {\textsc {sat}}(v,\alpha )$, which is the final requirement. So indeed, . (Here, the assumption ${\textsc {esc}}(X,\alpha ) {\setminus } F(U) \subseteq {\textsc {sat}}(v,\alpha )$ and the fact that $X\in {\mathcal {C}}$ were not needed.)

Proof of (ii): Let $x \in {\textsc {esc}}(X,\alpha ) {\setminus } F(U)$.

Non-emptiness of the set $\{(x,y)\mid y\in A(x) \cap X\}$ follows from the fact that $x\in X$ and $X\in {\mathcal {C}}$.

Choose $y \in A(x) \cap X$. We need to show that . We trivially have $x\in X{\setminus } F(U)$ and $y\in X$. Now, let $v\in {\textsc {viable}}(y,\alpha )$ and assume that ${\textsc {esc}}(X,\alpha ) {\setminus } F(U) \subseteq {\textsc {sat}}(v,\alpha )$. Here, the fact that $x\in {\textsc {sat}}(v,\alpha )$ follows trivially from the assumption that ${\textsc {esc}}(X,\alpha ) {\setminus } F(U) \subseteq {\textsc {sat}}(v,\alpha )$.

Proof of (iii): Let $x \in F(U)\cap X$.

We have $U(x) \in {\textsc {safestep}}(x,\delta ) \subseteq {\textsc {safestep}}(x,\alpha )$ by Lemma 14-(iii). We have ${\textsc {safestep}}(x,\delta ) \subseteq X$ by the fact that $X\in {\mathcal {W}}(U,\delta )$. These results together show that $U(x) \in {\textsc {safestep}}(x,\delta ) \subseteq {\textsc {safestep}}(x,\alpha ) \cap X$. Hence, $(x,U(x)) \in \{(x,y)\mid y \in {\textsc {safestep}}(x,\alpha ) \cap X \}$.

Let $y\in {\textsc {safestep}}(x,\alpha ) \cap X$. We need to show that . The requirements $x\in F(U) \cap X$ and $y\in X$ are trivially satisfied. Now, let $v\in {\textsc {viable}}(y,\alpha )$ and assume that ${\textsc {esc}}(X,\alpha ) {\setminus } F(U) \subseteq {\textsc {sat}}(v,\alpha )$. The fact that $y\in {\textsc {safestep}}(x,\alpha )$ implies $x\in {\textsc {sat}}(v,\alpha )$ (the assumption ${\textsc {esc}}(X,\alpha ) {\setminus } F(U) \subseteq {\textsc {sat}}(v,\alpha )$ is not needed). This shows that . $\square$

Lemma 26

Let $X\subseteq S$ and let $\mathbf {e}$ and $\mathbf {f}$ be two $\alpha$-exit sequences from X disregarding U. If $\mathbf {x}(\mathbf {e}) \subseteq \mathbf {x}(\mathbf {f})$, then ${\textsc {cap}}(X,\mathbf {e},U,\alpha ) \subseteq {\textsc {cap}}(X,\mathbf {f},U,\alpha )$ and ${\textsc {hat}}(X,\mathbf {e},U,\alpha ) \subseteq {\textsc {hat}}(X,\mathbf {f},U,\alpha )$.

Proof

Assume that $\mathbf {x}(\mathbf {e}) \subseteq \mathbf {x}(\mathbf {f})$. Let $(x,y)\in {\textsc {cap}}(X,\mathbf {e},U,\alpha )$. We will verify that $(x,y)\in {\textsc {cap}}(X,\mathbf {f},U,\alpha )$. Trivially, we have $x\in X{\setminus } F(U)$ and $y\in X$. Now, let $v\in {\textsc {viable}}(y,\alpha )$ and assume that

$$\begin{aligned} \mathbf {x}(\mathbf {f}) \cup ({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \subseteq {\textsc {sat}}(v,\alpha ). \end{aligned}$$

Then also

$$\begin{aligned} \mathbf {x}(\mathbf {e}) \cup ({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \subseteq {\textsc {sat}}(v,\alpha ), \end{aligned}$$

as $\mathbf {x}(\mathbf {e}) \subseteq \mathbf {x}(\mathbf {f})$. Now, $x\in {\textsc {sat}}(v,\alpha )$ follows from the fact that $\mathbf {e}$ is an $\alpha$-exit sequence from X disregarding U and the fact that (x, y) is an $\alpha$-cap for $(X,\mathbf {e},U)$. Then $(x,y) \in {\textsc {cap}}(X,\mathbf {f}, U, \alpha )$. The proof that ${\textsc {hat}}(X,\mathbf {e},U,\alpha ) \subseteq {\textsc {hat}}(X,\mathbf {f},U,\alpha )$ is entirely similar. $\square$

5.5.3 Graphs of $\alpha$-caps and $\alpha$-hats and their basic properties

For $X\in {\mathcal {W}}(U,\delta )$ and an $\alpha$-exit sequence $\mathbf {e}$ from X disregarding U, let us define ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$ as the graph with vertex set X and edge set

$$\begin{aligned} {\textsc {cap}}(X,\mathbf {e}, U,\alpha )\cup {\textsc {hat}}(X,\mathbf {e}, U,\alpha ). \end{aligned}$$

Notice that ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$ is indeed a graph with vertex set X, i.e., for every edge (x, y) of ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$, both x and y are trivially elements of X, by definition of the sets ${\textsc {cap}}(X,\mathbf {e}, U,\alpha )$ and ${\textsc {hat}}(X,\mathbf {e}, U,\alpha )$.

Let us also define ${\mathbf {H}}(X,\mathbf {e}, U,\alpha )$ as the graph with vertex set X and edge set

$$\begin{aligned} {\textsc {cap}}(X,\mathbf {e}, U,\alpha )\cup \{(t,U(t))\mid t\in F(U)\cap X \}. \end{aligned}$$

The graph ${\mathbf {H}}(X,\mathbf {e}, U,\alpha )$ is a subgraph of ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$, since for every $t\in F(U) \cap X$, we have $(t,U(t)) \in {\textsc {hat}}(X,\mathbf {e}, U,\alpha )$, by Lemmas 25-(iii) and 26.

Both graphs ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$ and ${\mathbf {H}}(X,\mathbf {e}, U,\alpha )$ have the property that, for every $x\in X$, there exists $y\in X$ such that (x, y) is an edge of the graph. Indeed, for $x\in X{\setminus } ({\textsc {esc}}(X,\alpha ) \cup F(U))$, this is implied by Lemma 25-(i) and Lemma 26; for $x\in {\textsc {esc}}(X,\alpha ) {\setminus } F(U)$, this is implied by Lemma 25-(ii) and Lemma 26; for $x\in F(U)$, it is implied by Lemmas 25-(iii) and 26. As we now see that Lemma 8 applies to these two graphs, we can freely use the fact that they have ergodic sets, and that there is a path in these graphs from each $x\in X$ to one of their ergodic sets.

Lemma 27

Let $X\in {\mathcal {W}}(U,\delta )$, let $\mathbf {e}$ be an $\alpha$-exit sequence from X disregarding U. Then

• (i) for every ergodic set Z of the graph ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$, we have

  $$\begin{aligned} {\textsc {esc}}(Z,\alpha ) = Z \cap {\textsc {esc}}(X,\alpha ); \end{aligned}$$

• (ii) for every ergodic set Y of the graph ${\mathbf {H}}(X,\mathbf {e}, U,\alpha )$, we have

  $$\begin{aligned} {\textsc {esc}}(Y,\alpha ){\setminus } F(U) = (Y \cap {\textsc {esc}}(X,\alpha )) {\setminus } F(U). \end{aligned}$$

Proof

Let $X\in {\mathcal {W}}(U,\delta )$ and let $\mathbf {e}$ be an $\alpha$-exit sequence from X disregarding U.

Proof of (i): Let Z be an ergodic set of ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$. We will prove first that ${\textsc {esc}}(Z,\alpha ) \subseteq Z \cap {\textsc {esc}}(X,\alpha )$. Let $x\in {\textsc {esc}}(Z,\alpha )$. We trivially have $x\in Z$, so it remains to prove that $x\in {\textsc {esc}}(X,\alpha )$.

Suppose that $x\in X{\setminus } ({\textsc {esc}}(X,\alpha ) \cup F(U))$. Then for all $y\in {\textsc {safestep}}(x,\alpha )$, the edge (x, y) is an edge of the graph ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$, by Lemmas 25-(i) and 26. Therefore, every such $y\in {\textsc {safestep}}(x,\alpha )$ is also an element of Z, by the properties of an ergodic set. It follows that ${\textsc {safestep}}(x,\alpha ) \subseteq Z$. This implies $x\notin {\textsc {esc}}(Z,\alpha )$. Contradiction.

We can already conclude that $x\in {\textsc {esc}}(X,\alpha ) \cup F(U)$. Suppose that $x\in F(U)$. Then for every $y\in {\textsc {safestep}}(x,\alpha )\cap X$, the edge (x, y) is an edge of the graph ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$, by Lemmas 25-(iii) and 26. Therefore, every such y is also an element of Z by the properties of an ergodic set. It follows that ${\textsc {safestep}}(x,\alpha )\cap X \subseteq Z$. Now, we choose $y\in {\textsc {safestep}}(x,\alpha )$ with $y\in (S\cup S^*) {\setminus } Z$, which is possible by the fact that $x\in {\textsc {esc}}(Z,\alpha )$. We must have $y\notin X$ then. The fact that $y\in {\textsc {safestep}}(x,\alpha )$ and $y\notin X$ demonstrates that $x\in {\textsc {esc}}(X,\alpha )$.

We will now prove that ${\textsc {esc}}(Z,\alpha ) \supseteq Z \cap {\textsc {esc}}(X,\alpha )$. Let $x\in Z \cap {\textsc {esc}}(X,\alpha )$. Since $x\in {\textsc {esc}}(X,\alpha )$, we can choose $y\in (S\cup S^*) {\setminus } X$ with $y\in {\textsc {safestep}}(x,\alpha )$. Then obviously $y\in (S\cup S^*) {\setminus } Z$, since $Z\subseteq X$. It follows that $x\in {\textsc {esc}}(Z,\alpha )$.

Proof of (ii): Let Y be an ergodic set of ${\mathbf {H}}(X,\mathbf {e}, U,\alpha )$.

We will prove first that ${\textsc {esc}}(Y,\alpha ) {\setminus } F(U) \subseteq (Y \cap {\textsc {esc}}(X,\alpha )) {\setminus } F(U)$. Let $x\in {\textsc {esc}}(Y,\alpha ) {\setminus } F(U)$. We trivially have $x\in Y{\setminus } F(U)$, so it remains to prove that $x\in {\textsc {esc}}(X,\alpha )$.

Suppose that $x\in X{\setminus } {\textsc {esc}}(X,\alpha )$. Then $x\in X{\setminus } ({\textsc {esc}}(X,\alpha ) \cup F(U))$, since $x\notin F(U)$. It follows that, for every $y\in {\textsc {safestep}}(x,\alpha )$, the edge (x, y) is an edge of the graph ${\mathbf {H}}(X,\mathbf {e}, U,\alpha )$, by Lemmas 25-(i) and 26. Therefore, every $y\in {\textsc {safestep}}(x,\alpha )$ is also an element of Y, by the properties of an ergodic set. It follows that ${\textsc {safestep}}(x,\alpha ) \subseteq Y$. This implies $x\notin {\textsc {esc}}(Y,\alpha )$. Contradiction. Thus, $x\in {\textsc {esc}}(X,\alpha )$.

We will now prove that ${\textsc {esc}}(Y,\alpha ) {\setminus } F(U) \supseteq (Y \cap {\textsc {esc}}(X,\alpha )) {\setminus } F(U)$. Let $x\in (Y \cap {\textsc {esc}}(X,\alpha )) {\setminus } F(U)$. Since $x\in {\textsc {esc}}(X,\alpha )$, we can choose $y\in {\textsc {safestep}}(x,\alpha )$ with $y\in (S\cup S^*) {\setminus } X$. Then obviously $y\in (S\cup S^*) {\setminus } Y$, as $Y\subseteq X$. Thus, $x\in {\textsc {esc}}(Y,\alpha )$. Also obviously, $x\notin F(U)$. It follows that $x\in {\textsc {esc}}(Y,\alpha ) {\setminus } F(U)$. $\square$

Let $X\in {\mathcal {W}}(U,\delta )$. The $\alpha$-exit sequences $\mathbf {e}$ from X disregarding U can be ordered by the cardinality of the set $\mathbf {x}(\mathbf {e})$. Let us say that an $\alpha$-exit sequence $\mathbf {e}$ from X disregarding U is maximal if $|\mathbf {x}(\mathbf {e})|$ is maximal among the $\alpha$-exit sequences from X disregarding U.

Lemma 28

Let $X\in {\mathcal {W}}(U,\delta )$, let $\mathbf {e}$ be an $\alpha$-exit sequence from X disregarding U and let $\mathbf {e}^*$ be a maximal $\alpha$-exit sequence from X disregarding U. Then $\mathbf {x}(\mathbf {e}) \subseteq \mathbf {x}(\mathbf {e}^*)$.

Proof

Define $\mathbf {f} = (\mathbf {e}^*,\mathbf {e})$. The sequence $\mathbf {f}$ is an $\alpha$-exit sequence from X disregarding U by Lemma 23. Then $|\mathbf {x}(\mathbf {e}^*)| \ge |\mathbf {x}(\mathbf {f})| = |\mathbf {x}(\mathbf {e}^*) \cup \mathbf {x}(\mathbf {e})|$, where the inequality is by the maximality of $\mathbf {e}^*$. This is only possible if $\mathbf {x}(\mathbf {e}) \subseteq \mathbf {x}(\mathbf {e}^*)$. $\square$

Lemma 29

Let $X\in {\mathcal {W}}(U,\delta )$ and let $\mathbf {e}^{*}$ be a maximal $\alpha$-exit sequence from X disregarding U. Let Y be an ergodic set of the graph ${\mathbf {H}}(X,\mathbf {e}^{*},U,\alpha )$ and let $\mathbf {f}$ be an $\alpha$-exit sequence from Y disregarding U. Then $\mathbf {f}$ is an $\alpha$-exit sequence from X disregarding U.

Proof

We trivially have $\mathbf {x}(\mathbf {f}) \subseteq Y \subseteq X$ and $\mathbf {x}(\mathbf {f}) \cap F(U) = \varnothing$. The sequence $\mathbf {f}$ thus trivially satisfies these two requirements for an $\alpha$-exit sequence from X disregarding U.

We next prove the requirement $\mathbf {y}(\mathbf {f}) \subseteq (S\cup S^*) {\setminus } X$ by contradiction. Therefore, suppose that $\mathbf {y}(\mathbf {f}) \not \subseteq (S\cup S^*) {\setminus } X$. Then there must be $h\in \{1,\ldots , k(\mathbf {f})\}$ with the property $y_h(\mathbf {f}) \in X$. Choose the smallest h with this property. Let $f = (x_h(\mathbf {f}), y_h(\mathbf {f}))$ and let $\widetilde{\mathbf {f}} = (x_j(\mathbf {f}),y_j(\mathbf {f}))_{j=1}^{h-1}$.

In our proof, we need the fact that $\widetilde{\mathbf {f}}$ is an $\alpha$-exit sequence from X disregarding U. The requirements $\mathbf {x}(\widetilde{\mathbf {f}}) \subseteq X$ and $\mathbf {x}(\widetilde{\mathbf {f}}) \cap F(U) = \varnothing$ are trivially satisfied and the requirement $\mathbf {y}(\widetilde{\mathbf {f}}) \subseteq (S\cup S^*){\setminus } X$ is satisfied due to the choice of h. Let $j\in \{1,\ldots , h-1\}$, let $v\in {\textsc {viable}}(y_j(\widetilde{\mathbf {f}}),\alpha )$, and assume that

$$\begin{aligned} \{x_1(\widetilde{\mathbf {f}}),\ldots ,x_{j-1}(\widetilde{\mathbf {f}})\} \cup ({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \subseteq {\textsc {sat}}(v,\alpha ). \end{aligned}$$

We need to prove that $x_j(\widetilde{\mathbf {f}})\in {\textsc {sat}}(v,\alpha )$. We have ${\textsc {esc}}(Y,\alpha ) {\setminus } F(U) \subseteq {\textsc {esc}}(X,\alpha ) {\setminus } F(U)$, which follows by Lemma 27-(ii) applied to $\mathbf {e}^*$. Also, we trivially have $\{x_1(\widetilde{\mathbf {f}}),\ldots ,x_{j-1}(\widetilde{\mathbf {f}})\} = \{x_1(\mathbf {f}),\ldots ,x_{j-1}(\mathbf {f})\}$. Thus, it follows that

$$\begin{aligned} \{x_1(\mathbf {f}),\ldots ,x_{j-1}(\mathbf {f})\} \cup ({\textsc {esc}}(Y,\alpha ) {\setminus } F(U)) \subseteq {\textsc {sat}}(v,\alpha ). \end{aligned}$$

Then $x_j(\widetilde{\mathbf {f}}) = x_j(\mathbf {f}) \in {\textsc {sat}}(v,\alpha )$, as $\mathbf {f}$ is an $\alpha$-exit sequence from Y disregarding U. This proves our claim that $\widetilde{\mathbf {f}}$ is an $\alpha$-exit sequence from X disregarding U.

Now observe that the edge f is an $\alpha$-cap for $(X,\widetilde{\mathbf {f}},U)$. Indeed, the only reason why $(\widetilde{\mathbf {f}},f)$ fails to be an $\alpha$-exit sequence from X disregarding U is because ${\textsc {last}}(f) = y_h(\mathbf {f}) \in X$. We have $\mathbf {x}(\widetilde{\mathbf {f}}) \subseteq \mathbf {x}(\mathbf {e}^{*})$ by Lemma 28, as $\widetilde{\mathbf {f}}$ is an $\alpha$-exit sequence from X disregarding U and $\mathbf {e}^{*}$ is a maximal one. It subsequently follows by Lemma 26 that $f\in {\textsc {cap}}(X,\widetilde{\mathbf {f}},U,\alpha ) \subseteq {\textsc {cap}}(X,\mathbf {e}^{*},U,\alpha )$. Thus, f is an edge of the graph ${\mathbf {H}}(X,\mathbf {e}^{*},U,\alpha )$. Now, since ${\textsc {first}}(f) = x_h(\mathbf {f}) \in Y$ and since Y is an ergodic set of ${\mathbf {H}}(X,\mathbf {e}^{*},U,\alpha )$, it follows that ${\textsc {last}}(f) = y_h(\mathbf {f}) \in Y$. This contradicts that $\mathbf {f}$ is an $\alpha$-exit sequence from Y.

We proved that $\mathbf {y}(\mathbf {f}) \subseteq (S\cup S^*) {\setminus } X$, as required. To prove that $\mathbf {f}$ satisfies the remaining requirement for an $\alpha$-exit sequence from X disregarding U, let $j\in \{1,\ldots , k(\mathbf {f})\}$, let $v\in {\textsc {viable}}(y_j(\mathbf {f}),\alpha )$, and assume that

$$\begin{aligned} \{x_1(\mathbf {f}),\ldots ,x_{j-1}(\mathbf {f})\} \cup ({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \subseteq {\textsc {sat}}(v,\alpha ). \end{aligned}$$

We need to prove that $x_j(\mathbf {f})\in {\textsc {sat}}(v,\alpha )$. By Lemma 27-(ii), we have ${\textsc {esc}}(Y,\alpha ) {\setminus } F(U) \subseteq {\textsc {esc}}(X,\alpha ) {\setminus } F(U)$. Therefore,

$$\begin{aligned} \{x_1(\mathbf {f}),\ldots ,x_{j-1}(\mathbf {f})\} \cup ({\textsc {esc}}(Y,\alpha ) {\setminus } F(U)) \subseteq {\textsc {sat}}(v,\alpha ). \end{aligned}$$

Then $x_j(\mathbf {f})\in {\textsc {sat}}(v,\alpha )$ immediately follows, as $\mathbf {f}$ is an $\alpha$-exit sequence from Y disregarding U. $\square$

Lemma 30

Let $X\in {\mathcal {W}}(U,\delta )$ and let $\mathbf {e}$ be an $\alpha$-exit sequence from X disregarding U. Let further p be a path in ${\mathbf {K}}(X,\mathbf {e},U,\alpha )$ and let $g\in {\textsc {viable}}({\textsc {last}}(p),\alpha )$. Then

$$\begin{aligned} \mathbf {x}(\mathbf {e}) \cup ({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \subseteq {\textsc {sat}}(g,\alpha ) {\,\,\,\implies \,\,\,}\langle p,g\rangle \in {\textsc {viable}}({\textsc {first}}(p),\alpha ). \end{aligned}$$

Proof

Assume that

$$\begin{aligned} \mathbf {x}(\mathbf {e}) \cup ({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \subseteq {\textsc {sat}}(g,\alpha ) \end{aligned}$$

(9)

We write $p = (z_j)_{j=1}^k$, and we define $g_k = g$ and $g_j = \langle (z_j,\ldots ,z_k),g\rangle$ for $j\in \{1,\ldots ,k-1\}$.

Trivially, $g_k = g$ is $\alpha$-viable. Now, let $j\in \{1,\ldots , k-1\}$ and assume that $g_{j+1}$ is $\alpha$-viable. We will prove that $g_j = \langle (z_j, z_{j+1}), g_{j+1}\rangle$ is $\alpha$-viable. For this, it is sufficient to demonstrate that $z_j\in {\textsc {sat}}(g_{j+1},\alpha )$. We trivially have $z_j = {\textsc {first}}(g_j) \in X$, so we can distinguish between the cases $z_j\in X\cap F(U)$ and $z_j\in X{\setminus } F(U)$.

Case 1: $z_j\in X\cap F(U)$. In this case, the edge $(z_j,z_{j+1})$ is an $\alpha$-hat for $(X, \mathbf {e}, U)$. In assumption (9), we may replace the term ${\textsc {sat}}(g,\alpha )$ by the term ${\textsc {sat}}(g_{j+1})$, as $\phi (g_{j+1}) = \phi (g)$. We then see that $z_j\in {\textsc {sat}}(g_{j+1},\alpha )$ follows by definition of an $\alpha$-hat.

Case 2: $z_j\in X{\setminus } F(U)$. In this case, the edge $(z_j,z_{j+1})$ is an $\alpha$-cap for $(X, \mathbf {e}, U)$. We replace the term ${\textsc {sat}}(g,\alpha )$ by the term ${\textsc {sat}}(g_{j+1})$ in assumption (9), and we see that $z_j\in {\textsc {sat}}(g_{j+1},\alpha )$ follows by definition of an $\alpha$-cap.

We proved by induction that $g_j$ is $\alpha$-viable for all $j\in \{1,\ldots ,k\}$. In particular, $\langle p,g\rangle = g_1$ is $\alpha$-viable. $\square$

Lemma 31

Let $X\in {\mathcal {W}}(U,\delta )$ and let $\mathbf {e}$ be an $\alpha$-exit sequence from X disregarding U such that $\mathbf {x}(\mathbf {e}) \cap {\textsc {pos}}(X,\alpha ) = \varnothing$. Then there exist ergodic sets Y of ${\mathbf {H}}(X,\mathbf {e}, U,\alpha )$ and Z of ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$ such that ${\textsc {pos}}(Y,\alpha ) \ne \varnothing$ and $Y\subseteq Z$.

Proof

We first prove that an ergodic set Z of the graph ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$ exists with ${\textsc {pos}}(Z,\alpha ) \ne \varnothing$. Suppose therefore that ${\textsc {pos}}(Z,\alpha ) = \varnothing$ for every ergodic set Z of ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$. We will demonstrate that ${\textsc {pos}}(X,\delta ) = \varnothing$, contradicting that $X\in {\mathcal {W}}(U,\delta ) \subseteq {\mathcal {X}}(\delta ) \subseteq {\mathcal {P}}(\delta )$. Let $x\in X$.

Assume that x is element of an ergodic set Z of ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$. Then obviously $\alpha _x\le 0$, by the assumption that ${\textsc {pos}}(Z,\alpha ) = \varnothing$. If $x\in X{\setminus } F(U)$, then it follows immediately that $\delta _x = \alpha _x \le 0$. We assume further that $x\in F(U)$. The edge (z, U(z)) is an edge of ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$ for all $z\in F(U)\cap X$, since it is by definition an edge of ${\mathbf {H}}(X,\mathbf {e}, U,\alpha )$ and ${\mathbf {H}}(X,\mathbf {e}, U,\alpha )$ is a subgraph of ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$. Therefore, we have $U(z)\in Z$ for all $z\in F(U) \cap Z$, by the properties of an ergodic set of ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$. Thus, it is possible to choose a non-absorbing and U-compatible plan g with ${\textsc {S}}(g) \subseteq Z$ and with ${\textsc {first}}(g) = x$. Plan g is $\alpha$-viable by the assumption that ${\textsc {pos}}(Z,\alpha ) = \varnothing$. Then $g\in {\textsc {admiss}}(x,U,\alpha )$ as it satisfies AD-ii. It follows that $\delta _x \le \phi _{i_x}(g) = 0$.

Now assume that x is not an element of any ergodic set of ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$. Then we can choose an ergodic set Z of ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$ and a U-compatible path p in ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$ from x to an element of Z. We can also choose a non-absorbing and U-compatible plan g with ${\textsc {S}}(g) \subseteq Z$ and ${\textsc {first}}(g) = {\textsc {last}}(p)$. Plan g is $\alpha$-viable by the assumption ${\textsc {pos}}(Z,\alpha ) = \varnothing$. We claim that plan $\langle p,g\rangle$ is also $\alpha$-viable.

We have $\mathbf {x}(\mathbf {e}) \subseteq {\textsc {sat}}(g,\alpha )$ by the assumption $\mathbf {x}(\mathbf {e}) \cap {\textsc {pos}}(X,\alpha ) = \varnothing$. We also have

$$\begin{aligned} ({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \cap {\textsc {pos}}(X,\alpha ) \subseteq {\textsc {esc}}(X,\delta ) \cap {\textsc {pos}}(X,\delta ) = \varnothing . \end{aligned}$$

Here, the inclusion follows by ${\textsc {esc}}(X,\alpha ) {\setminus } F(U) \subseteq {\textsc {esc}}(X,\delta )$ [Lemma 14-(iv)] and ${\textsc {pos}}(X,\alpha ) \subseteq {\textsc {pos}}(X,\delta )$, and the equality follows by the fact that $X\in {\mathcal {W}}(U,\delta ) \subseteq {\mathcal {X}}(\delta ) \subseteq {\mathcal {E}}(\delta )$. Thus, ${\textsc {esc}}(X,\alpha ) {\setminus } F(U) \subseteq {\textsc {sat}}(g,\alpha )$. The claim that $\langle p,g\rangle$ is $\alpha$-viable now follows by Lemma 30.

The fact that $\langle p,g\rangle$ is $\alpha$-viable proves that $\alpha _x \le \phi _{i_x}(\langle p,g\rangle ) = 0$. If $x\in X{\setminus } F(U)$, we have $\delta _x = \alpha _x \le 0$. If $x\in F(U)$, then notice that $\langle p,g\rangle \in {\textsc {admiss}}(x,U,\alpha )$ due to AD-ii, which proves that $\delta _x \le \phi _{i_x}(\langle p,g\rangle ) = 0$. Then indeed ${\textsc {pos}}(X,\delta ) = \varnothing$. Contradiction.

So, we can choose an ergodic set Z of ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$ with ${\textsc {pos}}(Z,\alpha ) \ne \varnothing$. Now suppose that ${\textsc {pos}}(Y,\alpha ) = \varnothing$ for every ergodic set Y of ${\mathbf {H}}(X,\mathbf {e}, U,\alpha )$ that is a subset of Z. We will derive a contradiction by demonstrating that ${\textsc {pos}}(Z,\alpha ) = \varnothing$. Let $x\in Z$.

Assume that x is element of an ergodic set Y of ${\mathbf {H}}(X,\mathbf {e}, U,\alpha )$. Then $\alpha _x\le 0$, since we suppose that ${\textsc {pos}}(Y,\alpha ) = \varnothing$.

Now assume that x is not an element of any ergodic set of ${\mathbf {H}}(X,\mathbf {e}, U,\alpha )$. Then we choose an ergodic set Y of ${\mathbf {H}}(X,\mathbf {e}, U,\alpha )$ and a path p in ${\mathbf {H}}(X,\mathbf {e}, U,\alpha )$ from x to an element of Y. Notice that path p lies entirely inside Z, because p is a path in the graph ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$, the path starts in Z, and Z is an ergodic set of ${\mathbf {K}}(X,\mathbf {e}, U,\alpha )$. Similarly, we can argue that $Y\subseteq Z$. We can also choose a non-absorbing plan g with ${\textsc {S}}(g) \subseteq Y$ and with ${\textsc {first}}(g) = {\textsc {last}}(p)$. Plan g is $\alpha$-viable by the assumption ${\textsc {pos}}(Y,\alpha ) = \varnothing$. We claim that plan $\langle p,g\rangle$ is also $\alpha$-viable.

We have $\mathbf {x}(\mathbf {e}) \subseteq {\textsc {sat}}(g,\alpha )$ by the assumption $\mathbf {x}(\mathbf {e}) \cap {\textsc {pos}}(X,\alpha ) = \varnothing$. We also have

$$\begin{aligned} ({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \cap {\textsc {pos}}(X,\alpha ) \subseteq {\textsc {esc}}(X,\delta ) \cap {\textsc {pos}}(X,\delta ) = \varnothing . \end{aligned}$$

Here, the inclusion follows by ${\textsc {esc}}(X,\alpha ) {\setminus } F(U) \subseteq {\textsc {esc}}(X,\delta )$ [Lemma 14-(iv)] and ${\textsc {pos}}(X,\alpha ) \subseteq {\textsc {pos}}(X,\delta )$, and the equality follows by the fact that $X\in {\mathcal {W}}(U,\delta ) \subseteq {\mathcal {X}}(\delta ) \subseteq {\mathcal {E}}(\delta )$. Thus, ${\textsc {esc}}(X,\alpha ) {\setminus } F(U) \subseteq {\textsc {sat}}(g,\alpha )$. The claim that $\langle p,g\rangle$ is $\alpha$-viable now follows by Lemma 30.

The fact that $\langle p,g\rangle$ is $\alpha$-viable proves that $\alpha _x \le \phi _{i_x}(\langle p,g\rangle ) = 0$. So, we have indeed ${\textsc {pos}}(Z,\alpha ) = \varnothing$. Contradiction. $\square$

5.5.4 Existence of $\delta$-exit sequences

Let $X\in {\mathcal {W}}(U,\delta )$ and let $\mathbf {e}^{*}$ a maximal $\alpha$-exit sequence from X disregarding U. We will exploit the properties of the graphs ${\mathbf {H}}(X,\mathbf {e}^{*},U,\alpha )$ and ${\mathbf {K}}(X,\mathbf {e}^{*},U,\alpha )$ to establish the existence of a $\delta$-exit sequence from X.

Lemma 32

Let $X\in {\mathcal {W}}(U,\delta )$ and let $\mathbf {e}^{*}$ be a maximal $\alpha$-exit sequence from X disregarding U. If $\mathbf {x}(\mathbf {e}^{*}) \cap {\textsc {pos}}(X,\alpha ) = \varnothing$, then there exists an ergodic set Z in the graph ${\mathbf {K}}(X,\mathbf {e}^{*},U,\alpha )$ that satisfies ${\textsc {pos}}(Z,\alpha ) \ne \varnothing$ and $F(U)\cap Z \ne \varnothing$. Moreover, for all $t\in F(U) \cap Z$ and all $v\in {\textsc {viable}}(s,\delta )$ with $s\in A(t)$, we have

$$\begin{aligned} \{t\} \cup \mathbf {x}(\mathbf {e}^{*}) \cup ({\textsc {esc}}(X,\alpha ){\setminus } F(U)) \subseteq {\textsc {sat}}(v,\alpha ) {\,\,\,\implies \,\,\,}t\in {\textsc {sat}}(v,\delta ). \end{aligned}$$

Proof

Assume that $\mathbf {x}(\mathbf {e}^{*}) \cap {\textsc {pos}}(X,\alpha ) = \varnothing$. Then Lemma 31 applies, so we can choose ergodic sets Y of ${\mathbf {H}}(X,\mathbf {e}^{*},U,\alpha )$ and Z of ${\mathbf {K}}(X,\mathbf {e}^{*},U,\alpha )$ with ${\textsc {pos}}(Y,\alpha ) \ne \varnothing$ and $Y\subseteq Z$. With these choices, it is obvious that ${\textsc {pos}}(Z,\alpha ) \ne \varnothing$.

I: We prove by contradiction that $F(U)\cap Y \ne \varnothing$, which also proves $F(U) \cap Z \ne \varnothing$. Suppose therefore that $F(U)\cap Y = \varnothing$. We claim that $Y\in {\mathcal {X}}(\alpha )$. We trivially have $Y\in {\mathcal {P}}(\alpha )$ and we have $Y\in {\mathcal {C}}$ by the properties of an ergodic set. It remains to prove that $Y\in {\mathcal {E}}(\alpha )$. We obviously have ${\textsc {pos}}(Y,\alpha ) \subseteq {\textsc {pos}}(X,\delta )$. We also have

$$\begin{aligned} {\textsc {esc}}(Y,\alpha )= & {} {\textsc {esc}}(Y,\alpha ){\setminus } F(U) \\\subseteq & {} {\textsc {esc}}(X,\alpha ){\setminus } F(U) \\\subseteq & {} {\textsc {esc}}(X,\delta ) {\setminus } F(U) \\\subseteq & {} {\textsc {esc}}(X,\delta ). \end{aligned}$$

Here, the equality holds because we suppose $F(U) \cap Y = \varnothing$, the first inclusion is by Lemma 27-(ii), the second inclusion follows by Lemma 14-(iv), and the third inclusion is trivial. We now conclude that

$$\begin{aligned} {\textsc {esc}}(Y,\alpha ) \cap {\textsc {pos}}(Y,\alpha ) \subseteq {\textsc {esc}}(X,\delta ) \cap {\textsc {pos}}(X,\delta ) = \varnothing , \end{aligned}$$

where the equality is because $X\in {\mathcal {X}}(\delta ) \subseteq {\mathcal {E}}(\delta )$. This proves that $Y\in {\mathcal {E}}(\alpha )$.

So we have indeed $Y\in {\mathcal {X}}(\alpha )$. We can thus choose a positive $\alpha$-exit sequence $\mathbf {e}$ from Y, by the fact that $\alpha \in \Omega ^*$. We now claim that $\mathbf {e}$ is an $\alpha$-exit sequence from Y disregarding U.

The requirements $\mathbf {x}(\mathbf {e}) \subseteq Y$ and $\mathbf {y}(\mathbf {e}) \subseteq (S\cup S^*) {\setminus } Y$ are obviously satisfied, because $\mathbf {e}$ is an $\alpha$-exit sequence from Y. The requirement $F(U) \cap \mathbf {x}(\mathbf {e}) = \varnothing$ is satisfied due to the assumption $F(U) \cap Y = \varnothing$. We further need to prove that, for all $j\in \{1,\ldots ,k(\mathbf {e})\}$ and all $v\in {\textsc {viable}}(y_j(\mathbf {e}),\alpha )$, we have

$$\begin{aligned} \{x_1(\mathbf {e}), \ldots , x_{j-1}(\mathbf {e})\} \cup ({\textsc {esc}}(Y,\alpha ) {\setminus } F(U)) \subseteq {\textsc {sat}}(v,\alpha ) {\,\,\,\implies \,\,\,}x_j(\mathbf {e}) \in {\textsc {sat}}(v,\alpha ).\nonumber \\ \end{aligned}$$

(10)

By definition of an $\alpha$-exit sequence from Y, the sequence $\mathbf {e}$ satisfies, for all $j\in \{1,\ldots ,k(\mathbf {e})\}$ and all $v\in {\textsc {viable}}(y_j(\mathbf {e}),\alpha )$,

$$\begin{aligned} \{x_1(\mathbf {e}), \ldots , x_{j-1}(\mathbf {e})\} \cup {\textsc {esc}}(Y,\alpha ) \subseteq {\textsc {sat}}(v,\alpha ) {\,\,\,\implies \,\,\,}x_j(\mathbf {e}) \in {\textsc {sat}}(v,\alpha ). \end{aligned}$$

We see that (10) indeed holds, since we have ${\textsc {esc}}(Y,\alpha ) = {\textsc {esc}}(Y,\alpha ) {\setminus } F(U)$ due to the fact that we suppose $F(U)\cap Y = \varnothing$. This shows that $\mathbf {e}$ is indeed an $\alpha$-exit sequence from Y disregarding U.

Now, it follows by Lemma 29 that $\mathbf {e}$ is an $\alpha$-exit sequence from X disregarding U. It follows even that $\mathbf {e}$ is a positive $\alpha$-exit sequence from X disregarding U, as it is a positive $\alpha$-exit sequence from Y. But then $\mathbf {e}^{*}$ must be a positive $\alpha$-exit sequence from X disregarding U as well, by the maximality of $\mathbf {e}^{*}$. This contradicts that $\mathbf {x}(\mathbf {e}^{*}) \cap {\textsc {pos}}(X,\alpha ) = \varnothing$, a given assumption of this lemma.

II: Choose $t\in F(U) \cap Y$, let $s\in A(t)$, and let $g\in {\textsc {viacomp}}(s,U,\alpha )$. Assume that

$$\begin{aligned} \{t\} \cup \mathbf {x}(\mathbf {e}^{*}) \cup ({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \subseteq {\textsc {sat}}(g,\alpha ). \end{aligned}$$

(11)

We will prove that $t\in {\textsc {sat}}(g,\delta )$. The proof will be by contradiction, so we suppose that $t\notin {\textsc {sat}}(g,\delta )$. The contradiction will be derived in six steps.

II-i: For all $x\in Y{\setminus } \{t\}$, we construct a plan $h_x\in {\textsc {viacomp}}(t,U,\alpha )$ such that x lies on $h_x$, such that all states on $h_x$ from start to the first occurrence of x are different, and such that $h_x\notin {\textsc {admiss}}(t,U,\alpha )$.

For all $x\in Y{\setminus } \{t\}$, we can choose a path $p_x$ in ${\mathbf {H}}(X,\mathbf {e}^{*},U,\alpha )$ from t to x, as both t and x are elements of the ergodic set Y. We choose $p_x$ of minimum length to ensure that each state appears at most once on $p_x$. We can also choose a path $q_x$ in ${\mathbf {H}}(X,\mathbf {e}^{*},U,\alpha )$ from x to t. We now define the plan $h_x$ by $h_x = \langle p_x,q_x,(t,s),g\rangle$.

Notice that plan $\langle (t,s),g\rangle$ is $\alpha$-viable, which follows from the fact that $g\in {\textsc {viacomp}}(s,U,\alpha ) \subseteq {\textsc {viable}}(s,\alpha )$ and the fact that $t\in {\textsc {sat}}(g,\alpha )$ by assumption (11). Assumption (11) also implies that

$$\begin{aligned} \mathbf {x}(\mathbf {e}^{*}) \cup ({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \subseteq {\textsc {sat}}(\langle (t,s),g \rangle ,\alpha ). \end{aligned}$$

Further, $\langle p_x, q_x \rangle$ is a path in ${\mathbf {K}}(X,\mathbf {e}^{*},U,\alpha )$, as $p_x$ and $q_x$ are both paths in the subgraph ${\mathbf {H}}(X,\mathbf {e}^{*},U,\alpha )$ of ${\mathbf {K}}(X,\mathbf {e}^{*},U,\alpha )$. Thus, Lemma 30 applies to the plan $\langle (t,s),g \rangle$ and the path $\langle p_x,q_x\rangle$. It follows that $h_x = \langle p_x, q_x, (t,s),g\rangle \in {\textsc {viable}}(t,\alpha )$. Further, plan $h_x$ is U-compatible, because the path $\langle p_x, q_x, (t,s) \rangle$ and plan g are both U-compatible. Thus, $h_x \in {\textsc {viacomp}}(t,U,\alpha )$.

Now, by definition, we have $t\in {\textsc {sat}}(v,\delta )$ for all $v\in {\textsc {admiss}}(t,U,\alpha )$. Apparently then, $h_x \notin {\textsc {admiss}}(t,U,\alpha )$, as we suppose $t\notin {\textsc {sat}}(g,\delta ) = {\textsc {sat}}(h_x,\delta )$.

II-ii: We claim that $\alpha _t \le 0$ and that $\alpha _x\le \alpha _t$ for all $x\in S^{i_t} \cap Y$. Notice that $U(t) \in Y$, hence $Y{\setminus } \{t\} \ne \varnothing$. We can thus choose $x\in Y{\setminus } \{t\}$ and construct its associated plan $h_x$. The claim $\alpha _t \le 0$ immediately follows from the fact that $h_x$ does not satisfy condition AD-i of admissibility.

Now suppose that $x\in S^{i_t} \cap Y$ exists with $\alpha _x > \alpha _t$. Recall that plan $h_x$ was constructed such that all states on $h_x$ from start t to the first occurrence of x are different. Thus, state x is reached on plan $h_x$ before any state of F(U) appears for the second time. Then $h_x$ is $(t,U,\alpha )$-admissible due to AD-i. Contradiction.

II-iii: We claim that, for all $x\in Y{\setminus } S^{i_t}$, we have

$$\begin{aligned} \forall y\in A(x){\setminus } Y, \, \forall v\in {\textsc {viable}}(y,\alpha ): t\in {\textsc {sat}}(v,\alpha ) \vee x\in {\textsc {sat}}(v,\alpha ). \end{aligned}$$

(12)

Let $x\in Y {\setminus } S^{i_t}$, let $y\in A(x) {\setminus } Y$, and let $v\in {\textsc {viable}}(y,\alpha )$. We will check that the plan $h_x$ and the pair (x, v) satisfy conditions AD-iv-(a),(b),(c),(d).

(a): The first occurrence of x on $h_x$ is before the second occurrence of a state in F(U), because all states on $h_x$ from start t to the first occurrence of x are different. Thus, the pair (x, v) satisfies AD-iv-(a) of a threat pair for $h_x$.

(b): We have $i_x \ne i_t$ by the fact that $x\in Y{\setminus } S^{i_t}$. Thus, (x, v) satisfies condition AD-iv-(b).

(c): Plan v is an $\alpha$-viable plan with ${\textsc {first}}(v) = y \in A(x)$. Thus, (x, v) satisfies condition AD-iv-(c).

(d): Notice that the elements of $A(x){\setminus } Y$ do not coincide with the follower of x on plan $h_x$, since the follower of x is the second state on path $q_x$, which lies inside Y. Thus, (x, v) satisfies condition AD-iv-(d).

Part (e) of condition AD-iv must be violated then, as plan $h_x$ violates condition AD-iv. It follows that $t\in {\textsc {sat}}(v,\alpha )$ or $x\in {\textsc {sat}}(v,\alpha )$. This proves (12).

II-iv: We claim that $Y \in {\mathcal {X}}(\alpha )$. We trivially have $Y\in {\mathcal {P}}(\alpha )$ and we have $Y\in {\mathcal {C}}$ by the properties of an ergodic set. It remains to prove that $Y \in {\mathcal {E}}(\alpha )$. By the result of II-ii, we have $F(U) \cap {\textsc {pos}}(Y,\alpha ) = \varnothing$. We may therefore write

$$\begin{aligned} {\textsc {esc}}(Y,\alpha ) \cap {\textsc {pos}}(Y,\alpha ) = ({\textsc {esc}}(Y,\alpha ){\setminus } F(U)) \cap {\textsc {pos}}(Y,\alpha ). \end{aligned}$$

We have

$$\begin{aligned} {\textsc {esc}}(Y,\alpha ){\setminus } F(U) \subseteq {\textsc {esc}}(X,\alpha ) {\setminus } F(U) \subseteq {\textsc {esc}}(X,\delta ), \end{aligned}$$

where the first inclusion is by Lemma 27-(ii) and the second inclusion by Lemma 14-(iv). We also have ${\textsc {pos}}(Y,\alpha ) \subseteq {\textsc {pos}}(X,\delta )$, by the fact that $Y \subseteq X$ and $\alpha \le \delta$. Therefore,

$$\begin{aligned} {\textsc {esc}}(Y,\alpha ) \cap {\textsc {pos}}(Y,\alpha )= & {} ({\textsc {esc}}(Y,\alpha ){\setminus } F(U)) \cap {\textsc {pos}}(Y,\alpha ) \\\subseteq & {} {\textsc {esc}}(X,\delta ) \cap {\textsc {pos}}(X,\delta ) \\= & {} \varnothing , \end{aligned}$$

where the last equality is by the fact that $X\in {\mathcal {X}}(\delta ) \subseteq {\mathcal {E}}(\delta )$. This proves that $Y\in {\mathcal {E}}(\alpha )$, hence $Y\in {\mathcal {P}}(\alpha ) \cap {\mathcal {E}}(\alpha ) \cap {\mathcal {C}} = {\mathcal {X}}(\alpha )$.

II-v: We now prove the existence of a positive $\alpha$-exit sequence from Y disregarding U.

Since we have $Y\in {\mathcal {X}}(\alpha )$ by the result of II-iv and since we have $\alpha \in \Omega ^*$, we can choose a positive $\alpha$-exit sequence $\overline{\mathbf {e}}$ from Y. We can choose $\overline{\mathbf {e}}$ such that every edge is legitimate. Indeed, if this is not already the case, then we remove, one by one, every edge that is not legitimate. This results in a non-empty $\alpha$-exit sequence from Y in which every edge is legitimate, by Lemma 18-(ii). The resulting sequence is still positive, by Lemma 18-(v).

Let $\mathbf {e}$ be the sequence that results from $\overline{\mathbf {e}}$ by deleting all edges $(x_j(\overline{\mathbf {e}}), y_j(\overline{\mathbf {e}}))$ with the property $x_j(\overline{\mathbf {e}}) \in F(U)$. We claim that $\mathbf {e}$ is a positive $\alpha$-exit sequence from Y disregarding U.

Let us investigate the relation between $\overline{\mathbf {e}}$ and $\mathbf {e}$ a bit more. If $F(U) \cap {\textsc {esc}}(Y,\alpha ) \ne \varnothing$, then the sequence $\overline{\mathbf {e}}$ contains no edges of the form (x, y) with $i_x = i_t$ and $\alpha _x \le \alpha _t$, as these are then not legitimate. Then in fact, the sequence contains $\overline{\mathbf {e}}$ no edges of the form (x, y) with $i_x = i_t$ at all, as there are no states in Y with $i_x = i_t$ and $\alpha _x > \alpha _t$, by the result of II-ii. Thus,

$$\begin{aligned} F(U) \cap {\textsc {esc}}(Y,\alpha ) \ne \varnothing {\,\,\,\implies \,\,\,}\mathbf {x}(\mathbf {e}) \cap S^{i_t} = \varnothing \hbox { and } \mathbf {e} = \overline{\mathbf {e}}. \end{aligned}$$

(13)

If $F(U) \cap {\textsc {esc}}(Y,\alpha ) = \varnothing$, then we may have $\mathbf {e} \ne \overline{\mathbf {e}}$. Assume that this is indeed the case. Then let $h\in \{1,\ldots , k(\overline{\mathbf {e}})\}$ be such that $x_h(\overline{\mathbf {e}}) \in F(U)$. Now, there may exist $j\in \{1,\ldots , k(\overline{\mathbf {e}})\}$ with $i_{x_j(\overline{\mathbf {e}})} = i_{x_h(\overline{\mathbf {e}})} = i_t$ and $j\ne h$. If this is so, then the relevant thing to see is that this implies $j<h$. Indeed, if we suppose $j>h$, then $\alpha _{x_j(\overline{\mathbf {e}})} > \alpha _t$ by Lemma 18-(vi), which contradicts the result of II-ii. Thus,

$$\begin{aligned} F(U) \cap {\textsc {esc}}(Y,\alpha ) = \varnothing \hbox { and } x_h(\mathbf {e}) \in S^{i_t} {\,\,\,\implies \,\,\,}\forall j\le h: x_j(\overline{\mathbf {e}}) = x_j(\mathbf {e}). \end{aligned}$$

(14)

Let us now prove that $\mathbf {e}$ is a positive $\alpha$-exit sequence from Y disregarding U. We have $\mathbf {x}(\mathbf {e}) \cap F(U) = \varnothing$ due to the construction of $\mathbf {e}$. We have $\mathbf {x}(\mathbf {e}) \subseteq \mathbf {x}(\overline{\mathbf {e}}) \subseteq Y$ and $\mathbf {y}(\mathbf {e}) \subseteq \mathbf {y}(\overline{\mathbf {e}}) \subseteq (S\cup S^*) {\setminus } Y$ due to the fact that $\overline{\mathbf {e}}$ is an $\alpha$-exit sequence from Y.

Now, let $j\in \{1,\ldots ,k(\mathbf {e})\}$, let $v\in {\textsc {viable}}(y_j(\mathbf {e}))$, and assume that

$$\begin{aligned} \{x_1(\mathbf {e}),\ldots ,x_{j-1}(\mathbf {e})\} \cup ({\textsc {esc}}(Y,\alpha ) {\setminus } F(U)) \subseteq {\textsc {sat}}(v,\alpha ). \end{aligned}$$

(15)

We need to prove that $x_j(\mathbf {e}) \in {\textsc {sat}}(v,\alpha )$.

First assume that $x_j(\mathbf {e}) \in S^{i_t}$. Then we have $F(U) \cap {\textsc {esc}}(Y,\alpha ) = \varnothing$, by the result of (13). In assumption (15), we may therefore replace the term ${\textsc {esc}}(Y,\alpha ){\setminus } F(U)$ by the term ${\textsc {esc}}(Y,\alpha )$. We also have $\{x_1(\mathbf {e}), \ldots , x_{j-1}(\mathbf {e})\} = \{x_1(\overline{\mathbf {e}}), \ldots , x_{j-1}(\overline{\mathbf {e}})\}$ by the result of (14). Assumption (15) is therefore equivalent to

$$\begin{aligned} \{x_1(\overline{\mathbf {e}}),\ldots ,x_{j-1}(\overline{\mathbf {e}})\} \cup {\textsc {esc}}(Y,\alpha ) \subseteq {\textsc {sat}}(v,\alpha ). \end{aligned}$$

It follows that $x_j(\overline{\mathbf {e}}) \in {\textsc {sat}}(v,\alpha )$ by the fact that $\overline{\mathbf {e}}$ is an $\alpha$-exit sequence from Y. Then $x_j(\mathbf {e}) \in {\textsc {sat}}(v,\alpha )$, as $x_j(\mathbf {e}) = x_{j}(\overline{\mathbf {e}})$ by the result of (14).

Now assume that $x_j(\mathbf {e}) \in Y{\setminus } S^{i_t}$. Then the result of II-iii applies, since we have $x_j(\mathbf {e}) \in Y{\setminus } S^{i_t}$ and $y_j(\mathbf {e}) \in A(x) {\setminus } Y$. Thus, we have $t\in {\textsc {sat}}(v,\alpha )$ or $x_j(\mathbf {e}) \in {\textsc {sat}}(v,\alpha )$. In fact, $x_j(\mathbf {e})\in {\textsc {sat}}(v,\alpha )$ always holds. Indeed, when $t\in {\textsc {sat}}(v,\alpha )$ holds, we have $s\in {\textsc {sat}}(v,\alpha )$ for all $s\in F(U)$. It then follows that

$$\begin{aligned} \{x_1(\overline{\mathbf {e}}),\ldots ,x_{i-1}(\overline{\mathbf {e}})\} \cup {\textsc {esc}}(Y,\alpha ) \subseteq {\textsc {sat}}(v,\alpha ), \end{aligned}$$

where $i\in \{1,\ldots , k(\overline{\mathbf {e}})\}$ is such that $x_i(\overline{\mathbf {e}}) = x_j(\mathbf {e})$. It subsequently follows that $x_j(\mathbf {e}) = x_i(\overline{\mathbf {e}}) \in {\textsc {sat}}(v,\alpha )$, by the fact that $\overline{\mathbf {e}}$ is an $\alpha$-exit sequence from Y. We proved that $\mathbf {e}$ is indeed an $\alpha$-exit sequence from Y disregarding U. The sequence $\mathbf {e}$ is also positive, since $\overline{\mathbf {e}}$ is positive and since $\mathbf {e}$ was obtained from $\overline{\mathbf {e}}$ by the deletion of edges (x, y) that satisfy $\alpha _x = \alpha _t \le 0$.

II-vi: We can now derive the desired contradiction. By Lemma 29, the sequence $\mathbf {e}$ is not only an $\alpha$-exit sequence from Y disregarding U, but it is also an $\alpha$-exit sequence from X disregarding U. It follows that $\mathbf {x}(\mathbf {e}) \subseteq \mathbf {x}(\mathbf {e}^*)$, by Lemma 28. Hence, $\mathbf {x}(\mathbf {e}) \cap {\textsc {pos}}(X,\alpha ) \subseteq \mathbf {x}(\mathbf {e}^*) \cap {\textsc {pos}}(X,\alpha ) = \varnothing$. This contradicts that $\mathbf {e}$ is positive.

III: Now let $t\in F(U) \cap Z$, let $s\in A(t)$, and let $g\in {\textsc {viacomp}}(s,U,\alpha )$. Assume further that

$$\begin{aligned} \{t\} \cup \mathbf {x}(\mathbf {e}^{*}) \cup ({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \subseteq {\textsc {sat}}(g,\alpha ). \end{aligned}$$

(16)

We will prove that $t\in {\textsc {sat}}(g,\delta )$. If $t\in F(U) \cap Y$, then the result of II applies and we are done. Assume further that $t\in F(U) \cap (Z{\setminus } Y)$.

We choose $t^\prime \in F(U) \cap Y$, which is possible because the set is non-empty. We further choose a U-compatible path p in the graph ${\mathbf {K}}(X,\mathbf {e}^{*},U,\alpha )$ from $U(t^\prime )$ to t and a U-compatible path q in ${\mathbf {K}}(X,\mathbf {e}^{*},U,\alpha )$ from t to $t^\prime$. Observe that $\langle p, q, (t^\prime ,U(t^\prime )), p,(t,s),g\rangle$ is a U-compatible plan that starts at $U(t^\prime ) \in A(t^\prime )$. We claim that the plan is $\alpha$-viable.

The plan $\langle (t,s),g\rangle$ is $\alpha$-viable, since $g\in {\textsc {viacomp}}(s,U,\alpha ) \subseteq {\textsc {viable}}(s,\alpha )$ and since $t\in {\textsc {sat}}(g,\alpha )$ due to assumption (16). Further, $\langle p, q, (t^\prime ,U(t^\prime )), p \rangle$ is a path in ${\mathbf {K}}(X,\mathbf {e}^{*},U,\alpha )$, and assumption (16) implies that $\mathbf {x}(\mathbf {e}^{*}) \cup ({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \subseteq {\textsc {sat}}(g,\alpha )$. We see that Lemma 30 applies, and it follows indeed that $h = \langle p, q, (t^\prime ,U(t^\prime )), p,(t,s),g\rangle$ is $\alpha$-viable.

We proved that $h\in {\textsc {viacomp}}(U(t^\prime ),U,\alpha )$. We now apply the result of II to deduce that $t,t^\prime \in {\textsc {sat}}(g,\delta )$.

IV: Now let $t\in F(U) \cap Z$, let $s\in A(t)$, and let $g\in {\textsc {viable}}(s,\delta )$. Assume further that Eq. (16) holds. We will prove that $t\in {\textsc {sat}}(g,\delta )$ by contradiction. Suppose therefore that $t\notin {\textsc {sat}}(g,\delta )$. Then plan g does not contain any elements of F(U), as g is $\delta$-viable. This implies that g is U-compatible. Plan g is also $\alpha$-viable, as $g\in {\textsc {viable}}(s,\delta ) \subseteq {\textsc {viable}}(s,\alpha )$. It follows that $g\in {\textsc {viacomp}}(s,U,\alpha )$. We see that the result of III applies and it follows that $t\in {\textsc {sat}}(g,\delta )$. Contradiction. $\square$

Lemma 33

Let $X\in {\mathcal {W}}(U,\delta )$ and let $\mathbf {e}^{*}$ be a maximal $\alpha$-exit sequence from X disregarding U. If $\mathbf {x}(\mathbf {e}^{*}) \cap {\textsc {pos}}(X,\alpha ) = \varnothing$, then there exists a $(\delta , \mathbf {x}(\mathbf {e}^{*}))$-exit from X of the form (t, s) with $t\in F(U)$.

Proof

Assume that $\mathbf {x}(\mathbf {e}^{*}) \cap {\textsc {pos}}(X,\alpha ) = \varnothing$. Then, by Lemma 32, we can choose an ergodic set Z in the graph ${\mathbf {K}}(X,\mathbf {e}^{*},U,\alpha )$ that satisfies ${\textsc {pos}}(Z,\alpha ) \ne \varnothing$ and $F(U)\cap Z \ne \varnothing$, and that satisfies, for all $t\in F(U) \cap Z$ and all $v\in {\textsc {viable}}(s,\delta )$ with $s\in A(t)$,

$$\begin{aligned} \{t\} \cup \mathbf {x}(\mathbf {e}^{*}) \cup ({\textsc {esc}}(X,\alpha ) {\setminus } F(U))\subseteq {\textsc {sat}}(v,\alpha ) {\,\,\,\implies \,\,\,}t\in {\textsc {sat}}(v,\delta ). \end{aligned}$$

(17)

First assume that $F(U) \cap {\textsc {esc}}(Z,\alpha ) \ne \varnothing$. Then we choose $t\in F(U) \cap {\textsc {esc}}(Z,\alpha )$. Notice that $t\in {\textsc {esc}}(X,\alpha )$, as we have ${\textsc {esc}}(Z,\alpha ) = Z\cap {\textsc {esc}}(X,\alpha )$ by Lemma 27-(i). Thus, we can choose additionally $s\in {\textsc {safestep}}(t,\alpha )$ with $s\in (S\cup S^*) {\setminus } X$. We claim that (t, s) is the required edge. The requirements $t\in X$ and $s\in (S\cup S^*) {\setminus } X$ are obviously satisfied.

Let $g\in {\textsc {viable}}(s,\delta )$ and assume that

$$\begin{aligned} \mathbf {x}(\mathbf {e}^{*}) \cup {\textsc {esc}}(X,\delta ) \subseteq {\textsc {sat}}(g,\delta ). \end{aligned}$$

(18)

To see that (t, s) is indeed the required edge, it now suffices to prove that $t \in {\textsc {sat}}(g,\delta )$. We have $s\in {\textsc {safestep}}(t,\alpha )$ and $g\in {\textsc {viable}}(s,\delta ) \subseteq {\textsc {viable}}(s,\alpha )$. Then $t\in {\textsc {sat}}(g,\alpha )$, by definition of the set ${\textsc {safestep}}(t,\alpha )$. We also have

$$\begin{aligned} \mathbf {x}(\mathbf {e}^{*}) \cup ({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \subseteq \mathbf {x}(\mathbf {e}^{*}) \cup {\textsc {esc}}(X,\delta ) \subseteq {\textsc {sat}}(g,\delta ) \subseteq {\textsc {sat}}(g,\alpha ), \end{aligned}$$

where the first inclusion is by Lemma 14-(iv) and the second inclusion is by assumption (18). Combining our results, we obtain

$$\begin{aligned} \{t\} \cup \mathbf {x}(\mathbf {e}^{*}) \cup ({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \subseteq {\textsc {sat}}(g,\alpha ). \end{aligned}$$

It follows that $t\in {\textsc {sat}}(g,\delta )$ by assumption (17).

Now assume that $F(U) \cap {\textsc {esc}}(Z,\alpha ) = \varnothing$. We then claim that $Z\in {\mathcal {X}}(\alpha )$. We have $Z\in {\mathcal {P}}(\alpha )$ by Lemma 32, and we have $Z\in {\mathcal {C}}$ by the properties of an ergodic set. Thus, to prove $Z\in {\mathcal {X}}(\alpha )$, it remains to prove that $Z\in {\mathcal {E}}(\alpha )$. We have

$$\begin{aligned} {\textsc {esc}}(Z,\alpha )= & {} {\textsc {esc}}(Z,\alpha ) {\setminus } F(U) \\= & {} (Z \cap {\textsc {esc}}(X,\alpha )) {\setminus } F(U) \\\subseteq & {} {\textsc {esc}}(X,\alpha ) {\setminus } F(U) \\\subseteq & {} {\textsc {esc}}(X,\delta ), \end{aligned}$$

where the first equality is by the assumption $F(U) \cap {\textsc {esc}}(Z,\alpha ) = \varnothing$, the second equality is by Lemma 27-(i), the first inclusion is trivial, and the second inclusion is by Lemma 14-(iv). We also have ${\textsc {pos}}(Z,\alpha ) \subseteq {\textsc {pos}}(X,\delta )$, as $Z\subseteq X$ and $\alpha \le \delta$. It follows that

$$\begin{aligned} {\textsc {esc}}(Z,\alpha )\cap {\textsc {pos}}(Z,\alpha ) \subseteq {\textsc {esc}}(X,\delta ) \cap {\textsc {pos}}(X,\delta ) = \varnothing . \end{aligned}$$

This proves $Z\in {\mathcal {X}}(\alpha )$. We can therefore choose a positive $\alpha$-exit sequence $\mathbf {f}$ from Z, as $\alpha \in \Omega ^*$.

Define $\widetilde{\mathbf {f}} = ({x}_j(\mathbf {f}), \mathbf {y}_j(\mathbf {f}))_{j=1}^h$, where h is the largest index such that ${x}_j(\mathbf {f}) \notin F(U)$ for all $j\le h$. Thus, $h=0$ in case ${x}_1(\mathbf {f}) \notin F(U)$ and $h = k(\mathbf {f})$ in case $\mathbf {x}(\mathbf {f}) \subseteq F(U)$.

We claim that $\widetilde{\mathbf {f}}$ is an $\alpha$-exit sequence from X disregarding U. We have $\mathbf {x}(\widetilde{\mathbf {f}}) \cap F(U) = \varnothing$ by construction, and we trivially have $\mathbf {x}(\mathbf {f}) \subseteq Z \subseteq X$. To prove that $\widetilde{\mathbf {f}}$ satisfies the other requirements as well, we define $\ell$ as the largest index in $\{0,\ldots ,h\}$ such that $\{y_1(\mathbf {f}), \ldots , y_\ell (\mathbf {f})\} \subseteq (S\cup S^*) {\setminus } X$. We will first prove that the sequence $\widehat{\mathbf {f}} = ({x}_j(\mathbf {f}), \mathbf {y}_j(\mathbf {f}))_{j=1}^{\ell }$ is an $\alpha$-exit sequence from X disregarding U, and we will then prove that $\ell = h$.

Let $j\in \{1,\ldots , \ell \}$, let $g\in {\textsc {viable}}(\mathbf {y}_j({\mathbf {f}}),\alpha )$ and assume that

$$\begin{aligned} \{ {x}_1({\mathbf {f}}), \ldots , {x}_{j-1}({\mathbf {f}}) \} \cup {\textsc {esc}}(X,\alpha ) {\setminus } F(U) \subseteq {\textsc {sat}}(g,\alpha ). \end{aligned}$$

We need to prove that ${x}_j({\mathbf {f}}) \in {\textsc {sat}}(g,\alpha )$. We have

$$\begin{aligned} {\textsc {esc}}(Z,\alpha ) = {\textsc {esc}}(Z,\alpha ) {\setminus } F(U) = (Z \cap {\textsc {esc}}(X,\alpha )) {\setminus } F(U)) \subseteq {\textsc {esc}}(X,\alpha ) {\setminus } F(U),\nonumber \\ \end{aligned}$$

(19)

where the first equality is by the assumption $F(U)\cap {\textsc {esc}}(Z,\alpha ) = \varnothing$ and the second equality is by Lemma 27-(ii). It follows that

$$\begin{aligned} \{ {x}_1({\mathbf {f}}), \ldots , {x}_{j-1}({\mathbf {f}}) \} \cup {\textsc {esc}}(Z,\alpha ) \subseteq {\textsc {sat}}(g,\alpha ). \end{aligned}$$

Then indeed ${x}_j({\mathbf {f}}) \in {\textsc {sat}}(g,\alpha )$, since ${\mathbf {f}}$ is an $\alpha$-exit sequence from Z.

We proved that the sequence $\widehat{\mathbf {f}} = ({x}_j(\mathbf {f}), \mathbf {y}_j(\mathbf {f}))_{j=1}^{\ell }$ is an $\alpha$-exit from X disregarding U. We now prove that $\widehat{\mathbf {f}} = \widetilde{\mathbf {f}}$, i.e., that $\ell = h$, by contradiction. So suppose that $\ell < h$. Observe then that the edge $({x}_{\ell +1}({\mathbf {f}}) , \mathbf {y}_{\ell +1}({\mathbf {f}}))$ is an $\alpha$-cap for $(X, \widehat{\mathbf {f}}, U)$. The edge is then also an $\alpha$-cap for $(X, \mathbf {e}^{*}, U)$, by Lemma 26 and the maximality of $\mathbf {e}^{*}$. This means that $({x}_{\ell +1}({\mathbf {f}}) , {y}_{\ell +1}({\mathbf {f}}))$ is an edge of the graph ${\mathbf {K}}(X,\mathbf {e}^{*},U,\alpha )$. It follows that ${y}_{\ell +1}({\mathbf {f}}) \in Z$, since Z is an ergodic set of ${\mathbf {K}}(X,\mathbf {e}^{*},U,\alpha )$. This contradicts that $\mathbf {f}$ is an $\alpha$-exit sequence from Z.

We proved that $\widetilde{\mathbf {f}}$ is an $\alpha$-exit sequence from X disregarding U. We therefore have $\mathbf {x}(\widetilde{\mathbf {f}}) \subseteq \mathbf {x}(\mathbf {e}^{*})$ by the maximality of $\mathbf {e}^{*}$. Since $\mathbf {f}$ is a positive sequence and $\mathbf {e}^{*}$ is not, we have $\mathbf {x}(\mathbf {f}) \not \subseteq \mathbf {x}(\mathbf {e}^{*})$. Thus, we have $\widetilde{\mathbf {f}} \ne \mathbf {f}$, i.e., we have $h < k(\mathbf {f})$. The edge $({x}_{h+1}(\mathbf {f}), \mathbf {y}_{h+1}(\mathbf {f}))$ therefore exists. The edge is of the form (t, s) with $t\in F(U)$, because h was defined as the largest index such that ${x}_j(\mathbf {f}) \notin F(U)$ for all $j\le h$.

Now, let $g\in {\textsc {viable}}(s,\delta )$, and assume that

$$\begin{aligned} \mathbf {x}(\mathbf {e}^{*}) \cup {\textsc {esc}}(X,\delta ) \subseteq {\textsc {sat}}(g,\delta ). \end{aligned}$$

(20)

We will prove that $t \in {\textsc {sat}}(g,\delta )$. We saw earlier that $\mathbf {x}(\widetilde{\mathbf {f}}) \subseteq \mathbf {x}(\mathbf {e}^{*})$, because $\widetilde{\mathbf {f}}$ is an $\alpha$-exit sequence from X disregarding U and $\mathbf {e}^{*}$ is a maximal one. We also have ${\textsc {esc}}(Z,\alpha ) \subseteq {\textsc {esc}}(X,\alpha ) {\setminus } F(U)$ by the result of (19), and we have ${\textsc {esc}}(X,\alpha ) {\setminus } F(U) \subseteq {\textsc {esc}}(X,\delta )$ by Lemma 14-(iv). Thus, we have

$$\begin{aligned} \{ {x}_1({\mathbf {f}}), \ldots , {x}_h({\mathbf {f}}) \} \cup {\textsc {esc}}(Z,\alpha ) \subseteq {\textsc {sat}}(g,\delta ) \subseteq {\textsc {sat}}(g,\alpha ). \end{aligned}$$

It follows that ${x}_{h+1}({\mathbf {f}}) = t\in {\textsc {sat}}(g,\alpha )$, since $\mathbf {f}$ is an $\alpha$-exit sequence from Z. In combination with assumption (20), we obtain

$$\begin{aligned} \{t\} \cup \mathbf {x}(\mathbf {e}^{*}) \cup {\textsc {esc}}(X,\delta ) \subseteq {\textsc {sat}}(g,\alpha ), \end{aligned}$$

and as ${\textsc {esc}}(X,\alpha ) {\setminus } F(U) \subseteq {\textsc {esc}}(X,\delta )$ by Lemma 14-(iv), it follows that

$$\begin{aligned} \{t\} \cup \mathbf {x}(\mathbf {e}^{*}) \cup ({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \subseteq {\textsc {sat}}(g,\alpha ). \end{aligned}$$

We now see that $t\in {\textsc {sat}}(g,\delta )$ holds, by the implication of (17).

Finally, we prove that $s\in (S\cup S^*) {\setminus } X$. Suppose that this is not true. We then claim that (t, s) is an $\alpha$-hat for $(X,\mathbf {e}^*,U)$. We obviously have $t\in F(U)$ and we suppose that $s\in X$. Now, let $g\in {\textsc {viable}}(s,\delta )$, and assume that

$$\begin{aligned} \mathbf {x}(\mathbf {e}^{*}) \cup ({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \subseteq {\textsc {sat}}(g,\alpha ). \end{aligned}$$

We have ${\textsc {esc}}(Z,\alpha ) \subseteq {\textsc {esc}}(X,\alpha ) {\setminus } F(U)$ by the result of (19), and we have $\{ x_1(\mathbf {f}), \ldots , x_h(\mathbf {f}) \} = \mathbf {x}(\widetilde{\mathbf {f}}) \subseteq \mathbf {x}(\mathbf {e}^*)$, since $\widetilde{\mathbf {f}}$ is an $\alpha$-exit sequence from X disregarding U and $\mathbf {e}^*$ is a maximal one. Therefore,

$$\begin{aligned} \{ x_1(\mathbf {f}), \ldots , x_h(\mathbf {f}) \} \cup {\textsc {esc}}(Z,\alpha ) \subseteq {\textsc {sat}}(g,\alpha ). \end{aligned}$$

It follows that $t = x_{h+1}(\mathbf {f}) \in {\textsc {sat}}(g,\alpha )$, as $\mathbf {f}$ is an $\alpha$-exit sequence from Z. This proves that (t, s) is indeed an $\alpha$-hat for $(X,\mathbf {e}^*,U)$. This means that (t, s) is an edge of the graph ${\mathbf {K}}(X,\mathbf {e}^{*},U,\alpha )$. The fact that $t\in Z$ therefore implies $s\in Z$, as Z is an ergodic set of the graph ${\mathbf {K}}(X,\mathbf {e}^{*}, U,\alpha )$. This contradicts that (t, s) is an edge of $\mathbf {f}$, which is an $\alpha$-exit sequence from Z.

We proved that the edge (t, s) with $t\in F(U)$ satisfies all requirements for a $(\delta , \mathbf {x}(\mathbf {e}^{*}) )$-exit from X. $\square$

Lemma 34

Let $X\in {\mathcal {W}}(U,\delta )$. Then there exists a positive $\delta$-exit sequence from X.

Proof

Let $\mathbf {e}^{*}$ be a maximal $\alpha$-exit sequence from X disregarding U. If $\mathbf {e}^{*}$ is a positive $\alpha$-exit sequence from X disregarding U, then it is also a positive $\delta$-exit sequence from X, by Lemma 24. In this case, we are done. Assume from here that $\mathbf {x}(\mathbf {e}^{*}) \cap {\textsc {pos}}(X,\alpha ) = \varnothing$.

We see that the result of Lemma 33 applies, so we can choose a $(\delta , \mathbf {x}(\mathbf {e}^{*}))$-exit from X, say (t, s), with $t\in F(U)$. If $t\in {\textsc {pos}}(X,\delta )$, then $(\mathbf {e}^{*},(t,s))$ is the required positive $\delta$-exit sequence from X. Indeed, in this case, the sequence is obviously positive, and it is a $\delta$-exit sequence from X, by Lemma 24 and the fact that (t, s) is a $(\delta , \mathbf {x}(\mathbf {e}^{*}))$-exit. Assume further that $t\notin {\textsc {pos}}(X,\delta )$.

We prove for this remaining case that $X\in {\mathcal {X}}(\alpha )$. We have $X\in {\mathcal {C}}$, because $X\in {\mathcal {W}}(U,\delta ) \subseteq {\mathcal {C}}$. The fact that $t\notin {\textsc {pos}}(X,\delta )$ implies that $\alpha _s \le \delta _s = \delta _t \le 0$ for all $s\in F(U)$. We also have $\alpha _x = \delta _x$ for all $x\in X{\setminus } F(U)$. It follows that ${\textsc {pos}}(X,\alpha ) = {\textsc {pos}}(X,\delta ) = {\textsc {pos}}(X,\delta ) {\setminus } F(U)$. Then $X\in {\mathcal {P}}(\alpha )$, as ${\textsc {pos}}(X,\alpha ) = {\textsc {pos}}(X,\delta ) \ne \varnothing$, where non-emptiness follows by the fact that $X\in {\mathcal {W}}(U,\delta ) \subseteq {\mathcal {P}}(\delta )$. To see that $X\in {\mathcal {E}}(\alpha )$, we observe that

$$\begin{aligned}&{\textsc {esc}}(X,\alpha ) \cap {\textsc {pos}}(X,\alpha ) = {\textsc {esc}}(X,\alpha ) \cap ({\textsc {pos}}(X,\alpha ) {\setminus } F(U)) \\&\quad =({\textsc {esc}}(X,\alpha ) {\setminus } F(U)) \cap {\textsc {pos}}(X,\alpha ) \subseteq {\textsc {esc}}(X,\delta ) \cap {\textsc {pos}}(X,\delta ) = \varnothing . \end{aligned}$$

Here, the inclusion follows by Lemma 14-(iv) and the final equality is by the fact that $X\in {\mathcal {E}}(\delta )$.

We can choose a positive $\alpha$-exit sequence $\mathbf {f}$ from X, since we proved that $X\in {\mathcal {X}}(\alpha )$ and since we have $\alpha \in \Omega ^*$. We claim that $\mathbf {h} = (\mathbf {e}^*,(t,s),\mathbf {f})$ is the required positive $\delta$-exit sequence from X.

The sequence $\mathbf {h} = (\mathbf {e}^*,(t,s),\mathbf {f})$ obviously satisfies $\mathbf {x}(\mathbf {h}) \subseteq X$ and $\mathbf {y}(\mathbf {h}) \subseteq (S\cup S^*) {\setminus } X$. The sequence $\mathbf {h}$ is positive with respect to $\delta$, because part $\mathbf {f}$ is positive with respect to $\alpha$ and $\alpha \le \delta$. Every edge in $\mathbf {h} = (\mathbf {e}^{*}, (t,s), \mathbf {f})$ of the form $(x_j(\mathbf {e}^{*}), y_j(\mathbf {e}^{*}))$ is a $(\delta ,\{x_1(\mathbf {e}^{*}),\ldots ,x_{j-1}(\mathbf {e}^{*})\})$-exit from X, because $\mathbf {e}^{*}$ is a $\delta$-exit sequence from X by Lemma 24. The edge (t, s) is a $(\delta , \mathbf {x}(\mathbf {e}^{*}))$-exit from X, by the result of Lemma 33. It remains to prove that every edge in $\mathbf {f}$, say $(x,y) = (x_j(\mathbf {f}), y_j(\mathbf {f}))$, is a $(\delta ,\mathbf {x}(\mathbf {e}^{*}) \cup \{t\} \cup \{x_1(\mathbf {f}),\ldots ,x_{j-1}(\mathbf {f})\})$-exit from X.

Let $g\in {\textsc {viable}}(y,\delta )$, and assume that

$$\begin{aligned} \mathbf {x}(\mathbf {e}^{*}) \cup \{t\} \cup \{x_1(\mathbf {f}), \ldots , x_{j-1}(\mathbf {f})\} \cup {\textsc {esc}}(X,\delta ) \subseteq {\textsc {sat}}(g,\delta ). \end{aligned}$$

(21)

We need to prove that $x\in {\textsc {sat}}(g,\delta )$. If $x\in F(U)$, this follows immediately, because $t\in {\textsc {sat}}(g,\delta )$ is implied by assumption 21. We assume further that $x\in X{\setminus } F(U)$.

We have $\{t\} \cup {\textsc {esc}}(X,\delta ) \subseteq {\textsc {sat}}(g,\delta )$ by assumption (21). Then $F(U) \cup {\textsc {esc}}(X,\delta ) \subseteq {\textsc {sat}}(g,\delta )$, since $\alpha _s = \alpha _t$ for all $s\in F(U)$. We also have ${\textsc {esc}}(X,\alpha ) \subseteq {\textsc {esc}}(X,\delta ) \cup F(U)$ by Lemma 14-(iv) and ${\textsc {sat}}(g,\delta ) \subseteq {\textsc {sat}}(g,\alpha )$ by the fact that $\alpha \le \delta$. It follows that

$$\begin{aligned} {\textsc {esc}}(X,\alpha ) \subseteq {\textsc {esc}}(X,\delta ) \cup F(U) \subseteq {\textsc {sat}}(g,\delta ) \subseteq {\textsc {sat}}(g,\alpha ). \end{aligned}$$

(22)

As assumption (21) also implies $\{x_1(\mathbf {f}), \ldots , x_{j-1}(\mathbf {f})\} \subseteq {\textsc {sat}}(g,\delta ) \subseteq {\textsc {sat}}(g,\alpha )$, we obtain

$$\begin{aligned} \{x_1(\mathbf {f}), \ldots , x_{j-1}(\mathbf {f})\} \cup {\textsc {esc}}(X,\alpha ) \subseteq {\textsc {sat}}(g,\alpha ). \end{aligned}$$

Then $x = x_j(\mathbf {f}) \in {\textsc {sat}}(g,\alpha )$ by the fact that $\mathbf {f}$ is an $\alpha$-exit sequence from X. As we assume $x \in X{\setminus } F(U)$, it follows immediately that $x\in {\textsc {sat}}(g,\delta )$. $\square$

The following result is a direct consequence of Lemmas 17, 22 and 34 .

Corollary 1

$\delta = \delta (U,\alpha ) \in \Omega ^*$.

5.6 Existence of a fixed point in $\Omega ^*$

We have arrived at the main result of this section, which is the existence of a fixed point with respect to the update procedure described in Sect. 3.

Of course, since $\alpha \in \Omega ^*$ and $U\in {\mathcal {U}}(\alpha )$ were fixed, but chosen arbitrarily, the results of Sects. 5.3, 5.4 and 5.5 are valid for all $\alpha \in \Omega ^*$ and $U\in {\mathcal {U}}(\alpha )$. From here, we do not assume anymore that $\alpha \in \Omega ^*$ and $U \in {\mathcal {U}}(\alpha )$ are fixed.

Theorem 2

There exists a vector $\alpha ^*\in \Omega ^*$ such that $\delta (U,\alpha ^*) = \alpha ^*$ for all $U\in {\mathcal {U}}(\alpha ^*)$.

Proof

Define

$$\begin{aligned} \Omega ^{**} = \{\alpha \in \Omega ^*\mid \hbox { for all } t\in S, \hbox { there exists } x\in S \hbox { such that } \alpha _t = r_{i_t}(x) \hbox { or } \alpha _t = 0 \}. \end{aligned}$$

The set $\Omega ^{**}$ is obviously finite and it is non-empty by Lemma 19. We claim that

$$\begin{aligned} \alpha \in \Omega ^{**} \hbox { and } U\in {\mathcal {U}}(\alpha ) {\,\,\,\implies \,\,\,}\delta (U,\alpha ) \in \Omega ^{**}. \end{aligned}$$

(23)

To prove (23), let $\alpha \in \Omega ^{**}$, let $U\in {\mathcal {U}}(\alpha )$, and let $t\in S$.

If $t\in S{\setminus } F(U)$, then we have $\delta _t(U,\alpha ) = \alpha _t$, in which case $\delta _t(U,\alpha ) = 0$ or the existence of $x\in S$ such that $\delta _t(U,\alpha ) = r_{i_t}(x)$ follows trivially from the fact that $\alpha _t$ has this property.

If $t\in F(U)$, then we have $\delta _t(U,\alpha ) = \gamma (U,\alpha )$. By definition of the number $\gamma (U,\alpha )$, there exists $s\in F(U)$ such that $\gamma (U,\alpha ) = \beta (s,U,\alpha )$. By definition of the number $\beta (s,U,\alpha )$, there exists a plan g such that $\beta (s,U,\alpha ) = \phi _{i_s}(g) = \phi _{i_t}(g)$. Thus, $\delta _t(U,\alpha ) = \phi _{i_t}(g)$. If g is a non-absorbing plan, we have $\delta _t(U,\alpha ) = 0$, and if g absorbs at $x\in S$, we have $\delta _t(U,\alpha ) = r_{i_t}(x)$. This proves claim (23).

For two vectors $\alpha , \beta \in {{\mathbb {R}}}^S$, we have already used the notation $\alpha \ge \beta$ to mean $\alpha _t \ge \beta _t$ for all $t\in S$. Clearly, the relation ’$\ge$’ defines a partial order on the set $\Omega ^{**}$. As any finite poset has at least one maximal element, we can choose a maximal element in $\Omega ^{**}$, which we denote by $\alpha ^*$.

Now, let $U\in {\mathcal {U}}(\alpha ^*)$. We proved $\delta (U,\alpha ^*) \in \Omega ^{**}$. Then we cannot have $\delta (U,\alpha ^*) \ge \alpha ^*$ and $\delta (U,\alpha ^*) \ne \alpha ^*$, as this would contradict the choice of $\alpha ^*$ as a maximal element in $\Omega ^{**}$. We do have $\delta (U,\alpha ^*) \ge \alpha ^*$ by Lemma 13. Therefore, $\delta (U,\alpha ^*) = \alpha ^*$.

It follows that $\delta (U,\alpha ^*) = \alpha ^*$ for all $U\in {\mathcal {U}}(\alpha ^*)$. $\square$