Abstract
This paper analyzes the set of pure strategy subgame perfect Nash equilibria of any finitely repeated game with complete information and perfect monitoring. The main result is a complete characterization of the limit set, as the time horizon increases, of the set of pure strategy subgame perfect Nash equilibrium payoff vectors of the finitely repeated game. This model includes the special case of observable mixed strategies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper provides a full characterization of the limit set, as the time horizon increases, of the set of pure strategy subgame perfect Nash equilibrium payoff vectors of any finitely repeated game. The obtained characterization is in terms of appropriate notions of feasible and individually rational payoff vectors of the stage-game. These notions are based on Smith’s (1995) notion of Nash decomposition and appropriately generalize the classic notion of feasible payoff vectors as well as the notion of effective minimax payoff defined by Wen (1994). The main theorem nests earlier results of Benoit and Krishna (1985), Smith (1995), and Demeze-Jouatsa and Wilson (2019).
Whether non-Nash outcomes of the stage-game can be sustained via subgame perfect Nash equilibria of the finitely repeated game depends on whether players can be incentivized to abandon their short term interests and to follow some collusive paths that have greater long-run average payoffs. There are two extreme cases. On the one hand, in any finite repetition of a stage-game that has a unique Nash equilibrium payoff vector such as the prisoners’ dilemma, only the stage-game Nash equilibrium payoff vector is sustainable by subgame perfect Nash equilibria of finite repetitions of that stage-game. On the other hand, for stage-games in which all players receive different Nash equilibrium payoffs such as the battle of sexes, the limit perfect folk theorem holds: any feasible and individually rational payoff vector of the stage-game is achievable as the limit payoff vector of a sequence of subgame perfect Nash equilibria of the finitely repeated game as the time horizon goes to infinity.
Benoit and Krishna (1985) established that for the limit perfect folk theorem to hold, it is sufficient that the dimension of the set of feasible payoff vectors of the stage-game equals the number of players and that each player receives distinct payoffs at Nash equilibria of the stage-game.Footnote 1 Smith (1995) provided a weaker, necessary and sufficient condition for the limit perfect folk theorem to hold. Smith (1995) showed that it is necessary and sufficient that the Nash decomposition of the stage-game is complete.Footnote 2 The distinct Nash payoffs condition and the full dimensionality of the set of feasible payoff vectors as in Benoit and Krishna (1985) or the complete Nash decomposition of Smith (1995) allow us to construct credible punishment schemes and to (recursively) leverage the behavior of any player near the end of the finitely repeated game. These are essential to generate a limit perfect folk theorem. In the case that the stage-game admits a unique Nash equilibrium payoff vector, Benoit and Krishna (1985) demonstrated that the set of subgame perfect Nash equilibrium payoff vectors of the finitely repeated game is reduced to the unique stage-game Nash equilibrium payoff vector.
A part of the puzzle remains unresolved. Namely, for stage-games that do not admit a complete Nash decomposition, what is the exact range of payoff vectors that are achievable as the limit payoff vector of a sequence of subgame perfect Nash equilibria of finite repetitions of that stage-game?Footnote 3
If the stage-game has an incomplete Nash decomposition, then the set of players naturally breaks up into two blocks where the first block contains all the players whose behavior can recursively be leveraged near the end of the finitely repeated game (see Footnote 2 for details). In contrast, it is not possible to control short run incentives of players of the second block. Therefore, each player of the second block has to play a stage-game pure best response at any profile that occurs on a pure strategy subgame perfect Nash equilibrium play path. Stage-game action profiles eligible for pure strategy subgame perfect Nash equilibrium play paths of the finitely repeated game are therefore exactly the stage-game pure Nash equilibria of what one could call the effective one shot game, the game obtained from the initial stage-game by setting the utility function of each player of the first block equal to a constant.
This restriction of the set of eligible actions for pure strategy subgame perfect Nash equilibrium play paths has two main implications. Firstly, for a feasible payoff vector to be approachable via pure strategy subgame perfect Nash equilibria of the finitely repeated game, it has to be in the convex hull of the set of payoffs to profiles of actions that are Nash equilibria of the effective one shot game. I introduce the concept of enforceable payoff vector. I call a payoff vector enforceable if it belongs to the convex hull of the set of payoff vectors to profile of actions that are Nash equilibria of the effective one shot game. Secondly, as subgame perfect Nash equilibria are protected against unilateral deviations even off-equilibrium paths, any player of the second block has to be at her best response at any action profile occurring on a credible punishment path. Therefore, only pure Nash equilibria of the effective one shot game are eligible for credible punishment paths in any finite repetition of the original stage-game. Consequently, a player of the first block can guarantee herself a payoff that is strictly greater than her effective minimax payoff. I call this new reservation payoff the enforceable minimax payoff.
The main finding of this paper says that, as the time horizon increases, the set of payoff vectors to pure strategy subgame perfect Nash equilibria of the finitely repeated game converges to the set of enforceable payoff vectors that dominate the enforceable minimax payoff vector.
The paper proceeds as follows. In Sect. 2 I introduce the model and the definitions. Section 3 states the main finding of the paper and sketches the proof, and Sect. 4 concludes the paper. Proofs are provided in the Appendix.
2 The model
2.1 The stage-game
Let \(G=(N,A=\times _{i \in N}A_{i},u=(u_{i})_{i\in N})\) be a stage-game where the set of players \(N=\{1,\ldots ,n\}\) is finite and where for all player \(i \in N\) the set \(A_{i}\) of actions of player i is compact. Given a player \(i\in N\) and an action profile \(a=(a_{1},\ldots ,a_{n})\in A\), let \(u_{i}(a)\) denote the stage-game utility of player i given the action profile a. Given an action profile \(a\in A\), \(i\in N\) a player, and \(a_{i}^{\prime }\in A_{i}\) an action of player i, let \((a_{i}^{\prime },a_{-i})\) denote the action profile in which all players except player i choose the same action as in a, while player i chooses \(a_{i}^{\prime }\). A stage-game pure best response of player i to the action profile a is an action \(b_{i}(a)\in A_{i}\) that maximizes the stage-game payoff of player i given that the choice of other players is given by \(a_{-i}\). An action profile \(a\in A\) is a pure Nash equilibrium of the stage-game G (denoted by \(a\in {\text {Nash}}(G)\)) if \(u_{i}(a_{i}^{\prime },a_{-i})\le u_{i}(a)\) for all player \(i\in N\) and all action \(a_{i}^{\prime }\in A_{i}\).
Each stage-game considered in this paper is compact in the sens that each \(A_i\) is compact, and u is continuous. A stage-game could for instance be finite, the mixed extension of another finite stage-game, or a game with a continum of actions for some players.
Let \(\gamma \) be a real number that is strictly greater than any payoff a player might receive in the stage-game G.Footnote 4 A player is said to have distinct pure Nash payoffs in the stage-game if there exist two pure Nash equilibria of the stage-game in which this player receives different payoffs. Let \(\tau (G)=(N,A,(u'_i)_{i \in N}) \) be the normal form game where the utility function of player i is defined by
Let \(G^{0}:=G\) and \(G^{l+1}:=\tau (G^{l})\) for all \(l\ge 0\). For all \(l\ge 0,\) let \(N_{l}\) be the set of players with a utility function that is constant to \(\gamma \) in the game \(G^{l}\). As N is finite, there is an \(h\in [0,+\infty )\) such that \(N_{l+1}=N_{l}\) for all \(l \ge h\). Let \({\widetilde{A}}={\text {Nash}}(G^{h})\) be the set of pure Nash equilibria of the game \(G^h\). We call \({\widetilde{A}}\) the enforceable action set. The set of enforceable payoff vectors of the game G is defined as the convex hull \(Conv[u({\widetilde{A}})]\) of the set \(u( {\widetilde{A}})=\{u(a) \mid a \in {\widetilde{A}}\}\). The sequence \(0\varsubsetneq N_1 \varsubsetneq \cdots \varsubsetneq N_h\) is the Nash decomposition of the game G, and the Nash decomposition is complete if \(N_h=N\).Footnote 5
Let \(\sim \) be the equivalence relation defined on the set of players as follows: player i is equivalent to j (denoted by \(i\sim j\)) if there exist \(\alpha _{ij}>0\) and \(\beta _{ij} \in {\mathbb {R}}\) such that for all \(a\in {\widetilde{A}}\), we have \(u_{i}(a)=\alpha _{ij}\cdot u_{j}(a)+\beta _{ij}\). For all \(i\in N\), let \({\mathcal {J}}(i)\) be the equivalence class of player i and let
The payoff \({\widetilde{\mu }}_{i}\) is the enforceable minimax of player i in the stage-game G.Footnote 6
Call a payoff vector e-rational if it dominates the enforceable minimax payoff vector \({\widetilde{\mu }}\). Let \({\widetilde{I}}=\{x=(x_1,\ldots ,x_n) \in {\mathbb {R}} \mid x_i \ge {\widetilde{\mu }}_i \text { for all } i \in N \}\) be the set of e-rational payoff vectors.
The name “enforceable action” comes from Fudenberg et al. (2009) notion of enforceability, which requires an action to be incentive compatible given some set of continuation payoffs. The concepts of enforceable payoff and enforceable minimax are respective generalizations of the classic concepts of feasible payoff and effective minimax, viewed as indicators to derive the perfect folk theorem for finitely repeated games. If each player receives (recursively) distinct payoffs at Nash equilibria of the stage-game, then the behavior of each player can be leveraged if the game is finitely repeated. In that case, the enforceable action set \({\widetilde{A}}\) equals the whole set A of action profiles, the enforceable minimax equals the classic effective minimax, and the set of enforceable payoffs vectors equals the set of feasible payoff vectors. In the other case, the set of enforceable actions \({\widetilde{A}}\) is a proper subset of the whole set of profile of pure actions, the set of enforceable payoff vectors is a proper subset of the classic set of feasible payoff vectors, and the enforceable minimax of a player can be strictly greater than her effective minimax.Footnote 7 Figure 1 uses the example of Footnote 3 to illustrate the differences between our newly introduced concepts and the classic ones. Only payoffs of players 1 and 2 are displayed. In that game, pure action profiles where player 1 chooses OM and player 2 chooses C are not enforceable. The effective minimax payoff vector equals (1, 0, 0, 0) and the enforceable minimax payoff vector equals (1, 1, 0, 0).Footnote 8
2.2 The finitely repeated game
Let G be the stage-game. Given \(T>0\), let G(T) denote the T-fold repeated game obtained by repeating the stage-game T times. A pure strategy of player i in the repeated game G(T) is a contingent plan that provides for each history the action chosen by player i given this history. That is, a strategy is a function \(\sigma _{i}:\bigcup \nolimits _{t=1}^{T}A^{t-1}\rightarrow A_{i}\) where \(A^{0}\) contains only the empty history.Footnote 9 The strategy profile \(\sigma =(\sigma _{1},\ldots ,\sigma _{n})\) of G(T) generates a play path \(\pi (\sigma )=[\pi _1({\sigma }),\ldots ,\pi _T({\sigma })]\in A^{T}\) and player \(i\in N\) receives a sequence \((u_{i}(\pi _{t}(\sigma ))_{1\le t\le T}\) of payoffs. The preferences of player \(i\in N\) among strategy profiles are represented by the average payoff \(u_{i}^{T}(\sigma )=\frac{1}{T} \sum \nolimits _{t=1}^{T}u_{i}[\pi _t(\sigma )]\). A strategy profile \(\sigma =(\sigma _{1},\ldots ,\sigma _{n})\) is a pure strategy Nash equilibrium of G(T) if \(u_{i}^{T}(\sigma _{i}^{\prime },\sigma _{-i})\le u_{i}^{T}(\sigma )\) for all \(i\in N\) and for all pure strategies \(\sigma _{i}^{\prime }\) of player i. A strategy profile \(\sigma =(\sigma _{1},\ldots ,\sigma _{n})\) is a pure strategy subgame perfect Nash equilibrium of G(T) if given any \( t\in \{1,\ldots ,T\}\) and any history \(h^{t}\in A^{t-1}\), the restriction \(\sigma _{\mid h^{t}}\) of \(\sigma \) to the history \(h^{t}\) is a Nash equilibrium of the finitely repeated game \(G(T-t+1)\).
For any \(T>0\), let E(T) be the set of pure strategy subgame perfect Nash equilibrium payoff vectors of G(T). Let E be such that the Hausdorff distance between E(T) and E goes to 0 as T goes to infinity.Footnote 10 The set E is the Hausdorff limit of the set of pure strategy subgame perfect Nash equilibrium payoff vectors of the finitely repeated game. As I show later in the Appendix A, the limit set E exists, is nonempty, convex, and compact.
3 Main result
Theorem 1
Let G be a compact stage-game. As the time horizon increases, the set of pure strategy subgame perfect Nash equilibrium payoff (average payoff) vectors of the finitely repeated game converges (in the Hausdorff sense) to the set of enforceable and e-rational payoff vectors.
A constructive proof of Theorem 1 is provided in the appendix. It uses four main lemmata. Lemma 3 states that as the time horizon increases, the set of pure strategy subgame perfect Nash equilibrium payoffs of the finitely repeated game converges to a well defined set, \({\text {ASPNE}}(G)\), which is the set of payoffs that are approachable via pure strategy subgame perfect Nash equilibria. Lemmata 4 and 5 together say that the limit set of the set of pure strategy subgame perfect Nash equilibrium payoff vectors, which equals the set \({\text {ASPNE}}(G)\), is included in the set of enforceable and e-rational payoff vectors. Lemma 6 states that every enforceable and e-rational payoff vector belongs to the set \({\text {ASPNE}}(G)\). The enforceability and the e-rationality can therefore be observed as necessary and sufficient conditions on feasible payoffs to be approachable via pure strategy subgame perfect Nash equilibria of the finitely repeated game.
Theorem 1 assumes no discounting. This assumption is without loss of generality. One can indeed check that as the discount factor goes to 1, the discounted average converges to the average payoff. Therefore, if the average payoff of a player to a path \(\pi \) is strictly greater than her average payoff to another path \(\pi ^{\prime }\), then the discounted average payoff of that player to the path \(\pi \) is strictly greater than her discounted average to \(\pi ^{\prime }\), given that the discount factor is high enough. One can also make use of the payoff continuation lemma for finitely repeated games and prove a stronger result.Footnote 11 With a fixed discount factor, one can show that the limit set of the set of pure strategy subgame perfect Nash equilibrium payoffs of the discounted finitely repeated game equals the set of enforceable and e-rational payoffs, given that the discount factor exceeds a threshold \({\underline{\delta }}\).
4 Conclusion
This paper analysed the set of pure strategy subgame perfect Nash equilibrium payoff vectors of the finitely repeated games with complete information. The main finding is an effective folk theorem. It is a complete characterization of the limit set, as the time horizon increases, of the set of pure strategy subgame perfect Nash equilibrium payoff vectors of the finitely repeated game. As the time horizon increases, the limiting set always exists, is compact, convex and can be strictly in-between the convex hull of the set of stage-game Nash equilibrium payoff vectors and the classic set of feasible and individually rational payoff vectors. This finding exhibits the exact range of cooperative payoffs that players can achieve via subgame perfect Nash equilibria of the finitely repeated game.
One point of this work is that it provides a full characterization of the optimal punishment payoff of finitely repeated games with complete information and perfect monitoring (Benoit and Krishna 1985, Gossner and Hörner 2010).
The method of this paper applies to the Nash equilibrium case. In this particular case, to leverage the behaviour of a player near the end of the finitely repeated game, it is necessary and sufficient that the latter player either has a pure Nash equilibrium payoff that is strictly greater than her pure minimax payoff, or that there exists a recursive Nash equilibrium in which the latter player receives a payoff that is different from her pure minimax payoff. Pure actions eligible for pure strategy Nash equilibrium play paths of the finitely repeated game are therefore the pure Nash equilibrium profiles of a new stage-game obtained from the original stage-game by setting the utility functions of players whose behaviour can be leverage near the end of the finitely repeated game to a constant. I refer to the convex hull of the set of original payoffs to eligible profiles as the set of Nash-feasible payoffs. As the time horizon increases, the set of pure strategy Nash equilibrium payoff vectors of the finitely repeated game converges to the set of Nash-feasible payoffs vectors that dominate the pure minimax payoff vector. This characterization of the limit set of the set of Nash equilibrium payoff vectors of the finitely repeated game nests early results of Benoit and Krishna (1987) and González-Díaz (2006).
One might wonder if similar method applies in the case that players can employ unobservable mixed strategies (Gossner 1995), in the case that the monitoring technology is imperfect (see Fudenberg et al. 2007 for the infinite horizon case, and with public monitoring), or in the case that equilibrium strategies are protected against renegotiation (Benoit and Krishna 1993).
Notes
Fudenberg and Maskin (1986) introduced the notion of full dimensionality of the set of feasible payoff vectors and used it to provide a sufficient condition for the perfect folk theorem for infinitely repeated games.
The Nash decomposition of a normal form game is a strictly increasing sequence of non-empty groups of players. Players of the first group are those who receive at least two distinct Nash equilibrium payoffs in the stage-game. The second group of players of the Nash decomposition, if any, contains each player of the first group as well as some new players. New players are those who receive at least two distinct Nash equilibrium payoffs in the new game that is obtained from the stage-game by setting the utility function of each player of the first group equal to a constant. This idea can be iterated. After a finite number of iterations, the player set no longer changes. The Nash decomposition is complete if its last element equals the whole set of players.
Consider the following 4-player stage-game. Player 1 is a social planer who wishes to maximize the welfare of a representative agent, player 2 is a monopolist in the market, and players 3 and 4 are potential entrants to the market. The latter entrants need both approval and support of the planer (player 1) to enter the market and make profit. Player 1 can choose either to open the market to the potential entrants (OM) or to keep it closed (CM), player 2 can choose either to cooperate (C) or to deviate (D) and maximize her profit in the detriment of consumers. Player 3 can choose up (U) or down (D) and player 4 can choose L or R. The Payoffs of the game are given by the following table:
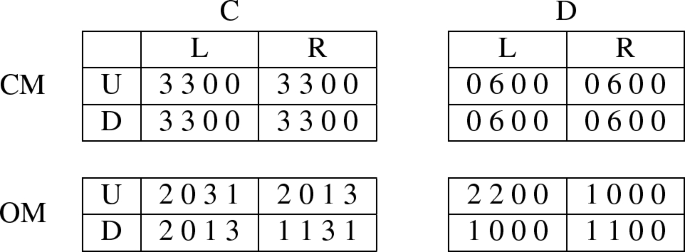
This game admits two pure Nash equilibrium profiles with respective payoff vectors (2,2,0,0) and (1,1,0,0), which are both strictly Pareto-dominated, for instance by the feasible payoff \((\frac{17}{8},\frac{19}{8},1,1)\). One might wonder if in the finite repetitions of this game players could cooperate and achieve efficiency via equilibrium strategies of the repeated game. As only players 1 and 2 receive distinct payoffs at pure Nash equilibria of the stage-game, the distinct Nash payoff condition of Benoit and Krishna (1985) does not hold. Furthermore, given any fixed profile of action of players 1 and 2, the 2-player induced game (played by players 3 and 4) does not admit a pure Nash equilibrium that has a payoff that is different from (0, 0). This means that the complete Nash decomposition condition of Smith (1995), which is necessary and sufficient for the finite horizon perfect folk theorem, does not hold. As a consequence, the finite horizon perfect folk theorem does not hold for this game. If it is immediate that players can cooperate and achieve some payoffs that are weakly Pareto-superior to any stage-game Nash equilibrium payoff, for instance (2.7, 2.7, 0, 0) in 10 repetitions, it is not clear what is the exact set of payoffs vectors that can be achieved via subgame perfect equilibria of the finitely repeated game.
As the set A of action profiles is compact and the utility function u is continuous on A, the set \(u(A)=\{u(a) \mid a \in A\}\) is compact and therefore bounded. This guarantees the existence of \(\gamma \).
While being equivalent to Smith’s (1995) definition of Nash decomposition, ours is simpler and requires to analyse no more than n simple transformations of the stage-game, while Smith’s definition requires, in many cases, to analyse at least \(2^{n-1}\) subgames, n being the number of players. Smith (1995) proved that having a complete Nash decomposition is a necessary and sufficient condition for the limit perfect folk theorem to hold. Under a complete Nash decomposition, the set of enforceable payoff vectors equals the classic set of feasible payoff vectors and the enforceable minimax payoff vector equals the classic effective minimax payoff vector. In that case, the main result (see Theorem 1) says that any feasible payoff vector that dominates the effective minimax payoff vector is approachable via pure strategy subgame perfect Nash equilibria of the finitely repeated game. That is the message of the limit perfect folk theorem. Benoit and Krishna (1985) showed that, if the dimension of the set of feasible payoff vectors of the stage-game equals the number of players and each player receives at least two distinct payoffs at pure Nash equilibria of the stage-game, then the limit perfect folk theorem holds. This result is a particular case of the main result of this paper, Theorem 1. Indeed, under the distinct stage-game Nash equilibrium payoffs condition of Benoit and Krishna (1985), the Nash decomposition of the stage-game equals \(\varnothing \varsubsetneq N_h=N\) which is complete and therefore the set of the enforceable payoff vectors equals the classic set of the feasible payoff vectors and the enforceable minimax payoff vector equals the classic effective minimax payoff vector. Furthermore, under the full dimensionality condition, the effective minimax payoff vector equals the minimax payoff vector.
If the stage-game G does not have any pure Nash equilibrium, then the set of pure strategy subgame perfect Nash equilibrium payoff vectors of the finitely repeated game is empty. If the stage-game G admits at least one pure Nash equilibrium, then \({\widetilde{A}}\) is non-empty and \({\widetilde{\mu }}\) is well defined.
Exceptions are degenerated games where at least one player has a constant utility function.
Note that the enforceable minimax payoff vector weakly Pareto-dominates the effective minimax payoff vector.
If the stage-game G is the mixed extension of another finite stage-game and mixed actions are observable, then players can condition their actions on the mixed actions themselves instead of outcomes of randomization devices.
Let d be the Euclidean distance of \({\mathbb {R}}^n\), A and B be two closed and bounded non-empty subsets of the metric space \(({\mathbb {R}}^{n},d)\). The Hausdorff distance (based on d) between A and B is given by \( d_{H}(A,B)=\max \left\{ \sup _{x\in A}d(x,B),\sup _{y\in B}d(y,A)\right\} , \) where \(d(x,Y)=\inf _{y\in Y}d(x,y).\)
Fudenberg and Maskin (1991) provides a payoff continuation lemma for infinitely repeated games with discounting. The payoff continuation lemma for finitely repeated games say that: for any \(\varepsilon >0,\) there exists \(k>0\) and \(\underline{\delta }<1\) such that for any feasible payoff vector x, there exists a deterministic sequence of profile of stage-game actions \(\left\{ a^{\tau }\right\} _{\tau =1}^{k}\) whose discounted average payoff is within \(\varepsilon \) of x for all discount factor \(\delta \ge {\underline{\delta }}\). A proof of this lemma is provided in Demeze-Jouatsa (2019).
A feasible payoff vector x is approachable via pure strategy subgame perfect Nash equilibria of the finitely repeated game if for all \(\varepsilon >0 \ \) there exists an integer \(T_{\varepsilon }\) such that for all \(T>T_{\varepsilon }\), the finitely repeated game G(T) has a pure strategy subgame perfect Nash equilibrium whose average payoff vector is within \(\varepsilon \) of x.
Indeed, as each pure Nash equilibrium of the stage-game G is a pure Nash equilibrium of the game \(G^h\) and each player plays a best response in Nash equilibrium, the Nash equilibrium payoff of any player is greater than or equal to her enforceable minimax payoff. It follows that any pure Nash equilibrium payoff vector weakly dominates the enforceable minimax payoff vector.
At the profile of actions \(w^i\), player i does not have to be at a pure best response. If she plays a pure best response to \(w^i\), she receives at least her stage-game pure minimax payoff but no more than her stage-game enforceable minimax payoff.
References
Abreu D, Dutta PK, Smith L (1994) The folk theorem for repeated games: a NEU condition. Econometrica 62(4):939–948
Benoit JP, Krishna V (1985) Finitely repeated games. Econometrica 53(1):905–922
Benoit JP, Krishna V (1987) Nash equilibria of finitely repeated games. Int J Game Theory 16(3):197–204
Benoit JP, Krishna V (1993) Renegotiation in finitely repeated games. Econom J Econom Soc 62:303–323
Demeze-Jouatsa GH (2019) Essays on finitely repeated games (doctoral dissertation). Universität Bielefeld, Bielefeld
Demeze-Jouatsa GH, Wilson A (2019) Comment on “smith (1995): Perfect finite horizon folk theorem”. Econometrica. https://www.econometricsociety.org/content/comment-%E2%80%9Csmith-1995-perfect-finite-horizon-folk-theorem (online)
Fudenberg D, Maskin E (1986) The folk theorem in repeated games with discounting or with incomplete information. Econometrica 54(3):533–554
Fudenberg D, Maskin E (1991) On the dispensability of public randomization in discounted repeated games. J Econ Theory 53(2):428–438
Fudenberg D, Levine DK, Takahashi S (2007) Perfect public equilibrium when players are patient. Games Econ Behav 61(1):27–49
Fudenberg D, Levine D, Maskin E (2009) The folk theorem with imperfect public information. In: A long-run collaboration on long-run games, World Scientific, pp 231–273
González-Díaz J (2006) Finitely repeated games: a generalized Nash folk theorem. Games Econ Behav 55(1):100–111
Gossner O (1995) The folk theorem for finitely repeated games with mixed strategies. Int J Game Theory 24(1):95–107
Gossner O, Hörner J (2010) When is the lowest equilibrium payoff in a repeated game equal to the minmax payoff? J Econ theory 145(1):63–84
Smith L (1995) Necessary and sufficient conditions for the perfect finite horizon folk theorem. Econometrica 63(2):425–430
Wen Q (1994) The “folk theorem” for repeated games with complete information. Econometrica 62(4):949–954
Funding
Open Access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
I acknowledges DAAD and the DFG (Deutsche Forschungsgemeinschaft/German Research Foundation) via Grant Ri 1128-9-1 (Open Research Area in the Social Sciences, Ambiguity in Dynamic Environments) for funding support and thank Christoph Kuzmics, Frank Riedel, Lones Smith, Michael Greinecker, Karl Schlag, Roland Pongou, Tondji-Jean Baptiste and Olivier Gossner for useful comments. I also thank seminar and conference participants at Bielefeld University, Cardiff University, University of Yaoundé I, Stony Brook University, Lisbon School of Economics and Management, and University of Graz for positive inputs. I thank two anonymous reviewers and an associated editor for their comments and suggestions.
Appendices
Appendix
A. Existence of the limit set of the set of equilibrium payoffs
In this section, I show that the limit set of the set of pure strategy subgame perfect Nash equilibrium payoff vectors of any finitely repeated game is well defined. Precisely, I prove that for any compact stage-game, the set of feasible payoff vectors that are approachable via pure strategy subgame perfect Nash equilibria of the finitely repeated game equals the limit set E. As corollary, I obtain that the limit set E is a compact and convex subset of the set of feasible payoff vectors of the stage-game. The main ingredient of this proof is the conjunction lemma-henceforth, Lemma CBK-established by Benoit and Krishna (1985). Lemma CBK states that the conjunction of two subgame perfect Nash equilibrium play paths is a subgame perfect Nash equilibrium play path of the corresponding finitely repeated game.
Let G be a compact stage-game and let \({\text {ASPNE}}(G)\) be the set of all feasible payoff vectors of G that are approachable via pure strategy subgame perfect Nash equilibrium payoff vectors of the finitely repeated game.Footnote 12
Lemma 1
The set \({\text {ASPNE}}(G)\) is compact and convex.
Proof of Lemma 1
The reader can check that \({\text {ASPNE}}(G)\) is a closed subset of the set of feasible payoff vectors which is compact. The set \({\text {ASPNE}}(G)\) is therefore compact. Since \({\text {ASPNE}}(G)\) is closed, its convexity holds if \(z=\frac{1}{2}(x+y)\in {\text {ASPNE}}(G)\) for all \( x,y\in {\text {ASPNE}}(G)\), which follows from Lemma CBK. \(\square \)
Lemma 2
For all \(T>0, \ E(T)\subseteq {\text {ASPNE}}(G).\)
Proof of Lemma 2
Let \(\sigma \) be a pure strategy subgame perfect Nash equilibrium of the finitely repeated game G(T) and \(\pi (\sigma )=(\pi _1(\sigma ),\cdots ,\pi _T(\sigma ))\) be the play path generated by \(\sigma \). Let \(x=u^T(\sigma )\). For all \(s\ge 0\) and \(t \in \{2,\cdots ,T\}\), let
be a play path of \(G((s+1)T-t+1)\). From Lemma CBK, \(\pi (s,l)\) is a pure strategy subgame perfect Nash equilibrium play path of the finitely repeated game \(G((s+1)T-t+1)\). Moreover, the sequence of payoff vectors \(\left( u^{(s+1)T-t+1}[\pi (s,l)]\right) _{s\ge 0}\) converges to x. \(\square \)
Lemma 3
As the time horizon increases, the set of pure strategy subgame perfect Nash equilibrium payoff vectors of the finitely repeated game converges (in the Hausdorff sense) to the set \({\text {ASPNE}}(G)\).
Proof of Lemma 3
Let \(\varepsilon >0\). We search for \(T_{\varepsilon }>0\) such that for all \(T>T_{\varepsilon }\), \(d_{H}({\text {ASPNE(G)}},E(T))\) \(<\varepsilon \). Let \(\{B(x^{l},\frac{\varepsilon }{2}) \ \mid x^{l},l=1,\ldots ,L\}\) be a finite covering of \({\text {ASPNE}}(G)\), where \(B(x,\varepsilon )=\left\{ y\in {\mathbb {R}}^{n}\text { }/\text { }d(x,y)<\varepsilon \right\} \). For all \(l=1,\ldots ,L\) take \(T_{0}^{l} \) given by the definition of “\(x^{l}\in {\text {ASPNE}}(G)\)” with \(\frac{\varepsilon }{2}\). Pose \(T_{0}=\max _{l\le L}T_{0}^{l}\). Let \(T>T_{0}\) and let \(x\in {\text {ASPNE}}(G)\). Let \( x^{l_{0}}\in {\text {ASPNE}}(G)\) be such that \(x\in B(x^{l_{0}},\frac{\varepsilon }{2})\) and let \(y\in E(T)\) be such that \(d(x^{l_{0}},y)<\frac{\varepsilon }{2}\). We have \( d(x,y)\le d(x,x^{l_{0}})+d(x^{l_{0}},y)<\varepsilon .\) This implies that \( d(x,E(T))<\varepsilon .\) Consequently, \(\sup _{x\in {\text {ASNPE}}(G)}d(x,E(T))\le \varepsilon .\) Furthermore, from Lemma 2, \(d(y,{\text {ASPNE}}(G))=0\) for all \(y\in E(T).\) That is \(\sup _{y\in E(T)}d(y,{\text {ASPNE}}(G))=0.\) It follows that \( d_{H}({\text {ASPNE}}(G),E(T))\) \(=\sup _{x\in P}d(x,E(T))\le \varepsilon \) for all \(T>T_{0}.\) Take \(T_{\varepsilon }=T_{0}\). \(\square \)
B. Necessity of enforceability
Lemma 4
Let G be a compact normal form game, let \(T>0\), and let \(\sigma \) be a pure strategy subgame perfect Nash equilibrium of G(T). The support \({\text {Supp}}(\pi (\sigma ))=\{\pi _1(\sigma )\ldots \pi _T(\sigma ) \}\) of the subgame perfect Nash equilibrium play path \(\pi (\sigma )=(\pi _1(\sigma )\ldots \pi _T(\sigma ) )\) is included in the set \({\text {Nash}}(G^{h})\) of pure Nash equilibrium profiles of the effective game \(G^h\).
Proof of Lemma 4
If \(N_{h}=N,\) then \({\text {Nash}}(G^{h})=A\) and \({\text {Supp}}(\pi (\sigma ))\subseteq {\text {Nash}}(G^{h})\). Now assume that \(N\backslash N_{h}\ne \emptyset \).
Let’s proceed by induction on the time horizon T.
For \(T=1\), the pure strategy subgame perfect Nash equilibrium \(\sigma \) is a pure Nash equilibrium of the stage-game G, and \({\text {Nash}}(G)={\text {Nash}}(G^0)\subseteq {\text {Nash}}(G^h)\).
Suppose that \(T>1\) and that the support of any pure strategy subgame perfect Nash equilibrium play path of the finitely repeated game G(t) with \(t \in \{1,\ldots ,T-1\}\) is included in the set \({\text {Nash}}(G^h)\) and let’s show that \(\{\pi _1(\sigma ),\ldots , \pi _T(\sigma ) \} \subseteq {\text {Nash}}(G^h)\). The restriction \(\sigma _{\left| \pi _{1}(\sigma )\right. }\) of \(\sigma \) to the history \(\pi _1(\sigma )\) is a pure strategy subgame perfect Nash equilibrium of the game \(G(T-1)\) and the induction hypothesis implies that the support \(\{\pi _2(\sigma )\ldots \pi _T(\sigma ) \}\) of the play path \(\pi (\sigma _{\left| \pi _{1}(\sigma )\right. })\) generated by the strategy profile \(\sigma _{\left| \pi _{1}(\sigma )\right. }\) is included in \({\text {Nash}}(G^h)\).
It remains to show that \(\pi _{1}(\sigma ) \in {\text {Nash}}(G^h)\).
At this point I proceed by contradiction. Assume that \(\pi _{1}(\sigma ) \notin {\text {Nash}}(G^{h})\). Then, in the game \(G^h\), there exists a player \(i\in N\) who has a strict incentive to deviate from the pure action profile \(\pi _{1}(\sigma )\). This player has to be in the block \(N \backslash N_h\) since any player of the block \(N_h\) has a constant utility function in the game \(G^h\). Let \(\sigma _{i}^{\prime }\) be a pure strategy one shot deviation of player i from \(\sigma \) that consists in playing a stage-game pure best response \(b_{i}[\pi _{1}(\sigma )]\) to \(\pi _{1}(\sigma )\) in the first round of the finitely repeated game G(T), and conforming to \(\sigma _{i}\) from the second round on. At the pure strategy profile \((\sigma _{i}^{\prime },\sigma _{-i})\), player i receives \(u_{i}(\pi ^{1})+e\) (with \(e>0\)) in the first round. Let \(h^{1}=(b_{i}(\pi _{1}(\sigma )),\pi _1(\sigma )_{-i})\) be the observed history after this first round and \(\sigma _{\left| h^{1}\right. }\) be the restriction of \(\sigma \) to the history \(h^{1}\). We have \((\sigma _{i}^{\prime },\sigma _{-i})_{\left| h^{1}\right. }=\sigma _{\left| h^{1}\right. }\) and \( \sigma _{\left| h^{1}\right. }\) is a pure strategy subgame perfect Nash equilibrium of \(G(T-1)\). By induction hypothesis, the support of the play path generated by \(\sigma _{\left| h^{1}\right. }\) is included in \({\text {Nash}}(G^{h})\). Therefore, at the profile \((\sigma _{i}^{\prime },\sigma _{-i})\) player i receives the sequence of stage-game payoffs \(\{u_{i}(\pi ^{1})+e,n_{i},\dots ,n_{i}\}\) where \(n_{i}\) is her unique stage-game pure Nash equilibrium payoff. Since player i receives \(\{u_{i}(\pi _{1}(\sigma )),n_{i},\ldots n_{i}\}\) at the strategy profile \(\sigma \), we have \(u_{i}^{T}(\sigma _{i}^{\prime },\sigma _{-i})>u_{i}^{T}(\sigma )\). This contradicts the fact that \(\sigma \) is a pure strategy subgame perfect Nash equilibrium of G(T) and concludes the proof. \(\square \)
Let \({\widetilde{F}}\) be the set of enforceable payoff vectors. We have the following corollary.
Corollary 1
Let G be a compact normal form game, let \(T>0\), and let \(\sigma \) be a pure strategy subgame perfect Nash equilibrium of G(T). Then the average payoff vector \(u^{T}(\sigma )\) belongs to the set \({\widetilde{F}}\).
C. Necessity of the e-rationality
Wen (1994) shows that any subgame perfect Nash equilibrium payoff vector of the infinitely repeated game weakly dominates the effective minimax payoff vector. This domination also holds for finitely repeated games. The following lemma provides a sharper lower bound of the set of equilibrium payoffs of the finitely repeated game. The lemma says that, any pure strategy subgame perfect Nash equilibrium payoff vector of the finitely repeated game weakly dominates the enforceable minimax payoff vector.
Lemma 5
Let G be a compact normal form game, let \(T\ge 1\), and let \(\sigma \) be a pure strategy subgame perfect Nash equilibrium of the finitely repeated game G(T). Then the average payoff vector \(u^T(\sigma )\) dominates the enforceable minimax payoff vector of the stage-game.
Proof of Lemma 5
I proceed by induction on the time horizon T.
At \(T=1\), pure strategy subgame perfect Nash equilibria of the game G(T) are pure Nash equilibria of the stage-game G and \(u^T(\sigma )\) dominates \({\widetilde{\mu }}\).Footnote 13
Assume that \(T>1\) and that the average payoff vector to any pure strategy subgame perfect Nash equilibrium of the finitely repeated game G(t) with \(0<t<T\) dominates the enforceable minimax payoff vector \({\widetilde{\mu }}\). Let us show that the payoff vector \(u^T(\sigma )\) dominates \({\widetilde{\mu }}\).
Let \(\pi _{1}(\sigma )\) be the action profile played in the first round of the game G(T) according to \(\sigma \). The restriction \(\sigma _{\left| \pi _{1}(\sigma )\right. }\) of the strategy \(\sigma \) to the history \(\pi _{1}(\sigma )\) is a pure strategy subgame perfect Nash equilibrium of the finitely repeated game \(G(T-1)\) and by induction hypothesis, we have that the payoff vector \(u^{T-1}(\sigma _{\left| \pi _{1}(\sigma )\right. })\) dominates \({\widetilde{\mu }}\). Suppose now that \(u^{T}(\sigma )\) does not dominates \({\widetilde{\mu }}\). Then there exists a player \(i \in N\) such that \(u_i^{T}(\sigma )<{\widetilde{\mu }}_i\). It follows that \(u_i[\pi _1(\sigma )]<{\widetilde{\mu }}_i\) since \(u_{i}^{T}(\sigma )\) is a convex combination of \(u_{i}[\pi _{1}(\sigma )]\) and \(u_{i}^{T-1}(\sigma _{\left| \pi _{1}(\sigma )\right. })\). Moreover, as \(\pi _1(\sigma ) \in {\text {Nash}}(G^h)\), we have \(u_j[\pi _1(\sigma )]<{\widetilde{\mu }}_j\) for all \(j \in {\mathcal {J}}(i)\). From the definition of \({\widetilde{\mu }}\), there exists a player \(i_0 \in {\mathcal {J}}(i)\) and a pure action \(a_{i_0} \in A_{i_0}\) of player \(i_0\) such that \(u_{i_0}[a_{i_0},\pi _1(\sigma )_{-i_0}] \ge {\widetilde{\mu }}_{i_0}\). Consider the pure strategy one shot deviation \(\sigma _{i_{0}}^{\prime }\) of player \(i_{0}\) from \(\sigma \) in which she plays \( a_{i_{0}}\) in the first round of the finitely repeated game G(T) and conforms to her strategy \(\sigma _{i_{0}}\) from the second round on. We have
which is greater than or equal to \({\widetilde{\mu }}_{i_0}\). Indeed, since \( \sigma _{\left| (a_{i_{0}},\pi _1(\sigma ) _{-i_{0}})\right. }\) is a pure strategy subgame perfect Nash equilibrium play path of the finitely repeated game \(G(T-1)\), the induction hypothesis implies that \(u^{T-1}(\sigma _{\left| (a_{i_{0}},\pi _1(\sigma ) _{-i_{0}})\right. })\) dominates \({\widetilde{\mu }}\). It follows that the deviation \(\sigma _{i_{0}}^{\prime }\) of player is profitable. This contradicts the fact that \(\sigma \) is a subgame perfect Nash equilibrium.\(\square \)
D. Proof of the complete perfect folk theorem
From Corollary 1 and Lemma 5, the set of pure strategy subgame perfect Nash equilibrium payoff vectors of any finite repetition of the stage-game G is included in the set of enforceable and e-rational payoff vectors. To complete the proof of Theorem 1, it is left to show that any enforceable and e-rational payoff vector belongs to the limit set E. In what follows, I prove that any enforceable and e-rational payoff vector is approachable via pure strategy subgame perfect Nash equilibria of the finitely repeated game (see Lemma 3).
Lemma 6
Let G be a compact normal form game. We have \( {\widetilde{F}}\cap {\widetilde{I}}\subseteq {\text {ASPNE}}(G)\).
Proof of Lemma 6
Let G be a compact normal form game. If G admits no pure Nash equilibrium, then \({\widetilde{F}} =\emptyset \) and \({\widetilde{F}}\cap {\widetilde{I}}\subseteq {\text {ASPNE}}(G)\). If G admits a unique pure Nash equilibrium payoff vector x, then \({\widetilde{F}}=\{x\}={\text {ASPNE}}(G)\) and \({\widetilde{F}}\cap {\widetilde{I}}\subseteq {\text {ASPNE}}(G)\). Now suppose that G admits at least two distinct pure Nash equilibrium payoff vectors. Normalize the game such that the enforceable minimax of each player equals 0 and such that two equivalent players have the same utility function on \({\widetilde{A}}\). Consider
It is immediate that the closure of \(F_{1}\cap I_{1}\) is equal to the set \( {\widetilde{F}}\cap {\widetilde{I}}\). From Lemma 1, \({\text {ASPNE}}(G)\) is closed. Therefore, it is enough to show that \(F_{1}\cap I_{1}\subseteq {\text {ASPNE}}(G)\). Let \(y=\frac{1}{p}\sum \nolimits _{1\le l\le p}u(a^{l})\in \) \(F_{1}\cap I_{1}\). For all \(i \in N_h\), let \(w^i \in arg \min _{a\in {\widetilde{A}}}\max _{j\in {\mathcal {J}}(i)}\max _{a_{j}^{\prime }\in A_{j}} u_i(a_{j}^{\prime },a_{-j})\).Footnote 14
I use a suitable but minimal adjustment of the 5-phase strategy presented in Smith (1995) and Demeze-Jouatsa and Wilson (2019) to cases where the Nash decomposition is incomplete to approximate the target payoff vector y.
For each \(g\in \{1,\ldots ,h\}\), let \(e_{N_{g-1}}, f_{N_{g-1}}\in \times _{i \in N_{g-1}}A_i \) be two profiles of actions of players of the bloc \(N_{g-1}\) such that there exists two Nash equilibria \(z(e_{N_{g-1}})\) and \(z(f_{N_{g-1}})\) respectively for games \(G(e_{N_{g-1}})\) and \(G(f_{N_{g-1}})\), with distinct payoff for each player of the block \(N_{g}\backslash N_{g-1} \), where \(G(e_{N_{g-1}})\) (respectively \(G(f_{N_{g-1}})\)) is a stage-game with players \(N\backslash N_{g-1}\) obtained from G by fixing the actions of players of the block \(N_{g-1}\) to \(e_{N_{g-1}}\) (respectively \(f_{N_{g-1}}\)). Define \(c_g=min_{i\in N_g\backslash N_{g-1}}||u(z(e_{N_{g-1}}))-u(z(f_{N_{g-1}}))||\). Let \(y^{g}\) denote alternating between the action profiles \(z(e_{{\mathcal {J}}_{g-1}})\) (in even periods) and \(z(f_{{\mathcal {J}}_{g-1}})\) (in odd periods). Let \(z^{i,g}\) be the Nash equilibrium profile among \( z(e_{N_{g-1}})\) and \( z(f_{N_{g-1}})\) which is the worst for player \(i\in N_g\).
The 5-phase strategy profile is adjusted as follows. The phase length variables -namely q (Phase 3), r (Phase 4), and \(t_{g}(qp+rp)\) (\(g=1,2,\ldots ,h\), Phases 2 and 5)- will be chosen at the end of the construction, along with the reward vectors \(x^{j}\) (\( \forall j\in N_h\)) used in Phase 4. Early (late) deviations are those occurring up to (after) period \( T-t_{h}(qp+rp)-(qp+rp)\), ie deviation is “early” if there is still time to run Phases 3 and 4 before period \(T-t_{h}(qp+rp)+1\).
Strategy profiles.
-
1.
(Main Path) Play \(a^l\) at period \(t=l[mod \ p]+t_{h}(qp+rp)\) until period \(T-t_{h}(qp+rp)\). [After an early deviation by \(i\in N_h\), go to Phase 3; after a late deviation by \(i\in N_{g^\prime }\), go to Phase 5.] Go to Phase 2.
-
2.
(Good Recursive Nash) For \(g=h,\ldots ,1\): Play \(y^{g}\) in periods \(T-t_{g}(qp+rp)+1,\ldots ,T-t_{g-1}(qp+rp)\). [After a deviation by \(i\in N_{g^\prime }\) with \(g^{\prime }<g\), start Phase 5.]
-
3.
(Minmax Phase for i): Play \(w^{i}\) for qp periods. [If any \(j \in N \backslash {\mathcal {J}}(i)\) deviates early, start Phase 4; if any \(j\in N_{g^\prime }\) deviates late, start Phase 5 with \(i\leftarrow j\). If any \( j \in {\mathcal {J}}(i)\) deviates early, set \(i\leftarrow j\) and restart Phase 3.] Then set \(j\leftarrow i\) and start Phase 4.
-
4.
(Reward Phase) Repeat the path \(\pi ^{p,j}\) for r rounds. [If any \(i\in N_h\) deviates early, restart Phase 3; if any \(i\in N_{g^\prime }\) deviates late, start Phase 5.] Then return to Phase 1.
-
5.
(Bad Recursive Nash) Play \(z^{g^{\prime },i}\) until period \(T-t_{g^{\prime }}(qp+rp)\). [If \(j\in N_{g^{\prime \prime }}\) deviates, where \(g^{\prime \prime }<g^{\prime }\), set \(g^{\prime }\leftarrow g^{\prime \prime }\) and \(i\leftarrow j\) and restart Phase 5.] Then go to Phase 2.
So along the equilibrium path, the sequence of action profiles is
Length of phases: Let \(\rho \) be the largest gap between best and worst payoffs across all players in G. For all \(i\in N_h,\) let \(\pi ^{p^\prime ,i}\) be a sequence of length \(p^\prime \) of pure Nash equilibria of the effective game such that the sequence of average payoffs \(x^i=u(\pi ^{p^\prime ,i}), i\in N_h\) satisfies \(x^{i}\gg 0\) \(\forall i \in N_h\), \(x_{i}^{i}<x_{i}^{j}\) \(\forall j \notin (N\backslash N_h)\cup {\mathcal {J}}(i)\), \(x^{i}=x^{j}\) \(\forall j\in {\mathcal {J}}(i)\), and \(x_{i}^{i}<y_i \ \forall i\in N_h\). (Such vectors exist following Abreu et al. (1994)). There is no loss of generality to assume that \(p^\prime =p\). Choose q such that \(\rho <qp\cdot x_{i}^{i}\) and r such that \(\rho +\max \left\{ 0,qp\cdot \left( y_j-u _{j}(w^{i})\right) \right\} <rp\cdot (x_{j}^{i}-x_{j}^{j})\) for all \(i\in N_h\) and \(j\in N_h\backslash {\mathcal {J}}(i)\).
For any number k, let \(\psi _{g}(k)\) be the least even number above \( 2k\rho /c_{g}\), so that that a player \(i\in N_g\) is willing to play k periods of any action followed by \(\psi _{g}(k)\) periods of \( y^{g}\), if deviations switch each \(y^{g}\) to \(z^{g,i}\). Recursively define
Then set \(t_{0}(m)=0\) and \(t_{g}(m)=s_{1}(m)+\cdots +s_{g}(m)\), for \(g=1,2,\ldots ,h\).
Subgame perfect verification: By construction, no one-shot deviation by a player of the block \(N_h\) is profitable (see Smith (1995), Demeze-Jouatsa and Wilson (2019)). Observe that only Nash equilibria of the effective game appears on equilibrium paths of each subgame. Therefore, no player of the block \(N\backslash N_h\) can profitably deviate from the constructed strategy. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Demeze-Jouatsa, GH. A complete folk theorem for finitely repeated games. Int J Game Theory 49, 1129–1142 (2020). https://doi.org/10.1007/s00182-020-00735-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-020-00735-z
Keywords
- Finitely repeated games
- Pure strategy
- Observable mixed strategies
- Subgame perfect Nash equilibrium
- Limit perfect folk theorem