Queen reflections: a modification of Wythoff Nim

Abstract

Wythoff Nim is a classical combinatorial game of queen moves on a chessboard. There are many ways to describe its P-positions (safe positions to move to). One way is to code them by the Fibonacci word 010010100100101..., which is the unique fixed point of the substitution of 0 by 01, and of 1 by 0. The coordinates of the n-th P-position are encoded by the location of the n-th zero and the n-th one in the Fibonacci word. We show that a minor modification of the rules of Wythoff Nim leads to a game with P-positions that are coded by 010010010010100100... This word can be derived by deleting all 2’s from the Tribonacci word, which is the unique fixed point of the substitution of 0 by 01, of 1 by 02, and of 2 by 0.

1 Introduction

Wythoff Nim is played by two people, taking alternate turns. Alice places a chess Queen on a large chessboard and Bob moves first. The Queen moves in the usual way but only west, south, or southwest, always moving closer to the lower left corner of the board. The player who gets the Queen in this corner is the winner. A position is safe if Alice can place the Queen there, knowing that if she does not make any mistake later on, then Bob cannot win. This game has been extensively studied and modified because of the remarkable properties of the coordinates of the safe positions. The survey articles Duchêne et al. (2017) and Larsson (2020) give a comprehensive account.

Fig. 1

Possible moves of a reflecting Queen in our modification of Wythoff Nim

In our modification of Wythoff Nim, the Queen can bounce against a side and continue her way, as long as the overall (Manhattan) distance to the corner decreases. More specifically, a move in the southwest direction can bounce against the left side and continue in the southeast direction. Or it can bounce against the bottom side and continue in the northwest direction. We need to consider only one bounce. A second bounce would result in a symmetric position. The Queen cannot return to the starting position, and cannot bounce when positioned at the side of the board, because the distance to the corner has to decrease.

The order of the coordinates in a safe position is unimportant because of the symmetry of the game with respect to the main diagonal. We take the first coordinate to be smaller than the second. We can line up the safe positions $(a_n,b_n)$ in an increasing sequence. If we denote the sequence $(a_n)$ by A and $(b_n)$ by B and if we ignore the trivial safe position (0, 0) then we get the following table:

Table 1 The first fifteen non-zero safe positions for our modification of Wythoff Nim, alongside their differences $\varDelta$ and sums $\varSigma$ in the header and the footer of the table

Some patterns emerge from this table. The A and B sequences are complementary, and the sequences of differences and sums are complementary as well. The differences $b_n-a_n$ increase slowly, sometimes skipping a number. The $b_n$-th entry in A is either equal to $a_n+b_n$ or to $a_n+b_n-1$. These properties are very similar to those of the safe positions of Wythoff Nim. The sequences A and B for Wythoff Nim are also complementary and they satisfy $b_n-a_n=n$ and $a_{b_n}=a_n+b_n$, see Gardner (1977). By allowing the Queen to bounce against a side, we have created slight irregularities in the sequence of safe positions, but the pattern of these irregularities can be precisely described.

The Tribonacci word $\omega ^3$ is an infinite string of the three symbols 0, 1, 2:

$$\begin{aligned} \omega ^3 = 0102010010201010201001020102010010201010201\cdots . \end{aligned}$$

(1)

It belongs to a family of k-bonacci words $\omega ^k$, which are infinite strings of k symbols, of which the Fibonacci word $\omega ^2$ is the best known and most studied Baake and Grimm (2013) and Lothaire (2002). We will encounter these words below in our analysis of Table 1. The steps that we need to take to prove our results generalize to arbitrary k-bonacci words. That is why we put our analysis of the game in this wider setting.

The Tribonacci word is listed as A080843 in the Online Encyclopedia of Integer Sequences. It is constructed by iteratively applying the Tribonacci or Rauzy map $\theta (0)=01, \theta (1)=02, \theta (2)=0$, introduced in Rauzy (1982). Starting from 0, the finite words

$$\begin{aligned} 0,\ 01,\ 0102,\ 0102010,\ 0102010010201,\ \ldots \end{aligned}$$

produce $\omega ^3$ in the limit. If $w_n$ is the n-th finite word in this iteration, then $w_n=w_{n-1}w_{n-2}w_{n-3}$, hence the name ‘Tribonacci’. It is listed in the OEIS as A305386. If we delete all 2’s from the Tribonacci word, then we get

$$\begin{aligned} \nu = 0100100100101001001001001001001010010010010\cdots . \end{aligned}$$

(2)

A quick comparison of this sequence and Table 1 indicates that the location of the n-th zero and the n-th one corresponds to $(a_n,b_n)$.

Table 1 has appeared before in the analysis of an impartial game by Duchêne and Rigo. They proved that $\varDelta$ and $\varSigma$ are complementary (Duchêne and Rigo 2008a, Cor. 3.6). The sequences A and B from that table are listed as A140100 and A140101 in the OEIS. They also appear in the Greedy Queens on the spiral problem, which was solved by Dekking et al. (2020). The problem here is to place Queens on an infinite ${\mathbb {Z}}\times {\mathbb {Z}}$ chess board, in such a way that none of the Queens attack each other. The squares of the chess board are numbered along a square spiral, on which a new Queen is placed if it does not attack any earlier Queen.

The structure of our paper is as follows. We first define our modification of Wythoff Nim as a take-away game and show how Table 1 can be generated by a mex-rule. Our main result Theorem 1 states that the locations of the 0’s and 1’s in sequence 2 indeed correspond to $a_n$ and $b_n$. To prove it we introduce the notion of differencing tables of general k-bonacci words. It turns out that the sequences A and B can be obtained by differencing. The sequences $\varDelta$ and $\varSigma$ can be obtained by differencing once more. We prove in Theorem 2 that if we difference twice, then we get sequences that partition the integers. Then we show in Theorem 3 that Table 1 is indeed a table with differences and double differences, which settles our main result. Theorem 3 also settles that the differences $b_n-a_n$ skip a number at index n if and only if the n-th letter of the Tribonacci word is equal to 1.

We have searched for take-away games that can be coded by the 4-bonacci words but were unable to find any. We do establish a mex-rule to generate the tables of the 4-bonacci word in Theorem 4. We conjecture that $a_{b_n}-a_n-b_n$ is either $-1$ or 0 and we prove that it is bounded by $-2$ and 1 in Theorem 5.

Substitutions are studied in combinatorics of words (Lothaire 2002), which is a well-developed field of study. We adopt some of the terminology from combinatorics of words throughout the paper.

2 Splithoff: a modification of Wythoff Nim

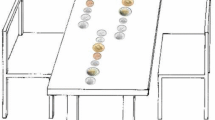
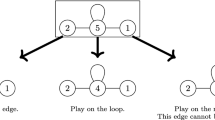
Wythoff Nim can also be defined as a take-away game on two piles of counters. Two players alternately either take a positive number of counters from a single pile (at most the whole pile), or an equal positive number from both piles (at most the number of the smallest pile). We modify Wythoff Nim by adding an option. If a player takes an equal number of counters from both piles leading to a single pile (taking away the smallest pile), then he can split the remaining pile into two. For instance, from position (2, 6) (as in the chess diagram in Fig. 1) it is possible to move to (1, 3) by taking 2 counters from both piles and splitting the remainder into 1 and 3. A split is only allowed after taking counters from both piles. We call this Splithoff. We refer to the three possible moves as single, double, and split.

We denote a position in this game as (x, y), in which x is the number of counters on the smallest pile. In particular, x and y are in ${\mathbb {N}}\cup \{0\}$. We write $d(x,y)=y-x$ and $s(x,y)=x+y$ (note that this is the Manhattan distance to the corner).

Lemma 1

There is a move from (x, y) to $(x',y')$ if and only if the following two conditions hold

• 1. $s(x,y)>s(x',y')$

• 2. $\{x,y\}\cap \{x',y'\}$ is non-empty or $d(x,y)\in \{d(x',y'),s(x',y')\}$.

Proof

If there is a move between (x, y) and $(x'y')$, then condition (1) guarantees that it is from (x, y) to $(x',y')$. It suffices to check that condition (2) is equivalent to the fact that there is a single, double, or split between the positions. The intersection $\{x,y\}\cap \{x',y'\}$ is non-empty if and only if a pile in (x, y) is equal to a pile in $(x',y')$. Or equivalently, $\{x,y\}\cap \{x',y'\}$ is non-empty if and only if there is a single between the two positions. Similarly, $d(x,y)=d(x',y')$ if and only if there is a double between the two positions. Finally, $d(x,y)=s(x',y')$ if and only if there is a split from (x, y) to $(x',y')$ (note that $x=0$ is ruled out in this case, by condition (1)). $\square$

The standard method of constructing the ${\mathcal {P}}$-positions (safe positions) is by recursion, starting from the losing position (0, 0) which has no move. Let $N^0$ be the positions with a move to (0, 0); these are all ${\mathcal {N}}$-positions (unsafe positions). Remove $N^0$ from the game. Let $P^1$ be the positions with no move in this reduced game; these are all ${\mathcal {P}}$-positions. Let $N^1$ be the positions with a move to $P^1$. Remove $N^1$ from the game, etc. The union of all $P^i$ including $\{(0,0)\}$ is equal to the set of all ${\mathcal {P}}$-positions. If we carry out this procedure for Splithoff, it turns out that it produces one new ${\mathcal {P}}$-position at a time, i.e., one column in Table 1 at a time.

2.1 A mex-rule for the P-positions

Let ${\mathbb {N}}=\{1,2,\ldots \}$ denote the natural numbers. For a proper subset $S\subset {\mathbb {N}}$, the minimal excludant $\textrm{mex}(S)$ is the smallest element of the complement ${\mathbb {N}}\setminus S$. It is well-known how the ${\mathcal {P}}$-positions for Wythoff Nim can be generated from the mex. We will derive a similar rule for the ${\mathcal {P}}$-positions in Splithoff in Table 1.

For $S\subset {\mathbb {N}}$, let $s_i$ denote the i-th element of S, and let $S_i=\{s_1,\ldots ,s_i\}$ be the subset of the first i elements of S. In particular, $S_0$ is the empty set. Table 1 contains four rows $\varSigma , A,B, \varDelta$, which are all subsets of ${\mathbb {N}}$. We denote their elements by $\varSigma =\{\sigma _1,\sigma _2,\ldots \}$ and $A=\{a_1,a_2,\ldots \}$, etc. The following rule set generates one new element at a time, for each of these sets.

$$\begin{aligned} \delta _{i+1}= & \textrm{mex}\left( \varDelta _i\cup \varSigma _i\right) \nonumber \\ a_{i+1}= & \textrm{mex}\left( A_i\cup B_i\right) \nonumber \\ b_{i+1}= & a_{i+1}+\delta _{i+1}\nonumber \\ \sigma _{i+1}= & a_{i+1}+b_{i+1} \end{aligned}$$

(3)

Think of this as a column generation. Since A and $\varDelta$ are defined by the $\textrm{mex}$, both $\{\varDelta , \varSigma \}$ and $\{A, B\}$ partition ${\mathbb {N}}$. The sequence $(a_n,b_n)$ of ${\mathcal {P}}$-positions of Splithoff Nim is produced by this rule.

The number zero is rather special and we do not include (0, 0) in the table of safe positions, even though $P^0=\{(0,0)\}$. The set of unsafe positions $N^0$, as defined above, consists of all positions (x, y) such that $x=0$ or $x=y$. If we remove $N^0$ from the game, then the remaining positions (x, y) satisfy $0<x<y$. In the reduced game, the only position without a move is (1, 2), i.e., $P^1=\{(1,2)\}$. It is the first safe position in our table.

Lemma 2

Let $a_i$ and $b_i$ be the i-th element generated by the mex-rule for A and B. Then $P^i=\{(a_i,b_i)\}$.

Proof

By induction. We already know it is true for $i=1$. Assume that the statement is true for all $i\le k$. We need to prove that it is true for $k+1$. At this stage, we remove the set $N^k$ of all positions with a move to $(a_k,b_k)$. By construction, the reduced game consists of all positions that have no move to $(a_i,b_i)$ for $i\le k$. We need to show that $P^{k+1}$, the set of positions with no move in the reduced game, is equal to $\{(a_{k+1},b_{k+1})\}$.

First of all, observe that $(a_{k+1},b_{k+1})$ is a position in the reduced game, i.e., admits no move to $(a_i,b_i)$ for $i\le k$. Indeed, if there would be such a move, then Lemma 1 implies that either $\{a_{k+1},b_{k+1}\}\cap \left( A_k\cup B_k\right)$ is non-empty or $\delta _{k+1}=d(a_{k+1},b_{k+1})\in \varDelta _k\cup \varSigma _k$. The latter is impossible by the definition of $\delta _{k+1}$. By the definition of $a_{k+1}$ we have $a_{k+1}\not \in A_k\cup B_k$. Since $b_{k+1}=a_{k+1}+\delta _{k+1}>a_k+\delta _k=b_k$, we have $b_{k+1}\not \in A_k\cup B_k$. Therefore $\{a_{k+1},b_{k+1}\}\cap \left( A_k\cup B_k\right)$ is empty. It follows that $(a_{k+1},b_{k+1})$ is a position in the reduced game.

Let (x, y) be a position in the reduced game. Suppose $\{x,y\}\cap \left( A_k\cup B_k\right)$ is non-empty, or $d(x,y)\in \varDelta _k\cup \varSigma _k$. It follows from condition (2) in Lemma 1 that there is a move between (x, y) and $(a_i,b_i)$ for some $i\le k$ if $s(x,y)>s(a_i,b_i)$. Since (x, y) is in the reduced game, there is no move from (x, y) to $(a_i,b_i)$, hence $s(a_i,b_i)>s(x,y)$. It follows from Lemma 1 that there is a move from $(a_i,b_i)$ to (x, y). Now $(a_i,b_i)$ only has moves to unsafe positions, i.e., positions that have a move to $(a_j,b_j)$ for $j<i$, or a move to (0, 0). It follows that (x, y) has a move to $(a_j,b_j)$ or (0, 0), which is nonsense. We conclude that $\{x,y\}\cap \left( A_k\cup B_k\right) =\emptyset$ and $d(x,y)\not \in \varDelta _k\cup \varSigma _k$ for all positions (x, y) in the reduced game. In particular, $x\ge a_{k+1}$ and $y\ge a_{k+1}+\delta _{k+1}=b_{k+1}$. It follows that $(a_{k+1},b_{k+1})$ is the position that is closest to the corner in the reduced game. Furthermore, all other positions (x, y) have a move in the reduced game. If $x=a_{k+1}$ then there is a single from (x, y) to $(a_{k+1},b_{k+1})$. If $x>a_{k+1}$ then there is a double from (x, y) to $(a_{k+1},a_{k+1}+d(x,y))$, which is in the reduced game by Lemma 1. We conclude that the mex-rule in Eq. 3 generates the columns in Table 1. $\square$

3 The positions table of the k-bonacci substitution

We show that Table 1 can be derived from the Tribonacci word $\omega ^3$. A more general statement is possible, at no extra effort. This is why we study tables that are generated by general k-bonacci substitutions, instead of just the Tribonacci substitution. The k-bonacci substitution $\theta _k$ on the alphabet $\{0,\ldots ,k-1\}$ is given by

$$\begin{aligned} \theta _k:\left\{ \begin{array}{llll} j&{}\mapsto &{} 0\,(j+1),&{}\textrm{if }\ j<k-1\\ k-1&{}\mapsto &{} 0 \end{array}.\right. \end{aligned}$$

The k-bonacci word $\omega ^{k}$ is the unique fixed point of this substitution. In particular, $\omega ^2$ is the Fibonacci word and $\omega ^3$ is the Tribonacci word. If $k=4$, then starting from 0, the finite words

$$\begin{aligned} 0,\ 01,\ 0102,\ 01020103,\ 010201030102010,\ 01020103010201001020103010201 \end{aligned}$$

converge to $\omega ^4$. In our analysis, $k>2$ is fixed and we will sometimes write $\theta$ and $\omega$ instead of $\theta _k$ and $\omega ^k$.

The k-bonacci word $\omega$ is a fixed point of $\theta$. If we apply $\theta$ to the string $\omega =\omega _1\omega _2\omega _3\omega _4\omega _5\cdots$ then we get the concatenated string

$$\begin{aligned} \theta (\omega _1)\theta (\omega _2)\theta (\omega _3)\theta (\omega _4)\theta (\omega _5)\cdots , \end{aligned}$$

which is equal to $\omega$. Each $\theta (\omega _i)$ contains exactly one 0 (and is equal to 0 if $\omega _i$ is equal to $k-1$). Therefore, the i-th occurence of 0 is in $\theta (\omega _i)$ and the difference between the i-th occurence and the $(i+1)$-th occurence is equal to two, unless $\omega _i=k-1$ in which case the difference is one. This can be seen in the first row of the positions table of the Quadribonacci word $\omega ^4$ below. The difference between entries in the first row is equal to two, unless the entry is headed by 3 (Table 2).

Table 2 The positions table of the Quadribonacci word $\omega ^4$, which is displayed in the gray heading line

If we apply $\theta ^{i+1}$ for $i<k$ to $\omega =\omega _1\omega _2\omega _3\omega _4\omega _5\cdots$ then we get the concatenated string

$$\begin{aligned} \theta ^{i+1}(\omega _1)\theta ^{i+1}(\omega _2)\theta ^{i+1}(\omega _3)\theta ^{i+1}(\omega _4)\theta ^{i+1}(\omega _5)\cdots , \end{aligned}$$

which is again equal to $\omega$. It turns out that each of these words contains the letter i exactly once.

Lemma 3

For each $i<k$ and each letter $j\in \{0,1,\ldots ,k-1\}$ the word $\theta ^{i+1}(j)$ contains the letter i exactly once and always at position $2^{i}$. Indeed, it occurs in $\theta ^{i+1}(j)$ as the final letter of $\theta ^i(0)$.

Note that in $\theta ^{i+1}$, the exponent has i as a number but the word $\theta ^{i+1}(j)$ has i as a letter.

Proof

We prove that i occurs only once in $\theta ^{i+1}(j)$ as the final letter of $\theta ^i(0)$. This is true if $i=0$, which occurs in each $\theta (j)$ at the first position. By induction, assume that the statement is true for $i-1$. Since i is in $\theta (j)$ if $j=i-1$, we have that i occurs only once in $\theta (\theta ^{i}(j))$, as the final letter of $\theta (\theta ^{i-1}(0))$. Since this substitution doubles the length, as long as $i<k$, the result follows. $\square$

The positions of i can now easily be found from the concatenated string $\theta ^{i+1}(\omega _1)\theta ^{i+1}(\omega _2)\theta ^{i+1}(\omega _3)\theta ^{i+1}(\omega _4)\theta ^{i+1}(\omega _5)\cdots$ by using the lengths of the words $\theta ^{i+1}(j)$ and the string of letters in the k-bonacci word. We summarize this as a lemma.

Lemma 4

Let $\ell ^i(j)$ be the length of $\theta ^{i+1}(j)$. If a column is headed by j in the positions table, then the difference between that column and the next is given by

$$\begin{aligned} \left[ \begin{array}{c} \ell ^0(j)\\ \ell ^1(j)\\ \vdots \\ \ell ^{k-1}(j) \end{array} \right] \end{aligned}$$

(4)

If we add 4 to the final row in Table 1, we get a subsequence of the row right above it. The same happens if we subtract 4. This is a general property of the positions table.

Lemma 5

For a subset V of the integers, let $V+a$ be its translate by a. Consider the rows of the positions table as sets. We have that

$$\begin{aligned} X^i=\left\{ X^{i+1}-2^{i}\right\} \cup \left\{ X^{i+1}+2^i\right\} . \end{aligned}$$

Furthermore $\left\{ X^{i+1}-2^{i}\right\} \cap \left\{ X^{i+1}+2^i\right\}$ contains the elements $m+2^i$ with m taken from the columns labeled by $k\!-\!1$.

Proof

The letter $i+1$ occurs once in every word of the concatenation

$$\begin{aligned} \theta ^{i+2}(\omega _1)\theta ^{i+2}(\omega _2)\theta ^{i+2}(\omega _3)\theta ^{i+2}(\omega _4)\theta ^{i+2}(\omega _5)\cdots \end{aligned}$$

at position $2^{i+1}$ as the final letter of $\theta ^{i+1}(0)$. In each $\theta ^{i+1}(\omega _j)$ we have that i occurs at most twice. To see that, write $\theta ^{i+1}(j)=\theta ^i(\theta (j))$. If $j<k\!-\!1$ then $\theta (j)$ consists of the two letters $0(j\!+\!1)$, and i occurs twice in $\theta ^{i+1}(0)\theta ^{i+1}(j+1)$. If $j=k\!-\!1$ then $\theta (j)=0$ and i only occurs once in $\theta ^{i+1}(\omega _j)$, while $i\!+\!1$ occurs as its final letter. The result now follows from Lemma 3. $\square$

4 The difference table

Consider the positions table of the Tribonacci word below. If we subtract the first row from the second, and the second from the third, then we get the ${\mathcal {P}}$-positions of Table 1. We prove this below (Table 3).

Table 3 The positions table for the Tribonacci word

The difference table of the k-bonacci word has rows $\varDelta ^j=X^{j+1}-X^j$. We will prove that its rows again form a partition of ${\mathbb {N}}$. It follows from Lemma 4 and Eq. 4 that the difference table can be derived from $\omega$. The step size is

$$\begin{aligned} \left[ \begin{array}{c} \ell ^1(j)-\ell ^0(j)\\ \ell ^2(j)-\ell ^1(j)\\ \vdots \\ \ell ^{k-1}(j)-\ell ^{k-2}(j) \end{array} \right] \end{aligned}$$

(5)

if j is the letter heading the column (Table 4).

Table 4 The difference table for the Quadribonacci word

Lemma 6

For each $1\le i\le k-1$ and each letter j

$$\begin{aligned} \ell ^{i}(j)=2\ell ^{i-1}(j)-\delta ^{k-1}_{i+j}, \end{aligned}$$

where $\delta ^i_j$ is Kronecker’s delta.

Proof

We defined $\ell ^i(j)$ as the length of $\theta ^{i+1}(j)$. The substitution $\theta$ replaces each letter by two letters, except the final letter $k\!-\!1$, which is replaced by a single 0. It suffices to prove that $\theta ^i(j)$ contains no letter $k\!-\!1$ unless $k-1=i+j$, in which case it contains a single $k\!-\!1$.

If we start from j, the only instance that reaches $k-1$ is produced from $j\rightarrow j+1\rightarrow \cdots$. All other instances can only be produced from a 0, but do not reach $k\!-\!1$ because $i\le k-1$. The sequence $j\mapsto j+1$ produces $k\!-\!1$ after $k-1-j$ substitutions. Hence, we have one non-doubling letter if $i=k-1-j$. $\square$

In the positions table, the difference between consecutive entries in a row is minimal if an entry is in a column labeled by $k\!-\!1$, and maximal if a row is labeled by 0. This is because $\ell ^{i}(j)$ is minimal if $j=k\!-\!1$ and maximal if $j=0$. The same holds in the difference table.

Lemma 7

The difference between consecutive entries in row $\varDelta ^i$ is at least $2^i$ and at most $2^{i+1}$. In row $\varDelta ^{k\!-\!2}$ the maximum difference is $2^{k-1}-1$.

Proof

The differences in row $\varDelta ^i$ are equal to $\ell ^{i+1}(j)-\ell ^i(j)$ for the letters j. By the previous lemma, these differences are

$$\begin{aligned} \ell ^i(j)-\delta _{i+j+1}^{k-1}. \end{aligned}$$

Now $\ell ^i(j)$ is the length of $\theta ^{i+1}(j)$ which is at most $2^{i+1}$. It is equal to $2^i$ if $j=k-1$, in which case $\delta _{i+j+1}^{k-1}=0$.

Finally, if $i=k-2$ then $\delta _{i+j+1}^{k-1}=1$ at $j=0$ and the other substitutions have length $<2^{k-1}$. Therefore, the upper bound is $2^{k-1}-1$ in this case. $\square$

The following result is analogous to Lemma 5.

Lemma 8

Consider the rows of the difference table as sets. We have that

$$\begin{aligned} \varDelta ^i=\left\{ \varDelta ^{i+1}-2^{i}\right\} \cup \left\{ \varDelta ^{i+1}+2^i\right\} . \end{aligned}$$

Furthermore $\left\{ \varDelta ^{i+1}-2^{i}\right\} \cap \left\{ \varDelta ^{i+1}+2^i\right\}$ contains the elements $m+2^i$ with m taken from the columns labeled by $k\!-\!1$.

Proof

By Lemma 5 we have

$$\begin{aligned} \varDelta ^i=X^{i+1}-X^i= \left( X^{i+2}-2^{i+1}\cup X^{i+2}+2^{i+1}\right) - \left( X^{i+1}-2^{i}\cup X^{i+1}+2^{i}\right) . \end{aligned}$$

If an entry in $X^{i+1}$ is in $X^{i+2}-2^{i+1}$ then the corresponding entry in $X^{i}$ is in $X^{i+1}-2^{i}$, and vice versa. Therefore we can write this intersection as

$$\begin{aligned} \varDelta ^i=\left( X^{i+2}-X^{i+1}-2^{i+1}+2^i\right) \cup \left( X^{i+2}-X^{i+1}+2^{i+1}-2^i\right) , \end{aligned}$$

which is $\varDelta ^{i+1}-2^i \cup \varDelta ^{i+1}+2^i$. The intersection $\varDelta ^{i+1}-2^i \cap \varDelta ^{i+1}+2^i$ contains $m+2^i$ for which the difference between m and the consecutive entry is $2^{i+1}$, which is the least possible difference according to Lemma 7. It occurs in columns labeled by the letter $k\!-\!1$. $\square$

Lemma 9

The rows in the difference table are disjoint as sets:

$$\begin{aligned} \varDelta ^i\cap \varDelta ^j=\emptyset \ \mathop {\textrm{if }}i\not =j. \end{aligned}$$

Proof

Suppose $j>i$. By iterating Lemma 8 we find that each element of $\varDelta ^i$ is in some $\varDelta ^j\pm 2^{j-1}\pm \cdots \pm 2^{i}$. By Lemma 7 the minimal distance in $\varDelta ^j$ is $2^j$ and $2^{j-1}+\cdots +1<2^j$. Therefore, $\varDelta ^i$ and $\varDelta ^j$ are disjoint. $\square$

Lemma 10

The rows in the difference table form a partition of ${\mathbb {N}}$.

Proof

We only need to prove that the rows cover ${\mathbb {N}}$. By iterating Lemma 8 each $\varDelta ^i$ is the union of all $\varDelta ^{k-2}\pm 2^{k-2}\pm \cdots \pm 2^{i}$, with $\varDelta ^{k-2}$ the bottom row of our table. The union of the rows is equal to the union of $\varDelta ^{k-2}+n$ for all integers n that can be written as $\pm 2^{k-2}\pm \cdots \pm 2^{i}$ for some i and some choice of the signs. Here we take $n=0$ if $i=k-2$. It is not hard to verify that each $n\in \{-2^{k-2}+1,\ldots , 2^{k-2}-1\}$ admits such an expansion. The result now follows from Lemma 7 which says that the maximum difference in $\varDelta ^{k-2}$ is $2^{k-1}-1$. $\square$

Theorem 1

The word $\nu$, which is derived from the Tribonacci word by deleting the 2’s, codes the ${\mathcal {P}}$-positions of Splithoff. More specifically, the ${\mathcal {P}}$-positions are $(a_n,b_n)$ where $a_n$ is the location of the n-th 0 and $b_n$ is the location of the n-th 1 in $\nu$.

Proof

The difference table of $\omega ^3$ consists of two rows. We will prove below in Theorem 3 that the difference table of $\omega ^3$ gives the ${\mathcal {P}}$-positions of Splithoff. The step size in the first row of this table is two in columns headed by 0 and it is one in the columns headed by 1 or 2. This implies that the first row corresponds to the locations of 0 if we apply the coding $0\mapsto 01,\ 1\mapsto 0,\ 2\mapsto 0$ to $\omega ^3$. We denote this coding by $\kappa$. The Tribonacci word $\omega ^3$ is the limit of $\theta ^n(0)$. We conclude that $\nu$ is the limit of $\kappa (\theta ^n(0))$.

Let $\lambda$ be the coding $0\mapsto 0,\ 1\mapsto 1,\ 2\mapsto \epsilon$, where $\epsilon$ denotes the empty word. The coding $\lambda \circ \theta$ is equal to $\kappa$. Therefore $\lambda (\theta ^{n+1}(0))=\kappa (\theta ^n(0))$ and taking limits gives $\lambda (\omega ^3)=\nu$. $\square$

5 The double-difference table

We continue by differencing the differences

$$\begin{aligned} d\varDelta ^{i}=\varDelta ^{i+1}-\varDelta ^i \end{aligned}$$

and collect these as rows in a double-difference table. It turns out that we need to add a bottom row containing the sum

$$\begin{aligned} \varSigma =\varDelta ^0+\cdots +\varDelta ^{k-2} \end{aligned}$$

to turn the rows of the table into a partition. We call this the sum row and we call the other rows the difference rows. Again, we add the k-bonacci word $\omega$ in the header. For the Tribonacci word we have one difference row and one sum row. These are the $\varDelta$ and $\varSigma$ of Table 1.

Table 5 The double-difference table for the Quadribonacci word, in which we add the sum $\varSigma =\varDelta ^0+\varDelta ^1+\varDelta ^2$ as a final row

Lemma 6 implies that the step between columns is

$$\begin{aligned} \left[ \begin{array}{c} \ell ^2(j)-2\ell ^1(j)+\ell ^0(j)\\ \vdots \\ \ell ^{k-1}(j)-2\ell ^{k-2}(j)+\ell ^{k-3}(j)\\ \ell ^{k-1}(j)-\ell ^0(j) \end{array} \right] = \left[ \begin{array}{rcl} \ell ^0(j)&{}-&{}\delta ^{k-1}_{2+j}\\ &{}\vdots &{}\\ \ell ^{k-3}(j)&{}-&{}\delta ^{k-1}_{k-1+j}\\ \ell ^{k-1}(j)&{}-&{}\ell ^0(j) \end{array} \right] . \end{aligned}$$

(6)

Consider the row $d\varDelta ^1$ in Table 5, in particular the entries that are headed by the letter 1. These differences are $5, 18, 30, 43, \ldots$, and if we add 2, then we get the sequence $\varSigma$. For a general k, let $M\subset d\varDelta ^{k-3}$ be the subsequence of entries headed by the letter 1. We will prove below that $M+2^{k-3}$ is equal to the sum row $\varSigma$, by showing that both sequences have the same initial element, and the same steps (differences between consecutive elements).

By Lemma 3 the 1’s occur in $\omega ^k$ as the second letters in the concatenation $\theta ^2(\omega _1)\theta ^2(\omega _2)\theta ^2(\omega _3)\cdots$. Note that $\theta ^2(h)$ is equal to $010(h+2)$ if $h<k-2$, equal to 010 if $h=k-2$, and equal to 01 if $h=k-1$. If we write $\omega ^k$ as a concatenation $0w_1w_2w_3\ldots$ of words $w_j$ with initial letter 1 and no other occurences of that letter (i.e., return words as defined in Durand (1998)), then the $w_j$ are either equal to $10(h\!+\!2)0$ or 100 or 10. In other words, the return word $w_j$ is equal to $\theta ^2(\omega _j)$ if we delete the initial zero, and add a zero to the end.

Lemma 11

The j-th step in M has length $\ell ^{k-1}(\omega _j)-\ell ^{0}(\omega _j)$. Therefore, the steps in M are equal to the steps of $\varSigma$.

Proof

The steps in $\varDelta ^{k-3}$ are equal to $\ell ^{k-3}(j)-\delta ^{k-1}_{k-1+j}$. The Kronecker-delta is zero, unless $j=0$. If the j-th return word is $10(h\!+\!2)0$ for $h<k-2$, then the j-th step in M is equal to

$$\begin{aligned} \ell ^{k-3}(1)+\ell ^{k-3}(0)+\ell ^{k-3}(h\!+\!2)+\ell ^{k-3}(0)-2. \end{aligned}$$

If we extend our notation and let $\ell ^{k-3}(w)$ be the sum of the $\ell ^{k-3}(j)$ over the letters in w, then we can write this as

$$\begin{aligned} \ell ^{k-3}(w_j)-2=\ell ^{k-3}(\theta ^2(\omega _j))-\ell ^0(\omega _j), \end{aligned}$$

(7)

where $w_j$ is the return word. This equation holds because $\theta ^2(\omega _j)$ has the same letters as $w_j$ and because $\omega _j<k-2$. If $\omega _j=k-2$ then the return word is 100 which contains two zeroes, and the same equation holds. If $\omega _j=k\!-\!1$ then the return word 10 contains only one zero, but $\ell ^0(k\!-\!1)=1$. Again Equation 7 holds. Now $\ell ^{k-3}(\theta ^2(\omega _j))=\ell ^{k-1}(\omega _j)$. $\square$

We now repeat Lemmas 8 and 9 for the difference rows in the double-difference table.

Lemma 12

$d\varDelta ^i=\left\{ \varDelta ^{i+1}-2^{i}\right\} \cup \left\{ \varDelta ^{i+1}+2^i\right\}$.

Proof

The same as the proof of Lemma 8, with minor editing.

$$\begin{aligned} d\varDelta ^j=\varDelta ^{j+1}-\varDelta ^j= \left( \varDelta ^{j+2}-2^{j+1}\cup \varDelta ^{j+2}+2^{j+1}\right) - \left( \varDelta ^{j+1}-2^{j}\cup \varDelta ^{j+1}+2^{j}\right) \end{aligned}$$

Again, the signs depend on locations and so this is equal to

$$\begin{aligned} \left( \varDelta ^{j+2}-\varDelta ^j-2^{j+1}+2^j\right) \cup \left( \varDelta ^{j+2}-\varDelta ^{j+1}+2^{j+1}-2^j\right) \end{aligned}$$

which is $d\varDelta ^{j+1}-2^j \cup d\varDelta ^{j+1}+2^j$. $\square$

Lemma 13

$d\varDelta ^i\cap d\varDelta ^j=\emptyset \ \mathop {\textrm{if }}i\not =j$.

Proof

Suppose $j>i$. By iterating Lemma 8 we find that each element of $\varDelta ^i$ is in some $d\varDelta ^j\pm 2^{j-1}\pm \cdots \pm 2^{i}$. It follows from Eq. 6 that the minimal step size in $d\varDelta ^j$ is $2^j$ and $2^{j-1}+\cdots +1<2^j$. Therefore, $d\varDelta ^i$ and $d\varDelta ^j$ are disjoint. $\square$

The rows of the double differences $d\varDelta ^i$ are disjoint, but they no longer cover ${\mathbb {N}}$. The maximum step in the final difference row $d\varDelta ^{k-3}$ occurs in columns with label 1. These lead to missing values in the union of the $d\varDelta ^i$ for which we need to use the sequence $\varSigma$ as a filler.

Lemma 14

Let $S\subset {\mathbb {N}}$ be the set $S=M+2^{k-3}$. The difference rows in the double-difference table form a partition of ${\mathbb {N}}\setminus S$.

Proof

We only need to prove that the difference rows cover ${\mathbb {N}}\setminus S$. By iterating Lemma 12 each $d\varDelta ^i$ is the union of all $d\varDelta ^{k-3}\pm 2^{k-4}\pm \cdots \pm 2^{i}$, with $d\varDelta ^{k-3}$ the final difference row of our table. The union of these rows is the union of $d\varDelta ^{k-3}+n$ for all integers $|n|<2^{k-3}$. The maximal step in $d\varDelta ^{k-3}$ is $2^{k-2}$, which occurs in the 1-columns. Therefore, the union of the difference rows is ${\mathbb {N}}\setminus S$. $\square$

Theorem 2

The rows in the double-difference table form a partition of ${\mathbb {N}}$.

Proof

We need to prove that S is equal to $\varSigma$. By Lemma 11 these sequences have equal steps. We need to show that they have the same initial element. The initial element of $\varSigma$ is the sum of the initial elements of the difference sequences. This is $\ell ^{k-1}(0)-\ell ^0(0)=2^{k-1}-1$. The initial element of S is $m+2^{k-3}$ with m the initial element of M. Now m is the second element of $d\varDelta ^{k-3}$. The first element of $d\varDelta ^{k-3}$ is $2^{k-3}$ and the second element is $2^{k-3}+\ell ^{k-3}(0)-1=2^{k-3}+2^{k-2}-1$. Therefore, the initial element of S is $2^{k+3}+2^{k-3}+2^{k-2}-1=2^{k-1}-1$. S and $\varSigma$ have the same initial element. $\square$

6 The table of safe positions of Splithoff

We already showed in Theorem 1 that deleting the 2’s from $\omega ^3$ gives a string that codes the difference table. We will now show that the difference table corresponds to the safe positions in Table 1. In particular, we show that we can generate this difference table by the same mex-rule that generates the safe positions in Equation 3.

We denote the elements of the difference sequence $\varDelta ^j$ by $a^j_1,a^j_2,\ldots$ and the elements of $d\varDelta ^j$ by $d^j_1,d^j_2,\ldots$. As before, $X_i$ denotes the first i entries of a sequence X.

Lemma 15

$a^0_{i+1}=\textrm{mex}\left( \varDelta ^0_i\cup \varDelta ^1_i\cup \cdots \cup \varDelta ^{k-2}_i\right)$ .

Proof

The rows partition ${\mathbb {N}}$ and therefore $\textrm{mex}\left( \varDelta ^0_i\cup \varDelta ^1_i\cup \cdots \cup \varDelta ^{k-2}_i\right)$ occurs in one of the rows. Both rows and columns are strictly increasing. This mex has to be in the first row. $\square$

By the same argument we find the following result.

Lemma 16

$d^0_{i+1}=\textrm{mex}\left( d\varDelta ^0_i\cup d\varDelta ^1_i\cup \cdots \cup d\varDelta ^{k-3}_i\cup \varSigma _i\right)$.

We can now complete the proof of our main result.

Theorem 3

Let $x_i, y_i, z_i$ be the locations of the i-th 0, 1, 2, respectively, in the Tribonacci word. Then the i-th ${\mathcal {P}}$-position $(a_i,b_i)$ in Table 1 is given by $a_i=y_i-x_i$ and $b_i=z_i-y_i$.

Proof

If $k=3$ there are only the rows $\varDelta _0, \varDelta _1, d\varDelta _0, \varSigma$. The previous two lemmas state that

$$\begin{aligned} d^0_{i+1}= & \textrm{mex}\left( d\varDelta ^0_i\cup \varSigma _i\right) \nonumber \\ a^0_{i+1}= & \textrm{mex}\left( \varDelta _i^0\cup \varDelta _i^1\right) \end{aligned}$$

(8)

By definition $a^1_{i+1}=a^0_{i+1}+d^0_{i+1}$ and if $s_i$ denotes the entries in $\varSigma$ then by definition $\sigma _{i+1}=a^0_{i+1}+a^1_{i+1}$. These rules are the same as for the table of ${\mathcal {P}}$-positions in Eq. 3. We conclude that the difference table of the Tribonacci word is identical to the rows of Table 1. The double difference table is identical to the header and footer of that table. $\square$

Corollary 1

Let $(\delta _n)$ be the sequence $\varDelta$ in Table 1. The steps $\delta _{n+1}-\delta _n$ are either 1 or 2. A step is equal to 2 if and only if $\omega _n=1$.

Proof

$\varDelta$ is equal to the top row of the double-difference table, for $k=3$. According to Eq. 6 the step is equal to $\ell ^0(j)-\delta ^{2+j}_2$. This is equal to 1 if $j\in \{0,2\}$ and equal to 2 if $j=1$. $\square$

7 A mex-rule for the Quadribonacci table

Duchêne and Rigo asked if there exists an impartial game with positions that can be coded with the Quadribonacci word (Duchêne and Rigo 2008b). We were unable to find such a game from our results. The best that we can come up with is a $\textrm{mex}$-rule to generate the positions table of the Quadribonacci word.

Lemma 17

The bottom row of the k-bonacci positions table can be written as a sum

$$\begin{aligned} X^{k-1}=E+X^0+\cdots +X^{k-1}, \end{aligned}$$

where E denotes the enumerating sequence $1,2,3,\ldots$.

Proof

This is true for the initial column. Each next column is an increment by the vector in Eq. 4. We need to show that

$$\begin{aligned} \ell ^{k-1}(i)=1+\ell ^{0}(i)+\cdots +\ell ^{j-2}(i). \end{aligned}$$

This is a consequence of the following observation. Suppose you start from 1 and double each time, except once, when you double and subtract one. Then the final number is the sum of the other numbers. We leave the verification to the reader. The equality above follows from the observation for $i<k-1$. In that case, we have $\ell ^0(i)=2$ and each next $\ell ^{j}(i)$ is doubled, unless $k-1$ appears in $\theta ^j(i)$, which happens once. If $i=k-1$ then $\ell ^{j}(k-1)=2^{j}$ and again the equation holds. $\square$

According to this lemma it suffices to generate the first three rows of the Quadribonacci table, and compute the fourth row as a sum. These three rows can be derived from the first two rows of the difference table, which can be derived from the first row of the double-difference table, which follows from the $\textrm{mex}$ rule. That is the idea behind Theorem 4 below, in which we generate all three tables of the Quadribonacci word simultaneously.

We write $x^j_i$ for the elements of the positions table.

Theorem 4

The following rules generate the three tables for the Quadribonacci word:

$$\begin{aligned} a^0_{i+1}= & \textrm{mex}\left( \varDelta ^0_i\cup \varDelta ^1_i\cup \varDelta ^{2}_i\right) \\ b^0_{i+1}= & \textrm{mex}\left( d\varDelta ^0_i\cup d\varDelta ^1_i\cup \varSigma _i\right) \\ x_{i+1}^0= & \textrm{mex}\left( X^0_i\cup X^1_i\cup X^{2}_i\cup X^3_i\right) \\ a^1_{i+1}= & a^0_{i+1}+b^0_{i+1}\\ x^1_{i+1}= & x^0_{i+1}+a^0_{i+1}\\ x^2_{i+1}= & x^1_{i+1}+a^1_{i+1}\\ x^3_{i+1}= & x^0_{i+1}+x^1_{i+1}+x^2_{i+1}+i+1\\ a^2_{i+1}= & x^3_{i+1}-x^2_{i+1}\\ b^2_{i+1}= & a^1_{i+1}+a^2_{i+1}+a^3_{i+1} \end{aligned}$$

Proof

The first and second equation follow from Lemma 15 and 16. The third equation can be derived in an equivalent manner. The other equations follow from Lemma 16 and the definition of the difference tables. $\square$

8 An additive property of the safe positions

It is well-known that consecutive pairs of Fibonacci numbers occur as safe positions in Wythoff Nim.

$$\begin{aligned} (1,2), (3,5), (8, 13), (21, 34),\ldots . \end{aligned}$$

This follows from the fact that $a_{b_n}=a_n+b_n$ in Wythoff Nim. For Splithoff we conjecture that $-1\le a_{b_n}-a_n-b_n\le 0.$ We establish a slightly weaker bound below. To do that, we need some combinatorial properties of the Tribonacci word.

The number of letters j in a word w is denoted by $|w|_j$. A word w is c-balanced if $||u|_j-|v|_j|\le c$ for each letter j and all subwords u, v of equal length. The Tribonacci word $\omega ^3$ is 2-balanced, see (Richomme et al. 2010, Theorem 1.3). If w is a prefix of $\omega ^3$, then jw is also a subword for any letter $j\in \{0,1,2\}$, see (Tan and Wen 2007, Remark 1.3).

Theorem 5

The coordinates $(a_n,b_n)$ of the safe positions in Splithoff satsisfy $-2\le a_{b_n}-a_n-b_n\le 1$.

Proof

Recall from the proof of Theorem 1 that the coding $\kappa (0)=01,\ \kappa (1)= 0,\ \kappa (2)=0$ converts $\omega ^3$ to $\nu$. Let w be the prefix of length n of $\omega ^3$. Then $\kappa (w)$ is a prefix of $\nu$ containing n zeroes. Let j be the final letter of w and write $w=w'j$. Then $a_n$ is equal to the length of $\kappa (w')0$. In particular,

$$\begin{aligned} a_n=|w'|_0+n \end{aligned}$$

because $\kappa$ adds a 1 for each 0 in $w'$.

Let v be the prefix of $\omega ^3$ that ends with the n-th zero. Then $b_n$ is equal to the length of $\kappa (v)$, which contains n ones and $b_n-n$ zeroes. To get to $a_{b_n}$ we need n more zeroes. Extend the prefix v to vu with u of length n. Let j be the final letter of u and write $u=u'j$. Then

$$\begin{aligned} a_{b_n}=b_n+|u'|_0+n. \end{aligned}$$

It follows that

$$\begin{aligned} a_{b_n}-b_n-a_n=|u'|_0-|w'|_0 \end{aligned}$$

Since the Tribonacci word is 2-balanced, we immediately get that $|a_{b_n}-b_n-a_n|\le 2$. Now suppose that $|u'|_0-|w'|_0=2$. Since vu is a prefix of $\omega ^3$ and since the final letter of v is 0, we get that $0u'$ is a subword of $\omega ^3$. Since $w'$ is a prefix, $1w'$ is a subword of $\omega ^3$. By 2-balancedness we have that $|0u'|_0-|1w'|_0\le 2$. It follows that $|u'|_0-|w'|_0\le 1$. $\square$

9 Final remarks

For Wythoff Nim, each row, column, and diagonal of ${\mathbb {N}}\times {\mathbb {N}}$ contains each Sprague-Grundy value once and only once. For Splithoff, it looks like every row or column contains each Sprague-Grundy value once and only once, see Table 6. We do not have a proof for that. Diagonals, however, do not contain each value. For instance, the diagonal $(n,n+3)$ does not contain Sprague-Grundy value zero because 3 is missing from the difference sequence $\varDelta$.

Table 6 The Sprague-Grundy values of Splithoff for piles (m, n) containing up to sixteen counters

There is a connection between Wythoff Nim and Fibonacci numeration that has been extended to other Wythoff-like games by Fraenkel (2010). We did not consider the relation between the ${\mathcal {P}}$-positions of Splithoff and the Tribonacci numeration system, but it is central in the analysis of the Greedy Queens problem in Dekking et al. (2020). The link between numeration and words is well known and extensively studied. Sirvent introduced the k-bonacci substitution in Sirvent (1997) to generalize results on Fibonacci and Tribonacci numbers. The link between words and ${\mathcal {P}}$-positions is much less clear and has been explored by Duchêne and Rigo (2008b). Recently, Fraenkel and Larsson (2019) introduced the notion of playability to describe the complexity of the ${\mathcal {P}}$-positions, which may be a more fruitful approach.

Splithoff is one of the many modifications of Wythoff Nim. A well-studied modification, called a-Wythoff, allows a player to remove x coins from one pile and y coins from the other, if $|x-y|<a$ for a fixed number a. It is equal to the original game if $a=1$. We can modify our game in the same way to get a-Splithoff. We say that a move is a double if it removes coins from both piles. If one of the piles is cleared by a double, then in a-Splithoff the player may split the remaining pile. We conjecture that 2-Splithoff can also be coded by the Tribonacci word, as illustrated by Table 7. The B-row appears to be equal to the difference between the first row and the third row in the positions table of $\omega ^3$.

Table 7 The ${\mathcal {P}}$-positions for 2-Splithoff

Wythoff led a secluded life and was not a man of many words (Fokkink 2016). At the end of his very short paper (Wythoff 1907), he left two remarks, both a bit cryptic, on the existence of certain complementary sequences $\{A_n\}$ and $\{B_n\}$. His first remark was that for any natural number a there exist $A_n=\lfloor n\alpha \rfloor$ and $B_n=\lfloor n\beta \rfloor$ such that $B_n-A_n=na$. Wythoff specified $\alpha$ and $\beta$ (they are quadratic numbers) and mentioned that there are games that have $(A_n,B_n)$ as ${\mathcal {P}}$-positions, leaving the rules of the games to the reader. These games were later rediscovered by Holladay (1968) and are now known as a-Wythoff Nim, the games we encountered in the above paragraph. His second remark was that for natural numbers $0< b\le a$ there exist $A_n=\lfloor n\alpha +\gamma \rfloor$ and $B_n=\lfloor n\beta +\delta \rfloor$ such that $B_n-A_n=na+b$. Here again $\alpha ,\beta ,\gamma ,\delta$ are quadratic numbers. Kimberling (2011) rediscovered $A_n$ and $B_n$, and called them $na\!+\!b$ Wythoff sequences.