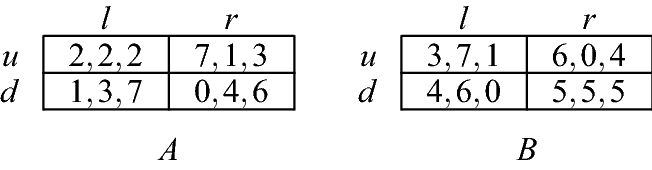Abstract
We prove some interesting properties of unilaterally competitive games when there are more than two players. We show that such games possess: (1) a Nash equilibrium, (2) maximin-solvability, (3) strong solvability in the sense of Nash, and (4) weak acyclicity, all in pure strategies of finite or infinite games.





Similar content being viewed by others
Notes
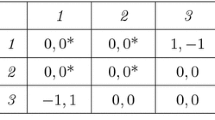
A simpler example of UC game that is not a potential game is given by De Wolf (1999):
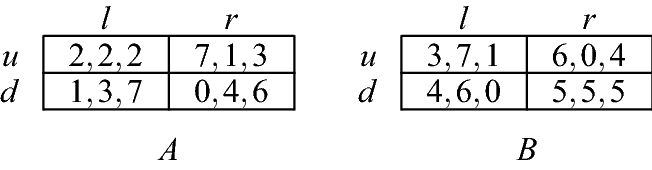
The solvability in the sense of Nash is an immediate consequence of strategy eliminations. For the strong solvability, note that if \(s \in E(G)\), \((s'_i,s_{-i}) \in S\), \(u_i(s'_i,s_{-i})=u_i(s)\), and \((s'_i,s_{-i}) \notin E(G)\), then IENBR cannot remove \(s'_i\), and the game cannot be IENBR-solvable; a similar reasoning applies to the necessity of strong solvability for IESDS-solvability.
References
Ania AB (2008) Evolutionary stability and Nash equilibrium in finite populations, with an application to price competition. J Econ Behav Organ 65:472–488
De Wolf O (1999) Optimal strategies in \(n\)-person unilaterally competitive games, CORE discussion paper 9949
Fabrikant A, Jaggard AD, Schapira M (2013) On the structure of weakly acyclic games. Theory Comput Syst 53:107–122
Fehr E, Schmidt KM (1999) A theory of fairness, competitition, and cooperation. Q J Econ 114:817–868
Iimura T, Watanabe T (2016) Pure strategy equilibrium in finite weakly unilaterally competitive games. Int J Game Theory 45:719–729
Iimura T, Maruta T, Watanabe T (2019) Equilibria in games with weak payoff externalities. Econ Theory Bull 7:245–258
Kats A, Thisse J-F (1992) Unilaterally competitive games. Int J Game Theory 21:291–9
Matsumura T, Matsushima N (2012) Competitiveness and stability of collusive behavior. Bull Econ Res 64:s22–s31
Monderer D, Shapley LS (1996) Potential games. Games Econ Behav 14:124–143
Nash J (1951) Non-cooperative games. Ann Math 54:286–295
Osborne MJ, Rubinstein A (1994) A course in game theory. The MIT Press, Cambridge
Schaffer ME (1989) Are profit-maximizers the best survivors? A Darwinian model of economic natural selection. J Econ Behav Organ 12:29–45
Shubik M (1984) Game theory in the social sciences: concepts and solutions. The MIT Press, Cambridge
Von Neumann J, Morgenstern O (1953) Theory of Games and Economic Behavior, 3rd edn. Princeton University Press, Princeton
Voorneveld M, Norde H (1997) A characterization of ordinal potential games. Games Econ Behav 19:235–242
Acknowledgements
An earlier version was presented at the UECE Lisbon Meetings in Game Theory and Applications 2018. This work is supported by JSPS Grant-in-Aid for Scientific Research (C) (KAKENHI) 25380233, 16K0355301, and 20K01549. The author thanks a co-editor and anonymous reviewers for their valuable comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 A proof of Theorem 5
In this proof, we take a viewpoint that a UC game can be seen as a collection of two-person zero-sum games, to which we then apply Theorem 1.
Proof
Suppose that G is an n-person UC game with \(n \ge 2\) and \(E(G) \ne \emptyset\). By Lemma 1, we have that player i chooses \(s_i\) to maximize \(u_i(s_i,s_{-i})\) given \(s_{-i}\) and player \(-i\) (“other than i”) chooses \(s_{-i}\) to minimize \(u_i(s_i,s_{-i})\) given \(s_i\), and this is true for any \(i \in N\). Since minimizing \(u_i(s_i,\cdot )\) is the same as maximizing \(-u_i(s_i,\cdot )\), we can think of player i as playing a two-person zero-sum game \(G_i=(\{i,-i\},(S_i,S_{-i}),(u_i,-u_i))\) with player \(-i\), for any \(i \in N\). Let \(E(G_i)\) and \(M(G_i)\) be the set of equilibria of \(G_i\) and the set of maximin profiles of \(G_i\), for each \(i \in N\).
Now, let \(s \in E(G)\). It is not difficult to see that \(s=(s_i,s_{-i}) \in E(G_i)\) for every \(i \in N\) (use Lemma 1 to see the optimality of \(s_{-i}\) against \(s_i\)). Then, by Theorem 1, \(s=(s_i,s_{-i}) \in M(G_i)\) for every \(i \in N\). By the definition of maximin strategy in G, \(s_i\) is also a maximin strategy of player i in G, for any \(i \in N\). Hence \(s \in M(G)\).
Let then \(s \in M(G)\). By the definition of maximin strategy in G, we have \(s=(s_i,s_{-i}) \in M(G_i)\) for any \(i \in N\). Then, since \(E(G) \ne \emptyset\), and hence \(E(G_i) \ne \emptyset\) for any \(i \in N\), we have \(E(G_i)=M(G_i)\) for any \(i \in N\) by Theorem 1. Hence \(s=(s_i,s_{-i}) \in E(G_i)\) for any \(i \in N\), and \(s \in E(G)\), for obvious reasons. \(\square\)
Rights and permissions
About this article
Cite this article
Iimura, T. Unilaterally competitive games with more than two players. Int J Game Theory 49, 681–697 (2020). https://doi.org/10.1007/s00182-020-00724-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-020-00724-2
Keywords
- Unilaterally competitive games
- Existence of a pure strategy equilibrium
- Maximin
- Strongly solvable games
- Weak acyclicity