School starting age and the impact on school admission

Abstract

This study employs Chilean administrative data to investigate the impact of school starting age on the characteristics of students’ initial enrolled schools. Employing minimum age requirements and an RD design to mitigate endogeneity concerns, we identify benefits linked to commencing school at a later age. Our findings demonstrate that children starting school at an older age enroll in institutions with higher average scores in standardized tests and interact with older peers whose parents have higher education levels. Furthermore, they display a heightened likelihood of entering schools employing academic selection methods, a greater proportion of full-time teachers, and a larger percentage of instructors with a 4-year college degree. The analysis by level of education of the parents and gender reveals that most of our results are driven by parents with lower levels of education and girls. Subgroup analyses further reveal that many of our results are driven by parents with lower levels of education and parents of girls.

1 Introduction

There is an extensive literature studying the relationship between the age at school entry (school starting age, SSA) and short-, medium-, and long-run outcomes. In general, this literature on SSA shows a positive short- and medium-run impact of SSA on students (Bedard and Dhuey 2006; Datar 2006; McEwan and Shapiro 2006; Elder and Lubotsky 2009; Dhuey and Lipscomb 2010: Mühlenweg and Puhani 2010a; Lubotsky and Kaestner 2016; Attar and Cohen-Zada 2018; Dee and Sievertsen 2018: Caceres-Delpiano and Giolito 2019).¹ As pointed out by Dhuey et al. (2019), these previous results imply that initial variations in maturity, often referred to as readiness, can impact human capital accumulation across an individual’s life with potentially significant implications for adult outcomes. However, studies investigating the long-term effects of SSA present more mixed results across diverse dimensions (Angrist and Kruger 1991; Cascio and Lewis 2006; Black et al. 2011; Dobkin and Ferreira 2010; Fredriksson and Öckert 2014; Cook and Kang 2016; Landersø et al. 2016; Peña 2017).²

The consistency observed in short- and medium-term outcomes, coupled with the less definitive conclusions regarding adult outcomes, may suggest that the mechanisms driving the persistence of early childhood advantages may operate differently depending on the characteristics of the educational system. This study specifically focuses on exploring one potential mediating channel: the elementary school where children begin their education. More specifically, we investigate the impact of SSA on the characteristics of the school where children first enroll, using Chilean public administrative records for the national population of students. On the one hand, if the initial impact of age on readiness enables children to access better schools, it is more likely for this initial effect to persist over time. On the other hand, the extent of this mechanism will be influenced by the degree to which the institutional framework allows for such sorting.

To address potential unobserved variables influencing SSA, we utilize minimum age requirement rules to introduce a discontinuous change in the likelihood of starting school at an older age. Specifically, we employ a fuzzy regression discontinuity (RD) approach that relies on precise birth dates. It’s important to emphasize that our study focuses on an educational context characterized by a generalized voucher system, a period during which schools were permitted to actively select their students. This particular context offers the opportunity to unveil a mechanism that could also apply to other educational settings, though its impact may vary.

Our findings reveal that children starting elementary school at an older age attend schools that differ across several dimensions. First, they enroll in schools with better perceived quality, as evidenced by their average scores on standardized exams. More precisely, we find that older children are 5 percentage points more likely to enroll in schools situated in the upper quartile of the score distribution. Secondly, they have older classmates, on average, and their classmates’ parents possess 0.15 more years of education. Thirdly, they are more likely to attend schools employing some form of academic selection, featuring a higher proportion of full-time teachers, and boasting a larger fraction of teachers holding a 4-year college degree. The analysis, when stratified by parents’ level of education and gender, reveals that the results are driven by parents with lower levels of education and female students.

These results indicate that starting school at an older age allows families to enroll their children in schools associated with better opportunities. However, it’s crucial to interpret our reduced form analysis as reflecting the combined effects resulting from both parental school choice decisions and schools’ selection of students. This selection process could potentially be influenced by the enhanced maturity of children starting school at a later age.

This paper is part of an expanding body of literature that focuses on the relationship between the persistent effects of school starting age (SSA) and the structure of the educational system, which could enhance the benefits of starting school at an older age (Bedard and Dhuey 2006; Mühlenweg and Puhani 2010b; Zweimüller 2013; Schneeweis and Zweimüller 2014; Fredriksson and Öckert 2014; Nam 2014; Peña 2017; Oosterbeek et al. 2021). Although the initial readiness advantage gained from starting school older naturally diminishes over time (Elder and Lubotsky 2009; Lubotsky and Kaestner 2016), the level of selectivity within an educational system or the presence of an early tracking system might contribute to sustaining these early advantages. The timing of the interaction with the educational system’s characteristics also seems crucial. For instance, Fredriksson and Öckert (2014) discover that SSA boosts educational attainment in Sweden; however, this effect is less pronounced among those who delay tracking.³

In a paper analyzing the long-run effect of relative age in Mexico, Peña (2017)⁴ presents a model to demonstrate that the extent of selectivity in the educational system and the wage premium can lead to larger relative age effects, even under less age-biased allocation mechanisms than a tracking system. Our paper is particularly relevant to Peña (2017) as we examine the impact of SSA in an institutional context where elementary schools actively select students. Specifically, if SSA contributes to school readiness, a selective environment could result in older children being more likely to enroll in schools with better resources or interact with more capable peers. Consequently, the impact of SSA might endure if it enables children to access enhanced opportunities at an early age.

Recognizing that we are examining a specific context, our findings could offer an extra avenue to elucidate recent discoveries about the long-term impacts of SSA within the same setting (Celhay and Gallegos 2022).⁵ Nonetheless, it’s probable that in different environments, certain levels of school selectivity exist (e.g., private schools). In such instances, it’s conceivable that the influence of SSA on student outcomes might also encompass the influence of school attributes.

The paper is structured as follows. Section 2 provides a brief overview of Chile’s educational system. In Sect. 3, we outline the conceptual framework for our study, our empirical approach, the data utilized in the analysis, and the defined outcomes. Section 4 presents the primary findings. Lastly, Sect. 5 offers concluding remarks.

2 Institutional background

2.1 Chilean educational system

Since the early 1980s, Chile’s primary and secondary educational system has experienced substantial decentralization and increased private sector involvement.⁶$^{,}$⁷ The student population, which is around 3.5 million, is divided among three types of schools: public or municipal schools (constituting 41% of total enrollment), subsidized private schools (making up 51% of total enrollment), and unsubsidized private schools (representing 7% of total enrollment). Municipal schools are overseen by the comunas (similar to counties in the USA), while the private sector manages the other two types of schools.⁸

Both municipal and subsidized private schools receive state funding through a voucher scheme, with the subsidy amount varying based on each school’s enrollment. Subsidized private schools are often called voucher schools. Importantly, parents are not obligated to select a school within their county of residence, although approximately 90% of parents choose to do so. This system is similar to other extensive voucher programs in countries like the Netherlands, Denmark, and Sweden, as well as some smaller-scale programs in the USA (Epple et al. 2017).

Initially, public and subsidized private schools in Chile were intended to be free of charge. However, starting in 1994, these schools were permitted to charge tuition and fees in addition to the government subsidy they received. Subsequently, Law 20.845 of 2015 required schools with tuition to gradually reduce the co-payment to zero or transition to unsubsidized private schools. Despite the majority of public schools remaining free of charge, approximately 30% of students attended voucher schools with co-payment during this period.

This paper focuses on studying the population of Chilean students who entered primary school between 2002 and 2008, a time when schools were allowed to actively select students. The law of the year 2015 explicitly prohibited voucher schools from engaging in student selection. Instead, it established a Centralized Admission System for both public and voucher schools. This system was implemented gradually by regions and was fully in place at the national level by 2020.

2.2 Minimum age requirements

In Chile, the minimum age requirement rules stipulate that children must have turned six before a specific date during the academic year in order to be enrolled in first grade at primary school.⁹ Children whose birthday falls before this cutoff date are eligible to start school in the year they turn six, while those born after this date must wait until the following academic year to begin school.

Initially, Chile’s official enrollment cutoff was set on April 1st. However, from 1992 until recently, the Ministry of Education allowed schools some flexibility to set other cutoff dates, but not later than July 1st. Schools have distributed themselves over seven cutoff dates between January 1st and July 1st.¹⁰ McEwan and Shapiro (2006) used the four most common cutoffs (April 1st, May 1st, June 1st, and July 1st) to estimate the impact of SSA on students’ outcomes in Chile.

Fig. 1

Fraction of students starting older around different cutoffs

Figure 1 visually illustrates the variation induced by minimum age requirement rules. Each panel of the figure shows the fraction of students who start elementary education in the year of their seventh birthday (“Older”) within a 15-day window around different age cutoffs. Panel (a) presents this fraction by stacking up all the cutoffs. Notably, approximately 15% of students to the left of any cutoff start school at an older age, and this fraction nearly doubles to the right of these cutoffs.

Upon closer examination in Panels (b) to (d), we observe that among students with early-year birthdays, only a small fraction are “redshirted” (i.e., they delay enrollment). Practically none of the students with birthdays before April 1st are redshirted, but this fraction progressively increases to approximately 45% among students with a birthday in June. Two elements explain this pattern. First, students born early in the year are already older at the start of the academic year, making them less likely to postpone enrollment. Second, due to the Chilean institutional setting of multiple cutoffs across schools, children with birthdays closer to July 1st face a larger increase in the pool of schools to choose from if they decide to wait.¹¹ These factors likely contribute to the heterogeneity in the discontinuity induced by minimum age rules.

Additionally, it is important to note that children born after June 30th are “forced” to postpone enrollment until the next year, leading to an approximately 55 percentage point increase in the likelihood of starting school older compared to those born before July 1st. The probability of waiting until the next year changes by less than 1 percentage point for the January–March cutoff (Panel (b)) and by around 10 percentage points around the April–June cutoff (Panel (c)).

3 Methods

3.1 Conceptual framework

To define the scope of our paper, we make slight modifications to a framework initially introduced by Hanushek (1979) and also by Boardman and Murnane (1979).¹² Consider a three-period setting where $t=0$ represents the time before school entry, and $t=1$ and $t=2$, the first and second years of school, respectively. We define $A_{t}$ as children’s achievement at the beginning of period t. Let $F_{t}$ represents family investments in children’s learning during period t, W be the family wealth, $\mu$ be children’s innate ability, and a be their SSA. Therefore, if SSA influences children’s intellectual maturity, we can define the achievement at school entry as:

$$\begin{aligned} A_{1}=g_{0}(F_{0},\mu ,a). \end{aligned}$$

Similarly, achievements at the beginning of second year depend on the history of family inputs, $F_{0}$ and $F_{1}$ and on school inputs, $S_{1}$, as well as children cognitive ability:

$$\begin{aligned} A_{2}=g_{1}\left( S_{1},F_{1,}F_{0},\mu ,a\right) \end{aligned}$$

As in Todd and Wolpin (2003), we distinguish between two types of school inputs: the amount of inputs chosen by the family at the time of schooling decision, denoted by ${\overline{S}}_{1}$, and the actual level of school inputs, $S_{1}.$ We will refer to these inputs broadly as “school inputs,” which include factors such as teachers’ qualifications and potential sources of peer effects, like classmates’ parental education or classmates’ age. Within the context of our paper, families have the flexibility to approximate their desired school inputs (${\overline{S}}_{1}$) by directly selecting schools in a voucher system. For the sake of simplifying notation in the analysis that follows, let’s assume that family decisions regarding school inputs are solely determined by family wealth and children’s innate ability (independent of $A_{1}$).

$$\begin{aligned} {\overline{S}}_{1}=\theta \left( W,\mu \right) \end{aligned}$$

Schools also decide how to allocate inputs to children, for example, by “tracking” based on their previous achievement. In the case of Chile during the period under consideration, schools were allowed to select students depending on their achievements at the time of school entry. Therefore,

$$\begin{aligned} S_{1}=\psi \left( A_{1},\mu \right) \end{aligned}$$

Finally, the family decides on direct investments in children’s learning depending on their wealth, previous children’s achievement, their ability, and the deviation between actual and desired school inputs. Under the assumption that families observe these deviations before deciding on investments, we have:

$$\begin{aligned} F_{1}=\phi \left( A_{1},W,\mu ,S_{1}-{\overline{S}}_{1}\right) . \end{aligned}$$

In this context, we can examine the effect of an exogenous increase in SSA on children’s achievement at the beginning of the second year, $A_{2}$. For simplicity, we assume that SSA has only a direct effect on $A_{1}$, meaning that pre-school family investments (other than school choice) are independent of SSA: $\frac{dF_{0}}{da}=0$. Therefore, we have:

$$\begin{aligned} \frac{dA_{2}}{da}=\frac{\partial g_{1}}{\partial a}+\left[ \frac{\partial g_{1}}{\partial F_{1}}\frac{\partial \phi }{\partial A_{1}}+\left( \frac{\partial g_{1}}{\partial S_{1}}+\frac{\partial g_{1}}{\partial F_{1}}\frac{\partial \phi }{\partial \left( S_{1}-{\overline{S}}_{1}\right) }\right) \frac{\partial \psi }{\partial A_{1}}\right] \frac{\partial g_{0}}{\partial a} \end{aligned}$$

The impact of SSA on students’ achievement consists of a direct effect ($\frac{\partial g_{1}}{\partial a}$) and a series of indirect effects caused by changes in pre-school achievement ($\frac{\partial g_{0}}{\partial a}$):

• (i) The impact of changes in school direct inputs: $\left( \frac{\partial g_{1}}{\partial S_{1}}\frac{\partial \psi }{\partial A_{1}}\frac{\partial g_{0}}{\partial a}\right)$.

• (ii) The impact of family adjusting investments in reaction to changes in pre-school achievement: $\left( \frac{\partial g_{1}}{\partial F_{1}}\frac{\partial \phi }{\partial A_{1}}\frac{\partial g_{0}}{\partial a}\right)$.

• (iii) The impact of changes in family investments in reaction to the deviation between actual and targeted school inputs $\left( \frac{\partial g_{1}}{\partial F_{1}}\frac{\partial \phi }{\partial \left( S_{1}-{\overline{S}}_{1}\right) }\frac{\partial \psi }{\partial A_{1}}\frac{\partial g_{0}}{\partial a}\right)$.

In this paper, our main objective is to estimate the effect of SSA on school inputs, which are broadly defined and measured at the time of school entry. The reduced form parameter $\alpha =\frac{\partial \psi }{\partial A_{1}}\frac{\partial g_{0}}{\partial a}$ captures the combined impact of SSA on pre-school achievements $\left( \frac{\partial g_{0}}{\partial a}\right)$ and the subsequent effect of these achievements on school inputs $\left( \frac{\partial \psi }{\partial A_{1}}\right)$, considering the interaction between parents and schools. For simplicity, we have assumed that parents’ choice of school characteristics is independent of pre-school achievement and, consequently, independent of SSA ($\frac{\partial \theta }{\partial A_{{1}}}=0$). However, this reduced form does not allow us to distinguish between changes in school inputs resulting from parents’ school choice decisions and schools selecting children based on their improved pre-school achievement due to SSA. Moreover, since we are estimating a Local Average Treatment Effect (LATE), the estimated impact corresponds to the subgroup of compliers rather than the one for the full population.¹³

Recent literature have shown evidence about the different channels. While some recent papers explore the immediate impact in terms of school readiness,$\frac{\partial g_{1}}{\partial a}$ (e.g., Dhuey et al. 2019), other studies have explored the contribution of families (Elder and Lubotsky 2009; Landersø et al. 2020; Celhay and Gallegos 2022).¹⁴ Depending on the context, the papers that analyze the connection between SSA and family investments are either capturing the direct adjustment of parents to the improvement in children’s skills (channel (ii)), or a combination of the direct effect and parents’ response to changes in school inputs (channels (ii) and (iii) combined).

3.2 Data

The primary data source for our analysis comes from public administrative records provided by the Ministry of Education of Chile for the period 2002–2008. Our analysis focuses on students born between the years 1996 and 2001. From this dataset, we obtain for each student in the population their masked identification number,¹⁵ exact dates of birth, gender, municipality of residence, first school identifier, and type of school (public, voucher, or unsubsidized private). Additionally, we use the individual records to determine the average age of students’ classmates. We identify the schools’ minimum age cutoffs by considering the entire student population. In any given year or period under analysis, we establish the cutoff date for each school by using the birth date of the youngest child enrolled.

Our second data source is the SIMCE standardized test records, obtained from the Agencia de Calidad de la Educación.¹⁶ Firstly, we utilize the parental survey module within the SIMCE survey to determine the parents’ level of education. Secondly, we aggregate scores at the school level for the year preceding each cohort’s entry using individual student records, along with information about the average schooling of their classmates’ parents. Finally, we gather parental opinions about the school selection process at the time of the survey through the parental survey.¹⁷

The third source of information comes from administrative records regarding teachers, provided by the Ministry of Education of Chile for the period 2003–2009. From this source, we acquire data on teachers’ weekly total working hours and total teaching hours, which we aggregate at the school level. Additionally, we obtain information about teachers’ education from the teacher evaluation database, which we also aggregate at the school level.¹⁸

3.3 Empirical specification

Estimating the effects of SSA poses challenges due to potential SSA manipulation, including practices like redshirting (Dhuey et al. 2019) or strategic birth timing (Buckles and Hungerman 2013).¹⁹ As the determinants of school entry decisions are often unknown or unobserved by researchers, there is a risk of omitted variable bias when comparing outcomes among children who start school at different ages.

To tackle the issue of endogeneity, we employ a quasi-experimental approach by utilizing the minimum age requirement rule as source of variation. In particular, we utilize a fuzzy regression discontinuity (RD) strategy that relies on precise birth dates. To address concerns regarding weak instruments, we concentrate solely on the July cutoff, which exhibits the most significant and identifiable discontinuity among the seven different cutoffs in Chile.²⁰

In the scenario where students are indexed by i, their year of birth by t, and their birthday over the calendar year by b, the specification used to estimate the impact of SSA on school characteristics for student i ($y_{it}$) can be expressed as follows:

$$\begin{aligned} {y_{it}}{=}{\rho _{t}+X_{i}^{'}\mathbf {\psi }+{\alpha }\,Older{}_{i}+g(b_{i})+\epsilon _{it}}&, \end{aligned}$$

(1)

The variable $Older_{i}$ is a dummy variable that takes the value of one if a child started primary school during the academic year of their seventh birthday, and zero otherwise. Moreover, $\rho _{t}$ represents the year of birth, and $X_{i}$ a vector of individual covariates.²¹ Finally, $g(b_{i})$ is a flexible polynomial specification in the day of birth for a student, which we allow to have a different slope at each side of the cutoff. By adding to the specification a polynomial specification in the day of birth, $g(b_{i})$,²² we deal with the possibility that students born at different dates differ in a systematic manner. We cluster the error term at the student’s day of birth.

In Eq. (1), our primary focus is on the parameter $\alpha$, which represents the reduced form impact of SSA on school characteristics. As explained in Sect. 3.1, this parameter captures the interplay between schools, (which are allowed to select students), and parents (who may choose a better match from a larger number of schools). This interplay arises in response to the child’s skills improvement due to SSA.

As stated above, the variable indicating whether or not a child starts schooling at an older age ($Older_{i}$) is a non-random variable. To address this endogeneity, we use the discontinuity determining SSA and estimate the following first-stage regression:

$$\begin{aligned} Older_{i}=\rho _{t}+X_{i}^{'}\psi +\delta \times 1\{b_{i}-C>0\}+g(b_{i})+v_{i} \end{aligned}$$

(2)

Here, the parameter of interest, \delta, captures the discontinuity in the endogenous variable. The operator 1{*} serves as an indicator function, and C represents the July cutoff.

Following Calonico et al. (2014, 2017), we select two data-driven bandwidths for each of the outcomes. The first method tries to balance some form of bias-variance trade-off by minimizing the mean squared error (MSE) of the local polynomial RD point estimator (MSE-optimal bandwidth). The second bandwidth minimizes an approximation to the coverage error rate (CER) of the confidence intervals, that is, the discrepancy between the empirical coverage of the confidence interval and the theoretical level. See Appendix A for details.²³

The primary identifying assumption for our analysis is that there are no factors other than SSA changing discontinuously at cutoffs. To ensure the plausibility of that assumption, we perform several robustness checks.²⁴ In Appendix B.1 we show that the individual covariates (gender, parents’ education, and municipality of residence) behave smoothly at the cutoff. Additionally, in Appendix B.2, we present both visual and formal evidence, following McCrary (2008), that there is no manipulation based on birth dates around the cutoff.

In the context of “essential heterogeneity” (Heckman et al. 2006), the estimated parameters can be interpreted as weighted “Local Average Treatment Effects” (LATE)²⁵ across all individuals (Lee and Lemieux 2010). However, for this interpretation to hold, it is crucial to ensure that the monotonicity assumption is not violated. In the context of our paper, the monotonicity assumption implies that a change in the instrument’s value (in our case, being born after the July cutoff) should increase the school starting age (SSA) for all students or, at the very least, not decrease it. Although we cannot directly test this assumption, we provide some arguments to mitigate concerns below and discussed them in more detail in Appendix B.3.

The need for the monotonicity assumption arises due to the presence of heterogeneity, combined with students strategically choosing their SSA based on expected outcomes (“sorting on gains”). To gauge the extent of this heterogeneity, we include covariates that can reasonably serve as indicators for income, such as parental education, and specifically within the Chilean context, the municipality of residence. If the violation of monotonicity posed a notable empirical concern in our analysis, we would anticipate the estimates to display sensitivity when covariates like these are incorporated (Dhuey et al. 2019). Nonetheless, our estimates are in general insensitive to the inclusion of these covariates (see Appendix C.2). This observation suggests that potential violations of monotonicity are unlikely to significantly influence our results.

However, we acknowledge that we cannot rule out the presence of heterogeneity and sorting on gains. Therefore, we will now examine the plausibility of the monotonicity assumption in relation to our paper, assuming independence between the instrument and the potential treatment assignment.

When heterogeneity and sorting on gains are present, as highlighted by Barua and Lang (2016), a violation of monotonicity can occur when there are “defiers”—children who start school early only when they are not allowed to do so. However, in our working sample, we find that approximately half of the June-born children are redshirted, while hardly any July-born children start school early.²⁶ This observation effectively rules out the biggest concerns regarding defiers.

The primary risk of potential monotonicity violation in our sample arises from redshirted June-born children, who would have faced a slight decrease in their SSA if they were born after July (simply because they would start school at the same time but be a few days younger). Nonetheless, our confidence is boosted by the availability of precise date of birth information, allowing us to include a daily time trend to mitigate these concerns. This daily time trend enables us to estimate the treatment effect at a singular point (or infinitely small approximation) of the cutoff (Dhuey et al. 2019). While we cannot definitively rule out a violation of monotonicity, following Fiorini and Stevens (2021), we can infer that the parameter we are estimating in our fuzzy RD design closely approximates the Local Average Treatment Effect (LATE) of interest.

3.4 Outcomes

We utilize the data described in Sect. 3.2 to construct variables related to school inputs and peer characteristics at the school when students enroll in first grade of elementary school. These variables help us characterize schools by their average score in the national standardized test, by their degree of selectivity as reported by parents, and certain direct observable measures such as parental schooling and teachers’ characteristics.

To assess school “quality,” we use the average SIMCE score of each school, measured a year before students enroll. We create three categories to show if a school’s score is higher than the 25th, 50th, or 75th percentile. Additionally, we include a dummy variable indicating if the school is a subsidized private, which are addressed as Voucher school.

Even though test scores are not a perfect way to measure school quality because they can be influenced by other factors (Kramarz et al. 2008), in Chile, the average SIMCE score is frequently used to provide families insights into their school choices.(Mizala and Urquiola 2013). Moreover, school average scores are considered a good predictor of the probability of college admission. As shown in Fig. 2, there is a strong correlation between the school average score and the probability of admission to selective universities in Chile.²⁷

Fig. 2

Source: Departamento de Evaluación, Medición y Registro Educacional (DEMRE) and Agencia de Calidad de Educación

Average standardized SIMCE school and probability of admission to selective colleges

Until recent reforms, the school selection process typically involved active involvement from both families and schools. To gain a clearer understanding of how school choice worked, we use data from the parents’ survey of the SIMCE standardized test. From this data, we create a variable that shows the percentage of parents who reported that their child went through a selection process mainly based on academic factors. We consider academic selection as situations where students take exams, participate in play sessions, or schools ask for past academic records (like preschool attendance).²⁸

A second group of variables pertains directly to visible school resources, with a specific focus on teachers at the school level. These variables include the average age of teachers, the percentage of full-time teachers, the ratio of teaching hours to total hours, and the share of teachers possessing a 4-year college degree.²⁹

The final two variables in this second group, aim to characterize the students’ classmates. These variables represent the average education level of parents among the classmates and the average age of the classmates themselves. The importance of the latter variable has been highlighted by recent research that examines how the age of peers can influence learning (Cascio and Whitmore Schanzenbach 2016; Peña 2017).³⁰

Table 1 Descriptive statistics

Furthermore, in an educational system where schools have the authority to choose students, those who begin school at an older age might find themselves among older classmates. This situation could indicate that these students are enrolling in schools that consistently admit older students.

Table 1 presents the descriptive statistics. The upper panel reports the statistics for students born from January to July during the period under consideration, while the bottom panel shows the statistics for students with birthdays within an 8-day interval around July’s cutoff.

Notably, the working sample’s statistics closely resemble those of the whole population. Each cohort comprises roughly 250,000 students, split evenly between boys and girls. The average age of school entry is 6.14 years, with roughly 21% beginning school at a later age. This percentage increases around July’s cutoff (Panel B), due to the explained institutional setup.

Fig. 3

Evolution of selected outcomes according to the student’s birthday

Concerning school type, about 52% of students are in voucher schools. The average schooling level of classmates’ parents is approximately 11 years. For selection procedures, around 65% of students attend schools historically known to pick students based on academics. The portion of full-time teachers is about 32%, with around 64% holding a 4-year college degree.

Fig. 4

Evolution of selected outcomes according to the student’s birthday

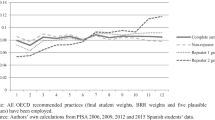
Figures 3 and 4 portray how each outcome corresponds to the student’s birthday.³¹ It’s important to note a distinct jump at the discontinuity for most of the considered variables. Specifically, Fig. 3 emphasizes that students born just after the cutoff often enroll in schools with higher test scores and some degree of academic selection.

Furthermore, Fig. 4 suggests that children born on or after July 1st are more likely to be surrounded by older classmates with better-educated parents. They also have a higher chance of being taught by teachers holding 4-year college degrees. This descriptive observation implies that starting school at an older age is linked to an overall “quality” improvement in the school environment.

4 Results

4.1 First stage: impact of minimum age requirements on the probability to start school older

Table 2 shows the calculated change in the likelihood of starting school at an older age (the year of the seventh birthday) for children born in the early days of July compared to those with a birthday in the final days of June. This difference, denoted as $\delta$ in Eq. (2), is displayed in three panels for different samples: Panel A shows the results for the complete sample, Panel B considers parents’ education, and Panel C breaks down the results by students’ gender.

For each of these samples, we estimate $\delta$ using bandwidths of 5 days (columns 1–2), 10 days (columns 3–4), and 15 days (columns 5–6).³² For each of the bandwidths, the first column shows the results using only a local linear specification for $g(b_{i})$ as a control,³³ and the second column includes all other control variables.

Notably, the estimates remain qualitatively robust across all samples when additional variables are included in the model. This robustness to other covariates is consistent with the lack of correlation between observed predetermined variables and the source of variation coming from the minimum age requirements (see Appendix B.1). The estimates are also robust to changes in the bandwidth used.

Table 2 First-stage estimates

Regarding the estimated $\delta$, it is observed that being born after the cutoff increases the probability of starting school at an older age by approximately 45 to 50 percentage points compared to students with a birthday just before July 1st. Figure 1 further supports this finding, as it shows that fewer than half of the children born before July are redshirted. Furthermore, in an IV approach equivalence, the value of the F-statistic (reported at the bottom of each panel/sample) suggests disregarding any concerns about weak instruments.³⁴

In Panels B and C of Table 2, we explore the heterogeneity in the source of variation by parents’ education and students’ gender. This analysis allows us to confirm relevant variation for these two subsamples. In addition, it also demonstrates the robustness of our estimates across families with varying levels of parental education and among male and female students.

The difference in point estimates suggests a larger complier group among families with less educated parents and female students. Specifically, regardless of the specification used, we find that students from families with lower levels of parental education are approximately 8 percentage points more likely to start school older due to minimum age requirements. On the other hand, the differences by students’ gender are relatively smaller, with girls showing an additional increase of approximately 5 percentage points in the probability to start at an older age, compared to boys. Despite these differences in the degrees of compliance, it is important to note that for all the subsamples, we observe a relevant source of variation induced by the discontinuity determined by the entry rules.

4.2 SSA and school characteristics

Tables 3 and 4 present the estimates of $\alpha$ in Eq. (1) for two groups of variables: school quality and selectivity, and proxies for school inputs, respectively. Panel A of each table shows the OLS estimates,³⁵ while Panels B to D display the RD estimates for the complete sample, as well as subsamples defined by parents’ education (Panel C)³⁶ and students’ gender (Panel D). The RD estimates reported are based on the specification using the MSE-optimal point estimate bandwidth.³⁷ Moreover, for each outcome and bandwidth, we provide the weak instrument Effective F statistic (Olea and Pflueger 2013), which is valid under heteroscedastic or serially correlated errors.³⁸ These tests help us address concerns related to weak instruments.

Table 3 Impact of SSA on school characteristics. MSE-optimal bandwidth

Table 4 Impact of SSA on school inputs

Focusing on the RD estimates for the complete sample (Panel B), we see that starting school at an older age increases the average SIMCE score of the first school by 0.09 standard deviation. Columns (2) to (4) display results showing this improvement across the entire score distribution. There’s a rise in the likelihood of attending a school above the 25th percentile by 2 percentage points, above the 50th percentile by 5 percentage points, and above the 75th percentile by 5 percentage points. When comparing OLS and RD estimates, we notice a positive bias in the OLS estimates regarding the impact of starting older on school SIMCE scores. This bias is evident in both the average SIMCE score and across the score distribution. This implies that some parents deliberately delay their children’s school entry to enhance their chances of gaining admission to schools perceived to have better quality. Moreover, we observe a 3 percentage point increase in the likelihood of attending a voucher school, which roughly corresponds to a 6% increase based on the sample mean.

In the Chilean context during the period analyzed, families compelled to postpone school entry might invest more time in searching for the most suitable school for their children. However, it’s important to note that schools also have the freedom to choose students. Columns (6) and (7) in Table 3 present estimates for two variables crafted at the school level based on parents’ responses from previous years. The outcomes in the first column reveal that students who start school at a later age enroll in schools where a higher proportion of parents reported some form of academic selection. Specifically, initiating school at an older age leads to a 7.5 percentage point increase in this proportion (roughly a 12% increase considering the sample mean).

The differences among parents’ education (Panel C) imply that students from less educated backgrounds are primarily responsible for the improvements associated with SSA in terms of school average scores and selectivity. Among children with more educated parents, the benefits of SSA are confined to a higher likelihood of attending schools in the upper range of the SIMCE distribution (beyond the 75th percentile) and a 5 percentage point rise in the portion of parents reporting academic selection. This evidence, combined with a precisely zero impact on the likelihood of entering a voucher school for families with higher education levels, suggests that the impact of SSA is on intensive margins. To put it another way, some families who were already sending their children to private schools are able to transition to other private schools in the upper part of the SIMCE distribution, which tend to be more academically selective.

For families with less educated parents, we observe a significant increase of 0.11 standard deviations in the school SIMCE score across the entire score distribution. This group also experiences a 5.4 percentage point rise in the likelihood of starting in a voucher school and a greater proportion of parents (9 percentage points) reporting academic selection. Elder and Lubotsky (2009) discovered that the initial benefits of SSA in terms of test scores are more pronounced among higher-income families. They use this evidence, combined with the timing of the effect, to argue that SSA is influenced by skill development before kindergarten. In the context of a voucher system where school choice is itself an investment factor and schools actively select students, our findings lend support to the notion that families with lower incomes can offset these disparities in previous skill development.³⁹

In Panel D, the variation by students’ gender highlights greater improvements in SSA for girls, resulting in a significant 0.12 standard deviation increase in the school SIMCE score. This positive change is noticeable throughout the entire SIMCE distribution. Additionally, the probability of girls attending a voucher school is almost double that of male students, and they encounter a higher level of academic selection compared to boys (8.6 percentage points versus 6.8 percentage points).

We have conducted robustness checks in three different ways to validate the findings. First, in Appendix C.1, we provide estimates for each of the different outcomes and samples using the CER-optimal bandwidth, which is our second data-driven bandwidth reported in Appendix C.1. The results obtained using this alternative bandwidth show similar magnitudes and conclusions.

Secondly, in Appendix C.2.2, we provide the reduced form estimates for each outcome both with and without covariates, using three different bandwidths (5, 10, and 15 days). These estimates consistently show a benefit for students born in July when compared to those born in the final days of June. Moreover, the results remain robust regardless of whether covariates are included and which bandwidth is employed.

Lastly, in Appendix C.4, we present the reduced form estimates for a Placebo analysis using different cutoffs, specifically at the 1st of September and the 1st of October, along with three distinct bandwidths, both with and without controls. Across all specifications, we do not detect a significant discontinuity, suggesting that the observed effects are not driven by spurious factors.

4.3 SSA, school peers and school teachers

The impact of starting primary school at an older age on the characteristics of school peers and teachers is presented in Table 4, using a similar structure to the one used for school characteristics. It’s important to highlight that the test for weak instruments helps alleviate any concerns regarding these outcomes.

The RD estimates for the complete sample indicate that students who begin school at an older age join a school with more “advantaged” peers, as measured by the education level of classmates’ parents. Specifically, students entering school in the year of their seventh birthday show an increase of around 0.2 years in the average education level of parents within the school. Analyzing the variation by gender and parents’ education, we find that, similar to estimates for school scores and selectivity, bigger improvements are seen for students with less educated parents and girls.

Column (2) of Table 4 demonstrates that starting school at an older age increases the average age of classmates by around 0.06 years. This outcome remains consistent across different samples. This finding holds significance for two reasons. Firstly, it implies that students commencing school at an older age are more likely to enroll in schools that systematically choose older students (using earlier cutoff dates) or employ academic selection (where older students tend to perform better in academic assessments). Secondly, this discovery aligns with previous evidence on the impact of relative age (Cascio and Whitmore Schanzenbach 2016; Peña 2017), suggesting an additional pathway through which SSA can benefit students.⁴⁰

Examining teacher characteristics, we notice that students who begin school at an older age witness a decrease of around 0.7 years in the average age of teachers at the school. While this discovery might not inherently be positive, as it could signify a decline in teacher experience, we also identify that these students enroll in schools with a larger portion of teachers possessing a 4-year college degree. Concretely, there is a 2-percentage-point increase, which corresponds to a 3% difference compared to the sample mean.

Regarding school inputs, we discover that students who start school at an older age join institutions with about 1.3 percentage points more full-time contract teachers, signifying a 4% rise relative to the sample average. Furthermore, there’s a decrease in the proportion of teaching hours compared to the total, implying a potential allocation of more time toward class preparation.

As for the previous group of outcomes, the RD results are robust to alternative bandwidths (Appendix C.1 and C.2.2). The placebo analysis in Appendix C.4 does not reveal a discontinuity for any of the outcomes, with the exception of the share of teachers with a 4-year college degree. However, this impact is considerably smaller than the main analysis, has an opposite sign, and is only statistically significant at the 10% level.

5 Conclusions

In this paper, we investigate how the school starting age (SSA) affects the attributes of the initial school that students attend, utilizing data from Chile’s public administrative records. To address potential endogeneity, we leverage minimum age requirement rules as a source of variation in the likelihood of starting school at an older age.

We find that beginning school at an older age leads to noteworthy changes in school options. Firstly, students who delay school entry are placed in schools with an approximately 0.1 standard deviation higher average score on standardized tests. Secondly, their classmates tend to be older and have parents with higher education levels. Thirdly, these students are more likely to enter schools that implement some type of academic selection, have a higher portion of full-time teachers, and a greater share of teachers with a 4-year college degree. Further analysis by parental education level and gender highlights that most of these effects are driven by parents with lower education levels and girls.

This paper contributes to the existing literature that examines the relationship between the lasting impacts of SSA and the educational system’s structure, which could enhance the benefits of beginning school at an older age. Our results contribute evidence to an alternative pathway through which SSA affects students’ long-term outcomes.