Abstract
Using a regression discontinuity design and public educational administrative data for Chile, this chapter studies the impact of age at school entry on children’s outcomes. In contrast to previous studies, the authors are able to track this impact on school achievement over 11 years of the school life of a cohort of students. The results confirm previous findings that a higher age at entry has a positive effect on grade point average (GPA) and the likelihood of passing a grade, but also that this impact tends to wear off over time. However, we also find that this impact on school achievement is still present 11 years after a child has started school.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
This chapter studies the impact of age at entry on school performance using public administrative data for Chile.Footnote 1 In contrast to previous literature, the authors are able to track this impact on a selected group of outcomes by following a cohort of students over 11 years of their school life. This not only allows the authors to understand the evolution of the impact, but also sheds light on alternative channels that explain the pattern over time.
Since Deming and Dynarski (2008) pointed out a trend in the United States (US) towards delayed school entry, an increasing number of studies have explored the short- and long-term effects of age at entry.Footnote 2 ,Footnote 3 Despite the observed positive correlation between age at entry and academic achievements (Stipek 2002), a series of recent studies reveal mixed results for these and other long-term outcomes once the endogeneity of age at entry is addressed. Among children in primary school, age at entry has been negatively associated with grade retention and positively linked with scores in standardized tests (McEwan and Shapiro 2006). The evidence for older students shows that age at entry is associated with lower IQ and increased rates of teen pregnancy and mental health problems (Black et al. 2011). Earlier age at school entry is also associated with a negative effect on completed years of education (Angrist and Kruger 1991), lower earnings in young adulthood (20s and early 30s) (Angrist and Kruger 1991; Black et al. 2011), and an insignificant effect on the Armed Forces Qualifying Test (Cascio and Lewis 2006). Therefore, although a positive effect occurs in early school outcomes, age at entry seems to have an ambiguous long-term effect.
In this chapter, the analysis is focused on the impact of age at school entry on children of school age. This work is closely related to that of McEwan and Shapiro (2006), who also study the benefits of delaying enrollment on educational outcomes in Chile. They show that an increase of 1 year in the age of enrollment is associated with a reduction in grade retention, an increase in grade point average (GPA) during the first years, and an increase in higher education participation. Also, like McEwan and Shapiro (2006), the authors address the endogeneity of age at entry by using the quasi-random assignment stemming from the discontinuity in age at entry produced by the minimum age requirements. In the present study, however, the authors use the complete population of students.Footnote 4 This is important given the recognized sorting of better students into schools with better teachers (Tincani 2014). Second, the authors follow a cohort of students for over 11 years of their school life. By following this cohort, there is no need to restrict the analysis to a specific grade, which is a function of the number of grades repeated; rather, the analysis considers the number of years elapsed since a child started primary school. This is particularly relevant for Chile, where over 30% of the students in a particular cohort have repeated a grade at least once during the course of their school life. Third, by following a cohort of students for 11 years, the authors investigate the evolution of the impact of age at entry and its reported decline over the student’s school life. In Chile, in contrast to other countries, laws on mandatory education are linked to years of education rather than to a student’s age. In fact, for the period under analysis, the completion of secondary education is mandatory. This institutional feature enables study of the long-term return of delaying school entry over a child’s school life, even into secondary education, without concern that the impact of dropping out is captured simultaneously. Finally, by using other outcome variables going beyond school achievements, the authors are able to study the channels by which age at entry affects educational performance, and to assess the evolution of the impact associated with a delay in the age at entry. Specifically, the authors study the impact on school type, the type of academic track followed by the students and whether or not delaying school entry is associated with being in a school where higher cream skimming can be observed.Footnote 5
The findings confirm that delaying school entry has a positive effect on GPA, attendance, and the likelihood of passing a grade, but also that this impact tends to wear off over time.Footnote 6 Nevertheless, in contrast to previous studies, the findings reveal that this impact may still be observed 11 years after a child has started school. Moreover, evidence on the effect of age at entry on school type provides a potential explanation for the decline in the impact of age entry on academic achievement over a child’s school life. Specifically, a higher age at entry decreases the likelihood that a child is enrolled in a municipal school, such schools being characterized by less active selection of students and lower-quality teachers. Consistent with these differences in academic selection, children who are older when they start school have a higher probability of being enrolled in schools where children coming from other schools have a GPA that is higher than the mean in the school where the student was enrolled for first time. There is also evidence that age at entry has a positive effect on the likelihood that a child follows an academic track in high school. Finally, the authors provide evidence that age at entry is associated with an increase in the probability that a child is enrolled in a school which is actively engaged in cream skimming, which also explains the drop in the impact of age at entry on school achievements.
The chapter is organized as follows. Section 2 describes the authors’ empirical strategy. Section 3 briefly sketches Chile’s educational system, presents the dataset used in the analysis, and defines the sample and the selected outcomes in the analysis. In Sect. 4 the results are presented, and Sect. 5 concludes.
2 Empirical Specification
The specification of interest in this analysis can be expressed as follows:
with y it as one of the educational outcomes observed for a student, i, t years after she/he started school. Aentry i corresponds to the age at entry and X i to other predetermined variables. The parameter of interest is γ t, which corresponds to the impact of age at entry on a selected outcome. The time superscript highlights the fact that this impact is allowed to change over time. As extensively reported in the literature, it is suspected that estimating Eq. (1) by ordinary least squares (OLS) will produce inconsistent estimates of γ.t Families who decide to delay school entry are more likely to have relatively higher (lower) gains (costs) associated with this delay.Footnote 7 Unobserved variables correlated with these gains and costs, such as parents’ education, parents’ motivation, and so on, can also have a direct effect on a student’s achievement; the OLS estimates are likely to pick up the impact of these unobserved factors as well as the impact of age at entry.
To overcome the problem of this omitted variable and to estimate the impact of age at entry, γ t, the minimum age at entry rules is used as a source of variation in the age at enrollment in first grade of primary school. These rules establish that children, in order to be enrolled in first grade at primary school, must have turned 6 before a given date in the academic year. Children whose birthday occurs before this cutoff date are entitled to start school the year they turn 6. Those whose birthday is after this cutoff must wait until the next academic year to start school. This discontinuity in the age at entry, together with the assumption that parents cannot fully control the date of birth, provides a potential quasi-experimental variation in the age at entry that constitutes the core of our “fuzzy” regression discontinuity (RD) strategy.Footnote 8
Chile’s official enrollment cutoff used to be 1 April but, since 1992, the Ministry of Education has provided some degree of flexibility to schools, allowing them to set other cutoffs between 1 April and 1 July. In fact McEwan and Shapiro (2006) show that in practice four cutoff dates are used in Chile: 1 April, 1 May, 1 June, and 1 July.
Hahn et al. (2001) show that the estimation of causal effects in this regression discontinuity framework is numerically equivalent to an instrumental variable (IV) approach within a small interval around the discontinuity.Footnote 9 In particular, following the equivalence with an IV approach, the instruments in the analysis correspond to four dummy variables taking a value of 1 for those children whose birthday is just after one of the cutoffs, and 0 otherwise.
Finally, in Eq. (1), we include \(g^{n}(x_{i}^{n})\), which is a flexible polynomial specification in the date of birth for a student whose birthday is around the n cutoff.Footnote 10 By including \(g^{n}(x_{i}^{n})\) in the previous equation the authors recognize that students born at different times of year might differ in a systematic manner. In fact, Buckles and Hungerman (2013), for the US, show that season of birth is correlated with some mothers’ characteristics. Specifically, they show that the mothers of children born in winter are more likely to have lower levels of education, to be teen mothers, and to be Afro-American. The fact that these mothers’ characteristics are correlated simultaneously with birthday and child’s educational outcomes does not invalidate the RD approach taken here. The fact that these observed and unobserved factors do not change discontinuously in the mentioned cutoffs is the basis for this identification.
3 Data and Variables
Since a major educational reform in the early 1980s,Footnote 11 Chile’s primary and secondary educational system has been characterized by its decentralization and by a significant participation of the private sector. By 2012, the population of students was approximately 3.5 million, distributed in three types of school: public or municipal (41% of total enrollment), non-fee-charging private (51% of total enrollment), and fee-charging private (7% of total enrollment).Footnote 12 Municipal schools, as the name indicates, are managed by municipalities, while the other two types of schools are controlled by the private sector. Though both municipal and non-fee-charging private schools receive state funding through a voucher scheme, only the latter are usually called voucher schools.Footnote 13
Primary education consists of 8 years of education while secondary education depends on the academic track chosen by a student. A “Scientific-Humanist” track lasts 4 years and prepares students for a college education. A “Technical-Professional” track in some cases lasts 5 years, with a vocational orientation aiming to help transition into the workforce after secondary education. Until 2003, compulsory education consisted of 8 years of primary education; however, a constitutional reform established free and compulsory secondary education for all Chilean inhabitants up to the age of 18. Despite mixed evidence on the impact of a series of reforms introduced in the early 1980s on the quality of education,Footnote 14 Chile’s primary and secondary education systems are comparable, in terms of coverage, to any system in any developed country.
The data used in this analysis come primarily from public administrative records on educational achievement provided by the Ministry of Education of Chile for the period 2002–2012. These records contain individual information for the whole population of students during the years that a student stays in the system. Moreover, an individual’s unique identification allows each student to be tracked over her/his whole school life. This dataset is essential to this study for four reasons. First, for every student in the system, there are several measures of school performance. Second, for the cohort of children born in 1996 or later, one can observe the age at which students were enrolled in first grade of elementary school. In fact, we define “age at entry” as the age at which a student is observed at the beginning of the school year when she/he was enrolled in first grade. The analysis is focused on the oldest cohort that was eligible to start school the first year for which there are data, that is, children born in 1996. These children, in complying with school’s minimum age at entry rule, should have started school either in 2002 (those eligible to start school the year they turned 6) or in 2003 (in the case of those children whose entry into school was delayed until the year they turned 7). Third, these administrative records provide an opportunity to follow every child over her/his complete school life, and to analyze the impact of age at entry beyond the first year of enrollment. Depending on the age at entry in primary school, these children are observed either 11 or 12 times (years) in the records. Given this last constraint, the analysis is focused on the impact of age at entry over the first 11 years of a student’s school life. Finally, because the whole population of students is observed, and the student’s school can be identified at every year, it is possible to determine not only some characteristics of the school, but also whether or not a student is enrolled in a school engaged in cream skimming.
By using students’ records two sets of outcomes are constructed. The first group of variables attempts to characterize the impact of age at entry on school performance. The first variable, attendance, corresponds to the percentage of days, out of the total, that a child has attended school during a given school year. Attendance, however, might well be capturing a school’s effort, since, for those institutions receiving funding through the voucher system, funding is a function of students’ attendance. To account for the fact that attendance is able to capture this and other school effects, we define a dummy variable “attendance below the median,” which takes a value of 1 for students with attendance below the median in the class, and 0 otherwise. The next variable is the annual average GPA over all subjects. As well as the variable attendance, GPA could reflect a school’s characteristics rather than a student’s own achievements.Footnote 15 As with attendance, a dummy variable is defined as indicating whether or not the GPA for a student in a particular year is above the class median. Finally, for this group of outcomes, the variable “Pass” is defined as a dummy variable taking a value of 1 when a student passes to the next grade, and 0 otherwise.
The second group of variables is composed of variables describing the movement of students between schools and variables related to the school’s characteristics. First, a dummy variable describes the movement between schools in a given year and takes a value of 1 when a child is observed in two (or more) different schools for two consecutive years. The rest of the outcomes in this second group characterize a school in three dimensions. The first dummy variable, “Public school,” takes a value of 1 if a child is enrolled in a public school, and 0 otherwise. A second variable, “Scientific-Humanist,” takes a value of 1 if a child who is attending secondary education is enrolled in a school following an academic track to prepare students for college, and 0 otherwise. Finally, since the classmates in the cohort may be observed over the 11 years followed in this study, the rest of the outcomes are useful for measuring the degree of cream skimming observed in the school, that is, the extent to which schools are able to select better students and remove students at the bottom of the distribution. First, a variable is created with the fraction of students among those coming from other schools who had grades above the median in the previous school. Since a standardized examination comparable across schools is not used here, this variable also helps to assess something about the quality of classmates. Specifically, this variable will increase when the rotation of students into the school is lowered (smaller denominator), or when more of the students who move come from the upper part of the distribution in their previous school (larger numerator). Both of these movements could be related to a higher quality of school. The next dummy variable takes a value of 1 if the GPA in first grade is higher than the median of the students that still remain from the first grade. For a child with a GPA above the median in first grade, this variable will take a value of 1. However, if the school is actively cream skimming, this variable will be less likely to take a value of 1 later on. Two dummy variables are also defined that indicate whether or not a particular student has, first, a GPA higher than that of the median of students who have ever moved and, second, a GPA higher than that of the students just moving into the school.Footnote 16 Finally, the last outcomes correspond to the average GPA of the rest of the classmates, not counting in this average the student’s own GPA.
The descriptive statistics are presented in Table 1. The sample is composed of approximately 250,000 students observed for approximately 10.2 years; 13% of the students attend schools in rural areas and 91% of the children starting primary school do so in a school in their own municipality. The average age at entry is 6.23 years (2282 days), with 40% of the students starting school the year they turn 6. In terms of the selected outcomes, the average attendance in a given year is over 91%. The average GPA is 5.6,Footnote 17 with approximately 93% of the students being promoted to the next class in every period. In a given year over the period under analysis, approximately 20% of students change school. In relation to the school type, approximately 47% of the students in a given year are enrolled in a public school. Although approximately 16% of the children are following an academic track, this fraction is driven down for the periods in primary school. When the sample is restricted to students in secondary school, this fraction increases to approximately 60%.Footnote 18
4 Results
4.1 Discontinuity in the Age at Entry
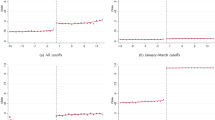
The RD design as a source of randomization of the treatment not only should ensure that other observed and unobserved factors are uncorrelated with the treatment, but also, and equally importantly, provides a significant variation of the treatment defined as the age at entry to the educational system.Footnote 19 Figure 1 presents the source of variation associated with the minimum age at entry using two definitions of the variable of interest: age at entry (in days) and a dummy variable indicating whether or not a child started school in the year she/he turned 6. Firstly, it is observed that those children born at the end of the calendar year are older when starting school and are also less likely to start school the year that they turn 6 (they are more likely to start school the year that they turn 7 or even later). However, conditional on being eligible to start school the year they turn 6 (being born before 1 April or being subject to the same eligibility rule as those born after 1 April but before 1 July), those students born later but to the left of a particular cutoff are the younger ones in their class. Secondly, a distinguishable jump in the age of starting school is observed for children born around 1 April, 1 May, 1 June, and 1 July. However for each of these thresholds a discontinuity in the treatment can be observed; the largest jump, for those children born around the threshold of 1 July, is noteworthy. This large jump around 1 July is explained by the perfect compliance associated with the rule of turning 6 before 1 July. In fact, the fraction of students starting school the year that they turn 6 (as opposed to the alternative of turning 7 or more) drops to practically zero for those children born after 1 July.
Table 2 presents the estimated discontinuities for the “age at entry” (in days) at start of primary school. The results confirm the graphical analysis. Being born after the cutoff date causes entry to be delayed for some students, that is, increases the average age at entry. This impact is significant for each of the cutoffs, but the largest discontinuity is observed for those individuals born after 1 July, who experience an average increase of approximately half a year in the age at entry. The average increase for the rest of the cutoffs is between 15 and 45 days approximately. The results are robust to the selection of the bandwidths, the degree of the polynomial, and the inclusion of other covariates in the specification. Finally, following the equivalence with an IV approach, the value of the F-statistic for the null of the relevance of the excluded instruments is large enough to disregard any concern about weak instruments in all the specifications and selected bandwidths.
4.2 Impact of Age at Entry on Selected Outcomes
The impact of age at entry on the two selected groups of outcomes is reported in Table 3. The overall picture from Table 3 regarding the impact of increasing age at entry on the different school achievement outcomes is not only that it is positive but also that the impact is still present 11 years after starting primary school. The only exception regarding this positive impact of increasing age at entry is observed for some of the outcomes (attendance) for the ninth year after school entry, which would correspond to the first year of secondary school for those children who had not repeated a grade.
Specifically, first, for the variable “attendance” it is observed that children with a higher age at entry increase their attendance by between 1 and 2 percentage points during the first 2 years after starting primary school and the second year of secondary school. This impact in terms of school days, given an average attendance of 91% in the population, means that increasing age at entry by 1 year is associated with approximately 2–5 more days of classes during a specific school year. The exception in the size of the impact of age at entry is found for the first year of secondary school, when attendance falls by an average of 3 percentage points. However, even in the ninth year after starting school, by looking at the impact on the probability of having an attendance rate higher than the median in the class, one can discern a positive effect associated with age at entry. This finding suggests that the negative effect on attendance rate captured during the first year of secondary school reflects some school effects rather than an individual reduction in attendance.
Second, a higher age at entry is associated with a higher annual GPA for all years for which this cohort of students is followed. However, this impact tends to diminish with time. Specifically, the impact on average GPA falls from approximately 0.5 points for a child during her/his first year in the school system to 0.15 points 11 years after entry into the system (which would be the third year of secondary school for those children who have not repeated a grade). These magnitudes are not only statistically significant but also economically important. The magnitude of the increase in GPA (0.5 or 0.15 points) is equivalent to the difference between a student on the median of the GPA distribution and one on the 75th (60th) percentile of this distribution. Can this observed impact on GPA be driven by differences in grade inflation between schools, or differences in the requirements established in schools? The results for the outcomes indicating the place on the distribution of GPA in relation to the students within the same school cohort do not support this hypothesis. A higher age at entry increases by almost 31 percentage points the likelihood that a child’s GPA is above the median in their first year of school, and increases it by approximately 7 percentage points 11 years after school entry.Footnote 20 Consistent with this positive impact on GPA, it is found that a higher age at entry is associated with an increase in the probability of passing a grade of between 2 and 5 percentage points.
In this way, and in contrast to other studies, these results show an impact of age at entry that is still observed 11 years after the start of primary school. Tincani (2014) shows that, in Chile, private schools (privately and voucher funded) not only specialize in higher-ability students, but are also able to attract higher-quality teachers from public schools and from other sectors, by offering them better salaries. In relation to the current problem, it has been shown that a higher age at entry provides some advantage in terms of school achievement. Thus, in light of Ticani’s findings, these better students will be more likely (at some point in their school life) to sort into better schools. Although the absolute impact of this sorting process on average GPA is ambiguous,Footnote 21 the relative advantage associated with delayed entry should decrease with average quality of classmates. The rest of the analysis seeks to measure the effect of age at entry on schools’ characteristics and movement between schools.
Mixed results are observed for the outcomes characterizing movement between schools. Although children whose entry to school is delayed are less likely to change schools in the fourth year after the start of primary school, a year later they are more likely to move to other schools. In fourth grade, children take a National Examination (SIMCE). This examination aims to measure the quality of the education provided by schools, and the results might later be used by parents to choose schools. Moreover, there is anecdotal evidence indicating that schools have some leeway in selecting which students take this examination. Along these lines, this finding that a higher age at entry is associated not only with better grades but also with being less likely to change school in the year when this national examination takes place suggests that schools might have some power to retain these better students, at least in the short run (the year that this examination takes place). Also, during the first year of secondary school it is observed that delayed entry is associated with an increase in the chance of changing schools. In fact, an additional year in child’s age at school entry is associated with an increase of approximately 6 percentage points in the likelihood of changing school between the ninth (first year of secondary school) and tenth years after starting primary school. The start of secondary school in Chile is characterized by approximately 50% of the students in the educational system switching schools. This amount of friction might induce some students to actively search for a new school. Where this search effort is positively correlated with early educational outcomes, it would explain why higher age at entry results in an increased search effort in the periods with higher friction in the system. In fact, this greater search effort is consistent with a reduction in the probability of switching schools between the tenth and eleventh years. Also consistent with this increase in the fraction of students switching school at the beginning of secondary school is the already reported drop in school attendance during the first year of secondary school.
Regarding school type, it is first observed that a higher age at entry is associated with a decrease in the probability that a child attends a public school for almost all years under analysis. Second, it is observed that delaying school entry increases the likelihood that a child will follow an academic track by approximately 13 percentage points. In terms of the sample, this means that this last impact corresponds to an approximately 25% increase in the fraction of students in the educational track that aims to prepare students for college.
For the outcomes characterizing the school measured by the classmates choosing the school (who have moved there), it is observed that increasing the age at entry is associated with a rise in the fraction of students arriving from the upper part of the GPA distribution in their previous school, but specifically in secondary school. Therefore, the results reveal not only that higher age at entry is associated with a lower probability of being enrolled in schools linked to lower-quality teachers, as observed in public schools (Tincani 2014), but also that these students have better-quality classmates in secondary school, where they are more likely to follow an academic track. In fact, it can be assumed that all of these factors contribute to the drop in the GPA in secondary school, due to a tougher academic track and the lower likelihood of grade inflation reported in better schools. It is worth noting that the timing of these impacts is consistent with the drop in the GPA observed when starting secondary school. The last four outcomes explore the impact of age at entry on the probability of being enrolled in a school that is actively cream skimming. It has been shown that children with a higher age at entry have a greater likelihood of having a GPA higher than the mean of their classmates. Where some of these schools were actively engaged in cream skimming, however, the probability of having a GPA higher than the median of the students moving into the school should not only be lower but also fall over time. This is what is observed from the impact of age at entry on the outcomes that measure the probability of having a GPA higher than the median of students moving into the school in a given year, or of those who have moved to the school at some point in the past. That is, it is observed that age at entry increases the probability of having a GPA higher than the median of students moving into the school, but this increase in the probability is lower than the increase in the probability of having a GPA higher than the median of all students in the class (fourth column in Table 3) for almost all the years. Secondly, over the school life this probability decreases and by the time secondary school is reached it is not statistically significant. Also consistent with the hypothesis that age at entry increases the likelihood of being enrolled in a school actively cream skimming, analysis of the GPA in first grade over the years, but with the mean of the classmates arriving from first year of primary school, shows that this probability decreases over time. Finally, it is observed for some years, and with the exception of the first year of secondary school, that age at entry increases the probability of being enrolled in a school where classmates have, on average, a higher GPA.
5 Conclusions
The findings of this study confirm not only that delaying school entry has a positive effect on GPA, attendance and the likelihood of passing a grade but also that this impact tends to wear off across time. Nevertheless, in contrast to previous studies, the findings reveal that this impact can still be observed 11 years after a child has started school. Moreover, evidence of the effect of age at entry on school type provides a potential explanation for the fading of the impact on academic achievement throughout the school life. Specifically, a higher age at entry decreases the likelihood that a child will be enrolled in municipal (public) schools, which are characterized by a less active selection of students and lower-quality teachers. Consistent with these differences in academic selection (competition), children with a higher age at entry have a higher probability of being enrolled in schools where the children arriving from other schools were in the upper GPA distribution in their previous school. Evidence is also found that age at entry has a positive effect on the likelihood that a child follows an academic track in high school. Finally, evidence is found that age at entry is associated with an increase in the probability that a child will be enrolled in a school actively engaged in cream skimming, which also explains the drop in the impact of age at entry on school achievements.
Notes
- 1.
Age at entry is expected to affect educational achievement over divergent channels, with various effects on individual outcomes. First, holding back a student is associated with a higher propensity to learn (school readiness). Second, delaying school entry means that students will be evaluated at an older age than other students who started earlier (age at test). In comparing children in the same grade, these two channels cannot be set apart from each other due to the perfect multicollinearity of these variables (Black et al. 2011). Third, by altering age at entry, parents affect the relative age of the students with ambiguous effect on educational outcomes. Fourth, the combination of minimum age entry rules and rules on mandatory education has been shown to affect dropout decisions (Angrist and Kruger 1991). Finally, a late start in school implies delaying entry into the labor market, that is, a reduction in the accumulation of labor experience (Black et al. 2011).
- 2.
As mentioned by the authors, one-fourth of this change is explained by legal changes, while the rest is attributed to families, teachers, and schools.
- 3.
A related part of the literature has focused on the impact of age per se, rather than age at entry. Among these studies is that of Kelly and Dhuey (2006), who found, among a sample of countries that are members of the Organisation for Economic Co-operation and Development (OECD), that younger children obtain considerably lower scores than older ones at fourth and eighth grades.
- 4.
McEwan and Shapiro (2006) focus part of their analysis on publicly funded schools in urban areas.
- 5.
The term cream skimming has been used in the voucher literature to describe the fact that a voucher is more likely to be used by the parents of “high-ability” students or, more generally, students who are less costly to teach. These parents/students move from public, lower-performing, schools to better, private, ones, leaving the students who are more costly to teach to the public schools. In this chapter the concept of cream skimming is used to describe the active or passive process by which some schools end up capturing high-achievement students while other schools, as a result of this process, are left with students from lower levels of capacity/achievement.
- 6.
As mentioned above, (footnote 1), the channels by which age at entry can affect individual outcomes are diverse. Depending on which channel is more important, it will be more likely to observe a particular long-lasting effect associated with holding back a student. For example, it is argued that an age at test channel should wear off over time (Black et al. 2011). So, whether or not a positive long-lasting effect may be observed is an empirical question. Moreover, this study explores an additional channel that is often ignored, but which is of relevance in a system using a voucher scheme. This is the progressive sorting of students into schools, which we refer to in this chapter as cream skimming.
- 7.
Parents decide to delay a child’s school entry based on individual benefits and costs. On the side of benefits, the literature has stressed the concept of “readiness” for learning (Stipek 2002). On the cost side, families must face the cost of the labor income forgone by the household member responsible for childcare, or the market cost of childcare for the unenrolled children. These and other factors defining the decision to delay school entry are not always observed by the researcher, and are potentially correlated with school outcomes. For example, a mother’s labor force participation has been shown to affect her child’s health, which might affect school performance (Sandler 2011).
- 8.
In a fuzzy RD treatment, status is not perfectly determined by the running variable. On the other hand, where the treatment is a deterministic function of date of birth, the probability of treatment would change from 1 to 0 at the cutoff day. For more details, see Lee and Lemieux (2010).
- 9.
By focusing on the observations around these four discontinuities, the study first concentrates on those observations where the age at entry is as if it were randomly assigned. This randomization of the treatment ensures that all other factors (observed and unobserved) determining a given outcome must be balanced on either side of these discontinuities. Second, and for a given parametrization of g(.), the estimated function can be seen as the non-parametric approximation of the true relationship between a given outcome and the variable date of birth, that is, it is less likely that the estimated impacts are driven by an incorrect specification of g n(.). In particular, use is made of a bandwidth of 15 days around each of the discontinuities in the baseline specification. Two of the most popular methods are used to define this bandwidth. First, using the rule-of-thumb approach (Lee and Lemieux 2010), the bandwidth ranges from 5 to 10 days. Alternatively, using a method based on the calculation of the cross-validation function (Lee and Lemieux 2010) leads to a bandwidth of 20 days around the discontinuities. Moreover, the authors show in the working paper version that their results are robust to different bandwidths but also to the degree of g(.).
- 10.
Specifically, \(x_{i}^{n}=BD_{i}-C,^{n}\), where BD i is the birth date in the calendar year of a student and C n is one the four cutoffs.
- 11.
The management of primary and secondary education was transferred to municipalities, payment scales and civil service status for teachers were abolished, and a voucher scheme was established as the funding mechanism for municipal and non-charging private schools. Municipal and non-fee-charging private schools received the same rates, tied strictly to attendance, and parents’ choices were not restricted by residence. Although with the return to democracy some of the earlier reforms have been abolished or offset by new reforms and policies, the Chilean primary and secondary educational system is still considered one of the few examples in a developing country of a national voucher system. In 2009 it covered approximately 93% of primary and secondary enrollment. For more details, see Gauri and Vawda (2003).
- 12.
There is a fourth type of school, “corporations,” which are vocational schools administered by firms or enterprises with a fixed budget from the state. In 2012, they accounted for less than 2% of the total enrollment. Throughout this analysis, they are treated as municipal schools.
- 13.
Public schools and subsidized private schools may charge tuition fees, with parents’ agreement. However, these complementary tuition fees cannot exceed a limit established by law.
- 14.
The bulk of research has focused on the impact of the voucher funding reform on educational achievements. For example, Hsieh and Urquiola (2006) find no evidence that school choice improved average educational outcomes as measured by test scores, repetition rates and years of schooling. Moreover, they find evidence that the voucher reform was associated with an increase in sorting. Other papers have studied the impact of the extension of school days on children’s outcomes (Berthelon and Kruger 2012), teacher incentives (Contreras and Rau 2012), and the role of information about the school’s value added in school choice (Mizala and Urquiola 2013). For a review of these and other reforms since the early 1980s, see Contreras et al. (2005).
- 15.
Anecdotal evidence exists on grade inflation, which has not been equally observed among all schools.
- 16.
These two variables make an attempt to capture whether or not a student is doing better than other students who remain in a given school, or in relation to those just moving into this school. By looking at the evolution of this parameter over time, together with other outcomes, one is able to establish a better picture of the relative return of age at entry and the type of schools these students are moving to over time. Although the absolute impact of this sorting process on average GPA is ambiguous, the relative advantage associated with age at entry should decrease with average quality of classmates. Where some of these schools were actively engaged in cream skimming, the probability of having a GPA higher than the median of the students moving into the school should not only be lower but should also fall over time, specifically in relation to the new students in these schools.
- 17.
The grade scale in Chile goes from 0 to 7, with 7 being the highest grade. To pass a subject or test, students must obtain a grade of 4 or higher.
- 18.
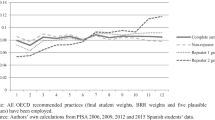
The graphic analysis presenting the relationship between each of the outcomes and the student’s date of birth is reported in the working paper. For each outcome, a flexible second-degree polynomial is fitted at every side of the four discontinuities. Two observations are noticeable from the figures: first, the existence of a series of discontinuities around the cutoff, and, second, a heterogeneous jump around them.
- 19.
Analysis using an RD design is built on the fact that the variation of the treatment (age at entry) is as good as a randomized assignment for those observations near a particular discontinuity. Formal testing was carried out for discontinuities in baseline characteristics (highest parent’s education and gender) for alternative polynomial specifications and different bandwidths. Finally, following McCrary (2008), testing was also carried out for a discontinuity in the distribution of the running variable, by estimating the density of the variable date of birth and formally testing for a discontinuity for each of these cutoffs. First, no evidence was found of a discontinuity in the baseline characteristics. Second, for any of the four thresholds the null hypothesis which supports the graphical analysis can be rejected, and there is no evidence of a precise manipulation of the date of birth. For reasons of space, these checks were left in the working paper version.
- 20.
Although the same qualitative results are observed for the other variables indicating whether or not a student is above the 75th, 50th, or 25th percentiles, the strongest impacts are observed in the upper part of the distribution of the GPA. In fact, only in the first years of school life it is observed that a higher age at entry increases the probability of being above the 10th percentile in the GPA distribution of the class.
- 21.
Anecdotal evidence suggests higher grade inflation among worse schools (http://www.uchile.cl/portal/presentacion/historia/luis-riveros-cornejo/columnas/5416/inflacion-de-notas), that is, the effect of age at entry should be negatively correlated with grade inflation, and the impact of age at entry will be more likely to be observed among better schools. If, on the other hand, better schools set higher standards, it will be harder to observe a stronger effect of age at entry as children move to better schools.
References
Angrist JD, Kruger AB (1991) Does compulsory schooling attendance affect schooling and earnings? Q J Econ 106:979–1014
Berthelon M, Kruger D (2012) Risky behavior among youth: Incapacitation effects of school on adolescent motherhood and crime in Chile. J Public Econ 95(1–2):41–53
Black S, Devereaux P, Salvanes P (2011) Too young to leave the nest? The effect of school starting age. Rev Econ Stat 93(2):455–467
Buckles K, Hungerman D (2013) Season of birth and later outcomes: old questions, new answers. Rev Econ Stat 95(3):711–724
Cascio EU, Lewis EG (2006) Schooling and the armed forces qualifying test. Evidence from school-entry laws. J Hum Resour 41(2):294–318
Contreras D, Rau T (2012) Tournament incentives for teachers: evidence from a scaled-up intervention in Chile. Econ Dev Cult Chang 61(1):219–246
Contreras D, Larranaga O, Flores L, Lobato F, Macias V (2005) Politicas educacionales en Chile: vouchers, concentracion, incentivos y rendimiento. In: Cueto S (ed) Usos e impacto de la informacion educativa en America Latina. Preal, Santiago, pp 61–110
Deming D, Dynarski, S (2008) The lengthening of childhood. J Econ Perspect 22(3):71–92
Gauri V, Vawda A (2003) Vouchers for basic education in developing countries. A principal-agent perspective. World bank policy research working paper 3005. World Bank, Washington
Hahn J, Todd P, van der Klaauw W (2001) Identification and estimation of treatment effects with a regression-discontinuity design. Econometrica 69(1):201–209
Hsieh C, Urquiola M (2006) The effects of generalized school choice on achievement and stratification: evidence from Chile’s voucher program. J Public Econ 90(8–9):1477–1503
Kelly B, Dhuey E (2006) The persistence of early maturity: International evidence of long-run age effects. Q J Econ 121(4):1437–1472
Lee DS, Lemieux T (2010) Regression discontinuity designs in economics. J Econ Lit 48:281–355
McCrary J (2008) Manipulation of the running variable in the regression discontinuity design: a density test. J Econ 142(2):698–714
McEwan P, Shapiro J (2006) The benefit of delayed primary school enrollment. Discontinuity estimates using exact birth dates. J Hum Resour 43(1):1–29
Mizala A, Urquiola M (2013) School markets: the impact of information approximating schools? effectiveness. J Dev Econ 1003:313–335
Sandler M (2011) The effects of maternal employment on the health of school-age children. J Health Econ 30(2):240–257
Stipek D (2002) At what age should children enter kindergarten? A question for policy makers and parents. Soc Policy Rep 16(2):3–16
Tincani MM (2014) School vouchers and the joint sorting of students and teachers. HCEO Working Paper No. 2014-02. Human capital and economic opportunity global working group, University of Chicago
Acknowledgements
We want to thank seminar participants at the Departments of Economics at Carlos III and Universidad Alberto Hurtado for comments and suggestions. Julio Cáceres-Delpiano gratefully acknowledges financial support from the Spanish Ministry of Education (Grant ECO2009-11165), Spanish Ministry of Economy and Competitiveness (MDM 2014-0431), and Comunidad de Madrid MadEco-CM (S2015/HUM-3444).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this chapter
Cite this chapter
Cáceres-Delpiano, J., Giolito, E.P. (2019). The Impact of Age of Entry on Academic Progression. In: Crato, N., Paruolo, P. (eds) Data-Driven Policy Impact Evaluation. Springer, Cham. https://doi.org/10.1007/978-3-319-78461-8_16
Download citation
DOI: https://doi.org/10.1007/978-3-319-78461-8_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-78460-1
Online ISBN: 978-3-319-78461-8
eBook Packages: Political Science and International StudiesPolitical Science and International Studies (R0)