1 Introduction

Laser cutting technology has gained significant attention in recent years due to its capability to trim and refine thin workpiece parts by removing excess materials or rough edges in high-speed machining. In the automotive industry, challenges arise when attempting to maintain a perpendicular laser beam on three-dimensional stamped parts without compromising precision. Moreover, the employment of expansive 3D laser cutting machines, initially intended for the precision severing of sizable automobile components, poses challenges in enhancing efficiency when confronted with tiny sizes through holes distributed at different locations on the component, subject to the forces of perpendicular and substantial loads. This paper addresses these challenges and explores a potential strategy to enhance productivity in cutting such tiny sizes through holes on automotive parts.

Numerous research studies [1,2,3] have been dedicated to enhance cutting speed through the optimization of laser parameters. However, these endeavors to maximize cutting speed through laser parameter adjustments have not completely addressed the main challenges associated with 3D cutting.

Meanwhile, some researchers [4,5,6] have explored the relationship between speed enhancement and orientation error by adopting an oblique cutting strategy. Yet, these analyses have primarily focused on the aspects of laser cutting technology, overlooking the potential benefits that may arise from the manufacturing tolerance achieved through an inclined laser beam posture [7].

Furthermore, the utilization of process tolerance to enhance performance without compromising manufacturing quality is a common practice in various other manufacturing applications, including welding [8], spray painting [9], and drilling [10]. Weingartshofer [11] developed a general optimization-based path planner for industrial robots, incorporating certain deviations in posture to avoid collisions and singular joint configurations. Similarly, posture optimization has shown benefits in manufacturing dynamics, particularly in robotic milling processes, as demonstrated by Lei [12] with an energy deformation model. For laser relevant applications, Tang [13] controls the laser head vector to enhance the contour precision for laser additive manufacturing. Xu [14] optimized the laser head orientation by minimizing the rotatory axes’ energy consumption. However, the incorporation of cutting angle tolerance for 3D laser cutting has received limited attention so far.

Considering the thin thickness of automotive parts, it is worth noting that a slight slope in cutting through holes may indeed be deemed acceptable without compromising the overall quality of the part. Therefore, by exploiting this manufacturing tolerance, there is potential to further enhance the efficiency of 3D laser cutting processes, especially in cases where precision can be maintained while achieving higher cutting speeds.

This paper presents a novel cutting strategy that utilizes a conic-shaped laser beam posture for hole paths, addressing challenges associated with speed and servo control precision in large-scale axes. By adhering strictly to the specified Cartesian manufacturing path while allowing for deviations in laser beam posture, the proposed strategy achieves a balance between cutting accuracy and process flexibility. A multi-objective optimization problem is formulated to determine the optimal vertex location of the cone, evaluating the quality and smoothness of the cutting process. The optimization process minimizes both laser beam taper error and kinetic energy consumption along the path. Furthermore, a time minimization approach is proposed to achieve enhanced efficiency in cutting a significant quantity of through holes using the conic posture cutting strategy, resulting in a substantial enhancement of productivity.

The remainder of this work is organized as follows: Sect. 2 discusses laser cutting, particularly regarding the inclined laser beam resulting in taper error, and introduces the prototype machine developed by EFORT Intelligent Equipment Co., Ltd [15], characterized by redundancy property. In Sect. 3, the objective holes-cutting conic posture trajectory is modeled in both Cartesian and joint coordinates together with the computation of the conic posture through the inverse kinematics of the redundant machine. Sect. 4 describes the formulation of the optimization problem and the use of a multi-objective genetic algorithm as the core process in the hole-cutting time minimization approach. A time minimization of global holes cutting on a singular part is proposed in Sect. 5. Sect. 6 presents the results of the experiment performed on a real B-pillar part with the 3D laser cutting machine prototype. Lastly, Sect. 7 concludes the paper with a comprehensive summary of the key findings and contributions from the previous sections, along with potential avenues for future research in 3D laser cutting processes.

Fig. 1
figure 1

Schematic representation of laser cutting principle and characteristics

Full size image
Fig. 2
figure 2

Inclined laser beam and taper error. a geometric transformation of the laser beam in the coordinate system; b localized graphic view of the tilt angle error in the yz plane; c localized graphic view of the lead angle error in the xz plane

Full size image

2 Preliminaries

2.1 3D laser cutting

Laser cutting is a highly precise manufacturing technique that employs a focused laser beam to cut through various materials. This process has found extensive applications in the manufacturing industry due to its ability to produce intricate and complex shapes with exceptional accuracy. As illustrated in Fig. 1, the laser beam is directed onto the material’s surface, leading to either melting or vaporization of the material, which is subsequently blown away by a jet of gas. The choice of laser cutting parameters significantly influences the final cutting quality, and numerous research works [1, 16, 17] have presented predictable models to simulate and optimize the cutting process for various materials [2, 18]. These models play a crucial role in enhancing manufacturing efficiency and achieving desired cutting outcomes.

To achieve optimal cutting performance in laser cutting, it is crucial to optimize laser parameters such as power, standoff distance, cutting speed, and auxiliary gas pressure [19]. The maximum achievable cutting speed for a given material thickness is a critical factor, as it depends on the rate of material fusion required for successful cutting. The laser beam must deliver sufficient energy to cut through the material without causing excessive melting or vaporization. Therefore, careful balance of laser parameters is necessary to achieve the highest feasible cutting speed for a specific material thickness while ensuring the desired cutting quality is met [20].

Fig. 3
figure 3

CAD scheme of the redundant 3D laser cutting machine prototype. a overall view of the entire machine; b detailed close-up of the machine’s head part

Full size image

In contrast to 2D laser cutting machines, which move the laser beam along flat surfaces, 3D laser cutting offers greater flexibility by allowing the laser beam’s movement to extend, providing more degrees of freedom in cutting angles. This flexibility is particularly useful for adjusting the laser beam’s attitude while cutting complex shapes on workpieces with irregular contours. However, achieving the ideal condition of perfect perpendicularity between the laser beam direction and the workpiece surface along all trajectories can be challenging due to various factors:

  • Workpiece shape: When the workpiece’s thickness and shape are irregular, maintaining perpendicularity becomes difficult.

  • Machine feasible workspace: In some cases, the desired configuration for the laser beam may be unreachable within the machine’s feasible workspace.

  • Interference and singularity avoidance: There are instances where certain laser beam configurations may interfere with the workpiece or lead to singularity issues.

The angle between the intended laser beam and the actual inclined laser beam is known as taper error. This taper error can be decomposed into lead angle in the feed direction of motion and tilt angle perpendicular to the feed direction. Figure 2 shows how to define the inclined laser beam and shows the decomposition of the error angle. The lead angle is the one between the laser beam and the normal to the workpiece surface, which is the z-axis of the coordinate system, while the x-axis is along the feed direction. The tilt angle lays in the xy plane. The lead angle and tilt angle can related to \(\alpha _{x}\) and \(\alpha _{y}\) through geometric transformation. In our study, we primarily focus on materials with thin thickness. Consequently, we consider the laser incline angle as being equivalent to the workpiece’s taper error. This approach simplifies our analysis by not accounting for the curved taper of the kerf, similar to what has been assumed in past efforts [21].

The management of taper error in manufacturing production necessitates a careful equilibrium between minimizing the taper error to enhance cutting precision and permitting an acceptable degree of taper error within defined tolerances to expedite cutting trajectories and boost productivity. Within computer-aided manufacturing (CAM) simulations, programmers strive to optimize cutting paths by taking into account the taper error, aiming to achieve the desired level of cutting quality and efficiency. Nevertheless, the incorporation of an autonomous solution for taper error management proves to be a challenging task, owing to the multitude of non-linear constraints and the intricate interplay between laser parameters.

The permissible limit of taper error is often contingent upon the thickness of the workpiece being cut and the particular demands of the application. Thinner workpieces may withstand slightly greater taper errors without substantially compromising the overall excellence of the end product, while thicker workpieces may require more stringent regulation of the taper error in order to uphold precise cutting. The determination of an acceptable tolerance level entails the contemplation of factors such as material characteristics, cutting specifications, and the intended purpose of the final workpiece.

Given the complexity of managing the taper error and the variety of factors involved, the human expertise of programmers and operators remains crucial in finding the optimal balance between precision and productivity in laser cutting processes. As technology and research advance, there may be potential for developing more sophisticated autonomous solutions to manage the taper error, but for now, human intervention and optimization play a central role in achieving the desired cutting outcomes in manufacturing production.

2.2 The prototype machine for 3D laser machine

The motion required for cutting applications typically involves only five degrees of freedom, thus limiting flexibility and dexterity in the 3D motion. In contrast, the prototype machine presented in this paper is configured with redundancy, featuring an additional prismatic joint integrated into the cutting head. Figure 3a illustrates the 3D laser cutting machine used in our study. The machine consists of a Cartesian robot that actuates the first three prismatic joints (\(q_1, q_2, q_3\)), on which the laser cutting head is mounted. The head is actuated through two revolute joints (\(q_4,q_5\)) and one prismatic joint \(q_6\). The cutting head features a restructured design that eliminates the offset between the two rotational axes, commonly found in traditional five-axis machines. It is important to note that our mechanical structure for the head incorporates an arc motor mechanism to drive the second rotational axis, as detailed in Fig. 3b. This innovative design ensures the alignment of all three axes at a single point on the head, known in technical terms as the wrist center point, closely mirroring a concept commonly seen in industrial robots.

Table 1 DH parameter table of the laser cutting machine
Full size table

2.2.1 Direct kinematics

The joint variables of the cutting machine, represented as generalized coordinates, are denoted as \(\textbf{q}=[q_1,\ldots ,q_6]^T \in \mathbb {R}^6\). In this study, we analyze the direct kinematics of the end-effector frame e, which is positioned at the nozzle tip, with respect to the machine base frame b. We express the direct kinematics in the form of a homogeneous transformation matrix denoted as \(\textbf{A}_{e}^{b} =\left[ \begin{array}{cc} \textbf{R}_{e}^{b} &{} \textbf{p}_{e}^{b} \\ \textbf{0} &{} 1\end{array}\right] \in SE(3)\), where \(\textbf{R}_{e}^{b}\) represents the rotation matrix, \(\textbf{p}_{e}^{b}\) represents the translation vector, and SE(3) denotes the special Euclidean group. The homogeneous transformation matrix is computed based on the Denavit-Hartenberg convention, utilizing the parameters listed in Table 1. The graphical representation depicted in Fig. 4 presents a visual portrayal of the machine kinematic chain. In this figure, the origins of joint frames are separated by the distance \(q_i\) along the specific direction traversed by the prismatic joints; as the joints move towards their respective home positions, the origins of the individual frames associated with each joint will converge to a common point.

Fig. 4
figure 4

Geometrical kinematic chain equivalent of the cutting machine

Full size image

According to the parameters reported in Table 1, the homogeneous transformation matrix \(\textbf{A}_6^0\) is computed as:

$$\begin{aligned} \begin{aligned} \textbf{A}_6^0&= \textbf{A}_1^0 \textbf{A}_2^1 \textbf{A}_3^2 \textbf{A}_4^3 \textbf{A}_5^4 \textbf{A}_6^5 \\&= \left[ \begin{array}{cccc} c4c5 &{} -s4 &{} c4s5 &{} q_1 +q_6 c4s5\\ c5s4 &{} c4 &{} s4s5 &{} q_2 +q_6 s4s5\\ -s5 &{} 0 &{} c5 &{} q_3 +q_6 c5\\ 0 &{} 0 &{} 0 &{} 1 \end{array}\right] , \end{aligned} \end{aligned}$$
(1)

where the abbreviations s4 and c4 denote the trigonometric functions \(\sin (q_4)\) and \(\cos (q_4)\) respectively, same for s5 and c5, for the purpose of conciseness. These abbreviations are used to represent these functions in all subsequent instances of this paper.

Since the end-effector frame e corresponds to the last joint frame, only the transformation from the base frame must be included to complete the overall transformation from the base to the end-effector of the robot. In the considered case, the base frame denoted as b is positioned on a stable point located on the basement of the cutting machine, ensuring its stationary nature. The initial base transformation matrix indicates a fixed displacement from the original point of frame 0, as

$$\begin{aligned} \textbf{A}_0^b = \left[ \begin{array}{cccc} 0 &{} 0 &{} 1 &{} p_{x0}\\ 1 &{} 0 &{} 0 &{} p_{y0}\\ 0 &{} 1 &{} 0 &{} p_{z0}\\ 0 &{} 0 &{} 0 &{} 1 \end{array}\right] . \end{aligned}$$
(2)

The complete homogeneous transformation matrix computed from base frame b to the end-effector frame e is then given by the following:

$$\begin{aligned} \textbf{A}_e^b = \left[ \begin{array}{cccc} c_4c_5 &{} -s_4 &{} c_4s_5 &{} p_{x0}+q_1 +q_6c_4s_5\\ c_5s_4 &{} c_4 &{} s_4s_5 &{} p_{y0} + q_2 +q_6s_4s_5\\ -s_5 &{} 0 &{} c_5 &{} p_{z0} + q_3 +q_6c_5\\ 0 &{} 0 &{} 0 &{} 1 \end{array}\right] . \end{aligned}$$
(3)

2.2.2 Inverse kinematic analysis

In the realm of conventional machine mechanism modeling, the importance of inverse kinematic solutions cannot be overstated. Numerous efforts have been undertaken to analyze and solve the generalized five-axis machine kinematic model with various typical configurations [22,23,24]. Nevertheless, the presence of redundant machine configurations poses a more complex challenge with an additional degree of freedom. Caputi [25] utilized the differential inverse kinematics technique on a TRRTTT redundant milling machine by addressing an optimization-based problem that aims to minimize torque at rotary axes and position errors. This approach encounters difficulties due to the high-dimensional \(6 \times 6\) Jacobian matrix associated with a six-axis machine.

However, Chu [26] suggested that the rotational performance of five-axis machine tools can be effectively evaluated by analyzing the determinant of the Jacobian matrix within a simplified \(2 \times 2\) sub-model of the two rotary axes only, rather than considering the entire kinematic chain. In other words, the machine is similar to two cooperating robots, one robot carrying the tool and another rotating the tool, and the kinematic performance of the machine is determined by the latter. Moreover, another example of the adoption of redundant architecture is the study of manufacturing by using industrial robots, which are characterized by six degrees of freedom. The concept of kinematic decoupling, as employed by Bottin [27] on an industrial robot, has exhibited efficient handling of redundant tasks, particularly around the wrist center point with the division of the robot into an anthropomorphic manipulator and a spherical wrist.

In this study, the present research addresses the redundant inverse kinematic problem by employing a decoupling technique. The kinematic chain is divided into two distinct components, namely the Cartesian robot chain and the Polar robot chain. The head axes mechanism, designed with zero-offset, greatly contributes to the significance of the wrist center point, as it accurately represents the motion of the Cartesian robot and determines the positioning of the Polar robot. The direct decoupling information can be noticed from the displacement column of \(\textbf{A}_{e}^{b}\) in Eq. (3), Let w represent the intermediate frame located at the wrist center point with its orientation aligned to the frame b. Notably, the displacement \(\textbf{p}_{w}^0\) of the frame w is directly affected by the first three joint variables, collected in \(\textbf{q}_h= \left[ q_{1}, q_{2}, q_{3}\right] ^T\). Moreover, a particular attention is placed on solving the inverse displacement \(\textbf{p}_{e}^{w}\) from the frame w to the frame e to determine the values of the remaining three wrist joints \(\textbf{q}_w = \left[ q_{4}, q_{5}, q_{6}\right] ^T\). Therefore, the solution for \(\textbf{q}_h\) is unique and straightforward to compute; it can be written as follows:

$$\begin{aligned} \textbf{q}_h = \textbf{p}_{e}^{0} - \textbf{p}_{e}^w. \end{aligned}$$
(4)

To provide a clearer discussion of the solution in the wrist domain, we will use the following symbolic substitutions:

  • Let \(\textbf{p}_{w}\) represent the Cartesian coordinates of the moving wrist center point substituting the displacement \(\textbf{p}_{w}^0\).

  • Let \(\textbf{s}_w\) represent the displacement \(\textbf{p}_{w}^{e}\), which specifically depends on the wrist joints \(\textbf{q}_w\).

The displacement \(\textbf{s}_w\) depends only on the geometry of the mechanism. The solution can be expressed as follows:

$$\begin{aligned} \textbf{s}_w = \left[ \begin{array} {l} q_{6}c4s5\\ q_{6}s4s5\\ q_{6}c5 \end{array}\right] . \end{aligned}$$
(5)

The technique of differential inverse kinematics can be adopted to resolve the joint conversion from the displacement; therefore, the instantaneous linear velocity \(\dot{\textbf{s}}_{w}\) is computed as follows:

$$\begin{aligned} {\dot{\textbf{s}}_{w}} = \textbf{J}_{w}{\dot{\textbf{q}}_{w}}, \end{aligned}$$
(6)

where \(\dot{\textbf{q}}_w\) is the wrist joint velocity vector and \(\textbf{J}_w\) is the \(3 \times 3\) analytical wrist Jacobian matrix of \(\textbf{q}_w\), given by

$$\begin{aligned} \textbf{J}_w = \left[ \begin{array}{ccc} -q_6 c_5 s_4 &{} -q_6 c_4 s_5 &{} c_4 c_5\\ q_6 c_4 c_5 &{} -q_6 s_4 s_5 &{} c_5 s_4\\ 0 &{} q_6 c_5 &{} s_5 \end{array}\right] . \end{aligned}$$
(7)

2.2.3 Singularity analysis

The solution of the inverse kinematics through the differential approach requires a careful handling of the singular configurations. It is worth mentioning that the wrist singularity becomes degenerated [28] in correspondence of the configuration for which the determinant of \(\textbf{J}_w\) is equal to zero, that is, when the second rotational axis is 0\(^{\circ }\) or 180\(^{\circ }\). The damped least squares (DLS) method, introduced by Wampler [29], overcomes the ill-conditioned issues often encountered with the pseudo-inverse method by stabilizing the solution. To further enhance performance in regions close to singularities, the pseudo-inverse DLS method was proposed as an extension in [30]. As a result, the singular robust (SR) wrist Jacobian matrix, denoted as \(\textbf{J}_w^*\), can be expressed as

$$\begin{aligned} \textbf{J}_w^*=\left( \textbf{J}_w^T\mathbf {~J}_w+\lambda \textbf{I}\right) ^{-1} \mathbf {~J}_w^T, \end{aligned}$$
(8)

where the scale damping value \(\lambda \) is introduced when the matrix becomes degenerated, and \(\textbf{I} \in \mathbb {R}^{3 \times 3}\) is the identity matrix. With the aim of computational convenience, Eq. (8) can be rewritten into the following form:

$$\begin{aligned} \textbf{J}_w^*=\mathbf {~J}_w^T\left( \textbf{J}_w^T\mathbf {~J}_w+\lambda \textbf{I}\right) ^{-1}. \end{aligned}$$
(9)

Parameter \(\lambda \) can be computed as a function of the manipulability \(\omega _w\triangleq \sqrt{{\text {det}}\left( \textbf{J}_w \textbf{J}_w^T\right) }\), providing a measure of the distance from the singular value of the Jacobian matrix, as follows:

$$\begin{aligned} \lambda =\left\{ \begin{array}{cl} \lambda _0\left( 1-\omega _w / \omega _{w0}\right) ^2 &{} \text{ for } \omega _w<\omega _{w0} \\ 0 &{} \text{ for } \omega _w \ge \omega _{w0} \end{array}\right. , \end{aligned}$$
(10)

where \(\lambda _0\) is a constant scale factor and \(\omega _{w0}\) defines the size of the boundary of the neighborhood of singularity. The wrist joint velocity vector \({\dot{\textbf{q}}}_w\) can be then represented as a function of the SR wrist Jacobian matrix and the Cartesian linear velocity of the displacement as follows:

$$\begin{aligned} {\dot{\textbf{q}}_{w}} = \mathbf {~J}_w^*{\dot{\textbf{s}}_{w}}. \end{aligned}$$
(11)

To sum up, the machine’s inverse kinematics, denoted as \(\mathbf {\Psi }\left( \cdot \right) \), can be resolved in two steps. The first stage involves addressing the redundancy problem by utilizing an intermediate variable \(\textbf{p}_w\) for the position of the wrist center, which will be determined by the solution of the optimization problem in Sect. 4, thus leading to the attainment of the target pose \(\textbf{A}_{e}^{b}\). In the second stage, the joint configuration \(\textbf{q}\) is determined by Eqs. (4), (6), (9), taking the singularity issue into account, as

$$\begin{aligned} \textbf{q} = \Psi \left( \textbf{A}_{e}^{b}, \textbf{p}_w\right) . \end{aligned}$$
(12)

3 Through hole path and conic posture

In this section, we present a mathematical model for the through hole path in 3D laser cutting, taking into account the geometric constraints during motion. Before delving into the details of the model, we first introduce the distinct cutting events for individual holes, each segmented by the movement between holes. The hole path consists of the inner contour of the hole and an approach path leading to the contour’s edge.

3.1 Interpolation of the hole path

The through hole assumes a critical role in the manufacturing process, serving as the blueprint for accurately positioning and shaping the holes on the automotive parts. Achieving precise and consistent cutting execution along the through hole path is of paramount importance to ensure optimal fit, desired functionality, and structural integrity of the final automotive product. The cutting paths of through holes in the context of automotive parts refer to the specific trajectory along which holes are systematically cut through the components. The path exhibits a range of shapes and complexities, encompassing circle, oblong, or rounded rectangle contours, among others, dictated by the design specifications. Moreover, by starting with an inner piercing point and establishing a connecting path to the contour’s edge, the quality of hole path cutting can be shielded from the potential impacts of laser shots during the piercing process. This approach should be recognized as an integral component of the cutting path.

In customary practice, individual through holes are represented as macro instructions encompassing a series of distinct geometric segments. The objective of achieving precise hole placement is pursued through the establishment of a localized reference coordinate system at the geometric center of each hole. This methodological approach finds a visual representation of a simple circular hole path, as illustrated in Fig. 5.

Fig. 5
figure 5

Circular hole-cutting path and interpolation

Full size image

The S-shaped velocity profile method [31] is adopted to outcome the continuity and smoothness at the level of acceleration of curves with predefined motion parameters and path length. After the continuous hole cutting path is obtained by the parameterized curves, each series of N discrete intermediate points \(\textbf{p}_k\) can be computed with path interpolation sampling interval \(\Delta t\), as requested by the computer numerical control (CNC) as

$$\begin{aligned} \textbf{p}_k = \textbf{p}_{1} + \left( \textbf{p}_N - \textbf{p}_1\right) \frac{k\Delta {t}}{t_{N} - t_1} S\left( k\Delta {t}\right) , \end{aligned}$$
(13)

where \(\forall k\in 1, \dots , N\), \(\textbf{p}_1\), \(\textbf{p}_N\) are the starting and ending point of the hole-cutting path, \(t_1\), \(t_N\) are the starting and ending time, and \(S(\cdot )\) is the S-shaped function to generate the scale length value according to the current \(k\Delta {\textbf{t}}\).

Fig. 6
figure 6

Conic posture on a circle hole path. a stationary wrist center point \(\textbf{p}_w\). b dynamic wrist center \(\textbf{p}_w\) resulting from the conic vertex positioned away from the plane of the circular path

Full size image

3.2 Conic posture

Through holes on the part are typically cut while maintaining a consistent laser beam posture along the hole’s path, which implies that the rotational wrist joints remain stationary throughout the operation. In this paper, we propose a strategy for holes capable of accommodating a tapered cut. The hole size to be tackled with conic posture should be relatively small. However, defining a specific size limitation is challenging, due to the interplay of numerous complex factors. In the following section, we will deal with the relationship between the hole dimensions and its vertex search area, which can affect the optimization result. This method employs a conic posture, which is a specific orientation that assumes the shape of a cone during the cutting process. This posture is dictated by a determined vertex, which serves as the point of origin for the conical shape. The use of the conic posture introduces flexibility in the cutting trajectories, a feature that is particularly beneficial for the hole path cutting process, and this is attributed to the lightweight nature of the wrist axes.

The graphic representations of the conic posture are shown in Fig. 6, where the coordinate of the cone vertex \(\textbf{p}_v\) affects two distinct scenarios due to the physical stroke of the ultimate prismatic joint \(q_6\). In the first instance, the wrist center position \(\textbf{p}_w\) overlaps the cone vertex \(\textbf{p}_v\), as each intermediate point \(\textbf{p}_k\) falls within the feasible domain of the wrist workspace. As a result of the vertex’s distant position, an alternative scenario could generate a dynamic wrist center point path constrained by the maximum extension of \(q_6\) stroke. This path can potentially mirror the hole’s geometry but on a smaller scale.

The assigned conic posture to \(\textbf{p}_k\) in the form of a rotation matrix is determined by the following three orthogonal unit vectors:

  1. 1.

    the unit vector \(\hat{\textbf{v}}_{k,z}\) is directed along the vector pointing from \(\textbf{p}_k\) to \(\textbf{p}_v\) as z-axis;

  2. 2.

    the unit vector \(\hat{\textbf{v}}_{k,x}\) is directed along the vector aligned with tangential direction from \(\textbf{p}_{k-1}\) to \(\textbf{p}_k\) as x-axis;

  3. 3.

    the unit vector \(\hat{\textbf{v}}_{k,y}\) is directed along the cross product in \(\hat{\textbf{v}}_{k,z}\) and \(\hat{\textbf{v}}_{k,x}\) as y-axis.

Thus, obtaining comprehensive pose information in SE(3) entails specifying the coordinates of the intermediate point \(\textbf{p}_k\) and the vertex \(\textbf{p}_v\). As deduced from Eq. (12), the inverse kinematics produces the subsequent expression, whereby \(\textbf{p}_k\) gives rise to \(\textbf{q}_k\) as

$$\begin{aligned} \textbf{q}_k = \Psi \left( \textbf{p}_k,\textbf{p}_v\right) . \end{aligned}$$
(14)

The evaluation of cutting quality in terms of the taper error \(\alpha _k\) on an intermediate point \(\textbf{p}_k\) is given by

$$\begin{aligned} {\alpha }_{k} = \arccos \left( \frac{\textbf{n} \cdot \textbf{l}}{\Vert \textbf{n}\Vert \Vert \textbf{l}\Vert }\right) , \end{aligned}$$
(15)

where \(\textbf{n}\) is the normal vector to the cutting plane, and \(\textbf{l}\) is laser beam vector along the \(\hat{\textbf{v}}_{k,z}\) direction. Additionally, \(\cdot \) is the dot product for two vectors, and \(\Vert \cdot \Vert \) is the norm of a vector.

To depict the conic posture strategy more effectively and particularly highlight the minor movements primarily executed by the wrist joints, Fig. 7 shows the machining process for a circular hole path using the conic posture strategy, followed by the inverse kinematic transformation mentioned above.

Fig. 7
figure 7

Circular hole path machining with conic posture strategy

Full size image

4 Conic posture optimization

4.1 Objective functions

This section expands on the preliminary discussions and focuses on the optimization of the conic posture along the through hole path. The spatial location of the conical vertex exerts an influence on the configuration of the laser beam’s posture during the cutting procedure. Consequently, we treat \(\textbf{p}_v\) as the design variable, represented by a three-dimensional vector \(\textbf{x} \in \mathbb {R}^3\), in the context of the optimization problem.

The conic shape posture is known to produce angular differences as the taper error. Thus, the objective of the optimization problem should be to minimize such a deviation. However, it is evident that the minimization of taper angle error alone may prove insufficient in addressing the intricate optimization challenges inherent in the conic posture. This limitation arises due to the geometric characteristics of cones, where an increase in the spatial separation between the vertex and the cutting plane can potentially lead to a reduction in taper errors.

Therefore, a holistic optimization approach should not be confined merely to minimizing the taper error only. It necessitates the incorporation of supplementary reference variables to aptly govern the optimization of the vertex position. Hence, an additional objective is introduced to minimize the kinetic energy consumption to evaluate the machine’s actuators. By reducing the magnitude of acceleration under a constant target speed, the second objective function can improve the smoothness of the trajectory, consequently, the overall quality of the machining process. Meanwhile, the penalty of the axes mass is introduced to encourage the utilization of the wrist joints for enhanced dynamic performance.

The representation of the multi-objective function \(F(\textbf{x})\), encapsulating the two goals mentioned before can be expressed as follows:

$$\begin{aligned} F \left( \textbf{x}\right) = \left( 1 - \varphi \right) f_1\left( \textbf{x}\right) + \varphi f_2\left( \textbf{x}\right) , \end{aligned}$$
(16)

where the weight \(\varphi \), within the range of [0,1], plays a crucial role in the selection of an optimal solution that aligns with the designated functionality of the hole, as

  • \(\varphi = 0\): minimize \(f_1(\textbf{x})\) only;

  • \(\varphi = 1\): minimize \(f_2(\textbf{x})\) only.

The first objective \(f_1(\textbf{x})\) represents the mean value of the taper error \(\alpha _k\), which is defined according to Eq. (15). This objective function evaluates the global cutting quality along the cutting path, and it is defined as

$$\begin{aligned} f_1\left( \textbf{x}\right) = \frac{1}{N}\sum _{k=1}^{N} \alpha _k. \end{aligned}$$
(17)

In the definition of the second objective function \(f_2(\textbf{x})\), evaluating the kinetic energy consumption of the actuators, the inclusion of acceleration \(\ddot{\textbf{q}}\) emerges as a fundamental factor, similar to what has been done in another effort in the literature [14]. This is attributed to its influence on the torque or force demanded, which depends on the current output from the servo system’s amplifier. In this study, the matrix of acceleration samples \(\ddot{\textbf{q}}\) during the motion, represented by N sets of intermediate points along the path, is derived from the joint configurations \(\textbf{q} \in \mathbb {R}^{N \times 6}\) with the finite-differential matrix \(\textbf{D}\) as

$$\begin{aligned} \ddot{\textbf{q}} = \textbf{D} \textbf{q}, \text {with} \end{aligned}$$
(18)
$$\begin{aligned} \textbf{D} = \left[ \begin{array}{cccccccc} 1 &{} 0 &{} 0 &{} \cdots &{} 0 &{} 0 &{} 0 &{} 0 \\ -2 &{} 1 &{} 0 &{} \cdots &{} 0 &{} 0 &{} 0 &{} 0 \\ 1 &{}-2 &{} 1 &{} \cdots &{} 0 &{} 0 &{} 0 &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} -2&{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} \cdots &{} 1 &{} -2 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} \cdots &{} 0 &{} 1 &{} -2 &{} 1 \end{array}\right] \in \mathbb {R}^{N \times N}, \end{aligned}$$
(19)

where \(\textbf{q}\) is determined by the inverse kinematics conversion from Cartesian points \(\textbf{p} \in \mathbb {R}^{N \times 3}\), as described by Eq. (14), applied to \(\textbf{p}\) corresponding to the cone vertex candidate \(\textbf{x}\).

Table 2 Joint physical constraints
Full size table
Fig. 8
figure 8

Graphic representation of the vertex searching area

Full size image

The evaluation of the kinetic energy consumption during posture optimization is then performed by incorporating the sum of squared accelerations, which captures the magnitudes of the energy provided by the system. This assessment can be further enhanced by considering the varying effects of different load mass or inertia through the use of the weight vector \(\textbf{M}^T = \left[ m_1,\dots , m_{6}\right] \). Hence, we define

$$\begin{aligned} f_2\left( \textbf{x}\right) = \frac{1}{2} \left( \ddot{\textbf{q}} \textbf{M} \right) ^T\left( \ddot{\textbf{q}} \textbf{M}\right) . \end{aligned}$$
(20)

Substituting \(\ddot{\textbf{q}}\) from Eq. (18) into Eq. (20), and defining \(\textbf{Q}\) and \(\textbf{D}\) as

$$\begin{aligned} \mathbf {Q = qM}, \end{aligned}$$
(21)
$$\begin{aligned} \textbf{U} = \textbf{D}^T\textbf{D}, \end{aligned}$$
(22)

we can simplify and represent the kinetic energy consumption objective function \(f_2(\textbf{x})\) in a quadratic form as

$$\begin{aligned} f_2\left( \textbf{x}\right) = \frac{1}{2}\textbf{Q}^T\textbf{U}\textbf{Q}. \end{aligned}$$
(23)

4.2 Constraints

The constraints of the proposed conic posture optimization problem are the following:

  1. 1.

    The taper error \(\alpha _k\) can never exceed the specified maximum tolerance of taper error \(\alpha _{\max }\).

  2. 2.

    The motion of the machine along the trajectory must satisfy physical constraints such as joint stroke limits, joint velocity limits, and joint acceleration limits, as detailed in Table 2.

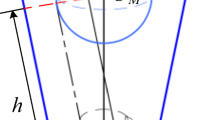
The boundary of the \(\textbf{x}\) variable is dependent on the geometric features of the specific hole being cut, which serves to confine the search area, as shown in Fig. 8. The parameter d denotes the maximum inner distance of the hole; for a circular hole, d represents the diameter of the circle. The minimum search height \(h_0\) above the cutting plane should be adequately set to meet the taper error constraint, as specified below

$$\begin{aligned} h_0 = \beta \textbf{q}_{6,\max } \cos \left( \alpha _{\max }\right) , \end{aligned}$$
(24)

where \(\beta \) represents a scale factor that determines the initial search height based on the percentage of extension of \(q_6\) stroke; here we choose \(\beta = 0.8\) as an illustrative example.

Hence, the lower boundary \(\textbf{lb}\) and upper boundary \(\textbf{ub}\) of the 3D search as

$$\begin{aligned} \textbf{l b}=\left[ \begin{array}{c} -3 d \\ -3 d \\ h_0 \end{array}\right] , \quad \textbf{u b}=\left[ \begin{array}{c} 3 d \\ 3 d \\ h_0+3 d \end{array}\right] . \end{aligned}$$
(25)

In summary, the optimization model is governed by the following constraints:

$$\begin{aligned}{} & {} 0 \le \alpha _k \le \varvec{\alpha }_{\max }, \quad k = 1, \dots , N \nonumber \\{} & {} \textbf{q}_{i,\min } \le q_{i,k} \le \textbf{q}_{i,\max }, \quad i = 1, \dots , 6, k = 1, \dots , N \nonumber \\{} & {} \textbf{v}_{i,\min } \le \dot{q}_{i,k} \le \textbf{v}_{i,\max }, \quad i = 1, \dots , 6, k = 1, \dots , N \nonumber \\{} & {} \textbf{a}_{i,\min } \le \ddot{q}_{i,k} \le \textbf{a}_{i,\max }, \quad i = 1, \dots , 6, k = 1, \dots , N \nonumber \\{} & {} \textbf{lb}_j \le \textbf{x}_j \le \textbf{ub}_j, \quad j = 1, \dots , 3 \end{aligned}$$
(26)

4.3 Multi-objective genetic algorithm

The multi-objective genetic algorithm (MOGA) is a type of Genetic algorithm (GA), which uses the non-dominated classification of a GA population to move the population toward the Pareto front, which stands for a set of solutions that are non-dominated by each other but are superior to the rest of solutions in the search space. MOGA was introduced by Fonseca and Fleming [32]. Subsequently, various dominance-based Pareto techniques [33] have been developed, such as NPGA [34], NSGA/NSGA-II [35]. GA is particularly effective at searching for optimal solutions in complex and nonlinear spaces, characteristics that align with our evaluation functions. Furthermore, the multi-objective methodology facilitates an exploration of trade-offs between the two objectives, enabling the selection of the most suitable solution tailored to customized preferences. In this study, we employed an elitist genetic algorithm to address the conic posture optimization problem. During the evolution process, lower rank individuals are preferable to be selected as the parents considering crowding distance. The newly created population is again passed through the mechanism of genetic operators to generate another new offspring population.

To summarize, we can leverage Eqs. (16) and (26) to formulate the conic posture optimization problem in a comprehensive form, as

$$\begin{aligned} \begin{aligned}&\quad \min _{\textbf{x} \in \mathbb {R}^3} F\left( \textbf{x}\right) = \left( 1 - \varphi \right) f_1\left( \textbf{x}\right) + \varphi f_2\left( \textbf{x}\right) \\&{\textbf {Subject to}} \\&\quad \varphi \in [0,1] \in \mathbb {R}\\&\quad i = 1, \dots , 6 \in \mathbb {Z}\\&\quad j = 1, \dots , 3 \in \mathbb {Z}\\&\quad k = 1, \dots , N \in \mathbb {Z}\\&\quad 0 \le \alpha _k \le \varvec{\alpha }_{\max }\\&\quad \textbf{q}_{i,\min } \le q_{i,k} \le \textbf{q}_{i,\max }\\&\quad \textbf{v}_{i,\min } \le \dot{q}_{i,k} \le \textbf{v}_{i,\max }\\&\quad \textbf{a}_{i,\min } \le \ddot{q}_{i,k} \le \textbf{a}_{i,\max }\\&\quad \textbf{lb}_j \le \textbf{x}_j \le \textbf{ub}_j \\ \end{aligned} \end{aligned}$$
(27)

The optimization problem is solved using the gamultiobj solver from the MATLAB Global Optimization Toolbox. Non-inferior solutions are obtained from the iterative optimization process after completing 150 generations with a population size of 100 candidate solutions. Pareto optimal solutions and the Pareto front representing the average of taper error and the sum of weighted squared accelerations are illustrated in Fig. 9 for an instant hole-cutting path.

Fig. 9
figure 9

Optimal Pareto front and its search history for hole 2

Full size image
Fig. 10
figure 10

Result of conic posture optimization for hole 2 in joint space

Full size image

The selected solution features a vertex at coordinates \(\textbf{x} = \left[ 1305.72, 76.59,11.68\right] \), which is determined by the selective weight \(\varphi = 0.6\). This solution is conditioned with a tangential cutting speed of 7500 mm/min and an acceleration of 4000 mm/s\(^2\). The evolution of the six joints after optimization by MOGA, including joint speeds and accelerations, are graphically represented in Fig. 10.

5 Approach for minimizing machining time for the hole-cutting path

In this section, we present an approach aimed at further improving the result advisable by the optimization process illustrated in the previous sections, minimizing the overall machining time required for cutting paths of individual holes on a single workpiece. The primary objective is to achieve global time optimization by determining the maximum achievable cutting speeds \(\textbf{V}_{\text {tan}}\), considering maximum taper error tolerance \(\alpha _{\max }\) and spatial positions on the workpiece.

The non-linearity in their mapping from the local coordinate system to the machine coordinate system, which is influenced by the setup position of the workpiece fixture and inverse kinematics transformation, leads to varying achievable maximum speeds for each hole-cutting path. Therefore, we propose an approach to minimize the time required for hole cutting that aims to maximize the speed of each hole j, while still satisfy specified constraints. This approach involves to gradually decrease the speed \(v_j\) by multiplying it with the reduction rate \(\gamma \) from its maximized technical speed \(v_{\max }\), encompassing a continuous speed descent process to search achievable maximum speed. A smaller \(\gamma \) provides a more precise determination of the speed. Taking into account our computational capabilities, we have chosen \(\gamma = 0.9\), which reduces the speed by 10% at each step. Once the optimal solution for the conic posture is identified, the post-processor will generate the corresponding Macro G-code to facilitate the utilization of the most advantageous vertex discovered.

Additionally, it is important to acknowledge that this approach will no longer execute the conical posture optimization for holes that demand high precision in orientation errors. Instead, it will adopt the canonical cutting strategy when the cutting speed decreases to a level that can be achieved normally. The implementation of the holes-cutting time minimization algorithm is detailed in Algorithm 1.

Algorithm 1
figure a

Pseudo code of Holes-cutting time minimization algorithm.

Full size image

6 Experiments and results

6.1 Experiments and software setup

In order to validate the improvements introduced by our conic cutting strategy in the manufacturing process, we conducted a comparative experiment. This experiment involved applying both the canonical strategy and our proposed approach to parts with identical model specifications.

For our experimental setup, an automotive B-pillar was chosen as a significant case study, featuring 26 holes distributed across its surface, varying in location and size. Geometric parameters for the hole-cutting path are detailed in a table in Appendix A. The experimental material was high-strength stainless steel (HSS) with a thickness of 1.5 mm. Our prototype machine is equipped with a 3KW fiber laser, producing a laser beam with a focused diameter of 50 \(\upmu \)m from the generator. To fulfill the machining requirements, the G41 G-code instruction is utilized for tool dimension compensation. The standoff distance, the gap between the nozzle tip and the workpiece surface, is precisely set at 1.5 mm. Compressed air was employed as the auxiliary gas, supplied at a pressure of 13 bar to ensure optimal cutting quality. The experimental setup is depicted in Fig. 11.

The benchmark cutting speed, set at 8000 mm/min as a reference point, was derived from the G-code program used by a manufacturer for an identical B-pillar workpiece. However, it is important to note that the actual maximum cutting speed may be equal to or lower than such a reference. Such a discrepancy depends on the specific length of each individual hole path and the overall machining performance. In our application, the rate of material removal is significantly related to the laser power density and frequency. For the HHS material mentioned above, an analysis of technological constraints indicated that the maximum achievable cutting speed for achieving good cutting quality is 14,000 mm/min.

Fig. 11
figure 11

Experimental setup and 3D laser cutting machine prototype

Full size image

To ensure the effectiveness of our experimental evaluations, we divided the algorithm’s implementation into two primary components. The post-processing component is designed to generate optimized vertex coordinates for each individual part based on predefined specifications and constraints. We constructed this part using MATLAB R2022b according to the procedure developed in Sect. 4 and a simple post-processor for exporting the corresponding G-code post program, ensuring compatibility with the interpolator. On the other hand, the real-time execution component is responsible for interpolating specific hole positions and is integrated into the CNC using G-code format. A detailed implementation of the circular hole path executed using a conic posture is comprehensively described in Appendix B. This component was developed within the Robox Development Environment 5.45 software platform in C++.

6.2 Results and discussion

The results from the optimization procedure applied to the 26 holes are presented in Fig. 12. The provided data in the figure offer a comprehensive depiction of the achieved speed, the reduction in hole-cutting cycle time, and a comparative analysis of taper tolerance and average values along the path of each specific hole-cutting operation after the optimization procedure.

Fig. 12
figure 12

Experimental results overview

Full size image
Fig. 13
figure 13

B-Pillar workpiece post-conic posture cutting. Hole indexes are marked in blue, with a zoomed-in view of the through-holes provided

Full size image

The primary optimized cutting speeds demonstrate a significant increase compared to the reference speed, where the differences are quantified through standard error bars in Fig. 12. It is worth mentioning that the sections within the range of index 8 to 19 exhibit a comparatively less significant enhancement in velocity compared to the outcomes observed on the remaining holes. This occurrence can be reasonably attributed to the particular placement of these holes, primarily on the frontal surface of the component. This underlines the optimization strategy’s effectiveness in enhancing cutting speed, particularly for holes located at the top or bottom side of the part and where a higher acceptable taper error is admissible. The only exception in this trend appears in the case of hole 21, which demonstrates a lower improvement rate (9180 mm/min compared to the reference). This anomaly could potentially be explained by the concave nature of the hole’s surface. It is noteworthy that the location and orientation of the holes significantly affect the optimization outcome, indicating the need for a tailored approach in executing the optimization strategy. The cut part is shown in Fig. 13.

Fig. 14
figure 14

Representations of the conic posture cutting strategy at different positions on the workpiece. a bottom position; b front position; c top position

Full size image
Fig. 15
figure 15

Comparison of through holes obtained by a canonical strategy, b conic posture strategy

Full size image

The optimization outcomes consistently exhibit diminished values in relation to the specified tolerance when considering the average taper error. Figure 14 illustrates the inclined laser head posture during the hole-cutting process on the bottom, front, and top positions. This representation emphasizes the effectiveness of the optimization process in preserving the accuracy and quality of the cuts, even when operating at higher cutting speeds. We observe that some holes show increased taper errors. This is attributed to their unique geometric characteristics of the conic posture, as assessed by the calculated mean taper error. However, these deviations remain within acceptable thresholds.

The time efficiency aspect should also be noted. A direct comparison of the total cutting time before and after optimization, 16.71 s and 10.46 s respectively, reveals significant improvement on a singular part. Overall, the optimization process has successfully reduced the average time of laser beam on for holes cutting. These improvements in speed and time efficiency could lead to substantial cost savings and increased productivity in a manufacturing setting.

While the conic posture strategy has improved efficiency, maintaining the cutting quality and positional precision is crucial. Figure 15 compares the results of the conventional strategy with our proposed strategy. In Fig. 15b, we observe that the selected cone vertex led to a taper error of about 13.45 degrees in average, causing a slight tilt in the hole walls. Additionally, this method resulted in a small drift — around 0.36 mm — between the upper and lower circular hole surface. To address this issue, we added a compensation feature in our post-processing. This feature adjusts the center of the hole to offset in the opposite direction of the vertex’s projection on the plane of the hole by an amount equal to the displacement.

7 Conclusion

In this paper, an effective approach is proposed to reduce the cycle time of cutting through holes on the automotive parts in 3D laser cutting application. The objective of this methodology is to present an innovative method for hole cutting, known as the conic cutting strategy. This approach effectively improves the tangential cutting speed along the hole path by leveraging the flexibility provided by the kinematic redundancy of the structure. The conic posture strategy demonstrates superior performance compared to the canonical cutting strategy that employs a perpendicular laser beam driven by fixed Cartesian axes. Furthermore, a multi-objective optimization problem is formulated with the objective of searching for the optimized coordinate position of the conic vertex, while simultaneously minimizing the taper error and kinetic energy consumption.

The proposed approach is validated through experiments on a 3D laser cutting machine prototype. The experiments show the practicality and efficiency of the conic cutting strategy on the through holes. Some through holes situated on the side have been demonstrated to have better adaptability of being cut with the conic strategy. The dedicated processing tolerance in the specifications has been guaranteed by the optimization constraints. The cycle time of 26 holes cutting, including 3 holes not being optimized, is reduced by around 37% on a single part after the conic posture optimization.

Our study explores the possibility of achieving a higher cutting speed by cutting through holes in a conical shape, given that these holes are intentionally designed to have low taper accuracy, for instance, cable passing holes or liquid leak holes. It is important to acknowledge that the aforementioned method is rooted in the notion of redundancy and the decoupling of kinematics. This methodology contributes to boost machine’s dynamic performance through the optimization of the proper position of the wrist center point. This concept is crucial due to its applicability to other non-contact machining applications, especially 3D laser cutting machines, provided that the standoff servo axis is extended as we did. Furthermore, our work will be extended to improve the speed of the open cutting path on the complex surface in 3D space by controlling the redundancy, which nowadays is mainly limited by the path geometry and the capacity of the machine dynamics’ itself.