Simple adaptive control for industrial feed drive systems using a jerk-based augmented output signal

Abstract

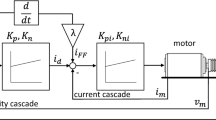
In the manufacturing industry, there is an extensive use of high-precision motion control techniques to achieve high performance in the feed drive system. This study deals with the simple adaptive control (SAC) technique for simultaneous high-precision motion and energy-saving of the feed drive system. The application of the SAC requires that the “almost strictly positive real (ASPR)” property is satisfied and there is a command general tracking solution for the plant and the reference model. This paper presents to use the jerk-based augmented output signal for the ASPR property. The proposed approach allows the SAC to track the desired signal at high frequencies more precise and is achieved by placing the zeros of the system at effective locations. To verify the feasibility of the proposed approach, simulation and experiment are conducted. The results are compared with those of the commonly used parallel feedforward compensation (PFC) approach. Experimental results revealed that the proposed approach reduced the tracking error by about 80% compared to PFC without any additional control input. Moreover, the proposed approach has been proved to be energy-efficient by about 21% than PFC under similar tracking conditions.

Appendix. Stability analysis

This appendix shows the stability analysis for the proposed method. The perfect tracking requires $y^*_p = y_m$ condition is met. The ideal state and input correspond to the state and input of the reference model as

$$\begin{aligned} {} & {} x^*_p = X{x}_m + Uu_m, \nonumber \\ &{}{}&u^*_p = \tilde{\varvec{k}}^T_x{x}_m + \tilde{k}_uu_m, \end{aligned}$$

(A1)

where X and U are the time-varying coefficient matrices. $\tilde{\varvec{k}}_x$ and $\tilde{k}_u$ are the constant vector and parameter, respectively. Introducing the terms $A_{p1}x^*_p + B_{p1}u^*_p - A_{p1}x^*_p - B_{p1}u^*_p$ into derivative of ${x}^*_p$ and substituting the term $\dot{x}_m$ from (2) into $\dot{x}^*_p$ lead to

$$\begin{aligned} {} & {} \dot{x}^*_p = A_{p1}x^*_p + B_{p1}u^*_p + [\dot{X} + XA_m - A_{p1}X - \nonumber \\ &{}{}&B_{p1}\tilde{\varvec{k}}^T_x]x_m + [XB_m + \dot{U} - A_{p1}U - B_{p1}\tilde{k}_u]u_m+\nonumber \\ &{}{}&U \dot{u}_m.\ \end{aligned}$$

(A2)

The state error is defined as $e_x = x^*_p - x_p$ and its derivative $\dot{e}_x = \dot{x}^*_p - \dot{x}_p$. The system dynamics (1) derives the states of position and velocity for the actuator and table. Thus, a different representation is required to provide accessibility to the higher order derivatives of table position [42]. Therefore, the following state space representation is used:

$$\begin{aligned} {} & {} \underbrace{ \begin{bmatrix} \dot{x}_e \\ \ddot{x}_e \\ \dddot{x}_e \\ \ddddot{x}_e \\ \end{bmatrix}}_{\dot{x}_p}= \underbrace{ \begin{bmatrix} 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1\\ \frac{-\sigma _{5}}{\sigma _{1}} &{} \frac{-\sigma _{4}}{\sigma _{1}} &{} \frac{-\sigma _{3}}{\sigma _{1}} &{} \frac{-\sigma _{2}}{\sigma _{1}}\\ \end{bmatrix}}_{A_{p1}}\underbrace{ \begin{bmatrix} {x}_e \\ \dot{x}_e \\ \ddot{x}_e \\ \dddot{x}_e \\ \end{bmatrix}}_{{x}_p} + \nonumber \\ &{}{}&\underbrace{ \begin{bmatrix} 0 &{} 0 &{} 0 &{} \frac{g}{\sigma _{1}} \\ \end{bmatrix}^T}_{B_{p1}}{u}_p. \end{aligned}$$

(A3)

The values of $\sigma _{1},...,\sigma _{5}$ are defined in (14). Substituting $\dot{x}^*_p$ from (A2) and $\dot{x}_p$ from (A3) into state error derivative, the equation becomes

$$\begin{aligned} {} & {} \dot{e}_x = A_{p1}e_x + B_{p1}(u^*_p - u_p) + M,\ \end{aligned}$$

(A4)

where M contains the rest of the terms. Adding and subtracting $B_{p1}\tilde{k}_ee_a$ into (A4) lead to

$$\begin{aligned} {} & {} \dot{e}_x = A_{p1}e_x - B_{p1}\tilde{k}_e e_a - B_{p1}[\varvec{k}-\tilde{\varvec{k}}]^T\varvec{r} + M. \end{aligned}$$

(A5)

The augmented error signal is defined as $e_a = y_{ma} - y_{pa}$ given as

$$\begin{aligned} {} & {} e_a = \bar{C}_{p1}x^*_p + D_{p1}u^*_p - \bar{C}_{p1}x_p - D_{p1}u_p, \end{aligned}$$

(A6)

where $\bar{C}_{p1}$ is from (22). Substituting $u^*_p$ from (A1) and $u_p$ from (6) into (A6) leads to

$$\begin{aligned} {} & {} e_a = \bar{C}_{pc}e_x - D_{pc}[\varvec{k}-\tilde{\varvec{k}}]^T\varvec{r}, \end{aligned}$$

(A7)

where $\bar{C}_{pc} = \bar{C}_{p1}(1 + D_{p1}\tilde{k}_e)^{-1}$. Hence, substituting (A7) into (A5) leads to

$$\begin{aligned} {} & {} \dot{e}_x = A_{pc}e_x - B_{pc}[\varvec{k}-\tilde{\varvec{k}}]^T\varvec{r} + M, \end{aligned}$$

(A8)

where $A_{pc} = A_{p1} - B_{p1}\tilde{k}_e(1+D_p\tilde{k}_e)^{-1}\bar{C}_p$ and $B_{pc} = B_{p1} - B_p\tilde{k}_e(1+D_{p1}\tilde{k}_e)^{-1}D_{p1}$. Substituting $\dot{e}_{x}$ from (A8) and $\dot{\varvec{k}}_{I}$ from (11) and replacing $e_y$ with $e_a$ into (24) give

$$\begin{aligned} {} & {} \dot{V} = \left[ A_{pc}e_x - B_{pc}[\varvec{k}-\tilde{\varvec{k}}]^T\varvec{r} + M\right] ^TPe_{x} \nonumber \\ {} & {} + e^T_{x}P\left[ A_{pc}e_x - B_{pc}[\varvec{k}-\tilde{\varvec{k}}]^T\varvec{r} + M\right] + \nonumber \\ {} & {} 2\text {tr} \left\{ S^T(\varvec{k}_{I}-\tilde{\varvec{k}}) \Gamma ^{-1}_I \left[ e^T_a\Gamma _{I}\varvec{r} - \xi \varvec{k}^T_{I}\right] S \right\} , \end{aligned}$$

(A9)

from Eq. (9) and replacing $e_y$ with $e_a$; $\varvec{k}_{I} =\varvec{k} - \varvec{k}_{p} = \varvec{k} - e_a\Gamma _{p}\varvec{r}$, (A9) leads to

$$\begin{aligned} {} & {} \dot{V} = e^T_x \left( A^T_{pc}P + PA_{pc}\right) e_x\nonumber \\ {} & {} - B^T_{pc}[\varvec{k}-\tilde{\varvec{k}}]\varvec{r}^TPe_{x} - e^T_{x}PB_{pc}[\varvec{k}-\tilde{\varvec{k}}]^T\varvec{r} \nonumber \\ {} & {} + M^TPe_{x} + e^T_{x}PM + e^T_a[\varvec{k}-\tilde{\varvec{k}}]\varvec{r}S^TS \nonumber \\ {} & {} + \varvec{r}^T[\varvec{k} -\tilde{\varvec{k}}]^Te_aS^TS -2e^T_ae_a\varvec{r}^T\varvec{r}\Gamma _{p}S^TS \nonumber \\ {} & {} - 2\xi \text {tr} \left\{ [\varvec{k}_{I}-\tilde{\varvec{k}}]\Gamma ^{-1}_{I}\varvec{k}^T_{I} S^TS \right\} . \end{aligned}$$

(A10)

The passivity relation (25), (A10), and constraint on the output matrix $\bar{C}_{pc}=(S^TS)^{-1}(B^T_{pc}P) + L^TW$ which lead to

$$\begin{aligned} {} & {} \dot{V} = -e^T_xQe_x - e^T_xL^TLe_x\nonumber \\ {} & {} - \bar{C}^T_{pc}[\varvec{k}-\tilde{\varvec{k}}]\varvec{r}^Te_{x}S^TS + L^TW[\varvec{k}-\tilde{\varvec{k}}]\varvec{r}^Te_{x} \nonumber \\ {} & {} - \bar{C}^T_{pc}e^T_{x}[\varvec{k}-\tilde{\varvec{k}}]^T\varvec{r}S^TS + L^TWe^T_{x}[\varvec{k}-\tilde{\varvec{k}}]^T\varvec{r} \nonumber \\ {} & {} + \bar{C}^T_{pc}e^T_x[\varvec{k}-\tilde{\varvec{k}}]\varvec{r}S^TS-D^T_{pc}[\varvec{k}-\tilde{\varvec{k}}]^T\varvec{r}^T[\varvec{k}-\tilde{\varvec{k}}]\varvec{r} \nonumber \\ {} & {} + \bar{C}_{pc}e_x\varvec{r}^T[\varvec{k}-\tilde{\varvec{k}}]^TS^TS-D_{pc}[\varvec{k}-\tilde{\varvec{k}}]\varvec{r}^T[\varvec{k}-\tilde{\varvec{k}}]^T\varvec{r} \nonumber \\ {} & {} -2e^T_ae_a\varvec{r}^T\varvec{r}\Gamma _{p}S^TS - 2\xi \text {tr} \left\{ [\varvec{k}_{I}-\tilde{\varvec{k}}]\Gamma ^{-1}_{I}\varvec{k}^T_{I} S^TS \right\} \nonumber \\ {} & {} + 2e^T_{x}PM. \end{aligned}$$

(A11)

The third and fifth terms cancel with the seventh and ninth terms, respectively. With the choice of $\varvec{k} = \tilde{\varvec{k}}$ which is required for implementation, rearranging Eq. (A11) becomes

$$\begin{aligned} {} & {} \dot{V} = -e^T_xQe_x - e^T_xL^TLe_x -2e^T_ae_a\varvec{r}^T\varvec{r}\Gamma _{p}S^TS \nonumber \\ {} & {} - 2\xi \text {tr} \left\{ S^T[\varvec{k}_{I}-\tilde{\varvec{k}}]\tilde{\varvec{k}}^T\Gamma ^{-1}_{I} S \right\} \nonumber \\ {} & {} - 2\xi \text {tr} \left\{ S^T[\varvec{k}_{I}-\tilde{\varvec{k}}]^T[\varvec{k}_{I}-\tilde{\varvec{k}}]\Gamma ^{-1}_{I} S \right\} \nonumber \\ {} & {} + 2e^T_{x}PM. \end{aligned}$$

(A12)

Introducing positive coefficients $\beta _1,\beta _2,\beta _3...,\beta _7$ leads to

$$\begin{aligned} {} & {} \dot{V} \le -\beta _1\Vert e_x\Vert ^2 -\beta _2\Vert e_a\Vert ^4 -\beta _3\Vert e_a\Vert ^2 \Vert x_m\Vert ^2 \nonumber \\{} & {} -\beta _4\Vert e_a\Vert ^2 \Vert u_m\Vert ^2 -\beta _5\Vert \varvec{k}_I-\tilde{\varvec{k}}\Vert -\beta _6\Vert \varvec{k}_I-\tilde{\varvec{k}}\Vert ^2 \nonumber \\{} & {} + \beta _7\Vert e_x\Vert . \end{aligned}$$

(A13)

When either $\Vert e_x\Vert$, $\Vert e_a\Vert$, or $\Vert \varvec{k}_{I}-\tilde{\varvec{k}}\Vert$ increases beyond a certain bound, the negative definite quadratic terms in (A13) become dominant making $\dot{V}$ negative semi-definite guarantees all signals (namely, $e_x$, $\varvec{k}_I$, and $e_a$) are bounded.

Since V in (23) is lower bounded and $\dot{V}$ is negative semi-definite, to apply the Barbalat’s lemma requires $\dot{V}$ to be uniformly continuous. The derivative of $\dot{V}$ is

$$\begin{aligned} {} & {} \ddot{V} = -2\dot{e}^T_xQe_x - 2\dot{e}^T_xL^TLe_x -\nonumber \\{} & {} -4\dot{e}^T_ae_a\varvec{r}^T\varvec{r}\Gamma _{p}S^TS -4e^T_ae_a\dot{\varvec{r}}^T\varvec{r}\Gamma _{p}S^TS\nonumber \\{} & {} - 2\xi \text {tr} \left\{ S^T\dot{\varvec{k}}_I\tilde{\varvec{k}}^T\Gamma ^{-1}_{I} S \right\} \nonumber \\{} & {} - 2\xi \text {tr} \left\{ S^T[\varvec{k}_{I}-\tilde{\varvec{k}}]\Gamma ^{-1}_{I}\dot{\varvec{k}}^T_I S \right\} + 2\dot{e}^T_{x}PM. \end{aligned}$$

(A14)

The derivative of $e_x$ from (A8); $\dot{e}_x = A_{pc}e_x + M$ when $\varvec{k} = \tilde{\varvec{k}}$ is selected and as $e_x$ is shown to be bounded from (A13), then $\dot{e}_x$ is also bounded. The augmented tracking error $e_a$ is bounded from (A13), and its derivative is given as $\dot{e}_a = \bar{C}_{pc}\dot{e}_x$ with $\varvec{k} = \tilde{\varvec{k}}$ selected for implementation, and since $\dot{e}_x$ is shown to be bounded, then $\dot{e}_a$ is also bounded.

It is assumed that the reference signals $u_m$ and $\dot{u}_m$ are bounded and piece wise continuous, thus the state $x_m$ is bounded. This in turn implies from (2) that $\dot{x}_m$ and $y_m$ are also bounded. The regressor vector $\varvec{r}$ on this design contains signals $e_a$, $x_m$, and $u_m$ which are all bounded, and their derivatives $\dot{e}_a$, $\dot{x}_m$, and $\dot{u}_m$ are also bounded, making the regressor derivative $\dot{\varvec{r}}$ bounded.

The derivative of integral gain term from (11); $\dot{\varvec{k}}_I = e_a\Gamma _{I}\varvec{r} - \xi \varvec{k}_{I}$, the signals $e_a$ and $\varvec{k}_I$ are bounded from (A13) and $\varvec{r}$ is bounded, and thus, the term $\dot{\varvec{k}}_I$ is bounded. This shows that $\ddot{V}$ is bounded; hence, $\dot{V}$ is uniformly continuous and the Barbalat’s lemma can be applied.