1 Introduction

In view of the increased global environmental awareness and the associated strict energy requirements for society and industry, thorough energy efficiency considerations are coming more and more into focus. The growing global energy demand from industrial sectors results in significant ecological as well as economical costs [24]. Aiming to reduce the impact of machining operations on the global energy consumption, led to a great number of research activities and publications regarding energy efficient machine tools and machining processes [2, 6, 7, 9, 10]. However, this contribution will focus on the cooling of machine tools. On the one hand, industrial cooling and temperature control systems represent an essential component of industrial production systems, since they strongly affect the product quality, service life of thermally stressed  parts, and the stability of the entire production process. On the other hand, cooling systems are responsible for a significant share of the energy consumption in the industrial sector [29]. Therefore, measures to increase the efficiency of cooling and temperature control systems can not only save costs but also contribute to reducing \(\text {CO}_{2}\) emissions associated with machine cooling [29].

The remaining part of the article is structured as follows: In the next section, the authors present the basic thermo-physical background for heat transfer enhancement by means of static mixers inside cooling channels. It will be shown that the increase of the convective heat transfer coefficient is associated with different mechanisms. Section 3 is devoted to a detailed presentation of strategies for the efficient numerical modeling of mold cooling scenarios. Since machine tools can be subjected to stationary and transient thermal loading, these both loading regimes are discussed. These considerations serve as a basis for the numerical setup in Section 3. Here, extensive computational studies are carried out. The achieved results are presented and discussed in Section 4. A short summary of the research implications in Section 5 concludes the paper.

The novelty of the contribution at hand comes from the fact that the specific application limits of static mixers for the enhancement of the convective heat transfer are systematically elaborated by means of extensive numerical simulations. The studies include all relevant layout parameters for machine tools such as tool material, flow rate of the coolant, heat flux during exposition and thermal loading regime (stationary vs. transient). This information is not provided in the state of the art and will help process engineers in optimizing existing cooling systems of machine tools as well as increasing the effectiveness of the overall production process.

Fig. 1
figure 1

Description of the numerical simulation model

Full size image

2 Basic strategies and mechanisms of heat transfer enhancement

With increasing concern about the sustainability of the global energy supply, techniques to increase energy efficiency have attracted considerable attention within the scientific community as well as in industry. In many modern industrial processes, the exchange of thermal energy between a flowing fluid and its confining channel is a ubiquitous transfer mechanism. In order to enhance the fluid-to-wall or wall-to-fluid convective heat transfer, two distinct categories of techniques have been developed in the sense of active and passive methods, cf. [21].

Active methods are characterized by their requirement of an external power/energy input to operate. According to Sheikholeslami et al. [25], such methods include for example

  • rotating mechanical devices like screws, mixing units and rotors in order to stir the fluid and thus inducing additional flow energy, cf. [22, 26, 34].

  • high frequency surface or fluid vibration like pulsation flows resulting in higher convective heat transfer coefficients, cf. [11, 32].

  • electrostatic fields like electric or magnetic fields or a combination of both inducing greater bulk mixing, force convection or electromagnetic pumping to enhance heat transfer in dielectric fluid flows, cf. [1, 16, 18].

  • special devices for injection and suction involving porous heat transfer interfaces [19].

Although active methods provide the ability to control heat transfer enhancement, they are generally not as widely used as passive methods due to their complexity, additional maintenance effort and increased costs. Furthermore, it is often not possible to integrate active devices for heat transfer enhancement into existing plants and processes.

Conversely, passive methods do not require external power input in terms of the above-mentioned strategies for active heat transfer enhancement. Passive methods are the most common form of heat transfer enhancement due to their simplicity, low costs and effort of integration. These methods usually employ geometrical or surface modifications in the channel flow by additional inserts such as static mixers or alternating the wall surface of the channel by dimples. In this way, it is possible to drastically increase the contact area between the fluid and the inner wall and/or disrupt the flow to enhance circulation or induce turbulence. From an energy perspective, the improved heat transfer is always accompanied by an increased pressure loss [8]. In order to drive the flow by compensating the induced pressure drop the use of stronger and therefore more expensive pumps is required. This leads to a multi-objective optimization problem with conflicting objectives (heat transfer enhancement vs. induced pressure drop). Since there is no optimum for both objectives simultaneously, an elaborate trade-off among the objectives is required to ensure that the savings from the heat transfer enhancement exceed the cost of a larger pressure drop.

Following the recent classifications for the most popular passive methods [21, 25], the subsequent types of inserts and surface modifications can be listed:

  • Twisted tape inserts are usually made of metallic strips which are twisted by appropriate techniques to a predefined shape and dimension. In literature, these inserts are often referred to as so-called static mixers [14, 15, 20]. By the insertion of static mixers, the heat transfer is enhanced by different mechanisms. Firstly, a part of the achieved heat transfer enhancement is associated with an increase of flow velocity due to a reduction of the hydraulic diameter. Secondly, due to the twisted geometry of the insert the fluid is forced to flow in the twisted pathway, creating an effective increase in flow length. Moreover, a swirl mixing occurs increasing agitation and inducing turbulence providing a further contribution to heat transfer enhancement. Finally, the inserts can act as baffles and fins increasing the surface area of contact with the fluid.

  • Coiled wire inserts have some advantages over other passive such as low cost due to their simple manufacturing as well as good integration and removement properties. Coiled wires unfold their thermal-hydraulic gains especially in turbulent flow regimes because they enable agitation of the laminar sublayer near the channel walls due to their geometry, cf. [12, 21, 25].

  • Surface modifications act in a similar way on the heat transfer enhancement like coiled wire inserts [28]. By means of corrugated/ribbed tubes or surface dimples additional roughness structures are added in order to increase turbulence which is associated with a heat transfer enhancement [13]. Such modifications are used exclusively in turbulent flow regimes due to their strongly localized effects within the viscous sublayer. For laminar flow regimes, twisted tape inserts provide the best performance among all passive methods.

In the scope of this contribution, the authors focus on helical static mixers as devices to enhance the convective heat transfer in mold cooling.

3 Strategies for the numerical modeling of mold cooling

In this section, the authors want to present numerical modeling strategies for describing the relevant mechanisms in mold cooling. As a representative application scenario for cyclically loaded machine tools, the cooling of a simple injection mold including the corresponding process conditions is investigated. However, the procedure to build up the numerical model as well as the obtained results can easily be transferred to other classes of water-cooled, thermally-loaded machine tools such as furnace rolls, heat shields or other components which are exposed to stationary or recurring thermal loading regimes. The research focus is intentionally put on investigating the influence of static mixers on the heat transfer between the coolant and the injection mold by means of numerical simulations. The implemented CFD model involves all relevant thermal mechanisms of the underlying fluid-structure interaction in terms of thermal conduction within the mold as well as the convective heat transfer in the cooling channel.

The application of static mixers aims to reduce cycle times and/or increase the surface quality of the injection molded part. This is achieved by a faster and more homogeneous cooling of the polymer melt.

3.1 Definition of a Representative Volume Element (RVE)

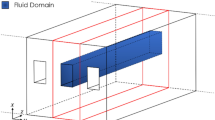
All numerical investigations are performed on a representative section of an injection mold. The mold is made of steel. The cooling channel is \(500\,\text {mm}\) long and has a circular cross-section with an inner diameter of \(8\,\text {mm}\). The center of the cooling channel has a distance of \(25\,\text {mm}\) from the top surface of the mold in order to reproduce the technically relevant close-contour cooling scenario. The mold section is cube-shaped and has a length of \(500\,\text {mm}\), a width of \(30\,\text {mm}\) and a height of \(65\,\text {mm}\). Due to the periodic boundary conditions on the side faces of the mold section, larger tool widths can be easily reproduced by placing several sections next to each other. On the top surface of the mold section, the model involves a homogeneous \(1\,\text {mm}\) thick layer of polymer melt (Fig. 1), with the material data of an ABS polymer. The interface between the metal and polymer volumes is modeled as an ideal thermal interface without thermal contact resistance.

Since the actual injection process including the filling of the mold cavity as well as the solidification of the polymer melt is not considered within the scope of this investigation, the polymer volume is regarded here as a solid for the sake of simplification. For a thorough simulation of the mold-filling process, the authors refer to their former work, cf. [3,4,5]. Water with an inlet temperature of \(T_{\text {inlet}}=30\,^{\circ }\text {C}\) is employed as the cooling medium. Further initial thermal conditions of \(30\,^{\circ }\text {C}\) are selected for the mold and \(250\,^{\circ }\text {C}\) for the polymer melt. Therefore, the polymer layer acts as a source of heat in the model. Within the CFD framework, a constant flow velocity is specified at the inlet of the cooling channel. Possible turbulence is captured by the k-\(\omega \) SST turbulence model. The material properties for the density \(\rho \), specific heat capacity \(c_{p}\), thermal conductivity \(\lambda \) and viscosity \(\eta \) of the involved model components are summarized in Table 1.

Table 1 Material properties of the steel, polymer and water
Full size table

3.2 Transfer from transient to steady-state simulation

The transient simulation of the model includes 15 injection molding cycles with a cycle duration of \(20\,\text {s}\). This quantity of cycles is required to bring the system to a steady state. Only in the steady-state regime, it is possible to make a sound comparison of different cooling channel configurations. Within the first cycles, the influence of the selected boundary and initial conditions of the mold dominate. Since the injection process is not simulated, the temperature of the entire polymer volume is set back abruptly to \(250\,^{\circ }\text {C}\) at the beginning of each new cycle as a simplification. During each cycle, the temperature of the polymer melt changes due to heat conduction into the mold. Figure 2 presents the temporal evolution of the volume-averaged polymer melt temperature \(T_{\text {melt}}\) over the first 15 cycles (with a total duration of \(300\,\text {s}\)) and a cooling channel without any swirl generating installations. This serves as a reference configuration for later simulations.

Fig. 2
figure 2

Temperature profile of the melt over 15 cycles in an empty cooling channel

Full size image

In addition to the melt temperature, special results on the spatial temperature distribution in the contact surface between the mold and the polymer are used to evaluate the different variants of swirl generating installations. These include the area-averaged temperature \(T_{\text {avg}}\) as well as the temperature difference \(\Delta T\) between the minimum \(T_{\text {min}}\) and maximum temperature \(T_{\text {max}}\) within this area. The knowledge of the temporal changes of these quantities is important for the later evaluation of the results (cf. Section 4) and represents the essential advantage of the transient simulation method. A disadvantage is a large number of iterations and the associated high computing time. In order to be able to investigate as many variants and influencing factors as possible with a low computational effort, the possibility of transferring the transient injection molding process to an equivalent stationary model is investigated. For this purpose, the results of the transient simulation after the first cycle are employed and the cooling mechanism of the polymer melt is converted into an equivalent constant heat flux on the contact surface of the mold \(\dot{q}\). The equation for the heat flux is based on an energy balance (first law of thermodynamics) regarding the polymer layer as a lumped system and is therefore defined as follows:

$$\begin{aligned} \dot{q}=\frac{\dot{Q}}{A}=\frac{c_{p,\text {melt}}\cdot V_{\text {melt}}\cdot \rho _{\text {melt}}\cdot \Delta T_{\text {cooling}}}{t_{\text {cooling}}\cdot A_{\text {melt}}} \end{aligned}$$
(1)

In this equation, the material properties of the polymer layer are taken from Table 1. The melt volume \(V_{\text {melt}}\) has a height of \(1\,\text {mm}\) and a base area \(A_{\text {melt}}\) of \(15000\,\text {mm}^{2}\). More details are given in Section 3.1. A cycle time \(t_{\text {cooling}}\) of \(20\,\text {s}\) is used for cooling the polymer by \(\Delta T_{\text {cooling}}=216\,\text {K}\), cf. Fig. 2. This gives an approximated heat flux of \(\dot{q}=13400\,\text {W/m}^{2}\) on the contact surface of the mold. With the constant heat flux calculated in this way, a steady-state calculation based on the same model is performed without the polymer melt layer. A comparison of the results for the different evaluation parameters is shown in Figs. 3, 4, and 5.

Fig. 3
figure 3

Time-dependent evolution of the minimum and maximum contact surface temperature and comparison with the respective steady-state solution \(T_{\text {min,stat}}\) and \(T_{\text {max,stat}}\)

Full size image
Fig. 4
figure 4

Time-dependent evolution of the temperature difference \(\Delta T\) in the contact surface and comparison with the steady-state solution \(\Delta T_{\text {stat}}\)

Full size image
Fig. 5
figure 5

Time-dependent evolution of the difference between the mass-flow-weighted outlet and inlet temperature and comparison with the steady-state solution

Full size image

The steady-state simulation gives a time-averaged value of the transient curve for all temperatures in the contact surface to the mold, cf. Fig. 3. The same applies to the time-averaged temperature difference \(\Delta T_{\text {stat}}\) in a steady-state cycle within the contact surface, cf. Fig. 4. The time-averaged temperature difference is described in Eq. 2. In this equation, \(T_{\text {max,stat}}\) denotes the maximum and \(T_{\text {min,stat}}\) the minimum of the time-averaged temperature on the contact surface.

$$\begin{aligned} \Delta T_{\text {stat}} = T_{\text {max,stat}}-T_{\text {min,stat}} \end{aligned}$$
(2)

Figure 5 shows the temperature difference \(\Delta T_{\text {outlet}}\) between the outflow temperature \(T_{\text {outlet}}\) and the supply temperature \(T_{\text {inlet}}\) of the cooling channel and provides the limit value for the steady-state observation. Please note that for the calculation of these temperatures, the mass-flow-weighted average is used. The transient simulation approaches the above-mentioned limit value asymptotically. Although all information about the time-dependent processes is lost by the steady-state observation, the steady-state values can still be considered as good indicators for the comparison of different cooling strategies. In the following, the steady-state simulation are used to explore the influence of the quantity and spacing of mixers, the thermal conductivity of the mold steel, the magnitude of the heat flux, and the flow velocity (Reynolds number) on the heat transfer between the mold and the coolant. Based on these results, selected variants are subjected to a transient analysis to identify and evaluate time-dependent effects that may enable a reduction in cycle time.

4 Computational studies

The numerical simulations are performed with ANSYS Fluent 2020 R2. The meshing of the model is also done with ANSYS Fluent Meshing. To guarantee the comparability of the results and to minimize the mesh influences, the same parameters for the automatic polyhedron meshing are used for all models. The meshes are prepared with a maximum element size of \(4\,\text {mm}\) and 5 inflation layers at the walls. Please note that the spatial discretization is done by polyhedral elements for the fluid as well as for the solid. On the basis of the region types (solid or fluid) the code numerically solves the Navier-Stokes equations for the fluid and the heat equation for the solid, respectively. For the temporal discretization an implicit framework with adaptive time-steps is employed. Figure 6 shows an exemplary mesh for the configuration with one static mixer. In addition to the ANSYS Fluent default convergence criteria, an additional convergence target of \(10^{-5}\) for the change in the average outlet temperature is employed in all stationary simulations after a minimum number of 200 iterations.

Fig. 6
figure 6

Mesh in ANSYS Fluent with one static mixer

Full size image

Throughout the subsequent investigations, the gravitational force is neglected since natural convection inside the cooling channel, caused by the change in fluid density during heating, is only relevant at extremely low flow velocities (e.g., \(v\le 0.2\,\text {m/s}\)) accompanied by high heat fluxes. Such conditions are not common to typical scenarios of machine cooling and are therefore not considered. All other boundary conditions are implemented as symmetry conditions (in terms of heat conduction). In addition to the reference of the empty cooling channel, four other variations including different installations of static mixers are investigated. The variation is expressed in terms of the number (1, 4, 7 and 13 static mixers) and the distances, but not in the design and the orientation within the cooling channel.

4.1 Influence of the flow velocity in an empty cooling channel

The reference for all variants is the calculation with a process-typical Reynolds number of 9633, which corresponds to a flow velocity of \(1{.}21\,\text {m/s}\) for a cooling channel cross-section of \(8\,\text {mm}\) [30]. With a Reynolds number clearly above 2300, a completely turbulent pipe flow can be assumed in the cooling channel without static mixer as well [23, 27]. Figure 7 shows the change in the area-weighted average surface temperature in the mold-to-melt contact surface \(T_{\text {avg}}\) and the average temperature of the cooling water at the outlet as a function of the flow velocity \(T_{\text {outlet}}\).

Fig. 7
figure 7

Average temperature in the contact surface and at the outlet as a function of flow velocity at \(13400\,\text {W/m}^{2}\) in an empty cooling channel

Full size image

Both functions have a similar hyperbolic characteristic that is proportional to the reciprocal of the flow velocity 1/v. The velocity-dependent evolution of the outlet temperature corresponds well to the analytical solution for the heating due to a constant heat flow, cf. Fig. 8. From the steady-state energy balance at the differential fluid element in the circular tube subjected to a constant specific heat flux, the analytical solution (Eq. 3) can be derived for the change in fluid temperature along the flow direction. This equation contains the fluid temperature \(T_{\text {fluid}}\), inlet temperature \(T_{0}\), heat flux \(\dot{q}\), hydraulic diameter d in m, mass flow rate \(\dot{m}\) in kg/s, specific heat capacity \(c_{p}\) and the distance from the inlet x given in m.

$$\begin{aligned} T_{\text {fluid}}\left( x\right) =T_{0}+\frac{\dot{q} \cdot d \cdot \pi }{\dot{m} \cdot c_{p}} \cdot x \end{aligned}$$
(3)
Fig. 8
figure 8

The numerical and theoretical values of the difference between the averaged outlet and inlet temperature

Full size image

The average fluid temperature at the outlet approaches asymptotically the inlet temperature of \(30\,^{\circ }\text {C}\) at high flow velocities. For this configuration, the average temperature in the contact surface approaches a limit value of approximately \(42{.}5\,^{\circ }\text {C}\). Figure 9 shows an analysis of the average temperature \(T_{\text {avg}}\) and the average coolant temperature at the outlet normalized to the respective reference \(T_{\text {ref}}\) at \(v=1{.}21\,\text {m/s}\). This demonstrates that the temperature at the outlet is slightly less affected by a change in the flow velocity compared with the averaged temperature in the contact surface.

Fig. 9
figure 9

Average temperature in the contact surface and at the outlet (normalized to the reference at \(v=1{.}21\,\text {m/s}\)) as a function of flow velocity at \(13400\,\text {W/m}^{2}\) in an empty cooling channel

Full size image

4.2 Influence of the static mixer number and the static mixer distance

In order to improve the heat transfer, static helical mixers are inserted into the cooling channel in various configurations. The employed static mixers have a length of \(26\,\text {mm}\) and a material thickness of \(0{.}58\,\text {mm}\), cf. Fig. 10. They are basically built up from two metallic strips which are twisted \(180^{\circ }\) and reassembled with alternating orientation.

Fig. 10
figure 10

Static helical mixers — single element and location in the cooling channel

Full size image

The static mixers with a diameter of \(8\,\text {mm}\) are used to avoid the gap between the static mixers and the cooling channel wall. In all cases, the static mixers are placed at an equal mutual distance of h. The distance of \(10\,\text {mm}\) from the first static mixer to the inlet is the same in all configurations. The same flow velocities as in Section 4.1 are used for the simulations.

Fig. 11
figure 11

Contact surface temperature as a function of the velocity (normalized to the value of the respective variant at \(v=1{.}21\,\text {m/s}\))

Full size image

Figure 11 shows the change in the average temperature in the contact surface for all variants \(T_{\text {avg,i}}\). Please note that for the sake of comparability, all results are normalized to the value of the reference variant at \(v=1{.}21\,\text {m/s}\) in each case \(T_{\text {avg,ref,i}}\). This shows that the use of static mixers strongly reduces the dependence on the flow velocity. For the empty cooling channel, a reduction of the velocity to \(0{.}1\,\text {m/s}\) increases the temperature by \(52\,\%\) compared to the reference value at \(1{.}21\,\text {m/s}\). In contrast, the 13 static mixer variant shows a change of only \(18\,\%\) to the reference set. The same applies to the case of an increase in the velocity to \(6\,\text {m/s}\). This results in a decrease of about \(5\,\%\) for the empty cooling channel. The variant with 13 static mixers amounts to only \(2\,\%\). In this observation, the variant with only one static mixer near the inlet shows a comparatively small difference to the empty cooling channel.

Fig. 12
figure 12

Average temperature in the contact surface (normalized to the value of the empty cooling channel at the respective velocity) as a function of the flow velocity at \(13400\,\text {W/m}^{2}\)

Full size image

Figure 12 presents the results of the average temperature in the contact surface \(T_{\text {avg}}\) normalized to the value of the empty cooling channel \(T_{\text {avg,empty}}\) at the respective velocity. The use of static mixers gives a maximum improvement (i.e., decrease) in the average temperature of around \(4\,\%\) relative to the reference at a velocity of \(1{.}21\,\text {m/s}\). This applies to a similar effect for the variants with 7 and 13 static mixers. In the configuration with one static mixer, there is no further decrease at this Reynolds number. This also applies to increasing the flow rate of the coolant. At a velocity of \(3\,\text {m/s}\), there are almost no noticeable differences in the average temperatures compared to the empty cooling channel. This result is due to the strong turbulence within the pipe flow, which is already present in the empty cooling channel at high flow velocities. An additional increase in turbulence due to static mixers has no significant effect on heat transfer, which is also reported in the literature [21, 25]. Significant advantages can be seen in a laminar or low turbulent flow range. For example, 13 static mixers at a flow velocity of \(v=0{.}5\,\text {m/s}\) and a Reynolds number of \(\text {Re}=4132\) can reduce the temperature by \(9\,\%\). At a flow velocity of \(v=0{.}1\,\text {m/s}\) and a Reynolds number of \(\text {Re}=826\), even \(25\,\%\) can be achieved. Compared to the average temperature in the contact surface, clear advantages of the static mixers are shown regarding the maximum temperature difference \(\Delta T\) within the contact surface, cf. Eq. 4 and Fig. 13. In this equation, \({T}_{\text {min}}\) represents the minimum and \(T_{\text {max}}\) the maximum temperature in the contact surface, respectively.

$$\begin{aligned} \Delta T = {T}_{\text {max}}-{T}_{\text {min}} \end{aligned}$$
(4)

Regarding this parameter, the static mixers generate a significant decrease on \(\Delta T\) and a homogenization of the temperature profile. With a Reynolds number of 9633, a temperature difference of \(1{.}2\,\%\) reduction is possible by using 4 static mixers. The improvement is more pronounced when 7 static mixers are used. In this case, the temperature difference \(\Delta T\) is reduced from \(1{.}23\,\text {K}\) to \(0{.}86\,\text {K}\), resulting in an improvement of \(29{.}8\,\%\). An exception in this consideration is the single static mixer configuration. Due to the single static mixer near the inlet, the temperature of the surface in the inlet region is significantly reduced locally. However, there is almost no change on the outlet side. This results in a considerably more inhomogeneous temperature distribution within the contact surface and a temperature difference of \(2{.}28\,\text {K}\), which is \(86\,\%\) higher.

Fig. 13
figure 13

Temperature distribution in the contact surface in \(^{\circ }\)C (\(1{.}21\,\text {m/s}\), \(\dot{q}=13400\,\text {W/m}^{2}\))

Full size image

4.3 Influence of the heat flux and the specific thermal conductivity of the mold steel

After investigating the influence of velocity and static mixer configuration (quantity and distance) at a heat flux of \(13400\,\text {W/m}^{2}\), the heat flux is now also varied at different flow velocities. This allows an approximate consideration of, for example, changes in the polymer layer, such as the thickness of the layer, initial temperature, and specific heat capacity. The additional heat flux makes the effect between the variants more obvious.

Fig. 14
figure 14

Normalized average temperature in the contact surface at a flow velocity of \(1{.}21\,\text {m/s}\)

Full size image

Figure 14 shows the normalized values of the average contact surface temperature \(T_{\text {avg,i}}/T_{\text {avg,empty}}\) at a flow velocity of \(1{.}21\,\text {m/s}\) and heat fluxes of \(13400\,\text {W/m}^{2}\), \(30000\,\text {W/m}^{2}\) and \(60000\,\text {W/m}^{2}\). Independent of the heat fluxes, it can be observed that by increasing the number of static mixers, the average contact surface temperature decreases. The effect is more noticeable at low Reynolds numbers.

Fig. 15
figure 15

Normalized average temperature in the contact surface at a flow velocity of \(0{.}5\,\text {m/s}\)

Full size image
Fig. 16
figure 16

Normalized average temperature in the contact surface at a flow velocity of \(6\,\text {m/s}\)

Full size image

As depicted in Fig. 15, at a flow velocity of \(0{.}5\,\text {m/s}\) and a heat flux of \(60000\,\text {W/m}^{2}\), there is a temperature reduction of up to \(17\,\%\). At a heat flux of \(13400\,\text {W/m}^{2}\) this is up to \(7\,\%\). In contrast, the differences at high heat fluxes decrease significantly between the high flow rate variants. At a flow velocity of \(6\,\text {m/s}\), no significant differences can be observed, cf. Fig. 16. The maximum improvement for the 13 static mixer variants is only approximately \(1{.}5\,\%\). The last influencing variable to be changed as part of the steady-state investigation is the thermal conductivity of the mold steel used. Higher specific thermal conductivity enhances heat transfer from the contact surface to the cooling channel. This results in lower temperatures on the contact surface, whereas a lower specific thermal conductivity will result in significantly higher temperatures. Figure 17 shows an example of this relationship for the empty cooling channel at a flow velocity of \(1{.}21\,\text {m/s}\) and a heat flux of \(30000\,\text {W/m}^{2}\). The reference for normalization is the model without static mixers with the initial specific thermal conductivity of \(\lambda _{0} = 28\,\text {W/(m K)}\).

Fig. 17
figure 17

Normalized average temperature in the contact surface (empty cooling channel variant) relative to the value at \(\lambda _{0}=28\,\text {W/m}^{2}\)

Full size image

The temperature reduction associated with the increased specific thermal conductivity can be further improved by including static mixers. This applies in particular to high values of thermal conductivity. At \(\lambda =56\,\text {W/(m K)}\), \(\dot{q}=30000\,\text {W/m}^{2}\), \(v=1{.}21\,\text {m/s}\), an additional reduction of about \(7\,\%\) compared to the reference configuration (empty cooling channel) can be achieved by using 13 static mixers. Figure 18 shows the ratio of the contact surface temperatures of individual variants to the reference contact surface temperature of the empty cooling channel at the respective thermal conductivity.

Fig. 18
figure 18

Average temperature in the contact surface (normalized on the empty cooling channel) as a function of specific thermal conductivity at a flow velocity of \(1{.}21\,\text {m/s}\) and a heat flux of \(30000\,\text {W/m}^{2}\)

Full size image

The results indicate that the static mixers have a great impact on the heat transfer enhancement when a boundary layer with a higher temperature is formed on the wall in an empty cooling channel. As shown in Fig. 19, the static mixers break up this boundary layer. This is caused as a result of the turbulence generated by the static mixers and effects in a homogenization of the temperature distribution in the coolant. The resulting increased temperature gradient between coolant and mold improves the heat transfer.

Fig. 19
figure 19

Temperature profile at the outlet (\(v=1{.}21\,\text {m/s}\); \(\dot{q}=60000\,\text {W/m}^{2}\)) — without static mixers (left) and with 13 static mixers (right)

Full size image

4.4 Comparison to the transient simulations

After the steady-state preliminary investigations, selected variants are examined in more detail with a transient simulation. In addition to the steady-state individual values, the time curves of individual variables can also be observed. These can give indications of a possible reduction in the cycle times. Figure 20 shows the comparison of the time histories of the volume-averaged melt temperature \(T_{\text {melt}}\) of the reference model \(T_{\text {melt,ref}}\) without static mixers with that of the 7 static mixer variant at a Reynolds number of 9633. With this configuration, a \(1{.}28\,\text {K}\) lower temperature at the end of the 15 cycles can be achieved by using static mixers. This corresponds to a reduction of the temperature of around \(3\,\%\). This result corresponds to the forecasts of the steady-state simulations for this flow velocity (cf. Section 4.2). Now, the demolding temperature \(T_{\text {melt}}\) after cycle 15 of about \(41\,^{\circ }\text {C}\) is considered as the target temperature to observe the possibility of cycle time reduction. This objective temperature is already reached about \(3{.}5\,\text {s}\) earlier with the 7 static mixer variant, cf. Fig. 20. Due to the nonlinearity of the melt temperature evolution in all cycle profiles, a conservative reduction of \(10\,\%\) from \(20\,\text {s}\) to \(18\,\text {s}\) is investigated.

Fig. 20
figure 20

Evolution of the melt temperature at the end of the last cycle (empty cooling channel and 7 static mixer variant)

Full size image

This assumption is verified by another transient simulation of the 7 static mixer variant with a reduced cycle time of \(18\,\text {s}\). The results of this simulation are shown in Fig. 21. It can be seen that after 15 cycles, only minor differences of \(0{.}12\,\text {K}\) (\(\approx 0{.}3\,\%\)) in the demolding temperature are discernible. The same applies to the surface area’s minimum and maximum wall temperatures. With the selected boundary conditions, the 7 mixer variant with a reduced cycle time of \(18\,\text {s}\) and the reference with the cycle time of \(20\,\text {s}\) can be regarded as approximately equivalent.

Fig. 21
figure 21

Evolution of the melt temperature at the end of the last cycle (empty cooling channel, 7 static mixer variant for a \(20\,\text {s}\) cycle, 7 static mixer variant for a \(18\,\text {s}\) cycle)

Full size image

In addition to the possible reduction of the cycle time, which only can be investigated within the framework of the transient simulation methodology, the results also confirm the predictions of the steady-state preliminary investigations. The temperature difference in the mold-melt contact surface at the end of the last cycle is reduced by \(26{.}6\,\%\) (cycle time \(20\,\text {s}\)) and \(21{.}5\,\%\) (cycle time \(18\,\text {s}\)) when using 7 static mixers. The steady-state simulation for 7 static mixers and a heat flux of \(13400\,\text {W/m}^{2}\) suggest a possible improvement of \(43{.}6\,\%\). As pointed out in Section 3.2, this value can be considered as the average of the whole time course and not as a single value at the end of the cycle. Taking this into account, the steady-state result is in good agreement with the transient simulations. The transient investigation of the melt temperature at different flow velocities of the 7 static mixer variant and the reference also confirm the results of the steady-state preliminary investigations. Figure 22 shows the average temperature of the melt at the end of the fifteenth cycle (each with a duration of \(20\,\text {s}\)) for the 7 static mixer variants and different flow velocities. The results show that a change in flow velocity has relatively little effect on the static mixer variant compared to the reference. The reduction of the velocity from \(1{.}21\,\text {m/s}\) to \(0{.}5\,\text {m/s}\) results in an absolute temperature increase of only \(1{.}4\,\text {K}\). In the same case, an increase of almost \(3\,\text {K}\) is observed for the reference. Considering the average temperature of the contact surface in the steady-state analysis, similar results were obtained, cf. Section 4.2 and Fig. 11.

Fig. 22
figure 22

Comparison of an empty cooling channel to static mixer variants with different flow velocities at the end of the last cycle

Full size image

Both transient and steady-state simulations indicate the advantages of using static mixers in the considered configuration. In addition, the static mixers ensure homogenization of the temperature distribution in the contact surface. This positively affects the surface quality of the polymer component [17, 31]. However, the effect of the numerically determined advantages in real injection molds depends strongly on the geometry of the cooling channel. Changes in direction or kinks in the cooling channel can lead to increased turbulence, similar to static mixers, thus improving heat transfer. This would reduce the benefit of static mixers. In addition, the pressure loss in the cooling channel induced by the static mixer was not considered in this study. Depending on the static mixer configuration, this can be considerable and result in significantly increased energy requirements for the coolant pump.

5 Conclusion and outlook

In the scope of this contribution, the impact of all relevant layout parameters for machine tools was investigated by means of extensive numerical studies. The obtained numerical results clearly demonstrate that general statements on the performance of static mixers for the heat transfer enhancement in mold cooling are not possible. It is always crucial to take into account the individual boundary conditions, such as the mold material, thermal loading regime in terms of cycle times and values of heat fluxes from the machine process, and the thermal-hydraulic properties of the cooling system. The configuration of the cooling system is extremely important in order to decide what type of method of heat transfer enhancement is suitable. For complicated cooling channel geometries with many redirections as well as for turbulent flow regimes, the effect of static mixers on the heat transfer enhancement is very limited and usually does not overweigh the induced additional pressure loss. In straight cooling channels with long inlet sections as well as laminar flow regimes, static mixers can lead to a significant enhancement of the convective heat transfer. In the presented case of injection molding, even slight temperature gains in mold temperature can lead to a drastic reduction in cycle times due to the nonlinear nature of the injected polymer cooling. Please note that the longer the cycle time the greater effect can be achieved by means for heat transfer enhancement. From an economic point of view, even small reductions in the cycle time have an enormous impact on the effectiveness of the production process.

The obtained results are not restricted to injection molding processes. Moreover, the findings may serve as decision criteria for the application of static mixers in other convective cooling settings as well as other types of machine tools.

The plausibility of the results was verified by agreement with analytical models in Section 4.1. An additional experimental validation is therefore not necessary and would go far beyond the scope of this contribution. From a technical point of view, a set up for a thorough experimental validation would be very costly, laborious and not effective, because clearly specified and reproducible heat fluxes, mold materials, etc. with spatially homogeneous characteristics cannot be provided. Furthermore, it is not possible to measure the spatial distribution of temperature within the cavity during the injection molding process. The only plausible perspective for an experimental validation is a point-wise temperature measurement within the mold body including Kalman filter techniques in order to estimate the spatial temperature distribution, cf. [33].