Skip to main content
SpringerLink
Log in

Study on temperature of cylindrical wet grinding considering lubrication effect of grinding fluid

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

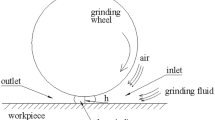
Abstract

The improved cylindrical wet grinding temperature (ICWGT) model considering the lubrication effect of the grinding fluid is established and solved numerically. In doing so, the Newton–Raphson method is used to solve the hydrodynamic pressure of grinding fluid, and the fast Fourier transform (FFT) method is employed to accelerate the deformation calculation. Furthermore, the convective heat transfer coefficient (CHTC) is calculated based on the heat transfer theory, and the moving heat source method is adopted to obtain the grinding temperature. Meanwhile, the effectiveness of ICWGT is verified through the grinding temperature measurement experiment of alloy steel. Then, the cylindrical wet grinding temperature for alloy steel considering the lubrication effect of grinding fluid is studied and compared at varied grinding process parameter, and some rules are revealed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Data availability

All data supporting the findings of this study are included in this article.

Code availability

The method codes involved in this paper are not applicable.

Abbreviations

a gmax :

Undeformed chip thickness (mm)

B w, B s :

Widths of workpiece and wheel (mm)

c f , c s , c w :

Specific heat capacities of grinding fluid, wheel, and workpiece (J/(kg·K))

C :

Ratio of the chip width to chip thickness

d g :

Equivalent diameter of abrasive grain (mm)

D s , D w :

Diameters of wheel and workpiece (mm)

E s, E w :

Young’s moduli of wheel and workpiece (GPa)

f r :

Radial infeed fate of wheel (mm/min)

F n, F t :

Normal grinding force and tangential grinding force (N)

h, h c :

Local and central grinding fluid thicknesses (μm)

h f, h w :

Convection heat transfer coefficients of grinding fluid and workpiece (W/(m2·K))

i, j, k :

Discrete position indexes along x-, y- and z-directions

k f, k s, k w :

Thermal conductivities of grinding fluid, wheel, and workpiece (W/(m·K))

l c :

Real contact arc length (mm)

n w :

Speed of workpiece (r/min)

N d :

Active grits number per unit area

N x, N y :

Numbers of grid nodes along x- and y-directions

O-xyz :

Global coordinate system

p :

Hydrodynamic pressure of grinding fluid (MPa)

q ch, q f :

Heat flux into the chips and grinding fluid (W/mm2)

q s, q w :

Heat flux into the grinding wheel and workpiece (W/mm2)

r 0 :

Effective contact radius of grains (mm)

R r :

Roughness factor of wheel

R x, R y :

Equivalent curvature radii of workpiece and grinding wheel along the x- and y-directions (mm)

R w :

Heat partition ratio of workpiece

R wch , R ws :

Workpiece-chip partition ratio and workpiece-wheel partition ratio

u e :

Entrainment velocity of grinding fluid (m/s)

U :

Velocity of grinding fluid along x-direction (m/s)

v :

Total elastic deformation

U a :

Average speed of grinding fluid (m/s)

v s :

Speed of grinding wheel (m/s)

x s, x e :

Starting and end positions of computation domain in x-direction

y s, y e :

Starting and end positions of computation domain in y-direction

α w :

Thermal diffusivities of workpiece (m2/s)

β w, β f :

Thermal property parameters for workpiece and grinding fluid (m2/s)

υ s , υ w :

Poisson’s ratios of wheel and workpiece

θ :

Half apex angle of abrasive grain (°)

φ :

Shear angle (°)

γ :

Shear strain

\({\rho }_{f}\) :

Density of grinding fluid (kg/m3)

\({\eta }_{f}\) :

Viscosity of grinding fluid (Pa·s)

\({\omega }_{p}\) :

Pressure relaxation factor

\({\omega }_{F}\) :

Load relaxation factor

References

  1. Rowe WB (2009) Principles of modern grinding technology. William Andrew Publishing, USA

    Google Scholar 

  2. Lin B, Zhou K, Guo J, Liu QY, Wang WJ (2018) Influence of grinding parameters on surface temperature and burn behaviors of grinding rail. Tribol Int 122:151–162

    Article  Google Scholar 

  3. Jaeger JC (1942) Moving sources of heat and the temperature at sliding contacts. J Proc Roy Soc New South Wales 76:203–204

    Google Scholar 

  4. Desruisseaux NR, Zerkle RD (1970) Temperature in semi-infinite and cylindrical bodies subjected to moving heat sources and surface Cooing. J Heat Trans 92:456–464

    Article  Google Scholar 

  5. Kim NK, Guo C, Malkin C (1997) Heat flux distribution and energy partition in creep-feed grinding. CIRP Ann Manuf Technol 46:227–232

    Article  Google Scholar 

  6. Jin T, Stephenson DJ (2006) Heat flux distributions and convective heat transfer in deep grinding. Int J Mach Tools Manuf 46:1862–1868

    Article  Google Scholar 

  7. Li BZ, Zhu DH, Pang JZ, Yang JG (2011) Quadratic curve heat flux distribution model in the grinding zone. Int J Adv Manuf Technol 54:931–940

    Article  Google Scholar 

  8. Lavin AS (1998) A simple model for convective cooling during the grinding process. J Eng Ind 110:1–6

    Article  Google Scholar 

  9. Miao Q, Li HN, Ding WF (2020) On the temperature field in the creep feed grinding of turbine blade root: Simulation and experiments. Int J Heat Mass Tran 147:118957-1–119013

    Article  Google Scholar 

  10. Rowe WB, Morgan MN, Allanson DR (1991) An advance in the modelling of thermal effects in the grinding process. CIRP Ann Manuf Technol 40:339–342

    Article  Google Scholar 

  11. Zhang L, Rowe WB, Morgan MN (2013) An improved fluid convection solution in conventional grinding. Proc Inst Mech Eng B J Eng Manuf 227:832–838

    Article  Google Scholar 

  12. Lin B, Morgan MN, Chen XW, Wang YK (2009) Study on the convection heat transfer coefficient of coolant and the maximum temperature in the grinding process. Int J Adv Manuf Technol 42:1175–1186

    Article  Google Scholar 

  13. Chang CC (1997) An application of lubrication theory to predict useful flow-rate of coolants on grinding porous media. Tribol Int 30:575–581

    Article  Google Scholar 

  14. Jin T, Stephenson DJ, Rowe WB (2003) Estimation of the convection heat transfer coefficient of coolant within the grinding zone. Proc Inst Mech Eng B J Eng Manuf 217:397–407

    Article  Google Scholar 

  15. Li CH, Mao W, Hou YL, Ding YC (2011) Investigation of hydrodynamic pressure in high-speed precision grinding. Procedia Eng 15:2809–2813

    Article  Google Scholar 

  16. Hryniewicz P, Szeri AZ, Jahanmir S (2001) Application of lubrication theory to fluid flow in grinding: part I—flow between smooth surfaces. J Tribol 123:94–100

    Article  Google Scholar 

  17. Hryniewicz P, Szeri AZ, Jahanmir S (2001) Application of lubrication theory to fluid flow in grinding: Part II—influence of wheel and workpiece roughness. J Tribol 123:101–107

    Article  Google Scholar 

  18. Meng FM, Cui XF, Pu C (2019) Effect of three-dimensional surface crack on the elastohydrodynamic lubrication performance of ellipsoid contact. Proc Inst Mech Eng J J Eng Tribol 233:975–991

    Article  Google Scholar 

  19. Liu SB, Wang QJ, Liu G (2000) A versatile method of discrete convolution and FFT (DC-FFT) for contact analyses. Wear 243:101–111

    Article  Google Scholar 

  20. Meng FM (2013) On influence of cavitation in lubricant upon tribological performances of textured surfaces. Opt Laser Technol 48:422–431

    Article  Google Scholar 

  21. Rowe WB, Qi HS, Morgan MN, Zhang HW (1993) The effect of deformation in the contact area in grinding. CIRP Ann Manuf Technol 42:409–412

    Article  Google Scholar 

  22. Zhu XH (1988) Grinding principle. China Machine Press, Beijing

    Google Scholar 

  23. Li GF, Wang LS (2001) Simulation and optimum for plunge grinding. Key Eng Mater 202–203:219–226

    Article  Google Scholar 

  24. Black SCE (1996) The effect of abrasive properties on the surface integrity of ground ferrous materials. Doctoral thesis, Liverpool John Moores University, Liverpool

  25. Rowe WB (2017) Temperatures in grinding-a review. J Manuf Sci E 139:121001-1–121006

    Google Scholar 

  26. Jin T, Stephenson DJ (2006) Analysis of grinding chip temperature and energy partitioning in high-efficiency deep grinding. Inst Mech Eng B J Eng Manuf 220:615–625

    Article  Google Scholar 

  27. Thanedar A, Dongre GG, Joshi SS (2019) Analytical modelling of temperature in cylindrical grinding to predict grinding burns. Int J Precis Eng Man 20:13–25

    Article  Google Scholar 

  28. Rowe WB, Black S, Mills B, Qi MNMS (1997) Grinding temperatures and energy partitioning. P Roy Soc A 453:1083–1104

    Article  Google Scholar 

  29. Bai XY, Dong QB, Zheng H, Zhou K (2021) Modelling of non-Newtonian starved thermal-elastohydrodynamic lubrication of heterogeneous materials in impact motion. Acta Mech Solida Sin 34(6):954–976

    Article  Google Scholar 

  30. He D, Dong QB, Zhao G (2021) Modeling mixed lubrication in point and line contact by non-normalized discretization. Int J Appl Mech 13(07):2150080-1-23

  31. Bai XY, Dong QB, Zheng H, Zhou K (2021) A finite element model for non-Newtonian starved thermal-elastohydrodynamic lubrication of 3D line contact. Int J Appl Mech 13(09):2150107-1-32

  32. Dong QB, Zhou K (2015) Modeling heterogeneous materials with multiple inclusions under mixed lubrication contact. Int J Mech Sci 103:89–96

    Article  Google Scholar 

  33. Sakakura M, Ohnishi T, Shinoda T (2012) Temperature distribution in a workpiece during cylindrical plunge grinding. Prod Eng Res Devel 06:149–155

    Article  Google Scholar 

  34. Nie ZG, Wang G, Wang LP, Rong YM (2019) A coupled thermomechanical modeling method for predicting grinding residual stress based on randomly distributed abrasive grains. J Manuf Sci E 141:081005-1–81012

    Google Scholar 

  35. Mihić SD, Cioc S, Marinescu ID, Weismiller MC (2013) Detailed study of fluid flow and heat transfer in the abrasive grinding contact using computational fluid dynamics methods. J Manuf Sci E 141:041002-1–41012

    Google Scholar 

  36. Pang JZ, Wu CJ, Shen YM, Liu SQ, Wang QG, Li PZ (2019) Heat flux distribution and temperature prediction model for dry and wet cylindrical plunge grinding. Proc Inst Mech Eng B J Eng Manuf 233:2047–2060

    Article  Google Scholar 

  37. Ding ZS, Jiang XH, Guo MX, Liang SY (2018) Investigation of the grinding temperature and energy partition during cylindrical grinding. Int J Adv Manuf Technol 97:1767–1778

    Article  Google Scholar 

  38. Yin GX, Marinescu ID (2017) A Heat transfer model of grinding process based on energy partition analysis and grinding fluid Cooling application. J Manuf Sci E 139:121015–121111

    Article  Google Scholar 

  39. Zhang L, Rowe WB (2020) Study of convective heat transfer in grinding applied to tool carbide. J Manuf Sci E 142:021001–021009

    Article  Google Scholar 

  40. Yi J, Jin T, Zhou W, Deng ZH (2020) Theoretical and experimental analysis of temperature distribution during full tooth groove form grinding. J Manuf Process 58:101–115

    Article  Google Scholar 

Download references

Funding

This study was supported by the National Natural Science Foundation of China (Nos. 52175160 and 51975381), and the Research and Innovation Projects of Graduate Students in Chongqing City (No. CYS19003).

Author information

Authors and Affiliations

  1. The State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing, 400044, China

    Yong Zheng, Changqing Wang, Yifei Zhang & Fanming Meng

  2. Harbin Dong’an Engine Co., Ltd., Harbin, 150066, Heilongjiang, China

    Changqing Wang

Authors
  1. Yong Zheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Changqing Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yifei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Fanming Meng
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Yong Zheng: investigation, methodology, software, validation, data curation, writing—review and editing. Changqing Wang: investigation, software, data curation, writing—original draft. Yifei Zhang: investigation, formal analysis, visualization. Fanming Meng: conceptualization, funding acquisition, project administration, supervision, writing—review and editing.

Corresponding author

Correspondence to Fanming Meng.

Ethics declarations

Ethics approval

The authors declare that this manuscript was not submitted to more than one journal for simultaneous consideration. The submitted work is original and has not been published elsewhere in any form or language.

Consent to participate and publish

The authors declare that they consent to participate in and publish this paper.

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zheng, Y., Wang, C., Zhang, Y. et al. Study on temperature of cylindrical wet grinding considering lubrication effect of grinding fluid. Int J Adv Manuf Technol 121, 6095–6109 (2022). https://doi.org/10.1007/s00170-022-09658-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-022-09658-3

Keywords

Search

Navigation