Geometrical process design during continuous generating grinding of cutting tools

Abstract

Modern cutting tools like end mills, drilling tools, and reamers underlie high requirements regarding geometrical accuracy, cutting edge quality, and production costs. However, the potential for process optimization is limited due to the process kinematics during grinding. Consequently, a novel tool grinding process for the manufacture of cutting tools has been developed recently at the Institute for Production Engineering and Machine Tools (IFW). This continuous generating grinding process allows the simultaneous production of all flutes and circumferential flank faces of rotational symmetrical cutting tools. The present paper focuses on the geometrical process design and develops a method to determine the necessary basic rack and process parameters in order to create a desired cutting edge geometry by continuous generating grinding. The developed method can define all parameters with an accuracy of up to 5 µm and 0.2° within a simulation in five iteration steps and allows not only the quantitative design of the cutting tool geometry but a qualitative modification of the flute geometry as well. Subsequently performed grinding tests showed that the presented method allows the design of grinding worms for continuous generating grinding of cutting tools and enables the successful implementation of these processes.

1 Introduction

The production of modern precision tools like end mills, drilling tools, reamers, or saw blades from cylindrical blanks requires several different process steps during grinding. Usually, the different flutes of the mentioned cutting tools are manufactured subsequently by using 1A1- or 1V1-shaped grinding wheels that move parallel to the axis of the cutting tool. The disadvantages of this conventional tool grinding process are the auxiliary process times due to the necessary movements of the grinding tool between the machining of subsequent flutes and the requirement of different tools for the production of the flank and rake faces [1]. Consequently, the process kinematic limits the productivity of the manufacturing process. The discontinuous machining of the cutting edges may reduce the pitch accuracy of the ground cutting tool.

To understand the mechanisms of these discontinuous tool grinding processes and increase the productivity of these processes, a wide range of different investigations has been performed in the literature. The optimization of grinding tool properties is one approach chosen in the literature to investigate the points mentioned above. Such investigation often includes an application-specific choice of the grinding tool bond [2,3,4], an optimization of the bond properties [5,6,7,8], or optimization of the properties of the used abrasive and their distribution in the bond [9, 10]. Optimization of the tool grinding process design poses another research field in this context. This includes investigations of the influence of the chosen process parameters on cutting edge quality [1, 11,12,13] as well as investigations of the influence of these parameters and the single grain chip thickness on residual stress states resulting from these tool grinding processes [14]. The resulting residual stress states of the cutting tools can be used as a measure for the mechanical and thermal loads in the grinding process [15, 16] and are relevant for subsequent coating processes [16, 17] and for the tool life [3, 18]. But despite the efforts in the literature to increase the productivity of tool grinding processes, the processing time of flute grinding, which depends on the process kinematics, continues to be the largest economic cost factor of discontinuous tool grinding processes.

The same disadvantages as mentioned for the discontinuous grinding of cutting tools also occur during discontinuous profile grinding of gears due to similar process kinematics. However, an alternative process kinematic, namely the continuous generating gear grinding, has been established to produce gears in large badge sizes during the last century. This process imitates the kinematics in a gear worm drive (Fig. 1) and allows very high production rates and an increased surface quality due to wear compensation by shifting the grinding worm [19]. A transfer of continuous generating grinding processes to the manufacturing of cutting tools would therefore pose a possibility for a significant increase in productivity for tool grinding processes, as this would address the existing limitations concerning the process kinematics. But the possibility of transferring continuous generating grinding processes to tool grinding processes has not yet been extensively investigated or transferred to industrial practice.

Fig. 1

Process kinematics during continuous generating grinding [19]

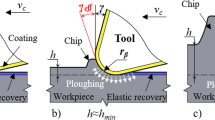
However, recent publications have shown that the continuous generating grinding process can be used to produce rotationally symmetric cutting tools [20, 21]. An adaptation of the grinding worm’s basic rack and the process parameters allows the creation of the undercut at the rake face and simultaneously the creation of a flank face with an adjustable orthogonal clearance (Fig. 2). Thus, the flutes and the circumferential cutting edges of most industrial available cutting tools with equal pitch may be produced by the novel continuous generating grinding process. Consequently, neither the utilization of different grinding tools nor auxiliary process times for the repositioning of the grinding tool between the manufacture of different flutes nor cutting edges are necessary. Therefore, these factors pose a further addition to the possible increase of the productivity of tool grinding processes which could be realized by a transfer of continuous generating grinding processes to tool grinding processes.

Fig. 2

Engagement conditions near the cutting edge during continuous generating grinding of cutting tools [21]

But the geometrical process design of continuous generating grinding processes is very challenging since several different process parameters and the basic rack of the grinding worm have a significant influence on the resulting geometry of the cutting tool.

Although there are already simulation-based studies in the literature aiming to understand, improve and design continuous generating grinding processes of gears [22,23,24,25,26,27,28,29,30,31], such studies have not been carried out for transferring continuous generating grinding processes to tool grinding. For this reason, a user-independent method for a geometrical process design of continuous generating grinding processes of cutting tools is currently not available. But since the availability of such a method is essential to make the use of continuous generating grinding processes for the manufacture of cutting tools possible, the lack of such a method is an obstacle to the exploitation of the above-mentioned potentials for increasing productivity in tool grinding. Therefore, this paper investigates and presents a method that allows the determination of all relevant processes and basic rack parameters to produce a desired cutting edge geometry of a cutting tool to be machined by continuous generating grinding.

The paper is organized as follows: Firstly, Sect. 2 presents the experimental setup of this study, including the simulation tool used, the grinding and dressing tools, and the machine tool, as well as the measuring equipment. Section 3 then starts with a description of the basics and the parameters of the method for the geometrical process design in Sect. 3.1. Subsequently, the necessity to use dampening factors and their design is explained in Sect. 3.2 before the usability of the method for its intended purpose is checked in Sect. 3.3. After that, the applicability of the presented method for the design of continuous generating grinding processes of cutting tools is validated via grinding experiments in Sect. 3.4. Finally, all results are concluded in Sect. 4.

2 Experimental setup

The current paper focuses on the theoretical analysis of the novel tool grinding process. Due to the complex process kinematics and engagement conditions during continuous generating grinding, solely analytical approaches are not expedient. Thus, a numerical material removal simulation called IFW-CutS is utilized to determine the interrelationship between the process parameters, the basic rack of the grinding worm, and the resulting geometry of the cutting tool. This simulation works dexel-based and allows one to imitate whole machine tools, including their axes movements by evaluating machine-readable NC-Code [32]. In the present case, a WALTER Helitronic Vision 400-L tool grinding machine is represented in the simulation environment. The grinding worm is parameterized by the basic rack after [20, 21] (Fig. 3) and cuts the workpiece, which is discretized in all directions in space by 1024 dexels each. This leads the investigated tools with a diameter of 10–12 mm to a maximum dexel distance of d_x = d_z = 11.7 µm. This maximum geometrical error of the simulation is further reduced by rotating the dexels about 45° around the cutting tool axis. This rotation of the dexels reduces the maximum geometric error because, as a result of the rotation of the dexels, no dexels are aligned parallel or perpendicular to the workpiece axis. This reduces potential sampling errors in the simulation and thus increases its accuracy, especially at undercuts and steep geometry sections of the workpiece, such as the tooth flanks of the workpiece. Furthermore, a time step of t_s = 100 µs is utilized for all simulations as proposed in [20, 21], and the sweep volume of the grinding worm path is calculated. That means that the grinding worm path between the mentioned time steps is also considered for the calculation of the material removal. Taking into account the aforementioned dexel resolution, the measures taken result in a geometrical error of the final cutting tool geometry of less than 5 µm.

Fig. 3

Basic rack for the production of cutting tools with adjustable orthogonal clearance [20]

After performing the simulation in IFW-CutS, the resulting dexel-field is exported to a MATLAB script, which evaluates the geometry of the cutting tools. This includes the rake angle, the orthogonal clearance, and the inner and outer diameter of the ground tool. Furthermore, the cross-section of the workpiece is presented to allow the investigation of qualitative changes regarding flute geometry.

In addition, an NC code for the continuous generating grinding of the simulated tools on the Walter Helitronic Vision 400 L is generated via IFW-CutS to validate the applicability of the investigated method for the manufacturing of milling tools by continuous generating grinding. The respective grinding experiments are performed with a grinding wheel with vitrified bond and CBN with a grain size of 64 µm (B64) as abrasive (29B 64 M4 V242 150, Hermes Schleifmittel GmbH). A cutting speed of 23 m/s and a feed of 1 µm are used in the process. The grinding worm geometry is generated via a dressing process. The dressing process is performed in two steps with a dressing spindle (C72FCA2, Dr. Kaiser Diamantwerkzeuge GmbH & Co. KG) that is integrated into the tool grinding machine. In the first dressing step, rough machining is performed with a CVD diamond form roll of the type NC10-C-150–2-1.5-R1-40–12-TK (Dr. Kaiser Diamantwerkzeuge GmbH & Co. KG). Subsequently, finishing is done in the second dressing step with a CVD diamond form roll of the type NC40-C-150-R0.25-W40-12-TK (Dr. Kaiser Diamantwerkzeuge GmbH & Co. KG). Both process steps are performed with a feed velocity of the rotational axis of 95,000°/min, a cutting speed of the grinding tool of v_cd = 1.38 m/s, and a dressing speed ratio of q_d = 32.4. The profile of the grinding worm is divided into lines for the dressing processes, which are then machined with a step size of Δx_d = 60 µm (horizontal) and Δy_d = 8 µm (vertical). In the grinding tests, steel of type 1.3343 is used as workpiece material. A Leitz PMM 866 coordinate measuring machine is used to measure the geometry of the grinding worm after dressing and after the grinding experiments. The geometry of the manufactured cutting tool is investigated via a Walter HeliCheck transmitted-light microscope and a Zeiss EVO 60 VP scanning electron microscope.

3 Results & discussion

3.1 Parameters and basics of the method

Cutting tools, i.e., end mills and their cutting wedge, are generally defined by the characteristic values rake angle γ, clearance angle α, core (d_k), and outer diameter (d). Those values may be manipulated by different process variables and grinding worm parameters during continuous generating grinding. To identify all parameters that have a significant influence on the mentioned parameters and thus are suitable to create the desired geometry of the ground cutting tool, preliminary simulations have been performed [21]. The results of these simulations for the rake angle are shown in Fig. 4. The results show that the module directly influences the core and outer diameter of the cutting tool. However, the ratio of both diameters stays constant when varying the module since it is a linear scaling factor for the size of the grinding worm’s teeth. Consequently, the core and the outer diameter increase to the same extent, and their ratio stays constant. Furthermore, the normalized addendum modification x^*, the normalized tip clearance c_P^* (see Fig. 5), and the tooth root angle α_fP,l (see Fig. 3) influence the geometrical parameters of the ground cutting tool and thus are eligible for process design. In gearing technology, tip clearance describes the distance between the addendum circle of one gear and the root circle of the corresponding gear. Transferred to the continuous generating grinding of cutting tools, this means a variation of the tip clearance leads to a variation of the core and outer diameter of the cutting tool, e.g., by changing the flute depth, as shown in Fig. 5.

Fig. 4

The influence of different parameters on the rake angle of the ground cutting tool

Fig. 5

The influence of a variation of the tip clearance on cutting tool geometry

However, contrary to the module, the latter mentioned variables have a strongly varying, non-linear influence on the core diameter and outer diameter as well as on the clearance angle and the rake angle. Those complex interdependencies between the four setting variables and the four geometrical target values of the cutting tool impede the process design since all output variables are influenced by every input variable differently. Therefore, a consecutive modification of the different input variables to gradually achieve the desired output variables is not possible. Instead, another method must be developed to find suitable process variables and grinding worm parameters for the desired cutting wedge geometry.

One possibility to find the suitable grinding worm geometry for a specific cutting tool is “reverse machining” within the simulation environment. For this purpose, the continuous generating grinding process is reversed within the material removal simulation. Instead of machining the tool blank with a specified grinding worm geometry, the desired cutting tool geometry machines a grinding worm blank. The result of this simulation is a grinding worm geometry that may be used to create the utilized cutting tool geometry. However, this approach has a disadvantage: the process kinematics must be clearly defined before the simulation starts. This means that the user must select the addendum modification since it represents the axial distance between the grinding worm and the cutting tool blank and thus directly influences the process kinematics. This leads to a user-dependent result of the described approach and may avoid successful determination of the grinding worm’s basic rack if the wrong addendum modification has been chosen.

Consequently, a second approach has been developed. This method is based on the mathematically well-known Newton–Raphson method and takes all four mentioned input variables, including the addendum modification and, thus, the process kinematics, into consideration. This numerical method approximates the zeroes of a real-valued function in an iterative procedure. Starting from an initial guess x₀, the derivative ƒ′ (x) of a single variable function ƒ(x) is determined. Subsequently, the root of the function is approximated by using the calculation procedure shown in Eq. (1). This iterative method may be repeated until a sufficient precise approximation of the desired function root is reached.

$${x}_{n+1}= {x}_{n}- \frac{f({x}_{n})}{{f}^{^{\prime}}({x}_{n})}$$

(1)

This method may also be transferred to the multidimensional room if there is more than one input and one output variable, as in the present case during continuous generating grinding. The Newton–Raphson method can therefore be applied to this application using Eq. (2).

$$\overrightarrow{{T}_{MT}}=f\left({\phi }_{n}\right)-\frac{f\left({\phi }_{n}\right)}{{f}^{^{\prime}}({\phi }_{n})}=f\left({\phi }_{n}\right)-{\left(J\left({\phi }_{n}\right)\right)}^{-1}\cdot f\left({\phi }_{n}\right)$$

(2)

The vector T_MT represents the target geometry of the milling tool to be ground which is defined in this case by outer and core diameter as well as the rake and clearance angle. The function ƒ(ϕ) describes the machining result of the grinding process performed with a grinding worm whose geometry is defined by the parameters α_fP,l, x^*, c_P^*, and m_n. The function ƒ(ϕ) depends on all four influencing variables (see Eq. (3)). Consequently, the root of the function is also multidimensional and defined by the geometrical parameters of the ground tool:

$$f\left(\phi \right)=f\left({\alpha }_{fP,l}, {x}^{*}, {{c}_{P}}^{*}, {m}_{n}\right)=\left(\begin{array}{c}\begin{array}{c}d\\ {d}_{k}\end{array}\\ \alpha \\ \gamma \end{array}\right)$$

(3)

It should be noted, in contrast to the conventional application of the Newton–Raphson method, f(ϕ) is neither known nor analytically describable with the current state of the art. Therefore, numerical simulation results determined with IFW-CutS are used as input (α_fP,l, x^*, c_P^*, m_n) and output values (d, d_k, α, γ) of Eq. (3). These input and output values can subsequently be used to numerically calculate the secants of the unknown function f(ϕ) and their gradients in the investigated points. The gradients of these secants can be determined by an isolated and successive variation of α_fP,l, x^*, c_P^*, and m_n within IFW-CutS. However, this means that initial values for α_fP,l, x^*, c_P^*, and m_n, as well as an initial gradient of the secants Δϕ_s (representing ƒ′(ϕ)), must be chosen to give a starting point for the calculations. If no experience-based values are available, it can be recommendable to perform preliminary simulations of the continuous generating grinding process to identify suitable values for α_fP,l, x^*, c_P^*, m_n. For the selection of Δϕ_s, the restrictions mentioned in Sect. 3.2 must be considered.

Besides that, a 4 × 4 Jacobian matrix J(ϕ) must be formed based on Eq. (3), as shown in Eq. (4), to acquire the derivative ƒ′ (ϕ) needed for the application of the Newton–Raphson method. It must be mentioned that it is not possible in this case to form partial derivatives as an analytical solution is unknown. The partial derivatives are replaced with the gradients of the numerically determined secants at the investigated point and can be used in J(ϕ). After that, the roots of this linearization of f(ϕ) can be determined for the point ϕ_n using J(ϕ) in Eq. (2). The Newton–Raphson method shown in Eq. (2) can then be repeated iteratively, with ϕ_n+1 approaching the root of the linearized function with each iteration step. In this process, the linearization of f(ϕ)gets closer to the root of the original nonlinear version of f(ϕ) with every iteration step. This means that the deviation from the intended cutting tool geometry ($\overrightarrow{{T}_{MT}}$) decreases with an increase in iteration steps.

$$J\left(\phi \right):={\left(\frac{\partial {f}_{i}}{{\partial \phi }_{j}}\right)}_{ij}=\left(\begin{array}{cc}\begin{array}{c}\begin{array}{cc}\frac{\partial d}{\partial {\alpha }_{fP,l}}& \frac{\partial d}{\partial {x}^{*}}\end{array}\\ \begin{array}{cc}\frac{\partial {d}_{k}}{\partial {\alpha }_{fP,l}}& \frac{\partial {d}_{k}}{\partial {x}^{*}}\end{array}\end{array}& \begin{array}{c}\begin{array}{cc}\frac{\partial d}{\partial {{c}_{P}}^{*}}& \frac{\partial d}{\partial {m}_{n}}\end{array}\\ \begin{array}{cc}\frac{\partial {d}_{k}}{\partial {{c}_{P}}^{*}}& \frac{\partial {d}_{k}}{\partial {m}_{n}}\end{array}\end{array}\\ \begin{array}{c}\begin{array}{cc}\frac{\partial \alpha }{\partial {\alpha }_{fP,l}}& \frac{\partial \alpha }{\partial {x}^{*}}\end{array}\\ \begin{array}{cc}\frac{\partial \gamma }{\partial {\alpha }_{fP,l}}& \frac{\partial \gamma }{\partial {x}^{*}}\end{array}\end{array}& \begin{array}{c}\begin{array}{cc}\frac{\partial \alpha }{\partial {{c}_{P}}^{*}}& \frac{\partial \alpha }{\partial {m}_{n}}\end{array}\\ \begin{array}{cc}\frac{\partial \gamma }{\partial {{c}_{P}}^{*}}& \frac{\partial \gamma }{\partial {m}_{n}}\end{array}\end{array}\end{array}\right)$$

(4)

The method shows a local quadratic convergence if J(ϕ) is invertible at the root of the function and if it is Lipschitz continuous near this point. This is always the case if the first flank face of the cutting tool is generated by the tooth root of the grinding worm. As long as the flank faces are generated by the tooth root of the grinding worm, all faces of the manufactured cutting tool are generated in a continuous process. The associated function is, therefore, continuous. The limited tooth root angle also limits the maximal gradient of the function and ensures Lipschitz continuity.

3.2 Dampening factors

However, the used function is non-linear in some sections due to the kinematics of continuous generating grinding processes and the resulting interactions with the workpiece. This non-linearity reduces the rate of convergence and can lead to tooth root angles α_fP > 90° or α_fP < 0°. These angles cannot be manufactured and do not lead to the creation of the intended cutting tool geometry. Besides that, α_fP must be greater than 60° or equal to it to ensure that the flank face is generated by the tool root of the grinding worm. For α_fP lower than 60°, the flank face is generated by the tooth tip, and it is therefore no longer possible to adjust the clearance angle and the rake angle in the grinding process by varying α_fP. For this reason, a dampening factor f_d is introduced. This factor is taken into account if the Newton–Raphson method calculates a tooth root angle that is not between 60° and 85°. The dampening factor limits the adjustment of the tooth root angle in the iteration steps and ensures that the angle remains in an area suitable for the intended process. The dampening factor can be calculated according to Eqs. (5) and (6). But the function can not only have non-linear sections depending on the tooth root angle but also in correlation with the addendum modification and the tip clearance. This can lead to Newton–Raphson-method no longer converging, e.g., if the teeth of the cutting tool to be produced are removed in the process due to a high addendum modification. The maximal change of x^* and c_P^* between each iteration step gets limited to 0.3 by applying the dampening factor analogous to α_fP, as shown in Eqs. (7) and (8) to avoid this. The application of the dampening factor reduces the rate of convergence but ensures that reasonable cutting tool geometries are created by the method and prevents the method from becoming divergent. If a dampening factor must be applied, ϕ_n+1 can therefore be calculated by using Eqs. (9) and (10).

$${f}_{d,n}=\frac{80^\circ -{\alpha }_{fP,n-1}}{\Delta {\alpha }_{fP}} \ for \ {\alpha }_{fP}>85^\circ$$

(5)

$${f}_{d,n}=\frac{65^\circ -{\alpha }_{fP,n-1}}{\Delta {\alpha }_{fP}} \ for \ {\alpha }_{fP}<60^\circ$$

(6)

$${f}_{d,n}=\frac{0.3-{{x}^{*}}_{n-1}}{\Delta {x}^{*}} \ for \ \left|\Delta {x}^{*}\right|>0.3$$

(7)

$${f}_{d,n}=\frac{0.3-{{cp}^{*}}_{n-1}}{\Delta {{c}_{P}}^{*}} \ for \ \left|\Delta {cp}^{*}\right|>0.3$$

(8)

$$\begin{aligned}{\phi }_{n+1}=&\left({\phi }_{n}+{\Delta \phi }_{n}\right)\cdot {f}_{d,n} \ with \ {f}_{d,n}=1 \ for \ 60^\circ \le {\alpha }_{fP}\le 85^\circ , \ \\& \left|{\Delta x}^{*}\right|\le 0.3 \ \mathrm{and} \ \left|\Delta {{c}_{P}}^{*}\right|\le 0.3\end{aligned}$$

(9)

$$\Delta {\phi }_{n}:=-{\left(J\left(\phi \right)\right)}^{-1}\cdot f\left(\phi \right)$$

(10)

3.3 Usability of the method for the determination of the basic rack of the grinding worm

The method is then used to design a continuous generating grinding process for two different milling tools to verify its usability for determining the basic rack and process parameters of the grinding worm. The tool geometries of the milling tools is characterized by their outer diameter, their core diameter, their clearance angle and their rake angle. The chosen values for these parameters can be seen in Eqs. (11) and (12). Besides this, the number of teeth z and the helix angle β is varied between the two tools. The first tool (d = 11.9 mm) has four teeth and a helix angle of 30°, while the second one (d = 12 mm) has six teeth and a helix angle of 40°. Since the number of teeth depends on the module and the helix angle depends on the ratio of outer and core diameter, these two factors do not have to be included separately in the calculations [21].

$$\overrightarrow{{T}_{MT,1}}=\left(\begin{array}{c}d\\ \begin{array}{c}{d}_{k}\\ \alpha \end{array}\\ \gamma \end{array}\right)=\left(\begin{array}{c}11.9 \ mm\\ \begin{array}{c}7 \ mm\\ 8^\circ \end{array}\\ 11^\circ \end{array}\right)$$

(11)

$$\overrightarrow{{T}_{MT,2}}=\left(\begin{array}{c}d\\ \begin{array}{c}{d}_{k}\\ \alpha \end{array}\\ \gamma \end{array}\right)=\left(\begin{array}{c}12 \ mm\\ \begin{array}{c}8 \ mm\\ 14^\circ \end{array}\\ 12^\circ \end{array}\right)$$

(12)

Based on the equations presented previously, the parameters sought can be approximated to the target values by iterative application of Eq. (2) until the target vector is reached with sufficient accuracy. The starting point ϕ₁ for the method is shown in Eq. (13). To allow the replacement of the partial derivatives in J(ϕ) by the gradients of the linearization as described before, the starting point values are initially varied by Δϕ_s (see Eq. ((14)) to allow the calculation of the initial gradients of the linearization.

$${\phi }_{1}=\left(\begin{array}{c}{\alpha }_{fP,l}\\ \begin{array}{c} {x}^{*}\\ {c}_{P}^{*}\end{array}\\ {m}_{n}\end{array}\right)=\left(\begin{array}{c}70^\circ \\ \begin{array}{c}0\\ 0\end{array}\\ 2.5 \ mm\end{array}\right)$$

(13)

$$\overrightarrow{\Delta {\phi }_{s}}=\left(\begin{array}{c}{\Delta \alpha }_{fP,l}\\ \begin{array}{c} {\Delta x}^{*}\\ {\Delta c}_{P}^{*}\end{array}\\ {\Delta m}_{n}\end{array}\right)=\left(\begin{array}{c}-5^\circ \\ \begin{array}{c}0.1\\ -0.1\end{array}\\ 0.1 \ mm\end{array}\right)$$

(14)

To give an example of the necessity and application of the dampening factor, the calculation results of Eq. (2) for ϕ₁ and ϕ₂ of the first cutting tool (d = 11.9 mm) are shown below in Eqs. (15)–(17). The given starting point results in a cutting tool geometry that clearly shows deviations from the intended geometry, as shown in Eq. (15). Applying the next iterative step without a dampening factor by using Eqs. (2), (4), (10), and (14) would lead to the calculation of a ϕ₂ with the values shown in Eq. (16). It can be seen in this case that α_fP,l increases and gets closer to an angle of 90°, which could lead to the calculation of an unmanufacturable grinding worm geometry. To prevent this, the dampening factor shown in Eq. (5) is applied according to Eq. (9), as α_fP,l is greater than 85°. This leads to the calculation of the values shown in Eq. (17) for ϕ_2, which results in the calculation of a manufacturable grinding worm geometry and a calculation of a cutting tool geometry that deviates less from the intended geometry.

$${f}_{MT,1}\left({\phi }_{1}\right)=\left(\begin{array}{c}d\\ \begin{array}{c}{d}_{k}\\ \alpha \end{array}\\ \gamma \end{array}\right)=\left(\begin{array}{c}10.818 \ mm\\ \begin{array}{c}6.523 \ mm\\ 20.262^\circ \end{array}\\ 15.300^\circ \end{array}\right)$$

(15)

The resulting deviations of the diameters and angles of the designed milling tools from the target geometry are shown in Figs. 6 and 7 for each iteration step. It can be seen that in both cases, starting from the specified initial value, the method reduces the diameter and angle deviations occurring on the milling tool to be designed. For the milling tool with four teeth, this means that the diameters show a maximal deviation of 9 µm and a maximal deviation of the investigated angles of 0.5° after five iteration steps (see Fig. 6), which can be considered a sufficiently accurate result for the design of the continuous grinding process and the grinding worm. For the geometrically more complex milling tool, the method produces much higher deviations in the first iteration steps and shows that at least one more iteration step is needed to reach a value of diameter deviation comparable to the milling tool with four teeth (see Fig. 7). But at this point, the maximal deviation of the investigated angles is still 3° which means that further iteration steps have to be performed if a higher accuracy of the angles of the milling tool has to be achieved in the continuous generating grinding process.

Fig. 6

Diameter and angle deviations for a milling tool with 4 teeth

Fig. 7

Diameter and angle deviations for a milling tool with 6 teeth

$${\phi }_{2( fd.2 = 1)}=\left(\begin{array}{c}{\alpha }_{fP,l}\\ \begin{array}{c} {x}^{*}\\ {c}_{P}^{*}\end{array}\\ {m}_{n}\end{array}\right)=\left(\begin{array}{c}70^\circ +16.94\\ \begin{array}{c}0-0.280\\ 0-0.148\end{array}\\ 2.5 \ mm+0.449 \ mm\end{array}\right)=\left(\begin{array}{c}86.940^\circ \\ \begin{array}{c}-0.280\\ -0.148\end{array}\\ 2.949 \ mm\end{array}\right)$$

(16)

$$\begin{aligned}{\phi }_{2( fd.2 = 0.59)}=&\left(\begin{array}{c}{\alpha }_{fP,l}\\ \begin{array}{c} {x}^{*}\\ {{c}_{P}}^{*}\end{array}\\ {m}_{n}\end{array}\right)=\left(\begin{array}{c}80^\circ \\ \begin{array}{c}-0.166\\ -0.088\end{array}\\ 2.765 \ mm\end{array}\right) \ resulting \ in \ {f}_{MT,1} \\&\left({\phi }_{2}\right)=\left(\begin{array}{c}d\\ \begin{array}{c}{d}_{k}\\ \alpha \end{array}\\ \gamma \end{array}\right)=\left(\begin{array}{c}11.388 \ mm\\ \begin{array}{c}6.790 \ mm\\ 13.534^\circ \end{array}\\ 9.533^\circ \end{array}\right)\end{aligned}$$

(17)

It is particularly important to achieve a high degree of accuracy in the application of the method regarding the diameters and angles considered in the design, as these can influence the operational behavior of the cutting tools produced. The ratio of the mentioned diameters, for example, influences the flute geometry of the cutting tool, which in turn influences chip formation, chip removal as well as friction between chips and cutting tool in the cutting processes [33, 34]. Rake and clearance angle also influence the chip formation in these processes as well as the mechanical stability of the cutting wedges of the cutting tool and the friction between the workpiece and cutting tool. The clearance angle has a high influence on the friction between the workpiece and the cutting tool and thus on the thermal load in the cutting process. Since the clearance angle also influences the mechanical stability of the cutting wedges, it should therefore be carefully selected and manufactured with sufficient accuracy.

However, in both cases, a lower speed of convergence can be observed for the angular deviations of the milling tools than for the diameter deviations. The reason for the lower speed of convergence for the angular deviations is numerical errors or inaccuracies in the calculations resulting from the limited dexel density and discretization of the grinding worm in the simulation. These errors or inaccuracies especially influence the angles and limit the speed of convergence of the method for these parameters. Furthermore, they can cause an overshoot of the angles in the method, as can be seen in the change of the angular deviation from iteration steps three to four in Fig. 6 and steps four to five in Fig. 7, respectively.

But in general, the use of the presented method leads to a reduction of the deviations of all investigated parameters in a few iteration steps and, therefore, to the sensible design of the grinding worm. However, it converges slower for geometrically more complex tools than for geometrically less complex tools. It can therefore be assumed that the method is suitable to design the grinding worms for the continuous generating grinding of rotational cutting tools with different numbers of teeth and helix angles and is thus verified as a method suitable for this purpose.

To complete the design of the grinding worm, it is not only necessary to design the cutting tool quantitatively (see Fig. 8, left side) but to modify the flutes of the cutting tool qualitatively as well. This can be done by modifying the kink point shift and the tooth thickness shift, as shown in Fig. 8. By varying the tooth thickness shift, the thickness of the cutting tool’s teeth can be adjusted (see Fig. 8, middle), while varying the kink point shift allows an adjustment of the curvature of the teeth (see Fig. 8, right side). It must be mentioned that if these two factors are varied, α_fP,l, x^*, c_P^*, and m_n must be kept constant to prevent the cutting wedge from changing and to ensure that the tooth roots of the grinding worm continue to generate the flank faces of the cutting tool. Otherwise, this would alter the basic geometry of the cutting tool and, e.g., alter the clearance angle of the cutting tool. This would then make a repetition of the Newton–Raphson method necessary to adapt the grinding tool to the changed geometry of the cutting wedge. Considering these restrictions, there is a limit for the kink point shift at −0.6. Kink point shifts higher than −0.6 would alter the cutting wedge geometry, as shown in Fig. 8 (right side), and would therefore make a repetition of the Newton–Raphson method necessary to adapt the grinding worm to the new requirements. But besides this, no further restrictions for the variation of the tooth thickness shift and kink point shift must be considered in adapting the flute geometry.

Fig. 8

Qualitative adjustment of the flute geometry by varying tooth thickness shift and kink point shift

3.4 Validation of the applicability of the method for the design of continuous generating grinding processes

With the help of the geometry of the grinding worm determined using the previously presented method and the NC-code generated on this basis, grinding tests can then be carried out to validate the applicability of the method for designing continuous generating grinding processes of milling tools. The result of a continuous generating grinding process designed by this means is shown in Fig. 9. It can be seen that it was possible to manufacture a milling tool with six teeth via continuous generating grinding as intended. It can therefore be assumed that the method allows for the design of grinding worm geometries for the continuous generating grinding of milling tools and thus makes the realization of such grinding processes possible.

Fig. 9

Milling tool manufactured by continuous generating grinding

But compared to the results of the simulations, the ground milling tools show geometrical deviations from the intended result. Although the geometric deviation of the cross-section geometry of the ground tool from the simulated tool is less than 35 µm in most areas of the tool, this is not true for the head of the teeth of the milling tool. In this area of the tools, the geometry of the milling tool deviates up to 140 µm from the intended and simulated geometry. Measurements of the grinding worm profile identify deviations of the grinding worm geometry from the target profile as a possible source for the geometry deviations of the ground milling tool. A comparison of the intended and targeted grinding worm profiles is shown in Fig. 10. While the deviation from the target profile is at the tooth tips and flanks of the teeth of the grinding worm less than 50 µm, deviations of up to 150 µm can be observed at the tooth roots. Possible reasons for the deviation of the grinding worm profile are a mutual displacement of the grinding worm and the diamond form roll as a result of the acting process forces acting during dressing and wear of the diamond form roll during the process. But in this case, it can be assumed that the wear of the diamond form roll is the dominant effect since geometry deviations resulting from a displacement in the dressing process should affect all areas of the grinding worm geometry and not only the tooth root in particular. The profile measurements of the grinding worm profile support this hypothesis, as the corner radius of the dressing tool that has worn from its initial radius of 0.25 to 0.65 mm, can be identified in the profile of the grinding worm. This wear especially influences the grinding worm geometry in areas in which the tooth root angle is lower than the angle of the diamond form roll (40°). This applies in this case as the tooth root angle of 10° is lower than the angle of the diamond form roll. However, the measured deviation of the grinding worm geometry of less than 50 µm at the tooth tips and of up to 150 µm at the tooth roots correlate well with the measured milling tool geometry deviations of less than 35 µm at most parts of the cross-sectional geometry and of 140 µm at the teeth of the tool. It can therefore be assumed that the measured deviations from the intended milling tool geometry are a result of wear-caused inaccuracies of the dressing process and are not directly linked with the presented method for the design of the continuous generating grinding process of cutting tools. Based on these results, it can therefore be assumed that the presented methodology for designing the basic rack of the grinding worm and the needed parameters is suitable for continuous generating grinding of cutting tools.

Fig. 10

Comparison of the target profile and the actual profile of the grinding worm after dressing

4 Conclusions

The application of continuous generating grinding processes offers a possibility to increase the productivity of tool grinding processes. However, due to the complex kinematics of such processes and the complex interactions between grinding worm geometry and the resulting cutting tool geometry, the design of the grinding worms needed for these grinding processes poses a challenge. Therefore, this paper presents a method for the geometrical process design of continuous generating grinding processes of cutting tools to meet these challenges. Based on the results of this investigation, the following conclusions can be drawn:

• Tip clearance, module, addendum modification, and tooth root angle are important factors for the geometrical design of continuous generating grinding processes of cutting tools and should therefore be used in models which aim at the design of such processes.

• The use of the Newton–Raphson method enables the iterative calculation of all parameters needed for the design of a continuous generating grinding process of cutting tools.

• The application of dampening factors is necessary to ensure the calculation of sensible and manufacturable grinding worm geometries, although these factors can influence the rate of convergence of the method.

• The flute geometry of the designed cutting tool can be adjusted by varying the kink point shift and the tool thickness shift. However, α_fP,l, x^*, c_P^*, and m_n must be kept constant in this procedure, and the kink point shift may not be greater than −0.6.

• The presented method allows the determination of the basic rack of the grinding worm and the parameters needed for the design of a continuous generating grinding process of cutting tools without being user dependent. The method can determine the needed parameters with sufficient accuracy within five iteration steps, although the number of needed iteration steps may increase with the complexity of the cutting tool to be designed.

• The grinding experiments show that grinding worms designed with the presented method can perform the manufacturing of milling tools via a continuous generating grinding process in the intended way. But the results also show that influence factors like the wear of the dressing tools can influence the geometric accuracy of the manufactured tool. Future investigations should therefore investigate the relevance of grinding process-related influence factors and their significance for the process result to allow further improvement of the accuracy and productivity of the continuous generating grinding of cutting tools.