Skip to main content

Advertisement

SpringerLink
Log in

Sequential optimization of the injection molding gate locations using parallel efficient global optimization

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

Abstract

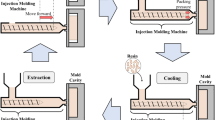
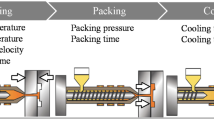
Injection molding (IM) is a versatile manufacturing process capable of rapid prototyping and mass-producing high-quality polymer parts. The present study mainly investigates the challenge of designing multiple molding gates on the complex arbitrary part surface in 3D. Currently, this problem is a challenge in mold design and engineering experience still plays an important role in designing the molding gates. To reduce the human intervention in the design process, the present study proposed a novel methodology with the following major steps: 1) using Poisson disk sampling (PDS) to preselect candidate gate locations automatically within the suitable gating region specified by designers; 2) using a space-filling initialization strategy and efficient global optimization to find the optimal gate locations. In the present setting, the molding gate design problem is formalized as a discrete optimization problem. The PDS is employed to construct the discrete solution space and EGO is used to efficiently search through a large solution space for the best design. To further promote optimization efficiency, a parallel implementation of EGO is also proposed. The effectiveness of the proposed methods is validated in two design cases. The results demonstrate the proposed EGO and Parallel EGO method is superior that the Genetic Algorithm (GA) and Surrogate Optimization (SO). Moreover, the proposed Parallel EGO converges faster than all other alternatives.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Code availability

Moldex3D, open3d.

References

  1. Gao Y, Wang X (2008) An effective warpage optimization method in injection molding based on the Kriging model. Int J Adv Manuf Technol 37(9):953–960. https://doi.org/10.1007/s00170-007-1044-6

    Article  Google Scholar 

  2. Wang X, Gu J, Shen C, Wang X (2015) Warpage optimization with dynamic injection molding technology and sequential optimization method. Int J Adv Manuf Technol 78(1–4):177–187. https://doi.org/10.1007/s00170-014-6621-x

    Article  Google Scholar 

  3. Zhai M, Shen C (2005) An optimization scheme based on flow resistance to locate optimum gate of complex part. J Reinf Plast Compos 24(15):1559–1566. https://doi.org/10.1177/0731684405050389

    Article  Google Scholar 

  4. Lam YC, Jin S (2001) Optimization of gate location for plastic injection molding. J Inject Molding Technol 5(3):180

    Google Scholar 

  5. Shen C, Zhai M (2004) Algorithm to optimise number of gates and locations in an injection mould. Plast Rubber Compos 33(8):330–334. https://doi.org/10.1179/174328904X22323

    Article  Google Scholar 

  6. Deng Y-M, Zheng D, Lu X-J (2008) Injection moulding optimisation of multi-class design variables using a PSO algorithm. Int J Adv Manuf Technol 39(7–8):690–698. https://doi.org/10.1007/s00170-007-1258-7

    Article  Google Scholar 

  7. Pandelidis I, Zou Q (1990) Optimization of injection molding design. Part I: Gate location optimization. Polym Eng Sci 30(15):873–882. https://doi.org/10.1002/pen.760301502

    Article  Google Scholar 

  8. Chen S-C, Turng L-S (2019) Advanced injection molding technologies. In: Chen SC and Turng LS (eds) Advanced Injection Molding Technologies. Carl Hanser Verlag GmbH & Co. KG, p I–XV. https://doi.org/10.3139/9781569906040.fm

  9. Chen Z, Turng L-S (2005) A review of current developments in process and quality control for injection molding. Adv Polym Technol 24(3):165–182. https://doi.org/10.1002/adv.20046

    Article  Google Scholar 

  10. Irani RK, Kim BH, Dixon JR (1995) Towards automated design of the feed system of injection molds by integrating CAE, iterative redesign and features. J Eng Ind 117(1):72–77. https://doi.org/10.1115/1.2803281

    Article  Google Scholar 

  11. Lam YC, Britton GA, Liu DS (2004) Optimisation of gate location with design constraints. Int J Adv Manuf Technol 24(7–8):560–566. https://doi.org/10.1007/s00170-004-1633-6

    Article  Google Scholar 

  12. Lee BH, Kim BH (1996) Automated selection of gate location based on desired quality of injection-molded part. Polym-Plast Technol Eng 35(2):253–269. https://doi.org/10.1080/03602559608000583

    Article  Google Scholar 

  13. Young W-B (1994) Gate location optimization in liquid composite molding using genetic algorithms. J Compos Mater 28(12):1098–1113. https://doi.org/10.1177/002199839402801202

    Article  Google Scholar 

  14. Zhai M, Lam YC, Au CK (2005) Algorithms for two gate optimization in injection molding. Int Polym Process 20(1):14–18. https://doi.org/10.3139/217.1860

    Article  Google Scholar 

  15. Kitayama S, Natsume S (2014) Multi-objective optimization of volume shrinkage and clamping force for plastic injection molding via sequential approximate optimization. Simul Model Pract Theory 48:35–44. https://doi.org/10.1016/j.simpat.2014.07.004

    Article  Google Scholar 

  16. Garud SS, Karimi IA, Kraft M (2017) Design of computer experiments: a review. Comput Chem Eng 106:71–95. https://doi.org/10.1016/j.compchemeng.2017.05.010

    Article  Google Scholar 

  17. Gramacy RB (2020) Surrogates: Gaussian process modeling, design, and optimization for the applied sciences. Boca Raton: Chapman and Hall/CRC. https://doi.org/10.1201/9780367815493

    Article  Google Scholar 

  18. Garrido-Merchán EC, Hernández-Lobato D (2020) Dealing with categorical and integer-valued variables in Bayesian Optimization with Gaussian processes. Neurocomputing 380:20–35. https://doi.org/10.1016/j.neucom.2019.11.004

    Article  Google Scholar 

  19. Turk G (1992) Re-tiling polygonal surfaces. In: Proceedings of the 19th annual conference on Computer graphics and interactive techniques, New York, NY, USA, p 55–64. https://doi.org/10.1145/133994.134008

  20. Nehab D, Shilane P (2004) Stratified point sampling of 3D models. Eurograph Assoc. https://doi.org/10.2312/SPBG/SPBG04/049-056

    Article  Google Scholar 

  21. Yuksel C (2015) Sample elimination for generating Poisson disk sample sets. Comput Graph Forum 34(2):25–32. https://doi.org/10.1111/cgf.12538

    Article  Google Scholar 

  22. Alliez P, Meyer M, Desbrun M (2002) Interactive geometry remeshing. ACM Trans Graph 21(3)

  23. Johnson A (1997) Spin-images: a representation for 3-D surface matching. Undefined. Accessed 16 Sep 2021 [Online]. Available at: https://www.semanticscholar.org/paper/Spin-Images%3A-A-Representation-for-3-D-Surface-Johnson/4c09532c6ef9afd5f0dd1f3d2b0af313199a8520

  24. Zhou Q-Y, Park J, Koltun V (2018) Open3D: a modern library for 3D data processing. arXiv:1801.09847

  25. Jones DR, Schonlau M, Welch WJ (1998) Efficient global optimization of expensive black-box functions. J Glob Optim 13(4):455–492. https://doi.org/10.1023/A:1008306431147

    Article  MathSciNet  MATH  Google Scholar 

  26. Lophaven SN (2002) DACE – a MATLAB Kriging Toolbox – Version 2.0

  27. Santner TJ, Williams BJ, Notz WI (2003) The design and analysis of computer experiments. New York: Springer-Verlag. https://doi.org/10.1007/978-1-4757-3799-8

    Article  MATH  Google Scholar 

  28. Regis R, Shoemaker C (2007) A stochastic radial basis function method for the global optimization of expensive functions. Inf J Comput. https://doi.org/10.1287/ijoc.1060.0182

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The research is supported by CoreTech System Co., Ltd. The source CAE model, license of Moldex3D, and technical support are highly appreciated by the authors.

Author information

Authors and Affiliations

  1. Center for Intelligent Maintenance Systems, Department of Mechanical Engineering, University of Cincinnati, PO Box 210072, Cincinnati, OH, 45221-0072, USA

    Yuan-Ming Hsu, Xiaodong Jia, Wenzhe Li & Jay Lee

  2. Department of Material Science, Purdue University, West Lafayette, IN, 47907, USA

    Panayotis Manganaris

Authors
  1. Yuan-Ming Hsu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaodong Jia
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wenzhe Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Panayotis Manganaris
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jay Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiaodong Jia.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hsu, YM., Jia, X., Li, W. et al. Sequential optimization of the injection molding gate locations using parallel efficient global optimization. Int J Adv Manuf Technol 120, 3805–3819 (2022). https://doi.org/10.1007/s00170-022-09012-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-022-09012-7

Keywords

Search

Navigation