1 Introduction

Trailing edge (TE) noise, also known as airfoil self-noise, is one of the main sources of noise pollution generated by airfoils moving through homogeneous flows. Keeping this noise source at a reasonable level is a major challenge for the development of onshore wind energy [1] or aviation. Therefore, improving the accuracy of low-order TE noise models that can be integrated into optimization methodologies is an active research topic in the aeroacoustics community.

TE noise is generated by surface pressure fluctuations (SPF) that are caused by unsteady flow structures in the transitional or turbulent boundary layer. These SPFs undergo a sharp discontinuity at the trailing edge of the airfoil [2], resulting in acoustic scattering of the SPF into acoustic waves.

Most theoretical models of the sound radiated by pressure fluctuations in the vicinity of a sharp trailing edge are derived from Lighthill’s acoustic analogy [3]. An early review of the resulting theories was done by Howe [4], and a more general and recent overview of aeroacoustic models and prediction techniques can be found in Lee et al. [5]. Aeroacoustic models can generally be regarded as transfer functions that predict far-field acoustics based on near-field pressure fluctuations. However, most current theoretical approaches rely on empirical or semi-empirical models of SPFs for turbulent flows [5, 6]. These models often rely on experimental datasets rather than first principles, and their accuracy is highly dependent on the similarity between the studied cases and the original dataset. Consequently, it is challenging to estimate a priori how noise reduction techniques that modify the flow field will impact these SPF models [5].

Nonetheless, theoretical models provide valuable insights into TE noise. Of particular relevance to the present work is the “scattering condition” resulting from theory [7], which suggests that only perturbations with spanwise wavenumbers lower than the acoustic wavenumbers are effectively radiated as sound at the trailing edge. The acoustic wavenumber is defined as \(k_0=\omega /a_0\), where \(a_0\) is the speed of sound and \(\omega \) the angular frequency.

Alternatively, high-fidelity compressible simulations can simultaneously capture the hydrodynamic and acoustic fluctuations of the flow from first principles [8, 9]. These simulations, especially when combined with empirical flow decomposition techniques like spectral proper orthogonal decomposition (SPOD) [10, 11], provide high-quality reference data for reduced-order models by identifying the main coherent structures related to TE noise generation. However, their computational cost remains prohibitive for engineering applications. One approach to mitigate this cost is employing hybrid methods, where hydrodynamic fluctuations are solved using an incompressible solver, while acoustic radiation is handled with acoustic analogies. Such methods have achieved success in reproducing TE noise [12], but remain computationally expensive and lack predictive capabilities.

A promising technique to gain further insight into the mechanisms behind TE noise, and ultimately to reduce the degrees of freedom for optimizing noise reduction techniques, is to combine a physics-based but low-order model of SPFs with an acoustic analogy. This paper aims to develop and evaluate such a model by using linearized mean flow analysis (LMFA) to model the coherent structures in the turbulent boundary layer and using the resulting SPFs as input to an acoustic analogy. An approach similar to the present work has been successfully applied to estimate the sound generated by turbulent jets from LMFA-based models [13,14,15], and the present work is inspired from the developments obtained in this field.

LMFA and the related linear stability analysis has been widely employed over the last century to investigate unsteadiness in various flow applications [16], including the analysis of coherent structures in turbulent flows [17, 18] and more recently by Kuhn et al.  [19] among others. In particular, the resolvent analysis [20] has gained popularity in recent years, and has been successfully used to extract the coherent structures maximizing the disturbance energy gain from a turbulent mean flow by McKeon & Sharma [21] and Hwang & Cossu [22]. Since then, many studies have applied these techniques to the transitional and turbulent flows around airfoils and explored the connection between hydrodynamic instabilities and TE noise (e.g. Fosas de Pando et al. [23, 24], Yeh and Taira [25], Symon et al. [26], Abreu et al. [27], and Ricciardi et al. [28, 29], among others). However, the main goal of these studies was to uncover the underlying mechanisms of TE noise, rather than devising reduced-order model that reproduces the acoustic spectra and directivity of experimental or high-fidelity simulation data, as is the objective of the present work.

In this work, we analyze the flow around a NACA0012 airfoil at low angle of attack (\(\alpha =3\) deg) and a transitional Reynolds number (\(\text {Re}=5\times 10^4\)), which is the same setup as in the analysis of Ricciardi et al. [29]. This case offers the advantage of numerical tractability while showcasing a complex acoustic spectrum and flow dynamics typical of applications in this regime. At such low-to-moderate Reynolds numbers, a feedback mechanism occurs between upstream-traveling acoustic waves and downstream propagating hydrodynamic instability waves in the boundary layer. This results in tonal TE noise, characterized by multiple equally spaced sharp peaks in the acoustic spectrum [28, 30, 31], i.e., the tones. The results of Ricciardi et al. [29] further suggest that the tonal noise at these conditions is primarily caused by the scattering of spanwise coherent structures, in line with the aforementioned scattering condition. This allows to restrict our empirical and physics-based modeling to zero spanwise wavenumbers only.

We employ resolvent analysis based on the mean field to model the coherent flow structures that cause the SPF. This method allows to identify the most amplified coherent structures at each frequency from the linearized mean flow operator. To keep the physics-based model simple, an incompressible resolvent analysis is performed as a first step. The modes obtained from the resolvent analysis are then combined with an acoustic analogy. Based on the scattering condition and the spanwise-invariant geometry of our setup, we employ a closed form of Lighthill’s acoustic analogy derived by Curle [32], which accounts for the scattering of dipolar sources on a solid boundary. The present model is evaluated by comparing the resolvent analysis with results obtained from SPOD of the LES snapshots [33].

In previous works, promising attempts with a similar methodology were reported in Wagner et al. [34, 35], for a NACA0012 airfoil at a lower Reynolds number (\(\text {Re}=2\times 10^4\)), and of Prinja et al. [36], for the experimental flow around a cylinder. In both cases, the acoustic spectrum was dominated by a single frequency, and the analysis was focused on this discrete frequency. In contrast, the present work extends these previous analyses to a more complex case. Here, we must consider the hydrodynamic and acoustic fluctuations over a broad range of frequencies due to the presence of multiple tones.

The paper is organized as follows: The numerical dataset together with the acoustic spectrum is presented in Sect. 2. Next, Sect. 3 introduces the SPOD, resolvent, and aeroacoustic methods used to obtain the empirical and physics-based TE noise models. In particular, the radiated acoustic field from the aeroacoustic analogy is compared with a spectral analysis of the LES snapshots in Sect. 4.2 to assess its accuracy without any modeling of the SPF. The results of the proposed physics-based model are then compared with reference data from the SPOD analysis in Sect. 5, both in terms of wavepackets near the airfoil, SPFs, and the radiated acoustic field. Finally, conclusions are drawn in Sect. 7.

2 Dataset

This work is based on a numerical dataset obtained from LES of the flow around a NACA0012 airfoil at angle of attack \(\alpha =3\) deg. The trailing edge of the airfoil is rounded with a radius of approximately \(0.16\%\) of the chord length c. The geometry is described with Cartesian coordinates \((x,\,y,\,z)\) denoting the streamwise, vertical, and spanwise directions respectively, while the corresponding components of the velocity are denoted as \(\textbf{u}=[u,\,v,\,w]^\text {T}\) The Reynolds number based on the chord length is \(Re = \rho _{\infty } u_{\infty } c/\mu _{\infty }=5\times 10^4\), where \(u_{\infty }\), \(\rho _{\infty }\), and \(\mu _{\infty }\) denote the freestream velocity, density, and dynamic viscosity, respectively. The freestream Mach number is \(M=u_{\infty }/a_0=0.3\), where \(a_0\) is the speed of sound. The surface of the airfoil is smooth, such that no forced transition occurs. On the suction side, the flow is initially laminar with a thin recirculation bubble stretching over a large portion of the airfoil, from \(x/c\approx 40\%\) to \(x/c\approx 80\%\). At the reattachment location, the flow is turbulent, having transitioned from the laminar state near the end of the bubble. These features are highlighted in Fig. 1a, which shows contours of the mean turbulent kinetic energy \(k=0.5\left( \overline{u'^2}+\overline{v'^2}+\overline{w'^2}\right) \), with primes denoting fluctuations around the mean (defined in Sect. 3.2), near the surface of the airfoil, along with the recirculation region.

The open source, high order flux-reconstruction, numerical framework PyFR [37] is used for wall-resolved implicit large eddy simulations (iLES). Unlike LES with an explicit sub-grid scale model, iLES introduces the numerical dissipation through the discretization, see Park et al. [38] for details. The framework is designed to solve a range of governing systems on mixed unstructured grids containing various element types. The discrete set of equations obtained from the spatial discretization are integrated in time using an explicit fourth-order Runge–Kutta method. The simulation is performed on a cluster of Nvidia A100 GPUs, and 840 snapshots are collected over 40 convective flow through times (CTUs), at a sampling Strouhal number of \(\text {St} = fc/u_\infty = 33.3\), where f denotes the frequency. At least 20 CTUs were discarded before collecting snapshots, in order to evacuate the transient flow behavior resulting from the initialization.

To resolve near-wall flow structures, an O-grid type mesh is applied around the airfoil region with structured hexahedral type of elements. The maximum resolution at about the mid-chord given in terms of wall unit is \(\triangle x^+ < 20\), \(\triangle z^+ < 10\) and \(\triangle y^+ < 1.0\). At the trailing edge, the resolution in streamwise direction is kept as \(\triangle x^+ < 5\). A structured mesh is also applied in the wake region, until 2 chord lengths after the trailing edge. In the acoustic region, an unstructured mesh with tetrahedra elements type is applied in order to reduce numerical costs and avoid high aspect ratios. However, the acoustic wavelengths are still resolved for up to \(\text {St} < 10\), assuming five points to resolve one wave length. The acoustic region has been extended until 15 chord lengths away from the airfoil surface and the domain width is \(40\%\) of the chord length in the spanwise direction. Periodic boundary conditions are used at the spanwise lateral boundaries of the domain, while a no-slip, adiabatic wall is assumed for the airfoil surface. A designed sponge region is added via a forcing term \(-\xi (q - q_0)\) to the equation system. Here, \(\xi \) is the sponge strength, which is carefully chosen to assure that no acoustic waves are reflected back inside the domain.

Fig. 1
figure 1

a Contours of the time-span-averaged turbulent kinetic energy near the airfoil surface (higher values in darker color), the recirculation regions are highlighted by the dashed line at \(\bar{u}=0\); b Spanwise-averaged snapshot of pressure fluctuations obtained from the LES, the contour levels are saturated to highlight the origin of acoustic waves at the trailing edge. Additionally, the red rectangle indicates the resolvent domain

Full size image

In this work, we focus on spanwise-coherent structures, i.e., with zero spanwise wavenumber \(k_{\text {z}}=0\). Based on previous numerical [11, 27] and theoretical [39] results, these structures are known to be most relevant for TE noise and they satisfy the TE scattering condition \(k_{\text {z}}<k_0\) [6] for all frequencies. Thus, the LES snapshots are initially averaged in the spanwise direction before undergoing further analysis. An illustration of the resulting two-dimensional snapshot is presented in Fig. 1b. Here, the pressure fluctuation contour levels are saturated to emphasize the acoustic waves that originate at the trailing edge.

Figure 2a shows the power spectral density (PSD) of the spanwise-averaged pressure fluctuations one chord length above the trailing edge. It was estimated from the LES data employing the Welch method. The spectrum displays discrete, equally spaced, tones, typical for airfoils at transitional Reynolds number and moderate angle of attack [30, 31].

The present geometry setup and flow parameters are the same as in the work of Ricciardi et al. [29]. A very good agreement is found between the present surface pressure distribution on the airfoil and the one reported by their paper, as shown in Fig. 2b. Other mean flow quantities, such as mean boundary-layer profiles are also in very good agreement. Similarly, the frequency of the tones in the acoustic spectrum reported in their work matches well with the one recovered in this work, as shown in Fig. 2a.

Fig. 2
figure 2

a Power spectral density of the pressure fluctuations probed one chord length above the trailing edge (\(x,\, y) = (1,\,1)\). The frequencies of the main tones identified by Ricciardi et al. [29] are added for comparison (\(\hbox {-}\,\hbox {-}\,\hbox {-}\)); b pressure distribution over the airfoil (\(\hbox {---}\)) from the present work and from the LES from Ricciardi et al. [29] (\(+\))

Full size image

3 Coherent structures identification and modeling

This section describes the methods by which coherent structures, i.e. time-periodic flow patterns with an organized spatial structure, are extracted from the LES dataset and modeled via linearized analysis.

3.1 Spectral proper orthogonal decomposition

Proper orthogonal decomposition (POD) is a data-driven method which extracts a set of orthogonal basis functions from flow realizations [40, 41], here the LES snapshots, describing spatially coherent structures in the flow. In the spectral version of POD (termed SPOD), this basis is defined by the eigenvalue decomposition of the cross spectral density (CSD) matrix of the Fourier-transformed realizations at each frequency, resulting in the spatio-temporal coherence of the structures. Following the so-called snapshot method [42], the decomposition is based on the inner product between different flow realizations \(q_{\text {i}}\), given by

$$\begin{aligned} \langle q_{\text {i}}, q_{\text {j}}\rangle = \int _{\Omega }q_{\text {j}}^H\mathcal {W}q_{\text {i}} \text {d}\textbf{x}= q_{\text {j}}^H{\textbf {W}}q_{\text {i}}\text {,} \end{aligned}$$
(1)

where \(\Omega \) is the region of interest, the superscript “H” denotes the Hermitian transpose, and the discretized weighting operator, \({\textbf {W}}\), is chosen as such that the sum of the eigenvalues defines an energy (related to the variance of the CSD). In the present work, the flow realizations are defined as the velocity fluctuations \(q'(\textbf{x},\,t)=\left[ u'\,v'\right] ^\text {T}\) around the stationary time-averaged velocity field \(\overline{\textbf{u}}(\textbf{x})=\left[ \overline{u}~\overline{v}\right] ^\text {T}\), and \(\mathcal {W}\) is a diagonal matrix with uniform energy weights

$$\begin{aligned} \mathcal {W} =\begin{bmatrix}1 &{}\quad 0\\ 0 &{}\quad 1 \end{bmatrix} \text {.} \end{aligned}$$
(2)

The eigenvalues and eigenvectors of the CSD represent the optimal coherent structures in terms of turbulent kinetic energy \(\Vert \textbf{u}' \Vert ^2 \) at each frequency. Note that the Chu norm [43] is another common choice of norm for compressible flows, but is not chosen here to remain coherent with the incompressible resolvent analysis introduced in the following section.

The SPOD analysis is also conducted on the pressure fluctuations alone, yielding optimal structures in terms of a \(\Vert p'^2\Vert \)-energy, akin to the sound power, in order to provide an empirical model of the trailing edge noise.

The analysis is performed with the numerical code from Schmidt [42], using \(N_{\text {b}}=6\) blocks with an overlap of \(75\%\), resulting in \(N_{\text {FFT}}=187\) frequency bins per block. Although this number of blocks is rather low for SPOD, it is considered suitable for the analysis of the tones, considering the quasi-periodic nature of the flow [29]. It was confirmed by observing that although the frequency resolution was reduced with higher \(N_\text {b}\), the separation between the leading and sub-leading SPOD eigenvalues remained similar and the leading mode shapes remained almost identical when the number of blocks was doubled. Similarly to the spectral analysis of pressure fluctuations used to recover the acoustic spectrum in Fig. 2a, the SPOD analysis is done on the spanwise-averaged flow quantities.

3.2 Resolvent analysis

A resolvent analysis of the mean flow is used as the physics-based model of coherent hydrodynamic fluctuations. Following Reynolds and Hussain [17], flow quantities \(q=[\textbf{u},\,p]^{\text {T}}\) are decomposed into \(q=\bar{q}+\tilde{q}+q''\), where fluctuations around the time-averaged \(\bar{q}\) are split between a coherent term \(\tilde{q}\) with a quasi-periodic behavior, and a stochastic term \(q''\) corresponding to turbulent motion. Coherent fluctuations are defined by the difference of the ensemble average and the mean flow: \(\tilde{q}=\langle q\rangle - \bar{q}\).

The following derivations are based on the incompressible Navier-Stokes equations due to the low Mach number studied. After substituting the triple decomposition into the governing equations, transport equations of the coherent fluctuations are obtained by phase-averaging and subtracting the mean flow equations, leading to

$$\begin{aligned}{} & {} \nabla \cdot \tilde{u}=0\text {,} \end{aligned}$$
(3a)
$$\begin{aligned}{} & {} \frac{\partial \tilde{u}}{\partial t} + (\overline{u}\cdot \nabla ) \tilde{u} + (\tilde{u}\cdot \nabla ) \overline{u} + \nabla \tilde{p} - \nabla \cdot (\nu \nabla \tilde{u}) = \tilde{f}\text {,} \end{aligned}$$
(3b)

where \(\nu \) is the molecular viscosity and the nonlinear terms have been lumped into the forcing term

$$\begin{aligned} \tilde{f} = -\nabla \cdot \left( \tilde{u}\tilde{u} + \overline{\tilde{u}\tilde{u}}\right) - \nabla \cdot \widetilde{u''u''}, \end{aligned}$$
(4)

where the last term of \(\tilde{f}\) can be interpreted as the coherent fluctuation of the Reynolds stress [17].

Since we focus our analysis on the near-field of the airfoil, where the flow is either laminar or transitional, we assume that the influence of turbulent fluctuations on the forcing is negligible \(\widetilde{u''u''}\ll \tilde{f}\). In this case, the resulting formulation is equivalent to the one derived from the classical Reynolds decomposition without turbulence modeling [44], similar to Ricciardi et al. [29] for the same case.

The analysis is carried out in the frequency domain by applying a Fourier transform onto the fluctuations in time. Owing to the spanwise homogeneity of the setup and the periodic lateral boundary conditions in the LES, the time-averaged state is also spanwise averaged, while the fluctuations and forcing term are also Fourier-transformed in the spanwise direction, resulting in

$$\begin{aligned} \tilde{q}(x,\,y,\,z,\,t)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\widehat{q}(x,\,y)\text {e}^{i\left( k_{\text {z}}z-\omega t\right) }\text {d}k_{\text {z}}\text {d}\omega \text {,} \end{aligned}$$
(5)

with \(\omega \) the angular frequency and \(k_\text {z}\) the spanwise wavenumber. Analog to the SPOD analysis, only \(k_\text {z}=0\) is considered.

The equations with appropriate boundary conditions are then discretized, leading to the following system

$$\begin{aligned} \left( {\textbf {L}} - \omega {\textbf {B}}\right) \widehat{q}={\textbf {B}}_\text {f}\widehat{f}\text {,} \end{aligned}$$
(6)

where \({\textbf {L}}\), \({\textbf {B}}\), and \({\textbf {B}}_\text {f}\) are sparse matrices resulting from the finite-element discretization of the system (3). In contrast to linear stability analyses, the resolvent framework retains the harmonic forcing term \(\widehat{f}\) on the right hand side of Eq. (6), with the matrix \({\textbf {B}}_\text {f}\) defined such that no forcing is applied to the continuity equation. The system is then rearranged to explicitly express the relationship between the inputs \(\widehat{\eta }\) and outputs \(\widehat{y}\), reading

$$\begin{aligned} \widehat{y} = {\textbf {R}}(\omega )\widehat{\eta }\text {,} \end{aligned}$$
(7)

where \({\textbf {R}}\) is the resolvent operator which linearly maps any arbitrary volume forcing onto the response, at the real-valued angular frequency \(\omega \).

Similar to Towne et al. [33], the input and response are related to the forcing and coherent fluctuation terms of eq (6) through

$$\begin{aligned} \widehat{f}= & {} \mathcal {F}_\text {f}\,\widehat{\eta }\text {,}\nonumber \\ \widehat{y}= & {} \mathcal {F}_\text {y}\,\widehat{q}\text {,} \end{aligned}$$
(8)

where the \(\mathcal {F}_\text {f}\) and \(\mathcal {F}_\text {y}\) matrices are used to restrict the forcings and responses to a subset of the spatial domain near to the airfoil surface, similarly to Ricciardi et al. [29]. The resolvent domain is shown in Fig. 1b. This configuration focuses the analysis on perturbations near the surface, while filtering out spurious modes that have significant support in the freestream [29]. The resolvent operator is therefore explicitly given as

$$\begin{aligned} {\textbf {R}}=\mathcal {F}_\text {y}\left( {\textbf {L}} - \omega {\textbf {B}}\right) ^{-1}{} {\textbf {B}}_\text {f}\mathcal {F}_\text {f}. \end{aligned}$$
(9)

The objective of the resolvent analysis is then to find the pairs of inputs-outputs leading to the maximum gains of energy, where the gain, \(\sigma \), is defined as

$$\begin{aligned} \sigma ^2 = \frac{\langle \widehat{y},\,\widehat{y}\rangle }{\langle \hat{\eta },\,\hat{\eta }\rangle } = \frac{ \widehat{y}^\text {H} {\textbf {W}}_\text {y} ~ \widehat{y} }{ \widehat{\eta }^\text {H} {\textbf {W}}_{\eta }\widehat{\eta } }, \end{aligned}$$
(10)

with \({\textbf {W}}_\text {y}\) and \({\textbf {W}}_\eta \) the discretized matrices corresponding to the weights from the definition of the inner product (1) for the responses and forcing terms, respectively. In the present study, \({\textbf {W}}_\text {y}={\textbf {W}}_\eta ={\textbf {W}}\), such that \(\sigma \) represents the gain in terms of turbulent kinetic energy, analog to the SPOD analysis of Sect. 3.1.

Finally, it can be shown [45, 46] that pairs of forcing and response that maximize the gain at a given frequency are the solutions of the eigenvalue problem

$$\begin{aligned} {\textbf {W}}^{-1}{} {\textbf {R}}^{H}{} {\textbf {W}}{} {\textbf {R}}\widehat{\eta }=\lambda \widehat{\eta }\text {,} \end{aligned}$$
(11)

obtained by substituting Eqs. (7) and (9) into Eq. (10). The resulting eigenvalues \(\lambda \) are the optimal, squared gains \(\sigma _i^2\), and the corresponding eigenvectors \(\widehat{\eta }_i\) are used to obtain the optimal forcing modes \(\widehat{f}=\mathcal {F}_\text {f}\widehat{\eta }_i\), which define an orthogonal basis of forcings. Applying the resolvent operator on the set of optimal forcings yields the optimal response modes \(\widehat{y}_i\) that also span an orthogonal basis. The resulting triplets of \(\{\widehat{\eta },\,\sigma ,\,\widehat{y}\}_i(\omega )\) are ranked according to the gain-magnitude in descending order. If the first, i.e., the leading, gain is significantly larger than the remaining ones, the resolvent operator is said to exhibit low-rank behavior at this particular frequency. In this case, and provided that the forcing is not biased toward sub-optimal resolvent forcing modes [47], the response to a forcing can be approximated by the leading optimal gain, forcing and response alone.

The resolvent analysis is performed using the Finite Element Linearized (Combustion) Solver FELiCS [48]. We assume Dirichlet boundary conditions in the far field \(\left( \widehat{q}=0\right) \) for all quantities. Away from the airfoil, the otherwise constant molecular viscosity \(\nu \) is artificially increased to act as a sponge region and damp spurious solutions. The shape of the sponge region is the same as in Ricciardi et al. [29]. At the airfoil surface, Dirichlet conditions are imposed for the velocity fluctuations and a Neumann condition is imposed for the pressure. Computations are conducted over the same range of frequency as the SPOD analysis.

4 Hybrid acoustic modeling approach

This section describes the acoustic model used to retrieve the radiated sound field from SPFs. The results of this model are compared with the acoustic field extracted directly from the LES snapshots.

4.1 Curle’s acoustic analogy

As with most current aeroacoustic models [5], we use a formulation derived from Lighthill’s acoustic analogy [3] to model trailing edge noise. This formulation was proposed by Curle [32] in order to include solid boundaries in the acoustic wave propagation equation and will be referred to as Curle’s acoustic analogy.

For a two-dimensional domain, an analytical solution of Curle’s acoustic analogy may be derived by using a free-field Green’s function for the convected wave equation. According to Schram et al. [49], the sound pressure \(\widehat{p}_{\text {obs}}\) at an observer point \(\textbf{x}_{\text {obs}}\) can be related to the SPF \(\widehat{p}_{{\mathcal {S}}}\) on an impenetrable surface \(\mathcal {S}\) in the frequency domain by

$$\begin{aligned} \widehat{p}_{\text {obs}}\left( \textbf{x}_{\text {obs}},\,\omega \right) =\frac{ik_0}{4} \int _{\partial \mathcal {S}} \frac{r_{\text {i}} n_{\text {i}}}{r} H_1^{(2)}\left[ \frac{k_0}{\beta ^2} \left( r+M \left( \textbf{x}_{\mathcal {S}}-\textbf{x}_{\text {obs}}\right) \right) \right] \widehat{p}_{\mathcal {S}}\left( \textbf{x}_{\mathcal {S}},\,\omega \right) \text {d}x_{\mathcal {S}}\text {,} \end{aligned}$$
(12)

where n is the unit normal vector out of the airfoil surface, r is the distance to the observer, \(H_1^{(2)}\) is the Hankel function of second kind, \(\beta =\sqrt{1-M^2}\) is the Prandtl-Glauert factor, and \(\textbf{x}_{\mathcal {S}}\) is the surface coordinate.

Equation (12) considers only dipolar acoustic sources on the solid surface and neglects quadrupole sources related to velocity fluctuations in the flow, which is reasonable at low Mach numbers [32, 50]. In addition, the term between the brackets in Eq. (12) was added to the original formulation by Schram et al. [49] to account for uniform mean flow convection, similar to Sandberg et al. [8]. Non-uniform effects may play a role and modify sound radiation, as will be shown later.

The present formulation also assumes that the solid body is acoustically compact [49], which can be assessed by defining a Helmholtz number based on the chord length of the airfoil \(\mathcal {H}=c/\lambda _0=St\,M\), where \(\lambda _0=\) is the acoustic wavelength. For \(\mathcal {H}<1\), the body is acoustically compact and the model presented holds. However, Eq. (12) neglects the scattering of sound generated by the body over itself [49] for \(\mathcal {H}>1\), which may become relevant if it is not already accounted for in \(\widehat{p}_{{\mathcal {S}}}\).

To improve the convergence of the power spectral density from the sound pressure calculation, Eq. (12) is embedded in a Welch-like method and applied to each flow realization (or pressure-based SPOD mode). The final PSD is then obtained by averaging

$$\begin{aligned} \Vert \widehat{p}_{\text {obs}}^{\text {tot}}(\omega )\Vert ^2= \frac{1}{N_{\text {b}}} \sum _i^{N_{\text {b}}}\left\| \widehat{p}_{\text {obs}}^{\text {i}}(\omega )\right\| ^2, \end{aligned}$$
(13)

where \(N_{\text {b}}\) is the number of blocks to average over and \(\widehat{p}_{\text {obs}}^{\text {i}}\) is the sound pressure of the i-th realization. The corresponding sound pressure level in decibel is then defined as

$$\begin{aligned} L_{p}=10 \log _{10} \left( \frac{\widehat{p}_{\text {obs}}^{2}}{{p}_{0}^{2}}\right) \textrm{dB}, \end{aligned}$$
(14)

with a reference sound pressure \({p}_{0}=2 \times 10^{-5}~\textrm{Pa}\).

4.2 Sound-field from Curle’s analogy vs. LES data

To demonstrate the accuracy of Curle’s analogy, we apply the method to the LES surface pressure fluctuations and compare the resulting sound field against that directly extracted from the LES data using Welch method. The comparison is done in terms of radiated sound power and directivity.

Sound power is an important quantity for engineering applications as it is equivalent to the total noise emitted. It is readily obtained by integrating the PSD of the sound pressure over a surface when considering far-field conditions. Figure 3a shows the arc circle used for integration in the present two-dimensional framework. It excludes the wake region since pressure fluctuations associated with the turbulent wake are not captured by the acoustic model. Note that a rather short radius \(r=2\) is used here to avoid regions where the LES mesh becomes coarser and high-frequency acoustic waves are potentially filtered out.

Figure 3b–e show the comparison between the acoustic analogy and the LES. Overall, there is very good agreement between the two in terms of the sound power spectrum, although Curle’s analogy slightly underestimates the sound power for Strouhal \(\text {St}<9\). This trend is accentuated at higher frequencies, where the most of sound sources shift to smaller scale flow structures associated with the turbulent boundary layer near the trailing edge and wake. As quadrupole sources associated with turbulence are not included in the acoustic analogy, this discrepancy with the LES data is expected, but is limited to frequencies where the acoustic pressure is weak anyway.

Similarly, there is good agreement in terms of directivity, which has been normalized in the plots to compensate for the differences in PSD. The number and overall position of lobes in the directivity patterns, typical of airfoil trailing edge noise [50,51,52], are well captured for Strouhal numbers corresponding to both acoustically compact (\(\text {St}=0.53\)), in Fig. 3c, and non-compact (\(\text {St}=[{3.4},\,5.91]\)), in Fig. 3d, e, surfaces. The remaining discrepancies in directivity may be related to the non-uniformity of the flow around the airfoil, but the results of the acoustic analogy are considered satisfactory for the purposes of this study.

Fig. 3
figure 3

a Integration path (\(\hbox {-}\,\hbox {-}\,\hbox {-}\)) used to compute the sound power level around the airfoil, the contours indicate the distribution of the PSD at \(\text {St}=3.4\) for illustration purposes; b–e comparison of the sound power levels directly computed on LES pressure fluctuations (\(\hbox {---}\)) and from Curle’s acoustic analogy using the SPFs (\({\text {-}\,\cdot \,\text {-}}\)) in terms of b sound power level and (c–e) directivity

Full size image

5 Resolvent-based hydrodynamic modeling

In this section, we evaluate the ability of the incompressible resolvent analysis to capture the relevant hydrodynamic features of the flow, as resolvent modes form the basis of our trailing edge noise model.

5.1 Resolvent vs. SPOD modes

The SPOD analysis provides a reference for comparison with the resolvent modes. Figure 4a shows the SPOD spectrum obtained from velocity fluctuations near the airfoil (the domain considered is shown in Fig. 6). The eigenvalues associated with the most energetic SPOD mode display sharp peaks at the frequencies of the tones identified in the acoustic spectrum probed above the trailing edge (see Fig. 2a). These peaks are also observable for the first sub-leading mode, but become increasingly difficult to distinguish from the rest of the spectrum when considering the following sub-leading modes. At the tones, the large separation between the leading and sub-leading SPOD eigenvalues indicates a low-rank dynamic behavior, similar to the case of Symon et al. [26]. This gain separation is less pronounced for frequencies in-between the tones, as emphasized in Fig. 4b showing the normalized energy decay for the different SPOD modes. Hence, the hydrodynamic behavior of the flow is well approximated by the leading SPOD mode at the tones, while the system is governed by higher-order dynamics in-between the tones.

Fig. 4
figure 4

SPOD analysis of the LES data: a SPOD spectrum obtained from velocity snapshots. Asterisks indicate the frequencies for which mode shapes will be compared later in this paper; b Energy of the SPOD modes, normalized by the cumulative energy of all modes, at the main tone \(\text {St}=3.4\) (black) and in-between tones \(\text {St}=3.67\) (red). Results are shown for the velocity (\(\hbox {---}\)) and pressure (\(\hbox {-}\,\hbox {-}\,\hbox {-}\)) fluctuations

Full size image

The SPOD analysis is further performed on the pressure fluctuations. Similarly to the velocity field, spanwise-averaged realizations are also considered. Overall, the characteristics of pressure-based SPOD eigenvalues are similar to that based on the velocity fluctuations. In the spectrum, the same peaks are recovered (not shown). The separation between the eigenvalues also follows the same pattern as for the velocity SPOD, as shown in Fig. 4b. This suggests that the acoustic field at the tones is well approximated by the leading SPOD mode. This will be confirmed in the following sections.

Next, the results of the resolvent analysis are analyzed and compared against that of the SPOD. Beforehand, we emphasize two of the main differences between the present SPOD and resolvent analyses: (i) the SPOD is based on a compressible LES, which allows for the presence of acoustic feedback, whereas acoustic waves are absent in the incompressible resolvent; (ii) the SPOD is based on the nonlinear flow dynamics determined from LES, while the resolvent is based on the linearized mean field operator. Therefore, the latter cannot capture triadic interactions between nonzero frequency fluctuations. However, it does account for the interaction of fluctuations with the base state through linearization around the time-average.

The resolvent gain for the three leading modes are displayed in Fig. 5 as a function of the Strouhal number. A large gain separation is observed between the optimal and subsequent modes for most of the frequency range, except in the very low and high frequency limits. In contrast to the SPOD, we do not observe low gain separation in between the tones. Generally speaking, the large gain separation is indicative for a strong linear amplification mechanisms typical of flows with strong shear, like laminar separation bubbles, backwards facing step [53] and jets [54, 55]. It further suggests that the leading resolvent mode is a good approximation of the incompressible flow dynamics [26].

Fig. 5
figure 5

Three leading gains from the resolvent analysis of LES mean field

Full size image

The leading resolvent gain exhibits regularly spaced peaks of small relative amplitude. The frequency steps separating the peaks differ from that of the SPOD spectrum, suggesting a difference in the feedback mechanism compared to the compressible LES. The position of the peaks is found to be robust to changes in the resolvent domain size and the position of the sponge region, suggesting that they are not related to spurious feedback from domain truncation [56]. Instead, we suspect that the peaks are due to an intrinsic resonance mechanism caused by a feedback loop between evanescent pressure waves traveling upstream at infinite speed from the trailing edge and the downstream traveling wave packets. However, such resonance mechanism is expected to differ from the results for compressible flow at Mach 0.3, and hence this is not investigated further.

Fig. 6
figure 6

Real part of the pressure fluctuations obtained from (left column) the leading SPOD and (right column) resolvent modes at (top row) \(\text {St} = 0.53\), (middle row) \(\text {St} = 3.4\), and (bottom row) \(\text {St} = 8.87\). Contours levels are saturated to highlight low-amplitude acoustic fluctuations in the SPOD modes. The same Strouhal numbers are indicated with the “\(*\)” symbol on Figs. 4a and 5. The boundary layer height (\(\hbox {-}\,\hbox {-}\,\hbox {-}\)) and recirculation region (\(\hbox {---}\)) are also indicated

Full size image

Figure 6 compares the mode shape of the leading SPOD and resolvent mode, in terms of pressure fluctuations. The depicted frequencies correspond to low, main, and high -frequency tones, respectively, as indicated in Figs. 4a and 5 by red “\(*\)” symbols. In all cases, the modes take the shape of wavepackets propagating along the suction side of the airfoil near the trailing edge. Similar observations were made in previous related studies [11, 27, 29].

Several distinctions can be made between SPOD and resolvent modes. First, the agreement is excellent at moderate frequency while it strongly deteriorates for the very low and high frequency limits. At low frequency, the SPOD wavepacket is detached from the surface and concentrated near the flow reattachment region, which is not captured by the resolvent mode. At high frequency the SPOD modes extend into the wake, while the resolvent mode is confined to the suction side of the airfoil and located further upstream. Moreover, the SPOD modes show low amplitude acoustic waves radiating from the trailing edge. In contrast, the resolvent mode’s pressure field is nearly uniform away from the surface and of opposite sign on each side of the airfoil, representing evanescent pressure fluctuations.

Fig. 7
figure 7

Alignment between the optimal resolvent mode and most energetic SPOD mode considering both velocity components (\(\hbox {---}\)) or pressure (\(\hbox {-}\,\hbox {-}\,\hbox {-}\)) fluctuations

Full size image
Fig. 8
figure 8

a Alignment of the SPFs obtained over the airfoil from the leading SPOD (\(\hbox {---}\)) mode and the optimal resolvent (\({\text {-}\,\cdot \,\text {-}}\)) response; Comparison between the SPOD and resolvent SPF mode at the main tone (\(\text {St} = 3.4\)) in terms of b magnitude and c unwrapped phase angle. The curvilinear coordinate “s” starts at the trailing edge and increases as the profile is traveled in the counter-clockwise direction

Full size image

The comparison between the leading optimal resolvent mode and leading SPOD mode is extended to the full frequency range by considering the alignment between mode shapes [27, 44]. It is defined with the inner product of Eq. 1 as

$$\begin{aligned} \gamma _{ij} = \frac{|\langle q_i,\, q_j\rangle |}{|q_i ||q_j |}\text {,} \end{aligned}$$
(15)

where the operand \(|q_i |\) is the norm of the complex mode shape \(q_i\). A perfect alignment between mode shapes is indicated by \(\gamma _{ij}=1\), while \(\gamma _{ij}=0\) indicates orthogonal vectors. Note that alignment is only computed within the physically relevant region for trailing edge noise, close to the airfoil surface. This corresponds to the input/output region in the resolvent shown in Fig. 1b.

Figure 7 shows the alignment as function of frequency computed based on the velocity and pressure fluctuations, respectively. Both quantities exhibit similar overall trends. High alignment of \(\gamma \approx 80\%\) is found at the main tones at moderate frequencies, and it drops below \(50\%\) for the high frequencies range of \(\text {St}>6.6\). These high frequencies correspond to the range of decreasing gain separation of the RA and the SPOD. Hence, the incompressible resolvent presented here turns out to be suitable to model the low rank flow dynamics present at low and moderate frequencies.

5.2 Resolvent-based modeling of SPFs

We now focus the analysis on the SPFs associated with the hydrodynamic features examined in the previous section, as they serve as input to the acoustic model. The SPFs are extracted from resolvent modes around the airfoil contour and compared with the pressure-based SPOD modes. For this purpose, a curvilinear coordinate system referred to as “s” is adopted. The system commences at the trailing edge (\(s=0\)) and progresses counter-clockwise around the profile.

Figure 8 displays the alignment between the SPFs obtained from the optimal resolvent and leading SPOD modes. Results show a similar trend to the alignment based on the velocity field shown in Fig. 7. The highest alignment is obtained for Strouhal numbers between \(1\le \text {St}\le 6\), with maximum values of about \(95\%\) at the main tones. With increasing frequency, the alignment between SPOD and resolvent modes decreases until they become approximately orthogonal at \(\text {St}=13\). Considering the very high alignments at moderate frequencies, we conclude that the incompressible resolvent analysis models the SPFs very accurately in the range where the tones occur.

The alignment between the SPF from the SPOD and the resolvent is, however, biased toward regions where the fluctuations have high amplitudes. As will be shown, low-amplitude pressure waves on the airfoil surface are also crucial when trying to reproduce the directional patterns of TE noise, but their relative importance is masked when relying solely on the alignment as defined in Eq. 15. This is highlighted in Fig. 8b where the SPF of SPOD and resolvent modes are plotted along the surface coordinate s using a semilogarithmic scale. Note that for this comparison the resolvent mode was first scaled such that its amplitude matches that of the SPOD at the point where the amplitude of the SPOD mode is maximum: \(s(\max (\Vert \tilde{p}_{\text {spod}}\Vert ))\). The figure reveals that if the SPOD and resolvent modes are aligned to have similar amplitudes near the trailing edge (near \(s=0\) and \(s=2\)), they however differ by one order of magnitude close to the leading edge (\(s=1\)).

The reason for this difference is explained when examining the phase angle of the SPFs, as shown in Fig. 8c. Both the resolvent and SPOD modes reveal downstream-traveling waves on the suction side near the trailing edge, as indicated by the positive slope of the phase angle \(\phi \) for \(0\le s\le 0.5\). However, the SPOD analysis also captures acoustic upstream-traveling waves propagating with the speed of sound toward the leading edge, as indicated by a negative (resp. positive) slope for \(s\le 1\) (resp. \(s\ge 1\)). In sharp contrast, the resolvent predicts nearly infinitely fast propagating waves (nearly zero slope), consistent with the incompressibility condition, which correspond to evanescent pressure fluctuations.

The acoustic nature of the upstream-traveling waves captured by the SPOD is confirmed by examining the phase speed of the SPF. It is defined as \(c_{\text {ph}}=\omega /k_{\text {s}}\), with \(k_{\text {s}}=\partial \phi /\partial s\) as the wavenumber along the airfoil surface. Note that the sign of the phase speed was adjusted to describe downstream- (upstream-) traveling waves for \(c_{\text {ph}} > 0\) (\(c_{\text {ph}}<0\)) respectively for all s. Figure 9 reveals that on the suction side near the trailing edge, both the resolvent and SPOD analyses show pressure fluctuations traveling downstream at roughly \(60\%\) of the freestream velocity, indicating the propagation of hydrodynamic structures. In other regions of the surface, however, the SPOD captures the upstream-propagating acoustic waves traveling at phase velocities corresponding to \(c_{\text {ph}}=-(a_0-u_{\infty })\). This is not captured by the resolvent modes, as it is based on an incompressible formulation. As will be shown later, this deviation has a non-negligible impact on the acoustic field obtained from the acoustic low-order model.

Fig. 9
figure 9

Comparison of the SPF phase speed over the surface of the airfoil obtained from the SPOD (\({\text {-}\,\cdot \,\text {-}}\)) and resolvent (\(\hbox {---}\)) modes for \(\text {St}=3.4\) (up) and \(\text {St}=8.87\) (down). The speed of upstream-traveling acoustic waves, \(c_{\text {ph}}=-(a_0-u_{\infty })\), is indicated with the dashed line. All speeds are normalized with the freestream velocity

Full size image

6 Low-order trailing edge noise prediction

Curle’s acoustic analogy is applied to the SPF extracted from both the SPOD and resolvent modes presented in the previous section. With the former, we will assess to what extend the acoustic field is driven by the most energetic coherent structure (the leading SPOD mode), while with the latter we intend to asses the quality of the physics-based TE noise model.

6.1 SPOD-based model

The acoustic field from the empirical model is obtained by inserting the SPF from the leading SPOD mode into Eq. (12). As the accuracy of Curle’s solution has been assessed in Sect. 4, the results of the acoustic analogy using the leading SPOD mode can be compared with those of the same analogy applied to the SPF extracted directly from the LES.

Figure 10a shows the acoustic power, integrated over a circle of radius \(r=2c\) and centered at the trailing edge. The predictions based on the leading SPOD mode is in very good agreement with that obtained from the LES data for most of the frequency range, with the exception of very high frequencies (\(\text {St}\ge 12\)). There, the dynamics are no longer low-rank and more SPOD modes should be considered to reconstruct the TE noise, as shown in Fig. 10c. This is also the case in-between the peaks where we also observe slight disagreements.

The directivity of the predicted acoustic fields is shown in Fig. 10b for the main tone frequency, and in Fig. 10c for a frequency in between tones. At the tones, the position of the lobes and amplitude of the PSD in the directivity pattern are very well predicted by the SPOD-based model. In between the tones, the position and number of the lobes is still well predicted, but the amplitude is under-predicted. Note that this observation held true for most of the frequency range.

Fig. 10
figure 10

Comparing results from Curle’s method applied to the SPFs from the SPOD modes against Curle’s results using directly the LES SPFs: a integrated acoustic power from the LES (black) and SPOD (orange); b directivity at the main tone (\(\text {St}=3.4\)) from the SPFs of the LES (\(\hbox {---}\)) and first SPOD mode (\(\hbox {-}\,\hbox {-}\,\hbox {-}\)); c directivity for frequency in-between tones, at \(\text {St}= 10.125\), using SPFs from the LES (\(\hbox {---}\)), and from the summation of an increasing number of SPOD modes (\(\hbox {-}\,\hbox {-}\,\hbox {-}\)), starting from the leading mode alone and including up to all modes (\(N_{\text {b}}=6\)) following the arrow

Full size image

Overall, the SPF extracted from the leading SPOD mode combined with Curle’s acoustic analogy proves to be an accurate estimate of the trailing edge noise radiated by the airfoil for most of the frequency range. The frequencies at which the model is less accurate, either in between tones or at the high end of the frequency range, correspond to low sound power levels and are therefore less relevant.

Fig. 11
figure 11

Comparison of the total acoustic power obtained from Curle’s acoustic analogy applied to the leading SPOD mode (\(\hbox {-}\,\hbox {-}\,\hbox {-}\)) and the optimal resolvent mode (\(\hbox {---}\)) scaled at: a the maximum amplitude of the SPOD mode; b a fixed position near the trailing edge (\(s=0.2\))

Full size image

6.2 Resolvent-based model

A similar procedure to that of the previous section is now applied to the SPF extracted from the optimal resolvent mode. The SPF from resolvent modes are calibrated at each frequency using a complex-valued weight [26] obtained from the pressure fluctuations of the leading SPOD mode at a single point on the airfoil surface. Complex factors are defined as the ratio of the complex SPOD and resolvent modes at this point:

$$\begin{aligned} \chi =\tilde{p}_{\text {spod}}(\omega ,\,s_{\text {p}})/\tilde{p}_{\text {RA}}(\omega ,\,s_{\text {p}}). \end{aligned}$$

Note that the sub-optimal resolvent modes are considered insignificant, due to the low-rank behavior of the system observed in both the SPOD and resolvent analyses at relevant frequencies

Two strategies are followed for choosing the position of the calibration factor probe \(s_{\text {p}}\). First, we use a fixed position for all frequencies and select a location where the hydrodynamic pressure fluctuations have significant amplitude on the suction side near the trailing edge (we selected \(s_{\text {p}}=0.1\) and \(s_{\text {p}}=0.2\)). Second, we use the position where the pressure amplitude of the SPOD mode is maximum on the airfoil surface, which varies as a function of frequency. Note that the former approach can easily be applied to experiments as it only requires a single well-positioned sensor, whereas the latter strategy would require an array of sensors placed along the chord.

Figure 11 compares the radiated sound power predicted by the acoustic analogy applied to the SPF of the optimal resolvent mode and with that of the leading SPOD mode. The PSD is again integrated over a circle of radius \(r=2c\) centered at the trailing edge, and results are shown for both the fixed and frequency-dependent calibration positions. Overall, a good agreement between the empirical and resolvent-based models is found, for both fixed calibration positions, in the range of frequencies \(0.35 \le \text {St}\le 6.8\), corresponding to a high alignment between resolvent and SPOD leading SPF modes. The agreement is even better for the frequency-dependent calibration position, with good agreement up to frequencies of \(\text {St}\approx 10\), thus covering most of the frequency range with significant sound power levels. Overall, both scaling methods result in an overshoot of about 4 dB at the main tone, however, the relative amplitudes of tones are well captured. As expected, the resolvent-based model underperforms at very low and high frequencies (\(\text {St}\le 0.35\), \(\text {St}\ge 10\)), where we also encountered poor alignment between SPOD and resolvent modes.

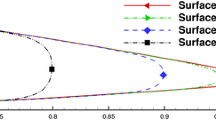
The evaluation of the resolvent-based model is completed by a comparison of the normalized directivity patterns, as shown in Fig. 12 for three different Strouhal numbers. At the lower Strouhal number of \(\text {St}=0.53\), the airfoil is acoustically compact, as characterized by \(\mathcal {H}=\text {St}\,M\approx 0.16\), which results in the dipolar directivity pattern observed in Fig. 12a. In this case, the resolvent-based model captures the position and respective amplitudes of the two lobes very well. A very similar result is presented by Wagner & Sandberg [35] using a similar method for a NACA0012 at \(\alpha =0\) deg and \(\text {Re}=2\times 10^4\). For higher frequencies, the agreement significantly deviates. The resolvent-based model retrieves only two lobes directed slightly downstream, while the SPOD-based model shows an increasing number of lobes directed upstream with increasing frequency.

Fig. 12
figure 12

Normalized directivity plots for the empirical (black) and physics-based (blue) models at a \(\text {St}=0.53\), b \(\text {St}=3.4\), and c \(\text {St}=8.87\). The directivity of a hybrid SPF distribution (\({\text {-}\,\cdot \,\text {-}}\)) between the resolvent and SPOD which effectively filters out the upstream-traveling acoustic waves from the SPOD is added to (b)

Full size image

The deviation of the resolvent-based prediction of the directivity at higher frequencies can be explained by constructing a hybrid model. This model is composed of the SPOD mode along the suction side near the trailing edge and the resolvent mode for the rest of the surface. This mode-merging procedure is performed at the main tone frequency (\(\text {St}=3.5\)), where the SPFs of the SPOD and resolvent modes are very similar. Figure 13 shows the SPF distribution of this hybrid model, where a smoothing spline function is used to avoid discontinuities between the two distributions. Practically, this hybrid model allows to decouple the influence of SPFs caused by the downstream-traveling hydrodynamic wavepacket from that of back-scattered acoustic waves in the radiated sound.

The directivity pattern predicted from this hybrid SPF model and Curle’s acoustic analogy is included in Fig. 12b. Accordingly, the hybrid model shows a much better agreement with the resolvent-based model than when using the full SPOD pressure fluctuations. The number and position of lobes match that of the physics-based model. This highlights the importance of small-amplitude back-scattered acoustic waves for the directivity pattern observed in the data.

Fig. 13
figure 13

At the main tone (\(\text {St}=3.5\)), real part of the SPF from the optimal resolvent (\(\hbox {-}\,\hbox {-}\,\hbox {-}\)) and leading SPOD (\(\hbox {---}\)) modes; as well as the hybrid SPF distribution () obtained by merging the two models on the suction side of the airfoil, upstream of the hydrodynamic wavepacket (\(s=0.44\)). A second merging of the SPF is done near the trailing edge on the pressure side in order to respect the Kutta condition

Full size image

To get an impression of the global sound field, the radiated acoustic field of the empirical and resolvent-based models are illustrated in Fig. 14. The comparison is shown for a low frequency where the airfoil is acoustically compact and at the main tone where this is not the case. For the latter, the sound field determined from the incompressible resolvent is mainly directed downstream of the trailing edge, while the opposite is observed for the empirical model. This is not the case for the low Helmholtz number case. Therefore, the applicability of the physics-based model in its current form is limited to low Helmholtz numbers for accurate directivity predictions. However, it may still estimate the radiated sound power with reasonable accuracy, as seen in Fig. 11.

Fig. 14
figure 14

Comparison of the acoustic fields radiated by using Curle’s solution on the SPF from the empirical model (left column) and the physics-based model (right column), at a low Strouhal number \(\text {St} = 0.53\) (top row) and at the main tone \(\text {St} = 3.4\) (bottom row). Contours show the real part of the complex pressure field and highlight the differences in terms of directivity from the two approaches

Full size image

7 Summary and Conclusions

In this study, we developed and evaluated a physics-based, reduced order model of the trailing edge noise generated by an airfoil at low angle of attack. Our model relies on pressure fluctuations on the airfoil surface, which are obtained from the leading incompressible resolvent mode about the mean flow. These pressure fluctuations are then incorporated into Curle’s solution to Lighthill’s acoustic analogy to compute the acoustic field. The input to the model are the mean flow and a single point surface pressure spectrum to scale the amplitude of the resolvent mode. While most state-of-the-art SPF models are based on empirical arguments [5], the advantage of the present physics-based model is that it is easily transferable to other airfoil shapes and flow parameters, provided that the mean flow is known and its dynamics are low rank over the frequency range of interest.

Our model was evaluated for the flow around a NACA0012 airfoil at transitional Reynolds number \(\text {Re}=5\times 10^4\), low Mach number \(M=0.3\), and low angle of attack \(\alpha =3\deg \). In this setup, tonal trailing edge noise dominates the sound field [29], which is characterized by regularly spaced peaks in the acoustic spectrum. The resolvent analysis is performed on the spanwise and time-averaged flow obtained from a compressible LES. Likewise, only spanwise coherent structures with spanwise wavenumber \(k_z=0\) are considered as they fulfill the edge scattering condition [11, 27, 39]. The results from the resolvent analysis are compared to the wavepackets determined from SPOD of the LES snapshots, considering velocity fluctuations in the airfoil’s boundary layer, associated SPFs, and radiated acoustic fields through Curle’s acoustic analogy.

A good agreement is found between the leading SPOD and optimal resolvent mode at the frequency of the main tones. Alignment values between resolvent and SPOD modes of up to \(80\%\) are observed at these frequencies, which suggests that the incompressible resolvent analysis is able to accurately model the dominant wavepackets propagating in the airfoil’s boundary layer as predicted by the compressible LES.

When assessing the SPFs employed to derive the radiated acoustic field via Curle’s analogy, an excellent match is found between the optimal resolvent and leading SPOD modes at the tonal frequencies. This is quantified by alignment values of up to \(95\%\). However, we demonstrate that the absence of back-scattered acoustic waves in the resolvent modes has a dramatic effect on the directivity patterns of the sound emitted by the resolvent-based model at frequencies where the airfoil is not acoustically compact. This observation extends the results of Wagner et al. [34, 35] who used a similar methodology to study a NACA0012 at \(\text {Re}=2\times 10^4\). Their results were obtained at a single frequency that resulted in a dipolar directivity pattern, which is typical of acoustically compact surfaces. However, this is not the case here, as the airfoil is not acoustically compact for \(\text {St}>c/M~\approx 3.3\) and back-scattered acoustics become relevant. A compressible formulation of the resolvent could potentially address this.

At high Strouhal numbers, the resolvent modes strongly deviate from the SPOD modes, even though a large separation is still found in the resolvent gain. This leads to a deviation of the acoustic prediction. We conjecture that this mismatch is caused by the nonlinear triadic interaction between the discrete modes at the tonal frequencies, which are not captured by the present resolvent approach. In this regard, the methodology proposed by Symon et al. [26] to obtain the nonlinear “parasitic modes” from a nonlinear forcing composed of limited triadic interactions of known resolvent modes could be used to extend the present work.

In conclusion, the resolvent-based model presented here can accurately predict the sound power emitted by the airfoil provided that the SPF-spectrum is known at a single surface point close to the trailing edge, within 4 dB of the reference provided by the leading SPOD mode. We further assessed that the leading SPOD mode alone offers an accurate data-driven model of TE noise across most of the frequency range for the case studied. By adjusting the scaling position of the resolvent modes, we observed improvements in the prediction at the main tones, achieving errors within \(2~{\textrm{dB}}\), but at the cost of accuracy in higher-frequency prediction.

In the future, this modeling approach could be utilized to optimize airfoil shapes with the aim of reducing the overall sound power emitted. This could be achieved by combining a low-fidelity mean field solver with an appropriate scaling strategy for the point-wise SPF spectrum. It remains to be seen how well this method can be applied to model the broadband TE noise encountered at higher Reynolds numbers. We expect higher spanwise wave numbers to become important in this case, which is easily implemented in this approach, and we expect the incompressible limit of the solver to be even better justified due to the absence of tonal frequencies and associated acoustic feedback mechanism.