1 Introduction

In modern engineering, one of the main challenges is to optimize processes regarding costs and efficiency. In simulation processes, the material model has a big impact on time efficiency and accuracy. All existing theories are a compromise between generality and applicability. On the one hand, there are detailed material models which are based on the micro-scale behavior of the material. In this case, the physical properties on the micro-scale are modeled. These calculations are very expensive especially in the case of structure models. On the other hand, there are phenomenological models which show the main features of the material on the macro-scale. An overview of different continuum mechanical models is given, e.g. in [4]. These models provide fast calculations but the accuracy strongly depends on the mathematical model and the understanding of the material behavior.

For predicting large plastic deformations of a material within the finite element program Abaqus there are generally two different possibilities. The first one is to use the Abaqus internal material laws with the NLGEOM option (non-linear geometry). The second possibility is to use the material subroutine UMAT. Here it is possible to develop own material laws which are able to predict the behavior of the material during large plastic deformation. In this article we will use the second option and develop a finite elasto-plasticity theory for large plastic deformations. For the elastic part of the model, we use the physically linear elastic St. Venant–Kirchhoff reference law (see for example [4]) which is constant and denoted with the \(2^{\textrm{nd}}\) Piola-Kirchhoff stress tensor. For the plastic part the isomorphy concept after [5,6,7,8,9] and [10,11,12] is used. They have developed a finite plasticity theory which is based on the transformation of the elastic law during yielding. For many materials, it is known that the elastic behavior remains almost unchanged during large plastic deformations in the sense that in every elastic region after any plastic deformation the local elastic law is obtained from a push-forward of the elastic reference law. Examples are crystal plasticity and isotropic von Mises plasticity. We use an isotropic yield condition following the \(J_2\) theory by [1, 2], and [3]. This means that the equivalent stress only depends on the second principle invariant of the deviatoric part of the Cauchy stresses. The yield condition is formulated using the principle of maximum plastic dissipation. After formulating the material equations we present the numerical implementation in the Abaqus user subroutine UMAT with the programming language Fortran. Finally, we validate the material model by comparing the results with the literature and with the Abaqus internal material law.

Subsequently, we use this material model to determine the effective stiffness of arbitrary inhomogeneous materials before and after large deformations. We will perform test deformations \({\mathop {{\varvec{ E}}}\limits ^{\tiny {\text {G}}}}\) on different materials. Together with the resulting \({\mathop {{\varvec{ T}}}\limits ^{\tiny {\text {2PK}}}}\) stresses, we calculate the stiffness tetrad \({\mathbb { K}}\) during the post-processing with the computer algebra system Mathematica. The entire program code is given in the Appendix. A detailed procedure is described to determine the material stiffness by applying small elastic test deformations. This procedure can be applied to an initial material or to a material after a certain deformation process. In [13] and [14], the utility of this procedure described here is extensively demonstrated. In particular, the development of material stiffness during deformation processes is discussed.

2 Material law

In the following section we develop the material law with its elastic and plastic part. We also present the numerical implementation into the Abaqus subroutine UMAT and the Fortran source code in the appendix.

2.1 St. Venant–Kirchhoff elasticity

For the elastic deformation of the material, we use the physically linear elastic St. Venant-Kirchhoff reference law. It is constant and denoted with the \(2^{\textrm{nd}}\) Piola-Kirchhoff stress tensor:

$$\begin{aligned} {\mathop {{\varvec{ T}}}\limits ^{\tiny {\text {2PK}}}}=J{\varvec{ F}}^{-1}{\varvec{ T}}{\varvec{ F}}^{-T} \end{aligned}$$
(1)

with J being the determinant of the deformation gradient \({\varvec{ F}}= \text {grad}\left( X \right) \), and \({\varvec{ T}}\) the Cauchy stress tensor. The initial elastic law \({\varvec{ K}}_0\) can be written with the Green strain tensor \({\mathop {{\varvec{ E}}}\limits ^{\tiny {\text {G}}}}= \frac{1}{2}\left( {\varvec{ C}}-{\varvec{ I}}\right) \), the right Cauchy-Green tensor \({\varvec{ C}}={\varvec{ F}}^{T}{\varvec{ F}}\), the second-order unity tensor \({\varvec{ I}}\) and the material stiffness tetrad of fourth-order \({\mathbb { K}}_0\) as

$$\begin{aligned} {\mathop {{\varvec{ T}}}\limits ^{\tiny {\text {2PK}}}} = {\varvec{ K}}_0\left( {\varvec{ F}}\right) = {\mathbb { K}}_0:{\mathop {{\varvec{ E}}}\limits ^{\tiny {\text {G}}}}\ . \end{aligned}$$
(2)

With the right Cauchy-Green tensor \({\varvec{ C}}={\varvec{ F}}^{T}{\varvec{ F}}\) we can write this elastic law as

$$\begin{aligned} {\mathop {{\varvec{ T}}}\limits ^{\tiny {\text {2PK}}}} = {\varvec{ K}}_0\left( {\varvec{ F}}\right) =\frac{1}{2} {\mathbb { K}}_0 : \left( {\varvec{ F}}^{\text {T}}{\varvec{ F}}-{\varvec{ I}}\right) \ . \end{aligned}$$
(3)

2.2 Isomorphy concept for large deformations

It is a well-known fact that the elastic behavior of a material hardly changes during large plastic deformations. Therefore, we want to use a plasticity theory with isomorphic elastic ranges. To transform between these elastic ranges, we use a second-order tensor \({\varvec{ P}}\). With this plastic transformation \({\varvec{ P}}\), we will be able to calculate the current elastic law \({\varvec{ K}}_{\text {p}}\) for the reference placement (see [12]) by the following equation:

$$\begin{aligned} \overset{\tiny {2PK}}{{\varvec{ T}}} = {\varvec{ K}}_{\text {p}}\left( {\varvec{ F}}\right) ={\varvec{ P}}{\varvec{ K}}_0 \left( {\varvec{ P}}^{\text {T}}{\varvec{ F}}^{\text {T}} {\varvec{ F}}{\varvec{ P}}\right) {\varvec{ P}}^{\text {T}} \ . \end{aligned}$$
(4)

If we now insert our chosen elastic reference law \({\varvec{ K}}_0\) Eq. (3) in Eq. (4), we will be able to calculate the \(2^{\textrm{nd}}\) Piola–Kirchhoff stress tensor in the reference placement

$$\begin{aligned} \overset{\tiny {2PK}}{{\varvec{ T}}} ={\varvec{ K}}_{\text {p}}\left( {\varvec{ F}}\right) ={\varvec{ P}}\left( \frac{1}{2} {\mathbb { K}}_0 : \left( {\varvec{ P}}^{\text {T}}{\varvec{ F}}^{\text {T}} {\varvec{ F}}{\varvec{ P}}-{\varvec{ I}}\right) \right) {\varvec{ P}}^{\text {T}} \ . \end{aligned}$$
(5)

which can also be written with the Rayleigh product

$$\begin{aligned} \overset{\tiny {2PK}}{{\varvec{ T}}} ={\varvec{ K}}_{\text {p}}\left( {\varvec{ F}}\right) =\frac{1}{2} \left( {\varvec{ P}}* {\mathbb { K}}_0 \right) : \left( {\varvec{ F}}^{\text {T}}{\varvec{ F}}- {\varvec{ P}}^{-T}*{\varvec{ I}}\right) \ . \end{aligned}$$
(6)

The Rayleigh product is defined between a second-order tensor and a tensor of arbitrary order

$$\begin{aligned} {\varvec{ A}}*\overset{\langle n \rangle }{{\mathbb { K}}}\ = K_{\underbrace{i \ldots p}_{n\text { indices}}} \underbrace{({\varvec{ A}}{\varvec{ e}}_i)\otimes \ldots \otimes ({\varvec{ A}}{\varvec{ e}}_p)}_{n\text { times}},\qquad K_{\underbrace{i \ldots p}_{n\text { indices}}}=\overset{\langle n \rangle }{{\mathbb { K}}}\underbrace{\cdot \ldots \cdot }_{n\text { dots}} \underbrace{{\varvec{ e}}_i\otimes \ldots \otimes {\varvec{ e}}_p}_{n\text { times}}. \end{aligned}$$
(7)

It changes the basis while keeping the components, which can be used, e.g., to represent rotations. For second-order tensors it can be written as \({\varvec{ A}}*{\varvec{ T}}={\varvec{ A}}{\varvec{ T}}{\varvec{ A}}^\text {T}\). It is associative in the first factor, i.e. \(({\varvec{ A}}{\varvec{ B}})*{\mathbb { K}}={\varvec{ A}}*({\varvec{ B}}*{\mathbb { K}})\) and linear in the second factor, i.e. \({\varvec{ A}}*({\mathbb { K}}_1+\alpha {\mathbb { K}}_2)={\varvec{ A}}*{\mathbb { K}}_1+\alpha {\varvec{ A}}*{\mathbb { K}}_2\). Now we continue with Eq. (5) and use the relation

$$\begin{aligned} \widetilde{{\varvec{ F}}} = {\varvec{ F}}{\varvec{ P}} \end{aligned}$$
(8)

resulting from the isomorphy condition and notate the stresses in all three placements.

  • Reference placement:

    $$\begin{aligned} \overset{\tiny {2PK}}{{\varvec{ T}}}={\varvec{ P}}\left( \frac{1}{2} {\mathbb { K}}_0 :\left( \widetilde{{\varvec{ F}}}^{\text {T}}\widetilde{{\varvec{ F}}}-{\varvec{ I}}\right) \right) {\varvec{ P}}^{\text {T}} \end{aligned}$$
    (9)

  • Intermediate placement:

    $$\begin{aligned} \overset{\widetilde{\tiny {2PK}}}{{\varvec{ T}}}=\frac{1}{2} {\mathbb { K}}_0:\left( \widetilde{{\varvec{ F}}}^{\text {T}}\widetilde{{\varvec{ F}}}-{\varvec{ I}}\right) \end{aligned}$$
    (10)

  • Current placement:

    $$\begin{aligned} {\varvec{ T}}=\frac{1}{\widetilde{J}} \widetilde{{\varvec{ F}}}\left( \frac{1}{2}{\mathbb { K}}_0:\left( \widetilde{{\varvec{ F}}}^{\text {T}}\widetilde{{\varvec{ F}}}-{\varvec{ I}}\right) \right) \widetilde{{\varvec{ F}}}^{\text {T}} \end{aligned}$$
    (11)

2.3 Yield condition

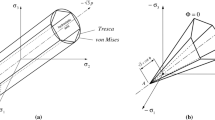
In this section we will introduce a suitable yield condition. We use an isotropic yield condition following the \(J_2\) theory by [1, 2] and [3]. This means that the equivalent stress only depends on the second principle invariant of the deviatoric part of the Cauchy stresses. Together with the yield stress \(\sigma _{\text {F}} = const.\), we get the yield condition as

$$\begin{aligned} \sqrt{\frac{3}{2}} \Vert {\varvec{ T}}^{'} \Vert - \sigma _{\text {F}} = 0\ . \end{aligned}$$
(12)

We start with the stress power defined as

$$\begin{aligned} l = \frac{1}{\rho } {\varvec{ T}}: {\varvec{ L}}\ . \end{aligned}$$
(13)

Together with Eq. (8), we write the velocity gradient \({\varvec{ L}}\) as

(14)

and insert it into Eq. (13)

(15)

with \(\widetilde{{\varvec{ F}}} = {\varvec{ F}}{\varvec{ P}}\), and assume the principle of maximum plastic dissipation. The dissipation D will be maximal if the scalar product is maximal and this is the case for with an undetermined skew part of which is arbitrary. Together with the consistency parameter \(\lambda \) the yield condition has the following form:

(16)

Now we replace the Cauchy stress tensor \({\varvec{ T}}\) by the \(2^{\textrm{nd}}\) Piola-Kirchhoff stress tensor \(\overset{\widetilde{\tiny {2PK}}}{{\varvec{ T}}}\)

(17)

We use the relation \(\rho _0 = \widetilde{J} \rho \) and rewrite as follows:

(18)

We take the deviatoric part of the right Cauchy-Green tensor \(\widetilde{{\varvec{ C}}}\) because \({\text {det} }\left( {\varvec{ P}} \right) = 1\) and therefore

(19)

and end up with the final form of our evolution equation

$$\begin{aligned} \dot{{\varvec{ P}}}= -\widetilde{\lambda } {\varvec{ P}}\left( \overset{\widetilde{\tiny {2PK}}}{{\varvec{ T}}} \widetilde{{\varvec{ C}}}\right) ^{'} \ . \end{aligned}$$
(20)

2.4 Numerical implementation

This section shows the implementation of the material model in the Abaqus user subroutine UMAT with the programming language Fortran. To solve the problem, we use the implicit Euler scheme (see [15])

$$\begin{aligned} {\varvec{ P}}_{n+1} = {\varvec{ P}}_{n} + \Delta t \dot{{\varvec{ P}}}_{n+1} \end{aligned}$$
(21)

together with the flow rule we get

$$\begin{aligned} {\varvec{ P}}_{n} = {\varvec{ P}}_{n+1}\left( {\varvec{ I}}+ \lambda \left( \overset{\widetilde{\tiny {2PK}}}{{\varvec{ T}}}_{n+1}\widetilde{{\varvec{ C}}}_{n+1}\right) ^{'} \right) \ . \end{aligned}$$
(22)

As the next step, we use the exponential map (see [16]) to ensure \({\varvec{ P}}\in \textit{Unim}^+\). With the power series for the \({\text {exp} }\left( x \right) \) function

$$\begin{aligned} {\text {exp} }\left( x \right) = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + ... \approx 1 + x \ , \end{aligned}$$
(23)

we obtain

$$\begin{aligned} {\varvec{ P}}_{n} \approx {\varvec{ P}}_{n+1} \ {\text {exp} }\left( \lambda \left( \overset{\widetilde{\tiny {2PK}}}{{\varvec{ T}}}_{n+1} \widetilde{{\varvec{ C}}}_{n+1}\right) ^{'} \right) \ . \end{aligned}$$
(24)

The final residuum to solve the problem with Newton’s method (see [17]) reads

$$\begin{aligned} {\varvec{ R}}= {\text {ln} }\left( {\varvec{ P}}^{-1}_{n+1}{\varvec{ P}}_{n} \right) - \lambda \left( \overset{\widetilde{\tiny {2PK}}}{{\varvec{ T}}}_{n+1} \widetilde{{\varvec{ C}}}_{n+1}\right) ^{'} \ . \end{aligned}$$
(25)

The algorithm for this method is found in Appendix B.5.

3 Python script

For a better overview, the Python script generating the RVEs and performing the starting and test calculations is divided into different parts. In Fig. 1 a flowchart provides an overview over the different Python scripts, Fortran subroutines and functions and the Mathematica post-processing.

Fig. 1
figure 1

Flowchart giving an overview of the used Python, Fortran, and Mathematica codes

Full size image

3.1 Starting calculation 1: “0_A.py”

The main part which has to be started is called “0_A.py” (see Appendix A.1). This script first calls “0_subroutines.py” (see Appendix A.9) to initialize subrountines like the calculation of a matrix determinant or a matrix multiplication. Afterward the displacement gradient \({\varvec{ H}}_0\) is prescribed. Next the script “0_RVE.py” is called.

After that, the material parameters will be imported from the file 0_material.py (see Appendix A.11). At this point, the subrountine 0_rve.py is finished.

The next step is to write the Abaqus input file. We are able to distinguish between different operating systems like Windows or Linux on which the Python script is running. The syntax slightly differs.

Hereinafter, the Abaqus Step definitions are given. Step 1 is the loading step prescribing the deformation as displacement following \({\varvec{ H}}_0\). In Step 2, the unloading takes place. Two different methods are distinguished. In case of uni-directional tension, the load is gradually removed (tension components, two shear components, finally the whole \({\varvec{ H}}_0\)) to avoid rotations. \({\varvec{ H}}_0\) is removed at once in all other cases.

After the step definitions, the subroutine “0_job.py” is called (see Appendix A.10) using the before defined input file name “inpname” and the “cpunumber”. The script will detect when the job is finished by checking the lock file. Also the successful execution is verified, else an error file is generated.

figure a

In the last section of the Python script “0_A.py”, the post-processing is performed. Therefore the node numbers of the three artificial nodes are searched. Then the output database ODB is opened and the reaction forces (RF1, RF2 and RF3) such as the displacements (U1, U2 and U3) are read out. The predeformation is saved in the text file “K0_ANLAUFRECHNUNG_H0.txt” and the unloaded placement as \({\varvec{ H}}_1\) as “K0_ANLAUFRECHNUNG_H1.txt”.

3.2 Starting calculation 2: “0_A2.py”

Next we need a second starting calculation “0_A2.py” (see Appendix A.2) to calculate the \(2^{\textrm{nd}}\) Piola-Kirchhoff stresses \({\mathop {{\varvec{ T}}}\limits ^{\tiny {\text {2PK}}}}_1\). For this purpose, we prescribe \({\varvec{ H}}_1\) from “0_A1.py” directly after the pre-deformation \({\varvec{ H}}_0\). Following the post-processing is performed like described for “0_A1.py”. Additionally, the reaction forces divided by the volume result in the 1\(^{\textrm{st}}\) Piola-Kirchhoff stresses \({\mathop {{\varvec{ T}}}\limits ^{\tiny {\text {1PK}}}}_1\). Using the equations

$$\begin{aligned} {\varvec{ F}}_1 = {\varvec{ H}}_1 + {\varvec{ I}} \end{aligned}$$
(26)

and

$$\begin{aligned} {\mathop {{\varvec{ T}}}\limits ^{\tiny {\text {2PK}}}}_1 = {\varvec{ F}}_1^{-1} {\mathop {{\varvec{ T}}}\limits ^{\tiny {\text {1PK}}}}_1 \ , \end{aligned}$$
(27)

we are able to calculate the \(2^{\textrm{nd}}\) Piola-Kirchhoff stresses \({\mathop {{\varvec{ T}}}\limits ^{\tiny {\text {2PK}}}}_1\). The stresses are saved in the text file “K0_ANLAUFRECHNUNG_T1.txt”.

figure b

3.3 Elastic test strain calculations : “0_1.py” to “0_6.py”

Now the unloaded placement \({\varvec{ H}}_1\) and the residual stresses in the unloaded placement \({\mathop {{\varvec{ T}}}\limits ^{\tiny {\text {1PK}}}}_1\) are known. In the six elastic test calculations (i=1...6) to determine the stiffness tetrad \({\mathbb { K}}_1\) the following three steps are applied:

  • Step 1: load step by prescribing \({\varvec{ H}}_0\)

  • Step 2: unload step by prescribing \({\varvec{ H}}_1\)

  • Step 3: elastic test strain by prescribing \({\varvec{ H}}_2^i\) .

In the post-processing part the differences

$$\begin{aligned} \Delta {\mathop {{\varvec{ E}}}\limits ^{\tiny {\text {G}}}}= {\mathop {{\varvec{ E}}}\limits ^{\tiny {\text {G}}}}_{2} - {\mathop {{\varvec{ E}}}\limits ^{\tiny {\text {G}}}}_{1} \end{aligned}$$
(28)

and

(29)

are calculated. Therefore Green’s strain tensor of the placements \({\varvec{ H}}_1\) and \({\varvec{ H}}_2\) are needed:

$$\begin{aligned} {\mathop {{\varvec{ E}}}\limits ^{\tiny {\text {G}}}}_{1}&= \frac{1}{2} \left( {\varvec{ F}}_1^{\text {T}} {\varvec{ F}}_1 - {\varvec{ I}}\right) \end{aligned}$$
(30)
$$\begin{aligned} {\mathop {{\varvec{ E}}}\limits ^{\tiny {\text {G}}}}_{2}&= \frac{1}{2} \left( {\varvec{ F}}_2^{\text {T}} {\varvec{ F}}_2 - {\varvec{ I}}\right) \ . \end{aligned}$$
(31)

The \(2^{\textrm{nd}}\) Piola-Kirchhoff stresses \({\mathop {{\varvec{ T}}}\limits ^{\tiny {\text {2PK}}}}_1\) are already known. The \({\mathop {{\varvec{ T}}}\limits ^{\tiny {\text {2PK}}}}_2\) stresses are calculated according to Eqs. (26) and (27). For the further post-processing with the computer algebra system Mathematica, two files are generated. Both are saved as text file. The first one is “K0_matheEGREEN_einzeln.txt” and consists of the difference \(\Delta E_G\) in the Abaqus notation of Cowin:

(32)

of all six calculation so that the file has 36 entries (see Appendix). Analogously the second file consists of the difference of the \(2^{\textrm{nd}}\) Piola-Kirchhoff stresses \({\mathop {{\varvec{ T}}}\limits ^{\tiny {\text {2PK}}}}\) and is saved in the text file “K0_matheT2PK_einzeln.txt” as

(33)

4 Validation of the material model

In this section we validate the material with its elastic and plastic behavior. Therefore we compare with the Abaqus internal material model.

4.1 Elastic

First we validate the elastic behavior of our material model by calculating the stiffness tetrad of a homogeneous material and compare the results with literature and the Abaqus material. To determine the stiffness tetrad, we use the difference quotient with a small elastic test deformation \(\delta \). In Fig. 2, we compare the deviation of the resulting stiffness tetrad to the analytically one in dependence of \(\delta \). Our own material model shows a better convergence even for larger \(\delta \)-values. Within the shown figure, the largest relative error (0.0001) for the St. Venant-Kirchhoff model corresponds to the smallest error of the Abaqus model within the range \(1e^{-9}< \delta < 0.001\). As a result, we find that our model firstly calculates the correct stiffness tetrads and secondly this is done with a better convergence.

Fig. 2
figure 2

Error regarding the original stiffness tetrad of the St. Venant-Kirchhoff user material and the Abaqus material over \(\delta \) value of difference quotient (log-log)

Full size image

4.2 Plastic

To validate the plastic behavior of our material model, we perform a tensile (see Fig. 3) and a shear test (see Fig. 4) with the material parameters Young’s modulus \(\hbox {E} = 100\hbox {GPa}\), Poisson’s ratio \(\nu =0.3\) and yield stress of \(\sigma _{\text {F}}=100\hbox {MPa}\).

Fig. 3
figure 3

Tensile test: 100% strain

Full size image
Fig. 4
figure 4

Shear test: shear number \(\gamma =1\)

Full size image

The results show, as expected, a constant stress level while yielding for the tensile and the shear test. This means, we get proper results. The slope of both curves differs slightly due to the application of the different boundary conditions.

For a final test, we compare the results of a 10% tensile test of our material model and the Abaqus elastic–plastic material applied on a notched cylindrical bar (Fig. 5) with the same material parameters as above. As a result, the von Mises stresses in Fig. 6 show a very good agreement comparing both material models. Additionally, we find a very good agreement of the von Mises stress distribution depicted in Fig. 6. Even small details look exactly the same.

Fig. 5
figure 5

Mesh of a notched cylindrical bar

Full size image
Fig. 6
figure 6

Von Mises stresses of the Abaqus material (left) and the St. Venant-Kirchhoff user material (right)

Full size image

5 Calculation of the effective material stiffness

In this section, we introduce an example inhomogeneous fiber material and present a method to determine the effective stiffness of it before and after large deformations using the described material model.

Fig. 7
figure 7

RVE with uni-directional reinforcement. Left: Fiber parts, Middle: Matrix parts, Right: Assembly

Full size image
Fig. 8
figure 8

One unit-cell of the uni-directional RVE with effectively transversal isotropic symmetry. Left: undeformed, Right: largely deformed unit-cell

Full size image

5.1 Representative volume element of the example material

We will use a representative volume element (RVE) of an uni-directionally reinforced material with an effective transversal isotropic material symmetry (see Figs. 7 and 8) to perform test deformations \({\mathop {{\varvec{ E}}}\limits ^{\tiny {\text {G}}}}\). Together with the resulting \({\mathop {{\varvec{ T}}}\limits ^{\tiny {\text {2PK}}}}\) stresses, we calculate the stiffness tetrad \({\mathbb { K}}\) during the post-processing with the computer algebra system Mathematica. We will determine the stiffness of the undeformed material (\({\mathbb { K}}_0\)) and the stiffness tetrad of a deformed material after a large plastic deformation (\({\mathbb { K}}_1\)). The stiffness tetrads will be calculated and compared in the reference placement and therefore we use the \(2^{\textrm{nd}}\) Piola-Kirchhoff stresses \({\mathop {{\varvec{ T}}}\limits ^{\tiny {\text {2PK}}}}\) and Green’s strain tensor \({\mathop {{\varvec{ E}}}\limits ^{\tiny {\text {G}}}}\). For calculating the stiffness tetrads, we use the difference quotient out of six test calculations. Within the test calculations, six different small elastic test strains \(\delta _i\) with i=1...6 are applied to the presented materials (RVEs). With the definitions

  • \({\varvec{ H}}_0\): displacement gradient of the unloaded placement

  • \(\Delta {\varvec{ H}}_i\): displacement gradients of the 6 different elastic deformations

and the scheme in Fig. 9, we are able to calculate a stiffness tetrad by the equation:

$$\begin{aligned} \Delta {\mathop {{\varvec{ T}}}\limits ^{\tiny {\text {2PK}}}}_i = {\mathbb { K}}:\Delta {\mathop {{\varvec{ E}}}\limits ^{\tiny {\text {G}}}}_i \ . \end{aligned}$$
(34)
Fig. 9
figure 9

Scheme to determine the test stresses \(\Delta {\mathop {{\varvec{ T}}}\limits ^{\tiny {\text {2PK}}}}_i\) and the test strains \(\Delta {\mathop {{\varvec{ E}}}\limits ^{\tiny {\text {G}}}}_i\) out of the test displacement gradients \(\Delta {\varvec{ H}}_i\) for calculating the stiffness tetrad \({\mathbb { K}}\)

Full size image

5.2 Validation of the stiffness calculation

We will compare the calculated stiffness tetrads to the literature to validate our implementation. If we prescribe \({\varvec{ F}}_0 = {\varvec{ 0}}\) we will get the stiffness of the undeformed material \({\mathbb { K}}_0\). For \({\varvec{ F}}_1\) being the unloaded placement after a large plastic deformation we will get the stiffness \({\mathbb { K}}_1\). To compare both, it is necessary to push-forward \({\mathbb { K}}_1\) to the new stress-free placement using the deformation gradient \({\varvec{ F}}\) and the Rayleigh product \(*\).

$$\begin{aligned} {\mathbb { K}}_0 = {\varvec{ F}}* {\mathbb { K}}_1 \end{aligned}$$
(35)

The Rayleigh product is defined between a second-order tensor and a tensor of arbitrary order,

$$\begin{aligned} {\varvec{ A}}*\overset{\langle n \rangle }{{\mathbb { K}}}\ = K_{\underbrace{i \ldots p}_{n\text { indices}}} \underbrace{({\varvec{ A}}{\varvec{ e}}_i)\otimes \ldots \otimes ({\varvec{ A}}{\varvec{ e}}_p)}_{n\text { times}},\qquad K_{\underbrace{i \ldots p}_{n\text { indices}}}=\overset{\langle n \rangle }{{\mathbb { K}}}\underbrace{\cdot \ldots \cdot }_{n\text { dots}} \underbrace{{\varvec{ e}}_i\otimes \ldots \otimes {\varvec{ e}}_p}_{n\text { times}}. \end{aligned}$$
(36)

It changes the basis while keeping the components, which can be used, e.g., to represent rotations. For second-order tensors it can be written as \({\varvec{ A}}*{\varvec{ T}}={\varvec{ A}}{\varvec{ T}}{\varvec{ A}}^\text {T}\). It is associative in the first factor, i.e. \(({\varvec{ A}}{\varvec{ B}})*{\mathbb { K}}={\varvec{ A}}*({\varvec{ B}}*{\mathbb { K}})\) and linear in the second factor, i.e. \({\varvec{ A}}*({\mathbb { K}}_1+\alpha {\mathbb { K}}_2)={\varvec{ A}}*{\mathbb { K}}_1+\alpha {\varvec{ A}}*{\mathbb { K}}_2\).

First, we study an isotropic material. The material parameters of the matrix and the fiber are identically and chosen as example (see Table 1). The components of the stiffness tetrad of an isotropic material can be found in the literature and are represented in Table 2. Using our implementation, we get the following stiffness tetrad \({\mathbb { K}}_0\) (values given in [GPa]) for the undeformed material (Table 3). It correctly represents an isotropic material. The next step is to validate the implementation for a plastically deformed material and to calculate the stiffness tetrad \({\mathbb { K}}_1\). First, we choose a 50% tensile test, unload the material sample and measure the stiffness tetrad. The resulting stiffness tetrad \({\varvec{ F}}*{\mathbb { K}}_1\) in Table 4 is identical to \({\mathbb { K}}_0\). The second test is a shear test with \(\gamma =0.5\) perpendicular to the fiber direction. After unloading and measuring the stiffness tetrad \({\varvec{ F}}*{\mathbb { K}}_1\), we find it is again identical to \({\mathbb { K}}_0\) (see Table 5). In the foregoing section, the material was isotropic. We want to study an anisotropic material and again use the RVE with the uni-directional reinforcement. But now the material parameters of the matrix and fiber material are different (see Table 6). The stiffness tetrad of a transversal isotropic material is given in literature with the following five different material parameters (see Table 7). Using again our implementation, we get the following stiffness tetrad \({\mathbb { K}}_0\) for the undeformed transversal isotropic material (see Table 8). It correctly represents the transversal isotropic material from literature. Next, we validate the implementation for the plastically deformed material and calculate the stiffness tetrad \({\mathbb { K}}_1\). First, we choose a 50% tensile test, unload the material sample and measure the stiffness tetrad. The resulting stiffness tetrad \({\varvec{ F}}*{\mathbb { K}}_1\) in Table 9 is identical to \({\mathbb { K}}_0\) of the transversal isotropic material. Again, the second test is a shear test with \(\gamma =0.5\) perpendicular to the fiber direction. After unloading and measuring the stiffness tetrad \({\varvec{ F}}*{\mathbb { K}}_1\), we find it is not identical to \({\mathbb { K}}_0\) (see Table 10). The shear test of this anisotropic material shows the first time that the calculation of \({\mathbb { K}}_0={\varvec{ F}}*{\mathbb { K}}_1\) fails when we change the symmetry of the material during the deformation. There is a difference between both stiffness tetrads which means that for certain deformation the stiffness tetrad evolves.

Table 1 Material parameters for the isotropic material on the micro-scale
Full size table
Table 2 Stiffness tetrad of an isotropic material
Full size table
Table 3 Stiffness tetrad \({\mathbb { K}}_0\) of the calculated isotropic material
Full size table
Table 4 Initially isotropic material after the tension test
Full size table
Table 5 Initially isotropic material after the shear test
Full size table
Table 6 Material parameters for the anisotropic material on the micro-scale
Full size table
Table 7 Stiffness tetrad of a transversal isotropic material
Full size table
Table 8 Stiffness tetrad \({\mathbb { K}}_0\) of the calculated transversal isotropic material
Full size table
Table 9 Initially transversal isotropic material after the tension test
Full size table
Table 10 Initially transversal isotropic material after the shear test
Full size table

5.3 Results for an uni-directional reinforcement

The following three examples will show the deviation between the initial stiffness tetrad \({\mathbb { K}}_0\) and the stiffness tetrad \({\mathbb { K}}_1\) measured after a large deformation. We will investigate the three characteristic shear tests for the uni-directional reinforced material \(H_{\text {xy}}\) (equivalent to \(H_{\text {yx}}\)), \(H_{\text {xz}}\) (equivalent to \(H_{\text {yz}}\)) and \(H_{\text {zx}}\) (equivalent to \(H_{\text {zy}}\)). The first case is the shear test with \(H_{\text {xy}}\). Figure 10a shows that we have a transport of the fibers which leads to a change of the symmetry. The fiber direction remains the same. This type of deformation leads to a change of about 8% between the stiffness tetrads.

$$\begin{aligned} {\mathbb { K}}_1 - {\varvec{ F}}^{-1} * {\mathbb { K}}_0 \ / \ {\mathbb { K}}_1 = 7.7\% \end{aligned}$$
(37)

In Fig. 10b, we see the shear test \(H_{\text {xz}}=0.5\) and no transport of the fibers. Instead, the fiber direction changes which leads to a change of the symmetry. We find the largest change in the stiffness tetrad as shown in Eq. (38).

$$\begin{aligned} {\mathbb { K}}_1 - {\varvec{ F}}^{-1} * {\mathbb { K}}_0\ / \ {\mathbb { K}}_1 = 35.2\% \end{aligned}$$
(38)

The shear test \(H_{\text {zx}}=0.5\) is depicted in Fig. 10c and shows that we have a transport of fibers in the fiber direction. The fiber direction remains the same so this motion has nearly no effect on the symmetry.

$$\begin{aligned} {\mathbb { K}}_1 - {\varvec{ F}}^{-1} * {\mathbb { K}}_0\ / \ {\mathbb { K}}_1 = 0.5\% \end{aligned}$$
(39)

We see that the deviation of the stiffness tetrad \({\mathbb { K}}_1\) from \({\mathbb { K}}_0\) can be considerable. A shear parallel to the fiber normal plane with \(\gamma =0.5\) results in a deviation by approximately 35%.

Fig. 10
figure 10

Three different shear tests of the uni-directional reinforced material

Full size image

6 Conclusion

In this paper, an elastic–plastic material model for large deformations was presented. The elastic behavior was captured by the St. Venant–Kirchhoff elasticity and the plastic behavior by the mentioned isomorphy concept. The yield condition follows the isotropic \(J_2\) theory by [1, 2] and [3]. The yield condition was written in terms of the principle of maximum plastic dissipation. The model was validated regarding the elastic and plastic material behavior. We can conclude that the material model on the micro-scale provides reliable results during large plastic deformations following our validation process. To use this material model we show the entire Fortran implementation in the Appendix B and C. The main part of this article deals with the determination of material stiffness. The procedure was described in detail and the implementation was presented as Python code. This can be viewed in the Appendix A. The described procedure can easily be applied to the most diverse material classes, microstructures or composites. All that is required is to create a representative sample within the Abaqus program environment and insert it into the existing code. All calculations are then performed automatically.