1 Introduction

The field of topology optimisation has enjoyed rapid growth owing to improved computing power, new optimisation techniques, and application to a wide range of design problems (Bendsøe and Sigmund 2004; Deaton and Grandhi 2013; Sigmund and Maute 2013). Classical computational methods for topology optimisation include density-based methods (Bendsøe 1989; Rozvany et al. 1992) in which the design variables are material densities of elements/nodes in a mesh, and level set-based methods (Wang et al. 2003; Allaire et al. 2004) in which the boundary of the shape is implicitly tracked as the zero level set of a higher dimensional level set function. Conventional level set methods rely on the Hamilton–Jacobi evolution equation to update the design according to a normal velocity field defined on the boundary (e.g. Wang et al. 2003; Allaire et al. 2004). An important aspect of these methods is extending the normal velocity away from the boundary. To this end, the Hilbertian velocity extension-regularisation framework, which is well known in the context of level set methods (see discussion by Allaire et al. (2021b)), can be used to generate a velocity field that guarantees a descent direction and has additional regularity (smoothness) over the whole computational domain.

Topology optimisation problems often include multiple constraints. In density-based topology optimisation (Bendsøe 1989; Rozvany et al. 1992), the application of constraints is usually straightforward and handled by the optimisation algorithm (e.g. Method of Moving Asymptotes (Svanberg 1987)). In the context of conventional level set-based methods, applying constraints is more complicated. The augmented Lagrangian method (Nocedal and Wright 2006; Birgin and Martínez 2009) is a classical approach for constrained optimisation problems. It converts a constrained optimisation problem into a sequence of unconstrained problems that are a combination of the classical Lagrangian method and quadratic penalty method. In a level set framework, applying the method is straightforward: the shape sensitivity of the augmented Lagrangian is used to inform the normal velocity for the Hamilton–Jacobi equation (e.g. Guo et al. 2014; Allaire et al. 2016; Cao et al. 2021). However, the difficulty associated with tuning the accompanying parameters is problem dependent and scales with the number of constraints (Allaire et al. 2021b). The level set sequential linear programming method (SLP) (Dunning and Kim 2015; Dunning et al. 2015) involves linearising the optimisation problem into a number of sub-problems that are then solved using a linear programming method (e.g. the simplex method (Kambampati et al. 2020)). For level set-based topology optimisation, applying SLP is fairly straightforward except for implementing appropriate trust region constraints (Dunning and Kim 2015). The projection method (Wang and Wang 2004; Challis et al. 2008) projects the objective shape sensitivity onto a space that will leave the constraints unchanged and combines this with constraint shape sensitivities. This approach has been used to successfully design material microstructures subject to isotropy constraints (Challis et al. 2008) but has not been widely adopted in the literature. However, similar methods have more recently been proposed in the literature by Barbarosie et al. (2020) and Feppon et al. (2020) for level set topology optimisation. The projection method and these two recent works are examples of general null space gradient methods (e.g. Nocedal and Wright 2006).

It is natural to consider methods of constrained optimisation that take advantage of the Hilbertian extension-regularisation framework. For example, Allaire et al. (2021b) recently presented an SLP method in the Hilbertian framework. In this paper we revisit the projection method from Challis et al. (2008) and combine it with the Hilbertian extension-regularisation procedure. Our method constructs an orthogonal basis that spans the set of extended constraint shape sensitivities and an orthogonal projection operator that projects onto the set perpendicular to the extended constraint shape sensitivities. We then define the normal velocity for the level set function as a linear combination of the orthogonal projection operator applied to the extended objective function shape sensitivity and a weighted sum of basis functions for the extended constraint shape sensitivities. This normal velocity is naturally extended onto the bounding domain and endowed with additional regularity due to the Hilbertian extension-regularisation. Whilst our method is similar to other recently proposed approaches (Barbarosie et al. 2020; Feppon et al. 2020), our formulation utilising an orthogonal basis provides significant benefits.

To demonstrate our presented Hilbertian projection method we consider several linear elastic microstructure optimisation (i.e. inverse homogenisation) problems with multiple constraints. The constraints naturally arise under the enforcement of symmetries for the effective material properties, such as isotropy. Irrespective of optimisation method, microstructure optimisation has been used successfully for a range of design problems including linear elastic materials with extremal properties (e.g. Gibiansky and Sigmund 2000; Andreassen et al. 2014), multifunctional composites (e.g. Challis et al. 2008), auxetic materials (e.g. Vogiatzis et al. 2017), piezoelectric materials (e.g. Silva et al. 1998; Wegert et al. 2022), and multi-material composites (e.g. Zhuang et al. 2010; Faure et al. 2017). In this work, we consider maximising the bulk modulus with and without isotropy constraints and the design of auxetic and multi-phase materials. We compare our Hilbertian projection method with a Hilbertian sequential linear programming (SLP) method (Sect. 5.3.2, Allaire et al. 2021b) and show that the Hilbertian projection method is able to successfully handle these optimisation problems with little-to-no parameter tuning.

The remainder of the paper is as follows. In Sect. 2, we discuss the mathematical background for the level set method, Hilbertian extension-regularisation procedure, and linear elastic microstructure optimisation. In Sect. 3, we formulate the Hilbertian projection method and compare our formulation to the null space method presented by Feppon et al. (2020). In Sect. 4, we discuss our numerical implementation. In Sect. 5, we present and discuss the example optimisation problems and results. Finally, in Sect. 6, we present our concluding remarks.

2 Mathematical background

In this section we give a brief introduction to the level set method for topology optimisation and shape derivatives. We then discuss the Hilbertian extension-regularisation framework. We conclude by describing linear elastic microstructure optimisation for single- and multi-phase materials.

2.1 The level set method

Level set methods track the boundary of a domain \(\Omega\) inside a bounding domain \(D\subset \mathbb {R}^d\) implicitly via the zero level set of a function \(\phi :D\rightarrow \mathbb {R}\) (Sethian 1996; Osher and Fedkiw 2006). For a domain \(\Omega\) inside a bounding domain D, the level set function \(\phi\) is typically defined as

$$\begin{aligned} {\left\{ \begin{array}{ll}\phi (\varvec{x})<0&{}\text {if } \varvec{x} \in \Omega, \\ \phi (\varvec{x})=0 &{}\text {if } \varvec{x} \in \partial \Omega, \\ \phi (\varvec{x})>0 &{}\text {if } \varvec{x} \in D \backslash \bar{\Omega }.\end{array}\right. } \end{aligned}$$
(1)

Using this definition and assuming that the interface may evolve in time, a material derivative of \(\phi\) on \(\partial \Omega\) gives

$$\begin{aligned} \frac{\partial \phi }{\partial t}(t,\varvec{x}) + v(t,\varvec{x})|\nabla \phi (t,\varvec{x})|= 0, \end{aligned}$$
(2)

where v is the normal velocity of the interface. In practice, the above is solved over the whole bounding domain D instead of only on the interface \(\partial \Omega\) by extending the velocity v away from the boundary. Assuming that the time interval (0, T) is small so that the velocity does not vary in time gives the Hamilton–Jacobi evolution equation (Sethian 1996; Osher and Fedkiw 2006; Allaire et al. 2021b):

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial \phi }{\partial t}(t,\varvec{x}) + v(\varvec{x})|\nabla \phi (t,\varvec{x})|= 0,\\ \phi (0,\varvec{x})=\phi _0(\varvec{x}),\\ \varvec{x}\in D,~t\in (0,T), \end{array}\right. } \end{aligned}$$
(3)

where \(\phi _0(\varvec{x})\) is the initial condition for \(\phi\) at \(t=0\).

It is often useful to reinitialise the level set function as the signed distance function \(d_\Omega\). This ensures that the level set function is neither too steep nor too flat near the boundary of \(\Omega\) (Osher and Fedkiw 2006). The signed distance function may be defined as follows (Allaire et al. 2021b):

$$\begin{aligned} d_{\Omega }(\varvec{x})={\left\{ \begin{array}{ll} -d(\varvec{x}, \partial \Omega )&{}\text {if }\varvec{x} \in \Omega , \\ 0&{}\text {if } \varvec{x} \in \partial \Omega , \\ d(\varvec{x}, \partial \Omega )&{}\text {if } \varvec{x} \in D \backslash \bar{\Omega }, \end{array}\right. } \end{aligned}$$
(4)

where \(d(\varvec{x}, \partial \Omega ):=\min _{\varvec{p} \in \partial \Omega }|\varvec{x}-\varvec{p}|\) is the minimum Euclidean distance from \(\varvec{x}\) to the boundary \(\partial \Omega\). Several methods are available for constructing the signed distance function and the reader is referred to Osher and Fedkiw (2006) and Allaire et al. (2021b) and the references therein for a detailed discussion. In this work we use the following reinitialisation equation (Peng et al. 1999; Osher and Fedkiw 2006) to reinitialise a pre-existing level set function \(\phi _0(\varvec{x})\) as the signed distance function:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial \phi }{\partial t}(t,\varvec{x}) + S(\phi _0(\varvec{x}))\left( |\nabla \phi (t,\varvec{x})|-1\right) = 0,\\ \phi (0,\varvec{x})=\phi _0(\varvec{x}),\\ \varvec{x}\in D, t>0. \end{array}\right. } \end{aligned}$$
(5)

Here, S is the sign function and Eq. 5 is solved until close to steady state. Similar numerical schemes may be used to solve for Hamilton–Jacobi evolution and reinitialisation (Eqs. 3 and 5).

2.2 Shape derivatives

To find a normal velocity v that reduces some functional \(J(\Omega )\) via solution of the Hamilton–Jacobi equation (Eq. 3) we use the notion of shape derivatives. We recall the following useful results from Allaire et al. (2004, 2021b).

Suppose that we consider smooth variations of the domain \(\Omega\) of the form \(\Omega _{\varvec{\theta }} =(\varvec{I}+\varvec{\theta })(\Omega )\), where \(\varvec{\theta } \in W^{1,\infty }(\mathbb {R}^d,\mathbb {R}^d)\). Then the following definition and lemma follow:

Definition 1

(Allaire et al. 2004) The shape derivative of \(J(\Omega )\) at \(\Omega\) is defined as the Fréchet derivative in \(W^{1, \infty }(\mathbb {R}^d, \mathbb {R}^d)\) at \(\varvec{\theta }\) of the application \(\varvec{\theta } \rightarrow J(\Omega _{\varvec{\theta }})\), i.e.

$$\begin{aligned} J(\Omega _{\varvec{\theta }})(\Omega ))=J(\Omega )+J^{\prime }(\Omega )(\varvec{\theta })+\textrm{o}(\varvec{\theta }) \end{aligned}$$
(6)

with \(\lim _{\varvec{\theta } \rightarrow 0} \frac{|\textrm{o}(\varvec{\theta })|}{\Vert \varvec{\theta }\Vert }=0,\) where the shape derivative \(J^{\prime }(\Omega )\) is a continuous linear form on \(W^{1, \infty }(\mathbb {R}^d, \mathbb {R}^d)\).

Lemma 1

(Allaire et al. 2004) Let \(\Omega\) be a smooth-bounded open set and \(f \in W^{1,1}(\mathbb {R}^d)\). Define

$$\begin{aligned} J(\Omega )=\int _{\Omega } f~\textrm{d} \Omega. \end{aligned}$$
(7)

Then J is differentiable at \(\Omega\) and

$$\begin{aligned} J^{\prime }(\Omega )(\varvec{\theta })=\int _{\Omega } {\text {div}}(\varvec{\theta } f)~ \textrm{d} \Omega =\int _{\partial \Omega } f~\varvec{\theta } \cdot \varvec{n} ~ \textrm{d} \Gamma, \end{aligned}$$
(8)

for any \(\varvec{\theta } \in W^{1, \infty }(\mathbb {R}^d, \mathbb {R}^d)\).

Céa’s formal method (Céa 1986) can be applied to find the shape derivative of a functional J that depends on fields that satisfy specified state equations (e.g. Allaire et al. 2004, 2021b). The method relies on defining a Lagrangian functional \(\mathcal {L}\) that satisfies the two following properties:

  1. 1.

    The state equations are generated by stationarity of \(\mathcal {L}\) under variations of the fields.

  2. 2.

    \(\mathcal {L}\) is equal to the functional of interest J at the solution to the state equations.

Once these properties are satisfied the shape derivative of the functional of interest can be found using Lemma 1 (Allaire et al. 2004).

2.3 Hilbertian extension-regularisation

To infer a descent direction from \(J^\prime (\Omega )\) we utilise the Hilbertian extension-regularisation method as discussed by Allaire et al. (2021b). This involves solving an identification problem over a Hilbert space H on D with inner product \(\langle \cdot ,\cdot \rangle _H\): Find \(g_\Omega \in H\) such that

$$\begin{aligned} \langle g_\Omega ,w\rangle _H=-J^{\prime }(\Omega )(w\varvec{n})~\forall w\in H. \end{aligned}$$
(9)

For an unconstrained optimisation problem the resulting field \(g_\Omega\) is the extended shape sensitivity that is used to evolve the interface with \(\varvec{\theta }=\tau g_\Omega \varvec{n},\) where \(\tau >0\) is sufficiently small.

The Hilbertian extension-regularisation method provides two important benefits: it naturally extends the shape sensitivity from \(\partial \Omega\) onto the bounding domain D and ensures a descent direction for \(J(\Omega )\) with additional regularity (i.e. H as opposed to \(L^2(\partial \Omega )\)) (Allaire et al. 2021b). As discussed by Allaire et al. (2021b), this may be viewed as an analogue to the sensitivity filtering used in density-based topology optimisation algorithms.

A common choice for the Hilbert space H is \(H^1(D)\) with the inner product

$$\begin{aligned} \langle u,v\rangle _{H}=\beta ^2\int _D\nabla u\cdot \nabla v~\textrm{d}\Omega +\int _Duv~\textrm{d}\Omega, \end{aligned}$$
(10)

where \(\beta\) is the so-called regularisation length scale (e.g. Allaire et al. 2016; Feppon et al. 2019; Allaire et al. 2021a). For microstructure optimisation, we use the periodic Sobolev space \(H=H^1_{\text {per}}(D)\) and use the inner product defined in Eq. 10.

2.4 Linear elastic microstructure optimisation

In this section we briefly discuss computational homogenisation and topology optimisation in the context of periodic microstructure design.

The state equations for linear elastic homogenisation over a domain \(\Omega\) contained in a representative volume element (RVE) \(D\subset \mathbb {R}^d\) under an applied strain field \(\bar{\varepsilon }_{i j}\) are (e.g. Yvonnet 2019)

$$\begin{aligned} - \sigma _{ij,i}&= 0~\text {in }\Omega, \end{aligned}$$
(11)
$$\begin{aligned} \sigma _{ij}n_j&= 0~\text {on }\partial \Omega, \end{aligned}$$
(12)
$$\begin{aligned} \sigma _{i j}&=C_{i j k l} \varepsilon _{k l},\end{aligned}$$
(13)
$$\begin{aligned} \varepsilon _{ij}&=\frac{1}{2}\left( u_{i,j}+u_{j,i}\right), \end{aligned}$$
(14)
$$\begin{aligned} \frac{1}{{\text {Vol}}(D)}\int _{\Omega }{\varepsilon _{kl}}~\textrm{d}\Omega&=\bar{\varepsilon }_{kl}, \end{aligned}$$
(15)

where \(\sigma _{i j}\) is the stress tensor, \(\varepsilon _{i j}=\varepsilon _{i j}(\varvec{u})\) is the D-periodic strain field with displacement \(\varvec{u}\), and \(C_{i j k l}\) is the spatially dependent elasticity tensor. Note that in the above we use summation notation for indices and comma notation for derivatives.

To compute the homogenised stiffness tensor \(\bar{C}_{ijkl}\) of a periodic material, the above state equations are solved over \(\Omega\) for three (\(d=2\)) or six (\(d=3\)) different combinations of macroscopic strain fields. These macroscopic strain fields are applied by decomposing the strain into the constant macroscopic strain field and fluctuation strain field as \(\varepsilon _{i j}=\bar{\varepsilon }_{i j}+\tilde{\varepsilon }_{i j}\). The macroscopic strain fields are then given by the unique components of \(\bar{\varepsilon }_{i j}^{(k l)}=\frac{1}{2}\left( \delta _{i k} \delta _{j l}+\delta _{i l} \delta _{j k}\right)\) in k and l. For example, in two dimensions, the unique macroscopic strains are \(\bar{\varepsilon }_{i j}^{(11)}\), \(\bar{\varepsilon }_{i j}^{(22)}\), and \(\bar{\varepsilon }_{i j}^{(12)}\). The notation \(\tilde{\varepsilon }_{i j}^{(k l)}\) is used to denote the strain field fluctuation arising from the applied strain field \(\bar{\varepsilon }_{i j}^{(k l)}\).

In practice, Eqs. 11–15 are solved using a finite element method and the weak formulation given here:

Weak form 1

For each unique constant macroscopic strain field \(\bar{\varepsilon }_{i j}^{(k l)}\), find \(\tilde{\varvec{u}}^{(kl)}\in H^1_{\text {per}}(\Omega )^d\) such that

$$\begin{aligned} \begin{aligned}&\int _{\Omega } C_{pqrs} \varepsilon _{rs}(\tilde{\varvec{u}}^{(k l)}) \varepsilon _{pq}(\varvec{v}) ~\textrm{d} \Omega \\ {}&= -\int _{\Omega } C_{pqrs} \bar{\varepsilon }_{rs}^{(kl)} \varepsilon _{pq}(\varvec{v}) ~\textrm{d} \Omega ~~\forall \, \varvec{v}\in H^1_{\text {per}}(\Omega )^d, \end{aligned} \end{aligned}$$
(16)

where \(\varepsilon _{ij}(\varvec{v})=\frac{1}{2}\left( v_{i,j}+v_{j,i}\right).\)

2.4.1 Single-phase problems

For single-phase problems (one solid and a void phase), once the solution \(\tilde{\varvec{u}}^{(ij)}\) to Weak Form 1 has been found for each unique macroscopic strain \(\bar{\varepsilon }_{pq}^{(ij)}\), the resulting homogenised stiffness tensor may be computed via (Yvonnet 2019)

$$\begin{aligned} \bar{C}_{ijkl}(\Omega ) = \int _\Omega C_{pqrs}({\varepsilon }_{pq}(\tilde{\varvec{u}}^{(ij)})+{\bar{\varepsilon }}^{(ij)}_{pq}){\bar{\varepsilon }}_{rs}^{(kl)}~\textrm{d}\Omega, \end{aligned}$$
(17)

assuming that \({\text {Vol}}(D)=1\).

To evaluate Weak Form 1 and the homogenised stiffness tensor above, we utilise the ersatz material approximation. This method, which is classical in the literature (e.g. Allaire et al. 2004), fills the void phase with a soft material so that the state equations can be resolved without a body-fitted mesh. To this end, for small \(\varepsilon _{\textrm{void}}\) we take

$$\begin{aligned} C_{ijkl}(\varvec{x}) = {\left\{ \begin{array}{ll} C_{ijkl}&{} \text{if }\varvec{x}\in \Omega, \\ \varepsilon _{\textrm{void}} C_{ijkl}&{} \text{if }\varvec{x}\in D\setminus \Omega, \end{array}\right. } \end{aligned}$$
(18)

and relax integration to be over D. We can provide a smooth approximation to Eq. 18 using a smoothed Heaviside function \(H_{\eta }\)

$$\begin{aligned} H_\eta (\phi )={\left\{ \begin{array}{ll} 0&{}\text {if }\phi <-\eta, \\ \frac{1}{2}+\frac{\phi }{2\eta }+\frac{1}{2\pi }\sin \left( \frac{\pi \phi }{\eta }\right) &{}\text {if }|\phi |\le \eta, \\ 1&{}\text {if }\phi >\eta, \end{array}\right. } \end{aligned}$$
(19)

where \(\eta\) is half the length of the small transition region of \(H_\eta (\phi )\) between 0 and 1. Equation 18 can then be replaced with

$$\begin{aligned} C_{ijkl}(\phi ) = C_{ijkl}(1-H_\eta (\phi )) + \varepsilon _{\textrm{void}} C_{ijkl} H_\eta (\phi ). \end{aligned}$$
(20)

It is important to note that the ersatz material approximation is consistent (Allaire et al. 2021b). That is, as \(\varepsilon _{\textrm{void}}\rightarrow 0\), the approximation becomes exact.

We conclude this section by stating the shape derivative of the homogenised stiffness tensor:

Lemma 2

The shape derivative of Eq. 17 is given by

$$\begin{aligned} \begin{aligned}&\bar{C}_{ijkl}^{\prime }(\Omega )(\varvec{\theta })= \int _{\partial \Omega }C_{pqrs}({\varepsilon }_{pq}(\tilde{\varvec{u}}^{(ij)})+\bar{\varepsilon }_{pq}^{(ij)})\\ {}&\hspace{2cm}\times ({\varepsilon }_{rs}(\tilde{\varvec{u}}^{(kl)})+\bar{\varepsilon }_{rs}^{(kl)})~\varvec{\theta }\cdot \varvec{n}~\textrm{d}{\Gamma }. \end{aligned} \end{aligned}$$
(21)

Proof

See Appendix 1.

2.4.2 Multi-phase problems

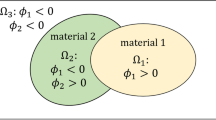
For multi-phase problems, we utilise the colour level set method in which up to \(2^M\) phases can be represented by the sign of M level set functions (Wang and Wang 2004; Allaire et al. 2014a). For example, in the case of four phases \(\Omega _1,\Omega _2, \Omega _3\) and \(\Omega _4\) with two level set functions \(\phi _1\) and \(\phi _2\), we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi _1<0~ \& ~\phi _2>0&{}\text{if }\varvec{x}\in \Omega _1,\\ \phi _1>0~ \& ~\phi _2<0&{}\text{if }\varvec{x}\in \Omega _2,\\ \phi _1<0~ \& ~\phi _2<0&{}\text{if }\varvec{x}\in \Omega _3,\\ \phi _1>0~ \& ~\phi _2>0&{}\text{if }\varvec{x}\in \Omega _4. \end{array}\right. } \end{aligned}$$
(22)

We further denote the domains associated with each level set function \(\phi _1\) and \(\phi _2\) as \(\mathcal {D}_1\) and \(\mathcal {D}_2\), respectively.

Fig. 1
figure 1

An illustration of colour level sets with two level set functions and four phases. a and b show the domain \(\mathcal {D}_1\) and \(\mathcal {D}_2\) represented via the level set function \(\phi _1\) and \(\phi _2\), respectively. c shows the colour representation of \(\Omega _1,\) \(\Omega _2\), \(\Omega _3\), and \(\Omega _4\) for different signs of \(\phi _1\) and \(\phi _2\)

Full size image

Figure 1 shows an illustration of this case.

In a similar way to Eq. 20 we can interpolate the value of the stiffness tensor between these domains via

$$\begin{aligned} \begin{aligned} C_{ijkl}(d_{\mathcal {D}_1},d_{\mathcal {D}_2})&\\ {}&\hspace{-2cm}=C_{ijkl,1}(1-H_{\eta }(d_{\mathcal {D}_1}))H_{\eta }(d_{\mathcal {D}_2}) \\ {}&\hspace{-2cm}~+ C_{ijkl,2} H_{\eta }(d_{\mathcal {D}_1})(1-H_{\eta }(d_{\mathcal {D}_2})) \\ {}&\hspace{-2cm}~+ C_{ijkl,3} (1-H_{\eta }(d_{\mathcal {D}_1}))(1-H_{\eta }(d_{\mathcal {D}_2})) \\ {}&\hspace{-2cm}~+ C_{ijkl,4} H_{\eta }(d_{\mathcal {D}_1})H_{\eta }(d_{\mathcal {D}_2}), \end{aligned} \end{aligned}$$
(23)

where \(C_{ijkl,\alpha }\) is the elasticity tensor for the phase occupying \(\Omega _{\alpha }\). In this multi-phase case we have replaced the level set functions \(\phi _1\) and \(\phi _2\) with \(d_{\mathcal {D}_1}\) and \(d_{\mathcal {D}_2}\) denoting their respective signed distance functions. This change facilitates shape differentiation. Unlike the situation discussed by Allaire et al. (2016), periodicity of D ensures that this replacement is valid provided the level set functions are reinitialised often. Additional care should then be taken regarding the calculation of certain quantities and their shape derivatives. Namely, the homogenised stiffness tensor (Eq. 17) becomes

$$\begin{aligned} \begin{aligned}&\bar{C}_{ijkl}(\mathcal {D}_1,\mathcal {D}_2)&\\\hspace{-1.9cm}&= \int _D C_{pqrs}(d_{\mathcal {D}_1},d_{\mathcal {D}_2})({\varepsilon }_{pq}(\tilde{\varvec{u}}^{(ij)})+{\bar{\varepsilon }}^{(ij)}_{pq}){\bar{\varepsilon }}_{rs}^{(kl)}~\textrm{d}\Omega. \end{aligned} \end{aligned}$$
(24)

The volume of \(\Omega _1\) is given by

$$\begin{aligned} {\text {Vol}}_{\Omega _1}(\mathcal {D}_1,\mathcal {D}_2)=\int _D (1-H_{\eta }(d_{\mathcal {D}_1}))H_{\eta }(d_{\mathcal {D}_2})~\textrm{d}\Omega. \end{aligned}$$
(25)

Similar expressions are used for \(\Omega _2\), \(\Omega _3\), and \(\Omega _4\).

Integration over the whole cell D in Eqs. 24 and 25 with dependence on the signed distance functions differs from the single-phase case where integration is over the domain \(\Omega\) occupied by the solid phase (see Eq. 17). Shape differentiability of the signed distance function and a coarea formula can be used in this multi-phase case to derive the shape derivative. We utilise the “approximate” formula discussed by Allaire et al. (2014a). This assumes that the Heaviside smoothing parameter \(\eta\) is small and that the principal curvatures of \(\partial \Omega\) vanish.

Lemma 3

The approximate shape derivatives of Eqs. 24 and 25 under variation of the domain \(\mathcal {D}_1\) by \(\varvec{\theta }_1\) are

$$\begin{aligned} \begin{aligned}&\bar{C}_{ijkl}^{\prime }(\mathcal {D}_1,\mathcal {D}_2)(\varvec{\theta }_1)\\ {}&\quad \approx -\int _{\partial \mathcal {D}_1}\frac{\partial C_{pqrs}}{\partial g}({\varepsilon }_{pq}(\tilde{\varvec{u}}^{(ij)})+\bar{\varepsilon }_{pq}^{(ij)})\\ {}&\quad \quad \quad \quad \quad \times ({\varepsilon }_{rs}(\tilde{\varvec{u}}^{(kl)})+\bar{\varepsilon }_{rs}^{(kl)})~\varvec{\theta }_1\cdot \varvec{n}~\textrm{d}{\Gamma }, \end{aligned} \end{aligned}$$
(26)

where \(g=H_\eta (d_{\mathcal {D}_1})\) and

$$\begin{aligned} \begin{aligned} {\text {Vol}}^{\prime }_{\Omega _1}(\mathcal {D}_1,\mathcal {D}_2)(\varvec{\theta }_1)\approx \int _{\partial \mathcal {D}_1} H_{\eta }(d_{\mathcal {D}_2})~\varvec{\theta }_1\cdot \varvec{n}~\textrm{d}\Gamma. \end{aligned} \end{aligned}$$
(27)

Analogous expressions follow for \(\varvec{\theta }_2\) and \(\Omega _2\), \(\Omega _3\), and \(\Omega _4\).

Proof

See Appendix 2.

We note that comparisons between the “true” formula, “Jacobian-free” formula (zero principal curvatures), and “approximate” formula have been discussed for compliance elsewhere in the literature (Allaire et al. 2014a, 2016). It suffices to mention that Allaire et al. (2016) found that the “approximate” formula does not capture the distortion that arises due to the ray integration and approximation of the principal curvatures in the “true” formula.

3 Hilbertian projection method

The Hilbertian framework yields a descent direction \(\varvec{\theta }=\tau g_\Omega \varvec{n}\) for unconstrained optimisation problems. However, for constrained optimisation problems such as

$$\begin{aligned} \begin{aligned} \underset{\Omega \in \mathcal {U}_{\textrm{ad}}}{\min }~&J(\Omega )\\ \text {s.t.}~~&C_i(\Omega )=0,~i=1,\dots ,N,\\&a(\varvec{u},\varvec{v})=l(\varvec{v}),~\forall \varvec{v}\in V, \end{aligned} \end{aligned}$$
(28)

the choice of \(\varvec{\theta }\) is more difficult.

In the literature a variety of optimisation methods deal with this problem but few of these take advantage of the Hilbertian framework. Allaire et al. (2021b) recently presented a sequential linear programming (SLP) method in the Hilbertian framework. The projection method uses orthogonal projections to evolve the design in a direction that aims for best possible improvement of the objective functional whilst improving the constraint functionals (Challis et al. 2008). In the following, we present a Hilbertian extension of the projection method for constrained topology optimisation.

3.1 Preliminaries

We proceed by first solving the following set of scalar Hilbertian extension-regularisation problems over H for an objective functional \(J(\Omega )\) and constraint functionals \(C_i(\Omega )\):

Find \(g_\Omega \in H\) and \(\mu _{\Omega i}\in H\) such that

$$\begin{aligned} \langle g_\Omega ,v\rangle _H&=-J^{\prime }(\Omega )(v\varvec{n}),~\forall v\in H,\text { and} \end{aligned}$$
(29)
$$\begin{aligned} \langle \mu _{\Omega i},v\rangle _H&=-C_i^{\prime }(\Omega )(v\varvec{n}),~\forall v\in H \end{aligned}$$
(30)

for all \(i=1,\dots ,N,\) with inner product \(\langle \cdot ,\cdot \rangle _H\) and norm \(\Vert \cdot \Vert _H=\sqrt{\langle \cdot ,\cdot \rangle _H}\).

Next we use Gram–Schmidt orthogonalisation to remove linearly dependent constraints from the set \(\{\mu _{\Omega i}\}_{i=1}^{N}\) to obtain the set \(\{\mu _{\Omega p}\}_{p=1}^{\bar{N}}\), where \(\bar{N}\le N\). We use \(\{\bar{\mu }_{\Omega p}\}\) to denote the corresponding orthogonal basis that spans the set \(C\subset H\) of extended constraint shape sensitivities. The basis \(\{\bar{\mu }_{\Omega p}\}\) can be used to construct an orthogonal projection operator \(P_{C^\perp }\) that projects the shape sensitivity \(g_\Omega\) onto the set \(C^\perp\) perpendicular to the set of extended constraint shape sensitivities. We define this operator as

$$\begin{aligned} P_{C^\perp }{g_\Omega } = g_\Omega - \sum _{p=1}^{\bar{N}}\frac{\langle \bar{\mu }_{\Omega p},g_\Omega \rangle _H}{\Vert \bar{\mu }_{\Omega p}\Vert _H^2}\bar{\mu }_{\Omega p}. \end{aligned}$$
(31)

Then, by construction, evolving the level set function using normal velocity \(P_{C^\perp }{g_\Omega }\) would to first order improve the objective functional \(J(\Omega )\) whilst leaving the constraint functionals \(C_i(\Omega )\) unchanged. On the other hand, the set of basis functions \(\{\bar{\mu }_{\Omega p}\}\) describes directions that to first order improve the constraint functionals \(C_i(\Omega )\).

3.2 Formulation

The Hilbertian projection method can then be formulated as follows: For some rate parameter \(\lambda \in \mathbb {R}\), suppose we choose \(v_\Omega \in H\) in the deformation field \(\varvec{\theta }=\tau v_\Omega \varvec{n}\) so that \(J(\Omega )\) and \(C_i(\Omega )\) decrease via (Challis et al. 2008)

$$\begin{aligned} \left\{ \begin{aligned}&J^\prime (\Omega )(v_\Omega \varvec{n}) = \text { min possible},\\&C_i^\prime (\Omega )(v_\Omega \varvec{n}) = -\lambda C_i. \end{aligned}\right. \end{aligned}$$
(32)

It is important to note that we purposefully pose the former requirement as “min possible” so that the objective functional may increase when required to improve constraints. Furthermore, linearly dependent constraints in the optimisation problem need to be consistent to ensure that the second line of Eq. 32 is well posed. Specifying constraints that have linearly dependent shape sensitivities but for which the directions of improvement are in contradiction would violate this requirement.

In the Hilbertian framework, Eq. 32 may be rewritten as

$$\begin{aligned} \left\{ \begin{aligned}&\langle g_\Omega ,v_\Omega \rangle _H = \text { max possible},\\&\langle \mu _{\Omega i},v_\Omega \rangle _H = \lambda C_i. \end{aligned}\right. \end{aligned}$$
(33)

Note that the change in sign comes from the application of Eqs. 29 and 30. We choose the following linear combination for \(v_\Omega\):

$$\begin{aligned} v_{\Omega }=\sqrt{1-\sum _{p=1}^{\bar{N}} \alpha _p^2} \frac{P_{C^{\perp }} g_{\Omega }}{\Vert P_{C^{\perp }} g_{\Omega }\Vert _H}+\sum _{p=1}^{\bar{N}} \alpha _p \frac{\bar{\mu }_{\Omega p}}{\Vert \bar{\mu }_{\Omega p}\Vert _H}, \end{aligned}$$
(34)

where \(\alpha _p\in \mathbb {R}\) are determined using \(\langle \mu _{\Omega p},v_\Omega \rangle _H = \lambda C_p\) for \(p=1,\dots ,\bar{N}\). This generates a lower-triangular linear system of the form

$$\begin{aligned} \lambda C_p = \sum _{l=1}^{p-1} \alpha _l\frac{\langle \bar{\mu }_{\Omega l}, \mu _{\Omega p}\rangle _H}{\Vert \bar{\mu }_{\Omega l}\Vert _H} + \alpha _p\Vert \bar{\mu }_{\Omega p}\Vert _H, \end{aligned}$$
(35)

which can easily be solved via forward substitution (Challis et al. 2008).

To first order, the first term of Eq. 34 improves the objective whilst leaving the constraints unchanged due to orthogonality, whilst the second term improves the constraints with extended shape sensitivities that contribute to the basis \(\{\bar{\mu }_{\Omega p}\}\). In the numerical examples, we have observed satisfaction of all constraints at convergence of the optimisation algorithm, including those that have linearly dependent shape sensitivities. The square root term of Eq. 34 is included to facilitate a balance between improving the objective and constraints.

3.3 Parameters

As discussed by Challis et al. (2008), the rate parameter \(\lambda\) should be chosen to ensure \(1-\sum _{p=1}^{\bar{N}} \alpha _p^2 \ge 0\) and \(\sum _{p=1}^{\bar{N}} \alpha _p^2 \ge \alpha _{\text {min}}^2\). The new parameter \(\alpha _{\text {min}}\) then controls the balance between improving the objective or constraints. For example, \(\alpha _{\textrm{min}}=1\) ignores the objective function in Eq. 28 and instead solves a constraint satisfaction problem. As a result, the method only has a single parameter \(\alpha _{\text {min}}\), whilst \(\lambda\) is dictated by the inequalities above. In general, we find that \(\alpha _{\text {min}}\) does not require fine tuning and unless otherwise stated we choose \(\alpha ^2_{\textrm{min}}=0.1\).

3.4 Comparison to null space methods

Our formulation is similar to null space methods recently developed by Barbarosie et al. (2020) and Feppon et al. (2020), both of which present a similar formulation. In the following we discuss some differences between our Hilbertian projection method and the null space method proposed by Feppon et al. (2020).

Most notably, our formulation makes use of an orthogonal basis for the set of extended constraint shape sensitivities. This avoids a possibly expensive matrix inversion that appears in the algorithm presented by (Feppon et al. 2020). Our use of the orthogonal basis also avoids reliance on the linear independence constraint qualification (LICQ) condition (Sect. 2.1, Feppon et al. 2020). Our method therefore naturally handles linearly dependent constraint shape sensitivities. Such dependencies often appear in microstructure optimisation problems when symmetries are imposed on the effective material properties (e.g. Sects. 5.2 and 5.4 below). Multi-phase level set-based topology optimisation via the colour level set method (Wang and Wang 2004; Allaire et al. 2014a) can also give rise to such linear dependency (e.g. Sect. 5.4 below). The ability of the Hilbertian projection method to naturally handle these situations gives the user more freedom in how topology optimisation problems are posed and avoids additional special treatment of linearly dependent constraint sensitivities.

For equality constrained problems when LICQ is satisfied, both the null space method (Feppon et al. 2020) and our Hilbertian project method give equivalent directions for improvement of the objective and violated constraints, up to coefficients \(\alpha _p\) and constant \(\lambda\). However, the method of attaining this improvement is quite different. In this work, the second term of Eq. 34 is a linear combination of the orthogonal basis of the set of extended constraint shape sensitivities. The coefficients \(\alpha _p\) are chosen to improve constraints exponentially, as per the second requirement in Eq. 33. The null space instead uses a Gauss–Newton direction for ensuring exponential decay of violated constraints (Lemma 2.5 and Proposition 2.6, Feppon et al. 2020). This again relies on LICQ and possibly expensive matrix inversion discussed above.

Finally, unlike the null space methods proposed by Barbarosie et al. (2020) and Feppon et al. (2020), the Hilbertian projection method as formulated above is unable to handle inequality constraints. Such an extension could be considered in the future using slack variables or by adopting the procedure used by either Barbarosie et al. (2020) or Feppon et al. (2020). Interestingly, in terms of the total length covered to reach the optimum, Feppon et al. (2020) found that their dual quadratic programming method for handling inequality constraints yielded equivalent performance when compared to the method of slack variables. However, using slack variables introduces additional computational cost and possibly further parameter tuning (Feppon et al. 2020). For our implementation this additional cost should be small owing to the use of orthogonalisation. As such the slack variable method would be an appropriate first recourse for implementing inequality constraints within the Hilbertian projection method. This would be similar to the approach taken by Schropp and Singer (2000).

4 Numerical implementation

In the following we describe the numerical implementation of our topology optimisation algorithm. We first discuss the resolution of state equations and Hamilton–Jacobi-type equations followed by an overview of the optimisation algorithm. We finish with a brief discussion of the Hilbertian SLP method which is compared to our presented Hilbertian projection method.

4.1 Resolving state and Hamilton–Jacobi-type equations

To solve the state equations and the Hilbertian extension-regularisation problems we use the finite element package Gridap (Badia and Verdugo 2020; Verdugo and Badia 2022) in the programming language Julia. In particular, we discretise the periodic domain \(D\subset \mathbb {R}^d\) into \(n^d\) linear quadrilateral (d = 2) or hexahedral (d = 3) elements with element width \(\Delta x\) and discretise the level set function at the nodes of the triangulation. To reduce computational cost when solving the state equations, we remove any elements that are completely void phase and leave a strip of ersatz material near the phase interface. The resulting linear systems for the state equations and Hilbertian extension-regularisation problems are then solved using a direct method in 2D or a GPU-based Jacobi pre-conditioned conjugate gradient method in 3D.

For the Hamilton–Jacobi evolution equation and signed distance reinitialisation equation (Eqs. 3 and 5), we use standard first-order Godunov upwind finite difference schemes (Peng et al. 1999; Allaire et al. 2004; Osher and Fedkiw 2006) that have been implemented on GPUs using CUDA.jl (Besard et al. 2018). For the Hamilton–Jacobi evolution equation we use \(\lfloor n/10\rfloor\) or \(\lfloor n/3\rfloor\) number of time steps in two dimensions or three dimensions, respectively. We are more conservative in three dimensions because we have less elements along each axial direction. For the reinitialisation equation we iterate until reaching a stopping condition

$$\begin{aligned} \Vert \phi ^{q}-\phi ^{q-1}\Vert _\infty < 5\times 10^{-5}, \end{aligned}$$
(36)

where q is the iteration number. In addition, for the sign function S we use the common approximation

$$\begin{aligned} S(\phi )=\frac{\phi }{\sqrt{\phi ^2+|\nabla \phi |^2\Delta x^2}} \end{aligned}$$
(37)

that applies on a Cartesian grid with square elements of side length \(\Delta x\) (Osher and Fedkiw 2006).

4.2 Algorithm overview

In Algorithm 1 we present our optimisation algorithm that is based on the theory discussed in Sects. 2 and 3. Algorithm 1 is similar to Algorithm 5 presented by Allaire et al. (2021b), with the addition of a line search method for determining the Courant–Friedrichs–Lewy (CFL) coefficient \(\gamma\) for solving the Hamilton–Jacobi evolution equation (e.g. Allaire et al. 2021a) with time step (Osher and Fedkiw 2006)

$$\begin{aligned} {\Delta t = \frac{\gamma \Delta x}{\Vert {v_\Omega }\Vert _{\infty }}}. \end{aligned}$$
(38)

Note that we omit the indices on \(\gamma\) that appear in Algorithm 1 for sake of clarity. In general, the line search method helps to remove oscillations in the optimisation history and improve convergence. For the stopping criterion we require that the current objective value compared to the previous five is stationary and that the constraints are satisfied within specified tolerances.

The Hilbertian projection method is implemented using the package DoubleFloats.jl that gives a machine epsilon of roughly \(5\times 10^{-32}\). This prevents accumulation of round-off error when generating the projection operator that can affect the optimisation history. All other computations are completed in standard double precision.

figure a

Table 1 gives the parameter values used for all the optimisation examples unless otherwise stated in Sect. 5.

Table 1 Parameter values used for optimisation examples
Full size table

4.3 Comparison to sequential linear programming (SLP)

We compare the Hilbertian projection method to the Hilbertian SLP method presented by Allaire et al. (2021b) (Sect. 5.3.2). We make two adjustments to the method. Firstly, to match our formulation we replace the inequality constraints with equality constraints. In addition, we change the trust region constraints for the constraint functionals to be

$$\begin{aligned} |\lambda _i|\le \frac{\Delta x}{2\Vert \varvec{\theta }_i\Vert _H} \end{aligned}$$
(39)

for \(i=1,\dots ,N\). For several two-dimensional problems we find that this choice promotes convergence and better optimisation results. However, as we will discuss later, choosing trust region constraints is not straightforward for our example optimisation problems.

We implement Hilbertian SLP by adjusting line 5 of Algorithm 1 accordingly. To solve the resulting linearised optimisation problem we use the Julia packages JuMP.jl (Dunning et al. 2017) and Ipopt.jl (Wächter and Biegler 2006).

5 Example problems

In the following we give the optimisation results for several example problems that have been solved with both the Hilbertian projection method and Hilbertian SLP method.

5.1 Example 1: maximum bulk modulus

In this example we consider a bounding domain \(D=[0,1]^d\) that contains a solid phase and void phase. The solid phase is constructed from an isotropic medium with \(E=1\) and \(\nu =0.3\). Subject to a volume constraint \({\text {Vol}}(\Omega )=1/2\), we maximise the effective bulk modulus \(\bar{\kappa }(\Omega )\) of the material. The bulk modulus is a measure of stiffness to volumetric strain given by

$$\begin{aligned} \bar{\kappa } = \frac{1}{4}(\bar{C}_{1111}+\bar{C}_{2222}+2\bar{C}_{1122}) \end{aligned}$$
(40)

in two dimensions or

$$\begin{aligned} \begin{aligned} \bar{\kappa } = \frac{1}{9}(&\bar{C}_{1111}+\bar{C}_{2222}+\bar{C}_{3333}\\ {}&+2(\bar{C}_{1122}+\bar{C}_{1133}+\bar{C}_{2233})) \end{aligned} \end{aligned}$$
(41)

in three dimensions. In other words, we seek to solve the optimisation problem:

$$\begin{aligned} \begin{aligned} \underset{\Omega \in \mathcal {U}_{\textrm{ad}}}{\min }~&-\bar{\kappa }(\Omega )\\ \text {s.t.}~~&\textrm{Vol}(\Omega )=1/2,\\&a(\varvec{u},\varvec{v})=l(\varvec{v}),~\forall \varvec{v}\in V. \end{aligned} \end{aligned}$$
(42)

The last line represents the satisfaction of the state equations.

In two dimensions we use a periodic starting structure with four equally spaced holes. For three dimensions the initial boundary between void and solid material is given by a Schwarz P minimal surface. It is well known that in two dimensions hole nucleation is not possible under Hamilton–Jacobi evolution (e.g. Allaire et al. 2004). For this reason we initialise the two-dimensional optimisation problems with more holes than required. Topological derivatives could be incorporated to rectify this, but this is outside of the scope of the current paper. We also note that different starting structures could be used provided they are periodic and have non-zero stiffness.

Fig. 2
figure 2

Two-dimensional optimisation results for Example 1: maximum bulk modulus. For the starting structure a, b and c show the final structures for the Hilbertian projection method and SLP, respectively, whilst d and e show the respective iteration histories. The Hashin–Shtrikman upper bound for the bulk modulus is given by the dashed black line

Full size image
Fig. 3
figure 3

Three-dimensional optimisation results for Example 1: maximum bulk modulus. For the starting structure a, b and c show the final structures for the Hilbertian projection method and SLP, respectively, whilst d and e show the respective iteration histories. The Hashin–Shtrikman upper bound for the bulk modulus is given by the dashed black line

Full size image

Figures 2 and 3 show the starting structures and optimisation results for two and three dimensions, respectively, for both the Hilbertian projection method and SLP. In addition, we compare the objective value with the Hashin–Shtrikman (HS) upper bound (Hashin and Shtrikman 1963). Table 2 shows a summary of the results.

Table 2 Summary of optimisation results for Example 1: maximum bulk modulus
Full size table

In two dimensions both the Hilbertian projection method (Fig. 2b, d) and Hilbertian SLP (Fig. 2c, e) perform well, converging in 32 and 12 iterations, respectively, at 99.71% and 99.51% of the HS bound. In addition, the resulting structures are geometrically similar and match classical results in the literature (Sect. 2.10.3, Bendsøe and Sigmund 2004). It is worth noting that no topological changes occur in this example.

In three dimensions the Hilbertian projection method converges to 99.86% of the HS bound, whilst Hilbertian SLP converges to 71.07% of the bound. Over the course of the iteration history, topological changes occur for the Hilbertian projection method, whilst SLP fails to evolve from the initial topology. The resulting structure from the Hilbertian projection method matches other classical results (Sect. 2.10.3, Bendsøe and Sigmund 2004).

5.2 Example 2: maximum bulk modulus with isotropy

In Example 2, we consider the same problem setup as Example 1 with the addition of macroscopic isotropy constraints. This ensures that the resulting homogenised stiffness tensor is invariant under rotation.

In two dimensions the optimisation problem is given by

$$\begin{aligned} \begin{aligned} \underset{\Omega \in \mathcal {U}_{\textrm{ad}}}{\min }~&-\bar{\kappa }(\Omega )\\ \text {s.t.}~~&\textrm{Vol}(\Omega )=1/2,\\&C_i(\Omega )=0,~i=1,\dots ,6,\\&a(\varvec{u},\varvec{v})=l(\varvec{v}),~\forall \varvec{v}\in V. \end{aligned} \end{aligned}$$
(43)

The constraints \(C_i(\Omega )\) are given by

$$\begin{aligned}&\sqrt{4\bar{\kappa }^2+8\bar{\mu }^2}C_1=\bar{C}_{1111}-\bar{\kappa }-\bar{\mu }, \end{aligned}$$
(44)
$$\begin{aligned}&\sqrt{4\bar{\kappa }^2+8\bar{\mu }^2}C_2=\bar{C}_{2222}-\bar{\kappa }-\bar{\mu }, \end{aligned}$$
(45)
$$\begin{aligned}&\sqrt{4\bar{\kappa }^2+8\bar{\mu }^2}C_3=\sqrt{2}(\bar{C}_{1122}-\bar{\kappa }+\bar{\mu }), \end{aligned}$$
(46)
$$\begin{aligned}&\sqrt{4\bar{\kappa }^2+8\bar{\mu }^2}C_4=2\bar{C}_{1112}, \end{aligned}$$
(47)
$$\begin{aligned}&\sqrt{4\bar{\kappa }^2+8\bar{\mu }^2}C_5=2\bar{C}_{2212}, \end{aligned}$$
(48)
$$\begin{aligned}&\sqrt{4\bar{\kappa }^2+8\bar{\mu }^2}C_6=2(\bar{C}_{1212}-\bar{\mu }), \end{aligned}$$
(49)

where \(\bar{\mu }\) is the isotropic shear modulus given by

$$\begin{aligned} \bar{\mu } = \frac{1}{8}(\bar{C}_{1111} + \bar{C}_{2222}) - \frac{1}{4}\bar{C}_{1122} + \frac{1}{2}\bar{C}_{1212}. \end{aligned}$$
(50)

Analogous expressions appear in three dimensions and the number of isotropy constraints increases from 6 to 21 (Challis 2009). It should be noted that the term \(\sqrt{4\bar{\kappa }^2+8\bar{\mu }^2}\) appears as a normalisation coefficient and is considered constant for the purpose of the shape differentiation. Furthermore, owing to the symmetry of the isotropy constraints the extended constraint shape sensitivities have a nullity of two. Our method handles these with no special treatment.

To visualise the behaviour of the isotropy constraints in the iteration history, we define the effective anisotropy \(\bar{\mathcal {A}}\) to be the sum of squares of the violation of these constraints. That is,

$$\begin{aligned} \bar{\mathcal {A}}(\Omega )=\sqrt{\sum C_i(\Omega )^2}. \end{aligned}$$
(51)

For the two-dimensional problem we implement both the full set of isotropy constraints as well as the single constraint \(\bar{A}=0\). We find that the SLP method struggles with the full set of constraints. For this reason we instead use \(\bar{\mathcal {A}}=0\) as the isotropy constraint for the SLP method. For the Hilbertian projection method we find that the full set of constraints is more effective. This matches previous literature (e.g. Challis et al. 2008; Challis 2009).

Fig. 4
figure 4

Two-dimensional optimisation results for Example 2: maximum bulk modulus with isotropy. a–c show the final structures for the Hilbertian projection method with the full set of constraints, single anisotropy constraint, and SLP with the single anisotropy constraint, respectively, whilst d–f show the respective iteration histories. The Hashin-Shtrikman upper bound for the bulk modulus is given by the dashed black line. Due to very little change between iteration 600 and 1000, the upper bound on the x-axis in f has been reduced to 700

Full size image
Fig. 5
figure 5

Three-dimensional optimisation results for Example 2: maximum bulk modulus with isotropy. a and b show the final structures for the Hilbertian projection method and SLP, respectively, whilst c and d show the respective iteration histories. The Hashin–Shtrikman upper bound for the bulk modulus is given by the dashed black line

Full size image

Figure 4 shows the two-dimensional results for the Hilbertian projection method with the full set of constraints and single anisotropy measure constraint, and SLP with the anisotropy measure constraint. We omit the starting structure as this is the same as previously (Fig. 2a). Figure 5 shows the three-dimensional results for the Hilbertian projection method and SLP. Table 3 shows a summary of the results for this example.

Table 3 Summary of optimisation results for Example 2: maximum bulk modulus with isotropy
Full size table

In two dimensions, the Hilbertian projection method performs well for the full set of constraints and the single anisotropy measure constraint. The number of iterations is markedly lower when using the full set of constraints (78 vs. 220). This is unsurprising because including the individual symmetry constraints enables the projection method to improve each constraint separately (Challis et al. 2008; Challis 2009). The final optimisation values with the full set or single constraint are very similar, being 99.68% and 99.69% of the HS bound, whilst the final structures are geometrically identical under a periodic shift of half the cell edge length along each coordinate direction. The resulting structures match other classical results (Sect. 2.10.3, Bendsøe and Sigmund 2004). In contrast, the SLP method does not manage to reduce the measure of anisotropy to zero and reaches the maximum number of iterations. However, the final structure obtained with SLP (Fig. 4c) is very close to those obtained with the Hilbertian projection method (Fig. 4a and b). We suspect that SLP fails to converge due to the difficulty associated with choosing the trust region constraints.

For the three-dimensional results, we find that the Hilbertian projection method with the full set of constraints converges in 53 iterations to 99.12% of the HS bound. The final structure again matches known results from the literature (Sect. 2.10.3, Bendsøe and Sigmund 2004). For SLP, the optimisation algorithm fails to converge in 1000 iterations and the final structure is clearly not optimal.

These results demonstrate that the Hilbertian projection method is able to handle a large number of constraints (22 in 3 dimensions) without requiring any parameter tuning of \(\alpha _{\textrm{min}}\) or \(\lambda\). In addition, the optimisation histories for the Hilbertian projection method with the full set of isotropy constraints (Figs. 4d and 5c) are smooth and converge fairly quickly.

5.3 Example 3: auxetic materials

In this example we consider two-dimensional minimum volume auxetic materials with a Poisson’s ratio of \(-0.5\). For the problem setup, we consider a bounding domain \(D=[0,1]^2\) that contains a solid phase and void phase. As previously mentioned, the solid phase is constructed from an isotropic material with \(E=1\) and \(\nu =0.3\).

To obtain an effective Poisson’s ratio \(\bar{\nu }=-0.5\), we require that \(\bar{C}_{1111}=\bar{C}_{2222}\) and prescribe a value to \(\bar{C}_{1111}\) and \(\bar{C}_{1122}\) so that the effective Poisson’s ratio \(\bar{\nu }\) given by

$$\begin{aligned} \bar{\nu }=\frac{\bar{C}_{1122}}{\bar{C}_{1111}} \end{aligned}$$
(52)

gives the required \(\bar{\nu }=-0.5\).

It may be noted that this is similar to the approach taken by Vogiatzis et al. (2017). However, they instead minimise a weighted sum of the square of the difference between \(\bar{C}_{ijkl}\) and its prescribed value subject to a volume constraint.

For the purpose of this example we choose \(\bar{C}_{1111}=0.1\), which results in \(\bar{C}_{1122}=-0.05\). The resulting optimisation problem is then

$$\begin{aligned} \begin{aligned} \underset{\Omega \in \mathcal {U}_{\textrm{ad}}}{\min }~&\textrm{Vol}(\Omega )\\ \text {s.t.}~~&\bar{C}_{1111}(\Omega )=0.1,\\&\bar{C}_{2222}(\Omega )=0.1,\\&\bar{C}_{1122}(\Omega )=-0.05,\\&\bar{C}_{1112}(\Omega )=0,\\&\bar{C}_{2212}(\Omega )=0,\\&a(\varvec{u},\varvec{v})=l(\varvec{v}),~\forall \varvec{v}\in V. \end{aligned} \end{aligned}$$
(53)

For this example we use \(\gamma _{\textrm{max}}=0.05\) and \(\alpha _{\textrm{min}}^2=0.5\). This means that the optimiser favours improvement of the constraints rather than the objective and does not move too quickly to avoid disconnecting in the first few iterations.

Fig. 6
figure 6

Optimisation results for Example 3: auxetic materials. For the starting structure a, b shows the final structure, whilst c shows the iteration history for the Hilbertian projection method. The desired Poisson’s ratio of \(-\) 0.5 is given by the dashed black line

Full size image

Figure 6 shows the starting structure (Fig. 6a) and optimisation results (Fig. 6b and c) for this problem using the Hilbertian projection method. We use a periodic starting structure with sixteen equally spaced holes. The method converges in 61 iterations with a final volume of 0.3159 and Poisson’s ratio of \(-\) 0.4998. In contrast, SLP fails because the optimiser prioritises the objective leading to a disconnected solid phase and the algorithm is unable to recover.

5.4 Example 4: multi-phase materials

For our final example we consider two-dimensional multi-phase maximum bulk modulus problems with and without isotropy constraints. We consider a bounding domain \(D=[0,1]^2\) that contains two solid phases and void. The solid phase contained in \(\Omega _2\) is an isotropic material with \(E=1\) and \(\nu =0.3\), whilst \(\Omega _3\) contains isotropic material with \(E=1/2\) and \(\nu =0.3\). The void phase is contained in \(\Omega _1\) and \(\Omega _4\). As previously, most void phase is removed from the mesh (see Sect. 4) whilst any material close to the interface is specified as weak material with \(E=10^{-3}\) and \(\nu =0.3\).

We consider two optimisation problems. The first is maximum bulk modulus subject to volume constraints on \(\Omega _2\) and \(\Omega _3\) given by

$$\begin{aligned} \begin{aligned} \underset{\mathcal {D}_1,\mathcal {D}_2\in \mathcal {U}_{\textrm{ad}}}{\min }~&-\bar{\kappa }(\mathcal {D}_1,\mathcal {D}_2)\\ \text {s.t.}~~&\textrm{Vol}_{\Omega _2}(\mathcal {D}_1,\mathcal {D}_2)=1/4,\\&\textrm{Vol}_{\Omega _3}(\mathcal {D}_1,\mathcal {D}_2)=1/4,\\&a(\varvec{u},\varvec{v})=l(\varvec{v}),~\forall \varvec{v}\in V. \end{aligned} \end{aligned}$$
(54)

The second is maximum bulk modulus subject to macroscopic isotropy constraints and volume constraints on \(\Omega _2\) and \(\Omega _3\) given by

$$\begin{aligned} \begin{aligned} \underset{\mathcal {D}_1,\mathcal {D}_2\in \mathcal {U}_{\textrm{ad}}}{\min }~&-\bar{\kappa }(\mathcal {D}_1,\mathcal {D}_2)\\ \text {s.t.}~~&\textrm{Vol}_{\Omega _2}(\mathcal {D}_1,\mathcal {D}_2)=1/4,\\&\textrm{Vol}_{\Omega _3}(\mathcal {D}_1,\mathcal {D}_2)=1/4,\\&C_i(\mathcal {D}_1,\mathcal {D}_2)=0,~i=1,\dots ,6,\\&a(\varvec{u},\varvec{v})=l(\varvec{v}),~\forall \varvec{v}\in V, \end{aligned} \end{aligned}$$
(55)

where the constraints \(C_{i}\) are as in Example 2. For SLP, we use the single anisotropy constraint and for the Hilbertian projection method we use the full set of isotropy constraints. For these examples we use \(\gamma _{\textrm{max}}=0.05\) so that the optimiser does not evolve the designs too quickly. It should be noted that for the case of only volume constraints the extended constraint shape sensitivities have a nullity of one (in \(\varvec{\theta }_1\)) and zero (in \(\varvec{\theta }_2\)) owing to the structure of the shape derivatives for the volume constraints. For the case of volume and isotropy constraints the extended constraint shape sensitivities have a nullity of three (in \(\varvec{\theta }_1\)) and two (in \(\varvec{\theta }_2\)) due to the underlying symmetry of the shape derivatives for the volume and isotropy constraints. Our method handles these with no special treatment.

We initialise with two overlapping level set functions that give a starting structure completely comprised of the less stiff material (\(\Omega _3\)) and the void phase. Regions of stiffer material (\(\Omega _2\)) are readily generated during the optimisation via independent evolution of the two level set functions. We use a starting structure of four equally spaced holes for the optimisation problem without isotropy constraints and nine equally spaced holes for the problem with isotropy constraints.

Fig. 7
figure 7

Optimisation results for Example 4: maximum bulk modulus multi-phase materials without isotropy constraints. For the starting structure a, b and c show the final structures for the Hilbertian projection method and SLP, respectively, whilst d and e show the respective iteration histories. The Hashin–Shtrikman–Walpole upper bound for the bulk modulus is given by the dashed black line. Note that the volume constraint for each phase is 0.25

Full size image
Fig. 8
figure 8

Optimisation results for Example 4: maximum bulk modulus multi-phase materials with isotropy constraints. For the starting structure a, b and c show the final structures for the Hilbertian projection method and SLP, respectively, whilst d and e show the respective iteration histories. The Hashin–Shtrikman–Walpole upper bound for the bulk modulus is given by the dashed black line. Note that the volume constraint for each phase is 0.25

Full size image

Figures 7 and 8 show the optimisation results and history without and with isotropy constraints, respectively. We denote the stiff and less stiff material phase by blue and green, respectively, whilst the smooth interface is given by the dark green overlap. We include the Hashin–Shtrikman–Walpole (HSW) upper bound (Walpole 1966) for this problem as the black-dashed line in these figures. Table 4 shows a summary of the results.

Table 4 Summary of optimisation results for Example 4: two-dimensional maximum bulk modulus multi-phase materials
Full size table

For the case of no isotropy constraints, both the Hilbertian projection method and SLP converge to roughly 96% of the HSW bound, whilst the resulting structures (Fig. 7b and c) are geometrically similar apart from the thin interface that presents in the results for the Hilbertian projection method. The difference between our results and the theoretical upper bound is likely due to the use of the approximate formula for the shape derivative. Indeed, results from Allaire et al. (2014a) showed that the approximate formula yields slightly less optimal results than the true or Jacobian-free counterpart. The iteration history for the Hilbertian projection method (Fig. 7d) is fairly smooth, whilst the history for SLP (Fig. 7e) moves rapidly at the beginning of the optimisation to satisfy the volume constraints and increase the objective. As previously noted, this is likely due to the trust region constraints that, in this case, need to be chosen to be more conservative.

With the addition of isotropy constraints, we again find that the Hilbertian projection method works well without significant parameter tuning. In 148 iterations, the optimisation algorithm is able to satisfy all constraints and obtain a final objective value that is 93.44% of the HS bound. In contrast, SLP does not converge within 1000 iterations.

6 Conclusion

In this paper we have presented a Hilbertian extension of the projection method for constrained level set-based topology optimisation. At its core, the method relies on the Hilbertian extension-regularisation method in which a set of identification problems are solved over a Hilbert space H on D with inner product \(\langle \cdot ,\cdot \rangle _{H}\). This procedure naturally extends shape sensitivities onto the bounding domain D and enriches them with the regularity of H. For a constrained optimisation problem the projection method framework aims for the best first-order improvement of the objective in addition to first-order improvement of the constraints. These requirements for the projection method may then be reposed in the Hilbertian framework in terms of H and \(\langle \cdot ,\cdot \rangle _{H}\). We satisfy these reposed requirements by defining the normal velocity of the level set function as a linear combination of the orthogonal projection operator applied to the extended objective shape sensitivity and basis functions for the extended constraint shape sensitivities. Owing to the Hilbertian extension-regularisation of shape sensitivities, the chosen normal velocity is already extended onto the bounding domain D and endowed with the regularity of H.

To demonstrate the Hilbertian projection method for constrained level set-based topology optimisation we have solved several example microstructure optimisation problems with multiple constraints. We showed that the Hilbertian projection method successfully handled all of these optimisation problems with little-to-no tuning of the parameter \(\alpha _\textrm{min}\) that controls the balance between improving the objective and constraints. The Hilbertian projection method also naturally handles linearly dependent constraint shape sensitivities. Such linear dependencies often appear in microstructure optimisation and multi-phase optimisation problems.

We found that our method performs well when compared to a Hilbertian sequential linear programming (SLP) method (Allaire et al. 2021b). For problems only involving volume constraint(s), both methods converged to appropriate optimised microstructures. However, SLP did not successfully solve some of the more complex example optimisation problems. These results demonstrate the capacity of the Hilbertian projection method and likely other projection/null space methods (e.g. Barbarosie et al. 2020; Feppon et al. 2020) for solving constrained level set-based topology optimisation problems.

Applying multiple constraints is challenging in level set-based topology optimisation owing to the reliance on implicitly defined domains. Alongside other recent work (Barbarosie et al. 2020; Feppon et al. 2020; Allaire et al. 2021b), our proposed Hilbertian projection method makes significant progress towards improving the capacity of conventional level set-based methods for constrained topology optimisation. Furthermore, due to its generality, the Hilbertian projection method is not confined to microstructure optimisation. It may be applied to any topology optimisation problem to be solved in a level set framework, including macroscopic or multi-physics problems. Inequality constraints could likely be incorporated into the method using slack variables. In addition, the method is not confined to Eulerian level set methods and can be readily applied to Lagrangian or body-fitted level set methods (e.g. Allaire et al. 2014b). These extensions could be considered in the future work.